| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201425539 | |
| Published online | 10 August 2015 | |
Sequential planet formation in the HD 100546 protoplanetary disk?
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: pinilla@strw.leidenuniv.nl
2 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
Received: 18 December 2014
Accepted: 25 May 2015
Context. The disk around the Herbig Ae star, HD 100546, shows structures that suggest the presence of two companions in the disk at ~10 and ~70 AU. The outer companion seems to be in the act of formation.
Aims. Our aims are to provide constraints on the age of the planets in HD 100546 and to explore the potential evidence for sequential planet formation in transition disks such as HD 100546.
Methods. We compare the recent resolved continuum observations of the disk around HD 100546 with the results of dust evolution simulations using an analytical prescription for the shapes of gaps carved by massive planets.
Results. An inner pressure bump must have been present since early in the disk lifetime to have good agreement between the dust evolution models and the continuum observations of HD 100546. This pressure bump may have resulted from the presence of a very massive planet (~20 MJup), which formed early in the inner disk (r ~ 10 AU). If only this single planet exists, the disk is likely to be old, comparable to the stellar age (~5−10 Myr). Another possible explanation is an additional massive planet in the outer disk (r ~ 70 AU): either a low-mass outer planet (≲ 5 MJup) injected at early times, or a higher mass outer planet (≳15 MJup) formed very recently, traps the right amount of dust in pressure bumps to reproduce the observations. In the latter case, the disk could be much younger (~3.0 Myr).
Conclusions. In the case in which two massive companions are embedded in the disk around HD 100546, as suggested in the literature, the outer companion could be at least ≳2.5 Myr younger than the inner companion.
Key words: protoplanetary disks / circumstellar matter / planet-disk interactions
© ESO, 2015
1. Introduction
Transition disks display different interesting structures such as dust depleted cavities (e.g. Brown et al. 2009; Andrews et al. 2011), azimuthal asymmetries (e.g. Isella et al. 2013; Casassus et al. 2013; van der Marel et al. 2013; Pérez et al. 2014), spiral arms (e.g. Fukagawa et al. 2004; Muto et al. 2012; Grady et al. 2013), and spatial segregation of small and large particles (e.g. Follette et al. 2013; Garufi et al. 2013; Zhang et al. 2014; Hashimoto et al. 2015). These structures suggest that these disks host a massive planet or multiple planets. Observations of planet candidates in transition disks (e.g Huélamo et al. 2011; Kraus & Ireland 2012; Biller et al. 2012; Quanz et al. 2013) have further supported this idea. Nonetheless, other mechanisms such as photoevaporation may also play an important role and explain some of the observed structures (e.g. Alexander et al. 2006; Owen & Clarke 2012; Rosotti et al. 2013).
Observations of the disk around the Herbig Ae star HD 100546 have indicated the presence of two potential companions. By modelling the [O I] 6300 Å emission line obtained with VLT/UVES in HD 100546, Acke & van den Ancker (2006) suggested the presence of a massive planet (≳ 20 MJup) at ~ 6.5 AU distance from the star. Using VLTI/AMBER at H- and K-band, Tatulli et al. (2011) proposed a less massive planet (~ 1−8 MJup) in the inner disk. However, using MIDI/VLT observations and by constraining the curvature of the disk wall of the inner cavity, Mulders et al. (2013) found a lower limit for the mass of the inner companion. Taking temperature changes when a planet opens a gap into account, Mulders et al. (2013) conclude that the mass of a potential planet located at ~ 10 AU is 20−30 MJup. On the other hand, high-contrast imaging with VLT/NACO shows signatures of a massive planet (~ 15 MJup) at ~ 70 AU, which may be its formation stage (Quanz et al. 2013, 2015). Currie et al. (2014) reported Gemini/NICI thermal infrared data and detected the outer protoplanet at the same location and brightness as that found by Quanz et al. (2013). This emission seems to have an extended structure which may come from a circumplanetary disk. In addition, spiral arms have been observed in scattered light images (e.g. Grady et al. 2001; Ardila et al. 2007; Boccaletti et al. 2013; Avenhaus et al. 2014), which may be related to the presence of these planets.
Previous observations of protoplanetary disks have revealed that the disk radial extent can be much larger for the molecular gas than for the millimetre-sized particles. This is the case for TW Hya, whose CO emission extends up to ~215 AU, while the mm grains extend to only ~60 AU from the star (Andrews et al. 2012). Birnstiel & Andrews (2014) suggest that radial drift may be responsible for the different radial extents of the gas and large dust grains. However, the disk around HD 100546 appears to be a special case: the radial extent of the gas is ~ 400 AU, while most of the emission at millimetre wavelengths comes from a narrow ring concentrated at ~ 26 AU, with a width of ~21 AU. In addition, a much fainter ring of emission (a factor of ~100 lower) comes from the outer disk, which is centred at ~ 190 AU, with a width of ~75 AU (Walsh et al. 2014). This double-ring emission is consistent with the two-planet scenario (Walsh et al. 2014). Ring-like emission in transition disks can be explained by the dust evolution, which occurs when a single massive planet or multiple planets interact with the disk (e.g. Pinilla et al. 2012a, 2015; Zhu & Stone 2014). An alternative explanation for multiple rings is magneto-rotational instability in the outer regions of disks (e.g. Pinilla et al. 2012b; Flock et al. 2015). In protoplanetary disks, particles migrate inward because of the sub-Keplerian motion of the gas (e.g. Weidenschilling 1977; Nakagawa et al. 1981; Tanga et al. 1996; Birnstiel et al. 2010). When a massive planet opens a gap, particles stop their inward migration due to the positive pressure gradient at the outer edge of that gap. Dust grains accumulate and grow in this preferential region known as a pressure trap, whose location and structure depend on disk viscosity, the mass and location of the planet (e.g. Rice et al. 2006).
In this work, we investigate the influence of the two suggested planets in HD 100546 on the dust distribution in the disk, and compare the resulting predicted continuum emission with the most recent mm observations. By computing dust evolution models for different parameters, we aim to put constraints on different planet properties, and to address the following questions: can dust evolution, without any planet(s) in the disk, explain the two-component emission observed with ALMA? What happens when a single inner companion is assumed? What if two companions are assumed? To answer these questions, we cover a large parameter space, which includes the mass, location, and age of the planets1, and disk viscosity.
For HD 100546, proper hydrodynamical simulations for the planet-disk interaction are highly computationally demanding because of the large radial separation between the two planet candidates. Since we aim to study several cases with different planet properties, we instead use analytical solutions to model the shapes of gaps in the disk. We use the Crida et al. (2006) prescription for the width, and the Fung et al. (2014) prescription for the depth. In Sect. 2, we explain the assumptions for the carved gaps, the potential caveats, and the connection with dust evolution models. In Sect. 3 we present the results of the dust evolution models, the computed visibilities at different wavelengths (λ = [0.87,1.0,3.0,7.0] mm), and the comparison with ALMA and ATCA observations of HD 100546. Sections 4 and 5 are the discussion and conclusions of this work.
 |
Fig. 1 Comparison between the analytical gap prescriptions and hydro-simulations when a massive planet opens a gap. The disk is assumed to be a flared disk, i.e. H/r = h0rf, with h0 = 0.05 the aspect ratio at the position of the planet, and f flaring index equal to 0.25. The planet-to-star mass ratio is q = 1 × 10-3 (left panel) and q = 1 × 10-2 (right panel), and the planet position is rp = 1. The disk viscosity is assumed to be α = 10-3 for both cases. |
2. Models and set-up
In this section, the analytical approximation for the shape of the gaps carved by planets is described, together with the dust evolution models, and the computation of the visibilities. To test this analytical approach and the validity of the resulting dust density distributions, different benchmark cases are considered.
2.1. Carved gaps
Because of the large separation between the potential planets in HD 100546 (~ 10 AU and ~ 70 AU), hydrodynamical simulations are computationally expensive. High grid resolution is needed close to the planet locations, and the inner and outer radial boundaries should be far enough from the planet positions to avoid unphysical results. Because our interest is focussed on the influence of the gas surface density carved by planets on the radial dust evolution, we use an approximation of the radial shape of the gaps in protoplanetary disks rather than full hydrodynamical simulations. We assume the analytical results presented in Crida et al. (2006) and Fung et al. (2014). Crida et al. (2006) proposed an equilibrium profile considering the viscous torque (tν), gravitational torque (tg), and the torque removed by pressure supported waves or pressure torque (tP). This analytical profile therefore satisfies that tν + tg + tP = 0. In an α-disk (Shakura & Sunyaev 1973), where disk viscosity is parametrised as 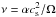 , the equilibrium solution for the gas surface density (Σ) when a planet located at rp is interacting with the disk (see Crida et al. 2006, Eqs. (11), (13), and (14)) is
, the equilibrium solution for the gas surface density (Σ) when a planet located at rp is interacting with the disk (see Crida et al. 2006, Eqs. (11), (13), and (14)) is 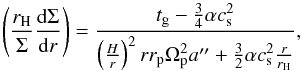 (1)with rH being the Hill radius of the planet (rH = rp(q/ 3)1/3, where q is the planet-stellar mass ratio MP/M⋆, and rp the planet orbital radii), Ωp the angular orbital velocity of the planet, H/r the aspect ratio, cs the sound speed, and a′′ a dimensionless function given by
(1)with rH being the Hill radius of the planet (rH = rp(q/ 3)1/3, where q is the planet-stellar mass ratio MP/M⋆, and rp the planet orbital radii), Ωp the angular orbital velocity of the planet, H/r the aspect ratio, cs the sound speed, and a′′ a dimensionless function given by 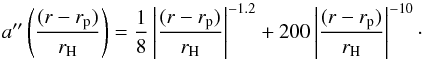 (2)This dimensionless function a′′ is an ansatz from 2D vertically isothermal simulations. When Eq. (1) is solved, a boundary condition needs to be imposed, which in our case is assumed to be the unperturbed density. Because the equilibrium solution of Eq. (1) assumes the gravitational and pressure torques to be null close to the planet (−2rH<r−rp< 2rH), the depth of the gap is not perfectly constrained.
(2)This dimensionless function a′′ is an ansatz from 2D vertically isothermal simulations. When Eq. (1) is solved, a boundary condition needs to be imposed, which in our case is assumed to be the unperturbed density. Because the equilibrium solution of Eq. (1) assumes the gravitational and pressure torques to be null close to the planet (−2rH<r−rp< 2rH), the depth of the gap is not perfectly constrained.
An analytical solution for the depth of the gap close to the planet is difficult to calculate because of the strong tidal gravitational field of the planet in this region. Using two independent codes (PEnGUIn and ZEUS90), Fung et al. (2014) provided an empirical relation of the depth of the gap carved by a non-migrating giant planet in a locally isothermal disk. They consider a large parameter space for the planet-stellar mass ratio q, viscosity α, and aspect ratio H/r, finding very similar results with both codes.
We imitate the gas gaps carved by massive planets by solving Eq. (1) and correcting the depth of the gap with the empirical scalings (Eqs. (12) and (14) from Fung et al. 2014), between −2rH<r−rp< 2rH. Both the width and the depth of the gaps are essential for the final dust distributions in disks. The width determines the location of the pressure maximum at the outer edge of the gap and therefore the location of the peak of the millimetre emission (e.g. Pinilla et al. 2012a). The depth is also important because of the possible dust filtration (e.g. Rice et al. 2006; Zhu et al. 2012).
To compare the results from these approximations, Fig. 1 displays the comparison of the gas surface density between hydrodynamical simulations done with FARGO (Masset 2000), and the gap shape obtained using the solution by Crida et al. (2006) and corrected by the empirical relations from Fung et al. (2014). For this comparison, it is considered that a massive planet, with q = 1 × 10-3 (left panel) and q = 1 × 10-2 (right panel), opens a gap in a flared disk, i.e. H/r = h0rf, with h0 = 0.05 being the aspect ratio at the position of the planet, and f a flaring index equal to 0.25. The disk viscosity is assumed to be α = 10-3. From the hydrodynamical simulations, the gas surface density is azimuthally averaged after the disk reaches a steady-state, 1000 and 2000 planet orbits for q = 1 × 10-3 and q = 1 × 10-2 respectively. As shown in Fig. 1, this approximation for the shape of the gaps is very good for the case of q = 1 × 10-3. In the case of q = 1 × 10-2, the width is under-predicted compared to the azimuthally-averaged profile from the hydrodynamical simulations. When a very massive planet q ≳ 5 × 10-3 interacts with the disk, the formed gaps become eccentric (Kley & Dirksen 2006), making the radial gap profile wider and less steep. The location of the pressure bump at the outer edge of the gap may change from 7−8 RH to 9−10 RH for a non-eccentric to an eccentric gap. Thus, in the case of transition disks, to reproduce the peak of the millimetre emission at a certain distance from the star using this analytical approach, we give an approximate value for the planet location rather than a specific position when q ≳ 5 × 10-3. Since the match between the hydrodynamical simulations and the analytical approach only works for the gap shape, and potential differences become significant far from the gap location (Fig. 1), we assume the gas surface density to follow the unperturbed density far from the location of the planet. Additional azimuthal features that may exist when a massive planet interacts with the disk, such as vortices or spiral arms (e.g. Kley & Dirksen 2006; Ataiee et al. 2013; Fung et al. 2014; Zhu & Stone 2014; Juhasz et al. 2015), are not considered in this work. Instead, we focus on the radial distribution of particles.
 |
Fig. 2 Left panel: comparison of the gas radial velocity obtained by hydrodynamical simulations using FARGO for q = 1 × 10-3, H/r = h0rf with h0 = 0.05 and f = 0.25, and α = 10-3, when νr,d is calculated from viscous accretion (Eq. (5)), assuming Σ by azimuthally averaging the gas surface density from FARGO simulations, and when the gas surface density is calculated analytically (Sect. 2.1) and νr,d from Eq. (5). Other panels: dust density distribution at the same time of evolution (~ 1 Myr) for the same assumptions. White line corresponds to St = 1 (Eq. (3)), which is proportional to the gas surface density. |
2.2. Dust evolution and radial gas velocity
To model the dust evolution, we use the formulation of Birnstiel et al. (2010). This model solves the advection-diffusion differential equation for the dust surface density Σd, and simultaneously simulates the growth, fragmentation, and erosion of dust grains by considering collisions of particles. For the relative velocities between particles, Brownian motion, turbulent velocities, settling to the midplane, and radial dust velocities are taken into account. The detailed explanation of this dust evolution model is in Birnstiel et al. (2010). This model has been used extensively to investigate dust distributions in different types of disks, including comparisons with observations (e.g. Birnstiel et al. 2013; van der Marel et al. 2013; Pinilla et al. 2013; de Juan Ovelar et al. 2013). We investigate the evolution of 180 species of dust grains, defined by size from 1 μm to 200 cm. The radial velocity of dust depends on the coupling of the dust particles to the gas. The Stokes number (St) quantifies this coupling, which in the Epstein regime, where the mean free path of the gas molecules λmfp is higher than the size of particles a (λmfp ≥ 4/9a), is defined as 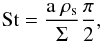 (3)where ρs is the volume density of a dust grain of size a. In terms of the Stokes number, the total radial dust velocity is
(3)where ρs is the volume density of a dust grain of size a. In terms of the Stokes number, the total radial dust velocity is 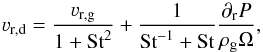 (4)with ρg being the total gas surface density. The first term of Eq. (4) depends on the radial gas velocity νr,g, which in a disk evolving by viscous accretion is
(4)with ρg being the total gas surface density. The first term of Eq. (4) depends on the radial gas velocity νr,g, which in a disk evolving by viscous accretion is 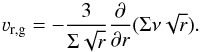 (5)When the dust evolution models are combined with hydrodynamical simulations, the gas surface density and gas radial velocities can be directly taken as initial conditions for the dust evolution models, once the disk has reached a steady-state. Alternatively, the gas surface density can be based on the hydrodynamical simulations and the gas radial velocity from Eq. (5) as in Pinilla et al. (2012a). When a non-migrating planet is in the disk, Σ is calculated with the analytical solution described in Sect. 2.1 and using this Σ-profile, the gas radial velocities are calculated assuming Eq. (5). To see the potential differences of assuming the gas radial velocities from hydrodynamical simulations or viscous accretion, Fig. 2 compares the gas radial velocities obtained by hydrodynamical simulations using FARGO for q = 1 × 10-3, H/r = h0rf with h0 = 0.05 and f = 0.25, and α = 10-3 (azimuthally averaged and averaging over the last 100 orbits of evolution i.e orbits 1000−1100), when νr,d is calculated from viscous accretion (Eq. (5)) and assuming Σ from FARGO; and when the gas surface density is calculated analytically (Sect. 2.1) and νr,d from Eq. (5). In addition the dust density distributions after ~ 1 Myr of evolution are displayed for each case. The main differences of the gas radial velocities are close to the planet where strong perturbation waves due to the planet create a wiggle profile. However, the dust density distribution is similar for each case, because radial drift and diffusion are more important than the drag term in Eq. (4). Hence, we have also proved the reliability of this analytical approach compared to the hydrodynamical simulations to obtain proper radial density distribution of dust particles.
(5)When the dust evolution models are combined with hydrodynamical simulations, the gas surface density and gas radial velocities can be directly taken as initial conditions for the dust evolution models, once the disk has reached a steady-state. Alternatively, the gas surface density can be based on the hydrodynamical simulations and the gas radial velocity from Eq. (5) as in Pinilla et al. (2012a). When a non-migrating planet is in the disk, Σ is calculated with the analytical solution described in Sect. 2.1 and using this Σ-profile, the gas radial velocities are calculated assuming Eq. (5). To see the potential differences of assuming the gas radial velocities from hydrodynamical simulations or viscous accretion, Fig. 2 compares the gas radial velocities obtained by hydrodynamical simulations using FARGO for q = 1 × 10-3, H/r = h0rf with h0 = 0.05 and f = 0.25, and α = 10-3 (azimuthally averaged and averaging over the last 100 orbits of evolution i.e orbits 1000−1100), when νr,d is calculated from viscous accretion (Eq. (5)) and assuming Σ from FARGO; and when the gas surface density is calculated analytically (Sect. 2.1) and νr,d from Eq. (5). In addition the dust density distributions after ~ 1 Myr of evolution are displayed for each case. The main differences of the gas radial velocities are close to the planet where strong perturbation waves due to the planet create a wiggle profile. However, the dust density distribution is similar for each case, because radial drift and diffusion are more important than the drag term in Eq. (4). Hence, we have also proved the reliability of this analytical approach compared to the hydrodynamical simulations to obtain proper radial density distribution of dust particles.
2.3. Visibilities at mm-wavelenghts
To compare the results from the dust evolution models with millimetre observations, we calculate the real part of the visibilities in the uv-plane: VReal(ruv) is given by (Berger & Segransan 2007) 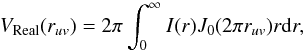 (6)where J0 is the zeroth-order Bessel function of the first kind and I(r) is the radial-dependent emergent intensity, which is directly calculated using the vertically integrated dust density distribution σ(r,a) from the dust evolution results at a specific time of evolution. Thus, σ(r,a) is different at each location for all the dust particle sizes (180 species) assumed in this work. For a given wavelength (λ), the intensity is given by,
(6)where J0 is the zeroth-order Bessel function of the first kind and I(r) is the radial-dependent emergent intensity, which is directly calculated using the vertically integrated dust density distribution σ(r,a) from the dust evolution results at a specific time of evolution. Thus, σ(r,a) is different at each location for all the dust particle sizes (180 species) assumed in this work. For a given wavelength (λ), the intensity is given by, ![\begin{equation} I(r)=B_\lambda (T (r))\left[1-\exp^{-\tau_\lambda(r)}\right], \label{intensity} \end{equation}](/articles/aa/full_html/2015/08/aa25539-14/aa25539-14-eq75.png) (7)with Bλ(T(r)) being the Planck function at the temperature T(r) and τλ the optical depth, which is computed as
(7)with Bλ(T(r)) being the Planck function at the temperature T(r) and τλ the optical depth, which is computed as 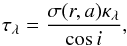 (8)where the opacities at a particular wavelength κλ are calculated for each grain size, assuming Mie theory and a mix of magnesium-iron silicates (e.g. Dorschner et al. 1995). The optical constants are taken from the Jena database2.
(8)where the opacities at a particular wavelength κλ are calculated for each grain size, assuming Mie theory and a mix of magnesium-iron silicates (e.g. Dorschner et al. 1995). The optical constants are taken from the Jena database2.
2.4. Set-up
We assume the disk mass to be 0.05 M⊙, consistent with the dust mass from Mulders et al. (2013), and a canonical dust-to-gas mass ratio of 100; however, disk masses are very uncertain. From optically thin mm emission, the disk mass can be estimated assuming dust opacities and a dust-to-gas mass ratio (e.g. Andrews & Williams 2005). Nonetheless, this calculation is unreliable since the dust opacity depends on composition and shape of the dust (e.g. Min 2005; Demyk et al. 2013), and the gas and dust are not necessarily co-spatial (e.g. Birnstiel & Andrews 2014). The gas mass can also be calculated from observations of CO and its isotopologues (e.g. Williams & Best 2014); however, this estimation can depend on the chemical disk evolution, such as isotope selective processes (Miotello et al. 2014). The disk mass assumed for HD 100546 is broadly consistent with the mass estimate from e.g. Henning et al. (1998), but it remains a very uncertain parameter and thus we keep it fixed in this work.
We fix the gas disk extent to [2−400] AU, in agreement with the CO J = 3−2 emission from Walsh et al. (2014). The initial gas surface density is a power law, such that Σ(r) = Σ0(r/rp1)-1. We use a temperature profile specific for HD 100546 and derived by Bruderer et al. (2012), who constrained the gas temperature via detailed modelling of the observed low-J CO line emission from single dish observations with the Atacama Pathfinder Experiment (APEX; Panić et al. 2010), mid/high-J CO lines observed with Herschel-PACS (Sturm et al. 2010), and continuum emission. For the dust evolution models, we impose the dust temperature as the gas temperature in the midplane, where Tgas ≃ Tdust (with values of T20 AU ≃ 100 K, T400 AU ≃ 25 K). This temperature is an upper limit, since it is obtained from observations of the warm gas in the disk atmosphere. However, CO channel maps from ALMA observations (Walsh et al. 2014) do not show the double lobe signature, which indicates the presence of a CO freeze-out zone (see e.g. de Gregorio-Monsalvo et al. 2013). Hence, HD 100546 is a warm disk (Tmidplane ≳ 20−25 K everywhere). Thus, we do not expect that the disk temperature considerably differs from the adopted temperature. This temperature is used for the dust evolution models and assumed to be the temperature of the vertically integrated dust density distribution for the calculation of the intensity and visibilities at mm-wavelengths, which are mostly sensitive to the distribution of large grains. Because large (mm-sized) grains efficiently settle towards the midplane, the surface density of large grains in the disk atmosphere (where the temperature is higher) is negligible (Dullemond & Dominik 2005). Therefore, adopting the midplane temperature only in the calculation of the emergent continuum emission is an appropriate assumption.
Based on that temperature, the aspect ratio is calculated as cs/vK = H/r = h0rf, obtaining h0 = 0.045 and f = 0.33 at the position where the inner planet is located (10 AU). This aspect ratio is directly used for obtaining the analytical shape of carved gaps. The disk viscosity is assumed to be 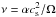 , with α = [2 × 10-3,5 × 10-3] as in Mulders et al. (2013). For the visibilities, the disk is taken to be at a distance of 103 pc with an inclination (i) of 45° (van den Ancker et al. 1997), and a position angle (PA) of 146° (east from north).
, with α = [2 × 10-3,5 × 10-3] as in Mulders et al. (2013). For the visibilities, the disk is taken to be at a distance of 103 pc with an inclination (i) of 45° (van den Ancker et al. 1997), and a position angle (PA) of 146° (east from north).
We assume a large range of planet masses according to previous studies (Acke & van den Ancker 2006; Tatulli et al. 2011; Mulders et al. 2013; Quanz et al. 2013; Currie et al. 2014). For an inner companion located rp1 ~ 10 AU, we assume the planet-stellar mass ratio to be ~ [4.2 × 10-4,2.1 × 10-3,4.2 × 10-3,8.3 × 10-3,1.3 × 10-2], which corresponds to Mp1 = [1,5,10,20,30] MJup planets around a 2.4 M⊙ star. For the outer planet located at rp2 ~ 70 AU, we consider Mp2 = [5,10,15,20] MJup.
Finally, for the dust evolution models, we assume that the velocity threshold above which particles fragment, the so-called fragmentation velocity, is νf = 10 m s-1. For the initial dust density distribution, we assume all particles to be 1 μm-sized. The dust particles are considered to have a volume density of ρs = 1.2 g cm-3, according to the averaged values of the volume density for silicates (e.g. Blum & Wurm 2008). All parameters are summarised in Table 1.
Stellar, disk, and planets parameters.
 |
Fig. 3 Dust density distribution at different times of evolution (upper panel) and real part of the visibilities at 870 μm (bottom panel) at different times of dust evolution, when no planet is embedded in the disk. ALMA Cycle 0 data at this wavelength are over-plotted (data from Walsh et al. 2014). In the upper panel, the white and blue line correspond to adrift (Eq. (10)), and afrag (Eq. (9)), respectively. |
 |
Fig. 4 Dust density distribution after 1.5 Myr of evolution and real part of the visibilities at 870 μm at different times of dust evolution, when a single planet interacts with the disk for two different values of disk viscosity, α = 2 × 10-3 (left column) and α = 5 × 10-3 (right column). From top to bottom, the masses of the planet are: 1, 5, and 10 MJup. ALMA Cycle 0 data are over-plotted in Fig. 3. In the dust density distribution plots, the white and blue lines correspond to St = 1 (Eq. (3)), and afrag (Eq. (9)) respectively. |
3. Results
In this section, we present the results for the case of no planet, and for the cases where either one or two planets are embedded in the disk. For the latter case, we consider the two scenarios where the second (outer) planet is injected either at the same time as the inner planet, or at a later time.
For the models where the planets are injected at later times, we do not assume an actual model to introduce the planet and let it grow. Our main aim is to study the final dust density distributions assuming that the planets are already formed and embedded in the disk. Massive planets such as those assumed in this work are expected to have slow Type II migration, in which case migration timescales follow the viscous diffusion time of the gas, as do the pressure bumps and the dust. Thus, potential dust traps are likely to follow the migration of the planets, keeping qualitatively similar results.
3.1. No planets in the disk
Figure 3 illustrates the dust density distribution at different times of evolution, and the corresponding real part of the visibilities at 870 μm, when no planet is embedded in the disk. Moreover, ALMA Cycle 0 data at this wavelength are also plotted for comparison. Note that the errors are also plotted and they are smaller than the point size (because of the very high signal-to-noise ratio of the ALMA data, Walsh et al. 2014). For this simulation α = 2 × 10-3 is assumed. At early times (t ≲ 1 Myr), the dust particles grow to the maximum grain size before particles fragment. When fragmentation is mainly because of turbulent relative velocities, afrag is (Birnstiel et al. 2012), 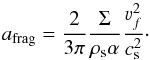 (9)
(9)
At later times, the dust surface density decreases, so the drift barrier moves to smaller sizes and possibly below the fragmentation size (Eq. (9)). In such cases, adrift is (Birnstiel et al. 2012) 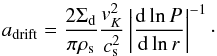 (10)
(10)
Before particles start to drift, millimetre particles are distributed in the entire disk (Fig. 3), creating a visibility profile in disagreement with observations, which suggest a more concentrated ring centred at ~ 26 AU (~ 290 kλ) (Walsh et al. 2014). Once the particles grow to sizes for which radial drift dominates (t ≳ 1 Myr), the disk is quickly depleted of millimetre dust particles. This is reflected in the profile of the real part of the visibilities where the flux at 870 μm drastically reduces after 1 Myr of evolution, becoming already very low at 2 Myr.
As a consequence, any mechanism that helps to reduce the rapid inward drift is needed to explain the millimetre emission of this disk. We assume that a pressure trap is formed at the outer edge of a gap carved by a massive planet, motivated also by the companion candidates suggest in the literature (e.g. Acke & van den Ancker 2006; Tatulli et al. 2011; Brittain et al. 2014). Particles concentrate in the regions of highest pressure (e.g. Weidenschilling 1977; Brauer et al. 2008), and therefore the assumed pressure bump can help to reduce the radial drift.
3.2. A planet is embedded in the inner disk
Assuming the analytical profiles for gaps carved by massive planets described in Sect. 2.1, we consider an inner planet of different masses Mp1 = [1,5,10,20,30] MJup at rp1 ~ 10 AU to investigate the trapping efficiency and the comparison with observations. Since we neglect the possible effect of an eccentric gap in our simulations, we give an approximated value for the location of the planets (Sect 2.1).
 |
Fig. 5 Dust density distribution at different times of evolution (upper row) and the corresponding real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm (lower row) at different times of dust evolution, when a 20 MJup planet (left column) and 30 MJup planet (right column) is embedded in the inner disk. Data from ALMA Cycle 0 from Walsh et al. (2014) and ATCA from Wright et al. (2014) are over-plotted. In the upper panels, the white and blue line correspond to St = 1 (Eq. (3)), and afrag (Eq. (9)) respectively. |
Figure 4 shows the dust density distribution after 1 Myr of evolution, and the corresponding real part of the visibilities at 870 μm for α = [2 × 10-3,5 × 10-3], when a 1, 5 or 10 MJup planet is embedded in the inner part of the disk. The results of these simulations suggest that a planet whose mass is lower than 10 MJup is not massive enough to result in trapping of millimetre-sized dust particles, sufficient to create a visibility curve that is in agreement with ALMA Cycle 0 observations. In any of these cases, the flux is already under-predicted after 1.5 Myr of evolution. Pinilla et al. (2012a) show that when a planet of q = 10-3, i.e. a 1 MJup around a solar-type star, carves a gap in the disk, particles can be trapped at the outer edge when α = 10-3. The reason why trapping is more difficult in this case is because of the larger difference between the maximum grain size or afrag (Eq. (9)), and the particle size in which dust feels the highest radial drift i.e. St = 1. Particles with St ~ 1 are the easiest to trap, however afrag is in this case around one order of magnitude lower than the grain size that corresponds to St = 1. These smaller particles are more difficult to trap because the drift is inefficient for particles with St ≲ α. For these models, the maximum grain size is lower because of the higher temperatures and α-viscosity considered here compared with those in Pinilla et al. (2012a). The visibility shape does not change significantly for the two values of the viscosity. For this reason, for the following results, we only focus on the cases with α = 2 × 10-3. Increasing α decreases the maximum grain size even further (Eq. (9)), making the particle trapping more difficult. Assuming a lower viscosity or a higher fragmentation velocity can help to trap the particles (Pinilla et al. 2015).
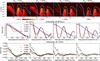 |
Fig. 6 Upper panels: dust density distribution at 1.5 Myr of evolution when two planets are injected in the disk simultaneously. The mass of the inner planet is 20 MJup and it is located at rp1 ~ 10−15 AU, while the outer planet at rp2 ≳ 70 AU is assumed to be Mp2 = [5,10,15,20] MJupfrom left to right panels respectively. The white line is St = 1, and the blue line is afrag. The corresponding real part of the visibilities for each Mp2 at λ = 0.87 mm (middle panels) and λ = 7.0 mm (lower panels) are displayed for different times of dust evolution, for each Mp2. ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
When the mass of the inner planet is increased, the trapping becomes more efficient. Figure 5 shows the dust density distribution at different times of evolution and the real part of visibilities at λ = [0.87,1.0,3.0,7.0] mm, when a 20 and 30 MJup planet is embedded in the inner part of the disk. ALMA Cycle 0 data from Walsh et al. (2014) and ATCA data from Wright et al. (2014) are over-plotted for comparison. For the case of a 20 MJup planet, the visibilities better fit the data; nonetheless, to obtain the best fit with the data, the dust needs to evolve for long timescales (≳ 5 Myr) to grow, drift, and concentrate the millimetre grains in a narrow ring. Already at 5 Myr, most of the millimetre particles are concentrated in a narrow region; however, the large amount of these grains leads to a over-prediction of the fluxes. The continuous fragmentation that occurs in the pressure bump, together with some small-sized dust crossing the gap, reduce the amount of millimetre grains, enabling a better fit to the data at 10 Myr. The total flux is under-predicted at 7 mm because the maximum grain size in the trap is around 1mm. The null of the visibilities at ~ 290 kλ is in good agreement with the observations, implying that a 20 MJup planet located in the inner part of the disk, can create a pressure maximum at ~26 AU, where the centre of the inner narrow ring was observed with ALMA Cycle 0.
If the planet is located at the same location, and its mass is increased to 30 MJup, the resulting carved gap is wider, moving the location of the pressure maximum outwards and therefore the peak of the millimetre emission. For this reason, the null of the visibilities is at shorter baselines (~ 245 kλ, Fig. 5). In addition, the total flux is higher because the gap is also deeper, filtering more dust, and as a result, a larger number of millimetre particles remain in the trap. However, the fluxes at 7 mm are lower than in the case of a 20 MJup planet. This is because the maximum grain size has decreased slightly in the trap as the pressure maximum is further away, where the gas surface density is also lower, decreasing afrag (Eq. (9)) within the bumps. An important remark is that at 7 mm the emission likely has a ≳ 10% contamination from free-free emission (Wright et al. 2014), which is neglected in our calculations. Hence, we expect the models to underestimate the 7 mm flux.
From the simulations with one single planet in the inner disk, the best model that reproduces the observations at different wavelength is for a 20 MJup planet and α = 2 × 10-3, consistent with the results from Mulders et al. (2013), who found similar results from modelling mid-infrared data. For these parameters, the best fit is for an old disk (~ 5−10 Myr). Nevertheless, with one single planet, the outer ring of mm emission observed with ALMA remains unexplained (Walsh et al. 2014) .
3.3. Two planets are embedded in the disk
In this section, the results with two planets embedded in the disk are presented. We use the analytical shapes described in Sect. 2.1 for both gaps. For all cases, the gas surface density is always scaled such that the disk mass is 0.05 M⊙. For the planet embedded in the inner disk, we consider the best single-planet fit of Mp1 = 20 MJup, and a disk viscosity of α = 2 × 10-3. For the outer planet, it is assumed Mp2 = [5,10,15,20] MJup and rp2 ~ 70 AU. There are two sets of simulations: one where the two planets are assumed to interact with the disk from the same stage of evolution, and a second, where the outer planet is assumed to interact with the disk from a later stage.
3.3.1. Simultaneous injection of both planets
Figure 6 illustrates the dust density distribution at 1.5 Myr of evolution when two planets are interacting in the disk from the same stage of evolution (t ~ 1000 yr). The inner planet is a 20 MJup planet at rp1 ~ 10 AU, while the outer planet at rp2 ~ 70 AU is assumed to be Mp2 = [5,10,15,20] MJup. In addition, the real part of the visibilities at λ = [0.87,7.0] mm are displayed for each Mp2, and at different times of dust evolution. When a second planet is assumed, the gas surface density sharply decreases with radius in the region between the two planets. As a consequence of the high negative pressure gradient, the dust particles move quickly inward (timescales shorter than ~1 Myr) and stop their migration in the pressure maximum at the outer edge on the inner gap. This effect creates a narrow ring-like concentration of large particles centred at ~ 26 AU in shorter timescales than in the case of a single inner planet.
 |
Fig. 7 Upper panels: dust density distribution at 2.5 Myr of evolution when a 20 MJup planet is embedded in the inner disk (10−15 AU) and a second planet (15 MJupleft panels, 20 MJupright panels) is injected in the outer region (rp2 ≳ 70 AU) after 2 Myr of dust evolution. The white line is St = 1, and the blue line is afrag. Bottom panels: real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm at different times of dust evolution; ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
In this case, a second trap also exists at the outer edge of the gap carved by the planet at rp2 ~ 70 AU. The amount of dust concentrated in this second trap depends on the mass of the outer planet. When the planet is more massive, dust filtration becomes more effective and the millimetre flux increases. This has a significant influence on the resulting real part of the visibilities. Because of the dust trapping in both pressure maxima, the visibility profiles show strong oscillations. For the case of Mp2 = 5 MJup, these oscillations are smoothed out late in the evolution (~10 Myr) because of the continued crossing of dust particles through the outer gap, which is filling the inner trap (middle and bottom left panels of Fig. 6). In this case, there is a similar contrast of the inner to the outer ring emission as that observed with ALMA Cycle 0 (of the order of ~100), generating similar visibility profiles to those observed. Nevertheless, for the case of a higher mass planet (Mp2 ≳ 10 MJup), the amount of dust concentrated in both traps is similar, and the undulating shape is more extreme and persists at late times, in contradiction to observations. The total flux at λ = 0.87 mm is slightly lower than in the case of the 20 MJup single planet; however, these fluxes can be higher if the disk mass or dust-to-gas ratio are assumed to be higher, or they can change by assuming different dust composition (Min 2005). We keep these two values the same for all the simulations to have a clear distinction of the effect of the planet parameters on the final dust distributions.
From these two-planets simulations, in which both planets are considered to interact with the disk from early in the disk lifetime, we conclude that the outer planet should be a low-mass planet (≲ 5 MJup) compared to the inner planet (20 MJup), and the disk may be as old as in the single planet scenario (~5−10 Myr).
3.3.2. Later injection of the outer planet
High-contrast imaging of this disk with VLT/NACO shows signatures of a massive planet (~ 15−20 MJup) in the outer region at ~ 70 AU (Quanz et al. 2013; Currie et al. 2014). However, in the previous section we showed that if the planet in the outer disk is as old as the one in the inner disk, the resulting visibility profiles are in disagreement with observations. To have a very massive planet in the outer disk and similar millimetre emission contrast between the inner and the outer ring (~ 100), the outer planet must be younger than the inner planet. In this scenario, at the time that the outer planet is injected in the disk, most of the dust has already moved towards the inner trap, decreasing the mass of dust available for trapping in the second pressure bump.
Figure 7 shows the dust density distribution at 2.5 Myr of evolution when a 20 MJup planet is embedded in the inner disk, and a second planet (Mp2 = [15,20] MJup) is injected in the outer region (rp2 ~ 70 AU) after 2 Myr of dust evolution. In comparison with the corresponding cases of Fig. 6, it is important to notice that the outer ring is fainter in this case than when the two planets are assumed to interact with the disk over the same timescale. The oscillations on the visibility profiles are much smoother in these cases, and better fit the total flux. The null in the visibility profiles remains similar as in the single planet case (~ 290 kλ). A 15 MJup outer planet fits the visibility shapes better and total fluxes than a 20 MJup planet, in agreement with the Gemini/NICI observations reported by Currie et al. (2014), who constrain the mass of the outer planet to be at most 15 MJup. The real part of the visibilities still have smooth oscillations; however, this can be further smoothed out by assuming than the planet is injected even later in the simulations. Figure 8 displays the case of a 20 MJup planet embedded in the inner disk from early stages, and an outer 15 MJup planet injected after 3 Myr of dust evolution. To reproduce the observations, the lower the mass of the planet, the earlier it needs to be introduced into the outer disk. Therefore, assuming the mass predicted by Quanz et al. (2013, 2015) and Currie et al. (2014) for the outer planet (and its possible circumplanetary disk), implies that this planet must be at least ≳ 2−3 Myr younger than the planet in the inner disk.
4. Discussion
We have shown that radial drift alone cannot reproduce the dust distribution observed for HD 100546 (Sect. 3.1). To obtain good agreement between the dust evolution models, which include radial drift, with the millimetre observations, an inner pressure bump must exist since early in the disk lifetime (<0.1 Myr).
Observations of HD 100546 indicate the presence of at least two companions in this disk (see e.g. Acke & van den Ancker 2006; Quanz et al. 2013). The mass of the inner companion has largely been discussed by several authors (e.g. Tatulli et al. 2011). If the required inner pressure bump is induced by a planet, we demonstrated that the required planet must be massive (~ 20 MJup) for a disk viscosity of α = 2 × 10-3. This in agreement with Mulders et al. (2013) results, but is derived from different observations (Sect 3.2). The trapping in HD 100546 disk is difficult because of the high disk temperature (as derived in Bruderer et al. 2012) and disk viscosity, which both increase the relative motion of the particles due to turbulence, and decrease the maximum grain size that particles can reach under these assumptions. This maximum grain size is one order of magnitude lower than the size corresponding to St = 1, which are the particles that feel the highest radial drift and are the easiest to trap in a pressure bump. Assuming a higher viscosity would make the trapping even more difficult and a more massive inner planet, located closer to the star, would be needed to explain the millimetre emission. In the case of a single planet embedded in the inner part of the disk, the disk is more likely to be old (~5−10 Myr).
In addition to the inner planet, we also assumed an outer planet as suggested by various authors e.g. Boccaletti et al. (2013) and Quanz et al. (2013). When the two planets are assumed to interact with the disk from the same stage of evolution, we demonstrated that the mass of the outer planet needs to be lower than the inner planet (≲ 5 MJup), otherwise the resulting dust density distributions are in disagreement with millimetre observations. This is because, if a second massive planet is coeval with the inner planet, it traps inward drifting grains too effectively in the outer bump, and the contrast ratio between the bumps becomes too strong compared with observations. However, the mass suggested by various authors for the outer planet is higher than 5 MJup. As in the single planet case, the models are more consistent with observations when the disk is old (~5−10 Myr). To test how sensitive the resulting timescales are to the assumed gas surface density profile, we considered the best-fit single planet model and adopted an exponentially tapered disk rather than a power law. For this case, mm-grains are concentrated in a much narrower ring, shifting the null of the visibilities to longer baselines, in disagreement with observations. In addition, at very early times, there is an oscillating behaviour (similar to the previous two-planet simulations). Hence, with this gas surface density profile, stronger oscillating behaviour is expected for the visibilities for the case of two planets. Thus, a power law for the gas surface density gives us a better fit to the observations.
 |
Fig. 8 Real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm at different times of dust evolution when a 20 MJup planet is embedded in the inner disk (10−15 AU) from early stages, and a second planet (15 MJup) is injected after 3 Myr of dust evolution. ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
If the mass of the outer planet is assumed to be large, as suggested by Quanz et al. (2013) (~ 15 MJup), we demonstrated that the outer planet must be at least ~ 2−3 Myr younger than the inner planet, favouring a significantly younger outer planet observed in the act of formation. In this case, the disk can be much younger than when the disk only hosts a single planet. The required time to be in agreement with observations is a few tenths of a Myr after the outer planet is injected. Figure 9 summarises our main findings and compares the cases of no planet, a single planet, two planets injected simultaneously, and two planets where the outer planet is injected after 3 Myr of evolution. One of the uncertainties of these predictions is the disk midplane temperature, which may be slightly lower than obtained by Bruderer et al. (2012) (Sect. 2.4). The temperature profile used is an upper limit; however, ALMA Cycle 0 CO J = 3−2 observations show no signs of CO freeze-out, i.e. we also have a lower limit of ~20 K. A slightly lower midplane temperature decreases the dust drift velocities (Eq. (4)), and increase the maximum grain size (Eqs. (10) and (9)). Observations with higher angular resolution and sensitivity of optically thin emission from multiple transitions of CO isotopologues are needed to give better constraints on the disk midplane temperature and confirm the current predictions. However, we expect that the overall trends remain similar with a slight lowering of the dust temperature.
 |
Fig. 9 Real part of the visibilities at 870 μm. Case 1: no planet embedded in the disk and t = 2 Myr. Case 2: a single planet embedded in the disk of 20 MJup mass at ~10 AU and t = 10 Myr. Case 3: two planets simultaneously interacting with the disk, 20 MJup at ~10 AU and 5 MJup at ~70 AU, and t = 10 Myr. Case 4: two planets in the disk, but the outer planet is injected t = 3 Myr after the inner planet, 20 MJup at ~10 AU and 15 MJup at ~70 AU, and t = 3.5 Myr. ALMA Cycle 0 is over-plotted for comparison. |
 |
Fig. 10 ALMA Cycle 0 continuum contours at 870 μm (red dashed lines) and the contours corresponding to the models (blue solid lines) when an inner 20 MJup planet alone (top panel) is embedded in the disk, and with two planets in the disk (bottom panel), where the outer planet is injected after 3 Myr of evolution. Contours are every 3, 10, 30, 100, 300, and 1000 times the rms (0.5 mJy beam-1). |
 |
Fig. 11 Synthetic images at 870 μm convolved with a 0.1″ × 0.1″ beam from the models of a single planet (20 MJup at ~10 AU) and two planets (20 MJup at ~10 AU and 15 MJup at ~70 AU), injected 3 Myr after the inner planet. |
 |
Fig. 12 Radial variations of the spectral index, calculated between 1 and 3 mm, when a single inner planet of 20 MJup mass is embedded in the disks and when two planets are in the disk, but the outer planet (15 MJup) is injected 3 Myr after the inner planet (20 MJup). The vertical lines correspond to the positions of the pressure maxima at the outer edge of the gap(s) carved by the planet(s). |
Moreover, Fig. 10 shows the synthetic ALMA Cycle 0 contour lines image at 870 μm (imaged using identical (u, v) coordinates as the ALMA observations), for the cases of one single planet and an old disk, and two massive planets and a younger disk. The latter scenario reproduces a more extended emission than with a single planet, but it is not as extended as observed. This discrepancy is because the width of the carved gaps (thus the location of the pressure maximum at the outer edge of the gap) is underestimated in our models compared to proper hydrodynamical simulations (Sect. 2.1). The location of the pressure maximum of a gap carved by a 15 MJup planet at 70 AU is expected to be ~ 190 AU i.e. at 9−10rH from the planet location, where the peak of the outer ring emission is observed. Figure 11 illustrates the synthetic images at 870 μm convolved with a 0.1″ × 0.1″ beam from the same models used for Fig. 10, showing that with high angular resolution observations, two rings can be resolved in the two-planet scenario.
The age of HD 100546 itself is very uncertain (~ 3−10 Myr Acke & van den Ancker 2006) and a more precise measurement of the age of this star can give us hints as to the nature of the potential planets embedded in this disk. An observation to ultimately test dust trapping in two pressure bumps, would be to measure spectral index variations inside and outside these pressure maxima locations (Pinilla et al. 2014), which are testable with future ALMA capabilities. Figure 12 shows the expected radial variations of the spectral index, calculated between 1 and 3 mm, when a single inner planet of 20 MJup mass is embedded in the inner disk at ~10 AU, and when two planets are in the disk, but the outer planet (15 MJup) is injected 3 Myr after the inner planet (20 MJup). At the location of the pressure trap, the spectral index is lower because of the accumulation of mm-grains and vice versa.
We also used ATCA observations to compare the visibility profiles at 3 and 7 mm with the models. The models with two planets predict slightly better the total flux, and estimate well the observed null of the real part of the visibilities at these wavelengths. The null at 7 mm is at a moderately longer kλ than at shorter wavelengths. This happens because larger grains are expected to be more concentrated. Nonetheless, for all cases, the total flux at 7 mm is under-predicted, which partially comes from the neglect of free-free emission in the models, and because of the small maximum grain size (~1 mm) under the assumed temperature and disk viscosity in the outer disk.
5. Conclusion
To obtain good agreement between dust evolution models and millimetre observations of the disk around HD 100546, an inner pressure trap must exist from early in the disk lifetime (≲1 Myr). If this pressure bump is formed because of a planet embedded in the inner disk (r ~ 10 AU), the mass of the planet should be high (~ 20 MJup) for a disk viscosity of α = 2 × 10-3, in agreement with Mulders et al. (2013), who found similar results from modelling mid-infrared data. In the case in which this is the only planet embedded in the disk, the disk is more likely to be old (~5−10 Myr). In this case the outer ring of emission observed with ALMA remains unexplained (Fig. 10). If an outer planet is also embedded in the disk, and it is as massive as suggested by Quanz et al. (2013, 2015) and Currie et al. (2014) (~ 15 MJup), this outer planet should be at least ~ 2−3 Myr younger than the inner planet, supporting the hypothesis that the outer planet may be in the act of formation. In this case, the models produce an outer ring of emission that is 100 times fainter than the inner ring of emission as observed with ALMA Cycle 0 (Fig. 10). If the outer planet is embedded in the disk at the same time as the inner planet, inward drifting grains are efficiently trapped in the outer bump, and the contrast of the millimetre fluxes between the two pressure traps becomes too strong compared with the observations. The ATCA observations at 3 and 7 mm also favour the two-planets scenario. Future high angular resolution and sensitivity observations of multiple transitions of optically thin emission from CO isotopologues, which can constrain better the disk gas surface density and temperature profiles, and continuum images with ALMA will allow us to resolve potential rings (Fig. 11), to measure spectral index variations inside and outside pressure maxima locations (Fig. 12), and to confirm particle trapping by one or two planets in this disk.
http://www.astro.uni- jena.de/Laboratory/Database/databases.html, with a specific silicate composition of: 10% MgFeSiO4, 28% MgSiO3, 31% Mg2SiO4, 1% NaAlSi2O6.
Acknowledgments
The authors are very grateful to E. F. van Dishoeck and D. Harsono for all their comments and fruitful discussions. We thank to S. Bruderer for providing his data for the disk temperature and C. Wright for the ATCA data. P.P. is supported by Koninklijke Nederlandse Akademie van Wetenschappen (KNAW) professor prize to Ewine van Dishoeck. T.B. acknowledges support from NASA Origins of Solar Systems grant NNX12AJ04G. C.W. acknowledges support from the Netherlands Organisation for Scientific Research (NWO, grant number 639.041.335). Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, and by the European Union A-ERC grant 291141 CHEMPLAN. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00863.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Acke, B., & van den Ancker, M. E. 2006, A&A, 449, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 369, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Ardila, D. R., Golimowski, D. A., Krist, J. E., et al. 2007, ApJ, 665, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Ataiee, S., Pinilla, P., Zsom, A., et al. 2013, A&A, 553, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Meyer, M. R., et al. 2014, ApJ, 790, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, J. P., & Segransan, D. 2007, New A Rev., 51, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., & Andrews, S. M. 2014, ApJ, 780, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Pinilla, P. 2013, A&A, 550, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Pantin, E., Lagrange, A.-M., et al. 2013, A&A, 560, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brittain, S. D., Carr, J. S., Najita, J. R., Quanz, S. P., & Meyer, M. R. 2014, ApJ, 791, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., van der Plas, G., M, S. P., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Currie, T., Muto, T., Kudo, T., et al. 2014, ApJ, 796, L30 [NASA ADS] [CrossRef] [Google Scholar]
- de Juan Ovelar, M., Min, M., Dominik, C., et al. 2013, A&A, 560, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demyk, K., Meny, C., Leroux, H., et al. 2013, Proc. The Life Cycle of Dust in the Universe: Observations, Theory, and Laboratory Experiments LCDU2013, eds. A. Andersen, M. Baes, H. Gomez, C. Kemper, & D. Watson [Google Scholar]
- Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Follette, K. B., Tamura, M., Hashimoto, J., et al. 2013, ApJ, 767, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, W., Li, H., Lubow, S., & Li, S. 2014, ApJ, 788, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Fukagawa, M., Hayashi, M., Tamura, M., et al. 2004, ApJ, 605, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., Shi, J.-M., & Chiang, E. 2014, ApJ, 782, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Avenhaus, H., et al. 2013, A&A, 560, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Polomski, E. F., Henning, T., et al. 2001, AJ, 122, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, J., Tsukagoshi, T., Brown, J. M., et al. 2015, ApJ, 799, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Burkert, A., Launhardt, R., Leinert, C., & Stecklum, B. 1998, A&A, 336, 565 [NASA ADS] [Google Scholar]
- Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isella, A., Pérez, L. M., Carpenter, J. M., et al. 2013, ApJ, 775, 30 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Juhasz, A., Benisty, M., Pohl, A., et al. 2015, MNRAS, 451, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M. 2005, Ph.D. Thesis [Google Scholar]
- Miotello, A., Bruderer, S., & van Dishoeck, E. F. 2014, A&A, 572, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Paardekooper, S.-J., Panić, O., et al. 2013, A&A, 557, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Nakazawa, K., & Hayashi, C. 1981, Icarus, 45, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Clarke, C. J. 2012, MNRAS, 426, L96 [NASA ADS] [CrossRef] [Google Scholar]
- Panić, O., van Dishoeck, E. F., Hogerheijde, M. R., et al. 2010, A&A, 519, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012a, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012b, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Benisty, M., et al. 2013, A&A, 554, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., Birnstiel, T., et al. 2014, A&A, 564, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2013, ApJ, 766, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2015, ApJ, 807, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Rosotti, G. P., Ercolano, B., Owen, J. E., & Armitage, P. J. 2013, MNRAS, 430, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, T., et al. 2010, A&A, 518, L129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanga, P., Babiano, A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., Benisty, M., Ménard, F., et al. 2011, A&A, 531, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Ancker, M. E., The, P. S., Tjin A Djie, H. R. E., et al. 1997, A&A, 324, L33 [NASA ADS] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walsh, C., Juhász, A., Pinilla, P., et al. 2014, ApJ, 791, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Best, W. M. J. 2014, ApJ, 788, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. M., Maddison, S. T., Wilner, D. J., et al. 2014, MNRAS, submitted [Google Scholar]
- Zhang, K., Isella, A., Carpenter, J. M., & Blake, G. A. 2014, ApJ, 791, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., & Stone, J. M. 2014, ApJ, 795, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison between the analytical gap prescriptions and hydro-simulations when a massive planet opens a gap. The disk is assumed to be a flared disk, i.e. H/r = h0rf, with h0 = 0.05 the aspect ratio at the position of the planet, and f flaring index equal to 0.25. The planet-to-star mass ratio is q = 1 × 10-3 (left panel) and q = 1 × 10-2 (right panel), and the planet position is rp = 1. The disk viscosity is assumed to be α = 10-3 for both cases. |
| In the text | |
 |
Fig. 2 Left panel: comparison of the gas radial velocity obtained by hydrodynamical simulations using FARGO for q = 1 × 10-3, H/r = h0rf with h0 = 0.05 and f = 0.25, and α = 10-3, when νr,d is calculated from viscous accretion (Eq. (5)), assuming Σ by azimuthally averaging the gas surface density from FARGO simulations, and when the gas surface density is calculated analytically (Sect. 2.1) and νr,d from Eq. (5). Other panels: dust density distribution at the same time of evolution (~ 1 Myr) for the same assumptions. White line corresponds to St = 1 (Eq. (3)), which is proportional to the gas surface density. |
| In the text | |
 |
Fig. 3 Dust density distribution at different times of evolution (upper panel) and real part of the visibilities at 870 μm (bottom panel) at different times of dust evolution, when no planet is embedded in the disk. ALMA Cycle 0 data at this wavelength are over-plotted (data from Walsh et al. 2014). In the upper panel, the white and blue line correspond to adrift (Eq. (10)), and afrag (Eq. (9)), respectively. |
| In the text | |
 |
Fig. 4 Dust density distribution after 1.5 Myr of evolution and real part of the visibilities at 870 μm at different times of dust evolution, when a single planet interacts with the disk for two different values of disk viscosity, α = 2 × 10-3 (left column) and α = 5 × 10-3 (right column). From top to bottom, the masses of the planet are: 1, 5, and 10 MJup. ALMA Cycle 0 data are over-plotted in Fig. 3. In the dust density distribution plots, the white and blue lines correspond to St = 1 (Eq. (3)), and afrag (Eq. (9)) respectively. |
| In the text | |
 |
Fig. 5 Dust density distribution at different times of evolution (upper row) and the corresponding real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm (lower row) at different times of dust evolution, when a 20 MJup planet (left column) and 30 MJup planet (right column) is embedded in the inner disk. Data from ALMA Cycle 0 from Walsh et al. (2014) and ATCA from Wright et al. (2014) are over-plotted. In the upper panels, the white and blue line correspond to St = 1 (Eq. (3)), and afrag (Eq. (9)) respectively. |
| In the text | |
 |
Fig. 6 Upper panels: dust density distribution at 1.5 Myr of evolution when two planets are injected in the disk simultaneously. The mass of the inner planet is 20 MJup and it is located at rp1 ~ 10−15 AU, while the outer planet at rp2 ≳ 70 AU is assumed to be Mp2 = [5,10,15,20] MJupfrom left to right panels respectively. The white line is St = 1, and the blue line is afrag. The corresponding real part of the visibilities for each Mp2 at λ = 0.87 mm (middle panels) and λ = 7.0 mm (lower panels) are displayed for different times of dust evolution, for each Mp2. ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
| In the text | |
 |
Fig. 7 Upper panels: dust density distribution at 2.5 Myr of evolution when a 20 MJup planet is embedded in the inner disk (10−15 AU) and a second planet (15 MJupleft panels, 20 MJupright panels) is injected in the outer region (rp2 ≳ 70 AU) after 2 Myr of dust evolution. The white line is St = 1, and the blue line is afrag. Bottom panels: real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm at different times of dust evolution; ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
| In the text | |
 |
Fig. 8 Real part of the visibilities at λ = [0.87,1.0,3.0,7.0] mm at different times of dust evolution when a 20 MJup planet is embedded in the inner disk (10−15 AU) from early stages, and a second planet (15 MJup) is injected after 3 Myr of dust evolution. ALMA Cycle 0 and ATCA data are over-plotted for comparison. |
| In the text | |
 |
Fig. 9 Real part of the visibilities at 870 μm. Case 1: no planet embedded in the disk and t = 2 Myr. Case 2: a single planet embedded in the disk of 20 MJup mass at ~10 AU and t = 10 Myr. Case 3: two planets simultaneously interacting with the disk, 20 MJup at ~10 AU and 5 MJup at ~70 AU, and t = 10 Myr. Case 4: two planets in the disk, but the outer planet is injected t = 3 Myr after the inner planet, 20 MJup at ~10 AU and 15 MJup at ~70 AU, and t = 3.5 Myr. ALMA Cycle 0 is over-plotted for comparison. |
| In the text | |
 |
Fig. 10 ALMA Cycle 0 continuum contours at 870 μm (red dashed lines) and the contours corresponding to the models (blue solid lines) when an inner 20 MJup planet alone (top panel) is embedded in the disk, and with two planets in the disk (bottom panel), where the outer planet is injected after 3 Myr of evolution. Contours are every 3, 10, 30, 100, 300, and 1000 times the rms (0.5 mJy beam-1). |
| In the text | |
 |
Fig. 11 Synthetic images at 870 μm convolved with a 0.1″ × 0.1″ beam from the models of a single planet (20 MJup at ~10 AU) and two planets (20 MJup at ~10 AU and 15 MJup at ~70 AU), injected 3 Myr after the inner planet. |
| In the text | |
 |
Fig. 12 Radial variations of the spectral index, calculated between 1 and 3 mm, when a single inner planet of 20 MJup mass is embedded in the disks and when two planets are in the disk, but the outer planet (15 MJup) is injected 3 Myr after the inner planet (20 MJup). The vertical lines correspond to the positions of the pressure maxima at the outer edge of the gap(s) carved by the planet(s). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


