| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425001 | |
| Published online | 20 August 2015 | |
VLT/X-Shooter spectroscopy of the afterglow of the Swift GRB 130606A⋆,⋆⋆,⋆⋆⋆
Chemical abundances and reionisation at z ~ 6
1
Anton Pannekoek Institute for Astronomy, University of
Amsterdam, Science Park
904, PO Box
94249
1090 GE
Amsterdam, The
Netherlands
e-mail:
olgahartoog@gmail.com
2
Dark Cosmology Centre, Niels Bohr Institute, Copenhagen
University, Juliane Maries Vej
30, 2100
Cøpenhagen O,
Denmark
3
Institute of Astronomy and Department of Physics, National Tsing
Hua University, No. 101, Section 2,
Kuang-Fu Road, 30013
Hsinchu, Taiwan,
R.O.C
4
European Southern Observatory, Alonso de Córdova 3107, Vitacura, 19001 Casilla,
Santiago 19,
Chile
5
Department of Particle Physics and Astrophysics, Faculty of
Physics, Weizmann Institute of Science, 76100
Rehovot,
Israel
6
European Southern Observatory, Karl-Schwarzschildstrasse 2, 85748
Garching bei München,
Germany
7
INAF, Osservatorio Astronomico di Brera, via E. Bianchi
46, 23807
Merate,
Italy
8
INAF-Osservatorio Astronomico di Roma, via Frascati
33, 00040
Monteporzio Catone,
Italy
9
ASI-Science Data Center, via Galileo Galilei,
00044
Frascati,
Italy
10
Laboratoire GEPI, Observatoire de Paris,
CNRS-UMR8111, Univ. Paris-Diderot, 5 place Jules Janssen, 92195
Meudon,
France
11
APC, Astroparticule et Cosmologie, Université Paris Diderot,
CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie
Duquet, 75205
Paris Cedex 13,
France
12
Centre for Astrophysics and Cosmology, Science Institute,
University of Iceland, Dunhagi
5, 107
Reykjavk,
Iceland
13
Department of Physics, University of Warwick,
Coventry
CV4 7AL,
UK
14
The Oskar Klein Centre, Department of Astronomy,
AlbaNova, 106 91
Stockholm,
Sweden
15
University of Leicester, Department of Physics and Astronomy,
University Road, Leicester
LE1 7RH,
UK
16
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
17
Tuorla Observatory, Department of Physics and Astronomy,
University of Turku, 20014
Turku,
Finland
18
Finnish Centre for Astronomy withESO, University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
19
Department of Physics and Astronomy, Michigan State
University, East
Lansing, MI
48824,
USA
20
Institute of Theoretical Astrophysics, University of
Oslo, PO Box 1029,
Blindern, 0315
Oslo,
Norway
21
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, Orsay,
France
Received: 16 September 2014
Accepted: 15 June 2015
Context. The reionisation of the Universe is a process that is thought to have ended around z ~ 6, as inferred from spectroscopy of distant bright background sources, such as quasars (QSO) and gamma-ray burst (GRB) afterglows. Furthermore, spectroscopy of a GRB afterglow provides insight in its host galaxy, which is often too dim and distant to study otherwise.
Aims. For the Swift GRB 130606A at z = 5.913 we have obtained a high S/N spectrum covering the full optical and near-IR wavelength region at intermediate spectral resolution with VLT/X-Shooter. We aim to measure the degree of ionisation of the intergalactic medium (IGM) between z = 5.02−5.84 and to study the chemical abundance pattern and dust content of its host galaxy.
Methods. We estimated the UV continuum of the GRB afterglow using a power-law extrapolation, then measured the flux decrement due to absorption at Lyα,β, and γ wavelength regions. Furthermore, we fitted the shape of the red damping wing of Lyα. The hydrogen and metal absorption lines formed in the host galaxy were fitted with Voigt profiles to obtain column densities. We investigated whether ionisation corrections needed to be applied.
Results. Our measurements of the Lyα-forest optical depth are consistent with previous measurements of QSOs, but have a much smaller uncertainty. The analysis of the red damping wing yields a neutral fraction xH i< 0.05 (3σ). We obtain column density measurements of H, Al, Si, and Fe; for C, O, S and Ni we obtain limits. The ionisation due to the GRB is estimated to be negligible (corrections <0.03 dex), but larger corrections may apply due to the pre-existing radiation field (up to 0.4 dex based on sub-DLA studies). Assuming that [ Si/Fe ] = +0.79 ± 0.13 is due to dust depletion, the dust-to-metal ratio is similar to the Galactic value.
Conclusions. Our measurements confirm that the Universe is already predominantly ionised over the redshift range probed in this work, but was slightly more neutral at z> 5.6. GRBs are useful probes of the ionisation state of the IGM in the early Universe, but because of internal scatter we need a larger statistical sample to draw robust conclusions. The high [Si/Fe] in the host can be due to dust depletion, α-element enhancement, or a combination of both. The very high value of [ Al/Fe ] = 2.40 ± 0.78 might be due to a proton capture process and is probably connected to the stellar population history. We estimate the host metallicity to be −1.7 < [ M/H ] < −0.9 (2%−13% of solar).
Key words: gamma-ray burst: individual: GRB 130606A / cosmology: observations / dark ages, reionization, first stars / ISM: abundances
Based on observations carried out under prog. ID 091.C-0934(C) with the X-Shooter spectrograph installed at the Cassegrain focus of the Very Large Telescope (VLT), Unit 2 – Kueyen, operated by the European Southern Observatory (ESO) on Cerro Paranal, Chile. Partly based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Partly based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, under programme A26TAC_63.
Appendix A is available in electronic form at http://www.aanda.org
The reduced spectrum (FITS file) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/580/A139
© ESO, 2015
1. Introduction
The potential of gamma-ray bursts (GRBs) as probes of star formation and the physics of the inter-galactic medium (IGM) back to the epoch of the first galaxies was appreciated very early in the so-called afterglow era (e.g., Wijers et al. 1998; Lamb & Reichart 2000; Ciardi & Loeb 2000). This promise has been bolstered by the rapid increase in the highest recorded spectroscopic redshift for GRBs from z = 4.5 in 2000 to z = 8.2 in 2009 (Andersen et al. 2000; Tanvir et al. 2009; Salvaterra et al. 2009). There are three main objectives in using GRBs to probe star formation and the IGM at high redshifts: to measure chemical abundances in very “primitive” conditions (e.g., dominated by Population III stars, Price et al. 2007; Wang et al. 2012; Sparre et al. 2014), to measure the neutral fraction of the IGM from the shape of the red damping wing (e.g., Miralda-Escudé 1998; Totani et al. 2006; Xu & Wei 2009; Greiner et al. 2009; Patel et al. 2010), and to pinpoint locations of star formation (Berger et al. 2007; Ruiz-Velasco et al. 2007; Tanvir et al. 2012). The last objective advances with each new detection, the full potential is still far from realised especially for the first two objectives.
GRB afterglows can be extremely bright, but also fade very rapidly. To obtain high-quality spectra, rapid follow-up at the largest optical telescopes is required. Primarily thanks to the Swift mission (Gehrels et al. 2004), studying the high-redshift universe though GRB afterglows has progressed well over the last years (e.g., Kawai et al. 2006; Price et al. 2007; Ruiz-Velasco et al. 2007; Thöne et al. 2013; Sparre et al. 2014). Traditionally, high-redshift galaxies are selected as Lyman-break galaxies (LBGs, Giavalisco 2002; Steidel et al. 2003), Lyα emitters (Stark et al. 2010; Ono et al. 2012; Pentericci et al. 2014), and damped Lyα absorbers towards quasars (QSO-DLAs, Wolfe et al. 2005). GRB host galaxies studied in absorption through afterglows (sometimes referred to as GRB-DLAs) are analysed using similar methods as those applied to QSO-DLAs, but intrinsic and observational biases are very different between these two classes of objects (see e.g. Prochaska et al. 2007a; Fynbo et al. 2008). In contrast to LBGs, for example, GRB host galaxies are not selected by their brightness; this provides the opportunity to explore a different range of luminosities and therefore sizes and masses of high-redshift galaxies.
We present spectroscopic observations of the afterglow of the z = 5.913 GRB 130606A obtained with X-Shooter on the European Southern Observatory (ESO) Very Large Telescope (VLT). The objective of the paper is to address the questions of chemical abundances in the host galaxy and the ionisation state of the IGM. Independent analyses of this event used data of significantly lower spectral resolution and with smaller wavelength coverage, for example, Chornock et al. (2013), Castro-Tirado et al. (2013a) and Totani et al. (2014). Our results are discussed in the context of the results from these earlier reports. The superior resolution and wavelength range we achieve with the data presented here, with the associated ability to perform direct line fits for abundances, provide the motivation for this paper.
For the cosmological calculations we assume a ΛCDM universe with ΩΛ = 0.6911, Ωm = 0.3089, and H0 = 67.74 km s-1 Mpc-1 from the 2013 Planck data (Planck Collaboration XVI 2014). Magnitudes are given in the AB system throughout the paper. Column densities are given as log (N/ cm-2). We use 1σ error bars unless explicitly noted otherwise.
Log of the NOT, TNG (top), and VLT/X-Shooter observations (bottom).
2. Observations
GRB 130606A was detected by Swift on June 6, 2013 at 21:04:39 UT (Ukwatta et al. 2013). The burst was relatively long with a T90 duration of 277 ± 19 s (Barthelmy et al. 2013).
We first observed the field of GRB 130606A with the Nordic Optical Telescope (NOT) equipped with the MOsaic CAmera (MOSCA) in the r band (3×200 s). Table 1 lists the observation log, including those obtained with the Telescopio Nazionale Galileo (TNG). Observations started at 20:35 UT or 0.5 h after the GRB trigger (Ukwatta et al. 2013; Xu et al. 2013b). Consistent with the Swift/XRT position (Osborne et al. 2013), we detected a new source with an r-band magnitude of 20.8 mag at RA (J2000) = 16h37m35.188s, Dec (J2000) = +29°47′47.03′′ (Xu et al. 2013b). The source coincided with the one reported by Jelinek et al. (2013). Observations in the near-infrared revealed that the afterglow was extremely bright (Ks = 15.0 about half an hour after the burst; Nagayama 2013a,b). We observed the field again 3 h later with NOT/MOSCA in the r and i bands. In Fig. 1 we show our i-band image compared to a pre-explosion image from the Sloan Digital Sky Survey. It soon became clear through spectroscopy and multi-band photometry at a number of telescopes that GRB 130606A was a very distant GRB (Castro-Tirado et al. 2013b; Lunnan et al. 2013; Afonso et al. 2013; Littlejohns et al. 2014). We subsequently acquired a medium-resolution spectrum with the X-Shooter spectrograph mounted at the ESO/VLT (Vernet et al. 2011), using nodding mode with 1 × 2 binning (i.e., binning in the dispersion direction, Xu et al. 2013a). Because we used a K-band blocking filter to increase the signal-to-noise ratio (S/N) at shorter near-IR wavelengths, the spectral coverage extends from 3000 to about 20 000 Å, corresponding to 430−2900 Å in the GRB rest frame. Observation started at 03:57:41 UT on 7 June, 2013 (see Table 1). Because the atmospheric dispersion corrector was not working at the time of the observation, we aligned the slit according to the parallactic angle and spread the observation over three observing blocks (OBs) of 2 × 600 s each in the UVB, VIS, and NIR arm. After each OB, we reset the position angle to the new parallactic angle to minimise flux losses in the UVB and VIS arm. The mid-exposure time is 7.829 h post burst (Xu et al. 2013a). The slit widths were matched to the seeing conditions, that is, we chose a 1.̋0, 0.̋9, and 0.̋9 slit in the UVB, VIS, and NIR arm, respectively. For this given instrument setup, the nominal resolving power R = λ/ Δλ is 5100, 8800, and 5300 in the UVB, VIS and NIR, respectively. For the VIS and NIR spectra we were able to directly measure the resolving power from the width of telluric absorption lines and find it to be 8700 and 6200, respectively. The NIR resolving power is higher than the nominal one because during most of the observations the seeing in this wavelength range was smaller than the slit width. The UVB spectrum shows no afterglow signal, as expected, given that the coverage of this arm falls below the Lyman break at the redshift of the GRB, and is not discussed further in the remainder of this paper.
 |
Fig. 1 80′′ × 80′′ field around the position of GRB 130606A in the i band. The left panel shows a pre-explosion image from the Sloan Digital Sky Survey and the right panel our i band image obtained with the NOT 3.5 h after the burst. North is up and east is to the left. |
VLT/X-Shooter data were reduced with the X-Shooter pipeline version 2.2.01 (Goldoni 2011). The wavelength binning was chosen to be 0.2 Å/px in the VIS, and 0.6 Å/px in the NIR. All spectra were flux calibrated with the spectrophotometric standard star LTT3218. We transformed the wavelength solution to vacuum and to the heliocentric frame. We corrected the VIS and NIR spectra for telluric absorption using the spectra of the telluric standard star Hip095400 observed just after the afterglow with the same slit width and at a similar airmass. The telluric corrections built with those spectra were applied with the Spextool software (Vacca et al. 2003). This corrected version was only used for line measurements in contaminated regions, because the uncorrected results showed a slightly higher S/N in unaffected regions.
3. Results
3.1. Astrometry
Based on the i-band image shown in Fig. 1, we determine the position of the afterglow of RA(J2000) = 16:37:35.143, Dec(J2000) = +29:47:46.62 calibrated to the USNO-A2.0 catalogue (Monet et al. 1998). The estimated error on the absolute position is 0.3′′ (Deutsch 1999). The position relative to stars in the field is much more precise, with an uncertainty of about 0.05′′.
 |
Fig. 2 Afterglow spectral energy distribution. The red spectrum is the X-Shooter spectrum, the filled circles on the left are the GROND photometric points (Afonso et al. 2013), and the data points on the right are the (binned) Swift/XRT points. The solid line is the synchrotron spectrum with interstellar absorption, while the dashed line shows the unabsorbed synchrotron spectrum with best fit β = 1.02. |
3.2. Fitting the spectral energy distribution
We constructed a broad-band spectral energy distribution (SED) for the afterglow of GRB 130606A spanning the wavelength range from the NIR K band to the X-ray energy range. We followed the methodology outlined in Krühler et al. (2011) and used the X-Shooter spectroscopy, photometric data from the Gamma-Ray Burst Optical/Near-Infrared Detector (GROND) as given in Afonso et al. (2013) and public X-ray data from the Swift/X-Ray Telescope (XRT) repository (Evans et al. 2007, 2009). We corrected for the Galactic foreground extinction of AV,Gal = 0.08 (Schlegel et al. 1998; Schlafly & Finkbeiner 2011).
After scaling the NIR spectroscopy to the photometry (data bluewards of Lyα were not fitted) to account for slit losses and different observing times, the complete data set is well described with a single power-law continuum Fν ∝ ν−β with index β = 1.02 ± 0.03, without evidence for reddening towards the GRB in addition to the Galactic component (see Fig. 2).
We set a 3σ upper limit of AV< 0.2 mag at ~zGRB assuming local extinction laws from the SMC, LMC, or MW (Pei 1992). The intrinsic X-ray absorption is also consistent with zero; given the GRB’s high redshift, we obtain a 3σ upper limit of 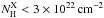 .
.
3.3. Analysis of the red damping wing
We used the SED obtained in Sect. 3.2 to normalise the spectrum. The normalisation is generally much more secure for GRB afterglows, which are intrinsically simple power-laws (pure synchrotron emission), compared to the more complex spectra of QSOs. To constrain the ionisation state of the IGM, we followed Miralda-Escudé (1998) and Totani et al. (2006) and jointly fitted the hydrogen column density in the GRB host galaxy, log NH i, and the neutral fraction of the IGM, xH i. In this analysis the redshift was kept fixed to that of the strongest component of the metal lines (z = 5.91285, see Sect. 3.4 and Table 2), and we assumed a constant neutral fraction xH i between z = 5.8 (the results are not very sensitive to this value) and z = 5.91285. The b parameter was also kept fixed in this fit. Each model specified by log NH i and xH i was normalised to the observed spectrum at 8730 Å. The χ2 sum was calculated over the region 0 to 2000 km s-1 with respect to Lyα. We performed the fit for three different slopes of the underlying afterglow continuum, β = 0.96,1.02,1.08 corresponding to the ±3σ allowed region for the spectral slope (Sect. 3.2). The minimum χ2 is reached for a fit with xH i = 0 (xH i< 0.05 at 3σ significance) and log NH i = 19.91 ± 0.02. The best fit to the Lyα red wing is shown in Fig. 3 and the 1, 2, and 3σ confidence regions in Fig. 4.
 |
Fig. 3 Top panel: spectral region around the Lyα feature with our best fit to the red wing overplotted in red. The model consists of a fully ionised intergalactic medium and a column density in the GRB host of log NH i = 19.91 ± 0.02. The 1σ noise is plotted as a dotted line. Bottom panel: residuals from the fit, with the ± 1σ region marked with a dotted line. The skyline residual in the bottom of the Lyα line should not be interpreted as Lyα emission. |
Redshift and Doppler parameter of the velocity components fitted to the metal lines of low- and high-ionisation species and for the fit to the Lyα line.
 |
Fig. 4 1, 2 and 3σ contours for a joint fit of the neutral hydrogen column density in the host galaxy, log NH i, and the neutral fraction of the intergalactic medium, xH i. The fit has been performed for three different normalising power-law SEDs: β = 0.96, β = 1.02 (best fit), and β = 1.08. The dot indicates the peak likelihood. |
3.4. Metal absorption lines
In Figs. A.1 and A.1 we show the afterglow spectrum redwards of the Lyα absorption line at 8400 Å up to 18 000 Å, which marks the end of the H band. The spectrum has a relatively high S/N (~20 per 0.2 Å pixel in VIS redwards of Lyα; ~10 per 0.6 Å pixel in NIR), and many metal absorption lines are detected. Most of these are from the host galaxy, but there is a number of intervening absorbers, see Sect. 3.5.
To determine the host-galaxy metal abundances, we proceeded with Voigt-profile fits to the metal lines around z = 5.913, with VPFIT version 10.02. A Voigt-profile fit to the red wing of the Lyα absorption lines results in log NH i = 19.925 ± 0.019; the blue wing is not visible due to ionisation in the IGM (see Sect. 3.6). This is consistent with the value from the combined fit for log NH i and xH i (Sect. 3.3); for the remainder of this analysis we adopt log NH i = 19.91 ± 0.02. Following the log NH i distinctions for QSO absorbers, this system is formally a sub-DLA, but only a factor of two below the DLA threshold (e.g., Wolfe et al. 2005).
We detected metal absorption lines of both low and high ionisation. We assumed that the redshift z and Doppler parameter b of a specific velocity component is the same for all metal lines of neutral, singly, and doubly ionised species. This assumption is commonly made for absorption spectra at intermediate spectral resolution. The z and b of components in the N v lines were not constrained to be the same as those of the low-ionisation species because these species are expected to reside in different locations (see Sect. 3.4.1). The resulting Voigt-profile fits are shown in Fig. 5. C iv and Si iv are not included in the overall fit with free z and b because they are strongly saturated, but we assumed the same velocity structure as N v and left the column densities free to fit. They are shown for completeness. Table 2 shows the redshifts and b parameters of the Lyα line and the components of the metal lines that follow from the fits. Because the values of b indicate that the velocity broadening is mostly due to turbulent motion of the gas and not to temperature, we did not weight the b values with the ion mass. We also included undetected lines, as long as they were located in regions without strong telluric contamination, in fitting the ensemble of lines to constrain the b values and reduce the effect of (hidden) saturation. We took into account contributions from intervening absorbers; for details on these, see Sect. 3.5.
 |
Fig. 5 Voigt-profile fits to the host-galaxy metal lines. We label the intervening metal lines (see Sect. 3.5) that contaminate the host galaxy lines; their contribution to the observed profile is taken into account. In orange (light grey) we show an atmospheric transmission spectrum matching the observing conditions and spectral resolution of our observations, generated with ESO’s SkyCalc tool. Residuals such as those close to the Fe ii lines are due to subtracted telluric emission lines. |
Derived column densities from the host galaxy absorption lines.
Table 3 shows the resulting column densities for several ion species and states, per component, total, and in the metallicity notation [ X/H ] ≡ log (N(X) /N(H))GRB − log (n(X) /n(H))⊙ based on the total column density and using reference solar abundances n from Asplund et al. (2009) following the recommendations by Lodders et al. (2009). These numbers are not corrected for ionisation or dust-depletion effects; for these, see Sects. 3.4.3 and 3.4.4, respectively.
3.4.1. Kinematic structure of absorption lines
Table 2 lists the redshifts and b parameters of the three components of low- (2, 4, 5) and high-ionisation lines (1, 3, 6) and their relative velocity. In the C ii, Si ii, and Fe ii lines component 4 is stronger than 5, while this is opposite in Al ii and Al iii, which show structures that are very similar to one another. N v shows a very different structure, which is broader, and where the absorption is strongest at the highest relative velocities. The N v lines are not significantly affected by lines from intervening absorbers (see Sect. 3.5). High-ionisation lines such as N v are common in GRB afterglow spectra (see, e.g., Fox et al. 2008). Prochaska et al. (2008) found that six out of seven GRB afterglow spectra show N v absorption, and the majority has N(N v) ≥ 1014 cm-2; for GRB 130606A we find log (N(N v)/cm-2) = 14.59 ± 0.03. However, these features are usually kinematically “cold” in GRB afterglow spectra: the lines are narrow and have velocity offsets δv ≲ 20 km s-1 with respect to the location of the neutral gas. Our resolution is not high enough to make strong statements about the width of the lines, but we do see a much larger offset: δv ≳ 60 km s-1 for the bulk of the N v absorption. In QSO-DLAs the detection rate of N v is much lower, and the lines are weaker (Fox et al. 2007; Prochaska et al. 2007b).
For QSO-DLAs it is known that the velocity width of optically thin lines, Δv90, is sensitive to the stellar mass of the host galaxy (Christensen et al. 2014); together with the metallicity of the gas, it can therefore be used to explore the evolution of the mass-metallicity (MZ) relation of galaxies from high redshifts to the local Universe (e.g., Ledoux et al. 2006). In a recent study, Møller et al. (2013) found that the redshift evolution of the MZ relation for QSO-DLAs is flat in the early Universe, but that it features a break at a redshift z ~ 2.6 after which it evolves steeply (see Fig. 6). Neeleman et al. (2013) reported a slightly flatter slope, but found no evidence for a break.
 |
Fig. 6 Results from Møller et al. (2013) with the high-redshift measurement of GRB 130606A included. [M/H]100 km s-1 is the metallicity expected for DLAs with ΔV = 100 km s-1, based on the overall mass-metallicity relation. The data of Møller et al. (2013; filled circles) favour a break in the evolution of the mass-metallicity relation at z ~ 2.6 (dashed line), which is also supported by our measurement of GRB 130606A (filled square). We assumed for this point ΔV = 90 km s-1 and [ M/H ] = −1.3 ± 0.2; see text. |
While QSO-DLAs sample complete sightlines through galaxies, GRB-DLAs are found inside galaxies, and therefore they sample (on average) only half sightlines. Arabsalmani et al. (2015) recently studied how this might alter the relations known from intervening DLA studies. Based on all the possible tests they could perform, they concluded that all evidence indicates that GRB-DLAs follow the same relations as QSO-DLAs. They also found from their sample that the evolution including a break (Møller et al. 2013) presented a somewhat better fit (probability 100:6) than the flatter evolution with no break (Neeleman et al. 2013).
Using the definition by Prochaska & Wolfe (1997), Δv90 is the width in velocity space containing 90% of the total optical depth of a line. For GRB 130606A we measure Δv90 = 120 ± 1 km s-1 from the Si ii λ1526 transition, which is the best line available for this analysis according to the criteria set by Ledoux et al. (2006). For a wider selection of lines (loosening these criteria) we find on average Δv90 = 140 ± 25 km s-1, which agrees with the value of Si ii λ1526. We applied the appropriate resolution correction using the method described by Arabsalmani et al. (2015) and obtained an intrinsic Δv90 = 90 km s-1. GRB 130606A is the highest redshift object for which Δv90 is determined, and it is therefore well suited to determine whether there is a break in the evolution of the MZ relation or not. We have included GRB 130606A in Fig. 6. Keeping in mind that this is only a single point of a relation that has a significant internal scatter (0.38 dex in [M/H]), the point is clearly consistent with the evolution with a break, as reported in Møller et al. (2013). The metallicity adopted here is [ M/H ] = −1.3 ± 0.23. The relation reported by Neeleman et al. (2013) (less steep and with no break) predicts a much lower metallicity for this Δv90: [ M/H ] = −2.25 ± 0.75. This value marginally agrees with our metallicity measurement, but only as a result of the large scatter. We repeated the analysis of Arabsalmani et al. (2015) including our new data point at z = 5.9 and found that considering only GRB-DLAs, the relative probability is 100:3 in favour of the redshift evolution with a break at z = 2.6.
3.4.2. Fine-structure and metastable lines
Absorption lines from Si ii 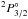 (Si ii∗) are regularly detected in high-z GRB spectra (e.g., Vreeswijk et al. 2004; Kawai et al. 2006; Sparre et al. 2014) and were also detected in GRB 130606A. They indicate that a considerable fraction of these ions are in an excited state (32% of total Si ii; see Table 3). However, fine-structure and metastable lines from Fe ii and Ni ii, which are also usually present in high S/N GRB afterglow spectra (see, e.g., Vreeswijk et al. 2007; Hartoog et al. 2013), were not convincingly detected here. Assuming that these lines have the same velocity structure (i.e. keeping z and b fixed) as the resonance lines, we estimated upper limits on the gas-phase column densities of Fe ii
(Si ii∗) are regularly detected in high-z GRB spectra (e.g., Vreeswijk et al. 2004; Kawai et al. 2006; Sparre et al. 2014) and were also detected in GRB 130606A. They indicate that a considerable fraction of these ions are in an excited state (32% of total Si ii; see Table 3). However, fine-structure and metastable lines from Fe ii and Ni ii, which are also usually present in high S/N GRB afterglow spectra (see, e.g., Vreeswijk et al. 2007; Hartoog et al. 2013), were not convincingly detected here. Assuming that these lines have the same velocity structure (i.e. keeping z and b fixed) as the resonance lines, we estimated upper limits on the gas-phase column densities of Fe ii 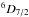 (Fe ii∗) and Ni ii
(Fe ii∗) and Ni ii 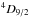 (Ni ii∗), which are listed in Table 3. These lines are probably absent because the host of GRB 130606A is a relatively weak absorber for a GRB host (not even a DLA), and the populations of the ground state levels of these excited ions are already very small due to the combined effect of a low gas column and dust depletion (Sect. 3.4.4).
(Ni ii∗), which are listed in Table 3. These lines are probably absent because the host of GRB 130606A is a relatively weak absorber for a GRB host (not even a DLA), and the populations of the ground state levels of these excited ions are already very small due to the combined effect of a low gas column and dust depletion (Sect. 3.4.4).
3.4.3. Ionisation correction
Because the neutral hydrogen column density of the GRB 130606A absorber is relatively low (sub-DLA), the hydrogen and metals are less shielded from ionising photons than in a DLA. As a result, the assumption that the overwhelming majority of an element is in a single neutral or lowly ionised state (e.g., NSi ii/NH i = NSi/NH), which is valid for DLAs (Vladilo et al. 2001; Prochaska et al. 2002), may not hold for this system. Moreover, the interstellar UV radiation field in a GRB host galaxy does not have to be similar to that in a QSO-sub-DLA, since the GRB host is known to be actively forming massive stars, while this is not necessarily the case in a random foreground line-of-sight object causing the QSO-sub-DLA. Chen et al. (2009) estimated the UV radiation field in a sample of 15 GRB host galaxies to be tens to hundreds of times that of the Galactic value, while the radiation field in QSO-DLAs, whose counterparts are notoriously difficult to detect, appears to be much more moderate (e.g., Wolfe et al. 2003). The ionisation induced by the UV/X-ray afterglow of the GRB needs to be considered in addition to this pre-burst ionisation correction. Both the pre- and post-burst ionisation effects are investigated in this section.
To estimate the pre-burst ionisation correction, we compared the situation with self-consistent sub-DLA ionisation studies from the literature. Dessauges-Zavadsky et al. (2003) reported on a detailed study with a sample of QSO-sub-DLAs and used the logarithmic ratio [ Al ii/ Al iii ] or [ Fe ii/ Fe iii ] as an indicator for the degree of ionisation to calibrate the ionisation parameter U in their photoionisation model. The conclusion of this work is that sub-DLAs need small corrections ≲0.2 dex for all measured elements except Al and Zn, which are more strongly influenced. For GRB 130606A, we measure [ Al ii/ Al iii ] = 0.81 ± 0.804, which is a typical value for sub-DLAs, but its large error does not allow us to constrain the ionisation parameter U very well. However, because the H i column density of the GRB 130606A absorber is only a factor of about two below the DLA definition limit, the ionisation corrections for the elements Fe, Si, and S that we are interested in are moderate regardless of what is assumed for U. For example, the sub-DLA in GRB 130606A is very similar to the z = 3.142 sub-DLA in QSO PSS J2155+1258 that was presented in Fig. 32 in Dessauges-Zavadsky et al. (2003): the neutral hydrogen and total Fe ii column densities are practically the same, and the Si ii column densities are the same within a factor of 2. This analogy suggests that the ionisation correction for the GRB 130606A sub-DLA for the Fe, S, and Si abundances can be constrained to −0.05 ≲ ϵFe< 0, −0.2 ≲ ϵS< 0 and −0.4 ≲ ϵSi< 0, respectively. These limits are independent of the value for U or the strength of the UV radiation field for the calculations considered by Dessauges-Zavadsky et al. (2003). Similar constraints on Fe and Si have been inferred for sub-DLAs by Meiring et al. (2009); see their Figs. 3 and 4. Vladilo et al. (2001) presented a similar study with DLAs, but since our sub-DLA has a column density close to the DLA lower limit, we can extrapolate their model results down to log NH i ~ 20, yielding ϵSi ~ −0.21, ϵS ~ −0.30, ϵFe ~ −0.04, and ϵNi ~ −0.17. We note that these corrections are negative (X+/ H0> [ X/H ] total), meaning that parts of singly ionised metals are in regions where hydrogen is ionised instead of neutral because the lower column density shields itself less effectively.
The ionisation due to the afterglow of GRB 130606A was calculated with a method similar to the one used in De Cia et al. (2012) and Vreeswijk et al. (2013). From published near-IR photometry of GRB 130606A (Nagayama 2013b; Butler et al. 2013; Im et al. 2013; Morgan 2013; Afonso et al. 2013) and assuming a constant spectral index β = −1 (see Sect. 3.2) and a single power-law light curve, we obtain a temporal index α = −1, at least until the time at which the spectrum was taken. The absorbing cloud is at distance d from the GRB and is illuminated on one side by the afterglow between t0 and tobs, the time of our observations. The onset of the afterglow t0 is unknown and introduces an uncertainty; we assumed different values to see its effect. The free parameters are the pre-burst NH i and NFe ii. The distance d was obtained from a separate fit using the observed ratio NSi ii∗/NSi ii in the cloud and was estimated to be d = 2.1 ± 0.5, 1.9 ± 0.4, and 1.8 ± 0.4 kpc for t0 = 60, 180, and 300 s in the rest frame, respectively. These values agree reasonably well with the lower limit d> 2.2 ± 0.2 kpc derived from the upper limit of NFe ii∗/NFe ii. The column densities of the ions (except H i and Fe ii) are assumed to be equal to their measured values at the start of the simulation (Table 3). This is not entirely correct, but it shows how much they would change when placed at the distance d and were illuminated by the afterglow. From the differences in column density between t0 and tobs, we conclude that the ionisation effects due to the afterglow are very minor. H i did not change at all, Fe ii is lowered by 0.03 dex, O i by 0.01, Si ii by 0.02, C ii by 0.01, Al ii by 0.02, and Al iii by 0.01 dex by using t0 = 60 s and even lower for the higher values of t0 and the larger distance d> 2.2 kpc.
Because our estimates for the ionisation corrections are not the result of fully consistent modelling, we did not apply them directly to our measured abundances. We discuss the estimated metallicity when the corrections are taken into account in Sect. 4.2.
 |
Fig. 7 Galactic warm disk depletion abundance pattern (solid line, Savage & Sembach 1996), in which Al is assumed to be depleted as strongly as Fe (Phillips et al. 1982), and depletion of O is assumed to be negligible (Jenkins 2009), fit to the observed pattern (diamonds) following Savaglio (2001). This fit yields DTM = 1.00 ± 0.01. Aluminium is not included in this fit. The limit on S is taken from Castro-Tirado et al. (2013a). |
3.4.4. Dust depletion
Although the optical extinction in the line of sight is low (AV< 0.2 mag at the 3σ level, see Sect. 3.2), the abundance pattern (Table 3) suggests that there is dust depletion at play. Elements that are locked up into dust by greater amounts (e.g. Si, Fe) have lower column densities in the gas phase than minimally depleted elements (e.g. S) when compared to the relative abundance pattern in the solar photosphere (Savage & Sembach 1996; Phillips et al. 1982; Jenkins 2009).
For the analysis of the dust depletion we assumed that the metallicity is [ S/H ] = −0.88 (using the limit log NS< 14.17 from Castro-Tirado et al. 2013a) and included only Si and Fe in the depletion-pattern fit. We followed the method described by Savaglio (2001) and refer to depletion levels reported by Savage & Sembach (1996). We assumed the depletion of oxygen to be negligible (Jenkins 2009) and the depletion of aluminium to be the same as iron, as suggested in Phillips et al. (1982). The observed abundances are formally best fit by the depletion pattern typical of a warm disk (WD) environment, although the other Galactic depletion patterns (Savage & Sembach 1996) cannot be ruled out based on these two measurements. The results are displayed in Fig. 7. Aluminium is a clear outlier, although the errors on the Al ii column density (log NAl ii = 14.66 ± 0.78) are too large to be constraining. We excluded Al from the fit because it shows an evidently peculiar abundance. Therefore, we cannot compare it to the Galactic depletion patterns of Savage & Sembach (1996), where solar relative abundances are assumed. We also tested whether an enhancement in the abundance of the α-elements could alleviate this discrepancy, but aluminium still remained an outlier. There must be some process that causes an Al enhancement, which we discuss in Sect. 4.3.1.
The dust-to-metal ratio (DTM, expressed as a fraction of the average Galactic value, Watson 2011) derived from the depletion-pattern analysis (DTM = 1.00 ± 0.01) agrees well, as expected, with the one derived from only the observed [Si/Fe] (DTM = 1.03 ± 0.04), using the method described in De Cia et al. (2013). A similar DTM was also found when other depletion patterns were used. This means that, assuming the underlying pattern is similar to that of a solar environment (see Sect. 4.3), the dust-to-metal ratio of the host galaxy environment is consistent with the Galactic value, which is remarkable at this redshift.
3.5. Intervening absorption systems
We confirm the detection of several intervening absorbers in addition to the host galaxy. Based on the preliminary reduction of the same X-Shooter spectrum as discussed here, Xu et al. (2013a) reported z1 = 2.3103 (Mg ii) and z3 = 3.4515 (Mg ii, Fe ii), which we confirm. We additionally detect z2 = 2.5207 (Mg ii, Fe ii), z4 = 4.6448, 4.6468, 4.6495 (C iv, Mg ii, Al ii Si ii, Fe ii) reported earlier by Chornock et al. (2013). We cannot unambiguously confirm the existence of the z5 = 5.806 system reported by these authors. Lines that are possibly present at this redshift are Si ii λ1260, Si ii* λ1265, O i λ1302, C ii λ1334, and C ii* λ1335, but many strong features are lacking: we do not see any Fe ii transitions, no Si ii λ1526, and no C iv λ1548, although the expected locations of these intrinsically strong lines are in regions with high S/N and only little telluric contamination and should not be blended with the other identified absorbers. At the redshifts z = 4.4660, 4.5309, 4.5427, and 4.6497 we tentatively detect additional C iv absorbers, but contamination by other lines and atmospheric features hampers strong conclusions on these systems.
3.6. Lyα forest constraints on the IGM
In this section we analyse the ionisation state of the IGM at z ~ 5−6 via the Gunn-Peterson optical depth (Gunn & Peterson 1965).
3.6.1. Lyα absorption
We measured the Lyα absorption by the IGM from 1200 Å in the rest frame, which is the limit not affected by the blue wing of Lyα, to 1040 Å, the shortest wavelength that is not affected by possible Lyβ emission from the GRB host. Within this range, we used redshift intervals of Δz of 0.15, which corresponds to ~60 Mpc in comoving distance, for comparison purposes with previous work. Using this redshift range and wavelength interval, we measured the transmission as 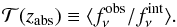 (1)The measured transmitted flux (
(1)The measured transmitted flux (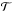 ) is shown in Table 4 and plotted in Fig. 8. The continuum level is determined first by fitting a power law to the near-infrared part of the spectrum, taking advantage of the broad wavelength coverage of X-Shooter. Then, we fixed the slope and fitted the normalisation to the optical part of the spectrum (8530−8950 Å). We masked strong identified absorption features (both telluric and extragalactic) in this process. When using QSOs for this type of analysis, continuum determination is often the largest source of uncertainty because of the complicated shape of their spectrum.
) is shown in Table 4 and plotted in Fig. 8. The continuum level is determined first by fitting a power law to the near-infrared part of the spectrum, taking advantage of the broad wavelength coverage of X-Shooter. Then, we fixed the slope and fitted the normalisation to the optical part of the spectrum (8530−8950 Å). We masked strong identified absorption features (both telluric and extragalactic) in this process. When using QSOs for this type of analysis, continuum determination is often the largest source of uncertainty because of the complicated shape of their spectrum.
A GRB continuum can be more accurately predicted as a result of its relatively flat shape that shows no broad features. We estimated errors on the transmission by changing the continuum slope within 1σ (see Sect. 3.2), added in quadrature to the noise in the spectra and the errors in determining the unabsorbed continuum level. The latter dominates the errors on 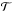 .
.
It is conventional to express the optical depth τ in terms of 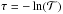 . We present τ as a function of redshift in Fig. 9.
. We present τ as a function of redshift in Fig. 9.
 |
Fig. 8 Lyα transmission in the spectrum of GRB 130606A (squares). Lyβ (diamonds) and Lyγ (crosses) measurements are converted to equivalent values at Lyα. The small black triangles, diamonds, and the grey squares are measurements based on quasars from Fan et al. (2006), Goto et al. (2011), and Songaila (2004), respectively. The solid line is the best power-law fit to the data at z< 5.5 by Fan et al. (2006, their Eq. (5)). The uncertainties of the QSO points are typically a factor of two. |
IGM absorption towards the GRB 130606A at z = 5.913.
3.6.2. Lyβ absorption
At the same neutral hydrogen density, the optical depth τ is proportional to fλ0, where f and λ0 are the oscillator strength and rest-frame wavelength of the transition, respectively. Therefore, the optical depth of Lyβ is a factor of 6.2 smaller than that of Lyα in a homogeneous medium illuminated by a uniform radiation field. This means that Lyβ probes into a larger amount of neutral hydrogen than Lyα. In this section we measure the optical depth using Lyβ absorption from the spectra.
We assumed the same continuum as we used for Lyα. We chose the minimum wavelength to be 970 Å, above which it is not affected by Lyγ absorption. This results in a redshift range of 5.59 <zabs< 5.74 for Lyβ. The Lyβ absorptions overlap with Lyα absorption at lower redshift. Therefore, we corrected the Lyα absorption to measure τβ. We used Eq. (5) of Fan et al. (2006) to estimate Lyα absorption from lower redshift and corrected the Lyβ transmission measurements. Table 4 shows the results, which are graphically represented in Fig. 8 as blue diamonds.
To convert Lyβ transmission to τα, different optical depths between Lyα and Lyβ have to be considered. The difference depends on the UV background and its uniformity, the clumpiness of the IGM, and its equation of state. According to simulations (e.g., Oh & Furlanetto 2005) and empirical measurements (Fan et al. 2006), the τα/τβ conversion is in the range of 2.2−2.9. The τα/τγ conversion lies in the range of 4.4−5.7. Following the discussion in Fan et al. (2006), we used τα/τβ = 2.25 and τα/τγ = 4.4. These values are based on measurements of transmitted flux at 5.4 <z< 5.8 in the QSO sample of Fan et al. (2006).
 |
Fig. 9 Effective Gunn-Peterson Lyα optical depth of the IGM from the spectrum of GRB 130606A. The large squares, diamonds, and crosses are measurements with error estimates from Lyα, Lyβ, and Lyγ, respectively, the latter two converted to the Lyα optical depth. The small black triangles, diamonds, and the grey squares are measurements based on QSO spectra from Fan et al. (2006), Goto et al. (2011), and Songaila (2004), respectively. The uncertainties of the QSO points are typically a factor of two. The solid line is the best power-law fit to the data at z< 5.5 by Fan et al. (2006, their Eq. (5)). |
Figure 9 shows constraints on the τα from Lyβ absorption measurements. We note that τ is converted to the Lyα optical depth in Fig. 9.
3.6.3. Lyγ absorption
Similar to Lyβ, the Lyγ optical depth (fλ0) is a factor of 17.9 lower than that of Lyα, providing us with a chance to probe into even more neutral hydrogen. The more neutral regions are denser in general. Therefore, Lyγ transmission also provides the opportunity to probe regions with different density, potentially constraining the density-temperature relation.
The Lyγ absorption measurement is restricted by Lyβ absorption at lower redshifts and the Lyδ absorption at the higher redshifts (closer to the GRB). Therefore, we used a smaller bin size of Δz = 0.06 than for the Lyα and Lyβ transmission. The Lyγ transmission measurements were corrected for overlapping lower redshift Lyα and Lyβ absorptions using the best-fit power laws to lower redshift data (Fan et al. 2006, their Eqs. (5) and (6)). The optical depth was converted to τα, using τα/τγ = 4.4. The results are listed in Table 4 and shown in Fig. 9.
The Lyγ absorption measurements are much more challenging than those of Lyα and Lyβ. Since the overlapping foreground Lyα and Lyβ lines absorb ~98% of the continuum flux in the wavelength ranges of Lyγ, we need to measure absorption in the remaining ~2%. Errors in the continuum determination are also larger in this region since we use the bluer part of the spectrum.
In Figs. 8 and 9, small triangles and grey squares represent previous data based on quasars from Fan et al. (2006) and Songaila (2004). The solid line shows the best power-law fit to the data at z< 5.5 based on Fan et al. (2006, their Eq. (5)). Within the scatter, our measurements agree with earlier findings. At z> 5.7, our data points deviate from the fit to z< 5.5 data, suggesting that the Universe was not yet completely ionised at z> 5.7.
 |
Fig. 10 Excerpt of the X-Shooter spectrum with the same model fit as shown in Fig. 3. The lower panel shows the residuals and deviations from the fit. The hatched region is range III in Totani et al. (2014), where their spectrum is inconsistent with a single DLA model. With our data, we can obtain a good fit with this model. The difference is most likely due to a different spectral index β, see Sect. 4.1. |
4. Discussion
4.1. Analysis of the red damping wing
Totani et al. (2014) reported evidence for a high neutral fraction based on their spectrum of the afterglow. In particular, they found that a Voigt-profile fitted to the red wing of the absorption trough is inconsistent with the data in a region referred to as wavelength range III by these authors, from about 8650 to 8700 Å. In Fig. 10 we show this wavelength range III in our spectrum including our fit and the deviations from the fit. Our spectrum is fully consistent with the Voigt-profile fit without a neutral hydrogen IGM component (see also Sect. 3.3). One important difference between our analysis and that of Totani et al. (2014) is that the value of the spectral slope adopted by these authors (β = −0.74) is inconsistent with the one we find.
We subsequently discussed this with Dr Totani and collaborators and made our spectrum available to them. The difference between the obtained neutral fractions seems to some extent to be dependent on the fitting method and on which sections of the spectrum are fitted. Dr Totani and collaborators will carry out an independent analysis of our spectrum (Totani et al., in prep.).
4.2. Metallicity of the host of GRB 130606A
The “raw” measured column density values and limits we derived for the host-galaxy ISM (Table 3) agree well with the results from Chornock et al. (2013) and Castro-Tirado et al. (2013a). Because our data have a higher spectral resolution and a larger wavelength coverage and because all results of other observations have been published, we try to explain the effects of ionisation and dust depletion to better constrain metallicity and true abundance pattern in the host galaxy of GRB 130606A. Estimates on the effects of ionisation are provided in Sect. 3.4.3, where we conservatively assumed the following contraints on the ionisation corrections, including both pre-burst and post-burst effects: ϵFe ~ 0, −0.4 ≲ ϵS< 0 and −0.4 ≲ ϵSi< 0. Here, we discuss their possible implications. We measured [ S/H ] < −0.60, while the spectrum by Castro-Tirado et al. (2013a), taken earlier in time, provides are more stringent upper limit of log NS< 14.17 and [ S/H ] < −0.88. Sulphur is only minimally depleted onto dust, and considering that the sulphur ionisation correction would only make this abundance smaller, this value should reflect a real upper limit on the metallicity. For silicon, we measured [ Si/H ] = −1.30 ± 0.08; adding the strongest ionisation correction, this values becomes [ Si/H ] ic = −1.7, which is a stringent lower limit on the metallicity. From the dust depletion analysis we know that a fraction of the Si is in dust, but the analysis is not robust enough to estimate an exact value. The effect is included, while Si provides the lower limit. The iron abundance [ Fe/H ] = −2.09 ± 0.08 is negligibly affected by ionisation, but severely so by dust depletion and does not provide additional information on the metallicity. The metallicity is constrained to be −1.7 < [ M/H ] < −0.9, since Si provides a lower limit and S the upper limit. This is relatively high when compared to QSO-DLAs at z> 5 (Rafelski et al. 2012, 2014), but not unexpected given predictions in recent models (Salvaterra et al. 2013). The difference in metallicity evolution in GRB-DLAs and QSO-DLAs has also recently been discussed in Thöne et al. (2013), Sparre et al. (2014), and Cucchiara et al. (2015), for instance.
4.3. Nucleosynthetic history
The high value of [Si/Fe] can be fully attributed to dust depletion, but the effects of this, and those of an underlying pattern that is different from that in the solar photosphere (e.g., α-element enhancement), are degenerate. At this redshift, one would expect to see more elements in the ISM created by shorter-lived massive stars, α-elements (C, N, O, Ne, Mg, S, Si, Ar, Ca, Ti) from core-collapse supernovae (SNe) instead of products of SNe originating in longer-living stars: the iron peak elements created by type Ia SNe (V, Cr, Mn, Fe, Co, Ni). This has not unambiguously been detected in high-redshift GRB host galaxies to date because there usually is the combined effect of the dust depletion (see, e.g., Thöne et al. 2013; Sparre et al. 2014). With the limited information we have for GRB 130606A, we cannot draw strong conclusions on either the dust depletion or α-element enhancement. With a pure dust-depletion explanation, the dust-to-metal ratio is about the same as the Galactic value. The dust extinction (AV< 0.2 mag at 3σ) can still be low due to the low total metal column density (see also, e.g., Zafar et al. 2011). A peculiarity that we cannot explain with dust depletion is the very high abundance of aluminium, which we discuss in Sect. 4.3.1.
4.3.1. High aluminium abundance at z ~ 6: a relic of Population III stars?
The analysis of the X-Shooter spectrum of the host galaxy of GRB 130606A yields a remarkably high aluminium abundance: [ Al ii/ H i ] = + 0.31 ± 0.78, given the low iron abundance of [ Fe/H ] = −2.09 ± 0.08. While the relatively large errors on the aluminium abundance cause this observation to be only marginally significant (≈3σ), it is not the only unusual abundance ratio in this system. The oxygen abundance is very low: Chornock et al. (2013) found [ O/H ] ~ −2.0, and we derive a lower limit of [ O/H ] > −1.85, while the silicon abundance, [ Si/H ] = −1.30 ± 0.08, is much higher than the iron abundance.
This unusual abundance pattern is not observed for the first time in a GRB host. In the host galaxy of GRB 120327A (z = 2.8145, D’Elia et al. 2014) the aluminium abundance was also high ([ Al/H ] = 0.00 ± 0.11; [ Al/Fe ] = 1.73 ± 0.07), although saturation of the Al ii and Al iii lines prevents an accurate abundance analysis of the three individual absorption line components. The oxygen abundance ([ O/H ] = −1.98 ± 0.13) is also lower than that of iron ([ Fe/H ] = −1.73 ± 0.10), and the silicon abundance is again high ([ Si/H ] = −1.16 ± 0.09). The similarity between these two unusual patterns deserves some discussion, and we here consider possible causes.
One explanation might be ionisation corrections due to the fairly low column density of GRB 130606A, but as shown in Sect. 3.4.3, this correction is less than 0.4 dex for GRB 130606A5. Furthermore, the host of GRB 120327A has an H i column density of log (NH i/ cm-2) = 22.01 and therefore will need no ionisation corrections. Taken together, it is very unlikely that this is the cause.
Another possibility is depletion onto dust grains. Our understanding of dust depletion is still very far from complete, and much is yet to be learned in this field. However, the depletion of Al and Fe is is expected to be very similar (Phillips et al. 1982), so again while hypothetically possible, we consider this an unlikely scenario.
An interesting, and possibly related, observation is the relatively high aluminium abundance that has been measured in the atmospheres of red giants in metal-poor ([ Fe/H ] < −1) globular clusters (e.g., Kraft et al. 1997). In these atmospheres, [Al/Fe] seems to be always ≲1.5 (Cordero et al. 2014), consistent with our value of + 2.40 ± 0.78, as well as that of GRB 120327A (+1.73 ± 0.07), although both of the GRB host measurements are in the upper range. In these globular clusters a strong anti-correlation has been found between the oxygen and sodium abundance. This anti-correlation has been interpreted as being due to proton-capture nucleosynthesis, where Na and Al are produced at the expense of Ne and Mg in regions where C and O are converted into N, that is, where the CNO cycle is active (Cavallo et al. 1998). Likewise, Si would be produced by proton capture of Al. Regarding these metal-poor globular clusters, the question is whether the proton capture occurred within the observed red giants, that is, during shell burning when the temperature is high enough for the CNO cycle, and convection dredged up the metals produced in these deeper layers within the stars (evolutionary scenario). Alternatively, these abundance “anomalies” might have been produced by proton capture in a previous generation of massive (perhaps even the first) stars (primordial scenario). The detection of similar abundance anomalies in main-sequence, turn-off and early sub-giant stars (Gratton et al. 2001) suggests the latter scenario. Denissenkov & Hartwick (2014) proposed that the abundance anomalies of proton-capture elements in globular clusters were produced by supermassive stars with M ~ 104M⊙, products of the runaway collisions of massive stars in dense clusters (Portegies Zwart et al. 2004).
It appears therefore that the measured abundances in the two GRB host galaxies discussed here find their simplest and most logical explanation as the result of proton-capture at work. Given the high redshift (z = 5.913) of GRB 130606A and the corresponding look-back time (~12.6 Gyr), these observations are consistent with the scenario that a previous generation of massive stars must have produced the chemical enrichment via proton capture.
4.4. Reionisation of the IGM
Prompt follow-up spectroscopy of GRB 130606A has enabled to reliably measure Gunn-Peterson optical depths using a GRB instead of a QSO as a background source (see also Chornock et al. 2013; Totani et al. 2014). The only other GRB for which this has been attempted is GRB 050904 (Totani et al. 2006). Given a high S/N afterglow spectrum, GRBs have several advantages over QSOs; the simple power-law continuum of a GRB spectrum is much easier to estimate than the complicated shape of a QSO spectrum, including a possibly broken power-law UV continuum, whose break is in the heavily absorbed UV range at high-redshift and broad emission lines. As a consequence of this, the uncertainties of the measured optical depths based on our GRB spectrum are much smaller than typical uncertainties on values in previous work based on QSOs, which are about a factor of 2. In addition, GRBs can be much brighter than QSOs if observed early enough. At the time of our reported spectroscopy, GRB 130606A had a near-IR brightness (Y,J,H) of around the 18th magnitude (Butler et al. 2013). This is much brighter than z ~ 6 QSOs used in previous work (mz ~ 20 mag). While obtaining high S/N spectra of fainter QSOs with current 8 m class telescopes becomes progressively more difficult at higher redshift with fainter QSOs, we can in principle extend the Gunn-Peterson test to much higher redshifts by using GRBs, without having to rely on future larger optical telescopes.
Another advantage of GRBs over QSOs is that the sightlines towards them suffer from different biases. GRB host galaxies differ from typical field galaxies (Fruchter et al. 2006; Savaglio et al. 2009; Wang & Dai 2014). At low redshift they are found to be low-mass, metal-poor galaxies, which reside in representative regions of the Universe. On the other hand, QSOs tend to be contained in massive haloes. The surroundings of QSOs could be overdense on scales of several tens of Mpc (for example see Overzier et al. 2009; Utsumi et al. 2010). In this case, the IGM in front of QSOs could be more ionised than a typical region of the Universe. Furthermore, the QSO background light has been present for a long time, which may have affected the degree of ionisation of the material in the sight line, in particular close to the source: the proximity effect. This is not the case for GRB afterglows.
However, despite our accurate measurements, the optical depths show significant variation across the redshift window we used (5.0 <z< 5.8). The variation is much larger than our measurement errors, and therefore, intrinsic. This suggests a strong spatial variation in optical depths at this epoch of the Universe. To fully understand the reionisation history of the Universe, it is therefore important to expand the statistical sample. GRBs will probably play a prominent role in this.
5. Conclusions
We reported the analysis of the z = 5.913 GRB 130606A afterglow spectrum obtained with VLT/X-Shooter. The analysis can be divided into two main parts: the study of the abundance pattern in the host galaxy measured by the afterglow absorption lines, and the study of the ionised fraction of the IGM through the shape of the red wing of Lyα at zGRB and through the Gunn-Peterson optical depth in front of the GRB (5.02 <z< 5.84).
Although many host absorption lines were detected, the abundances can only be well constrained for H, Si, Fe, and Al; for C, O, S, and Ni we obtained limits. The high [ Si/Fe ] = + 0.79 ± 0.13 can be explained with dust depletion with a dust-to-metal ratio similar to the Galactic value or α-element enhancement. The abundance of aluminium is very high: [ Al/H ] = +0.31 ± 0.78 and [ Al/Fe ] = +2.40 ± 0.78 based on Al ii alone, and even higher when taking into account Al iii, which shows a similar line structure, suggesting that the region where this resides is associated with the region in which Al ii is located. With log NH i = 19.91 ± 0.02 the absorber is a sub-DLA and might not be as efficiently shielding the ions from ionisation as DLAs. We estimated the ionisation corrections both in the pre-burst sub-DLA and due to the UV radiation GRB afterglow. While the former results in corrections of up to 0.4 dex, the latter is in this case negligible with corrections below 0.03 dex. When these corrections and the more stringent upper limit on S by Castro-Tirado et al. (2013a) are taken into account, the metallicity is estimated to be −1.7 < [ M/H ] < −0.9 (2−13% of solar). The metallicity and low-ionisation line width measured at this high redshift are consistent with the break in the evolution of the mass-metallicity relation for DLAs proposed in Møller et al. (2013), but also marginally with a model that assumes a shallower slope and no break (Neeleman et al. 2013).
From fitting the red wing of the Lyα absorption line of the GRB host galaxy, we concluded that the IGM is predominantly neutral: the ionised fraction xH i = 0 (xH i< 0.03 at 3σ significance). We measured the effective Gunn-Peterson Lyα optical depth of the IGM at 5.02 <z< 5.84. Our well-constrained data points agree with earlier test with background QSOs, which showed that the IGM was increasingly neutral at z> 5.6 but still overwhelmingly ionised. However, the intrinsic scatter within the measurement is much larger than the errors on the individual data points, which most likely reflects that the reionisation is a complicated process with a strong spatial variation. A larger statistical sample is required to understand the IGM state at the end of reionisation.
Online material
Appendix A: Full absorption spectra
 |
Fig. A.1 Afterglow spectrum op GRB 130606A, starting from Lyα. The absorption lines are indicated with the ion that produces them and the rest wavelength. We use different colours for the various absorbers (see Sect. 3.5), as indicated in the legend; z = 5.9127 in red is the signature of the host galaxy. The error spectrum is shown in purple, the orange spectrum is the scaled atmospheric transmission spectrum. The spectrum continues in Fig. A.1. |
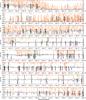 |
Fig. A.1 continued. |
This value results from our discussion in Section 4.2 where we take into account possible effects of ionisation and dust depletion. We assume that the estimated range −1.7 < [ M/H ] < −0.9 represents a 2σ confidence interval and that the metallicity is in the centre.
Larger ionization corrections for [Al/Fe] are supported by the calculations of Vladilo et al. (2001), with corrections potentially as large as ~1.4 dex. If we were to consider this (much larger) ionisation correction, we would still conclude that GRB 130606A exhibits an unusually large enhancement in [Al/Fe].
Acknowledgments
We thank the anonymous referee for careful inspection of the manuscript and constructive comments. We thank Max Pettini, Darach Watson, Georges Meynet, and Tomonori Totani for helpful discussions. We thank Andrea Rossi for careful reading of the manuscript. We thank Maryam Arabsalmani, who re-ran her code for us including our data point in Sect. 3.4.1. O.E.H. acknowledges the Dutch Research School for Astronomy (NOVA) for a Ph.D. grant. D.M. acknowledges the Instrument center for Danish Astrophysics (IDA) for funding. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007−2013)/ERC Grant agreement No. EGGS-278202 (J. P. U. F). T.K. acknowledges support by the European Commission under the Marie Curie Intra-European Fellowship Programme in FP7. The research of A.d.U.P. is supported by the Spanish project AYA2012-39362-C02-02 and by the European Commission under the Marie Curie Career Integration Grant programme (FP7-PEOPLE-2012-CIG 322307). The Dark Cosmology Centre is funded by the DNRF.
References
- Afonso, P., Kann, D. A., Nicuesa Guelbenzu, A., et al. 2013, GRB Coordinates Network, 14807 [Google Scholar]
- Andersen, M. I., Hjorth, J., Pedersen, H., et al. 2000, A&A, 364, L54 [NASA ADS] [Google Scholar]
- Arabsalmani, M., Møller, P., Fynbo, J. P. U., et al. 2015, MNRAS, 446, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Baumgartner, W. H., Cummings, J. R., et al. 2013, GRB Coordinates Network, 14819 [Google Scholar]
- Berger, E., Chary, R., Cowie, L. L., et al. 2007, ApJ, 665, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, N., Watson, A. M., Kutyrev, A., et al. 2013, GRB Coordinates Network, 14799 [Google Scholar]
- Castro-Tirado, A. J., Sánchez-Ramírez, R., Ellison, S. L., et al. 2013a, ArXiv e-prints [arXiv:1312.5631] [Google Scholar]
- Castro-Tirado, A. J., Sanchez-Ramirez, R., Gorosabel, J., et al. 2013b, GRB Coordinates Network, 14796 [Google Scholar]
- Cavallo, R. M., Sweigart, A. V., & Bell, R. A. 1998, ApJ, 492, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-W., Perley, D. A., Pollack, L. K., et al. 2009, ApJ, 691, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Chornock, R., Berger, E., Fox, D. B., et al. 2013, ApJ, 774, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Møller, P., Fynbo, J. P. U., & Zafar, T. 2014, MNRAS, 445, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardi, B., & Loeb, A. 2000, ApJ, 540, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Cordero, M. J., Pilachowski, C. A., Johnson, C. I., et al. 2014, ApJ, 780, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchiara, A., Fumagalli, M., Rafelski, M., et al. 2015, ApJ, 804, 51 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A., Ledoux, C., Fox, A. J., et al. 2012, A&A, 545, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Ledoux, C., Savaglio, S., Schady, P., & Vreeswijk, P. M. 2013, A&A, 560, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Elia, V., Fynbo, J. P. U., Goldoni, P., et al. 2014, A&A, 564, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & Hartwick, F. D. A. 2014, MNRAS, 437, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dessauges-Zavadsky, M., Péroux, C., Kim, T.-S., D’Odorico, S., & McMahon, R. G. 2003, MNRAS, 345, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, E. W. 1999, AJ, 118, 1882 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, A. J., Petitjean, P., Ledoux, C., & Srianand, R. 2007, A&A, 465, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, A. J., Ledoux, C., Vreeswijk, P. M., Smette, A., & Jaunsen, A. O. 2008, A&A, 491, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruchter, A. S., Levan, A. J., Strolger, L., et al. 2006, Nature, 441, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M. 2002, ARA&A, 40, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P. 2011, Astron. Nachr., 332, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Utsumi, Y., Hattori, T., Miyazaki, S., & Yamauchi, C. 2011, MNRAS, 415, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greiner, J., Krühler, T., Fynbo, J. P. U., et al. 2009, ApJ, 693, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Hartoog, O. E., Wiersema, K., Vreeswijk, P. M., et al. 2013, MNRAS, 430, 2739 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Sung, H.-I., & Urata, Y. 2013, GRB Coordinates Network, 14800 [Google Scholar]
- Jelinek, M., Gorosabel, J., Castro-Tirado, A. J., et al. 2013, GRB Coordinates Network, 14782, 1 [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Kawai, N., Kosugi, G., Aoki, K., et al. 2006, Nature, 440, 184 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kraft, R. P., Sneden, C., Smith, G. H., et al. 1997, AJ, 113, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Greiner, J., Schady, P., et al. 2011, A&A, 534, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, D. Q., & Reichart, D. E. 2000, ApJ, 536, 1 [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Littlejohns, O. M., Butler, N. R., Cucchiara, A., et al. 2014, AJ, 148, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein, 44 [Google Scholar]
- Lunnan, R., Drout, M., Chornock, R., & Berger, E. 2013, GRB Coordinates Network, 14798 [Google Scholar]
- Meiring, J. D., Lauroesch, J. T., Kulkarni, V. P., et al. 2009, MNRAS, 397, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J. 1998, ApJ, 501, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P., Fynbo, J. P. U., Ledoux, C., & Nilsson, K. K. 2013, MNRAS, 430, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D., Bird, A., Canzian, B., et al. 1998, VizieR Online Data Catalog: I/252 [Google Scholar]
- Morgan, A. N. 2013, GRB Coordinates Network, 14802 [Google Scholar]
- Nagayama, T. 2013a, GRB Coordinates Network, 14794 [Google Scholar]
- Nagayama, T. 2013b, GRB Coordinates Network, 14784 [Google Scholar]
- Neeleman, M., Wolfe, A. M., Prochaska, J. X., & Rafelski, M. 2013, ApJ, 769, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S. P., & Furlanetto, S. R. 2005, ApJ, 620, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Mobasher, B., et al. 2012, ApJ, 744, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, J. P., Beardmore, A. P., Evans, P. A., & Goad, M. R. 2013, GRB Coordinates Network, 14811 [Google Scholar]
- Overzier, R. A., Guo, Q., Kauffmann, G., et al. 2009, MNRAS, 394, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, M., Warren, S. J., Mortlock, D. J., & Fynbo, J. P. U. 2010, A&A, 512, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Vanzella, E., Fontana, A., et al. 2014, ApJ, 793, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, A. P., Gondhalekar, P. M., & Pettini, M. 1982, MNRAS, 200, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., & McMillan, S. L. W. 2004, Nature, 428, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Price, P. A., Songaila, A., Cowie, L. L., et al. 2007, ApJ, 663, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., & Wolfe, A. M. 1997, ApJ, 487, 73 [CrossRef] [Google Scholar]
- Prochaska, J. X., Henry, R. B. C., O’Meara, J. M., et al. 2002, PASP, 114, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Chen, H.-W., Dessauges-Zavadsky, M., & Bloom, J. S. 2007a, ApJ, 666, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Wolfe, A. M., Howk, J. C., et al. 2007b, ApJS, 171, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Dessauges-Zavadsky, M., Ramirez-Ruiz, E., & Chen, H.-W. 2008, ApJ, 685, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Wolfe, A. M., Prochaska, J. X., Neeleman, M., & Mendez, A. J. 2012, ApJ, 755, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Neeleman, M., Fumagalli, M., Wolfe, A. M., & Prochaska, J. X. 2014, ApJ, 782, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Velasco, A. E., Swan, H., Troja, E., et al. 2007, ApJ, 669, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Della Valle, M., Campana, S., et al. 2009, Nature, 461, 1258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Salvaterra, R., Maio, U., Ciardi, B., & Campisi, M. A. 2013, MNRAS, 429, 2718 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Savaglio, S. 2001, in The Extragalactic Infrared Background and its Cosmological Implications, eds. M. Harwit, & M. G. Hauser, IAU Symp., 204, 307 [Google Scholar]
- Savaglio, S., Glazebrook, K., & Le Borgne, D. 2009, ApJ, 691, 182 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A. 2004, AJ, 127, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Hartoog, O. E., Krühler, T., et al. 2014, ApJ, 785, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2012, ApJ, 754, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., Fynbo, J. P. U., Goldoni, P., et al. 2013, MNRAS, 428, 3590 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Kawai, N., Kosugi, G., et al. 2006, PASJ, 58, 485 [NASA ADS] [Google Scholar]
- Totani, T., Aoki, K., Hattori, T., et al. 2014, PASJ, 66, 63 [NASA ADS] [Google Scholar]
- Ukwatta, T. N., Barthelmy, S. D., Gehrels, N., et al. 2013, GRB Coordinates Network, 14781 [Google Scholar]
- Utsumi, Y., Goto, T., Kashikawa, N., et al. 2010, ApJ, 721, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vladilo, G., Centurión, M., Bonifacio, P., & Howk, J. C. 2001, ApJ, 557, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Vreeswijk, P. M., Ellison, S. L., Ledoux, C., et al. 2004, A&A, 419, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vreeswijk, P. M., Ledoux, C., Smette, A., et al. 2007, A&A, 468, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vreeswijk, P. M., Ledoux, C., Raassen, A. J. J., et al. 2013, A&A, 549, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, F. Y., & Dai, Z. G. 2014, ApJS, 213, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F. Y., Bromm, V., Greif, T. H., et al. 2012, ApJ, 760, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D. 2011, A&A, 533, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijers, R. A. M. J., Bloom, J. S., Bagla, J. S., & Natarajan, P. 1998, MNRAS, 294, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Prochaska, J. X., & Gawiser, E. 2003, ApJ, 593, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Xu, D., Malesani, D., Schulze, S., et al. 2013a, GRB Coordinates Network, 14816 [Google Scholar]
- Xu, D., Malesani, D., Schulze, S., et al. 2013b, GRB Coordinates Network, 14783 [Google Scholar]
- Xu, Z., & Wei, D. 2009, Science in China G: Physics and Astronomy, 52, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., Watson, D., Fynbo, J. P. U., et al. 2011, A&A, 532, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Redshift and Doppler parameter of the velocity components fitted to the metal lines of low- and high-ionisation species and for the fit to the Lyα line.
All Figures
 |
Fig. 1 80′′ × 80′′ field around the position of GRB 130606A in the i band. The left panel shows a pre-explosion image from the Sloan Digital Sky Survey and the right panel our i band image obtained with the NOT 3.5 h after the burst. North is up and east is to the left. |
| In the text | |
 |
Fig. 2 Afterglow spectral energy distribution. The red spectrum is the X-Shooter spectrum, the filled circles on the left are the GROND photometric points (Afonso et al. 2013), and the data points on the right are the (binned) Swift/XRT points. The solid line is the synchrotron spectrum with interstellar absorption, while the dashed line shows the unabsorbed synchrotron spectrum with best fit β = 1.02. |
| In the text | |
 |
Fig. 3 Top panel: spectral region around the Lyα feature with our best fit to the red wing overplotted in red. The model consists of a fully ionised intergalactic medium and a column density in the GRB host of log NH i = 19.91 ± 0.02. The 1σ noise is plotted as a dotted line. Bottom panel: residuals from the fit, with the ± 1σ region marked with a dotted line. The skyline residual in the bottom of the Lyα line should not be interpreted as Lyα emission. |
| In the text | |
 |
Fig. 4 1, 2 and 3σ contours for a joint fit of the neutral hydrogen column density in the host galaxy, log NH i, and the neutral fraction of the intergalactic medium, xH i. The fit has been performed for three different normalising power-law SEDs: β = 0.96, β = 1.02 (best fit), and β = 1.08. The dot indicates the peak likelihood. |
| In the text | |
 |
Fig. 5 Voigt-profile fits to the host-galaxy metal lines. We label the intervening metal lines (see Sect. 3.5) that contaminate the host galaxy lines; their contribution to the observed profile is taken into account. In orange (light grey) we show an atmospheric transmission spectrum matching the observing conditions and spectral resolution of our observations, generated with ESO’s SkyCalc tool. Residuals such as those close to the Fe ii lines are due to subtracted telluric emission lines. |
| In the text | |
 |
Fig. 6 Results from Møller et al. (2013) with the high-redshift measurement of GRB 130606A included. [M/H]100 km s-1 is the metallicity expected for DLAs with ΔV = 100 km s-1, based on the overall mass-metallicity relation. The data of Møller et al. (2013; filled circles) favour a break in the evolution of the mass-metallicity relation at z ~ 2.6 (dashed line), which is also supported by our measurement of GRB 130606A (filled square). We assumed for this point ΔV = 90 km s-1 and [ M/H ] = −1.3 ± 0.2; see text. |
| In the text | |
 |
Fig. 7 Galactic warm disk depletion abundance pattern (solid line, Savage & Sembach 1996), in which Al is assumed to be depleted as strongly as Fe (Phillips et al. 1982), and depletion of O is assumed to be negligible (Jenkins 2009), fit to the observed pattern (diamonds) following Savaglio (2001). This fit yields DTM = 1.00 ± 0.01. Aluminium is not included in this fit. The limit on S is taken from Castro-Tirado et al. (2013a). |
| In the text | |
 |
Fig. 8 Lyα transmission in the spectrum of GRB 130606A (squares). Lyβ (diamonds) and Lyγ (crosses) measurements are converted to equivalent values at Lyα. The small black triangles, diamonds, and the grey squares are measurements based on quasars from Fan et al. (2006), Goto et al. (2011), and Songaila (2004), respectively. The solid line is the best power-law fit to the data at z< 5.5 by Fan et al. (2006, their Eq. (5)). The uncertainties of the QSO points are typically a factor of two. |
| In the text | |
 |
Fig. 9 Effective Gunn-Peterson Lyα optical depth of the IGM from the spectrum of GRB 130606A. The large squares, diamonds, and crosses are measurements with error estimates from Lyα, Lyβ, and Lyγ, respectively, the latter two converted to the Lyα optical depth. The small black triangles, diamonds, and the grey squares are measurements based on QSO spectra from Fan et al. (2006), Goto et al. (2011), and Songaila (2004), respectively. The uncertainties of the QSO points are typically a factor of two. The solid line is the best power-law fit to the data at z< 5.5 by Fan et al. (2006, their Eq. (5)). |
| In the text | |
 |
Fig. 10 Excerpt of the X-Shooter spectrum with the same model fit as shown in Fig. 3. The lower panel shows the residuals and deviations from the fit. The hatched region is range III in Totani et al. (2014), where their spectrum is inconsistent with a single DLA model. With our data, we can obtain a good fit with this model. The difference is most likely due to a different spectral index β, see Sect. 4.1. |
| In the text | |
 |
Fig. A.1 Afterglow spectrum op GRB 130606A, starting from Lyα. The absorption lines are indicated with the ion that produces them and the rest wavelength. We use different colours for the various absorbers (see Sect. 3.5), as indicated in the legend; z = 5.9127 in red is the signature of the host galaxy. The error spectrum is shown in purple, the orange spectrum is the scaled atmospheric transmission spectrum. The spectrum continues in Fig. A.1. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


