| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 7 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201525878 | |
| Published online | 01 July 2015 | |
A study of the past dynamics of comet 67P/Churyumov-Gerasimenko with fast Lyapunov indicators
1 Università degli Studi di Padova, Dipartimento di Matematica, via Trieste, 63 – 35121 Padova Italy
e-mail: guzzo@math.unipd.it
2 Université de Nice Sophia Antipolis, CNRS UMR 7293, Observatoire de la Côte d’Azur, Bv. de l’Observatoire, C.S. 34229, 06304 Nice Cedex 4, France
e-mail: elena.lega@oca.eu
Received: 12 February 2015
Accepted: 13 April 2015
Comet 67P/Churyumov-Gerasimenko is the target of the Rosetta mission. On the basis of backward numerical integrations of a large set of simulated comets whose initial conditions were obtained from small variations of the orbital parameters of comet 67P, and using the analysis of suitable chaos indicators, we detect the phase-space structure of the past close encounters of the comet with Jupiter. On the basis of these computations we find that the probability that the comet could have been injected into the inner solar system from distances larger than 100 AU from the Sun in the past 150 000 years is about 60 percent.
Key words: celestial mechanics / chaos / comets: individual: 67P/Churyumov-Gerasimenko
© ESO, 2015
1. Introduction
The past dynamics of comet 67P/Churyumov-Gerasimenko become rapidly uncertain for increasing time intervals because of the several close encounters it had with Jupiter: very small errors in the initial conditions, as well as in the parameters determining the force model, can be amplified at any close encounter with Jupiter or other planets. This behaviour is typical of the comets of the so-called Jupiter family (see e.g. Kazimirchak-Polonskaya 1967; 1976; Levison & Duncan 1994; 1997; Valsecchi & Manara 1997). Specifically, for comet 67P/Churyumov-Gerasimenko, a sequence of deep close encounters with Jupiter (the last deep one occurred in 1959, see Carusi et al. 1985; 1995; Belyaev et al. 1985) limits the precision of its orbit computation to few centuries (see Groussin et al. 2007; Królikowska 2003). This uncertainty is unfortunate, since a detailed knowledge of the long–term past dynamics of the comet would be a useful complement to some of the outcomes of the experiments of the Rosetta mission (see Altwegg et al. 2015; Sierks et al. 2015).
In this paper we perform an analysis of the dynamics of comet 67P with a technique developed in the last decade in the framework of hyperbolic dynamical systems (Froeschlé et al. 1997 and 2000; Guzzo et al. 2002; Guzzo & Lega 2013b), recently modified to analyse close encounters in the three-body problem approximation (Guzzo & Lega 2013a; 2014a,b; see also Lega et al. 2011). In this study we adapt the technique to study the close encounters of a real body with a planet using a model of the solar system compatible with the JPL DE431 ephemerides, which in particular takes into account the gravitational interactions with the planets and with the four most massive asteroids, general relativity, and the non–gravitational cometary forces predicted by the so-called standard model of cometary dynamics.
Though it is not possible to determine the precise orbit of an individual object performing multiple close encounters with a planet in a fixed time interval [0,T], we determine the phase-space structure of all the initial conditions whose orbits have close encounters in [0,T]. On suitably chosen sections of the phase-space, the structure of the close encounters appears as the ridges of a chaos indicator, precisely the fast Lyapunov indicator (Lega et al. 2011; Guzzo & Lega 2013a), modified by filtering the contributions due to any single close encounter (Guzzo & Lega 2014a). The skeleton of this structure is represented by the collision manifold, which is the set of initial conditions whose orbits have a collision with the barycentre of the planet in [0,T]. Since we do not know the initial conditions of the comet with infinite precision, we do not know its exact location relative to the structure of close encounters, but we have hints about all the typical dynamics that are compatible with the uncertainties in the orbital determination. Profiting from the knowledge of the collision manifolds, these typical dynamics can be analysed with statistical purposes by changing the initial conditions only on a one-dimensional direction transverse to the collision manifold, rather than through the six-dimensional confidence ellipsoid, with considerable saving of CPU time: a sampling of N initial conditions with our method corresponds to a sampling of N6 initial conditions in the six-dimensional space of initial positions and velocities of the comet. Moreover, the topological coherence of the detected structures provides an indication of good control of round-off approximations. Our analysis can be performed on any Jupiter family comet; we treat the 67P/Churyumov-Gerasimenko as a case study, since as an outcome of the Rosetta mission we have a particularly good determination of the orbital parameters and of the parameters A1,A2,A3 entering the definition of the standard model of cometary dynamics. Our results, reported in Sect. 3, are specific to comet 67P, and cannot be exported to other Jupiter family comets without specific analysis.
For 67P/Churyumov Gerasimenko, we find in particular that within the uncertainties for the initial conditions provided by the JPL ephemerides system, the comet could have visited in the past150 000 years regions that are more than 50 AU from the Sun with a probability1 of 72 per cent (and regions more than 100 AU from the Sun with a probability of 60 per cent), before being injected in the inner solar system, and could have passed under the Jupiter Roche limit with a probability of about 4 per cent. Do these results indicate a certain dynamical origin for the comet? We return to this delicate question in the Conclusion.
The paper is organized as follows. In Sect. 2 we describe the fast Lyapunov indicator method for the computation of the structure of close encounters; in Sect. 3 we report theresults obtained for comet 67P/Churyumov-Gerasimenko; in Sect. 4 we provide conclusions.
2. The fast Laypunov indicator analysis of close encounters
We refer to the dynamics of comet 67P as the dynamics obtained from the initial conditions provided by the JPL ephemerides system with a numerical integration of the force model described in Yeomans et al. (2004), Sect. 1.2, accounting for the gravitation of the planets from Mercury to Pluto; the most important post-Newtonian contributions from general relativity; the non-gravitational forces modelled by the standard-model of cometary dynamics (Marsden et al. 1973, with values of the parameters A1,A2,A3 provided by the JPL ephemerides system); and the gravitational interaction with four asteroids (Ceres, Pallas, Vesta, Hygea). The small–scale analysis that we consider is sensitive to all these contributions in different extents; other effects, such as additional asteroidschosen among the most massive ones, have very little impact (see Sect. 3, Fig. 3), while the non-sphericity of the Sun does not seem to have any relevance;Jupiter’s satellites have been taken into account by integrating the barycentre of Jupiter’s system. Our analysis is based on the numerical integrations of the orbits of hundreds of thousands of simulated comets, whose initial conditions are obtained by slightly changing the initial conditions of comet 67P. We denote by ξ = (r,ṙ) = (x,y,z,ż,ẏ,ż) the vector of Cartesian components of the position r and velocity ṙ of a simulated comet in a heliocentric reference frame, and by 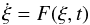 (1)the first-order differential equations defining the dynamics of the comet. For any initial condition ξ0 (the initial condition of the comet will be denoted by ξ∗) at a given reference epoch2, we numerically integrate backward Eq. (1) and its variation equations,
(1)the first-order differential equations defining the dynamics of the comet. For any initial condition ξ0 (the initial condition of the comet will be denoted by ξ∗) at a given reference epoch2, we numerically integrate backward Eq. (1) and its variation equations, ![\begin{equation} \dot w = \left [{\partial F\over \partial \xi}(\xi(t) ,t)\right]w \label{varfirseq} , \end{equation}](/articles/aa/full_html/2015/07/aa25878-15/aa25878-15-eq11.png) (2)with some initial conditions w(0) ∈ R6 (
(2)with some initial conditions w(0) ∈ R6 (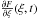 denotes the Jacobian matrix of F(ξ,t); and ξ(t) denotes the solution of (1) with initial conditions ξ(0) = ξ0). The growth of the norm of the tangent vector ∥w(t)∥ with time, where w(t) is the solution of the variational equations with initial conditions (ξ(0),w(0)) = (ξ0,w0), is a well-known method of characterizing the divergence of orbits with initial conditions very close to ξ0. Even if the traditional technique of computation of characteristic Lyapunov exponents, that is of quantities
denotes the Jacobian matrix of F(ξ,t); and ξ(t) denotes the solution of (1) with initial conditions ξ(0) = ξ0). The growth of the norm of the tangent vector ∥w(t)∥ with time, where w(t) is the solution of the variational equations with initial conditions (ξ(0),w(0)) = (ξ0,w0), is a well-known method of characterizing the divergence of orbits with initial conditions very close to ξ0. Even if the traditional technique of computation of characteristic Lyapunov exponents, that is of quantities 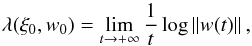 is not suitable for the case of close encounters (the equations are singular and orbits can escape from the solar system), all the simulated comets with initial conditions close to ξ∗ are characterized by some strong growth of ∥w(t)∥. The growth of tangent vectors due to close encounters has analogies with the growth of tangent vectors for initial conditions close to the stable and unstable manifolds of hyperbolic orbits (see Guzzo & Lega 2013a), a case which has been analysed in detail in Guzzo & Lega (2014a). In this analogy, the stable manifold is identified with the collision manifold, which is the set of initial conditions whose orbits have a collision with the barycentre of the planet in [0,T]. As a consequence, the distance of an initial condition from an initial condition on a collision orbit is well characterized by a dynamical indicator obtained from the fast Lyapunov indicator. In Guzzo & Lega (2014a) we modified the indicator with the introduction of a window function whose effect is that of filtering out all the contributions to the indicator that are not due to close encounters. Precisely, the fast Lyapunov indicator of ξ0 modified with a window function u(ξ) at time T is defined by (Guzzo & Lega 2014a,b)
is not suitable for the case of close encounters (the equations are singular and orbits can escape from the solar system), all the simulated comets with initial conditions close to ξ∗ are characterized by some strong growth of ∥w(t)∥. The growth of tangent vectors due to close encounters has analogies with the growth of tangent vectors for initial conditions close to the stable and unstable manifolds of hyperbolic orbits (see Guzzo & Lega 2013a), a case which has been analysed in detail in Guzzo & Lega (2014a). In this analogy, the stable manifold is identified with the collision manifold, which is the set of initial conditions whose orbits have a collision with the barycentre of the planet in [0,T]. As a consequence, the distance of an initial condition from an initial condition on a collision orbit is well characterized by a dynamical indicator obtained from the fast Lyapunov indicator. In Guzzo & Lega (2014a) we modified the indicator with the introduction of a window function whose effect is that of filtering out all the contributions to the indicator that are not due to close encounters. Precisely, the fast Lyapunov indicator of ξ0 modified with a window function u(ξ) at time T is defined by (Guzzo & Lega 2014a,b) 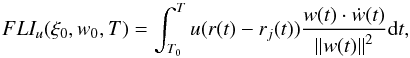 (3)where ξ(t) and w(t) are the solutions of Eqs. (1) and (2) with initial conditions (ξ(0),w(0)) = (ξ0,w0), and rj(t) denotes the orbit of the jth planet, which is Jupiter for Jupiter-family comets. A suitable choice for u (see Guzzo & Lega 2014a), obtained from the so-called Hanning window, is
(3)where ξ(t) and w(t) are the solutions of Eqs. (1) and (2) with initial conditions (ξ(0),w(0)) = (ξ0,w0), and rj(t) denotes the orbit of the jth planet, which is Jupiter for Jupiter-family comets. A suitable choice for u (see Guzzo & Lega 2014a), obtained from the so-called Hanning window, is ![\begin{equation} u(r)=\left \lbrace \begin{array}{lcl} &1&\ {\rm if}\ \ \norm{r}\leq \dfrac{\rho}{2} \\ & \dfrac{1}{2} \left[\cos \left(\left(\dfrac{\norm{r}}{\rho}-\dfrac{1}{2}\right)\pi \right)+1\right] & {\rm if}\ \ \dfrac{\rho}{2} < \norm{r}\leq \dfrac{3\rho}{2}\\ &0& \ {\rm if}\ \ \norm{r}> \dfrac{3\rho}{2}, \end{array}\right. \label{uzgamma} \end{equation}](/articles/aa/full_html/2015/07/aa25878-15/aa25878-15-eq27.png) (4)where ρ is a parameter that will be chosen of the same order as the Hill radius. The fast Lyapunov indicator defined in (3), hereafter simply denoted by FLI, measures the chaotic effects on an orbit due to the close encounters with Jupiter in the time interval [T0,T]. By computing the FLI on two-dimensional surfaces of different initial conditions the collision manifold appears as the ridges of the indicator: the initial conditions close to the top of a ridge have close encounters that give rise to significant divergence of their nearby orbits. Moreover, since the FLI rapidly decreases by increasing the distance from the top of the ridge (see Guzzo & Lega 2014a), the collision manifold is sharply identified and the distribution of FLI values provides the topological structure of close encounters. We note that a property of the ridge structures of close encounters is its stability with respect to small variations of the force model, while the individual orbits are not. Actually, even if a small change in the force model can produce a big change to an orbit with initial conditions ξ0, the ridges will be only slightly moved. In fact, the dynamics of ξ0 in the former force model is found for a different close initial condition in the latter force model (see Sect. 3 for examples).
(4)where ρ is a parameter that will be chosen of the same order as the Hill radius. The fast Lyapunov indicator defined in (3), hereafter simply denoted by FLI, measures the chaotic effects on an orbit due to the close encounters with Jupiter in the time interval [T0,T]. By computing the FLI on two-dimensional surfaces of different initial conditions the collision manifold appears as the ridges of the indicator: the initial conditions close to the top of a ridge have close encounters that give rise to significant divergence of their nearby orbits. Moreover, since the FLI rapidly decreases by increasing the distance from the top of the ridge (see Guzzo & Lega 2014a), the collision manifold is sharply identified and the distribution of FLI values provides the topological structure of close encounters. We note that a property of the ridge structures of close encounters is its stability with respect to small variations of the force model, while the individual orbits are not. Actually, even if a small change in the force model can produce a big change to an orbit with initial conditions ξ0, the ridges will be only slightly moved. In fact, the dynamics of ξ0 in the former force model is found for a different close initial condition in the latter force model (see Sect. 3 for examples).
 |
Fig. 1 Representation of the FLI (3) computed a grid of 500 × 500 initial conditions regularly spaced on (ẋ,ż) (the axes in the picture represent (ẋ0−ẋ∗,ż0−ż∗); the other initial conditions are x0 = x∗,y0 = y∗,z0 = z∗,ẏ0 = ẏ∗), computed for |T| = 300 yrs (top panels) and |T| = 500 yrs (bottom panels); the left panels are a zoom-in of the right ones. The FLI is reported using a colour scale, such that the highest FLI values are shown in yellow. In this way, the yellow curves in the picture correspond to the ridges of the FLI indicator, and pinpoint the set of initial conditions whose orbits have had past close encounters with Jupiter, in addition to the deep close encounter of 1959. |
 |
Fig. 2 Zooming in on selected ridges of the FLI. In the left panel, we select a faint ridge to zoom in on, marked with an asterisk. Since the ridges are almost parallel to the ẋ axis, we can suitably represent their one-dimensional section by computing again the FLI on many more initial conditions close to the ridge, but having the same value of ẋ. The result of the one-dimensional FLI computation is represented in the right panel: zooming in on the ridge we better detect its amplitude, and initial conditions having deeper encounters. The integration time is |T| = 400 yrs. |
3. Results
FLI detection of the collision manifold. We obtain sharp representations of the structure of close encounters by computing the FLI for refined grids of initial conditions in the two-dimensional surface of the space of the Cartesian coordinates and velocities, 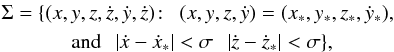 (5)where (x∗,y∗,z∗,ẋ∗,ẏ∗,ż∗) is the initial condition of comet 67P provided by the JPL Horizon ephemerides system, and σ = σ1 = 10-6 or σ = σ2 = 10-7 AU/day. The values of σ1 and σ2 have been chosen according to the errors on the determination of the initial conditions, and according to the stability of the detected structures with respect to small changes of the force model. The FLI (3) is computed using the same initial tangent vector w(0); the numerical integration of the variational equations is performed with negative time steps from the initial epoch of November 14, 2014, here identified by t = 0, while T0 is set just prior to the deep close encounter of 1959 (which is experienced by all the initial conditions that we consider), and different values of T<T0. Then, the FLI is represented using a colour scale, providing in this way snapshots of the structure of the close encounters occurring in the time interval [T,T0]. The results of the FLI computations are represented in Fig. 1. Since in Fig. 1 the yellow colour represents the higher values of the FLI, the top of the ridges of the FLI appear as yellow curves3, with many typical lobes visible on the zoomed-out picture obtained for σ = 10-6. All these curves pinpoint the set of initial conditions whose orbits have had past close encounters with Jupiter in addition to the deep close encounter of 1959. By increasing |T|, ridges corresponding to other close encounters appear in the pictures: since the ridges do not intersect, it is easy to understand how the ridges are expected to densely fill the picture by increasing the time |T| further.
(5)where (x∗,y∗,z∗,ẋ∗,ẏ∗,ż∗) is the initial condition of comet 67P provided by the JPL Horizon ephemerides system, and σ = σ1 = 10-6 or σ = σ2 = 10-7 AU/day. The values of σ1 and σ2 have been chosen according to the errors on the determination of the initial conditions, and according to the stability of the detected structures with respect to small changes of the force model. The FLI (3) is computed using the same initial tangent vector w(0); the numerical integration of the variational equations is performed with negative time steps from the initial epoch of November 14, 2014, here identified by t = 0, while T0 is set just prior to the deep close encounter of 1959 (which is experienced by all the initial conditions that we consider), and different values of T<T0. Then, the FLI is represented using a colour scale, providing in this way snapshots of the structure of the close encounters occurring in the time interval [T,T0]. The results of the FLI computations are represented in Fig. 1. Since in Fig. 1 the yellow colour represents the higher values of the FLI, the top of the ridges of the FLI appear as yellow curves3, with many typical lobes visible on the zoomed-out picture obtained for σ = 10-6. All these curves pinpoint the set of initial conditions whose orbits have had past close encounters with Jupiter in addition to the deep close encounter of 1959. By increasing |T|, ridges corresponding to other close encounters appear in the pictures: since the ridges do not intersect, it is easy to understand how the ridges are expected to densely fill the picture by increasing the time |T| further.
Within a ridge, the depth of all these encounters is related to the FLI value: to detect the orbits with deeper and deeper close encounters one needs to zoom in on the ridge (see Fig. 2). The ridges detected in Fig. 1 remain stable even when there are small changes of the model, even if the individual orbits are not. This is shown in Fig. 3, where we compare the detection of the ridge structures and the individual orbits of simulated comets computed with two different force models: model (A), corresponding to the force model described in Sect. 1, which also includes the four most massive asteroids, and model (B) corresponding to model (A) with seven additional asteroids (Euphrosyne, Eunomia, Davida, Interamnia, Cybele, Juno, and Psyche). In the top panels we represent the value of the FLI computed for many initial conditions with |T| = 400 yrs, by numerically integrating model (A) of the solar system (black line), and model (B) (blue line). All the initial conditions have x0 = x∗,y0 = y∗,z0 = z∗, ẋ0 = ẋ∗,ẏ0 = ẏ∗, and |ż0−ż∗| ≤ 10-7 AU/day (top-left panel). The FLI profile represented in the top panels provides one-dimensional sections of the ridges represented in Fig. 1, left panels. From the top-left panel in Fig. 3 we can see that the FLI profile of the black and blue curves are very similar, and to appreciate the differences we need to represent a zoom-in (top-right panel). In the zoom-in, we clearly see that for both models a peak of the FLI is detected, and the effect of the seven additional asteroids moves the peak by only 50 centimeters/day. The computation of the ridges is very stable with respect to the small perturbation due to the seven additional asteroids, even if individual orbits are not: from the bottom panels we note that two sample orbits obtained from the same initial conditions, but integrated with the two models, are well separated at 450 years ago. A similar phenomenon has been found in Milani et al. (2009).
 |
Fig. 3 Effects of the small variations of the force model to the ridge structure of close encounters and to individual orbits. In the top panels we represent the value of the FLI computed for many initial conditions with |T| = 400 yrs by numerically integrating the model of the solar system including the four most massive asteroids (model (A), black line), and another model including seven additional asteroids (model (B), blue line). All the initial conditions have x0 = x∗,y0 = y∗,z0 = z∗, ẋ0 = ẋ∗,ẏ0 = ẏ∗, and different ż0 ~ ż∗. From the top-left panel we can see that the FLI profiles obtained with both models (A) and (B) are very similar, and to appreciate the differences we represent a sample zoom-in in the top-right panel. We clearly appreciate that for both models a peak of the FLI is detected, and the effect of the additional asteroids moves the peak by only 50 centimeters/day. In the bottom panels we represent instead the effect of the additional asteroids on the orbit with initial conditions corresponding to the top of the left-peak (marked with an arrow). In the bottom-left panel the FLI evolution for a time interval ranging from 0 to 450 years ago is represented: the impulsive variations of the FLI occur at the close encounters: the very small difference between the two models changes the time of some close encounters, and this is amplified at the other close encounters. The close encounter occurring at 400 yrs ago determines the strong divergence of the two orbits, whose projection on the x-y plane is represented in the bottom-right panel. Up to 400 years the two orbits are almost identical, but between 400 and 450 years ago the two orbits are well separated. |
 |
Fig. 4 Representation of the maximum distance from the Sun reached in the interval [T,T0] by orbits with initial conditions on a grid of 500 × 500 initial conditions regularly spaced on (ẋ,ż) (the axes in the picture represent (ẋ0−ẋ∗,ż0−ż∗); the other initial conditions are the same as comet 67P), for |T| = 500 yrs (top panels). The colour scale represents the maximum distance, so that yellow means distances larger than 20 AU (top-left panel) or 30 AU (top-right panel). The top-right panel is a zoom-in of the top-left panel. The curves in the pictures are clearly correlated to the ridges of the FLI (see Fig. 1); the topology detected in the zoomed-in picture indicates that we can continue the exploration by fixing the value of ẋ0 = ẋ∗: in the bottom panels we represent the maximum distance from the Sun reached in the interval [T,T0] by 10 000 orbits with all the initial conditions equal to ξ∗, except for ż0, and times T = 1000 (bottom-left panel) and T = 2000 (bottom–right panel). |
Cumulative dynamical effect of close encounters. We discuss here the cumulative effect on the dynamics due to the several close encounters of the comet with Jupiter. In particular, we consider the statistics of the passages of the comet below the so-called Roche limit (where the comet can disintegrate as a result of Jupiter’s tidal forces), and the measure of the past maximum distance from the Sun reached in some interval [T,T0].
First, we represent a maximum distance D for a large set of simulated comets with initial conditions in Σ, for |T| = 500 yrs (Fig. 4, top panels). The curves of the largest maximum distance are clearly correlated to the ridges of the FLI (compare with Fig. 1), but at first glance, the zoomed-out picture (top-left panels) seems to reveal that only a few initial conditions on a selected ridge reach distances larger than 15 AU (corresponding to orange in the picture). This impression is disproved by zooming in around the origin (Fig. 4, top-right panel): we understand thatthe top of one of the ridges is uniformly characterized by initial conditions with maximum distances larger than 15 AU. Therefore, on the one hand, to correctly detect the probability of finding orbits with large maximum distances we need to suitably zoom in on the ridges; on the other hand, to compute such probabilities we are allowed to consider a line transverse to the ridge. Near the initial condition ξ∗, this line can be obtained by fixing one additional initial condition, such as ẋ0 = ẋ∗, as we can appreciate from the top panels of Fig. 4. We note that the initial condition to be fixed depends on the local topology of the collision manifold: in other places of the phase-space, where the collision manifold is almost vertical with respect to the ẋ0 axis (see Fig. 4, top-left panel), the choice must be different.
In the bottom panels of Fig. 4 we represent the computation of the maximum distance D for 10 000 initial conditions, obtained from ξ∗ by changing only ż∗, for |T| = 1000 yrs and |T| = 2000 yrs (a cut-off distance of 100 AU has been also introduced; the integrations are not stopped even if the comet passes under the Roche limit). By increasing the integration time, we obtain a significant increase in the number of ridges characterized by a large value of D. Because of the sharp oscillations of D with respect to ż0, only a statistical interpretation of these results is possible.In Fig. 5 we represent the statistics regarding the time evolution of D for a sample of N = 1000 simulated comets, whose initial conditions regularly spaced on ż0 in the interval |ż0−ż∗| ≤ 10-7 (the other initial conditions are the same as ξ∗). Given our knowledge of the collision manifold, our one-dimensional sampling of initial conditions is representative of a multi-dimensional sampling of N6 elements. Precisely, for any time |T| ranging from 0 to 150 000 yrs, we report the percentages of simulated comets whose maximum distance from the Sun has been smaller than 30 AU, between 30 and 50 AU, between 50 and 100 AU, and larger than 100 AU. We also report the percentage passed under Jupiter’s Roche limit. For Fig. 5, we note a large probability for the comet of having being injected in the inner solar system from large distances from the Sun: from distances larger than 100 AU from the Sun with a probability of60 per cent in the past150 000 years and, from distances larger than 50 AU from the Sun with a probability of72 per cent. Moreover, the comet could have passed under the Jupiter’s Roche limit with a probability ofabout 4 per cent in the same time interval.
Details on the numerical integrations. All the numerical integrations have been performed in double precision with an integrator which we specifically designed for this experiment. The comet and all the planets are integrated at the same time, with individual integration steps performed with a well known 6th-order Runge-Kutta integrator, but the step-size is adjusted within the code to treat close encounters as follows: if the comet is outside 3/2 Hill radii of any planet, all the bodies are integrated with a step-size τ0 of 2.4 h; if the comet is at a distance from a planet smaller than 3/2 Hill radii, the integration step-size τ is reduced so that in modulus it is the smallest between τ0/ 10,10-8d2/GM,10-5/ |ṙ|, where d denotes the distance between the comet and the closest planet and GM the product of the gravitation constant G and the mass of that planet.These thresholds have been chosen so that τGM/d2,τ|ṙ| are much smaller than the product between τ0 and the gravitational force acting on the comet in the unperturbed (without Jupiter) problem. The variational equations are integrated the same way. The results remain stable for further reductions of the time step:by reducing all the time steps by a factor of 10 on sample orbits, we do not notice differences in their orbits before and after deep close encounters.
 |
Fig. 5 Statistical evolution of the maximum distance from the Sun reached in the time interval [T,0],obtained by backward integrating a sample of simulated comets for 150 000 years. The initial epoch is identified by T = 0, the final one by T = −150 000 years. The sample of simulated comets is defined by 1000 initial conditions regularly spaced on ż0, with |ż0−ż∗| ≤ 10-7 (the other initial conditions are the same as ξ∗). At any given value of the time T, we represent the percentage ofsimulated comets whose maximum distance from the Sun in [T,0] is smaller than 30 AU, between 30 AU and 50 AU, between 50 and 100 AU, and larger than 100 AU. We also represent the percentage ofsimulated comets that passed under Jupiter’s Roche limit ( identified as collisions). |
4. Conclusions
The computation of the FLI indicator on a large number of initial conditions provides us with the knowledge of the collision manifold of the comet 67P/Churyumov-Grasimenko with Jupiter, and with the structure of the close encounters that determine divergence of the orbits. On the basis of these computations, we have been able to choose a direction that is transverse to the branches of the collision manifold. By computing the backward time evolution of many orbits with initial conditions along this direction, we obtained that a large fraction of them, corresponding to 60 per cent, have visited in the past 150 000 years regions of the solar system that are more than 100 AU from the Sun. Therefore, we find a strong dynamical link between these regions of the phase-space and the present values of orbital parameters of the comet. Does this indicate a certain dynamical origin of the comet? The answer could be quite complex, as the paradigmatic case of comet Encke suggests (see Valsecchi et al. 1995; Levison at al. 2006). The first aspect to consider is the intimate nature of statistics, which is valid for the many simulated comets with orbital parameters very close to those of 67P, but does not apply to the single real object. The second aspect to consider concerns backward integrations of systems with dissipation. It is well known that strongly dissipative systems cannot always be integrated backward, for example to reconstruct captures into attractors, but this seems not to be the case of comet 67P since dissipation is weak and acting mainly close to the perycentre; in any case, this point should be developed further. The third aspect concerns astronomical considerations since it is generally accepted that the probability of a comet transiting from the Oort cloud to the Jupiter family (with forward integrations) is very small. For all these reasons, we think that our results could be used to understand the origin of the comet only in the presence of additional knowledge, independent from dynamics.
Acknowledgments
We thank G.B. Valsecchi for a preliminary reading of our manuscript, and for a long discussion about the origin of comets. M. Guzzo has been supported by the Italian project PRIN “Teorie geometriche e analitiche dei sistemi Hamiltoniani in dimensioni finite e infinite”, and by the project CPDA149421/14 of University of Padova “New Asymptotic Aspects of Hamiltonian Perturbation Theory”. The numerical computations were done on the “Mesocentre SIGAMM” machine, hosted by the Observatoire de la Cote d’Azur.
References
- Altwegg, K., Balsiger, H., Bar-Num, A., et al. 2015, Science, 347, 6220 [CrossRef] [Google Scholar]
- Belyaev, N. A., Kresák, L., Pittich, E. M., & Pushkarev, A. N. 1985, Catalogue of Short-Period Comets (Bratislava: Veda) [Google Scholar]
- Carusi, A., Kresák, L., Perozzi, E., & Valsecchi, G. B. 1985, Long-Term Evolution of Short-Period Comets (Bristrol & Boston, Adam Hilger Ltd) [Google Scholar]
- Carusi, A., Kresák, L., & Valsecchi, G. B. 1995, Atlas of Dynamical Evolutions of Short–Period Comets, Formerly available at http://www.ias.rm.cnr.it/ias-home/comet/catalog.html [Google Scholar]
- Froeschlé, Cl., Lega, E., & Gonczi, R. 1997, Celest. Mech. Dynam. Astron., 67, 41 [CrossRef] [Google Scholar]
- Froeschlé, Cl., Guzzo, M., & Lega, E. 2000, Science, 289, 2108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Groussin, O., Hahn, G., Lamy, P. L., Gonczi, R., & Valsecchi, G. B. 2007, MNRAS, 376, 1399 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, M., & Lega, E. 2013a, MNRAS, 428, 2688 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, M., & Lega, E. 2013b, Chaos 23, 023124 [Google Scholar]
- Guzzo, M., & Lega, E. 2014a, SIAM J. Appl. Math., 74, 1086 [Google Scholar]
- Guzzo, M., & Lega, E. 2014b, Computation of transit orbits in the three-body-problem by Fast Lyapunov Indicators, Proc. of the XVII Ncas, Belgrade, in press [Google Scholar]
- Guzzo, M., Lega, E., & Froeschlé, C. 2002, Physica D, 163, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haller, G. 2014, Ann. Rev. Fluid. Mech., 47, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kazimirchak-Polonskaya, E. I. 1967, Sov. Astron., 11, 349 [NASA ADS] [Google Scholar]
- Kazimirchak-Polonskaya, E. I. 1976, in NASA, Goddard Space Flight Center The Study of Comets, NASA ADS Part 1, 490 [Google Scholar]
- Królikowska, M. 2003, Acta Astron., 53, 195 [NASA ADS] [Google Scholar]
- Lega, E., Guzzo, M., & Froeschlé, C. 2011, MNRAS, 418, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 1, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [Google Scholar]
- Levison, H. F., Terrell, D., Wiegert, P. A., Dones, L., & Duncan, M. J. 2006, Icarus 182, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Chesley, S. R., & Sansaturio, M. E., et al. 2009, Icarus, 203, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Shadden, S. C., Lekien, F., & Marsden, J. E. 2005, Physica D, 212, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lawy, P.L., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Valsecchi, G. B., & Manara, A. 1997, A&A 323, 986 [NASA ADS] [Google Scholar]
- Valsecchi, G. B., Morbidelli, A., Gonczi, R., et al. 1995, Icarus, 118, 1, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Yeomans, D. K., Chodas, P. W., Sitarski, G., Szutowicz, S., & Królikowska, M. 2004, Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 745, 137 [Google Scholar]
All Figures
 |
Fig. 1 Representation of the FLI (3) computed a grid of 500 × 500 initial conditions regularly spaced on (ẋ,ż) (the axes in the picture represent (ẋ0−ẋ∗,ż0−ż∗); the other initial conditions are x0 = x∗,y0 = y∗,z0 = z∗,ẏ0 = ẏ∗), computed for |T| = 300 yrs (top panels) and |T| = 500 yrs (bottom panels); the left panels are a zoom-in of the right ones. The FLI is reported using a colour scale, such that the highest FLI values are shown in yellow. In this way, the yellow curves in the picture correspond to the ridges of the FLI indicator, and pinpoint the set of initial conditions whose orbits have had past close encounters with Jupiter, in addition to the deep close encounter of 1959. |
| In the text | |
 |
Fig. 2 Zooming in on selected ridges of the FLI. In the left panel, we select a faint ridge to zoom in on, marked with an asterisk. Since the ridges are almost parallel to the ẋ axis, we can suitably represent their one-dimensional section by computing again the FLI on many more initial conditions close to the ridge, but having the same value of ẋ. The result of the one-dimensional FLI computation is represented in the right panel: zooming in on the ridge we better detect its amplitude, and initial conditions having deeper encounters. The integration time is |T| = 400 yrs. |
| In the text | |
 |
Fig. 3 Effects of the small variations of the force model to the ridge structure of close encounters and to individual orbits. In the top panels we represent the value of the FLI computed for many initial conditions with |T| = 400 yrs by numerically integrating the model of the solar system including the four most massive asteroids (model (A), black line), and another model including seven additional asteroids (model (B), blue line). All the initial conditions have x0 = x∗,y0 = y∗,z0 = z∗, ẋ0 = ẋ∗,ẏ0 = ẏ∗, and different ż0 ~ ż∗. From the top-left panel we can see that the FLI profiles obtained with both models (A) and (B) are very similar, and to appreciate the differences we represent a sample zoom-in in the top-right panel. We clearly appreciate that for both models a peak of the FLI is detected, and the effect of the additional asteroids moves the peak by only 50 centimeters/day. In the bottom panels we represent instead the effect of the additional asteroids on the orbit with initial conditions corresponding to the top of the left-peak (marked with an arrow). In the bottom-left panel the FLI evolution for a time interval ranging from 0 to 450 years ago is represented: the impulsive variations of the FLI occur at the close encounters: the very small difference between the two models changes the time of some close encounters, and this is amplified at the other close encounters. The close encounter occurring at 400 yrs ago determines the strong divergence of the two orbits, whose projection on the x-y plane is represented in the bottom-right panel. Up to 400 years the two orbits are almost identical, but between 400 and 450 years ago the two orbits are well separated. |
| In the text | |
 |
Fig. 4 Representation of the maximum distance from the Sun reached in the interval [T,T0] by orbits with initial conditions on a grid of 500 × 500 initial conditions regularly spaced on (ẋ,ż) (the axes in the picture represent (ẋ0−ẋ∗,ż0−ż∗); the other initial conditions are the same as comet 67P), for |T| = 500 yrs (top panels). The colour scale represents the maximum distance, so that yellow means distances larger than 20 AU (top-left panel) or 30 AU (top-right panel). The top-right panel is a zoom-in of the top-left panel. The curves in the pictures are clearly correlated to the ridges of the FLI (see Fig. 1); the topology detected in the zoomed-in picture indicates that we can continue the exploration by fixing the value of ẋ0 = ẋ∗: in the bottom panels we represent the maximum distance from the Sun reached in the interval [T,T0] by 10 000 orbits with all the initial conditions equal to ξ∗, except for ż0, and times T = 1000 (bottom-left panel) and T = 2000 (bottom–right panel). |
| In the text | |
 |
Fig. 5 Statistical evolution of the maximum distance from the Sun reached in the time interval [T,0],obtained by backward integrating a sample of simulated comets for 150 000 years. The initial epoch is identified by T = 0, the final one by T = −150 000 years. The sample of simulated comets is defined by 1000 initial conditions regularly spaced on ż0, with |ż0−ż∗| ≤ 10-7 (the other initial conditions are the same as ξ∗). At any given value of the time T, we represent the percentage ofsimulated comets whose maximum distance from the Sun in [T,0] is smaller than 30 AU, between 30 AU and 50 AU, between 50 and 100 AU, and larger than 100 AU. We also represent the percentage ofsimulated comets that passed under Jupiter’s Roche limit ( identified as collisions). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


