| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526176 | |
| Published online | 04 June 2015 | |
Mass of WASP-33b⋆
1 Thüringer Landessternwarte Tautenburg, 07778 Tautenburg, Germany
e-mail: lehm@tls-tautenburg.de
2 National Astronomical Research Institute of Thailand, 191 Huay Kaew Road, Muang, 50200 Chiangmai, Thailand
Received: 24 March 2015
Accepted: 16 April 2015
We analysed an extended time series of high-resolution spectra of the δ Sct star WASP-33 with the aim to determine the effect of its planet WASP-33b. We found ten frequencies in the measured radial velocities. Three of them we can attribute to previously observed photometric oscillations due to non-radial pulsations. One frequency exactly agrees with the orbital period of the planet. The semi-amplitude of the corresponding variation is 304 ± 20 m s-1. This finding allows us to give a new estimate of the mass of WASP-33b of 2.1 ± 0.2 Jupiter masses. Its mean density probably is at least 0.6 g cm-3, a value that can be expected for a planet of its mass that orbits an A-type star in 1.22 d.
Key words: planets and satellites: fundamental parameters / planets and satellites: gaseous planets / planetary systems / stars: variables: δScuti
Table 3 is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Up to now, most surveys of extrasolar planets have concentrated on stars of solar-type or later. Our knowledge of the properties of planets of stars more massive than the Sun is limited. Studying such objects would help us to better understand the formation and evolution of planets. An important prediction of planet formation models is that more massive stars have a higher frequency of massive planets. Studies of giant stars apparently confirm these results (Johnson et al. 2010, 2013; Lloyd 2011; Schlaufman & Winn 2013). However, models also predict that close-in planets of massive stars are rare because the life-time of the disks of such stars could be too short for the planets to migrate inwards (e.g. Currie 2009; Alibert et al. 2011). The observation of close-in planets of A-type stars thus constrains the speed with which planets migrate. Another interesting aspect is that A-stars are much brighter than solar-like stars and exhibit stronger winds (Babel 1995; Simon et al. 2002). The investigation of close-in planets also constrains models of the evaporation and inflation of planets (Ehrenreich & Désert 2011), and they are important for testing the mass-radius relation of the exoplanets (e.g. Batygin et al. 2011; Enoch et al. 2012).
For all these studies the radii and masses of close-in planets of A-stars are needed, which can be best measured for transiting planets. Up to now, we know of only 16 planets that orbit stars of more than 1.5 M⊙ and have an orbital period shorter than ten days. Apart from WASP-33 (=HD 15082) and Kepler-13b (Shporer et al. 2011), all these planets are orbiting F-stars, or even sub-giants, not A-stars. Unfortunately, Kepler-13b is a triple star, and it is not known which of its components hosts the planet. Thus, WASP-33b is the only known transiting planet of an A-star for which we can determine the mass and radius in order to determine whether close-in planets of A-stars have particularly low densities or not.
WASP-33 is a fast-rotating (vsini ≈ 90 km s-1) δ Scuti star of spectral type A5 that shows non-radial p-mode oscillations with a photometric semi-amplitude of about 0.1% (e.g. Herrero et al. 2011). It was discovered within the transit survey of the WASP project (Pollacco et al. 2006) by Christian et al. (2006) to show planet-like transits with a period of 1.22 d. WASP-33b, the first short-period planet of an A-type star, was finally confirmed by Collier Cameron et al. (2010, CC10 hereafter). CC10 derived from their combined photometric-spectroscopic analysis the mass and radius of the star to be 1.50 M⊙ and 1.44 R⊙, respectively, and the radius of the planet to be 1.50 RJ. For the mass of the planet, they derived an upper limit of 4.1 MJ. Sada et al. (2012) re-observed the transit in the z-band and improved the ephemeris. They derived a radius of the planet that agrees well with that given in CC10.
WASP-33b has a short orbital period of 1.219868 ± 0.00001 d (von Essen et al. 2014) and a separation of only 3.68 stellar radii, which makes it one of the hottest planets known. Its thermal emission was measured by several authors. Smith et al. (2011) detected the secondary transit photometrically at 0.91 μm with a depth of 0.109%, corresponding to a brightness temperature of 3600 K. Deming et al. (2012) detected the secondary eclipse at 2.15, 3.6, and 4.5 μm, using the 2.1 m telescope at Kitt Peak National Observatory and observations with (warm) Spitzer. Their measurements can be reproduced with a model atmosphere that is carbon-rich, non-inverted, and has a temperature of 3400 K at a level of one bar. The measurements also fit a model with solar composition that has an inverted temperature structure and a temperature of about 2700 K. Finally, de Mooij et al. (2013) derived a brightness temperature of 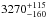 K from Ks-band observations using the LIRIS instrument on the William Herschel Telescope.
K from Ks-band observations using the LIRIS instrument on the William Herschel Telescope.
Recent investigations of WASP-33 were performed by Kovács et al. (2013, K13 hereafter) and von Essen et al. (2014, vE14 hereafter) , where vE14 included pulsation in their transit analysis. K13 presented 12 radial-velocity (RV) measurements from which they derived a mass of Mp = 3.18 ± 0.82 MJ. Here, we investigate the RVs of the star to determine the effect of the planet and to derive more precise estimates of its mass and density.
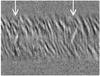 |
Fig. 1 Part of the time series of differential LSD profiles from the observations in 2013, horizontally arranged in a running order. The vertical axis spans ±150 km s-1. The RME was covered in two nights, which is indicated by the two white arrows. |
2. Observations
The time series of high-resolution spectra was observed in October and November 2013 (248 spectra) in the framework of a ground-based spectroscopic and photometric campaign organized around observations of WASP-33 with the MOST satellite (Walker et al. 2003) and later in January and February 2015 (39 spectra). All spectra were taken with the Coude-Echelle-spectrograph attached to the 2 m Alfred Jensch Telescope of the Thüringer Landessternwarte Tautenburg. They have a typical signal-to-noise ratio (S/N) of 90, a resolving power of 32 000, and cover the wavelength range 470 to 740 nm. The exposure time was 10 min. We used standard MIDAS routines for the spectrum reduction. This included bias-subtraction, flat-fielding, optimum extraction of the echelle orders, wavelength calibration using a ThAr lamp, corrections for instrumental shifts by using a larger number of telluric O2-lines, and normalisation to the local continuum.
3. Radial velocities
First, we used the least-squares deconvolution (LSD) technique (Donati et al. 1997) to compute LSD profiles from the observed spectra to determine the effect of pulsations on the line profiles. Figure 1 shows a part of the time series of differential LSD profiles after subtracting the mean profile. It illustrates the influence of multi-mode non-radial pulsations on the line profiles. The corresponding bumps run from the upper left to the lower right. The Rossiter-McLaughlin effect (Rossiter 1924, RME hereafter) can also be seen as the two short, bright streaks running from the lower left to the upper right.
The strong line profile variation (LPV) arising from high-degree l modes disturb the basically Gaussian-like LSD profiles. We decided to use the cross-correlation with a synthetic template spectrum that resembles the pulsationally undistorted spectrum of WASP-33 for determing the RVs1. The resulting cross-correlation functions (CCFs) can be very well fitted by Gaussians. The template was computed with SynthV (Tsymbal 1996), based on stellar parameters close to those given by CC10, that is, Teff = 7400 K, log g = 4.3, and [M/H] = 0.1. The CCFs were calculated on the wavelength interval 4895–5672 Å. The data set is very homogenous, and the error from fitting the CCFs by Gaussians gave an almost constant internal error of 65 m s-1.
4. Frequency search
For the analysis, we used the program Period04 (Lenz & Breger 2005). The periodogram of the measured RVs is dominated by the 1 d alias period (Fig. 2, top). The corresponding peak vanishes after subtracting a long-term frequency, f1, showing the highest peak below 1 c d-1 and resulting from the slight deviation between the mean values of the data groups. Next, we find f2 = 0.82 c d-1. Its 1 d alias at 1.82 c d-1 and some peaks at lower frequencies can also be seen (Fig. 2, second panel), most of them introduced by the window function of the data. These peaks vanish after subtracting f2 (Fig. 2, third panel). Applying the empirical S/N criterion by Breger et al. (1993), we continued the successive pre-whitening as long as the newly found frequency had a S/N> 4. The bottom panel of Fig. 2 shows the periodogram of the residuals. Table 1 lists the results. The errors were calculated from a Monte Carlo simulation based on 10 000 artificial data sets.
 |
Fig. 2 Periodograms (logarithmic plots) calculated with Period04. From top to bottom: original data, after subtracting the long-term trend, after also subtracting f2, and after subtracting all 10 frequencies. |
Results of the frequency search.
 |
Fig. 3 RVs from the spectra taken in 2013 (open circles) and 2015 (filled squares). a) Original RV data folded with f2; b) RVs after subtracting all frequency contributions but not f2, folded with f2; c) as b) but for f3, the solid lines show the best fitting orbital curve; d) as b) but for f1, the crosses represent phase-binned values. |
Frequency f2 corresponds to a period of 1.2197 ± 0.0003 d and agrees with the orbital period of the planet within 1σ. A crucial test for whether we really found the reflex motion of the star that is caused by the planet is a comparison of the phase of the calculated RV contribution with the photometric orbit of the star. We used the RVs cleaned of all frequencies but f2 to fit the orbit. The periods agree very well, we obtain 1.2199 ± 0.0006 d compared to 1.219868 ± 0.00001 derived by vE14. To compare the transit time, T0, we set the orbital period to the period known from photometry. The resulting T0 of 2 455 507.5218 ± 0.0002 agrees with the photometric value of 2 455 507.5222 ± 0.0003 to within 1σ.
From Fig. 3a we see that f2 can already be found in the raw RV data. Figure 3b shows the phase diagram calculated from our best-fit orbital solution together with the best-fitting orbital RV-curve. An over-plotted orbital curve based on the ephemeris given by vE14 cannot be distinguished from this best fit by eye. The semi-amplitude of the orbital RV curve follows to K = 304 ± 20 m s-1, the same value as obtained from the multi-frequency fit (Table 1). Frequencies f4 and f10 are close to those found by vE14 in the photometry of the star, also f9 if it is the 1 d alias of 34.1252 c d-1 found by these authors. Frequency f6 corresponds to the rotation period of WASP-33 of 0.84 d, as expected from the given radius and vsini of the star. The high S/N frequency f3 was not found by any of the photometric studies. We suspect that it is an alias period introduced by the time sampling of our data. The corresponding period of 0.72 d is approximately the mean daytime gap between consecutive nightly runs. This assumption is supported by the phase plot shown in Fig. 3c, where all spectra taken in 2013 are arranged in a straight line. From Fig. 3d we see that f1 and the related amplitude are very uncertain and do not allow for the determination of a dedicated long-term variation.
5. Mass and density of the planet
We used the spectroscopic mass function to derive the mass of the planet. Input parameters were the measured K-value, the very precisely known orbital period, the mass of the star, and the orbital inclination. From the calculated mass of the planet Mp and its radius Rp, we directly obtain its mean density.
Mass and radius of WASP-33 as well as the radius of the planet have been determined by three authors so far. Table 2 compares the masses and densities of the planet and its orbital separations following from their data and our new K-value. The given errors rely on the errors of Ms, K, P, i, and Rp and were computed according to the propagation of errors when calculating Mp, ρp, and a. The masses of the star and the inclinations of the orbit derived by the three authors agree well, and in all three cases we obtain a planet mass of 2.1 ± 0.2 MJ. The mean density of the planet is very sensitive to its derived radius. The values based on CC10 and S11 agree well, but K13 obtained a planet radius larger by about 10% and thus a distinctly lower density follows.
Mass, density, and orbital separation of WASP-33b based on our K-value and the data given by CC10, S11 (Smith et al. 2011), and K13.
6. Discussion
WASP-33b is the transiting planet orbiting one of the most massive stars known so far. Thus it is expected to be most affected by the heating, stellar wind, and tidal forces applied by its host star. In the following we compare the density of WASP-33b with that of other transiting exoplanets. We selected all transiting planets for which a full characterisation of the planet and its host star was available from the Extrasolar Planets Encyclopaedia2. From these, we furthermore selected the 152 planets with Mp> 0.1 and eccentricity <0.1.
Figure 4 shows the density versus the mass of the planets. A logarithmic, second-degree polynomial fit using 3σ-clipping gives the solid line. The positions of WASP-33 based on our newly determined mass (square) and the parameters given by CC10 and K13 (triangle) are indicated in the figure. For the comparison, we calculated the equilibrium temperatures Tp of all planets in a simplified way, using the equations given by Kane & Gelino (2011), approximating the luminosity of the host stars by the Stefan-Boltzmann law and assuming an albedo of 5% and bounded rotation, as is typical for the close-in planets for all of the planets. For WASP-33b we obtain Tp ≈ 3200 K in this way, which agrees well with the Tp derived by de Mooij et al. (2013) mentioned in the introduction.
 |
Fig. 4 Logarithmic plot of the density of transiting exoplanets versus their mass. The solid line results from a polynomial fit. The positions of WASP-33b according to CC10 (square) and K13 (triangle) are labelled. The cross indicates the typical error bars. |
Figure 5 shows the normalised deviation of the density from the fit shown in Fig. 4, q = ρ(M) /ρmean(M) –1, versus the calculated equilibrium temperature. It shows a general trend of the planets to have lower densities than typical for the corresponding mass for higher Tp, but the scatter for low-mass planets is very large. We looked for a density range where a clear trend can be seen and found that this is the case for planets with Mp> 1.4 MJ. We indicate these 46 planets in Fig. 5 with filled dots. The planetary and stellar parameters of this sample comprise P = 0.8–34 d, Mp = 1.4–27 MJ, Rs = 0.8–1.7 R⊙, Ms = 0.7–1.6 M⊙, Rs = 0.7–2.3 R⊙, and log g = 3.9–4.6. WASP-33b lies within the 1σ confidence range of the third-degree polynomial fit obtained for the higher-mass planets applying a 3σ clipping.
Unfortunately, we do not know the density-mass distribution of short-period, non-inflated planets so that we cannot discuss Figs. 4 or 5 in a quantitative way. There are only two planets in this mass range observed so far, PH1-Kepler-64b (Schwamb et al. 2013) and HAT-P-44c (Hartman et al. 2014), that have a separation of more than 0.5 AU. The first one is a circumbinary planet in a four-star system, and we do not know the radius of the second planet. Figure 5 shows, however, that WASP-33b fits well into the empirical density-temperature distribution of higher-mass transiting exoplanets.
7. Conclusions
The spectrum of WASP-33 shows strong LPV caused by multi-mode non-radial pulsations typical for a δ Sct star. The moving bumps that can be seen in the line profiles by eye complicate the RV and the spectrum analysis. In the first part of our investigation of a large set of observed spectra, we focused on the RVs. Their analysis revealed ten frequencies where two frequencies were previously found from light-curve analysis by several authors (Deming et al. 2012; K13; vE14), and one only by vE14. The frequency showing the largest amplitude agrees very well with the period of the planetary orbit. The analysis of its contribution to the RV variations showed that it perfectly fits the variation expected from the photometric orbital solution and confirms that we really found the effect of the planet in the RVs.
The results of the frequency search also show that it is possible to detect RV variations with amplitudes down to 120 m s-1, which is half of the mean scatter of the residuals in our case, from the spectra of an early-type, fast-rotating star if only the number of measurements is large enough. Moreover, in the case of large vsini and strong LPV, spectra providing undistorted line profiles are probably better suited for a precise RV measurement than spectra taken with an iodine cell.
The main result of the present investigation is the value of the RV semi-amplitude of the reflex motion of the star caused by its planet, K = 304 ± 20 m s-1. It allows us to calculate the mass and density of WASP-33b if precise values of the stellar mass and, in particular, the radius of the planet, are known. We determined a mass of 2.1 ± 0.1 MJ and densities of 0.64 or 0.88 g cm-3, based on the values derived by CC10 and K13,
respectively. Alternatively, taking the errors into account, we derived a range for the mean density of WASP-33b of between 0.6 and 1 g cm-3.
 |
Fig. 5 Deviation of the density from the mean value versus equilibrium temperature for planets with M< 1.4 MJ (open circles) and M> 1.4 MJ (filled circles). A polynomial fit and its 1σ confidence limits are shown by the solid and the dotted lines, respectively. |
Although WASP-33 is the hottest star to host a hot Jupiter and WASP-33b is peculiar in the amount of tidal distortion and radiation that it receives from its star, it fits the density-temperature distribution observed for other short-term exoplanets very well. Its density lies within the range that is typical for planets of its mass, separation, and spectral type of the host star.
In a next step, we plan to investigate the effect of pulsation on the WASP-33 spectra. We aim to derive more precise atmospheric parameters in this way and to perform an asteroseismic analysis of the star.
Online material
Barycentric Julian dates at mean exposure and the radial velocities determined from cross-correlation with a synthetic template.
References
- Alibert, Y., Mordasini, C., & Benz, W. 2011, A&A, 526, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babel, J. 1995, A&A, 301, 823 [Google Scholar]
- Batygin, K., Stevenson, D. J., & Bodenheimer, P. H. 2011, ApJ, 738, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Christian, D. J., Pollacco, D. L., Skillen, I., et al. 2006, MNRAS, 372, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Guenther, E., Smalley, B., et al. 2010, MNRAS, 407, 507 (CC10) [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T. 2009, ApJ, 694, L171 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2013, A&A, 550, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Fraine, J. D., Sada, P. V., et al. 2012, ApJ, 754, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ehrenreich, D., & Désert, J.-M. 2011, A&A, 529, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2014, AJ, 147, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Morales, J. C., Ribas, I., & Naves, R. 2011, A&A, 526, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Morton, T. D., & Wright, J. T. 2013, ApJ, 763, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, S. R., & Gelino, D. M. 2011, ApJ, 741, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Kovács, T., Hartman, J. D., et al. 2013, A&A, 553, A44 (K13) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Comm. Asteroseismol., 146, 53 [Google Scholar]
- Lloyd, J. P. 2011, ApJ, 739, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sada, P. V., Deming, D., Jennings, D. E., et al. 2012, PASP, 124, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Schlaufman, K. C., & Winn, J. N. 2013, ApJ, 772, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Schwamb, M. E., Orosz, J. A., Carter, J. A., et al. 2013, ApJ, 768, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., Jenkins, J. M., Rowe, J. F., et al. 2011, AJ, 142, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2002, ApJ, 579, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A. M. S., Anderson, D. R., Skillen, I., Collier Cameron, A., & Smalley, B. 2011, MNRAS, 416, 2096 (S11) [NASA ADS] [CrossRef] [Google Scholar]
- Tsymbal, V. 1996, in M.A.S.S., Model Atmospheres and Spectrum Synthesis, eds. S. J. Adelman, F. Kupka, & W. W. Weiss, ASP Conf. Ser., 108, 198 [Google Scholar]
- von Essen, C., Czesla, S., Wolter, U., et al. 2014, A&A, 561, A48 (vE14) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mass, density, and orbital separation of WASP-33b based on our K-value and the data given by CC10, S11 (Smith et al. 2011), and K13.
Barycentric Julian dates at mean exposure and the radial velocities determined from cross-correlation with a synthetic template.
All Figures
 |
Fig. 1 Part of the time series of differential LSD profiles from the observations in 2013, horizontally arranged in a running order. The vertical axis spans ±150 km s-1. The RME was covered in two nights, which is indicated by the two white arrows. |
| In the text | |
 |
Fig. 2 Periodograms (logarithmic plots) calculated with Period04. From top to bottom: original data, after subtracting the long-term trend, after also subtracting f2, and after subtracting all 10 frequencies. |
| In the text | |
 |
Fig. 3 RVs from the spectra taken in 2013 (open circles) and 2015 (filled squares). a) Original RV data folded with f2; b) RVs after subtracting all frequency contributions but not f2, folded with f2; c) as b) but for f3, the solid lines show the best fitting orbital curve; d) as b) but for f1, the crosses represent phase-binned values. |
| In the text | |
 |
Fig. 4 Logarithmic plot of the density of transiting exoplanets versus their mass. The solid line results from a polynomial fit. The positions of WASP-33b according to CC10 (square) and K13 (triangle) are labelled. The cross indicates the typical error bars. |
| In the text | |
 |
Fig. 5 Deviation of the density from the mean value versus equilibrium temperature for planets with M< 1.4 MJ (open circles) and M> 1.4 MJ (filled circles). A polynomial fit and its 1σ confidence limits are shown by the solid and the dotted lines, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


