| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201525765 | |
| Published online | 11 June 2015 | |
Investigating the rotational evolution of young, low-mass stars using Monte Carlo simulations
1 LATO–DCET, Universidade Estadual de Santa Cruz, UESC, Rodovia Jorge Amado, km 16, Bairro Salobrinho, CEP 45662-900, Ilhéus, Brazil
e-mail: mjvasc@uesc.br
2 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France,
CNRS, IPAG, 38000 Grenoble, France
Received: 29 January 2015
Accepted: 17 April 2015
Context. Young stars rotate well below break-up velocity, which is thought to result from the magnetic coupling with their accretion disk.
Aims. We investigate the rotational evolution of young stars under the disk-locking hypothesis through Monte Carlo simulations.
Methods. Our simulations included 280 000 stars, each of which was initially assigned a mass, a rotational period, and a mass accretion rate. The mass accretion rate depends on both mass and time, following power-law indices of 1.4 and −1.5, respectively. A mass-dependent accretion threshold was defined below which a star was considered as diskless, which resulted in a distribution of disk lifetimes that matches observations. Stars were evolved at constant angular spin rate while accreting and at constant angular momentum when they became diskless.
Results. Starting with a bimodal distribution of periods for disk and diskless stars, we recovered the bimodal period distribution seen in several young clusters. The short-period peak mostly consists of diskless stars, and the long-period peak is mainly populated by accreting stars. Both distributions, however, present a long tail toward long periods, and a population of slowly rotating diskless stars is observed at all ages. We reproduced the observed correlations between disk fraction and spin rate, as well as between IR excess and rotational period. The period-mass relation we derived from the simulations only shows the same global trend as observed in young clusters when we released the disk-locking assumption for the lowest mass stars. Finally, we find that the time evolution of median specific angular momentum follows a power-law index of −0.65 for accreting stars, as expected from disk locking, and of −0.53 for diskless stars, a shallower slope that results from a wide distribution of disk lifetimes. At the end of the accretion phase, our simulations reproduce the angular momentum distribution of the low-mass members of the 13 Myr h Per cluster.
Conclusions. Using observationally documented distributions of disk lifetimes, mass accretion rates, and initial rotation periods, and evolving an initial population from 1 to 12 Myr, we reproduced the main characteristics of pre-main sequence angular momentum evolution, which supports the disk-locking hypothesis.
Key words: methods: statistical / stars: pre-main sequence / stars: rotation
© ESO, 2015
1. Introduction
Several determinations of the rotational properties of young clusters have shown that the stellar period changes as a function of time (e.g., Bouvier 2013, for a review). The distribution of rotational periods of the Orion nebula cluster (ONC) with an age of 2 Myr presents values that range from shorter than 1 day to >15 days. The older cluster NGC 2547, which is 40 Myr old, shows almost the same amplitude of periods, but with lower mass stars (M∗ ≲ 0.5M⊙) that on average rotate faster. Main-sequence (MS) stars, like the Sun, rotate much more slowly than young stars.
During the first few Myr of evolution, stars that show evidence of disks, such as infrared excess emission, broad Hα lines, or excess UV emission, rotate slower on average than diskless stars, according to several studies (e.g., Rebull et al. 2006; Cieza & Baliber 2007). These observations are explained by the disk-locking hypothesis: during the time the star remains attached to the disk, the stellar rotation rate remains constant. As soon as the star loses its disk, it starts to spin-up as a result of the expected radius contraction on the Hayashi track. According to Gallet & Bouvier (2013), the star does not conserve its angular momentum from the zero-age main sequence (ZAMS) to the MS. The angular momentum can be lost via magnetic stellar winds, and eventually, all stars end up on the MS with the same angular velocity.
There are, however, some open problems related to this picture. Based on the disk frequency in several young clusters, Mamajek (2009) pointed out that the disk fraction as a function of time decreases exponentially. The mean disk lifetime is expected to be around 2−3 Myr, although some results indicate higher values (5−6 Myr, Bell et al. 2013). Measurements of the mass accretion rate in clusters of different ages point to a dependency on the age t of the star and its mass M∗ in the form 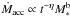 . However, there is no general agreement about the value of the exponents. According to the self-similar accretion theory (Hartmann et al. 1998), the mass accretion rate is independent of the mass and η = 3/2 or at least η> 1. Several works have provided different values for η and b. For example, Manara et al. (2012) analyzed a sample of stars in the ONC and found that η varies with the stellar mass, reaching values lower than 1 for M∗ ≳ 0.5 M⊙. They also obtained that the exponent b varies with age and evolves from 1.15 for t ~ 0.8 Myr to 2.43 for t ~ 10 Myr. Spezzi et al. (2012) found η = 0.3 and b = 0.82 in star-forming regions of the Large Magellanic Cloud, while Rigliaco et al. (2011) found b = 1.6 for the σ Ori region. Venuti et al. (2014) analyzed the accretion and variability of stars in NGC 2264 and obtained b = 1.4 ± 0.3. There is also some controversy related to the period − mass relation, that is, to the scarcity of slow rotators among lower mass stars (M∗< 0.5M⊙), which was reported, for example, by Henderson & Stassun (2012) in the period − mass diagrams of several clusters. However, neither Affer et al. (2013) for NGC 2264 nor Moraux et al. (2013) for h Persei found any evidence of this relation above 0.4 M⊙.
. However, there is no general agreement about the value of the exponents. According to the self-similar accretion theory (Hartmann et al. 1998), the mass accretion rate is independent of the mass and η = 3/2 or at least η> 1. Several works have provided different values for η and b. For example, Manara et al. (2012) analyzed a sample of stars in the ONC and found that η varies with the stellar mass, reaching values lower than 1 for M∗ ≳ 0.5 M⊙. They also obtained that the exponent b varies with age and evolves from 1.15 for t ~ 0.8 Myr to 2.43 for t ~ 10 Myr. Spezzi et al. (2012) found η = 0.3 and b = 0.82 in star-forming regions of the Large Magellanic Cloud, while Rigliaco et al. (2011) found b = 1.6 for the σ Ori region. Venuti et al. (2014) analyzed the accretion and variability of stars in NGC 2264 and obtained b = 1.4 ± 0.3. There is also some controversy related to the period − mass relation, that is, to the scarcity of slow rotators among lower mass stars (M∗< 0.5M⊙), which was reported, for example, by Henderson & Stassun (2012) in the period − mass diagrams of several clusters. However, neither Affer et al. (2013) for NGC 2264 nor Moraux et al. (2013) for h Persei found any evidence of this relation above 0.4 M⊙.
In this work, we investigate the main variables that can influence the spin rate evolution of a cluster of stars. To do this, we use Monte Carlo simulations and compare the results to observations available in the literature. We randomly assign a mass, a mass accretion rate, and an initial period for each star. We control the disk lifetime assuming a mass accretion rate threshold below which the star is considered to be diskless. We run our tests from 1 Myr to 12.1 Myr. In Sect. 2, we explain the main assumptions of the simulations. In Sect. 3, we present and discuss our results. In Sect. 4, we draw our conclusions.
2. Monte Carlo simulations
To calculate the evolution of the rotational period P, we assumed that a disk star has a constant period and that a diskless star changes its angular-velocity in conserving angular momentum following the equation 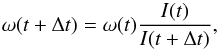 (1)where ω(t) = 2π/ P(t) is the angular velocity of the star at time t and I(t) is its moment of inertia at the same age. We calculated the moments of the inertia from the stellar evolutionary models of Baraffe et al. (1998) for five mass bins: 0.3 M⊙, 0.4 M⊙, 0.5 M⊙, 0.8 M⊙ and 1.0 M⊙. Figure 1 shows the interpolated moments of inertia for each mass bin as a function of the time interval considered in these simulations. As expected, the moment of inertia decreases with time because the star is contracting. This increases the stellar rotation rate and decreases the period of rotation if the star is free from its disk.
(1)where ω(t) = 2π/ P(t) is the angular velocity of the star at time t and I(t) is its moment of inertia at the same age. We calculated the moments of the inertia from the stellar evolutionary models of Baraffe et al. (1998) for five mass bins: 0.3 M⊙, 0.4 M⊙, 0.5 M⊙, 0.8 M⊙ and 1.0 M⊙. Figure 1 shows the interpolated moments of inertia for each mass bin as a function of the time interval considered in these simulations. As expected, the moment of inertia decreases with time because the star is contracting. This increases the stellar rotation rate and decreases the period of rotation if the star is free from its disk.
 |
Fig. 1 Moments of inertia of 0.3, 0.4, 0.5, 0.8, and 1.0 M⊙ stars as a function of time. |
We generated period, mass, and mass accretion rate distributions. Then, a population of about 280 000 stars was evolved from 1 Myr to 12.1 Myr in time steps of 0.1 Myr. The number of stars in each mass bin was obtained following the canonical IMF (Kroupa et al. 2013), ![\begin{equation} \label{imf} \xi (m) = \begin{cases} {k \left(\frac{m}{0.07}\right)^{-1.3}} & {0.07 < m \leq 0.5}, \\ {k \left[\left(\frac{0.5}{0.07}\right)^{-1.3}\right] \left(\frac{m}{0.5}\right)^{-2.3}} & {0.5 < m \leq 150}, \end{cases} \end{equation}](/articles/aa/full_html/2015/06/aa25765-15/aa25765-15-eq26.png) (2)where m is the mass in solar mass units (Fig. 2). The exact shape of the IMF does not affect our results.
(2)where m is the mass in solar mass units (Fig. 2). The exact shape of the IMF does not affect our results.
 |
Fig. 2 Initial mass distribution for the five mass bins considered in this work. |
 |
Fig. 3 Initial distributions of the mass accretion rate in each mass bin. |
 |
Fig. 4 Disk fraction as a function of time (solid black line) obtained from our simulations considering η = 1.5 and tth = 2.2 Myr. The colored dashed lines are the exponential decay laws expected from disk e-folding times 2.5 Myr (red line) and 5.5 Myr (blue line). The colored dots are data for nine young nearby associations from Ribas et al. (2014, circles), Hernández et al. (2007), and Hernández et al. (2008, squares). |
 |
Fig. 5 Period distributions obtained from model M1 for disk (red) and diskless (gray) stars. Outlined in blue is the period distribution for all stars (disk + diskless). In the top panels we show the distributions at t = 1 Myr, in the central panels those at 2.1 Myr, and in the bottom panels the distributions at 12.1 Myr. At the left side, the period distributions are shown on a linear scale, at the right side, the abscissa is given in log units. |
 |
Fig. 6 Period distributions obtained from model M2 for disk (red) and diskless (gray) stars. Outlined in blue is the period distribution for all stars (disk + diskless). In the top panels we show the distributions at t = 1 Myr, in the central panels those at 2.1 Myr, and in the bottom panels the distributions at 12.1 Myr. At the left, the period distribution are shown on a linear scale, at the right, the abscissa is given in log units. |
To obtain the initial mass accretion rate for each star, we calculated five different values, one for each mass bin, according to the equation 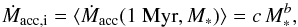 (3)where M∗ is the value of the stellar mass and b = 1.4(Venuti et al. 2014). The constant c was obtained considering that a 1 M⊙ has a mass accretion rate equal to 1.0 × 10-8M⊙ yr-1 at t = 1.0 Myr. The values are shown in Table 1. We then created five random log-normal distributions with means given by Ṁacc,i (see Eq. (3)and Table 1) and σlog Ṁacc = 0.8.
(3)where M∗ is the value of the stellar mass and b = 1.4(Venuti et al. 2014). The constant c was obtained considering that a 1 M⊙ has a mass accretion rate equal to 1.0 × 10-8M⊙ yr-1 at t = 1.0 Myr. The values are shown in Table 1. We then created five random log-normal distributions with means given by Ṁacc,i (see Eq. (3)and Table 1) and σlog Ṁacc = 0.8.
Mass accretion rate distributions.
With this initial setup, the mass accretion rate of each star evolves following the equation 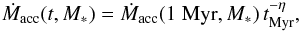 (4)where the time tMyr is expressed in Myr and η = 1.5(Hartmann et al. 1998). In this equation, Ṁacc(1Myr,M∗) is the initial value of the mass accretion rate of a given star (at 1 Myr). We then chose a criterion through which the stars will loose their disks. If, for a given star at a given age, Ṁacc(t,M∗) ≤ Ṁacc,th(M∗), the star will be released from its disk and will start to spin up, conserving angular momentum. Otherwise it will keep its disk and its rotational period will be held constant. The threshold mass accretion rate, Ṁacc,th, was obtained taking Eq. (4) at tMyr = tth, the threshold time, which was chosen to reproduce the observational disk fraction as a function of age (e.g., Mamajek 2009). We took tth = 2.2 Myr, which means that 50% of the stars will have lost their disk by this age. The mass accretion threshold values for each mass bin are shown in Table 1. All mass accretion rate values, including the initial ones, that fall below the threshold were set equal to Ṁacc,th, which causes the appearance of a peak at this value in the initial distributions shown in Fig. 3. Initially diskless stars start to spin up according to Eq. (1). Eventually, different stars will reach the mass accretion rate threshold, will be released from their disks, and will start to spin up according to the same equation.
(4)where the time tMyr is expressed in Myr and η = 1.5(Hartmann et al. 1998). In this equation, Ṁacc(1Myr,M∗) is the initial value of the mass accretion rate of a given star (at 1 Myr). We then chose a criterion through which the stars will loose their disks. If, for a given star at a given age, Ṁacc(t,M∗) ≤ Ṁacc,th(M∗), the star will be released from its disk and will start to spin up, conserving angular momentum. Otherwise it will keep its disk and its rotational period will be held constant. The threshold mass accretion rate, Ṁacc,th, was obtained taking Eq. (4) at tMyr = tth, the threshold time, which was chosen to reproduce the observational disk fraction as a function of age (e.g., Mamajek 2009). We took tth = 2.2 Myr, which means that 50% of the stars will have lost their disk by this age. The mass accretion threshold values for each mass bin are shown in Table 1. All mass accretion rate values, including the initial ones, that fall below the threshold were set equal to Ṁacc,th, which causes the appearance of a peak at this value in the initial distributions shown in Fig. 3. Initially diskless stars start to spin up according to Eq. (1). Eventually, different stars will reach the mass accretion rate threshold, will be released from their disks, and will start to spin up according to the same equation.
In Fig. 4, we show the disk fraction as a function of age obtained from our simulations superimposed on data from Ribas et al. (2014), Hernández et al. (2007), and Hernández et al. (2008) for nine young nearby associations. The combination of model parameters makes the number of diskless stars approximately equal to 25% initially. Our simulated disk fraction describes the observed fraction well, and it stays between the two exponential limiting curves based on the short disk lifetimes claimed by, for example, Dahm & Hillenbrand (2007) and the longer disk lifetimes proposed by Bell et al. (2013). At 12 Myr, the disk fraction is around 8%.
3. Results and discussion
We considered two models M1 and M2 that differ from each other by the initial distribution of periods of disk and diskless stars. Both have b = 1.4, η = 1.5 (see Eqs. (3)and (4)), tth = 2.2 Myr, and the same mass and initial mass accretion rate distributions. The resulting disk fraction (shown in Fig. 4) is then the same for both models since it only depends on the choice of the threshold time, η and the mass accretion rate distribution.
Changing the mass dependency of the mass accretion rate in our models does not change the main results we obtain below: the disk fraction, the period distributions, and the time dependency of the median specific angular momentum remain the same. Of course, it changes the distribution of mass accretion rates. The values are higher for a model with, for example, b = 0.82, as observed by Spezzi et al. (2012) at some star-forming regions of the Large Magellanic Cloud. However, the mass accretion rate as a function of time (Eq. (4)) and the mass accretion rate threshold also depend on the mass in the same way, which means that the entire problem in this sense is scale free. Thus, our models cannot be used to determine the mass dependency of the mass accretion rate, although they show a strong dependency on η and the mass accretion rate dispersion (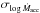 ). If the mass accretion rate dispersion is lower than the rate we have considered in this work, the time dependency must change to reproduce the observed disk fraction as a function of time. For example, if the mass accretion rate dispersion is lower than 2 orders of magnitude, that is, narrower than we considered here, η can be as low as 0.3. The reason for this is that there will be fewer stars with high mass accretion rate values, and then the disk fraction will fall off very quickly. To compensate for this, the mass accretion rate must slowly decrease with time. To have a time dependency that agrees with the self-similar accretion theory (i.e., η>1; Hartmann et al. 1998), we require a great amplitude of mass accretion rate values, as is observed in several young clusters (Venuti et al. 2014; Manara et al. 2012).
). If the mass accretion rate dispersion is lower than the rate we have considered in this work, the time dependency must change to reproduce the observed disk fraction as a function of time. For example, if the mass accretion rate dispersion is lower than 2 orders of magnitude, that is, narrower than we considered here, η can be as low as 0.3. The reason for this is that there will be fewer stars with high mass accretion rate values, and then the disk fraction will fall off very quickly. To compensate for this, the mass accretion rate must slowly decrease with time. To have a time dependency that agrees with the self-similar accretion theory (i.e., η>1; Hartmann et al. 1998), we require a great amplitude of mass accretion rate values, as is observed in several young clusters (Venuti et al. 2014; Manara et al. 2012).
 |
Fig. 7 Disk fraction as a function of period for different ages for model M2. |
3.1. Model M1
In model M1, we considered that the initial period distribution is the same for disk and diskless stars. It is given by a Gaussian function with a mean period equal to eight days and a standard deviation equal to six days (e.g., Rebull et al. 2004; Bouvier et al. 2014). The Gaussian is truncated at both ends, at 0.5 days, and at 18.5 days. In Fig. 5 we show the distributions of the rotational periods at t = 1.0, 2.1, and 12.1 Myr. At t = 1.0 Myr, our model assumptions establish an initial random distribution of periods and mass accretion rates for the whole population. According to the initial fraction of diskless stars derived from Fig. 4 (equal to 26%), there are fewer diskless stars than there are disk stars. This changes at t = 2.1 Myr, with the fraction of diskless stars increasing, and the distributions now peak at Ppeak = 8 − 9 days for disk stars and at Ppeak = 4 − 6 days for diskless stars. Our simulations indicate a significant overlap between the rotational distributions of disk and diskless stars at all ages. Diskless stars tend to rotate faster than disk stars, but exhibit a long tail toward long periods. Conversely, a fraction of fast rotators is found among disk stars.
Henderson & Stassun (2012) analyzed a sample of stars in NGC 6530 (1−2 Myr) and found that the mean period of stars showing near-IR (NIR) excess is around 6.3 days and 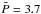 days for stars without NIR excess. Affer et al. (2013) also found
days for stars without NIR excess. Affer et al. (2013) also found 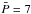 days for CTTS and
days for CTTS and 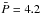 days for WTTS in a sample of stars in NGC 2264 (3 Myr). Cieza & Baliber (2007) found that stars with a spectral type M2 and earlier with and without disks also present different period distributions for NGC 2264 (1−5 days for diskless stars and a flatter distribution for disk stars) and the ONC (peak at ~2 days for diskless and at ~8 days for disk stars). Our results agree reasonably well with these observations. However, at 12.1 Myr, our simulation does not reproduce the bimodal rotational distribution of h Per cluster members, which exhibit one peak at ≤1 day and another at 3−7 days (Moraux et al. 2013). Instead, the period distribution of diskless stars in our simulation moves to shorter periods as a whole by an age of 12.1 Myr with a single peak at Ppeak ~ 2 days. This suggests that the initial conditions of the simulations might have to be modified.
days for WTTS in a sample of stars in NGC 2264 (3 Myr). Cieza & Baliber (2007) found that stars with a spectral type M2 and earlier with and without disks also present different period distributions for NGC 2264 (1−5 days for diskless stars and a flatter distribution for disk stars) and the ONC (peak at ~2 days for diskless and at ~8 days for disk stars). Our results agree reasonably well with these observations. However, at 12.1 Myr, our simulation does not reproduce the bimodal rotational distribution of h Per cluster members, which exhibit one peak at ≤1 day and another at 3−7 days (Moraux et al. 2013). Instead, the period distribution of diskless stars in our simulation moves to shorter periods as a whole by an age of 12.1 Myr with a single peak at Ppeak ~ 2 days. This suggests that the initial conditions of the simulations might have to be modified.
3.2. Model M2
To determine whether we can obtain a bimodal distribution for the whole population of stars up to 13 Myr, we ran model M2, for which the initial period distribution is different for disk and diskless stars. For disk stars, the period distribution was the same as was considered in model M1 (Pmean = 8 days and σ = 6 days). For the initial population of diskless stars, the period distribution was a truncated Gaussian with a peak at three days and a dispersion equal to two days. There are no stars with periods shorter than 0.5 days, and all the stars that originally had periods shorter than this value were smoothly redistributed around three days. These parameters were chosen assuming that at 1.0 Myr the stars in a given cluster have already experienced some disk and rotational evolution. That there is some disk loss at this age is seen in very young clusters such as NGC 1333, which is 1 Myr old and has a disk fraction equal to 66% ± 6%(Ribas et al. 2014, Fig. 4). Then we assumed that at 1 Myr there is a diskless population that is spinning up. In the somewhat older ONC, Cieza & Baliber (2007) found that stars without signs of dust disks rotate faster than the disk stars, with a mean period of two days, but with a tail toward longer periods. Assuming that at 1 Myr these stars rotate more slowly than at 2 Myr, we chose the mean period of the diskless population to be equal to three days, but with a dispersion value great enough to allow the existence of diskless stars with periods as long as ten days.
3.2.1. Evolution of the rotational distributions
In Fig. 6 we show the period distribution at 1.0, 2.1, and 12.1 Myr. The distinct initial period distributions for disk and diskless stars are shown at 1 Myr. While there are no diskless stars with periods greater than ten days, there are still fast rotators among disk stars. At 2.1 Myr, the period distribution clearly remains bimodal. The peak of the fast rotators is around two days, that of the slow rotators is around eight days, as reported by Cieza & Baliber (2007) for the ONC. We also recover a bimodal distribution shown in the logarithm distribution of the period at 12.1 Myr for h Per stars, quite in contrast with model M1 above. At this age, the peaks of the simulated distribution lie at 0.7 and 3.2 days. While the former agrees well with the peak of h Per fast rotators reported by Moraux et al. (2013), the latter is located at shorter periods than observed in h Per, where it lies at about three to seven days in the mass range 0.4−1.1 M⊙.
 |
Fig. 8 Disk fraction as a function of period obtained from model M2 (red circles) for t = 2.1 Myr (left panel) and for t = 3.1 Myr (right panel). The superimposed black circles show the disk fraction as a function of the period obtained for the ONC (left panel) and for NGC 2264 (right panel) for stars with a spectral type M2 and earlier extracted from Cieza & Baliber (2007). |
 |
Fig. 9 Ṁacc normalized to the mass accretion rate threshold is plotted versus period at t = 1.0 Myr (panel a)), t = 3.1 Myr (panel b)), t = 6.1 Myr (panel c)), and t = 12.1 Myr (panel d)). For clarity, we show a subsample of 464 stars randomly selected from model M2. Different colors represent different mass bins. Circles are for disk stars, crosses for diskless stars. |
 |
Fig. 10 Left: Ṁacc normalized to the mass accretion rate threshold vs. period at t = 2.1 Myr for a sample of 464 stars randomly chosen from our M2 model simulation. Different colors represent different mass bins. Circles are for disk stars and crosses are for diskless stars. Right: [3.6] − [8] IRAC colors for 464 stars with measured periods in the Orion region. Figure adapted from Rebull et al. (2006). |
3.2.2. Connection of rotation – disk fraction
Cieza & Baliber (2007) stated in a different way that disk stars rotate more slowly on average than diskless stars. They showed that the fraction of disk stars increases with period for a sample of young stars in NGC 2264. In Fig. 7 we plot the fraction of disk stars as a function of period for model M2 at different ages. There is a general trend of increasing disk fraction with increasing period. At 1 Myr, all stars with periods greater than ten days are disk stars (i.e., disk fraction equal to 1.0), following the M2 initial period distributions. As the system evolves, the disk fraction as a whole decreases, but the decrease rate is greater at shorter periods. This is because slowly rotating stars that loose their disk start to spin up, thus leading to an accumulation of diskless stars at shorter periods.
In Fig. 8 we compare our results at 2.1 and 3.1 Myr with the data of Cieza & Baliber (2007) for stars of ONC and NGC 2264 with a spectral type M2 and earlier. We used the same period bins to facilitate the comparison. Our results agree well with those of Cieza & Baliber (2007), taking into account the error bars, which in our case are equal to the standard errors of a Poisson counting. The disk fraction smoothly increases with rotational period at 2.1 Myr and 3.1 Myr as observed, which supports the M2 model assumptions, including disk locking and an initial bimodal distribution of periods for disk and diskless stars.
 |
Fig. 11 Left: slope of the log P− mass relationship as a function of age recovered from the simulations (green dots) and superimposed to data points from Henderson & Stassun (2012) for seven nearby clusters. The error bars of the green dots are equal to the standard errors of the estimate of the least-squares fits. Right: same plot for a modified model without disk locking for the 0.3 M⊙ stars. |
3.2.3. Connection of rotation – accretion
To investigate in detail whether we can see a segregation in period due to a disk, we plot in Fig. 9 the mass accretion rate normalized to the mass accretion rate threshold versus rotational period for the simulated sample at an age of 1.0, 3.1, 6.1, and 12.1 Myr. At t = 1.0 Myr, diskless stars (Ṁacc ≤ Ṁacc,th) are set at Ṁacc = Ṁacc,th , and none has a period longer than ten days. Conversely, there are only few disk stars at short periods. As the population evolves, the period distribution of diskless stars increases, both toward longer and shorter periods. The former effect is caused by the evolution of disk stars that only recently have lost their disks and that have not had enough time to significantly spin up, thus yielding a population of long-period diskless stars; the latter is due to the free spin up of initially diskless stars as they contract, thus shifting the bulk of the rotational period distribution of the diskless stars toward shorter periods. After a few Myr, the initially peaked diskless star period distribution spreads over the full range of periods from shorter than 1 day up to 15 days as a result. In contrast, disk stars tend to fill the locus of longer periods because they remain locked to their disk as they evolve. Over time, the initial correlation between rotational periods and disks therefore remains, but becomes blurred by the widening of the period distribution of diskless stars. But the short-period locus remains depleted of disk stars at all ages, up to 12.1 Myr.
In Fig. 10, we compare the simulated Ṁacc − log P plot at 2.1 Myr with the plot of observed Spitzer IR excess vs. period for the Orion region from Rebull et al. (2006). It is not straightforward to translate mass accretion rate into Spitzer IR excess, and we therefore did not attempt such a conversion. Nevertheless, the mid-IR excess is expected to scale, at least in a statistical sense, with mass accretion rate. In this figure, Rebull et al. (2006) showed the [3.6] − [8] IRAC colors for 464 stars with measured periods in the Orion region for which the mean age is about 2 Myr. Colors above [3.6] − [8] = 1 are indicative of the presence of disks. We clearly see in this figure a deficit of disk stars at short periods and an accumulation of diskless stars at all periods. As discussed above, similar trends are seen at 2.1 Myr in our simulations: the diskless stars cover the full range of periods, and there is a strong deficit of disk stars at P ≲ 4 days. Hence, the simulated results of model M2 agree well with the observed IR − rotation plots.
3.2.4. Period – mass relationship
Henderson & Stassun (2012) investigated the period − mass relationship of seven clusters (NGC 6530, ONC, NGC 2264, NGC 2362, IC 348, NGC 2547, and NGC 2516) with ages ranging from 1−2 Myr to 150 Myr. By analyzing low-mass (0.2−0.5 M⊙) cluster members, they found a positive correlation for older clusters, meaning that lower mass stars spin up faster than higher mass stars. Since the mass range we explored in our simulations does not extend down to 0.2 M⊙, we cannot claim that we can recover such a relationship, but we might expect some weaker correlation among the lowest mass stars of our sample. Following Henderson & Stassun (2012), we plot the slope of the log P− mass relationship as a function of age in Fig. 11. The slopes were calculated1 for the 75th percentile of a random sample of 500 stars in the mass interval 0.3 ≤ M/M⊙ ≤ 0.5 as a function of mass. The slopes obtained from model M2 do not vary much with age and remain close to zero. This suggests that the rotational distributions are fairly independent of mass at very low masses in our simulations, a result clearly at odds with observations.
We therefore attempted another model with the same assumptions and parameters as model M2, but relaxing the disk-locking assumption for the lowest mass stars. In the lowest mass bin, 0.3 M⊙, even a disk star is now assumed to evolve, conserving its angular momentum. The results, shown in Fig. 11, yield positively increasing slopes as a function of time, which qualitatively matches the observations. This suggests that the disk locking might be less efficient at very low masses, thus allowing these stars to spin up faster than higher mass stars (cf. Lamm et al. 2005; Bouvier et al. 2014).
 |
Fig. 12 Gyration radius squared (left) and stellar radius in solar radius (right) as a function of time obtained from the stellar evolution models of Baraffe et al. (1998) for the mass bins considered in this work (colored solid lines). The colored dashed lines are obtained assuming the contraction of a fully convective polytropic pre-main sequence star (R ∝ t− 1/3). |
 |
Fig. 13 Specific angular momentum evolution for 100 stars randomly extracted from our simulations over the mass range 0.4−1.0 M⊙ compared to observed samples. Simulated data are shown as light gray symbols, squares for disk stars, and crosses for diskless ones. Two stars chosen from the sample are highlighted as magenta filled circles (disk) or crosses (diskless) to illustrate the individual evolution depending on disk lifetime and initial period. Observations: Taurus-Auriga and ONC (black symbols) samples are from Davies et al. (2014), whose j values were recomputed taking the gyration radius from the models of Baraffe et al. (1998). Squares represent Class II stars, crosses Class III stars. At 13 Myr, the specific angular momenta of h Per members from Moraux et al. (2013) are plotted as gray diamonds. |
3.2.5. Specific angular momentum evolution
Davies et al. (2014) calculated the specific angular momentum evolution of a sample of fully convective stars in Taurus-Auriga and in the ONC. They used new estimates of stellar radii and ages and classified their sample as Class II or Class III stars based on Spitzer IRAC fluxes. They found that the decreasing rate of the specific angular momentum during Class II phase is given by jstar ∝ t− β2, with β2 = 2.0−2.5, which is faster than expected if the angular velocity is maintained constant. They interpreted this result as indicating that the braking rate of accreting young stars is higher than expected from disk locking alone. They also observed the same time dependency for Class III objects, which they interpreted as initially accreting stars being sequentially released from their disks over a timescale of about 10 Myr.
Using model M2, we calculated the specific angular momentum distribution of our population. As stated before, while a star has a disk in our simulations, its angular velocity is kept constant. Then, for disk stars, we expect that the specific angular momentum, jstar(t) = k2R2ω, varies with time as jstar ∝ t2(α + β), if k ∝ tα and R ∝ tβ, assuming that the time dependency of the gyration radius k and the stellar radius R can be expressed as power laws. Both are obtained from the stellar evolution models of Baraffe et al. (1998) and are shown in Fig. 12 for each mass bin considered in this work. From 1 Myr to ~3 Myr, the gyration radius is approximately constant for all mass bins. At most, the gyration radius varies 1% for the 0.3 M⊙ mass bin. Beyond 3 Myr, the more massive stars start to develop a radiative core, and the gyration radius of the 1 M⊙ decreases by about 15% at an age of 10 Myr, while the reduction is much less in lower mass stars. For the asymptotic power-law form above, we thus adopt α ≃ 0, while in the simulations we used the actual, time-dependent values of the gyration radius provided by the stellar evolution models.
The variation of the stellar radius during the first few Myr mimics that of a fully convective polytrope (n = 1.5), that is, β = −1/3. Figure 12 show that for M = 0.3−0.5M⊙, the stellar radius slightly decreases more rapidly with time (β< −1/3), while the opposite is true for more massive stars. The exact values of β, as derived from the stellar evolutionary models, are shown in Table 2. The mean value, however, is around −0.33, and we consider that β = −0.33 for the asymptotic form above. Then, the expected time dependency of the specific angular momentum in our simulations for disk-locked stars would be j ∝ t-0.66. For diskless stars, the angular momentum is held constant.
 |
Fig. 14 Logarithm distributions of the specific angular momentum of our full sample at 12.1 Myr (red) obtained with model M2 and of h Per members (blue). These last values were extracted from Moraux et al. (2013). |
In Fig. 13, the specific angular momentum, jstar, is plotted as a function of time for our simulated sample and compared to observed samples of young stars. At t = 1 Myr, ~75% of the simulated sample consists of disk stars. The magenta symbols show the specific angular momentum of two objects chosen from our simulations. One is initially fast rotating and diskless and thus evolves conserving its initial angular momentum. The other is initially a slower rotator and has a disk lifetime of about 3 Myr. During this time, its specific angular momentum decreases as t-0.66 as expected, while it is held constant once the star is eventually released from its disk. When considered as a group, we find that the median specific angular momentum of disk stars in our simulation decreases with time as jmed ∝ t-0.65, that is, close to the expectation for constant angular velocity. For diskless stars, we derive jmed ∝ t-0.53. Thus, while individual diskless stars evolve at constant angular momentum, when considered as a group, their median angular momentum decreases in time nearly as fast as for disk stars. As already noted by Davies et al. (2014), this is the result of the stars being sequentially released from their disk over a wide range of disk lifetimes, from about 1 to 10 Myr.
We compared our simulations to the jstar distribution of the Taurus-Auriga and Orion samples from Davies et al. (2014)2. The Taurus-Auriga and ONC j estimates fall well within our range of values. We also plot the angular momentum values of h Per low-mass members as derived by Moraux et al. (2013) at an age of 13 Myr, benchmarking the end of the accretion phase. A more detailed comparison of the angular momentum distribution of h Per members and that predicted by our simulations at 12.1 Myr is shown in Fig. 14. While the distributions show differences, especially in the location of the peaks, the overall range of specific angular momentum is well accounted for. Indeed, this suggests that the angular momentum distribution of low-mass stars at the end of the PMS accretion phase builds up during the first few Myr, as the result of disk locking acting over a wide range of disk lifetimes, effectively widening the initial j distribution (Bouvier et al. 1993; Rebull et al. 2004).
4. Conclusions
The Monte Carlo simulations presented here reproduced the main observed rotational properties of young low-mass stars during their pre-main sequence evolution. We have shown that starting from now well-documented initial distributions of periods, mass-accretion rates and disk lifetimes, a model that assumes disk locking for accreting stars and angular momentum conservation for diskless stars succeeds in reproducing both the evolution of rotational period distributions in young clusters and the accretion-rotation connection observed between IR excess and rotational period at young ages. To also reproduce the mass-rotation connection, we furthermore assumed that disk locking is less efficient in very low mass stars, below 0.3 M⊙. Finally, the Monte Carlo simulations naturally produced the distribution of angular momentum observed at the end of the accretion phase, that is, past 10 Myr. We showed that this distribution, which is the starting point for the subsequent ZAMS and MS rotational evolution of low-mass stars, builds up during the PMS as the disk-locking process acts over a wide range of disk lifetimes, thus effectively widening the initial distribution of periods during PMS evolution.
Note that to allow for the comparison, we had to recompute their values of j using actual gyration radii obtained from the models of Baraffe et al. (1998). Davies et al. (2014) used for most of their sample k2 = 2/3, which applies to uniform density shells, while a value of k2 = 0.205 is appropriate for fully convective PMS stars. We also neglected centrifugal effects in our simulations because they do not significantly affect the results.
Acknowledgments
M.J.V. is grateful to Florian Gallet and to Claire Davies for providing theoretical and observational data to this work, to Adriano Hoth Cerqueira and Andre Luis Batista Ribeiro for very useful discussions, and to Florian Gallet and to Adriano Hoth Cerqueira for a careful reading of the manuscript. M.J.V. would like also to thank for the financial support provided by CAPES (fellowship No. 2565-13-7) under the program “Science without borders” and by the project PROCAD CNPq/CAPES number 552236/2011-0. J.B. acknowledges the support of ANR grant 2011 Blanc SIMI5-6 020 01 Toupies: Towards understanding the spin evolution of stars (http://ipag.osug.fr/Anr_Toupies/).
References
- Affer, L., Micela, G., Favata, F., Flaccomio, E., & Bouvier, J. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 2013, in EAS Publ. Ser., 62, 143 [Google Scholar]
- Bouvier, J., Cabrit, S., Fernandez, M., Martin, E. L., & Matthews, J. M. 1993, A&A, 272, 176 [NASA ADS] [Google Scholar]
- Bouvier, J., Matt, S. P., Mohanty, S., et al. 2014, Protostars and Planets VI, 433 [Google Scholar]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E., & Hillenbrand, L. A. 2007, AJ, 133, 2072 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, C. L., Gregory, S. G., & Greaves, J. S. 2014, MNRAS, 444, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, C. B., & Stassun, K. G. 2012, ApJ, 747, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Megeath, T., et al. 2007, ApJ, 662, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Calvet, N., et al. 2008, ApJ, 686, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Verlag), 115 [Google Scholar]
- Lamm, M. H., Mundt, R., Bailer-Jones, C. A. L., & Herbst, W. 2005, A&A, 430, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E. 2009, in AIP Conf. Ser. 1158, eds. T. Usuda, M. Tamura, & M. Ishii, 3 [Google Scholar]
- Manara, C. F., Robberto, M., Da Rio, N., et al. 2012, ApJ, 755, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Moraux, E., Artemenko, S., Bouvier, J., et al. 2013, A&A, 560, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Megeath, S. T., Hora, J. L., & Hartmann, L. 2006, ApJ, 646, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, Á., Merín, B., Bouy, H., & Maud, L. T. 2014, A&A, 561, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Natta, A., Randich, S., Testi, L., & Biazzo, K. 2011, A&A, 525, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spezzi, L., de Marchi, G., Panagia, N., Sicilia-Aguilar, A., & Ercolano, B. 2012, MNRAS, 421, 78 [NASA ADS] [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Moments of inertia of 0.3, 0.4, 0.5, 0.8, and 1.0 M⊙ stars as a function of time. |
| In the text | |
 |
Fig. 2 Initial mass distribution for the five mass bins considered in this work. |
| In the text | |
 |
Fig. 3 Initial distributions of the mass accretion rate in each mass bin. |
| In the text | |
 |
Fig. 4 Disk fraction as a function of time (solid black line) obtained from our simulations considering η = 1.5 and tth = 2.2 Myr. The colored dashed lines are the exponential decay laws expected from disk e-folding times 2.5 Myr (red line) and 5.5 Myr (blue line). The colored dots are data for nine young nearby associations from Ribas et al. (2014, circles), Hernández et al. (2007), and Hernández et al. (2008, squares). |
| In the text | |
 |
Fig. 5 Period distributions obtained from model M1 for disk (red) and diskless (gray) stars. Outlined in blue is the period distribution for all stars (disk + diskless). In the top panels we show the distributions at t = 1 Myr, in the central panels those at 2.1 Myr, and in the bottom panels the distributions at 12.1 Myr. At the left side, the period distributions are shown on a linear scale, at the right side, the abscissa is given in log units. |
| In the text | |
 |
Fig. 6 Period distributions obtained from model M2 for disk (red) and diskless (gray) stars. Outlined in blue is the period distribution for all stars (disk + diskless). In the top panels we show the distributions at t = 1 Myr, in the central panels those at 2.1 Myr, and in the bottom panels the distributions at 12.1 Myr. At the left, the period distribution are shown on a linear scale, at the right, the abscissa is given in log units. |
| In the text | |
 |
Fig. 7 Disk fraction as a function of period for different ages for model M2. |
| In the text | |
 |
Fig. 8 Disk fraction as a function of period obtained from model M2 (red circles) for t = 2.1 Myr (left panel) and for t = 3.1 Myr (right panel). The superimposed black circles show the disk fraction as a function of the period obtained for the ONC (left panel) and for NGC 2264 (right panel) for stars with a spectral type M2 and earlier extracted from Cieza & Baliber (2007). |
| In the text | |
 |
Fig. 9 Ṁacc normalized to the mass accretion rate threshold is plotted versus period at t = 1.0 Myr (panel a)), t = 3.1 Myr (panel b)), t = 6.1 Myr (panel c)), and t = 12.1 Myr (panel d)). For clarity, we show a subsample of 464 stars randomly selected from model M2. Different colors represent different mass bins. Circles are for disk stars, crosses for diskless stars. |
| In the text | |
 |
Fig. 10 Left: Ṁacc normalized to the mass accretion rate threshold vs. period at t = 2.1 Myr for a sample of 464 stars randomly chosen from our M2 model simulation. Different colors represent different mass bins. Circles are for disk stars and crosses are for diskless stars. Right: [3.6] − [8] IRAC colors for 464 stars with measured periods in the Orion region. Figure adapted from Rebull et al. (2006). |
| In the text | |
 |
Fig. 11 Left: slope of the log P− mass relationship as a function of age recovered from the simulations (green dots) and superimposed to data points from Henderson & Stassun (2012) for seven nearby clusters. The error bars of the green dots are equal to the standard errors of the estimate of the least-squares fits. Right: same plot for a modified model without disk locking for the 0.3 M⊙ stars. |
| In the text | |
 |
Fig. 12 Gyration radius squared (left) and stellar radius in solar radius (right) as a function of time obtained from the stellar evolution models of Baraffe et al. (1998) for the mass bins considered in this work (colored solid lines). The colored dashed lines are obtained assuming the contraction of a fully convective polytropic pre-main sequence star (R ∝ t− 1/3). |
| In the text | |
 |
Fig. 13 Specific angular momentum evolution for 100 stars randomly extracted from our simulations over the mass range 0.4−1.0 M⊙ compared to observed samples. Simulated data are shown as light gray symbols, squares for disk stars, and crosses for diskless ones. Two stars chosen from the sample are highlighted as magenta filled circles (disk) or crosses (diskless) to illustrate the individual evolution depending on disk lifetime and initial period. Observations: Taurus-Auriga and ONC (black symbols) samples are from Davies et al. (2014), whose j values were recomputed taking the gyration radius from the models of Baraffe et al. (1998). Squares represent Class II stars, crosses Class III stars. At 13 Myr, the specific angular momenta of h Per members from Moraux et al. (2013) are plotted as gray diamonds. |
| In the text | |
 |
Fig. 14 Logarithm distributions of the specific angular momentum of our full sample at 12.1 Myr (red) obtained with model M2 and of h Per members (blue). These last values were extracted from Moraux et al. (2013). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


