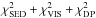| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201425372 | |
| Published online | 01 June 2015 | |
The evolved circumbinary disk of AC Herculis: a radiative transfer, interferometric, and mineralogical study⋆
1
Instituut voor Sterrenkunde (IvS), KU Leuven, Celestijnenlaan
200D,
3001
Leuven,
Belgium
e-mail:
Michel.Hillen@ster.kuleuven.be
2
AlbaNova University Centre, Stockholm University, Department of
Astronomy, 106 91
Stockholm,
Sweden
3
Stockholm University Astrobiology Centre,
106 91
Stockholm,
Sweden
4
Sterrenkundig Instituut Anton Pannekoek, University of
Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
5
Lunar and Planetary Laboratory, The University of Arizona, 1629 E.
University Blvd., Tucson
AZ
85721,
USA
Received: 19 November 2014
Accepted: 11 March 2015
Context. Many post-asymptotic giant branch (post-AGB) stars in binary systems have an infrared (IR) excess arising from a dusty circumbinary disk. The disk formation, current structure, and further evolution are, however, poorly understood.
Aims. We aim to constrain the structure of the circumstellar material around the post-AGB binary and RV Tauri pulsator AC Her. We want to constrain the spatial distribution of the amorphous and of the crystalline dust.
Methods. We present very high-quality mid-IR interferometric data that were obtained with the MIDI/VLTI instrument. We analyze the MIDI visibilities and differential phases in combination with the full spectral energy distribution, using the MCMax radiative transfer code, to find a good structure model of AC Her’s circumbinary disk. We include a grain size distribution and midplane settling of dust self-consistently in our models. The spatial distribution of crystalline forsterite in the disk is investigated with the mid-IR features, the 69 μm band and the 11.3 μm signatures in the interferometric data.
Results. All the data are well fitted by our best model. The inclination and position angle of the disk are precisely determined at i = 50 ± 8° and PA = 305 ± 10°. We firmly establish that the inner disk radius is about an order of magnitude larger than the dust sublimation radius. The best-fit dust grain size distribution shows that significant grain growth has occurred, with a significant amount of mm-sized grains now being settled to the midplane of the disk. A large total dust mass ≥10-3 M⊙ is needed to fit the mm fluxes. By assuming αturb = 0.01, a good fit is obtained with a small grain size power law index of 3.25, combined with a small gas/dust ratio ≤10. The resulting gas mass is compatible with recent estimates employing direct gas diagnostics. The spatial distribution of the forsterite is different from the amorphous dust, as more warm forsterite is needed in the surface layers of the inner disk.
Conclusions. The disk in the AC Her system is in a very evolved state, as shown by its small gas/dust ratio and large inner hole. Mid-IR interferometry offers unique constraints, complementary to mid-IR features, for studying the mineralogy in disks. A better uv coverage is needed to constrain in detail the distribution of the crystalline forsterite in the disk of AC Her, but we find strong similarities with the protoplanetary disk HD 100546.
Key words: stars: AGB and post-AGB / circumstellar matter / binaries: general / techniques: photometric / infrared: stars / techniques: interferometric
© ESO, 2015
1. Introduction
Post-asymptotic giant branch stars (post-AGB stars) are an evolved evolutionary phase of low- to intermediate-mass stars. They show a large variety of circumstellar characteristics (van Winckel 2003), but a significant fraction of the optically bright objects show a distinctive near-IR excess (de Ruyter et al. 2006; Kamath et al. 2014). This excess can be explained as being due to thermal emission of warm dust in the close environment of the central source (de Ruyter et al. 2006). It is now well established that this spectral energy distribution (SED) characteristic indicates the presence of a stable and compact dusty reservoir, likely a Keplerian disk (e.g. de Ruyter et al. 2006; Deroo et al. 2007a; Hillen et al. 2013, 2014). This was confirmed when the Keplerian rotation of the gas was first resolved by Bujarrabal et al. (2005) in one object, and recently endorsed by the most detailed position-velocity maps of the same object with the Atacama Large Millimeter Array (ALMA) by Bujarrabal et al. (2013b). A survey using single-dish CO line data confirms that rotation is widespread (Bujarrabal et al. 2013a), which is a strong observational indicator of stability. While neither the formation nor the evolution of these disks is well understood, both are linked to binary interaction processes, as evidence is mounting that sources with disk-like SEDs are indeed all binaries (van Winckel et al. 2009; Gorlova et al. 2013).
The longevity of the disk is further corroborated by the strong processing of the dust grains as attested by the infrared spectral dust-emission features (e.g. Gielen et al. 2008, 2011) and the mm continuum fluxes that indicate the presence of large grains (de Ruyter et al. 2005). A striking result is the large abundance and almost ubiquitous presence of crystalline grains (Molster et al. 2002c; Gielen et al. 2011).
Crystalline olivine grains ((Mg,Fe)2SiO4) are formed by high temperature (>1000 K) processes, either condensation from the gas phase or annealing of amorphous dust grains. This makes crystalline dust a tracer of high temperature regions and processes in the disk. In protoplanetary disks crystalline dust is dominantly observed in the inner parts, close to the central star where temperatures are high enough (van Boekel et al. 2004), but are also found farther out due to radial mixing mechanisms (Gail 2004). In situ processes that locally increase the temperature and pressure can also form crystalline grains at larger distances from the central star where it would otherwise be too cold. Examples of such mechanisms are formation by collisions (Morlok et al. 2010), by shocks (Harker & Desch 2002) or by stellar outbursts (Ábrahám et al. 2009). Crystalline dust abundances in protoplanetary disks are also locally enhanced in the walls of gaps that are likely formed by planets (Mulders et al. 2011, 2013).
The spatial distribution of the crystalline dust may hold unique clues about the formation and/or evolution of the disks in post-AGB systems. A distribution equal to that of the amorphous dust might suggest that all the crystalline material was formed during the early formation of the disk. It is not clear whether the formation of the disk involved predominantly Roche-Lobe overflow or a common-envelope phase. In either case the specific physical and chemical conditions in various mass flows within the system may have been beneficial to forming crystalline dust before the disk formed. Conversely, a very centrally condensed distribution may be a hint that the crystalline material formed primarily via a disk-related process. Even if radial mixing may transport some material outwards, the detailed spatial distribution of crystalline olivines can thus hold information about the disk’s history.
One can probe the spatial distribution and grain properties of crystalline olivine by modeling its multiple mid-IR and far-IR spectral features. These features contain a wealth of information because their precise peak-wavelength position, relative band strengths, and the band shapes are dependent on the temperature, composition, and abundance of the grains (Koike et al. 2003; Suto et al. 2006). Based on optically thin fits to the mid-IR features, Gielen et al. (2008, 2011) found that the dust in post-AGB disks is relatively well mixed, with a similar dust composition throughout the disk. These results still need to be confirmed with full radiative transfer models to rule out any influence of optical depth effects. Here we present a first attempt at such a study and we show the role that mid-IR interferometry can play for the study of post-AGB disks, and their mineralogy.
We focus on one of the brightest systems, AC Her, which is also one of the most regular and best studied RV Tauri pulsators. Van Winckel et al. (1998) presented the orbital solution as well as a photospheric abundance analysis, which showed the close resemblance between AC Her and the, then few, known post-AGB stars in binary systems with disks. Their detected photospheric abundance pattern was simultaneously found by Giridhar et al. (1998). The mm continuum fluxes have been measured by Sahai et al. (2011). The Keplerian kinematics of the outer disk is resolved in CO rotational lines, resulting also in an estimate of the disk’s mass (Bujarrabal et al. 2015, 2013a). Several authors have attempted to image AC Her’s disk with conflicting results. Most recently, Close et al. (2003) and Gallenne et al. (2012) both found AC Her to be unresolved in the thermal-IR on scales greater than 0.2″ using diffraction-limited imaging with different instruments. A crude radiative transfer disk model was constructed by Gielen et al. (2007), who also analyzed the mid-IR features with an optically thin approach (see Sect. 2).
We return to these results in the coming sections, where we discuss our observations (Sect. 2) and our estimation of the stellar parameters (Sect. 3). The stellar properties are needed as input for our radiative transfer models (Sects. 5–7). In this last section we will for the first time add crystalline olivine to a full radiative transport model and study the resulting features in the mid-IR, at 69 μm, and in the interferometric data.
2. Observations
In this section we describe the sources and data reduction strategies of the data sets to be used in the remainder of this paper. Being an RV Tauri pulsator, the pulsation phase is taken into account in the selection of the data that are fitted. The light curve of AC Her was retrieved from the AAVSO and AFOEV databases.
2.1. Literature photometric data
We collected photometric and spectroscopic observations of AC Her from various sources in the literature to construct its full SED (see Fig. 1). Although AC Her has been observed extensively, mostly the measurements do not cover a full pulsation cycle. Nevertheless, we gathered optical to near-IR photometric data for three typical pulsation phases, although from different cycles: primary and secondary minimum as well as maximum light.
For the near-maximum and -minimum pulsation phases, we used the near-IR JHKL photometry from Taranova et al. (2010) as well as the optical photometry in the Geneva system from de Ruyter et al. (2006). In addition, we used the Johnson UBV fluxes from Dawson (1979) and Zsoldos (1993) near maximum, and from Zsoldos (1993) and Shenton et al. (1992) near minimum. From this last source we also took Cousins R and I fluxes. At the secondary minimum phase, we used the Johnson-Cousins UBVRI data from Goldsmith et al. (1987) and the JHKL SAAO photometry from Shenton et al. (1992).
At mid-IR and longer wavelengths we collected publicly available photometric data from the Infra-Red Astronomy Satellite (IRAS, Neugebauer et al. 1984), the AKARI satellite (Murakami et al. 2007), as well as the Submillimetre Common-User Bolometer Array (SCUBA, Holland et al. 1999) 850 μm measurement published in de Ruyter et al. (2006), and the 1.3 and 3 mm fluxes measured with the Combined Array for Research in Millimeter-wave Astronomy (CARMA) by Sahai et al. (2011). The fluxes extracted from VISIR images by Gallenne et al. (2012) were also included in our analysis.
AC Her has been claimed to be photometrically variable even at mid-IR wavelengths (Shenton et al. 1992; Gehrz 1971), where the disk totally dominates the energy output. More recent observations of this variability are not available. We are confident that variability will not influence the results of this paper because 1) it is likely that only the inner rim of the disk will significantly respond to the varying stellar luminosity, hence fluxes beyond ~25 μm should be unaffected; 2) we exclude the IRAS fluxes at 12 and 25 μm as well as the AKARI fluxes at 9 and 18 μm from our SED fit owing to their uncertain phase attributions; and 3) all other data were taken near a secondary minimum phase or at phases with comparable V band magnitudes.
 |
Fig. 1 SED of AC Her. The gray dot-dashed line shows the input Kurucz model, reddened with an interstellar contribution of E(B − V) = 0.135 (see Sect. 3). The dotted blue line is the best single-power-law model (see Sect. 6.2). The dashed red line corresponds to our base model (i.e., the best double-power-law model obtained in Sect. 6.3). The full green line is the best-fit model with the alternative dust composition (Sect. 6.3.2). The inset shows a zoom-in of the near- to mid-IR wavelength range. We note that the ISO spectrum is included in our fit through the indicated anchor points (see the legend). |
2.2. SPIRE photometry
The Spectral and Photometric Imaging Receiver (SPIRE, Griffin et al. 2010; Swinyard et al. 2010) instrument on board the Herschel satellite (Pilbratt et al. 2010) was used to acquire new far-IR photometric data of AC Her in February 2012 (Herschel Observation ID 1342239790). A 169 s exposure in the small-map photometry observing mode was obtained simultaneously in three passbands, which are centered at 250 μm, 350 μm, and 500 μm. We refer to Hillen et al. (2014) for a description of the flux extraction procedures. The errors on the final fluxes are dominated by the absolute flux calibration, assumed to be at a precision level of 15% (Swinyard et al. 2010). The SPIRE data are included in Fig. 1.
2.3. Spectroscopic data: ISO and PACS/Herschel
AC Her was observed with the short (SWS) and long (LWS) wavelength spectrometers on board the Infrared Space Observatory (ISO; Molster et al. 1999, 2002a,b,c). This spectrum was taken close to a secondary minimum pulsation phase. The absolute calibration of the spectrum is closely in agreement with the near-IR K and L bands and with the mid-IR VISIR fluxes, that all correspond to a similar pulsation phase, and with the IRAS and AKARI photometry beyond 25 μm, which are averages of scans taken at several epochs. The flux-calibrated spectrum is also included in Fig. 1.
The full spectrum shows prominent spectral bands in the mid-IR from crystalline olivine grains (Molster et al. 1999), mainly from its Mg-rich end-member forsterite. Typical features of magnesium-rich crystalline olivine are located at 11.3, 16.2, 19.7, 23.7, 28.0, and 33.6 μm. The most recent analysis of these features was performed by Gielen et al. (2007). They fitted the mid-IR spectral bands with an optically thin model. Their best fit included a hot (800 K) population and an almost as abundant cold (100 K) population of forsterite grains. Both populations contained small (0.1 μm) and large (1.5 μm) forsterite crystals.
Crystalline olivine has now also been detected in the far-IR at 69 μm. This far-IR spectral band is a strong diagnostic of especially the crystal composition and the crystal temperature (Koike et al. 2003; Suto et al. 2006), very complementary to the mid-IR features. The 69 μm band shifts to the red and broadens as a function of increasing grain temperature and iron content. The Photodetector Array Camera and Spectrometer (PACS) on board the Herschel Space Observatory (Pilbratt et al. 2010; Poglitsch et al. 2010) was used to take a spectrum of AC Her in the wavelength range of 67−72 μm. The observation was performed as part of the GT program “Forsterite dust in the circumstellar environment of evolved stars” (GT1_jblommae_1). The spectrum has been published by Blommaert et al. (2014) as part of a large and diverse sample of evolved stars targeted with PACS. Details about the adopted observational setup and the data reduction procedure, can be found in the same paper.
Analysis of the peak wavelength positions and shapes of all these spectral bands show that the crystalline olivine grains contain no iron and are purely forsteritic (Mg2SiO4, Molster et al. 1999; Blommaert et al. 2014). Blommaert et al. (2014) moreover showed that the 69 μm band is dominated by flux from ~200 K forsterite grains and they found a peak-to-continuum-strength ratio of the 69 μm band of 0.06 ±/−0.004.
2.4. Mid-IR interferometry
We used the MID-infrared Interferometric instrument (MIDI) on the Very Large Telescope Interferometer (VLTI) to observe AC Her with the Unit Telescopes (UTs) during three nights in 2005. On each night a single MIDI observation was acquired in the GRISM spectral mode (R = 230) with the UT3-UT4 baseline on 25 May (baseline length and position angle: BL ~ 60 m, PA ~ 104°), and with the UT2-UT3 baseline on 26 June (BL ~ 45 m, PA ~ 47°) and on 23 July (BL ~ 37 m, PA ~ 50°). We reduced the data with version 2.0 of the Expert Work Station (EWS) software (Jaffe 2004)1.
Calibration of the raw target visibility occurs by division with the instrumental visibility (Vins, i.e., the interferometer’s response to a point source) for each wavelength. The Vins is interpolated from calibrator observations for which the intrinsic visibility is known and that were obtained immediately before and after the science measurement. Variability of the transfer function is taken into account by adding to the errors in quadrature the standard deviation of the Vins, including all calibrators within four hours of the science measurement. The resulting errors are very small, which attests to the good quality of all three nights.
The three MIDI observations are separated in time by about one month, corresponding to pulsation phases of ~0.8, ~0.3, and ~0.55, respectively, so we checked whether the data show any sign of variability. In the V passband, the corresponding fluxes differ by at most half a magnitude. Moreover, direct calibration of MIDI’s total flux spectrum for each of the three observations reveals no detectable difference, except that all three are consistently above the ISO fluxes by ~20%. Finally, even if the total flux is intrinsically variable in the AC Her system, the visibilities are likely to remain unaffected, because the physical morphology of the object cannot change on such short timescales. We conclude that variability is not an issue for these MIDI data.
In addition to the visibility amplitudes, MIDI measures differential phases. These are not the real Fourier phases, but have a linear component in wavenumber (i.e., inverse wavelength) subtracted (Jaffe 2004). The raw differential phases are corrupted by the different amount of water vapour that is experienced by the two beams, as a result of their different path lengths in the delay-line system. We calibrate the science data by subtracting the introduced phase shift, which is estimated by linearly interpolating the raw calibrator differential phase versus delay-line path length difference (per wavelength bin). The error on the differential phase is taken as the standard deviation of the calibrator measurements around this linear relation, added in quadrature to the statistical error on the phase. Differential phases can be used as a general indicator for asymmetry of the observed object, but they can also be included directly in model fitting. We refer to, e.g., Tristram et al. (2014) or Deroo et al. (2007b), for some successful examples of differential-phase modeling and for a deeper discussion on its diagnostic power. In summary, one can state that the differential phase measures the wavelength dependence of the symmetry of the object: if the object has different asymmetries across wavelengths, the differential phase will be nonzero.
3. The central star(s)
To construct a proper radiative transfer model of the circumbinary disk in the AC Her system requires correctly configuring the properties of the central heating source, i.e., defining the fundamental parameters of the post-AGB star.
Stellar and orbital parameters of AC Her.
Table 1 gives an overview of the adopted values for the relevant systemic and stellar parameters. There are three groups of parameters: those that have no direct impact on any of our observables, i.e., the orbital elements and pulsation period, taken from Van Winckel et al. (1998) and from the General Catalogue of Variable Stars (GCVS, Samus et al. 2009), respectively; parameters that do have an influence and are therefore fitted; and parameters that are indirectly derived from the former groups.
The parameters that affect the SED are the effective temperature Teff, the gravity log g, the angular diameter θ⋆, the interstellar reddening EISM(B − V), and the metallicity [Fe/H]. The metallicity was determined spectroscopically by Van Winckel et al. (1998) and by Giridhar et al. (1998). The values derived by these authors are consistent within the errors, but we assume the value derived by Van Winckel et al. (1998) since their Teff and log g are in better agreement with what we find in the following. We also fix the value of EISM(B − V) based on the consistent values of EISM(B − V) ~ 0.14 derived from the Galactic extinction maps of Schlegel et al. (1998) and Drimmel & Spergel (2001).
The Teff, log g, and θ⋆ are subsequently fitted to the stellar part of the SED, using the grid-based method detailed in Degroote et al. (2011). With this approach correlations between parameters can be easily identified and taken into account in determining the final uncertainties. The goodness of fit, and the confidence intervals (CI) derived from it, are determined with a χ2 statistic; in this case with three degrees of freedom. In practice, a Kurucz model SED is first reddened with the reddening law of Fitzpatrick (2004), subsequently integrated over the relevant photometric passbands, and ultimately scaled to the measured fluxes by optimizing the angular diameter. The resulting best-fit parameter values are listed in Table 1 and the CI are shown in Figs. 2 and 3.
 |
Fig. 2 Confidence interval of the stellar SED fit: Teff versus log g. |
 |
Fig. 3 Confidence interval of the stellar SED fit: log g versus θ⋆. |
 |
Fig. 4 Upper panel: measured MIDI visibilities of AC Her, color coded with respect to the baseline as listed in the legend, overplotted (full thick lines) with the best-fit single-power-law radiative transfer model (see Sect. 6), as a function of spatial frequency. Also shown in black are the uniform disk and uniform ring models mentioned in Sect. 4. Lower panel: residuals with respect to the radiative transfer model. |
 |
Fig. 5 Upper panel: MIDI differential phases of AC Her, similarly color coded and overplotted with the same radiative transfer model as in Fig. 4, as a function of wavelength. Lower panel: residuals with respect to the radiative transfer model. |
We use the P-L relation of Alcock et al. (1998) to estimate the absolute V band magnitude that corresponds to the pulsation period of AC Her. We integrate the best-fit SED model over the V passband and thus find a distance of 1.6 ± 0.3 kpc for a corresponding luminosity of 2500 L⊙.
Finally, we note that any scattering contribution to the stellar part of the SED is not properly taken into account in this analysis. Hillen et al. (2013) recently found – on the basis of a combined optical and near-IR interferometric data set – that a significant fraction (~35%) of all optical light in a similar system, 89 Herculis, is in fact circumstellar scattered light. For no other post-AGB binary system has the scattered light fraction been measured yet. We assume that the scatter in the P-L relation of Alcock et al. (1998) incorporates a similar spread in scattered light fraction as is present in the Galactic RV Tauri population, so that population-wise the estimated distances should be correct. For any individual system, however, the stellar luminosity is likely biased. Since we do not have data to constrain the scattered light fraction of AC Her, we ignore the optical to near-IR part of the SED for the rest of this paper.
4. A simple analysis of the interferometric data
Before continuing to the radiative transfer analysis of our data, we analyze the interferometric data on a qualitative level.
The calibrated MIDI visibilities are shown in Fig. 4 as a function of spatial frequency. The differential phases are shown in Fig. 5 as a function of wavelength. Thanks to the spectral range of MIDI that encloses the N band (8–13 μm), and the limited range in baseline length, the three observations overlap in their radial spatial frequency coverage. From the shapes of the three visibility and differential phase spectra, we can already draw several conclusions independent of any quantitative modeling.
-
The two shortest-baseline observations, which have similar position angles, are consistent with each other and show a clear minimum in visibility amplitude at more or less the same radial spatial frequency, hence at different wavelengths (see Fig. 4). This implies that the morphology of the source, and not its spectral characteristics, is controlling the shape of the visibility spectrum at these spatial frequencies.
-
The measured visibility amplitudes are overall very low, i.e., the data probe high spatial frequencies near two consecutive visibility minima. The “global geometry” of the system thus dominates the shape of the observed visibility spectra.
-
The visibility amplitude minima do not reach a full null. For the 60 m baseline (blue squares), the minimum amplitude is reached near 8 μm and is ~0.012–0.025. This is consistent with the estimated fraction of unresolved stellar flux of ~2%, based on the directly calibrated total MIDI flux and the SED model found in Sect. 3. This means that the circumstellar component does pass through a null at this baseline. The minimum visibilities at the shorter baselines are reached near 9.3 and 11.5 μm, respectively, and are in the range 0.04−0.06, significantly above the estimated stellar flux fractions of ~1% and ~0.5% at the respective wavelengths.
-
A strong differential phase signal (see Fig. 5) is detected on the 60 m baseline, and moderate signals are present on the 45 and 36 m baselines (green dots and red crosses, respectively). The differential phase on the 60 m baseline seems to be dominated by the source morphology. The strong signal near 8 μm is a clear example of a 180° phase jump (which is the result of a crossing of a visibility null); the signal is a result of the changing spatial resolution of the interferometer with wavelength (see the previous item). The fact that this transition is not step-like, but smooth yet steep, implies that the source morphology along this baseline direction is not entirely point-symmetric but is close to it. The shape of the differential phase signal at the shortest baselines is remarkably similar to the silicate feature in the ISO spectrum, as is illustrated in Fig. 6. The fact that the feature induces a signal in the differential phase at these baselines means that the position of the photocenter of the emission folded along this baseline direction is different between the continuum and the feature.
To define a range of sensible inner rim radii for our radiative transfer disk models, we first estimate the overall size of the mid-IR emission with simple geometric models. Figure 4 shows two such models: a uniform disk (UD) and a uniform ring (UR), as the full and dashed black lines, respectively. The UD diameter and UR inner diameter have been optimized so that the curves reach their first null coincident with the observed position on the two shortest baselines. In this exercise we keep the UR’s outer-to-inner-diameter ratio fixed at two. We find that the circumstellar emission seems to arise from within ~50−60 mas from the central source. Of course, these simple models cannot account for the full complexity of the wavelength-dependent source morphology, which is influenced by optical depth effects and by the thermal structure of the emitting material. Nevertheless, based on the visibility amplitudes, we can conclude that the source has a brightness distribution that does not look too different from a UD overall.
A circularly symmetric brightness distribution cannot, however, explain the striking features listed above: it does not fit with the shifted photocenter in and outside the silicate feature, nor with the smooth differential phase signal on the longest baseline or with the higher visibility plateau in the first null.
In the following sections we show that a circumbinary disk can explain the MIDI data set naturally, as well as the SED.
 |
Fig. 6 Comparison between the differential phase signal on the shortest MIDI baseline and the ISO spectrum in the same wavelength range. The red squares show the MIDI differential phases after subtraction of a linear trend (fit to the blue points), inversion, and normalization. The ISO spectrum was first smoothed with a Gaussian kernel (σ = 0.025 μm, comparable to the resolution of the MIDI grism at 13 μm). The full black line shows this smoothed ISO spectrum after subtraction of a linear trend (fit to the green points) and normalization. The differential phase of the intermediate baseline can be scaled similarly, but without sign inversion and with a smaller normalization factor, because these spatial frequencies fall largely in the second lobe of the radial visibility curve along this direction. The ISO spectrum of the base model added with 1% of 0.1 μm forsterite grains (see Sect. 7) is shown as the dashed line. We note that this model is normalized independently. |
Parameters of the MCMax radiative transfer disk models.
5. Radiative transfer modeling
Radiative transfer disk models of AC Her have been computed previously by Gielen et al. (2007) with the 2D Monte Carlo radiative transfer code MCMax. Here we use the code with different settings and include additional physics. The models of Gielen et al. (2007) were not yet computed with a grain size distribution up to mm-sized grains in combination with a full treatment of dust settling, which are both needed to fit the far-IR to the mm part of the SED. In all the models presented here, these effects are included.
5.1. The code
The MCMax code (Min et al. 2009) has been widely and successfully applied to model observables obtained for gas-rich disks in a variety of environments (Mulders et al. 2011; Verhoeff et al. 2011; Acke et al. 2013). We refer to these papers for a full description of the basic features of the MCMax code. To include the settling of dust we follow the approach that was presented in Mulders & Dominik (2012), and first applied in a post-AGB context in Hillen et al. (2014). In short, MCMax first computes the radiative equilibrium temperature structure throughout the disk. The vertical density structure of the disk is then self-consistently determined by solving the equations of vertical hydrostatic equilibrium, implicitly assuming thermal coupling between the gas and dust, but taking dynamical decoupling to model dust settling. Both steps are iterated until convergence is reached. Dust scattering can be treated in a full angle-dependent way or, to speed up the computations (Min et al. 2009), by assuming isotropic scattering. We apply isotropic scattering in this paper.
5.2. The dust model(s)
Two different compositions are tried for the amorphous dust component in this paper. Our standard mixture consists of the composition measured in the interstellar dust towards the Galactic center by Min et al. (2007) – 12.11% MgFeSiO4, 33.63% Mg2SiO4, 37.67% MgSiO3, 1.58% NaAlSi2O6 – co-added with 15% metallic iron (all mass fractions). The shapes of the grains are irregular, approximated by the distribution of hollow spheres (DHS, Min et al. 2005). Next to the standard composition, we also computed a grid of models consisting of only MgFeSiO4 (see Sect. 6.3) the opacities of which were computed from the optical constants of Dorschner et al. (1995) in the same way as before (fmax = 0.8).
The forsterite opacities that will be added to the model in Sect. 7 are calculated from the optical constants of Suto et al. (2006) in the same manner as the amorphous grains (using DHS). Since the forsterite opacities are temperature dependent, we use optical constants at the temperatures of 50, 100, 150, 200, and 295 K. MCMax can use temperature-dependent opacities (for more details, see, e.g., de Vries et al. 2014; Mulders et al. 2011), meaning the model correctly predicts the temperature-dependent spectral features of the forsterite grains.
6. A structural model
6.1. The strategy
Extensive grids of radiative transfer disk models are to be compared to our observations: the SED, the MIDI visibilities and the MIDI differential phases. The goal is to infer the density and thermal structure of the circumstellar material.
Although MCMax self-consistently computes the vertical structure of the disk, the radial (or surface density) distribution of the material is required as input for the models. Similarly to the disk in the 89 Her system (Hillen et al. 2014), we start by parameterizing the surface density distribution with a single power law, Σ ∝ r− pout.
Throughout this paper we keep the turbulent mixing strength α fixed at 0.01 (Hartmann et al. 1998), the outer disk radius at 200 AU, and the minimum dust grain size at 0.01 μm, since these parameters either have a minimal influence on our observables or are coupled with other parameters (e.g., α and the gas/dust ratio). The value of pout, which can only be constrained with resolved millimeter observations, is fixed at 1.0, the typical value found in protoplanetary disks (Williams & Cieza 2011).
The remaining free physical parameters are the inner radius Rin, the global gas/dust ratio, the grain size distribution power-law index q, the maximum grain size, and the total dust mass Md. In addition, there are two geometrical parameters: the inclination i and the position angle of the disk on the sky. Table 2 lists the allowed values for each parameter in our grid.
For each model, the computed spectrum is reddened with EISM(B − V) = 0.14, as determined in Sect. 3, and integrated over the photometric passbands. We include the ISO spectrum by taking the monochromatic flux at seven continuum wavelengths in the 4–25 μm region (see the legend in Fig. 1). MCMax provides the complex visibility for each model, from which we extract the visibility amplitude and compute the MIDI differential phase. To save computation time, we calculate complex visibilities only for 20 wavelengths between 7.5 and 13.5 μm, which are then linearly interpolated to the observed wavelength grid when calculating synthetic visibilities and differential phases. For each observable a separate χ2 is computed, i.e., for the SED, the MIDI visibility amplitudes and the MIDI differential phases.
To find models that fit all the data sets, we use the following criterion. A model is selected as good enough if it satisfies 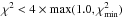 for all of the data sets. The lower limit of 1.0 is imposed to the
for all of the data sets. The lower limit of 1.0 is imposed to the 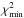 to avoid excluding too many models if a particular data set is over-fitted, which we do not expect given the complexity of these objects.
to avoid excluding too many models if a particular data set is over-fitted, which we do not expect given the complexity of these objects.
6.2. Single-power-law models
Although an extensive grid of models was computed, only two of our single-power-law models conform to the acceptance criterion. The best of these two is included in Table 2 (“Best Single”) and Figs. 1, 4, and 5. The χ2 values for both models are still high, 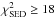 ,
, 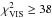 , and
, and 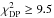 . In particular the visibilities and the SED do not fit well. The differential phases are already well represented by both models. Yet the amplitude at the shortest baseline is smaller than observed, because the silicate feature is almost completely absent in this model owing to a lack of small grains (see also the SED in Fig. 1). The SED does not fit very well in the 10–50 μm nor in the mm regime. It is also apparent that the shape of the visibility amplitude spectra agree well, but the absolute scaling for the shortest baselines do not. In summary, we interpret the general good agreement, i.e., the visibility and differential phase shapes, as a confirmation that a well-oriented disk model captures the basic features of the source morphology. The orientation of the disk on the sky is strongly constrained by the combined observations at different baseline position angles, and in particular by the long baseline that probes a secondary null and is almost aligned with the major axis of the disk. The remaining discrepancies can be attributed to the detailed inner rim shape. Because of the single-power-law parameterization of the surface density, the inner rim of these models is wall-like (see also Hillen et al. 2014; Dullemond & Monnier 2010). This explains the lower inclination compared to the best-fit models in the following sections: when the inclination is increased to 50°, the
. In particular the visibilities and the SED do not fit well. The differential phases are already well represented by both models. Yet the amplitude at the shortest baseline is smaller than observed, because the silicate feature is almost completely absent in this model owing to a lack of small grains (see also the SED in Fig. 1). The SED does not fit very well in the 10–50 μm nor in the mm regime. It is also apparent that the shape of the visibility amplitude spectra agree well, but the absolute scaling for the shortest baselines do not. In summary, we interpret the general good agreement, i.e., the visibility and differential phase shapes, as a confirmation that a well-oriented disk model captures the basic features of the source morphology. The orientation of the disk on the sky is strongly constrained by the combined observations at different baseline position angles, and in particular by the long baseline that probes a secondary null and is almost aligned with the major axis of the disk. The remaining discrepancies can be attributed to the detailed inner rim shape. Because of the single-power-law parameterization of the surface density, the inner rim of these models is wall-like (see also Hillen et al. 2014; Dullemond & Monnier 2010). This explains the lower inclination compared to the best-fit models in the following sections: when the inclination is increased to 50°, the 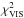 increases significantly because the inner rim appears too sharp.
increases significantly because the inner rim appears too sharp.
6.3. Double-power-law models
6.3.1. Our standard model
To improve upon our fit, we explore double-power-law models that smooth the inner disk rim. We parameterize the radial surface density profile by two power laws that are joined at an intermediate radius Rmid. This introduces two new parameters: the Rmid/Rin ratio and pin. We therefore fix the value of the grain size distribution power-law index at 3.25, given the relative lack of small grains compared to the observations in our best-fit single-power-law model. We allow pin to be between −0.5 and −3.0, while the turnover radius can be up to 2.5 times the inner radius.
Four models satisfy our acceptance criterion, of which two fit slightly better. We include the one with the smallest dust mass (see Sect. 8.2) in Table 2 as “Best Double”. The values of χ2 have significantly improved: 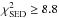 ,
, 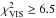 and
and 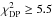 . This model is used as our base model in the remainder of this paper. Assuming this base model for the disk structure, the distribution of allowed inclinations and PAs is illustrated by the χ2 map in Fig. 7. There is a clearly defined minimum at an inclination and PA of 50° and 305°, respectively. Another minimum occurs at the same inclination but at a PA of 125°, because only the differential phases allows the 180° ambiguity in the disk position angle on the sky to be resolved. All well-fitting models have inclinations and PAs that fall within the first contour.
. This model is used as our base model in the remainder of this paper. Assuming this base model for the disk structure, the distribution of allowed inclinations and PAs is illustrated by the χ2 map in Fig. 7. There is a clearly defined minimum at an inclination and PA of 50° and 305°, respectively. Another minimum occurs at the same inclination but at a PA of 125°, because only the differential phases allows the 180° ambiguity in the disk position angle on the sky to be resolved. All well-fitting models have inclinations and PAs that fall within the first contour.
 |
Fig. 7 χ2 map of the disk inclination versus its orientation on the sky. We note that we adopt the convention that a PA of 0° corresponds to a disk oriented with its major axis along the N-S direction and with its far (prominent) side directed east. |
 |
Fig. 8 A visual rendering of our best-fit double power-law model at a wavelength of 12.5 μm. The intensity is shown on a linear scale. North is up and east is to the left. The field-of-view of this image is 200 by 200 mas. |
Although each of the model parameters influences our observables (or at least some of then), we do not expect to accurately constrain all parameters independently. This is consistent with the finding that a set of models fits our data equally well, so some degeneracy remains (see also Sect. 6.3.3). For certain parameters there are, however, clear trends. The inner radius is well constrained by our interferometric data at 34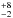 AU. The dust mass is also constrained to be 2.5–5.0 × 10-3 M⊙. The gas/dust ratio, which influences the data by its effect on the inner rim shape and on the feature/continuum ratio, is also smaller than 100 in all these models. Although this effect correlates with the turbulent mixing strength parameter α, we note that there are other indications for a low gas mass (see Sect. 8.2). The preferred ratio Rmid/Rin is clearly 2.0 or 2.5, and mostly pin is −3.0.
AU. The dust mass is also constrained to be 2.5–5.0 × 10-3 M⊙. The gas/dust ratio, which influences the data by its effect on the inner rim shape and on the feature/continuum ratio, is also smaller than 100 in all these models. Although this effect correlates with the turbulent mixing strength parameter α, we note that there are other indications for a low gas mass (see Sect. 8.2). The preferred ratio Rmid/Rin is clearly 2.0 or 2.5, and mostly pin is −3.0.
The SED, visibility amplitudes, and differential phases following from the base model are shown in Figs. 1, 9, and 10, respectively. A visual rendering is given, in Fig. 8. A closer inspection of the observables shows that they all fit the observations well, except for three small discrepancies. First, there is a deficit in the model SED in the 2–8 μm region. In particular the slope between 4 μm and 8 μm is not matched by the model (see Sect. 6.3.2). Second, the predicted visibilities for the two short baselines are larger than the observed values at 8–9 μm. Given the limited uv coverage one cannot, however, expect to constrain the shape of the inner rim in full detail. Some of the degeneracy in inner rim shape will be disclosed in Sect. 6.3.3. Third, the differential phase at the shortest baseline lacks the dip near 11 μm. This is to be expected because our model does not include crystalline forsterite, which is clearly present in the spectrum near 11.3 μm. We examine the effect of adding forsterite to our model in Sect. 7.
6.3.2. An alternative composition as a solution for the flux deficit?
Here we describe a grid of models with an alternative amorphous dust composition. We take the extreme case where there is only silicate dust consisting of amorphous MgFeSiO4. Large particles with this composition have higher absorption efficiencies in the wavelength range where we observe the flux deficit, compared to particles with our standard composition (see Fig. 11). We want to see 1) whether our derived model parameters depend significantly on our assumed dust composition; and 2) whether the 4–8 μm spectral slope mismatch can be linked to the dust composition.
 |
Fig. 9 MIDI visibilities of AC Her at the three baselines (one in each panel) as a function of wavelength. Overplotted are predictions for four double-power-law radiative transfer models: the standard best-fit model (full blue lines, Model 2 in Table 2); the standard model added with 1% of 0.1 μm forsterite grains (dashed green lines); the standard model added with 1% of forsterite grains with a size distribution between 0.1 and 2.0 μm (dotted red lines); and the New Forst model from Sect. 7.2.2 which has 1% of 0.1 μm forsterite grains, but with a different spatial distribution (thin black lines). |
 |
Fig. 10 MIDI DPs of AC Her at the three baselines (one in each panel) as a function of wavelength. Overplotted are the predictions for the same radiative transfer models as in Fig. 9. |
 |
Fig. 11 Mass absorption coefficients of the mixtures used in this work. Our “standard” mixture (the full lines) contains 15% metallic iron, while the alternative mixture (the dashed lines) consists of only MgFeSiO4. Only five grain sizes are shown for clarity. |
 |
Fig. 12 χ2 map of the inner radius Rin versus the inner surface density power-law pin. For each value of these two parameters, the model with the lowest |
The same trends are found as for the standard models previously, except that a higher inclination of 55° is now slightly preferred. One model that stands out is incorporated as the best fit in Table 2. The SED of this model is included in Fig. 1. The flux deficit is clearly diminished, but not completely removed. All observables fit better except the differential phases for which there is little change, as attested by the χ2 values. Although this model fits noticeably better, in the remainder of this paper we build upon our base model with the standard ISM dust composition. Our main conclusion is that our derived model parameters are not very dependent on the assumed dust composition.
6.3.3. Inner rim degeneracies
In Sect. 6.3.1 we parameterized the radial surface density distribution with two power-laws in order to smooth the inner rim, which is necessary to fit the interferometric data. The various parameters are, however, not all fully constrained because of the limited uv and wavelength coverage of our data. The inner rim can thus appear different for similarly fitting models. Here we explore the parameter space further, i.e., of pin, to explicitly show the degeneracies.
We now extend our grid and compute models up to pin = −7.0. Figure 12 shows the resulting χ2 distribution for the extended grid, folded onto a 2D surface containing pin and Rin. So, for each value of pin and Rin, the best-fit model for all the other free parameters is included in the figure. We note that for graphical purposes we take the sum of the three values of χ2. From the figure it is obvious that one has to be careful with the interpretation of the best-fit inner rim radius. Our data clearly exclude optically thick emission within ~30 AU (models with pin up to −3.0), but allow optically thin emission up to inner radii of 20 AU, when the extreme values for pin are used. For such models the optical τ = 1 surface in the midplane is generally still located at ~30–35 AU.
7. The forsterite features
In this section we describe how our base model (Best Double) looks when forsterite is included as a dust species. We investigate the signatures of forsterite in the mid-IR, at 69 μm and in the interferometric data. We do not attempt to fit the feature shapes in full detail, but merely focus on the relative feature strengths.
7.1. The base model with forsterite
In Fig. 13 are shown the continuum-subtracted mid-IR spectral bands of forsterite as observed with ISO. In order to extract the features from the ISO spectrum we take the following wavelength regions to linearly estimate the continua (all in μm): 14.5−15.4; 16.5–18.04; 20.1–21.9; 26.5–26.7; 29.4–31.3; 36.7–37.8; 68.0–68.4; 70.5–72.0. From blue to red wavelengths we identify features of forsterite at 16, 18, 24, 27, and 33 μm, and a band at 69.0 μm. The exact wavelength position of each feature is a function of grain size, temperature, and composition, but we use these wavelengths to refer to the different features.
 |
Fig. 13 Forsterite features. The left panel shows the mid-IR features in the ISO spectrum; the right panel contains the 69 μm band as observed by Herschel/PACS. The same models are overplotted as in Figs. 9 and 10, except for the base model without forsterite. |
Our base model is also included in Fig. 13, but now added with 1% of 0.1 μm forsterite grains that are distributed through the disk in the same way as the amorphous dust. This model reproduces the 18, 24, 27, and 33 μm bands well. The 16 μm band is too red in our model compared to the detection in the ISO spectrum. This was also reported by Gielen et al. (2007). Even though the peak wavelength position of the 16 μm band of forsterite is dependent on grain size, temperature, and composition, these parameters cannot explain its blueshifted location, as they shift the band to redder wavelengths.
The base model with forsterite also shows a strong 69 μm band, but it differs from the Herschel/PACS detection. The observed band is broader and its wavelength position redder than the one in our base model. The opacities of the 69 μm band significantly broaden and shift to the red with increasing temperature, which means that our model misses warm forsterite grains of several hundred degrees K. Such temperatures do not require it to be within the inner rim which has a temperature of ~400 K.
The 10 μm region also contains forsterite features; most prominently at 11.3 μm. The 10 μm region of the ISO spectrum is shown in Fig. 14. A strong and wide emission feature is seen from amorphous silicate, centered at 9.7 μm, with on top a clear 11.3 μm band of forsterite. The base model without forsterite reproduces the amorphous silicate band very well. Adding forsterite to our base model introduces an 11.3 μm band on top of the 9.7 μm band (see the green curve in Fig. 14). It compares well with the measured band, but is slightly narrower. The addition of forsterite to our base model reduces the quality of the fit to the 9.7 μm band in Fig. 14. This shows that the other fit parameters also require minor adjustments because of the added forsterite, but such details are beyond the scope of this work.
As discussed in Sect. 4, the contribution from forsterite to the 10 μm complex can also be seen in the differential phases (see Fig. 6), and weakly in the visibilities of the 45 m baseline. The very similar baseline-dependent behavior of the forsterite compared to the amorphous component, at first sight, suggests that the forsterite emission has a very similar spatial distribution to the amorphous feature emission.
In Figs. 9 and 10, the dashed green lines correspond to the visibilities and differential phases, respectively, of the base model to which 1% of forsterite is added. The model distinctly shows the 11.3 μm band in the visibilities of the 60 m and 36 m baselines, but not in the visibilities of the 45 m baseline, in stark contrast to the observations. The 11.3 μm band clearly appears in the differential phase of the 45 m baseline, although the observations show no such feature. Additionally, the observed differential phase of the 36 m baseline contains a clear 11.3 μm forsterite signature, which is only very weakly present in the model.
The discrepancies can be interpreted in the following way. Because of the much higher opacity in the features compared to the surrounding continuum, the τ = 1 surface is reached at much shallower depths into the disk. As a result, a wavelength-differential signal is induced in the interferometric data because the forsterite emission arises from a more compact, centrally concentrated region in the disk. This is illustrated by the left panel in Fig. 15. It shows the relative distribution of the azimuthally integrated 11.3 μm flux as a function of the vertical and radial position in the disk. MCMax can compute these flux contributions as output when ray-tracing the spectrum. The continuum and feature contributions are shown separately in the upper and lower panels, respectively. The continuum contribution is computed by linear interpolation from the flux distributions at two neighboring continuum wavelengths. The feature contribution is then obtained by subtracting the continuum contribution from the total. Even though the low-intensity tail in the feature is somewhat larger than in the continuum (e.g., the dark blue contour), the region where most of the flux originates is more compact and at higher disk layers in the feature than in the continuum. The difference in flux distribution seems to be rather subtle (considering the scales), although the effect pops up distinctly in the observables.
Summary
We can summarize the discussion of the forsterite signatures in this section by saying 1) that our model shows strong features in the visibilities while the observations do not; 2) that the 11.3 μm band is strongly present in the model differential phase of the 45 m baseline and only weakly in that of the 36 m baseline, which is opposite to the observations; and 3) that the spectrum is well fit over a wide wavelength range, except for the red component in the 69 μm band. Our model thus needs corrections. The 69 μm band requires more warm forsterite, which could be added to the model by increasing the forsterite abundance in the inner part of the disk. The interferometry on the other hand indicates that the hot forsterite in our model gives an emission distribution that is too centered; the 11.3 μm emission needs to be more extended than is currently the case in our base model. Although it is outside the scope of this paper to perfectly reproduce all forsterite features, we will show in the next section the effect of several parameters.
 |
Fig. 14 The 10 μm complex. The full black line is the smoothed ISO spectrum (as in Fig. 6). The overplotted models are the same as in Figs. 9 and 10. The inset shows the continuum-subtracted spectra (using a simple linear continuum fit). |
7.2. Effect of model parameters on the features
Adding forsterite to our base model does not have the desired effect on the interferometric observables. We identified the discrepancy as the result of an optical depth effect. Here we briefly explore two ways to change the optical depth in the innermost disk regions at 11.3 μm. First we will decrease the forsterite opacity at 11.3 μm by increasing the size of the crystals. Second, we will explore whether the degeneracies in inner disk structure can help to solve the forsterite problem.
 |
Fig. 15 Flux contribution at 11.3 μm as a function of radius and height in the disk, for the continuum (from interpolating nearby continuum wavelengths) and the feature. The red dashed and dotted lines represent the vertical and radial τ = 1 surfaces at 11.3 μm, respectively. Left panel: the base model with 1% of 0.1 μm forsterite grains. Right panel: the “New Forst.” model explained in Sect. 7.2. The arrow indicates the viewing direction. |
7.2.1. The forsterite grain size
Grain size has the effect of weakening, shifting, and broadening the spectral features of crystalline dust grains (see, e.g., Maaskant et al. 2015). The forsterite added to our base model (Sect. 7.1) had a grain size of 0.1 μm. If instead we use forsterite with a grain size distribution from 0.1 to 2.0 μm (with a power-law slope of −3.5), then the opacity in the 11.3 μm band drops by a factor of two. This opacity reduction decreases the optical depth at 11.3 μm in the inner disk. As can be seen in Figs. 9 and 10, this decline in optical depth diminishes the forsterite signal in the visibilities and differential phases (the red dotted line), but not sufficiently. The differential phase signal at the 36 m baseline remains unaffected, and the faulty signal at the 45 m baseline is only slightly diminished. The mid-IR spectral features (Fig. 13) are not changed much, although the 24, 27, and 33 μm complexes become slightly weaker. The 69 μm band remains unchanged, as expected.
7.2.2. The inner disk density distribution
Another way to improve the forsterite signatures may be to alter the inner density structure of the disk. The forsterite emission at 11 μm arises solely from the innermost disk regions and may be affected by our particular choice of base model. The optical depth profiles may be quite different at 11 μm between the various models included in Fig. 12. After all, one must not forget that the parameters of our base model were determined from a fit to the interferometric data in which forsterite was neglected.
For all the models within the extended grid computed in Sect. 6.3.3 for which each of the values of χ2 is smaller than 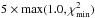 , we now recompute the visibilities and differential phases with 1% of 0.1 μm grains of forsterite included. These models are indicated as white dots in Fig. 12. From this newly computed set, models with very optically thin inner rims (pin< −4.0 and Rin< 30 AU) do not lead to a significantly improved interferometric forsterite signature, nor do the more extended rims (Rin> 36 AU). For the following qualitative discussion we select the model that matches the differential phases best, since the immediate effect of the forsterite on the fit quality is more apparent in the differential phases than in the visibilities. This model is included in Figs. 9, 10, 13, and 14 as the thin black full line (referred to as “New Forst” in the legends). For this model, a small signal appears in the 36 m baseline measurement, while the erroneous signal at the 45 m baseline is significantly diminished. The visibility signals are also reduced to an acceptable level. At the same time the mid-infrared features are little affected. Only the 69 μm fit is worse: the blue part of the band becomes less strong, and the broad red-shifted component is still not reproduced. Finally, we note that the amorphous contribution to the 10 μm complex is too strong for this model.
, we now recompute the visibilities and differential phases with 1% of 0.1 μm grains of forsterite included. These models are indicated as white dots in Fig. 12. From this newly computed set, models with very optically thin inner rims (pin< −4.0 and Rin< 30 AU) do not lead to a significantly improved interferometric forsterite signature, nor do the more extended rims (Rin> 36 AU). For the following qualitative discussion we select the model that matches the differential phases best, since the immediate effect of the forsterite on the fit quality is more apparent in the differential phases than in the visibilities. This model is included in Figs. 9, 10, 13, and 14 as the thin black full line (referred to as “New Forst” in the legends). For this model, a small signal appears in the 36 m baseline measurement, while the erroneous signal at the 45 m baseline is significantly diminished. The visibility signals are also reduced to an acceptable level. At the same time the mid-infrared features are little affected. Only the 69 μm fit is worse: the blue part of the band becomes less strong, and the broad red-shifted component is still not reproduced. Finally, we note that the amorphous contribution to the 10 μm complex is too strong for this model.
We show the flux distribution at 11.3 μm in the right panel of Fig. 15. This model fits the interferometric data better than the base model with forsterite because the forsterite emission is now distributed over a more extended area (see in particular the light blue region in the upper part of the disk).
This is the result of the combined effect of the three parameters that have changed compared to the base model:
-
The decrease in maximum grain size from 1.0 to 0.3 mm causes an increase in the dust mass of small particles (for the same total dust mass and power-law index of the grain size distribution), hence an increase in the continuum optical depth. The forsterite remains unaffected by this parameter.
-
The steeper pin = −4.0 results in a decreased density, and hence optical depth, at the inner rim. This parameter also shifts some forsterite from the inner regions in the direction of the turnover radius. Hence, the abundance in the upper disk layers increases at radii ~40 AU, and thereby also the emission from these regions.
-
The decreased inclination of 45° causes the viewing direction to be more vertical. As a result, the integrated optical depth in the line of sight towards farther-out disk radii decreases, so that more photons can escape these regions in the direction of the observer (compare the regions delineated by the vertical and radial τ = 1 surfaces included as red dotted and red dashed lines in Fig. 15, respectively).
In summary, although the New Forst model fits the interferometric data better than our base model with 1% of forsterite, this model does not reflect the global structure of the disk better than our base model (e.g., the mm fluxes are now too small). The new parameter values do, however, alter the spatial distribution of the forsterite emission in the innermost regions, differentially with respect to the continuum. The optical depth due to the forsterite is decreased in the innermost upper disk regions, without too much change to the continuum at these wavelengths. This model illustrates how the spatial distribution of the forsterite emission should change to fit the interferometric data better. We conclude that the details of the inner rim density structure may subtly affect the distribution of the forsterite emission, and thereby the features in the interferometric data.
8. Discussion
In this paper we have clearly demonstrated that the mid-IR brightness distribution of the AC Her system appears asymmetric, and that this is due to the circumstellar material being in a passive dusty puffed-up circumbinary disk that we see under a well-constrained inclination of 50 ± 5°. We have shown this by applying state-of-the-art Monte Carlo radiative transfer disk models in hydrostatic equilibrium to three interferometric measurements from the MIDI instrument on the VLTI of very high quality, combined with the full SED and the mid- to far-IR spectral features of crystalline forsterite. Overall we find a very good agreement between our best-fit models and the observables. To accurately fit the MIDI visibilities, and in particular the differential phases at the different baseline position angles, requires a highly asymmetric apparent source morphology which is, as we have shown, naturally generated by a disk model.
The inclusion of mm-sized grains that are allowed to settle to the midplane of the disk leads to a very good match with the full measured SED, just like for the 89 Her system (Hillen et al. 2014). Although there is still a flux-deficit in the 2−8 μm wavelength range, we argued that the discrepancy is within the uncertainties of our models and assumptions. We investigated this by putting into question the assumed composition of the amorphous dust component, but there are other possible origins. For one, our models ignore the effect of molecular opacity on the thermal structure of the disk (as well as the resulting direct emission contribution to the spectrum). Malek & Cami (2014) claim this to be significant for the similar HR4049 system. Similarly, optically thin dust might be present within the inner hole, e.g., in an accretion flow. Our exploration of inner rim shapes in Sect. 7.2, and the degeneracies with respect to the current data, shows that there are still several degrees of freedom.
Our results, nevertheless, resolutely confirm the disk hypothesis for the AC Her system that was raised by Van Winckel et al. (1998) based on less direct arguments. AC Her is, moreover, one of the objects among the sample of suspected post-AGB binaries with disks of de Ruyter et al. (2006) for which the near-IR excess is least pronounced. Therefore, our results corroborate that most of the objects listed by de Ruyter et al. (2006) must indeed be disks as well.
Our results, however, also raise several questions.
8.1. The inner hole
One of the most striking results of this paper is the large inner radius of the circumbinary disk in AC Her. The typical τ = 1 radius in the midplane of the disk is in the 30–35 AU range, irrespective of any speculative inner optically thin contribution. Following Eq. (12) of Dullemond & Monnier (2010), one can simply estimate the dust sublimation radius expected for the stellar parameters of AC Her, which we find to be in the range of 1.5–5.0 AU, depending on the assumed value of their ϵ. This parameter incorporates all inner rim properties that have an influence on the evaporation of the dust (like grain size and composition). We thus find that the actual inner rim in the AC Her system lies about an order of magnitude beyond the expected dust condensation radius. We note that both radii are dependent on the adopted distance, so their ratio is independent of it.
AC Her is the first post-AGB disk system for which it is now firmly established that the inner disk radius is significantly beyond the dust condensation radius. One can only speculate about the physical origin of this large inner hole. Several mechanisms have been proposed in the literature for the formation of holes or gaps in protoplanetary disks, such as photoevaporation, accretion, or the dynamical influence of a planetary-mass companion. More systems like AC Her need to be studied with high angular resolution techniques and across the full electromagnetic spectrum to show which of these mechanisms are at work in post-AGB disks.
8.2. The total disk mass and its composition
One of the parameters that is fairly well constrained in our modeling is the dust mass thanks to the inclusion of the mm fluxes. In each of the grids our best-fit dust mass is larger than 10-3 M⊙. In fact, the only model in which the dust mass is smaller than 2.5 × 10-3 M⊙ is the best-fit single-power-law model, which clearly lacks emission in the mm regime. In summary, under the assumptions made in our modeling (in particular the composition of our dust, pout = 1.0, Rout = 200 AU, and α = 0.01), the minimum dust mass needed to fit the SED is ≥10-3 M⊙.
If the gas/dust ratio were 100, then the total disk gas mass would be 0.1 M⊙. Our modeling indicates, however, that the global gas/dust ratio is likely smaller. Although our best-fit model has a ratio of 10.0, there are models that formally fit our acceptance criteria with a ratio of 1.0. We come to the conclusion that the total gas mass must be at least 10-3 M⊙, and can be one or two orders of magnitude larger, depending on the theoretically ill-understood parameter α. We note that α and the gas/dust ratio have a similar influence in our models (see, e.g., Mulders & Dominik 2012). Interestingly, the total gas mass found for AC Her by Bujarrabal et al. (2013a) is ~8 × 10-4 M⊙. If we correct for their smaller adopted distance, their gas mass is about a factor of five smaller than our best-fit value. This is within the respective errors of both methods. It would nevertheless be useful to examine how much their results may be influenced by optical depth effects. In addition, resolved observations with ALMA would allow us to constrain some of the model parameters assumed in this work, like pout and Rout, even though we do not expect them to significantly alter our results.
One assumption that may significantly affect our derived mass, is the dust composition. Although we have checked and ruled out a serious influence of the chosen silicate (+metallic Fe) composition, one cannot exclude other dust species with a high (sub-)mm opacity that would lower the effective dust mass. For protoplanetary disks a component of amorphous C is often assumed. There are claims that in certain post-AGB disks amorphous C may be present as well (e.g., Acke et al. 2013). Hillen et al. (2014) showed that for the 89 Her disk, models with amorphous C can fit the observations equally well. The presence of C-rich dust in an otherwise O-rich environment, however, requires an explanation.
Finally, one can do an interesting exercise to check how realistic our derived dust mass is, keeping in mind that all the circumstellar material has its origin in the central post-AGB star. Assuming that the post-AGB star started its evolution with a solar metallicity, one can compute how much mass of Fe, Si, and Mg the star has lost throughout its evolution. Assuming the star lost 1 M⊙ of hydrogen, we arrive at ~1.8, 0.9, and 1.0 × 10-3 M⊙ of Fe, Si, and Mg, respectively. Assuming that the disk’s current dust mass is indeed 2.5 × 10-3 M⊙, and taking our standard dust composition, then about 0.5 × 10-3 M⊙ of Fe, Si, and Mg would be currently locked up in dust in the disk. This means that between 30 and 50% of all the Fe, Si, and Mg that was released by the star should still be present in the form of dust in the disk. Such large fractions seem unrealistically high, as they would imply that the disk mass had once been close to 0.5 M⊙, and definitely warrants further investigation. All potential sources of bias mentioned previously should be checked thoroughly.
8.3. Forsterite
AC Her joins the short list of disk objects for which the mineralogy of crystalline dust species like forsterite has been studied with interferometry. Although rare, such studies are powerful. Based on a few MIDI observations, van Boekel et al. (2004) for the first time directly measured a gradient in the chemical composition of the dust in several protoplanetary disks. Using the interferometric correlated fluxes as a proxy for the inner disk spectrum, they fitted the mineralogy in the inner and outer disk separately. Deroo et al. (2006) later did a similar analysis for the post-AGB system HD52961, and found that the crystalline dust in that disk is also concentrated in the hotter inner regions. These disks were less resolved than in the current work, so their analysis was not complicated by the detailed morphologies of the objects. The few interferometric measurements analyzed in this paper are, however, dominated by the geometry, so that radiative transfer models are needed to draw conclusions concerning the morphology and mineralogy of the disk. We have shown in this paper that wavelength-differential interferometric observables have a strong diagnostic value in order to constrain the spatial distribution of minerals thanks to their high reliability and resolving power. Even without the presence of a signal (see, e.g., our longest baseline), constraints can be derived.
We find that by including forsterite with a similar radial distribution throughout AC Her’s disk to the amorphous dust and a global abundance of 1%, the mid-IR features of crystalline forsterite are well reproduced. This model does not reproduce the 69 μm band well, nor the forsterite signatures in the MIDI data. The observed 69 μm band shows that there must be an enhanced abundance of warm forsterite of several hundreds of kelvin. Based on our parameter study in Sect. 7.2, we conclude that the interferometric data require a similar change to the forsterite emission at 11.3 μm: less emission from the hot innermost AU of the disk and more emission from the warm forsterite in the upper disk layers a few AU farther out (See Fig. 15).
8.4. Comparison with protoplanetary disks
In this section we compare AC Her with some recent results concerning protoplanetary disks. The most extensive statistical and purely empirical comparison between the galactic post-AGB disks and a set of protoplanetary disks was done by de Ruyter et al. (2006). They used the empirical separation in two groups of Herbig AeBe disks determined by Acke et al. (2004) to show that all post-AGB disks are similar to those of the second group. These group II sources are generally believed to be flatter and more continuous disks than the group I objects, which have much more pronounced and redder far-IR excesses due to their flaring upper layers. Recently, Maaskant et al. (2013) concluded that all group I sources are indeed likely flaring disks with gaps. It is interesting to note that AC Her is one of the post-AGB objects that is most closely located to the dividing line between the group I and II sources. The inner hole in AC Her is in absolute scale similar in size to the largest gaps found in the small sample of group I Herbig sources by Maaskant et al. (2013). However, in terms of the Rin/Rcond ratio, AC Her’s hole is smaller than the gaps in the Herbig sources as a consequence of the large difference in stellar luminosity. A very relevant question is, why are there no group I post-AGB disks? In addition to the presence of a gap, the defining characteristic of a Herbig group I source seems to be a high degree of flaring. Our results combined with the statistics from de Ruyter et al. (2006) suggest that, although there are post-AGB disks with large inner holes, the presence of holes does not seem to go hand in hand with a large degree of flaring.
Next we compare our results concerning the forsterite in AC Her to the protoplanetary disk sample studied by Maaskant et al. (2015). Using the observations from the Herschel DIGIT programme, Maaskant et al. (2015) analyzed a sample of Herbig disks (containing both group I and II sources) to search for trends in the forsterite emission characteristics and study how these compare with typical radiative transfer models assuming various disk evolution scenarios. One of their main results concerns the relation between the 69 μm band luminosity and the integrated feature strength ratio of the 23 over the 69 μm bands (their Fig. 3). They find a clear separation in forsterite behavior between group I and II sources. Group I objects are scattered in this diagram, but typically show larger 69 μm band strengths. Group II objects on the other hand have very weak 69 μm bands, often below the detection threshold of the PACS instrument, even though the corresponding 23 μm features are well detected in the Spitzer spectra. Maaskant et al. (2015) conclude that the weak 69 μm bands in group II sources are the result of inefficient radial mixing in such disks, so that they only contain warm forsterite.
The integrated feature strengths of AC Her (L69/L⋆ ~ 2.6 × 10-5 and I23/I69 ~ 75) make it falls in a region only populated by group I protoplanetary disks. Although some group II Herbig sources have similar I23/I69 ratios, high 69 μm luminosities only seem to be reached by group I objects. Interestingly, out of the six post-AGB disk sources targeted with Herschel/PACS, the 69 μm band was only detected in AC Her and the Red Rectangle (Blommaert et al. 2014), which both have peculiar disks. The sample of Blommaert et al. (2014) combined with our detailed modeling of AC Her confirms the link between the presence of a detectable 69 μm band and the inner structure of the disk, as found by Maaskant et al. (2015) and following the work of Mulders et al. (2011).
Mulders et al. (2011) fitted for the first time the mid-IR features and 69 μm band of a disk source, HD 100546, with detailed radiative transfer models to investigate the influence of optical depth effects arising from the disk structure. They showed that the mid-IR bands can be reproduced with a forsterite abundance of 30% at the inner wall and falling as r-2 throughout the inner half of the disk. For this model the 69 μm band is, however, too narrow and its wavelength position too blue compared to the observations. They varied the spatial distribution of the forsterite in various ways and found that a model with a very high (40–60% by mass) local abundance of forsterite in the inner wall and inner disk surface layers can reproduce the mid-IR features and the 69 μm band simultaneously. Our forsterite modeling highlights the similarity with the forsterite features of AC Her, although the L69 is lower. The forsterite abundance in the inner disk surface layers of AC Her might thus be similarly enhanced as in HD 100546. It is beyond the scope of this paper to investigate such a model in detail for AC Her. Interferometric observations with a better uv coverage would be needed to constrain the details. It would be worthwhile to do a similar investigation of the forsterite signatures in the interferometric data of HD 100546. An extensive MIDI data set exists for this object (Mulders et al. 2013; Panić et al. 2014). Our results confirm the suggestion by Mulders et al. (2011) that the strength of crystalline features may be a reflection of the spatial distribution of the forsterite in the disk, intimately related to the structure of the disk, rather than the overall crystal abundance.
A higher abundance of forsterite in the inner disk, just like in several protoplanetary disks, would imply that the forsterite in AC Her’s disk is largely created as the result of disk processing, after the disk formed. Nonetheless, the current inner radius of AC Her’s disk at ~34 AU makes it unlikely that the observed crystalline material was assembled where it is presently observed. A larger and more quantitative exploration of possible spatial distributions of the forsterite needs to be performed before a final conclusion can be drawn about its formation history. Our finding of an enhanced abundance in the inner disk nevertheless suggests that it may not have formed alongside with the amorphous dust when the disk was created.
8.5. Evolutionary constraints
Finally, using our newly derived constraints one can ponder the evolution of the AC Her system into its current state. Adopting the PARSEC stellar evolutionary tracks (Bressan et al. 2012), one finds that our derived stellar luminosity is reached at the tip of the red giant branch for a star with initial mass Mi ~ 1.0−1.4M⊙. This makes AC Her a candidate to be a Galactic counterpart to the rather abundant post-RGB disk systems found in the Small Magellanic Cloud by Kamath et al. (2014). This conclusion is only tentative, however, given the large luminosity error due to the significant spread in the PL-relation.
Assuming then the log g and stellar radius as listed in Table 1, one finds a primary mass of 0.6 ± 0.2 M⊙. Combining this value with our interferometrically determined inclination (assuming co-planarity between the disk and the binary) and the orbital solution of Van Winckel et al. (1998), we find a companion mass of 1.2 ± 0.2 M⊙, or a M1/M2 mass ratio of 0.5 ± 0.1. The primary’s Roche lobe radius is then 180 ± 20 R⊙, which means that the system is currently not interacting. This is consistent with the lack of observational evidence of ongoing activity.
The radius that the primary would have had at the tip of the RGB ranges between 170 and 150 R⊙, which is remarkably similar to the current size of the Roche lobe. This suggests that the disk in AC Her was indeed formed by Roche-lobe overflow. Where all the envelope mass of the primary went is not clear. The secondary cannot have accreted much more than ~0.2 M⊙ because otherwise the initial mass ratio would have been so high that the Roche-lobe overflow would have been unstable and the system would have evolved into a common envelope scenario.
In a series of analytical calculations and smooth particle hydrodynamics simulations, Artymowicz et al. (1991) and Artymowicz & Lubow (1994, 1996) have shown various effects resulting from interactions between circumbinary disks and their central binaries. These studies found that the resonant interactions can lead to the formation of a stable inner hole in the disk with a size up to ~3 times the binary separation. For AC Her this would be at maximum ~8 AU, which is beyond the dust sublimation radius but well within our inner rim radius. Artymowicz & Lubow (1996) later found that for thicker disks than in the original simulations, accretion streams can exist within the otherwise stable hole. Can such accretion streams be responsible for the large inner hole in AC Her’s disk, possibly induced by the large-scale luminosity variations throughout the pulsation cycle?
9. Conclusions
In this paper we have extensively analyzed the circumstellar environment of the AC Her post-RGB/AGB binary system. First, we carefully collected pulsation-phase dependent photometric data to get a precise determination of the stellar parameters at the pulsation phase where our selected near- and mid-IR data were obtained. Given the large pulsation amplitudes of RV Tauri variables this is essential in order to reliably model the circumstellar environment. A basic analysis of our mid-IR interferometric data showed that the circumstellar material needs to be present in a globally asymmetric form that is moreover compact. This is consistent with the current state of the art concerning these objects which affirms that they have gas and dust in Keplerian circumbinary disks. With a detailed radiative transfer analysis we firmly established this conclusion: a (semi-)stable circumbinary disk in hydrostatic equilibrium can explain all the existing observational constraints on this system. In this work we focus on a simultaneous fitting of the full SED and our mid-IR interferometric data, which succeeds very well by including a rounding off of the inner disk rim.
We determined disk parameters like dust mass, inner radius, maximum grain size, inclination and position angle on the sky, and found our results to be robust against several of our modeling assumptions. We found that the disk in AC Her is seen under a significant inclination, that it has a rather high total dust mass and a large dust-poor inner hole. These derived values raise several questions concerning the current state and the evolution of the system. Although the precision on our distance and luminosity estimate is insufficient to make very strong statements, the newly derived stellar and disk parameters at least suggest that 1) AC Her may either be a post-RGB or a post-AGB star; 2) the circumbinary disk is in an evolved state as shown by the large inner radius and low gas/dust ratio; 3) the disk in AC Her used to be very massive; and 4) the system may be an exemplary case of binary-disk (resonant) interaction.
In addition to the global structure of the disk in AC Her, we also considered its mineralogy. The MIDI spectral range includes the 11.3 μm feature of crystalline forsterite, which also makes these data a powerful probe of the spatial distribution of the crystalline material in the disk. In combination with the mid-IR and the 69 μm spectral features, we have found evidence in favor of an enhancement of the forsterite abundance in the inner disk surface layers compared with a distribution that is similar to the amorphous dust. Based on the features alone, similar modifications have been proposed for the forsterite distribution in protoplanetary disks, most notably for the well-studied star HD 100546. Although our results are inconclusive, we have clearly demonstrated the value that interferometric data can have for mineralogical studies. With a more extensive filling of the uv-plane, such as the MATISSE 2nd generation VLTI instrument will be able to provide, the spatial distribution of crystalline material in disks can be studied more efficiently and in much greater detail. Ultimately this will give an interesting and unique perspective on the formation and evolutionary history of post-AGB disks.
Acknowledgments
We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research. J.M. is funded as a Ph.D. fellow of the Research Foundation Flanders (FWO). We thank Rens Waters for the discussions about this research. M.H. also thanks Sara Regibo for her help with the SPIRE data. M.H. and H.V.W. acknowledge support from the Research Council of the KU Leuven under grant number GOA/2013/012.
References
- Ábrahám, P., Juhász, A., Dullemond, C. P., et al. 2009, Nature, 459, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Acke, B., van den Ancker, M. E., Dullemond, C. P., van Boekel, R., & Waters, L. B. F. M. 2004, A&A, 422, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acke, B., Degroote, P., Lombaert, R., et al. 2013, A&A, 551, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 1998, AJ, 115, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., Clarke, C. J., Lubow, S. H., & Pringle, J. E. 1991, ApJ, 370, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Blommaert, J. A. D. L., de Vries, B. L., Waters, L. B. F. M., et al. 2014, A&A, 565, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Neri, R. 2005, A&A, 441, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Alcolea, J., Van Winckel, H., Santander-García, M., & Castro-Carrizo, A. 2013a, A&A, 557, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., et al. 2013b, A&A, 557, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Van Winckel, H. 2015, A&A, 575, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Close, L. M., Biller, B., Hoffmann, W. F., et al. 2003, ApJ, 598, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, D. W. 1979, ApJS, 41, 97 [NASA ADS] [CrossRef] [Google Scholar]
- de Ruyter, S., van Winckel, H., Dominik, C., Waters, L. B. F. M., & Dejonghe, H. 2005, A&A, 435, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ruyter, S., van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vries, B. L., Blommaert, J. A. D. L., Waters, L. B. F. M., et al. 2014, A&A, 561, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Acke, B., Samadi, R., et al. 2011, A&A, 536, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., van Winckel, H., Min, M., et al. 2006, A&A, 450, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., Acke, B., Verhoelst, T., et al. 2007a, A&A, 474, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., van Winckel, H., Verhoelst, T., et al. 2007b, A&A, 467, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 33 [Google Scholar]
- Gail, H.-P. 2004, A&A, 413, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., & Mérand, A. 2012, A&A, 538, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrz, R. D. 1971, Ph.D. Thesis, University of Minnesota [Google Scholar]
- Gielen, C., van Winckel, H., Waters, L. B. F. M., Min, M., & Dominik, C. 2007, A&A, 475, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., van Winckel, H., Min, M., Waters, L. B. F. M., & Lloyd Evans, T. 2008, A&A, 490, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., Bouwman, J., van Winckel, H., et al. 2011, A&A, 533, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giridhar, S., Lambert, D. L., & Gonzalez, G. 1998, ApJ, 509, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, M. J., Evans, A., Albinson, J. S., & Bode, M. F. 1987, MNRAS, 227, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Gorlova, N., Van Winckel, H., Vos, J., et al. 2013, in EAS Pub. Ser., 64, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Harker, D. E., & Desch, S. J. 2002, ApJ, 565, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hillen, M., Verhoelst, T., Van Winckel, H., et al. 2013, A&A, 559, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillen, M., Menu, J., Van Winckel, H., et al. 2014, A&A, 568, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jaffe, W. J. 2004, in SPIE Conf. Ser., 5491, ed. W. A. Traub, 715 [Google Scholar]
- Kamath, D., Wood, P. R., & Van Winckel, H. 2014, MNRAS, 439, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Koike, C., Chihara, H., Tsuchiyama, A., et al. 2003, A&A, 399, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maaskant, K. M., Honda, M., Waters, L. B. F. M., et al. 2013, A&A, 555, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maaskant, K. M., de Vries, B. L., Min, M., et al. 2015, A&A, 574, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malek, S. E., & Cami, J. 2014, ApJ, 780, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Waters, L. B. F. M., de Koter, A., et al. 2007, A&A, 462, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molster, F. J., Yamamura, I., Waters, L. B. F. M., et al. 1999, Nature, 401, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., Tielens, A. G. G. M., & Barlow, M. J. 2002a, A&A, 382, 184 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., & Tielens, A. G. G. M. 2002b, A&A, 382, 222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., Tielens, A. G. G. M., Koike, C., & Chihara, H. 2002c, A&A, 382, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlok, A., Koike, C., Tomioka, N., Mann, I., & Tomeoka, K. 2010, Icarus, 207, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Waters, L. B. F. M., Dominik, C., et al. 2011, A&A, 531, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Paardekooper, S.-J., Panić, O., et al. 2013, A&A, 557, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Panić, O., Ratzka, T., Mulders, G. D., et al. 2014, A&A, 562, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahai, R., Claussen, M. J., Schnee, S., Morris, M. R., & Sánchez Contreras, C. 2011, ApJ, 739, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Samus, N. N., Durlevich, O. V., et al. 2009, VizieR Online Data Catalog, II/25 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shenton, M., Albinson, J. S., Barrett, P., et al. 1992, A&A, 262, 138 [NASA ADS] [Google Scholar]
- Suto, H., Sogawa, H., Tachibana, S., et al. 2006, MNRAS, 370, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
- Taranova, O. G., Shenavrin, V. I., & Tatarnikov, A. M. 2010, VizieR Online Data Catalog, 903, 60144 [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 336, L17 [NASA ADS] [Google Scholar]
- van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Zsoldos, E. 1993, A&A, 268, 149 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SED of AC Her. The gray dot-dashed line shows the input Kurucz model, reddened with an interstellar contribution of E(B − V) = 0.135 (see Sect. 3). The dotted blue line is the best single-power-law model (see Sect. 6.2). The dashed red line corresponds to our base model (i.e., the best double-power-law model obtained in Sect. 6.3). The full green line is the best-fit model with the alternative dust composition (Sect. 6.3.2). The inset shows a zoom-in of the near- to mid-IR wavelength range. We note that the ISO spectrum is included in our fit through the indicated anchor points (see the legend). |
| In the text | |
 |
Fig. 2 Confidence interval of the stellar SED fit: Teff versus log g. |
| In the text | |
 |
Fig. 3 Confidence interval of the stellar SED fit: log g versus θ⋆. |
| In the text | |
 |
Fig. 4 Upper panel: measured MIDI visibilities of AC Her, color coded with respect to the baseline as listed in the legend, overplotted (full thick lines) with the best-fit single-power-law radiative transfer model (see Sect. 6), as a function of spatial frequency. Also shown in black are the uniform disk and uniform ring models mentioned in Sect. 4. Lower panel: residuals with respect to the radiative transfer model. |
| In the text | |
 |
Fig. 5 Upper panel: MIDI differential phases of AC Her, similarly color coded and overplotted with the same radiative transfer model as in Fig. 4, as a function of wavelength. Lower panel: residuals with respect to the radiative transfer model. |
| In the text | |
 |
Fig. 6 Comparison between the differential phase signal on the shortest MIDI baseline and the ISO spectrum in the same wavelength range. The red squares show the MIDI differential phases after subtraction of a linear trend (fit to the blue points), inversion, and normalization. The ISO spectrum was first smoothed with a Gaussian kernel (σ = 0.025 μm, comparable to the resolution of the MIDI grism at 13 μm). The full black line shows this smoothed ISO spectrum after subtraction of a linear trend (fit to the green points) and normalization. The differential phase of the intermediate baseline can be scaled similarly, but without sign inversion and with a smaller normalization factor, because these spatial frequencies fall largely in the second lobe of the radial visibility curve along this direction. The ISO spectrum of the base model added with 1% of 0.1 μm forsterite grains (see Sect. 7) is shown as the dashed line. We note that this model is normalized independently. |
| In the text | |
 |
Fig. 7 χ2 map of the disk inclination versus its orientation on the sky. We note that we adopt the convention that a PA of 0° corresponds to a disk oriented with its major axis along the N-S direction and with its far (prominent) side directed east. |
| In the text | |
 |
Fig. 8 A visual rendering of our best-fit double power-law model at a wavelength of 12.5 μm. The intensity is shown on a linear scale. North is up and east is to the left. The field-of-view of this image is 200 by 200 mas. |
| In the text | |
 |
Fig. 9 MIDI visibilities of AC Her at the three baselines (one in each panel) as a function of wavelength. Overplotted are predictions for four double-power-law radiative transfer models: the standard best-fit model (full blue lines, Model 2 in Table 2); the standard model added with 1% of 0.1 μm forsterite grains (dashed green lines); the standard model added with 1% of forsterite grains with a size distribution between 0.1 and 2.0 μm (dotted red lines); and the New Forst model from Sect. 7.2.2 which has 1% of 0.1 μm forsterite grains, but with a different spatial distribution (thin black lines). |
| In the text | |
 |
Fig. 10 MIDI DPs of AC Her at the three baselines (one in each panel) as a function of wavelength. Overplotted are the predictions for the same radiative transfer models as in Fig. 9. |
| In the text | |
 |
Fig. 11 Mass absorption coefficients of the mixtures used in this work. Our “standard” mixture (the full lines) contains 15% metallic iron, while the alternative mixture (the dashed lines) consists of only MgFeSiO4. Only five grain sizes are shown for clarity. |
| In the text | |
 |
Fig. 12 χ2 map of the inner radius Rin versus the inner surface density power-law pin. For each value of these two parameters, the model with the lowest |
| In the text | |
 |
Fig. 13 Forsterite features. The left panel shows the mid-IR features in the ISO spectrum; the right panel contains the 69 μm band as observed by Herschel/PACS. The same models are overplotted as in Figs. 9 and 10, except for the base model without forsterite. |
| In the text | |
 |
Fig. 14 The 10 μm complex. The full black line is the smoothed ISO spectrum (as in Fig. 6). The overplotted models are the same as in Figs. 9 and 10. The inset shows the continuum-subtracted spectra (using a simple linear continuum fit). |
| In the text | |
 |
Fig. 15 Flux contribution at 11.3 μm as a function of radius and height in the disk, for the continuum (from interpolating nearby continuum wavelengths) and the feature. The red dashed and dotted lines represent the vertical and radial τ = 1 surfaces at 11.3 μm, respectively. Left panel: the base model with 1% of 0.1 μm forsterite grains. Right panel: the “New Forst.” model explained in Sect. 7.2. The arrow indicates the viewing direction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.