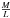| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425339 | |
| Published online | 25 May 2015 | |
The dark matter distribution in the spiral NGC 3198 out to 0.22 Rvir
1 SISSA/ISAS, International School for Advanced Studies, via Bonomea 265, 34136 Trieste, Italy
e-mail: ekarukes@sissa.it
2 INFN, Sezione di Trieste, via Valerio 2, 34127 Trieste, Italy
3 Department of Physics and Astrophysics, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
4 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281, 9000 Gent, Belgium
Received: 14 November 2014
Accepted: 11 March 2015
Aims. We use recent very extended HI kinematics (out to 48 kpc) along with previous Hα kinematics of the spiral galaxy NGC 3198 in order to derive its distribution of dark matter (DM).
Methods. First, we used a chi-square method to model the rotation curve (RC) of this galaxy in terms of different profiles of its DM distribution: the universal RC (URC) mass model (stellar disk + Burkert halo + gaseous disk), the NFW mass model (stellar disk + NFW halo + gaseous disk) and the baryon ΛCDM mass model (stellar disk + NFW halo modified by baryonic physics + gaseous disk). Second, to derive the DM halo density distribution, we applied a new method that does not require a global and often uncertain mass modelling.
Results. While according to the standard method, both URC and NFW mass models can account for the RC, the new method instead leads to a density profile that is sharply disagrees with the dark halo density distribution predicted within the Lambda cold dark matter (ΛCDM) scenario. We find that the effects of baryonic physics modify the original ΛCDM halo densities in such a way that the resulting profile is more compatible with the DM density of NGC 3198 derived using our new method. However, at large distances, r ~ 25 kpc, also this modified baryon ΛCDM halo profile appears to create a tension with the derived DM halo density.
Key words: dark matter / galaxies: kinematics and dynamics / galaxies: spiral
© ESO, 2015
1. Introduction
It has been known for several decades that the kinematics of disk galaxies leads to a mass discrepancy (e.g. Bosma 1978; Bosma & van der Kruit 1979; Rubin et al. 1980). While in their inner regions that range between one and three disk exponential scale lengths according to the galaxy luminosity (Salucci & Persic 1999), the observed baryonic matter accounts for the rotation curves (RCs; e.g. Athanassoula et al. 1987; Persic & Salucci 1988; Palunas & Williams 2000), we must add an extra mass component in the outer regions, namely a dark matter (DM) halo to account for that component. The kinematics of spirals is now routinely interpreted in the framework of a DM component. In the widely accepted Lambda cold dark matter (ΛCDM) scenario, the virialized structures are distributed according the well known NFW profile proposed by Navarro, Frenk, and White (Navarro et al. 19963). The ΛCDM scenario describes the large-scale structure of the Universe well (e.g. Springel et al. 2006), but it seems to fail on the scales of galaxies (de Blok & Bosma 2002; Gentile et al. 2004, 2005). Going into detail, the NFW density profile leads to the “core-cusp problem”: empirical profiles with a central core of constant density, such as the pseudo-isothermal (Begeman et al. 1991; Kent 1986) and the Burkert (Salucci & Burkert 2000), fit the available RCs much better than the mass models based on NFW haloes.
In the present paper, we derive the DM content and distribution in the spiral galaxy NGC 3198. This galaxy has been the subject of several investigations. It was studied by means of optical (Cheriguène 1975; Hunter et al. 1986; Bottema 1988; Wevers et al. 1986; Kent 1987; Corradi et al. 1991; Daigle et al. 2006) and HI-21 cm radio observations (Bosma 1981; van Albada et al. 1985; Begeman 1987, the latter established it as the object with the clearest evidence for DM, see also de Blok et al. 2008; Gentile 2008).
Our present analysis is mainly based on the HI observations by Gentile et al. (2013), part of the HALOGAS (Westerbork Hydrogen Accretion in LOcal GAlaxieS) survey. The main goal of HALOGAS is to investigate the amount and properties of extra-planar gas by using very deep HI observations. In fact, for this galaxy, they present a very extended RC out to 720 arcsec, corresponding to ~48 kpc for a galaxy distance at 13.8 Mpc (Freedman et al. 2001). The previous HI observations by de Blok et al. (2008) were only extended out to ~38 kpc, for the same galaxy distance. In Gentile et al. (2013) this extended RC was modelled in the framework of modified Newtonian dynamics (MOND). Here, we want to use such a uniquely extended kinematics to help resolving the DM core-cusp issue. To the very reliable kinematics available from 2 to 48 kpc we apply two different mass decomposition methods that will derive the DM halo structure. This is compared with a) the empirically based halo profiles coming from the URC; b) the NFW haloes and c) the baryon ΛCDM haloes, the outcome of scenarios in which baryonic physics has shaped the DM halo density.
 |
Fig. 1 Comparison between Hα and HI RCs black open triangles with error bars from Corradi et al. (1991), blue circles with error bars are from Daigle et al. (2006), and red circles with error bars are from Gentile et al. (2013). |
This paper is organized as follows. In Sect. 2 we present the HI and Hα kinematics used in this study. In Sect. 3 we model the RC by using the quadrature sum of the contributions of the individual mass components (stellar disk + dark halo + gas disk) where the dark halo has a NFW or a Burkert density profile, respectively. In Sect. 4 we obtain the results of standard mass modelling of the NGC 3198 RC. In Sect. 5 we use a recent mass modelling technique to obtain a very robust and careful determination of the DM halo density of NGC 3198 and to show that it is at variance with the NFW density profile in an unprecedented way. We consider the mass dependent density profiles obtained by hydro-dynamical simulations of ΛCDM haloes in Sect. 6. Our conclusions are drawn in Sect. 7.
2. Kinematics data
2.1. HI data
The HI data of NGC 3198 were taken in the framework of the HALOGAS survey (Heald et al. 2011) and they were presented in Gentile et al. (2013). The data were obtained with the WSRT (Westerbork Synthesis Radio Telescope) for 10 × 12 h, with a total bandwidth of 10 MHz subdivided into 1024 channels. The data cube used to derive the RC has a beam size of 35.2 × 33.5 arcsec, and we were able to detect emission down to ~1019 atoms cm-2.
To construct the gas distribution and the RC of this galaxy in a reliable way , we modelled the whole data cube by means of the TiRiFiC software (Józsa et al. 2007). We successfully modelled the HI observations of NGC 3198 with a thin and a thick neutral hydrogen disk, and, thanks to an increased sensitivity, we were able to trace the RC out to a distance of ~48 kpc (for the galaxy distance of 13.8 Mpc), i.e. to a larger radius than those reached in previous studies. More details about the data reduction analysis and modelling can be found in Gentile et al. (2013).
Stellar disk contribution Vd (km s-1; de Blok et al. 2008) and the circular velocity V (km s-1) mainly from Gentile et al. (2013), but also from Corradi et al. (1991) and Daigle et al. (2006), of the NGC 3198 with errors dV (km s-1).
2.2. Hα data
The Hα RCs of NGC 3198 have been published by many authors (Cheriguène 1975; Hunter et al. 1986; Bottema 1988; Wevers et al. 1986; Kent 1987; Corradi et al. 1991; Daigle et al. 2006). We notice that Corradi et al. (1991) and Daigle et al. (2006) measurements are a good representation of these data. In Fig. 1, these RCs are plotted along with the HI RC used in this work. Hα data provide us measurements of the circular velocity at five different new (inner) radii not mapped by the present HI RC and four more measurements at radii at which we can combine them with our HI data. The hybrid RC (HI+Hα data) is listed in Table 1. All together, HI and Hα RCs agree very well within the observational errors where they coexist. With respect to the HI RC of Gentile (2008), the present hybrid RC covers the innermost and the outermost regions significantly better; however, Hα RCs give us no new useful information for r< 2 kpc, owing to its large observational uncertainties and because in this very inner region the kinematics is strongly influenced by non-axisymmetric motions (see Corradi et al. 1991).
3. Mass models
We model the spiral galaxy NGC 3198 as consisting of three “luminous” components, namely the bulge and the stellar and the gaseous disks, which are embedded in a dark halo. To study the properties of luminous and DM in this galaxy, we model the RC in terms of the contributions from the stellar disk, the bulge, the gaseous disk, and the DM halo: 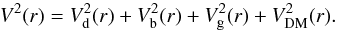 (1)
(1)
3.1. Luminous matter
We define Vd(r) as the contribution of the stellar disk to the circular velocity V(r). The surface brightness profile of NGC 3198 has been analysed very well by de Blok et al. (2008). We assume their one-component surface brightness profile to derive Vd(r). As a reference value we take the stellar mass-to-light ratio from de Blok et al. (2008): 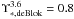 (referred to the Spitzer IRAC 3.6 μm band, which is a good proxy for the emission of the stellar disk). We thus set
(referred to the Spitzer IRAC 3.6 μm band, which is a good proxy for the emission of the stellar disk). We thus set 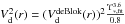 . Then, we leave the amplitude of the disk contribution to the circular velocity (i.e. the disk mass) as a free parameter to be derived by fitting the RC. No results of the present paper will change by assuming any other models of the dostribution of the stellar disk of NGC 3198 in de Blok et al. (2008) or in previous works.
. Then, we leave the amplitude of the disk contribution to the circular velocity (i.e. the disk mass) as a free parameter to be derived by fitting the RC. No results of the present paper will change by assuming any other models of the dostribution of the stellar disk of NGC 3198 in de Blok et al. (2008) or in previous works.
The contribution from the bulge component is Vb(r). We follow de Blok et al. (2008) and we consider their 1-component model which accounts for this inner stellar component. Hence, Vb(r) = 0 since the bulge is included in 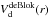 .
.
The helium corrected contribution of the gaseous disk derived from the HI surface density distribution Vg(r) taken from Gentile et al. (2013). We notice that, thanks to the accuracy of the HI measurements and to the excellent knowledge of the distance of this galaxy, this component is derived here much better than in the majority of the spirals studied to resolve the core-cusp controversy.
The “luminous” component of the circular velocity of this galaxy is then well known, except for the value of the disk mass which contributes to putting NGC 3198 at the front line of DM research.
3.2. Dark matter
We define 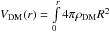 dR as the contribution to V(r) from the DM halo of the virial mass
dR as the contribution to V(r) from the DM halo of the virial mass 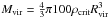 that could have a variety of density profiles. Here ρDM represents a DM halo density profile.
that could have a variety of density profiles. Here ρDM represents a DM halo density profile.
3.2.1. Burkert halo
The URC of galaxies and the kinematics of individual spirals (Salucci et al. 2007) points to dark haloes with a central constant-density core, in particular, to the Burkert halo profile (Burkert 1995; Salucci & Burkert 2000). The relative density distribution is given by  (2)where ρ0 (the central density) and rc (the core radius) are the two free parameters. The present data cannot distinguish these URC haloes from other cored profiles, for which limr → 0ρ(r) = const.
(2)where ρ0 (the central density) and rc (the core radius) are the two free parameters. The present data cannot distinguish these URC haloes from other cored profiles, for which limr → 0ρ(r) = const.
3.2.2. Navarro, Frenk, and White (NFW) halo
In numerical simulations performed in the (Λ) CDM scenario of structure formation, Navarro et al. (19963) found that virialized systems follow a universal DM halo profile. This is written as 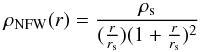 (3)where ρs and rs are the characteristic density and the scale radius of the distribution, respectively. These two parameters can be expressed in terms of the virial mass Mvir, the concentration parameter
(3)where ρs and rs are the characteristic density and the scale radius of the distribution, respectively. These two parameters can be expressed in terms of the virial mass Mvir, the concentration parameter 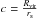 , and the critical density of the Universe ρcrit = 9.3 × 10-30 g cm-3. By using Eq. (3), we can write
, and the critical density of the Universe ρcrit = 9.3 × 10-30 g cm-3. By using Eq. (3), we can write 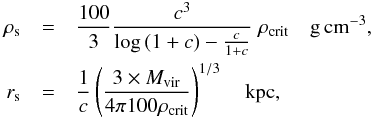 (4)where c and Mvir are not independent. It is well known from simulations that a c−Mvir relationship emerges (Klypin et al. 2011; Bullock et al. 2001; Wechsler et al. 2002):
(4)where c and Mvir are not independent. It is well known from simulations that a c−Mvir relationship emerges (Klypin et al. 2011; Bullock et al. 2001; Wechsler et al. 2002): 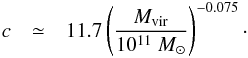 (5)We are testing the density profile of haloes made by collision-less cold DM particles. Variations in this scenario are not considered in this work, except one in Sect. 6.
(5)We are testing the density profile of haloes made by collision-less cold DM particles. Variations in this scenario are not considered in this work, except one in Sect. 6.
 |
Fig. 2 URC mass modelling of NGC 3198. Circular velocity data (filled circles with error bars) are modelled (thick red line) by the halo cored component (thick green line), the stellar disk (magenta line) and the HI disk (azure line). |
 |
Fig. 3 NFW mass modelling of NGC 3198. Circular velocity data (filled circles with error bars) are modelled (thick red line) by the stellar disk (magenta line), the NFW halo profile (green line) and the HI contribution (azure line). |
 |
Fig. 4 1, 2, 3σ confidence ellipses (purple, red, orange, respectively) of the best-fit parameters in the Burkert halo case. The central points indicate the best-fitting values. |
 |
Fig. 5 1, 2, 3σ confidence ellipses (purple, red, orange, respectively) of the best-fit parameters in the NFW halo case. The central points indicate the best-fitting values. |
4. Results from the χ2 fitting method
The mass modelling results for the Burkert and NFW profiles are shown in Figs. 2 and 3, respectively. The URC Burkert halo gives an excellent fit (see Fig. 2) with a reduced chi-square value of χ2 = 0.9. The best-fit parameters are 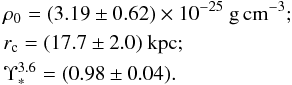 Then, we compute the mass of the stellar disk as
Then, we compute the mass of the stellar disk as 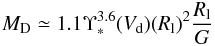 (6)where Vd(Rl) is the disk contribution to the circular velocity at the outermost radius Rl ≈ 48 kpc. This estimate is very solid and independent of the actual light profile in the inner part of the galaxy. We find MD ≃ 4.4 × 1010M⊙ (≈2 times bigger than the values found by de Blok et al. 2008) with a propagated uncertainty of about ten percent. The corresponding virial mass and virial radius are
(6)where Vd(Rl) is the disk contribution to the circular velocity at the outermost radius Rl ≈ 48 kpc. This estimate is very solid and independent of the actual light profile in the inner part of the galaxy. We find MD ≃ 4.4 × 1010M⊙ (≈2 times bigger than the values found by de Blok et al. 2008) with a propagated uncertainty of about ten percent. The corresponding virial mass and virial radius are 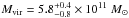 and
and 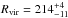 kpc. The 1,2,3σ confidence regions for the best-fit parameters are shown in Fig. 4. The central points correspond to the best-fit values.
kpc. The 1,2,3σ confidence regions for the best-fit parameters are shown in Fig. 4. The central points correspond to the best-fit values.
In the framework of the NFW mass models, we fitted data in terms of the free parameters: the virial mass, the concentration parameter and above defined the mass-to-light ratio (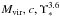 ). The results of the best-fit are
). The results of the best-fit are 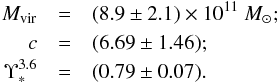 In this case the reduced chi-square is χ2 = 0.8, even slightly better value than found for the URC-halo model. The best-fit value of the concentration parameter c = 6.69 ± 1.46 is found to be somewhat lower than what is expected from Eq. (5): cNFW ≈ 10 ± 1. It is worth recalling that in other galaxies, this discrepancy in the concentration parameter is much larger (see McGaugh et al. 2003; Salucci et al. 2010; Memola et al. 2011).
In this case the reduced chi-square is χ2 = 0.8, even slightly better value than found for the URC-halo model. The best-fit value of the concentration parameter c = 6.69 ± 1.46 is found to be somewhat lower than what is expected from Eq. (5): cNFW ≈ 10 ± 1. It is worth recalling that in other galaxies, this discrepancy in the concentration parameter is much larger (see McGaugh et al. 2003; Salucci et al. 2010; Memola et al. 2011).
From Eq. (6) the disk mass, within a ten percent uncertainty, is MD = 3.5 × 1010M⊙, a somewhat smaller value than found for the URC-halo model. The best-fit values of the scale radius and the characteristic density are rs = (37.2 ± 11.0) kpc and ρs = (8.0 ± 4.1) × 10-26g cm-3.
The 1, 2, 3σ best-fit parameters confidence regions are shown in Fig. 5. The central points correspond to the best-fit values that result somewhat higher or lower than the N-body simulation outcome relative to a galaxy with Vmax ≃ 150 km s-1 as NGC 3198. The discrepancy, however, is within 1.5σ.
The standard mass modelling of the kinematical data of NGC 3198 is then not able to clearly select between a cored and a cuspy halo profile. In fact, in the case where a galaxy like NGC 3198 showing a flattish RC over a wide range of radii, we have a modelling degeneracy: the same best-fit solution corresponds to very different mass models (see Appendix of Gentile et al. 2004).
5. A new method of estimating the halo DM density and its results
A step forward in mass modelling spirals has come from the method of Salucci et al. (2010). This method was applied first to the Milky Way to derive the value of the DM density at the Sun’s location. In this paper we are applying it, for the first time, to the outermost parts of an external galaxy. Our aim is to derive, for the spiral galaxy with the most extended kinematics, the DM density at large radii, where the influence of the stellar and HI disks is respectively negligible and known.
The idea underlying the Salucci et al. (2010) method is to resort to the equation of centrifugal equilibrium holding in spiral galaxies: 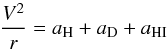 (7)where aH, aD and aHI are the radial accelerations, generated, respectively, by the halo, stellar disk, and HI disk mass distributions. Within the approximation of spherical DM halo, we have
(7)where aH, aD and aHI are the radial accelerations, generated, respectively, by the halo, stellar disk, and HI disk mass distributions. Within the approximation of spherical DM halo, we have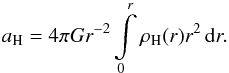 (8)Therefore, we compute the derivative of Eq. (7) by manipulating previous equations to get the DM density at any radius. We have
(8)Therefore, we compute the derivative of Eq. (7) by manipulating previous equations to get the DM density at any radius. We have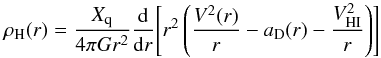 (9)where Xq is a factor correcting the spherical Gauss law used above in case of any oblateness of the DM halo. Since this value is very near to one, we assume Xq = 1 (see details in Salucci et al. 2010).
(9)where Xq is a factor correcting the spherical Gauss law used above in case of any oblateness of the DM halo. Since this value is very near to one, we assume Xq = 1 (see details in Salucci et al. 2010).
Equation (9) gives a very good estimation of the density when the contribution from the luminous components is small. In short, to work well the new method requires a high-resolution, high-quality, and very extended kinematics for a spiral of known distance. Of course, we are interested in the region well outside 3RD.
For simplicity, we model the disk component as a Freeman stellar exponential, infinitesimally thin disk (Freeman 1970) with the disk scale length RD = 3.7 kpc. No result in this paper will change by instead assuming the de Blok et al. (2008) disk mass profile, whose contribution to the circular velocity VD is given in Table 1. For MD we use the URC mass modelling value: MD ≃ 4.4 × 1010M⊙, and no result changes if assuming any other reasonable value for this quantity (see below).
The surface stellar density profile is given by 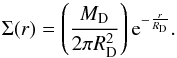 (10)We can write
(10)We can write 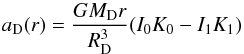 (11)where In and Kn are the modified Bessel functions computed at r/ (2RD).
(11)where In and Kn are the modified Bessel functions computed at r/ (2RD).
The HI disk component Vg(r) and its derivative are easily obtained from observations (Gentile et al. 2013). Finally, Eq. (9) becomes 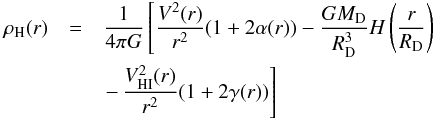 (12)where
(12)where 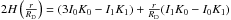 and α(r) and γ(r) are the logarithmic slopes of the circular velocity and of the HI+He disk contribution to the latter, both of which known.
and α(r) and γ(r) are the logarithmic slopes of the circular velocity and of the HI+He disk contribution to the latter, both of which known.
We stress that in galaxies with Vd(3RD) ≃ V(3RD), it is very difficult to use the standard mass modelling method to disentangle the circular velocity into its dark and luminous components and to obtain the DM density distribution out to r ≃ 6RD. Instead, the fundamental point of the present new method is that, for radii r ≳ 3RD the second term of RHS of Eq. (12) always goes rapidly to zero becoming much smaller than the first and the third terms, both known. Then, by means of Eq. (12), we can immediately derive ρ(r): the unknown term, proportional to the stellar disk mass becomes irrelevant as r ≳ 3RD. In Eq. (12), all terms have the dimensions of a density; specifically, the three terms of RHS can be considered as the effective density of the whole gravitating matter and the (sphericized) densities of the stellar and gaseous disks.
Thus, by means of Eq. (12) for r ≳ 3RD, we obtain a reliable DM density profile, the farther we get, the more precise the estimate becomes. In the range: r ≲ 3RD, Eq. (12) still holds, but it cannot give information about the DM halo since this is very sub-dominant there. In this region, however, we can use the latter equation to derive the stellar disk mass. This estimate, however, may turn out to be somewhat uncertain because, in this inner region, the first term of the RHS of Eq. (12) has some observational errors; moreover, moderate errors in the measured value of the disk scale length can affect the third term. Incidentally, we notice that the distance of the galaxy must be known with good precision (as it is in NGC 3198), because its uncertainty affects all three terms of the RHS in different ways.
 |
Fig. 6 Logarithmic slope of the RC of NGC 3198. |
 |
Fig. 7 Density profile of the DM halo of NGC 3198 and the effective density of the other components. We assume MD = 4.4 × 1010M⊙. The stellar disk (blue line), the HI disk (magenta line), the dark halo (red line) and the sum of all components (green line). The different colour regions correspond to the regions a) where we do not have any kinematical information due to the lack of data (dark purple); b) where the stellar disk dominates the DM density profile (light purple) and c) where DM dominates (white). |
In the case of NGC 3198 we take γ(r) = 0 for r ≳ 3RD, in order to simplify our calculations, since the gas contribution to the circular velocity, from s12 kpc, is nearly constant (see Fig. 2). The logarithmic slope of the RC instead varies with radius (see Table 1), even at rs17 kpc: we take dlog V(r) / dlog r as in Fig. 6. In Fig. 7 we obtain the density profile of the dark halo. We list the values of the obtained DM profile starting from 5.5 kpc in Table 1. We see that the DM component starts to dominate the luminous components from rs10 kpc; moreover, the stellar disk’s contribution in the RHS of Eq. (12) goes further below the gravitating matter for r ≳ 10 kpc and to zero for r ≳ 17 kpc, independently of its mass. This means that, starting from s17 kpc, the halo density profile, which obtained by means of Eq. (12), is virtually free from the uncertainty on the actual value of the disk mass, which usually plagues the standard mass modelling of RCs.
Next we discuss in detail the distribution of matter in the various regions of NGC 3198. In the innermost one, r ≲ 2 kpc we do not have any kinematical information due to the lack of data. In the region extended from s2 kpc to s10 kpc, the stellar component dominates over the DM component. No direct information on the latter can be extracted here. In this region, however, we can use the fair agreement between the stellar and the dynamical density (as defined in Eq. (12)) to derive the value of MD.
For r ≳ 17 kpc, the DM density is directly obtained by means of Eq. (12), see Fig. 7. Here, all quantities entering in Eq. (12) are known within a small uncertainty, and this leads to a robust determination of ρ(r).
The effect of the uncertainty in the value of the disk mass in the determination of ρ(r) is shown well in Fig. 8. We now do not take a specific value for MD, and we derive the DM density profiles through Eq. (12) by assuming different values for the disk mass. We see that the Salucci et al. (2010) method leads to a family of density profiles that all agree outside the stellar disk (i.e. for r ≳ 3RD), independently of the corresponding value of the disk mass (see the zoomed area in Fig. 9).
 |
Fig. 8 DM density profiles for different disk mass values MD = n × 1010M⊙ and n = 2,3,4.4,5 from the highest to the lowest curve (green, blue, azure and magenta triangles). The black solid line shows the NFW density profile with Mvir = 8.9 × 1011M⊙ corresponding to the best fit values found in the previous section. Two black dashed lines show the NFW density profiles taking 1σ uncertainties in Mvir and 10 percent of uncertainties in c into account. The URC halo is shown as red solid line. Two red dashed lines show the URC density profiles obtained by taking 1σ uncertainties in ρ0,rc into account. |
 |
Fig. 10 NFW case: the 1, 2, 3σ (purple region, red region and orange region, respectively) confidence ellipses for the global best-fit parameters. The blue solid line shows the c−Mvir relation from numerical simulations, the dashed blue lines show its 10 percent uncertainty. The green region shows the c−Mvir relation from the local density values obtained by the Salucci et al. (2010) method taking the 10 percent uncertainty into account. |
We compare the derived DM density with the URC and the NFW profiles, see Fig. 8. In the first case, the derived density bears no difference with that obtained by means of the first method, i.e. with Eqs. (1) and (2). We therefore found MD = (4.4 ± 1.0) × 1011M⊙. This is also evident in the zoomed area of Fig. 8 (see Fig. 9). In external regions of the NGC 3198, the Salucci et al. (2010) method yields a halo that is compatible with the URC halo, as derived by chi-square fitting of the RC of NGC 3198.
For NFW haloes the situation is very different. First, in Fig. 9 we realize that, independently of the disk mass we assume, the best-fit NFW halo profile is in poor agreement with the derived density. We consider this fault only as a hint and not as a definitive evidence against a NFW halo. Within the new modelling method, we derive the value of c and Mvir and their uncertainties by evaluating, from Eqs. (3), (4), and (12), the DM density (and its uncertainties) at the radius r = 45 kpc (where the stellar disk certainly does not contribute to the gravitating matter density profile). A more serious problem appears when we realize that the resulting values of the halo parameters Mvir and c are very different from the ones derived by means of the standard method applied in the previous section. In fact, for the virial mass and the concentration parameters we get Mvir = (8.9 ± 2.1) × 1011M⊙, c = 6.69 ± 1.46.
In Fig. 10 we plot the two solutions for (c−Mvir) with their uncertainties. We now compare these values of the concentration parameter and the virial mass (c−Mvir) obtained by each of the mass modelling techniques also in light of the (c−Mvir) relationship that emerged from numerical simulation (see Eq. (5)). They agree only for values of c that are much lower than those emerging in numerical simulations and for values of Mvir> 9 × 1011M⊙ far too high for this spiral galaxy which has Vmax ≲ 150 km s-1.
In short, by assuming a NFW halo in NGC 3198, we have two completely different solutions for its structure parameters, according to whether one adopts the local or the global method of mass modelling. The best intersection of these sets of results is in total disagreement with the properties of the simulated haloes in the N-body ΛCDM scenario. Noticeably, the problem for NFW haloes is different here and, if possible, more serious than that of the core-cusp discrepancy, usually occurring at ~0.05Rvir (Donato et al. 2009). We found, in fact, that the density of the DM halo around NGC 3198 is not very consistent with the NFW profiles well out to 0.22Rvir.
Of course, NFW haloes emerge out of DM only simulations in the leading ΛCDM scenario. However, this scenario actual haloes around galaxies may have undergone a compression by the stellar disk during the formation of the latter (e.g. Gnedin et al. 2004; Katz et al. 2014) and/or suffered a baryonic feedback during the subsequent history of the galaxy (Di Cintio et al. 2014). These processes could have modified the DM haloes original distribution. Furthermore, haloes today around galaxies, can be born within a different cosmological scenario like Warm or Self-Interacting DM, in which a NFW profile is not established (e.g. de Vega et al. 2014).
In spite of that, in this section we focused on the failure of the NFW halo profile because: a) it is important to fully expose the discrepancy between the density distribution of the dark haloes around galaxies and the predictions of the simplest dark particle scenario; b) NFW haloes are still used often to investigate important Cosmological issues in the belief that the discrepancy with actual galaxy haloes, though present, does not have much physical relevance; c) de facto, several cosmological investigations have been carried out considering that there is no discrepancy at all.
It goes without saying that the failure of NFW profiles is not the demise of the ΛCDM scenario (see next section).
6. Testing LCDM halo profiles modified by the physics of stellar disk formation
A line of thought holds that the cosmological core-cusp problem (CCCP) can be addressed by considering the present DM haloes around galaxies like NGC 3198 as very different with respect to those emerging out of N-body simulations. In fact, the formation and the growth in them of stellar disks and the related numerous and powerful supernova explosions could have modified the original N-body profile, by making it shallower and more in agreement with observations. We stress that such a dissolution of the CCCP is rarely studied.
 |
Fig. 11 Observed DM halo density profile (black points) of NGC 3198 and the obtained errors by the error propagation analysis (purple area). Di Cintio et al. (2014) mass-dependent model predictions (red line). |
One exception is the work by Di Cintio et al. (2014) based on the analysis of hydro-dynamically simulated galaxies drawn from the MaGICC project (Brook et al. 2012; Stinson et al. 2013). They did find, at the end of these simulations, that DM haloes had a completely new family of profiles, a generic double power-law density profile (Di Cintio et al. 2014). This was found to vary in a systematic manner in the stellar-to-halo mass ratio of each galaxy.
The mass-dependent density profile was derived by analysing hydrodynamical cosmological simulations. This profile (hereinafter referred to as DC14) accounts for the effects of feedback on the DM haloes due to gas outflows generated in high density star-forming regions during the history of the stellar disk. The resulting radial profile is far from simple, since it starts from an (α,β,γ) double power-law model (see Di Cintio et al. 2014) 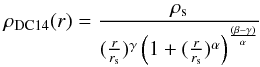 (13)where ρs is the scale density and rs the scale radius. The inner and the outer regions have logarithmic slopes −γ and −β, respectively, and α indicates the sharpness of the transition. These three parameters are fully constrained in terms of the stellar-to-halo mass ratio as shown in Di Cintio et al. (2014):
(13)where ρs is the scale density and rs the scale radius. The inner and the outer regions have logarithmic slopes −γ and −β, respectively, and α indicates the sharpness of the transition. These three parameters are fully constrained in terms of the stellar-to-halo mass ratio as shown in Di Cintio et al. (2014): 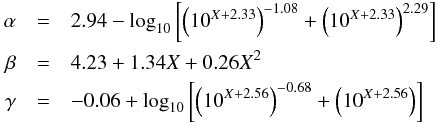 (14)where
(14)where 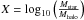 .
.
The concentration parameter of the halo is 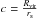 . An alternative definition, adopting the radius r-2, is
. An alternative definition, adopting the radius r-2, is 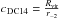 , where r-2 is the radius at which the logarithmic density slope of the profile is −2. This definition allows defining the same physical rs for different values of (α,β,γ)
, where r-2 is the radius at which the logarithmic density slope of the profile is −2. This definition allows defining the same physical rs for different values of (α,β,γ) 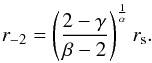 (15)Following Di Cintio et al. (2014), we reach the relation between the concentration parameter in the hydrodynamical simulations and the N-body haloes as a function of the stellar-to-halo mass ratio:
(15)Following Di Cintio et al. (2014), we reach the relation between the concentration parameter in the hydrodynamical simulations and the N-body haloes as a function of the stellar-to-halo mass ratio: 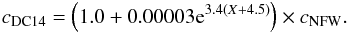 (16)Using the definition of the enclosed mass, we can write down the expression for the scale density of the DC14 profile:
(16)Using the definition of the enclosed mass, we can write down the expression for the scale density of the DC14 profile: 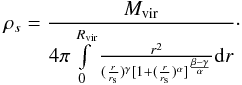 (17)To reduce the number of free parameters of the DC14 profile, it is necessary to adopt a value for the concentration parameter of the original NFW halo. For our purpose and since this quantity depends extremely weakly on the virial mass, we can adopt: cNFW = 10. By bringing together all the above equations of this section and noticing that Rvir = cDC14r-2, we can rewrite Eq. (13) just as a function of the scale radius and the stellar-to-halo mass ratio.
(17)To reduce the number of free parameters of the DC14 profile, it is necessary to adopt a value for the concentration parameter of the original NFW halo. For our purpose and since this quantity depends extremely weakly on the virial mass, we can adopt: cNFW = 10. By bringing together all the above equations of this section and noticing that Rvir = cDC14r-2, we can rewrite Eq. (13) just as a function of the scale radius and the stellar-to-halo mass ratio.
With this density profile, we can attempt a two-free parameter (X,rs) fit of the derived halo density profile of the NGC 3198 (Fig. 7). The result is in Fig. 11, the best-fit parameters are: 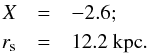 The inferred virial radius is Rvir ≃ 235 kpc and virial mass is Mvir ≃ 7.7 × 1011M⊙. As result, the CCCP is only partially resolved, and the DM core we detect in NGC 3198 can be explained as an effect of the energy that, in different ways, stars have injected in the galactic ambient. However, in the outer densities of the dark halo derived for the first time in this study, there are features that may conflict with the N-body simulation predictions that should be recovered at R> 25 kpc from the centre of NGC 3198.
The inferred virial radius is Rvir ≃ 235 kpc and virial mass is Mvir ≃ 7.7 × 1011M⊙. As result, the CCCP is only partially resolved, and the DM core we detect in NGC 3198 can be explained as an effect of the energy that, in different ways, stars have injected in the galactic ambient. However, in the outer densities of the dark halo derived for the first time in this study, there are features that may conflict with the N-body simulation predictions that should be recovered at R> 25 kpc from the centre of NGC 3198.
7. Conclusions
Galaxies with a flattish RC between 5 kpc to 50 kpc (e.g. the spiral NGC 3198, for many years the flagship of the evidence of the DM in galaxies) amount to only a few percent of the total number of disk systems. However, they play a crucial role in the core-cusp issue of the DM density. In fact, these “flat” RCs can be well fitted by either a cored DM halo or a cuspy DM halo, just by adjusting the amount of the stellar matter content. In contrast, in spirals in which | dlog V(r) / dlog r | is significantly far from zero, this quantity constraints the distribution of DM, usually towards a cored one (Gentile et al. 2005).
NGC 3198 is a special galaxy. The HI disk of this galaxy is very extended out to ~13 disk scale lengths or out to ~0.22 Rvir. Furthermore, for the innermost region, many complementary optical kinematical measurements are available. This object (of known distance of 13.8 Mpc) shows a spectacular evidence of a dark force in action: baryons of this galaxy are clearly unable to account for its (very extended) kinematics. We must assume that a large part of the circular velocity of NGC 3198 is due to a DM halo. In addition, the circular velocity of this galaxy is at variance with the MOND paradigm (Gentile et al. 2013), while it seems plausible within the F(R) scenario (see Salucci et al. 2014). It is then obvious that to resolve the core-cusp issue in NGC 3198 is of particular importance.
To do so, we used the old optical and new HI kinematics performed in the HALOGAS survey in combination with a new method of mass modelling a RC. First, we verified that with the standard χ2 mass modelling of the RC, both URC Burkert and the NFW dark halo models fit the available data well. Then, once assured of the conditions of its applicability, we used the new refined method developed by Salucci et al. (2010) to determine the DM halo density of NGC 3198. This result is inconsistent with the NFW haloes predictions, independently of any assumption about the luminous component we can take. Moreover, the derived density profile strongly supports a cored distribution of DM, adding independent evidence to the idea of cored DM distribution in galaxies.
Today, within the ΛCDM scenario, NFW haloes are often still assumed, although it has been recognized that in this scenario the actual DM halo density is not the one emerging from
cosmological N-body simulations. In fact, it has been agreed that they have been modified by the subsequent baryonic physics, leading to stellar disk formation and evolution. Di Cintio et al. (2014) have simulated this important phase of the history of spirals and found the emerging profiles of DM haloes. This baryonic ΛCDM halo profile prediction fits the detected halo of NGC 3198 very well, especially in its cored region. At very large distances, 25 kpc, however, the DM halo density derived here results in a clash; i.e., it is significantly higher than the outcome of the hydrodynamic N-body ΛCDM simulations. This disagreement is not an isolated one (see Gentile et al. 2007).
Acknowledgments
We would like to thank the referee, Albert Bosma, for comments that improved the quality of the paper.
References
- Athanassoula, E., Bosma, A., & Papaioannou, S. 1987, A&A, 179, 23 [NASA ADS] [Google Scholar]
- Begeman, K. G. 1987, Ph.D. Thesis, Kapteyn Institute [Google Scholar]
- Begeman, K. G., Broeils, A. H., & Sanders, R. H. 1991, MNRAS, 249, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A. 1978, Ph.D. Thesis, Groningen Univ. [Google Scholar]
- Bosma, A. 1981, AJ, 86, 1791 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A., & van der Kruit, P. C. 1979, A&A, 79, 281 [NASA ADS] [Google Scholar]
- Bottema, R. 1988, A&A, 197, 105 [NASA ADS] [Google Scholar]
- Brook, C. B., Stinson, G., Gibson, B. K., Wadsley, J., & Quinn, T. 2012, MNRAS, 424, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cheriguène, M. F. 1975, in La Dynamique des galaxies spirales, ed. L. Weliachew, 439 [Google Scholar]
- Corradi, R. L. M., Boulesteix, J., Bosma, A., Amram, P., & Capaccioli, M. 1991, A&A, 244, 27 [NASA ADS] [Google Scholar]
- Daigle, O., Carignan, C., Amram, P., et al. 2006, MNRAS, 367, 469 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Bosma, A. 2002, A&A, 385, 816 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- de Vega, H. J., Salucci, P., & Sanchez, N. G. 2014, MNRAS, 442, 2717 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cintio, A., Brook, C. B., Dutton, A. A., et al. 2014, MNRAS, 441, 2986 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, F., Gentile, G., Salucci, P., et al. 2009, MNRAS, 397, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G. 2008, ApJ, 684, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Salucci, P., Klein, U., Vergani, D., & Kalberla, P. 2004, MNRAS, 351, 903 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Tonini, C., & Salucci, P. 2007, A&A, 467, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gentile, G., Józsa, G. I. G., Serra, P., et al. 2013, A&A, 554, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnedin, O. Y., Kravtsov, A. V., Klypin, A. A., & Nagai, D. 2004, ApJ, 616, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Józsa, G., Serra, P., et al. 2011, A&A, 526, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, D. A., Rubin, V. C., & Gallagher, III, J. S. 1986, AJ, 91, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., McGaugh, S. S., Sellwood, J. A., & de Blok, W. J. G. 2014, MNRAS, 439, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Kent, S. M. 1986, AJ, 91, 1301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kent, S. M. 1987, AJ, 93, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A. A., Trujillo-Gomez, S., & Primack, J. 2011, ApJ, 740, 102 [Google Scholar]
- McGaugh, S. S., Barker, M. K., & de Blok, W. J. G. 2003, ApJ, 584, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Memola, E., Salucci, P., & Babić, A. 2011, A&A, 534, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Palunas, P., & Williams, T. B. 2000, AJ, 120, 2884 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., & Salucci, P. 1988, MNRAS, 234, 131 [NASA ADS] [Google Scholar]
- Rubin, V. C., Ford, W. K. J., & Thonnard, N. 1980, ApJ, 238, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., & Burkert, A. 2000, ApJ, 537, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., & Persic, M. 1999, A&A, 351, 442 [NASA ADS] [Google Scholar]
- Salucci, P., Lapi, A., Tonini, C., et al. 2007, MNRAS, 378, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., Nesti, F., Gentile, G., & Frigerio Martins, C. 2010, A&A, 523, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salucci, P., Frigerio Martins, C., & Karukes, E. 2014, Int. J. Mod. Phys. D, 23, 42005 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Frenk, C. S., & White, S. D. M. 2006, Nature, 440, 1137 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stinson, G. S., Brook, C., Macciò, A. V., et al. 2013, MNRAS, 428, 129 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S., Bahcall, J. N., Begeman, K., & Sancisi, R. 1985, ApJ, 295, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Wevers, B. M. H. R., van der Kruit, P. C., & Allen, R. J. 1986, A&AS, 66, 505 [NASA ADS] [Google Scholar]
All Tables
Stellar disk contribution Vd (km s-1; de Blok et al. 2008) and the circular velocity V (km s-1) mainly from Gentile et al. (2013), but also from Corradi et al. (1991) and Daigle et al. (2006), of the NGC 3198 with errors dV (km s-1).
All Figures
 |
Fig. 1 Comparison between Hα and HI RCs black open triangles with error bars from Corradi et al. (1991), blue circles with error bars are from Daigle et al. (2006), and red circles with error bars are from Gentile et al. (2013). |
| In the text | |
 |
Fig. 2 URC mass modelling of NGC 3198. Circular velocity data (filled circles with error bars) are modelled (thick red line) by the halo cored component (thick green line), the stellar disk (magenta line) and the HI disk (azure line). |
| In the text | |
 |
Fig. 3 NFW mass modelling of NGC 3198. Circular velocity data (filled circles with error bars) are modelled (thick red line) by the stellar disk (magenta line), the NFW halo profile (green line) and the HI contribution (azure line). |
| In the text | |
 |
Fig. 4 1, 2, 3σ confidence ellipses (purple, red, orange, respectively) of the best-fit parameters in the Burkert halo case. The central points indicate the best-fitting values. |
| In the text | |
 |
Fig. 5 1, 2, 3σ confidence ellipses (purple, red, orange, respectively) of the best-fit parameters in the NFW halo case. The central points indicate the best-fitting values. |
| In the text | |
 |
Fig. 6 Logarithmic slope of the RC of NGC 3198. |
| In the text | |
 |
Fig. 7 Density profile of the DM halo of NGC 3198 and the effective density of the other components. We assume MD = 4.4 × 1010M⊙. The stellar disk (blue line), the HI disk (magenta line), the dark halo (red line) and the sum of all components (green line). The different colour regions correspond to the regions a) where we do not have any kinematical information due to the lack of data (dark purple); b) where the stellar disk dominates the DM density profile (light purple) and c) where DM dominates (white). |
| In the text | |
 |
Fig. 8 DM density profiles for different disk mass values MD = n × 1010M⊙ and n = 2,3,4.4,5 from the highest to the lowest curve (green, blue, azure and magenta triangles). The black solid line shows the NFW density profile with Mvir = 8.9 × 1011M⊙ corresponding to the best fit values found in the previous section. Two black dashed lines show the NFW density profiles taking 1σ uncertainties in Mvir and 10 percent of uncertainties in c into account. The URC halo is shown as red solid line. Two red dashed lines show the URC density profiles obtained by taking 1σ uncertainties in ρ0,rc into account. |
| In the text | |
 |
Fig. 9 Zoom of Fig. 8 on linear scales. |
| In the text | |
 |
Fig. 10 NFW case: the 1, 2, 3σ (purple region, red region and orange region, respectively) confidence ellipses for the global best-fit parameters. The blue solid line shows the c−Mvir relation from numerical simulations, the dashed blue lines show its 10 percent uncertainty. The green region shows the c−Mvir relation from the local density values obtained by the Salucci et al. (2010) method taking the 10 percent uncertainty into account. |
| In the text | |
 |
Fig. 11 Observed DM halo density profile (black points) of NGC 3198 and the obtained errors by the error propagation analysis (purple area). Di Cintio et al. (2014) mass-dependent model predictions (red line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.