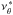| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425241 | |
| Published online | 11 June 2015 | |
Black hole spin inferred from 3:2 epicyclic resonance model of high-frequency quasi-periodic oscillations
1 Institute of Physics, Faculty of Philosophy and Science, Silesian University in Opava, Bezručovo nám. 13, 74601 Opava, Czech Republic
e-mail: gabriel.torok@physics.cz
2 Nicolaus Copernicus Astronomical Centre, Bartycka 18, 00716 Warsaw, Poland
Received: 30 October 2014
Accepted: 30 April 2015
Estimations of black hole spin in the three Galactic microquasars GRS 1915+105, GRO J1655-40, and XTE J1550-564 have been carried out based on spectral and timing X-ray measurements and various theoretical concepts. Among others, a non-linear resonance between axisymmetric epicyclic oscillation modes of an accretion disc around a Kerr black hole has been considered as a model for the observed high-frequency quasi-periodic oscillations (HF QPOs). Estimates of spin predicted by this model have been derived based on the geodesic approximation of the accreted fluid motion. Here we assume accretion flow described by the model of a pressure-supported torus and carry out related corrections to the mass-spin estimates. We find that for dimensionless black hole spin a ≡ cJ/GM2 ≲ 0.9, the resonant eigenfrequencies are very close to those calculated for the geodesic motion. Their values slightly grow with increasing torus thickness. These findings agree well with results of a previous study carried out in the pseudo-Newtonian approximation. The situation becomes different for a ≳ 0.9, in which case the resonant eigenfrequencies rapidly decrease as the torus thickness increases. We conclude that the assumed non-geodesic effects shift the lower limit of the spin, implied for the three microquasars by the epicyclic model and independently measured masses, from a ~ 0.7 to a ~ 0.6. Their consideration furthermore confirms compatibility of the model with the rapid spin of GRS 1915+105 and provides highly testable predictions of the QPO frequencies. Individual sources with a moderate spin (a ≲ 0.9) should exhibit a smaller spread of the measured 3:2 QPO frequencies than sources with a near-extreme spin (a ~ 1). This should be further examined using the large amount of high-resolution data expected to become available with the next generation of X-ray instruments, such as the proposed Large Observatory for X-ray Timing (LOFT).
Key words: X-rays: binaries / black hole physics / accretion, accretion disks
© ESO, 2015
1. Introduction
Studying the X-ray spectra and variability provides a useful tool for probing strong-field gravity effects and places constraints on the properties of compact objects, such as the mass or spin of a black hole. One of the commonly accepted ways to measure the black hole spin is related to fitting the X-ray spectral continuum or the relativistically broadened Fe K alpha lines. Using the spectral fitting methods, estimations of black hole spin have been carried out by many authors in the past (see e.g., McClintock et al. 2006, 2008, 2010, 2011, 2014; Middleton et al. 2006; Done et al. 2007; Miller 2007; Shafee et al. 2008).
There is another approach to estimating parameters of accreting black holes (BH) and neutron stars (NS) that has been gaining popularity in the past decade. It is the determination of compact object properties through the theory of high-frequency quasi-periodic oscillations (HF QPOs). These peaked features have been observed in the X-ray power density spectra of the BH and NS low-mass X-ray binaries for several decades (see e.g., van der Klis 2006; Belloni & Stella 2014, for a review). In the BH systems, the HF QPOs appear at frequencies that often form rational ratios with a preferred ratio of 3:2 (Abramowicz & Kluźniak 2001; McClintock & Remillard 2006).
1.1. Orbital models of HF QPOs
A rich variety of models has been proposed to explain the BH HF QPOs. Many of them are associated with motion of matter accreting onto the central compact object (e.g., Kato & Fukue 1980; Alpar & Shaham 1985; Lamb et al. 1985; Okazaki et al. 1987; Nowak & Wagoner 1991; Perez et al. 1997; Kluźniak 1998; Miller et al. 1998; Psaltis et al. 1999; Stella & Vietri 1998a,b; Wagoner 1999; Wagoner et al. 2001; Silbergleit et al. 2001; Abramowicz & Kluźniak 2001; Titarchuk & Wood 2002; Rezzolla et al. 2003; Pétri 2005; Zhang 2005; Šrámková et al. 2007; Kato 2007; Čadež et al. 2008; Stuchlík et al. 2008; Horák et al. 2009; Mukhopadhyay 2009; Lai et al. 2012; Ortega et al. 2014, and others). Despite the different involved physical mechanisms, several of the HF QPO models assign the observed frequencies to orbital frequencies that can under some approximations be expressed in terms of Keplerian and epicyclic frequencies of perturbed circular geodesic motion.
One of the early models, for instance, the so-called relativistic-precession model (Stella & Vietri 1998a,b, 1999), identifies the kHz QPO frequencies νU and νL with the Keplerian orbital frequency and the periastron-precession frequency, νU = νK,νL = νK − νr (where νr denotes the radial epicyclic frequency). Within the model framework, it is usually assumed that the observed kHz variability originates in a bright localized spot or blob orbiting the black hole at a slightly eccentric orbit. The photons emitted by the spot, which have a high orbital velocity of the order of percents of the speed of light, are then propagated from the strong gravity region towards the observer. Consequently, the detected X-ray flux is periodically modulated by the relativistic effects (see e.g., Schnittman & Bertschinger 2004; Bakala et al. 2014, and references therein).
A different class of models is based on the assumption that the light curve reflects variations in the emission of an accretion disc. A theory of normal modes of accretion disc oscillation, referred to as discoseismology, has been developed in the papers coauthored by Kato and by Wagoner. For instance, Kato & Fukue (1980) consider the g-mode of disc oscillation, whose frequency is close to the highest radial epicyclic frequency, while Silbergleit et al. (2001) developed a theory of c-mode (disc corrugation) whose frequency is related to the difference between the vertical epicyclic frequency and the orbital frequency.
Properties of the three microquasars GRO 1655-40, GRS 1915+105, and XTE 1550-564.
1.1.1. Resonance models
Kluźniak & Abramowicz (2001) have introduced another concept of orbital models. In these models, the relativistic effects acting on the emitted photons are also essential, but the HF QPOs are attributed to a non-linear resonance between two modes of accretion disc oscillations. This well explains the observed preferred frequency ratio, νU/νL = 3/2. Since the concept deals with a collective motion of accreted matter, it has a high potential of the observed flux modulation (Bursa et al. 2004; Mazur et al. 2013; Vincent et al. 2014; Bakala et al. 2014).
The framework of resonance models has been extensively developed (Abramowicz & Kluźniak 2001; Abramowicz et al. 2003; Kluźniak et al. 2004; Horák & Karas 2006; Horák et al. 2009) and miscellaneous combinations of disc oscillation modes have been considered. In several particular cases, the observed frequencies can be expressed in terms of Keplerian and epicyclic frequencies (see Török et al. 2005; Horák 2008; Kluźniak 2008, for details and references).
1.2. Spin estimation and epicyclic resonance model
In Kerr geometry, which describes the spacetime around a rotating black hole, the frequencies of the radial and vertical epicyclic oscillations depend on the mass and spin of the black hole. It is therefore possible to determine the BH mass or spin from the epicyclic resonance model and the observed 3:2 QPO frequencies. For three Galactic microquasars with the 3:2 HF QPOs (GRS 1915+105, GRO J1655-40, and XTE J1550-564), such BH spin estimations have been carried out in the past for the epicyclic resonance model and for several other HF QPO models (Strohmayer 2001a,b; Wagoner et al. 2001; Abramowicz & Kluźniak 2001; Kato 2004a,b; Török et al. 2005, 2011; Motta et al. 2014a,b). Analogous spin estimations have been obtained for the three sources through other methods by different groups of authors using the X-ray continuum-fitting procedure (McClintock et al. 2006, 2008; Middleton et al. 2006; Miller et al. 2009), and the iron line method (Miller 2007; Davis et al. 2006; McClintock & Remillard 2009; Blum et al. 2009; Steiner et al. 2011). The spin estimates obtained through the spectral and timing approaches are as yet somewhat inconsistent, however (see a detailed discussion in Török et al. 2011).
In this work, we consider one of the popular versions of resonance models represented by the epicyclic parametric (or internal) resonance model that assumes a 3:2 non-linear resonance between the axisymmetric radial and vertical epicyclic modes of accretion disc oscillations. All the estimates derived so far that were related to the epicyclic resonance model assume a geodesic approximation of the accreted fluid motion. Within this approximation, the two observable resonant frequencies are represented by the radial and vertical epicyclic frequencies, νr and νθ, of test particle motion. In more general accretion flows, non-geodesic effects connected for instance to pressure gradients, magnetic fields, or other forces may affect the properties of the considered oscillation modes and consequently the inferred spin predictions.
In the following, we explore black hole spin predictions implied by the epicyclic resonance QPO model considering non-geodesic influence that originates in pressure forces present in accretion flow, which is modelled by a small equilibrium-pressure-supported, perfect-fluid torus. Properties of the epicyclic modes of torus oscillations, such as modifications to their frequencies due to pressure gradients present in the torus, were calculated by Blaes et al. (2007) in the pseudo-Newtonian approximation and were later generalised by Straub & Šrámková (2009) for Kerr geometry. Using the results of Straub & Šrámková (2009), we apply the modified epicyclic frequencies to calculate the corresponding estimates of black hole spin based on the epicyclic resonance QPO model.
2. Resonant eigenfrequencies and black hole parameters implied by the epicyclic model
The explicit formulae of the epicyclic frequencies in Kerr geometry were first derived by Aliev & Galtsov (1981) and may be written in the Boyer-Lindquist coordinates t,r,θ,φ as (e.g., Silbergleit et al. 2001; Török & Stuchlík 2005)  where
where 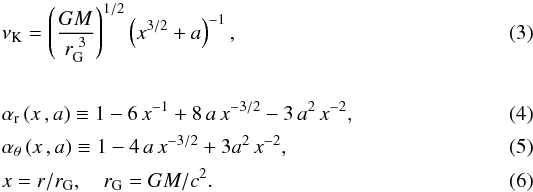 Here M and a denote the mass and the dimensionless angular momentum (spin) of the black hole.
Here M and a denote the mass and the dimensionless angular momentum (spin) of the black hole.
Within the epicyclic resonance (ER) model, it is assumed that the resonant eigenfrequencies are equal to epicyclic frequencies defined at the x3:2 orbit where we have  (7)Furthermore, it is assumed that the eigenfrequencies are equal to the observed upper and lower 3:2 QPO frequencies, νU and νL (e.g., Török et al. 2005). Using this set of formulae and the observed 3:2 HF QPO frequencies along with the independently estimated black hole masses, the intervals of spin predicted by the ER model were previously calculated for the three Galactic microquasars (GRS 1915+105, GRO J1655-40, and XTE J1550-564 – see Török et al. 2005, 2011). The obtained results and relevant properties of the three sources are summarized in Table 1.
(7)Furthermore, it is assumed that the eigenfrequencies are equal to the observed upper and lower 3:2 QPO frequencies, νU and νL (e.g., Török et al. 2005). Using this set of formulae and the observed 3:2 HF QPO frequencies along with the independently estimated black hole masses, the intervals of spin predicted by the ER model were previously calculated for the three Galactic microquasars (GRS 1915+105, GRO J1655-40, and XTE J1550-564 – see Török et al. 2005, 2011). The obtained results and relevant properties of the three sources are summarized in Table 1.
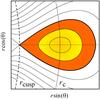 |
Fig. 1 Illustration of equipotential surfaces of the accretion torus. The dotted horizontal line denotes the equatorial plane. The yellow region illustrates tori of various thickness. The orange region, together with the yellow, illustrates a torus filling the equipotential surface with a cusp. |
2.1. Epicyclic frequencies in a slightly non-slender torus
We assumed a non-geodesic flow that was modelled by an equilibrium, slightly non-slender, pressure-supported perfect-fluid torus. The torus was assumed to have a constant specific angular momentum distribution and orbit a rotating Kerr black hole. We assumed that the torus is formed by a perfect fluid that fills up closed equipotential surfaces. One of these surfaces has a cusp in the equatorial plane, which embodies features similar to those of the L1 Lagrange point. The topology of the equipotential surfaces and the equilibrium torus is illustrated in Fig. 11.
In the investigated non-geodesic flow, the radial and vertical epicyclic oscillations of the fluid are modified by pressure forces. Using a perturbation theory, within the accuracy of a second order in the thickness of the torus, Straub & Šrámková (2009) calculated explicit formulae for the pressure corrections to epicyclic frequencies in a slightly non-slender, constant specific angular momentum torus orbiting a Kerr black hole. The calculated epicyclic frequencies can be written in the following form: 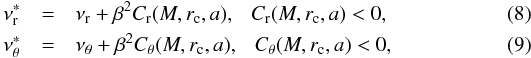 where Cr(M,rc,a) and Cθ(M,rc,a) denote the negative pressure corrections evaluated at the centre of the torus, r = rc. Explicit forms of expressions for the epicyclic frequencies (8) and (9) are given in formulae (52) and (56) of Straub & Šrámková (2009).
where Cr(M,rc,a) and Cθ(M,rc,a) denote the negative pressure corrections evaluated at the centre of the torus, r = rc. Explicit forms of expressions for the epicyclic frequencies (8) and (9) are given in formulae (52) and (56) of Straub & Šrámková (2009).
 |
Fig. 2 Epicyclic frequencies calculated at the centre of the torus, r = rc, plotted for various torus thicknesses (β) and black hole spins a. The curves are drawn solely within the region where the considered value of β does not exceed the critical value corresponding to a torus with a cusp. |
 |
Fig. 3 Ratio R of the vertical to radial epicyclic frequency and the resonant vertical epicyclic frequency |
The dimensionless parameter β determines the torus thickness. It is defined as (Blaes 1985) 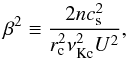 (10)where cs, νKc, and U are the sound speed, Keplerian frequency, and t-component of the contravariant four-velocity of the perfect fluid, all defined at the centre of the torus, r = rc. Within the perturbative approach applied by Straub & Šrámková (2009), it is expected that 0 ≤ β2 ≪ 1. For the critical β values corresponding to tori with a cusp, the limit of β → 0 corresponds to an infinitely slender torus located at the marginally stable circular orbit. High values of β< 1 then correspond to very large tori whose inner edge approaches the location of the marginally bound circular orbit. The behaviour of epicyclic frequencies for tori of different thickness, β ∈ {0, 0.1, 0.2, 0.4}, and a Kerr black hole with a ∈ {0.0, 0.5, 0.9, 0.99} is illustrated in Fig. 2.
(10)where cs, νKc, and U are the sound speed, Keplerian frequency, and t-component of the contravariant four-velocity of the perfect fluid, all defined at the centre of the torus, r = rc. Within the perturbative approach applied by Straub & Šrámková (2009), it is expected that 0 ≤ β2 ≪ 1. For the critical β values corresponding to tori with a cusp, the limit of β → 0 corresponds to an infinitely slender torus located at the marginally stable circular orbit. High values of β< 1 then correspond to very large tori whose inner edge approaches the location of the marginally bound circular orbit. The behaviour of epicyclic frequencies for tori of different thickness, β ∈ {0, 0.1, 0.2, 0.4}, and a Kerr black hole with a ∈ {0.0, 0.5, 0.9, 0.99} is illustrated in Fig. 2.
2.2. Behaviour of commensurable frequencies for moderately and rapidly rotating Kerr black holes
Using formulae (8) and (9), we investigated the behaviour of epicyclic frequencies in fluid tori when they are in the 3:2 ratio. For Schwarzschild and moderately rotating Kerr black holes, the resonant frequencies behave qualitatively in the same fashion. The resonant radius in this case decreases with growing torus thickness, while the individual epicyclic frequencies defined at this radius increase with growing torus size. This is illustrated in Fig. 3, which, for different values of a and β, displays the ratio R of the vertical to radial epicyclic frequency, and the vertical epicyclic frequency calculated at the resonant radius. Panels a) and c) of Fig. 3 drawn for a = 0 and a = 0.5 show that from certain value of β, there suddenly appear two different tori whose epicyclic frequencies display the 3:2 commensurability. This behaviour persists as we continue to increase the torus size until at some point the 3:2 resonant radius no longer exists. This phenomenon manifests itself in the form of a small loop in the profile of the resonant vertical epicyclic frequency plotted over β (panels b) and d) of Fig. 3). The same behaviour was found by Blaes et al. (2007), who carried out a similar analysis in the pseudo-Newtonian approximation. We find that for Kerr black holes, two different values of resonant frequency are allowed for the same value of β when a ≤ 0.86.
For higher values of a, the behavioural nature of the resonant frequencies begins to change significantly. The resonant radius retains its decreasing pattern with growing torus size, but two different tori with the 3:2 commensurability are no longer possible. Rather distinct modifications also appear in the character of the resonant frequency, which at first increases with rising β, but at some point starts to decrease rapidly. For a black hole spin approaching a ≐ 0.89, the resonant frequencies implied by the highest allowed values of β become lower than those calculated for the geodesic motion. This is illustrated in panels e) and f) of Fig. 3. For a still higher black hole spin (a ≳ 0.99), characteristic features of the resonant frequencies continue to change even further. While the resonant radius continues to drop monotonically with growing torus thickness, resonant frequencies are no longer higher than those of free test particles. They now decrease for tori of all sizes (β> 0), see panels g) and h) of Fig. 3. This is because the nature of epicyclic frequencies for rapidly rotating black holes is such that the decrease of frequencies due to higher β overrides the increase implied by lower resonant radius.
2.3. Comparison of predicted 3:2 epicyclic frequencies with observation
Figure 4 uses the relativistic 1 /M scaling of the orbital frequencies. It displays the M × νU(a) relation expected from the geodesic epicyclic resonance model marked by the thick black line. The shaded region describes the mass-spin interval predicted by the epicyclic resonance model for a slightly non-slender torus of various thickness. In the figure, we also present the conservative observational bounds on M × νU determined for the three microquasars (see Table 1). These bounds are indicated by the colour-coded areas. Apparently, while the geodesic line enters the observationally determined vertical range of microquasars when a ≳ 0.7, the non-geodesic line enters this range already for a ≳ 0.62.
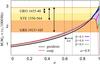 |
Fig. 4 Observational bounds on the quantity M × νU obtained for Galactic microquasars vs. relations predicted by the epicyclic resonance model. The vertical areas denote the observational bounds on M × νU determined for GRS 1915+105, XTE J1550−564, and GRO J1655−40. The areas are drawn assuming the conservative limits from Table 1. The solid black curve shows predictions of the model calculated for the geodesic flow. The shaded region indicates the interval predicted by the model for the family of equilibrium non-slender fluid tori of all thicknesses possible in the particular case. The red curve corresponds to the case of tori with a cusp. The arrow labelled Δ a indicates the shift of the lower limit on the spin of microquasars implied by considering the non-geodesic flow. |
Figure 4 clearly illustrates that for a ≲ 0.9, the highest possible increase of the predicted resonant frequency due to pressure effects is rather small, reaching about 10%. However, for a ≳ 0.9, the shaded region in the figure shifts from the area above the β = 0 curve to the area located mostly below this curve. The strongest possible shift of the resonant frequency is now much greater than it was for a ≲ 0.9. The coloured curves in Fig. 4 illustrate the mass-spin values predicted by the model for tori of β = 0.3, β = 0.4, and β = 0.5. In this case, predictions of the model with non-geodesic flow may significantly differ from those calculated for the geodesic flow. This has a direct link to observations, since the calculated shaded region overlaps a large part of the observationally determined yellow area.
3. Discussion and conclusions
Following the previous studies of Blaes et al. (2007), Straub & Šrámková (2009), and Török et al. (2011), we explored here the implications of consideration of pressure forces that originate in a pressure-supported fluid torus for the predictions of black hole spin inferred from the epicyclic resonance QPO model. Our findings for moderately rotating Kerr black holes with a ≲ 0.9 agree well with those carried out in the pseudo-Newtonian study of Blaes et al. (2007). The epicyclic resonance model with a non-geodesic flow predicts the black hole spin to be slightly lower than the spin estimated previously by the same model with a geodesic flow. The lower limit on the spin of Galactic microquasars inferred by the model is then decreased to a ~ 0.6. These findings indicate that for up to a ~ 0.9, the model has a high predictive power (falsifiability).
Different but very interesting results appear for rapidly rotating black holes with a ≳ 0.9. In this case, the behaviour of the resonant frequencies begins to markedly change in comparison to the pseudo-Newtonian case. This occurs in such a way that the predicted frequencies can be both higher and lower than those predicted by the geodesic model, with the strongest possible shift being much more significant towards the lower values. Therefore, when the source mass is determined from the 3:2 QPO frequencies, the epicyclic resonance model has a lower predictive power for rapidly rotating black holes than for moderately rotating black holes. On the other hand, our findings confirm the compatibility of the model with the rapid spin of the microquasar GRS 1915+105 (McClintock et al. 2006; Török et al. 2011; Fragos & McClintock 2015), since the expected mass interval almost overlaps with the interval constrained observationally. Furthermore, we provided highly testable predictions of the QPO frequencies. When the torus size (β) is not determined by some additional physical requirements, a wide range of commensurable frequencies is predicted for near-extreme rotating black holes3. Individual sources with a moderate spin (a ≲ 0.9) should therefore exhibit a smaller spread of the measured 3:2 QPO frequencies than sources with a near-extreme spin (a ~ 1). At present, there is a rather small amount of data needed for further analysis of this issue. Our predictions, however, can be explored using the large amount of high time-resolution data expected to become available with the next generation of X-ray instruments, such as the proposed Large Observatory for X-ray Timing (LOFT; Feroci et al. 2012).
For a detailed description of the model of the torus and further references see Straub & Šrámková (2009).
According to individual studies based on spectral and timing methods, it would also be possible to include several (vertical) bounds on the spin of microquasars. Within the figure, however, we focus primarily on the epicyclic resonance model of HF QPOs and its predictions. The discussion of various spectral and timing estimates of a can be found for instance in Miller (2007), McClintock et al. (2011, 2014), Steiner et al. (2013), Török et al. (2011), and Kotrlová (2014).
Values of β as high as β = 0.5 considered in panel h) of Fig. 3 may require additional treatment, since these values exceed the limits of full applicability of the adopted approximation. Nevertheless, the illustrated phenomenon is very significant and well apparent already for β ~ 0.3.
Acknowledgments
E.Š. and G.T. would like to acknowledge the Czech Science Foundation grant GAČR 209/12/P740. Z.S. acknowledges the Albert Einstein Centre for Gravitation and Astrophysics supported by the Czech Science Foundation grant No. 14-37086G. Furthermore, we acknowledge financial support from the internal grants of SU Opava, SGS/11/2013, SGS/23/2013, and IGS/9/2015.
References
- Aliev, A. N., & Galtsov, D. V. 1981, Gem. Rel. Grav., 13, 899 [Google Scholar]
- Abramowicz, M. A., & Kluźniak, W. 2001, A&A, 374, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowicz, M. A., Karas, V., Kluźniak, W., Lee, W. H., & Rebusco, P. 2003, PASJ, 55, 466 [Google Scholar]
- Alpar, M. A., & Shaham, J. 1985, Nature, 316, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Bakala, P., Török, G., Karas, V., et al. 2014, MNRAS, 439, 1933 [NASA ADS] [CrossRef] [Google Scholar]
- Beer, M. E., & Podsiadlowski, P. 2002, MNRAS, 331, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M., & Stella, L. 2014, Space Sci. Rev., 183, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O. M. 1985, MNRAS, 216, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O. M., Šrámková, E., Abramowicz, M. A., Kluźniak, W., & Torkelsson, U. 2007, ApJ, 665, 653 [Google Scholar]
- Blum, J. L., Miller, J. M., & Fabian, A. C. 2009, ApJ, 706, 66 [Google Scholar]
- Bursa, M., Abramowicz, M. A., Karas, V., & Kluzniak, W. 2004, ApJ, 617, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Čadež, A., Calvani, M., & Kostić, U. 2008, A&A, 487, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, S. W., Done, C., & Blaes, O. M. 2006, ApJ, 647, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroci, M., Stella, L., van der Klis, M., et al. 2012, Exp. Astron., 34, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J., Bailyn, Ch. D., & Orosz, J. A. 2001, ApJ, 554, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Cuby, J. G., & McCaughrean, M. J. 2001, Nature, 414, 522 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Horák, J. 2008, A&A, 486, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horák, J., & Karas, V. 2006, A&A, 451, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horák, J., Abramowicz, M. A., Kluźniak, W., Rebusco, P., & Török, G. 2009, A&A, 499, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kato, S. 2004a, PASJ, 56, 559 [NASA ADS] [Google Scholar]
- Kato, S. 2004b, PASJ, 56, 905 [NASA ADS] [Google Scholar]
- Kato, S. 2007, PASJ, 59, 451 [NASA ADS] [Google Scholar]
- Kato, S., & Fukue, J. 1980, PASJ, 32, 377 [NASA ADS] [Google Scholar]
- Kluźniak, W. 1998, ApJ, 509, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W. 2008, New Astron. Rev., 51, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., & Abramowicz, M. A. 2001, unpublished, ArXiv e-prints [arXiv:astro-ph/0105057] [Google Scholar]
- Kluźniak, W., Abramowicz, M. A., Kato, S., Lee, W. H., & Stergioulas, N. 2004, ApJ, 603, L89 [Google Scholar]
- Kotrlová, A., Török, G., Šramková, E., & Stuchlík, Z. 2014, A&A, 572, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lai, D., Fu, W., Tsang, D., Horak, J., Yu, C. 2013, Proc. IAU Symp. eds. 290, C. M., Zhang, T., Belloni, M., Mendez, S. N., & Zhang, 290, 57 [Google Scholar]
- Lamb, F. K., Shibazaki, N., Alpar, M. A., & Shaham, J. 1985, Nature, 317, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Mazur, G. P., Vincent, F. H., Johansson, M., et al. 2013, A&A, 554, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, M. C., Lamb, F. K., & Psaltis, D. 1998, ApJ, 508, 791 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, in Compact stellar X-ray sources, eds. W. Lewin, & M. van der Klis (Cambridge, UK: Cambridge University Press), Cambridge Astrophys. Ser., 39, 157 [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2009, in Astro2010: The A&A Decadal Survey (Science White Papers), 197 [Google Scholar]
- McClintock, J. E., Shafee, R., Narayan, R., et al. 2006, ApJ, 652, 518 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Narayan, R., & Shafee, R. 2008, In Black Holes, eds. M., Livio, & A. Koekemoer (Cambridge University Press) [Google Scholar]
- McClintock, J. E., Narayan, R., Gou, L., et al. 2010, AIP Conf. Proc., 1248, 101 [Google Scholar]
- McClintock, J. E., Narayan, R. D., Shane, W., et al. 2011, CQG, 28, 11 [Google Scholar]
- McClintock, J. E., Narayan, R., & Steiner, J. F. 2014, Space Sci. Rev., 183, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M., Done, Ch., Gierlinski, M., & Shane, D. W. 2006, MNRAS, 373, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M. 2007, ARA&A, 45, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Reynolds, C. S., Fabian, A. C., Miniutti, G., & Gallo, L. C. 2009, ApJ, 697, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S. E., Belloni, T. M., Stella, L., Munoz-Darias, T., & Fender, R. 2014a, MNRAS, 437, 3 2554 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S. E., Munoz-Darias, T., Sanna, A., et al. 2014b, MNRAS [Google Scholar]
- Mukhopadhyay, B. 2009, ApJ, 694, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Nowak, M. A., & Wagoner, R. V. 1991, ApJ, 378, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., Kato, S., & Fukue, J. 1987, PASJ, 39, 457 [Google Scholar]
- Orosz, J. A., Groot, P. J., van der Klis, M., et al. 2002, ApJ, 568, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Ortega-Rodríguez, M., Solís-Sánchez, H., López-Barquero, V., et al. 2014, MNRAS, 440, 3011 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, C. A., Silbergleit, A. S., Wagoner, R. V., & Lehr, D. E. 1997, ApJ, 476, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2005, A&A, 439, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Psaltis, D., Wijnands, R., Homan, J., et al. 1999, ApJ, 520, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., McClintock, J. E., Steiner, J. F., et al. 2014, ApJ, 796, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Yoshida, S., & Zanotti, O. 2003, MNRAS, 344, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Muno, M. P., McClintock, J. E., & Orosz, J. A. 2002, ApJ, 580, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Muno, M. P., McClintock, J. E., & Orosz, J. A. 2003, BAAS, 35, 648 [NASA ADS] [Google Scholar]
- Schnittman, J. D., & Bertschinger, E. 2004, ApJ, 606, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Shafee, R., McKinney, J. C., Narayan, R., et al. 2008, ApJ, 687, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Silbergleit, A. S., Wagoner, R. V., & Ortega-Rodríguez, M. 2001, ApJ, 548, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Šrámková, E., Torkelsson, U., & Abramowicz, M. A. 2007, A&A, 467, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steeghs, D., McClintock, J. E., Parsons, S. G., et al. 2013, ApJ, 768, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J. F., Reis, R. C., McClintock, J. E., et al. 2011, MNRAS, 416, 2, 941 [NASA ADS] [Google Scholar]
- Steiner, J. F., McClintock, J. E., & Narayan, R. 2013, ApJ, 762, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., Vietri, M. 1998a, in Abstracts of the 19th Texas Symposium on Relativistic Astrophysics and Cosmology, eds. J. Paul, T. Montmerle, & E. Aubourg (Saclay, France: CEA) [Google Scholar]
- Stella, L., & Vietri, M. 1998b, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., & Vietri, M. 1999, Phys. Rev. Lett., 82, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Straub, O., & Šrámková, E. 2009, CQG, 26, 055011 [Google Scholar]
- Strohmayer, T. E. 2001a, ApJ, 552, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E. 2001b, ApJ, 554, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., Konar, S., Miller, J. C., & Hledík, S. 2008, A&A, 489, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L., & Wood, K. 2002, ApJ, 577, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Török, G., & Stuchlík, Z. 2005, A&A 437, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., Abramowicz, M. A., Kluźniak, W., & Stuchlík, Z. 2005, A&A, 436, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, G., Kotrlová, A., Šramková, E., & Stuchlík, Z. 2011, A&A, 531, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Klis, M. 2006, in Compact Stellar X-Ray Sources, eds. W. H. G. Lewin, & M. van der Klis (Cambridge: Cambridge University Press), 39 [Google Scholar]
- Vincent, F. H., Mazur, G. P., Straub, O., et al. 2014, A&A, 563, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagoner, R. V., 1999, Phys. Rep., 311, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Wagoner, R. V., Silbergleit, A. S., & Ortega-Rodríguez, M. 2001, ApJ, 559, L25 [Google Scholar]
- Zhang, C. M. 2005, Chin. J. Astron. Astrophys., 5, 21 [Google Scholar]
All Tables
Properties of the three microquasars GRO 1655-40, GRS 1915+105, and XTE 1550-564.
All Figures
 |
Fig. 1 Illustration of equipotential surfaces of the accretion torus. The dotted horizontal line denotes the equatorial plane. The yellow region illustrates tori of various thickness. The orange region, together with the yellow, illustrates a torus filling the equipotential surface with a cusp. |
| In the text | |
 |
Fig. 2 Epicyclic frequencies calculated at the centre of the torus, r = rc, plotted for various torus thicknesses (β) and black hole spins a. The curves are drawn solely within the region where the considered value of β does not exceed the critical value corresponding to a torus with a cusp. |
| In the text | |
 |
Fig. 3 Ratio R of the vertical to radial epicyclic frequency and the resonant vertical epicyclic frequency |
| In the text | |
 |
Fig. 4 Observational bounds on the quantity M × νU obtained for Galactic microquasars vs. relations predicted by the epicyclic resonance model. The vertical areas denote the observational bounds on M × νU determined for GRS 1915+105, XTE J1550−564, and GRO J1655−40. The areas are drawn assuming the conservative limits from Table 1. The solid black curve shows predictions of the model calculated for the geodesic flow. The shaded region indicates the interval predicted by the model for the family of equilibrium non-slender fluid tori of all thicknesses possible in the particular case. The red curve corresponds to the case of tori with a cusp. The arrow labelled Δ a indicates the shift of the lower limit on the spin of microquasars implied by considering the non-geodesic flow. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.