| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424364 | |
| Published online | 04 June 2015 | |
Benchmarking spin-state chemistry in starless core models⋆
1 Max-Planck-Institute for Extraterrestrial Physics (MPE), Giessenbachstr. 1, 85748 Garching, Germany
e-mail: osipila@mpe.mpg.de
2 Department of Physics, PO Box 64, University of Helsinki, 00014 Helsinki, Finland
Received: 10 June 2014
Accepted: 16 January 2015
Aims. We aim to present simulated chemical abundance profiles for a variety of important species, giving special attention to spin-state chemistry, in order to provide reference results to which present and future models can be compared.
Methods. We employ gas-phase and gas-grain models to investigate chemical abundances in physical conditions that correspond to starless cores. To this end, we have developed new chemical reaction sets for both gas-phase and grain-surface chemistry, including the deuterated forms of species with up to six atoms and the spin-state chemistry of light ions and of the species involved in the ammonia and water formation networks. The physical model is kept simple to facilitate straightforward benchmarking of other models against the results of this paper.
Results. We find that the ortho/para ratios of ammonia and water are similar in both gas-phase and gas-grain models, particularly at late times, implying that the ratios are determined by gas-phase processes. Furthermore, the ratios do not exhibit any strong dependence on core density. We derive late-time ortho/para ratios of ~0.5 for ammonia and ~1.6 for water. We find that including or excluding deuterium in the calculations has little effect on the abundances of non-deuterated species and on the ortho/para ratios of ammonia and water, especially in gas-phase models where deuteration is naturally hindered by the presence of abundant heavy elements. Although we study a rather narrow temperature range (10–20 K), we find strong temperature dependence in, e.g., deuteration and nitrogen chemistry. For example, the depletion timescale of ammonia is significantly reduced when the temperature is increased from 10 to 20 K; this is because the increase in temperature translates into increased accretion rates, while the very high binding energy of ammonia prevents it from being desorbed at 20 K.
Key words: ISM: abundances / ISM: clouds / ISM: molecules / astrochemistry
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The ortho-to-para ratio of molecular hydrogen, H2, plays a large role in the development of deuterium chemistry at the high density and low temperature attributed to starless cores. The deuteration sequence begins with the exothermic reaction between  and HD:
and HD: 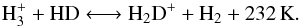 (1)The H2D+ ion can then donate its deuteron to other abundant species, such as CO and N2, yielding DCO+ and N2D+, respectively. However, spin-state effects complicate the reaction scheme.
(1)The H2D+ ion can then donate its deuteron to other abundant species, such as CO and N2, yielding DCO+ and N2D+, respectively. However, spin-state effects complicate the reaction scheme.
Chemical species with multiple protons, or deuterons, can exist in different spin configurations; for example, H2 has two distinct spin states where the nuclear spin wavefunction is either symmetric (ortho-H2; hereafter oH2) or antisymmetric (para-H2; hereafter pH2). The difference in energy between the ground states of these two spin states, ~170 K (Hugo et al. 2009), can be a very important energy reservoir at the low temperatures of starless cores. Indeed, reaction (1) can proceed relatively easily in the backward direction when the ortho forms of both H2D+ and H2 are involved. Consequently, the ortho-to-para (hereafter o/p) ratio of H2 is an important parameter that controls deuterium chemistry (Flower et al. 2006b). In addition to deuteration, spin-state effects play a large role in other areas of starless core chemistry. For example, the formation chain of ammonia depends critically on the N+ + H2 reaction, which requires the presence of oH2 to proceed efficiently at low temperatures (Dislaire et al. 2012).
Owing to its importance, spin-state chemistry is now widely adopted in numerical chemical models and has been applied to all the stages in the star formation process, i.e., diffuse clouds (Albertsson et al. 2014a), starless/prestellar cores (Walmsley et al. 2004; Flower et al. 2004; Pagani et al. 2009; Sipilä et al. 2010, 2013; hereafter S13), and protostellar systems (Taquet et al. 2013, 2014). However, spin-state chemistry is usually discussed in the context of specific problems adopting very different physical models, and comparison between the results of different works can be difficult. In this paper, we aim to remedy this by presenting relatively easily reproducible reference results pertaining to spin-state chemistry, in physical conditions that are appropriate to starless cores. To this end, we have developed a state-of-the-art spin-state chemical model that includes the spin states of light hydrogen-containing species (H2,  ...), and the spin states of the species taking part in the formation and destruction networks of ammonia and water. Our model also includes the deuterated forms of species with up to six atoms. To extend the usability of our results, we present results for both gas-phase and gas-grain models.
...), and the spin states of the species taking part in the formation and destruction networks of ammonia and water. Our model also includes the deuterated forms of species with up to six atoms. To extend the usability of our results, we present results for both gas-phase and gas-grain models.
The paper is organized as follows. Section 2 describes our physical and chemical models in detail. In Sect. 3, we present the results of our calculations. In Sect. 4, we discuss our results and in Sect. 5 present our conclusions. Appendices A to E include complementary discussion on our main results and also present additional modeling results.
2. Model
2.1. Physical parameters
To facilitate a straightforward comparison of future modeling works to the results presented in this paper, we have considered homogeneous models. That is, we fix the values of all physical parameters except the density of the medium. The model parameters (introduced below), along with their assumed values, are presented in Table 1. In all calculations, we set the gas temperature Tgas equal to the dust temperature Tdust. Although we restrict the temperature to T = 10 K in the main text, we present reference results also for T = 15 K and T = 20 K in Appendix C (briefly discussed in Sect. 4.5).
The binding energies of the various species, corresponding to a water ice surface, are mainly taken from Garrod & Herbst (2006; see also Sipilä 2012). Table 2 presents the binding energies of selected species. We assume that the binding energy of a deuterated species is equal to that of the corresponding undeuterated species. This approach has been previously adopted by Cazaux et al. (2010), Taquet et al. (2013), and S13, among others. To cover the typical density values associated with starless cores, we present results at four different densities ranging from 103 to 106 cm-3.
Adopted values of the various physical parameters (see text for definitions of the parameters).
Binding energies (corresponding to a water ice surface) of selected species.
2.2. Chemical code
We use the gas-grain chemical code discussed in Sipilä et al. (2010), Sipilä (2012), and S13, which uses the rate equation approach to calculate chemical evolution in the gas phase and on grain surfaces. The reaction rate coefficient is, for the majority of gas-phase reactions, defined with the modified Arrhenius equation as 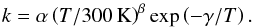 (2)However, there are some exceptions. For photodissociation reactions, the rate coefficient is defined as
(2)However, there are some exceptions. For photodissociation reactions, the rate coefficient is defined as 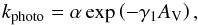 (3)where AV is the visual extinction. For cosmic-ray-induced dissociation, the rate coefficient is defined as
(3)where AV is the visual extinction. For cosmic-ray-induced dissociation, the rate coefficient is defined as 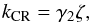 (4)where ζ is the cosmic ray ionization rate. In Eqs. (3) and (4), γ1 and γ2 are efficiency factors.
(4)where ζ is the cosmic ray ionization rate. In Eqs. (3) and (4), γ1 and γ2 are efficiency factors.
The abundance of dust grains is calculated as 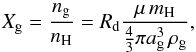 (5)where μ is the average particle mass (1.4), ρg is the grain material density, and Rd is the dust-to-gas mass ratio. For gas-phase chemical reactions involving a grain and another reactant with a different electric charge, the rate coefficient is multiplied by the “J-factor” taking increased reaction efficiency due to polarization into account (Draine & Sutin 1987; Pagani et al. 2009; Sipilä et al. 2010).
(5)where μ is the average particle mass (1.4), ρg is the grain material density, and Rd is the dust-to-gas mass ratio. For gas-phase chemical reactions involving a grain and another reactant with a different electric charge, the rate coefficient is multiplied by the “J-factor” taking increased reaction efficiency due to polarization into account (Draine & Sutin 1987; Pagani et al. 2009; Sipilä et al. 2010).
Gas-phase chemistry is linked with grain-surface chemistry through adsorption and desorption processes. The adsorption rate coefficient of species i is given by 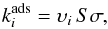 (6)where
(6)where 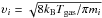 is the thermal speed of species i (kB is the Boltzmann constant and mi is the mass of species i); S is the sticking coefficient, set to unity for all species;
is the thermal speed of species i (kB is the Boltzmann constant and mi is the mass of species i); S is the sticking coefficient, set to unity for all species; 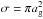 is the grain cross section assuming spherical grains with radius ag. The adopted desorption mechanism is cosmic-ray induced desorption, with the rate coefficient given by
is the grain cross section assuming spherical grains with radius ag. The adopted desorption mechanism is cosmic-ray induced desorption, with the rate coefficient given by ![\begin{equation} k_i^{\rm des} = f_{70} \, k_i^{\rm TD} (70 \, {\rm K}) = f_{70} \, \nu_{0,i} \exp \left[-E_{{\rm b},i}/70\, {\rm K} \right] , \end{equation}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq55.png) (7)where f70 = 3.16 × 10-19 is an efficiency factor, and
(7)where f70 = 3.16 × 10-19 is an efficiency factor, and 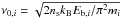 is the characteristic vibration frequency of species i (Hasegawa et al. 1992; Hasegawa & Herbst 1993). In the above, ns and Eb,i stand for the density of binding sites on the grain surface and the binding energy of species i on the grain surface, respectively. For simplicity, we consider only cosmic-ray induced desorption in this work, and neglect alternative desorption mechanisms such as photodesorption or reactive desorption.
is the characteristic vibration frequency of species i (Hasegawa et al. 1992; Hasegawa & Herbst 1993). In the above, ns and Eb,i stand for the density of binding sites on the grain surface and the binding energy of species i on the grain surface, respectively. For simplicity, we consider only cosmic-ray induced desorption in this work, and neglect alternative desorption mechanisms such as photodesorption or reactive desorption.
The rate coefficient for a grain-surface reaction between species i and j is given by 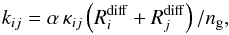 (8)where α is the branching ratio of the reaction; the efficiency factor κij = exp( − Ea/Tdust) or unity for exothermic reactions with or without activation energy (Ea), respectively; and ng is the number density of dust grains (see below). The (thermal) diffusion rate Rdiff is given by
(8)where α is the branching ratio of the reaction; the efficiency factor κij = exp( − Ea/Tdust) or unity for exothermic reactions with or without activation energy (Ea), respectively; and ng is the number density of dust grains (see below). The (thermal) diffusion rate Rdiff is given by 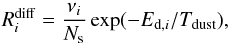 (9)where
(9)where 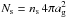 is the number of binding sites on the grain, and Ed,i is the diffusion energy of species i. The diffusion energy is determined by assuming a constant value for the diffusion-to-binding-energy ratio Ed/Eb.
is the number of binding sites on the grain, and Ed,i is the diffusion energy of species i. The diffusion energy is determined by assuming a constant value for the diffusion-to-binding-energy ratio Ed/Eb.
We assume that the gas is initially atomic with the exception of hydrogen and deuterium, which are locked in H2 and HD, respectively (Table 3). We use the same assumptions about the initial abundances as Semenov et al. (2010) except for HD, for which we adopted n(HD) /n(H) = 1.6 × 10-5 based on the D/H ratio measured in the local interstellar medium (ISM; Linsky et al. 1995). The initial H2 ortho/para ratio is (arbitrarily) set to 1 × 10-3.
Finally we note that we do not consider quantum tunneling on grain surfaces in the main body of the text. However, reference results including tunneling are presented in Appendix E, where we also discuss the modifications to the gas-grain model required when tunneling is included.
Initial chemical abundances with respect to nH, and the adopted initial H2 o/p ratio.
2.3. Gas-phase and grain-surface reaction sets
The chemical reaction sets for gas-phase and grain-surface reactions used in this work are reworked versions of the networks presented in S13. The present gas-phase network is based on osu_01_20091 instead of the modified version of osu_03_2008 (Semenov et al. 2010) adopted in S13. In the present model, the spin-state chemistry description of S13 is expanded by adding the spin states of the species involved in the formation of water and ammonia. Also, the present model contains deuterated forms of species with up to six atoms, including observationally important species, such as water, ammonia, and methanol. We discuss the various updates and additions in detail in the following.
2.3.1. Spin-state separation routine
In S13, a routine was developed to automatically spin-state separate any reaction involving light hydrogen-bearing species (H2, 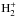 , and
, and  ). In practice, the routine creates new reactions based on predetermined branching ratios. In S13, the branching ratios for most reactions were deduced using the method of Oka (2004), in which representations of the nuclear spin wavefunctions of the various species are used to derive selection rules for reactive collisions. The resulting branching ratios correspond to pure nuclear spin statistical weights under the assumption that the nuclei are completely mixed in the reaction, and thus they are likely to be most applicable to highly exothermic reactions (Oka 2004). For example, the reaction
). In practice, the routine creates new reactions based on predetermined branching ratios. In S13, the branching ratios for most reactions were deduced using the method of Oka (2004), in which representations of the nuclear spin wavefunctions of the various species are used to derive selection rules for reactive collisions. The resulting branching ratios correspond to pure nuclear spin statistical weights under the assumption that the nuclei are completely mixed in the reaction, and thus they are likely to be most applicable to highly exothermic reactions (Oka 2004). For example, the reaction 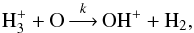 (10)with rate coefficient k, separates into three reactions when the spin states of the species containing multiple protons are considered explicitly:
(10)with rate coefficient k, separates into three reactions when the spin states of the species containing multiple protons are considered explicitly: 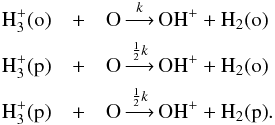 (11)In S13, the branching ratio matrices for some reacting systems were derived by hand and applied in the o/p separation routine. However, for more complicated reactions involving many protons and/or multiple products, custom separation rules were applied (see Appendix A in S13). The motivation for doing so was threefold. Firstly, Oka’s method may not be applicable when the exothermicity of a given reaction is very low. Secondly, we did not want to follow the spin states of species heavier than
(11)In S13, the branching ratio matrices for some reacting systems were derived by hand and applied in the o/p separation routine. However, for more complicated reactions involving many protons and/or multiple products, custom separation rules were applied (see Appendix A in S13). The motivation for doing so was threefold. Firstly, Oka’s method may not be applicable when the exothermicity of a given reaction is very low. Secondly, we did not want to follow the spin states of species heavier than  (with the exception of its deuterated forms), so in any reaction where such species (e.g., H2S) were present, we assumed that the species is in its para form. Thirdly, the branching ratio matrices were deduced by hand, which quickly becomes tedious when multiple protons and product species are present, even though the separation method itself is straightforward.
(with the exception of its deuterated forms), so in any reaction where such species (e.g., H2S) were present, we assumed that the species is in its para form. Thirdly, the branching ratio matrices were deduced by hand, which quickly becomes tedious when multiple protons and product species are present, even though the separation method itself is straightforward.
For this paper, we have developed a new version of the separation routine. In the new version, the branching ratios are calculated automatically using Oka’s method so that we easily obtain the branching ratio matrix of any reaction. Consequently, every species with multiple protons is separated into its ortho and para (and meta when applicable) states. However, to maintain the relative simplicity of the reaction network, we only keep the spin states of the light hydrogen-bearing species and of those species included in the formation networks of water and ammonia (see Sect. 2.3.2).
When spin species other than those mentioned above are present in a reaction, we recombine the reactions over the “unwanted” spin species. For example, consider the reaction 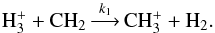 (12)When separated using spin selection rules, reaction (12) branches into the following set of reactions:
(12)When separated using spin selection rules, reaction (12) branches into the following set of reactions: 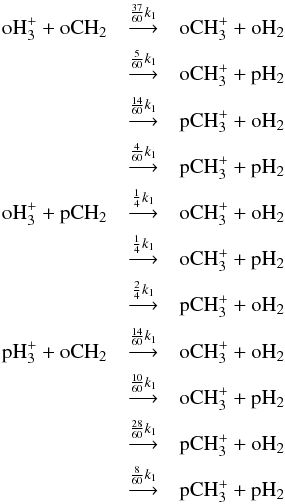
![\begin{eqnarray} \nonumber \\[-1.2cm] {\rm pH_3^+} + {\rm pCH_2} &\mathop{\longrightarrow}\limits^{\frac{1}{5}k_1}& {\rm oCH_3^+} + {\rm oH_2} \nonumber \\ &\mathop{\longrightarrow}\limits^{\frac{2}{5}k_1}& {\rm pCH_3^+} + {\rm oH_2} \nonumber \\ &\mathop{\longrightarrow}\limits^{\frac{2}{5}k_1}& {\rm pCH_3^+} + {\rm pH_2} \nonumber . \end{eqnarray}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq103.png) To determine the branching ratios of the
To determine the branching ratios of the 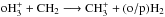 system, i.e., neglecting the spin states of CH2 and
system, i.e., neglecting the spin states of CH2 and 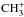 , we sum over the oH2 and pH2 production pathways and average the rate coefficients on the number of spin modifications of CH2 (two). A similar treatment of the
, we sum over the oH2 and pH2 production pathways and average the rate coefficients on the number of spin modifications of CH2 (two). A similar treatment of the  system finally results in four reactions:
system finally results in four reactions: 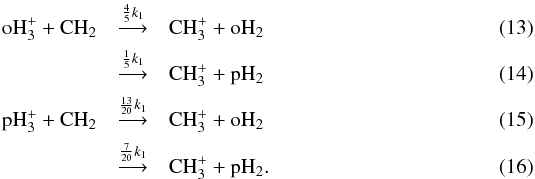 The branching ratios in Eqs. (13) to (16) are based on the assumption that the ortho and para forms of CH2 are equally abundant. Using the statistical ortho/para CH2 ratio (3:1), the four branching ratios are 33/40, 7/40, 27/40, and 13/40, while assuming that CH2 is completely in the para state yields the branching ratios 3/4, 1/4, 3/5, and 2/5. If we assume that the reaction proceeds through a proton hop process instead of complete scrambling, we obtain the branching ratios 1, 0, 1/2, and 1/2 (Oka 2004, Table 8b). Evidently, there are differences in the outcome depending on the assumed ortho/para ratio of CH2 or the assumed reaction mechanism (which is not known for the vast majority of reactions). We note, however, that heavier molecules have a negligible effect on the H2 ortho/para ratio, for example, and our assumptions seem justified in the present case where we only explicitly consider the spin states of a limited set of species.
The branching ratios in Eqs. (13) to (16) are based on the assumption that the ortho and para forms of CH2 are equally abundant. Using the statistical ortho/para CH2 ratio (3:1), the four branching ratios are 33/40, 7/40, 27/40, and 13/40, while assuming that CH2 is completely in the para state yields the branching ratios 3/4, 1/4, 3/5, and 2/5. If we assume that the reaction proceeds through a proton hop process instead of complete scrambling, we obtain the branching ratios 1, 0, 1/2, and 1/2 (Oka 2004, Table 8b). Evidently, there are differences in the outcome depending on the assumed ortho/para ratio of CH2 or the assumed reaction mechanism (which is not known for the vast majority of reactions). We note, however, that heavier molecules have a negligible effect on the H2 ortho/para ratio, for example, and our assumptions seem justified in the present case where we only explicitly consider the spin states of a limited set of species.
It should be noted that the Oka method allows the formation of oH2 from pH2, simply because this is statistically possible. However, the formation of oH2 should be unlikely at low temperatures where the collisional energies are low compared with the energy difference ΔE/k = 170 K between the ground states of oH2 and pH2, unless the reaction is sufficiently exothermic. In S13, we assumed that the required exothermicity is not reached in general, so that the network favored pH2 formation. In this paper, we slightly relax the assumptions of S13 and apply the separation routine to all reactions other than charge-transfer reactions, where we assume that spin states are conserved. However, we add an activation energy of 170 K to the γ coefficient in those reactions where oH2 is created by reactants whose spin states are not explicitly considered (for example, 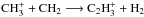 ; see also Albertsson et al. 2014a). The new approach modifies the results of S13 only very slightly; see Sect. 3.1. With these changes, the resulting network should be more applicable at higher temperatures (Albertsson et al. 2014b; see also 2014a). The combination of nuclear spin statistical weights and activation energies for probably endoergic reactions approximates the method that Hugo et al. (2009) used to calculate the thermal rate coefficients for the
; see also Albertsson et al. 2014a). The new approach modifies the results of S13 only very slightly; see Sect. 3.1. With these changes, the resulting network should be more applicable at higher temperatures (Albertsson et al. 2014b; see also 2014a). The combination of nuclear spin statistical weights and activation energies for probably endoergic reactions approximates the method that Hugo et al. (2009) used to calculate the thermal rate coefficients for the  isotopic system, but we note that a detailed state-to-state analysis, such as the one performed by Hugo et al. (2009), is required to study endothermic reactions consistently.
isotopic system, but we note that a detailed state-to-state analysis, such as the one performed by Hugo et al. (2009), is required to study endothermic reactions consistently.
We applied the same spin-state separation routine to grain-surface reactions. No rate coefficient corrections were made to the surface reactions, because in the base surface reaction set adopted here (Semenov et al. 2010), the non-addition reactions that create  (the asterisk denotes a surface species), for example
(the asterisk denotes a surface species), for example  , already present high activation barriers. Of course,
, already present high activation barriers. Of course, 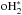 can be created by (cr-induced) photodissociations; we assume that these events are sufficiently energetic so that o
can be created by (cr-induced) photodissociations; we assume that these events are sufficiently energetic so that o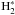 and p
and p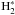 are produced in the statistical ratio 3:1.
are produced in the statistical ratio 3:1.
We note that the conservation of nuclear spin may not hold for grain-surface reactions since there is experimental evidence to the contrary (Fushitani & Momose 2002; Hama & Watanabe 2013). We discuss this issue briefly in Sect. 4.4.
2.3.2. Spin-state chemistry of ammonia and water
In this work, we have included the spin-state chemistry of nitrogen-containing species involved in the ammonia formation chain, recently studied using the Oka method by Le Gal et al. (2014; see also Flower et al. 2006a; Dislaire et al. 2012; Faure et al. 2013; Rist et al. 2013). We checked that our o/p separation routine produces the same branching ratios as given in Tables B.1. and B.2. in Le Gal et al. (2014), see also Sect. 4.2.
Because of the high exothermicities of the hydrogen addition reactions on grain surfaces creating 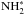 and
and 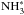 (~4.2 eV and 4.7 eV, respectively, as calculated from Eqs. (3) and (4) in Allen & Robinson 1977 and using data presented in Appendix C of Du et al. 2012), we assumed that the high-temperature statistical branching ratios for the formation reactions,
(~4.2 eV and 4.7 eV, respectively, as calculated from Eqs. (3) and (4) in Allen & Robinson 1977 and using data presented in Appendix C of Du et al. 2012), we assumed that the high-temperature statistical branching ratios for the formation reactions, 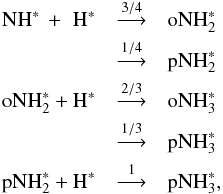 are valid. These branching ratios are, of course, given directly by the Oka method.
are valid. These branching ratios are, of course, given directly by the Oka method.
We also included the spin-state chemistry of the species involved in the water formation network. The branching ratios for the most important reactions in the water network are presented in Appendix B. Similar to the nitrogen chemistry, we adopted statistical branching for water formation on grain surfaces: 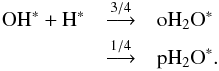 (17)
(17)
2.3.3. Deuteration
In S13, a deuteration routine was applied to the OSU network, and species with up to four atoms were deuterated. In the present work, the deuteration routine is extended to handle species with up to six atoms, so that the deuterated forms of important species, such as methanol and ammonia (whose formation depends on  ), can be included. The deuteration routine is based on the one presented by Rodgers & Millar (1996), in which deuterons are substituted for protons in the various reactions and branching ratios are calculated assuming complete scrambling (see also S13).
), can be included. The deuteration routine is based on the one presented by Rodgers & Millar (1996), in which deuterons are substituted for protons in the various reactions and branching ratios are calculated assuming complete scrambling (see also S13).
The calculation of the nuclear spin-state branching ratios for multiply deuterated species is more complicated than for undeuterated species. For species with three or more deuterium nuclei, Oka’s method, based on angular momentum algebra, is insufficient because there is no one-to-one correspondence between angular momentum and symmetry representations. The statistical branching ratios between the nuclear spin states of species with up to five hydrogen or deuterium nuclei can be obtained from Tables III and IV of Hugo et al. (2009). In the present paper, the spin-state chemistry in reactions between species containing H and/or D only is included using these rules, and they are mostly available in the literature. Specifically, we include the spin-state chemistry of the 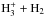 reacting system from Hugo et al. (2009), complemented by data for other reactions concerning light hydrogen-and-deuterium-bearing species (
reacting system from Hugo et al. (2009), complemented by data for other reactions concerning light hydrogen-and-deuterium-bearing species ( , H2D+, HD etc.) from Walmsley et al. (2004) and Flower et al. (2004). The rate coefficients for dissociative recombination between
, H2D+, HD etc.) from Walmsley et al. (2004) and Flower et al. (2004). The rate coefficients for dissociative recombination between  and its deuterated forms and electrons were taken from Pagani et al. (2009).
and its deuterated forms and electrons were taken from Pagani et al. (2009).
The nuclear spin chemistry of multiply deuterated molecules containing heavy elements is not considered in the present model, except that it is necessary to predict the ratio of oD2 and pD2 released in reactions involving heavy species to achieve a properly closed reaction network. Furthermore, oD2 and pD2 produced by these reactions can be relevant to the chemistry of light molecules containing only H and/or D, which are treated using the appropriate spin selection rules (see below).
The deuteration procedure used here directly propagates the hydrogen spin-state chemistry into the deuterium chemistry for molecules with up to two deuterium nuclei. For hydrogenated species like CH2, we assumed that the ortho and para forms of CH2 are equally abundant (see Sect. 2.3.1). However, copying the reaction scheme from hydrogenated to doubly deuterated molecules is equivalent to following the correct nuclear spin selection rules for spin-1 systems with the assumption that oD2 and pD2 are instead present in the ratio 2:1 (i.e., the statistical value) in complexes with heavy nuclei, e.g., CD2.
As an example of the spin-state separation of doubly deuterated species, we consider the reaction 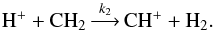 (18)Since our program performs the spin-state separation of hydrogen species prior to deuteration, the above reaction is first divided into the following two branches:
(18)Since our program performs the spin-state separation of hydrogen species prior to deuteration, the above reaction is first divided into the following two branches: ![\begin{eqnarray} \label{h2ex} {\rm H^+} + {\rm CH_2} &\mathop{\longrightarrow}\limits^{}& {\rm CH^+} + {\rm oH_2} , \;k=\frac{2}{3} k_2 \exp(-170/T) , \nonumber \\[2mm] &\mathop{\longrightarrow}\limits^{}& {\rm CH^+} + {\rm pH_2} , \;k=\frac{1}{3}k_2 . \end{eqnarray}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq126.png) (19)The branching ratio (2/3 oH2, 1/3 pH2) follows from the nuclear spin statistics under the implicit assumption that pCH2 and oCH2 have equal abundances, i.e. [pCH2] = [oCH2]. Deuterating both branches leads in our routine to the following reactions:
(19)The branching ratio (2/3 oH2, 1/3 pH2) follows from the nuclear spin statistics under the implicit assumption that pCH2 and oCH2 have equal abundances, i.e. [pCH2] = [oCH2]. Deuterating both branches leads in our routine to the following reactions: ![\begin{eqnarray*} {\rm H^+} + {\rm CHD} &\mathop{\longrightarrow}\limits^{\frac{2}{9}k_2\exp(-170/T)}& \rm CD^+ + oH_2 \\[1mm] &\mathop{\longrightarrow}\limits^{\frac{1}{9}k_2}& \rm CD^+ + pH_2 \\[1mm] &\mathop{\longrightarrow}\limits^{\frac{6}{9}k_2}& \rm CH^+ + HD \\[1mm] {\rm H^+} \,+\, {\rm CD_2} &\mathop{\longrightarrow}\limits^{\frac{2}{9}k_2}& \rm CH^+ + oD_2 \\[1mm] &\mathop{\longrightarrow}\limits^{\frac{1}{9}k_2\exp(-86/T)}& \rm CH^+ + pD_2 \\[1mm] &\mathop{\longrightarrow}\limits^{\frac{6}{9}k_2}& \rm CD^+ + HD \end{eqnarray*}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq128.png)
![\begin{eqnarray*} \\[-1.1cm] {\rm D^+} \,+\, {\rm CH_2} &\mathop{\longrightarrow}\limits^{\frac{2}{9}k_2\exp(-170/T)}& \rm CD^+ + oH_2 \\ &\mathop{\longrightarrow}\limits^{\frac{1}{9}k_2}& \rm CD^+ + pH_2 \\ &\mathop{\longrightarrow}\limits^{\frac{6}{9}k_2}& \rm CH^+ + HD \\ {\rm D^+} + {\rm CHD} &\mathop{\longrightarrow}\limits^{\frac{2}{9}k_2}& \rm CH^+ + oD_2 \\ &\mathop{\longrightarrow}\limits^{\frac{1}{9}k_2\exp(-86/T)}& \rm CH^+ + pD_2 \\ &\mathop{\longrightarrow}\limits^{\frac{6}{9}k_2}& \rm CD^+ + HD \\ {\rm D^+} \,+\, {\rm CD_2} &\mathop{\longrightarrow}\limits^{\frac{2}{3}k_2}& \rm CD^+ + oD_2 \\ &\mathop{\longrightarrow}\limits^{\frac{1}{3}k_2\exp(-86/T)}& \rm CD^+ + pD_2 . \end{eqnarray*}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq129.png) Reactions yielding pH2 or oD2 are assumed to have no activation energies, whereas those producing pD2 are assumed to have an activation energy of 86 K, corresponding to the energy separation between the ground states of pD2 and oD2 (Hugo et al. 2009). As noted above, the branching ratios for the reactions producing D2 are correct under the implicit assumption that [oCD2] : [pCD2] = 2:1. However, as in the case of H2, reactions involving heavy species have a negligible effect on the D2 o/p ratio. For the H+ + CHD and D+ + CH2 reactions above, one would expect H2 formation in the o/p ratio 3:1, but in the example the ratio is instead 2:1 because the deuterated reactions adopt the branching ratios from the undeuterated parent reactions, in this case reactions (19), where the three-proton system leads to an H2 o/p ratio of 2:1.
Reactions yielding pH2 or oD2 are assumed to have no activation energies, whereas those producing pD2 are assumed to have an activation energy of 86 K, corresponding to the energy separation between the ground states of pD2 and oD2 (Hugo et al. 2009). As noted above, the branching ratios for the reactions producing D2 are correct under the implicit assumption that [oCD2] : [pCD2] = 2:1. However, as in the case of H2, reactions involving heavy species have a negligible effect on the D2 o/p ratio. For the H+ + CHD and D+ + CH2 reactions above, one would expect H2 formation in the o/p ratio 3:1, but in the example the ratio is instead 2:1 because the deuterated reactions adopt the branching ratios from the undeuterated parent reactions, in this case reactions (19), where the three-proton system leads to an H2 o/p ratio of 2:1.
We have verified through testing that the spin separation of doubly deuterated (heavy) species is of little consequence to the results presented later in this paper, and therefore the separation method used here seems reasonable for the present work. We will discuss the spin separation of multiply deuterated molecules in depth in a future dedicated paper.
2.3.4. Other updates with respect to S13
In addition to the updates to the o/p separation and deuteration routines described above, the rate coefficients of several reactions have been updated. First of all, we now adopt the osu_01_2009 reaction set instead of (modified) osu_03_2008, so any updates of the base reaction set, including anion chemistry, are included in our new model. The modifications made to osu_03_2008 by Semenov et al. (2010), already included in S13, have been incorporated in the new model as well.
We have also included new rate coefficient data from the literature. We adopted the rate coefficients given in Tables 12 and 13 in Albertsson et al. (2013) – except for reactions involving hydrogen and/or deuterium only for which we use other data as detailed above. We also included selected data from Le Gal et al. (2014), which we summarize in Table B.2. We refer the reader to Albertsson et al. (2013) and Le Gal et al. (2014) for the original data references.
The impact of the rate coefficient updates is analyzed in Sect. 3.1.
3. Results
In this section, we present benchmarking results for spin-state chemistry for different values of density, using gas-phase and gas-grain models. All of the results presented below correspond to T = 10 K. Results for T = 15 K and T = 20 K are presented in Appendix C, while results without deuterium and with tunneling are presented in Appendices D and E, respectively. The data for the various figures presented below are available from the authors upon request.
3.1. Comparison of the new model to S13
 |
Fig. 1 Upper panels: abundances of selected non-deuterated (left), deuterated (middle), and grain-surface (both non-deuterated and deuterated, right) species as functions of time, as calculated with model T1 (solid lines) or model T2 (dashed lines). Middle panels: like the upper row, but comparing models T1 (solid lines) and T3 (dashed lines). Lower panels: like the other rows, but comparing models T1 (solid lines) and F1 (dashed lines). In all calculations, the density of the medium is set to nH = 105 cm-3. The abundances of H2O, NH3, and NH2D represent sums over their respective ortho and para states. |
 |
Fig. 2 Abundances of selected species calculated with model F2 (i.e., surface reactions and adsorption/desorption excluded) as functions of time at different densities, labeled in the upper left panel. The labels indicate densities of the medium; for example, 103 stands for nH = 103 cm-3. |
In our new model, there are two main sources of updates: 1) our new spin-state separation and deuteration routines and 2) the rate coefficient updates for various species from the literature and from the transition from osu_03_2008 to osu_01_2009. Qualitatively, the new spin-state separation routine may somewhat affect the abundances of the various species because of the increased emphasis on oH2 in the new separation routine (albeit with a 170 K barrier in most cases). However, the extension of deuteration from four to six atoms is not expected to have much of an impact on the overall chemistry. In the following, we study the effect of the various updates by successively introducing new updates into the S13 chemical model. The models introduced below are also described in Table 4.
Models discussed in this work.
 |
Fig. 3 As in Fig. 2, but calculated with model F1. The abundance scales are in some cases different than in Fig. 2. |
First, we constructed a test reaction set by spin-state separating the S13 base reaction set (modified osu_03_2008) with the new routine presented here, but using the old S13 deuteration routine and including no new rate coefficient data (model T2). The upper row in Fig. 1 plots the abundances of selected species as functions of time calculated using model T2 and using the old model of S13 (model T1). In these calculations, the density of the medium is set to nH = 105 cm-3, and the other physical parameters correspond to the values given in Table 1. In the righthand panel, the abundances of the respective ortho and para states of H2O∗, 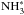 , and NH2D∗ have been summed over. It is observed that the new spin-state separation routine modifies only slightly the abundances of non-deuterated species at early times both in the gas phase and on grain surfaces, while the abundances of deuterated species are virtually identical in both cases. As a result, the new oH2-creating reactions with 170 K barriers included here (as opposed to S13) are of little consequence to the chemistry as a whole (although the situation might be different at high temperatures).
, and NH2D∗ have been summed over. It is observed that the new spin-state separation routine modifies only slightly the abundances of non-deuterated species at early times both in the gas phase and on grain surfaces, while the abundances of deuterated species are virtually identical in both cases. As a result, the new oH2-creating reactions with 170 K barriers included here (as opposed to S13) are of little consequence to the chemistry as a whole (although the situation might be different at high temperatures).
The middle row in Fig. 1 plots the abundances of selected species calculated with a test reaction set constructed by applying the new spin-state separation and deuteration routines to the modified osu_03_2008 reaction set; as before, no new rate coefficient data is included (model T3). It is observed that, overall, the extension of the deuteration scheme has little effect on the chemistry. However, deuteration is enhanced in the new model on long timescales because of less efficient HD depletion. Inspection of the reaction rates reveals that this effect is caused by the dissociation of HDO∗, the main grain-surface deuterium carrier in our model, whose dissociation produced only OD∗ + H∗ in S13 owing to a bug in the deuteration routine, but here also produces OH∗ + D∗. Consequently, more D∗ is available to form HD∗, replenishing the gas-phase HD abundance.
In the bottom row of Fig. 1, we again plot the abundances of selected species, now calculated with the full model presented in this paper, i.e., including the rate coefficient updates discussed in Sect. 2.3.4 (model F1). Evidently, the rate coefficient updates lead to significant differences with respect to the previous cases, both in the gas phase and on grain surfaces. For example, the CO formation timescale is much shorter with the updated rate coefficients, which is mainly due to numerous changes in electron DR rate coefficients. Accordingly, the electron abundance initially drops very rapidly in the new model. From an observational point of view, the most striking difference between the models is the abundance of N2H+, which is over an order of magnitude lower at late times in the new model, resulting mainly from increased (factor 2–3) electron DR rate coefficients and also from changes in neutral-neutral chemistry, with respect to the OSU values. The changes is N2H+ and HCO+ abundances propagate to their deuterated counterpart ions N2D+ and DCO+. Also, the abundance of ammonia decreases by a factor of 2–3 at late times in the new model with respect to S13.
Surface chemistry is also affected by the rate coefficient updates. In the new model, atomic hydrogen is at early times produced mainly by neutral-neutral reactions between light hydrocarbons instead of electron DR reactions of various ions (owing to decreased electron abundance), and there is more atomic hydrogen available in the gas phase. The hydrogen is then adsorbed onto grain surfaces, leading to efficient production of, for example, water and ammonia, which form mainly by hydrogenation. We stress that these effects are caused by changes in the gas-phase chemistry, because none of the surface reaction rates have been updated. These results emphasize the importance of constraining the reaction rate coefficients, particularly for key reactions.
Our chemical model predicts gas-phase and grain-surface abundances in physical conditions attributed to starless cores, and our model results could in principle be used to interpret ice observations. However, direct observations of grain-mantle species toward starless cores are extremely hard owing to the very high extinctions. Thus, we would need to rely on observations toward embedded Class 0 sources, for example, assuming that the ice feature originates in the source envelope. A detailed investigation of modeled ice abundances versus observations is left for future work, and we focus our attention on the gas-phase species in the present paper.
In what follows, all results have been produced with the new ortho/para separation and deuteration routines, and they include the rate coefficient updates from the literature as described in Sect. 2.3.4.
3.2. Gas-phase chemistry
Figure 2 presents the results of gas-phase modeling at different densities. Here, we have not considered adsorption or desorption of any species, and the formation of H2, HD, and D2 on grain surfaces is included in the form of gas-phase reactions as in the model of Kong et al. (2013).
Ion abundances decrease significantly with increasing density, which is a consequence of the increased electron DR rates at high density and of the high abundances of heavy neutral species owing to the absence of depletion. The abundances of heavy ions follow largely that of  , which is primarily destroyed by reactions between abundant neutral species like CO and N2 and electrons. One example of this tendency is HCO+, which is the most important reaction partner of free electrons at late times both at low and high densities. This ion is formed in a reaction between
, which is primarily destroyed by reactions between abundant neutral species like CO and N2 and electrons. One example of this tendency is HCO+, which is the most important reaction partner of free electrons at late times both at low and high densities. This ion is formed in a reaction between  and CO and destroyed mainly in electron recombination, which returns CO. At high densities, the enhanced production of free electrons by the cosmic ray ionization of H2 leads to an increase in the electron DR rates (at constant temperature), and the HCO+ abundance decreases accordingly. N2H+ is locked in a similar cycle (
and CO and destroyed mainly in electron recombination, which returns CO. At high densities, the enhanced production of free electrons by the cosmic ray ionization of H2 leads to an increase in the electron DR rates (at constant temperature), and the HCO+ abundance decreases accordingly. N2H+ is locked in a similar cycle (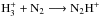 ; N2H+ + e− − → N2 + H), dependent on the abundance of
; N2H+ + e− − → N2 + H), dependent on the abundance of  . Also the N2H+ abundance decreases clearly when the density increases.
. Also the N2H+ abundance decreases clearly when the density increases.
Deuteration is also suppressed in the absence of depletion, because  reacts primarily with the abundant heavy species rather than with HD.
reacts primarily with the abundant heavy species rather than with HD.
3.3. Gas-grain chemistry
Figure 3 presents the results of gas-grain modeling at different densities, adopting the full model (F1) described above. Evidently, including depletion significantly decreases the abundances of carbon and oxygen-containing species with respect to the gas-phase model. The  abundance is much higher at late times in the full model with respect to the gas-phase model because of the depletion of its main reaction partners (e.g., CO) onto grain surfaces. The chemistry of nitrogen-containing species is different than that of, e.g., carbon and oxygen because nitrogen chemistry depends on slow neutral-neutral reactions. On the other hand, the binding energy of (atomic and molecular) nitrogen is relatively low (Table 2), so nitrogen chemistry can still occur efficiently after other heavy elements have been depleted onto grain surfaces. Consequently, an appreciable abundance of N2, the precursor molecule of both NH3 and N2H+ (see, e.g., Fontani et al. 2012), can be present in the gas at late times. This is demonstrated by two effects. Firstly, the abundance of NH3 is less than an order of magnitude lower in the full model than in the gas-phase model at high density, even though depletion tends to decrease its abundance. Secondly, the abundance of N2H+, dependent on
abundance is much higher at late times in the full model with respect to the gas-phase model because of the depletion of its main reaction partners (e.g., CO) onto grain surfaces. The chemistry of nitrogen-containing species is different than that of, e.g., carbon and oxygen because nitrogen chemistry depends on slow neutral-neutral reactions. On the other hand, the binding energy of (atomic and molecular) nitrogen is relatively low (Table 2), so nitrogen chemistry can still occur efficiently after other heavy elements have been depleted onto grain surfaces. Consequently, an appreciable abundance of N2, the precursor molecule of both NH3 and N2H+ (see, e.g., Fontani et al. 2012), can be present in the gas at late times. This is demonstrated by two effects. Firstly, the abundance of NH3 is less than an order of magnitude lower in the full model than in the gas-phase model at high density, even though depletion tends to decrease its abundance. Secondly, the abundance of N2H+, dependent on  , is orders of magnitude higher with respect to the gas-phase model even at high density (we assume that ions do not deplete onto grain surfaces, but can recombine with negatively charged grains).
, is orders of magnitude higher with respect to the gas-phase model even at high density (we assume that ions do not deplete onto grain surfaces, but can recombine with negatively charged grains).
Deuteration increases strongly when gas-grain interaction is taken into account. However, a local peak in deuteration is observed around the time that HD starts deplete, in line with the results of S13. HD depletion is somewhat less severe in the present model than in S13 because we do not consider quantum tunneling. In agreement with previous results in the literature, our results clearly show that depletion is needed to produce observable amounts of, say, oH2D+ and N2H+ at high density.
Figures 2 and 3 indicate that the o/p ratios of ammonia and water depend only slightly on density, both in the gas-phase and gas-grain models. We discuss this issue further below.
4. Discussion
4.1. The o/p ratios of water and ammonia
 |
Fig. 4 o/p ratios of NH3 (upper panels) and H2O (lower panels) as functions of time at different densities, labeled in the upper left panel. The left panels correspond to the gas-phase model (F2), while the right panels correspond to the gas-grain model (F1). |
Figure 4 plots the o/p ratios of NH3 and H2O at different densities according to gas-phase and gas-grain models. The o/p ratio of ammonia is very similar in both models up to nH = 105 cm-3. The ratio is greater at ~104 − 105 years at nH = 106 cm-3 in the gas-phase model, in which one of the main production pathways for  at t ~ 105 yr is the
at t ~ 105 yr is the  system, which forms all three spin variants of
system, which forms all three spin variants of  . However, m
. However, m , for example, only dissociates to oNH3 (see Table 2 in Le Gal et al. 2014). The detailed behavior of the spin-state chemistry is different in the gas-grain model, where the reaction pathways with H3O+ are practically absent at t ≳ 105 yr because of water depletion. Nevertheless, our results indicate that, at late times, o/p-NH3 is ~0.4–0.5 regardless of the considered model or assumed density.
, for example, only dissociates to oNH3 (see Table 2 in Le Gal et al. 2014). The detailed behavior of the spin-state chemistry is different in the gas-grain model, where the reaction pathways with H3O+ are practically absent at t ≳ 105 yr because of water depletion. Nevertheless, our results indicate that, at late times, o/p-NH3 is ~0.4–0.5 regardless of the considered model or assumed density.
The o/p ratio of H2O behaves similarly to that of NH3 in the sense that the largest differences between the gas-phase and gas-grain models are observed at nH = 106 cm-3. The o/p ratio of H2O is tied to that of H3O+, which evolves differently in the gas-grain model owing to multiple spin-state details (H3O+ and H2O are connected mainly through H2O+ + H2 − → H3O+ + H and the  system). The o/p-H2O ratios at different densities and in different models are, again, very close to each other at late times where we derive o/p-H2O ~ 1.5 − 1.7.
system). The o/p-H2O ratios at different densities and in different models are, again, very close to each other at late times where we derive o/p-H2O ~ 1.5 − 1.7.
Unlike the o/p ratio of H2, which is strongly influenced by grain-surface chemistry, the o/p ratios of H2O and NH3 are determined nearly completely by gas-phase chemistry because of their high binding energies (see Table 2). That the o/p ratios of the respective species are very similar in both gas-phase and gas-grain models supports this interpretation (Fig. 4). The late-time values of the o/p ratios can be justified by a rate coefficient analysis of the main formation and destruction paths of ammonia and water; this analysis is presented in Appendix A.
We note that the late-time H2O o/p ratios derived here are much lower than those typically observed in the ISM (van Dishoeck et al. 2013; see also the discussion in Keto et al. 2014). The disagreement is probably due to the fact that observations toward dark clouds with intermediate-to-high density are missing. To investigate this issue, we ran test calculations with our gas-grain model at conditions simulating translucent clouds (nH = 102 cm-3 and T = 10 K) with two values of AV, 10 mag, and 1 mag. We found that at AV = 10 mag, the H2O o/p ratio is ~1.6, but at AV = 1 mag the ratio is ~3, suggesting that photochemistry plays a large role in determining the o/p ratio in regions with low visual extinction. This result underlines the need for accurate physical models when interpreting observations.
Ammonia is a useful probe of the gas temperature in dark clouds (Tafalla et al. 2004; Juvela et al. 2012), and simulated NH3 line emission profiles can be used to constrain the kinetic temperature. However, a proper comparison of simulated line emission against a detection of pNH3, for instance, requires an estimate of the NH3 o/p ratio. Given that the NH3 o/p ratio changes very little with density in our models, we deduce that o/p-NH3 ~ 0.4−0.5 is a good conservative estimate of the ratio in dark clouds. This result is consistent with observations by Persson et al. (2012) and the models of Le Gal et al. (2014), see also Sect. 4.2.
Finally, we stress that we have not carried out a complete parameter-space study of the ammonia and water o/p ratios, and that such a study should be taken on in the future.
4.2. Comparison to Le Gal et al. (2014)
Recently, Le Gal et al. (2014) have presented gas-phase modeling results of nitrogen chemistry in dark clouds. They included in their model the spin-state chemistry pertaining to the ammonia formation network, as we do here. We ran some test calculations to compare our results to those of Le Gal et al. (2014), adopting the same physical conditions and initial chemical abundances for He, C, N, and Fe (we chose [C]/[O] = 0.8 and [S] = 8 × 10-8). Le Gal et al. (2014) do not explicitly state the initial H2 o/p ratio, but we assumed a value of 3.
Table 5 summarizes the results of these tests. In our model, there are many cosmic-ray-induced and photodissociation reactions with long timescales, which prevent the system from reaching a true steady state; the values given in the table correspond to late-time chemical evolution (t = 2.0 × 107 yr), after which temporal changes in chemical abundances are generally small. The Le Gal et al. steady-state values have been read off their Figs. 4 and 5. Evidently, our model gives lower NH and NH2 abundances and a higher NH3 abundance than the Le Gal et al. model, but the ortho/para ratios of both NH2 and NH3 are similar in both models.
We also tested an initial [C]/[O] ratio of 0.3 and found that in this case the late-time NH and NH2 abundances are lower by one and two orders of magnitude, respectively, than those predicted by Le Gal et al. (2014). However, the NH3 abundance and the NH2 and NH3 o/p ratios are again similar to the Le Gal et al. (2014) model.
Our test results indicate that there are minor differences in fractional abundances between our model and that of Le Gal et al. (2014). The two models predict similar o/p ratios for NH2 and NH3, which is expected since we adopt the same spin-state chemical description for these species as Le Gal et al. (2014).
Abundances and abundance ratios predicted by our gas-phase model (F2) and that of Le Gal et al. (2014).
4.3. H2 formation in gas-phase models
 |
Fig. 5 Abundances of selected species as functions of time at different densities (labeled in the figure), in a gas-phase model at T = 10 K, using different approaches to H2 formation. Dash-dotted lines correspond to the gas-phase reactions of Kong et al. (2013). Solid lines correspond to grain-surface H2 formation assuming only H and D adsorption and with the binding energies of H and H2 and their deuterated isotopologs set to 100 K. Dotted lines (superimposed on the dash-dotted lines) correspond to grain-surface H2 formation assuming only H and D adsorption and with the binding energies adopted in the main body of this work. The abundances of ammonia, water and H2D+ represent sums over the abundances of their respective ortho and para states. |
In the gas-phase results presented above, the formation of H2 (and its isotopologs HD and D2) is included in the form of gas-phase reactions (see Kong et al. 2013). From Fig. 2 it is evident that this approach leads to an increase in the H2 o/p ratio at late times, among other things. Another approach to including the formation of H2 and its isotopologs in a gas-phase model is to invoke grain-surface formation processes, but letting only atomic H and D be adsorbed onto the grain surfaces.
We ran test calculations at T = 10 K comparing the two approaches. The results of these calculations are presented in Fig. 5, where the abundances of selected species as functions of time are plotted at different densities, using different approaches to H2 formation. Evidently, the Kong et al. (2013) approach is practically equivalent to the grain-surface formation approach when “normal” binding energies (450 K for H and D) are used. (The dotted and dash-dotted lines are practically superimposed.) In the gas-grain model with very low H binding energy (100 K), H desorbs very fast, leading to inefficient H2 production on the grain surfaces regardless of the density. Increasing the binding energy increases the average time spent by H atoms on the grains and thus leads to more efficient H2 production.
The choice of the H2 formation efficiency has little effect on the abundance of H2D+ because deuterium chemistry is suppressed owing to the lack of depletion, and on the abundance of water because its formation pathway proceeds through exothermic reactions. However, the abundance of ammonia is slightly affected at late times because its formation starts with the N+ + H2 reaction, which is strongly endothermic when pH2 is involved (Le Gal et al. 2014).
We have checked that the o/p ratio of ammonia is hardly affected by the choice of the H2 formation efficiency, despite its effect on the total NH3 abundance. This is because the o/p ratio is mainly determined by reactions further up in the ammonia formation chain (see Appendix A). The o/p ratio of water is not affected because it is not sensitive to the H2 o/p ratio. However, the o/p ratio of H2D+ is affected because it is mainly determined by the H2 o/p ratio (Pagani et al. 1992; Gerlich et al. 2002; Hugo et al. 2007; Brünken et al. 2014). The late-time H2D+ o/p ratio changes by a factor of ≲2 depending on the choice of binding energies.
4.4. Conservation of spin in grain-surface reactions
In this work, we have assumed that high-temperature statistical branching ratios are applicable to both gas-phase and grain-surface reactions. However, it has been previously suggested that different selection rules may apply for grain-surface reactions (Fushitani & Momose 2002) and, in the case of H2 formation, that H2 ortho/para conversion may occur on the surface subsequent to H2 formation (Watanabe et al. 2010; Hama & Watanabe 2013).
To constrain the possible effect of uncertainties in grain-surface spin chemistry on our results, we constructed two test models in which grain-surface reactions can create either only para or only ortho states – with the exception of H2 and D2 for which we assume the high-temperature statistical formation ratios (i.e., both ortho and para are created). The result of this test is shown in Fig. 6. Evidently, the effect of reactions other than the fundamental H∗ + H∗ reaction (and of its deuterated counterparts) on the gas-phase spin-state chemistry is negligible, since both the upper and lower limits correspond almost exactly to our normal full model.
We carried out this test for all the medium densities considered in this paper (nH = 103 to 106 cm-3; with T = 10 K), and we conclude that the possible grain-surface branching ratio uncertainties related to spin-state chemistry do not modify the results of this paper. However, we note that Watanabe et al. (2010) discussed H2 ortho/para conversion subsequent to H2 formation. Such conversion processes might translate to modifications in the gas-phase chemistry as the H2 molecules desorb. We currently have no way to test this, meaning we have no data to form a rate coefficient. This issue should be investigated in the future.
 |
Fig. 6 Abundances of selected species as functions of time in a gas-grain model at T = 10 K and nH = 105 cm-3. The solid lines correspond to model F1, while the error bars correspond to test models in which grain-surface reactions can only create ortho species (upper limits) or para species (lower limits). |
4.5. Results at higher temperatures
In Appendix C, we present modeling results analogous to those shown in Figs. 2 to 4, but calculated assuming either Tgas = Tdust = 15 K or Tgas = Tdust = 20 K. No dramatic differences between the temperatures are seen in the gas-phase models, reflecting the weak temperature dependence of ion-molecule chemistry.
However, large differences between the temperatures are present in the gas-grain models. For example, nitrogen chemistry is much faster at high density at T = 20 K than at T = 10 K. The higher temperature increases the adsorption rates, but on the other hand, the very high binding energy of ammonia, for example, means that practically no desorption occurs even at T = 20 K. Consequently, ammonia and N2H+ deplete almost totally from the gas phase on a timescale of ~106 years at nH = 106 cm-3. Depletion also occurs at T = 10 K, but on a much longer timescale (Fig. 3). We note that in the case of N2H+, the “depletion" is caused by the freeze-out of N2 onto grain surfaces, because we assume that molecular ions (e.g., N2H+) dissociatively recombine with negatively charged grains, and the products (in this case N2 + H) are immediately returned to the gas phase.
Deuteration is also strongly affected by changes in temperature. For example, the (late-time) deuteration degree of  is much lower at T = 20 K than at T = 10 K because the higher temperature causes 1) the deuteration reactions (
is much lower at T = 20 K than at T = 10 K because the higher temperature causes 1) the deuteration reactions (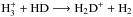 etc.) to proceed more efficiently in the backward direction and 2) less severe depletion of other important reaction partners of H2D+, such as CO and N2, observed also as enchanced deuterations of HCO+ and N2H+. Consequently, very little HD depletion is present at T = 20 K regardless of density.
etc.) to proceed more efficiently in the backward direction and 2) less severe depletion of other important reaction partners of H2D+, such as CO and N2, observed also as enchanced deuterations of HCO+ and N2H+. Consequently, very little HD depletion is present at T = 20 K regardless of density.
Although not readily apparent in the figures included here, we find a local minimum in deuteration at around 10 K if we study the abundances of deuterated species as a function of temperature but at fixed density. The temperature dependence is smoothed out if tunneling is included in the model, which also affects the deuteration degrees. This phenomenon might provide a way to investigate whether tunneling is indeed effective on grain surfaces by studying the temperature dependence of the deuterium fractionation. This will be the subject of a future paper.
5. Conclusions
We have developed new chemical reaction sets for gas-phase and grain-surface chemistry, using the osu_01_2009 reaction set as a template. The new sets presented here are evolved versions of those presented in S13. The present model includes deuteration of species with up to six atoms (so that we can include the formation pathways of, e.g., ammonia and methanol), and the spin-state chemistry for the species involved in the water and ammonia formation networks.
We chose a simplified physical model, carrying out chemical calculations with a pseudo-time-dependent chemical code at different densities and temperatures (but with otherwise fixed physical parameters) in order to facilitate straightforward comparison of future modeling results to those presented in this paper. Calculations were performed with gas-phase and gas-grain models. Special attention was given to the ortho/para ratios of water and ammonia and to the effect of either including or excluding deuterium in the chemical model.
We find that the o/p ratios of water and ammonia are ~1.6 and ~0.5, respectively, for t> 105 yr irrespective of density or model (gas-phase or gas-grain) used. The o/p ratio of water is clearly lower than the value (~3) observed toward translucent clouds, but we find that this apparent disagreement disappears if we consider low values of visual extinction (as opposed to AV = 10 assumed elsewhere in the present paper).
At early times, the o/p ratios vary with density, but little variation is seen between gas-phase and gas-grain models, implying that the o/p ratios are determined by gas-phase processes. Our results also show that, in the range of physical parameters considered, excluding deuterium from the model has only a marginal effect on the abundances of non-deuterated species.
We find that an increase in the temperature from 10 to 20 K generally decreases the depletion of heavy molecules onto grain surfaces, and this also decreases the deuteration degree. However, nitrogen chemistry proceeds differently: ammonia and N2H+ deplete more strongly at T = 20 K than at T = 10 K.
The physical model of the present paper was deliberately kept simple in order to facilitate straightforward benchmarking
of other models against the results presented here. However, we note that while the o/p ratio of ammonia did not show any density dependence in our calculations, a more complete parameter-space study of ammonia (and water) spin-state chemistry, in the context of a gas-grain model, is called for.
Online material
Appendix A: On the late-time ortho/para ratios of ammonia and water
In the ISM, ammonia production is dominated by the electron recombination of the ammonium ion, 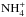 , and its destruction occurs mainly through a charge transfer reaction with H+. At late times of chemical evolution, the proton transfer reaction with
, and its destruction occurs mainly through a charge transfer reaction with H+. At late times of chemical evolution, the proton transfer reaction with 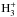 returns ammonia back to
returns ammonia back to 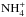 . The dominant reactions are shown schematically in Fig. A.1. The destruction rates of pNH3 and oNH3 in reactions with H+,
. The dominant reactions are shown schematically in Fig. A.1. The destruction rates of pNH3 and oNH3 in reactions with H+, 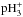 , and
, and 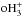 are equal, and consequently the o/p-NH3 ratio is determined by the nuclear spin branching ratios in the electron recombinations of para-, ortho-, and meta-
are equal, and consequently the o/p-NH3 ratio is determined by the nuclear spin branching ratios in the electron recombinations of para-, ortho-, and meta-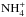 . One obtains the relationship
. One obtains the relationship 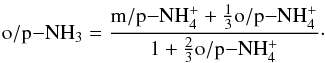 (A.1)The ammonium ion is predominantly formed in the reactions
(A.1)The ammonium ion is predominantly formed in the reactions 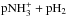 and
and 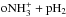 . These reactions determine the nuclear spin ratios of
. These reactions determine the nuclear spin ratios of 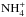 , because the electron recombination rates are equal for the different nuclear spin species. The following relationships are obtained:
, because the electron recombination rates are equal for the different nuclear spin species. The following relationships are obtained: ![\appendix \setcounter{section}{1} \begin{equation} \begin{array}{lll} {\rm m/p-}\nhfour &=& \dfrac{5}{8}{\rm o/p-}\ammplus \\[6mm] {\rm o/p\,-}\nhfour &=& \dfrac{15}{8}{\rm o/p-}\ammplus + \dfrac{3}{2} . \end{array} \label{eq:oprule2} \end{equation}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq210.png) (A.2)The primary production pathway to
(A.2)The primary production pathway to 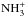 ,
, 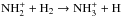 , becomes at late times less important than the charge transfer reaction between NH3 and H+, and in this situation one obtains roughly equal o/p ratios for NH3 and
, becomes at late times less important than the charge transfer reaction between NH3 and H+, and in this situation one obtains roughly equal o/p ratios for NH3 and 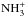 :
: 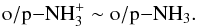 (A.3)Finally, substituting Eqs. (A.2) and (A.3) to Eq. (A.1), one obtains (with a little algebra) the steady-state ratio
(A.3)Finally, substituting Eqs. (A.2) and (A.3) to Eq. (A.1), one obtains (with a little algebra) the steady-state ratio 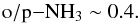 (A.4)This value is about 10% lower than the one predicted by our simulation with the full reaction set.
(A.4)This value is about 10% lower than the one predicted by our simulation with the full reaction set.
The ammonia abundance in interstellar molecular clouds is frequently derived using observations of the (1, 1) and (2, 2) inversion lines at λ = 1.2 cm, which both represent para-NH3. The total ammonia abundance is then derived by assuming o/p − NH3 = 1 or that the ortho and para states are populated according to LTE. The latter assumption implies at 10 K that o/p − NH3 = 3.3. Our result suggests that these previous observational estimates of the total ammonia abundance can be unrealistically large.
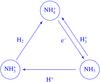 |
Fig. A.1 Ammonia cycle at late times of chemical evolution. |
Water is produced primarily in the electron recombination of the hydronium ion, H3O+ and, like ammonia, destroyed mainly in the charge transfer reaction with H+. The recombination of pH3O+ yields both oH2O and pH2O at equal ratios, whereas oH3O+ only yields ortho-water (along with hydroxyl). We obtain the relationship 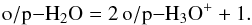 (A.5)
(A.5)
The H3O+ production is dominated by H2O+ + H2 → H3O+ + H. The spin selection rules result in the relationship 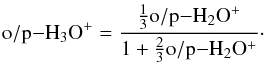 (A.6)
(A.6)
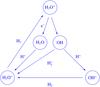 |
Fig. A.2 Dominant reactions involving water and hydroxyl. |
The most important reactions determining the abundance of water and related molecules in the gas phase are shown in Fig. A.2. The dominant pathway to H2O+ is the H atom abstraction reaction OH+ + pH2 → (poro)H2O+ + H, which leads to pH2O+ and oH2O+ with equal probability. The second reaction of importance is the charge transfer reaction H2O + H+ (with a 20% share of the H2O+ production), and the third is proton transfer from 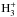 (~10%). Omitting the secondary reactions, one obtains
(~10%). Omitting the secondary reactions, one obtains 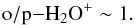 (A.7)The full reaction set yields o/p − H2O+ ~ 1.6 at late times. The substitution of Eqs. (A.6) and (A.7) to Eq. (A.5) yields a value
(A.7)The full reaction set yields o/p − H2O+ ~ 1.6 at late times. The substitution of Eqs. (A.6) and (A.7) to Eq. (A.5) yields a value 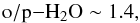 (A.8)representing steady state. This is about 20% lower than the late-time o/p ratio in our simulation. This discrepancy can be understood by the fact that in the very simple model described above, we have omitted the production of H2O+ from H2O and OH.
(A.8)representing steady state. This is about 20% lower than the late-time o/p ratio in our simulation. This discrepancy can be understood by the fact that in the very simple model described above, we have omitted the production of H2O+ from H2O and OH.
Appendix B: New branching ratios for water chemistry and updates to S13
Branching ratios of the most important reactions in the water formation network.
Rate coefficient data from Le Gal et al. (2014) included in the present model.
Appendix C: Calculations at different temperatures
In this appendix, we present the results of calculations otherwise similar to those presented in Sect. 3, but produced assuming either Tgas = Tdust = 15 K or Tgas = Tdust = 20 K.
Appendix D: Calculations without deuterium
Including deuterium in a chemical model may decrease the abundances of nondeuterated species especially at high densities in the presence of depletion, where deuterium fractionation is strong. To investigate how our results change when deuterium is excluded, we ran model calculations at T = 10 K setting the initial HD abundance (i.e., the initial deuterium abundance) to zero. The results of these calculations are presented in Figs. D.1 to D.3, which should be compared against Figs. 2 to 4 in the main text.
It is observed that in the gas-phase model, where there is little deuteration regardless of density, excluding deuterium from
the calculations makes virtually no difference in the abundances of the non-deuterated species. Even in the gas-grain model, only very small enhancements are observed in the abundances of non-deuterated species at high density. Also, the o/p ratios of H2O and NH3 are only very slightly modified in the gas-grain model, and hardly at all in the gas-phase model. Our models thus imply that disregarding deuteration in chemical models when T ≳ 10 K will likely not lead to large errors in the abundances of non-deuterated species. We note that we have not carried out a full parameter-space exploration of this issue here, and have only explored the effect of density (and temperature; Appendix C) on the results.
 |
Fig. D.1 Abundances of selected species in a gas-phase model excluding deuterium. This figure should be compared to Fig. 2. |
 |
Fig. D.2 Abundances of selected species in a gas-grain model excluding deuterium. This figure should be compared to Fig. 3. |
Appendix E: Calculations with quantum tunneling included
Below, we present the results of calculations performed at T = 10 K, but including quantum tunneling on grain surfaces. When tunneling is included, the thermal diffusion rate defined by Eq. (9) is replaced by the tunneling diffusion rate (Hasegawa et al. 1992) ![\appendix \setcounter{section}{5} \begin{equation} \label{eq:Rtunn} R_i^{\rm diff,q} = {\nu_i \over N_{\rm s}} \exp \left[-2 \, ( a/\hbar) \, (2 \, m \, k_{\rm B} E_i^{\rm diff})^{1/2} \right] , \end{equation}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq331.png) (E.1)where a is the width of the (rectangular) tunneling barrier. We assume a = 1 Å. Also, the reaction probability κij is in the presence of tunneling replaced by
(E.1)where a is the width of the (rectangular) tunneling barrier. We assume a = 1 Å. Also, the reaction probability κij is in the presence of tunneling replaced by ![\appendix \setcounter{section}{5} \begin{equation} \label{eq:ktunn} \kappa_{ij}^{\rm q} = \exp \left[-2 \, ( a/\hbar) \, (2 \, \mu \, k_{\rm B} E_a)^{1/2} \right] , \end{equation}](/articles/aa/full_html/2015/06/aa24364-14/aa24364-14-eq335.png) (E.2)
(E.2)
where μ is the reduced mass of the reactants (not to be confused with the mean molecular weight of the gas as defined in Eq. (5)). The reaction rate coefficient assumes the same form as when tunneling is excluded (Eq. (8)). In the present model, we only allow atomic H and D to tunnel; i.e., Eqs. (E.1) and (E.2) are only used for those reactions where either of these species is present as a reactant.
Figure E.1 presents the results of calculations at T = 10 K with quantum tunneling included. This figure should be compared against Fig. 3 in the main text. Evidently, tunneling influences our results only at long timescales (≳106 yr), and even then the influence on deuteration for example is small. The differences between the models arise because tunneling allows reactions with activation barriers to proceed efficiently. We refer the reader to S13 for more discussion on tunneling and its effects on deuteration.
Acknowledgments
We thank the anonymous referee for a thorough report and Malcolm Walmsley for helpful comments that improved the paper. O.S. acknowledges the financial support of the Academy of Finland grant 250741 and of the Department of Physics of the University of Helsinki. P.C. acknowledges financial support of the European Research Council (ERC; project PALs 320620).
References
- Albertsson, T., Semenov, D. A., Vasyunin, A. I., Henning, T., & Herbst, E. 2013, ApJS, 207, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Indriolo, N., Kreckel, H., et al. 2014a, ApJ, 787, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Albertsson, T., Semenov, D., & Henning, T. 2014b, ApJ, 784, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, M., & Robinson, G. W. 1977, ApJ, 212, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Sipilä, O., Chambers, E. T., et al. 2014, Nature, 516, 219 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cazaux, S., Cobut, V., Marseille, M., Spaans, M., & Caselli, P. 2010, A&A, 522, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Du, F., Parise, B., & Bergman, P. 2012, A&A, 538, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., Hily-Blant, P., Le Gal, R., Rist, C., & Pineau des Forêts, G. 2013, ApJ, 770, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2004, A&A, 427, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006a, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006b, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Zhang, Q., et al. 2012, A&A, 541, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fushitani, M., & Momose, T. 2002, J. Chem. Phys., 116, 10739 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerlich, D., Herbst, E., & Roueff, E. 2002, Planet. Space Sci., 50, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Hama, T., & Watanabe, N. 2013, Chem. Rev., 113, 8783 [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hugo, E., Asvany, O., Harju, J., & Schlemmer, S. 2007, Mol. Space Laboratory, 119 [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Juvela, M., Harju, J., Ysard, N., & Lunttila, T. 2012, A&A, 538, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keto, E., Rawlings, J., & Caselli, P. 2014, MNRAS, 440, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, S., Caselli, P., Tan, J. C., & Wakelam, V. 2013, ApJ, accepted [arXiv:1312.0971] [Google Scholar]
- Le Gal, R., Hily-Blant, P., Faure, A., et al. 2014, A&A, 562, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., Diplas, A., Wood, B. E., et al. 1995, ApJ, 451, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T. 2004, J. Mol. Spectrosc., 228, 635 [Google Scholar]
- Pagani, L., Salez, M., & Wannier, P. G. 1992, A&A, 258, 479 [NASA ADS] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A&A, 543, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rist, C., Faure, A., Hily-Blant, P., & Le Gal, R. 2013, J. Phys. Chem. A, 117, 9800 [Google Scholar]
- Rodgers, S. D., & Millar, T. J. 1996, MNRAS, 280, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O. 2012, A&A, 543, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Hugo, E., Harju, J., et al. 2010, A&A, 509, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2013, A&A, 554, A92 (S13) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, Ap&SS, 292, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Taquet, V., Peters, P. S., Kahane, C., et al. 2013, A&A, 550, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Charnley, S. B., & Sipilä, O. 2014, ApJ, 791, 1 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, N., Kimura, Y., Kouchi, A., et al. 2010, ApJ, 714, L233 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Adopted values of the various physical parameters (see text for definitions of the parameters).
Initial chemical abundances with respect to nH, and the adopted initial H2 o/p ratio.
Abundances and abundance ratios predicted by our gas-phase model (F2) and that of Le Gal et al. (2014).
Branching ratios of the most important reactions in the water formation network.
All Figures
 |
Fig. 1 Upper panels: abundances of selected non-deuterated (left), deuterated (middle), and grain-surface (both non-deuterated and deuterated, right) species as functions of time, as calculated with model T1 (solid lines) or model T2 (dashed lines). Middle panels: like the upper row, but comparing models T1 (solid lines) and T3 (dashed lines). Lower panels: like the other rows, but comparing models T1 (solid lines) and F1 (dashed lines). In all calculations, the density of the medium is set to nH = 105 cm-3. The abundances of H2O, NH3, and NH2D represent sums over their respective ortho and para states. |
| In the text | |
 |
Fig. 2 Abundances of selected species calculated with model F2 (i.e., surface reactions and adsorption/desorption excluded) as functions of time at different densities, labeled in the upper left panel. The labels indicate densities of the medium; for example, 103 stands for nH = 103 cm-3. |
| In the text | |
 |
Fig. 3 As in Fig. 2, but calculated with model F1. The abundance scales are in some cases different than in Fig. 2. |
| In the text | |
 |
Fig. 4 o/p ratios of NH3 (upper panels) and H2O (lower panels) as functions of time at different densities, labeled in the upper left panel. The left panels correspond to the gas-phase model (F2), while the right panels correspond to the gas-grain model (F1). |
| In the text | |
 |
Fig. 5 Abundances of selected species as functions of time at different densities (labeled in the figure), in a gas-phase model at T = 10 K, using different approaches to H2 formation. Dash-dotted lines correspond to the gas-phase reactions of Kong et al. (2013). Solid lines correspond to grain-surface H2 formation assuming only H and D adsorption and with the binding energies of H and H2 and their deuterated isotopologs set to 100 K. Dotted lines (superimposed on the dash-dotted lines) correspond to grain-surface H2 formation assuming only H and D adsorption and with the binding energies adopted in the main body of this work. The abundances of ammonia, water and H2D+ represent sums over the abundances of their respective ortho and para states. |
| In the text | |
 |
Fig. 6 Abundances of selected species as functions of time in a gas-grain model at T = 10 K and nH = 105 cm-3. The solid lines correspond to model F1, while the error bars correspond to test models in which grain-surface reactions can only create ortho species (upper limits) or para species (lower limits). |
| In the text | |
 |
Fig. A.1 Ammonia cycle at late times of chemical evolution. |
| In the text | |
 |
Fig. A.2 Dominant reactions involving water and hydroxyl. |
| In the text | |
 |
Fig. C.1 As for Fig. 2, but calculated with Tgas = Tdust = 15 K. |
| In the text | |
 |
Fig. C.2 As for Fig. 3, but calculated with Tgas = Tdust = 15 K. |
| In the text | |
 |
Fig. C.3 As for Fig. 4, but calculated with Tgas = Tdust = 15 K. |
| In the text | |
 |
Fig. C.4 As for Fig. 2, but calculated with Tgas = Tdust = 20 K. |
| In the text | |
 |
Fig. C.5 As for Fig. 3, but calculated with Tgas = Tdust = 20 K. |
| In the text | |
 |
Fig. C.6 As for Fig. 4, but calculated with Tgas = Tdust = 20 K. |
| In the text | |
 |
Fig. D.1 Abundances of selected species in a gas-phase model excluding deuterium. This figure should be compared to Fig. 2. |
| In the text | |
 |
Fig. D.2 Abundances of selected species in a gas-grain model excluding deuterium. This figure should be compared to Fig. 3. |
| In the text | |
 |
Fig. D.3 As for Fig. 4, but excluding deuterium. |
| In the text | |
 |
Fig. E.1 As for Fig. 3, but with quantum tunneling included. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


