| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 9 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526243 | |
| Published online | 21 May 2015 | |
Evolution of column density distributions within Orion A⋆,⋆⋆
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: stutz@mpia.de
Received: 2 April 2015
Accepted: 18 April 2015
We compare the structure of star-forming molecular clouds in different regions of Orion A to determine how the column density probability distribution function (N-PDF) varies with environmental conditions such as the fraction of young protostars. A correlation between the N-PDF slope and Class 0 protostar fraction has been previously observed in a low-mass star-formation region (Perseus); here we test whether a similar correlation is observed in a high-mass star-forming region. We used Herschel PACS and SPIRE cold dust emission observations to derive a column density map of Orion A. We used the Herschel Orion Protostar Survey catalog to accurately identify and classify the Orion A young stellar object content, including the cold and relatively short-lived Class 0 protostars (with a lifetime of ~0.14 Myr). We divided Orion A into eight independent regions of 0.25 square degrees (13.5 pc2); in each region we fit the N-PDF distribution with a power law, and we measured the fraction of Class 0 protostars. We used a maximum-likelihood method to measure the N-PDF power-law index without binning the column density data. We find that the Class 0 fraction is higher in regions with flatter column density distributions. We tested the effects of incompleteness, extinction-driven misclassification of Class 0 sources, resolution, and adopted pixel-scales. We show that these effects cannot account for the observed trend. Our observations demonstrate an association between the slope of the power-law N-PDF and the Class 0 fractions within Orion A. Various interpretations are discussed, including timescales based on the Class 0 protostar fraction assuming a constant star-formation rate. The observed relation suggests that the N-PDF can be related to an evolutionary state of the gas. If universal, such a relation permits evaluating the evolutionary state from the N-PDF power-law index at much greater distances than those accessible with protostar counts.
Key words: ISM: clouds / ISM: structure / stars: formation / ISM: individual objects: Orion A
Appendices are available in electronic form at http://www.aanda.org
The N(H) map as a FITS file is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/577/L6
© ESO, 2015
1. Introduction
The structure of molecular clouds can be described by the probability distribution function (N-PDF) of their column densities (e.g., Kainulainen et al. 2009). Observations (e.g., Hill et al. 2011; Hughes et al. 2013) and theoretical studies (Padoan et al. 2014; Federrath & Klessen 2013) suggested that the N-PDF depends on environmental conditions such as turbulence (e.g., Padoan et al. 1997), gravity (e.g., Klessen et al. 2000), magnetic field strength (e.g., Molina et al. 2012), and star formation (e.g., Schneider et al. 2013; Kainulainen et al. 2014; Abreu-Vicente et al. 2015). In particular, an increasing N-PDF slope has been shown to be correlated with an increasing fraction of Class 0 protostars in individual clumps within Perseus (Sadavoy 2013).
Here we aim to test whether a similar correlation is observed in a different star-forming region. We present a study of subregions within the Orion A molecular cloud that quantifies the link between the incidence of Class 0 protostars and the N-PDF slope. We bring together two data sets: column density measurements using Herschel observations and an accurate protostellar census from the Herschel Orion Protostar Survey (HOPS; Stutz et al. 2013; Fischer et al. 2013, Furlan et al., in prep.). With this analysis, we quantify spatial variations in the relationship between column density distributions and fractions of young protostars within Orion A.
2. Column density maps and source catalogs
2.1. Column density maps
We present the Orion A column density, N(H), map (Figs. 1 and A.1) derived from Herschel 160 μm to 500 μm emission maps calibrated against Planck and IRAS data (Bernard et al. 2010). The data were observed as part of the Herschel Gould Belt program (Polychroni et al. 2013). The column density and temperature maps were derived as in Stutz et al. (2010, 2013) and Launhardt et al. (2013). See Appendix A for more details.
2.2. Catalog of Class 0, Class I, and flat-spectrum young stellar objects
The young stellar object (YSO) catalog is the union of the PACS bright red sources (PBRS) sample (Stutz et al. 2013) of extremely young Herschel-detected Class 0 protostars (Heiderman & Evans 2015; van Kempen et al. 2009) and the HOPS sample (Furlan et al., in prep., and Fischer et al. 2013) of Class 0, Class I, and flat-spectrum YSOs. The HOPS YSO catalog is based on the Spitzer catalog from Megeath et al. (2012), which excludes extragalactic and stellar source contamination by means of infrared colors. The YSOs have well-sampled spectral energy distributions (SEDs) from near-infrared to the submillimeter wavelengths, including Herschel 70 μm, 100 μm, and 160 μm measurements as well as APEX LABOCA 870 μm data. We also included APEX SABOCA 350 μm data when available (Stanke et al. 2010; Stutz et al. 2013; Safron et al. 2015) to sample the peak of the cold envelope emission. The locations of the YSOs are indicated in Fig. 1.
 |
Fig. 1 Orion A N(H) map shown on a log scale; the N(H) = 3.7 × 1021 cm-2 contour is indicated in gray. The locations of protostars are indicated as ×-symbols. Numbered boxes (with 1/4 square degree area or 3.67 pc on a side) indicate the regions into which we divide the Orion A cloud. |
 |
Fig. 2 N(H) distributions for each region shown in Fig. 1. The combined N(H) distribution for all regions is shown in gray. The dashed curves show the best-fit slope assuming a power-law distribution of N(H); each value for the slope is listed (see Table 1 for slope errors). Here we show PDF data of bins containing more than 10 pixels, and each major tick mark represents a factor of 10. Mean-normalization, N(H) / ⟨ N(H) ⟩ in each region, has no effect on the derived PDF slopes because the operation simply results in a linear translation of the x-axis. |
3. Results
3.1. Power-law N(H) distributions
We analyze the high column density portion of the N-PDFs within the filamentary subregions of Orion A. Lombardi et al. (2015) demonstrated that the high-N(H) portion of the N-PDF can be reliably inferred from Herschel observations above AK ~ 0.2 mag even when accounting for complicating factors such as line-of-sight (LOS) blending and errors in the background emission or extinction estimates. We divide Orion A into eight separate square regions that are 3.67 pc on a side. The region locations are chosen such that they are independent (have no overlap), avoid the center of the Orion nebula cluster (ONC), which is affected by gross protostellar incompleteness and saturation in both Spitzer and Herschel observations, and cover regions that are currently forming stars. The region locations are shown in Fig. 1.
We extract the N-PDF and fit the high column density portion with a power law in each region. Our results are presented in Table 1 and Figs. 2 and 3. The Herschel 250 μm beam is ~18′′ FWHM; therefore we use an 18′′pixel scale to extract the N(H) distributions to minimize pixel-to-pixel correlations. Inspection of the N-PDFs reveals that they have an approximate power-law shape above log N(H)~ 22.0 to 22.4 and below log N(H)~22.7 to 23.0. For each region, the definition of the fitting regime is driven by the requirement of excluding areas with curvature in the N-PDFs. The lowest and highest N(H) values we use to derive the power-law indices are listed in Table 1.
We fit a power law to the N-PDF using a maximum-likelihood method that does not require binning the data and is therefore free of any potential errors due to bin size. We obtain power-law indices that vary from α = −0.93 to α = −2.95, or a factor of about 3. We test the effects of varying the beam size and pixel size on our derived indices and find that our fitting method is robust. We also test the effect of varying the upper bound of the fit and find that the effect on the indices is much waeker than the measured variations across regions. See Appendix B for more details.
Best-fit N-PDF power-law slopes and Class 0 protostar fractions.
3.2. Class 0 protostar fractions
Using the catalogs discussed in Sect. 2.2, we count the total number of YSOs and the subset of Class 0 protostars in each region (see Table 1 and Fig. 1). We define the Class 0 fraction as the number of Class 0 protostars divided by the total number of YSOs: NClass0 / NYSO. We define the Class 0 protostars as the subset of sources with bolometric temperatures Tbol< 70 K (Chen et al. 1995). Tbol is defined as the temperature of a blackbody with the same flux-weighted mean frequency as the observed SED (Myers & Ladd 1993). The original protostellar Tbol classification accounted for the effects of foreground extinction (Chen et al. 1995; see also Dunham et al. 2013). Here we calculate Tbol based on the observed SED, without additional extinction corrections. See text below and Appendix C for an analysis of the effects of foreground extinction. Our wavelength coverage samples the peak of even the coldest Class 0 protostellar SEDs and allows for a robust protostellar classification based on Tbol (Stutz et al. 2013; Dunham et al. 2014).
We estimate the errors on the fraction of Class 0 protostars to the total number of YSOs using the binomial distribution as follows. In each region the number of Class I protostars is (obviously) NClassI = NYSO−NClass0, where we include the flat-spectrum YSOs in the Class I sample. Since the YSOs in each region have a probability p of being Class I and a probability q = (1−p) of being Class 0, the expected number of Class 0 protostars is NYSO × q. The NClass0 error is 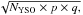 and the fractional error is therefore
and the fractional error is therefore 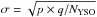 . The final numbers of YSOs, Class 0 protostars, fractions and respective errors in each region are presented in Table 1.
. The final numbers of YSOs, Class 0 protostars, fractions and respective errors in each region are presented in Table 1.
Two principal effects might alter the measured fractions of Class 0 protostars: incompleteness and misclassification. Variations in flux completeness across Orion A are dominated by the spatially varying level of nebulosity. We determine the completeness limits across the cloud by injecting fake sources into the PACS 70 μm images and measuring the flux at which 90% of the sources are recovered. Region 1 has the highest 70 μm flux completeness limit. We apply this limit to the entire YSO sample in each region and find that the Class 0 fractions are largely unaffected by incompleteness. We therefore do not correct the observational numbers presented in Table 1. See Appendix C and Fig. C.1 for more discussion.
 |
Fig. 3 Correlation between the power-law index of the N-PDF and Class 0 fraction across Orion A regions. The Class 0 fraction can be related to a timescale, as indicated, assuming a constant SFR (see text). Gray ×-symbols are the data from Perseus from Sadavoy (2013), Sadavoy et al. (2014), and Sadavoy (priv. comm., 2015). The dashed gray curve shows the linear fit to the data, which have a correlation coefficient of 0.7. |
With a reliable sample of YSOs and protostars, the main classification ambiguities that may hinder the identification of Class 0 protostars include any extrinsic effects (that is, effects acting independently of the Class 0 envelope) that will cause the observed SED to appear redder. The two main culprits are the inclination of the disk relative to the LOS and foreground reddening. Using a grid of protostellar SED models (Furlan et al., in prep.; Stutz et al. 2013), we test the effects of both on the Tbol-based classification. Even assuming the most elevated levels of extinction measured from our N(H) maps toward the positions of the protostars, we find that neither effect can account for the variations in the Class 0 fractions reported in Sect. 3.3. See Appendix C and Figs. C.3 and C.4 for more details.
3.3. Connection between the N-PDF and the Class 0 fraction
The N-PDF slopes and Class 0 fractions show a spatial variation within Orion A. From north to south, the N-PDF slope steepens and the Class 0 fraction decreases. Figure 3, which also includes data from Sadavoy (2013), Sadavoy et al. (2014), and Sadavoy (priv. comm., 2015), shows this observed correlation. A linear fit to the data results in a slope of 0.2 and an intercept of 0.7. We measure a correlation coefficient of 0.7. According to the t-test, there is a 0.3% chance of having a correlation coefficient this high in an uncorrelated random sample.
4. Discussion
The N-PDF slopes and Class 0 fractions indicate clear spatial variations within a single molecular cloud (Orion A). Making the simple assumption of a constant star-formation rate (SFR), the Class 0 fraction can be related to time (t). If the Class 0 and Class I lifetimes are 0.1 Myr and 0.4 Myr, respectively, then at t< 0.1 Myr the fraction will be equal to 1; at 0.1 Myr >t> 0.5 Myr the fraction is = [t/ (0.1 Myr)] -1; at t> 0.5 Myr, the fraction will be constant and equal to 1 / (1 + t1/t0) ~ 0.26, where t0 and t1 are the lifetimes of the Class 0 and Class I phases, respectively (Dunham et al. 2014). Under these assumptions, high fractions correspond to short evolutionary timescales of the on-going star formation event, and the N-PDFs change on timescales of ~0.3 Myr.
However, variations in the SFR might explain the observed trend. We know that Orion A has formed stars for longer than 0.5 Myr (e.g., Megeath et al. 2012). An elevated Class 0 fraction may therefore reflect an increasing SFR over time compared to regions with lower fractions of Class 0 protostars.
O-star feedback might compress the gas and cause a flattening of the N-PDF slopes. Regions 1 and 2 would be most affected by feedback because of the O-star population in the northern portion of Orion A. In Perseus O-stars themselves are not responsible because the region does not contain any such stars. However, Sadavoy et al. (2014) proposed that feedback from the low-mass protostars themselves may account for the observed correlation between Class 0 fraction and N-PDF slope. This mechanism might operate in Orion as well.
5. Conclusions
We analyze the N-PDF slopes and Class 0 protostellar fractions within subregions of the Orion A molecular cloud. Our conclusions are as follows.
We observe a progression from shallow to steep N-PDF slopes from north to south in the Orion A cloud. This progression shows that there is no unique N-PDF, but that the N-PDF shape depends on environment.
We observe a correlation between increasing N-PDF slope and increasing fraction of Class 0 protostars in subregions of Orion A. Under the assumption that the Class 0 fraction is related to time by assuming a constant SFR, evolutionary timescales for each region can be derived. This suggests that regions with shallower slopes have younger evolutionary states.
If universal, this relation permits an evaluation of the evolutionary state from the N(H) power-law index measurement, which is possible at much greater distances than regions that are accesible with protostar counts. A key aspect of this study is that the slopes do not change significantly with resolution; for fixed angular resolution we therefore expect to obtain the same slope measurement over a broad range of distances.
Online material
Appendix A: Column density map of Orion A
We have generated reduced data products for the Orion A region using HIPE processing to level 1 followed by final level 2 Scanamorphos processing (version 24.0, using the galactic option, Roussel 2013). The column density (and temperature) maps were derived in a similar way as those presented in Stutz et al. (2010, 2013) and Launhardt et al. (2013), with the total power emission levels at each of the four wavelengths calculated using Planck and IRAS data (Bernard et al. 2010). We briefly summarize the steps we used to generate the N(H) and temperature maps here and refer to the above works for more details. We applied the total power emission level corrections for each of the 160 μm, 250 μm, 350 μm, and 500 μm intensity maps (Bernard et al. 2010). We convolved the data to the largest beam: the 500 μm beam, with ~38′′ FWHM. We used the azimuthally averaged convolution kernels from Aniano et al. (2011). We then re-gridded the data to a matched coordinate system and pixel scale, in this case, we adopted an 18′′ pixel scale (see Appendix B for more details). The conversion to matched units assumes the beam sizes listed in the SPIRE instrument handbook. We fit the SED of each pixel assuming a modified blackbody function of the form 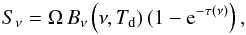 (A.1)where Ω is the solid angle of the emitting element, Bν(Td) is the Planck function at a dust temperature Td, and τ(ν) is the optical depth at frequency ν. Here, the optical depth is given by
(A.1)where Ω is the solid angle of the emitting element, Bν(Td) is the Planck function at a dust temperature Td, and τ(ν) is the optical depth at frequency ν. Here, the optical depth is given by 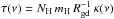 , where NH = 2 × N(H2) + N(H) is the total hydrogen column density, mH in the proton mass, κν is the assumed frequency dependent dust opacity law, and Rgd is the gas-to-dust ratio, assumed to be 110 (Sodroski et al. 1997). We used the Ossenkopf & Henning (1994) model dust opacities corresponding to Col. 5 of their Table 1 (sometimes referred to as the OH5 opacities). These opacities are meant to reflect grains with thin ice mantles after 105 years of coagulation time at an assumed gas density of 106 cm-3. See Stutz et al. (2013) and Launhardt et al. (2013) for discussions on the systematic uncertainties introduced by the model dust opacity assumption. To apply the color and beam size corrections recommended in the SPIRE and PACS instrument handbooks, we first fit the uncorrected pixel SED to estimate the temperature. We then applied the interpolated correction value at that temperature and re-fit the SED.
, where NH = 2 × N(H2) + N(H) is the total hydrogen column density, mH in the proton mass, κν is the assumed frequency dependent dust opacity law, and Rgd is the gas-to-dust ratio, assumed to be 110 (Sodroski et al. 1997). We used the Ossenkopf & Henning (1994) model dust opacities corresponding to Col. 5 of their Table 1 (sometimes referred to as the OH5 opacities). These opacities are meant to reflect grains with thin ice mantles after 105 years of coagulation time at an assumed gas density of 106 cm-3. See Stutz et al. (2013) and Launhardt et al. (2013) for discussions on the systematic uncertainties introduced by the model dust opacity assumption. To apply the color and beam size corrections recommended in the SPIRE and PACS instrument handbooks, we first fit the uncorrected pixel SED to estimate the temperature. We then applied the interpolated correction value at that temperature and re-fit the SED.
In an additional step, we used the 500 μm resolution temperature (Td) map to convert the 250 μm intensity map to a column density map to improve the final resolution (Figs. A.1 and 1). Both maps compare well; only minor differences are apparent on the smallest scales caused by resolution effects, as expected. The previously published Herschel-derived N(H) maps compare well to the maps we present here (e.g., Lombardi et al. 2014; Polychroni et al. 2013).
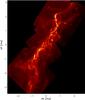 |
Fig. A.1 Orion A N(H) map, shown on a log scale. |
Appendix B: Fitting N(H) PDFs without binning
Here we describe the method we used to fit an index α to a power-law distribution of the form dN/ dZ ∝ Zα over a finite range in Z values from Zmin to Zmax. The differential probability of the column density Zi, given a power-law distribution Zα and total number of expected detections nexp in the interval between Zmin and Zmax , is 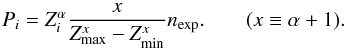 The likelihood ℒ is given by the product of the individual probabilities, or
The likelihood ℒ is given by the product of the individual probabilities, or 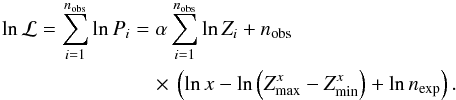 It is straightforward to show that the likelihood is maximized when the models are restricted to those with nexp = nobs. Hence, we simplify the notation by n = nexp = nobs and obtain
It is straightforward to show that the likelihood is maximized when the models are restricted to those with nexp = nobs. Hence, we simplify the notation by n = nexp = nobs and obtain 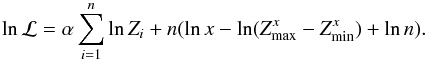 To determine where ℒ is maximized, we differentiate w.r.t. α (or x = α + 1) and set to zero
To determine where ℒ is maximized, we differentiate w.r.t. α (or x = α + 1) and set to zero 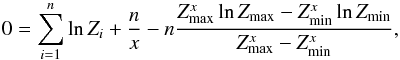 which can be rewritten as
which can be rewritten as 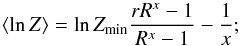 where
where 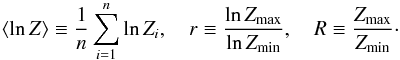 The error is given by Gould (1995) Eq. (2.4):
The error is given by Gould (1995) Eq. (2.4): ![\appendix \setcounter{section}{2} \begin{eqnarray*} {1\over \sigma(x)} = \sqrt{n\biggl[{1\over x^2} - {R^{-x}(\ln R)^2\over (R^{-x} - 1)^2}\biggr],} \end{eqnarray*}](/articles/aa/full_html/2015/05/aa26243-15/aa26243-15-eq68.png) which can be written more elegantly as
which can be written more elegantly as ![\appendix \setcounter{section}{2} \begin{eqnarray*} {1\over \sigma(x)} = {1\over |x|} \sqrt{n\biggl[1 - \biggl({Q\over \sinh Q}\biggr)^2\biggr]}, \qquad \biggl(Q\equiv {x\ln R\over 2}\biggr)\cdot \end{eqnarray*}](/articles/aa/full_html/2015/05/aa26243-15/aa26243-15-eq69.png) This expression can be Taylor-expanded:
This expression can be Taylor-expanded: 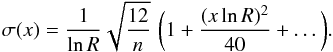 (B.1)Equation (B.1) represents the analytical error solution assuming the power-law model accurately reflects the distribution of data values. Therefore it represents a lower limit for the errors. Alternatively, the errors can be estimated using the Δ χ2 = 1.0 interval, which compares well to those derived using the minimum-variance bound (see Table B.1 for a comparison between the two). The power-law indices and Δ χ2 = 1.0 errors are listed in Table 1.
(B.1)Equation (B.1) represents the analytical error solution assuming the power-law model accurately reflects the distribution of data values. Therefore it represents a lower limit for the errors. Alternatively, the errors can be estimated using the Δ χ2 = 1.0 interval, which compares well to those derived using the minimum-variance bound (see Table B.1 for a comparison between the two). The power-law indices and Δ χ2 = 1.0 errors are listed in Table 1.
Comparison of power-law index errors.
Appendix B.1: Effects of resolution, pixel-size, and fitting range on the power-law index
As described above, the power-law indices for each region were extracted from 18′′ pixel N(H) maps derived from the 250 μm map of Orion A. Here we test the effect of adopting different pixel scales for the 250 μm N(H) map. As shown in Fig. B.1, the adopted pixel scale has a negligible effect on the indices, with a strongest effect on the best-fit indices of ~ 2%. The fractional errors increase with pixel size because the number of pixels decreases. We found similar results using the 500 μm N(H) map (with a beam size of ~36′′ FWHM) and adopting pixel sizes of 10′′, 20′′, 30′′, and 40′′: the power-law index is only marginally affected by the choice in pixel size. The fractional errors exhibit the same behavior as for the 250 μm, but are somewhat larger (at most 10% at 40′′) because of the smaller number of pixels available to fit. Finally, in Fig. B.2 we compare the indices derived from the 250 μm 18′′ pixel map with those derive from the 500 μm 40′′ pixel map. The two slope estimates agree well.
 |
Fig. B.1 Top: best-fit power-law index for each region as a function of N(H) map pixel size. The slope values are not affected by correlated pixel, and differences are 2% at most. Bottom: error for each region as a function of N(H) map pixel size. The error increases with pixel size because the number of counts decreases. All quantities shown here have been derived using the same N(H) limits presented in Table 1. |
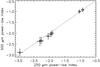 |
Fig. B.2 Indices derived from the 250 μm 18′′pixel map vs. those derived from the 500 μm 40′′pixel map, both using the N(H) limits presented in Table 1. |
We also tested varying the upper bound of the fitting range shown as Max log N(H) in Table 1. For a change ± Δlog N(H) = 0.3, the indices change by ~10% or less; this variation is much smaller than the differences between regions.
Appendix C: Effects of completeness and extinction on the Class 0 protostar fraction
Appendix C.1: Completeness of protostellar catalogs
The northern portion of Orion A (regions 1 and 2) are most affected by incompleteness because of the elevated levels of nebulosity. We estimated the completeness limit in the HOPS protostellar catalog as follows. We injected artificial sources into the 70 μm images and recovered them with our source-finding software (see Stutz et al. 2013, for details). We estimated the mean 90% completeness level for regions 1 and 2 to be 0.12 Jy, while for the rest of L1641 it is 0.03 Jy. We therefore applied a 0.12 Jy 70 μm flux limit to the HOPS protostar catalog, eliminating about 10% of protostars from the catalog. We then calculated Class 0 fractions from the remaining sources. The completeness-corrected and total raw sample fractions agree well, as shown in Fig. C.1.
 |
Fig. C.1 Class 0 fraction in regions. Diamonds indicate the total fraction (Table 1), while squares indicate the completeness corrected values. Results remain consistent with and without the application of the completeness limit. |
Appendix C.2: Effect of foreground extinction on Tbol
Our goal is to assess the effects of foreground extinction on the Tbol-based YSO classification. We assumed here that the main contribution to an erroneous Tbol classification is the misidentification of Class I sources as Class 0 protostars (Tbol) < 70 K). While other sources of contamination are also possible, scrutiny of the HOPS protostellar SEDs reveals that the current classification based on observed colors and fluxes, in combination with PACS and 870 μm data, is robust (Furlan et al., in prep.).
Upper limits to the distribution of protostellar extinction per region.
 |
Fig. C.2 Model Tbol values versus extincted SED Tbol,ext values. Colors indicate the assumed levels of extinction. Here we show 500 randomly chosen models. As the extinction AV increases, the model Tbol,ext decreases and the levels of contamination at Tbol,ext< 70 K increases. |
We obtained observational constraints on the levels of foreground extinction toward individual protostars from the Herschel N(H) map. We measured the N(H) toward each protostar using an annulus of size 18″ × [1.5,4] (or ~11 400 AU to 30 300 AU), adopted to avoid extinction intrinsic to the protostellar envelopes. Within each annulus we calculated the median value of N(H). In Table C.1 we list the median, minimum, and maximum protostellar N(H) values for each region, assuming a conversion of AV/N(H) = 1.85 × 1021 mag cm-2 (e.g., Bohlin et al. 1978,derived for the diffuse ISM, and used here for notational simplicity). These values are upper limits because the N(H) map integrates the extinction through the entire cloud. The protostellar AV values have at most 35 mag in regions 1 and 7. However, more typical values range from ~20 mag to ~10 mag.
To assess the levels of contamination in the Class 0 sample, we used the protostellar model grid presented in Stutz et al. (2013). We refer to this publication and to Furlan et al. (in prep.) for more details. In brief, we varied five parameters in our grid: the inclination of the disk relative to the LOS, the envelope density, the cavity opening angle, the disk size, and the luminosity of the central protostar. Our grid contains uniformly sampled paramaters and uses the Ormel et al. (2011) model dust opacities (icsgra3). In total, our grid contains 30 400 individual models. About ~30% of the models have Tbol< 70 K, similar to the observed protostellar distribution. We attenuated each model SED (adopting the wavelength coverage of the observations) with a range of AV values between 1 and 35 mag, spanning the observed range in AV toward the protostar sample (Table C.1). For consistency with the above protostellar YSO measurements, we attenuated the model SEDs with the same model as that used to derive the N(H) map (Ossenkopf & Henning 1994; OH5), assuming AV/AK = 14 (Nielbock et al. 2012). In Fig. C.2 we show the resulting extincted Tbol,ext values as a function of Tbol for a random subset of models. We then measured the fraction of models that have Tbol> 70 K and Tbol,ext< 70 K as a function of Tbol and AV, marginalizing over a uniform AV distribution. The probability that a given Class I protostar is masquerading as a Class 0 protostar is shown in Fig. C.3, top panel. The bottom panel of Fig. C.3 shows the probability that a given Class 0 protostar is correctly identified (has Tbol< 70 K).
 |
Fig. C.3 Top: probability that a source with a given Tbol> 70 K will have Tbol,ext< 70 K, marginalizing over a uniform foreground AV extinction distribution up to the listed value (shown in color). There is no Class 0 contamination from Class I models with Tbol> 400 K for the AV values we consider here. Bottom: probability that a source is correctly classified as a Class 0 source (has Tbol< 70 K). |
We obtained a maximum fraction of ~9% of Class I sources that may appear as Class 0 protostars if models are extincted by up to AV = 35 mag. For all models with Tbol> 400 K, there is zero contamination of Class 0 sources up to extinctions of AV ~ 60 mag. We conclude that the main source of extinction-driven contamination on the Class 0 sample is therefore from Class I sources with 70 K <Tbol< 400 K. We also find that there is < 5% contamination of Class 0 protostars below Tbol,ext~ 45 K and below foreground extinction levels of AV = 35 mag. For a median extinction value of AV = 20 mag, the fraction of Class 0 contamination is lower than 5% for Tbol,ext< 55 K.
Using the total contamination fractions shown in Fig. C.3 and both the median and maximum observed AV levels (Table C.1), we applied correction factors to the observed numbers of Class 0 protostars, keeping the total number of YSOs fixed at the observed value. The dependence of the Class 0 fraction on extinction contamination is presented in Fig. C.4. While the overall amplitude of the fraction is affected by the foreground extinction effects, the shape is not. As noted above, the bottom panel of Fig. C.3 demonstrates that at Tbol,ext< 55 K the amount of Class 0 contamination is lower than 5% for our expected levels of extinction. We therefore tested the effects of adopting a 55 K division between Class 0 and Class I protostars. The results are similar to those shown in Fig. C.4 for the median extinction-corrected values, as expected. We therefore conclude that contamination driven by foreground extinction cannot account for the observed trend presented in Fig. 3.
We note that our requirement of a PACS 70 μm detection and the inclusion of longer wavelengths covering the peak of the cold-dust SED, in combination with meticulous short-wavelength selection (Megeath et al. 2012), virtually guarantees the presence of an envelope. Therefore we do not consider Class I protostar contamination from more evolved sources to be a significant source of error (see also Heiderman & Evans 2015).
 |
Fig. C.4 Dependence of the fraction of Class 0 protostars on Tbol misclassification due to foreground extinction. Diamonds indicate the raw uncorrected observed fractions. Squares indicate the fractions derived by correcting for the sample median AV extinction levels toward protostars in each region. X-symbols indicate the fractions derived by correcting for the maximum AV observed toward protostars in each region. |
Acknowledgments
The authors thank Andrew Gould for extremely helpful discussions. The authors thank Jean-Philippe Bernard for providing the offsets Herschel for the Herschel maps. We thank Neal Evans for a helpful referee report. We are very grateful to the HOPS team for data use in advance of publication. The authors thank H. Linz, M. Nielbock, and A. Schmiedeke for assistance with the data reduction. The authors thank E. Keto, M. Fouesneau, L. Hartmann, L. Konstandin, S. T. Megeath, M. Ness, P. Myers, T. Robitaille and S. Sadavoy for helpful discussions. The work of A.S. and J.K. was partially supported by the Deutsche Forschungsgemeinschaft priority program 1573 ("Physics of the Interstellar Medium"). We include data from Herschel, a European Space Agency space observatory with science instruments provided by European-led consortia and with important participation from NASA. We use data from the Spitzer Space Telescope and the Infrared Processing and Analysis Center Infrared Science Archive, which are operated by JPL/Caltech under a contract with NASA. We also include data from APEX, a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
References
- Abreu-Vicente, J., Kainulainen, J., Stutz, A., Henning, Th., & Beuther, H. 2015, A&A, submitted [Google Scholar]
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H., Myers, P. C., Ladd, E. F., & Wood, D. O. S. 1995, ApJ, 445, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Arce, H. G., Allen, L. E., et al. 2013, AJ, 145, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 195 [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, W. J., Megeath, S. T., Stutz, A. M., et al. 2013, Astron. Nachr., 334, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 1995, ApJ, 440, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., & Evans, II, N. J. 2015, ApJ, submitted [arXiv:1503.06810] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, A., Meidt, S. E., Schinnerer, E., et al. 2013, ApJ, 779, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2014, Science, 344, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2012, AJ, 144, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, F. Z., Glover, S. C. O., Federrath, C., & Klessen, R. S. 2012, MNRAS, 423, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., & Ladd, E. F. 1993, ApJ, 413, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Min, M., Tielens, A. G. G. M., Dominik, C., & Paszun, D. 2011, A&A, 532, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Padoan, P., Nordlund, Å., & Jones, B. J. T. 1997, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Federrath, C., Chabrier, G., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 77 [Google Scholar]
- Polychroni, D., Schisano, E., Elia, D., et al. 2013, ApJ, 777, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Sadavoy, S. I. 2013, Ph.D. Thesis, University of Victoria [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Safron, E. J., Fischer, W. J., Megeath, S. T., et al. 2015, ApJ, 800, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Stanke, T., Stutz, A. M., Tobin, J. J., et al. 2010, A&A, 518, L94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A., Launhardt, R., Linz, H., et al. 2010, A&A, 518, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A. M., Tobin, J. J., Stanke, T., et al. 2013, ApJ, 767, 36 [NASA ADS] [CrossRef] [Google Scholar]
- van Kempen, T. A., van Dishoeck, E. F., Salter, D. M., et al. 2009, A&A, 498, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Orion A N(H) map shown on a log scale; the N(H) = 3.7 × 1021 cm-2 contour is indicated in gray. The locations of protostars are indicated as ×-symbols. Numbered boxes (with 1/4 square degree area or 3.67 pc on a side) indicate the regions into which we divide the Orion A cloud. |
| In the text | |
 |
Fig. 2 N(H) distributions for each region shown in Fig. 1. The combined N(H) distribution for all regions is shown in gray. The dashed curves show the best-fit slope assuming a power-law distribution of N(H); each value for the slope is listed (see Table 1 for slope errors). Here we show PDF data of bins containing more than 10 pixels, and each major tick mark represents a factor of 10. Mean-normalization, N(H) / ⟨ N(H) ⟩ in each region, has no effect on the derived PDF slopes because the operation simply results in a linear translation of the x-axis. |
| In the text | |
 |
Fig. 3 Correlation between the power-law index of the N-PDF and Class 0 fraction across Orion A regions. The Class 0 fraction can be related to a timescale, as indicated, assuming a constant SFR (see text). Gray ×-symbols are the data from Perseus from Sadavoy (2013), Sadavoy et al. (2014), and Sadavoy (priv. comm., 2015). The dashed gray curve shows the linear fit to the data, which have a correlation coefficient of 0.7. |
| In the text | |
 |
Fig. A.1 Orion A N(H) map, shown on a log scale. |
| In the text | |
 |
Fig. B.1 Top: best-fit power-law index for each region as a function of N(H) map pixel size. The slope values are not affected by correlated pixel, and differences are 2% at most. Bottom: error for each region as a function of N(H) map pixel size. The error increases with pixel size because the number of counts decreases. All quantities shown here have been derived using the same N(H) limits presented in Table 1. |
| In the text | |
 |
Fig. B.2 Indices derived from the 250 μm 18′′pixel map vs. those derived from the 500 μm 40′′pixel map, both using the N(H) limits presented in Table 1. |
| In the text | |
 |
Fig. C.1 Class 0 fraction in regions. Diamonds indicate the total fraction (Table 1), while squares indicate the completeness corrected values. Results remain consistent with and without the application of the completeness limit. |
| In the text | |
 |
Fig. C.2 Model Tbol values versus extincted SED Tbol,ext values. Colors indicate the assumed levels of extinction. Here we show 500 randomly chosen models. As the extinction AV increases, the model Tbol,ext decreases and the levels of contamination at Tbol,ext< 70 K increases. |
| In the text | |
 |
Fig. C.3 Top: probability that a source with a given Tbol> 70 K will have Tbol,ext< 70 K, marginalizing over a uniform foreground AV extinction distribution up to the listed value (shown in color). There is no Class 0 contamination from Class I models with Tbol> 400 K for the AV values we consider here. Bottom: probability that a source is correctly classified as a Class 0 source (has Tbol< 70 K). |
| In the text | |
 |
Fig. C.4 Dependence of the fraction of Class 0 protostars on Tbol misclassification due to foreground extinction. Diamonds indicate the raw uncorrected observed fractions. Squares indicate the fractions derived by correcting for the sample median AV extinction levels toward protostars in each region. X-symbols indicate the fractions derived by correcting for the maximum AV observed toward protostars in each region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


