| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201525781 | |
| Published online | 18 May 2015 | |
Calibrating the α parameter of convective efficiency using observed stellar properties
1
Key Laboratory of Optical Astronomy, National Astronomical Observatories,
Chinese Academy of Sciences,
20 Datun Road, Chaoyang District,
100012
Beijing
PR China
2
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
e-mail:
frank@grupp-astro.de
3
University of the Chinese Academy of Sciences,
19A Yuquan Road, Shijingshan District,
100049
Beijing, PR
China
4
Institute of Astronomy, Russian Academy of Sciences,
119017
Moscow,
Russia
5
Universitäts Sternwarte München, Scheinerstr. 1, 81679
München,
Germany
Received: 2 February 2015
Accepted: 29 March 2015
Context. Synthetic model atmosphere calculations are still the most commonly used tool when determining precise stellar parameters and stellar chemical compositions. Besides three-dimensional models that consistently solve for hydrodynamic processes, one-dimensional models that use an approximation for convective energy transport play the major role.
Aims. We use modern Balmer-line formation theory as well as spectral energy distribution (SED) measurements for the Sun and Procyon to calibrate the model parameter α that describes the efficiency of convection in our 1D models. Convection was calibrated over a significant range in parameter space, reaching from F-K along the main sequence and sampling the turnoff and giant branch over a wide range of metallicities. This calibration was compared to theoretical evaluations and allowed an accurate modeling of stellar atmospheres.
Methods. We used Balmer-line fitting and SED fits to determine the convective efficiency parameter α. Both methods are sensitive to the structure and temperature stratification of the deeper photosphere.
Results. While SED fits do not allow a precise determination of the convective parameter for the Sun and Procyon, they both favor values significantly higher than 1.0. Balmer-line fitting, which we find to be more sensitive, suggests that the convective efficiency parameter α is ≈2.0 for the main sequence and quickly decreases to ≈1.0 for evolved stars. These results are highly consistent with predictions from 3D models. While the values on the main sequence fit predictions very well, measurements suggest that the decrease of convective efficiency as stars evolve to the giant branch is more dramatic than predicted by models.
Key words: stars: fundamental parameters / stars: atmospheres / stars: late-type
© ESO, 2015
1. Introduction
One-dimensional (1D) stellar model atmospheres are widely used for determining basic physical parameters, such as effective temperatures, surface gravities, luminosities, masses, and chemical compositions of stars at different evolutionary stages. They also serve as boundary conditions for stellar evolution codes.
While codes for 3D model atmospheres self-consistently solve for convection in the atmospheric layers, 1D codes apply a simplified approach such as described by Böhm-Vitense (1958, BV hereafter) or Canuto & Mazzitelli (1991, 1992, CMA hereafter). As these formulations do not self-consistently determine the convective flux, at least one calibration parameter is required: the α-parameter, which sets the efficiency of convection.
Recent calibrations of the 1D α-parameter based on 3D theoretical model atmospheres have been presented by Magic et al. (2015, hereafter Magic15) and earlier by Ludwig et al. (1999). The primary goal of this paper is to compare observational constraints on αCMA, the α-parameter in the formulation of Canuto & Mazzitelli (1992), to theoretical predictions of 3D models. This will allow us to use a proper αCMA for 1D model atmospheres across a wide range of stellar parameter space.
We use the approach as Fuhrmann et al. 1993 (FAG93 hereafter), using the dependence of Balmer line profiles on the atmospheric structure, which we call the αCMA-parameter. For this test we use a sample of stars (including the Sun) with stellar parameter start values determined independently of model atmospheres, for example, by astrometrical methods. As another tool for determining αCMA, we use stellar spectral energy distributions (SED) in the visible and near-UV spectral range. This method is of course limited to objects with good absolute calibration of the SED. We here use the Sun and Procyon.
On the model side, the adopted model atmosphere code is the plane-parallel, chemically homogeneous, local thermodynamical equilibrium (LTE) code MAFAGS-OS presented by Grupp (2004a). Stellar convection is treated in MAFAGS-OS according to the formalism of CMA. The authors take into account a spectrum of turbulent eddies with different sizes, which is more advanced than the one single eddy in the mixing-length theory (MLT; Böhm-Vitense 1958). The molecular weight within the convective zone is variable, a detail neglected by MLT. Nevertheless, it is a parametric and simplified approach, not a self-consistent numerical formalism. MLT furthermore assumes that the turbulence is incompressible and sets the mixing-length Λ = αHp, where Hp denotes the local pressure scale height, and leaves the so-called mixing-length parameter α (hereafter, αMLT) as a free parameter. Therefore, calibrations by comparing the models with the observational data are necessary.
Some previous works suggest that αMLT is greater than unity for the Sun and varies with stellar parameters. For example, Miglio & Montalbán (2005) constrained αMLT of the α Centauri A+B systems using a method from asteroseismology and found an αMLT for component B higher by 10% than that of A. Moreover, αMLT was found to be strongly dependent on stellar mass (e.g., Yıldız et al. 2006), but not on metallicity (e.g., Ferraro et al. 2006). In contrast, using the solar-like stars in the Kepler field, Bonaca et al. (2012) indicated that αMLT correlates more significantly with metallicity than Teff or log g. With 2D hydrodynamical models of dwarf stars, Ludwig et al. (1999) showed that αMLT decreases with increasing Teff and log g, and this was confirmed by 3D simulations of Trampedach (2007).
Canuto & Mazzitelli (1992) introduced Λ = αz by taking into account local effects, where z is the distance to the top of the convective zone, and its value is close to the polytrope Hp. α = 1 correspond to the nonlocal Λ = z in Canuto & Mazzitelli (1991). In previous versions of the MAFAGS-OS program, the α according to the CMA theory (hereafter, αCMA) is fixed to 0.82, because the evolutionary stage of the Sun, as determined by its internal structure, can be well reproduced by this value (Bernkopf 1998). However, this is only one calibration point in parameter space, there is no evidence that stars throughout the whole Hertzsprung-Russell diagram (HRD) necessarily have the same αCMA values.
In this paper, we analyze a sample of extensively studied “standard stars”1 with different chemical compositions and evolutionary stages. All of them have angular diameter data obtained with modern interferometers, which – together with distance measurements from Hipparcos – enable direct measurements of stellar radii, effective temperature, and surface gravities. The variation of αCMA across the HRD can therefore be constrained.
Best-fitting αCMA.
2. Stellar samples and basic stellar parameters
Our sample consists of ten dwarf and turnoff stars as well as one giant, with effective temperatures ranging from 4600 K to 6600 K and metallicities ([Fe/H]) from −2.60 to +0.60. All objects have been observed with the Fiber Optics Cassegrain Echelle Spectrograph (FOCES; Pfeiffer et al. 1998) on the 2.2 m telescope at Calar Alto Observatory. The optical spectra have signal-to-noise ratios (S/Ns) of >200 and resolving powers (R = λ/ Δλ) of ≈60 000. Data reduction was performed using the FOCES EDRS software package (see Pfeiffer et al. 1998). Normalization was performed manually. The sample is shown in the physical HRD in Fig. 1.
 |
Fig. 1 HRD of the program stars. Color encodes metallicity, size encodes stellar diameter measurements. |
Interferometric diameter determination for eight of the program stars is available (see Table 1).
To minimize the different instrumental response effects, the spectroscopic parameters (Teff, log g, [Fe/H] and ξ) were taken from Fuhrmann (1998, 2004), who derived them with the same FOCES spectra as we used in this study. The available interferometric observations provide accurate bolometric fluxes (ℱBOL) with typical uncertainties of ~2% (e.g., Boyajian et al. 2012). Combined with the interferometrically measured stellar angular diameter (θ) measurements with typical relative uncertainties of 1 ~ 3% for our samples, the uncertainties of Teff = 2341(ℱBOL/θ2)1/4 are lower than 1.5%, which is precise enough as cross-validations of the spectroscopic data.
Therefore, whenever possible, we used interferometric Teff and θ given by recent measurements with VLTI or CHARA to compose interferometric parameters. The spectroscopic and interferometric parameters are summarized in Table 1.
The log g of stars that have interferometric measurements parameters was derived using the direct angular diameter of the star, its distance from the Hipparcos parallax (van Leeuwen 2007), and its mass, either from the astrometric measurements of a binary companion (for Procyon A), or by fitting the stellar evolutionary track in the HRD. The parameters metallicity ([Fe/H]) and micro-turbulence velocity (ξ), which cannot be obtained by interferometric means, were kept the same as those in the spectroscopic group. The solar abundance mixture was taken from Lodders et al. (2009). For the five low-metallicity stars in our sample with [Fe/H] < −0.60 (HD 6582, [Fe/H] = −0.83; HD 103095, [Fe/H] = −1.35; HD 122563, [Fe/H] = −2.60; HD 45282, [Fe/H] = −1.50; and HD 140283, [ Fe/H ] = −2.38), α-elements enhancements of [α/Fe] = +0.4 were adopted.
A model of Vega was calculated to consistently derive the theoretical zero-point of the spectrophotometric data.
3. Model atmospheres
For each set of stellar parameters, model atmospheres were calculated using the model atmosphere code MAFAGS-OS (Grupp 2004a,b; Grupp et al. 2009). The opacity-sampling (OS) code is based on the opacity distribution function (ODF) version of T. Gehren (1979). In the reprogrammed version of Reile (1987), the code relies on the following basic assumptions:
-
Plane-parallel 1D geometry.
-
Chemical homogeneity throughout the atmosphere.
-
Hydrostatic equilibrium.
-
Convection is treated according to the formalism of Canuto & Mazzitelli (1991, 1992).
-
No chromosphere or corona.
-
Local thermodynamical equilibrium.
-
Flux conservation throughout all 80 layers.
While these assumptions can break down for hot stars, stars with very extended atmospheres, and the coolest stars, they are valid for temperatures from 4000 through 15 000 K and for gravities from the main sequence down to log g ≈ 0.
The model was iterated until the flux was constant (<0.5% level) throughout the atmosphere.
3.1. Convection and atmospheric structure
 |
Fig. 2 Temperature (T), pressure (P), and electron pressure (Pe) versus optical depth log (τ5000) with three different mixing-length parameters αCMA in the MAFAGS-OS models of Sun. |
Figure 2 shows the influence of the convective efficiency parameter αCMA on temperature stratification, gas pressure, and electron pressure of a solar atmospheric model. While a low value of αCMA results in low convective flux, high αCMA leads to an increase of the convective flux and − as the total flux is preserved through all layers − lower radiative flux in the convection zone of the stellar atmosphere. Low radiative flux leads to lower temperature gradients. Therefore, the high-αCMA case shows a lower temperature in the inner region of the stellar atmosphere.
For our program stars, increasing αCMA from 0.5 to 2.5 leads to decreasing temperatures in the inner atmosphere by up to 1000−1300 K at log (τ5000) ≃ 1.5.
The effect of a variation of αCMA on the solar SED is shown in Fig. 3. Flux changes of up to 5% of the solar SED in the UV and of 1% in the near-IR region are notable. There are some node points at 550, 1350, and 2050 nm around which the fluxes are insensitive to mixing-length parameters, while the continuum of the SED between each two shows opposite tendencies with αCMA.
The trends in model structures and fluxes are similar for other stars in our sample, with the only exception of the A0V star Vega. As Vega has no convection zone reaching the stellar atmosphere, no change with αCMA is present in the stellar flux.
 |
Fig. 3 Upper panel: computed solar flux Fλ with different αCMA. The spectrum is sampled every 50 Å along the wavelength. The transmission curves of U, B, V, R, I in Bessell photometric system, and J, H, Ks in 2MASS system are also overplotted (from left to right). The residuals to fluxes with αCMA = 0.82 are plotted in the lower panel. |
4. Spectral energy distributions
In the following section we directly compare the computed absolute fluxes to the observational data to calibrate αCMA. Absolute flux data are only available for a few stars. For our sample, reliable absolute SED data are only available for the Sun and Procyon.
4.1. Near-UV – visible – near-IR domain
Neckel & Labs (1984) measured solar irradiance between 3300 and 12 500 Å by combining the absolute fluxes of high-resolution spectra obtained with the Fourier Transform Spectrometer (FTS) at the McMath Solar Telescope on Kitt Peak. The spectra were averaged every 10 Å between 3305 and 6295 Å, and every 20 Å between 6310 and 8690 Å.
Thuillier et al. (2003) presented the solar irradiance from 2000 Å to 24 000 Å obtained with the SOLSPEC and SOSP spectrometers mounted on space missions. However, for wavelength ranges above 8700 Å, their data are sampled with a rate different from that in visible and UV domains. Therefore we only adopted the spectra below 8700 Å to compare with our solar fluxes.
Figure 4 shows the data and absolute deviations of solar irradiance of Neckel & Labs (1984) and Thuillier et al. (2003) together with the computed solar fluxes for three different αCMA values of 0.5, 1.5, and 2.5. A visual check prefers a fit between blue (αCMA = 2.5) and green (αCMA = 1.5).
The left and right panels of Fig. 5 compare the measured and observed fluxes starting from 4500 and 5500 Å. The strong dependency on the blue end of the comparison window does not allow precisely determining αCMA from these data. Nevertheless, data points with values below 1.0 can be excluded from the Neckel data. The data of Thuillier et al. (2003) would only allow for very low convective efficiency if the blue region is ignored. In general, we find an overestimation of the solar flux in the regime below 5000 Å. This can be caused by missing atomic or molecular opacity. Variations of convective efficiency do not change this region significantly, thus can be excluded as the cause of this shortcoming.
4.2. Ultraviolet domain
The ultraviolet spectrum of Procyon A has been obtained with the Space Telescope Imaging Spectrograph (STIS) onboard the Hubble Space Telescope (HST) with high-quality calibration in the range from 220 nm up to 405 nm. As the STIS spectra span several echelle orders and overlap between each pair of orders, we averaged bins of 2 nm width for the STIS measured data and MAFAGS-OS model calculations to allow a most direct comparison. This comparison is shown in Fig. 6 for αCMA ranging from 0.5 to 2.5 for a model with a Teff/ log g/[Fe/H]/ξ = 6530/3.98/−0.05/2.10. MAFAGS-OS underestimates the fluxes by at most ~35% for Mg ii H & K at 280 nm. The average deviation is within 4%.
Figure 7 displays the 2D plots of χ2 versus αCMA (x axes) and the scaling factor of computed flux (y-axes) for four models with different temperatures. The difference of ~70 K in Teff causes a difference of ~4% in the total fluxes. The scaling factors were introduced to account for the offsets between the computed fluxes and the observational data to first-order approximation. The relative uncertainty (~1%) of the angular diameter can lead to an offset of up to 2% of the observational SED. Therefore the ±3% of the scaling factor on the total flux is reasonable. The derived αCMA for each model was estimated by minimizing the χ2 with the observational SED over the 2D plane. We found that model (c) and (d) led to smaller χ2 with the observational data, which favors higher Teff for Procyon A. Models (b), (c), and (d) led to quite consistent αCMA ≃ 1.4 to minimize χ2, while model (a) favors smaller αCMA ≃ 1.3.
 |
Fig. 4 Comparison of solar absolute fluxes (solid dots) to synthetic flux levels with αCMA = 0.5 (red), 1.5 (green), and 2.5 (blue). Observational data were taken from Neckel & Labs (1984) (upper panel) and Thuillier et al. (2003) (lower panel). The absolute deviation (Fmodel − Fobs) is plotted in the lower part of each panel. Offsets of 0.05 were added to improve the visualization. |
 |
Fig. 5 Relations of χ2 of observational and computed fluxes versus αCMA for the solar irradiance of Neckel & Labs (1984) and Thuillier et al. (2003). Observational data between 4500 and 8700 Å (left plots) and between 5500 and 8700 Å (right plots) were taken into account. |
5. NLTE calculations of Balmer-line profiles
Our analysis is based on the non-LTE (NLTE) line formation for H i using the method described in Mashonkina et al. (2008). In brief, the model atom includes levels with principal quantum numbers up to n ≤ 19. We checked the influence of inelastic collisions with neutral hydrogen atoms, as computed following Steenbock & Holweger (1984), on the statistical equilibrium (SE) of H i and resulting profiles of the Balmer lines in the models. The differences in normalized fluxes between including and neglecting H+H collisions are smaller than 0.0005 of the continuum flux for the core-to-wing transition region that is most sensitive to Teff variations. Therefore all the NLTE calculations were performed with pure electronic collisions with the exception of a very metal poor (VMP) giant atmosphere 4600/1.60/−2.6 and a metal-poor subgiant atmosphere 5777/3.70/−2.38, for which SH = 1.0 and 2.0 were adopted.
The coupled radiative transfer and SE equations were solved with a revised version of the code DETAIL (Butler & Giddings 1985). The update was described in Mashonkina et al. (2008). The obtained departure coefficients were then used by the code SIU (Reetz 1991) to calculate the synthetic line profiles. The absorption profiles of Balmer lines were computed by convolving the profiles resulting from the thermal, natural, and Stark broadening, as well as self-broadening. The Stark profile was based on the unified theory as developed by Vidal et al. (1970, 1973, VCS). The calculations of Stehle (1994) based on a different theory agreed reasonably well with the data of VCS. For self-broadening, we applied the Lorentz profile with a half-width computed using the cross-section and velocity parameter from Barklem et al. (2000). As shown by Barklem et al. (2000), “the complete profiles obtained from overlapping line theory are very closely approximated by the p-d component of the relevant Balmer line”. This gives ground to apply the impact approximation to describe the self-broadening effect on Hα, Hβ, and Hγ.
 |
Fig. 6 Comparison of absolute fluxes of Procyon A (solid lines) obtained with HST/STIS with MAFAGS-OS model fluxes with αCMA = 0.5 (red), 1.5 (green), and 2.5 (blue) in model (a). The fluxes were summed every 2 nm. The absolute deviation (Fmodel − Fobs) were plotted in the lower panel. Offsets of 1.0 in the upper panel and 0.5 in the lower panel were added for clarity. |
We selected the model 6530/3.96/−0.05 to show the behavior of the departure coefficients 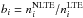 of the relevant levels of H i (Fig. 8). Here,
of the relevant levels of H i (Fig. 8). Here, 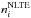 and
and 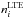 are the SE and thermal (Saha-Boltzmann) number densities, respectively. Very similar behavior of bi was found for all the model atmospheres investigated in this study. The ground state and the n = 2 level keep their thermodynamic equilibrium level populations throughout the atmosphere. Departures from LTE for the n = 3 level are controlled by Hα. In the layers where the continuum optical depth drops below unity, Hα serves as the pumping transition, which results in an overpopulation of the upper level. For instance, b(n = 3) ≃ 1.017 around log τ5000 = −0.57, where the Hα core-to-wing transition is formed. Starting from log τ5000 ≃ −2.8 and farther out, photons that escape from the Hα core cause an underpopulation of the n = 3 level. For Hα, NLTE leads to a weakening of the core-to-wing transition compared to the LTE case (Fig. 9).
are the SE and thermal (Saha-Boltzmann) number densities, respectively. Very similar behavior of bi was found for all the model atmospheres investigated in this study. The ground state and the n = 2 level keep their thermodynamic equilibrium level populations throughout the atmosphere. Departures from LTE for the n = 3 level are controlled by Hα. In the layers where the continuum optical depth drops below unity, Hα serves as the pumping transition, which results in an overpopulation of the upper level. For instance, b(n = 3) ≃ 1.017 around log τ5000 = −0.57, where the Hα core-to-wing transition is formed. Starting from log τ5000 ≃ −2.8 and farther out, photons that escape from the Hα core cause an underpopulation of the n = 3 level. For Hα, NLTE leads to a weakening of the core-to-wing transition compared to the LTE case (Fig. 9).
To compare them with observations, the computed synthetic profiles were convolved with a profile that combines instrumental broadening with a Gaussian profile of 3.2 km s-1 to 4.6 km s-1 for different stars and broadening caused by macroturbulence with a radial-tangential profile of 4 km s-1. Rotational broadening was only taken into account for Procyon, with Vsini = 2.6 km s-1 (Fuhrmann 1998). All the remaining dwarf and subgiant stars were assumed to be slow rotators, with Vsini ≤ 1 km s-1. It is worth noting that the thermal broadening of Balmer lines, with the most probable velocity of about Vt = 10 km s-1 in the atmospheres of the investigated stars, is more pronounced than the broadening caused by rotation, macroturbulence, and instrumental profile together. Therefore, the uncertainty in the external broadening parameters only has an minor effect on the computed Balmer-line wings.
6. Fitting procedure of Balmer-line wings
Our analysis of Hα is based on profile fitting in the wavelength range from 6473 to 6653 Å for Procyon and from 6520 to 6608 Å for the remaining stars. We analyzed Hβ in the wavelength range 4815−4908 Å only for the metal-poor stars HD 103095, HD 122563, HD 45282, and HD 140283. For HD 122563 and HD 140283 we also analyzed Hγ profiles in the wavelength range from 4315 to 4365 Å. Before fitting, we made the following preparations of the observed profiles for all stars.
We excluded the Balmer line cores up to 0.9 of the relative flux (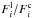 ), because the core half-width of the hydrogen line cannot be described in cool stars with classical model atmospheres. Thus only the pressure-broadened wings were analyzed. As our aim is to fit the profiles of Balmer lines, all blended lines should be removed from the observed profiles. The high resolution of the employed spectra allows us to assume that unblended spectral windows do exist and can be used for the fitting. We identified spectral windows across the line that are expected to be free from blends in the stars of interest. This was done by means of calculating Balmer line profiles with and without metal lines. Then we created a mask that was free from any blends. Based on the examination of the spectra, this is reasonable at Hα for all the reference stars, and at Hβ for HD 122563, HD 45282, and HD 140283, and at Hγ only for HD 122563 and HD 140283. It is impracticable to define spectral windows without any blends at Hβ and Hγ in solar metallicity stars.
), because the core half-width of the hydrogen line cannot be described in cool stars with classical model atmospheres. Thus only the pressure-broadened wings were analyzed. As our aim is to fit the profiles of Balmer lines, all blended lines should be removed from the observed profiles. The high resolution of the employed spectra allows us to assume that unblended spectral windows do exist and can be used for the fitting. We identified spectral windows across the line that are expected to be free from blends in the stars of interest. This was done by means of calculating Balmer line profiles with and without metal lines. Then we created a mask that was free from any blends. Based on the examination of the spectra, this is reasonable at Hα for all the reference stars, and at Hβ for HD 122563, HD 45282, and HD 140283, and at Hγ only for HD 122563 and HD 140283. It is impracticable to define spectral windows without any blends at Hβ and Hγ in solar metallicity stars.
 |
Fig. 7 χ2 versus αCMA and the scaling factor for the HST/STIS data and the computed absolute fluxes between 220 and 405 nm with models of different Teff for Procyon A. From a) to d): Teff = 6520/6530/6550/6590 K. |
 |
Fig. 8 Departure coefficients log bi for the five lowest levels of H i as a function of continuum optical depth τ5000 referring to λ = 5000 Å in the model atmosphere 6530/3.96/−0.05. Tick marks indicate the locations of core-to-wing transition (0.85 to 0.95 in normalized flux) formation depths for Hα and Hβ. |
 |
Fig. 9 Synthetic NLTE (continuous curve) and LTE (dashed curve) flux profile of Hα computed with the MAFAGS-OS 6530/3.96/−0.05 (αCMA = 2.3) model compared to the observed spectrum of Procyon (bold dots). |
The mask consists of a spectral window of pure Hα, Hβ, and Hγ (when available) lines with noise alone. The same mask was applied for all stars, but minor modifications were made for each star individually. Modifications of the mask were necessary to reject stars in some specific cases, for example, if there was an ingress of atmospheric lines in the spectral window or for Procyon, which has much stronger macroturbulence and Vsini than other stars. It is very important to clearly distinguish between noise fluctuations and weak metal lines in the spectra. In this context, we relied upon the spectral line database and inspected all Balmer line profiles.
We also investigated the effect of spectral resolution on the choice of which spectral windows to mask. It is necessary to have a proper number of spectral windows between blended lines because only by using such a mask are we able to derive the same result regardless of whether we use high-resolution spectra or the spectra degraded to the resolution of our observations. This mask is quite reliable in the case of Hα for all stars, but for Hβ and Hγ we were unable to define such a mask for all stars. This makes the results obtained from Hβ and Hγ profiles less reliable.
We also took into account the effect of rotational broadening and broadening caused by macroturbulence on the choice of spectral windows of mask. While all our sample stars are slow rotators with Vsini ≤ 1 km s-1 except for Procyon with Vsini = 2.6 km s-1, we were able to find a proper number of spectral windows between blending lines around Hα profiles. In the case of Hβ and Hγ profiles, this effect becomes important because there are many blending lines in the two profiles. This prevented us from defining a reliable mask for all stars, except for some metal-poor stars (HD 103095, HD 122563, HD 45282, and HD 140283), which only contain few blending lines in their Hβ and Hγ profiles.
In this work we used a method based on a reduced χ2 statistics. Statistical measurement of the goodness-of-fit was performed by comparing the theoretical profile and an observed profile through a χ2 minimization procedure (Nousek & Shue 1989). The estimator of the fit goodness is defined by 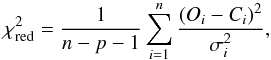 (1)where Oi is the relative flux measured at the wavelength λi, Ci is the relative flux computed from the model at the same wavelength λi, σi is the variance of the data point i that is defined as the (S/N)-1 ratio at the same wavelength λi, n is the number of data points, and p is the number of free parameters of the model so that n − p − 1 is the number of degrees of freedom (d.o.f).
(1)where Oi is the relative flux measured at the wavelength λi, Ci is the relative flux computed from the model at the same wavelength λi, σi is the variance of the data point i that is defined as the (S/N)-1 ratio at the same wavelength λi, n is the number of data points, and p is the number of free parameters of the model so that n − p − 1 is the number of degrees of freedom (d.o.f).
Estimated errors in CMA factor for Hα profiles.
For the spectra of HD 10700 and HD 122563, we did not have the σi at the wavelength λi. Although it is known that the S/N depends on the number of recorded photons I (~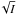 ), we adopted the mean constant S/N for these stars because we only fit the wings of each line up to 0.9 where the S/N is not changed dramatically. For Procyon, for example, the relative flux at a S/N of 0.85 is 10% lower than that with a S/N of 0.995. Apart from the inner wings, which have less strongly blended lines because they are saturated by the hydrogen line, equal weights were assigned for all spectral windows of a line profile.
), we adopted the mean constant S/N for these stars because we only fit the wings of each line up to 0.9 where the S/N is not changed dramatically. For Procyon, for example, the relative flux at a S/N of 0.85 is 10% lower than that with a S/N of 0.995. Apart from the inner wings, which have less strongly blended lines because they are saturated by the hydrogen line, equal weights were assigned for all spectral windows of a line profile.
There were two free parameters, αCMA and the effective temperature, while the other parameters (log g, [Fe/H], ξ) were fixed. Assuming the Poissonian error distribution, which approaches the normal distribution at high S/N, the minimization of χ2 provides the maximum-likelihood estimate of the parameters, in our case for αCMA and Teff.
We also compared a grid of Balmer-line profiles for a given model grid with a 25 K interval in Teff and a 0.1 interval in αCMA. By varying the free parameters of the model, we computed the value of χ2 at each step. First we fixed one of the two free parameters, Teff, and analyzed the function of χ2, which smoothly changes with varying αCMA and follows an asymmetric parabolic form with one single minimum. The best αCMA and Teff were chosen from the requirement of the lowest χ2 value. The variation of temperature within the error bars allows us to estimate the upper and lower values for our αCMA. An example of the fitting for Hα profile in the metal poor star HD 103095 is shown in Fig. 10.
 |
Fig. 10 Example of fitting the Hα wings in the metal-poor star HD 103095. Bold dots correspond to the observed data. The theoretical Hα profile was calculated with (dashed curve) and without (solid curve) blending lines. Only bold dots were used for determining the χ2 statistic. |
6.1. Errors
Estimated errors are presented in Table 2 for the program stars. The strength of the hydrogen line depends only weakly on the surface gravity or the metallicity. We considered how the typical errors (0.1 dex) for either of them may affect the result. Microturbulence does not affect the formation of the Balmer-line wings (Fuhrmann et al. 1993), therefore we did not consider the influence of microturbulence. Only the temperature can strongly affect the wings of hydrogen lines. With increasing temperature the wings of hydrogen lines tend to be stronger. The effective temperature is the main source of errors in our results. The influence of other sources of error, such as Stark-broadening, self-broadening, and He-broadening, were considered in Fuhrmann et al. (1993, 1994) and Barklem et al. (2002). The latter showed that the influence of Stark- and self-broadening on the behavior of Balmer lines is insignificant for solar metallicity stars, but tends to be stronger for metal-poor atmospheres. Moreover, the determination of the continuum placement is one of the most significant uncertainties in this work. For the sample spectra, the error in the continuum placement of the high-quality spectra is approximately 0.5% of the continuum flux, depending on the S/N. As a result of the interdependency of errors, it is difficult to precisely account for the combined effect, therefore we divided all errors into two groups: those propagated from the stellar parameters (Teff, log g, and [Fe/H]), and those caused by observational aspects (continuum placement and fitting error).
7. Results
 |
Fig. 11 Comparison of the line profiles of Hα, Hβ, and Hγ (from bottom to top) for HD 122563, HD 103095, and the Sun. The x-axis is the wavelength shift relative to the center of the Balmer lines. The colors are coded with different αCMA (from 0.5 to 1.5), while the solid lines and dashed lines represent profiles using LTE and NLTE line formations, respectively. The dotted lines are profiles with LTE models of αCMA = 0.5 but Teff + 100 K. For clarity, offsets of 0.2 and 0.4 are added to the Hβ and Hγ, respectively. |
In Fig. 11 we plot the profiles of the Balmer lines for three of our program stars (HD 122563, HD 103095, and the Sun). The profiles are only slightly different under LTE or NLTE assumptions for dwarfs, but exhibit significant variations with αCMA on their wings. The changes with αCMA from 0.5 to 2.5 are similar (for Hα) and even larger (for Hβ and Hγ) to that of Teff of a few hundreds of Kelvin. For the metal-poor giant HD 122563, the NLTE effect plays a more important role than αCMA for Hα profile, but is less sensitive than αCMA parameter. Figure 11 also indicates that if the αCMA parameter in the model atmosphere is not correct, the Teff may be biased by up to a few hundreds of Kelvin by fitting Hβ or Hγ line profiles. Therefore, caution must be exercised when choosing αCMA in 1D model atmospheres.
7.1. The Sun
The Sun is the best-known star with high-quality observations and accurate physical parameters. Following Fuhrmann et al. (1993), we attempted to calibrate αCMA for the solar atmosphere. Our work differs from that of Fuhrmann et al. (1993) in that we have used the self-broadening theory of Barklem et al. (2000). For investigations of the Sun we employed the solar atlas (Kurucz et al. 1984). We adopted an effective temperature of 5777 K with an error bar of ±40 K. By fitting theoretical Hα profiles to reduced observational profiles, the two parameters Teff and αCMA were varied within error bars and reasonable physical limits, respectively. The results are shown in Fig. 12, where the χ2 minimum indicates the best Teff and αCMA.
Figure 13 compares the left wing of Hα line profile for the Sun with the theoretical spectrum for αCMA = 2.0 (solid line).
The combination of Teff = 5770 ± 20 K and αCMA = 2.0 ± 0.2 is preferred based on the degree of agreement between the observational and theoretical Hα profiles. Nevertheless, it is important to note that the value of χ2 is still high, which suggests that our agreement between the observational and the theoretical Hα profiles is not perfect. This means that the quality of the observed solar flux spectra is higher than the quality of theoretical surveys.
From comparison with SED, a low value for αCMA< 1.0 is excluded. The lack of fitting in the region below 5000 Å does not allow precisely determining the convective efficiency, but the measurements are consistent with an αCMA of 2.0.
7.2. Procyon
Procyon (HD 61421, HR 2943) is one of the brightest stars in the night sky (V = 0.34). It is a binary system consisting of an F5 IV-V star (Procyon A) with a mass of 1.497 ± 0.037 M⊙ and a faint white dwarf (Procyon B) with a mass of 0.602 ± 0.015 M⊙, orbiting each other with a period of 40.8 years (Girard et al. 2000). Spectroscopic analyses gave rather discrepant effective temperatures, from 6470 K (by fitting the Balmer lines; Zhao & Gehren 2000) to 6850 K (by measuring the equivalent widths of a large set of iron lines; Heiter & Luck 2003). The proximity of Procyon (π = 284.56 ± 1.26 mas; van Leeuwen 2007) to the Earth allows us to directly measure its angular diameter (e.g., Hanbury Brown et al. 1974; Mozurkewich et al. 1991; Aufdenberg et al. 2005; Chiavassa et al. 2012). Kervella et al. (2004) found Teff = 6530 ± 50 K and log g = 3.96 ± 0.2, which agrees well with other works (e.g., Allende Prieto et al. 2002; Fuhrmann et al. 1997). We used a high-quality spectrum of Hα for Procyon and applied the same fitting method as described in the previous sections.
The results are displayed in Fig. 12, where the χ2 minimum indicates the best Teff and αCMA. For this star we find Teff = 6524 ± 50 K and αCMA = 1.9 ± 0.7. The error of αCMA is not symmetric in this case, but we adopted the largest. The left wing of the Hα line profile for Procyon is shown in Fig. 13, where two theoretical spectra with αCMA = 1.5 (solid line) and αCMA = 2.3 (dashed line) are plotted as well.
The value preferred from the SED fitting for αCMA ≈ 1.4, nevertheless, there are large uncertainties with respect to opacity data. As a result of the uncertain UV flux comparison, the values given by SED fitting and that by Balmer profiles do not contradict each other.
 |
Fig. 12 Survey of the reduced χ2 obtained from Hα profile fitting for the observed solar flux spectra (top panel) and spectra of Procyon (bottom panel) with different αCMA and Teff. The preferred parameter area is located where χ2 is minimal. All χ2 are not normalized and indicate a good fit in each case. |
 |
Fig. 13 Left wings of Hα line profiles for the Sun with αCMA = 2.0 (top panel) and Procyon (bottom panel), where two theoretical spectra with αCMA = 1.5 (solid line) and αCMA = 2.3 (dash line) are shown. |
7.3. Program stars
The final results of our fitting are given in Table 1, including the names of the program stars, their parameters, the best αCMA along with the limits, and the χ2 values that indicate the best fit in each case. We also present the best-fit Teff within the error bars that was obtained during the χ2 minimization procedure. Temperatures with asterisks are the best-fit temperatures. The results from Hβ and Hγ for some stars are less reliable. Even though good-quality observations of Hβ and Hγ are available for all remaining stars, these lines were not adopted because choosing a reliable mask was problematic.
The observed spectra and the best-fitting line profiles from this method are plotted in Fig. 14. When applying the above-mentioned method, we have to keep in mind that weak blending lines may, nevertheless, be presented in a chosen windows. Therefore, it would be better to inspect the best profiles visually to give preference to the case where all observed points are below the theoretical line profile, but the χ2 – method minimizes the deviations without considering whether the observed points are above or below the theoretical profile. In this context, for the χ2 method, αCMA will be slightly underestimated, while the best-fit Teff will be overestimated.
The derived Teff for stars HD 10700, HD 39587, HD 217014, HD 22049, HD 122563, HD 45282, and HD 140283 agree well with those derived from astrometric and IRFM methods. However, for HD 103095 we were unable to find an appropriate Teff in the temperature range Teff = 4820 ± 100 K. Thus, for this star we adopted a higher spectroscopic temperature of Teff = 5110 K.
 |
Fig. 14 Best fits of the Hα lines in our stellar sample. Solid lines are the theoretical spectra corresponding to the best fit and dotted lines represent the observed spectra that were used for determining the χ2 statistic. The horizontal dotted lines show the limit of reasonableness of the approximation and allows seeing residuals. |
The individual results for our stellar sample are reported below.
HD 6582 (μ Cas, 30 Cas, HR 321) is a close binary system that consists of a slightly metal-deficient subdwarf (component A, V = 5.17) and a component B fainter by 5.3 magn (V = 10.5), with a separation of only 0″.40 ~ 1″.40 (Mason et al. 2001). The spectroscopic parameters adopted here for HD 6582 A (Teff = 5387 K, log g = 4.45, [Fe/H] = −0.83, and ξ = 0.89 km s-1) were taken from Fuhrmann (2004). Boyajian et al. (2012) measured its limb-darkened angular diameter θLD = 0.972 ± 0.009 mas with CHARA, corresponding to the stellar radius of 0.790 ± 0.009 R⊙, combining with the Hipparcos parallax (π = 132.38 ± 0.82 mas; van Leeuwen 2007). This is agrees well with the spectroscopic radius (R = 0.8 R⊙), but the interferometric Teff = 5264 K is ~120 K lower than that of Fuhrmann (2004). By comparing the Hα profile, we found the best αCMA = 2.3 for spectroscopic parameters, while αCMA = 1.7 for interferometric parameters. Despite this large discrepancy, the fitting method with the interferometric model (b) led to lower χ2 and supports a higher Teff = 5370 K. This result supports the relative high Teff of 5339 K derived by the photometric b − y = 0.437 and c1 = 0.213 (Hauck & Mermilliod 1998) with the color–Teff relation of Alonso et al. (1996).
HD 10700 (τ Cet, 52 Cet, HR 509) is a nearby and inactive G8 V star, with a distance of only 3.650 ± 0.002 pc (π = 273.96 ± 0.17 mas; van Leeuwen 2007). It is one of the most frequently observed targets in several precise radial velocity surveys for extrasolar planets, and Tuomi et al. (2013) reported five planets with minimum masses of up to 6.6 M⊕ orbiting it. Spectroscopic analyses indicate that its Teff ranges from 5283 K (Valenti & Fischer 2005) to 5420 K (Takeda et al. 2005), and [Fe/H] range from −0.43 (Takeda et al. 2005) to −0.58 (Luck & Heiter 2005). Interferometric measurements with VLTI gave θLD = 2.078 ± 0.031 mas (Di Folco et al. 2004), and Teff was perfectly consistent with the spectroscopic parameters (Teff = 5377 K, log g = 4.53, [Fe/H] = −0.49, and ξ = 0.8 km s-1; Mashonkina et al. 2011). With a least χ2 fitting, we found the best αCMA = 1.8, and the best Teff = 5330 K agrees with the Teff = 5346 K inferred from the b − y and c1 color (Hauck & Mermilliod 1998; Alonso et al. 1996).
HD 22049 (ϵ Eri, 18 Eri, HR 1084) is a nearby (π = 310.94 ± 0.16 mas; van Leeuwen 2007), chromospherically active K2 V star orbited by a dusty ring (Greaves et al. 1998). Atmospheric parameter determinations based on high-resolution spectra gave very consistent results, with a Teff ranging from 5054 K (Fuhrmann 2004) to 5200 K (Luck & Heiter 2005), log g ranging from 4.40 (Mishenina et al. 2013) to 4.72 (Takeda et al. 2005), and [Fe/H] ranging from −0.18 (Ghezzi et al. 2010) to +0.06 (Takeda et al. 2005). We adopted the parameters of Fuhrmann (2004) (Teff = 5054 K, log g = 4.54, [Fe/H] = −0.09, and ξ = 0.9 km s-1). Di Folco et al. (2004) suggested an interferometric angular diameter of θLD = 2.148 ± 0.029 mas and an effective temperature of Teff = 5122 K. Hα profile fitting with spectroscopic and interferometric methods result in quite consistent αCMA = 2.2. The best-fit Teff = 5045 K also agrees with the photometric Teff = 5074 K from the b − y and c1 (Hauck & Mermilliod 1998).
HD 39587 (χ1 Ori, 54 Ori, HR 2047) is a variable star of RS CVn type, orbiting by a faint (VA = 4.4, VB = 8.8) companion with a mass of 0.15 ± 0.01 M⊙ (Irwin et al. 1992). Boyajian et al. (2012) measured its angular diameter θLD = 1.051 ± 0.009 mas with a precision of 0.9%. This yield a radius of 0.979 ± 0.009 R⊙ with a Hipparcos parallax of 115.43 ± 0.27 mas (van Leeuwen 2007). Boyajian et al. (2012) also gave its effective temperature as Teff = 5961 K, which generally agrees with the spectroscopic temperature reported by Fuhrmann (2004). We found the best-fit αCMA = 1.5 for spectroscopic parameters and αCMA = 1.9 for interferometric parameters.
HD 122563 (HR 5270) is the most metal-poor halo star ([ Fe/H ] ~ −2.6) that can be seen by the naked eye (V = 6.2) in the night sky. It is the only giant in our program stars and therefore provides unique constraints. Mashonkina et al. (2011) presented a detailed analysis of the NLTE formation of iron lines for this star, and we used the same parameters (Teff = 4600 K, log g = 1.60, [ Fe/H ] = −2.60, and ξ = 1.95 km s-1). Recent interferometric measurements with CHARA and PTI (Creevey et al. 2012) gave its angular diameter as θLD = 0.948 ± 0.012 mas, and Teff = 4598 ± 41 K, which is consistent with its spectroscopic temperature. We found the best-fit αCMA = 1.0 with Hα profile, while the fitting of Hβ and Hγ gave satisfactory agreement with αCMA = 0.5. The αCMA is lower than that of the dwarfs, implying that the stellar convective energy transport become less efficient after stars evolved off the main sequence.
 |
Fig. 15 Determined αCMA for the program stars. An error of αCMA of ≈ ± 0.4...0.7 maybe assumed for all stars except HD 140283, Teff = 5780 K, log g = 3.70 where the error reaches ≈ ± 1.1. |
HD 217014 (51 Peg, HR 8729) is a nearby (π = 64.07 ± 0.38 mass; van Leeuwen 2007) G5 V star with the first extrasolar planet ever discovered orbiting a Sun-like host (Mayor & Queloz 1995). Spectroscopic analysis gave its effective temperatures as ranging from 5710 K (Maldonado et al. 2012) to 5832 K (Ramírez et al. 2009). The narrow-band photometric color indices b − y = 0.416 and c1 = 0.371 (Hauck & Mermilliod 1998) indicate a rather low Teff = 5661 K (Alonso et al. 1996). The parameters adopted here (Teff = 5793 K, log g = 4.33, [Fe/H] = +0.20, and ξ = 0.95 km s-1, Fuhrmann 1998) agree for the effective temperature with the interferometric results of Teff = 5804 K and θLD = 0.748 ± 0.027 mas (Baines et al. 2008). We found a best-fit of αCMA = 2.0 with both parameters giving consistent results.
HD 45282 is a G 0 metal-poor star ([Fe/H] = −1.5) at low Galactic latitude (b = −3.9°). Previous spectroscopic analyses gave its Teff as ranging from 5150 K (Fulbright 2000) to 5344 K (Gratton et al. 2000). Considering its high reddening with E(B − V) ≃ 0.82 at this direction (Schlegel et al. 1998), we used the IRFM Teff from Casagrande et al. (2010), which is thought to be less affected by interstellar medium. The Balmer profile χ2 fitting gives αCMA = 1.0 for Hα and αCMA = 0.5 for Hβ with the best-fit Teff = 5310 K. The error of 0.05 on E(B − V) causes an uncertainty of ~300 K on Teff, therefore the photometric temperature is not reliable.
For the Sun we used the widely adopted parameters of Teff = 5777 K, log g = 4.44, [Fe/H] = 0.0, and ξ = 0.90 km s-1 and for Vega Teff = 9550 K, log g = 3.95, [Fe/H] = −0.50, and ξ = 2.00 km s-1 (Castelli & Kurucz 1994). The solar αCMA from the Hα Balmer line is 2.0, while a determination based on the solar flux suggests a value of 1.5−1.75. Although this is consistent within the error bars, it has to be noted that, for both the Sun and Procyon, SED fitting leads to a notably lower value of αCMA than Balmer-line fitting.
7.4. α CMA
Figure 15 shows our final results for the efficiency parameter αCMA as determined from Balmer-line fitting. Except for evolved stars, αCMA is consistent with a value of about 2.0 for all objects within the given insecurities. There is no obvious correlation with metallicity and a weak trend of increasing α for the coolest main-sequence objects in the investigated range of F- and G-type stars. This confirms the behavior and numerical values predicted by Magic et al. (2015) for this part of the HRD.
For the evolved stars of our sample αCMA is of about 1.0. Although Magic et al. (2015) predicted the same trend of lower convective efficiency for objects with lower log g, the magnitude of the change is much greater in our sample than that suggested by the 3D simulation of Magic et al. (2015). Our sample mainly consists of main-sequence stars and only contains three evolved objects with well-determined parameters. Nevertheless, the stars clearly show a behavior different from that suggested by Magic et al. (2015). The three objects span a wide range of temperatures, therefore the evolutionary state seems to be the main discriminator that separates them from the rest of the sample.
8. Discussion and implication
Figure 16 shows the difference between the suggested αCMA and that from Magic et al. (2015), who adopted a calibration using the entropy jump (Fig. 3 in their work). As described above, the differences are small along the main sequence and increase dramatically later in the evolutionary sequence, which suggests that there is either a stronger variation of αCMA as predicted by the STAGGER grid, or that our modeling of the Balmer lines is incorrect. The latter is excluded because we generally determined a temperature that agreed well with astrometric and IRFM data.
 |
Fig. 16 Difference between our determined αCMA and the one predicted by Magic et al. (2015). |
Based on the similar method of FAG93, our analysis indicates that if the theory of Barklem et al. (2000) for Balmer-line broadening is adopted instead of that of Vidal et al. (1970, 1973), while the old ODF version is replaced by the MAFAGS-OS version, it is very unlikely to derive a low value of αCMA = 0.82. For F- and G-type main-sequence stars, αCMA ≈ 2.0 is derived, and the value decreases toward 1.0 for more evolved stars.
A variation of the convective efficiency naturally influences the temperatures determined by the Balmer-line method. It furthermore changes stellar SEDs and in turn filter fluxes and color determinations. All stellar lines that have contribution functions down to the convection scone (very strong lines) are subject to potential changes as well.
Acknowledgments
We are grateful to K. Fuhrmann for providing some spectral observations. X.S.W. thanks R.Wittenmyer and H.N. Li for their useful comments and suggestions. X.S.W., L.W., and G.Z. are supported by the National Natural Science Foundation of China under grant No. 11390371 and 11233004. S.A. and L.M. are supported by the Russian Foundation for Basic Research (grants 14-02-31780 and 14-02-91153). F.G. would like to thank T. Gehren for his support, knowledgable comments, and so many helpful discussions.
References
- Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&AS, 117, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aufdenberg, J. P., Ludwig, H.-G., & Kervella, P. 2005, ApJ, 633, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., McAlister, H. A., ten Brummelaar, T. A., et al. 2008, ApJ, 680, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&A, 363, 1091 [NASA ADS] [Google Scholar]
- Barklem, P. S., Stempels, H. C., Allen de Prieto, C., et al. 2002, A&A, 385, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernkopf, J. 1998, A&A, 332, 127 [NASA ADS] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Bonaca, A., Tanner, J. D., Basu, S., et al. 2012, ApJ, 755, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, K., & Giddings, J. 1985, Newsletter on the analysis of astronomical spectra, No. 9 (University of London) [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1992, ApJ, 389, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 1994, A&A, 281, 817 [NASA ADS] [Google Scholar]
- Chiavassa, A., Bigot, L., Kervella, P., et al. 2012, A&A, 540, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Creevey, O. L., Thévenin, F., Boyajian, T. S., et al. 2012, A&A, 545, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A&A, 426, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferraro, F. R., Valenti, E., Straniero, O., & Origlia, L. 2006, ApJ, 642, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997, A&A, 323, 909 [NASA ADS] [Google Scholar]
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Gehren, T. 1979, A&A, 75, 73 [NASA ADS] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., et al. 2010, ApJ, 720, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Girard, T. M., Wu, H., Lee, J. T., et al. 2000, AJ, 119, 2428 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
- Greaves, J. S., Holland, W. S., Moriarty-Schieven, G., et al. 1998, ApJ, 506, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Grupp, F. 2004a, A&A, 420, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupp, F. 2004b, A&A, 426, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupp, F., Kurucz, R. L., & Tan, K. 2009, A&A, 503, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanbury Brown, R., Davis, J., & Allen, L. R. 1974, MNRAS, 167, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., & Luck, R. E. 2003, AJ, 126, 2015 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, A. W., Yang, S., & Walker, G. A. H. 1992, PASP, 104, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Morel, P., et al. 2004, A&A, 413, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm, NSO Atlas No. 1 [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein, 44 [Google Scholar]
- Luck, R. E., & Heiter, U. 2005, AJ, 129, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Magic, Z., Weiss, A., & Asplund, M. 2015, A&A, 573, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2012, A&A, 541, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., & Montalbán, J. 2005, A&A, 441, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishenina, T. V., Pignatari, M., Korotin, S. A., et al. 2013, A&A, 552, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mozurkewich, D., Johnston, K. J., Simon, R. S., et al. 1991, AJ, 101, 2207 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Nousek, J. A., & Shue, D. R. 1989, ApJ, 342, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Pfeiffer, M. J., Frank, C., Baumueller, D., Fuhrmann, K., & Gehren, T. 1998, A&AS, 130, 381 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reetz, J. K. 1991, Diploma Thesis (Universität München) [Google Scholar]
- Reile, C. 1987, Diplomarbeit, Universitäts Sternwarte München [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Stehle, C. 1994, A&AS, 104, 509 [NASA ADS] [Google Scholar]
- Takeda, Y., Ohkubo, M., Sato, B., Kambe, E., & Sadakane, K. 2005, PASJ, 57, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Hersé, M., Labs, D., et al. 2003, Sol. Phys., 214, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R. 2007, in Unsolved Problems in Stellar Physics: A Conference in Honor of Douglas Gough, eds. R. J. Stancliffe, G. Houdek, R. G. Martin, & C. A. Tout, AIP Conf. Ser., 948, 141 [Google Scholar]
- Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal, C. R., Cooper, J., & Smith, E. W. 1970, J. Quant. Spec. Radiat. Transf., 10, 1011 [Google Scholar]
- Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Yıldız, M., Yakut, K., Bakış, H., & Noels, A. 2006, MNRAS, 368, 1941 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., & Gehren, T. 2000, A&A, 362, 1077 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 HRD of the program stars. Color encodes metallicity, size encodes stellar diameter measurements. |
| In the text | |
 |
Fig. 2 Temperature (T), pressure (P), and electron pressure (Pe) versus optical depth log (τ5000) with three different mixing-length parameters αCMA in the MAFAGS-OS models of Sun. |
| In the text | |
 |
Fig. 3 Upper panel: computed solar flux Fλ with different αCMA. The spectrum is sampled every 50 Å along the wavelength. The transmission curves of U, B, V, R, I in Bessell photometric system, and J, H, Ks in 2MASS system are also overplotted (from left to right). The residuals to fluxes with αCMA = 0.82 are plotted in the lower panel. |
| In the text | |
 |
Fig. 4 Comparison of solar absolute fluxes (solid dots) to synthetic flux levels with αCMA = 0.5 (red), 1.5 (green), and 2.5 (blue). Observational data were taken from Neckel & Labs (1984) (upper panel) and Thuillier et al. (2003) (lower panel). The absolute deviation (Fmodel − Fobs) is plotted in the lower part of each panel. Offsets of 0.05 were added to improve the visualization. |
| In the text | |
 |
Fig. 5 Relations of χ2 of observational and computed fluxes versus αCMA for the solar irradiance of Neckel & Labs (1984) and Thuillier et al. (2003). Observational data between 4500 and 8700 Å (left plots) and between 5500 and 8700 Å (right plots) were taken into account. |
| In the text | |
 |
Fig. 6 Comparison of absolute fluxes of Procyon A (solid lines) obtained with HST/STIS with MAFAGS-OS model fluxes with αCMA = 0.5 (red), 1.5 (green), and 2.5 (blue) in model (a). The fluxes were summed every 2 nm. The absolute deviation (Fmodel − Fobs) were plotted in the lower panel. Offsets of 1.0 in the upper panel and 0.5 in the lower panel were added for clarity. |
| In the text | |
 |
Fig. 7 χ2 versus αCMA and the scaling factor for the HST/STIS data and the computed absolute fluxes between 220 and 405 nm with models of different Teff for Procyon A. From a) to d): Teff = 6520/6530/6550/6590 K. |
| In the text | |
 |
Fig. 8 Departure coefficients log bi for the five lowest levels of H i as a function of continuum optical depth τ5000 referring to λ = 5000 Å in the model atmosphere 6530/3.96/−0.05. Tick marks indicate the locations of core-to-wing transition (0.85 to 0.95 in normalized flux) formation depths for Hα and Hβ. |
| In the text | |
 |
Fig. 9 Synthetic NLTE (continuous curve) and LTE (dashed curve) flux profile of Hα computed with the MAFAGS-OS 6530/3.96/−0.05 (αCMA = 2.3) model compared to the observed spectrum of Procyon (bold dots). |
| In the text | |
 |
Fig. 10 Example of fitting the Hα wings in the metal-poor star HD 103095. Bold dots correspond to the observed data. The theoretical Hα profile was calculated with (dashed curve) and without (solid curve) blending lines. Only bold dots were used for determining the χ2 statistic. |
| In the text | |
 |
Fig. 11 Comparison of the line profiles of Hα, Hβ, and Hγ (from bottom to top) for HD 122563, HD 103095, and the Sun. The x-axis is the wavelength shift relative to the center of the Balmer lines. The colors are coded with different αCMA (from 0.5 to 1.5), while the solid lines and dashed lines represent profiles using LTE and NLTE line formations, respectively. The dotted lines are profiles with LTE models of αCMA = 0.5 but Teff + 100 K. For clarity, offsets of 0.2 and 0.4 are added to the Hβ and Hγ, respectively. |
| In the text | |
 |
Fig. 12 Survey of the reduced χ2 obtained from Hα profile fitting for the observed solar flux spectra (top panel) and spectra of Procyon (bottom panel) with different αCMA and Teff. The preferred parameter area is located where χ2 is minimal. All χ2 are not normalized and indicate a good fit in each case. |
| In the text | |
 |
Fig. 13 Left wings of Hα line profiles for the Sun with αCMA = 2.0 (top panel) and Procyon (bottom panel), where two theoretical spectra with αCMA = 1.5 (solid line) and αCMA = 2.3 (dash line) are shown. |
| In the text | |
 |
Fig. 14 Best fits of the Hα lines in our stellar sample. Solid lines are the theoretical spectra corresponding to the best fit and dotted lines represent the observed spectra that were used for determining the χ2 statistic. The horizontal dotted lines show the limit of reasonableness of the approximation and allows seeing residuals. |
| In the text | |
 |
Fig. 15 Determined αCMA for the program stars. An error of αCMA of ≈ ± 0.4...0.7 maybe assumed for all stars except HD 140283, Teff = 5780 K, log g = 3.70 where the error reaches ≈ ± 1.1. |
| In the text | |
 |
Fig. 16 Difference between our determined αCMA and the one predicted by Magic et al. (2015). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


