| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201425333 | |
| Published online | 06 May 2015 | |
The Gaia-ESO Survey: Tracing interstellar extinction⋆,⋆⋆
1 Université de Nice Sophia-Antipolis, CNRS, Observatoire de Côte d’Azur, Laboratoire Lagrange, 06304 Nice Cedex 4, France
e-mail: mathias.schultheis@oca.eu
2 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
3 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
4 Instituto de Astrofísica de Andalucía-CSIC, Apdo. 3004, 18080 Granada, Spain
5 Lund Observatory, Department of Astronomy and Theoretical Physics, Box 43, 221 00 Lund, Sweden
6 INAF−Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
7 Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
8 INAF−Padova Observatory, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
9 Centro de Astrobiología (INTA-CSIC), Departamento de Astrofísica, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
10 Suffolk University, Madrid Campus, C/Valle de la via 3, 28003 Madrid, Spain
11 INAF−Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
12 Dipartimento di Fisica e Astronomia, Sezione Astrofisica, Universitá di Catania, via S. Sofia 78, 95123 Catania, Italy
13 GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
Received: 13 November 2014
Accepted: 16 February 2015
Context. Large spectroscopic surveys have in recent years enabled computing three-dimensional interstellar extinction maps thanks to the accurate stellar atmospheric parameters and line-of-sight distances these surveys provide. Interstellar extinction maps are complementary to 3D maps extracted from photometry and allow a more thorough studying of the dust properties.
Aims. Our goal is to use the high-resolution spectroscopic survey Gaia-ESO to obtain with a good distance resolution the interstellar extinction and its dependency as a function of the environment and the Galactocentric position.
Methods. We used the stellar atmospheric parameters of more than 5000 stars, obtained from the Gaia-ESO survey second internal data release, and combined them with optical (SDSS) and near-infrared (VISTA) photometry as well as different sets of theoretical stellar isochrones to calculate line-of-sight extinction and distances. The extinction coefficients were then compared with the literature to discuss their dependency on the stellar parameters and position in the Galaxy.
Results. Within the errors of our method, our work does not show any dependence of the interstellar extinction coefficient on the stellar atmospheric parameters. We find no evidence of a variation of E(J − H) /E(J − K) with the angle from the Galactic centre or with Galactocentric distance. This suggests that we are dealing with a uniform extinction law in the SDSS ugriz bands and the near-IR JHKs bands. Therefore, extinction maps built from mean colour-excesses that assume a constant extinction coefficient can be used without introducing any systematic errors.
Key words: Galaxy: structure / dust, extinction / Galaxy: stellar content
Based on observations collected with the FLAMES spectrograph at the VLT/UT2 telescope (Paranal Observatory, ESO, Chile), for the Gaia-ESO Large Public Survey, programme 188.B-300.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Understanding the dust spatial distribution in the Milky Way is a crucial part of Galactic archeology. It can reveal important features of Galaxy evolution, such as the location and intensity of past star formation episodes (Boulanger 2007). In the literature, the most commonly used full-sky dust map is that of Schlegel et al. (1998) obtained with COBE/DIRBE data, later improved by Schlafly et al. (2010) and Schlafly & Finkbeiner (2011) by adding correction terms mainly due to the adopted reddening law. Other 2D extinction maps result from specific stellar populations. For example, red clump stars are considered to be an ideal tracer for extinction as their mean intrinsic colour varies only slightly with metallicity, which makes them reliable tracers of dust extinction (see for example Gonzalez et al. 2011, 2012; Nataf et al. 2013). However, such studies require a sufficient number of red clump stars to achieve a good spatial coverage, and hence they are limited to regions with high stellar density (close to the plane or towards the Bulge). On the other hand, Nidever et al. (2012) mapped the extinction with the so-called Rayleigh Jeans colour excess method (RJCE), which is based on a combination of near- and mid-infrared photometry (e.g. H and [4.5]). RJCE determines 2D star-by-star reddening at high resolution (2 × 2′), allowing penetrating the heavily obscured Galactic mid-plane.
The recent growth of large surveys together with the increasing volume of data has advanced extinction mapping and allowed tracing its distribution in three dimensions. The first of these 3D extinction models was constructed by Drimmel et al. (2003) by fitting the far- and near-IR data from the COBE/DIRBE instrument. Marshall et al. (2006) used the 2MASS colours together with the stellar population synthesis model of Besançon (Robin et al. 2003) to trace extinction in 3D for the Galactic Bulge region (| l | < 90, | b | < 10) with a spatial resolution of 15′.
A number of photometric techniques have been used to study the dust in 3D (Green et al. 2014; Schlafly et al. 2014, Bailer-Jones 2011; Hanson & Bailer-Jones 2014; Sale 2012; Sale et al. 2014; Lallement et al. 2014). Chen et al. (2014) traced the stellar locus similarly to the method of Berry et al. (2012) by combining optical, 2MASS, and WISE photometry and by defining the reference stellar locus as well as fixing the extinction law. Their map covers about 6000 square degrees with a small overlap on some of our GES fields (see Sect. 5).
Until now, most of the interstellar extinction studies were mainly conducted by using photometric techniques. The already available or upcoming large spectroscopic surveys (RAVE, APOGEE, Gaia-ESO, GALAH, 4MOST, etc.) provide an important quantity of accurate stellar parameters of different stellar populations. It is therefore possible to probe the 3D distribution of interstellar dust using the expected colours of the targets and comparing them with the observed ones. The Gaia space mission of ESA will provide 2D maps for most of the Galaxy in the coming years, but will also publish individual extinction estimates together with measured parallaxes (see Bailer-Jones et al. 2013, for more details). In this paper we use stellar properties derived from the Gaia-ESO survey (GES, Gilmore et al. 2012) to probe the interstellar extinction in three dimensions, as done by Schultheis et al. (2014b) using APOGEE data. They compared 3D extinction models in the Galactic Bulge region with Marshall et al. (2006) and Schultheis et al. (2014a) and found a steep rise in extinction in the first few kpc and a flattening of the extinction at about 4 kpc from the Sun. While Schultheis et al. (2014b) and Wang & Jiang (2014) probed the interstellar dust properties with APOGEE in the Galactic plane (), the GES fields are located at much higher Galactic latitudes (| b | > 20°). The GES data are thus complementary to APOGEE, allowing tracing the dust extinction at higher Galactic height | z | and compare them with available 3D dust models. In Sect. 2, we describe the sample of stars that has been used, in Sect. 3 we present the method employed in determining the extinction and the distances. In Sects. 4 and 5, we compare and discuss the extinctions to existing 2D and 3D maps, and we conclude in Sect. 6 with discussing the universality of the extinction law.
2. Sample
The GES is a public spectroscopic survey targeting ~105 stars. It covers all the major components of the Milky Way, from the halo to star-forming regions, with the purpose of characterising the chemistry and kinematics of these populations. It uses the FLAMES multi-object spectrograph on the VLT UT2 telescope to obtain high-quality uniformly calibrated spectra. The GES processing flow extends from target selection through data reduction, spectrum analysis, astrophysical parameter determination, calibration, and homogenisation. A detailed description of the data processing cascade and general characterisation of the data set can be found in Gilmore et al. (in prep.), In this paper, we analyse the second data release (DR2) GES results for ~10 000 Milky Way stars observed with the high-resolution gratings HR10 centred at 5488 Å (R ~ 19 800) and HR21 centred at 8757 Å (R ~ 16 200) of the GIRAFFE spectrograph. All the targets were selected from VISTA photometry, with colour cuts in the range 0.2 < (J − K) < 0.8 and magnitude cuts between 12.5 <J< 17.5 (cf. Gilmore et al. 2012). Additional SDSS photometry is also available, which we use in this work. Considerable effort has been invested in determining the stellar parameters. The stellar parameters have been derived with three different methods, MATISSE (Recio-Blanco et al. 2006), SME (Valenti & Piskunov 1996), and FERRE (Allende Prieto et al. 2006). This ensures a reliable determination of the derived stellar parameters, a crucial step in deriving accurate stellar abundances and line-of-sight distances. The homogenisation of the results from the three nodes, which was verified during the GES parameter validation process, leads to the so-called recommended stellar parameters. For our analysis we used these parameters, that is, the effective temperature (Teff), surface gravities (log g), global metallicities ([M/H]), and α-elements ([α/ Fe]). The relative error distributions peak at 70 K for Teff, 0.10 dex for log g, 0.08 dex for [M/H] , and 0.03 dex for [α/ Fe]. More details about the related GES parameterisation pipeline can be found in Recio-Blanco et al. (2014).
 |
Fig. 1 Field centres of the GES-DR2 fields in Galactic coordinates. |
To achieve the scope of this paper, we selected targets with available photometry from the VISTA Variables in the Via Lactea (VVV) survey (Minniti et al. 2010) or 2MASS, together with reliable atmospheric parameters obtained from spectroscopy. This implied selecting only the targets with spectra whose signal-to-noise S/N> 10, errors in radial velocity σ(RV) < 1.5 km s-1, and which have a low internal dispersion on Teff and log g between the three different nodes (see Sect. 3). The first two criteria ensure that the random errors of the algorithms are minimised, and the (σTeff,σlog g) criterium ensures a minimisation of the internal errors of the GES homogenisation pipeline. Our sample consists thus of 5603 stars with only near-IR photometry, while 1106 stars have ugrizJHK photometry.
Figure 1 shows the field centres of the GES-DR2 fields in Galactic coordinates.
3. Distance and extinction determination
The routine we used to determine the absolute magnitudes of the stars in different photometric bands (and from that the extinctions and the distances) is based on the routine described in Kordopatis et al. (2011b), which was previously successfully applied in Gazzano et al. (2013), Kordopatis et al. (2013), Recio-Blanco et al. (2014). Briefly, the method projects the measured atmospheric parameters (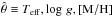 ), and colours on a given set of theoretical isochrones. The set of isochrones used is defined for a given age a and a range of iron abundances [Fe/H] within the [M/H] error bars. We here assumed that the [Fe/H] values of the isochrones are similar enough to [M/H] so that we could use the approximation [Fe/H] = [M/H] while performing the projection on the isochrones. According to Recio-Blanco et al. (in prep.), this is true for most of the stars in the GES iDR2.
), and colours on a given set of theoretical isochrones. The set of isochrones used is defined for a given age a and a range of iron abundances [Fe/H] within the [M/H] error bars. We here assumed that the [Fe/H] values of the isochrones are similar enough to [M/H] so that we could use the approximation [Fe/H] = [M/H] while performing the projection on the isochrones. According to Recio-Blanco et al. (in prep.), this is true for most of the stars in the GES iDR2.
The probability density function for a given star, W(a,m, [Fe/H]), is defined as 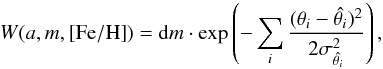 (1)where θi is the theoretical Teff, log g or [Fe/H],
(1)where θi is the theoretical Teff, log g or [Fe/H], 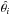 and
and 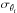 are the measured parameters and their respective errors, and dm is the mass step between two points of the same isochrone, introduced to impose a uniform prior on the stellar mass. We note that Zwitter et al. (2010) have shown that having such a flat prior on mass does not significantly affect the final derived distances when compared to the use of a combination of a more realistic mass function (e.g. Chabrier 2003) with a luminosity prior on the surveyed stars (see, Zwitter et al. 2010, their Sect. 2.2, for more details).
are the measured parameters and their respective errors, and dm is the mass step between two points of the same isochrone, introduced to impose a uniform prior on the stellar mass. We note that Zwitter et al. (2010) have shown that having such a flat prior on mass does not significantly affect the final derived distances when compared to the use of a combination of a more realistic mass function (e.g. Chabrier 2003) with a luminosity prior on the surveyed stars (see, Zwitter et al. 2010, their Sect. 2.2, for more details).
The expected value of the absolute magnitude Mτ in a given photometric band τ of a given star is then obtained by computing the weighted mean: 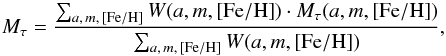 (2)where ∑ a,m, [Fe/H] is the triple sum over the ages, masses, and iron abundances. The associated variance of the expected absolute magnitude Mτ is obtained by
(2)where ∑ a,m, [Fe/H] is the triple sum over the ages, masses, and iron abundances. The associated variance of the expected absolute magnitude Mτ is obtained by ![\begin{equation} \sigma^2(M_\tau)\!=\!\frac{\sum_{a, \,m,\, \feh} W(a,\,m, {\feh}) \!\cdot \! [M_\tau \!-\!M_\tau(a,m,\feh)] ^2}{\sum_{a,m,\feh} W(a,m,\feh) }\cdot \end{equation}](/articles/aa/full_html/2015/05/aa25333-14/aa25333-14-eq44.png) (3)We used two sets of isochrones: those from Yonsei-Yale (Demarque et al. 2004) with the Lejeune et al. (1998) colour tables, and the Padova isochrones (Marigo 1998; Bressan et al. 2012). The Yonsei-Yale (YY) isochrones have been computed using the provided interpolation code of YY, from which we generated a set of isochrones with a constant step in age of , starting from to , which resulted in a flat prior on the age of the stars. The metallicities lie within a range of −3 < [Fe/H] < 0.8 dex, constantly spaced by 0.1 dex. The α-enhancements of the isochrones were selected in the following way:
(3)We used two sets of isochrones: those from Yonsei-Yale (Demarque et al. 2004) with the Lejeune et al. (1998) colour tables, and the Padova isochrones (Marigo 1998; Bressan et al. 2012). The Yonsei-Yale (YY) isochrones have been computed using the provided interpolation code of YY, from which we generated a set of isochrones with a constant step in age of , starting from to , which resulted in a flat prior on the age of the stars. The metallicities lie within a range of −3 < [Fe/H] < 0.8 dex, constantly spaced by 0.1 dex. The α-enhancements of the isochrones were selected in the following way:
-
[Fe/H] ≥ 0 dex, then [α/ Fe] = 0.0 dex;
-
−0.3 ≤ [Fe/H] ≤ −0.1 dex, then [α/ Fe] = +0.1 dex;
-
−0.6 ≤ [Fe/H] ≤ −0.4 dex, then [α/ Fe] = +0.2 dex;
-
−0.9 ≤ [Fe/H] ≤ −0.7 dex, then [α/ Fe] = +0.3 dex;
-
[Fe/H] ≤ −1 dex, then [α/ Fe] = +0.4 dex.
According to Carpenter et al. (2001), the (JK)ESO provided by the Yonsei-Yale isochrones match the (JKs)2MASS and (JKs)VHS very well, therefore no colour transformation is needed when manipulating the magnitudes from the different photometric systems.
Median errors in distance when adding an offset to the derived atmospheric parameters for giants (log g< 3) and dwarfs and subgiants (log g> 3).
The Padova isochrones were downloaded using the online interpolation interface1, which allows us to select the output photometric system (2MASS, SDSS, VISTA). The considered metallicity range is smaller than the one of YY (from −2.2 dex to + 0.2 dex in steps of 0.1 dex with solar-scale α-abundances), computed with steps in age of .
After the absolute magnitudes were computed, the colours were derived and the colour excess was deduced by subtracting the theoretical colour from the observed one in the five SDSS and three VISTA filters. The colour excess derived using this method is hereafter referred to as Eλ1 − λ2 with λ = u,g,r,i,z,J,H,Ks. About 5% of our stars show negative extinction, most of which are fainter than Ks> 14.5. We omitted them from our analysis. The distances were calculated using the usual relation 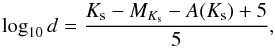 (4)with d expressed in pc, and adopting A(Ks) = 0.528 × E(J − Ks) (Nishiyama et al. 2009), similar to what has been done in Schultheis et al. (2014b). The errors in the derived distances include errors in Teff, log g and [M/H] and errors on the apparent magnitude J and Ks as well as the extinction AKs. For more details, we refer to Kordopatis et al. (2011a). Other than the internal errors in the stellar parameters, the absolute calibration in Teff, log g and [Fe/H] is also crucial for the errors in our derived distances.
(4)with d expressed in pc, and adopting A(Ks) = 0.528 × E(J − Ks) (Nishiyama et al. 2009), similar to what has been done in Schultheis et al. (2014b). The errors in the derived distances include errors in Teff, log g and [M/H] and errors on the apparent magnitude J and Ks as well as the extinction AKs. For more details, we refer to Kordopatis et al. (2011a). Other than the internal errors in the stellar parameters, the absolute calibration in Teff, log g and [Fe/H] is also crucial for the errors in our derived distances.
Table 1 shows the errors in the derived distances (in %) for an offset in Teff ± 100 K, log g ± 0.2 dex and [M/H] ± 0.1 dex. The strong impact of log g for giants with up to ~34% error in the derived distances is clearly visible, while temperature and metallicity offsets play only a minor role. For dwarf stars and subgiants, the effect of the surface gravity is the lowest (<10%) because the main sequences roughly overlap at all ages. On the other hand, offsets in Teff have a stronger effect for dwarf stars because of the overall steeper slope of the main sequences in the J vs. (J − K) plane. We note, however, that the effect of Teff offsets rarely exceeds 10%.
Figure 2 shows the difference between the GES Teff and log g and the projected value on the Padova isochrones as a function of σTeff and σlog g (the internal GES parameter dispersions resulting from the three individual nodes, see Sect. 2). It shows that when the internal GES parameter dispersions are large, then the absolute differences between the projected Teff and log g and the recommended GES ones also increase. In general, this indicates that for these few stars, the recommended parameters do not lie on top of theoretical isochrones and that offsets are performed during the projection. Given the trends illustrated in Fig. 3, we used for our analysis only the targets with σTeff< 300 K and σlog g< 0.3 dex, resulting to a total of 5603 stars.
 |
Fig. 2 Left: density plot of the difference between Teff and the corresponding temperature from the isochrones and the dispersion of Teff between the three nodes (see text). The black points indicate the mean (in 100 K steps) and the error bars the standard deviations. Right: same, but for log g. The black points indicate the mean (in 0.2 dex steps) and the error-bars the standard deviations. |
3.1. Effect of the stellar isochrone libraries
The choice of the stellar atmosphere models used to produce the isochrones affects the derived extinctions and distances. Below we compare the extinction and distance values derived from the same pipeline (see Sect. 3 and Kordopatis et al. 2011b) using alternatively the Padova and Yonsei-Yale models. We recall that Schultheis et al. (2014b) have shown that there are only small differences in the derived extinction and distances between the Padova isochrones and the corresponding Basel3.1 model library (Lejeune et al. 1997) for K/M giants observed by APOGEE. Here we wish to demonstrate the importance of the chosen model library for our GES sample, which covers a much larger Teff and log g range than APOGEE.
Figure 3 compares the Padova and Yonsei-Yale libraries for different combinations of ages and metallicities. The differences between the two libraries increase with decreasing metallicity. These differences concern the positions of the turn-off and the giant branch, in the sense that YY has an offset towards cooler temperatures, that is, towards redder colours. However, the known age-colour (or age-metallicity) degeneracy (e.g. Bergemann et al. 2014; Worthey 1994) causes the YY and the Padova models to partly overlap at a given metallicity when selecting younger YY isochrones. Since our procedure projects the observed Teff, log g, and [M/H] on all the ages of a set of isochrones (see above), the differences in the derived magnitudes are smaller for most types of stars than what is suggested by a simple one-to-one comparison between the isochrones. However, for the stars at the boundaries of the libraries (e.g. the hotter stars and the more metal-poor giants), the differences are expected to be the largest as a result of the described offset. Finally, we also investigated the effect on the shape of the isochrones (and therefore on the derived absolute magnitudes) of atmospheric models with different α-enhancements. The dashed and plain lines in Fig. 3, obtained for the YY isochrones, indicate only a very weak effect in the Teff vs. log g and J vs. (J − Ks) diagram. We conclude, in agreement with other studies (e.g. Breddels et al. 2010; Zwitter et al. 2010), that the adopted α-enhancement level of the isochrones does not significantly affect the final distance estimates.
Figure 4 shows the comparison of the derived extinctions (left panel) and distances (right panel). It is obvious from this comparison that the YY E(B − V) values are systematically lower than the Padova values. In agreement with what has been stated in the previous paragraph, this means that the intrinsic colours from the YY models are redder than the Padova colours. The effect in E(B − V) can reach up to 0.2 mag, showing that the choice of a certain stellar library is essential to determine the extinction. If one transforms this into distances (see right panel of Fig. 4), the distances from the YY isochrones are systematically larger, especially for . We traced these differences as a function of the stellar parameters, Teff, log g, and [M/H] , and could identify that they mainly arise for dwarf stars (log g > 4) with 5500 < Teff < 6500 K. This is consistent with Fig. 3, where the Padova isochrones predict bluer J − K colours. On the other hand, YY underestimate distances for cool giant stars with log g < 3 and 4000 < Teff < 5000 K. Finally, the difference between Padova and YY increases for the most metal-poor stars ([M/H] < − 1 dex). All these discrepancies indicate important differences in the stellar atmosphere models between Padova and YY. For most of our objects, the differences between the two stellar libraries are within 20% (right panel of Fig. 4). In the following Sect. 4, we compare the derived E(B − V) values with the dust map of Schlegel et al. (1998).
 |
Fig. 3 Left: isochrones in the Teff vs. log g space for different combinations of [M/H] and ages. The red line shows the Padova isochrones. The dashed black line indicates the Yonsei-Yale isochrones without α-elements, while the plain black line plots YY models with alpha enhancement. Right: similar as in the left panel, but in the J − K vs. K colour−magnitude diagram. |
4. Comparison with the 2D extinction maps: the Schlegel map
In contrast to the study of Schultheis et al. (2014b) with APOGEE, where the fields were concentrated in regions of high extinction towards the Galactic Bulge, we analysed here lower extinction fields at higher latitudes with GES. We used the dust map of Schlegel et al. (1998), hereafter referred to as SFD98, as it has the same sky coverage as our GES stars. We used the conversion E(J − KS) /E(B − V) = 0.527 (Rieke & Lebofsky 1985).
As already mentioned, stellar libraries can give systematically offset extinctions. Figure 5 shows the difference in E(B − V) between the values of SFD98 and those derived with the Padova isochrones (in black), and the YY isochrones (in red). The Padova isochrones clearly better match the E(B − V)SFD98 with a mean difference of 0.009 ± 0.075, which is the typical uncertainty of our method (derived from Eq. (3)). If we include low Galactic latitude fields with | b | < 10°, the dispersion increases to 0.18 mag, where it is suspected that SFD98 overestimates extinction (Schlafly et al. 2014). Schlafly & Finkbeiner (2011) measured the dust reddening using the colours of stars derived from stellar parameters from the SDSS. Their uncertainty is in the order of 30 mmag for high-latitude fields and E(B − V) < 0.04. Our larger dispersion is due to the lower Galactic latitude fields of the GES fields (see Fig. 7). The YY isochrones systematically overestimate E(B − V)SFD98 by 0.065 mag. For the remaining of our analysis, we decided to use the Padova isochrones because they match the values of SFD98 better.
Figure 6 shows the comparison between E(B − V)Padova and E(B − V)SFD98. While there is no shift in the derived E(B − V), a large scatter is seen, especially for E(B − V)SFD98> 0.5 where the values of SFD98 are higher than E(B − V)Padova. Our results agree with those of Schlafly et al. (2014), who compared their map based on PAN-STARRS photometry with the map of Schlegel. They found systematically higher E(B − V) of SFD98 for E(B − V)SFD98 > 0.3. The Planck dust map at 353 GHz shows a similar behaviour (see Schlafly et al. 2014), indicating that for higher E(B − V) the far-infrared modelling of the dust shows some systematical offsets. A revision of these models is therefore needed.
We now assess the existence of biases as a function of Teff, log g and [M/H] between our derived extinction and the map of SFD98. Figure 8 displays a mild trend of the differences in E(B − V) towards higher temperatures (Teff > 6000 K) in the sense that SFD98 derived higher E(B − V) than E(B − V)Padova. For cooler temperatures (Teff < 4500 K) SFD98 predicts higher E(B − V) than E(B − V)Padova. While for the range 1.5 < log g < 4.5 no trend is visible, giants with log g < 1.5 have a slightly overestimated extinction compared to E(B − V)SFD98. Interestingly, our E(J − K) estimate for dwarf stars with log g > 4.5 and 4000 < Teff < 6000 K is slightly offset towards higher values than E(J − K)SFD98.
 |
Fig. 4 Left: density distribution of the difference in E(B − V) derived from the Padova and the Yonsei-Yale (YY) isochrones as a function of E(B − V) from the YY isochrones. Right: ratio of distances derived from the Padova isochrones to the YY stellar library as a function of distance. The dashed horizontal lines indicate ± 20% difference. |
 |
Fig. 5 Histogram of the differences between our derived E(B − V) and the value of Schlegel SFD98 for high Galactic latitude stars (|b| > 10°). The black lines plot the derived extinction values using the Padova isochrones, the red lines those from the Yale isochrones. The mean value and the rms scatter is indicated in the top left corner. |
 |
Fig. 6 Density plot of E(B − V) against E(B − V) from SFD98. |
 |
Fig. 7 Difference of E(B − V) to E(B − V) from SDF98 vs. Galactic latitude. |
 |
Fig. 8 Difference in E(B − V) to SFD98 as a function of a) Teff; b) log g; and c) [Fe/H] for high Galactic latitude stars (|b| > 10°). The median value is indicated by black dots together with the standard deviation. |
The derived extinction depends on the corresponding matched colour of the isochrone as well as of the stellar parameters, the surface gravity being a particularly sensitive parameter. Indeed, systematic offsets of 0.2 dex can significantly shift the extinctions and distances (see Sect. 3). This mainly affects giant stars, while GES has mostly dwarf stars (see Fig. 2 of Recio-Blanco et al. 2014).
5. Comparison with three-dimensional maps
In this section, we compare our 3D extinction distributions with the model of Drimmel et al. (2003) and the map of Chen et al. (2014). The model of Drimmel et al. (2003) is based on the far- and near-IR data fits of the dust distribution made by Drimmel & Spergel (2001) from the COBE/DIRBE instrument. The spatial resolution of this map is approximately 21′× 21′; we recall, however, that the model of Drimmel et al. does not include features related to the Galactic bar or the nuclear disk, resulting in systematic overestimates of the extinction towards the Galactic Bulge (see Schultheis et al. 2014b, for further details).
We found only a limited spatial overlap with the 3D map of Chen et al. (2014) 3D with six GES fields. Chen et al. (2014) combined optical photometry (g, r, i) with 2MASS (J, H, K) and WISE (W1, W2) photometry and used the method of Berry et al. (2012) to trace the stellar locus in a multi-dimensional colour space. The constructed 3D map covers roughly 6000 square degrees towards the Galactic anti-centre region, with an angular resolution varying between 3−9′.
 |
Fig. 9 Extinction in the (X,Y) plane for different heights above the Galactic plane. In the left upper plot we superimpose an illustration of our Galaxy produced by R. Hurt. |
 |
Fig. 10 Extinction vs. distance for different lines of sight. The x- and y-axis approximately show the location in Galactic coordinates. The model of Drimmel et al. (2003) is superimposed in red. |
 |
Fig. 11 Extinction vs. distance for different lines of sight. In red the 3D extinction model of Drimmel et al. (2003) is superimposed, in green the 3D model of Chen et al. (2013). |
Figure 9 displays for different heights above the Galactic plane, the AK extinctions measured from the GES targets. The illustration is made in a Cartesian Galactocentric (X,Y) frame, with the Sun located at from the centre. Superimposed in the panel representing the closest distance from the plane is the illustration of our Galaxy produced by Robert Hurt based on the results of the Spitzer Infrared Space telescope (R. Benjamin). Compared with the APOGEE targets, most of which are located at distances larger than about 6 kpc, the GES targets probe a volume much closer to the Sun with typical distances d ~ 2 − 3 kpc. Figure 9 shows that GES also contains a line of sight in the direction of the Galactic bar (l = 28°, b = −3°), which shows a higher concentration of dust. According to Schultheis et al. (2014b), this is associated with a dust lane in front of the bar. Clearly visible is also the increased dust amount associated with the Perseus spiral arm, the Sagittarius arm, and the Scutum-Centaurus arm. Most of the low extinction is situated in the first few kpc around the position of the Sun.
Figures 10 and 11 show the 3D extinction for a few selected lines of sight and compare our results with those of Drimmel et al. and Chen et al. We present in Fig. A.1 additional lines of sight of 3D extinction for different GES fields. Below we describe a few trends:
-
In contrast to the APOGEE data, GES samples the first few kpc athigher spatial resolution in distance. In general,AV rises steeply (see Fig. 10).
-
The model of Drimmel et al. systematically underestimates AV for high Galactic latitudes (l > |50|). The map of Chen et al. predicts a steeper increase in AV for the first kpc than Drimmel et al., which seems to agree better with the GES data (see Fig. 11).
-
For most of the lines of sight, we see a steep rise in AV followed by a flattening afterwards, which is qualitatively described by the model of Drimmel. As a result of the low absolute extinction values, the errors in the derived extinction and distances become significant for distances larger than 4 kpc.
-
Puspitarini et al. (2015) studied the DIBS of 225 GES stars in five fields and found a good correlation between the DIB strength and the extinction. We have one field in common, which is the COROT-ANTICENTER field (see upper left panel of Fig. 11, located at (l,b) = (+212.87, −2.04)°. They found a steep increase in extinction of up to 1 kpc, a plateau between 1 to 2.5 kpc, and a second increase beyond 2.5 kpc (see their Fig. 6). We confirm the steep increase in AV between 0 and 1.5 kpc with a flattening starting at around 2 kpc. There are too few data points to see their second increase in AV.
-
The GES fields located at (l,b) = (+38.30, −6.51)°, (l,b) = (+14.60, + 21.85)°, and the field at (l,b) = (+147.13, −2.04)° span the full distance range and follow the AV vs. distance relation predicted by Drimmel et al.
-
The GES data seem to confirm the general shape of the 3D extinction with a steep rise in AV for distances up to 4 kpc and a flattening that occurs at shorter distances than indicated by the values found with the APOGEE sample of Schultheis et al. (2014b).
With the future data releases of GES in the coming years, we will be able to systematically trace the behaviour of distance vs. AV, allowing us to qualitatively compare spectroscopically derived extinction with 3D dust models. The combination of both GES and APOGEE data tracing the low-extinction fields in the visible as well as the highly obscured fields in the infrared clearly is a goal for the future for tracing 3D extinction.
6. Interstellar extinction law
Using the extinctions derived by the GES sample, we now investigate the universality of the extinction law as a function of the position on the sky and the stellar environment. Using APOGEE red clump stars, Wang & Jiang (2014) recently found a constant power law with alpha =1.95, yielding AJ/AKs = 2.88. They used stars with 3500 < Teff < 4800 K, log g < 3 and [Fe/H] > −1.0 dex. On the other hand, Yuan et al. (2013) combined SDSS, GALEX, 2MASS, and WIDE photometry to determine reddening coefficients from the far-UV to the near- and mid-IR by using the SDSS spectroscopic archive. They concluded that their newly derived extinction coefficients differ slightly, but favour the R(V) = 3.1 Fitzpatrick reddening law (Fitzpatrick 1999) over the reddening laws of Cardelli et al. (Cardelli et al. 1989) and O’Donnell et al. (O’Donnell 1994).
Derived slopes of the colour excesses.
Here we perform a similar study and aim to extend the analysis to investigating the systematic dependencies of the extinction law as a function of the stellar parameters (Teff,log g, [Fe/H]). In addition to the near-IR photometry, we used SDSS photometry in the filters u,g,r,i,z, which enabled us to simultaneously trace the extinction law in the optical and IR. For every band, the colour excess is simply the difference between the intrinsic colour derived from the isochrone-matching method and the observed colour. Figure 12 shows the linear fit results of the different colour excess similar as done by Yuan et al. (2013) and Wang & Jiang (2014). We forced the intercept to be zero, as done as in Wang & Jiang (2014). Figure 12 displays our best-fitting results, and Table 2 lists the fitting parameters as well as the comparison with Yuan et al. (2013) and Fitzpatrick (1999) and Cardelli et al. (1989).
 |
Fig. 12 Relation between different colour excesses. The red line denotes the best linear fitting. |
The extinction coefficients we derive agree within 10% with Yuan et al. (2013) except for u − g, where we find a value closer to the Fitzpatrick extinction law. The u − g dispersion we measure is higher than for other colours with some outliers not following the linear relation between E(u − g) and E(g − r) (see Fig. 12). The observed rms scatter is ~0.1 mag in the u band, which agrees with the estimated uncertainties.
 |
Fig. 13 Extinction coefficients as a function of Teff,log g, and [M/H]. |
Up to now, most of the studies have mainly concentrated on deriving interstellar extinction coefficients using a specific population or a mixture of stars with different stellar parameters. However, as first suggested by Wildey (1963), other factors such as the stellar abundance may affect the interstellar extinction. In particular, Grebel & Roberts (1995) showed that the colour dependence of interstellar extinction is a complicated function of the temperature, luminosity, and metallicity of the stellar probe. Even the ratio of total to selective extinction depends on these parameters, and RV can, according to their model, vary by more than 10% between a star with Teff = 3500 K and another with Teff = 10 000 K. Figure 13 shows the extinction coefficient (defined as the ratio of two colour excesses) as a function of Teff and log g. It is clear from Fig. 13 that our method does not have the required accuracy to detect variations at the level of 10% as predicted by the theoretical models of Grebel & Roberts (1995). However, within the accuracy of our procedure, large-scale variations of the different extinction coefficients as a function of Teff,log g, or [M/H] are not detected. We note, on the other hand, that the dispersion increases for higher log g.
As a result of the limited spatial overlap between SDSS and the GES, only a small number of our GES sources have SDSS ugriz photometry. For the targets for which we have SDSS photometry, the E(g − r) /E(r − i) ratio is overestimated for cool giant stars with Teff< 5000 K and log g< 3.5. Within the large dispersion of our method we do not note any hint of a dependence of the extinction coefficient on the Galactic environment, that is, the metallicity of the stars. However, we lack stars with [M/H] < − 1 dex, and small-scale variations cannot be excluded by our method. The nearly flat extinction coefficient in the near-IR (e.g. E(J − H) /E(J − K)) plane is striking, without variation as a function of the stellar parameters. Within the errors of our method, our work does not show any dependence of the interstellar extinction coefficient on the stellar atmospheric parameters. This suggests that extinction maps derived from mean colours of stars such as the RJCE method (Majewski et al. 2011) or the colour-excesses of stars (Lada et al. 1994; Gonzalez et al. 2012) can be generally used, assuming a constant extinction coefficient that does not depend on the stellar parameter. We fitted the E(J − H) vs. E(J − K) diagram in the same way as Wang & Jiang (2014). Our value E(J − H) = 0.651 ± 0.009 × E(J − Ks) is slightly higher than that of Wang & Jiang (2014), who measured E(J − H) = 0.641 ± 0.001 × E(J − Ks), resulting in a power-law index of α = 2.12 and AJ/AKs = 3.15 (assuming λeff = 1.25 μm,1.65 μm,2.15 μm for the J,H,KS bands). Our power-law index is similar to that of Stead & Hoare (2009) with α = 2.14 or Fritz et al. (2011) with α = 2.11.
Finally, we investigated the variation of the extinction coefficient along different lines of sight. Zasowski et al. (2009) and Gao et al. (2009) suggested strong variations in the extinction law in the mid-IR as a function of Galactic longitude or angle from the Galactic centre. Strong variation of the extinction law as a function of the Galactic latitude was also found by Chen et al. (2013) in the Galactic Bulge. Zasowski et al. (2009) suggested the existence of strong longitudinal variations in the infrared extinction law where the slopes increase as the wavelength increases (see their Fig. 5), resulting in a steeper extinction curve in the outer Galaxy. Gao et al. (2009) identified mild variations of the mid-IR extinction law with the location of the spiral arms. Figure 14 shows the extinction coefficient E(J − H) /E(J − K) as a function of the angle from the Galactic centre (see Fig. 14). Note that in contrast to APOGEE, GES probes different regions of the Galaxy and in particular avoids the Galactic plane, where interstellar extinction is very high.
Within the dispersion of our method, we do not find evidence for any trend of the variation of E(J − H) /E(J − K) with the angle from the Galactic centre or with Galactocentric distance, in agreement with the extinction coefficients in the SDSS bands. This suggests that the extinction law in the SDSS ugriz bands and the near-IR JHKs bands is uniform, confirming the result of Wang & Jiang (2014) obtained with APOGEE red clump stars.
 |
Fig. 14 Density plot of E(J − H) /E(J − K) vs. angle from the Galactic centre. The dashed black line plots the mean of our derived extinction coefficient. |
7. Conclusions
We used data from the GES survey, together with accurate stellar parameters (Teff,log g, [M/H]), to trace 3D interstellar extinction in intermediate and high-latitude regions of our Galaxy. We discussed the influence of different stellar isochrones (Yonsei-Yale & Padova) on the derived 3D extinction and compared our results with the SFD98 dust maps. We found on average good agreement with a mean difference of ΔE(B − V) = 0.009 ± 0.075, with increasing dispersion when low Galactic latitude regions were included (| b | < 10°). For larger E(B − V) > 0.5 SFD98 derived a higher extinction than our estimate of E(B − V)Padova.
We compared our 3D interstellar dust maps with those of Drimmel et al. (2003) and Chen et al. (2014). The GES data confirm the steep rise in AV for distances between 0 and 4 kpc with a flattening of the extinction at larger distances. We studied the influence of the stellar parameters on the extinction coefficients in the optical (SDSS-bands) and the near-IR (JHKs). We did not detect any significant dependence of the extinction coefficient on stellar parameters, indicating that a constant extinction coefficient can be assumed. Within the precision of our method, we did not find any evidence for the variation of the extinction coefficients with the angle from the Galactic centre or Galactocentric distance. We note, however, that our method does not allow tracing small-scale variations of the extinction coefficient. This suggests a uniform extinction law, as found in Wang & Jiang (2014). With the future data releases of GES in the coming years, we will be able to trace the behaviour of distance vs. AV, which will allow us to systematically compare qualitatively spectroscopically derived extinction with 3D dust models.
Online material
Appendix A: 3D extinction along different lines of sight of GES
 |
Fig. A.1 3D extinctions for GES lines of sight for GES field. The red straight line gives the corresponding model of Drimmel et al. (2003). |
 |
Fig. A.1 continued. |
Acknowledgments
We wish to thank the anonymous referee for the extremely useful comments. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme. We wish to thank C. Bailer-Jones and C. Babusiaux for extremely useful comments. M. Schultheis, A. Recio-Blanco, P. de Laverny, and V. Hill acknowledge the support of the “Programme National de Cosmologie et Galaxies” (PNCG) of CNRS/INSU, France. T.B. is funded by grant No. 621-2009- 3911 from the Swedish Research Council.
References
- Allen de Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L. 2011, MNRAS, 411, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Andrae, R., Arcay, B., et al. 2013, A&A, 559, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berry, M., Ivezić, Ž., Sesar, B., et al. 2012, ApJ, 757, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F. 2007, in IAU Symp. 237, eds. B. G. Elmegreen, & J. Palous, 47 [Google Scholar]
- Breddels, M. A., Smith, M. C., Helmi, A., et al. 2010, A&A, 511, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Hillenbrand, L. A., & Skrutskie, M. F. 2001, AJ, 121, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, B. Q., Schultheis, M., Jiang, B. W., et al. 2013, A&A, 550, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, B.-Q., Liu, X.-W., Yuan, H.-B., et al. 2014, MNRAS, 443, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, J., Jiang, B. W., & Li, A. 2009, ApJ, 707, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Gazzano, J.-C., Kordopatis, G., Deleuil, M., et al. 2013, A&A, 550, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grebel, E. K., & Roberts, W. J. 1995, A&AS, 109, 293 [NASA ADS] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D. P., et al. 2014, ApJ, 783, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, R. J., & Bailer-Jones, C. A. L. 2014, MNRAS, 438, 2938 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Recio-Blanco, A., de Laverny, P., et al. 2011a, A&A, 535, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kordopatis, G., Recio-Blanco, A., de Laverny, P., et al. 2011b, A&A, 535, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kordopatis, G., Hill, V., Irwin, M., et al. 2013, A&A, 555, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., Lada, E. A., Clemens, D. P., & Bally, J. 1994, ApJ, 429, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Zasowski, G., & Nidever, D. L. 2011, ApJ, 739, 25 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Marigo, P. 1998, A&A, 340, 463 [NASA ADS] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New A, 15, 433 [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Zasowski, G., & Majewski, S. R. 2012, ApJS, 201, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Kordopatis, G., et al. 2014, A&A, 567, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sale, S. E. 2012, MNRAS, 427, 2119 [NASA ADS] [CrossRef] [Google Scholar]
- Sale, S. E., Drew, J. E., Barentsen, G., et al. 2014, MNRAS, 443, 2907 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., Schlegel, D. J., et al. 2010, ApJ, 725, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Green, G., Finkbeiner, D. P., et al. 2014, ApJ, 789, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schultheis, M., Chen, B. Q., Jiang, B. W., et al. 2014a, A&A, 566, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schultheis, M., Zasowski, G., Allen de Prieto, C., et al. 2014b, AJ, 148, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, S., & Jiang, B. W. 2014, ApJ, 788, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Wildey, R. L. 1963, AJ, 68, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, H. B., Liu, X. W., & Xiang, M. S. 2013, MNRAS, 430, 2188 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Majewski, S. R., Indebetouw, R., et al. 2009, ApJ, 707, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Zwitter, T., Matijevič, G., Breddels, M. A., et al. 2010, A&A, 522, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Median errors in distance when adding an offset to the derived atmospheric parameters for giants (log g< 3) and dwarfs and subgiants (log g> 3).
All Figures
 |
Fig. 1 Field centres of the GES-DR2 fields in Galactic coordinates. |
| In the text | |
 |
Fig. 2 Left: density plot of the difference between Teff and the corresponding temperature from the isochrones and the dispersion of Teff between the three nodes (see text). The black points indicate the mean (in 100 K steps) and the error bars the standard deviations. Right: same, but for log g. The black points indicate the mean (in 0.2 dex steps) and the error-bars the standard deviations. |
| In the text | |
 |
Fig. 3 Left: isochrones in the Teff vs. log g space for different combinations of [M/H] and ages. The red line shows the Padova isochrones. The dashed black line indicates the Yonsei-Yale isochrones without α-elements, while the plain black line plots YY models with alpha enhancement. Right: similar as in the left panel, but in the J − K vs. K colour−magnitude diagram. |
| In the text | |
 |
Fig. 4 Left: density distribution of the difference in E(B − V) derived from the Padova and the Yonsei-Yale (YY) isochrones as a function of E(B − V) from the YY isochrones. Right: ratio of distances derived from the Padova isochrones to the YY stellar library as a function of distance. The dashed horizontal lines indicate ± 20% difference. |
| In the text | |
 |
Fig. 5 Histogram of the differences between our derived E(B − V) and the value of Schlegel SFD98 for high Galactic latitude stars (|b| > 10°). The black lines plot the derived extinction values using the Padova isochrones, the red lines those from the Yale isochrones. The mean value and the rms scatter is indicated in the top left corner. |
| In the text | |
 |
Fig. 6 Density plot of E(B − V) against E(B − V) from SFD98. |
| In the text | |
 |
Fig. 7 Difference of E(B − V) to E(B − V) from SDF98 vs. Galactic latitude. |
| In the text | |
 |
Fig. 8 Difference in E(B − V) to SFD98 as a function of a) Teff; b) log g; and c) [Fe/H] for high Galactic latitude stars (|b| > 10°). The median value is indicated by black dots together with the standard deviation. |
| In the text | |
 |
Fig. 9 Extinction in the (X,Y) plane for different heights above the Galactic plane. In the left upper plot we superimpose an illustration of our Galaxy produced by R. Hurt. |
| In the text | |
 |
Fig. 10 Extinction vs. distance for different lines of sight. The x- and y-axis approximately show the location in Galactic coordinates. The model of Drimmel et al. (2003) is superimposed in red. |
| In the text | |
 |
Fig. 11 Extinction vs. distance for different lines of sight. In red the 3D extinction model of Drimmel et al. (2003) is superimposed, in green the 3D model of Chen et al. (2013). |
| In the text | |
 |
Fig. 12 Relation between different colour excesses. The red line denotes the best linear fitting. |
| In the text | |
 |
Fig. 13 Extinction coefficients as a function of Teff,log g, and [M/H]. |
| In the text | |
 |
Fig. 14 Density plot of E(J − H) /E(J − K) vs. angle from the Galactic centre. The dashed black line plots the mean of our derived extinction coefficient. |
| In the text | |
 |
Fig. A.1 3D extinctions for GES lines of sight for GES field. The red straight line gives the corresponding model of Drimmel et al. (2003). |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


