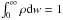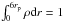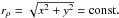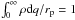| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 6 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201425576 | |
| Published online | 24 March 2015 | |
Chaotic enhancement of dark matter density in binary systems
1 Institut UTINAM, Observatoire des Sciences de l’Univers THETA, CNRS & Université de Franche-Comté, 25030 Besançon, France
e-mail: rollin@obs-besancon.fr, jose.lages@utinam.cnrs.fr
2 Laboratoire de Physique Théorique du CNRS, IRSAMC, Université de Toulouse, UPS, 31062 Toulouse, France
e-mail: dima@irsamc.ups-tlse.fr
Received: 23 December 2014
Accepted: 9 February 2015
We study the capture of galactic dark matter particles (DMP) in two-body and few-body systems with a symplectic map description. This approach allows modeling the scattering of 1016 DMPs after following the time evolution of the captured particle on about 109 orbital periods of the binary system. We obtain the DMP density distribution inside such systems and determine the enhancement factor of their density in a center vicinity compared to its galactic value as a function of the mass ratio of the bodies and the ratio of the body velocity to the velocity of the galactic DMP wind. We find that the enhancement factor can be on the order of tens of thousands.
Key words: chaos / celestial mechanics / binaries: general / dark matter
© ESO, 2015
1. Introduction
In 1890, Henri Poincaré proved that the dynamics of the three-body gravitational problem is generally non-integrable (Poincaré 1890). Even 125 yr later, many aspects of this problem remain unsolved. Thus the capture cross-section σ of a particle that scatters on the binary system of Sun and Jupiter has only recently been determined, and it has been shown that σ is much larger than the area of the Jupiter orbit (Khriplovich & Shepelyansky 2009; Lages & Shepelyansky 2013). The capture mechanism is described by a symplectic dynamical map that generates a chaotic dynamics of a particle. The scattering, capture, and dynamics of a particle in a binary system recently regained interest with the search for dark matter particles (DMP) in the solar system and the Universe (Bertone et al. 2005; Garrett & Dūda 2011; Merritt 2013). Thus it is important to analyze the capture and ejection mechanisms of a DMP by a binary system. Such a system can be viewed as a binary system with a massive star and a light body orbiting it. This can be the Sun and Jupiter, a star and a giant planet, or a super massive black hole (SMBH) and a light star or black hole (BH). In this work we analyze the scattering process of DMP galactic flow, with a constant space density, in a binary system. One of the main questions here is whether the density of captured DMPs in a binary system can be enhanced compared to the DMP density of the scattering flow.
The results obtained by Lages & Shepelyansky (2013) show that a volume density of captured DMPs at a distance of the Jupiter radius r<rp = rJ is enhanced by a factor ζ ≈ 4000 compared to the density of Galactic DMPs which are captured after one one orbital period around the Sun and which have an energy corresponding to velocities 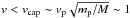 km s-1 ≪ u. Here, mp,M are the masses of the light and massive bodies, respectively, u ≈ 220 km s-1 is the average velocity of a Galactic DMP wind for which, following Bertone et al. (2005), we assume a Maxwell velocity distribution:
km s-1 ≪ u. Here, mp,M are the masses of the light and massive bodies, respectively, u ≈ 220 km s-1 is the average velocity of a Galactic DMP wind for which, following Bertone et al. (2005), we assume a Maxwell velocity distribution: 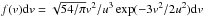 .
.
Our results presented below show that for an SMBH binary system with vcap>u there is a large enhancement factor ζg ~ 104 of the captured DMP volume density, taken at a distance of about a binary system size, compared to its galactic value for all scattering energies (and not only for the DMP volume density at low velocities v<vcap ≪ u, as discussed by Lages & Shepelyansky 2013). We note that the Galactic DMP density is estimated at ρg ~ 4 × 10-25 g cm-3, while the typical intergalactic DMP density is estimated to be ρg0 ~ 2.5 × 10-30 g cm-3 (Garrett & Dūda 2011; Merritt 2013). At first glance, this high enhancement factor ζg ~ 104 seems to be rather unexpected because it apparently contradicts Liouville’s theorem, according to which the phase space density is conserved during a Hamiltonian evolution. Because of this, it is often assumed (Gould & Alam 2001; Lundberg & Edsjö 2004) that the volume (or space) DMP density cannot be enhanced for DMPs captured by a binary system, and thus ζg ~ 1. Below we show that this restriction is not valid for the following reasons: first, we have an open system where DMPs can escape to infinity, being ejected from the binary system by a time-dependent force induced by binary rotation. This means that the dynamics is not completely Hamiltonian. Second, DMPs are captured (or they linger, or are trapped) and are accumulated from continuum at negative coupled energies near the binary during a certain capture lifetime (although not forever). Thus, the longer the capture lifetime, the higher the accumulated density. Third, we obtain the enhancement for the volume density and not for the density in the phase space, for which the enhancement is indeed restricted by Liouville’s theorem. We discuss the details of this enhancement effect in the next sections.
The scattering and capture process of a DMP in a binary system can be an important element of galaxy formation. This process can also be useful to analyze cosmic dust and DMP interaction with a supermassive black hole binary. This is expected to play a prominent role in galaxy formation, see Graham et al. (2015). Thus we hope that analyzing this process will be useful for understanding the properties of velocity curves in galaxies, which was started by Zwicky (1933) and Rubin et al. (1980). We note that the velocity curves of captured DMPs in our binary system have certain similarities with those found in real galaxies.
2. Symplectic map description
Following the approach developed by Petrosky (1986), Chirikov & Vecheslavov (1989), Malyshkin & Tremaine (1999), and Lages & Shepelyansky (2013), we used a symplectic dark map description of the DMP dynamics in one orbital period of a DMP in a binary system 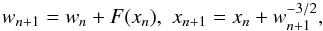 (1)where xn = tn/Tp(mod1) is given by time tn taken at the moment of DMP nth passage through perihelion, Tp is the planet period, and
(1)where xn = tn/Tp(mod1) is given by time tn taken at the moment of DMP nth passage through perihelion, Tp is the planet period, and 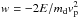 . Here E,md,andvp are the energy, mass of the DMP, and the velocity of the planet or star. The amplitude J of the kick F-function is proportional to the mass ratio J ~ mp/M. The shape of F(x) depends on the DMP perihelion distance q, the inclination angle θ between the planetary plane (x,y) and DMP plane, and the perihelion orientation angle ϕ, as discussed by Lages & Shepelyansky (2013). In the following we use for convenience units with md = vp = rp = 1 (here md is the DMP mass, which does not affect the DMP dynamics in gravitational systems).
. Here E,md,andvp are the energy, mass of the DMP, and the velocity of the planet or star. The amplitude J of the kick F-function is proportional to the mass ratio J ~ mp/M. The shape of F(x) depends on the DMP perihelion distance q, the inclination angle θ between the planetary plane (x,y) and DMP plane, and the perihelion orientation angle ϕ, as discussed by Lages & Shepelyansky (2013). In the following we use for convenience units with md = vp = rp = 1 (here md is the DMP mass, which does not affect the DMP dynamics in gravitational systems).
For q>rp the amplitude J drops exponentially with q and F(x) = Jsin(2πx), as shown by Petrosky (1986). This functional form of F(x) is significantly simpler than the real one at q<rp, while it still produces chaotic dynamics at 0 <w ≪ 1 and integrable motion with invariant curves above a chaos border w>wch. In this regime the map takes the form 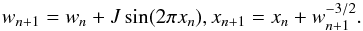 (2)The same map describes a microwave ionization of excited hydrogen atoms that is called the Kepler map (see Casati et al. 1987; Shepelyansky 2012). There, the Coulomb attraction plays the role of gravity, while a circular planet rotation is effectively created by the microwave polarization. The microwave ionization experiments performed by Galvez et al. (1988) were made for three-dimensional atoms, but the ionization process is still well described by the Kepler map (see Casati et al. 1990; Shepelyansky 2012). These results provide additional arguments in favor of a simplified Kepler map description of DMP dynamics in binary systems. The dynamics of the Kepler map can be locally described by the Chirikov standard map (see Chirikov 1979). We note that the approach based on the Kepler map has recently been used to determine chaotic zones in gravitating binaries, see Shevchenko (2015).
(2)The same map describes a microwave ionization of excited hydrogen atoms that is called the Kepler map (see Casati et al. 1987; Shepelyansky 2012). There, the Coulomb attraction plays the role of gravity, while a circular planet rotation is effectively created by the microwave polarization. The microwave ionization experiments performed by Galvez et al. (1988) were made for three-dimensional atoms, but the ionization process is still well described by the Kepler map (see Casati et al. 1990; Shepelyansky 2012). These results provide additional arguments in favor of a simplified Kepler map description of DMP dynamics in binary systems. The dynamics of the Kepler map can be locally described by the Chirikov standard map (see Chirikov 1979). We note that the approach based on the Kepler map has recently been used to determine chaotic zones in gravitating binaries, see Shevchenko (2015).
The similarity of dynamics of dark (1) and Kepler (2) maps is also well visible from comparing their Poincaré sections, shown in Fig. 1, for the typical dark map parameters corresponding to the Halley comet (see Fig. 1a in Lages & Shepelyansky 2013) and the corresponding parameter J of the Kepler map.
To take into account that J decreases with q, we use the relation J = J0 = const. for q<qb and J = J0exp( − α(q − qb))) for q ≥ qb (below J is used instead of J0). We use qb = 1.5 and α = 2.5, corresponding to typical dark map parameters (see Fig. 1 in Lages & Shepelyansky 2013), but we checked that the obtained enhancement is not affected by a moderate variation of qborα. The simplicity of map (2) allows increasing the number Np of injected DMPs by a factor one hundred compared to map (1). The correspondence between (1) and (2) is established by the relation J = 5mp/M, which works approximately for the typical parameters of Halley comet case.
Of course, as discussed by Lages & Shepelyansky (2013), the dark map and moreover the Kepler map give an approximate description of DMP dynamics in binary systems. However, this approach is much more efficient than the exact solution of Newton equations used by (Peter 2009a,b), and Sivertsson & Edsjö (2012) and allows obtaining results with very many DMPs injected during the lifetime of the solar system (SS) tS = 4.5 × 109 yr. The validity of such a map description is justified by the results obtained by Petrosky (1986), Chirikov & Vecheslavov (1989), Malyshkin & Tremaine (1999), Lages & Shepelyansky (2013), Rollin et al. (2015), and Casati et al. (1990).
3. Capture cross-section
 |
Fig. 1 Poincaré sections for the dark map (1) (top) and the Kepler map (2) (bottom) for parameters of the Halley comet case in Eq. (1) and J = 0.007 in Eq. (2) (see text). |
The capture cross-section σ is computed as previously described by Lages & Shepelyansky (2013) with 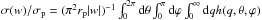 , where h is a fraction of DMPs captured after one map iteration from w< 0 to w> 0, given by an interval length inside the F(x) envelope at | w| = const.,
, where h is a fraction of DMPs captured after one map iteration from w< 0 to w> 0, given by an interval length inside the F(x) envelope at | w| = const., 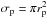 . The equation for σ(w) is based on the expression for the scattering impact parameter
. The equation for σ(w) is based on the expression for the scattering impact parameter 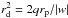 . For the Kepler map the h-function only depends on q, and the numerical computation is straightforward. The differential energy distribution of captured DMPs is dN/ dw = σ(w)ngf(w)/2 with ng = ρg/md.
. For the Kepler map the h-function only depends on q, and the numerical computation is straightforward. The differential energy distribution of captured DMPs is dN/ dw = σ(w)ngf(w)/2 with ng = ρg/md.
The results for σ(ω) and dN/dw/Np, obtained for maps (1) and (2), are shown in Fig. 2. Here 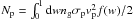 is the number of DMPs crossing the planet orbit area per unit of time. The results of Fig. 2 show that both maps give similar results, which provides additional support for the Kepler map description. The theoretical dependence σ ∝ 1/|w |, predicted by Khriplovich & Shepelyansky (2009), is clearly confirmed. The only difference between maps (1) and (2) is that the kick amplitude J ≈ 5mp/M for (2) is restricted, and thus after one kick we may have only | w| ≤ J, while for (1) some orbits can be captured with | w| >J = 5mp/M as a result of close encounters. However, the probability of such events is low.
is the number of DMPs crossing the planet orbit area per unit of time. The results of Fig. 2 show that both maps give similar results, which provides additional support for the Kepler map description. The theoretical dependence σ ∝ 1/|w |, predicted by Khriplovich & Shepelyansky (2009), is clearly confirmed. The only difference between maps (1) and (2) is that the kick amplitude J ≈ 5mp/M for (2) is restricted, and thus after one kick we may have only | w| ≤ J, while for (1) some orbits can be captured with | w| >J = 5mp/M as a result of close encounters. However, the probability of such events is low.
 |
Fig. 2 a) Dependence of the capture cross-section σ on DMP energy w for Sun-Jupiter (black curve, data from Ref. (8)) and for the Kepler map at J = 0.005 (red curve); the dashed line shows the dependence σ ∝ 1/|w |. b) Dependence of the rescaled captured number of DMPs on energy w for the models of the left panel. Here wcap = 0.001. |
4. Chaotic dynamics
The injection, capture, evolution, and escape of DMPs is computed as described by Lages & Shepelyansky (2013): we numerically modeled a constant flow of scattered DMPs with an energy distribution d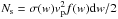 per time unit (we used q ≤ qmax = 4rp). For Jupiter we have u ≈ 17 ≫ 1 and dNs ∝ dqdw. However, for an SMBH we can have u2<J so that one kick captures almost all the DMPs from the galactic distribution f(w). In this case, we used the whole distribution f(w) (w = v2). Map (2) is simpler than (1) since the kick function only depends on q, which allows performing simulations with more DMPs.
per time unit (we used q ≤ qmax = 4rp). For Jupiter we have u ≈ 17 ≫ 1 and dNs ∝ dqdw. However, for an SMBH we can have u2<J so that one kick captures almost all the DMPs from the galactic distribution f(w). In this case, we used the whole distribution f(w) (w = v2). Map (2) is simpler than (1) since the kick function only depends on q, which allows performing simulations with more DMPs.
 |
Fig. 3 a) Number Ncap of captured DMPs as a function of time t in years for the energy range w> 0 (black curve), w> 4 × 10-5 corresponding to half the distance between Sun and the Alpha Centauri system (red curve), w> 1/20 corresponding to r< 100 AU (blue curve); NJ = 4 × 1011 DMPs are injected during SS lifetime tS; data are obtained from the map (2) at J = 0.005, u = 17 corresponding to the Sun-Jupiter case. b) Top part: density distribution ρ(w) ∝ dN/ dw in energy at time tS (normalized as |
The scattering and evolution processes were followed during the whole lifetime tS of the SS. The total number of DMPs, injected during time tS for | w| ≤ J and all q is NJ. For the Kepler map the highest value is NJ = 4 × 1011, which is 100 times higher than for the dark map.
 |
Fig. 4 a) Stationary radial density ρ(r) ∝ dN/ dr from the Kepler map at J = 0.005 with u = 17 at time tS (red curve) and u = 0.035 at time tu ≈ 4 × 108Tp (black curve); data from the dark map at mp/M = 10-3 are shown by the blue curve at u = 17 and time tS for the Sun-Jupiter case, and by the green curve at u = 0.035 and tS for the SMBH; the normalization is fixed as |
The time dependence Ncap(t) for the Kepler map, shown in Fig. 3, is very similar to that found for the dark map by Lages & Shepelyansky (2013). For a finite SS region w> 1/20 the growth of Ncap(t) saturates after a time scale of td ≈ 107 yr. This scale approximately corresponds to a diffusive escape time td ~ 12 yr /D ~ 106 yr, where the diffusion rate is taken in a random phase approximation to be D ≈ J2/ 2 (see, e.g., Casati et al. 1987). The diffusive spreading extends from w ~ 0 up to chaos border wch ≈ 0.3. This value agrees well with the theoretical value wch = (3πJ)2/5 = 0.29 obtained from the Chirikov criterion (Chirikov 1979; see discussion for DMP dynamics in Petrosky 1986; Casati et al. 1987; Khriplovich & Shepelyansky 2009). The validity of the Chirikov criterion in this system was also demonstrated in Shevchenko (2015). As for the dark map, we obtain a density distribution of ρ(w) ∝ 1 /w3/2, corresponding to the ergodic estimate according to which ρ(w) is proportional to time period at a given w. The results of Figs. 1–3 confirm the close similarity of dynamics described by maps (1) and (2).
5. Radial variation of the dark matter density
To compute the DMP density, we considered captured orbits NAC with w> 4 × 10-5. The radial density ρ(r) was computed by the method described by Lages & Shepelyansky (2013): NAC were determined at instant time tS; for them the dynamics in real space was recomputed during a time period Δt ~ 100 yr of planet. The value of ρ(r) was computed by averaging over k = 103 points randomly distributed over Δt for all NAC orbits.
We also checked that a semi-analytical averaging, using an exact density distribution over Kepler ellipses for each of NAC orbits, gives the same result: assuming ergodicity ρw,q(r)dr = w3/2dt/ 2π and using Kepler’s equation, the radial density of the DMPs on a given orbit is ρw,q(r) = (rw2/ 2π)((1 − qw)2 − (1 − rw)2)− 1/2, then adding the radial density of each NAC orbit, we retrieve the DMP radial density ρ(r) shown in Fig. 4. From the obtained space distribution we determine a fraction ηri of NAC DMP orbits located inside a range 0 ≤ r ≤ ri by computing ηri = ΔNi/ (kNAC), where ΔNi is the number of points inside the above range (we used ri/rp = 0.2,1,and6).
In Fig. 4 we show the dependence of radial ρ(r) and volume ρv = ρ/r2 densities on distance r. For the Kepler map data, the density ρ(r) has a characteristic maximum at rmax that is determined by the chaos border position rmax ≈ 2 /wch (this dependence, as well as the relation wch = (3πJ)2/5, is numerically confirmed for the studied range 10-3<J< 10-2 for the Kepler map with a given fixed J). The density profile ρ(r) is not sensitive to the value of u and remains practically unchanged for u = 17, 0.035. For the dark map a variation of the kick function with q and angles leads to a variation of wch that leads to a slow growth of ρ at large r. A power-law fit of ρv ∝ 1 /rβ in a range 2 <r< 100 gives β ≈ 2.25 ± 0.003 for the Kepler map data and β = 1.52 ± 0.002 for the dark map. We attribute the difference in β values to a larger fraction of integrable islands for the dark map, as is visible in Fig. 1 for typical parameters. We note that an effective range of radial variation is bounded by the kick amplitude with r<rcap ≈ 1 /J, and in the range rp<r<rcap the data are compatible with ρ ~ const. (dashed line in Fig. 4b).
We note that the value of u does not significantly affect the density variation with r, as is clearly seen in Fig. 4. The spacial density distribution of computed from the dark map at u = 0.035 shown in Fig. 5 is also very similar to those at u = 17 (see Fig. 5 by Lages & Shepelyansky 2013). This independence of u arises because ρ(r) is determined by the dynamics at w> 0, which is practically insensitive to the DMP energies at −J<w< 0 that are captured by one kick.
 |
Fig. 5 Density of captured DMPs at present time tS/Tp ≈ 4 × 108 for the dark map at mp/M = 10-3 and u/vp = 0.035. Top panels: DMP surface density ρS ∝ dN/ dzdrρ shown at the left in the cross plane (0,y,z) perpendicular to the planetary orbit (data are averaged over |
6. Enhancement of dark matter density
To determine the enhancement of the DMP density captured by a binary system we followed the method developed by Lages & Shepelyansky (2013). We computed the total mass of DMP flow crossing the range q ≤ 4rp during time tS: 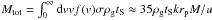 , where we used the cross-section
, where we used the cross-section 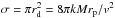 for injected orbits with q ≤ 4rp, w = v2, k is the gravitational constant. For SS at u/vp ≈ 17 we have Mtot ≈ 0.5 × 10-6M.
for injected orbits with q ≤ 4rp, w = v2, k is the gravitational constant. For SS at u/vp ≈ 17 we have Mtot ≈ 0.5 × 10-6M.
 |
Fig. 6 Dependence of the DMP density enhancement factor ζ = ρv(ri) /ρgJ on J at u/vp = 17 (Jupiter); here ρgJ is the galactic DMP volume density for an energy range of 0 < |w| <J and ri = 0.2rp,rp,6 rp (blue, black, red); points and squares show results for map (2) with the number of injected particles NJ = 4 × 109 and 4 × 1011, respectively; crosses show data for map (1) with NJ = 4 × 109 and J = 5mp/M. b) Dependence of the galactic enhancement factor ζg = ρv(ri) /ρg on u/vp at rζ = rp and J = 0.005 in (2) (points) and mp/M = 0.001 in (1) (crosses), here ρg is the global galactic density; lines show dependencies ζg ∝ 1 /u (red) and ζg ∝ 1 /u3 (blue). c) Dependence of ζg on J at u/vp = 17; d) the same at u/vp = 0.035, parameters of symbols are as in a), b). The green curve shows theory (3) in all panels. |
From the numerically known fractions ηri of the previous section and the fraction of captured orbits ηAC = NAC/Ntot we find the mass Mri = ηriηACMtot inside the volume 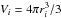 of radius r<ri (ri = 0.2rp;rp;6rp). Here Ntot is the total number of injected orbits during the time tS, while the number of orbits injected in the range | w| <J (only those can be captured) is
of radius r<ri (ri = 0.2rp;rp;6rp). Here Ntot is the total number of injected orbits during the time tS, while the number of orbits injected in the range | w| <J (only those can be captured) is 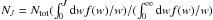 . For J ≪ u2 we have κ = Ntot/NJ = 2u2/ (3J) ≈ 3.8 × 104 for u/vp = 17 and κ = 1 for u/vp = 0.035 at J = 0.005. Thus for u/vp = 17 the number of orbits, injected at 0 < |w| <J, NJ = 4 × 1011, corresponds to the total number of injected orbits Ntot ≈ 1.5 × 1016. Finally, we obtain the global density enhancement factor ζg(ri) = ρv(ri) /ρg ≈ 16πηriηAC(rp/ri)3τSvp/u, where τS = tS/Tp is the injection time expressed in the number of planet periods Tp = 2πrp/vp. For u2 ≫ J it is useful to determine the enhancement ζ = ρv(ri) /ρgJ of the scattered galactic density in the range 0 < |w| <J, whose density is ρgJ ≈ 1.38ρgJ3/2(vp/u)3. Thus ζ = 0.72ζg(u/vp)3/J3/2.
. For J ≪ u2 we have κ = Ntot/NJ = 2u2/ (3J) ≈ 3.8 × 104 for u/vp = 17 and κ = 1 for u/vp = 0.035 at J = 0.005. Thus for u/vp = 17 the number of orbits, injected at 0 < |w| <J, NJ = 4 × 1011, corresponds to the total number of injected orbits Ntot ≈ 1.5 × 1016. Finally, we obtain the global density enhancement factor ζg(ri) = ρv(ri) /ρg ≈ 16πηriηAC(rp/ri)3τSvp/u, where τS = tS/Tp is the injection time expressed in the number of planet periods Tp = 2πrp/vp. For u2 ≫ J it is useful to determine the enhancement ζ = ρv(ri) /ρgJ of the scattered galactic density in the range 0 < |w| <J, whose density is ρgJ ≈ 1.38ρgJ3/2(vp/u)3. Thus ζ = 0.72ζg(u/vp)3/J3/2.
The results of the DMP density enhancement factors ζ and ζg are shown in Fig. 6. At (u/vp)2 ≫ J we have ζ ≫ 1 and ζg ≪ 1. At u/vp = 17 we find that ζ ∝ 1 /J (the fit gives exponent a = 1.04 ± 0.01) and 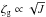 (the fit exponent is a = 0.46 ± 0.1) in agreement with the above relation between ζ and ζg. In general, we have ζg ∝ 1 /u for
(the fit exponent is a = 0.46 ± 0.1) in agreement with the above relation between ζ and ζg. In general, we have ζg ∝ 1 /u for 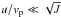 and ζg ∝ 1 /u3 for
and ζg ∝ 1 /u3 for 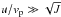 . There is only weak variation of ζg with J for
. There is only weak variation of ζg with J for 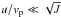 . The values of ζ and ζg have similar values for the dark and Kepler maps (a part of the fact that at ri = 0.2rp and ri = rp the dark map has approximately the same ζ since there ρv(r) ~ const. for r ≤ rp).
. The values of ζ and ζg have similar values for the dark and Kepler maps (a part of the fact that at ri = 0.2rp and ri = rp the dark map has approximately the same ζ since there ρv(r) ~ const. for r ≤ rp).
All these results can be summarized by the following formula for the chaotic enhancement factor of DMP density in a binary system: ![\begin{eqnarray} \label{eq3} \zeta_{\rm g} = A \sqrt{J} (v_{\rm p}/u)^3\Big/\left[1+B J (v_{\rm p}/u)^2\right], J=5 m_{\rm p}/M. \end{eqnarray}](/articles/aa/full_html/2015/04/aa25576-14/aa25576-14-eq214.png) (3)Here ζg is given for DMP density at ri = rp and A ≈ 15.5, B ≈ 0.7. This formula describes the numerical data of Fig. 6 well. For (u/vp)2 ≫ J we have ζg ≪ 1, but we still have an enhancement of ζ = 0.72ζg(u/vp)3/J3/2 ≈ 0.72A/J ≫ 1. For (u/vp)2 ≪ J we have the global enhancement
(3)Here ζg is given for DMP density at ri = rp and A ≈ 15.5, B ≈ 0.7. This formula describes the numerical data of Fig. 6 well. For (u/vp)2 ≫ J we have ζg ≪ 1, but we still have an enhancement of ζ = 0.72ζg(u/vp)3/J3/2 ≈ 0.72A/J ≫ 1. For (u/vp)2 ≪ J we have the global enhancement 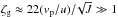 . The color representation of dependence (3) is shown in Fig. 7.
. The color representation of dependence (3) is shown in Fig. 7.
 |
Fig. 7 Logarithm of DMP density enhancement factor log 10ζg from (3), shown by color and log value-levels, as a function of u/vp and J; two points are for J = 0.005, u/vp = 17 (SS) and u/vp = 0.035 (SMBH; such vp is about 2% of the light velocity). |
Equation (3) can be understood on the basis of simple estimates. The total captured mass Mcap ≈ MAC is accumulated during the diffusive time td and hence 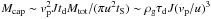 , where τd = td/Tp, and we omit numerical coefficients. This mass is concentrated inside a radius rcap ~ 1 /J so that at r ~ 1 /J the volume density is
, where τd = td/Tp, and we omit numerical coefficients. This mass is concentrated inside a radius rcap ~ 1 /J so that at r ~ 1 /J the volume density is 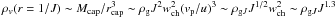 , where we use a relation
, where we use a relation 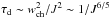 . (Our modeling of the injection process in the Kepler map with a constant injection flow in time, counted as the number of map iterations, shows that the number of absorbed particles scales as NK ~ τd ~ J− 6/5 at small J.) It is important to stress that ρv(r = 1 /J) ≪ ρgJ in contrast to the naive expectation that ρv(r = 1 /J) ~ ρgJ. Using our empirical density decay ρv ∝ 1 /rβ with β ≈ 2.25 for the Kepler map, we obtain ζ ∝ 1 /J0.95, which is close to the dependence ζ ~ 1 /J and ζg ~ J1/2/ (u/vp)3 from (3) at u2 ≫ J. For the dark map we have β ≈ 1.5 but wch ~ const. as a result of the sharp variation of F(x) with x, which again gives ζ ~ 1 /J. It is difficult to obtain the exact analytical derivation of the relation ζ ~ 1 /J due to contributions of different q values (which have different τd) and different kick shapes in (1) that affect τd and the structure of chaotic component. In the regime (u/vp)2 ≪ J the entire energy range of the scattering flow is absorbed by one kick, and Mcap is increased by a factor (u/vp)2/J, leading to an increase of ζg by the same factor, which yields
. (Our modeling of the injection process in the Kepler map with a constant injection flow in time, counted as the number of map iterations, shows that the number of absorbed particles scales as NK ~ τd ~ J− 6/5 at small J.) It is important to stress that ρv(r = 1 /J) ≪ ρgJ in contrast to the naive expectation that ρv(r = 1 /J) ~ ρgJ. Using our empirical density decay ρv ∝ 1 /rβ with β ≈ 2.25 for the Kepler map, we obtain ζ ∝ 1 /J0.95, which is close to the dependence ζ ~ 1 /J and ζg ~ J1/2/ (u/vp)3 from (3) at u2 ≫ J. For the dark map we have β ≈ 1.5 but wch ~ const. as a result of the sharp variation of F(x) with x, which again gives ζ ~ 1 /J. It is difficult to obtain the exact analytical derivation of the relation ζ ~ 1 /J due to contributions of different q values (which have different τd) and different kick shapes in (1) that affect τd and the structure of chaotic component. In the regime (u/vp)2 ≪ J the entire energy range of the scattering flow is absorbed by one kick, and Mcap is increased by a factor (u/vp)2/J, leading to an increase of ζg by the same factor, which yields 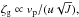 in agreement with (3).
in agreement with (3).
We note that for galaxies the value of exponent β is debated (see Merritt 2013). For the adiabatic growth model, we have 2.25 ≤ β ≤ 2.5, which is close to the value obtained from our symplectic map simulations.
 |
Fig. 8 Density distribution of DMPs ρ(q) over q obtained from the Kepler map at J = 0.005 and time tu ≈ 4 × 108Tp: a) u/vp = 17; b) u/vp = 0.04; the density is normalized to unity ( |
The nontrivial properties of the distribution of the captured DMPs in q are shown in Fig. 8 in a stationary regime at times tS/Tp ≈ 4 × 108 for the Kepler map. While for u/vp ~ 17 ≫ 1 we have a smooth drop of DMP density ρ(q) at q> 1.5rp, for u/vp = 0.04 ≪ 1 we have an increase of ρ(q) by a factor 3 for q/rp ≈ 2.5 compared to q/rp ≈ 1. We attribute this variation to different capture conditions at 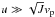 , where only DMPs at low velocities are captured by one kick, and
, where only DMPs at low velocities are captured by one kick, and 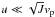 , where practically all DMPs are captured by one kick. As a result of the dependence of J on q, we also have various diffusive timescales td ∝ 1 /J2 that can affect the contribution of the DMPs at different q values in the volume density distribution on r.
, where practically all DMPs are captured by one kick. As a result of the dependence of J on q, we also have various diffusive timescales td ∝ 1 /J2 that can affect the contribution of the DMPs at different q values in the volume density distribution on r.
Finally, we stress the importance of the obtained result of large enhancement factors ζ and ζg. This result is drastically different from the frequent claims that there is no enhancement of the DMP density in the center vicinity of a binary system compared to its galactic value because of the Liouville theorem, which implies that the density of DM in the phase space is conserved during the evolution (Gould & Alam 2001; Lundberg & Edsjö 2004). However, this statement does not take into account the actual dynamics of captured DMPs. Indeed, the galactic space density ρg is obtained from all energies of DMPs in the Maxwell distribution. The analysis of symplectic DMP dynamics shows that DMPs at large q ≫ 1 are not captured, while DMPs with q ~ 1 are captured, and by diffusion, they penetrate up to high values w ~ wch, thus accumulating DMPs with typical distance values r ~ 1 /wch. The symplectic map approach also determines an effective size of our binary system of rcap ~ 1 /J corresponding to an energy range w ~ J. If we assume that the DMP density in this range is the same as its galactic value, then we should conclude that the enhancement factor should be ζg ~ (rcap/rp)β ~ 1 /wcapβ ~ 1 /Jβ ~ 1.5 × 105 for typical values J = 0.005 and β = 2.25 (we consider here the case 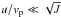 ). This estimate gives a value ζg that is even higher than that given by relation (3). In fact, relation (3) takes into account that only bounded values of q are captured, it also estimates the chaos region, where DMPs are accumulated during the chaotic diffusion process, populating a part of the phase space volume from w ~ 0 up to w ~ wch ~ 1. This gives a lower value of ζg than the above simplified estimate. We also note that at
). This estimate gives a value ζg that is even higher than that given by relation (3). In fact, relation (3) takes into account that only bounded values of q are captured, it also estimates the chaos region, where DMPs are accumulated during the chaotic diffusion process, populating a part of the phase space volume from w ~ 0 up to w ~ wch ~ 1. This gives a lower value of ζg than the above simplified estimate. We also note that at 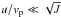 the typical kinetic energy of an ejected DMP
the typical kinetic energy of an ejected DMP 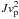 is significantly higher than the typical DMP energy u2 in the galactic wind. For these reasons, there is no contradiction with the Liouville theorem, and a large enhancement of the captured DMP density is possible.
is significantly higher than the typical DMP energy u2 in the galactic wind. For these reasons, there is no contradiction with the Liouville theorem, and a large enhancement of the captured DMP density is possible.
7. Few-body model
 |
Fig. 9 a) Radial density ρ(r) ∝ dN/ dr for the Kepler models of SS (red curve) and SMBH binary (black curve) at tS/Tp ≈ 4 × 108; the normalization is fixed as |
Above we considered the DMP capture in a two-body gravitating system. We expect that a central SMBH binary dominating the galaxy potential can be viewed as a simplified galaxy model. Recent observations of Graham et al. (2015) indicate that such systems may exist. Within the Kepler map approach it is easy to analyze the whole SS (an SMBH binary) including all eight planets (eight stars) with given positions ri and velocities vi measured in units of orbit radius rp and velocity vp of Jupiter for SS at u/vp = 17 (and of, e.g., the fifth star for an SMBH binary at u/vp = 0.035). Thus in (2) we have now for the SS eight kick terms with Ji ~ (mi/M)(vi/vp)2. For the SMBH binary model we consider eight stars modeled by map (2) with the values J1 = 2.5 × 10-4, J2 = 5 × 10-4, J3 = 7.5 × 10-4, J4 = 10-3, J5 = 2.5 × 10-3, J6 = 6.25 × 10-4, J7 = 5 × 10-4, and J8 = 1.25 × 10-4 with the same ratio ri/rp as for the SS. In both cases we injected NJ = 2.8 × 1010 particles considering evolution during τS orbital periods of Jupiter (fifth star). The steady-state density distribution is shown in Fig. 9. For the SS, ρ(r) is very close to the case of only one Jupiter discussed above. This result is natural since its mass is dominant in the SS. For the SMBH binary model we also find a similar distribution (see Fig. 4) with a slightly slower decay of ρv(r) with r (β = 2.06 ± 0.002) due to the contribution of more stars. We obtain ζ = 3000 (SS) and ζg = 3 × 104 (SMBH). These two examples show that the binary model captures the main physical effects of the DMP capture and evolution.
8. Discussion
Our results show that DMP capture and dynamics inside two-body and few-body systems can be efficiently described by symplectic maps. The numerical simulations and analytical analysis show that in the center of these systems the DMP volume density can be enhanced by a factor ζg ~ 104 compared to its galactic value. The values of ζg are highest for a high velocity vp of a planet or star rotating around the system center. We note that our approach based on a symplectic map description of the restricted three-body problem is rather generic. Thus it can also be used to analyze comet dynamics, cosmic dust, and free-floating constituents of the Galaxy.
References
- Bertone, G., Hooper, D., & Silk, J. 2005, Phys. Rep., 405, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Casati, G., Guarneri, I., & Shepelyansky, D. L. 1987, Phys. Rev. A, 36, 3501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Casati, G., Guarneri, I., & Shepelyansky, D. L. 1990, Phys. A Stat. Mech. Appl., 163, 205 [CrossRef] [Google Scholar]
- Chirikov, B. V. 1979, Phys. Rep., 52, 263 [Google Scholar]
- Chirikov, R. V., & Vecheslavov, V. V. 1989, A&A, 221, 146 [NASA ADS] [Google Scholar]
- Galvez, E. J., Sauer, B. E., Moorman, L., Koch, P. M., & Richards, D. 1988, Phys. Rev. Lett., 61, 2011 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garrett, K., & Dūda, G. 2011, Adv. Astron., 2011, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., & Alam, S. M. K. 2001, ApJ, 549, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. J., Djorgovski, S. G., Stern, D., et al. 2015, Nature, 518, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Khriplovich, I. B., & Shepelyansky, D. L. 2009, Int. J. Mod. Phys. D, 18, 1903 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lages, J., & Shepelyansky, D. L. 2013, MNRAS, 430, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lundberg, J., & Edsjö, J. 2004, Phys. Rev. D, 69, 123505 [NASA ADS] [CrossRef] [Google Scholar]
- Malyshkin, L., & Tremaine, S. 1999, Icarus, 141, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 2013, Dynamics and Evolution of Galactic Nuclei (Princeton University Press) [Google Scholar]
- Peter, A. H. G. 2009, Phys. Rev. D, 79, 103531 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosky, T. Y. 1986, Phys. Lett. A, 117, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Poincaré, H. 1890, Acta Math., 13, 1 [Google Scholar]
- Rollin, G., Haag, P., & Lages, J. 2015, Phys. Lett. A, 379, 1017 [CrossRef] [Google Scholar]
- Rubin, V. C., Ford, W. K. J., & Thonnard, N. 1980, ApJ, 238, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Shepelyansky, D. 2012, Scholarpedia, 7, 9795 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, I. I. 2015, ApJ, 799, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Sivertsson, S., & Edsjö, J. 2012, Phys. Rev. D, 85, 123514 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helv. Phys. Acta, 6, 110 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Poincaré sections for the dark map (1) (top) and the Kepler map (2) (bottom) for parameters of the Halley comet case in Eq. (1) and J = 0.007 in Eq. (2) (see text). |
| In the text | |
 |
Fig. 2 a) Dependence of the capture cross-section σ on DMP energy w for Sun-Jupiter (black curve, data from Ref. (8)) and for the Kepler map at J = 0.005 (red curve); the dashed line shows the dependence σ ∝ 1/|w |. b) Dependence of the rescaled captured number of DMPs on energy w for the models of the left panel. Here wcap = 0.001. |
| In the text | |
 |
Fig. 3 a) Number Ncap of captured DMPs as a function of time t in years for the energy range w> 0 (black curve), w> 4 × 10-5 corresponding to half the distance between Sun and the Alpha Centauri system (red curve), w> 1/20 corresponding to r< 100 AU (blue curve); NJ = 4 × 1011 DMPs are injected during SS lifetime tS; data are obtained from the map (2) at J = 0.005, u = 17 corresponding to the Sun-Jupiter case. b) Top part: density distribution ρ(w) ∝ dN/ dw in energy at time tS (normalized as |
| In the text | |
 |
Fig. 4 a) Stationary radial density ρ(r) ∝ dN/ dr from the Kepler map at J = 0.005 with u = 17 at time tS (red curve) and u = 0.035 at time tu ≈ 4 × 108Tp (black curve); data from the dark map at mp/M = 10-3 are shown by the blue curve at u = 17 and time tS for the Sun-Jupiter case, and by the green curve at u = 0.035 and tS for the SMBH; the normalization is fixed as |
| In the text | |
 |
Fig. 5 Density of captured DMPs at present time tS/Tp ≈ 4 × 108 for the dark map at mp/M = 10-3 and u/vp = 0.035. Top panels: DMP surface density ρS ∝ dN/ dzdrρ shown at the left in the cross plane (0,y,z) perpendicular to the planetary orbit (data are averaged over |
| In the text | |
 |
Fig. 6 Dependence of the DMP density enhancement factor ζ = ρv(ri) /ρgJ on J at u/vp = 17 (Jupiter); here ρgJ is the galactic DMP volume density for an energy range of 0 < |w| <J and ri = 0.2rp,rp,6 rp (blue, black, red); points and squares show results for map (2) with the number of injected particles NJ = 4 × 109 and 4 × 1011, respectively; crosses show data for map (1) with NJ = 4 × 109 and J = 5mp/M. b) Dependence of the galactic enhancement factor ζg = ρv(ri) /ρg on u/vp at rζ = rp and J = 0.005 in (2) (points) and mp/M = 0.001 in (1) (crosses), here ρg is the global galactic density; lines show dependencies ζg ∝ 1 /u (red) and ζg ∝ 1 /u3 (blue). c) Dependence of ζg on J at u/vp = 17; d) the same at u/vp = 0.035, parameters of symbols are as in a), b). The green curve shows theory (3) in all panels. |
| In the text | |
 |
Fig. 7 Logarithm of DMP density enhancement factor log 10ζg from (3), shown by color and log value-levels, as a function of u/vp and J; two points are for J = 0.005, u/vp = 17 (SS) and u/vp = 0.035 (SMBH; such vp is about 2% of the light velocity). |
| In the text | |
 |
Fig. 8 Density distribution of DMPs ρ(q) over q obtained from the Kepler map at J = 0.005 and time tu ≈ 4 × 108Tp: a) u/vp = 17; b) u/vp = 0.04; the density is normalized to unity ( |
| In the text | |
 |
Fig. 9 a) Radial density ρ(r) ∝ dN/ dr for the Kepler models of SS (red curve) and SMBH binary (black curve) at tS/Tp ≈ 4 × 108; the normalization is fixed as |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.