EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 576 (April 2015) A&A, 576 (2015) A117 Full HTML
Free Access
Issue
A&A
Volume 576, April 2015
Article Number A117
Number of page(s) 11
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201425418
Published online 16 April 2015

© ESO, 2015

1. Introduction

Early-type supergiants show strong line driven winds (CAK mechanism; Castor et al. 1975; Morton 1967; Lucy & Solomon 1970) and typical mass loss rates of a few 10-6 M⊙/ yr (e.g., Puls et al. 2006). These high velocity winds that can reach terminal velocities ν∞> 2000 km s-1 (e.g., Muijres et al. 2012) are perturbed and clumpy (Owocki et al. 1988; Feldmeier et al. 1997; Puls et al. 2006; Oskinova et al. 2012; Sundqvist & Owocki 2013) with over 90% of the wind mass concentrated in less than ~10% of the wind volume (Sako et al. 1999; Rahoui et al. 2011, for Vela X-1 and Cyg X-1, respectively). Binary systems consisting of an O/B-type giant and a compact object offer us the unique chance to investigate these winds by using the X-ray source as a test probe.

Cygnus X-1 is in such a high mass X-ray binary with the O9.7Iab supergiant HDE 226868 (Walborn 1973). Located ~1.86 kpc away (Reid et al. 2011; see also Xiang et al. 2011), it is one of the brightest and best-observed black hole binaries. The orbital period is P = 5.599829 ± 0.000016 d with T0 = 52 872.288 ± 0.009 (Gies et al. 2008). The source also shows a superorbital period that has been reported as ~300 d (Priedhorsky et al. 1983), then as ~150 d (Brocksopp et al. 1999; Benlloch et al. 2004; Ibragimov et al. 2007), and lately as having changed back to ~300 d (Zdziarski et al. 2011).

The intrinsic variability of Cyg X-1 on timescales of hours (Böck et al. 2011) to years (Pottschmidt et al. 2003; Wilms et al. 2006; Shaposhnikov & Titarchuk 2006; Axelsson et al. 2006; Grinberg et al. 2013) can be classified in terms of X-ray spectral states that also show distinct timing characteristics on timescales below 1 s and are similar for most black hole binaries (for a review see, e.g., Belloni 2010). In particular, the hard state spectrum above ~2 keV is dominated by a power law component with photon index Γ ~ 1.7, while in the soft state the thermal emission from the accretion disk is prominent and the contribution from a steeper power law component is low.

Orosz et al. (2011) determine the inclination of the binary system to 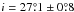\hbox{$i=27\fdg{}1\pm0\fdg{}8$}, the black hole mass to MBH = (14.8 ± 1.0) M⊙, and the companion mass to M⋆ = (19.2 ± 1.9) M⊙; the last value was questioned by Ziółkowski (2014), who estimate a range of 25–35  M⊙ with a most likely value of 27  M⊙. As HDE 226868 fills ≳90% of its Roche lobe (Gies et al. 2003) and has a strong (a few 10-6  M⊙ yr-1, Gies et al. 2003) fast wind, the black hole accretes via a focussed wind (Friend & Castor 1982; Gies & Bolton 1986a,b; Sowers et al. 1998; Miller et al. 2005; Hanke et al. 2009; Hell et al. 2013; Miškovičová et al. 2015, and others). Values for ν∞ for HDE 226868 vary in the literature: Davis & Hartmann (1983) obtain (2300 ± 400) km s-1 in the hard state, but Vrtilek et al. (2008) find 1420 km s-1 in the soft state. Herrero et al. (1995) adopt 2100 km s-1. Gies et al. (2008) obtain 1200 km s-1 during a soft state, but list 1600 km s-1 as more likely.

The inclination of the system implies that our line of sight probes different regions of the wind at different orbital phases. Orbital variability of the absorption column density in the hard state has been reported by Feng & Cui (2002), Ibragimov et al. (2005), and Boroson & Vrtilek (2010). Dips in the (soft) X-ray lightcurves of Cyg X-1 are interpreted as signatures of clumps in the stellar wind. They occur preferably at superior conjunction (φorb ~ 0), i.e., when the O-star companion is between the observer and the black hole (e.g., Li & Clark 1974; Mason et al. 1974; Parsignault et al. 1976; Pravdo et al. 1980; Remillard & Canizares 1984; Kitamoto et al. 1984; Bałucińska-Church et al. 2000; Poutanen et al. 2008; Boroson & Vrtilek 2010).

The 16 years of mainly bi-weekly Cyg X-1 observations (1996–2011) with Rossi X-ray Timing Explorer’s (RXTE’s) Proportional Counter Array (PCA; Jahoda et al. 2006) and High Energy X-ray Timing Experiment (HEXTE; Rothschild et al. 1998) allowed us to study the long term spectral and X-ray timing evolution of the source in unprecedented detail in the previous papers of the series (Pottschmidt et al. 2003; Gleissner et al. 2004b,a; Wilms et al. 2006; Grinberg et al. 2013, 2014). In this paper, we use these data to analyze the orbital variability of absorption due to the focussed wind. The exceptional exposure reveals subtle effects such as the orbital variability in intermediate states and rare events with very high absorption.

In Sect. 2, we introduce the data used and the spectral models applied to describe them. In Sect. 3, we discuss the observed orbital variability of absorption in hard, intermediate, and soft states. In Sect. 4, we compare our measurements with previous results and with different wind models, namely with a toy model for a CAK-wind and with simulations of clumpy winds in single stars. We summarize our results in Sect. 5.

2. Data and spectral analysis

Ibragimov et al. (2005) used 42 Ginga-OSSE and RXTE-OSSE observations of Cyg X-1 taken mainly in the hard state to show orbital variability of absorption by demonstrating an increased equivalent hydrogen column density, NH, around φorb ~ 0. In Wilms et al. (2006), we analyzed 202 observations from 1999–2004 using RXTE-PCA and, where available, RXTE-HEXTE spectra with models similar to the one presented below and with a time resolution of individual RXTE observations that were typically of several satellite orbits in length, i.e., had exposure times of 5–10 ks. Boroson & Vrtilek (2010) classified 102 of these observations as hard states and used them to demonstrate the orbital variability of absorption in the hard state, but did not have enough data taken during softer states. At the same time, higher sensitivity snapshots at different φorb with Chandra (Miller et al. 2005; Hanke et al. 2009; Hanke 2011; Miškovičová et al. 2015) and Suzaku (Nowak et al. 2011; Miller et al. 2012; Yamada et al. 2013) revealed a complex structure of the wind with highly variable local densities, but the orbital coverage was significantly worse than the RXTE measurements.

thumbnail Fig. 1

Histogram of the PCA exposure times of the individual satellite orbit-wise observations analyzed in this work. The mean exposure is 1.74 ks, the median 1.66 ks.

thumbnail Fig. 2

Number of orbitwise PCA observations with a given soft photon index Γ1 that do (red) or do not (blue) require a multitemperature disk component. Also highlighted are observations that do not require a disk and fall into the long hard state of MJD 53 900–55 375 (black). Dashed vertical lines indicate thresholds for hard (Γ1 ≤ 2.0), intermediate (2.0 < Γ1 ≤ 2.5), and soft (2.5 < Γ1) states according to Grinberg et al. (2013).

In this paper we therefore extend the earlier RXTE analyses, using the full mission-long database of RXTE observations of Cyg X-1, and using spectra taken with the exposure of one orbit of the RXTE satellite around Earth, or around 1.6 ks (Fig. 1). We thus probe average spectral parameters on shorter timescales than earlier RXTE studies over a variety of spectral shapes (Fig. 2). Our total sample consists of 2741 PCU 2 and HEXTE-spectra (Grinberg et al. 2013). The total exposure time of our observations is 4.77 Ms which corresponds to ~10 orbital periods of 5.6 d. The exposure is evenly distributed between the orbital phases. Advances in PCA calibration (Shaposhnikov et al. 2012) and a careful consideration of energy-dependent systematic uncertainties in different gain epochs of the PCA instrument (Hanke 2011; Grinberg et al. 2013) strengthen our analysis. For a detailed discussion of data treatment, see Grinberg et al. (2013). All analyses in this paper were performed with ISIS 1.6.2 (Houck & Denicola 2000; Houck 2002; Noble & Nowak 2008).

thumbnail Fig. 3

Histogram of χred2\hbox{$\chi^2_{\mathrm{red}}$} values for observations that do (red) and do not (blue) require a multitemperature disk component.

In performing our analysis we used the same approach as we used before (Grinberg et al. 2013), i.e., we modeled the data empirically with a broken power law with soft photon index Γ1, hard photon index Γ2, and a spectral break at ~10 keV (Wilms et al. 2006). This broken power law is modified by a high-energy cutoff, by an Fe Kα-line modeled with a Gaussian at ~6.4 keV, and by absorption. A multitemperature disk (diskbb, Mitsuda et al. 1984; Makishima et al. 1986) is added to the model where it improves the χ2 by more than 5% except in seven cases where the X-ray timing behavior and the correlation between Γ1 and Γ2 strongly prefer the model without a disk (Grinberg et al. 2014). Figure 3 shows that the model offers a very good description of the spectrum. As in Grinberg et al. (2013), we use Γ1-based state definitions derived from spectral and timing properties of Cyg X-1: the source is in hard state if Γ1 ≤ 2.0, in the intermediate state if 2.0 < Γ1 ≤ 2.5, and in the soft state if 2.5 < Γ1. The distribution of observations with Γ1 is shown in Fig. 2. Out of 1822 hard state observations, 1515 do not require a disk, but 384 out of 413 intermediate state observations and all 506 soft state observations require a disk component.

When studying variations of NH in an astronomical source, the measured column toward the source consists of two main components: absorption in the interstellar medium (ISM) that is constant on observable timescales and a variable absorption local to the X-ray source. For Galactic sources, X-ray data do not allow us to distinguish the two absorption components. In the case of Cyg X-1, we therefore take the constant ISM contribution into account by setting a minimum value for NH to NH,ISM = 4.8 × 1021 cm-2, as derived by Xiang et al. (2011) from studies of the dust scattering halo of the source. We describe absorption with the tbnew model, an improved version1 of tbabs (Wilms et al. 2000), using wilm abundances of Wilms et al. (2000) and vern cross sections of Verner et al. (1996). We note that optical depth at a frequency ν depends on the total cross section σν and the hydrogen column density NH as τν = σν·NH. The observed spectrum, Iobs, and the source spectrum, Isrc, are then related by Iobs,ν = Isrc,ν·e− τν. For the individual contribution to σν from different phases of the absorbing medium (e.g., gas or dust) and the different constituents (e.g., oxygen) see Wilms et al. (2000) or Gatuzz et al. (2015). Generally in the X-ray range, the optical depth is dominated by metals (Wilms et al. 2000) and σν ∝ E-3, i.e., the photoelectric absorption acts more strongly on the low energy photons.

We caution that the exact choice of absorption model, abundances, and cross sections can lead to differences in NH up to 20–30% between different approaches (Wilms et al. 2000), although they do not affect overall trends observed. We also caution that the absorption modeling is based on the absorption of neutral material, while in reality the material will be moderately photoionized by the strong X-ray source embedded in it. Especially when using proportional counters such as the PCUs, approximating the X-ray absorption by ionized material with absorption in neutral material is an appropriate assumption, since most absorption is due to K-shell absorption, which is only mildly dependent on ionization stage. However, our modeling will not pick up effects from fully ionized material, as it is mainly transparent to X-rays and the RXTE’s instruments did not have the resolution to detect absorption lines.

A second issue relates to the uncertainty of the NH measurements. For models such as the ones used here there is a well-known degeneracy between the power law slope, i.e., Γ1, and NH (e.g., Suchy et al. 2008). By calculating two-dimensional confidence contours we confirm that this degeneracy is not responsible for the variation of NH discussed here (for example contours see Hanke 2011). Because of the limited energy range of the PCA, in addition to the correlation with the power law continuum there is also a degeneracy between parameters of the accretion disk and NH. The effect of a stronger absorption can be counterweighted by a stronger disk component and vice versa. The values of NH from best fit models with and without a disk therefore have to be considered separately because of the different systematic effects and we do so throughout this paper. Unless discussed otherwise, we give all uncertainties at the 90% level.

thumbnail Fig. 4

Example spectra with 1.72 < Γ1< 1.73, but different absorption columns. PCA data and best fit models to PCA and HEXTE data are shown. The ratio plots show residuals of the best fit in color and residuals of an evaluation of the best fit model with NH = NH,ISM (i.e., no absorption local to the system) in black. All observations are from the hard state of 2006–2010 (Sect. 3.1).

thumbnail Fig. 5

Absorption column vs. unabsorbed energy flux during the hard state of 2006–2010. Red circles mark observations shown in Fig. 4.

3. Orbital variability of absorption

3.1. Hard state

We now turn to studying the variability of NH in the RXTE data. As an example, Fig. 4 shows spectra of different observations that have the same typical hard state continuum shape (Γ1 = 1.72...1.73), but different absorption columns. The residuals shown in the figure for various orbital phases illustrate the strong effect caused by the orbital variation compared to the influence of the interstellar medium alone. Absorption affects the whole spectrum up to energies of 10 keV.

thumbnail Fig. 6

Variation of NH with orbital phase for observations where the source was in the hard (left), intermediate (middle), and soft (right) state. Upper panels: orbit dependence of NH measurements for individual satellite orbit-wise spectra (black datapoints with gray uncertainties), as well as the average (red) and median (white) values for orbital phase bins with a width of Δφorb = 0.1. Lower panels: standard deviation σ { NH,22 } ≔ σ { NH/ (1022 cm-2) } of the NH measurements. The panels specifically show 1515 hard state (Γ1 ≤ 2.0) observations that do not require a disk component, 384 intermediate state (2.0 < Γ1 ≤ 2.5) observations that require a disk, and 506 soft state (2.5 < Γ1) observations (all soft state observations require a disk component).

When looking at the whole state-resolved sample, we determine the average and median values of NH and its standard deviation, σ { NH,22 } ≔ σ { NH/ (1022 cm-2) }, for phase bins of width Δφorb = 0.1 starting at φorb = 0. In the hard state, the average column values and the standard deviation, i.e., the variability of the wind between individual observations, increase around superior conjunction (Fig. 6, left).

Individual observations, especially for φorb ~ 0, show NH values much larger than the average for a given phase (Fig. 6, left, see also Fig. 4 for example spectra). We associate these observations with the prolonged deep absorption events (often dubbed “dips”) known from the literature (Sect. 1) and carefully check our data to find out whether these observations have systematic differences to other observations in the same spectral state. We find no such differences; in particular, these dips do not have larger uncertainties in NH and do not show clear trends in their exposure time, 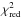χred2\hbox{$\chi^2_{\mathrm{red}}$}, unabsorbed 3–50 keV flux2 (see also Fig. 5), or the correlation between Γ1 and Γ2 known from Wilms et al. (2006). The dips cluster around superior conjunction, but individual strong absorption measurements occur as early as φorb ≈ 0.8 and as late as φorb ≈ 0.3 (Fig. 6, left).

The RXTE spectra do not allow a meaningful fit of partial covering models and so we cannot constrain possible partial covering either in physical space or in time (i.e., a clump or a group of clumps, possibly of different optical depth, passing through the line of sight for a part of the total exposure time of one spectrum). Thus, the NH values derived for individual observations are lower limits on the sum of the absorption columns of individual clumps with the ISM absorption over a given observation’s exposure time (i.e., on average 1.6–1.7 ks, Fig. 1).

thumbnail Fig. 7

Observations from the hard state of 2006–2010 (MJD 53 900–55 375, Grinberg et al. 2013) that do not require a disk. Left: normalized histograms (blue) and normalized cumulative histograms (red) for NH above the ISM value for individual orbital phase bins; n denotes the total number of observations in a given orbital phase bin. We note that the phase bin φorb = 0.7 − 0.8 contains one measurement in excess of 1023 cm-2. Right: orbital dependence of NH. The best fit focussed wind model introduced in Sect. 4.1.2 is shown in green.

Within the hard state, Cyg X-1 can display a range of spectral and timing behaviors (Pottschmidt et al. 2003; Wilms et al. 2006; Grinberg et al. 2014). At the same time, we expect the behavior of the absorption to depend on the broadband spectral shape of the X-ray source because of possible ionization of the wind. For a detailed analysis of absorption, we therefore need a hard state with stable spectral and timing characteristics, such as the long hard state of 2006–2010 (MJD 53 900–55 375, Grinberg et al. 2013, 2014). We show the results for this long hard state period in Fig. 7; it includes 383 observations that do not require a disk (Fig. 2) and that have a total exposure time of 660 ks or ~1.4 orbital periods of the system. The variability of absorption can be clearly seen in the (cumulative) probability distributions of NH values at different orbital phases (Fig. 7, left). The values are low and the distribution narrow at φorb ~ 0.5. At φorb ~ 0, the distribution is broad with a higher average (average values and their standard deviations are shown in Fig. 9, right). We will use this set for comparison with a toy model for the focussed wind and a clumpy wind model in Sects. 4.1.2 and 4.1.3, respectively.

3.2. Intermediate state and soft state

We now address observations of Cyg X-1 in the intermediate and the soft state, i.e., when the X-ray spectrum is much softer than in the hard state. Most data in the intermediate state require a disk component that leads to larger uncertainties in the NH determination and particularly to a systematically increased average value independent of orbital phase as well as a larger σ { NH,22 }. An increase of average NH at φorb ≈ 0 is, however, still visible (Fig. 6, middle).

Our data do not show orbital variability of absorption in the soft state (Fig. 6, right). The average values are comparable with the intermediate state, but in several phase bins we find median values of 4.8 × 1021 cm-2, i.e., the data are consistent with there being no neutral absorption intrinsic to the source. Because of the increased disk contribution, observations in the soft state are even more affected by systematics than those in the intermediate state, especially given that the disk in Cyg X-1 has a temperature ≲0.4 keV (≈4.6 × 106 K) even in the soft state (Wilms et al. 2006, and our fits), i.e., it peaks below the lower limit of our data so that the disk parameters show relatively large uncertainties.

4. Discussion

4.1. Hard state

4.1.1. Discussion and comparison to earlier results

Our results show that despite PCA’s energy coverage only above ~3 keV and comparatively low spectral resolution when compared to CCD or even grating instruments, PCA data can be used to assess trends in the behavior of the absorption. The changes in NH strongly influence the shape of the observed spectra (Fig. 4). The overall orbital variability of NH values found here is consistent with earlier results (Feng & Cui 2002; Ibragimov et al. 2005; Wilms et al. 2006; Boroson & Vrtilek 2010). To our knowledge, we are the first to quantify the variance of the equivalent hydrogen column, σ { NH,22 } (Fig. 6, lower panels).

The largest NH values seen during the hard state (Figs. 4 and 7) are on the order of 1023 cm-2. Kitamoto et al. (1984, using Tenma, Bałucińska-Church et al. (1997, using ASCA), and Hanke et al. (2008, using Chandra reported individual deep absorption events with NH ≳ 1023 cm-2. Periods of increased absorption that lasted longer than a few ks have been observed with various instruments, especially close to superior conjunction. For example, Feng & Cui (2002) discuss a long dip of at least ~3 ks that shows complex substructure. Prolonged periods of increased absorption are also clearly seen in the long uninterrupted observations possible with Chandra (Hanke et al. 2008). Given these previous measurements and the size of our sample, the detection of several strong absorption events as discussed in Sect. 3.1 is plausible.

Bałucińska-Church et al. (2000) have used mainly RXTE-All Sky Monitor (ASM; Levine et al. 1996) data to show orbital variability in ASM-based hardness ratios and in dip (defined by a threshold ASM hardness ratio) occurrence, both peaking at superior conjunction consistent with the behavior of the absorption column density that we observe. They observe a peak in the dip occurence at φorb = 0.95, but our sample is not large enough to track this possible assymetry of the NH distribution around φorb = 0. Poutanen et al. (2008) show that the orbital modulation of ASM count rates in the hard state depends on the superorbital phase: the number of ASM-defined dips shows a superorbital periodicity when assuming a ~150 d superorbital period. The smaller number of our measurements when compared to ASM data combined with the apparent stochastic nature and large variance of the absorption variations do not allow such an analysis here.

Despite these shortcomings, the exceptional coverage of the pointed observation allows us to compare the observational results to theoretical models. In particular we quantitatively compare a simple focussed CAK wind to our data from the stable hard state period of 2006–2010 (~250 orbits of the binary system) in Sect. 4.1.2, and, for the first time for a high mass black hole binary, qualitatively match the observed data from the same stable hard state period with predictions from a clumpy wind model for O-star winds in Sect. 4.1.3.

4.1.2. Focussed wind model in the hard state

We first compare the orbital variation of NH from MJD 53 900–55 370 with a toy model for the focussed wind as introduced by Gies & Bolton (1986b). This model is based on the previous work of Friend & Castor (1982) and depends on the angle θ between the wind direction and the donor-black hole axis. We emphasize that this is only a toy model that does not take into account details of both the physics of a real wind and the observations used. The model is, however, useful to assess general trends and to point out the directions in which better models have to be developed.

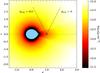thumbnail Fig. 8

Stellar wind density calculated following the focussed wind model of Gies & Bolton (1986a). The x- and z-axes are shown in units of orbital separation. The position of the black hole is marked with a black cross, the position of the center of mass with a green cross. Lines of sight toward the black hole at orbital phases 0 and 0.5 are indicated by dashed lines, the orbital plane by a dotted line. We note that there are no discotinuities in the wind.

For θ ≧ 20°, the wind is the radiatively driven CAK-wind of a single star (Castor et al. 1975). For θ< 20°, the wind varies smoothly with θ with terminal velocity and density peaking at θ = 0. In particular, we employ the model with the fill-out-factor of 0.98 with the correspondent values for terminal velocity and wind density listed in Table 1 of Gies & Bolton (1986a) and use masses, inclination, and orbital period as given in Sect. 1. Figure 8 shows the resulting distribution of wind density.

We obtain the total (neutral and ionized) column density by integrating along the line of sight toward the black hole at a given orbital phase. These values are on the order of 3–5 × 1022 cm-2, i.e., much higher than the measured average values and more reminiscent of dips (cf. Fig. 6, left), but this total column density is not the NH measured in our observations. The fully ionized part of the wind is transparent to X-rays and thus only some weakly to moderately ionized part of the wind will contribute to the measured absorption. We can hence assume that the absorption in the binary is restricted to the region of the wind with log ξ< log ξmax with the ionization parameter ξ defined after Tarter et al. (1969) as ξ = L/ (nr2) with n being the absorbing particle number density, r the distance from the ionizing source, and L the luminosity above the hydrogen Lyman edge (typical for Cyg X-1: L = 1037 erg s-1, Miškovičová et al. 2015). We consider only the contribution of those parts of the wind that satisfy this condition.

We take into account the ISM column density NH,ISM and fit the parameter log ξmax of this model to the data. We obtain log ξmax ≈ 2.7, however with 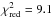χred2=9.1\hbox{$\chi^2_{\mathrm{red}} = 9.1$} for 382 degrees of freedom. The phase variation of NH that corresponds to our best fit value of log ξmax is shown in Fig. 7, right panel, as a green curve. The failure to describe the data well is expected since the toy model does not include the clumping that we expect to contribute greatly to the spread of the NH measurements at a given orbital phase. To conduct a simple test for the influence of clumping on our results, we remove the 13 measurements with NH> 5 × 1022 cm-2 and obtain a best fit 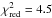χred2=4.5\hbox{$\chi^2_{\mathrm{red}} = 4.5$} for 369 degrees of freedom with a decreased best fit value (log ξmax ≈ 2.67 instead of previously log ξmax ≈ 2.71).

The toy model also neglects additional smaller effects such as a potential photoionization wake that would introduce asymmetries (Blondin 1994). Uncertainties in determination of the ISM absorption, NH,ISM, toward the source may lead to further problems (Xiang et al. 2011). However, it is interesting to note that when we account for the fact that our measurements include the clumping, our result is in rough agreement with the results (log ξ ≲ 2.6) found by Miškovičová et al. (2015), who infer NH values ranging from 6.8 × 1021 cm-2 to 1.3 × 1022 cm-2 from modeling the Ne edge in the non-dip parts of hard state Chandra observations at five different orbital phases.

thumbnail Fig. 9

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N = 1000 and the terminal porosity length h∞ = R∗ (see Sect. 4.1.3 for explanation of parameters). Left: model histograms for the distribution of equivalent absorption column density NH. Right: average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption.

4.1.3. Clumpy wind model for the hard state

We next consider whether the observed variability in the absorbing column could be due to wind structures, and how the characteristics of those structures compare to what is known about radiatively driven winds in other contexts, such as clumps (Abbott et al. 1981; Hillier & Miller 1998; Fullerton et al. 2006; Puls et al. 2006) or discrete absorption components (DACs; Prinja & Howarth 1986). To this end, we use a numerical code to simulate the column density between the observer and a point-like X-ray source, as the source orbits around a companion whose wind is composed of discrete clumps. For simplicity, the code does not account for the focussed wind properties of the system; moreover, the clumps are assumed to be spherical, rather than the pancake morphologies considered by other authors (e.g., Feldmeier et al. 2003; Oskinova et al. 2004). At a given orbital phase, the column-density evaluation is performed by casting a ray from the source to the observer, determining which ray segments lie inside clumps, and summing up the contributions from these segments (as the product of the segment length and the clump density).

The distribution of clumps throughout the wind follows a similar approach to that described in Appendix A of Sundqvist et al. (2012). Clumps are relased at the stellar surface r = R∗ in a random direction and with an initial radial size l∗, and then advect outward with the wind according to a canonical β velocity law ν(r) = ν∞(1 − R∗/r)β. As a clump advects its radial size grows as l(r) = (r/R∗)l∗, but its mass remains fixed at m = Ṁ/Ṅ where Ṁ is the overall wind mass loss rate and Ṅ is the clump release rate. The latter is most conveniently parameterized in terms of the number of clumps per wind flow time N = Ṅtflow, with tflow ≡ R∗/ ν∞. To relate these parameters to the porosity length h (essentially, the mean free path between clumps; see Owocki & Cohen 2006), we note that h(r) = h∞ν(r)/ν∞, where the terminal porisity length is 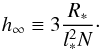h∞≡3R∗l∗2N·\begin{equation} h_{\infty} \equiv 3 \frac{R_{*}}{l_{*}^{2} N}\cdot \end{equation}(1)To apply the code to Cyg X-1, we assume β = 1.6, R∗ = 18 R⊙, ν∞ = 2400 km s-1, and Ṁ = 2 × 10-6 M⊙ yr-1, and adopt the orbital parameters given in Sect. 1. We ran a grid of simulations with N = 100,316,1000,3162, and 10 000, and h∞/R∗ = 0.1,0.316,1,3.162, and 10 to explore the level of variability expected on the timescales we probe here. For each grid point we calculated 1000 model orbits, with a phase resolution Δφorb = 0.001. Since typical RXTE observations of Cyg X-1 had an exposure of about 0.005 orbits, and since each observation is not subdivided into time slices, it is necessary to average the model to a timescale corresponding to the observations. Thus, we rebinned the models by a factor of five by taking a linear average of the model column density. A linear average over a phase bin does not correctly account for the non-linear addition of partial covering in time, but is adequate given the crude nature of our model. Likewise, rebinning by a factor of five is not an exact match to the actual observations, but it is an adequate approximation.

The statistical properties of each phase bin of 0.005 orbits do not change rapidly as a function of orbital phase, so these statistical properties were further averaged into phase bins of 0.1 orbits, corresponding to the grouping used to evaluate the observations. We show this statistical analysis of the column for N = 1000 and h∞ = R∗ in Fig. 9; the mean and standard deviation of this model are compared to those of the data in the right panel. We have chosen a model with a similar level of variability as the observations near phase 0.5, where our line of sight to the compact object mainly probes the part of the wind that is likely least perturbed by the peculiarities of the focussed part of the wind. For other model realizations see Figs. A.1 and A.2.

The choice of porosity length h∞ has a strong effect on determining the level of variability in the model (Fig. A.1). The choice of N has a weaker effect, with larger values of N (and thus small values of l∗) showing somewhat reduced variability (Fig. A.2). This is a result of single observations averaging over the transit of one or more clumps across the line of sight, thus washing out the variability expected on short timescales. We have explored the effect of different choices of averaging timescale (or equivalently observation duration) in our simulations, and as expected, we find that increasing the averaging timescale tends to reduce the variability (see also Sect. 3.1 for a discussion of exposure times on the measured NH). We also find that there is a maximum useful time resolution above which increasing the sampling rate does not increase the level of variability observed. This maximum rate corresponds roughly to the timescale for a typical clump to transit our line of sight to the compact object which is on the order of l∗/ ν∞ (when the wind velocity dominates over orbital velocity as is the case here). One obvious conclusion of these results is that the clump size scale could be constrained by obtaining spectra of high statistical quality (e.g., with Suzaku or Chandra satellites) and exploring the level of variability on shorter timescales.

The models with h∞ = R∗ have the best agreement with the data near φorb = 0.5, with the exception that for N = 10 000 the model with h∞ = 3.162 R∗ has the best agreement (Fig. A.2). Based on previous theoretical and observational investigations of single O stars, it is reasonable that h∞ should be comparable to or smaller than R∗ (Dessart & Owocki 2003; Owocki & Cohen 2006; Nazé et al. 2013). This is also consistent with the results of Leutenegger et al. (2013), who found that the spectrum of the single O supergiant ζ Pup could be fit with models having porosity lengths h∞ ≤ R∗. To test for the influence of terminal velocity on our results, we re-ran the simulations with ν∞ = 1600 km s-1. Although the resulting mean values for NH are higher (owing to the increased wind density), our results are otherwise similar to the original ν∞ = 2400 km s-1 grid, and thus our conclusions do not change.

Comparing Figs. 7 and 9, the model shows a Gaussian distribution of absorbing columns, while the data show a non-Gaussian tail near phase 0. It seems likely that this non-Gaussian tail reflects some unusual wind structure related to the focussed wind. However, since the impact parameter of our line of sight with respect to the optical companion is smallest near this orbital phase, the tail might also be a signature of a wind with pancake-shaped clumps, which would be effectively more porous when viewed edge on (Feldmeier et al. 2003; Oskinova et al. 2012). A more thorough exploration of these effects may give insight into their importance, but it is beyond the scope of this paper.

4.2. Intermediate state and soft state

Because of the lack of suitable observations in the previously analyzed samples, the variability of absorption in intermediate and soft states has not been previously analyzed using RXTE spectra, but only using ASM data. Boroson & Vrtilek (2010) analyzed orbital variability of absorption in five soft state periods. Boroson & Vrtilek see no variability in their soft states 2 and 5 that would be mostly classified as intermediate states using the more rigorous state definitions of Grinberg et al. (2013). Their soft state 3 shows orbital variability. Boroson & Vrtilek (2010) also point out that the intrinsic variability of the X-ray source in the softer periods hampers the search for periodicities in ASM data.

Based on the pointed RXTE data alone, we see no orbital variability in the soft state, while there are signs of an increase in the absorption toward φorb ≈ 0 in the intermediate state. These results qualitatively agree with the behavior seen in analyses of Chandra high resolution spectra: as the source softens, dipping becomes less pronounced (Miškovičová et al. 2015). However, dips have still been observed in the soft state with Suzaku (Yamada et al. 2013, but we note the strong changes in hardness ratio in their data that may be indicative of spectral evolution during the observation). Hanke (2011) shows lightcurves and softness ratios of all Chandra observations up to and including ObsID 13219 taken in 2011 February: some weak and short dipping can be seen in the soft state data.

The interpretation of these results in the context of the previous Suzaku and Chandra results is that the soft X-rays emitted from the vicinity of the black hole in the soft state are strong enough to fully ionize the wind and even some or all of the optically thick clumps. The wind thus becomes mainly transparent to X-rays and no orbital variation of absorption column can be seen.

5. Summary and conclusions

We have analyzed almost 5 Ms of RXTE observations of Cyg X-1 taken over a span of 16 years in different spectral states. We find clear orbital variability of absorption in the hard state of the X-ray source with an overall increase and additional deep absorption events (dips with NH ~ 1023 cm-2) around superior conjunction, in agreement with previous work with different instruments. Because of the presence of an additional multitemperature disk component in the spectra, the absorption column cannot be well constrained in the intermediate and soft states. However, there are signs for increased NH toward φorb = 0 in the intermediate state.

We compared the observed orbital variability of absorption with two wind models. A toy model for a focussed line-driven wind without clumps (Gies & Bolton 1986b) does not describe the data well and we attribute the differences to the absence of clumping in the model that would lead to the observed strong variations of NH at the same orbital phase. Qualitatively matching the observed NH distributions at a given orbital phase to a toy clumpy wind model (Owocki & Cohen 2006; Sundqvist et al. 2012) without a focussed wind and with spherical clumps results in the best match for models with porosity length, h∞, on the order of the stellar radius, R∗, at orbital phases φorb ≈ 0.5, in agreement with results from (effectively) single O stars (Leutenegger et al. 2013). Our models exclude both much lower and much higher porosities. The discrepancies between the toy clumpy wind model and data at φorb ≈ 0 could be due to either a focussed wind component or to a non-spherical shape of the clumps or to a combination of both. We note here that the existence of a focussed wind component in Cyg X-1 is supported by multiple lines of evidence such as optical measurements (Gies & Bolton 1986b; Sowers et al. 1998).

While we caution against an over-interpretation of details of the presented simple models, we would like to note that they firstly demonstate that RXTE data of Cyg X-1 can indeed be used for an analysis of the long term orbital variability of absorption and secondly clearly demand better models. In particular, a thorough exploration of the winds will require a model that includes both the focussed and the clumpy structures of the wind, and possibly also different clump shapes and/or sizes.

Online material

Appendix A: Clumpy wind model simulations

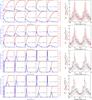thumbnail Fig. A.1

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N = 1000 and varying terminal porosity length h∞ = 10, 3.162, 0.316, and 0.1 R∗ (see Sect. 4.1.3 for explanation of parameters and Fig. 9 for the case of h∞ = 1). Left: model histograms for the distribution of equivalent absorption column density NH. Right: average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption.

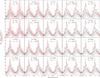thumbnail Fig. A.2

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N and varying terminal porosity length h∞. Shown are average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption. For the case of N = 1000 see Figs. 9 and A.1.

2

The X-ray flux of Cyg X-1 can vary by a factor of 4–5 at the same spectral shape (Wilms et al. 2006, and references therein).

Acknowledgments

Support for this work was provided by NASA through the Smithsonian Astrophysical Observatory (SAO) contract SV3-73016 to MIT for Support of the Chandra X-Ray Center (CXC) and Science Instruments; CXC is operated by SAO for and on behalf of NASA under contract NAS8-03060. It was partially completed by LLNL under Contract DE-AC52-07NA27344, and is supported by NASA grants to LLNL and NASA/GSFC. We thank the Bundesministerium für Wirtschaft und Technologie for funding through Deutsches Zentrum für Luft- und Raumfahrt grant 50 OR 1113. M.A.N. acknowledges support from NASA Grant NNX12AE37G. R.H.D.T. acknowledges support from NASA award NNX12AC72G. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. We thank John E. Davis for the development of the slxfig module used to prepare all figures in this work and Fritz-Walter Schwarm, Thomas Dauser, and Ingo Kreykenbohm for their work on the Remeis computing cluster. This research has made use of ISIS functions (isisscripts) provided by ECAP/Remeis observatory and MIT3. Without the hard work by Evan Smith and Divya Pereira to schedule the observations of Cyg X-1 so uniformly for more than a decade, this whole series of papers would not have been possible.

References

  1. Abbott, D. C., Bieging, J. H., & Churchwell, E. 1981, ApJ, 250, 645 [NASA ADS] [CrossRef] [Google Scholar]
  2. Axelsson, M., Borgonovo, L., & Larsson, S. 2006, A&A, 452, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bałucińska-Church, M., Takahashi, T., Ueda, Y., et al. 1997, ApJ, 480, L115 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bałucińska-Church, M., Church, M. J., Charles, P. A., et al. 2000, MNRAS, 311, 861 [NASA ADS] [CrossRef] [Google Scholar]
  5. Belloni, T. M. 2010, in The Jet Paradigm: From Microquasars to Quasars (Berlin: Springer Verlag), ed. T. Belloni, Lect. Notes Phys., 794, 53 [Google Scholar]
  6. Benlloch, S., Pottschmidt, K., Wilms, J., et al. 2004, in X-ray Timing 2003: Rossi and Beyond, eds. P. Kaaret, F. K. Lamb, & J. H. Swank, AIP Conf. Ser., 714, 61 [Google Scholar]
  7. Blondin, J. M. 1994, ApJ, 435, 756 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Böck, M., Grinberg, V., Pottschmidt, K., et al. 2011, A&A, 533, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Boroson, B., & Vrtilek, S. D. 2010, ApJ, 710, 197 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brocksopp, C., Fender, R. P., Larionov, V., et al. 1999, MNRAS, 309, 1063 [NASA ADS] [CrossRef] [Google Scholar]
  11. Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
  12. Davis, R., & Hartmann, L. 1983, ApJ, 270, 671 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dessart, L., & Owocki, S. P. 2003, A&A, 406, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
  15. Feldmeier, A., Oskinova, L., & Hamann, W.-R. 2003, A&A, 403, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Feng, Y. X., & Cui, W. 2002, ApJ, 564, 953 [NASA ADS] [CrossRef] [Google Scholar]
  17. Friend, D. B., & Castor, J. I. 1982, ApJ, 261, 293 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gatuzz, E., García, J., Kallman, T. R., Mendoza, C., & Gorczyca, T. W. 2015, ApJ, 800, 29 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gies, D. R., & Bolton, C. T. 1986a, ApJ, 304, 371 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gies, D. R., & Bolton, C. T. 1986b, ApJ, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gies, D. R., Bolton, C. T., Thomson, J. R., et al. 2003, ApJ, 583, 424 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gies, D. R., Bolton, C. T., Blake, R. M., et al. 2008, ApJ, 678, 1237 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gleissner, T., Wilms, J., Pooley, G. G., et al. 2004a, A&A, 425, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gleissner, T., Wilms, J., Pottschmidt, K., et al. 2004b, A&A, 414, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Grinberg, V., Hell, N., Pottschmidt, K., et al. 2013, A&A, 554, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Grinberg, V., Pottschmidt, K., Böck, M., et al. 2014, A&A, 565, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hanke, M. 2011, Ph.D. Thesis, Universität Erlangen-Nürnberg [Google Scholar]
  29. Hanke, M., Wilms, J., Nowak, M. A., et al. 2008, in Proc. VII Microquasar Workshop: Microquasars and Beyond [Google Scholar]
  30. Hanke, M., Wilms, J., Nowak, M. A., et al. 2009, ApJ, 690, 330 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hell, N., Miškovičová, I., Brown, G. V., et al. 2013, Phys. Scr. T, 156, 014008 [NASA ADS] [CrossRef] [Google Scholar]
  32. Herrero, A., Kudritzki, R. P., Gabler, R., Vilchez, J. M., & Gabler, A. 1995, A&A, 297, 556 [NASA ADS] [Google Scholar]
  33. Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
  34. Houck, J. C. 2002, in High Resolution X-ray Spectroscopy with XMM-Newton and Chandra, ed. G. Branduardi-Raymont, published electronically [Google Scholar]
  35. Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [Google Scholar]
  36. Ibragimov, A., Poutanen, J., Gilfanov, M., Zdziarski, A. A., & Shrader, C. R. 2005, MNRAS, 362, 1435 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ibragimov, A., Zdziarski, A. A., & Poutanen, J. 2007, MNRAS, 381, 723 [NASA ADS] [CrossRef] [Google Scholar]
  38. Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kitamoto, S., Miyamoto, S., Tanaka, Y., et al. 1984, PASJ, 36, 731 [NASA ADS] [Google Scholar]
  40. Leutenegger, M. A., Cohen, D. H., Sundqvist, J. O., & Owocki, S. P. 2013, ApJ, 770, 80 [NASA ADS] [CrossRef] [Google Scholar]
  41. Levine, A. M., Bradt, H., Cui, W., et al. 1996, ApJ, 469, L33 [NASA ADS] [CrossRef] [Google Scholar]
  42. Li, F. K., & Clark, G. W. 1974, ApJ, 191, L27 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
  44. Makishima, K., Maejima, Y., Mitsuda, K., et al. 1986, ApJ, 308, 635 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mason, K. O., Hawkins, F. J., Sanford, P. W., Murdin, P., & Savage, A. 1974, ApJ, 192, L65 [NASA ADS] [CrossRef] [Google Scholar]
  46. Miller, J. M., Wojdowski, P., Schulz, N. S., et al. 2005, ApJ, 620, 398 [NASA ADS] [CrossRef] [Google Scholar]
  47. Miller, J. M., Pooley, G. G., Fabian, A. C., et al. 2012, ApJ, 757, 11 [NASA ADS] [CrossRef] [Google Scholar]
  48. Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
  49. Miškovičová, I., Hell, N., Hanke, M., et al. 2015, A&A, submitted [Google Scholar]
  50. Morton, D. C. 1967, ApJ, 150, 535 [NASA ADS] [CrossRef] [Google Scholar]
  51. Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Nazé, Y., Oskinova, L. M., & Gosset, E. 2013, ApJ, 763, 143 [NASA ADS] [CrossRef] [Google Scholar]
  53. Noble, M. S., & Nowak, M. A. 2008, PASP, 120, 821 [NASA ADS] [CrossRef] [Google Scholar]
  54. Nowak, M. A., Hanke, M., Trowbridge, S. N., et al. 2011, ApJ, 728, 13 [NASA ADS] [CrossRef] [Google Scholar]
  55. Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
  56. Oskinova, L. M., Feldmeier, A., & Hamann, W.-R. 2004, A&A, 422, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Oskinova, L. M., Feldmeier, A., & Kretschmar, P. 2012, MNRAS, 421, 2820 [NASA ADS] [CrossRef] [Google Scholar]
  58. Owocki, S. P., & Cohen, D. H. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef] [Google Scholar]
  59. Owocki, S. P., Castor, J. I., & Rybicki, G. B. 1988, ApJ, 335, 914 [NASA ADS] [CrossRef] [Google Scholar]
  60. Parsignault, D. R., Epstein, A., Grindlay, J., et al. 1976, Ap&SS, 42, 175 [NASA ADS] [CrossRef] [Google Scholar]
  61. Pottschmidt, K., Wilms, J., Nowak, M. A., et al. 2003, A&A, 407, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [NASA ADS] [CrossRef] [Google Scholar]
  63. Pravdo, S. H., White, N. E., Becker, R. H., et al. 1980, ApJ, 237, L71 [NASA ADS] [CrossRef] [Google Scholar]
  64. Priedhorsky, W. C., Terrell, J., & Holt, S. S. 1983, ApJ, 270, 233 [NASA ADS] [CrossRef] [Google Scholar]
  65. Prinja, R. K., & Howarth, I. D. 1986, ApJS, 61, 357 [NASA ADS] [CrossRef] [Google Scholar]
  66. Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Rahoui, F., Lee, J. C., Heinz, S., et al. 2011, ApJ, 736, 63 [NASA ADS] [CrossRef] [Google Scholar]
  68. Reid, M. J., McClintock, J. E., Narayan, R., et al. 2011, ApJ, 742, 83 [NASA ADS] [CrossRef] [Google Scholar]
  69. Remillard, R. A., & Canizares, C. R. 1984, ApJ, 278, 761 [NASA ADS] [CrossRef] [Google Scholar]
  70. Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sako, M., Liedahl, D. A., Kahn, S. M., & Paerels, F. 1999, ApJ, 525, 921 [NASA ADS] [CrossRef] [Google Scholar]
  72. Shaposhnikov, N., & Titarchuk, L. 2006, ApJ, 643, 1098 [NASA ADS] [CrossRef] [Google Scholar]
  73. Shaposhnikov, N., Jahoda, K., Markwardt, C., Swank, J., & Strohmayer, T. 2012, ApJ, 757, 159 [NASA ADS] [CrossRef] [Google Scholar]
  74. Sowers, J. W., Gies, D. R., Bagnuolo, W. G., et al. 1998, ApJ, 506, 424 [NASA ADS] [CrossRef] [Google Scholar]
  75. Suchy, S., Pottschmidt, K., Wilms, J., et al. 2008, ApJ, 675, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  76. Sundqvist, J. O., & Owocki, S. P. 2013, MNRAS, 428, 1837 [NASA ADS] [CrossRef] [Google Scholar]
  77. Sundqvist, J. O., Owocki, S. P., Cohen, D. H., Leutenegger, M. A., & Townsend, R. H. D. 2012, MNRAS, 420, 1553 [NASA ADS] [CrossRef] [Google Scholar]
  78. Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] [Google Scholar]
  79. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
  80. Vrtilek, S. D., Boroson, B. S., Hunacek, A., Gies, D., & Bolton, C. T. 2008, ApJ, 678, 1248 [NASA ADS] [CrossRef] [Google Scholar]
  81. Walborn, N. R. 1973, ApJ, 179, L123 [Google Scholar]
  82. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
  83. Wilms, J., Nowak, M. A., Pottschmidt, K., Pooley, G. G., & Fritz, S. 2006, A&A, 447, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Xiang, J., Lee, J. C., Nowak, M. A., & Wilms, J. 2011, ApJ, 738, 78 [NASA ADS] [CrossRef] [Google Scholar]
  85. Yamada, S., Torii, S., Mineshige, S., et al. 2013, ApJ, 767, L35 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zdziarski, A. A., Pooley, G. G., & Skinner, G. K. 2011, MNRAS, 412, 1985 [NASA ADS] [CrossRef] [Google Scholar]
  87. Ziółkowski, J. 2014, MNRAS, 440, L61 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Histogram of the PCA exposure times of the individual satellite orbit-wise observations analyzed in this work. The mean exposure is 1.74 ks, the median 1.66 ks.
In the text
thumbnail Fig. 2

Number of orbitwise PCA observations with a given soft photon index Γ1 that do (red) or do not (blue) require a multitemperature disk component. Also highlighted are observations that do not require a disk and fall into the long hard state of MJD 53 900–55 375 (black). Dashed vertical lines indicate thresholds for hard (Γ1 ≤ 2.0), intermediate (2.0 < Γ1 ≤ 2.5), and soft (2.5 < Γ1) states according to Grinberg et al. (2013).
In the text
thumbnail Fig. 3

Histogram of χred2\hbox{$\chi^2_{\mathrm{red}}$} values for observations that do (red) and do not (blue) require a multitemperature disk component.
In the text
thumbnail Fig. 4

Example spectra with 1.72 < Γ1< 1.73, but different absorption columns. PCA data and best fit models to PCA and HEXTE data are shown. The ratio plots show residuals of the best fit in color and residuals of an evaluation of the best fit model with NH = NH,ISM (i.e., no absorption local to the system) in black. All observations are from the hard state of 2006–2010 (Sect. 3.1).
In the text
thumbnail Fig. 5

Absorption column vs. unabsorbed energy flux during the hard state of 2006–2010. Red circles mark observations shown in Fig. 4.
In the text
thumbnail Fig. 6

Variation of NH with orbital phase for observations where the source was in the hard (left), intermediate (middle), and soft (right) state. Upper panels: orbit dependence of NH measurements for individual satellite orbit-wise spectra (black datapoints with gray uncertainties), as well as the average (red) and median (white) values for orbital phase bins with a width of Δφorb = 0.1. Lower panels: standard deviation σ { NH,22 } ≔ σ { NH/ (1022 cm-2) } of the NH measurements. The panels specifically show 1515 hard state (Γ1 ≤ 2.0) observations that do not require a disk component, 384 intermediate state (2.0 < Γ1 ≤ 2.5) observations that require a disk, and 506 soft state (2.5 < Γ1) observations (all soft state observations require a disk component).
In the text
thumbnail Fig. 7

Observations from the hard state of 2006–2010 (MJD 53 900–55 375, Grinberg et al. 2013) that do not require a disk. Left: normalized histograms (blue) and normalized cumulative histograms (red) for NH above the ISM value for individual orbital phase bins; n denotes the total number of observations in a given orbital phase bin. We note that the phase bin φorb = 0.7 − 0.8 contains one measurement in excess of 1023 cm-2. Right: orbital dependence of NH. The best fit focussed wind model introduced in Sect. 4.1.2 is shown in green.
In the text
thumbnail Fig. 8

Stellar wind density calculated following the focussed wind model of Gies & Bolton (1986a). The x- and z-axes are shown in units of orbital separation. The position of the black hole is marked with a black cross, the position of the center of mass with a green cross. Lines of sight toward the black hole at orbital phases 0 and 0.5 are indicated by dashed lines, the orbital plane by a dotted line. We note that there are no discotinuities in the wind.
In the text
thumbnail Fig. 9

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N = 1000 and the terminal porosity length h∞ = R∗ (see Sect. 4.1.3 for explanation of parameters). Left: model histograms for the distribution of equivalent absorption column density NH. Right: average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption.
In the text
thumbnail Fig. A.1

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N = 1000 and varying terminal porosity length h∞ = 10, 3.162, 0.316, and 0.1 R∗ (see Sect. 4.1.3 for explanation of parameters and Fig. 9 for the case of h∞ = 1). Left: model histograms for the distribution of equivalent absorption column density NH. Right: average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption.

In the text
thumbnail Fig. A.2

Predictions of NH variability assuming a clumpy wind model with the total number of clumps per flow time N and varying terminal porosity length h∞. Shown are average values (circles) and standard deviations (error bars on the average values) in a given orbital phase for the theoretical model (red) and values measured in the hard state of MJD 53 900−55 375 (black). Average measured values are shown as “average − NH,ISM” to account for the ISM absorption. For the case of N = 1000 see Figs. 9 and A.1.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.