| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201423910 | |
| Published online | 16 April 2015 | |
Performance of the VLT Planet Finder SPHERE
II. Data analysis and results for IFS in laboratory
1 INAF−Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: dino.mesa@oapd.inaf.it
2 Aix Marseille Université, CNRS, LAM – Laboratoire d’Astrophysique de Marseille, UMR 7326, 13388 Marseille, France
3 Dipartimento di Fisica ed Astronomia – Universitá di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
4 INAF–Osservatorio Astrofisico di Arcetri – L.go E. Fermi 5, 50125 Firenze, Italy
5 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
6 LESIA, Observatoire de Paris, CNRS, University Pierre et Marie Curie Paris 6 and University Denis Diderot Paris 7, 5 place Jules Janssen, 92195 Meudon, France
7 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
8 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
9 CRAL, UMR 5574, CNRS, Université Lyon 1, 9 avenue Charles André, 69561 Saint Genis Laval Cedex, France
10 Laboratoire J.-L. Lagrange, UMR 7293, Observatoire de la Côte d’Azur (OCA), Université de Nice-Sophia Antipolis (UNS), CNRS, Campus Valrose, 06108 Nice Cedex 2, France
11 ONERA – The French Aerospace Lab BP72 – 29 avenue de la Division Leclerc, 92322 Chatillon Cedex, France
12 Observatoire de Genève, University of Geneva, 51 Chemin des Maillettes, 1290 Versoix, Switzerland
13 Sterrenkundig Instituut Anton Pannekoek, University of Amsterdam, Science Park 904, 1098 Amsterdam, The Netherlands
Received: 31 March 2014
Accepted: 26 February 2015
Aims. We present the performance of the Integral Field Spectrograph (IFS) of SPHERE, the high-contrast imager for the ESO VLT telescope designed to perform imaging and spectroscopy of extrasolar planets, obtained from tests performed at the Institut de Planétologie et d’Astrophysique de Grenoble facility during the integration phase of the instrument.
Methods. The tests were performed using the instrument software purposely prepared for SPHERE. The output data were reduced applying the SPHERE data reduction and handling software, adding an improved spectral deconvolution procedure. To this aim, we prepared an alternative procedure for the spectral subtraction exploiting the principal component analysis algorithm. Moreover, a simulated angular differential imaging procedure was also implemented to estimate how the instrument performed once this procedure was applied at telescope. The capability of the IFS to faithfully retrieve the spectra of the detected faint companions was also considered.
Results. We found that the application of the updated version of the spectral deconvolution procedure alone, when the algorithm throughput is properly taken into account, gives us a 5σ limiting contrast of the order of 5 × 10-6 or slightly better. The further application of the angular differential imaging procedure on these data should allow us to improve the contrast by one order of magnitude down to around 7 × 10-7 at a separation of 0.3 arcsec. The application of a principal component analysis procedure that simultaneously uses spectral and angular data gives comparable results. Finally, we found that the reproducibility of the spectra of the detected faint companions is greatly improved when angular differential imaging is applied in addition to the spectral deconvolution.
Key words: instrumentation: spectrographs / methods: data analysis / techniques: imaging spectroscopy / planetary systems
© ESO, 2015
1. Introduction
High-contrast direct imaging of extrasolar planets is very challenging because of the very high brightness contrast between the planets and their host (10-6 for young giant planets with intrinsic emission observed in the near infrared and 10-8 − 10-9 for old giant and rocky planets seen through stellar reflected light), and the very small angular separation between the planets and their hosts (few tenths of arcsec for planet at ~10 AU from their hosts and tens of parsec away). For this reason, only 47 low-mass companions out of more than 1000 planets discovered so far have been detected by exploiting high-contrast imaging (see Extrasolar Encyclopaedia1; Schneider et al. 2011). A new generation of instruments devoted to exploiting this technique is now becoming operational. They combine extreme adaptive optics (XAO), providing high Strehl ratio (SR) by correcting high-order wavefront aberrations, with high-efficiency coronagraphs to attenuate the diffracted light from the host star. To fully exploit the potential of these instruments, differential imaging techniques, such as angular differential imaging (ADI; see Marois et al. 2006b), simultaneous spectral differential imaging (S-SDI; see, e.g., Racine et al. 1999 and Marois et al. 2005) and spectral deconvolution2 (SD; see Sparks & Ford 2002 and Thatte et al. 2007) are also used. One of these instruments, Project 1640 (Crepp et al. 2011), is already operating at the 5 m Palomar Telescope and led to good scientific results (see, e.g., Oppenheimer et al. 2013). The Gemini Planet Imager (GPI; see Macintosh et al. 2006) is starting science operations at the Gemini South Telescope while SPHERE is currently in its science verification phase at Paranal. A fourth instrument called CHARIS is expected to become operative by the end of 2015 (Peters-Limbach et al. 2013) at the Subaru Telescope. This instrument is expected to expand the capabilities of SCExAO, already available at the same telescope (see e.g. Currie et al. 2014). Besides these instruments, the LBT telescope with its lower order adaptive optics system has proven to be a very powerful instrument for the imaging of extrasolar planets (see e.g. Skemer et al. 2012; Esposito et al. 2013).
The instrument SPHERE (Beuzit et al. 2006), dedicated to high-contrast imaging of faint planetary mass companions around nearby young stars, is installed on the Nasmyth platform of the ESO Very Large Telescope (VLT). It is divided into four subsystems:
-
the Common Path and Infrastructure (CPI) receives and transfers telescope light, feeds the other three subsystems with a highly stabilized adaptive optics (AO) corrected and coronagraphic beam. The Extreme AO system for SPHERE, called SAXO, produces a beam with a Strehl ratio better than 90% (Petit et al. 2012). The AO deformable mirror (DM) is described in Hugot et al. (2012);
the Zurich IMaging POLarimeter (ZIMPOL) produces direct and differential polarimetric images in the visible between 500 and 900 nm (Thalmann et al. 2008);
the InfraRed Dual-band Imager and Spectrograph (IRDIS) has various observing modes: classical imaging (CI), dual-band imaging (DBI; see Vigan et al. 2010), polarimetric imaging (DPI; see Langlois et al. 2010), or long-slit spectroscopy (LSS; see Vigan et al. 2008). It works in the near infrared between 0.95 and 2.32 μm with a field of view (FOV) of 12.5 × 11 arcsec (Dohlen et al. 2008);
the IFS also operates in the near infrared between 0.95 and 1.35 μm with a 2-pixel spectral resolution of 50 for the YJ-mode and between 0.95 and 1.65 μm with a spectral resolution of around 30 for the YH-mode (Claudi et al. 2008). Its FOV is of 1.7 arcsec square. The integral field unit (IFU) is composed of a double system of lenslets set on an a-focal configuration and tailored to reduce cross-talk between both adjacent lenslets and adjacent spectra (Antichi et al. 2009). The raw data for IFS is composed of around 21 000 spectra aligned with the detector columns over a hexagonal grid rotated by 10.9° with respect to the dispersion axis. The data reduction and handling (DRH) software (Pavlov et al. 2008) transforms each detector frame into a datacube composed of 39 monochromatic images of 291 × 291 pixels for both the observing modes.
In this paper we present the results of the laboratory tests performed and highlight the performance limits of the IFS in terms of contrast and signal-to-noise (S/N) as determined from laboratory data. We obtained these results with dedicated speckle subtraction algorithms, which we will describe. While on-sky data from SPHERE are currently becoming available we think that this paper exploiting the laboratory data is still useful given that it allows us to present the state-of-the-art data reduction algorithms for SPHERE IFS.
The outline of this paper is: in Sect. 2 we describe the test procedures, in Sect. 3 we describe the data reduction pipeline, in Sects. 4 and 5 we present the results of the data reduction for the YJ- and YH-mode, and in Sect. 6 we give our conclusions.
2. The IFS tests description
The whole SPHERE instrument is at present in its science verification phase at Paranal. Before shipment to ESO, it was assembled in a large dedicated clean room at the Institut de Planétologie et d’Astrophysique de Grenoble (IPAG). A large number of functional and performance tests were performed on the instrument from the end of 2011 to the end of 2013. The aim of this paper is to describe the tests performed on IFS. The first goal of these tests was to check that the instrument control software (INS) worked properly. It is organized in different components, defined as “templates”, which can be run autonomously or within observing blocks, according to the operational model adopted at VLT (see e.g. Baruffolo et al. 2012). These templates execute all the tasks needed to perform the calibration of the instrument and acquire scientific observations.
The main calibration templates perform the following tasks: detector dark and flat field acquisition, determination of the spectra positions, wavelength calibration and finally acquisition of the IFU flat field. The IFU flat field is required to calibrate different outputs from different lenslets composing the lenslet array. Other calibration templates were executed to monitor the instrument such as the gain and readout noise (RON), ghosts, distortion and background. All these templates were intensively and repeatedly tested and, when necessary, modifications were made to improve their outcome or to correct errors during their execution. Other calibration templates dedicated to the observations (e.g., sky flat) will be fully tested when the instrument is installed at the telescope.
Two templates enable the acquisition of scientific data: one of them is for observations of single objects with IFS in the YJ-mode IRDIFS, while the second is for the observations in the YH-mode (IRDIFS_EXT). All these templates run IFS in parallel with IRDIS. Several dichroic beamsplitters in the CPI, located after the coronagraphic focal mask and before the Lyot stops, allow for the feeding of both instruments simultaneously. IRDIS is used both for acquisition purposes, like fine coronagraphic centering and the noncommon path aberrations calibration, as well as for scientific purposes.
The laboratory tests performed at IPAG used a telescope simulator (TSIM) including rotating phase screens to emulate atmospheric turbulence corresponding to 0.6′′, 0.8′′, and 1.2′′ seeing conditions. The phase screens have adjustable rotation speed to simulate wind speeds ranging from 2 to 10 m/s. Stars of different brightness were emulated by inserting different neutral density filters. It is important to say that this method just simulates a fainter star from the IFS point of view, while this is not true for the AO. This is important given that the AO performance degrades for faint stars. Moreover, several coronagraphs (SPHERE allows the use of both apodized Lyot and 4-quadrant coronagraphs; see Boccaletti et al. 2008) have been tested. However, we report on results obtained only with the apodized Lyot coronagraph with a mask diameter of 185 mas (projected on sky) since the performance of the 4-quadrant coronagraph is not yet optimized. Possible explanations for performances loss, compared to expectations, with this type of coronagraph could be related to the presence of low-order aberrations, probably a defocus, or a possible aging of the optical components materials. These reasons could explain the higher level of performances obtained during the preliminary tests performed at LESIA (see e.g. Boccaletti et al. 2008). Figure 1 shows an example of IFS (in the YJ-mode) coronagraphic raw data, while Fig. 2 shows a zoom on the central part of the same image highlighting spectral layout. In this case, we used a simulated star with a J magnitude of 2.6 with typical seeing and wind speed condition for Paranal (0.8 arcsec seeing and 5 m/s wind speed).
 |
Fig. 1 Example of IFS coronagraphic raw data. The displayed image covers a square 1.77×1.77 arcsec FOV. This observation was performed in YJ-mode. |
3. Data reduction pipeline
We performed the data reduction using the DRH pipeline developed by the SPHERE consortium. This software is composed by different modules, called recipes, aimed to reduce specific data sets generated by the SPHERE instrument software. The data reduction pipeline includes the following steps:
-
creation of the master dark;
creation of the detector master flat field;
definition of the IFS spectra positions. At this step, each detector pixel is attached to a particular spectrum and a first guess wavelength is assigned to it, based on a model. The corresponding data set is obtained by illuminating the IFS with a broadband light source connected to an integrating sphere located in the calibration arm;
wavelength calibration of each spectra. At this stage the wavelength assigned to each pixel is refined using data obtained illuminating the IFS with several laser light sources (three for the YJ-mode and four for the YH-mode). Those lasers feed the same integrating sphere.
creation of IFU flat field to take the response to a uniform illumination of all the IFU lenslets properly into account;
reduction of the scientific images with the creation of monochromatic images datacubes. The datacubes are obtained by interpolating the individual spectra spectrally and spatially. A more detailed description of the procedure used in the DRH to create the calibrated datacube can be found in Pavlov et al. (2008);
subtraction of the speckle pattern by exploiting the SD method.
3.1. Spectral deconvolution for IFS
The aim of the SD algorithm is to reduce the speckle noise. This method is described in detail in Sparks & Ford (2002) and Thatte et al. (2007). It can be summarized by the following steps:
-
each single frame in the datacube is rescaled according to itswavelength in such a way that the speckle pattern for the starbecomes similar at all wavelenghts while its companion islocated at different positions for different frames;
-
a polynomial fit is performed along the wavelength direction for each pixel of the rescaled datacube;
-
the obtained fit is then subtracted from the rescaled datacube to reduce the speckle noise; and each frame of the datacube is rescaled back to the original dimensions in such a way that the companion image is set back to the same position in all the frames.
The main difficulties of the SD method for IFS is to properly estimate the center of each monochromatic image in the datacube and to rescale the images because the rescaling factor slightly varies with wavelength due to imperfect wavelength calibration. To overcome these problems, satellite spots were artificially introduced by generating periodic phase offsets on the deformable mirror as proposed in Langlois et al. (2013) for what concerns their use for SPHERE observations. The use of satellite spots was previously proposed by Sivaramakrishnan & Oppenheimer (2006) and by Marois et al. (2006a). These satellite images, symmetric with respect to the central star as shown in Fig. 3, are used to compute the star center position very accurately (with a precision of some tenths of spatial pixel) and, moreover, to calibrate the rescaling factor more accurately by exploiting their shifting outward with increasing wavelengths.
 |
Fig. 3 Example of a monochromatic (λ = 1.047 μm) reduced image where the four artificial satellite spots are clearly visible. This image was taken exploiting the SPHERE apodized Lyot coronagraph (ALC). The diameter of the coronagraphic mask used is 185 mas. A bar indicating the length of 0.1 arcsec has been superimposed to the image to make the scale clearer. |
A second order of problems consists in the fact that the image could not be uniformely illuminated because of an out of focus ghost on the telescope simulator optics. To solve this problem, we performed a bidimensional fit on the original image. The image resulting from this procedure is an inclined plane function that is subtracted to the original image. While this problem arises from the telescope simulator, we cannot exclude that a similar problem could arise for the on-sky data. For this reason this procedure should be maintained in the pipeline and used just in case it is needed. Besides, when rescaled properly according to their wavelength, the speckle FWHM varies with wavelength because it is not uniquely determined by diffraction. This results in an inaccurate subtraction of the speckles. To solve this problem, all the images are smoothed so that the speckle FWHM remains unchanged for all wavelengths. This method enables more precise speckle subtraction, but the smoothing slightly degrades the spatial resolution to about 1.5λ/D. Finally, to compensate the flux variations within original images and not properly corrected by the subtraction of the inclined plane function described above, each image is divided in eight radial sectors for which normalization factors are calculated using the median of the image for separation ranging from 6 to 15λ/D. The images were then divided by these normalization factors taking care to maintain comparable flux for all the images at different wavelengths before applying the SD procedure. These procedures generate images more uniform in flux and better aligned with the speckle pattern. As a final step, we developed the SD procedure to exclude the planet signal when fitting the function to be subtracted from spectra to reduce the speckle noise. This was done by excluding all the pixels around the maximum of the spectrum from the spectrum to be fitted if larger than its median plus fifteen times the standard deviation of the remaining part of the spectrum itself. The number of excluded pixels is calculated according to the fraction of the spectrum that would be covered by a possible planet at the separation under consideration according to the theory of the SD given in Thatte et al. (2007).
3.2. The PCA for IFS
As an alternative to the SD algorithm described above, we implemented a PCA procedure to be applied to the IFS data as described, e.g., in Soummer et al. (2012). In this case, the data prereduction is identical to what has been described in Sect. 3.1, but the normalization of the images is performed using the image median between 6 and 15λ/D, without division in sectors. A stellar profile, computed from the median of all the pixels equidistant from the central star, is then subtracted from each image. Only the central part of these resulting images is considered to fill the two-dimensional array needed to feed the PCA procedure. The size of these subimages can be selected by the user, but from our experience we have found that the optimal size is 200 pixels centered on the center of the star. This allows us to work on the most important part of the image near the center. Moreover, discarding the most external part of the image, we are able to avoid a procedure that is too expensive computationally. The PCA, relying on the singular value decomposition algorithm, generates three arrays which, combined in the correct way, lead to the eigenvectors and the eigenvalues used to reconstruct the original data. The principal components for this reconstruction are given by the matrix product of these two arrays. A principal components subset is used to generate an image with the quasi static noise pattern that can then be subtracted from the original image. The number of principal components used is adjustable by the user. These adjustments will be discussed in more detail in Sect. 4.2. Clearly, the larger the number of principal components used, the better the noise subtraction, but, on the other hand, the larger the cancellation of the signal from possible faint companion objects.
3.3. Angular differential imaging
During the laboratory tests continuous FOV rotation by the derotator was not possible because this would result in a misalignment of the Lyot stop when using the TSIM since the telescope pupil is inside the TSIM itself. So, strictly speaking, no implementation of the ADI technique was possible. We tried to evaluate the efficiency of this algorithm, however, by subtracting images taken at different epochs. To this aim, we implemented a very simple ADI procedure that subtracts from each image all the other images in the datacube excluding just the adjacent images. Each image was normalized before the subtraction dividing for the value of the total flux of the image itself. The analysis was performed using the data reduced with the speckle subtraction methods described in Sects. 3.1 and 3.2. In this configuration, SPHERE was proven to be extremely stable, with no significant decorrelation of the instrumental speckle pattern over several tens of minutes. Given the great stability of the speckle pattern in the laboratory images, which will not be reproduced for the on-sky data, these results give an optimistic estimation of the on-sky instrument performances, where we expect more rapid decorrelation of instrumental speckles with timescale of about ten minutes (see Martinez et al. 2013) with derotation. It is important to stress that the temporal stability will be very important for on-sky operation. Given that SPHERE was carefully designed with this aim in mind, however, we expect very good stability even for on-sky data.
3.4. Algorithm throughput
To properly evaluate the contrast level achievable by exploiting the speckle subtraction method described above we have to account for the algorithm throughput. This effect is inherent to the differential techniques used in high-contrast imaging. In fact, these techniques require the subtraction of two images: in one image the faint companion signal is present, and in the other it is either absent or weak. The two images should have a noise pattern, mainly due to speckles, as similar as possible to each other. This leads to select images with small differences in time for angular differential imaging or in wavelength for spectral differential imaging. The closer the images are in time and wavelength, the more likely the faint companion signal is present in the comparison image. Hence, once the two images are subtracted from each other, part of the signal from the faint companion is canceled together with noise. To optimize the detection, the S/N of the companion signal should be optimized. This optmization is typically achieved neither when the companion signal is not affected by any self-subtraction, nor when the speckle noise is best subtracted, leading to strong self-subtraction, but for some intermediate self-subtraction.
To evaluate the impact of the algorithm throughput, we injected in the scientific datacubes simulated planets at different separations (0.2, 0.3, 0.4, 0.5, 0.6, 0.7 and 0.8 arcsec). To be able to clearly determine the optimal algorithm throughput for the single planets a wide J-band contrast of 3 × 10-4 was used. The contrast value was evaluated using the off-axis PSF not affected by the coronagraph. The spectrum of the simulated planets was assumed to be gray. In this case, we assume that the simulated companions do not have identical spectra to that of the central star. It is important to point out that the algorithm used to subtract the speckles makes use of spectral information, and the throughput is dependent on the spectral properties of the simulated planets (see e.g. Maire et al. 2014,for the case of dual band image). Moreover, the planet flux, which is quite bright in our case, could impact the spectral fitting.
To simulate the rotation of the FOV, we inserted the simulated planets with rotation of 5° between two successive datacubes leading to a full FOV simulated rotation of 75° for 16 datacubes. The rotation considered here is of the order of 1° per minute corresponding at Paranal to the field rotation for a target with a declination between −10° and −38° and observed during its transit at the meridian. A continous rotation of 5° would of course introduce a smearing of a point source especially at the edge of the FOV. However, for this exercise we just wanted to check the speckle subtraction obtained from images taken at a distance of 5 min and a rotation of 5°. We, then, did not consider individual single exposures, rather we took a stack of the images at different times. On the other hand, in the real case the ADI algorithm should be modified to take the large smearing effect introduced by the rotation of the FOV into account.
4. Results for IFS YJ-mode
In this section we present the IFS data reduction for its YJ-mode, using the procedures detailed in Sect. 3. An overview of the data used for this analysis is given in Table 1.
Summary of data used.
4.1. Results obtained with the updated spectral deconvolution procedure
We obtained very good speckle noise subtraction using the updated version of the SD and evaluating the attenuation of the satellite spots described above. We obtained attenuation factors ranging from 30 to 50, depending on the function used to reproduce the speckle spectra. This factor is similar to the results obtained by Thatte et al. (2007) and Crepp et al. (2011). However, to estimate the gain in limiting contrast, the algorithm throughput on the companion’s after the SD procedure must be considered as described in Sect. 3.4. The final reduced image obtained from the considered data set where simulated planets were inserted is displayed in Fig. 4. In this figure, the segmentation near the star center is generated by the normalization performed in different sectors as described in Sect. 3.1. In the external part of the image, the data reduction method is very efficient at removing these artifacts unlike at close separation where the method is less effective.
 |
Fig. 4 Final reduced image obtained from the data set using the updated SD procedure where seven fake planets with contrast of 3 × 10-4 were inserted. |
 |
Fig. 5 5σ contrast plot with the IFS operating in YJ-mode while simulating observations of a bright star and using the updated SD method. The contrast solid curve in black is obtained without any speckle subtraction while the green curve is obtained applying the updated SD procedure. The red and orange dashed curves show the contrast obtained with the simulated ADI procedure in addition to the speckle subtraction. Different symbols are used to indicate the positions of known planets on this plot. |
In Fig. 5 we show the 5σ contrast curves obtained by applying the refined SD procedure described in Sect. 3.1 and taking the algorithm throughput into account. In the following, the contrast curves are calculated using the median image from the final datacube produced by the speckle subtraction procedure. The exact procedure used to calculate the contrast follows these steps (see e.g. Masciadri et al. 2005):
-
The standard deviation inside a 1.5λ/D wide box centered on each pixel is calculated for each pixel of the image.
A median of these standard deviations is calculated for all the pixels located at the same separation from the central star.
The contrast at different separations is then calculated by dividing these median values by the normalization factor. The normalization factor is obtained by multiplying the maximum of the off-axis PSF, derived from the star not affected by the coronagraph, the ratio between the coronagraphic image single exposure and the off-axis image exposure, and the ratio of the transmission of the neutral density filters used in the two cases to avoid the saturation of the detector.
Figure 5 shows the final results of this procedure. The contrast solid curve in black is obtained from the original coronagraphic images, the green curve is obtained from the application of the SD and the orange and red dashed curves represent the contrast after the application of the simulated ADI procedure. These contrasts were obtained by applying the SD and fitting a 1 degree function to obtain a good speckle subtraction while keeping the algorithm throughput to an high level. In this figure we do not show the contrast curves corresponding to a separation lower than 0.2 arcsec (smaller than the bifurcation radius as defined by Thatte et al. 2007) from the central star because at these separations the method is no more effective. On this plot we added the positions of some known planets to enlighten the capability of IFS to retrieve their signal. Since the J magnitude for HD95086b is not known we have exploited its known H-K color−color diagrams to infer their possible magnitudes assuming the same J-H index. The error bar displayed in the figure account for the uncertainties of the method. We can see that we will be able to image βPic b just using the SD and without applying the ADI while the planets of HR8799 are close to the limit for speckle deconvolution alone. On the other hand, we will have to use the ADI to be able to image HD95086b.
The algorithm throughput obtained for each planet is given in Fig. 6 for fitting function (used in the SD procedure) degrees of 0 (corresponding to a constant value given by the median of the spectra), 1, 2 or 3. In this figure and in the following, the algorithm throughput has a value of 1 for no flux loss of the fake planet while it has a value of 0 when the planet is completely canceled out. Clearly the throughput is much larger with lower fitting degrees. Besides, the difference between higher degrees (2 and 3) is smaller than the difference between lower degrees. Furthermore, as expected, the throughput is larger at larger separations. This occurs because companion objects extend on smaller fractions of the speckles field spectrum at large separations (see Sparks & Ford 2002).
 |
Fig. 6 Algorithm throughput obtained for various degrees of the fitting function used in the SD procedure. A detailed explanation of the meaning of these curves is given in the text. |
However, high-degree fitting functions provide a better reduction of the noise. For detection purposes, the best way to perform the SD is to optimize the S/N. These plots are shown in Fig. 7. The S/N is obtained by dividing the planet signal integrated within a 1 pixel radius aperture centered on the planet position, by the standard deviation estimated in a 10 × 10 pixels region located near the considered planet but at a separation such that the flux in this region is not affected by the planetary signal. This is an acceptable way to estimate the noise for our images since that the noise is very stable in the whole image. Figure 7 shows that at separation lower than 0.35 arcsec and larger than 0.75 arcsec, a fit with a low-degree polynomial function works better, while for intermediate separations the fit with a 3 degrees fitting function gives the best S/N. Edge effects are caused by the noisy structure at the edge of the IFS FOV that can be seen, e.g., in Fig. 3 or in Fig. 4 and are important at separations greater than 0.6 arcsec. They can explain the steep fall of the S/N value at large separations obtained with high-order fits.
 |
Fig. 7 S/N plots obtained with different degrees of the fitting function used in the SD procedure. A detailed explanation of the meaning of the plotted lines is given in the text. |
 |
Fig. 8 Contrast plots for the SD taking and not taking into account the algorithm throughput. |
Figure 8 displays the 5σ contrast curves obtained by taking the SD algorithm throughput (blue line) into account compared to the contrast obtained without taking it (red line) into account and before the application of the SD (green line). The difference from Fig. 5 is that these contrasts are obtained just considering the simulated planets. Despite this difference, the two latter curves are in good agreement with those shown in Fig. 5 at least at separations larger than 0.3 arcsec. The discrepancy at 0.3 arcsec can be given by the proximity to the central star and to the lower throughput of the SD at that separation. We have then tried to implement a very simple simultaneous spectral differential imaging (S-SDI) procedure by subtracting images obtained at different wavelengths after simulating a T7 spectral type planet. We have used the images at wavelengths between 1.10 and 1.19 micron where the signal is not present to be subtracted from the images at wavelengths in the ranges between 1.02 and 1.09 micron and between 1.22 and 1.29 micron where the signal from the planet is instead present. In this figure the contrast curve obtained by applying this method is represented by the orange curve. The S-SDI is more effective at small separations from the star (less than 0.3 arcsec) where the SD cannot be properly applied because the planet spectrum covers the entire spectrum provided by the IFS (see the definition of bifurcation point in Thatte et al. 2007).
4.1.1. Synthetic planets spectral retrieval
We performed a test to check the ability of the system to retrieve the spectra of the injected planets. The test was performed using the same data described in the previous paragraphs. The data were reduced using both the updated SD procedure alone and together with the simulated ADI procedure described in Sect. 3.3. The injected simulated planets had a mean contrast on the whole wavelength range of the IFS YJ-mode of 3 × 10-4. While the flux of the simulated planets was the same for all the instrument channels, the flux for the simulated star was variable and for this reason the contrast of the simulated planets changed for different channels. The output spectra for the planets at different separations are shown in Fig. 9 for the case in which we only used the SD procedure. In Fig. 10, however, we only used the ADI procedure. The latter gives a better reconstruction of the spectra and a lower dispersion of the results. In this second case all the spectra are very similar to each other indipendent from the separation from the central star. This is probably due to the high contrast of the simulated planets that we have used in this case. However, in both cases we found a loss of flux with respect to the original spectra (represented by the black solid line in both the figures). The final flux is around 44% of the original in the case of the spectral deconvolution alone, while it is of the order of 57% when we use the ADI procedure. This is due to the low algorithm throughput given by the speckle subtraction methods we describe.
A more refined analysis of the spectro-photometric capabilities of the IFS and IRDIS and a description of the methods adopted to improve the algorithm throughput is reported in Zurlo et al. (2014). In that work the effects of different types of input spectra for the simulated planets are enlightened too.
 |
Fig. 9 Output spectra for the 7 simulated planets obtained applying just the spectral deconvolution procedure. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
 |
Fig. 10 Output spectra for the 7 simulated planets obtained applying the spectral deconvolution procedure and the simulated ADI procedure. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
 |
Fig. 11 Final image obtained by applying the PCA method to a dataset containing simulated planets with a contrast of 3 × 10-4. The image is obtained retaining only the first 4 principal components out of 38 and without considering the rotation of the FOV. |
4.2. Results with the PCA procedure
Figure 11 shows the final image obtained by applying the PCA procedure on a single science datacube without considering rotation of the FOV. Similar to the SD case, seven fake planets with 3 × 10-4 contrast were injected at the same separation as above. In this figure negative features along the direction star-planets arising from the subtraction procedure are clearly visible. They are caused by the oversubtraction given by a not perfect spectral fitting around the planetary position. Figure 12 displays the final image obtained using all the datacubes and where the rotation of the FOV is simulated with a rotation of 5° between consecutive datacubes corresponding to a total FOV rotation of 75°. Here we have decided to insert simulated planets with a lower contrast of 10-5, which is nearer to the contrast limit for this image and has a smaller impact on a correct determination of the S/N probably because of the lower level of the strong subtraction structures described below. In the latter case, the image has been reconstructed using 32 principal components (see Sect. 3.2), while in the former case, without FOV rotation, only four principal components were used. Negative structure given by the subtraction algorithm are visible in Fig. 12. The strong level of the noise suppression that we can obtain with this technique combined with the very high contrast of the simulated planets enables these structures to be visible. In future improvements of this procedure, we want to address in detail these residual structures in the image. However, the presence of these structures does not affect the scientific results presented in this paper. Similar to the SD case, we exploited these images to calculate the algorithm throughput at different separations from the central star. The algorithm throughput versus the separation from the central star is shown in Fig. 13.
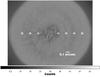 |
Fig. 12 Same as for Fig. 11 but in this case the image is obtained retaining the first 32 principal components out of 608 and considering the rotation of the FOV too. Moreover, in this case the simulated planets have a contrast of 10-5. |
 |
Fig. 13 Algorithm throughput versus separation for two sets of the PCA method parameters. The algorithm throughput is represented by the orange curve and corresponds to no rotation of the FOV and 4 principal components, as shown in Fig. 11 while the green line represents the FOV rotation case and 32 principal components as shown in Fig. 12. |
Using these algorithm throughputs, the contrast plot displayed in Fig. 14 were properly estimated. In this figure the solid black line represents the contrast without any speckle subtraction and the solid green line represents the contrast without field rotation (4 principal components out of 38 are used). The image resulting from the complete reduction of this data set is shown in Fig. 11. The dashed red line represents the contrast for the case where the FOV rotation is simulated and 32 principal components out of 608 are used. The final image obtained from this data set is shown in Fig. 12.
 |
Fig. 14 5σ contrast plot with the IFS operating in YJ-mode for bright star observations after PCA data reduction and with simulated ADI procedure. The solid black line represents the contrast before speckle subtraction, the green line represents the contrast after PCA data reduction method using only the 4 principal components and without any rotation (see Fig. 11). The red line is obtained applying the PCA method with 32 principal components and with simulated FOV rotation (see Fig. 12). |
 |
Fig. 15 Algorithm throughput by the PCA method for a planet at 0.4 arcsec using different numbers of principal components. |
We also focused on the variation of the S/N and of the algorithm throughput with the number of principal components used to reconstruct the original data. The throughput and S/N values for the planet at 0.4 arcsec separation are given in Figs. 15 and 16, respectively. As expected, the throughput reduces with the number of principal components used, but at the same time the noise decreases so that the S/N is maximum when 32 principal components are used. In order to find faint companions, the number of principal components to be used needs to be carefully considered since it changes from case to case and, for instance, it depends on the separation from the star (see e.g. Meshkat et al. 2014). However, for this analysis with simulated planets of known contrast we preferred to use a single number of principal components for the whole image. This choice is adequate for the objective of this analysis, which is mainly aimed at providing an initial estimate of the contrast that can be reached with this procedure. Moreover, this choice allowed us to use a simpler code and, as a consequence, to reduce the required computing time.
Tests made using different numbers of principal components have allowed to us to find that it is adequate to use 32 of them as shown in Fig. 14. We would like to stress that this number is adequate just for the present data set. Different data sets will certainly require the use of a different number of principal components that must be evaluated on a case-by-case basis.
 |
Fig. 16 S/N for the PCA method with a planet at 0.4 arcsec using different numbers of principal components. |
5. Results for IFS YH-mode
Following the scheme of Sect. 4, we present the results of the analysis of the data taken with IFS operating in the YH-mode. As seen in Table 1, the data used for this instrument mode were taken at a different epoch with respect to the data taken for the YJ-mode. Between the two epochs the condition of the instrument changed. In particular the telescope simulator lamp was changed and an additional neutral density filter was used to avoid saturation. Moreover, the spectra obtained from the telescope simulator presented a strong absorbing band at 1.4 μm caused by the OH− ions contained in the optical fiber used. This caused extremely low flux at the wavelengths around 1.4 μm making it more difficult to apply the SD. For these reasons the contrast obtained in this mode is worse than those for the YJ-mode. However, this problem should not occur on sky since the stellar spectra are flatter in this wavelength range with the resolving power of IFS, even considering the absorption due to water vapour in the Earth atmosphere.
5.1. Results with the updated spectral deconvolution procedure
In Fig. 17 the contrast plot obtained from the YH-mode IFS data is shown. These contrast levels are worse than those obtained with the instrument operating in the YJ-mode (see Fig. 5 for comparison). The worsening is particularly evident for the simulated ADI contrast plot while it is much less evident for the SD alone contrast plot. This worsening could be due, besides the reasons given above, to the shorter total integration time for the data set used in this test. As for YJ-mode case, we have inserted the positions of some known planets on the plot. In this case, we will be able to image the planet of βPicb without the application of the ADI, while to retrieve the signal from HD95086b and from the HR8799 planets, the use of ADI is mandatory.
 |
Fig. 17 Contrast plot obtained applying the SD and the ADI to the data taken with IFS operating in the YH-mode. The curves color codes are the same as in Fig. 5. The difference in time delays given in the label with respect to those in Fig. 5 is due to the different way in which the data have been taken at two epochs. See text for more detail. Different symbols are used to indicate positions of known planets on this plot. |
 |
Fig. 18 Spectral retrieval obtained for seven planets at different separations with the IFS operating in the YH-mode. In this case both the SD and the ADI were applied to the datacube before performing the spectral retrieval. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
5.1.1. Synthetic planets spectral retrieval
Similar to the YJ-mode analysis, seven simulated planets were added to the science datacube to estimate the precision in reconstructing the spectra of the injected planets. The introduced fake planets have the same flux for all the IFS channels. As a consequence, given that the flux of the simulated star was variable from one channel to the other, the contrast of the simulated planets with respect to the simulated star was variable. The mean contrast on the whole wavelength range of the IFS YH-mode is of 3 × 10-4. In Fig. 18 the results obtained with this datacube after the application of both SD and ADI are shown, while Fig. 19 shows the spectral retrieval obtained in this case after the application of ADI only on the original datacube.
The spectral retrieval is better in the second case, confirming the results already obtained for the YJ-mode. At the same time, this result confirms that the application of SD strongly distorts the original spectra. This effect is slightly decreased when the ADI procedure is directly applied to the original datacube without applying the SD. Moreover, a second problem that affects the analysis for the YH-mode is given by the great difference in flux between different images at different wavelengths in the YH datacube. This has the effect of inserting biases in the estimation of the normalization factors along the spectra and, in this way, leads to overestimate parts of the spectrum with respect to others. From the analysis of the results, we can conclude that the distortion of the spectra is about eight times larger than in the case of the YJ-mode. Moreover, in some cases, additional flux is added to the original in such a way that the flux is higher in the extracted spectra than in the simulated spectra. This could arise from the worse quality of the data in the YH-mode than the YJ-mode as explained in Sect. 5.1. Hence, careful analysis of YH-mode images will be then mandatory on on-sky data.
 |
Fig. 19 Spectral retrieval obtained for seven planets at different separations with the IFS operating in the YH-mode. In this case only ADI was applied to the datacube before performing the spectral retrieval. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
 |
Fig. 20 Contrast plot obtained applying the PCA procedure to the IFS YH-data. The solid green line represents the contrast obtained with the PCA applied to a single datacube without any rotation. The dashed red line represents the contrast obtained applying the PCA to all the datacubes with the rotation of the FOV. |
5.2. Results with the PCA procedure
Figure 20 shows the contrast plots obtained applying the PCA to the IFS YH-mode data. The green line has been obtained applying the procedure to a single datacube without any rotation of the FOV. We then applied the procedure to all ten datacubes to simulate FOV rotation as described in Sect. 4.1. The contrast plot obtained for this case is represented by the dashed red line in Fig. 20. As for all previous cases, the introduction of the field rotation allows us to obtain a contrast level better than 10-6.
Summary of the contrast obtained at different separations for the IFS YJ-mode.
Summary of the contrast obtained at different separations for the IFS YH-mode.
6. Conclusions
We have described the results of the functional and performance tests for the IFS instrument within SPHERE. While the functional tests performed using the instrument templates and the DRH recipes allowed us to validate and improve the software, the performance tests allowed us to get hints about the achievable contrast with IFS when used on sky and to optimize the calibration and data reduction procedures. The spectral deconvolution procedure currently implemented in the dedicated DRH recipe yields a contrast close to 10-5, while better results were expected from instrument simulations (Mesa et al. 2011). For this reason we implemented an updated version of the SD procedure taking several issues not properly addressed in the original procedure into account (e.g., more precise centering of the datacube images and more refined rescaling factor at different wavelengths). This updated procedure allowed us to improve the contrast by a factor of two to three. The final contrast obtained is of the order of 4 × 10-6 at 0.3 arcsec separation, taking the total throughput of the differential imaging procedures properly into account. To consider this last effect, several simulated planets located at different separation from the star were injected.
We also developed a new procedure for the speckle subtraction exploiting the PCA algorithm. In Table 2 we summarize the 5σ contrast we obtained with the IFS in the YJ-mode with various speckle subtraction methods described in this paper. Similar results are presented in Table 3 for the IFS YH-mode. In both of these tables the second column gives the results obtained when applying the SD to a single datacube, while in the third column lists the results obtained with our simulated ADI procedure after SD are displayed. In the fourth column, labeled PCA1, we list the results obtained applying the PCA to a single datacube and with only four principal components used (in this case no rotation of the FOV was simulated), while in the fifth column, labeled PCA2, we give the results of the PCA performed on the complete data set in this case using 32 principal components (in this latter case a rotation of the FOV was simulated). While the cancellation of the noise is similar for both SD and PCA, the throughput is much lower for the PCA method as shown in Table 2. This latter effect seems to be much less important in the case of the YH-mode as shown in Table 3. As explained in Sect. 5, however, these data were taken under different conditions with respect to the YJ case and proper comparison between the two cases is difficult. Moreover this caused a loss of effectiveness of the SD method for the YH data (see Table 3). All these uncertainties will be solved when on-sky data become available.
However, we can conclude that the PCA procedure can give results comparable to the SD results once the algorithm throughput is properly taken into account. A more refined method to take them into account will be presented in an associated paper (Zurlo et al. 2014). Moreover, the implementation of ADI procedure in the PCA procedure is much easier than the implementation of the ADI in the SD procedure. For this reason, the PCA procedure should probably be considered as a better solution for the final IFS pipeline.
Finally, we have verified that, whatever the choice for the IFS reduction pipeline (SD, PCA or other possible solutions), ADI is mandatory to reach the 10-6 5σ contrast threshold using IFS mounted on SPHERE. The effectiveness of the ADI, however, strongly depends on the rotation of the FOV and on the separation from the central star.
The authors are aware that the definition of spectral deconvolution is probably inadequate since no deconvolution is actually performed. However, this name is routinely used in the high-contrast imaging community. Moreover, the method is clearly explained in Sect. 3.1. For these reasons, we have decided to keep it in our paper.
Acknowledgments
We are grateful to the SPHERE team and all the people always available during the tests at IPAG in Grenoble. D.M., A.Z., and S.D. acknowledge partial support from PRIN INAF 2010 “Planetary systems at young ages”. SPHERE is an instrument designed and built by a consortium consisting of IPAG, MPIA, LAM, LESIA, Laboratoire Fizeau, INAF, Observatoire de Genéve, ETH, NOVA, ONERA, and ASTRON in collaboration with ESO.
References
- Antichi, J., Dohlen, K., Gratton, R. G., et al. 2009, ApJ, 695, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Baruffolo, A., Fantinel, D., Gluck, L., et al. 2012, in SPIE Conf. Ser., 8451 [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, The Messenger, 125, 29 [NASA ADS] [Google Scholar]
- Boccaletti, A., Abe, L., Baudrand, J., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Bonnefoy, M., Chauvin, G., Lagrange, A.-M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, B. P., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 723, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., McElwain, M. W., Turner, E. L., et al. 2013, ApJ, 764, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Claudi, R. U., Turatto, M., Gratton, R. G., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Crepp, J. R., Pueyo, L., Brenner, D., et al. 2011, ApJ, 729, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Guyon, O., Martinache, F., et al. 2014, in IAU Symp. 299, eds. M. Booth, B. C. Matthews, & J. R. Graham, 34 [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Esposito, S., Mesa, D., Skemer, A., et al. 2013, A&A, 549, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hugot, E., Ferrari, M., El Hadi, K., et al. 2012, A&A, 538, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langlois, M., Dohlen, K., Augereau, J.-C., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Langlois, M., Vigan, A., Moutou, C., et al. 2013, in Proc. Third AO4ELT Conf., eds. S. Esposito, & L. Fini [Google Scholar]
- Lavigne, J.-F., Doyon, R., Lafrenière, D., Marois, C., & Barman, T. 2009, ApJ, 704, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J., Palmer, D., et al. 2006, in SPIE Conf. Ser., 6272 [Google Scholar]
- Maire, A.-L., Boccaletti, A., Rameau, J., et al. 2014, A&A, 566, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marois, C., Doyon, R., Racine, R., et al. 2005, J. Roy. Astron. Soc. Canada, 99, 130 [Google Scholar]
- Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2006a, ApJ, 647, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Phillion, D. W., & Macintosh, B. 2006b, in SPIE Conf. Ser., 6269 [Google Scholar]
- Marois, C., Correia, C., Véran, J.-P., & Currie, T. 2014, in IAU Symp. 299, eds. M. Booth, B. C. Matthews, & J. R. Graham, 48 [Google Scholar]
- Martinez, P., Kasper, M., Costille, A., et al. 2013, A&A, 554, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Mesa, D., Gratton, R., Berton, A., et al. 2011, A&A, 529, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meshkat, T., Kenworthy, M. A., Quanz, S. P., & Amara, A. 2014, ApJ, 780, 17 [Google Scholar]
- Oppenheimer, B. R., Baranec, C., Beichman, C., et al. 2013, ApJ, 768, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, A., Möller-Nilsson, O., Feldt, M., et al. 2008, in SPIE Conf. Ser., 7019 [Google Scholar]
- Peters-Limbach, M. A., Groff, T. D., Kasdin, N. J., et al. 2013, in SPIE Conf. Ser., 8864 [Google Scholar]
- Petit, C., Sauvage, J.-F., Sevin, A., et al. 2012, in SPIE Conf. Ser., 8447 [Google Scholar]
- Pueyo, L., Soummer, R., Hoffmann, J., et al. 2015, ApJ, 803, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R., Walker, G. A. H., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sivaramakrishnan, A., & Oppenheimer, B. R. 2006, ApJ, 647, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Skemer, A. J., Hinz, P. M., Esposito, S., et al. 2012, ApJ, 753, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Thalmann, C., Schmid, H. M., Boccaletti, A., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Thatte, N., Abuter, R., Tecza, M., et al. 2007, MNRAS, 378, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Vigan, A., Langlois, M., Moutou, C., & Dohlen, K. 2008, A&A, 489, 1345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Zurlo, A., Vigan, A., Mesa, D., et al. 2014, A&A, 572, A13 [Google Scholar]
Appendix A: Contrast plot calculation
The method that we have used to calculate the contrast plot in this paper and described in Sect. 4.1 has in the past been demonstrated to be reliable (see e.g. Esposito et al. 2013). On the other hand, the most common method used to calculate the contrast plot is to calculate the standard deviation on a ring centered on the center of the star. Our choice was driven by the fact that this second method does not take the possible large scale inhomogeneities in the image properly into account, and that we need however to calculate some local noise when we are searching for a point source like a planet.
 |
Fig. A.1 Left: same of image 5 obtained with our method. Right: same contrast plot obtained using the standard method described in the text. |
 |
Fig. A.2 Left: same of image 5 obtained with our method where a smoothed version of the same image has been subtracted from the nonsubtracted image after applying a low-frequency filtering to subtract any possible large scale structure in the image. Right: same contrast plot obtained using the standard method described in the text. |
To compare the results of the two methods we have run both of them on one of the cases presented here. In particular, we have chosen the case presented in Fig. 5. On the left panel of Fig. A.1 we present the same image while on the right panel we present the contrast obtained using the classical method described above on the same data set. The difference between the two plots (black line) for nonsubtracted images is readily evident while it tends to diminish when we consider subtracted images and it is almost null when we consider images where the ADI is applied. The great difference for nonsubtracted images is given by the problem of the large scale inhomogeneities in the original image cited above. To demonstrate this, we have prepared the same plots presented in Fig. A.1 but applying a low-frequency filtering on the nonsubtracted image, subtracting from the original image a smoothed version of the image itself using the SMOOTH IDL procedure with a large value of the smoothing area (with a semi amplitude of 25 pixels corresponding to ~0.18 arcsec).
The results of this test are presented in Fig. A.2 where it is evident that now the contrast plots are very similar using both methods. The conclusion of this test is that the main difference between the two methods is on the nonsubtracted images where the large scale inhomogeneities in the image are not taken properly into account by the standard method. These differences can be reduced applying a low-frequency filtering on the images. The main problem with our method is that if the box that we are using for calculations has a dimension similar to the dimension of the speckle (~λ/D), we could have an underestimation of the noise. However, we took care that the dimension of the box was larger than this value (as said in the paper, of the order of ~1.5λ/D). Moreover, various tests with different dimensions of the box have been done arriving at the conclusion that boxes with larger dimensions do not significantly change the estimated contrast. From these tests, we can estimate an error of the order of 10% for our contrast estimation.
As a further test of the reliability of our contrast estimation we have introduced simulated planets with a contrast of 10-4 on the nonsubtracted image (black plot on both panels of Fig. A.1). The result of this test is presented in Fig. A.3 where, as foreseen by the contrast plot, the planets at separations of 0.3 arcsec and larger are visible (even just above the detection limit) while the planet at 0.2 arcsec is not visible. This is in good agreement with what we can infer from the analysis of the contrast plot displayed on the left panel and obtained exploiting our method.
The conclusion of these tests are that both methods can give a reliable estimation of the contrast when used in the correct way.
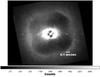 |
Fig. A.3 Nonsubtracted datacube median image with simulated planets with a contrast of 10-4. The planets with separation larger than 0.2 arcsec are just visible as foreseen by our contrast plot. |
All Tables
All Figures
 |
Fig. 1 Example of IFS coronagraphic raw data. The displayed image covers a square 1.77×1.77 arcsec FOV. This observation was performed in YJ-mode. |
| In the text | |
 |
Fig. 2 Zoom on the central part of the image from Fig. 1 showing the spectra more clearly. |
| In the text | |
 |
Fig. 3 Example of a monochromatic (λ = 1.047 μm) reduced image where the four artificial satellite spots are clearly visible. This image was taken exploiting the SPHERE apodized Lyot coronagraph (ALC). The diameter of the coronagraphic mask used is 185 mas. A bar indicating the length of 0.1 arcsec has been superimposed to the image to make the scale clearer. |
| In the text | |
 |
Fig. 4 Final reduced image obtained from the data set using the updated SD procedure where seven fake planets with contrast of 3 × 10-4 were inserted. |
| In the text | |
 |
Fig. 5 5σ contrast plot with the IFS operating in YJ-mode while simulating observations of a bright star and using the updated SD method. The contrast solid curve in black is obtained without any speckle subtraction while the green curve is obtained applying the updated SD procedure. The red and orange dashed curves show the contrast obtained with the simulated ADI procedure in addition to the speckle subtraction. Different symbols are used to indicate the positions of known planets on this plot. |
| In the text | |
 |
Fig. 6 Algorithm throughput obtained for various degrees of the fitting function used in the SD procedure. A detailed explanation of the meaning of these curves is given in the text. |
| In the text | |
 |
Fig. 7 S/N plots obtained with different degrees of the fitting function used in the SD procedure. A detailed explanation of the meaning of the plotted lines is given in the text. |
| In the text | |
 |
Fig. 8 Contrast plots for the SD taking and not taking into account the algorithm throughput. |
| In the text | |
 |
Fig. 9 Output spectra for the 7 simulated planets obtained applying just the spectral deconvolution procedure. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
| In the text | |
 |
Fig. 10 Output spectra for the 7 simulated planets obtained applying the spectral deconvolution procedure and the simulated ADI procedure. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
| In the text | |
 |
Fig. 11 Final image obtained by applying the PCA method to a dataset containing simulated planets with a contrast of 3 × 10-4. The image is obtained retaining only the first 4 principal components out of 38 and without considering the rotation of the FOV. |
| In the text | |
 |
Fig. 12 Same as for Fig. 11 but in this case the image is obtained retaining the first 32 principal components out of 608 and considering the rotation of the FOV too. Moreover, in this case the simulated planets have a contrast of 10-5. |
| In the text | |
 |
Fig. 13 Algorithm throughput versus separation for two sets of the PCA method parameters. The algorithm throughput is represented by the orange curve and corresponds to no rotation of the FOV and 4 principal components, as shown in Fig. 11 while the green line represents the FOV rotation case and 32 principal components as shown in Fig. 12. |
| In the text | |
 |
Fig. 14 5σ contrast plot with the IFS operating in YJ-mode for bright star observations after PCA data reduction and with simulated ADI procedure. The solid black line represents the contrast before speckle subtraction, the green line represents the contrast after PCA data reduction method using only the 4 principal components and without any rotation (see Fig. 11). The red line is obtained applying the PCA method with 32 principal components and with simulated FOV rotation (see Fig. 12). |
| In the text | |
 |
Fig. 15 Algorithm throughput by the PCA method for a planet at 0.4 arcsec using different numbers of principal components. |
| In the text | |
 |
Fig. 16 S/N for the PCA method with a planet at 0.4 arcsec using different numbers of principal components. |
| In the text | |
 |
Fig. 17 Contrast plot obtained applying the SD and the ADI to the data taken with IFS operating in the YH-mode. The curves color codes are the same as in Fig. 5. The difference in time delays given in the label with respect to those in Fig. 5 is due to the different way in which the data have been taken at two epochs. See text for more detail. Different symbols are used to indicate positions of known planets on this plot. |
| In the text | |
 |
Fig. 18 Spectral retrieval obtained for seven planets at different separations with the IFS operating in the YH-mode. In this case both the SD and the ADI were applied to the datacube before performing the spectral retrieval. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
| In the text | |
 |
Fig. 19 Spectral retrieval obtained for seven planets at different separations with the IFS operating in the YH-mode. In this case only ADI was applied to the datacube before performing the spectral retrieval. The black solid line represents the contrast for each IFS channel obtained from the input spectrum of the simulated objects. |
| In the text | |
 |
Fig. 20 Contrast plot obtained applying the PCA procedure to the IFS YH-data. The solid green line represents the contrast obtained with the PCA applied to a single datacube without any rotation. The dashed red line represents the contrast obtained applying the PCA to all the datacubes with the rotation of the FOV. |
| In the text | |
 |
Fig. A.1 Left: same of image 5 obtained with our method. Right: same contrast plot obtained using the standard method described in the text. |
| In the text | |
 |
Fig. A.2 Left: same of image 5 obtained with our method where a smoothed version of the same image has been subtracted from the nonsubtracted image after applying a low-frequency filtering to subtract any possible large scale structure in the image. Right: same contrast plot obtained using the standard method described in the text. |
| In the text | |
 |
Fig. A.3 Nonsubtracted datacube median image with simulated planets with a contrast of 10-4. The planets with separation larger than 0.2 arcsec are just visible as foreseen by our contrast plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


