| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424822 | |
| Published online | 04 March 2015 | |
Parameters of type IIP SN 2012A and clumpiness effects
1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
e-mail: utrobin@itep.ru
2 State Scientific Center of the Russian Federation – Institute for Theoretical and Experimental Physics of National Research Center “Kurchatov Institute”, B. Cheremushkinskaya St. 25, 117218 Moscow, Russia
3 Institute of Astronomy of Russian Academy of Sciences, Pyatnitskaya St. 48, 119017 Moscow, Russia
Received: 15 August 2014
Accepted: 2 February 2015
Context. The explosion energy and the ejecta mass of a type IIP supernova (SN IIP) derived from hydrodynamic simulations are principal parameters of the explosion theory. Few SNe IIP have been studied by hydrodynamic modeling so far, however. Some doubts exist about the reliability of the derived SN IIP parameters.
Aims. We studied the well-observed type IIP SN 2012A with hydrodynamic modeling. We examined its early spectra for ejecta clumpiness. We also explored other observational effects of clumpiness.
Methods. We determined the supernova parameters by means of standard hydrodynamic modeling. We used the early hydrogen Hα and Hβ lines as clumpiness diagnostics. We used a modified hydrodynamic code to study the clumpiness effect in the light curve and expansion kinematics.
Results. We found that SN 20012A is the result of the explosion of a red supergiant with a radius of 715 ± 100 R⊙. The explosion energy is (5.25 ± 0.6) × 1050 erg, the ejecta mass is 13.1 ± 0.7 M⊙, and the total 56Ni mass is 0.012 ± 0.002 M⊙. The estimated mass of a progenitor, a main-sequence star, is 15 ± 1 M⊙. The Hα and Hβ lines in early spectra indicate that outer ejecta are clumpy. Hydrodynamic simulations show that the clumpiness modifies the early light curve and increases the maximum velocity of the outer layers.
Conclusions. The pre-SN 2012A was a normal red supergiant with the progenitor mass of ≈ 15 M⊙. The outer layers of ejecta indicate the clumpy structure. The clumpiness of the external layers can increase the maximum expansion velocity.
Key words: supernovae: general / supernovae: individual: SN 2012A
© ESO, 2015
1. Introduction
The general picture of the phenomenon of type IIP supernovae (SNe IIP) has been understood decades ago (Grassberg et al., 1971; Falk & Arnett, 1977; Eastman et al., 1994). Central to this picture is the explosion of a massive red supergiant (RSG) with an energy of about 1051 erg. The major characteristics – the explosion mechanism and the progenitor mass – remain a matter of debate, however. The hydrodynamic modeling of the well-observed SNe IIP is the only way to determine the explosion energy and ejecta mass. The progenitor mass can be obtained by combining the ejecta mass with the mass of the neutron star and the estimated mass lost by the stellar wind. In some cases, the progenitor mass can be also recovered from pre-explosion images (Smartt, 2009). The hydrodynamic approach requires a well-observed SN IIP with a reliably defined duration of the light curve plateau. There are few such well-studied events: at present, only eight SNe IIP are studied hydrodynamically (Utrobin & Chugai, 2013). Every other well-observed SN IIP therefore is a bonanza for researchers.
The type IIP SN 2012A in the nearby galaxy NGC 3239 became the subject of detailed observational and theoretical study, including hydrodynamic modeling (Tomasella et al., 2013). The derived parameters seem reasonable except for the small pre-SN radius. Moreover, the hydrodynamic model of Tomasella et al. produced a surprisingly low velocity at the photosphere that does not exceed 3000 km s-1, although the early Hα profile shows an expansion velocity of up to ~104 km s-1; in addition, the Fe ii 5169 Å absorption indicates a photospheric velocity of 5500 km s-1 on day 15 (Tomasella et al., 2013). We therefore find it appropriate to revisit the hydrodynamic modeling of this object.
Another motivation for us to consider SN 2012A is that the early (t< 20 d) Hα and Hβ lines of type IIP SN 2008in reveal a serious problem (we dub it the Hα/Hβ problem): the modeled Hβ absorption is too weak compared to the observed absorption, the modeled Hα line is consistent with the observed line. It is remarkable that SN 1987A does not show the Hα/Hβ problem, from which we conclude that this problem is a specific feature of normal SNe IIP that originate from the RSG explosion (Utrobin & Chugai, 2013). The Hα/Hβ problem can be resolved by invoking the clumpy structure of the external ejecta (Chugai & Utrobin, 2014). Keeping in mind that SN 2012A is in many respects similar to SN 2008in, it is of great interest to explore whether the Hα/Hβ problem arises for SN 2012A as well. If confirmed, the next question should be the nature of the other observational effects of the proposed ejecta clumpiness. This question could be explored, for example, by means of one-dimensional hydrodynamic simulations that take into account the clumpy structure of the external ejecta.
Here we perform the hydrodynamic modeling of SN 2012A to derive the SN parameters using a standard approach that was previously applied to other SNe IIP. We then analyze the early spectra to determine whether the Hα/Hβ problem arises for SN 2012A, which would indicate clumpy ejecta. As we show below, this is indeed the case. We also explore the question of observational effects of the clumpiness with a modified one-dimensional hydrodynamic code. An additional motivation to study this subject stems from the unsuccessful search for a missing factor that would be responsible for the “mass problem” that was revealed first for SN 2005cs – the conflict between the high mass obtained from the hydrodynamic modeling (Utrobin & Chugai, 2008) and the low mass recovered from archival images (Maund et al., 2005).
2. Observational data
Hydrodynamic modeling with the one-group radiation transfer is aimed at reproducing a bolometric light curve and photospheric velocities. For SN 2012A the bolometric light curve was recovered using UBVRIJHK photometry measured by Tomasella et al. (2013) and was corrected for the reddening 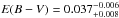 mag adopted by them. We used a blackbody spectral fit to calculate the integrated flux with the zero-points reported by Bessell et al. (1998). Following Tomasella et al. (2013), we adopted the distance modulus of m − M = 29.96 ± 0.15 mag to the nearby galaxy NGC 3239. We used our hydrodynamic model and the calculated R-band light curve together with the R magnitude at the SN detection (Moore et al., 2012) to fix the explosion epoch at MJD = 55 930.6. This date is 2.4 days before the explosion moment estimated by Tomasella et al. (2013). Both values are consistent within the errors, however. Below we count the time from our explosion date. The photospheric velocities for several moments were derived by modeling the line profiles. From the Hα and Hβ lines we derive velocity values of 9000, 6100, 5400, and 1800 km s-1 on day 5.5, 12.5, 22.4, and 52.4, respectively. The velocity uncertainty does not exceed ±100 km s-1.
mag adopted by them. We used a blackbody spectral fit to calculate the integrated flux with the zero-points reported by Bessell et al. (1998). Following Tomasella et al. (2013), we adopted the distance modulus of m − M = 29.96 ± 0.15 mag to the nearby galaxy NGC 3239. We used our hydrodynamic model and the calculated R-band light curve together with the R magnitude at the SN detection (Moore et al., 2012) to fix the explosion epoch at MJD = 55 930.6. This date is 2.4 days before the explosion moment estimated by Tomasella et al. (2013). Both values are consistent within the errors, however. Below we count the time from our explosion date. The photospheric velocities for several moments were derived by modeling the line profiles. From the Hα and Hβ lines we derive velocity values of 9000, 6100, 5400, and 1800 km s-1 on day 5.5, 12.5, 22.4, and 52.4, respectively. The velocity uncertainty does not exceed ±100 km s-1.
3. Model overview
3.1. Standard hydrodynamic model
The numerical modeling of a SN outburst exploits the implicit, Lagrangian, radiation hydrodynamics code Crab, which integrates the spherically symmetric hydrodynamic equations with a gravity force and radiation transfer equation in the one-group (gray) approximation (Utrobin, 2004, 2007). The one-group radiation transfer of the Crab code is a reasonably accurate approximation for the problems we deal with, which is supported by comparing the parameters of type IIP SN 1999em recovered by Utrobin (2007) with those obtained by Baklanov et al. (2005) in the framework of their multigroup radiation hydrodynamics code Stella.
SN 2012A photometrically and spectroscopically resembles the type IIP SN 2008in (Roy et al., 2011), which suggests that parameters of these SNe are similar and that for SN 2012A, the pre-SN is an RSG star as well. We used a non-evolutionary RSG model in the hydrostatic equilibrium for the pre-SN, which is exploded by a supersonic piston applied to the bottom of the stellar envelope at the boundary with the 1.4 M⊙ central core. The core presumably collapses into a neutron star and remains outside the computational domain.
3.2. Modification for clumpy ejecta
To explore the effects of the clumpy structure of the outer layers, we modified the Crab code by means of introducing the clumpiness only in the radiation transfer equation and leaving the hydrodynamics intact. However, the clumpiness affects the hydrodynamics implicitly because the radiative force is modified by the clumpiness through the radiation transfer effects of a clumpy medium.
3.2.1. Radiative transfer in a clumpy medium
The radiation transfer in a clumpy medium is treated by using the standard equations in which the absorption (or scattering) coefficient and the emissivity are modified by including the clumpiness. We considered the clumpy structure of the outer layers to be a medium composed of an ensemble of dense clumps with a density ρc. These are embedded in a more tenuous interclump medium of a density ρi. With the clump-to-average density contrast χ = ρc/ρ and the mass fraction of clumps μ, the volume-filling factor of clumpy component is f = μχ-1, while the clump and interclump densities are 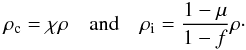 (1)We assume that clumps are uniform spheres of a radius a that are randomly distributed, but do not overlap. The number density of clumps is then
(1)We assume that clumps are uniform spheres of a radius a that are randomly distributed, but do not overlap. The number density of clumps is then 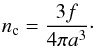 (2)A random photon traveling a length s shares its path between the clumps, fs, and the interclump medium, (1 − f)s (Kendall & Moran, 1963). This suggests that the absorption coefficient in a clumpy medium can be written as a sum
(2)A random photon traveling a length s shares its path between the clumps, fs, and the interclump medium, (1 − f)s (Kendall & Moran, 1963). This suggests that the absorption coefficient in a clumpy medium can be written as a sum 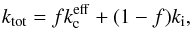 (3)where
(3)where 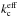 is the effective absorption coefficient for the clumps and ki is the absorption coefficient for the interclump medium. The absorption coefficient
is the effective absorption coefficient for the clumps and ki is the absorption coefficient for the interclump medium. The absorption coefficient 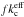 of the clumpy component enters the element of the optical depth dτcl along the linear displacement ds
of the clumpy component enters the element of the optical depth dτcl along the linear displacement ds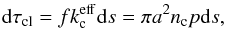 (4)where p is the average absorption probability for the photon to randomly strike the cloud. After elementary integration (e.g., Hobson & Padman, 1993), the absorption probability reads
(4)where p is the average absorption probability for the photon to randomly strike the cloud. After elementary integration (e.g., Hobson & Padman, 1993), the absorption probability reads 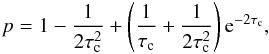 (5)where τc = kca is the clump optical thickness, kc is the microscopic absorption coefficient of the clump matter. As expected, the absorption probability p = 1 for the τc ≫ 1, and p = 4τc/ 3 for τc ≪ 1. Introducing the value q(τc) = (3/4τc)p(τc) reduces the effective absorption coefficient
(5)where τc = kca is the clump optical thickness, kc is the microscopic absorption coefficient of the clump matter. As expected, the absorption probability p = 1 for the τc ≫ 1, and p = 4τc/ 3 for τc ≪ 1. Introducing the value q(τc) = (3/4τc)p(τc) reduces the effective absorption coefficient 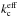 to
to 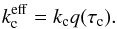 (6)The emissivity of the clumpy medium is treated in the same way as the absorption coefficient, viz.,
(6)The emissivity of the clumpy medium is treated in the same way as the absorption coefficient, viz., 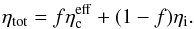 (7)The emissivity of the clumpy component is
(7)The emissivity of the clumpy component is 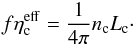 (8)where Lc = 4πa2F is the luminosity of a clump and F is the radiation flux escaping the clump surface. Assuming a homogeneous emissivity ηc across the clump, the emerging intensity in the direction at the angle θ to the outward normal is
(8)where Lc = 4πa2F is the luminosity of a clump and F is the radiation flux escaping the clump surface. Assuming a homogeneous emissivity ηc across the clump, the emerging intensity in the direction at the angle θ to the outward normal is ![\begin{eqnarray} I(\theta) = \int_{0}^{2 \tau_{\rm c} \cos \theta} \!\!\! \eta_{\rm c} \exp(-k_{\rm c} s) \; {\rm d}s = \frac{\eta_{\rm c}}{k_{\rm c}} \left[1-\exp(-2 \tau_{\rm c} \cos \theta)\right]. \label{eq:intemg} \end{eqnarray}](/articles/aa/full_html/2015/03/aa24822-14/aa24822-14-eq54.png) (9)Integrating the projection Icosθ over angles gives the flux escaping the spherical clump
(9)Integrating the projection Icosθ over angles gives the flux escaping the spherical clump 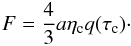 (10)The effective emissivity is thus reduced to
(10)The effective emissivity is thus reduced to 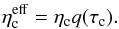 (11)Remarkably, the expressions for the effective absorption coefficient (6) and the effective emissivity (11) look similar; this is an outcome of the optical reversibility. The function q(τc) can be interpreted as the escape probability for a photon emitted in a spherical homogeneous clump (Osterbrock, 1989).
(11)Remarkably, the expressions for the effective absorption coefficient (6) and the effective emissivity (11) look similar; this is an outcome of the optical reversibility. The function q(τc) can be interpreted as the escape probability for a photon emitted in a spherical homogeneous clump (Osterbrock, 1989).
3.2.2. Setting-out clumpiness
The ejecta clumpiness suggested earlier for SN 2008in (Utrobin & Chugai, 2013; Chugai & Utrobin, 2014) is presumably generated during the shock wave propagation in the outermost layers of a RSG star, which are characterized by a density inversion and convection (e.g., Paczyński, 1969; Maeder, 1981; Chiavassa et al., 2011). The mass of these layers depends on the RSG mass and amounts to 0.01 − 0.2 M⊙ for the stellar mass in the range of 10 − 20 M⊙ (Fadeyev, 2012). Two mechanisms might be involved in producing the clumpiness. The first is related to the shock wave propagation through the density inversion layer, which should result in the Rayleigh-Taylor and Richtmyer-Meshkov instabilities. The second mechanism is related to the shock wave propagation through the outer convective zone. The convection velocity in a RSG probed by the macroturbulent velocity attains 6–10 km s-1 (Chiavassa et al., 2011), which is similar to the sound speed. The colliding tangential flows of the neighboring convective cells will produce supersonic collision accompanied by a significant compression. This suggests that the convective zone contains density perturbations of large amplitude, δρ/ρ ~ 1. The SN shock wave running through the inhomogeneous convection layer can produce the clumpy post-shock flow with a strong density contrast.
We set the inhomogeneous structure of the ejecta by turning on the clumpiness generation when the shock wave reached a level corresponding to a certain overlying mass, for example, ≈0.07 M⊙. The downstream clumpiness parameters μ and χ were set to grow with the local hydrodynamic time scale from zero to their final values, which are limited by the pre-set model values μ0 and χ0. The third parameter, the clump radius a, is assumed to be the constant fraction of the shell radius a/r = 0.016; the value is adopted following the estimate on the basis of the amplitude of flux fluctuations in the Hα line profile of SN 2008in (Chugai & Utrobin, 2014).
To facilitate calculating the clump temperature and that of the interclump medium, we assume that the clumps and the interclump medium are in a pressure equilibrium. In the optically thick medium the total pressure of gas and radiation is determined by the thermodynamic equilibrium. In contrast, the pressure equilibrium in the optically thin case is predominantly controlled by the gas pressure because the interaction between gas and radiation field is negligible, and the radiation field in both the clumps and the interclump medium is the same. To describe these extreme regimes, we introduce the effective pressure 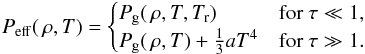 (12)The regimes intermediate between the optically thick and thin cases are described by the factor exp( − τ) in the radiation pressure, where τ is the total optical depth at a certain layer from the outer boundary of the envelope.
(12)The regimes intermediate between the optically thick and thin cases are described by the factor exp( − τ) in the radiation pressure, where τ is the total optical depth at a certain layer from the outer boundary of the envelope.
The hydrodynamic code works with a smooth medium described by the density ρ and the gas temperature T that specify the effective pressure Peff( ρ,T). The pressure equilibrium between the clumps and the interclump matter along with the effective pressure (12) permits us to calculate the gas temperature of the clumps (Tc) and interclump matter (Ti) from the equalities 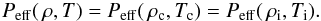 (13)The temperatures Tc and Ti combined with the corresponding densities ρc and ρi (1) and the radiation temperature Tr were used to calculate the absorption coefficients according to relation (3) and the total emissivity (7) for the clumpy medium that enter the radiation hydrodynamics equations.
(13)The temperatures Tc and Ti combined with the corresponding densities ρc and ρi (1) and the radiation temperature Tr were used to calculate the absorption coefficients according to relation (3) and the total emissivity (7) for the clumpy medium that enter the radiation hydrodynamics equations.
4. Supernova parameters
The parameters of SN 2012A were determined in a standard way by means of hydrodynamically simulating the bolometric light curve and the evolution of the photospheric velocity and their fitting to the observations. The main model parameters are the ejecta mass, the explosion energy, the pre-SN radius, and the total 56Ni mass. The latter value is fixed by the bolometric luminosity at the radioactive tail and in the case of SN 2012A is equal to 0.012 M⊙. Additional tuning parameters are the density distribution in the RSG envelope (Fig. 1), the mixing between the helium core and the hydrogen envelope, and the mixing of CNO elements and heavier metals dubbed “Fe” elements, which also include radioactive 56Ni (Fig. 2). The dependence of the observational properties of a SN IIP outburst on the parameter variations was studied in detail elsewhere (Utrobin, 2007). The results of the hydrodynamic modeling are almost independent of the helium-core mass, which is taken following the standard evolutionary models for a single star of a given initial mass. For SN 2012A we adopted a helium-core mass of 4 M⊙, which corresponds to a nonrotating star with a ZAMS mass of about 15 M⊙ (Hirschi et al., 2004).
 |
Fig. 1 Density distribution as a function of interior mass (panel a)) and radius (panel b)) for the best-fit pre-SN model of SN 2012A. The central core of 1.4 M⊙ is omitted. |
 |
Fig. 2 Mass fraction of hydrogen (solid line), helium (long dashed line), CNO elements (short dashed line), and Fe-peak elements including radioactive 56Ni (dotted line) in the ejecta of the best-fit model. |
 |
Fig. 3 Best-fit hydrodynamic model. Panel a): the bolometric light curve of the best-fit model (solid line) overplotted on the bolometric data of SN 2012A (crosses) evaluated from the UBVRIJHK magnitudes reported by Tomasella et al. (2013). Panel b): the calculated photospheric velocity (solid line) compared to the photospheric velocity derived from the Hα and Hβ lines (open circles) (Sect. 2) and from the He i 5876 Å line (filled circles, Tomasella et al. 2013). Panels c) and d): the calculated B and R light curves (solid line) compared to the observations of SN 2012A (crosses) obtained by Tomasella et al. Two open circles are the SN detection in R band (Moore et al., 2012). |
 |
Fig. 4 Density and the 56Ni mass fraction as a function of velocity for the best-fit model at t = 50 days (solid lines). The dash-dotted line is the density distribution fit ρ ∝ v-7.6. |
Exploring the parameter space results in the best-fit model (Fig. 3) with an ejecta mass Menv = 13.1 M⊙, an explosion energy E = 5.25 × 1050 erg, and a pre-SN radius R0 = 715 R⊙. The model reproduces not only the bolometric light curve, but also the B- and R-band light curves. The latter plot is especially valuable because it demonstrates that the earliest photometric points are fitted well and reliably indicate the explosion moment. The model density distribution in the freely expanding envelope on day 50 (Fig. 4) is similar to that of SN 2008in (Utrobin & Chugai, 2013) with an outer density power law of ρ ∝ v-7.6. The power-law index k = −∂lnρ/∂lnv depends on the density distribution of pre-SN outer layers, which in turn is constrained by the initial luminosity peak. The rule of thumb states that a more luminous and longer initial luminosity peak requires a shallower density distribution in the outer layers, that is, a lower k value. The modeling of four SNe IIP, namely, SN 2004et (Utrobin & Chugai, 2009), SN 2005cs (Utrobin & Chugai, 2008), SN 2008in (Utrobin & Chugai, 2013), and SN 2012A, results in a similar density gradient with k ≈ 7.6 in the outer layers.
Combining the ejecta mass with the mass of the neutron star gives a pre-SN mass of 14.5 M⊙. The progenitor ZAMS mass should be higher by the amount lost by the stellar wind. Following the estimate for SN 2003Z with a comparable progenitor mass (Utrobin et al., 2007), we adopted for SN 2012A a lost mass in the range of 0.2 − 0.8 M⊙, in which case the progenitor mass is M = 15.0 ± 0.3 M⊙.
The parameter errors can be estimated by varying the model parameters around the best-fit model. Adopting an uncertainty of 17% in the bolometric luminosity, 4% in the photospheric velocity, and 3% in the plateau duration, we find errors of ±100 R⊙ for the initial radius, ±0.7 M⊙ for the ejecta mass, ±0.6 × 1050 erg for the explosion energy, and ±0.002 M⊙ for the 56Ni mass. The error of the ejecta mass combined with the uncertainty in the mass loss suggests a progenitor mass error of ±1 M⊙.
5. Clumpiness effects
5.1. Evidence from hydrogen lines
 |
Fig. 5 Observed Hα (upper panels) and Hβ (lower panels) (Tomasella et al., 2013) in SN 2012A on days 7, 14, and 23 (thin line) compared to the model profiles (thick line). The model parameters are adjusted to fit the observed Hα. For these models, however, the calculated Hβ is unable to fit the observed profile. |
It was recently found that the Hα and Hβ lines in the early (t ≲ 20 d) spectra of SN 2008in cannot be reproduced for the standard spherically symmetric model (Utrobin & Chugai, 2013); the controversy was resolved by assuming a clumpy structure of the outer ejecta layers. To examine whether the early SN 2012A spectra reveal a similar Hα/Hβ problem, we applied the standard approach to the description of line profiles in an expanding envelope. We considered a freely expanding atmosphere at the top of the photosphere. The Hα and Hβ line profiles are then mainly determined by the radial distribution of the population of the second hydrogen level, n2(v), and the line source function S(v). The latter consists of the scattering and net emission, S = W + Se, where W is the dilution factor and Se is the term responsible for the net emission normalized to the photospheric brightness I.
In the framework of this model, it is easy to fit the Hα line on days 7, 14, and 23 (Fig. 5). However, the Hβ absorption component for the best-fit function n2(v) is too weak, that is, the Hβ line suggests the larger population of the second level. If we were to proceed in the opposite way, that is, first fit the Hβ line and then use the found function n2(v) to calculate the Hα line, we would obtain an unacceptably strong Hα absorption. This is exactly the problem we met in the case of SN 2008in. Note that a more sophisticated model based on radiation transfer with non-LTE effects revealed the same disparity for SN 2006bp on days 8–12 (Dessart et al., 2008, cf. Fig. 9). The modeled Hβ there fits the observed absorption component, while the modeled Hα absorption is substantially deeper than the observed one. Although apparent, this disparity was not mentioned in the refereed paper.
Following the earlier suggestion for SN 2008in, we assumed that the clumpiness of the external layers of the SN 2012A ejecta is responsible for the peculiar Hβ intensity. In this picture, the SN atmosphere consists of an ensemble of dense clouds with the filling factor f embedded in a rarefied intercloud medium. We fit both the Hα and Hβ lines with the filling factor f = (v/vf)-2.8 for v>vf = 5500 km s-1 and the velocity at the photosphere of 8900, 6200, and 5550 km s-1 on days 7, 14, and 23, respectively. This requires a clumpy structure of the outer ≈0.07 M⊙ of the ejecta in the best-fit hydrodynamic model.
The clumpy model invoked in this case suggests a high clump-to-interclump ratio of the Hα optical depth. On day 14, the Hα optical depth in clouds at the fiducial velocity of 8000 km s-1 is τ(Hα) = 80, while in the interclump gas it is τ(Hα) = 0.5 at the same velocity, that is, 160 times lower. Since the density contrast of the clouds probably does not significantly exceed ≈7, which is the compression ratio in the adiabatic-radiation-dominated shock, this factor of ~160 requires explanation. In this respect, we note that when the population rate of the second hydrogen level is dominated by recombination and the depopulation is controlled by the Lyα escape, one expects that the hydrogen concentration n2 is proportional to n3. This means that with a clump-to-interclump density ratio of 5–6, the required ratio of the Hα optical depth in these components can be attained.
5.2. Hydrodynamic model with clumpiness
The signatures of the clumpy structure of the ejecta indicated by hydrogen lines pose questions concerning other observational effects of the clumpiness. Following the proposed prescription for including the clumpiness into the hydrodynamic simulations (Sect. 3.2), we computed several models based on the best-fit homogeneous model. The clumpy structure is determined by the adopted mass fraction of clumps μ and the density contrast χ with the fixed ratio a/r = 0.016. The clumpiness generation is turned on when the shock wave reaches the external mass coordinate of ≈0.07 M⊙. The evolution of the distributions of μ and v between the shock breakout stage (day 1.4) and the free-expansion regime (day 50) is shown in Fig. 6 for the hydrodynamic model with μ0 = 0.95 and χ0 = 7. It is noteworthy that in the outermost layers the clumpiness generation is turned off at the shock breakout because of the shock radiative damping. This explains the sharp drop of the μ value in the outermost layers that is clearly seen on day 50.
 |
Fig. 6 Evolution of velocity and clumping in the hydrodynamic model (μ0 = 0.95, χ0 = 7) from the moment just before the shock breakout (panel a)) until day 50 (panel b)). The thick line is the velocity profile and the dotted line shows the mass fraction of clumps. Note that the clumpiness is turned off in the outermost layers as a result of the shock breakout. |
 |
Fig. 7 Dependence of the bolometric luminosity (thick line) at the initial peak on the mass fraction of clumps μ0 and the density contrast χ0 indicated in each panel. The bolometric luminosity peak of the best-fit model for the smooth medium is shown by the dotted line. |
We show the results for combinations of the mass fraction of the clumps (μ0 = 0.5 and 0.95) and the density contrast (χ0 = 4 and 7). These χ0 values correspond to the adiabatic compression factor for the matter- and radiation-dominated regimes, respectively. The main effect of the clumpiness is a decrease in the optical depth compared to the homogeneous case. This results in a luminosity enhancement during the first several days (Fig. 7). The effect is stronger for larger μ0 and insensitive to the density contrast χ0, in agreement with expression (1) for the density of the interclump medium. As a result of the flux increase, the external layers experience a stronger radiative acceleration, which results in a higher maximum velocity of the ejecta (Fig. 8). For a mass fraction of the clumps of μ0 = 0.95, the highest velocity is about 30% higher than that of the homogeneous model. The density minimum in the range of 10 000 − 12 000 km s-1 separates the main ejecta and the outer ~10-4M⊙ shell that formed as a result of the shock breakout.
 |
Fig. 8 Density as a function of velocity (thick line) for the different mass fraction of clumps μ0 and density contrast χ0 indicated in each panel. The density profile of the best-fit model for the smooth medium is shown by the dotted line. |
In addition to the enhanced flux, the homogeneous structure of the outermost layers (Fig. 6) is another crucial factor favoring the stronger radiative acceleration. Indeed, if the outermost layers were clumpy as well, the radiation-matter interaction would not be strong enough to produce the efficient acceleration. To verify this argument, we computed a hydrodynamic model in which the clumpy structure was set artificially throughout the external layers. This model did not show additional acceleration.
Observationally, velocities of the external ejecta could be probed by the blue wings of the absorption components of the Hα, Hβ, and He i 5876 Å lines. Unfortunately, the Hα and He i 5876 Å absorptions in the first spectrum of SN 2012A on day 7 (Tomasella et al., 2013) are too shallow for confident conclusion. The Hβ absorption indicates ejecta velocities of up to 11 000 − 12 000 km s-1, which is consistent with the velocity of the density minimum (Fig. 8) where the absorption intensity drops significantly. We estimate that the Hβ optical depth in the density minimum is ~10-2 on day 7, which is beyond the detection limit. Another manifestation of the higher expansion velocity in the clumpy model might be the higher photospheric velocity at the early (t< 5 d) stage compared to the homogeneous model (Fig. 9). Unfortunately, this cannot be confirmed because the spectra of SN 2012A are not available at that early stage. At the later (t> 5 d) stage, the photospheric velocities of smooth and clumpy models are similar and consistent with the observational data.
 |
Fig. 9 Photospheric velocity evolution (thick line) for the different mass fraction of clumps μ0 and density contrast χ0 indicated in each panel. The photospheric velocity of the best-fit model for the smooth medium is shown by the dotted line. |
6. Discussion and conclusions
Hydrodynamic models of type IIP supernovae.
We pursued three goals: to derive the basic parameters of SN 2012A, to probe the clumpiness using the Hα and Hβ lines, and to explore the possible effects of the ejecta clumpiness. We find the ejecta mass Menv = 13.1 ± 0.7 M⊙, the explosion energy E = (5.25 ± 0.6) × 1050 erg, the pre-SN radius R0 = 715 ± 100 R⊙, and the total 56Ni mass MNi = 0.012 ± 0.002 M⊙. We estimate the progenitor mass to be 15 ± 1 M⊙. The 56Ni mass estimate coincides with the value derived by Tomasella et al. (2013). Moreover, the ejecta mass and the explosion energy are close to those obtained by Tomasella et al. However, our pre-SN radius is three times larger. We rule out a significantly smaller radius because the pre-SN radius is constrained by the initial luminosity peak; it cannot be reproduced for a compact pre-SN star (Tomasella et al., 2013).
 |
Fig. 10 Explosion energy (panel a)) and 56Ni mass (panel b)) vs. hydrodynamic progenitor mass for SN 2012A and eight other core-collapse SNe (Utrobin & Chugai, 2013). The SN 2012A position in both scatter plots supports the correlations of “explosion energy vs. progenitor mass” and “56Ni mass vs. progenitor mass”. |
With SN 2012A, we now have the parameters of nine SNe IIP that are derived by the unique method of hydrodynamic simulations (Table 1). Among these objects, two events, SN 1987A and SN 2000cb, are produced by the explosion of a blue supergiant and one peculiar event, SN 2009kf, has an anomalously high explosion energy. The ejecta mass of SN 2012A is the lowest in this sample. In the scatter plots of “explosion energy vs. progenitor mass” and “56Ni mass vs. progenitor mass” (Fig. 10), the SN 2012A parameters fall into the bands that are occupied by other events. In this regard, SN 2012A is indeed a normal type IIP event.
The early spectra of SN 2012A show the Hα/Hβ problem – a weak model Hβ line for the model Hα line consistent with observations – which was recovered previously for SN 2008in (Utrobin & Chugai, 2013; Chugai & Utrobin, 2014). The disparity is resolved in the same way as for SN 2008in, that is, by invoking a clumpy structure of the external ejecta. The ejecta clumpiness is presumably produced during the shock wave propagation in the outer layers of a pre-SN, which are associated with the density inversion and the vigorous convection in a RSG atmosphere. The mass of the clumpy external layers is estimated to be ~0.07 M⊙. This value is consistent with the mass of RSG layers of 0.01−0.2 M⊙ above the density inversion for stars in the range of 10−20 M⊙ (Fadeyev, 2012). Although the solution we proposed for the Hα/Hβ problem seems to be reasonable, an independent decisive evidence is required to confirm this conjecture.
Hydrodynamic simulations with the modified best-fit model, which incorporates a clumpiness of the outer 0.07 M⊙ layers into the radiation transfer, demonstrated that the most pronounced effect is the increase in the maximum velocity of the ejecta. The physics behind this phenomenon is the clumpiness in the outer layers with an outermost low-mass smooth layer. The clumpiness favors a higher luminosity, which results in an efficient radiative acceleration of the outer layers.
The effect of a higher velocity in the clumpy outer ejecta is highly remarkable because the low photospheric velocity at very early phase is a specific feature of the hydrodynamic model of SNe IIP with a low pre-SN mass (Utrobin & Chugai, 2008). That
was the reason why the ejecta mass and the explosion energy of the model were pushed up to account for the observed high expansion velocity of the outer layers. The velocity increase of the outer ejecta in the clumpy model compared to the smooth model opens an interesting possibility of producing a hydrodynamic model of SNe IIP with the lower pre-SN mass. One can hope thus to resolve the mass problem, meaning the conflict between the high hydrodynamic mass for SNe IIP and the low mass based on the archival pre-explosion images. The problem was first uncovered for SN 2005cs (Utrobin & Chugai, 2008), for which we compared the progenitor mass of 17 − 19 M⊙ obtained from hydrodynamic modeling with the 7 − 12 M⊙ ZAMS mass recovered by Maund et al. (2005) from the archival images. This disparity has emerged in several other cases as well. For SN 2012A the hydrodynamic mass is slightly higher than the mass recovered from the pre-explosion image, although they are consistent within errors (Tomasella et al., 2013). The possibility of resolving the mass problem for SNe IIP by invoking the ejecta clumpiness is promising and requires a separate study.
Acknowledgments
We thank Lina Tomasella for kindly sending us spectra of SN 2012A. V.P.U. is grateful to Wolfgang Hillebrandt, Ewald Müller, and Hans-Thomas Janka for hospitality during his stay at the MPA. V.P.U. is supported by Russian Scientific Foundation grant 14-12-00203.
References
- Baklanov, P. V., Blinnikov, S. I., & Pavlyuk, N. N. 2005, Astron. Lett., 31, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Chiavassa, A., Freytag, B., Masseron, T., & Plez, B. 2011, A&A, 535, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chugai, N. N., & Utrobin, V. P. 2014, Astron. Lett., 40, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Blondin, S., Brown, P. J., et al. 2008, ApJ, 675, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, R. G., Woosley, S. E., Weaver, T. A., & Pinto, P. A. 1994, ApJ, 430, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Fadeyev, Y. A. 2012, Astron. Lett., 38, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, S. W., & Arnett, W. D. 1977, A&AS, 33, 515 [NASA ADS] [Google Scholar]
- Grassberg, E. K., Imshennik, V. S., & Nadyozhin, D. K. 1971, Ap&SS, 10, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobson, M. P., & Padman, R. 1993, MNRAS, 264, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, M. G., & Moran, A. P. 1963, Geometrical probability (London: Griffin) [Google Scholar]
- Maeder, A. 1981, A&A, 99, 97 [NASA ADS] [Google Scholar]
- Maund, J. R., Smartt, S. J., & Danziger, I. J. 2005, MNRAS, 364, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Newton, J., & Puckett, T. 2012, Central Bureau Electronic Telegrams, 2974, 1 [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, CA: University Science Books) [Google Scholar]
- Paczyński, B. 1969, Acta Astron., 19, 1 [NASA ADS] [Google Scholar]
- Roy, R., Kumar, B., Benetti, S., et al. 2011, ApJ, 736, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Tomasella, L., Cappellaro, E., Fraser, M., et al. 2013, MNRAS, 434, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2004, Astron. Lett., 30, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2007, A&A, 461, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2008, A&A, 491, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2009, A&A, 506, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2013, A&A, 555, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., Chugai, N. N., & Pastorello, A. 2007, A&A, 475, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Density distribution as a function of interior mass (panel a)) and radius (panel b)) for the best-fit pre-SN model of SN 2012A. The central core of 1.4 M⊙ is omitted. |
| In the text | |
 |
Fig. 2 Mass fraction of hydrogen (solid line), helium (long dashed line), CNO elements (short dashed line), and Fe-peak elements including radioactive 56Ni (dotted line) in the ejecta of the best-fit model. |
| In the text | |
 |
Fig. 3 Best-fit hydrodynamic model. Panel a): the bolometric light curve of the best-fit model (solid line) overplotted on the bolometric data of SN 2012A (crosses) evaluated from the UBVRIJHK magnitudes reported by Tomasella et al. (2013). Panel b): the calculated photospheric velocity (solid line) compared to the photospheric velocity derived from the Hα and Hβ lines (open circles) (Sect. 2) and from the He i 5876 Å line (filled circles, Tomasella et al. 2013). Panels c) and d): the calculated B and R light curves (solid line) compared to the observations of SN 2012A (crosses) obtained by Tomasella et al. Two open circles are the SN detection in R band (Moore et al., 2012). |
| In the text | |
 |
Fig. 4 Density and the 56Ni mass fraction as a function of velocity for the best-fit model at t = 50 days (solid lines). The dash-dotted line is the density distribution fit ρ ∝ v-7.6. |
| In the text | |
 |
Fig. 5 Observed Hα (upper panels) and Hβ (lower panels) (Tomasella et al., 2013) in SN 2012A on days 7, 14, and 23 (thin line) compared to the model profiles (thick line). The model parameters are adjusted to fit the observed Hα. For these models, however, the calculated Hβ is unable to fit the observed profile. |
| In the text | |
 |
Fig. 6 Evolution of velocity and clumping in the hydrodynamic model (μ0 = 0.95, χ0 = 7) from the moment just before the shock breakout (panel a)) until day 50 (panel b)). The thick line is the velocity profile and the dotted line shows the mass fraction of clumps. Note that the clumpiness is turned off in the outermost layers as a result of the shock breakout. |
| In the text | |
 |
Fig. 7 Dependence of the bolometric luminosity (thick line) at the initial peak on the mass fraction of clumps μ0 and the density contrast χ0 indicated in each panel. The bolometric luminosity peak of the best-fit model for the smooth medium is shown by the dotted line. |
| In the text | |
 |
Fig. 8 Density as a function of velocity (thick line) for the different mass fraction of clumps μ0 and density contrast χ0 indicated in each panel. The density profile of the best-fit model for the smooth medium is shown by the dotted line. |
| In the text | |
 |
Fig. 9 Photospheric velocity evolution (thick line) for the different mass fraction of clumps μ0 and density contrast χ0 indicated in each panel. The photospheric velocity of the best-fit model for the smooth medium is shown by the dotted line. |
| In the text | |
 |
Fig. 10 Explosion energy (panel a)) and 56Ni mass (panel b)) vs. hydrodynamic progenitor mass for SN 2012A and eight other core-collapse SNe (Utrobin & Chugai, 2013). The SN 2012A position in both scatter plots supports the correlations of “explosion energy vs. progenitor mass” and “56Ni mass vs. progenitor mass”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


