| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201424699 | |
| Published online | 09 February 2015 | |
Mass–concentration relation and weak lensing peak counts
1
INAF – Osservatorio Astronomico di Roma, via Frascati 33, 00040,
Monte Porzio Catone
Roma
Italy
email: winnyenodrac@gmail.com
2
CENTRA, Instituto Superior Técnico, Universidade de
Lisboa, Avenida Rovisco Pais
1, 1049-001
Lisboa,
Portugal
3
Jodrell Bank Centre for Astrophysics, The University of
Manchester, Alan Turing Building,
Oxford Rd, Manchester
M13 9PL,
UK
4
Dipartimento di Fisica e Astronomia, Alma Mater Studiorum
Università di Bologna, Viale Berti
Pichat 6/2, 40127
Bologna,
Italy
5
Dipartimento di Fisica, Università di Napoli “Federico
II”, Compl. Univ. di Monte S.
Angelo, via Cinthia, 80126
Napoli,
Italy
6
INFN, Sezione di Napoli, Compl. Univ. di Monte S. Angelo, via
Cinthia, 80126
Napoli,
Italy
7
Dipartimento di Fisica, Università di Roma “La
Sapienza”, Piazzale Aldo
Moro, 00185
Roma,
Italy
Received: 29 July 2014
Accepted: 11 September 2014
Context. The statistics of peaks in weak lensing convergence maps is a promising tool for investigating both the properties of dark matter haloes and constraining the cosmological parameters.
Aims. We study how the number of detectable peaks and its scaling with redshift depend upon the cluster’s dark matter halo profiles and use peak statistics to constrain the parameters of the mass-concentration (MC) relation. We investigate which constraints the Euclid mission can set on the MC coefficients taking degeneracies with the cosmological parameters into account, too.
Methods. To this end, we first estimated the number of peaks and its redshift distribution for different MC relations and found that the steeper the mass dependence and the greater the normalisation, the larger the number of detectable clusters, with the total number of peaks changing up to 40% depending on the MC relation. We then performed a Fisher matrix forecast of the errors on the MC relation parameters, as well as on cosmological parameters.
Results. We find that peak number counts detected by Euclid can determine the normalization Av, the mass Bv, redshift Cv slopes, and intrinsic scatter σv of the MC relation to an unprecedented accuracy, which is σ(Av) /Av = 1%, σ(Bv) /Bv = 4%, σ(Cv) /Cv = 9%, and σ(σv) /σv = 1% if all cosmological parameters are assumed to be known. If we relax this severe assumption, constraints are degraded, but remarkably good results can be restored by setting only some of the parameters or combining peak counts with Planck data. This precision can give insight into competing scenarios of structure formation and evolution and into the role of baryons in cluster assembling. Alternatively, for a fixed MC relation, future peak counts can perform as well as current BAO and SNeIa when combined with Planck.
Key words: gravitational lensing: weak / galaxies: clusters: general
© ESO, 2015
1. Introduction
A clear picture of the formation and evolution of cosmic structures requires a good understanding of the interplay between astrophysical processes and the cosmological framework. As dark matter-dominated, nearly virialised objects, clusters of galaxies should be relatively easy to sort out. The hierarchical cold dark matter scenario with a cosmological constant (ΛCDM) can explain many features of galaxy clusters. Their density profile over most radii is accurately reproduced by the Navarro-Frenk-White (NFW) density profile (Navarro et al. 1996, 1997), and the relationship between mass and concentration is accurately predicted.
The concentration measures the halo central density relative to outer regions and is related to the cluster properties at the formation time, in particular to its virial mass and redshift (Bullock et al. 2001). Lower mass and smaller redshift clusters should show higher concentrations, with a moderate evolution with mass and redshift (Bullock et al. 2001; Duffy et al. 2008). A flattening in concentration might appear towards the very high mass tail and high redshifts (Klypin et al. 2011; Prada et al. 2012), but the real presence of any turn-around is still being debated (Meneghetti & Rasia 2013).
The mass-concentration (MC) relation also depends upon cosmological parameters (Kwan et al. 2013; De Boni et al. 2013). Other than the normalisation of the matter power spectrum and the dark matter content, the dark energy equation of state also affects the MC relation for low-mass haloes (Kwan et al. 2013; De Boni et al. 2013), although the effect is secondary in very massive clusters.
This clear theoretical picture is challenged by conflicting observational pieces of evidence (Comerford & Natarajan 2007; Fedeli 2012). The normalisation factor of the MC relation is higher than expected, whereas the slope is steeper (Comerford & Natarajan 2007; Ettori et al. 2010). These results seem to be stable against redshift. A steep c(M) was found at 0.15 ≲ z ≲ 0.3 in the weak lensing analysis of 19 X-ray luminous lensing galaxy clusters (Okabe et al. 2010), at 0.3 ≲ z ≲ 0.7 in a combined strong and weak lensing analysis of a sample of 25 lenses from the Sloan Giant Arcs Survey (Oguri et al. 2012) and in a sample of 31 massive galaxy clusters at high redshift 0.8 ≲ z ≲ 1.5 (Sereno & Covone 2013). Concentrations measured in lensing-selected clusters are systematically higher than in X-ray analyses (Comerford & Natarajan 2007), and a significant number of over-concentrated clusters are detected at high masses (Broadhurst et al. 2008; Oguri & Blandford 2009; Umetsu et al. 2011). However, these conflicts can be partially reconciled by considering orientation and shape biases (Sereno & Umetsu 2011; Rasia et al. 2012), which severely affect strong lenses. In fact, the disagreement is reduced in strong lensing analyses of X-ray selected samples (Sereno & Zitrin 2012). It is also worth noting that the discrepancy can also be related to selection effects. Indeed, the recent analyses of the CLASH data (Merten et al. 2014) have shown that the MC relation determined from the data can be reconciled with the expectation from numerical simulations provided one carefully takes the details of the sample selection into account.
One of the main sources of concern in the measurement of the MC relation is the choice and size of the sample. Clusters selected according to their gravitational lensing features or X-ray flux may form biased samples that are primarily elongated along the line of sight (Hennawi et al. 2007; Meneghetti et al. 2011), and the strongest lenses are expected to be a highly biased population of haloes oriented mainly towards the observer (Oguri & Blandford 2009). Neglecting halo triaxiality can then lead to systematically higher, biased concentrations. Correcting for shape and orientation biases requires very deep multi-wavelength observations (Sereno et al. 2013; Limousin et al. 2013), which are expensive to carry out on a large sample. Furthermore, the orientation bias cannot fully account for the discrepancy between theory and observations for some very strong lenses (Sereno et al. 2010).
Another reason for concern is that the discrepancies between theory and observations are mitigated when stacking techniques are employed. Weak lensing analyses of stacked clusters of agree with theoretical predictions (Johnston et al. 2007; Mandelbaum et al. 2008; Sereno & Covone 2013). Oguri et al. (2012) find that the concentration measured with a stacked analysis was lower than what is expected from the individual clusters in their sample. Okabe et al. (2013) performed a weak-lensing stacked analysis of a complete and volume-limited sample of X-ray-selected galaxy clusters and found shallow density profiles that are consistent with numerical simulations. The stacked profile of 31 clusters at high redshift was in accordance with theoretical predictions, too (Sereno & Covone 2013).
Pending the debate about which MC relation has to be trusted – numerically motivated or observationally based – and given the systematics connected to the measurements of concentration, it is worth tackling the problem from a different perspective that relies on an alternative probe. Weak lensing peaks in the convergence map have recently attracted attention as a powerful tool for finding clusters up to very high redshift. While low statistics and difficulties with galaxy shape measurement from the ground have limited application of this technique to present data (but see, e.g., Shan et al. 2012 and refs. therein for recent results), the future availability of large galaxy surveys both from the ground (e.g. LSST1) and space (e.g. Euclid2) has motivated a renewed interest in this technique – not only as a tool for finding clusters, but also as a way to probe the cosmological parameters (Marian et al. 2009, 2011; Dietrich & Hartlap 2010; Kratochvil et al. 2010), the theory of gravity (Cardone et al. 2013), primordial non-Gaussianity (Maturi et al. 2011), and the dark matter halo properties (Bartelmann et al. 2002). Investigating whether such a methodology can allow us to distinguish among different MC relations is the aim of the present work.
As already hinted at above, peak number counts also depend on cosmological parameters so that one should pay attention to possible degeneracies between the two sets of quantities. Actually, the background cosmology can be held fixed when considering the peak number-count dependence on the MC relation, since most of the cosmological parameters play minor roles in determining peak statistics. Alternatively, one can combine peak counts with other probes, as we investigate here when taking the recent Planck covariance matrix as a prior.
The plan of the paper is as follows. In Sect. 2, we review how the number of detectable weak-lensing peaks can be estimated and also discuss questions concerning the filter choice and the role of the MC relation. The formulae obtained here are then used in Sects. 3 and 4 to infer the number of detectable peaks and its redshift distribution for five different MC relations, thus highlighting how the results strongly depend on the MC parameters. This encouraging outcome suggests that future surveys can put interesting constraints on the mass and redshift depencence and the normalization of the MC relation. We therefore devote Sect. 5 to discussing the Fisher matrix forecast for the case of the Euclid survey, also taking degeneracies with cosmological parameters into account and the impact of baryons. Lastly, Sect. 6 is devoted to conclusions.
2. Weak lensing peaks
As the largest and most massive mass concentrations, galaxy clusters are ideal candidates for lensing background galaxies. The spectacular arcs forming when the cluster and source are aligned along the line of sight are indeed remarkable evidence. In less favourable circumstances, clusters generate a shear field that can be reconstructed from the statistical properties of the shape distributions of background galaxies. In shear maps, clusters can then be detected as peaks clearly emerging out of the noise – thus offering an efficient technique for identifying them.
As a peak finder, we consider the aperture mass defined by (Schneider 1996) 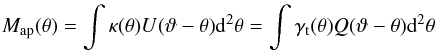 (1)where κ(θ) and γt(θ) = −ℛ [ γ(θ)exp(−2iφ) ] are the convergence and the tangential shear at position θ = (ϑcosφ,ϑsinφ), and U(ϑ), Q(ϑ) are compensated filter functions related to each other by the integral equation
(1)where κ(θ) and γt(θ) = −ℛ [ γ(θ)exp(−2iφ) ] are the convergence and the tangential shear at position θ = (ϑcosφ,ϑsinφ), and U(ϑ), Q(ϑ) are compensated filter functions related to each other by the integral equation 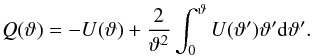 (2)To detect a cluster as a peak in the aperture mass map, we have to estimate the Map variance and then set a cut on the signal-to-noise ratio (S/N). To this end, we have to specify how we compute both signals, as is outlined in the next two sections.
(2)To detect a cluster as a peak in the aperture mass map, we have to estimate the Map variance and then set a cut on the signal-to-noise ratio (S/N). To this end, we have to specify how we compute both signals, as is outlined in the next two sections.
2.1. Halo model
For given lens and source redshifts (zl,zs), the aperture mass depends on the lens’s mass density profile. Justified by both simulations of structure formation and observations, we assume that cluster haloes are described by the NFW (Navarro et al. 1996, 1997) model 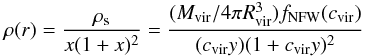 (3)with x = r/Rs, y = r/Rvir and
(3)with x = r/Rs, y = r/Rvir and 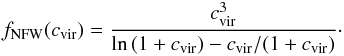 (4)Following a common practice, we use the virial mass Mvir as a mass parameter, i.e. the mass lying within the virial radius Rvir, where the mean mass density,
(4)Following a common practice, we use the virial mass Mvir as a mass parameter, i.e. the mass lying within the virial radius Rvir, where the mean mass density, 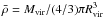 , equals Δvir(zl)ρcrit(zl) (with ρcrit(zl) the critical density at the cluster redshift). The critical overdensity Δvir(zl) should be computed according to the spherical collapse formalism (being hence a function of the adopted cosmological model) and turns out to depend on the redshift (see, e.g. Bryan & Norman 1998). However, it is normal to set Δvir = 200 at all redshift and replace (Mvir,cvir) with (M200,c200), which is what we do in the following.
, equals Δvir(zl)ρcrit(zl) (with ρcrit(zl) the critical density at the cluster redshift). The critical overdensity Δvir(zl) should be computed according to the spherical collapse formalism (being hence a function of the adopted cosmological model) and turns out to depend on the redshift (see, e.g. Bryan & Norman 1998). However, it is normal to set Δvir = 200 at all redshift and replace (Mvir,cvir) with (M200,c200), which is what we do in the following.
As a second parameter, we choose the halo concentration c200 = R200/Rs3. According to N-body simulations, the NFW model can be reduced to a one-parameter class since c200 correlates with the virial mass M200. Actually, the slope, the scatter, and the redshift evolution of the c200 − M200 relation are still matters of controversy, with different results available in the literature. However, most works do agree on the shape of the MC relation given by 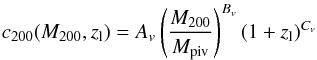 (5)with Mpiv a pivot mass and different values for the (Av,Bv,Cv) parameters. Equation (5) should actually be considered only as an approximate rather than exact relation. Indeed, for a given mass, halo concentrations scatter around the value predicted by Eq. (5). This gives rise to a distribution which can be reasonably well described as a lognormal with mean value and variance σv depending on the MC relation adopted. Such a scatter is usually neglected in peak count studies, but it must be taken into account if one aims at studying the impact of the MC relation on peaks statistics. We set Mpiv = 5 × 1014 M⊙ and
(5)with Mpiv a pivot mass and different values for the (Av,Bv,Cv) parameters. Equation (5) should actually be considered only as an approximate rather than exact relation. Indeed, for a given mass, halo concentrations scatter around the value predicted by Eq. (5). This gives rise to a distribution which can be reasonably well described as a lognormal with mean value and variance σv depending on the MC relation adopted. Such a scatter is usually neglected in peak count studies, but it must be taken into account if one aims at studying the impact of the MC relation on peaks statistics. We set Mpiv = 5 × 1014 M⊙ and 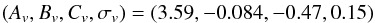 (6)as a fiducial case in agreement with Duffy et al. (2008, hereafter.
(6)as a fiducial case in agreement with Duffy et al. (2008, hereafter.
With these ingredients, it is now only a matter of algebra to compute the lensing properties of the NFW profile inserting the mass and concentration values in the analytical expressions of the convergence κ and shear γ given in Bartelmann (1996) and Wright & Brainerd (2000).
2.2. Filter function and S/N
Gravitational lensing probes the total matter distribution along the line of sight so that the observed aperture mass Map is eventually the sum of the cluster contribution, as well as of another that is due to the uncorrelated large-scale structure projected along the same line of sight, namely 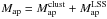 . Since it is a density contrast, one typically assumes that
. Since it is a density contrast, one typically assumes that 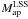 averages out to zero – thus not biasing the Map distribution, but only contributing to the variance (Hoekstra 2001). Then, the filter functional form and its parameters are chosen as a compromise between the need to find as many clusters as possible and the necessity of decreasing the number of fake peaks. To this end, shear field simulations, when taking both the underlying fiducial cosmology and the survey characteristics into account, are used to tailor the filter parameters (see e.g. Hetterscheidt et al. 2005). However, such a method is far from being perfect, since it is intimately related to the adopted cosmology and to the halo model assumed in the reference simulation.
averages out to zero – thus not biasing the Map distribution, but only contributing to the variance (Hoekstra 2001). Then, the filter functional form and its parameters are chosen as a compromise between the need to find as many clusters as possible and the necessity of decreasing the number of fake peaks. To this end, shear field simulations, when taking both the underlying fiducial cosmology and the survey characteristics into account, are used to tailor the filter parameters (see e.g. Hetterscheidt et al. 2005). However, such a method is far from being perfect, since it is intimately related to the adopted cosmology and to the halo model assumed in the reference simulation.
As a possible solution, Maturi et al. (2005, hereafter M05) proposes an optimal filter, explicitly taking both the cosmological model and the shape of the signal into account, i.e. the halo shear profile. According to M05, the Fourier transform of the filter reads as![\begin{eqnarray} \hat{\Psi}(\ell) = \frac{1}{(2 \pi)^2} \left [ \int{\frac{|\hat{\gamma}_{\rm t}(\ell)|^2}{P_{\rm N}(\ell)} {\rm d}^2 \ell} \right ]^{-1} \frac{\hat{\gamma}_{\rm t}(\ell)}{P_{\rm N}(\ell)}, \label{eq: defpsihat} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq50.png) (7)where
(7)where 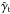 is the Fourier transform of the tangential shear component and PN(ℓ) the noise power spectrum as a function of the angular wavenumber ℓ. Two terms contribute to the noise so that it is
is the Fourier transform of the tangential shear component and PN(ℓ) the noise power spectrum as a function of the angular wavenumber ℓ. Two terms contribute to the noise so that it is 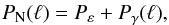 (8)with
(8)with 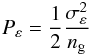 (9)the term caused by the finite number of galaxies (with number density ng) and their intrinsic ellipticities with variance σε; and Pγ(ℓ) = Pκ(ℓ) / 2 the noise due to the LSS, where the factor 1 / 2 comes from using only one shear component. Under the Limber flat sky approximation, we have
(9)the term caused by the finite number of galaxies (with number density ng) and their intrinsic ellipticities with variance σε; and Pγ(ℓ) = Pκ(ℓ) / 2 the noise due to the LSS, where the factor 1 / 2 comes from using only one shear component. Under the Limber flat sky approximation, we have 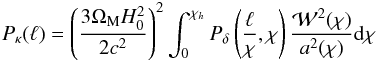 (10)with
(10)with 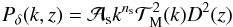 (11)the matter power spectrum, with spectral index ns and present day mass variance σ8 on scales R = 8 h-1 Mpc used to set the normalization constant
(11)the matter power spectrum, with spectral index ns and present day mass variance σ8 on scales R = 8 h-1 Mpc used to set the normalization constant 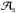 . Here,
. Here, 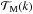 is the matter transfer function, approximated according to Eisenstein & Hu (1998), while D(z) is the growth factor (normalised to unity today) for the assumed cosmological model. In Eq. (10), the redshift is replaced by the comoving distance
is the matter transfer function, approximated according to Eisenstein & Hu (1998), while D(z) is the growth factor (normalised to unity today) for the assumed cosmological model. In Eq. (10), the redshift is replaced by the comoving distance 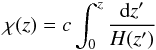 (12)with H(z) the Hubble rate. Finally,
(12)with H(z) the Hubble rate. Finally, 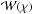 is the lensing weight function (assuming a spatially flat universe),
is the lensing weight function (assuming a spatially flat universe), 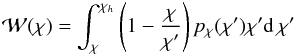 (13)and pχ(χ)dχ = pz(z)dz the source redshift distribution – which we here parameterise as (Smail et al. 1994)
(13)and pχ(χ)dχ = pz(z)dz the source redshift distribution – which we here parameterise as (Smail et al. 1994) ![\begin{eqnarray} p_z(z) \propto\frac{\beta}{z_0} \left ( \frac{z}{z_0} \right )^2 \exp{\left [ - \left ( \frac{z}{z_0} \right )^{\beta} \right ]} \label{eq: pz} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq73.png) (14)and normalise to unity. We set (β,z0) = (1.5,0.6) so that zm = 0.9 is the median redshift of the sources as expected for the Euclid mission (Marian et al. 2011).
(14)and normalise to unity. We set (β,z0) = (1.5,0.6) so that zm = 0.9 is the median redshift of the sources as expected for the Euclid mission (Marian et al. 2011).
Following Bartelmann (1996) and Wright & Brainerd (2000) for the shear profile of the NFW model, one finally gets for the Fourier transform of the filter4![\begin{eqnarray} \hat{\Psi}(\ell) &=&- \frac{1}{(2 \pi)^3} \left [ \left ( \frac{M_{200}/4 \pi R_{200}^2}{\Sigma_{\rm crit}} \right ) g(c_{200}) \left ( 2 \pi \theta_{\rm s}^2 \right ) \right ]^{-1}\nonumber \\ &&\times \frac{\tilde{\tau}(\ell \theta_{\rm s})}{P_{\rm N}(\ell) \tilde{{\cal{D}}}(\theta_{\rm s})} \label{eq: fourierpsi} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq76.png) (15)where Σcrit = c2Ds/ (4πGDdDds) is the critical density for lensing (depending on the lens and source redshift), g(cvir) = fNFW(c200) /c200, θs is the angular scale corresponding to Rs, and we have defined
(15)where Σcrit = c2Ds/ (4πGDdDds) is the critical density for lensing (depending on the lens and source redshift), g(cvir) = fNFW(c200) /c200, θs is the angular scale corresponding to Rs, and we have defined 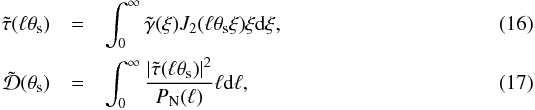 with
with 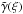 the NFW shear profile scaled with respect to ρsRs/ Σcrit (Bartelmann 1996; Wright & Brainerd 2000).
the NFW shear profile scaled with respect to ρsRs/ Σcrit (Bartelmann 1996; Wright & Brainerd 2000).
We now stress an important caveat about the values of (M200,c200) entering the filter function. The best choice would be to fix them to those of the halo we are interested in to find. Needless to say, such a strategy is unfeasible, and we have to set them to some fiducial values 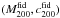 , thus obtaining a filter optimised for finding clusters with mass and concentration close to the fiducial ones. As we will see in a moment, the S/N does not critically depend on these values, but rather on the MC relation taken as fiducial.
, thus obtaining a filter optimised for finding clusters with mass and concentration close to the fiducial ones. As we will see in a moment, the S/N does not critically depend on these values, but rather on the MC relation taken as fiducial.
With this caveat in mind, we take the inverse Fourier transform of Eq. (15) and set Q = Ψ in the aperture mass definition to get eventually 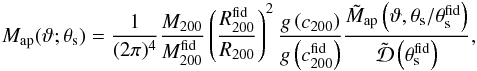 (18)with ϑ the filter aperture and the label “fid” denoting quantities referred to the fiducial case. In Eq. (18), we have also defined (with
(18)with ϑ the filter aperture and the label “fid” denoting quantities referred to the fiducial case. In Eq. (18), we have also defined (with 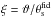 and
and 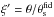 )
) ![\begin{eqnarray} \label{eq: defmaptilde} \tilde{M}_{\rm ap} &=& \int_{0}^{\xi}{\tilde{\gamma}\left [ \xi^{\prime} \left ( \theta_{\rm s}/\theta_{\rm s}^{\rm fid} \right ) \right ] \xi^{\prime} {\rm d}\xi^{\prime}} \nonumber\\ &&\times \int_{0}^{2 \pi}{\tilde{\Psi}\left [ \theta_{\rm s} \left ( \xi^2 + \xi^{\prime 2} - 2 \xi \xi^{\prime} \cos{\theta} \right )^{1/2} \right ] \cos{(2 \theta)} {\rm d}\theta} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq91.png) (19)and
(19)and 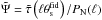 .
.
A conceptual remark is in order here. Equation (18) was obtained by assuming that the measured shear and cluster profiles are the same. Actually, what one measures is the shear field reconstructed from the observed galaxies ellipticities, which is only an approximation of the input cluster profile. However, the only way to get analytic prediction is to identify the reconstructed and theoretical shear profiles – what we have implicitly done here. Moreover, as a further approximation, we set γ ≃ gsh with gsh = γ/ (1 − κ) the measurable reduced shear. In the weak-lensing limit (κ ≪ 1), the difference is safely negligible.
To predict the number of peaks, we need the S/N. Then, we first compute the noise given by5 (Maturi et al. 2005) ![\begin{eqnarray} \sigma_{\rm ap}^2 &=& \frac{1}{2 \pi} \int_{0}^{\infty}{P_{\varepsilon} \left | \tilde{\Psi}(\ell) \right |^2 \ell {\rm d}\ell} \nonumber \\ & =& \frac{1}{(2 \pi)^7} \left( \frac{M_{200}^{\rm fid}/4 \pi R_{200}^{{\rm fid} \ 2}}{\Sigma_{\rm crit}} \right)^{-2} \frac{g^{-2} \left(c_{200}^{\rm fid} \right)} {\left ( 2 \pi \theta_{\rm s}^{{\rm fid} \ 2} \right )^2} \frac{P_{\varepsilon}}{\tilde{{\cal{D}}}(\theta_{\rm s}^{\rm fid})} \nonumber \\ & &\times \int_{0}^{\infty}{\frac{\tilde{\tau}^2(\ell \theta_{\rm s}^{\rm fid})}{[P_{\varepsilon} + (1/2) P_{\kappa}(\ell)]^2} \ell {\rm d}\ell}. \label{eq: defsigmaap} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq96.png) (20)Thus, the S/N reads
(20)Thus, the S/N reads 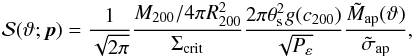 (21)where
(21)where 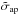 is the integral in the third row of Eq. (20). In the above relation, p summarizes the parameters which the S/N depends upon. Apart from the virial mass M200 explicitly appearing as a multiplicative term through the factor
is the integral in the third row of Eq. (20). In the above relation, p summarizes the parameters which the S/N depends upon. Apart from the virial mass M200 explicitly appearing as a multiplicative term through the factor 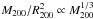 , there are the MC relation parameters (Av,Bv,Cv) used to estimate the halo concentration c200 and hence θs through Eq. (5). The lens and source redshift (zl,zs) enter through the critical density Σcrit and the conversion from the linear Rs to the angular scale θs. Finally, we remember that Eq. (5) is affected by a lognormal scatter σv, which is another parameter to be added to the list. To take both the source redshift distribution and the scatter in the MC relation fully into account, we therefore compute the final S/N as
, there are the MC relation parameters (Av,Bv,Cv) used to estimate the halo concentration c200 and hence θs through Eq. (5). The lens and source redshift (zl,zs) enter through the critical density Σcrit and the conversion from the linear Rs to the angular scale θs. Finally, we remember that Eq. (5) is affected by a lognormal scatter σv, which is another parameter to be added to the list. To take both the source redshift distribution and the scatter in the MC relation fully into account, we therefore compute the final S/N as 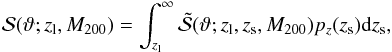 (22)with
(22)with 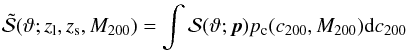 (23)and
(23)and ![\begin{eqnarray} p_{\rm c}(c_{200}; M_{200}) \propto \exp{\left \{- \frac{1}{2} \left [ \frac{\log{c_{200}} - \log{\langle c_{200} \rangle(M_{200})}}{\sigma_v} \right ]^2 \right \}} \label{eq: pclog}\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq104.png) (24)Here, ⟨ c200 ⟩ (M200) is defined as in Eq. (5) for given values of the MC relation parameters (Av,Bv,Cv) and scatter σv.
(24)Here, ⟨ c200 ⟩ (M200) is defined as in Eq. (5) for given values of the MC relation parameters (Av,Bv,Cv) and scatter σv.
Two sets of MC relation parameters actually enter Eqs. (22)–(24), the former fixed by the MC relation used to set the filter (hence determining 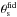 ) and the latter related to the MC relation used in the estimate of the expected number of clusters (giving θs). We use the D08 MC relation as a fiducial (with σv = 0.15) to set the filter function, while we consider different choices for (Av,Bv,Cv,σv) to investigate whether peak statistics can distinguish among MC relations.
) and the latter related to the MC relation used in the estimate of the expected number of clusters (giving θs). We use the D08 MC relation as a fiducial (with σv = 0.15) to set the filter function, while we consider different choices for (Av,Bv,Cv,σv) to investigate whether peak statistics can distinguish among MC relations.
3. Cluster detectability
Equations (21)–(24) allow us to estimate the S/N for a cluster of virial mass M200 and redshift zl provided the MC relation parameters (Av,Bv,Cv) and the scatter σv. To this end, we have to preliminarily set the survey characteristics and the background cosmology to estimate the noise σap. Moreover, we have to fix the filter scale ϑ.
We consider the survey specification for the photometric Euclid survey (Laureijs et al. 2011; Amendola et al. 2013) with an area of 15 000 deg2 and an ellipticity dispersion σϵ = 0.3. The total number of source galaxies is set to ng = 30 gal / arcmin2 and is assumed to be uniform over the full survey area. The results can be easily scaled to other choices, but noting that 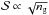 , while the total number of peaks linearly depends on the survey area.
, while the total number of peaks linearly depends on the survey area.
To be consistent with the recent Planck results (Planck Collaboration XVI 2014), we assume a flat ΛCDM model as fiducial cosmological scenario with 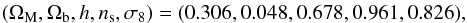 (25)where ΩM (Ωb) is the current matter (baryon) density, h = H0/ 100 km s-1 Mpc-1 the present-day dimensionless Hubble constant, ns the scalar spectral index, and σ8 the variance of perturbations on the scale 8 h-1 Mpc. The dark energy equation of state is described by the CPL (Chevallier & Polarski 2001; Linder 2003) ansatz
(25)where ΩM (Ωb) is the current matter (baryon) density, h = H0/ 100 km s-1 Mpc-1 the present-day dimensionless Hubble constant, ns the scalar spectral index, and σ8 the variance of perturbations on the scale 8 h-1 Mpc. The dark energy equation of state is described by the CPL (Chevallier & Polarski 2001; Linder 2003) ansatz 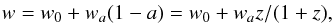 (26)with (w0,wa) held fixed to the ΛCDM values, (− 1,0). We also assume that dark energy does not cluster on the scales of interest. Thus, the growth factor is the solution of
(26)with (w0,wa) held fixed to the ΛCDM values, (− 1,0). We also assume that dark energy does not cluster on the scales of interest. Thus, the growth factor is the solution of 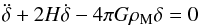 (27)with δ the density perturbation. The S/N has a negligible dependence on the cosmological parameters, so that the following results hold true independently of the fiducial cosmology adopted.
(27)with δ the density perturbation. The S/N has a negligible dependence on the cosmological parameters, so that the following results hold true independently of the fiducial cosmology adopted.
The choice of the filter scale ϑ requires some caution. The optimal filter is designed to account for the NFW profile to maximise the signal. Therefore, a natural scale would be ϑ = θs, since most of the mass contributing to the lensing signal is contained within this aperture. For a cluster with M200 = 5 × 1014 M⊙ at a typical cluster redshift zl = 0.3, the concentration predicted by the D08 relation reads as c200 = 2.65, thus giving θs ≃ 1 arcmin, while the virial radius subtends an angle θ200 ≃ 2.8 arcmin. However, not all the clusters have the same mass and redshift. Setting ϑ = 1 arcmin would be an optimal choice for these median values, but would strongly underestimate the signal for clusters that are more massive or are at a lower redshift. In contrast, a varying ϑ would allow maximisin the S/N at every redshift, but would make it difficult to compare peak counts in different bins. As a compromise, we therefore set ϑ = 2 arcmin noting that with this choice we cut the contribution on scales larger than θ200. Indeed, it can be smaller than 2 arcmin for low-mass and/or high-redshift clusters.
MC relations parameters for a pivotal mass Mpiv = 5 × 1014h-1 M⊙ for the different cases investigated, whose acronyms (ID) are shown in the first column.
Having set all the preliminary quantities, we can now investigate how the S/N depends on the virial mass and redshift for different MC relations. Table 1 lists the parameter choices for different models we take as representative cases, also giving the name we use for it in the following. The first two cases are theoretical relations motivated by the comparison with numerical simulations. In contrast, the Ok10 and Og12 MC relations have been inferred from observations6. The authors did not try to fit for a redshift dependence so that the parameter Cv is set to zero. To explore a possible redshift dependence, we therefore introduced the two other relations (Ok10z and Og12z) by arbitrarily setting the Cv parameter to the D08 value. Although the Ok10z and Og12z relations are not motivated by either numerical simulations or observations, they are useful for scrutinising the dependence of peak statistics on the MC relation. Numerically inspired B01 and D08 relations are shallower than the observationally motivated Ok10 and Og12, and also have a larger normalisation. In other words, for the pivot mass, a cluster at a given redshift zl is more concentrated according to Ok10 and Og12 than for B01 and D08. More concentrated haloes have higher masses within the scale radius, so one should expect that, for given (zl,M200), the S/N will be greater for Ok10 and Og12 MC. However, this is only partly true. Indeed, because of the different scaling with z of the considered MC relations and the use of a filter based on D08, the S/N will not simply scale with the concentration so that a full computation is needed to check the above qualitative prediction.
 |
Fig. 1 Top panels: S/N vs. cluster virial mass for fixed redshift (zl = 0.4,0.9,1.3from left to right) for different MC relations (black, red, blue, dashed blue, orange, dashed orange for B01, D08, Ok10, Ok10z, Og12, Og12z, respectively). Bottom panels: S/N vs. cluster redshift for fixed mass (log M200 = 14.5,15.5,16.5from left to right). |
 |
Fig. 2 Maximum S/N (left) and virial mass log Mmax (centre) at which the S/N is maximised as a function of the cluster redshift. Right panel: Mmax normalised to the value for the D08 relation (wiggles are merely interpolation features). Black, red, blue, dashed blue, orange, and dashed orange lines refer to B01, D08, Ok10, Ok10z, Og12, and Og12z, respectively. |
Figure 1 shows how the S/N, 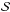 , depends on (zl,M200) for the different MC relations we consider. Although the filter is built using D08 as a fiducial case, the MC relation the gives the highest
, depends on (zl,M200) for the different MC relations we consider. Although the filter is built using D08 as a fiducial case, the MC relation the gives the highest 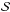 value depends on (zl,M200). As a general rule, for a given zl, the
value depends on (zl,M200). As a general rule, for a given zl, the 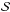 vs. M200 curve shows non-monotonic behaviour. It first increases with M200 up to a maximum value and then decreases again. The peak value is higher for steeper MC relations, while the opposite is observed for what concerns the width of the curve. As a consequence, the D08 relation provides the highest
vs. M200 curve shows non-monotonic behaviour. It first increases with M200 up to a maximum value and then decreases again. The peak value is higher for steeper MC relations, while the opposite is observed for what concerns the width of the curve. As a consequence, the D08 relation provides the highest 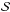 values for groups and intermediate-mass clusters, while the empirically motivated MC relations Ok10 and Og12 (and their redshift dependent counterparts) overcome D08 in the high-mass regime.
values for groups and intermediate-mass clusters, while the empirically motivated MC relations Ok10 and Og12 (and their redshift dependent counterparts) overcome D08 in the high-mass regime.
For fixed cluster mass, the dependence on the redshift is more complicated, and which MC relation provides the highest S/N depends on the mass regime. This can also be understood from Fig. 2, where we plot the maximum S/N as a function of the cluster redshift. As a further remark, we note that the Ok10z and Og12z curves always stay quite close to their redshift-independent counterparts, thus demonstrating that it is the concentration-mass dependence that drives the 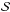 values.
values.
The above results can be qualitatively explained considering how 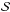 depends on the halo concentration. On the one hand, Eq. (22) shows that the S/N is the product of
depends on the halo concentration. On the one hand, Eq. (22) shows that the S/N is the product of 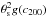 , an increasing function of the concentration, an integral depending on the ratio
, an increasing function of the concentration, an integral depending on the ratio 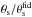 , and the filter aperture. One can naively expect that the higher the concentration, the greater the S/N. Should this be the dominant factor, the MC relation providing the higher concentration would also be the one preferred by a S/N viewpoint. However, a larger c200 also implies a smaller θs. Consequently, if θs<ϑ, the filter cuts away a large part of the cluster, thus leading to a lower aperture mass (hence a smaller integral term). The best compromise between these two somewhat opposite behaviours depend on the cluster mass and redshift.
, and the filter aperture. One can naively expect that the higher the concentration, the greater the S/N. Should this be the dominant factor, the MC relation providing the higher concentration would also be the one preferred by a S/N viewpoint. However, a larger c200 also implies a smaller θs. Consequently, if θs<ϑ, the filter cuts away a large part of the cluster, thus leading to a lower aperture mass (hence a smaller integral term). The best compromise between these two somewhat opposite behaviours depend on the cluster mass and redshift.
It is worth noting that the largest S/N does not guarantee the final detected number of peaks to also be the largest one. This can be understood by looking at Fig. 2, where we plot the maximum S/N as a function of zl for the different MC relations considered. For sources at the survey median redshift zs = 0.9, all the MC relations achieve a maximum S/N that is higher than for the D08 case. However, such a maximum corresponds to haloes as massive as log M200 ~ 16, which are few. If we limit our attention to the mass range corresponding to 0.1 ≤ zl ≤ 0.3, i.e. 13.5 ≤ log M200 ≤ 15.5, we see that the D08 maximum S/N is comparable to – if not even greater than – those of other MC relations. Although such a discussion only considers the maximum S/N, it nevertheless warns against inferring any conclusion on which MC relation provides the largest number of peaks based on S/N alone.
4. Peak number counts
 |
Fig. 3 Left: total number of peaks as a function of the threshold S/N |
The weak lensing peaks we are interested in are due to massive clusters. To compute their expected number, we first need to know how many massive haloes there are. This is given by the mass function7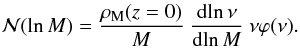 (28)Here, ν = δc/σ(M), δc is the critical overdensity for spherical collapse, and σ is the variance of the perturbations on the scale R corresponding to the mass M,
(28)Here, ν = δc/σ(M), δc is the critical overdensity for spherical collapse, and σ is the variance of the perturbations on the scale R corresponding to the mass M, ![\begin{eqnarray} \sigma^2[R(M)] = \frac{1}{(2 \pi)^3} \int{P_{\delta}(k) |W(kR)|^2 {\rm d}^3k}, \label{eq: sigmavardef} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq171.png) (29)where W(kR) is the Fourier transform of the spherical top hat function and the density power spectrum Pδ(k,z).
(29)where W(kR) is the Fourier transform of the spherical top hat function and the density power spectrum Pδ(k,z).
To compute the mass function through Eq. (28), one has to choose an expression for νϕ(ν). We adopt the Sheth et al. (2001) function ![\begin{eqnarray} \nu \varphi(\nu) = A \sqrt{\frac{2 a \nu^2}{\pi}} \left[1 + \left(a \nu^2\right)^{-p}\right] \exp{\left(-a \nu^2/2\right)}, \label{eq: stmf} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq175.png) (30)with (A,a,p) = (0.322,0.75,0.3). Although many other choices are possible (see for instance the extensive list in Murray et al. 2013, and refs. therein), we note that the choice of the mass function is not critical for our aims, since we are mainly interested in comparing the impact of different MC relations on peak count rather than forecasting exact numbers.
(30)with (A,a,p) = (0.322,0.75,0.3). Although many other choices are possible (see for instance the extensive list in Murray et al. 2013, and refs. therein), we note that the choice of the mass function is not critical for our aims, since we are mainly interested in comparing the impact of different MC relations on peak count rather than forecasting exact numbers.
Not all the clusters will give rise to detectable peaks, but only those with S/N greater than a fixed threshold. We have first to take into account that the shot noise from discrete background galaxy positions and the intrinsic ellipticity distribution introduce a scatter of the observed aperture mass Map around its theoretically expected value 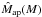 . As a consequence, a halo of mass M has a certain probability p(Map | M) of producing an aperture mass Map which we can model as a Gaussian, namely,
. As a consequence, a halo of mass M has a certain probability p(Map | M) of producing an aperture mass Map which we can model as a Gaussian, namely, ![\begin{eqnarray} p(M_{\rm ap} | M) \propto \exp{\left \{ - \frac{1}{2} \left [ \frac{M_{\rm ap} - \hat{M}_{\rm ap}(M)}{\sigma_{\rm ap}} \right ]^2 \right \}} \cdot \label{eq: mapprob} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq179.png) (31)The probability that the S/N will be higher than a given threshold will read as (Bartelmann et al. 2002)
(31)The probability that the S/N will be higher than a given threshold will read as (Bartelmann et al. 2002) ![\begin{eqnarray} p({\cal{S}} > {\cal{S}}_{\rm th} | M_{\rm vir}, z) = \frac{1}{2} {\rm erfc}\left [ \frac{{\cal{S}}(M_{\rm vir}, z) - {\cal{S}}_{\rm th}}{\sqrt{2}} \right ]\cdot \label{eq: snrprob} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq180.png) (32)Therefore, the number density of haloes giving a detectable weak lensing peak will be the product of the halo mass function and this probability, i.e.,
(32)Therefore, the number density of haloes giving a detectable weak lensing peak will be the product of the halo mass function and this probability, i.e., 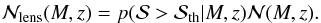 (33)Integrating over the redshift and the mass and multiplying by the survey area gives the total number of peaks generated by cluster haloes and a higher S/N than a threshold value
(33)Integrating over the redshift and the mass and multiplying by the survey area gives the total number of peaks generated by cluster haloes and a higher S/N than a threshold value 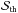 , which reads as
, which reads as 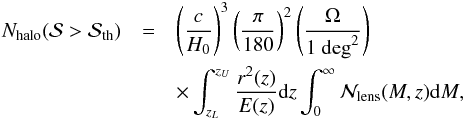 (34)with r(z) = (c/H0)-1χ(z). As redshift limits, we set (zL,zU) = (0.1,1.4) since the number of peaks outside this range is negligible – although the survey will very likely detect galaxies over a much wider range.
(34)with r(z) = (c/H0)-1χ(z). As redshift limits, we set (zL,zU) = (0.1,1.4) since the number of peaks outside this range is negligible – although the survey will very likely detect galaxies over a much wider range.
 |
Fig. 4 Left: number of peaks with |
The number of observed peaks is the sum of 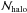 and a term due to the contamination from the LSS,
and a term due to the contamination from the LSS, 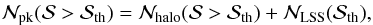 (35)where the LSS term reads as (Maturi et al. 2010, 2011)
(35)where the LSS term reads as (Maturi et al. 2010, 2011) ![\begin{eqnarray} {\cal{N}}_{\rm LSS} = \frac{1}{(2 \pi)^{3/2}} \left ( \frac{\sigma_{\rm LSS}}{\sigma_{\rm ap}} \right )^2 \frac{\kappa_{\rm th}}{\sigma_{\rm ap}} \exp{\left [ - \frac{1}{2} \left ( \frac{\kappa_{\rm th}}{\sigma_{\rm ap}} \right )^2 \right ]}, \label{eq: npklss} \end{eqnarray}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq190.png) (36)with
(36)with 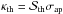 and
and 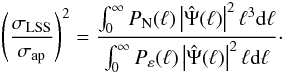 (37)Here,
(37)Here, 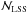 only depends on the noise properties and the threshold S/N, but not on the lens mass and redshift. This is an obvious consequence of this term being due to the LSS rather than a particular cluster. For this same reason,
only depends on the noise properties and the threshold S/N, but not on the lens mass and redshift. This is an obvious consequence of this term being due to the LSS rather than a particular cluster. For this same reason, 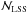 is determined by the matter power spectrum (hence the underlying cosmological scenario) entering PN(ℓ).
is determined by the matter power spectrum (hence the underlying cosmological scenario) entering PN(ℓ).
4.1. Cumulative peak number and S/N threshold
As a preliminary step, it is worth investigating how the total number of peaks (actual ones due to clusters and fake ones due to LSS) change as a function of the threshold S/N. This will also tell us how to choose the threshold S/N value to discriminate true from fake peaks.
Figure 3 helps us to highlight some important issues. First, in the left-hand panel, we plot the 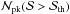 as a function of the threshold S/N for the six different MC relations in Table 1. Somewhat surprisingly, although the filter has been set using the D08 relation as fiducial, there are more peaks than for the other relations. This is better shown in the central panel where the number of peaks is scaled with respect to the D08 one. The quick increase in the ratio for large
as a function of the threshold S/N for the six different MC relations in Table 1. Somewhat surprisingly, although the filter has been set using the D08 relation as fiducial, there are more peaks than for the other relations. This is better shown in the central panel where the number of peaks is scaled with respect to the D08 one. The quick increase in the ratio for large 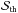 is not due to the number of peaks diverging, but rather to
is not due to the number of peaks diverging, but rather to 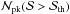 quickly approaching the null value for the reference D08 case.
quickly approaching the null value for the reference D08 case.
The larger number of peaks for MC relations other than the fiducial D08 one can be traced back to the higher S/N for clusters of mass log M200> 15, where, hereafter, M200 is the mass in solar units. The higher the cluster redshift, the higher the mass to pass the selection threshold. As z increases, the minimum mass a cluster should have in order to generate a detectable peak increases, too, but its value also depends on the adopted MC relation. Since the D08 model predicts the lower S/N values, the limiting mass is greater for this case so that the contribution to the total number of peaks in the highest redshift bins decreases as the threshold S/N increases. As a consequence, the MC relations predicting larger 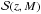 have a greater chance or producing haloes that are massive enough to pass the selection threshold, thus leading to the greater
have a greater chance or producing haloes that are massive enough to pass the selection threshold, thus leading to the greater 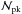 values.
values.
Up to now, we have considered the total number of detectable peaks, but what is actually of interest to investigate in the MC relation is the number of peaks due to clusters alone. The right-hand panel in Fig. 3, showing the ratio between the number of peaks due to clusters and the total ones, helps us to disentangle the clusters from fake peaks. As expected, 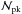 is dominated by the LSS term for low S/N; that is to say, the lower the S/N, the higher the probability that the detected peak is a fake one due to the LSS rather than the evidence for a cluster. This agrees with common-sense expectations and previous analyses in the literature using different cosmological models and survey parameters (Hetterscheidt et al. 2005; Maturi et al. 2010). The ratio
is dominated by the LSS term for low S/N; that is to say, the lower the S/N, the higher the probability that the detected peak is a fake one due to the LSS rather than the evidence for a cluster. This agrees with common-sense expectations and previous analyses in the literature using different cosmological models and survey parameters (Hetterscheidt et al. 2005; Maturi et al. 2010). The ratio 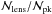 is, however, a strong increasing function of
is, however, a strong increasing function of 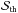 for
for 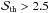 . Imposing the requirement
. Imposing the requirement 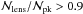 , one gets
, one gets  with a very weak dependence on the adopted MC relation. We can therefore safely argue that all the peaks with
with a very weak dependence on the adopted MC relation. We can therefore safely argue that all the peaks with 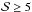 are due to clusters. We find a value for
are due to clusters. We find a value for 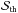 comparable to but higher than what is suggested in Maturi et al. (2010) because of differences in both the cosmological model and the survey characteristics.
comparable to but higher than what is suggested in Maturi et al. (2010) because of differences in both the cosmological model and the survey characteristics.
4.2. Number of peaks in redshift bins
The total number of peaks is obtained by integrating over the full redshift range as in Eq. (35). This obviously degrades the information on the dependence of the MC relation on z. It is worth investigating what can be learned by binning the peaks according to their redshift. The number of peaks in a bin centred on z and with width Δz can be computed using again Eq. (35) and replacing (zL,zU) with (z − Δz/ 2,z + Δz/ 2). Since we need a redshift measurement to assign a given peak to a bin, we implicitly assume that all the detected peaks are due to clusters, i.e. 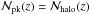 ; in other words, we disregard the LSS term. Actually, for a given threshold S/N, such a term makes a constant contribute to the number of peaks in each redshift bin. However, since we only consider peaks with
; in other words, we disregard the LSS term. Actually, for a given threshold S/N, such a term makes a constant contribute to the number of peaks in each redshift bin. However, since we only consider peaks with 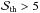 , one can be confident that the predicted numbers indeed refer to peaks with measurable redshift. For Δz = 0.1, we get the
, one can be confident that the predicted numbers indeed refer to peaks with measurable redshift. For Δz = 0.1, we get the 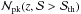 curves shown in the left-hand panel of Fig. 4 for the different MC relations listed in Table 1.
curves shown in the left-hand panel of Fig. 4 for the different MC relations listed in Table 1.
Binning the data indeed helps to distinguish better among the different MC relations. The number of peaks in each given bin happens to be quite different from one MC relation to another – with D08 dominating the signal for z< 0.5, but quickly decreasing for larger z. Indeed, a way to distinguish between D08 and other relations is by looking at bins with z> 1, where almost no peaks are expected for the D08 case, while a still significant number can be found for other relations. In particular, Ok10z and Og12z give the highest 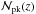 values.
values.
That redshift binning improves the efficiency when distinguishing among different MC relations can also be quantitatively shown by first considering the total number of clusters given in Table 2. The comparison of numbers for the relative difference with respect to the D08 case (reported in the third column8) with the ones referred to binned data (which can be read from the right panel of Fig. 4) convincingly shows that binning in z is utterly effective.
Total number of peaks 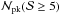 and percentage deviation
and percentage deviation ![\hbox{$\Delta = \left [ {\cal{N}}_{\rm pk}^{\rm id}({\cal{S}} \ge 5) - {\cal{N}}_{\rm pk}^{D08}({\cal{S}} \ge 5) \right ]/{\cal{N}}_{\rm pk}^{D08}({\cal{S}} \ge 5)$}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq213.png) for the different MC relations considered.
for the different MC relations considered.
5. Fisher matrix forecasts
To quantify the conclusions discussed above, we carry on a Fisher matrix analysis and consider observed data to be the total number of peaks with 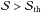 in equally spaced redshift bins centred on z and with width Δz = 0.1 over the range (0.1,1.4). As usual when dealing with number counts, we can assume Poisson errors and then quantify the agreement between data and model through the following likelihood function (Cash 1979):
in equally spaced redshift bins centred on z and with width Δz = 0.1 over the range (0.1,1.4). As usual when dealing with number counts, we can assume Poisson errors and then quantify the agreement between data and model through the following likelihood function (Cash 1979): 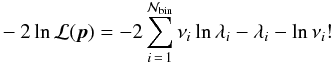 (38)where, to simplify the notation, we have respectively defined
(38)where, to simplify the notation, we have respectively defined 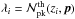 and
and 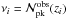 for the theoretical and observed number of peaks in the ith redshift bin, and p denotes the set of parameters we want to constrain and the sum runs over the
for the theoretical and observed number of peaks in the ith redshift bin, and p denotes the set of parameters we want to constrain and the sum runs over the 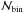 bins. The Fisher matrix elements are given by the second derivatives of the logarithm of the likelihood with respect to the parameters of interest evaluated at the fiducial values. Starting from Eq. (38), one gets (Holder et al. 2001)
bins. The Fisher matrix elements are given by the second derivatives of the logarithm of the likelihood with respect to the parameters of interest evaluated at the fiducial values. Starting from Eq. (38), one gets (Holder et al. 2001) 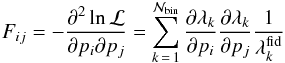 (39)where
(39)where 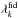 is the expected number of peaks in the kth bin for the fiducial model. The covariance matrix is then simply the inverse of the Fisher matrix, and its diagonal elements represent the lowest variance one can achieve on the model parameter measurement.
is the expected number of peaks in the kth bin for the fiducial model. The covariance matrix is then simply the inverse of the Fisher matrix, and its diagonal elements represent the lowest variance one can achieve on the model parameter measurement.
Although our main interest focusses on the MC relation, peak number counts do not depend on this relation alone. On the contrary, 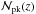 strongly depends on the background cosmological model, too, so that the Fisher matrix must be computed with respect to both sets of parameters. As a first approximation, one can hold the cosmology fixed and only derive the constraints on the MC parameters9. Otherwise, one can assume the MC relation known from a different probe and investigate to which extent peak number counts can constrain cosmology. Both possibilities will be considered below.
strongly depends on the background cosmological model, too, so that the Fisher matrix must be computed with respect to both sets of parameters. As a first approximation, one can hold the cosmology fixed and only derive the constraints on the MC parameters9. Otherwise, one can assume the MC relation known from a different probe and investigate to which extent peak number counts can constrain cosmology. Both possibilities will be considered below.
5.1. Constraints on the MC parameters
We first consider the case with the background cosmological model held fixed. An implicit assumption which the Fisher matrix forecast relies on is that the confidence regions may be approximated as a Gaussian ellipsoids, while it is not uncommon that the true ones have broad tails or significant curvature. Holder et al. (2001) investigated whether this is the case for number counts by comparing with Monte Carlo analysis of simulated datasets. They found that Fisher matrix forecasts can indeed be trusted. Therefore, we are confident that our estimated iso-likelihood contours, shown in Fig. 5, provide reliable accounts of the degeneracies in the MC relation parameters space. It is worth emphasising that these results have been obtained assuming that the cosmological parameters are known with infinite precision so that they can be hold fixed in the Fisher matrix derivation. We return to this point later.
 |
Fig. 5 Fisher matrix forecasts for the 68, 95, 99% CL assuming a fiducial D08 MC relation and a filter aperture ϑ = 2 arcmin. |
The marginalised 1σ errors on the MC parameters for the fiducial are 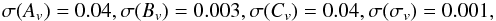 (40)which can also be rewritten conveniently as
(40)which can also be rewritten conveniently as 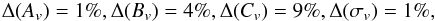 (41)with Δ(p) = σ(p) /p. Such numbers nicely show that peak number counts in redshift bins provide competitive constraints on the MC parameters, thus enabling us to discriminate convincingly among different MC relations. Indeed, comparing the differences of the (Av,Bv,Cv) values in Table 1 with the 1σ uncertainties given above, we can safely conclude that the B01, Ok10, and Og12 relations could be rejected with high confidence, should the actual MC relation coincide with fiducial D08.
(41)with Δ(p) = σ(p) /p. Such numbers nicely show that peak number counts in redshift bins provide competitive constraints on the MC parameters, thus enabling us to discriminate convincingly among different MC relations. Indeed, comparing the differences of the (Av,Bv,Cv) values in Table 1 with the 1σ uncertainties given above, we can safely conclude that the B01, Ok10, and Og12 relations could be rejected with high confidence, should the actual MC relation coincide with fiducial D08.
It is worth wondering whether the results depend on the adopted fiducial MC relation. We do not expect this to be the case since the Fisher matrix approach should provide a reliable description of the likelihood in the neighbourhood of the fiducial values regardless of these values. However, the Ok10 and Og12 mass slope parameters are so far away from those of D08 that some failure of the Fisher matrix cannot be excluded a priori. To check this, we therefore repeated the Fisher matrix evaluation, taking the Og12z as fiducial model for the MC relation while holding the cosmological parameters set to the Planck ones. We get 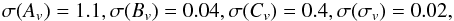 (42)for the marginalised 1σ errors; i.e.,
(42)for the marginalised 1σ errors; i.e., 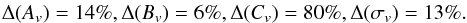 (43)Although there is a significant degradation of the constraints owing to the degeneracy between Bv and Cv, it is nevertheless still possible to distinguish the different MC relations10. Using the value of the mass slope parameter Bv as discriminator, we now get | Bv(Og12z) − Bv(mc) | /σ(Bv) = (11.5,12.6,4.8) for mc = B01, D08, Ok10, so that it is still possible to distinguish D08 and empirically motivated MC relations, in agreement with the previous result.
(43)Although there is a significant degradation of the constraints owing to the degeneracy between Bv and Cv, it is nevertheless still possible to distinguish the different MC relations10. Using the value of the mass slope parameter Bv as discriminator, we now get | Bv(Og12z) − Bv(mc) | /σ(Bv) = (11.5,12.6,4.8) for mc = B01, D08, Ok10, so that it is still possible to distinguish D08 and empirically motivated MC relations, in agreement with the previous result.
The above constraints have been obtained after assuming that the cosmological parameters are perfectly known. Relaxing this assumption introduces degeneracies which significantly enlarge the confidence ranges. For the cosmological model with DE EoS described by the CPL ansatz and fitting both the MC and seven cosmological parameters (ΩM,Ωb,w0,wa,h,nPS,σ8), the marginalised 1σ errors on the MC parameters now read as 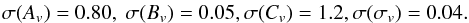 (44)It is possible to distinguish empirically (e.g. Ok10, Og12) and numerically inspired MC relations thanks to the radically different Bv value.
(44)It is possible to distinguish empirically (e.g. Ok10, Og12) and numerically inspired MC relations thanks to the radically different Bv value.
The situation can be improved by adopting an intermediate strategy. Forcing the model to have a Λ term (i.e. setting w0 = −1 and wa = 0) and fixing (Ωb,h,nPS) to their fiducial values, we get the following 1σ errors: 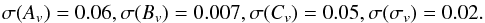 (45)Although the constraints are wider by roughly a factor of two than in the case obtained fixing background cosmology (not the case for Cv), they are still remarkably strong allowing for distinguishing among different MC relations.
(45)Although the constraints are wider by roughly a factor of two than in the case obtained fixing background cosmology (not the case for Cv), they are still remarkably strong allowing for distinguishing among different MC relations.
Although our focus here is on the use of peak number counts, this is not the only probe one can use. Degeneracies among cosmological and MC parameter can indeed be lifted by using different tracers. To this end, we combine our Fisher matrix with the one obtained by inverting the Planck covariance matrix11. By leaving all the seven cosmological and four MC relation parameters free to change, we get 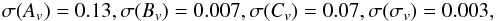 (46)which are dramatically tighter than the case with no Planck data and comparable (although looser) with those for the case with the cosmology set to the fiducial case. Setting (Ωb,w0,wa,h,nPS) to their fiducial values now only improves the constraint on Av (from 0.13 to 0.06), while those on (Bv,Cv,σv) are almost left unchanged. This is expected since the Planck data already set strong limits on the background cosmological model so that forcing it to be equal to the fiducial one now has a minor impact on the MC parameters confidence ranges.
(46)which are dramatically tighter than the case with no Planck data and comparable (although looser) with those for the case with the cosmology set to the fiducial case. Setting (Ωb,w0,wa,h,nPS) to their fiducial values now only improves the constraint on Av (from 0.13 to 0.06), while those on (Bv,Cv,σv) are almost left unchanged. This is expected since the Planck data already set strong limits on the background cosmological model so that forcing it to be equal to the fiducial one now has a minor impact on the MC parameters confidence ranges.
5.2. Constraints on cosmological parameters
We now explore the use of peak number counts as a tool for probing the background cosmological model. The most favourable case is the one with the fewest parameters so that we only vary (ΩM,σ8) and set all the remaining cosmological and MC quantities to their fiducial values. Only using peaks, we get 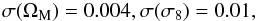 (47)which are already comparable to what one can obtain using the Planck data alone. A joint fit to peak number counts and Planck pushes the errors down further leading to
(47)which are already comparable to what one can obtain using the Planck data alone. A joint fit to peak number counts and Planck pushes the errors down further leading to 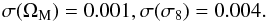 (48)This can be easily understood by looking at Fig. 6, where 1σ marginal error contours in the (ΩM,σ8) plane are shown as obtained from peak count alone, Planck alone, and the combination of the two probes. As a matter of fact, weak lensing and CMB temperature anisotropies suffer from different degeneracy for what concerns those two parameters, and this happens in a way that makes their combination more effective.
(48)This can be easily understood by looking at Fig. 6, where 1σ marginal error contours in the (ΩM,σ8) plane are shown as obtained from peak count alone, Planck alone, and the combination of the two probes. As a matter of fact, weak lensing and CMB temperature anisotropies suffer from different degeneracy for what concerns those two parameters, and this happens in a way that makes their combination more effective.
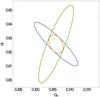 |
Fig. 6 Marginal error 1σ contours in the (ΩM,σ8) plane as obtained from peak counts alone (blue ellipse), Planck alone (green ellipse), and the combination of the two probes (yellow ellipse). |
Moving towards a more realistic case, we can allow the MC parameters to change, thereby introducing degeneracies among (ΩM,σ8) and (Av,Bv,Cv,σv). As a result, we now find 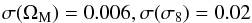 (49)from only the peak number counts. Instead, if we add Planck we have
(49)from only the peak number counts. Instead, if we add Planck we have 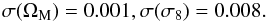 (50)Although the constraints have been weakened, the uncertainties on the MC parameters have not dramatically broadened the confidence ranges of (ΩM,σ8), which are still well constrained even when only peak number counts are used. Figure 7 illustrates this by plotting the marginal error ellipses for all the combinations of MC parameters with Ωm and σ8, for the case with or without Planck priors.
(50)Although the constraints have been weakened, the uncertainties on the MC parameters have not dramatically broadened the confidence ranges of (ΩM,σ8), which are still well constrained even when only peak number counts are used. Figure 7 illustrates this by plotting the marginal error ellipses for all the combinations of MC parameters with Ωm and σ8, for the case with or without Planck priors.
 |
Fig. 7 Marginal error 1σ contours for all the combinations of MC parameters with Ωm (top panels) and σ8 (bottom panels), for the case with (yellow curves) or without (blue curves) Planck priors. |
As a further step, we investigate the precision of peaks number counts to constrain all cosmological parameters under the assumption that the MC relation has been already constrained through a different method. Here, we only consider the case where Planck data are added to peaks, since the degeneracies among cosmological parameters cannot be lifted by a probe that is only sensitive to integrated quantities. Adding Planck and peak Fisher matrices and marginalising over the MC parameters gives 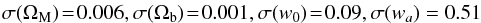 (51)and
(51)and 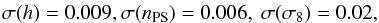 (52)which compares nicely to what can be obtained by combining Planck with other data, such as BAOs and SNeIa. In particular, there is significant improvement in the constraints on the dark energy equation of state. Specifically, we get
(52)which compares nicely to what can be obtained by combining Planck with other data, such as BAOs and SNeIa. In particular, there is significant improvement in the constraints on the dark energy equation of state. Specifically, we get 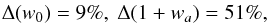 (53)to be compared with 18% and 51% from the combination of Planck, BAOs, and SNeIa data. However, it is worth stressing that the comparison is actually unfair given that we have contrasted future peak statistics with current SNeIa and BAO data. A fair comparison would ask for a preliminary Fisher matrix forecast based on, for instance, Euclid BAO data, which is, however, outside our aims here.
(53)to be compared with 18% and 51% from the combination of Planck, BAOs, and SNeIa data. However, it is worth stressing that the comparison is actually unfair given that we have contrasted future peak statistics with current SNeIa and BAO data. A fair comparison would ask for a preliminary Fisher matrix forecast based on, for instance, Euclid BAO data, which is, however, outside our aims here.
Moroever, we emphasise that this result is strongly bound to the assumption that the MC relation is perfectly known. If we relax it, the constraints in the eleven-dimensional parameter space weaken strongly. While (ΩM,Ωb,h,nPS,σ8) are still reasonably well constrained, the accuracy on dark energy parameters (w0,wa) read as 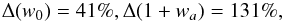 (54)thus asking for additional data to narrow down the confidence ranges.
(54)thus asking for additional data to narrow down the confidence ranges.
5.3. The impact of baryons
Both the B01 and D08 relations and the Sheth-Tormen mass function have been inferred from the results on N-body simulations that only include collisionless dark matter particles. As a matter of fact, galaxy clusters also contain baryons (both in galaxies and in hot gas), so that a realistic description should take their presence into account. As a consequence, we should also investigate the impact of baryons on peak number counts and hence on the constraints discussed above. While addressing how the MC and mass function are changed by the collapse of baryons is outside our aims, we can nevertheless draw some lessons by considering recent results for this question.
First, we note that baryons can alter the halo concentration, thus changing the normalisation of the MC relation. However, we expect that this effect is less and less important as the halo mass increases. Indeed, Fig. 8 in Duffy et al. (2010) shows that the ratio 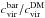 (with
(with 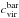 and
and 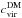 the halo concentration with and without baryons) deviates less than 10% from unity for log Mvir> 13.5, as inferred from comparing CDM only with hydrodynamical simulations that include baryons. Although this is not a direct proof that the MC relation is unaffected, we can reasonably infer that the mass and redshift power-law dependence we have adopted so far is a good approximation even when baryons are included. It is worth stressing that, while it is possible that the (Av,Bv,Cv,σv) parameters differ from the fiducial D08 case, this has no impact on our conclusion that peak number counts can differentiate different MC relations.
the halo concentration with and without baryons) deviates less than 10% from unity for log Mvir> 13.5, as inferred from comparing CDM only with hydrodynamical simulations that include baryons. Although this is not a direct proof that the MC relation is unaffected, we can reasonably infer that the mass and redshift power-law dependence we have adopted so far is a good approximation even when baryons are included. It is worth stressing that, while it is possible that the (Av,Bv,Cv,σv) parameters differ from the fiducial D08 case, this has no impact on our conclusion that peak number counts can differentiate different MC relations.
As discussed in Velliscig et al. (2014, and refs. therein), baryons also change the mass function by altering both the masses of single haloes and their abundances. Based on hydrodynamical simulations with different recipes for the details of baryons physics, Velliscig et al. (2014) provide approximated formulæ to convert the CDM-only mass function in its baryons-included counterpart. Using their formalism, we have thus recomputed 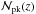 by adopting the D08 MC relation and changing the baryon model12. Figure 8 shows
by adopting the D08 MC relation and changing the baryon model12. Figure 8 shows 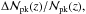 taking the CDM-only fiducial case as a reference for two choices of the threshold S/N value. While deviations from the CDM-only case can be significant, they are nevertheless less than 12% when only considering peaks with S/N ≥ 5, the ones used in our Fisher matrix forecasts. We therefore expect that including baryons does not significantly change our results.
taking the CDM-only fiducial case as a reference for two choices of the threshold S/N value. While deviations from the CDM-only case can be significant, they are nevertheless less than 12% when only considering peaks with S/N ≥ 5, the ones used in our Fisher matrix forecasts. We therefore expect that including baryons does not significantly change our results.
 |
Fig. 8 Percentage deviations |
5.4. The choice of the filter aperture and profile
As a final remark, we want to qualitatively discuss how the choice of the filter affects our results. Once the profile has been set (in our case resorting to the M05 optimal filter), one only has to choose the aperture ϑ. Our choice of ϑ = 2 arcmin was motivated by the need to match the filter aperture to the typical scale radius Rs of the NFW profile. Needless to say, Rs is not the same for all clusters, and moreover, its value in angular units also depends on the cluster redshift and the background cosmology. Our choice is therefore based on a median cluster with mass M200 ~ 5 × 1014 M⊙ at z ~ 0.3, where we expect the peak number counts to be the largest. Nevertheless, it is worth noting that this choice has not been done to maximise the S/N since this depends on the mass, the redshift, and MC relation. What is important is that, regardless of the ϑ value, the analysis presented here is still correct. Indeed, the Fisher matrix forecasts only rely on the assumption that the peaks detected are due to clusters and are not fake ones. This is guaranteed by the choice of a large enough S/N threshold. If we had chosen a different ϑ, we could have repeated the same analysis, provided the threshold S/N still selects only clusters peaks.
Although we do not aim here at optimising the filter aperture to minimise the constraints on the MC parameters, we nevertheless note that, holding fixed the threshold S/N (which is a good assumption for 1 ≤ ϑ/ arcmin ≤ 3), the larger the aperture, the higher the total peak number. However, this does not automatically translate into stronger constraints. Indeed, changing the filter aperture also changes the orientation of the confidence contours in the projected two-dimensional parameter spaces. This result can be qualitatively explained by noting that, for a given redshift, the larger aperture, the lower the minimum cluster mass to get a higher S/N value than the threshold. A similar consideration also holds for the critical detection redshift at a given mass. As a consequence, the effective redshift of the peak sample and the mass regime investigated change with the aperture size, thus making the orientation of the contours different depending on the ϑ values. Since the magnitude of the constraints also depends on the mass and redshift regime explored, one cannot use a rule of thumb to conclude that larger apertures lead to a smaller peak sample and weaker constraints.
The choice of the filter is even subtler. Ideally, the optimal filter should guarantee both completeness and purity; that is to say, it should make it possible to build up a catalogue containing all the peaks present in the survey with each one of them associated with a cluster and not caused by large scale structure noise. Although the M05 optimal filter we use here was designed to fulfil both these criteria (purity guaranteed by the S/N selection), it is nevertheless far from perfect since it is based on the assumption that noise and signal combine in a linear way. Nonetheless, from our viewpoint, a less than ideal filter can still work to infer constraints efficiently on the parameters of interest. Indeed, what we need is a peak catalogue whose redshift distribution can be theoretically predicted without any unaccounted-for systematics. This is the case for the optimal filter in the high S/N regime we have used here. Under these circumstances, the signal is dominated by the cluster itself so that it does not matter whether the noise combines linearly with it or not. As a result, the peak number counts are correctly predicted with the analytical formalism we use, so that we can confidently rely on the Fisher matrix forecasts we derive.
While the present paper was already completed, we became aware of a quite similar work by Mainini & Romano (2014, hereafter MR14). They forecast the constraints on MC relation parameters from peak number counts in Euclid, but they used a different filter and different redshift scaling of the MC relation. Also, the background cosmological model and the S/N threshold are different. As a result, a straightforward comparison is not possible. We nevertheless note that our constraints (for the case with MC and (ΩM,σ8) parameters left free to vary) are stronger than theirs. This very likely depends on how the filter has been dealt with. In our approach, we assume that the filter is fixed to the one computed assuming a fiducial D08 MC relation so that 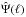 in Eq. (37) is the same regardless of the MC relation used to predict the peak number counts. Such a choice (mimicking what is actually done in building a catalogue from shear maps) allows maximising the differences among MC relations. Since this was not done in MR14, their predicted peak redshift distribution is less dependent on the MC parameters – thus weakening the forecast constraints.
in Eq. (37) is the same regardless of the MC relation used to predict the peak number counts. Such a choice (mimicking what is actually done in building a catalogue from shear maps) allows maximising the differences among MC relations. Since this was not done in MR14, their predicted peak redshift distribution is less dependent on the MC parameters – thus weakening the forecast constraints.
6. Conclusions
Weak-lensing peak statistics in an Euclid-like survey will offer an effective tool for studying the properties of galaxy clusters. In particular, the MC relation can be tightly constrained. Unlike ongoing studies that focus on detailed study of a small sample of objects – usually of a few dozen clusters – number counts can measure the MC relation in a statistical way by studying how it affects the number of thousands of detectable haloes and its evolution with redshift. The properties of the clusters are then measured from the whole population of haloes that pass the detectability threshold rather than from a limited sample of objects that might suffer from selection biases.
The massive end of the mass-concentration relation is of particular interest in the context of structure formation and evolution. The dynamical state of dark matter haloes might cause a non-monotonic relation between mass and concentration at high redshift (Prada et al. 2012; Ludlow et al. 2012). Massive systems at high redshift are most likely still accreting material in a transient stage of high concentration before virialisation (Ludlow et al. 2012). Peak statistics will determine the MC slope to ≲0.03 at M200> 1015 M⊙ with clusters all over the redshift range, from z ≲ 0.1 to ≳0.8, contributing significantly to the total number of detectable peaks. This will then probe the assembly history of massive haloes.
Peak number counts not only probe the MC relation, but also test the growth of structure through the dependence on the halo mass function. As we have shown, the peaks redshift distribution can nicely complement CMB data to further improve the constraints on the cosmological parameters. In particular, if the MC relation is known, peak number counts work better than the combination of current BAOs and SNeIa to constrain the present-day value of the dark energy equation of state. Even in the least favourable case of fully unknown MC parameters to be marginalised over, peak number counts still combine nicely with Planck to reduce the error on dark energy parameters and further decrease those on the other cosmological parameters.
The constraints we have discussed were obtained by relying on the peak redshift distribution. However, this is only a zeroeth-order statistics, while developing higher order ones (such as the correlation function between peaks) has only now begun (Marian et al. 2013). Although still in its infancy, such an approach is worth being investigated in order to see how it depends on the halo properties and whether it can help to strengthen constraints on MC relation parameters. Furthermore, a combined analysis of cluster number counts from different tracers (weak lensing peaks, X-ray, and Sunyaev-Zel’dovich) could represent a promising way to better constrain the scaling with mass and redshift of the MC relation, because each probe tests a different regime. In this case, one could finally find out which MC relation is the most reliable, hence opening the hunt for the physics needed to fill the gap between numerical results and the inferred MC relation.
Actually, Oguri et al. (2012) estimated the cvir–Mvir rather than the c200–M200 relation so that the parameters in Table 1 should be changed to take this difference into account. We have, however, neglected this correction.
It is worth noting that the difference in the total number of peaks and the difference in the binned peaks can have a different sign depending on which redshift bin is considered. Indeed, in the first case, we are referring to the total area under the curve in the left panel of Fig. 4, while in the second case, we consider the area under only a portion of the curve. For instance, since the B01 line stays almost always under the D08 one, it is clear that the Δ in Table 2 takes a negative value. Nonetheless, if we refer only to the peaks in a bin with z> 1, the D08 line is lower than the B01 one so that the difference is now positive.
We use the covariance matrix corresponding to the joint fit of Planck and WMAP polarisation data. We note that (after marginalising over nuisance parameters) this constrains 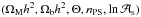 with Θ the angular scale of the sound horizon and
with Θ the angular scale of the sound horizon and 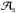 the power spectrum normalisation. We therefore first invert the covariance matrix and then project the corresponding Fisher matrix on our seven-dimensional parameter space (ΩM,Ωb,w0,wa,h,nPS,σ8).
the power spectrum normalisation. We therefore first invert the covariance matrix and then project the corresponding Fisher matrix on our seven-dimensional parameter space (ΩM,Ωb,w0,wa,h,nPS,σ8).
Acknowledgments
V.F.C. warmly thanks Silvia Galli for help with the Planck covariance matrix, Marco Velliscig for discussions on the impact of baryons, and Roberto Mainini for sharing his results in advance of publication. V.F.C. is funded by Italian Space Agency (ASI) through contract Euclid-IC (I/031/10/0). V.F.C., R.S., and M.S. acknowledge financial contribution from agreement ASI/INAF/I/023/12/0. S.C. is funded by FCT-Portugal under Post-Doctoral Grant No. SFRH/BPD/80274/11. G.C. acknowledges support form the PRIN-INAF 2011 “Galaxy Evolution with the VLT Survey Telescope (VST)”.
References
- Amendola, L., Appleby, S., Bacon, D., et al. 2013, Liv. Rev. Rel., 16, 6 [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Bartelmann, M., Perrotta, F., & Baccigalupi, C. 2002, A&A, 396, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broadhurst, T., Umetsu, K., Medezinski, E., Oguri, M., & Rephaeli, Y. 2008, ApJ, 685, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G., & Norman, M. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Cardone, V., Camera, S., Mainini, R., et al. 2013, MNRAS, 430, 2896 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallier, M., & Polarski, D. 2001, Int. J. Mod. Phys., D10, 213 [Google Scholar]
- Comerford, J. M., & Natarajan, P. 2007, MNRAS, 379, 190 [NASA ADS] [CrossRef] [Google Scholar]
- De Boni, C., Ettori, S., Dolag, K., & Moscardini, L. 2013, MNRAS, 428, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., & Hartlap, J. 2010, MNRAS, 402, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dal la Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C. 2012, MNRAS, 424, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., Dalal, N., Bode, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Hetterscheidt, M., Erben, T., Schneider, P., et al. 2005, A&A, 442, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoekstra, H. 2001, A&A, 370, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holder, G., Haiman, Z., & Mohr, J. 2001, ApJ, 560, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, D. E., Sheldon, E. S., Tasitsioni, A., et al. 2007, ApJ, 656, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A. A., Trujillo-Gomez, S., & Primack, J. 2011, ApJ, 740, 102 [Google Scholar]
- Kratochvil, J. M., Haiman, Z., & May, M. 2010, Phys. Rev. D, 81, 043519 [NASA ADS] [CrossRef] [Google Scholar]
- Kwan, J., Bhattacharya, S., Heitmann, K., & Habib, S. 2013, ApJ, 768, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., Augueres, J.-L., et al. 2011, ESA-SRE, 12 [Google Scholar]
- Limousin, M., Morandi, A., Sereno, M., et al. 2013, Space Sci. Rev., 177, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. V. 2003, Phys. Rev. Lett., 90, 091301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ludlow, A. D., Navarro, J. F., Li, M., et al. 2012, MNRAS, 427, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., & Hirata, C. M. 2008, JCAP, 0808, 006 [CrossRef] [Google Scholar]
- Marian, L., Smith, R. E., & Bernstein, G. M. 2009, ApJ, 698, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Marian, L., Hilbert, S., Smith, R. E., Schneider, P., & Desjacques, V. 2011, ApJ, 728, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Marian, L., Smith, R. E., Hilbert, S., & Schneider, P. 2013, MNRAS, 432, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Maturi, M., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2005, A&A, 442, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Angrick, C., Pace, F., & Bartelmann, M. 2010, A&A, 519, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Fedeli, C., & Moscardini, L. 2011, MNRAS, 416, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., & Rasia, E. 2013, MNRAS, submitted [arXiv:1303.6158] [Google Scholar]
- Meneghetti, M., Fedeli, C., Zitrin, A., et al. 2011, A&A, 530, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, S. G., Power, C., & Robotham, A. S. G. 2013, Astron. Comput., 3, 23 [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Bayliss, M. B., Dahle, H., et al. 2012, MNRAS, 420, 3213 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., Futamase, T., & Smith, G. P. 2010, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Okabe, N., Smith, G. P., Umetsu, K., Takada, M., & Futamase, T. 2013, ApJ, 769, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Meneghetti, M., Martino, R., et al. 2012, New J. Phys., 14, 055018 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P. 1996, MNRAS, 283, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Covone, G. 2013, MNRAS, 434, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Umetsu, K. 2011, MNRAS, 416, 3187 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Zitrin, A. 2012, MNRAS, 419, 3280 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Jetzer, P., & Lubini, M. 2010, MNRAS, 403, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Ettori, S., Umetsu, K., & Baldi, A. 2013, MNRAS, 428, 2241 [NASA ADS] [CrossRef] [Google Scholar]
- Shan, H., Kneib, J.-P., Tao, C., et al. 2012, ApJ, 748, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., Mo, H., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Ellis, R. S., & Fitchett, M. J. 1994, MNRAS, 270, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Broadhurst, T., Zitrin, A., et al. 2011, ApJ, 738, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. O., & Brainerd, T. G. 2000, ApJ, 534, 34 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
MC relations parameters for a pivotal mass Mpiv = 5 × 1014h-1 M⊙ for the different cases investigated, whose acronyms (ID) are shown in the first column.
Total number of peaks 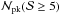 and percentage deviation
and percentage deviation ![\hbox{$\Delta = \left [ {\cal{N}}_{\rm pk}^{\rm id}({\cal{S}} \ge 5) - {\cal{N}}_{\rm pk}^{D08}({\cal{S}} \ge 5) \right ]/{\cal{N}}_{\rm pk}^{D08}({\cal{S}} \ge 5)$}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq213.png) for the different MC relations considered.
for the different MC relations considered.
All Figures
 |
Fig. 1 Top panels: S/N vs. cluster virial mass for fixed redshift (zl = 0.4,0.9,1.3from left to right) for different MC relations (black, red, blue, dashed blue, orange, dashed orange for B01, D08, Ok10, Ok10z, Og12, Og12z, respectively). Bottom panels: S/N vs. cluster redshift for fixed mass (log M200 = 14.5,15.5,16.5from left to right). |
| In the text | |
 |
Fig. 2 Maximum S/N (left) and virial mass log Mmax (centre) at which the S/N is maximised as a function of the cluster redshift. Right panel: Mmax normalised to the value for the D08 relation (wiggles are merely interpolation features). Black, red, blue, dashed blue, orange, and dashed orange lines refer to B01, D08, Ok10, Ok10z, Og12, and Og12z, respectively. |
| In the text | |
 |
Fig. 3 Left: total number of peaks as a function of the threshold S/N |
| In the text | |
 |
Fig. 4 Left: number of peaks with |
| In the text | |
 |
Fig. 5 Fisher matrix forecasts for the 68, 95, 99% CL assuming a fiducial D08 MC relation and a filter aperture ϑ = 2 arcmin. |
| In the text | |
 |
Fig. 6 Marginal error 1σ contours in the (ΩM,σ8) plane as obtained from peak counts alone (blue ellipse), Planck alone (green ellipse), and the combination of the two probes (yellow ellipse). |
| In the text | |
 |
Fig. 7 Marginal error 1σ contours for all the combinations of MC parameters with Ωm (top panels) and σ8 (bottom panels), for the case with (yellow curves) or without (blue curves) Planck priors. |
| In the text | |
 |
Fig. 8 Percentage deviations |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



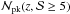
![\hbox{$\Delta {\cal{N}}_{\rm pk}(z)/{\cal{N}}_{\rm pk}(z) = \left [ {\cal{N}}_{\rm pk}^{\rm CDM}(z) - {\cal{N}}_{\rm pk}^{\rm bar}(z) \right ]/{\cal{N}}_{\rm pk}^{\rm CDM}(z)$}](/articles/aa/full_html/2015/02/aa24699-14/aa24699-14-eq262.png)