| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 32 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424672 | |
| Published online | 28 January 2015 | |
Simulations of an inhomogeneous stellar wind interacting with a pulsar wind in a binary system⋆
1 Departament d’Astronomia i Meteorologia, Institut de Ciènces del Cosmos, Universitat de Barcelona, IEEC-UB, Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: xparedes@am.ub.es
2 Departament d’Astronomia i Astrofísica, Universitat de València, Av. Vicent Andrés Estellés s/n, 46100 Burjassot, València, Spain
Received: 24 July 2014
Accepted: 9 November 2014
Context. Binary systems containing a massive star and a non-accreting pulsar present strong interaction between the stellar and the pulsar winds. The properties of this interaction, which largely determine the non-thermal radiation in these systems, strongly depend on the structure of the stellar wind, which can be clumpy or strongly anisotropic, as in Be stars.
Aims. We study numerically the influence of inhomogeneities in the stellar wind on the structure of the two-wind interaction region.
Methods. We carried out for the first time axisymmetric, relativistic hydrodynamical simulations, with Lorentz factors of ~6 and accounting for the impact of instabilities, to study the impact in the two-wind interaction structure of an over-dense region of the stellar wind. We also followed the evolution of this over-dense region or clump as it faces the impact of the pulsar wind.
Results. For typical system parameters, and adopting a stellar wind inhomogeneity with a density contrast χ ≳ 10, clumps with radii of a few percent of the binary size can significantly perturb the two-wind interaction region, pushing the two-wind interface to ≲40% of the initial distance to the pulsar. After it is shocked, the inhomogeneity quickly expands and is disrupted when it reaches the smallest distance to the pulsar. It eventually fragments, being advected away from the binary system. The whole interaction region is quite unstable, and the shocked pulsar wind can strongly change under small perturbations.
Conclusions. We confirm the sensitive nature of the two-wind interaction structure to perturbations, in particular when the stellar wind is inhomogeneous. For realistic over-dense regions of the stellar wind, the interaction region may shrink by a factor of a few, with the shocked flow presenting a complex spatial and temporal pattern. This can lead to strong variations in the non-thermal radiation.
Key words: hydrodynamics / X-rays: binaries / stars: winds, outflows / radiation mechanisms: non-thermal / gamma rays: stars
© ESO, 2015
1. Introduction
In binaries consisting of a massive star and a young non-accreting pulsar, the relativistic wind of the pulsar interacts with the non-relativistic wind of the stellar companion. This can result in efficient particle acceleration and in the production of non-thermal radiation, from radio to gamma rays. At present, PSR B1259−63 has been confirmed as a member of this class of objects, and there are several other high-mass binaries hosting a compact object whose nature is still unknown and may belong to this class as well (e.g., Dubus 2013; Paredes et al. 2013).
The properties of the non-thermal radiation in high-mass binaries hosting a non-accreting pulsar are determined to a large extent by the dynamics of the two-wind interaction structure. To study different aspects of this structure and its evolution along the orbit, heavy and detailed numerical simulations have been performed. Romero et al. (2007) carried out non-relativistic, smoothed particle hydrodynamic (SPH) simulations in three dimensions (3D) to study the orbital evolution of a hypothetic two-wind interaction region in LS I +61 303. Bogovalov et al. (2008) studied numerically the collision of the pulsar and the stellar wind in PSR B1259−63, treating the flows as laminar fluids by relativistic hydrodynamical simulations in two dimensions (2D). For the same system, Okazaki et al. (2011) and Takata et al. (2012) performed 3D SPH non-relativistic simulations to study the tidal and wind interactions between the pulsar and the decretion disc of the Be star, and Bogovalov et al. (2012) studied the collision of a magnetized anisotropic pulsar wind and the stellar wind adopting the same geometry and using a similar treatment as adopted in Bogovalov et al. (2008). Lamberts et al. (2012a) performed non-relativistic hydrodynamical simulations in planar geometry of the two-wind interaction structure for several orbits on large scales. Lamberts et al. (2012b) and Lamberts et al. (2013) performed 2D relativistic hydrodynamical (RHD) simulations in planar geometry of the interaction between the pulsar and the stellar wind on the scales of the binary system. Finally, Bosch-Ramon et al. (2012) performed 2D RHD simulations in planar geometry aimed at studying the interaction between the stellar and pulsar winds on scales at which the orbital motion is important.
Some relevant conclusions of the numerical work done up to now are the importance of instabilities, in particular the Rayleigh-Taylor (RT) and Kelvin-Helmholtz (KH)1 instabilities, in the spatial and temporal properties of the two-wind interaction structure on both small and large scales, the occurrence of shocked-flow re-acceleration, the impact of orbital motion through lateral, strong shocks, the effective mixing of the shocked winds downstream of the flow, the strong effects of the pulsar wind ram pressure on Be discs, and the relatively minor role of pulsar wind anisotropies and magnetic fields. However, all the simulations of binaries hosting a pulsar considered smooth winds, while the stellar wind is expected to be inhomogeneous, in particular for earlier spectral types (Lucy & Solomon 1970). The wind inhomogeneities (clumps hereafter) are expected to play an important role in the structure of the two-wind interaction region, and therefore in the non-thermal emission. The origin of these clumps can be explained by different mechanisms depending on their scale, either the stellar surface at the wind formation region, or a circumstellar disc in the Be system. For instance, the impact of a fragment of a Be star disc on the two-wind interaction region has been proposed to cause the GeV flare observed in the gamma-ray binary PSR B1259−63 (Abdo et al. 2011; Chernyakova et al. 2014). In addition, some sort of wind clumping could explain short flares on scales of seconds to hours found in the X-ray light curves of LS 5039 and LS I +61 303 (e.g., Bosch-Ramon et al. 2005; Paredes et al. 2007; Smith et al. 2009; Li et al. 2011). The clump-pulsar wind interaction problem has previously been studied analytically (see Bosch-Ramon 2013), but numerical calculations of the interaction between an inhomogeneous stellar wind and a relativistic pulsar wind have not been conducted yet.
In this work, we present 2D axisymmetric RHD simulations of the interaction between a wind clump and a relativistic pulsar wind. Orbital motion has not been accounted for because of the axisymmetric nature of the simulations; given the small spatial and temporal scales considered, this is a reasonable approximation. We simulated clumps with different sizes and densities to study the global variations induced in the two-wind interaction structure, as well as on the evolution of the clumps under the impact of the pulsar wind.
We note that this is the first time that relativistic simulations are carried out in a more realistic set-up, with axisymmetry along the two-star line, without suppressing the development of instabilities. The numerical results are compared with the analytical results found in Bosch-Ramon (2013). The paper is structured as follows: in Sect. 2 we describe the physical framework: the two-wind interaction region, the origin of the clumps in the winds of massive stars, and the analytical equations; in Sect. 3, we describe the numerical simulations: the numerical set-up and the obtained results; finally, a discussion and the conclusions can be found in Sects. 4 and 5.
2. Physical framework
The collision between the stellar wind and the wind from the young pulsar creates a shock structure bow-shaped towards the wind with the lower momentum flux. The contact discontinuity is located where the ram pressure of the two winds balances. As discussed in Bosch-Ramon (2013), the presence of clumps can significantly distort the overall interaction structure, although their dynamical impact is determined by their size and mass (see, e.g., Pittard 2007, for a similar non-relativistic scenario). Winds formed by small and light clumps will behave as uniform winds, while massive clumps will tend to come less frequently and be more damaging for the global stability of the interaction region (see Perucho & Bosch-Ramon 2012 for the effect of an inhomogeneous wind on a high-mass microquasar jet). A sketch of the physical scenario is shown in Fig. 1.
 |
Fig. 1 Cartoon representing a density map of the physical scenario: an inhomogeneous stellar wind interacts with the relativistic pulsar wind. The shocked stellar wind and the shocked pulsar wind are separated by a contact discontinuity. The distances are not to scale. The simulations presented in this paper only considered a stellar wind with one clump centered at the axis joinning the two stars. |
The instability of the line-driving mechanism in the inner wind is thought to be an important source of clumps in the wind structure of hot stars of spectral types O and B (Lucy & Solomon 1970). Runacres & Owocki (2002) suggested that the outer evolution of the inhomogeneous wind can be approximated as a pure gas dynamical problem, and the stellar wind clumps initiated close to the star can survive up to long distances (d ~ 1000 R⊙). Moffat (2008) suggested that all hot stellar winds are likely to be inhomogeneous because of radiative instabilities, with a multi-scale distribution of masses and sizes. Therefore, considering the outer wind evolution as a gas dynamical problem, the clumps could expand with the wind flow and large clumps could reach the interaction region between the stellar and the pulsar wind. However, the relatively small initial sizes (~0.01 R∗), and limitations on the clump growth (which can be parameterized as Rc = Rc0 (d/R∗)α, with α ≤ 1 and Rc0 being the initial clump radius) could prevent the formation of clumps as large as, Rc ~ R∗, for instance, which is required for the strongest variations of the two-wind interaction structure (see Bosch-Ramon 2013, and references therein). Typical massive star radii are R∗ ~ 10 R⊙.
Large clumps different from those related to radiative instabilities may be found in the stellar wind. For instance, early-type stars known as Be stars present a decretion disc formed by material ejected from the stellar equator by rapid rotation (Hanuschik 1996). The truncation of this disc, either caused by tidal forces or by direct pulsar wind ram pressure (see Okazaki et al. 2011), could explain the presence of large clumps in the stellar wind formed by chunks of disc. This possibility has been considered for instance to explain the GeV flare detected from the gamma-ray binary PSR B1259−63 by Chernyakova et al. (2014) (see Sect. 4.2.1). Other types of large-scale structures in the stellar wind, of size of the order of the stellar radius have also been inferred from the observed discrete absorption components (DACs) in the UV (e.g., Kaper et al. 1997). The appearance of DACs can be interpreted as co-rotating dense structures produced at the stellar surface and extending several tens of stellar radii (e.g., Lobel 2008), and can be attributed to the dynamical effects of rotation, magnetic fields, or non-radial pulsations (Cranmer & Owocki 1996). The arrival of any of those structures at the two-wind interaction region probably modify the latter in space and time.
Bosch-Ramon (2013), developed an analytical model for the two-wind interaction dynamics accounting for the lifetime of clumps under the pulsar-wind impact. It was concluded that for a clump radius Rc ≪ χ− 1/2ΔR, being ΔR the thickness of the two-wind interaction region and χ = ρc/ρw the density contrast between the clump density and the wind density, the clump is destroyed and deflected by the shocked wind medium before crossing the two-wind interaction region. Otherwise, for Rc approaching χ− 1/2ΔR or larger, the clump will penetrate into the unshocked pulsar wind. When R and R′ are the initial and final distances between the pulsar and the contact discontinuity, following Bosch-Ramon (2013), this approximate relation applies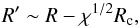 (1)which for Rc ~ R′ implies
(1)which for Rc ~ R′ implies 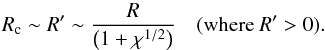 (2)The simulations presented here are intended to investigate in detail the dynamical consequences of the presence of clumps in the stellar wind. Below we compare analytical estimates with numerical results.
(2)The simulations presented here are intended to investigate in detail the dynamical consequences of the presence of clumps in the stellar wind. Below we compare analytical estimates with numerical results.
3. Numerical simulations
3.1. Numerical set-up
The simulations were performed using a finite-difference code based on a high-resolution shock-capturing scheme that solves the equations of relativistic hydrodynamics in two dimensions in a conservation form (Martí et al. 1997). The code is parallelized using open message passing (OMP; Perucho et al. 2005). The simulations were run in a workstation with two Intel(R) Xeon(R) CPU E5-2643 processors (3.30 GHz, 4 × 2 cores, with two threads for each core) and four modules of 4096 MB of memory (DDR3 at 1600 MHz).
We adopted an ideal relativistic gas without a magnetic field, one particle species, and a polytropic index of γ = 1.444, intermediate between a non-relativistic (stellar wind) and a relativistic (pulsar wind) index. The physical size of the domain is r ∈ [0,30 a] and z ∈ [0,50 a], where a = 8 × 1010 cm. The adopted resolution is 150 × 250 cells. The pulsar is located at (r,z) = (0,5 a), and the star at (r,z) = (0,60 a), outside the simulated grid. This yields a two-star separation of d = 4.4 × 1012 cm. The typical orbital separation distances in gamma-ray binaries are ~1013 cm (see, e.g., Dubus 2013, and references therein).
The initial conditions of the simulation were computed in spherical coordinates assuming adiabatic gas radial propagation and solving the Bernoulli equation for the pulsar and stellar winds. The initial two-wind separation point is derived as the approximate location where the on-axis wind ram pressures become equal (z = 22 a).
The chosen physical parameters of the pulsar wind are the total luminosity Lsd = 1037 erg s-1, the Lorentz factor Γ = 5, and the specific internal energy ϵpw = 9.0 × 1019 erg g-1. As a result of resolution limitations, the adopted Lorentz factor is smaller than expected in pulsar winds, Γ ~ 104–106 (see Khangulyan et al. 2012; Aharonian et al. 2012, and references therein), but high enough to capture important relativistic effects (see the discussion in Bosch-Ramon et al. 2012). For the stellar wind, the physical parameters are a mass-loss rate Ṁ = 10-7M⊙ yr-1, a radial velocity vsw = 3000 km s-1, and a specific internal energy ϵsw = 1.8 × 1015 erg g-1. The derived pulsar wind and stellar wind densities are ρpw = 1.99 × 10-19 g cm-3 and ρsw = 2.68 × 10-13 g cm-3, respectively. All the previous quantities, except for Lsd and Ṁ, are given at a distance r = a with respect to the pulsar and star centres. The values of Lsd, Ṁ and vsw were chosen as representative values of gamma-ray binaries hosting a pulsar because Lsd is to be high enough to power the gamma-ray emission, and the stellar wind properties correspond to those of an OB star. All these parameters are summarized in Tables 1 and 2.
The previous physical values lead to a pulsar-to-stellar wind thrust ratio of 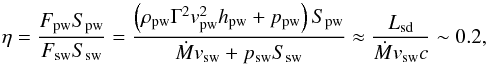 (3)where Fpw (Fsw) is the momentum flux of the pulsar wind (stellar wind), Spw (Ssw) the spherical surface at a distance r = a with respect to the pulsar (star), hpw the specific enthalpy of the pulsar wind given by
(3)where Fpw (Fsw) is the momentum flux of the pulsar wind (stellar wind), Spw (Ssw) the spherical surface at a distance r = a with respect to the pulsar (star), hpw the specific enthalpy of the pulsar wind given by 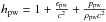 , and ppw/sw the pressure of the pulsar/stellar wind given by ppw/sw = (γ − 1)ρpw/swϵpw/sw.
, and ppw/sw the pressure of the pulsar/stellar wind given by ppw/sw = (γ − 1)ρpw/swϵpw/sw.
The pulsar wind is introduced by defining an injector with the mentioned properties and radius 3 a(2.4 × 1011 cm; 15 cells) as a boundary condition, and the stellar wind is injected according to its characterization at the upper boundary of the grid. The lower and right boundaries of the grid are set to outflow, while the left boundary of the grid is set to reflection.
The pulsar wind is injected with a Lorentz factor of 5, but because of adiabatic propagation, it reaches Lorentz factors of ~6 before termination.
Simulation parameters.
Pulsar and stellar parameters in code and CGS units.
The stellar wind clumps are introduced at (r,z) = (0,33 a) after the steady state is reached. The clumps are characterized by their radius Rc and their density contrast χ with respect to the average stellar wind value at their location. We present here the results for four different cases: χ = 10 and Rc = 1 a, 2.5 a, 5 a and χ = 30 and Rc = 1 a, corresponding to different degrees of wind inhomogeneity, from modest χ = 10 and Rc = 1 a to rather high χ = 10 (30) and Rc = 5 (1) a.
The axisymmetric nature of the simulations, in particular the reflection boundary conditions, the presence of a coordinate singularity, plus the concentration of fluxes, all at r = 0, lead to the generation of perturbations that quickly grow, posing difficulties to achieve a steady state. This effect makes the simulation also quite sensitive to the initial conditions, and the initial two-wind contact discontinuity has to be carefully chosen so as not to enhance the axis perturbations further. In this context, the modest resolution of most of the simulations and the pulsar wind Lorentz factor adopted were chosen to stabilize the solution of the calculations through a larger numerical dissipation and moderate wind density contrast. Given the fast growth of any perturbation (numerical or physical) in the simulated problem (as explained below), higher resolutions will enhance (as also shown below) the instability of the simulated structures through the penetration of small fragments of stellar wind material into the pulsar wind region. On the other hand, higher Lorentz factors would have enhanced the wind density contrast and thereby the instability growth rate. Finally, the grid size was also limited to prevent the instabilities from fully disrupting the two-wind interaction structure within the simulated region. With our resolution, larger grid sizes would have given enough time to the instabilities to develop and grow towards the downstream edge of the grid. The resulting structures would be similar to those found in the higher resolution simulations also presented in this work, and would also lead to the collapse of the two-wind interaction region. Albeit small, the grid size does not significantly affect the hydrodynamics within as the flow is supersonic at the outflow boundaries. We remark that because the clump is the strongest dynamical factor, its impact can be studied neglecting the role of numerical perturbations on the axis after a (quasi-)steady state has been reached.
 |
Fig. 2 Density distribution by colour at time t = 58 000 s. The coloured arrows represent the three-velocity at different locations (β = v/c). The axes units are a = 8 × 1010 cm. The density units are ρ0 = 22.5 × 10-22 g cm-3. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. The same units are used in all the figures. |
 |
Fig. 3 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 4 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 5 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 6 Density distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 7 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 4. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. |
 |
Fig. 8 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 9 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 10 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. 2. |
 |
Fig. 11 β distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
3.2. Results
Figure 2 shows the density map of the simulated flow in the (quasi-)steady state at t = 58 000 s. The shock structure is bow-shaped towards the pulsar, with the contact discontinuity at ~18 a from the pulsar. The thickness of the shocked two-wind region is ~8 a on the simulation axis. After being shocked, winds are accelerated side-wards because of the strong pressure gradient in the downstream region, as pointed out in Bogovalov et al. (2008). This is seen in the velocity maps presented in this section, for which the two-wind interaction structure has not yet been affected by the clump arrival. Because of this flow re-acceleration, the ratio of the momentum-flux to pressure shows that the flow becomes supersonic at the boundaries.
These axisymmetric simulations are quite sensitive to the initial conditions, and in particular, reaching steady state, is highly dependent on the initial set-up of the simulation. It is still an open question, to be answered with 3D simulations, to which extent this sensitivity to the initial set-up is caused by the geometry of the grid. Nevertheless, it is expected that instabilities quickly grow if perturbations are present, as shown by planar coordinate relativistic simulations (Bosch-Ramon et al. 2012; Lamberts et al. 2013). In the present simulations, the boundary conditions at the axis induce perturbations there that grow under the RT instability. These perturbations are then amplified by the KH instability as the flow propagates along the contact discontinuity. For grid sizes larger than 30 a in the r direction, the structures resulting from instability growth can reach deep into the pulsar wind, eventually disrupting the two-wind interaction region and filling the pulsar vicinity with shocked material. For small grids, on the other hand, these structures are advected out of the grid before it happens. The RT and KH instabilities grow faster for faster (and lighter) pulsar winds, which for a fixed η implies a stronger wind density contrast and thus a more unstable contact discontinuity. A Lorentz factor of Γ ~ 5–6 was adopted as a compromise: a rather relativistic flow with tenable instability-growth rates.
Despite numerical perturbations introducing a degree of deformation in the global structure of the two-wind collision region, as shown by the wave at r ~ 20 − 30 a in the two-wind interaction region in Fig. 2, the opening angle and width of the shocked wind zone are similar to those found in Bogovalov et al. (2008, 2012). Those simulations were similar to ours given their axisymmetry, although the simulated flows were laminar.
Figures 3–6 show the density map evolution for the clumps characterized by χ = 10 and Rc = 1 a, 2.5 a, 5 a, and χ = 30 and Rc = 1 a, respectively. The times of the map snapshots were chosen such that the images are illustrative of the structure evolution. The bigger clumps, characterized by χ = 10 and Rc = 2.5 a and Rc = 5 a, and the smallest but densest one, with χ = 30 and Rc = 1 a, strongly perturb the two-wind interaction region, pushing the contact discontinuity to less than a half its initial distance (see Fig. 2) to the pulsar (see Figs. 4−6, respectively).
We now focus on a clump with χ = 10 and Rc = 2.5 a, as it is illustrative of a strong impact by a clump of intermediate size. For this case, we also show Figs. 7−11, which display the evolution of the clump in the density map, the tracer map (1 for the clump material and 0 otherwise), the pressure map, the map of the momentum flux over the pressure (greater than a few for a super-sonic flow), and the map of β. These figures show how the two-wind interaction region is pushed by the clump, until the contact discontinuity reaches a minimum distance to the pulsar at 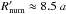 (
(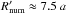 for the termination shock). After that, the clump starts to be pushed backwards by the pulsar wind, is shocked, and decelerates, eventually disrupting, with its fragments driven away from the simulation axis by the shocked flow. All this is clearly seen in the density maps (Figs. 4 and 7), and in the tracer (Fig. 8). In addition, Figs. 9−11 provide information on the presence of shocks, apparent as sudden increases in pressure or drops in the ratio of momentum-flux to pressure, and relevant for particle acceleration; flow re-acceleration, important for non-radiative cooling, flow relativistic motion, and flow-to-sound-speed relation; and flow speed and direction downstream of the shocks, determining Doppler effects on the flow emission. Equivalent images to Figs. 7−11 for the other three simulated clump cases are available in the on-line material. In all the simulations, a t = 0 is assigned to the steady state plus a clump at the initial position.
for the termination shock). After that, the clump starts to be pushed backwards by the pulsar wind, is shocked, and decelerates, eventually disrupting, with its fragments driven away from the simulation axis by the shocked flow. All this is clearly seen in the density maps (Figs. 4 and 7), and in the tracer (Fig. 8). In addition, Figs. 9−11 provide information on the presence of shocks, apparent as sudden increases in pressure or drops in the ratio of momentum-flux to pressure, and relevant for particle acceleration; flow re-acceleration, important for non-radiative cooling, flow relativistic motion, and flow-to-sound-speed relation; and flow speed and direction downstream of the shocks, determining Doppler effects on the flow emission. Equivalent images to Figs. 7−11 for the other three simulated clump cases are available in the on-line material. In all the simulations, a t = 0 is assigned to the steady state plus a clump at the initial position.
Concerning stability, under the perturbation induced by the clump with χ = 10 and Rc = 5 a, the system recovers steady state after the clump has been advected. In contrast, for the cases with χ = 10 and Rc = 2.5 a, and χ = 30 and Rc = 1 a, the instabilities eventually lead to the collapse of the two-wind interaction region, filling the region close to the pulsar with shocked pulsar wind. The clump with Rc = 1 a and χ = 10 only slightly perturbs the two-wind interaction region and pushes the contact discontinuity to ~2/3 of its initial distance (see Fig. 2) to the pulsar (see Fig. 3). Afterwards, the system recovers the (quasi-)steady state. We recall that although the steady-state solution is only metastable in the context of our simulations, the main features of the clump phase should be reliable because the clump represents a dominant perturbation over any other, physical or numerical, before it is assimilated by the two-wind flow.
 |
Fig. 12 Density distribution by colour at time t = 25 000 s for the simulation with a resolution of 300 × 500 cells. The remaining plot properties are the same as those of Fig. 2. |
Other simulations, not shown here, were carried out for clumps with Rc = 0.5–5 and χ = 10–100. As seen before, the impact on the two-wind interacting region is larger the denser the clump or the larger is its radius, so different combinations of these parameters yield results in line with those shown.
To show the impact of increasing resolution, we present the results of two simulations with the same set-up but, a resolution 2 and 1.5 times (i.e. 300 × 500 and 225 × 375 cells, respectively) higher than the resolution adopted for most of the simulations in the paper. For the highest resolution case, we were unable to reach steady state (without clump) because the higher resolution allowed the rapid development of instabilities already within the grid, leading to the collapse of the two-wind interaction region. A temporal state of this simulation taken shortly before the collapse of the interaction region is shown in Fig. 12. For the intermediate-resolution case, we reached (quasi-)steady state, but compared with the lower resolution simulations, it presented a more unstable pattern in the two-wind interaction region away from the simulation axis and a more compressed two-wind interaction region close to the axis singularity. A sequence of images showing the evolution of a clump characterized by χ = 10 and Rc = 2.5 a for the intermediate resolution simulation is shown in Fig.13. The higher resolution allowed the development of denser small-scale structures that pushed the pulsar wind termination shock closer to the neutron star. However, the general behaviour of the higher and lower resolution clump simulations is similar, which suggests that the main features resulting from the lowest resolution simulations, albeit smoother, are reliable.
4. Discussion
The interaction of a relativistic pulsar wind with the non-relativistic wind of a massive star was simulated through relativistic axisymmetric hydrodynamic calculations. The two-wind interaction structure reaches a (quasi-)steady state, although the solution is metastable and quite sensitive to the initial set-up parameters, such as the grid size or the wind density contrast. Therefore, even though the collision between the two winds forms a structure similar to those previously found in axisymmetric relativistic simulations, it shows some irregularity (Fig. 2). In the dynamical problem solved here, the axisymmetric geometry may introduce numerical perturbations to the physical solution that grow affected by the RT instability close to the axis, and by the KH instability farther away. However, similar irregularities have been also found in relativistic 2D simulations in planar geometry that have been attributed to the development of KH instabilities (Bosch-Ramon et al. 2012; Lamberts et al. 2013), which implies that the irregularities found in this work are not only related to the axisymmetric geometry adopted.
The growth of instabilities strongly affects the shocked pulsar-wind region in its (quasi-)steady state. Given the very high sound speed, this region can change within time intervals significantly shorter than the dynamical time of the simulation, ~d/vsw, dominated by the slow stellar wind. Nevertheless, we find that the interaction region globally follows the expected geometry both for the contact discontinuity and for the width of the two-wind collision region (Bogovalov et al. 2008, 2012).
The arrival of clumps can have a very strong impact on the whole interaction structure, overcoming the effect of any possible numerical perturbation related to the geometry of the calculations. The clumps trigger violent RT and KH instabilities because the structure is prone to suffer them, and thus the interaction between the clump and the two-wind collision region is highly non-linear, leading not only to a secular modification of the global geometry, but also to quick changes of the shocked pulsar-wind region. This is apparent in all the map time sequences (in particular in the zoomed-in sequence: Fig. 7), as the largest variations affect the shocked pulsar wind.
Below we discuss a few relevant points: the comparison between the analytical and the numerical approximation; the clump effect on the global structure and radiation, with a mention of the GeV flare of PSR B1259−63 as a possible instance of matter clump-perturbation of the two-wind interaction region, and work under development.
 |
Fig. 13 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a and a resolution of 225 × 375 cells for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
4.1. Numerical results vs. analytical estimates
An analytical estimate of the minimum distance between the two-wind interaction region and the pulsar, after the clump has penetrated the shocked pulsar wind, has been presented in Sect. 2. For comparison, the analytical and numerical values of the minimum distances from the contact discontinuity, and the termination shock, to the pulsar, are shown in Table 3 for all the simulated clumps.
The final distance between the pulsar and the contact discontinuity, for a given density contrast and a clump radius, computed using Eq. (1), agree well with the numerical results except for the clump with radius Rc = 5 a (see Table 3). The reason is that such a large clump is already outside of the application range of Eq. (1), which strictly applies only to clumps with Rc ≪ R′. For Rc → R′ or bigger, the clump behaves more as an homogeneous wind than as a discrete obstacle, but χ times denser than the average stellar wind. In this case, the minimum distance from the contact discontinuity to the pulsar can be computed from Eq. (3) and assuming momentum flux equality as 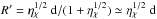 , with ηχ = χ-1η. For χ = 10 it gives
, with ηχ = χ-1η. For χ = 10 it gives 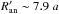 , which agrees well with the numerical result for the clump with Rc = 5 a (
, which agrees well with the numerical result for the clump with Rc = 5 a (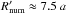 ).
).
Clump impact on the size of the two-wind interaction region.
The time required for the clump with χ = 10 and Rc = 2.5 a to become shocked is ~4000 s, and for full clump disruption, meaning that when the clump material is advected away already integrated in the shocked flows, the time required is ~10 000−15 000 s (see Fig. 7). These times are consistent with the analytical value of the clump lifetime, ~χ1/2Rc/vsw ≈ 2000 s (Bosch-Ramon 2013), or 4000 s, if the clump diameter is adopted as the characteristic clump size.
4.2. Clump effects on the global structure and radiation
On the scales simulated in this work, stellar winds with a modest inhomogeneity degree (χ = 10 and Rc = 1 a) present non-negligible variations of the interaction structure, and even smaller/lighter clumps can provide continuous perturbations for the development of instabilities in the contact discontinuity. In addition, medium-sized or denser clumps (Rc = 2.5, 5 a and χ = 10; Rc = 1 a and χ = 30) can lead to strong variations in the size of the two-wind interaction structure. Both small and medium-sized/denser clumps can generate quick and global variations in the shocked pulsar wind. This affects the location of the pulsar wind termination shock (i) and also introduces seeds for small-scale relativistic and transonic turbulence that would grow downstream of this shock (ii).
- (i)
The consequences of large variations in the termination shock location have previously been discussed in Bosch-Ramon (2013). In short, they can induce variations in the cooling, radiative as well as non-radiative, channels, and non-linear radiation processes, through synchrotron self-Compton or internal pair creation, for large reductions of the emitter size.
- (ii)
The relativistic flow variations on small spatial and temporal scales downstream of the pulsar wind shock, already apparent despite the modest resolution in Fig. 11, would lead to a complex radiative pattern in time and direction. This complex radiative pattern is caused by Doppler boosting because of the complex orientation of the fluid lines and the relativistic speeds achieved through re-acceleration of the shocked pulsar wind (see Khangulyan et al. 2014, for a study of the impact of Doppler boosting on radiation).
4.2.1. The flare in PSR B1259−63
The flare in PSR B1259−63, observed by Fermi about 30 days after periastron passage (Abdo et al. 2011), has a potential connection with the Be disc through the disruption and fragmentation of the latter. This may have led to the impact of a dense piece of disc on the two-wind interaction structure, largely reducing the size of the pulsar wind termination shock. This reduction could allow efficient Compton scattering by a population of GeV electrons on local X-ray photons, as proposed in Dubus & Cerutti (2013; see also Khangulyan et al. 2012, for a similar proposal involving infrared photons) as a result of the strong enhancement of the X-ray photon density. This idea is worth to be studied in more detail, although it remains unclear why such a modification of the GeV emitter has no clear effects at other wavelengths (Chernyakova et al. 2014).
It is worth estimating what fraction of the mass of a Be stellar disc the simulated clumps would represent. The mass of a typical Be disc can be derived from the disc mass-loss rate, ~10-12–10-9M⊙ yr-1, times the disc extension, say ~1 AU (quantities similar to those adopted in Okazaki et al. 2011 and Takata et al. 2012), with a typical disc radial velocity of ~1 km s-1 (Okazaki 2001). This yields a disc mass of ~1022–1025 g. In particular, for PSR B1259−63, Chernyakova et al. (2014) estimated a disc mass of 2 × 1025 g, with a disc radius of 0.42 AU, roughly similar to the values just mentioned. The masses of the simulated clumps are ~8 × 1018 g, ~1020 g, ~1021 g and ~2 × 1019 g for the clumps characterized by χ = 10 and Rc = 1 a, 2.5 a, 5 a and χ = 30 and Rc = 1 a, respectively. For comparison, the mass of the clump with Rc = 2.5 a would be ~0.001−1% the disc mass.
4.3. Future work
To distinguish the importance of numerical artefacts in our results and study a more realistic case, a 3D version of the simulations presented here is under way to more accurately characterize the instabilities that affect the two-wind interaction region. In addition, we are planning to carry out calculations of the radiation outcome expected from the two-wind interaction region, and most importantly, from the clump interaction with this structure, making full use of the dynamical information provided by these simulations.
5. Conclusions
We presented, for the first time, 2D axisymmetric RHD simulations of the interaction between an inhomogeneous stellar wind and a relativistic pulsar wind, focusing on the region inside the binary system. We simulated clumps with different sizes and densities to study different degrees of the stellar wind inhomogeneity. The presence of the clumps results in significant variations of the interaction region, which are expected to strongly affect the non-thermal radiation as well. Therefore, we confirm the sensitive nature of two-wind interaction structure under the presence of the stellar wind inhomogeneities. The shocked flow presents a complex spatial and temporal pattern, with fast changes in the shocked pulsar wind. This can lead to strong short time-scale flux variability in the non-thermal radiation of gamma-ray binaries, which might be observed for instance in gamma rays with the future Cherenkov Telescope Array (CTA; Acharya et al. 2013; Paredes et al. 2013).
Online material
Appendix A: Physical quantity maps for different clump parameters
The density zoom, tracer, pressure, ratio of momentum-flux to pressure, and velocity maps are presented in Figs. A.1–A.15 for different clump parameters: χ = 10 and Rc = 1 a; χ = 10 and Rc = 5 a; and χ = 30 and Rc = 1 a.
 |
Fig. A.1 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The coloured arrows represent the three-velocity at different locations (β = v/c). The axes units are a = 8 × 1010 cm. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. |
 |
Fig. A.2 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.3 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.4 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.5 β distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.6 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.7 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.8 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.9 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.10 β distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.11 Zoom-in of the density distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.12 Tracer distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.13 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.14 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
 |
Fig. A.15 β distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
RT: instability developed in the contact surface between two fluids of different densities, with the lightest fluid exerting a force on the densest one. KH: instability developed in the contact surface between two fluids of different parallel velocities (see Chandrasekhar 1961).
Acknowledgments
We thank the anonymous referee for his/her constructive and useful comments. We acknowledge support by the Spanish Ministerio de Economía y Competitividad (MINECO) under grants AYA2010-21782-C03-01, AYA2010-21322-C03-01, AYA2010-21097-C03-01, AYA2013-47447-C3-1-P, FPA2010-22056-C06-02 and FPA2013-48381-C6-6-P. We also acknowledge support by the “Generalitat Valenciana” grant “PROMETEO-2009-103”. This research has been supported by the Marie Curie Career Integration Grant 321520. X.P.-F. also acknowledges financial support from Universitat de Barcelona and Generalitat de Catalunya under grants APIF and FI (2014FI_B 01017), respectively. V.B-R. also acknowledges financial support from MINECO and European Social Funds through a Ramón y Cajal fellowship.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Acharya, B. S., Actis, M., Aghajani, T., et al. 2013, Astropart. Phys., 43, 3 [Google Scholar]
- Aharonian, F. A., Bogovalov, S. V., & Khangulyan, D. 2012, Nature, 482, 507 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D. V., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2008, MNRAS, 387, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2012, MNRAS, 419, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V. 2013, A&A, 560, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Paredes, J. M., Ribó, M., et al. 2005, ApJ, 628, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Barkov, M. V., Khangulyan, D., & Perucho, M. 2012, A&A, 544, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Clarendon) [Google Scholar]
- Chernyakova, M., Abdo, A. A., Neronov, A., et al. 2014, MNRAS, 439, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1996, ApJ, 462, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2013, A&ARv, 21, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., & Cerutti, B. 2013, A&A, 557, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuschik, R. W. 1996, A&A, 308, 170 [NASA ADS] [Google Scholar]
- Kaper, L., Henrichs, H. F., Fullerton, A. W., et al. 1997, A&A, 327, 281 [NASA ADS] [Google Scholar]
- Khangulyan, D., Aharonian, F. A., Bogovalov, S. V., & Ribó, M. 2012, ApJ, 752, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Bogovalov, S. V., & Aharonian, F. A. 2014, Internat. J. Mod. Phys. Conf. Ser., 28, 60169 [Google Scholar]
- Lamberts, A., Dubus, G., Lesur, G., & Fromang, S. 2012a, A&A, 546, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamberts, A., Dubus, G., Fromang, S., & Lesur, G. 2012b, in AIP Conf. Ser. 1505, eds. F. A. Aharonian, W. Hofmann, & F. M. Rieger, 406 [Google Scholar]
- Lamberts, A., Fromang, S., Dubus, G., & Teyssier, R. 2013, A&A, 560, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Torres, D. F., Zhang, S., et al. 2011, ApJ, 733, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lobel, A. 2008, in Clumping in Hot-Star Winds, Proc. internat. Workshop, held in Potsdam, eds. W.-R. Hamann, A. Feldmeier, & L. M. Oskinova, 81 [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J. M., Müller, E., Font, J. A., Ibáñez, J. M., & Marquina, A. 1997, ApJ, 479, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, A. F. J. 2008, in Clumping in Hot-Star Winds, eds. W.-R. Hamann, A. Feldmeier, & L. M. Oskinova, 17 [Google Scholar]
- Okazaki, A. T. 2001, PASJ, 53, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., Nagataki, S., Naito, T., et al. 2011, PASJ, 63, 893 [NASA ADS] [Google Scholar]
- Paredes, J. M., Ribó, M., Bosch-Ramon, V., et al. 2007, ApJ, 664, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M., Bednarek, W., Bordas, P., et al. 2013, Astropart. Phys., 43, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., & Bosch-Ramon, V. 2012, A&A, 539, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Martí, J. M., & Hanasz, M. 2005, A&A, 443, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pittard, J. M. 2007, ApJ, 660, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, A., Kaaret, P., Holder, J., et al. 2009, ApJ, 693, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, J., Okazaki, A. T., Nagataki, S., et al. 2012, ApJ, 750, 70 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cartoon representing a density map of the physical scenario: an inhomogeneous stellar wind interacts with the relativistic pulsar wind. The shocked stellar wind and the shocked pulsar wind are separated by a contact discontinuity. The distances are not to scale. The simulations presented in this paper only considered a stellar wind with one clump centered at the axis joinning the two stars. |
| In the text | |
 |
Fig. 2 Density distribution by colour at time t = 58 000 s. The coloured arrows represent the three-velocity at different locations (β = v/c). The axes units are a = 8 × 1010 cm. The density units are ρ0 = 22.5 × 10-22 g cm-3. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. The same units are used in all the figures. |
| In the text | |
 |
Fig. 3 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 4 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 5 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 6 Density distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 7 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 4. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. |
| In the text | |
 |
Fig. 8 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 9 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 10 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 11 β distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 12 Density distribution by colour at time t = 25 000 s for the simulation with a resolution of 300 × 500 cells. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. 13 Density distribution by colour for the case with clump parameters χ = 10 and Rc = 2.5 a and a resolution of 225 × 375 cells for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. 2. |
| In the text | |
 |
Fig. A.1 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The coloured arrows represent the three-velocity at different locations (β = v/c). The axes units are a = 8 × 1010 cm. The pulsar and the star are located at (r,z) = (0,5 a) and (r,z) = (0,60 a), respectively. |
| In the text | |
 |
Fig. A.2 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.3 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.4 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.5 β distribution by colour for the case with clump parameters χ = 10 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.6 Zoom-in of the density distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.7 Tracer distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.8 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.9 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.10 β distribution by colour for the case with clump parameters χ = 10 and Rc = 5 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.11 Zoom-in of the density distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.12 Tracer distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The tracer value ranges from 0 (pulsar and stellar wind) to 1 (clump). The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.13 Pressure distribution in units of ρ0c2 by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.14 Momentum flux over pressure distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The momentum flux is given by Fp = ρ Γ2v2(1 + ϵ + P/ρ) + P. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
 |
Fig. A.15 β distribution by colour for the case with clump parameters χ = 30 and Rc = 1 a for the times shown at the top of each plot. The remaining plot properties are the same as those of Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


