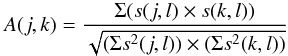| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A142 | |
| Number of page(s) | 38 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201423882 | |
| Published online | 09 February 2015 | |
Radial dependence of line profile variability in seven O9–B0.5 stars⋆
1
LUPM, Université Montpellier 2, CNRS, Place Eugène Bataillon, 34095
Montpellier,
France
email:
fabrice.martins@univ-montp2.fr
2
Observatório do Valongo, Universidade do Rio de
Janeiro, Ladeira Pedro António,
43, CEP
20080-090, Brasil
3
Department of Physics and Astronomy & Pittsburgh Particle
physics, Astrophysics and Cosmology Center (PITT PACC), University of
Pittsburgh, 3941 O’Hara
Street, Pittsburgh,
PA
15260,
USA
4
IRAP, CNRS & Univ. de Toulouse,
14 Av. E. Belin, 31400
Toulouse,
France
5
LAM–UMR 6110, CNRS & Université de Provence,
rue Frédéric Joliot-Curie,
13388, Marseille Cedex 13,
France
Received: 25 March 2014
Accepted: 15 September 2014
Context. Massive stars show a variety of spectral variabilities: discrete absorption components in UV P-Cygni profiles, optical line profile variability, X-ray variability, and radial velocity modulations.
Aims. Our goal is to study the spectral variability of single OB stars to better understand the relation between photospheric and wind variability. For that, we rely on high spectral resolution and on high signal-to-noise ratio optical spectra collected with the spectrograph NARVAL on the Télescope Bernard Lyot at Pic du Midi.
Methods. We investigated the variability of twelve spectral lines by means of the temporal variance spectrum. The selected lines probe the radial structure of the atmosphere from the photosphere to the outer wind. We also performed a spectroscopic analysis with atmosphere models to derive the stellar and wind properties and to constrain the formation region of the selected lines.
Results. We show that variability is observed in the wind lines of all bright giants and supergiants on a daily timescale. Lines formed in the photosphere are sometimes variable, sometimes not. The dwarf stars do not show any sign of variability. If variability is observed on a daily timescale, it can also (but not always) be observed on hourly timescales, albeit with lower amplitude. There is a very clear correlation between amplitude of the variability and fraction of the line formed in the wind. Strong anti-correlations between the different parts of the temporal variance spectrum are observed.
Conclusions. Our results indicate that variability is stronger in lines formed in the wind. A link between photospheric and wind variability is not obvious from our study, since wind variability is observed regardless of the level of photospheric variability. Different photospheric lines also show different degrees of variability.
Key words: stars: massive / stars: atmospheres / stars: winds, outflows / stars: variables: general
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Massive stars are important objects for several fields of astrophysics. Due to their high temperature and high luminosity, they have powerful ionizing spectra that create H ii regions. With their high initial mass, they are able to go beyond the fusion of carbon in their core, thus producing a large fraction of the elements that are heavier than oxygen and contributing to the chemical evolution of galaxies. They explode as core-collapse supernovae, leading to the formation of neutron stars and stellar black holes. They are also the precursors of long-soft gamma ray bursts (Woosley & Bloom 2006).
One of the main characteristics of massive stars is their strong winds. Because of the high luminosity, a large number of photons can be absorbed or scattered through spectral lines in the outer layers of massive stars, leading to a radiative acceleration that is strong enough to generate an outflow: the radiatively driven stellar wind. A massive star can lose 90% of its mass through such a wind during its life (Maeder & Meynet 2000). The rate of mass loss ranges from 10-9 to 10-4M⊙ yr-1, depending on the evolutionary status and luminosity. The velocity at which this stellar wind is driven can reach 4000 km s-1 in the most extreme cases. The amount of mechanical energy released by stellar wind over the lifetime of a massive star is similar to the energy produced by the final supernova. The consequence is that massive stars keep injecting energy into the interstellar medium, participating in the support of turbulence.
The process of acceleration through spectral lines is intrinsically unstable. The resulting acceleration is directly related to the velocity gradient in the atmosphere. As a result, a slight increase in the velocity gradient leads to stronger acceleration, which in turn increases the velocity gradient (Owocki & Rybicki 1984). This instability produces fluctuations in the velocity structure of a massive star’s atmosphere (MacGregor et al. 1979; Owocki et al. 1988; Feldmeier 1995). Owing to mass conservation, these velocity fluctuations induce density variations. Since spectral lines are sensitive to both velocity and density structures, they are also affected.
Spectroscopic variability is commonly observed in massive stars in general and O stars in particular. The UV resonance lines of O supergiants sometimes show discrete absorption components (DACs) corresponding to zones of over-absorption throughout the blue-shifted absorption part of the P-Cygni profile (Kaper et al. 1996; Fullerton 2011). They are usually attributed to the presence of large scale structures leading to optical depth enhancement. Such structures may be due to corotating interacting regions (CIRs) born in the photosphere, which are thought to be produced by surface brightness variations, leading to modulations of the launching velocity between adjacent surface regions and ultimately to interaction between slower and faster material. Thanks to rotation, CIRs may subsequently develop through a spiral pattern, thereby explaining how DACs are observed to move out of P-Cygni profiles with time. Optical observations also show line profile variability in the strongest wind lines of O stars, especially Hα (e.g. de Jong et al. 2001). Morel et al. (2004) report Hα variability in all their sample stars showing wind-dominated lines. Markova et al. (2005) studied a sample of O supergiants and conclude that the detected Hα variability is usually consistent with a model of broken shells for the atmosphere, at least for the stars with the strongest winds. Such a model is a way of representing the density fluctuations caused by the line-driving instability. Lines formed closer to the photosphere also vary. Fullerton et al. (1996) conducted a survey of 30 O stars and detected variability in HeI 5876 and sometimes CIV 5802−5812 for 77% of their sample, indicating that spectroscopic variability is widespread among O stars even in the deepest parts of the atmosphere. Subsequent studies have revealed variability in both the wind and photospheric lines of O stars (de Jong et al. 2001; Kaufer et al. 2002; Prinja et al. 2004; Prinja et al. 2006).
Whether there is a direct causal link between photospheric, surface variability and wind variability is still a matter of debate. It is not clear whether the line-driving instability can act on its own, at rather high velocities or if it is an amplifier of deeply seated variations. For the case of the O7.5III star ξ Per, de Jong et al. (2001) investigated this question using UV and optical spectroscopy. Although variability was observed in photospheric and wind features, a direct link was not obvious because of the different timescales of these variations. Kaufer et al. (2006) reached similar conclusions for the B0.5Ib supergiant HD 64760, although part of the Hα variability has a periodicity comparable to that of lines formed closer to the photosphere. On theoretical grounds, surface variability is expected if the star experiences non-radial pulsations, as is the case for several O stars (Smith 1978; Kambe et al. 1990; Fullerton et al. 1991; de Jong et al. 1999; Degroote et al. 2010). Surface inhomogeneities, possibly caused by magnetic spots, could also trigger variability.
To test this relationship between photospheric and wind variability further, more spectroscopic time series of O stars are required. As many photospheric and wind lines as possible should be monitored in order to sample the transition region between the stellar surface and the wind-dominated atmosphere. The classical indicators are usually Hα and He i 5876. In this study, we consider ten additional lines probing the inner part of the wind, down to the photosphere. We report on the spectroscopic variability of seven late-O/early-B stars using high resolution, high signal-to-noise spectra. We quantify the degree of variability by means of the temporal variance spectrum (TVS) analysis developed by Fullerton et al. (1996). We also model the average profiles with the atmosphere code CMFGEN. Based on the models, we constrain the line formation region of each line. We investigate the radial dependence of variability throughout the photosphere-wind transition region of the sample stars. Our spectroscopic analysis also provides the fundamental parameters of the sample stars.
The paper is organized as follows. We present the observations in Sect. 2 and the line profile variability in Sect. 3. We describe modelling of the stars and determination of the line formation region in Sect. 4. We discuss our results in comparison to previous studies in Sect. 5 and present our conclusions in Sect. 6.
2. Observations and data reduction
The sample stars were initially selected as part of a programme aiming at searching magnetic fields in massive stars. They are bright enough to allow repeated and frequent observations on a two-metre telescope. Previous variability in the sample giants and supergiants was used as a potential indication of magnetic field, based on previous detections (e.g. Donati et al. 2002, 2006). The dwarf stars were objects with very weak winds that, according to Martins et al. (2005) could be due to the presence of a magnetic field. We selected the stars with a sufficient number of spectra to allow a variability study. In total, seven O stars with spectral types from O9 to B0.5 and luminosity classes from V to Iab were chosen. None of them is a known binary.
We used the spectropolarimeter NARVAL mounted on the Télescope Bernard Lyot at the Pic du Midi observatory to obtain high signal-to-noise, high spectral resolution data (see Bouret et al. 2008; Martins et al. 2010). The observations were obtained between October 16 and October 25, 2007, in June 2008, and between July 20 and August 4, 2009. NARVAL provides échelle spectra between 3700 Å and 1.05 μm. The signal-to-noise ratio per 2.6 km s-1 resolution bin depends on weather conditions and wavelength but is always greater than 200. The resolving power is 65 000. Table A.1 gives the journal of observations.
The data were automatically reduced on site by the Libre Esprit software, a fully automatic reduction package for NARVAL data. Ample details on the reduction process can be obtained in Donati et al. (1997), to which we refer the reader for information.
3. Line profile variability
To study the spectral variability of our sample stars, we computed the TVS defined as 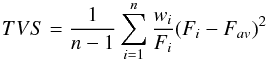 (1)
(1)
where Fi is the rectified flux, Fav the mean rectified flux, n the number of spectra available, and wi a weighting factor taking the variation in the signal-to-noise ratio from spectrum to spectrum into account (see Eq. (11) of Fullerton et al. 1996). Given the relatively long exposure time, we have assumed that the photon noise was the main source of noise, implying that the factor αij of Fullerton et al., encompassing the wavelength dependence of noise, is equal to the flux Fi. The TVS is computed at all wavelengths and quantifies the degree of variability in a series of spectra. We checked the effect of normalization uncertainties on the resulting TVS. One of us has normalized the same spectrum five times and used the five resulting spectra to compute the TVS. The intensity we obtain is usually lower than 0.005 and is seen over the entire spectrum, not just in lines. We present two types of TVS, depending on the data available: TVS computed for one night, when at least five spectra are available for the night; or TVS computed for several days. In the latter case, we used the average spectrum of the night (when several spectra are available) for each date.
We selected twelve spectral lines to look for spectroscopic variability. In addition to the classical Hα and He i 5876 features, we have added Hβ and Hγ, which probe deeper layers than Hα thanks to their reduced oscillator strength. We have also included three other He i lines (He i 4471, He i 4026, and He i 4712 in order of decreasing oscillator strength1), three He ii lines (He ii 4542, He ii 4686, He ii 5412), O iii 5592 and C iv 5802. The high ionization lines (C iv, He ii, O iii) probe deeper layers of the atmosphere compared to Balmer lines. The He i lines are triplets and belong to the 2p 3P° series. With these lines, we are able to sample variability throughout the atmosphere of the sample stars.
We used continuum regions adjacent to the lines of interest to evaluate the one and three σ levels. The one σ level is set to the standard deviation around the mean value of the TVS in this continuum region.
3.1. Daily variability
In Fig. 1 we show the TVS and individual spectra of ϵ Ori between October 16 and October 25, 2007. We detect variability in all H and He i lines, as well as in He ii 4686. The other He ii lines, as well as O iii 5592 and C iv 5802, do not show any significant variability. The shape of the TVS is similar in all lines where variability is detected. There is a triple peak system, with the central peak the strongest. It corresponds to variability in the line core. The two secondary peaks are located in the line wings, relatively far from the line core, at velocities up to 500 km s-1 in Hα. Variability is usually greater and more extended in stronger lines. For example, the TVS reaches 0.042 in Hα, 0.024 in Hβ, and 0.020 in Hγ. Variability extends up to 500 km s-1 in Hα, 200 km s-1 in Hβ, and 100 km s-1 in Hγ. The same trend toward greater variability in stronger lines is seen in He i with the largest TVS maximum in He i 5876, then He i 4471, He i 4026, and He i 4712, corresponding to decreasing oscillator strength (see above).
We gather in Figs. B.1 to B.6 the same figures as Fig. 1 for the other sample stars. The variability of these stars is summarized as follows:
-
HD 167264: this star shows variability in the same lines as ϵ Ori. The amplitude of the TVS is similar (e.g. 0.04 for Hα). The shape of the TVS is mostly single peaked, except for He i 4026, He i 4471, and He i 5876, for which a double-peaked structure is observed.
-
HD 207198: variability is observed in the H and He i lines, but also in all photospheric lines (He ii, O iii, C iv) although marginally in He ii 4542. The shape of the TVS is mostly double-peaked, as in HD 167264, with the red peak stronger than the blue one in the most strongly variable lines. In the He i lines, the amplitude of the blue peak in the TVS decreases with decreasing oscillator strength. (It vanishes in He i 4712.)
-
HD 188209: it is variable in all lines, whether photospheric or wind-dominated. The Balmer lines are mostly triple-peaked, the red component being the strongest. The TVS of the He i lines is double-peaked, with the red peak usually stronger than the blue one. The high ionization lines (from C iv, O iii, He ii) are clearly variable.
-
HD 209975: as in HD 188209, all lines show some degree of variability, with rather similar amplitudes. A double peak is seen in the TVS with an asymmetry between red and blue, with the red peak stronger at least in the most variable lines.
-
10 Lac and AE Aur: both late O dwarfs do not show any evidence of variability in any of the lines. The spectra are very stable over several nights.
In general, we observe strong variability in giants and supergiants on a daily timescale. All low ionization lines (H i and He i) are variable. In two cases (ϵ Ori and HD 167264), the high ionization lines (He ii, O iii, and C iv) are stable over days, while in the three other stars (HD 188209, HD 207198, and HD 209975), they also show clear changes from day to day. The former stars are B0-0.5 supergiants, while the latter are O9-9.5 supergiants. The two late-type O dwarfs (AE Aur and 10 Lac) do not show any variability on a daily timescale.
 |
Fig. 1 Variability of ϵ Ori on a daily timescale (from 16 to 25, October 2007). Upper panels: individual spectra in black (each spectrum corresponds to a night average) and global average spectrum in red. Lower panels: temporal variance spectrum, together with the one-sigma (dashed line) and three-sigma (dot-dashed line) limits. |
3.2. Hourly variability
If we now look at Figs. B.7 to B.9, we see how the lines vary during a few hours (for the stars for which we have at least five spectra over a night).
-
ϵOri: the changes during the night of October 19, 2007 are shown. The amplitude is reduced compared to Fig. 1 (e.g. 0.008 instead of 0.042 for Hα), but the same lines show variability (and the same lines remain stable). Figure 2 compares the TVS of the night of October 19, 2007 to the TVS obtained on the night-averaged spectra over the October 2007 month, for the Hα line. We see that on a timescale of hours, the variability is less than on a daily timescale. In addition, the strong variability observed over days extends up to 500 km s-1 away from the line core. The shorter timescale variability is restricted to the line cores, either because the physical origin of this shorter timescale variability is different or because the level of variability at high velocities is too low to be detected with our datasets. We have also computed the TVS during the night of October 22 and October 25, 2007, but we did not detect any significant variability. The number of spectra available is much larger during the night of October 19, but if we compute the TVS using only a sample of six spectra taken during that night, the variability is still present. Thus, the lower number of spectra available for the nights of October 22 and October 25 does not explain not detecting any variability.
-
HD 188209: Fig. B.8 reveals that HD 188209 is variable in all lines also on an hourly timescale during the night of June 25, 2008. The variations in the high ionization lines are marginal. The variability is observed again during the nights of June 27 and 28, 2008.
-
HD 209975: during the night of June 28, 2008, variability is observed in all lines except He ii 4542 and C iv 5802. OIII 5592 is also very marginally variable. The variability is less than observed on a daily timescale. The selected lines are also variable on the night of June 21, 22, and 27. The amplitude of the variations on June 21 are smaller than on June 28, and only the most strongly variable lines are actually changing during that night. The time span of the observations is the same during all nights (about 2 h).
The general conclusion is that stars showing variability on a daily timescale can also vary over a few hours. The variability on this shorter timescale is smaller (in intensity and velocity), and sometimes restricted to the strongest wind lines. Conversely, if a line does not vary on a daily basis, it does not vary either on an hourly timescale. If the processes responsible for the daily and hourly variability are the same, then our observations indicate that the associated timescale is longer than days. However, if the processes are different, Fig. 2 suggests that the one acting on longer timescales leads to stronger variability than the one acting on timescales of hours.
 |
Fig. 2 Daily and hourly Hα TVS of ϵ Ori. The largest TVS is for the daily timescale. The hourly TVS is observed during the night of October 19, 2007. |
4. Spatial distribution of variability
4.1. Stellar and wind parameters
To understand the origin of the observed variability better, we have identified the line formation region for all features displayed in Fig. 1 and Figs. B.1 to B.9. For that purpose, we analysed the spectroscopic data with atmosphere models computed with the code CMFGEN (Hillier & Miller 1998). Our goal was to reproduce the observed spectra in the best way for constraining the atmosphere structure and thus the line formation regions, which are directly accessible from the models. In practice, we worked on the grand average of all optical spectra for each star. To constrain the wind structure, we also relied on far-UV spectra retrieved from the IUE archive. We used averaged spectra to have the highest possible signal-to-noise ratio and to provide average parameters for the sample stars.
We used different diagnostics to compute the best-fitting model for each star. In practice, we proceeded as follows to determine those parameters:
 |
Fig. 3 Formation region of lines shown in Figs. 1. The contribution function for a given line (in arbitrary units) is shown as a function of height above the photosphere. Left: lines showing variability in Fig. 1. Right: lines not showing variability in Fig. 1. The black solid line in both panels is the velocity structure in the best fit model. |
-
Effective temperature: we used the ionization ratio method to constraint Teff. The He i and He ii lines were the main indicators: He i 4026, He i 4388, He i 4471, He i 4712, He i 4920, He i 5876, He ii 4200, He ii 4542, and He ii 5412. He ii 4686 is not considered since it also depends on the wind density.
-
Gravity: the wings of the Balmer lines are the main diagnostics of log g. They are broader at stronger gravities. We used Hβ, Hγ, Hδ, Hϵ, H i 3889, and H i 3835. The typical uncertainty on log g is 0.1 dex.
-
Luminosity: we fitted the UV-optical-infrared SED to constrain the luminosity. When reliable (i.e. uncertainty lower than 30%), we used the Hipparcos parallaxes as constraints on the distances. The distances we used are reported in Table 1. We used the Galactic extinction law of Seaton (1979) and Howarth (1983) to constrain the extinction.
-
Surface abundances: C and N abundances have been derived using the numerous carbon and nitrogen lines present in the optical range. C iii 4070, C iii 4153-56-63, C iii 4326, C iii 5305, and C iii 6205 were the main carbon abundance indicator. For nitrogen, we used N ii 3995, N ii 4041, N iii 4196, N iii 4216, N ii 4447, N iii 4511, N iii 4515, N iii 4523, N iii 4602, N ii 4607, N ii 4621, N iii 4907, N ii 5676, and N ii 5679.
-
Mass loss rate: the mass loss rate was determined from the strength of the UV P–Cygni lines (C iii 1176, N v 1238−1242, C iii 1247, Si iv 1393–1403, C iv 1548–1550) and from Hα. The typical uncertainty on Ṁ is 0.2 dex.
-
Wind terminal velocity: v∞ was directly measured from the blueward extinction of the UV P-Cygni profiles. A typical uncertainty of 100 km s-1 is achieved.
-
Clumping: clumping was treated by means of an exponential law in CMFGEN, where the volume-filling factor f has the following dependence on velocity:
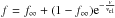 . The factor f∞ is the maximum clumping factor at the top of the atmosphere, and vcl determines the velocity at which clumping becomes non negligible. We adopted vcl = 30 km s-1 and derived f∞ from the shape of NIV 1720 line (Bouret et al. 2005).
. The factor f∞ is the maximum clumping factor at the top of the atmosphere, and vcl determines the velocity at which clumping becomes non negligible. We adopted vcl = 30 km s-1 and derived f∞ from the shape of NIV 1720 line (Bouret et al. 2005). -
Velocity slope: we constrained the slope of the velocity field − the so-called β parameter − from the condition that both Hα and the UV lines should be fitted for the same mass loss rate. Increasing the value of β allows the emission peak sometimes observed at the core of the broader Hα absorption to be reproduced. The UV P-Cygni profiles are usually reproduced simultaneously. For the almost pure photospheric Hα profiles of AE Aur end 10 Lac, β was adopted.
-
Rotational velocity/macroturbulence: we used the Fourier transform method (Simón-Díaz & Herrero 2007) to constrain the projected rotational velocity (Vsin i). We relied on the averaged spectrum to benefit from the highest signal-to-noise ratio. We used He i 4712 and O iii 5592 as diagnostics. Once the value of Vsin i was estimated, we used synthetic spectra (from our private database) to determine the macroturbulent velocity. We approximated macroturbulence by a Gaussian broadening. We tested several values of vmac to best reproduce the diagnostic lines for the estimated Vsin i. The best fit (selected by eye) provided vmac.
The internal velocity structure of the atmosphere was iterated: we first converged the populations, then computed the resulting radiative acceleration, and included it in a solution of the hydrodynamical equation to obtain a new velocity field. The populations was then re-converged with this hydrodynamical structure, and the process was iterated. After a couple of these hydrodynamical iterations, the structure was usually consistent with the radiative transfer solution, except around the sonic point where a discrepancy was still present. Once the model atmosphere was converged, we performed a formal solution of the radiative transfer equation by adopting a microturbulent velocity ranging from 10 km s-1 in the photosphere to 0.1 ×v∞ in the outer atmosphere. The resulting spectrum was compared to the observed spectra to constrain the stellar and wind parameters. The results of the spectroscopic analysis are gathered in Table 1.
4.2. Spatially resolved variability
Once a satisfactory fit was obtained, we retrieved the line formation region from the best fit model. The formation region is quantified by the contribution function, i.e. the fraction of the line produced as a function of radius. In Fig. 3, we show the formation region of the lines of ϵ Ori displayed in Fig. 1. The contribution function is evaluated at the line core. No correction for continuum was performed, but we verified that the continuum just outside the line wings forms closer to the photosphere than the line core. We separated the lines showing variability (left panel) and the lines showing no variability at the 3σ level (right panel). All lines are partly formed in the photosphere (i.e. below 10 km s-1). The main difference between both sets of lines is that the variable lines are formed in regions extending to high velocities, i.e. in the wind. This is clearly seen in Hα: the line is mainly formed between 1.1 and 1.25 Rstar above the photosphere, which corresponds to velocities between 5 and 200 km s-1. We thus conclude that the Hα variability observed in Figs. 1 and B.7 is rooted in the wind and not in the photosphere. More specifically, it is the inner part of the wind at velocities of a few tens to a few hundred km s-1, which is probed by Hα.
Using the best fit model for each star, we computed the fraction of the line formed above 10 km s-1, i.e. in the wind part of the atmosphere. We did that for all lines. The choice of 10 km s-1 is governed by the shape of the contribution function shown in Fig. 3. It corresponds to the velocity of the radius separating the two main peaks in the contribution function. A velocity of 10 km s-1 is also close to the sonic point considered to be around the transition between the photosphere and the wind. Figure 4 shows the intensity of the TVS as a function of the fraction of the line formed in the wind. We quantified the variability by the intensity of the TVS peak. We see a clear correlation: lines formed mostly in the wind are more variable than lines formed in the photosphere. The correlation is observed for all stars showing variability. This correlation between amplitude of variability and fraction of the line formed in the wind is valid for stars both showing and not showing changes in the photospheric lines. More specifically, the same level of Hα variability is observed in ϵ Ori and in HD 188209. The former star shows no sign of photospheric changes, while the latter is clearly variable in lines from high ionization states. It seems that the degree of variability in the photosphere is not directly correlated to the variability in the wind. This does not exclude a link between photospheric and wind changes in line profiles. But it suggests that instabilities in the wind can develop even if photospheric changes are absent (or at least weak).
Variability in lines formed mainly in the photosphere is quite complex. When present, variability is weaker than in wind lines. But lines formed at the bottom of the atmosphere do not behave similarly. For instance, the He ii and O iii lines in ϵ Ori do not vary, while He i 4026 and He i 4713 do. All lines have very similar contribution functions (see Fig. 3). Similar behaviour is observed in HD 167264. This shows that the line formation position in the atmosphere is not the only parameter controlling line variability. For instance, Reid et al. (1993) suggested that for the fast rotator ζ Oph, equator-to-pole temperature gradients lead to formation of He ii (He i) lines primarily at the pole (equator). A latitudinal variation of the variability mechanism could then naturally explain the observed different behaviour of He i and He ii lines.
In Fig. 5 we show the effect of the variation of mass loss rate on the Hα synthetic spectrum of ϵ Ori. The best fit model for ϵ Ori was used as a starting point. The TVS was computed by assigning the same weight to all models. The mass loss rate varies by ±25%. The associated TVS shows a single peak located close to the line core, slightly to its red side. The blue side of the TVS displays a shoulder. The TVS amplitude reaches 0.04, similar to what is observed in ϵ Ori. However, we do not observe the three-peak structure in the TVS. In Fig. 6, the influence of a change in the velocity law slope (β) is shown. Here again, the best fit model for ϵ Ori is the starting point, and β is varied between 0.8 and 1.4. The TVS is strongly peaked around the line core and is much narrower than the TVS, resulting from changes in mass loss rates or the observed TVS. Its amplitude reaches a maximum of 0.15, which is much higher than what is observed for ϵ Ori.
 |
Fig. 4 TVS peak intensity as a function of fraction of the line formed in the wind. Filled symbols correspond to the sample stars showing variability on a daily timescale. The solid open triangles show the variability of synthetic lines for which the mass loss rate varies by 25%, starting from the best fit model of ϵ Ori. The dotted triangles represent the theoretical variability due to changes in β (from 0.8 to 1.4) in the best fit model of ϵ Ori. The points for Hα, Hβ, and Hγ are out of the plot (amplitudes of 0.135, 0.104, and 0.070, respectively). |
The open black triangles in Fig. 4 correspond to the model shown in Fig. 5. A change in mass loss rate by 25% produces the same type of correlation between variability and fraction of line formed in the wind as what we observe for ϵ Ori (filled red triangles). Figure 4 illustrates the effect of a variation in the slope of the velocity field (the β parameter). We see that the same correlation is observed: the greater the fraction of the line formed in the wind, the stronger the variability. For the changes adopted (β between 0.8 and 1.4), the variability of the lines with the smallest wind contribution is correctly reproduced, but the main wind lines show variability that is too strong compared to what is observed in ϵ Ori (field triangles).
The strongest variability in wind lines (quantified by the absolute value of the TVS maximum intensity) does not necessarily imply that the underlying mechanism responsible for the variability is stronger in the wind. Indeed, lines formed in the outer parts of the atmosphere are on average stronger (i.e. they have a higher oscillator strength) and form over wider regions. To first order, one expects a stronger reaction to any instability in stronger lines. To investigate this issue further, we computed the ratio of the maximum amplitude of the TVS divided by the line optical depth at the photosphere (TVSpeak/τ), i.e. the depth at which the electron scattering optical depth is equal to two thirds. This is a first-order approximation to take line strength effects into account. The results are shown in Fig. 7. We see a different behaviour than in Fig. 4: in all stars, there is a large scatter of TVSpeak/τ close to the photosphere and a decrease from the maximum value of TVSpeak/τ towards a minimum as the fraction of the line formed in the wind increases.
Does this mean that the underlying variability mechanism is stronger close to the photosphere and that the stronger variability in lines formed mainly in the wind is only due to their higher strength and their formation over wider regions? It is not necessarily either. Indeed, lines formed over a wide region may be subject to cancellation effects: variability at a given wavelength and a given position in the wind can be compensated for by variability at another wavelength and another position corresponding to the same wavelength in the observer’s frame. Such cancellations effects are smaller in photospheric lines which all form in narrow regions.
Our investigations do not allow us to constrain the nature of the variability mechanism or its variation with depth. Nevertheless, we are able to show very clearly that there is a gradient of variability from the photosphere to the outer parts of the wind. Modulations in the wind parameters (mass loss rate, slope of the velocity field) can qualitatively explain the variability of the wind lines. We do not claim that true changes in the wind parameters are responsible for the observed variability. But the global density fluctuations they imply are qualitatively consistent with the observed line profile variations. In the photosphere, variability is quite complex, and lines formed in very close regions may show different variability patterns.
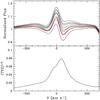 |
Fig. 5 TVS of a series of synthetic spectra computed from atmosphere models with Ṁ varying from 2.7 to 3.5 × 10-6M⊙ yr-1. The models are tailored to represent the observed spectra of ϵ Ori best. |
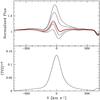 |
Fig. 6 TVS of a series of synthetic spectra computed from atmosphere models with β varying from 0.8 to 1.4 for the case of ϵ Ori. |
 |
Fig. 7 Same as Fig. 4 for the ratio of the TVS peak intensity to the line optical depth at the photosphere. |
4.3. TVS profile
The TVS provides more information than does the global level of variability. We illustrate this for the cases of ϵ Ori and HD 207198, which are typical of the types of variability observed: ϵ Ori does not show photospheric variability on the timescales we probe, while HD 207198 does. Both stars show wind line variability.
We use the autocorrelation function to extract information on the line profile variability. It is defined as
where s(j,l) is the lth spectrum at wavelength j. The l index in the sum has been dropped for clarity. For a perfect (anti-) correlation between wavelengths j and k, A(j,k) is equal to 1 (−1).
In the upper panels of Fig. 8 we show selected Hα and Hγ spectra of ϵ Ori illustrating the autocorrelation quantified in the matrixes displayed in the bottom panels. The triple-peak structure observed in Fig. 1 is also seen in the auto-correlation matrixes. There is a clear anti-correlation between the variability of the line core and of the line wings. The core is stronger when the wings are weaker. This type of anti-correlation is seen in all lines showing the triple-peak structure. A profile showing regular core strengthening and line narrowing could account for such behaviour. For instance, a change in the line broadening caused by a variable macro-turbulence could explain this behaviour. We simulated such a change by varying the macro-turbulent velocity between 50 and 75 km s-1 and we could reproduce a triple-peaked structure in the TVS, as well as the associated anti-correlation. One can also think of an extra emission on top of a photospheric profile. It could be caused by a shell of material initially just above the photosphere. At first, it would contaminate only the line core, making the overall profile less strong than a pure photospheric profile. The shell could subsequently expand, reaching higher velocity. The emission would then be spread over a range of velocities, and would consequently contaminate the wings more and the line core less. In that case the core would be stronger and the wings weaker than when the shell was just above the photosphere. This could reproduce the anti-correlation observed in ϵ Ori.
 |
Fig. 8 Top panels: selected Hα (left) and Hγ (right) spectra of ϵ Ori showing an anti-correlated variation (with the average spectrum as a bold line). Bottom panels: auto-correlation matrixes. White (black) corresponds to a full (anti-) correlation. Only the part of the spectrum showing variability on a daily timescale is displayed. |
Figure 9 shows the correlation matrixes and selected spectra for HD 207198. This star mainly shows double-peaked structures in its TVS (see Fig. B.2). The Hα and Hγ lines show a clear anti-correlation between their blue and red wings. One possibility for explaining such behaviour is a simple radial velocity shift. But since not all lines show variability, we can exclude a bulk motion of the star. In addition, the two peaks do not always have the same strength, which is inconsistent with a radial velocity modulation. A moving shell does not account for the observed anti-correlation of the red and blue wings (see above).
An asymmetry between the blue and red TVS peak can be explained by some types of wind asymmetries. For instance, Markova et al. (2005) performed simulations of clumpy winds with broken shells (see their Fig. 10). The resulting TVS is asymmetric, but with a stronger blue peak, contrary to what we observe. Their simulations of winds with a spiral pattern yield a symmetric TVS. The presence of blue and red variability could be explained in the case of winds confined by a magnetic field. Simulations by ud-Doula et al. (2013) show that if the star is not rotating too fast, material channelled along the field lines can settle in a disk-like structure and episodically fall back onto the star. Material reaching the equatorial plane at a greater distance or flowing away from the surface at the poles can escape the star. This can qualitatively explain blue and red variability. However, since both infall and ejection of material happen at the same time, no anti-correlation is expected. In addition, no magnetic field has been detected on HD 207198. In Fig. B.2 we see that as we move from lines mainly formed in the wind to photospheric lines (e.g. He ii 5412), the asymmetry of the TVS disappears. This implies that any mechanism leading to this asymmetry is linked to the wind itself and not to the photosphere.
In conclusion, the TVS shapes are complex and vary from star to star. But a qualitative interpretation indicates the important role of the wind in producing the observed structures, in agreement with the conclusions regarding the degree of variability (see Sect. 4.2).
Physical parameters of the sample stars.
5. Discussion
Several of our sample stars have been the subject of variability studies in the past. Kaper et al. (1996) reported variability of 10 Lac in the bluest part of the N v 1238−1242 UV line, but not for all of their time series. No Hα variability was detected by Kaper et al. (1997), and 10 Lac was found to be a non-radial pulsator by Smith (1978). Our time series do not show any variability.
HD 188209 was studied by Fullerton et al. (1996). They gathered spectra over one night and detected variability in He i 5876 and C iv 5802. The variation they observed span the range [−200; 100] km s-1 about the line centre. Our results obtained on the same timescale (night of June 25−26, 2008) are very similar, with variations in the range [−70; 150] km s-1. We also detect variability on June 27 and June 28. Markova et al. (2005) report Hα variability on a timescale of months. They conclude that changes in the mass loss rate by 17% could account for this variability. Israelian et al. (2000) report variability with a period of 6.4 days that they tentatively attribute to binarity, although there are difficulties with this scenario (see their Sect. 7).
HD 209975 was also part of the sample of Fullerton et al. (1996). They collected spectra over one day and reported a variability of He i 5876 with an extension over ±170 km s-1. We also detect variability in He i 5876 on an hourly timescale for all nights covered by our observations. The variability can be restricted to the first 100 km s-1or extend up to 200 km s-1 depending on the night, consistent with the findings of Fullerton et al. Markova et al. (2005) observed a monthly variability in Hα that they could reproduce by a 27% change in the mass loss rate of the star. Kaper et al. (1996) reported the presence of DACs in UV spectra of HD 209975, causing variations on a timescale of at least five days. Subsequent observations in the UV and Hα by Kaper et al. (1997) confirmed this timescale. The Hα variability was found to extend over the first 200 km s-1 around the line centre. In our case, the TVS extends up to ±300 km s-1 on the timescale of the observations (7 nights).
The source ϵ Ori was observed by Prinja et al. (2004). Variability was detected in several lines, including Hα and the weaker Si iii 4553 feature. They highlighted a periodicity of 1.9 d in the variations of both the strong wind line Hα and Si iii 4553, which is formed closer to the photosphere. They conclude that a direct link between photospheric and wind variability was revealed. Thompson & Morrison (2013) confirm the presence of periodic signals on timescales of two to seven days in both Hα and He i 5876, which they interpret as evidence of a connexion between photospheric and wind variability.
Our results are consistent in the sense that we detect a clear variability in the wind lines. But we do not see any change in many photospheric lines (the He ii, O iii, and C iv lines). We checked the behaviour of the Si iii 4553 and detected a variability with a peak of the TVS of the order of 0.010, in agreement with Prinja et al. (2004). As noted previously, some of the He i lines formed in the photosphere (He i 4026, He i 4713) do show variability, making the interpretation of the photospheric variability of ϵ Ori quite complex.
We investigated the periodic signals in the variability we detect for ϵ Ori. We focused on Hα since it is the most variable line, and we relied on its maximum emission as a proxy for our measurement. We performed a period search using the technique of Scargle (1982). We only detected a broad peak in the power spectrum at about two days. This is consistent with the findings of Prinja et al. (2004) and Thompson & Morrison (2013). However, our sampling is too coarse for a good period identification.
Previous analyses were based on only a few lines (mainly Hα, He i 5876, and C iv 5802). Our study extends the investigation of the line profile variability to a much longer list of spectral features. We confirm that variability is mainly observed in wind-sensitive lines. We show that there is a significant correlation between variability and the fraction of the line formed in the wind. The question of whether these instabilities can be triggered by a photospheric mechanism or if they can be self-sustained has not been settled. Our results indicate that some photospheric lines can be remarkably stable even if wind lines are variable. At the same time, different photospheric lines may be stable or not, as in the case of ϵ Ori or HD 167264. The effect of subsurface convection in evolved massive stars (Cantiello et al. 2009) may explain the properties of stars showing photospheric variability, but fail to account for the objects without detectable variability or variability in only selected photospheric lines.
The presence of small scale magnetic loops could trigger magnetic activity close to the photosphere. This could be the seeds for wind variability (e.g. Fullerton et al. 1996; Morel et al. 2004). All our sample stars were initially part of a sample dedicated to the search for magnetic field among O stars. We did not detect any evidence of Zeeman signatures in the analysis of the spectro-polarimetric data, excluding strong magnetic field (B> few 100 G, Grunhut et al., in prep.). In addition, all known O stars with a strong magnetic field show well-defined rotational modulations (e.g. Donati et al. 2002, 2006; Wade et al. 2012) thanks to the presence of the equatorial overdensities caused by magnetic wind confinment. In our sample stars, we detect variability on various timescales (hour-to-hour and night-to-night). This is not fully consistent with the presence of large scale magnetic fields. However, we cannot exclude much weaker fields of a few Gauss (as discovered by Lignières et al. 2009 on Vega). These fields could create surface inhomogeneities (temperature, composition) that might trigger photospheric variability subsequently amplified in the wind (e.g. by the line-driving instability). The photospheric variability could be weak so that we do not detect it in some of our sample stars.
It has been claimed that pulsations are the seeds of the spectral variability in OB-type stars. Kaufer et al. (2002) performed a large survey of the early B supergiant HD 64670 during ten nights and report periodic variability in photospheric lines. They explain it by a model of stellar oscillations. Variability was also observed in Hα. Some of the features observed in this line could be assigned a periodicity similar to that of the photospheric lines. Some other patterns escaped this relation. Kaufer et al. (2002) conclude that there is a clear link between photospheric and wind variability. Prinja et al. (2006) studied the late-O supergiant α Cam. They report hourly and daily variability in both Hα and He i 5876. From the daily variability of He i 5876, they suggest that photospheric variations are present in the time series analysis. In our analysis, we show that He i 5876 is one of the most variable lines after the Balmer lines. In ϵ Ori, He i 5876 has a formation region extending significantly in the wind (about 35% of the contribution function). Other lines are mainly photospheric (e.g. He ii lines) and show none or weak variability. In our sample stars, therefore, pulsations at the photosphere are difficult to relate to variability in lines formed farther out in the wind, at least for stars without clear photospheric variability.
Line profile variability in OB stars is a complex process. Our results seem to indicate that a photospheric seed is not mandatory to trigger wind variability; however, the behaviour of photospheric variability is difficult to interpret since lines formed over relatively similar regions in the photosphere may show different degrees of variability. In addition, the anti-correlations in the TVS are not easy to interpret. Dedicated simulations of specific variability mechanisms coupled to radiative transfer calculations are necessary to test possible excitation mechanisms.
6. Conclusion
We have performed time series analysis of the optical spectra of seven late-O early-B stars to investigate line profile variability. We used spectra collected with the spectropolarimeter NARVAL mounted on the Télescope Bernard Lyot at Pic du Midi. The spectra were obtained in several observing campaigns between 2007 and 2009. Depending on the star, spectra have been collected over a single night or over several nights (sometimes with several exposures during individual nights). We performed the analysis of the variability using the temporal variance spectrum (TVS, Fullerton et al. 1996). We also computed atmosphere models with the code CMFGEN to determine the fundamental properties of the sample stars and to constrain the formation regions of the lines for which variability was investigated. Unlike in most previous studies, we did not restrict ourselves to lines formed in the wind, but instead analysed twelve spectral lines, sampling the radial structure of the atmosphere. Our results can be summarized as follows:
-
Variability is detected in the wind lines of all bright giants and supergiants. The dwarf stars do not show any sign of line profile variability in any line.
-
Photospheric variability in lines from high ionization states is sometimes observed, sometimes not, even if wind lines variability is definitely detected.
-
In some cases the weakest photospheric He i lines may be variable even if the higher excitation lines are stable.
-
When variability is detected on daily timescales, it can also (but not always) be observed on hourly timescales with a much lower amplitude.
-
The shape of the temporal variance spectrum is usually double- or triple-peaked. Most of the double-peaked structures show a red/blue asymmetry, the former being the strongest.
-
Clear anti-correlations between these variable structures is observed.
-
We find a clear correlation between the amplitude of the variability and fraction of the line formed in the wind.
-
There is no obvious relation between photospheric variability and stellar or wind parameters.
Our results are the first to provide variability information for a large sample of lines probing the entire radial structure
of the atmosphere. They show for the first time a very clear correlation between the level of variability and the fraction of the line formed in the wind. At the same time, our results do not indicate that wind variability is always related to photospheric modulations.
Online material
Appendix A: Journal of observations
In Table A.1 we present the journal of observations for the target stars.
Journal of observations.
Appendix B: Temporal variance spectra of sample stars
 |
Fig. B.1 Variability of HD 167264 between July 25 and August 4, 2009. |
 |
Fig. B.2 Variability of HD 207198 between July 25 and August 4, 2009. |
 |
Fig. B.3 Variability of HD 188209 between June 21 and June 30, 2008. |
 |
Fig. B.4 Variability of HD 209975 between June 21 and June 27, 2008. |
 |
Fig. B.5 Variability of AE Aur between October 15 and October 19, 2007. |
 |
Fig. B.6 Variability of 10 Lac between October 15 and October 24, 2007. |
 |
Fig. B.7 Variability of ϵ Ori on the night of October 19 to 20, 2007. |
 |
Fig. B.8 Variability of HD 188209 during the night of June 25–26, 2008. |
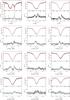 |
Fig. B.9 Variability of HD 209975 during the night of June 22 to 23, 2008. |
Appendix C: Best fits to the UV/optical spectra of the sample stars
 |
Fig. C.1 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of ϵ Ori. |
 |
Fig. C.2 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of ϵ Ori. |
 |
Fig. C.3 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 207198. |
 |
Fig. C.4 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 207198. |
 |
Fig. C.5 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 167264. |
 |
Fig. C.6 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 167264. |
 |
Fig. C.7 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 188209. |
 |
Fig. C.8 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 188209. |
 |
Fig. C.9 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 209975. |
 |
Fig. C.10 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 209975. |
 |
Fig. C.11 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of 10 Lac. |
 |
Fig. C.12 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of 10 Lac. |
 |
Fig. C.13 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of AE Aur. |
 |
Fig. C.14 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of AE Aur. |
Acknowledgments
We thank an anonymous referee for a careful reading of the manuscript and his/her constructive report. F.M. thanks the Agence Nationale de la Recherche for financial support (grant ANR-11-JS56-0007). D.J.H. acknowledges support from STScI theory grant HST-AR-12640.01.
References
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., Donati, J.-F., Martins, F., et al. 2008, MNRAS, 389, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. A., Henrichs, H. F., Schrijvers, C., et al. 1999, A&A, 345, 172 [NASA ADS] [Google Scholar]
- de Jong, J. A., Henrichs, H. F., Kaper, L., et al. 2001, A&A, 368, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Briquet, M., Auvergne, M., et al. 2010, A&A, 519, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Howarth, I. D., Bouret, J.-C., et al. 2006, MNRAS, 365, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, A. 1995, A&A, 299, 523 [NASA ADS] [Google Scholar]
- Fullerton, A. W. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 136 [Google Scholar]
- Fullerton, A. W., Gies, D. R., & Bolton, C. T. 1991, in BAAS, 23, 1379 [Google Scholar]
- Fullerton, A. W., Gies, D. R., & Bolton, C. T. 1996, ApJS, 103, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D. 1983, MNRAS, 203, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Israelian, G., Herrero, A., Musaev, F., et al. 2000, MNRAS, 316, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Kambe, E., Ando, H., & Hirata, R. 1990, in Progress of Seismology of the Sun and Stars (Berlin: Springer Verlag), Lect. Notes Phys., 367, eds. Y. Osaki, & H. Shibahashi, 449 [Google Scholar]
- Kaper, L., Henrichs, H. F., Nichols, J. S., et al. 1996, A&AS, 116, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaper, L., Henrichs, H. F., Fullerton, A. W., et al. 1997, A&A, 327, 281 [NASA ADS] [Google Scholar]
- Kaufer, A., Prinja, R. K., & Stahl, O. 2002, A&A, 382, 1032 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufer, A., Stahl, O., Prinja, R. K., & Witherick, D. 2006, A&A, 447, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lignières, F., Petit, P., Böhm, T., & Aurière, M. 2009, A&A, 500, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., Hartmann, L., & Raymond, J. C. 1979, ApJ, 231, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Markova, N., Puls, J., Scuderi, S., & Markov, H. 2005, A&A, 440, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Donati, J.-F., Marcolino, W. L. F., et al. 2010, MNRAS, 407, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., Marchenko, S. V., Pati, A. K., et al. 2004, MNRAS, 351, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1984, ApJ, 284, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Castor, J. I., & Rybicki, G. B. 1988, ApJ, 335, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Prinja, R. K., Rivinius, T., Stahl, O., et al. 2004, A&A, 418, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinja, R. K., Markova, N., Scuderi, S., & Markov, H. 2006, A&A, 457, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, A. H. N., Bolton, C. T., Crowe, R. A., et al. 1993, ApJ, 417, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1979, MNRAS, 187, 73P [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. A. 1978, ApJ, 224, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, G. B., & Morrison, N. D. 2013, AJ, 145, 95 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., Sundqvist, J. O., Owocki, S. P., Petit, V., & Townsend, R. H. D. 2013, MNRAS, 428, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Grunhut, J., Gräfener, G., et al. 2012, MNRAS, 419, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Variability of ϵ Ori on a daily timescale (from 16 to 25, October 2007). Upper panels: individual spectra in black (each spectrum corresponds to a night average) and global average spectrum in red. Lower panels: temporal variance spectrum, together with the one-sigma (dashed line) and three-sigma (dot-dashed line) limits. |
| In the text | |
 |
Fig. 2 Daily and hourly Hα TVS of ϵ Ori. The largest TVS is for the daily timescale. The hourly TVS is observed during the night of October 19, 2007. |
| In the text | |
 |
Fig. 3 Formation region of lines shown in Figs. 1. The contribution function for a given line (in arbitrary units) is shown as a function of height above the photosphere. Left: lines showing variability in Fig. 1. Right: lines not showing variability in Fig. 1. The black solid line in both panels is the velocity structure in the best fit model. |
| In the text | |
 |
Fig. 4 TVS peak intensity as a function of fraction of the line formed in the wind. Filled symbols correspond to the sample stars showing variability on a daily timescale. The solid open triangles show the variability of synthetic lines for which the mass loss rate varies by 25%, starting from the best fit model of ϵ Ori. The dotted triangles represent the theoretical variability due to changes in β (from 0.8 to 1.4) in the best fit model of ϵ Ori. The points for Hα, Hβ, and Hγ are out of the plot (amplitudes of 0.135, 0.104, and 0.070, respectively). |
| In the text | |
 |
Fig. 5 TVS of a series of synthetic spectra computed from atmosphere models with Ṁ varying from 2.7 to 3.5 × 10-6M⊙ yr-1. The models are tailored to represent the observed spectra of ϵ Ori best. |
| In the text | |
 |
Fig. 6 TVS of a series of synthetic spectra computed from atmosphere models with β varying from 0.8 to 1.4 for the case of ϵ Ori. |
| In the text | |
 |
Fig. 7 Same as Fig. 4 for the ratio of the TVS peak intensity to the line optical depth at the photosphere. |
| In the text | |
 |
Fig. 8 Top panels: selected Hα (left) and Hγ (right) spectra of ϵ Ori showing an anti-correlated variation (with the average spectrum as a bold line). Bottom panels: auto-correlation matrixes. White (black) corresponds to a full (anti-) correlation. Only the part of the spectrum showing variability on a daily timescale is displayed. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 for HD 207198. |
| In the text | |
 |
Fig. B.1 Variability of HD 167264 between July 25 and August 4, 2009. |
| In the text | |
 |
Fig. B.2 Variability of HD 207198 between July 25 and August 4, 2009. |
| In the text | |
 |
Fig. B.3 Variability of HD 188209 between June 21 and June 30, 2008. |
| In the text | |
 |
Fig. B.4 Variability of HD 209975 between June 21 and June 27, 2008. |
| In the text | |
 |
Fig. B.5 Variability of AE Aur between October 15 and October 19, 2007. |
| In the text | |
 |
Fig. B.6 Variability of 10 Lac between October 15 and October 24, 2007. |
| In the text | |
 |
Fig. B.7 Variability of ϵ Ori on the night of October 19 to 20, 2007. |
| In the text | |
 |
Fig. B.8 Variability of HD 188209 during the night of June 25–26, 2008. |
| In the text | |
 |
Fig. B.9 Variability of HD 209975 during the night of June 22 to 23, 2008. |
| In the text | |
 |
Fig. C.1 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of ϵ Ori. |
| In the text | |
 |
Fig. C.2 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of ϵ Ori. |
| In the text | |
 |
Fig. C.3 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 207198. |
| In the text | |
 |
Fig. C.4 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 207198. |
| In the text | |
 |
Fig. C.5 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 167264. |
| In the text | |
 |
Fig. C.6 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 167264. |
| In the text | |
 |
Fig. C.7 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 188209. |
| In the text | |
 |
Fig. C.8 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 188209. |
| In the text | |
 |
Fig. C.9 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of HD 209975. |
| In the text | |
 |
Fig. C.10 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of HD 209975. |
| In the text | |
 |
Fig. C.11 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of 10 Lac. |
| In the text | |
 |
Fig. C.12 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of 10 Lac. |
| In the text | |
 |
Fig. C.13 Best CMFGEN fit (red solid line) of the UV spectrum (black solid line) of AE Aur. |
| In the text | |
 |
Fig. C.14 Best CMFGEN fit (red solid line) of the optical spectrum (black solid line) of AE Aur. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.