| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201424851 | |
| Published online | 10 December 2014 | |
Systematic trend of water vapour absorption in red giant atmospheres revealed by high resolution TEXES 12 μm spectra⋆
1 Department of Astronomy and Theoretical PhysicsLund Observatory, Lund University, Box 43, 221 00 Lund, Sweden
e-mail: ryde@astro.lu.se
2 Department of Physics, University of California at Davis, CA 95616, USA
3 UPM, Université Montpellier II, Montpellier, France
4 Astrophysics Research Group, Trinity College Dublin, Dublin 2, Ireland
5 Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
6 Southwest Research Institute, Division 15, 6220 Culebra Road, San Antonio, TX 78228, USA
Received: 22 August 2014
Accepted: 14 October 2014
Context. The structures of the outer atmospheres of red giants are very complex. Recent interpretations of a range of different observations have led to contradictory views of these regions. It is clear, however, that classical model photospheres are inadequate to describe the nature of the outer atmospheres. The notion of large optically thick molecular spheres around the stars (MOLspheres) has been invoked in order to explain spectro-interferometric observations and low- and high-resolution spectra. On the other hand high-resolution spectra in the mid-IR do not easily fit into this picture because they rule out any large sphere of water vapour in LTE surrounding red giants.
Aims. In order to approach a unified scenario for these outer regions of red giants, more empirical evidence from different diagnostics are needed. Our aim here is to investigate high-resolution, mid-IR spectra for a range of red giants, spanning spectral types from early K to mid M. We want to study how the pure rotational lines of water vapour change with effective temperature, and whether we can find common properties that can put new constraints on the modelling of these regions, so that we can gain new insights.
Methods. We have recorded mid-IR spectra at 12.2 − 12.4 μm at high spectral resolution of ten well-studied bright red giants, with TEXES mounted on the IRTF on Mauna Kea. These stars span effective temperatures from 3450 K to 4850 K.
Results. We find that all red giants in our study cooler than 4300 K, spanning a wide range of effective temperatures (down to 3450 K), show water absorption lines stronger than expected and none are detected in emission, in line with what has been previously observed for a few stars. The strengths of the lines vary smoothly with spectral type. We identify several spectral features in the wavelength region that are undoubtedly formed in the photosphere. From a study of water-line ratios of the stars, we find that the excitation temperatures, in the line-forming regions, are several hundred Kelvin lower than expected from a classical photospheric model.
Conclusions. All stars in our sample show several photospheric features in their 12 μm spectra, which can be modelled with a classical model photosphere. However, in all stars showing water-vapour lines (stars cooler than ~4300 K), the water lines are found to be much deeper than expected. The line ratios of these pure-rotational lines reveal low excitation temperatures. This could either be due to lower temperatures than expected in the outer regions of the photospheres caused by for example extra cooling, or due to non-LTE level populations, affecting the source function and line opacities, but this needs further investigation. We have demonstrated that these diagnostically interesting water lines are a general feature of red giants across spectral types, and we argue for a general explanation of their formation rather than explanations requiring specific properties, such as dust. Since the water lines are neither weak (filled in by emission) nor do they appear in emission, as predicted by LTE MOLsphere models in their simplest forms, the evidence of the existence of such large optically-thick, molecular spheres enshrouding the stars is weakened. It is still a challenge to find a unifying picture of the outer regions of the atmospheres of red giants, but we have presented new empirical evidence that needs to be taken into account and explained in any model of these regions.
Key words: infrared: stars / stars: atmospheres / stars: fundamental parameters / stars: late-type
Table 4 is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Recent investigations of K and M giants and supergiants have led to a divergent, and sometimes a somewhat contradictory picture of their outer atmospheres. Existing observations range from interferometric and spectro-interferometric to low- and high-resolution spectra in different bands. Here, we will discuss the picture that has emerged based mostly on near- and mid-IR data.
Low-resolution spectra of a range of giants and supergiants (see e.g. Tsuji et al. 1997; Yamamura et al. 1999; Tsuji 2000) have been interpreted as evidence of a structure, beyond the photosphere, of a molecular condensation of large radial extent, named a MOLsphere (Tsuji et al. 1997; Tsuji 2000). Tsuji (2008, 2009) concludes, based on high-resolution near-IR spectra, that these structures appear to be a basic feature of all K and M red giants. The structure is supposed to be composed of water vapour and CO. It would be a quasi-static molecular layer situated of the order of a stellar radius beyond the classical extent of the photosphere (see e.g. Tsuji 2003). In the case of early-K giants like Arcturus, it could be interpreted as an aggregation of molecular clouds connected to the outer photosphere (Tsuji 2009). Spectro-interferometric K-band observations have also been interpreted as evidence of molecular layers of water and CO in extended atmospheres of K and M giants (see e.g. Ohnaka et al. 2012; Ohnaka 2013) and of red supergiants (see e.g. Perrin et al. 2004a, 2007; Wittkowski et al. 2012; Ohnaka et al. 2013; Arroyo-Torres et al. 2013). These spatial extensions cannot be modelled with current atmospheric models, indicating that the model atmospheres are too compact (Ohnaka 2013; Arroyo-Torres et al. 2013).
High-resolution spectra in the mid-IR of both giants and supergiants have not been able to corroborate this idea. On the contrary, resolved 12 μm spectra show strong absorption lines of OH and H2O, absorption that is actually even larger than that expected from a classical photosphere without a MOLsphere (Ryde et al. 2002, 2003a, 2006a,b). Even though it depends on the parameters assumed in the MOLsphere realisation, deep H2O lines are not expected from an extended, optically-thick MOLsphere, since the water lines will be filled-in with emission from the extended shell (for an explanation see Tsuji 2000, 2003, 2006; Ryde et al. 2006b). In short, the reason is that, at wavelengths longward of ~5 μm, the cool MOLsphere of large extent will, in optically thick lines, outshine the hotter stellar continuum from the geometrically smaller star (see, for the case of μ Cep, Ryde et al. 2006b). This leads to predicted weak absorption or even emission lines (see the spectra for a few MOLsphere realisations in Ryde et al. 2006a). The same MOLsphere phenomenon is suggested to be active in normal giants too (Tsuji 2001). We note that MOLspheres, as molecular clouds closer to the photosphere, will not have the same effect (see Tsuji 2009).
Similarly, but based on low-resolution infrared spectra, several papers have also noted that synthetic spectra underestimates observed molecular bands. For example, Price et al. (2002) demonstrated clearly that synthetic spectra of late K-giants observed with the Short Wavelength Spectrometer (SWS) on board the Infrared Space Observatory, ISO at R ~ 1500, underpredict the CO bands at 4.5 μm and the SiO molecular bands at 8 μm. Recently, Sloan et al. (2014) also showed, based on spectra obtained with the Infrared Spectrograph (IRS) on the Spitzer Space Telescope of 33 K giants at R ~ 100, that the observed strengths of the SiO band at 8 μm and the OH lines at 14 − 17 μm are deeper than expected from synthetic spectra, with the interesting finding that the discrepancy for the SiO is smaller than that of the OH lines, i.e. that it seems to grow with wavelength. They also show that this underprediction is an issue for all K giants observed. Likewise, Van Malderen et al. (2004) demonstrated, although more qualitatively, the underprediction of, most prominently, the OH lines at 14 − 17 μm also observed with ISO/SWS. There seems to be a consensus that for the outer, tenuous regions of the atmospheres of red giants where the strong molecular lines form, existing model atmospheres have problems in adequately representing them (Ryde et al. 2002; Price et al. 2002; Decin et al. 2003; Farzone et al. 2013; Sloan et al. 2014). In these regions the heat capacity per volume is low, which means that even small alterations of the heating or cooling terms in the energy equation (for example due to dynamic processes or uncertainties and errors in the calculations of radiative cooling) easily can lead to changes in the temperature structure.
Thus, based on a large number of both spectroscopic and interferometric studies of a range of giants and supergiants, it is clear that classical model atmospheres are inadequate to describe the nature of the outer atmospheres of these stars (see e.g. Tsuji 2003, 2008). It is, however, unclear whether the physics that these different observations are revealing have a common origin or whether there are several different explanations for different wavelengths, observing method, or different stars in the range of effective temperature and surface gravity that has been investigated. Tsuji (2006) concludes that even for the case of the well-studied supergiant Betelgeuse, our understanding of the outer atmosphere has not converged. The controversy between the different pictures that emerge from the interpretations of interferometric and high-resolution spectroscopic investigations could be a result of the extreme complexity of the outer atmospheres and could provide a clue to the underlying physical reality (Tsuji 2006).
More data are needed to be added to the bank of empirical evidence in order to approach a unified picture. In this paper, we add new insights by investigating the way the 12 μm H2O lines change with spectral type for a range of K and M giants. This will show whether the larger-than-expected water absorption is general feature for cool giants across spectral types or due to a specific property, such as the presence of alumina dust, as suggested by Tsuji (2006, 2008) for Betelgeuse and μ Cep.
Since the origin of formation of these water lines are not clear, high-resolution spectra are needed to retrieve as much information as possible. Resolving the stellar spectrum has the advantages that (1) several resolved H2O lines of different excitation can be analysed to provide an excitation temperature at the location where they are formed; (2) photospheric features, if any, can be detected between the water lines; (3) velocity shifts between photospheric features and the water lines can be measured; (4) line broadening can be measured; (5) emission in lines from an extended shell should be present, either as pure emission lines or as emission filling in photospheric absorption lines to different degrees. Detailed line strengths of different resolved lines can also be tested against line-formation models.
With our high-resolution TEXES spectra of a range of K and M giants, we are now in a position to examine these issues.
2. Observations
K, N magnitudes, parallaxes, distances, and observed signal-to-noise ratios (per spectral pixel) of the programme stars.
A total of 10 early-K to mid-M giants and subgiants, ranging from spectral type K0 to M3, were observed in the 12 μm region with TEXES, the Texas Echelon Cross Echelle Spectrograph (Lacy et al. 2002), mounted on the InfraRed Telescope Facility, IRTF, on Mauna Kea. The observations were performed on 31 Oct., 27 Nov. 2000, 2 and 4 Feb. 2001, and on 9 Jul. 2006. Table 1 presents the basic data of the observed stars.
Mid-IR observations at high spectral resolution have become practical in the past decade due to the development of large-grating spectrographs that take advantage of large-format detector arrays at these wavelengths. The detector arrays are able to record a weak stellar signal on top of a very bright background. It is, however, still only possible to observe the very brightest stars with a decent signal-to-noise ratio within a reasonable observing time. Indeed, the observed stars are all very bright (K ≲ 0) and lie in the solar neighbourhood, i.e at a distance of less than 100 pc from the Sun. According to the SIMBAD astronomical database1, there are around 50 stars that meet these criteria. Thus, a fifth of these giants and subgiants in the solar neighbourhood, are represented in our data set. Table 1 presents the bright K and N magnitudes and the final signal-to-noise ratio per pixel of the observations, ranging from 70 to 290. The N-band extinction towards the stars are minimal (see e.g. Cardelli et al. 1989).
The stars were observed with TEXES at high spectral resolution. The spectral resolution, as determined by Gaussian fits to telluric atmospheric lines, has a full width at half maximum (FWHM) corresponding to R = 85 000 or 3.5 km s-1 and the slit width was 1.5′′ and length 8′′. The cross-dispersed spectra consist of approximately 20 orders, each order being larger than the 2562 pixel detector array, which results in gaps between the orders in the final merged spectrum. The spectral coverage ranges from 806.5 to 821.5 cm-1 (that is approximately 12.2 − 12.4 μm). Ryde et al. (2002) describe the determination of the frequency scale, which is subject to systematic offsets of a half2 to one km s-1. One pixel represents approximately 0.9 km s-1. The total integration times of the stars range from 60 − 600 s. For details about the observing method, see for example Ryde et al. (2006b).
The observations were reduced using standard TEXES procedures (Lacy et al. 2002) and the continua are normalised with the IRAF3 task continuum (Tody 1993) by a fifth-order Legendre polynomial. Figure 1 shows an example of an un-normalised spectrum, demonstrating the non-linear form of the blaze function. This spectrum of β Peg shows two distinct water lines in the middle order. The normalisation function at the blue edge (at higher wave numbers) is very uncertain due to the turn-over of the blaze function. This should be held in mind when studying features at the blue edges, where extra care should be exercised. The normalised spectrum of β Peg is presented later in the top panel of Fig. 3.
Subsequently, telluric lines were removed by dividing the normalised spectra with that of a normalised, telluric standard of high signal-to-noise ratio, which we observed in the same setting and reduced in the same way, using custom IDL routines.
Figures 3 and 4 present a part of the reduced, normalised spectra (816.5−821.5 cm-1) in black. The stars are shown in order of increasing effective temperature, Teff. In Fig. 3 these are β Peg, δ Vir, δ Oph, μ UMa, and α Lyn, with effective temperatures between 3448 to 3836 K. Figure 4 shows the other stars, namely α Tau, α Hya, α Boo, α Ser, and β Gem, with temperature ranging from 3871 to 4858 K.
Apart from water lines (we have concentrated our analysis on the ones marked with vertical dashed lines in Figs. 3 and 4) several emission lines of Mg, Si, and Ca are detected in the spectra. Figure 5 shows these in detail. Figures 3 and 4 also indicate the photospheric OH quartet at 820 cm-1 as well as the rotational line of HF at 819.1 cm-1. The HF line is discussed in detail in a paper of its own (Jönsson et al. 2014).
 |
Fig. 1 Un-normalised spectrum of β Peg around 817.0 cm-1. One full order and parts of two neighbouring orders on either side are presented. Three distinct water lines can be seen in the middle order. The non-linear form of the blaze function is indicated by the dashed line, which is a fifth order Legendre polynomial used to fit the continuum. |
3. Analysis
In our analysis, we calculate synthetic spectra of the wavelength region with the Bsyn code, version 7.09 (for details see Ryde et al. 2002). Bsyn is based on the same routines as the MARCS code (Gustafsson et al. 2008). This MARCS code is used to construct model atmospheres (in our case in spherical geometry), which are used when calculating the synthetic spectra. The MARCS code computes hydrostatic model photospheres under the assumption of local thermodynamic equilibrium (LTE), chemical equilibrium, homogeneity and the conservation of the total flux. The fundamental parameters defining a stellar atmosphere model are (i) the effective temperature, Teff; (ii) the surface gravity, log g; (iii) the metallicity, [Fe/H]; (iv) the microturbulence, ξmicro; and (v) the α element enhancement, [α/Fe]. Therefore, we have to determine these parameters for our observed stars, which is done in the following section, Sect. 3.1.
When generating the synthetic spectra with the Bsyn code, the continuous opacities are taken from the model atmosphere calculations. Section 3.2 describes the line data. Subsequently, the spectra were broadened by macroturbulence velocity in order for the synthetic spectrum to fit the observed one. The Eqwi code (version 7.06) calculates equivalent widths for a given model atmosphere and line list (Sect. 3.2). Our observed equivalent widths are measured within the IRAF task splot, by measuring the total area in the absorption or emission line.
 |
Fig. 2 Hertzsrpung-Russell diagram presenting the surface gravities (log g) vs. the effective temperatures (Teff) for the stars investigated in this paper (shown with plus signs). We have also indicated, with triangles, the supergiants and α Boo, that have been investigated at high spectral resolution earlier in the literature (Jennings & Sada 1998; Ryde et al. 2002, 2006a,b). |
3.1. Stellar parameters
Here we describe our method of determining the stellar parameters, of which the surface gravity is the most uncertain. These are provided in Table 2 and plotted in Fig. 2.
3.1.1. The effective temperature, Teff
All our stars are bright and nearby. Angular diameters can therefore be acquired with good accuracy. Knowing the bolometric flux, Fbol, and the limb-darkened diameter of a star, θLD, its effective temperature can be determined directly from 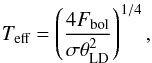 (1)where σ is the Stefan Boltzmann constant. Mozurkewich et al. (2003) measured limb-darkened diameters with the Mark II stellar Interferometer, and provide bolometric fluxes for 85 stars, among others the giants in our sample. They used quadratic limb-darkening laws based on ATLAS9 models to derive the diameters. Table 2 gives the effective temperatures and their uncertainties derived by Mozurkewich et al. (2003). The uncertainties are of the order of 50 K.
(1)where σ is the Stefan Boltzmann constant. Mozurkewich et al. (2003) measured limb-darkened diameters with the Mark II stellar Interferometer, and provide bolometric fluxes for 85 stars, among others the giants in our sample. They used quadratic limb-darkening laws based on ATLAS9 models to derive the diameters. Table 2 gives the effective temperatures and their uncertainties derived by Mozurkewich et al. (2003). The uncertainties are of the order of 50 K.
Mérand et al. (2010) showed that for a K0III star, the uncertainty in the diameter due to different models do not exceed 0.5% (and is thus negligible for the determination of Teff). It may be worse for M stars but the uncertainty should not exceed ~100 K. We note that, recently, Arroyo-Torres et al. (2014) derived an effective temperature of Teff = 3909 ± 187 K for our coolest star β Peg based on VLTI/AMBER diameters, more than 450 K warmer than the temperature of Mozurkewich et al. (2003). Dehaes et al. (2011) derived Teff = 3600 ± 300 K from modelling the spectral energy distributions (SED), for the same star. For the warmer stars α Tau and α Boo, they, however, find excellent agreement. This demonstrates the difficulties for the cooler stars. However, these estimates of the effective temperature of β Peg, are higher than the one we adopt, which will only increase the discrepancy between the observed and the modelled H2O lines in the 12 μm spectra, which we will discuss later.
 |
Fig. 3 Observations of the five coolest stars. The observed spectra are shown with black lines and the synthetic spectra with red lines. The blue ticks above the spectra indicate spectral features of H2O whereas green marks OH(ν = 3 − 3) lines. Dashed lines mark the spectral features of interest which are ultimately used in the calculation of the formation region temperatures. In addition, one emission feature in the form of neutral Mg is visible at 818.1 cm-1, and the HF line is also marked. The lack of observational data between the orders of the spectrometer, is indicated by the vertical solid black lines. |
3.1.2. The surface gravity, log g, and metalliciy, [Fe/H]
Fundamental stellar parameters which are used when generating model atmospheres for our stars.
The surface gravity is given by 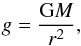 (2)where G is the gravitational constant, and r the stellar radius. The radius is derived from the measured limb-darkened angular diameter, θLD, and the distance to the star through its Hipparcos parallax, π, in the same unit as the angular diameter (van Leeuwen 2007):
(2)where G is the gravitational constant, and r the stellar radius. The radius is derived from the measured limb-darkened angular diameter, θLD, and the distance to the star through its Hipparcos parallax, π, in the same unit as the angular diameter (van Leeuwen 2007): 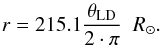 (3)The stellar mass, M, we determine from evolutionary tracks, knowing the star’s luminosity, effective temperature, and metallicity. The stellar metallicities we find from the literature, picking the iron abundances from the references that provide effective temperatures and surface gravities in the proximity of our values, see the references in Table 2. The literature values can vary (see e.g. Dehaes et al. 2011; Cruzalèbes et al. 2013; Jönsson et al. 2014), but will not influence our conclusions. We use the sets of evolutionary tracks from Bertelli et al. (2008, 2009) who use isochrones from Girardi et al. (2000). We find that the masses vary from 0.9 M⊙ for α Lyn to 2.7 M⊙ for α Hya. The uncertainties in the derived luminosities and effective temperatures provide estimates of the uncertainties in the masses, which together with the uncertainties in the radii provide our uncertainties in the surface gravity. Table 2 summarises the surface gravities and the metallicities, which have typical uncertainties of 0.15 dex, for our stars.
(3)The stellar mass, M, we determine from evolutionary tracks, knowing the star’s luminosity, effective temperature, and metallicity. The stellar metallicities we find from the literature, picking the iron abundances from the references that provide effective temperatures and surface gravities in the proximity of our values, see the references in Table 2. The literature values can vary (see e.g. Dehaes et al. 2011; Cruzalèbes et al. 2013; Jönsson et al. 2014), but will not influence our conclusions. We use the sets of evolutionary tracks from Bertelli et al. (2008, 2009) who use isochrones from Girardi et al. (2000). We find that the masses vary from 0.9 M⊙ for α Lyn to 2.7 M⊙ for α Hya. The uncertainties in the derived luminosities and effective temperatures provide estimates of the uncertainties in the masses, which together with the uncertainties in the radii provide our uncertainties in the surface gravity. Table 2 summarises the surface gravities and the metallicities, which have typical uncertainties of 0.15 dex, for our stars.
We have also determined the surface gravities for our stars directly from the PARAM 1.1 web interface (da Silva et al. 2006). It provides a Bayesian estimate of the stellar parameters M, log (g) and r with the use of the Girardi et al. (2000) isochrones, through prior knowledge of the probabilities associated with the placement of a star in the HR-diagram. The input parameters needed are the star’s effective temperature, metallicity, V-magnitude, and parallax. Table 2 gives the PARAM gravities in the fourth column.
We can conclude that the surface gravities determined with the two methods agree nicely, within the estimated uncertainties, for all stars except for the two coolest giants. The PARAM gravities are systematically and significantly lower than ours. The only difference in methodology between the two methods is the determination of the stellar luminosity and thereby the stellar radius. PARAM uses the V magnitude and a bolometric correction, (B.C., from Girardi et al. 2008), which together with the input parameters Teff and parallax, π, provides the radius. We use the angular diameter, parallax, and measured bolometric flux to obtain the luminosity. Although, we are not certain for the cause of the difference in log g, we note that the main difference is the introduction of the B.C., which gets increasingly larger and more uncertain the cooler the star is. Values from recent literature provide even higher surface gravities, with our log g being closer to these. Although they also find a higher temperature, Soubiran et al. (2008)4 for instance derive log g = 1.2 for β Peg, our coolest star, whereas we find log g = 0.5 and PARAM provides log g = 0.2. In our discussion later about the spectral features in our TEXES spectra, the surface gravity will, however, not play an important role.
3.1.3. The microturbulence and macroturbulence
The microturbulence parameter, χmicro, is difficult to determine empirically, but is nevertheless important and especially so when analysing lines that are saturated. The microturbulence will then affect the line strengths for a given abundance, and is therefore a crucial parameter when analysing strong lines. We have, therefore, looked at two different sets of microtubulence determination for giants. One is the values used in the investigations of high-resolution near-IR spectra of red giants by T. Tsuji (see, for instance, Tsuji 1985, 2008) and the second is an empirically found function of Teff, log g, and [Fe/H] with a scatter of ~0.1 dex, developed within the Gaia-ESO survey (Gilmore et al. 2012) from high-resolution optical spectra. We present them in different columns in Table 2.
As we can see from these values, Tsuji’s microturbulent velocities are in general 1 km s-1 larger than the values determined from the empirical Gaia-ESO relation. Since we are not able to determine the microturbulent velocities ourselves, we will take an average of 2.0 km s-1 as our default value, and later discuss its influence on the spectral lines in the Discussion section, see Sect. 5.6.1.
To match synthetic spectra with the observed ones, a “macroturbulent” broadening, χmacro, is introduced, which takes into account the macroturbulence of the stellar atmosphere and instrumental broadening. Since our water lines are far from matched by our model spectra, we have convolved our synthesised spectra with reasonable values that match the lines that are modelled well, which are the OH lines and the HF line. We have used a Gaussian function, specified by its FWHM which Table 2 provides. The macroturbulent broadening changes only the form of a line and not the intrinsic line strength.
Molecular data of the most prominent H2O lines in the 808−822 cm-1 region (λair = 12.162−12.373 μm), partly from Ryde et al. (2002) data.
3.1.4. [α/Fe] and CNO abundances
A few of the α elements5 are important electron donors in the continuum- and line-forming regions of the stellar atmosphere. Especially, Mg alone contributes more than half of the electrons, but also Si is important at least in the continuum forming regions. The continuous opacity in the mid-IR is due to H 6, an opacity which is proportional to the electron density (see e.g. Eq. (2.76) from Rutten 2003). The strength of a weak line is proportional to the line opacity and inversely proportional to the continuous opacity, thus directly influenced by the electron density.
6, an opacity which is proportional to the electron density (see e.g. Eq. (2.76) from Rutten 2003). The strength of a weak line is proportional to the line opacity and inversely proportional to the continuous opacity, thus directly influenced by the electron density.
In our atmospheric models and spectral synthesis we have prescribed an α element over-abundance which is + 0.4 for metallicities below [Fe / H] = −1 and linearly decreasing to a solar ratio at solar metallicity.
Since we are modelling red giants and the first dredge-up that these stars have experienced will lead to an increased C abundance and an accompanied decrease of N, such that C+N is constant, we have used CN-processed models (see e.g. Gustafsson et al. 2008). However, as these authors point out, the effects on the model structure is moderate.
3.2. Line data
Spectral lines detected in the recorded wavelength range include H2O, OH, HF, and metallic emission lines (for the metallic emission lines, see Sect. 4.2). When synthesising the modelled spectra, we have included an atomic line list and the most common molecules that might have transitions in the N band7. For our temperature range, however, only H2O, OH, HF, and atoms show features detectable at the signal-to-noise level of the observations. Neither are atomic absorption lines detected nor are there any expected from a spectral synthesis of the wavelength region. The only atomic lines that are detected are emission lines due to a very specific non-LTE process, see Sect. 4.2.
The line lists for our calculation of the photospheric synthetic spectra are taken from the compilation of Goldman et al. (1998) for OH and from Jönsson et al. (2014) for HF. The H2O line list is based on the compilation of Barber et al. (2006), but for a dozen of the strongest lines, Ryde et al. (2002) identified the transitions from laboratory measurements by Polyansky et al. (1996, 1997a,b). Uncertainties in the line positions of these measurements are less than 0.002 cm-1 (for details see Ryde et al. 2002, 2006a,b). Table 3 gives the line data for the most prominent H2O lines. All molecular lines are synthesised with the Bsyn code with corresponding partition functions that are consistent with the line lists.
4. Results
In Figs. 3 and 4, parts of the TEXES spectra of our red giants are shown. The observations are presented in black and the synthetic spectra in red. Water lines that affect the synthetic spectra are marked with blue tick marks and the most prominent water lines, that we will be using in the analysis, are marked with vertical, dashed lines. Absorption lines of OH are shown with green tick marks, and the HF line and the emission line due to Mg are marked. From the spectra, no molecular emission lines are detected. Furthermore, the strengths of the H2O lines vary smoothly with effective temperature and, as expected, the coolest stars have the strongest and most H2O lines present. The wavelengths of the strongest water lines are accurate enough for our spectra, whereas several weaker lines do not match up as well. This is expected based on the accuracy of the H2O line list, see Sect. 3.2. In the following sections we are more interested in the lines that appear over a range of stellar temperatures, in other words only the strongest lines, those marked with vertical, dashed lines in Figs. 3 and 4.
All lines in the region are modelled and synthesised, except for the metallic emission lines that require a specific non-LTE process (see Sect. 4.2), which are not modelled for here (for a model of these lines, see Sundqvist et al. 2008). From Figs. 3 and 4 and the other parts of our recorded TEXES spectra, we immediately see that the synthetic spectra fail to match the observations of the OH(ν = 0 − 0) quartets, failing by a bit, and the H2O lines, failing by a large amount. The OH(ν = 2 − 2), OH(ν = 3 − 3), and the HF lines are, however, modelled well with a photospheric model with the stellar parameters derived in Sect. 3.1.
This result for all our stars is identical to the results and conclusions for Arcturus by Ryde et al. (2002). Now, we see the same trend for all the giants in our investigation, stars with spectral types ranging from K to M.
 |
Fig. 4 Observations of the five warmest stars. The observed spectra are shown with black lines and the synthetic spectra with red lines. See also figure caption of Fig. 3. |
Table 4 presents our measured equivalent widths of the water lines, Wobs (in mÅ), and their strengths in the form of log (Wobs/λ). We see that the lines are normally weaker than log (Wobs/λ) = −5.0 and that they vary smoothly with the effective temperatures of the stars. In the table we also present the modelled equivalent widths, Wmod (also in mÅ), for the water lines. In addition, here we can conclude that the synthetic lines are too weak for all stars and all lines. For the coolest star, β Peg, the synthetic lines are too weak by a factor of ~two, and for the warmer stars, a factor of between 5 and 50.
Photospheric emission lines with line identifications from Chang & Noyes (1983); Chang (1984); Brault & Noyes (1983); Ryde et al. (2004); Sundqvist et al. (2008).
4.1. The formation of the continuum at 12 μm
None of the red giants we have observed are expected to have large continuum emission due to dust in the 12 μm region. This is verified from low spectral-resolution SWS01 spectra observed with ISO (Kessler et al. 1996). We therefore assume that the continua recorded from the red giants originate in their photospheres. For an Arcturus model atmosphere, the near- and mid-IR continua, which are dominated by the H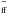 opacity, is formed at an optical depth of log τ500 ~ −0.5. This can be compared with the continuum at 1.6 μm, which is formed at log τ500 ~ +0.6, and is the deepest point in the atmosphere the optical/near-IR continuum is formed. Even a MOLsphere would not contribute much continuous opacity (see e.g. the realisations of a MOLsphere in Ryde et al. 2006b). The MOLsphere continuum, due to Hff and H
opacity, is formed at an optical depth of log τ500 ~ −0.5. This can be compared with the continuum at 1.6 μm, which is formed at log τ500 ~ +0.6, and is the deepest point in the atmosphere the optical/near-IR continuum is formed. Even a MOLsphere would not contribute much continuous opacity (see e.g. the realisations of a MOLsphere in Ryde et al. 2006b). The MOLsphere continuum, due to Hff and H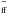 , is therefore expected to be transparent. Other stars, such as the supergiants α Ori and μ Cep, show large dust emission in the wavelength region of 9−13 μm. In these cases this has to properly be taken into account when synthesising this spectral region (see Ryde et al. 2006a,b).
, is therefore expected to be transparent. Other stars, such as the supergiants α Ori and μ Cep, show large dust emission in the wavelength region of 9−13 μm. In these cases this has to properly be taken into account when synthesising this spectral region (see Ryde et al. 2006a,b).
4.2. Emission lines of Mg, Al, Si, and Ca
In the parts of our TEXES spectra in Figs. 3 and 4, emission lines due to Mg i at 818.06 cm-1 are clearly detected in all the stars, apart from those where the line falls into a gap between orders.
Carlsson et al. (1992) explained in detail the formation process of the emission lines of Mg i in the solar spectrum. The lines are formed in the photosphere due to a non-LTE process, in which a flow cycle between states of Mg i and Mg ii, refilling neutral magnesium again via its Rydberg states, is established. This results in an underpopulation of the levels from which the lines originate. A small difference in the departure coefficients between the upper and lower levels is the direct cause of the emission.
Ryde & Richter (2004) were the first to report these emission lines in a star apart from the Sun. They showed that the same non-LTE mechanism is at play in Procyon (F5IV-V), a star with an effective temperature of Teff = 6512 K and a surface gravity of log g = 3.9 (cgs). Later, Sundqvist et al. (2008) detected even stronger emission lines in three K giants. They succeeded in modelling these lines by using the same non-LTE mechanism also for these giants. An expanded model atom of Mg and inclusion of neutral hydrogen collisions was, however, needed in order to reproduce the emission strengths in these giants. Sundqvist et al. (2008) also showed that the emission lines are formed in atmospheric layers below the temperature minimum. They are therefore clearly photospheric features.
Table 5 gives possible metallic emission lines in our wavelength region, in addition to the Mg i emission lines. Carlsson et al. (1992) and Baumüller & Gehren (1996) explained and modelled the emission lines due to Si i and Al i in the solar spectrum, which are weaker than the Mg emission, with a similar process as for magnesium. Stellar emission lines at 12 μm due to Si i and Al i were first identified in α Boo by Lacy et al. (2002) and analysed by Sundqvist et al. (2008) in the three K giants they investigated. Here, we detect emission lines due to Si i, Al i, and Ca i lines for all our giants. Figure 5 presents these and Table 6 gives their equivalent widths (when measurable). The metallic emission lines at 12 μm thus seems to be a common feature in a variety of stars, and can be explained by the non-LTE flow cycle in the stellar photospheres. For red giants the lines are formed at an optical depth of log τ500 ~ − 1.7, i.e. quite deep in. It is then clear that we are recording the photospheric spectrum of the red giants.
Equivalent widths in mÅ of the photospheric emission lines identified with their wavenumber in cm-1.
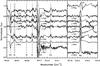 |
Fig. 5 Normalised spectra shifted with respect to each other showing emission lines from Si, Al, Ca, and Mg, which are marked. Two OH lines in absorption are also indicated along with one H2O line in β Peg at 818.1 cm-1. |
4.3. The HF line
We detect the rotational HF line at 12.21 μm (819.11 cm-1) for all the spectra of our stars, except for α Ser, for which the HF line falls beyond the recorded spectrum. This line can be used to derive the fluorine abundance of the stars. This was done by Jönsson et al. (2014), who synthesised these successfully only with photospheric models. Earlier studies in the literature of the photospheric fluorine abundances in stars have all used the vibration-rotation HF lines at 2.3 μm instead. Jönsson et al. (2014) used both sets of lines to determine the photospheric fluorine abundances for our stars. They gave consistent abundances, indicating that also the 12 μm HF lines are photospheric in origin and well described by a standard model atmosphere. Again, this indicates that we are recording the photospheric spectrum of the red giants at these wavelengths.
4.4. Velocity shifts between water, OH, and emission lines
Table 7 presents the mean velocity shifts between the water lines, OH(ν = 0 − 0) lines, and the emission line of Mg relative to the HF line. The Mg and the HF lines are most certainly photospheric in origin. The uncertainties given there are the standard deviation of the mean for the cases where we can measure several lines. We estimate the random measurement uncertainties to ± 0.5 km s-1 and the systematic uncertainties (mainly due to the wavelength calibration) to lie in the range of ≈0.5 − 1 km s-1. Since the OH lines lie at lower wavenumbers than the Mg and HF lines, these systematic uncertainties might be the reason that the OH-line shifts for all the stars are systematically negative, but within the estimated uncertainties. For a few stars, such as α Tau and β Peg, there might be a formal systematic offset between the H2O lines and the OH lines, but not between the photospheric HF line and the H2O lines. However, in the case of the α Tau spectrum, the uncertainties are in the range of this offset. The photospheric Mg emission line is for example shifted by the same magnitude but in the opposite direction. The same trend is seen in other stars but within the estimated uncertainties. β Peg is the coolest star, which means that molecules start contributing severely and start blending lines. This leads to larger systematic offsets in the wavelength determinations. Thus, we conclude that at this accuracy, within ± 1.5 km s-1, all the spectral lines are at the same velocity.
This means that either the water lines in all our stars are formed in the photospheres or that the MOLspheres have no velocity relative to the stellar photospheres.
Velocity offsets, and standard deviations of the mean when there are several lines, in km s-1 of the water, OH, and Mg lines relative to the HF line, are shown in Cols. 2–4, respectively.
5. Discussion
Previously, water lines in the mid-IR have been investigated in only four stars, namely the red giant α Boo (Ryde et al. 2002) and the red supergiants α Sco (Jennings & Sada 1998), α Ori (Ryde et al. 2006a), and μ Cep (Ryde et al. 2006b). The question is whether the properties of the strong water lines are specific to a few particular stars or whether they are a general feature of red giants and supergiants. Our goal is to present empirical evidence for how the strengths of the water lines change with spectral type for a range of K and M giants to test for a trend with temperature. Before discussing the general trends and its possible causes, we start off by discussing the published results from the literature.
In the case of the well-studied K giant Arcturus, Ryde et al. (2002) firmly establish the mid-IR OH lines to be photospheric by determining identical velocity shifts and line widths of the vibration-rotation lines at 1.6 μm, a definite photospheric feature8, and the 12 μm rotation lines, as well as successfully synthesising lines of different excitation energies, including the strong H2O lines at 12 μm, based only on a modified photospheric model. They find that the outer temperatures have to be lowered by of the order of 10%, that is approximately 300 K compared to the radiative-equilibrium temperatures of 2000−2500 K, in the layers described by log τ500< − 4 (see Fig. 7 of Ryde et al. 2002). This was a so called semi-empirical model atmosphere, constructed in order to fit the water lines. In addition, the metallic emission lines detected in this region, especially the Mg line emission, is shown to be formed by a photospheric line-formation process (Sundqvist et al. 2008), establishing also that the continuum most likely originates in the photosphere.
Although K giants do not have direct evidence of MOLspheres (Tsuji 2003), Tsuji (2009) find indirect evidence from lines originating from the fundamental band of CO that is interpreted as suggesting a MOLsphere for Arcturus. However, the Ryde et al. (2002) observations do not register the molecular layers and therefore either contradict the MOLsphere hypothesis9 or put new strong constraints on the nature and interpretation of the MOLspheres. With a MOLsphere, it would be unlikely that the velocity shifts, line widths, and degree of excitation would match so closely to the photospheric values.
It can be noted that Cohen et al. (2005) find that the continuum of α Boo is reasonably well modelled by a classical model photosphere in the region of 40 − 125 μm, that is, wavelengths that sample the upper photosphere, but they also show that it is not until wavelengths beyond 1−3 mm that the continuum is formed in photospheric regions corresponding to where Ryde et al. (2002) need to start cooling their upper photosphere. This is also a location which is well above the depth of the onset of the coexisting chromospheric temperature rise of the Arcturus model of Ayres & Linsky (1975). Chromospheric free-free continuum radiation also contributes at submillimetre or millimetre wavelengths.
Later, Ryde et al. (2006a) and Ryde et al. (2006b) also found stronger than expected H2O lines both in the supergiant Betelgeuse and in the prototypical MOLsphere supergiant μ Cep (Tsuji 2000). Suggested LTE MOLsphere models in the literature for these stars, based on low-resolution spectra and interferometric measurements (Tsuji 2000; Ohnaka 2004; Verhoelst et al. 2006), would all result in strong emission features at 12 μm, which are not detected. In these cases too, lower temperature structures in the outer photospheric layers, inspired by the discussion for Arcturus (Ryde et al. 2002) but also by that in Jennings & Sada (1998), made it possible to model the spectra well. The conclusion of Ryde et al. (2006a,b) is that also in these cases the water lines are most likely formed in the photospheres, albeit in non-classical ones, and that there is no need for MOLspheres to explain this wavelength region. From the line widths it is suggested that the features are formed close to the photosphere, perhaps in connection with the coexisting, inhomogeneous chromosphere. The column densities of H2O also fit closely what is expected from the spectra (Jennings & Sada 1998).
A cool temperature structure is able to synthesise all the spectral features of the 12 μm region simultaneously because is the relative response of the different spectral features to the outer, cooler layers due to different heights of formation. Whilst the models that explain this wavelength region are semi-empirical model atmospheres, constructed solely to fit the lines, insights may still be gained from such an exercise. It could, for instance, indicate lower excitation temperatures of the levels of water forming the lines, or indicate extra cooling.
The ultimate goal, however, is to find a model that can explain all empirical data. This is not yet the case, since a photospheric temperature structure as suggested by the 12 μm wavelength region predicts strong TiO bands in the optical, which are not seen in Arcturus (Ryde et al. 2003b). Furthermore, the MOLsphere model of μ Cep predicts emission from water bands at 6 and 40 μm, as suggested from low-resolution, ISO spectra (Tsuji 2000). This scenario predicts the 12 μm lines to be in emission as well. However, Ryde et al. (2006b) detect the contrary. High-resolution spectra of the 6 and 40 μm water bands, resolving the individual lines, will be able to reveal the nature of the emission lines, providing line profiles, excitation temperatures, velocity shifts, turbulent velocities, and the existence of absorption lines or components. Indeed, 6 μm observations have now been performed during the science verification flight in April 2014 of the EXES spectrometer onboard the Stratospheric Observatory For Infrared Astronomy, SOFIA (see DeWitt et al. 2014). No results have been presented yet.
5.1. New TEXES observations
We begin by summarising the results based on our new observations at high spectral resolution in the mid-IR; the water vapour lines in all our stars from α Boo and cooler show absorption lines stronger than expected from a classical model photosphere. The continuum is most likely formed in the photosphere, as is the HF line, metallic emission lines, and the OH(ν = 2 − 2) and OH(ν = 3 − 3) lines. What is then the cause of the strong absorption of only the water lines and the OH(ν = 0 − 0) lines? We note that these show no net velocity shift compared to the photospheric lines.
5.2. The general behaviour across spectral types
The water lines we detect for giants of effective temperatures spanning the range from 3400 to 4900 K show a smooth trend in the strengths of the water lines. The strong lines and lack of emission, therefore, seems to be a general feature of red giants. An explanation of the stronger-than-expected lines must therefore be found in a general cause, applicable to all late-type giants. The general nature of the observed molecular mid-IR lines, underpredicted by synthetic spectra, was also found by Sloan et al. (2014) for all K giants in their sample. For the cases of the supergiants Betelgeuse and μ Cep Tsuji (2006, 2009) suggested a specific solution to explain the strong H2O lines at 12 μm shown by Ryde et al. (2006a). In this case, optically thin 12 μm lines were suggested to be formed in the MOLsphere, in absorption against a continuum formed from an alumina shell. Our stars do not have surrounding dust.
5.3. Excitation temperatures of the water lines
In the wavelength recorded, we actually have water lines with quite a spread in excitation energies of the lower levels of the transitions: 0.398−1.398 eV, see Table 3. In the discussion of μ Cep (Ryde et al. 2006b), the range was smaller: 1.014−1.150 eV. This means that we can derive the temperature of the site of line-formation from line-strength ratios. The dotted lines in Figs. 3 and 4 mark the lines that can be used in the calculation of such temperatures.
In order to derive analytical relations, we make the following hypotheses:
-
1.
For a given star, all water lines are formed in layers with aconstant temperature. As the outer parts of static red giantatmospheres, where molecular line contribution functions arebelieved to peak, exhibit a rather flat temperature profile, thishypothesis should be valid (we note, however, that resonancelines have relatively broad contribution functions).
-
2.
The continuum opacity is constant over the considered wavelength range. In the infrared, the main continuum opacity source is due to H− free-free absorption, which approximately varies as ν-2, ν being the frequency. The water lines considered here cover a range between 808 cm-1 and 821 cm-1, i.e. a relative variation of only ~1.5%. This hypothesis is thus fully justified.
-
3.
We assume that all lines are formed in the optically thin limit, that is, lines are not saturated; in other words, they are located in the linear part of the curve of growth (weak-line approximation).
-
4.
The lines are not blended. This gets increasingly untrue for the cooler stars. Some lines are blended by as much as 40%.
The last two hypotheses are the most questionable ones. In spite of the simplifying assumptions, we will calculate the temperatures of the line forming regions. Under these assumptions, the equivalent widths of water lines obey to the relation 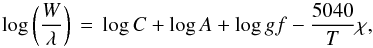 (4)where C is a constant parameter (for given star and species), including the continuum opacity and the partition function (the constancy of the temperature implies the same partition function and the same molecular equilibrium), A the water abundance, and χ the line excitation energy.
(4)where C is a constant parameter (for given star and species), including the continuum opacity and the partition function (the constancy of the temperature implies the same partition function and the same molecular equilibrium), A the water abundance, and χ the line excitation energy.
In other words, line-strength ratios allow the determination of the temperature (assumed to be uniform) at which they are formed, or the excitation temperature in the case of non-LTE effects. Considering two lines with excitation energies and oscillator strengths χ1, gf1 and χ2, gf2, respectively, one gets 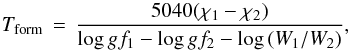 (5)where W1 and W2 are the measured equivalent widths.
(5)where W1 and W2 are the measured equivalent widths.
Table 8 displays the obtained values of the temperatures of the line-formation regions both from the observed lines-strength ratios and those from synthetic spectra. The standard deviation due to temperature determination from different combinations of line ratios lie between 100−300 K, originating mostly from the simplicity of the assumptions of non-saturated lines and non-blended lines. The temperature from the observed spectra lie around 2500 K and systematically show cooler temperatures compared with the synthetic spectra by 300−1000 K. Thus, either an additional cooling of the outer atmospheric layers, or an additional extension of the atmosphere, compared to the static, LTE model atmosphere such as a MARCS model, is required to explain the relative strengths of the water lines. Figure 6 illustrates this for the case of α Boo.
These temperatures should be seen as indicative. For example, the reason for the larger temperature difference for Arcturus (600 K) than that found by Ryde et al. (2002) (300−350 K) is that the observed water lines are weak in the spectrum leading to very uncertain line ratios. The line ratios from the synthetic spectrum are, however, quite accurate since these lines are not saturated and not blended in this star, being the warmest in our sample. In addition, the synthetic spectrum is noise-free.
In any case, what is found is that the formation temperatures are in general of the order of 300 − 600 K cooler as derived from the observed spectra compared to those derived from the modelled ones. This is also consistent with the temperature decreases (300−400 K) needed in the model atmospheres of Arcturus (Ryde et al. 2002), Betelgeuse (Ryde et al. 2006a), and μ Cep (Ryde et al. 2006b). In addition, it is found to be a general feature for all the giants observed here, from K to M giants. It should be noted that the derived temperature could also be the temperature of the MOLsphere if the water lines are formed in such a circumstellar environment.
 |
Fig. 6 Temperature profile from a MARCS model atmosphere with parameters relevant for α Boo. The (red) horizontal dashed line indicates the expected water line formation temperature, assuming LTE. The (blue) full line indicates the average formation temperature computed from Eq. (5) (the dotted lines indicate the full range of temperatures). |
 |
Fig. 7 Absorption lines of H2O and HF calculated based on a non-modified Arcturus model atmosphere (black spectrum) and based on a semiempirical model constructed to fit observed water lines with cooler outer regions (red spectrum), see Ryde et al. (2002). The HF line is formed deeper in the atmosphere and is therefore not affected by the cooler outer parts. |
5.4. Detected photospheric features
As we have discussed, the observed metallic emission lines at 12 μm are without doubt photospheric in origin in all our stars. They are formed though a very specific non-LTE process giving rise to them. As mentioned above, they are well explained with this photospheric process for the Sun and giants (see Sundqvist et al. 2008) anchoring them to the photosphere. The HF line is also undoubtably photospheric, since it gives the same abundance as near-IR HF lines (Jönsson et al. 2014), as expected from a photosphere. Were they formed in a cooler MOLsphere, the derived abundances would not have matched that closely. The H2O lines in this wavelength region are, however, poorly modelled. As mentioned, Ryde et al. (2002, 2006) thus constructed a semi-empirical model atmosphere which could explain the formation of strong water lines. A cooling of the outer atmosphere of a few 100 K, at log τ500< −4, was needed. This extra outer cooling does not, however, significantly affect the HF line, since it is formed deeper in the photosphere: the derived fluorine abundance is only 0.07 dex lower (see Fig. 7).
The lack of any velocity shift between the photospheric HF and Mg lines is expected. The lack of any shifts of the OH and H2O lines means either that these lines are photospheric or that they are formed in a MOLsphere that is static, to within a few km s-1, relative to the photosphere. Ryde et al. (2002) argued that also the OH rotation lines in Arcturus are formed in the photosphere. This was based on velocity and FWHM similarities between the rotation OH lines and the vibration-rotation OH lines at 1.6 μm, the later being photospheric. We have no reason to believe that this should not be the case for the other stars too, since Arcturus nicely fits into the trend of lines strengths, and velocities.
Thus, the metallic emission lines, the HF line, and the adjacent continua, are most likely photospheric in origin. The wavelength shifts of the water lines are, within uncertainties, identical to those of the photospheric emission lines and HF line. This indicates that also the water lines might be of a photospheric origin.
5.5. Strong H2O lines
We have shown that the approximate temperature at the location of formation of the water lines are a few hundred degrees lower than expected from a model photosphere. This is empirically determined from water lines from different excited levels. If the H2O lines are formed in such a stellar photosphere, lines in LTE would show a larger absorption than expected. We see this for all our giants.
An important point when discussing the formation of the water lines is that they are optically thick at these temperatures and with the column densities that are assumed in MOLsphere realisations (Tsuji 2000, 2003). At the line centre, ν0, assuming a broadened line with a characteristic line width of 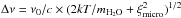 , the optical depth is given by
, the optical depth is given by 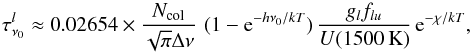 (6)
(6)
where Ncol is the column density of water vapour, U is the partition function of water vapour and has a value of 2713 for a temperature of 1500 K (Partridge & Schwenke 1997), and χ is the excitation energy of the level (for details see Ryde et al. 2006b). For example, 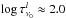 for the water line at 818 cm-1.
for the water line at 818 cm-1.
Thus, if the lines were to be formed in a large MOLsphere of these typical temperatures, the sheer size of it will weaken any absorption dramatically, or even show emission (see the discussions in Ryde et al. 2006a,b). Most MOLsphere realisations are of such a size that emission lines are expected at 12 μm. The reason for this is indeed that the water lines are very optically thick, even in non-LTE, and therefore probe the MOLsphere. The continuum between the H2O lines, on the other hand, probe the stellar photosphere. The angular size of a MOLsphere compared to the continuum forming stellar surface, will lead to absorption lines weaker than expected or even to emission in the lines. However, we do not find any indication of emission lines of water from any of our red giants, on the contrary they are all deeper than expected.
5.6. Possible solutions to the mismatch of the H2O lines
Here we discuss possible mechanisms that could increase the strengths of the H2O lines.
5.6.1. Spectroscopic uncertainties
Increasing the oxygen abundance would increase the strength of the water lines, but it would require an increase of the order of 0.6 dex to fit some of the lines. Other H2O lines, which are not observed, would then also emerge. This would also greatly affect the OH lines. The oxygen abundances of these stars are quite well determined. For example, Ramírez & Allende Prieto (2011) determine the oxygen abundance of Arcturus to better than 0.05 dex. Normally, the abundance determinations are good to within 0.1 dex.
A change in the stellar parameters in the range of their uncertainties will only change the equivalent widths by 20% for a change in effective temperature for the coolest star and by up to a factor of 2 for the warmest star, where water is on the verge of being visible. A change in log g of 0.1 will change the equivalent width of the H2O lines by 10−20%. These changes are too small to explain the strong H2O lines.
If the lines are saturated, their strengths will be sensitive to the adopted microturbulence. The lines will broaden but they will not appear deeper. A different microturbulence will therefore not be able to fit the strong water lines.
Thus, none of these uncertainties are enough to explain the lines strengths of the H2O lines.
5.6.2. Non-LTE line formation of H2O
The need for considering a situation in which the water lines might not be formed in LTE, was stated already in Ryde et al. (2002) and discussed by Ohnaka et al. (2013). Different behaviours of rotation lines and vib-rotation lines of H2O might be caused by different non-LTE effects (see Tsuji 2006; Perrin et al. 2004b). Lambert et al. (2013a) estimated the critical density and showed that it is indeed higher than that of the outer atmosphere or MOLsphere, requiring a proper non-LTE analysis of the formation of water lines either in the photosphere or in a MOLsphere. Preliminary results show that the source function, level populations, and cooling rates are affected (Lambert et al., 2013a,b). Either the molecular levels, of for example H2O, from which the cooling lines originate (which not necessarily are the lines we have observed) are overpopulated leading to an increased cooling, or the non-LTE level populations could affect the source function and line opacities of the lines discussed. In the latter case the strengths of the lines is a line-formation effect and not an increased abundance of water vapour as such.
5.6.3. Extra cooling in the upper layers of the photosphere
If we assume that the outer regions in the photosphere are cooler, as indicated by our line-ratio analysis, how should this additional cooling be interpreted? Is it a non-LTE effect or a dynamic effect? Non-LTE usually results from either a strong radiation field or a low density of collisional partners. The photospheric radiation field itself may lead to such effects, but it may also be increased by chromospheric emission. This chromospheric emission would in particular manifest itself in the ultraviolet, which would increase the molecular photodissociation, and thus a weakening of water lines. We naturally do not rule out the presence of a chromospheric activity in the observed stars, but it does not seem to generate a significant photospheric non-LTE effect. More generally, a strong radiation field would generate over-excitation (i.e. an excitation temperature larger than the kinetic temperature) and over-dissociation, and thus a lowering of the cooling function. If non-LTE effects cause the observed strong water lines, it would thus be mostly through low collision rates compared to radiative ones, leading to a stronger cooling. An additional cooling may also be due to a dynamic effect, such as an adiabatic expansion, leading to extra dilution of the outer atmosphere. Radiation pressure, which is potentially sensitive to non-LTE effects, could also produce a similar effect. Furthermore, as the observed giants are believed to be static, non-LTE effects should dominate over dynamic effects.
As mentioned earlier, Lambert et al. (2013b) indeed show that in cool evolved stars, non-LTE effects may be important to the formation of water lines. These effects reveal themselves through an overpopulation of lower levels, an increase in the cooling function (the contribution of water to cooling being multiplied by up to factor of 4 in the outer layers) and increased radiation pressure. This extra water cooling of the outer photosphere could be a reason for the detected cooler temperatures of the line-formation regions.
Short & Hauschildt (2003) discussed another reason for a cooler outer photosphere in their Arcturus model photosphere. They relaxed the assumption of LTE in the calculation of the photospheric structure by treating atomic opacity (continuous and line opacity) in non-LTE using large model atoms. They demonstrated that overionisation of Fe can decrease the temperatures by a few hundred Kelvin in the outer atmospheric layers. It has to be investigated whether this is a general feature for red giants or not.
In the outer layers where the water lines are suggested to form for all stars across the range of spectral types investigated in this paper, the hot chromospheric regions10 appear to coexist with cooler areas where water can be formed in sufficient quantities to match our observations. Chromospheres are dynamic and, at least for the solar case, a wave-driven phenomenon of spatially and temporally intermittent structures. The classical modelling neglects mechanical energy and momentum deposition that leads to the chromospheric heating and mass loss, which shows that the classical atmospheric modelling is inadequate for a complete treatment of these regions. This is in line with the discussion by Wiedemann et al. (1994) of the COmosphere, that is, the cool regions (determined from CO fundamental lines) coexisting with the chromosphere. They conclude that their CO spectra suggest a dominance of cool regions having large filling factors.
Temperature inhomogeneities, due to surface granulations in the photospheres, could affect the water spectrum. In the mid-IR, the continuum intensity contrast is small. However, the column density of water in the cool, sinking gas would likely be larger than in an homogeneous photosphere. The cooler areas in inhomogeneous photospheric models with both cool areas and hotter ones, will mainly affect the mid-IR spectrum. Optical and UV wavelengths are more biased towards hotter regions (see the discussion in Ryde et al. 2006a). Hydrodynamic simulations of granules in giants such as by Chiavassa et al. (2009, 2010a,b) will help in understanding a more realistic formation of molecular lines in the outer photospheres. The 12 μm lines provides a good test for three-dimensional model photospheres of red giants and supergiants, which are starting to be realised (see the development in e.g. Collet et al. 2007; Chiavassa et al. 2010a; Ludwig & Kučinskas 2012; Dobrovolskas et al. 2013).
6. Conclusions
We have observed a range of late-type giants in the N band, at 12.2 − 12.4 μm, at a high enough spectral resolution so as to resolve individual stellar spectral-lines. We detect photospheric metallic emission-lines (which are formed in non-LTE), OH, and HF lines. In addition we detect stronger-than-expected absorption lines of water vapour in all the stars showing water lines, that is, for stars cooler than ~4300 K. The strengths of these H2O lines vary smoothly with the spectral types of the stars. This shows that an explanation for the formation of these water lines has to generally apply to all giants across spectral types, ranging 4500 to 3450 K (K1.5-M3.0).
We have shown that the 12 μm continuum is formed in the photosphere and that several observed features in the spectra are photospheric in origin (the metallic emission lines, OH lines, and the HF lines). The water lines in this continuum, could either be formed in the suggested molecular sphere, a MOLsphere, around the stars, or in the photosphere. The strong absorption lines of H2O, indicating a lack of emission from an extended sphere and the lack of any velocity shifts between the photospheric features and the water vapour lines, indicate that they might be formed close to the stars or in the photospheres rather than in a MOLsphere of a large extent.
From a simple analysis of the excitation balance of the different water lines, we show that, for all the stars across spectral types, they are formed at temperatures several hundred Kelvin cooler than the temperatures expected in the outer photospheres. Thus, if the H2O lines are formed in the photospheres, the temperature of the outer photosphere of red giants in general need to be cooler. The physical structure of the outer photospheres of late-type giants (log τ500< − 4) are very uncertain due to low densities and complicated structures (see e.g. Tsuji 2008, 2009). Small changes in the description of cooling in the energy equations, can lead to a change in the temperature structure in tenuous boundary layers where the heat capacity per volume is small.
Non-LTE treatment of either atomic, molecular, and/or continuous opacities might be necessary. Non-LTE effects in atoms, such as suggested by Short & Hauschildt (2003), may provide an explanation to a cooler temperature structure. Other non-LTE effects, which might be important, are those in important molecular opacities affecting the energy balance in the outer boundary layers. Examples are strong water and even CO lines which sample these layers (Lambert et al. 2013a). Non-LTE level populations will directly affect the source function and line opacities, and could also offer a viable explanation for the strong water line absorption. Inhomogeneties as such are also a source of cooler regions.
The formation of the water lines is still a mystery, but with the high-resolution spectra, we have now gathered empirical facts of the nature of the water lines, adding new constraints to the emerging picture of the outer atmospheres of red giants and that will help solving this issue in the future. We note that recently, Sloan et al. (2014) showed that the mid-IR bands of SiO and OH are stronger than expected for K giants too, based on Spitzer/IRS spectra. They might thus be probing the same phenomenon described here.
Online material
Equivalent widths of water lines in mÅ as observed and the equivalent widths from synthetic spectra for the stars calculated for standard marcs models.
Assuming that there is no specific selection of only H2O and CO in the MOLspheres, but that there is simultaneously hydrogen and other molecules, like OH, available. In the MOLsphere realisations of Ryde et al. (2006b), the continuous opacity is due to Hff and H , which is very small. The continuum from the MOLsphere is therefore expected to be very optically thin, i.e. transparent.
, which is very small. The continuum from the MOLsphere is therefore expected to be very optically thin, i.e. transparent.
Mg II h/k emission fluxes are reported for all these stars in Pérez Martínez et al. (2011).
Acknowledgments
The referee Dr. Greg Sloan is warmly thanked for a very constructive and careful referee’s report that improved the paper. N.R. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation, and acknowledges support from the Swedish Research Council, VR (project number 621-2008-4245), Funds from Kungl. Fysiografiska Sällskapet i Lund (Stiftelsen Walter Gyllenbergs fond and Märta och Erik Holmbergs donation), and financial support from the Swedish Karl Trygger’s foundation under grants CTS 12:408 and 13:388 and its investment for science and astrophysics. Moreover, we thank the French National Agency for Research (ANR) through programme number ANR-06-BLAN-0105, and from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. This publication made use of the SIMBAD database, operated at CDS, Strasbourg, France, NASA’s Astrophysics Data System, and the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
References
- Arroyo-Torres, B., Wittkowski, M., Marcaide, J. M., & Hauschildt, P. H. 2013, A&A, 554, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arroyo-Torres, B., Martí-Vidal, I., Marcaide, J. M., et al. 2014, A&A, 566, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayres, T. R., & Linsky, J. L. 1975, ApJ, 201, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Baumüller, D., & Gehren, T. 1996, A&A, 307, 961 [NASA ADS] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brault, J., & Noyes, R. 1983, ApJ, 269, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 253, 567 [NASA ADS] [Google Scholar]
- Chang, E. S. 1984, J. Phys. B At. Molec. Phys., 17, L11 [Google Scholar]
- Chang, E. S., & Noyes, R. W. 1983, ApJ, 275, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Chiavassa, A., Plez, B., Josselin, E., & Freytag, B. 2009, A&A, 506, 1351 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiavassa, A., Collet, R., Casagrande, L., & Asplund, M. 2010a, A&A, 524, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Haubois, X., Young, J. S., et al. 2010b, A&A, 515, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, M., Carbon, D. F., Welch, W. J., et al. 2005, AJ, 129, 2836 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruzalèbes, P., Jorissen, A., Rabbia, Y., et al. 2013, MNRAS, 434, 437 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Vandenbussche, B., Waelkens, C., et al. 2003, A&A, 400, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehaes, S., Bauwens, E., Decin, L., et al. 2011, A&A, 533, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeWitt, C. N., Richter, M., Kulas, K., et al. 2014, in AAS Meet. Abstr., 224, 418.04 [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Steffen, M., et al. 2013, A&A, 559, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farzone, M., Ryde, N., Harper, G. M., et al. 2013, in EAS Pub. Ser. 60, eds. P. Kervella, T. Le Bertre, & G. Perrin, 155 [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Dalcanton, J., Williams, B., et al. 2008, PASP, 120, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Goldman, A., Schoenfeld, W., Goorvitch, D., et al. 1998, JQSRT, 59, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jennings, D. E., & Sada, P. V. 1998, Science, 279, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Joint Iras Science Working Group 1994, VizieR Online Data Catalog: II/125 [Google Scholar]
- Jönsson, H., Ryde, N., Harper, G. M., Richter, M. J., & Hinkle, K. H. 2014, ApJ, 789, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Koleva, M., & Vazdekis, A. 2012, A&A, 538, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacy, J. H., Richter, M. J., Greathouse, T. K., Jaffe, D. T., & Zhu, Q. 2002, PASP, 114, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, J., Josselin, E., Ryde, N., & Faure, A. 2013a, A&A, submitted [Google Scholar]
- Lambert, J., Josselin, E., Ryde, N., & Faure, A. 2013b, in EAS Pub. Ser., 60, eds. P. Kervella, T. Le Bertre, & G. Perrin, 111 [Google Scholar]
- Leep, E. M., Wallerstein, G., & Oke, J. B. 1987, AJ, 93, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., & Kučinskas, A. 2012, A&A, 547, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallik, S. V. 1998, A&A, 338, 623 [NASA ADS] [Google Scholar]
- McWilliam, A. 1990, ApJSS, 74, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Kervella, P., Barban, C., et al. 2010, A&A, 517, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Ohnaka, K. 2004, A&A, 421, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K. 2013, A&A, 553, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Schertl, D., et al. 2012, A&A, 537, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Schertl, D., et al. 2013, A&A, 555, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Partridge, H., & Schwenke, D. 1997, J. Chem. Phys., 106, 4618 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez Martínez, M. I., Schröder, K.-P., & Cuntz, M. 2011, MNRAS, 414, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, G., Ridgway, S. T., Coudé du Foresto, V., et al. 2004a, A&A, 418, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Ridgway, S. T., Mennesson, B., et al. 2004b, A&A, 426, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Verhoelst, T., Ridgway, S. T., et al. 2007, A&A, 474, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polyansky, O. L., Busler, J. R., Guo, B., Zhang, K., & Bernath, P. F. 1996, J. Mol. Spectr., 176, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Polyansky, O. L., Tennyson, J., & Bernath, P. F. 1997a, J. Mol. Spectr., 186, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Polyansky, O. L., Zobov, N. F., Viti, S., et al. 1997b, J. Mol. Spectr., 186, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. D., Sloan, G. C., & Kraemer, K. E. 2002, ApJ, 565, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Allen de Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres (Utrecht University) [Google Scholar]
- Ryde, N., & Richter, M. J. 2004, ApJ, 611, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Lambert, D. L., Richter, M. J., & Lacy, J. H. 2002, ApJ, 580, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Lambert, D. L., Richter, M. J., Lacy, J. H., & Greathouse, T. K. 2003a, in ASP Conf. Ser. 293, 3D Stellar Evolution, eds. S. Turcotte, S. C. Keller, & R. M. Cavallo, 214 [Google Scholar]
- Ryde, N., Lambert, D. L., Richter, M. J., Lacy, J. H., & Greathouse, T. K. 2003b, in 3D Stellar Evolution, ASP Conf. Ser., 293, 214 [Google Scholar]
- Ryde, N., Korn, A. J., Richter, M. J., & Ryde, F. 2004, ApJ, 617, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Harper, G. M., Richter, M. J., Greathouse, T. K., & Lacy, J. H. 2006a, ApJ, 637, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Richter, M. J., Harper, G. M., Eriksson, K., & Lambert, D. L. 2006b, ApJ, 645, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Short, C. I., & Hauschildt, P. H. 2003, ApJ, 596, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Herter, T. L., Charmandaris, V., et al. 2014, AJ, in press [arXiv:1408.5922] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1985, ApJ, 294, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, A&A, 480, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Ryde, N., Harper, G. M., Kruger, A., & Richter, M. J. 2008, A&A, 486, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
- Tsuji, T. 1985, in Cool Stars with Excesses of Heavy Elements, eds. M. Jaschek, & P. C. Keenan, ASSL, 114, 295 [Google Scholar]
- Tsuji, T. 2000, ApJ, 538, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2001, A&A, 376, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuji, T. 2003, in Exploiting the ISO Data Archive. Infrared Astronomy in the Internet Age, ESA SP, 511, 93 [NASA ADS] [Google Scholar]
- Tsuji, T. 2006, ApJ, 645, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2008, A&A, 489, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuji, T. 2009, A&A, 504, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuji, T., Ohnaka, K., Aoki, W., & Yamamura, I. 1997, A&A, 320, L1 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Malderen, R., Decin, L., Kester, D., et al. 2004, A&A, 414, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhoelst, T., Decin, L., van Malderen, R., et al. 2006, A&A, 447, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiedemann, G., Ayres, T. R., Jennings, D. E., & Saar, S. H. 1994, ApJ, 423, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Hauschildt, P. H., Arroyo-Torres, B., & Marcaide, J. M. 2012, A&A, 540, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamamura, I., de Jong, T., & Cami, J. 1999, A&A, 348, L55 [NASA ADS] [Google Scholar]
All Tables
K, N magnitudes, parallaxes, distances, and observed signal-to-noise ratios (per spectral pixel) of the programme stars.
Fundamental stellar parameters which are used when generating model atmospheres for our stars.
Molecular data of the most prominent H2O lines in the 808−822 cm-1 region (λair = 12.162−12.373 μm), partly from Ryde et al. (2002) data.
Photospheric emission lines with line identifications from Chang & Noyes (1983); Chang (1984); Brault & Noyes (1983); Ryde et al. (2004); Sundqvist et al. (2008).
Equivalent widths in mÅ of the photospheric emission lines identified with their wavenumber in cm-1.
Velocity offsets, and standard deviations of the mean when there are several lines, in km s-1 of the water, OH, and Mg lines relative to the HF line, are shown in Cols. 2–4, respectively.
Equivalent widths of water lines in mÅ as observed and the equivalent widths from synthetic spectra for the stars calculated for standard marcs models.
All Figures
 |
Fig. 1 Un-normalised spectrum of β Peg around 817.0 cm-1. One full order and parts of two neighbouring orders on either side are presented. Three distinct water lines can be seen in the middle order. The non-linear form of the blaze function is indicated by the dashed line, which is a fifth order Legendre polynomial used to fit the continuum. |
| In the text | |
 |
Fig. 2 Hertzsrpung-Russell diagram presenting the surface gravities (log g) vs. the effective temperatures (Teff) for the stars investigated in this paper (shown with plus signs). We have also indicated, with triangles, the supergiants and α Boo, that have been investigated at high spectral resolution earlier in the literature (Jennings & Sada 1998; Ryde et al. 2002, 2006a,b). |
| In the text | |
 |
Fig. 3 Observations of the five coolest stars. The observed spectra are shown with black lines and the synthetic spectra with red lines. The blue ticks above the spectra indicate spectral features of H2O whereas green marks OH(ν = 3 − 3) lines. Dashed lines mark the spectral features of interest which are ultimately used in the calculation of the formation region temperatures. In addition, one emission feature in the form of neutral Mg is visible at 818.1 cm-1, and the HF line is also marked. The lack of observational data between the orders of the spectrometer, is indicated by the vertical solid black lines. |
| In the text | |
 |
Fig. 4 Observations of the five warmest stars. The observed spectra are shown with black lines and the synthetic spectra with red lines. See also figure caption of Fig. 3. |
| In the text | |
 |
Fig. 5 Normalised spectra shifted with respect to each other showing emission lines from Si, Al, Ca, and Mg, which are marked. Two OH lines in absorption are also indicated along with one H2O line in β Peg at 818.1 cm-1. |
| In the text | |
 |
Fig. 6 Temperature profile from a MARCS model atmosphere with parameters relevant for α Boo. The (red) horizontal dashed line indicates the expected water line formation temperature, assuming LTE. The (blue) full line indicates the average formation temperature computed from Eq. (5) (the dotted lines indicate the full range of temperatures). |
| In the text | |
 |
Fig. 7 Absorption lines of H2O and HF calculated based on a non-modified Arcturus model atmosphere (black spectrum) and based on a semiempirical model constructed to fit observed water lines with cooler outer regions (red spectrum), see Ryde et al. (2002). The HF line is formed deeper in the atmosphere and is therefore not affected by the cooler outer parts. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


