| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423731 | |
| Published online | 04 December 2014 | |
Large-scale simulations of solar type III radio bursts: flux density, drift rate, duration, and bandwidth
1
Centre for Fusion, Space and Astrophysics, Department of Physics,
University of Warwick, CV4 7AL, UK
e-mail:
h.ratcliffe@warwick.ac.uk
2
SUPA School of Physics & Astronomy, University of Glasgow, G12 8QQ,
UK
Received: 28 February 2014
Accepted: 22 October 2014
Non-thermal electrons accelerated in the solar corona can produce intense coherent radio emission, known as solar type III radio bursts. This intense radio emission is often observed from hundreds of MHz in the corona down to the tens of kHz range in interplanetary space. It involves a chain of physical processes from the generation of Langmuir waves to non-linear processes of wave-wave interaction. We develop a self-consistent model to calculate radio emission from a non-thermal electron population over a large frequency range, including the effects of electron transport, Langmuir wave-electron interaction, the evolution of Langmuir waves due to non-linear wave-wave interactions, Langmuir wave conversion into electromagnetic emission, and finally escape of the electromagnetic waves. For the first time we simulate escaping radio emission over a broad frequency range from 500 MHz down to a few MHz and infer key properties of the radio emission observed: the onset (starting) frequency, identification as fundamental or harmonic emission, peak flux density, instantaneous frequency bandwidth, and timescales for rise and decay. By comparing these large-scale simulations with the observations, we can identify the processes governing the major type III solar radio burst characteristics.
Key words: Sun: particle emission / Sun: radio radiation / Sun: flares
© ESO, 2014
1. Introduction
Type III solar radio bursts, easily identified by their high brightness temperatures and rapid frequency drift, are a common signature of fast electron beams in the solar corona. It is known that they arise from accelerated electrons propagating in the decreasing density plasma of the corona and solar wind, which generate Langmuir waves and subsequently electromagnetic emission at the plasma frequency and its harmonics. The frequency of these bursts therefore traces the local plasma frequency, and so information about the electron beam velocity can be inferred if the density profile is known. However, because of the complicated nature of particle transport and emission, it is not straightforward to recover any additional information about the electrons. Nevertheless, type III observations have the potential to offer unique information supplementary to that from e.g. hard X-rays (HXR; e.g. Dennis 1988; Holman et al. 2011, as a review) and gyrosynchrotron radio emission observations (e.g. Gary & Hurford 1990; Melnikov et al. 2002; Fleishman et al. 2013), in order to understand electron acceleration in the corona.
The plasma emission mechanism, which we assume is responsible for type III burst production, was first proposed by Ginzburg & Zhelezniakov (1958) and is summarised in the books by Melrose (1980); Tsytovich (1995), and reviews by Dulk (1985); Bastian et al. (1998); Nindos et al. (2008); Melrose (2009); Reid & Ratcliffe (2014). Large amounts of work have been invested in the problem yet the exact details of type III production are still not fully understood. The mechanism involves multiple steps, several of which are non-linear, and these must all be considered self-consistently. Broadly, one needs to take into account four elements leading to escaping radio emission. First, the spatially non-uniform electron beam propagates through the coronal and solar wind plasma and generates Langmuir waves; second, the Langmuir waves evolve both spectrally and in space; third, electromagnetic waves are generated by the Langmuir waves; and finally, this radio emission escapes the source and reaches the observer.
These main processes operate on similar scales, requiring a self-consistent treatment, and so numerical simulations are essential in order to reproduce the basic burst properties, such as drift rate, exciter speed, frequency bandwidth, and rise/decay times. Specifically, the consideration of electron transport including the generation and absorption of Langmuir waves requires a numerical treatment to achieve self-consistency. Langmuir waves generated by the beam electrons are subsequently reabsorbed by the beam (e.g. Zaitsev et al. 1972; Takakura & Shibahashi 1976; Magelssen & Smith 1977; Mel’Nik et al. 1999), which allows the electrons to propagate over more than 1 AU accompanied by a high level of plasma waves. The presence of plasma inhomogeneity substantially complicates the evolution of these Langmuir waves (e.g. Smith & Sime 1979; Goldman & Dubois 1982; Melrose 1987; Yoon et al. 2005; Daldorff et al. 2011) as can be seen in numerical simulations (e.g. Kontar 2001b; Ledenev et al. 2004; Ratcliffe et al. 2012). The overall level of Langmuir waves induced by the beam is decreased but the scattering of Langmuir waves to lower wavenumber can lead to acceleration of electrons.
Large-scale 1D numerical simulations of electron transport, including the effects of Langmuir wave generation, have recently been developed (Kontar & Reid 2009; Reid & Kontar 2010, 2013), and show significant effects on the electron spectra below ~50 keV observed at 1 AU. Specifically, an injected power-law spectrum develops into a broken power-law, and the low energy electrons arrive sooner than their high-energy counterparts, both of which are due to Langmuir wave evolution in the decreasing density plasma of the corona and heliosphere. Simulations of type III burst production have also recently been developed for rather narrow frequency range by e.g. Li et al. (2006, 2008, 2011); Li & Cairns (2013), and can reproduce some features of observed type III dynamic spectra.
In this paper we present type III burst simulations based on the description of electron propagation and Langmuir wave evolution in inhomogeneous plasma of Reid & Kontar (2013). We add an angle-averaged model for plasma radio emission, described in Ratcliffe & Kontar (2014), in order to simulate the type III burst generation process from electrons to radio waves. We calculate the duration and the frequency bandwidth of emission over a wide frequency range. The frequency drift of the emission is used to infer the velocity of the emission source, which may then be compared to the true velocity of the generating electrons. We discuss the physical origins of these major characteristics, allowing clarification of the details of the standard model of emission and ruling out some suggestions as to dominant effects. Finally, we also consider the characteristics of the fast-electron injection in the corona, specifically the injection timescale, and the effects this has on the observed emission.
2. Simulation model
2.1. Electron-Langmuir wave interactions
We start from the simulations of beam propagation and Langmuir wave generation described in Reid & Kontar (2013), which treat the propagation and evolution of a fast electron population streaming from the Sun outwards through the expanding corona. The model assumes that the dynamics of electrons and Langmuir waves are 1D along the direction of ambient magnetic field. Because the magnetic field expands with distance (spherically symmetrically) the electron beam has a cross-sectional area increasing with distance. The whole system has azimuthal symmetry around the direction of ambient magnetic field. The quasi-linear equations describing the electron and Langmuir wave evolution are based on those in Drummond & Pines (1962); Vedenov et al. (1962), but modified to account for additional processes described below, and are 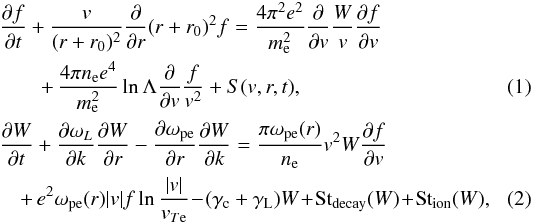 where f(v,r,t) is the electron beam distribution function, and W(k,r,t) the spectral energy density of Langmuir waves, with k their wavenumber. S(v,r,t) is the electron injection rate discussed in Sect. 3.
where f(v,r,t) is the electron beam distribution function, and W(k,r,t) the spectral energy density of Langmuir waves, with k their wavenumber. S(v,r,t) is the electron injection rate discussed in Sect. 3.
The first two terms on the RHS of Eqs. (1) and (2) describe the interaction of Langmuir waves and electrons. As in Reid & Kontar (2013), the electron transport assumes radial expansion of the beam due to expansion of magnetic field in the corona (described by the second term on the RHS of Eq. (1)). The ambient magnetic field is assumed to expand in a cone, with opening angle 34° determined by the constant r0 = 3.4 × 109 cm in the second term on the LHS of Eq. (1) (Reid & Kontar 2013). The cross-sectional area of the electron beam therefore expands, and the electron density correspondingly decreases. As the Langmuir wave group velocity is a fraction of the electron thermal speed, the Langmuir waves are generated/absorbed locally and the role of magnetic flux expansion on Langmuir waves is negligible. The electrons and Langmuir waves interact resonantly, ωpe = kv, so that the electrons with velocity v interact with Langmuir waves of equal phase velocity ωpe/k. The second term on the RHS of Eq. (1) also accounts for the (total) electron energy losses in plasma.
The electron distribution function f(v,r,t) and the spectral energy density of Langmuir waves W(k,r,t) are one-dimensional functions, with positive direction of v and k corresponding to the direction away from the Sun. In the following sections we also distinguish so-called forwards (positive k) and backwards Langmuir waves, that is those with a component of their wavevector away from the Sun, and those towards the Sun.
A small part of the energy lost by electrons to the plasma (second term on the RHS of Eq. (1)) goes to generation of Langmuir waves near ωpe. This so called spontaneous Langmuir wave generation (the second term on the RHS of Eq. (2)), is treated as in e.g. Zheleznyakov & Zaitsev (1970a); Takakura & Shibahashi (1976); Kontar et al. (2012). The third term on the LHS of Eq. (2) describes the change in wavenumber of Langmuir waves due to density gradients in the background plasma. The third term on the RHS describes collisional absorption of Langmuir waves by background plasma (Lifshitz & Pitaevskii 1981) with coefficient 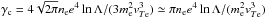 with the Coulomb logarithm lnΛ taken as 20 for the solar corona. The background plasma electrons also absorb Langmuir waves due to Landau damping in Maxwellian plasma with coefficient
with the Coulomb logarithm lnΛ taken as 20 for the solar corona. The background plasma electrons also absorb Langmuir waves due to Landau damping in Maxwellian plasma with coefficient 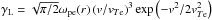 given by third RHS term of Eq. (2), where
given by third RHS term of Eq. (2), where 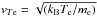 . This latter term is included because we do not explicitly simulate the thermal plasma electrons below approximately 3vTe and their effect is therefore not accounted for by the first RHS terms. Finally, we have two source terms, denoted St(W) and describing the scattering of Langmuir waves by plasma ions and their interactions with ion-sound waves respectively, given in the next section.
. This latter term is included because we do not explicitly simulate the thermal plasma electrons below approximately 3vTe and their effect is therefore not accounted for by the first RHS terms. Finally, we have two source terms, denoted St(W) and describing the scattering of Langmuir waves by plasma ions and their interactions with ion-sound waves respectively, given in the next section.
2.2. Non-linear Langmuir and ion-sound wave evolution
The two terms StIon and StDecay in Eq. (2) describe the scattering off ions (non-linear Landau damping) L + i ⇄ L′ + i′ and decay of Langmuir waves L ⇄ L′ + s, where i,i′ denote an initial and scattered plasma ion and s is an ion-sound wave. The general expressions describing these processes (e.g. Melrose 1980; Tsytovich 1995) have been written under the same one-dimensional approximation as in e.g. Kontar & Pécseli (2002), which is that the fast-electron generated Langmuir waves propagate approximately parallel to the generating electrons and therefore the ambient magnetic field. In this case, both of these non-linear processes produce back-scattered (negative wavenumber) Langmuir waves, approximately antiparallel to the initial Langmuir waves. The ion-sound waves produced are also approximately beam parallel or anti-parallel, and the dynamics remain 1D. Hereafter, we omit the explicit time and space dependence of the spectral energy densities for clarity of notation. Hence the evolution of Langmuir wave spectrum due to scattering by ions is described by ![\begin{eqnarray} \label{eqn:LIonA} {\rm St}_{\rm ion}(W(k))&=&\int {\rm d}k_{L'} \frac{\alpha_{\rm ion}}{|k-k_{L'}|} \exp{\left(-\frac{(\omega_{L}-\omega_{L'})^2}{2|k-k_{L'}|^2 {v}_{T{\rm i}}^2}\right)} \notag\\ &&\times \left[\frac{1}{k_{\rm B}T_{\rm i}}\frac{\omega_{L'}-\omega_{L}}{\omega_{L}}W(k_{L'})W(k)\right], \end{eqnarray}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq25.png) (3)where k,kL′,ωL,ωL′ are the wavenumber and frequency of the initial and scattered Langmuir waves, and
(3)where k,kL′,ωL,ωL′ are the wavenumber and frequency of the initial and scattered Langmuir waves, and 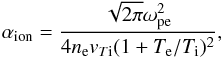 (4)with \begin{lxirformule}${v}_{T{\rm i}}=\sqrt{k_{\rm B} T_{\rm i}/M_{\rm i}}$\end{lxirformule} the ion thermal speed, and Mi the mass of a plasma ion. It is evident from the exponential factor that the scattering is strongest for ωL ≃ ωL′ and kL′ ≃ −k, i.e. for backscattering of the waves. The resulting momentum change for the Langmuir wave is absorbed by the ions which we assume to have a Maxwellian distribution at temperature Ti. This momentum transfer is small, so the deviation of the ion distribution from thermal can be neglected (Tsytovich 1995).
(4)with \begin{lxirformule}${v}_{T{\rm i}}=\sqrt{k_{\rm B} T_{\rm i}/M_{\rm i}}$\end{lxirformule} the ion thermal speed, and Mi the mass of a plasma ion. It is evident from the exponential factor that the scattering is strongest for ωL ≃ ωL′ and kL′ ≃ −k, i.e. for backscattering of the waves. The resulting momentum change for the Langmuir wave is absorbed by the ions which we assume to have a Maxwellian distribution at temperature Ti. This momentum transfer is small, so the deviation of the ion distribution from thermal can be neglected (Tsytovich 1995).
The second source term describes Langmuir wave decay, and is given by ![\begin{eqnarray} \label{eqn:4ql_sSrc} &&{\rm St}_{\rm decay}(W(k))=\alpha_S\omega_{k} \int {\rm d}k_S \omega_{k_S}^S \notag \\ && \times\Biggl[ \left( \frac{W(k_{L})}{\omega^L_{k_{L}}}\frac{W_S(k_S)}{\omega^S_{k_S}}\!-\! \frac{W(k)}{\omega^L_k}\left(\frac{W(k_{L})}{\omega^L_{k_{L}}}\!+\! \frac{W_S(k_S)}{\omega^S_{k_S}}\right)\right)\delta (\omega^L_{k}\!-\!\omega^L_{k_{L}}\!-\!\omega^S_{k_S})\Biggr. \notag \\ && \qquad -\left. \left( \frac{W(k_{L'})}{\omega^L_{k_{L'}}}\frac{W_S(k_S)}{\omega^S_{k_S}}- \frac{W(k)}{\omega^L_k}\left(\frac{W(k_{L'})}{\omega^L_{k_{L'}}}- \frac{W_S(k_S)}{\omega^S_{k_s}}\right)\right)\right. \notag \\ && \qquad\Biggl.\times\delta\left(\omega^L_{k}-\omega^L_{k_{L'}}+\omega^S_{k_S}\right) \Biggr], \end{eqnarray}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq32.png) (5)where
(5)where 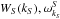 are the spectral energy density and frequency of ion-sound waves, given by
are the spectral energy density and frequency of ion-sound waves, given by 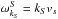 with
with 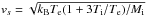 the sound speed, and the constant is
the sound speed, and the constant is 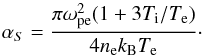 (6)For a given initial Langmuir wavenumber, k, we have two possible processes, namely L → L′ + s and L + s → L′. The wavenumbers of the resulting Langmuir wave, kL,kL′, respectively, and the participating ion-sound wave, kS, are found from simultaneous solution of the equations of energy conservation (encoded by the delta functions in Eq. (5)), and momentum conservation, given by kL = k − kS and kL′ = k + kS for the two processes. For example, for the process L → L′ + s we find kL ≃ −k, and kS ≃ 2k, and the initial Langmuir wave is backscattered. More precisely, we have kL = −k + Δk with the small increment
(6)For a given initial Langmuir wavenumber, k, we have two possible processes, namely L → L′ + s and L + s → L′. The wavenumbers of the resulting Langmuir wave, kL,kL′, respectively, and the participating ion-sound wave, kS, are found from simultaneous solution of the equations of energy conservation (encoded by the delta functions in Eq. (5)), and momentum conservation, given by kL = k − kS and kL′ = k + kS for the two processes. For example, for the process L → L′ + s we find kL ≃ −k, and kS ≃ 2k, and the initial Langmuir wave is backscattered. More precisely, we have kL = −k + Δk with the small increment 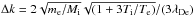 . Thus repeated scatterings tend to accumulate Langmuir waves at small wavenumbers.
. Thus repeated scatterings tend to accumulate Langmuir waves at small wavenumbers.
Similarly, the evolution of the ion-sound wave distribution is given by 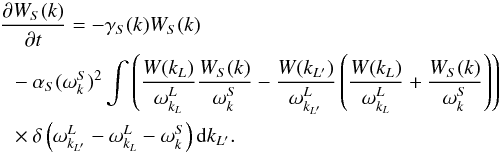 (7)The second term here is analogous to Eq. (5), describing the interaction of an ion-sound wave at wavenumber k with a Langmuir wave at wavenumber kL, producing a Langmuir wave at wavenumber kL′. Again, these participating wavenumbers are found from simultaneous solution of energy (frequency) and momentum (wavenumber) conservation. The first term is Landau damping of the waves, with coefficient
(7)The second term here is analogous to Eq. (5), describing the interaction of an ion-sound wave at wavenumber k with a Langmuir wave at wavenumber kL, producing a Langmuir wave at wavenumber kL′. Again, these participating wavenumbers are found from simultaneous solution of energy (frequency) and momentum (wavenumber) conservation. The first term is Landau damping of the waves, with coefficient ![\begin{equation} \gamma_S(k)=\sqrt{\frac{\pi}{2}}\omega^S_k\left[\frac{{v}_s}{{v}_{T{\rm e}}}+\left(\frac{{v}_s}{{v}_{T{\rm i}}}\right)^3\exp\left[- \left(\frac{{v}_s}{2{v}_{T{\rm i}} }\right)^2 \right]\right]\cdot \end{equation}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq50.png) (8)
(8)
2.3. Electromagnetic emission
Electromagnetic emission is described in terms of its brightness temperature, TT, which is defined from the Rayleigh-Jeans law for the radiation intensity as a function of frequency f = ω/ (2π) by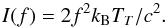 (9)As stated above, the electrons, Langmuir waves, and ion-sound waves are treated one-dimensionally, along the ambient magnetic field. Although the electromagnetic emission pattern produced from Langmuir waves is azimuthally symmetric around the beam direction, it is not aligned along the beam and requires a different approach. Radio emission near the plasma frequency has a dipole pattern with a peak at polar angle π/ 2 to the direction of the beam, while electromagnetic waves produced near double the plasma frequency (the harmonic) peak at π/ 4 and 3π/ 4 radians (Zheleznyakov & Zaitsev 1970b). Because our model assumes azimuthal symmetry around the beam direction, we do not distinguish the lobes at + π/ 2 and at −π/ 2, and similarly those at ± π/ 4 and ± 3π/ 4.Here, we use an angle-averaged model as described in previous work (Ratcliffe & Kontar 2014), by averaging the emission probability over angles using the assumed small angular spread of the Langmuir waves, and including the constraints on the wavevectors involved as described in the following sections. The resulting angle-averaged electromagnetic spectral energy density depends only on the magnitude of the wavevector, and so the derived brightness temperature is also angle independent. We do not assume that the harmonic wavenumber is far smaller than the Langmuir wavenumber, as is often done in the so-called head-on approximation (Melrose & Stenhouse 1979).
(9)As stated above, the electrons, Langmuir waves, and ion-sound waves are treated one-dimensionally, along the ambient magnetic field. Although the electromagnetic emission pattern produced from Langmuir waves is azimuthally symmetric around the beam direction, it is not aligned along the beam and requires a different approach. Radio emission near the plasma frequency has a dipole pattern with a peak at polar angle π/ 2 to the direction of the beam, while electromagnetic waves produced near double the plasma frequency (the harmonic) peak at π/ 4 and 3π/ 4 radians (Zheleznyakov & Zaitsev 1970b). Because our model assumes azimuthal symmetry around the beam direction, we do not distinguish the lobes at + π/ 2 and at −π/ 2, and similarly those at ± π/ 4 and ± 3π/ 4.Here, we use an angle-averaged model as described in previous work (Ratcliffe & Kontar 2014), by averaging the emission probability over angles using the assumed small angular spread of the Langmuir waves, and including the constraints on the wavevectors involved as described in the following sections. The resulting angle-averaged electromagnetic spectral energy density depends only on the magnitude of the wavevector, and so the derived brightness temperature is also angle independent. We do not assume that the harmonic wavenumber is far smaller than the Langmuir wavenumber, as is often done in the so-called head-on approximation (Melrose & Stenhouse 1979).
For thermal radiation (free-free emission), the brightness temperature is TT = Te, where Te is the plasma temperature. From Kirchoff’s law the thermal emission rate P(k) = γdTe is related to the damping rate γd giving the thermal radiation level. Thus, from the bremsstrahlung damping rate, 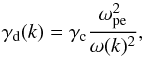 (10)one can find the thermal emission rate.
(10)one can find the thermal emission rate.
2.4. Escape of electromagnetic emission
To treat the propagation of radiation between the source and observer, we assume the simple case of travel approximately along the ambient magnetic field, and thus along the plasma density gradient. At these distances (<10Rsun) this is approximately parallel to the plasma density gradient (e.g. Parker 1958). The equation describing electromagnetic radiation transfer in inhomogeneous, magnetised plasma along the direction of the magnetic field and inhomogeneity is (Zheleznyakov 1969, Eq. (10)) 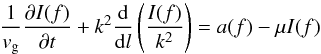 (11)where l is the path length along a ray, I(f) is the spectral intensity, vg = ∂ω/∂k is the group velocity of electromagnetic waves with the dispersion relation
(11)where l is the path length along a ray, I(f) is the spectral intensity, vg = ∂ω/∂k is the group velocity of electromagnetic waves with the dispersion relation 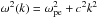 . a(f) is the radiation source and μ is the absorption coefficient. The absorption is assumed to be due to collisions, so that μ = γd/vg. The emission a(f) includes the thermal radiation and the coherent plasma radiation by Langmuir waves (noting that the latter depends on radiation intensity I(f).)
. a(f) is the radiation source and μ is the absorption coefficient. The absorption is assumed to be due to collisions, so that μ = γd/vg. The emission a(f) includes the thermal radiation and the coherent plasma radiation by Langmuir waves (noting that the latter depends on radiation intensity I(f).)
Using the Rayleigh-Jeans law (Eq. (9)) to relate the spectral intensity and the radiation brightness temperature, and expanding d/dl (Zheleznyakov 1996, Eq. (4.28) with Eq. (4.23)), we obtain the equation for the evolution of radiation brightness temperature namely 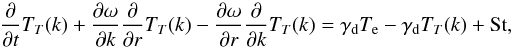 (12)where r is the direction of beam propagation, the first term on the RHS is the thermal emission rate and the second term is the collisional absorption. St are the source terms describing the production of electromagnetic waves via the non-linear processes described in the following subsections.
(12)where r is the direction of beam propagation, the first term on the RHS is the thermal emission rate and the second term is the collisional absorption. St are the source terms describing the production of electromagnetic waves via the non-linear processes described in the following subsections.
2.5. Fundamental electromagnetic source terms
The processes for emission at the fundamental are L ⇄ t ± s where L,s are Langmuir and ion-sound waves, and t is an electromagnetic (EM) wave, and L + i ⇄ t + i′, for i,i′ an initial and final plasma ion. The probability of both processes (e.g. Tsytovich 1995) has a maximum when the wavevector of the EM wave is perpendicular to the initial Langmuir wave (dipole emission peaking at π/ 2 rad).
The latter process, L + i ⇄ t + i′, is analogous to that described by Eq. (3) for the conversion of Langmuir waves into EM waves. However, the growth rate for this process is much lower than that for the ion-sound wave interaction, and for the cases considered here is expected to be negligible in comparison to this (e.g. Cairns 2000). Therefore we do not consider direct ion scattering in this work.
For EM emission by the process L ⇄ t ± s to be efficient, we require ion-sound waves to be present. These can be generated by the decay of Langmuir waves described above. It is important that these ion-sound waves, and the Langmuir waves, are not confined exactly to angles parallel to the electron beam, as the emission probability is proportional to | k × kT | for k the wavenumber of the participating ion-sound wave and kT the EM wave. We therefore assume that the beam-generated Langmuir waves have some small angular spread in wavenumber space, covering a solid angle of ΔΩ. Further assuming that this solid angle forms a cone around the beam direction, we require it has a half-angle of the order of 10 degrees for almost all waves to satisfy the kinematic conditions for interactions. For beam-generated Langmuir waves, backscattered Langmuir waves and the generated ion-sound waves, this condition is easily satisfied. For example, 2D simulations of beam-plasma relaxation (Churaev & Agapov 1980; D’Iachenko et al. 1989; Ziebell et al. 2008) suggest that the beam remains relatively narrow and the magnetic field tends to support beam-plasma interaction in 1D (Dum & Nishikawa 1994).
Further assuming the Langmuir waves are uniform within this angle, the resulting EM emission may be assumed approximately isotropic. Then using the general expressions in (e.g. Melrose 1980; Tsytovich 1995), averaging over angles and rewriting in terms of the hemisphere-averaged brightness temperature, given by 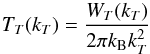 (13)for WT(kT) the EM wave spectral energy density, we obtain the expression given in Ratcliffe & Kontar (2014)
(13)for WT(kT) the EM wave spectral energy density, we obtain the expression given in Ratcliffe & Kontar (2014)![\begin{eqnarray} \label{eqn:FundS} &&{\rm St}_{\rm fund}^{\rm lts}(T_T(k))= \frac{\pi \omega_{\rm pe}^4{v}_s\left(1+\frac{3T_{\rm i}}{T_{\rm e}}\right)}{ 24 {v}_{T{\rm e}}^2n_{\rm e}T_{\rm e}} \notag \\ &&\times\! \!\int\!\! {\rm d}k_{L}\! \left\{ \left[\!\frac{W_S(k_S)}{\omega_{k_S}^S} \frac{2\pi^2}{ k_{\rm B} k_{L}^2\Delta\Omega} \frac{W_{L}({k}_{L})}{\omega_{k_{L}}^L}\!-\!\frac{T_T({k})}{\omega_{k}^T}\left( \frac{ W_S(k_S)}{\omega_{k_S}^S} \!+\! \frac{W_{L}(k_{L})}{\omega_{k_{L}}^L}\right)\right]\right. \notag \\ &&\quad \times\,\delta\left(\omega_{k_{L}}^L +\omega_{k_S}^S-\omega_{k}^T\right) \notag\\ &&~+\left.\left[\frac{W_S(k_{S'})}{\omega_{k_{S'}}^S} \frac{2\pi^2}{k_{\rm B} k_{L}^2\Delta\Omega} \frac{W_{L}({k}_{L})}{\omega_{k_{L}}^L}-\frac{T_T({k})}{\omega_{k}^T}\left( \frac{ W_S(k_{S'})}{\omega_{k_{S'}}^S} - \frac{W_{L}(k_{L})}{\omega_{k_{L}}^L}\right)\right]\right.\notag \\&&\left.\phantom{\left[\frac{W_S(k_S)}{\omega_{k_S}^S} \right]}\quad\times, \delta\left.(\omega_{k_{L}}^L -\omega_{k_{S'}}^S-\omega_{k}^T\right)\right\}, \end{eqnarray}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq89.png) (14)where the participating wavenumbers are obtained from energy and momentum conservation (equivalent to frequency and wavenumber conservation). However, in this case the momentum conservation condition must be obtained from the 3D description of the process. Using our assumption that the EM emission occurs approximately perpendicular to the initial Langmuir wave, the wavenumbers kL,kS,kT form a right-triangle and thus we find that
(14)where the participating wavenumbers are obtained from energy and momentum conservation (equivalent to frequency and wavenumber conservation). However, in this case the momentum conservation condition must be obtained from the 3D description of the process. Using our assumption that the EM emission occurs approximately perpendicular to the initial Langmuir wave, the wavenumbers kL,kS,kT form a right-triangle and thus we find that 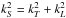 .
.
2.6. Harmonic electromagnetic emission source terms
Emission at the harmonic of the plasma frequency occurs due to the coalescence of two Langmuir waves, L + L′ ⇄ t. The probability peaks when the angle between initial Langmuir and final EM wavevectors is π/ 4 or 3π/ 4, noting that the whole problem has azimuthal symmetry around the beam direction. However, the probability also depends on the magnitudes of the wavenumbers k1,k2 for the participating Langmuir waves, and kT for the EM wave. Rather than assume head-on coalescence, we instead assume that emission occurs primarily at the angle where the probability is maximised, which is close to a π/ 4 or 3π/ 4 angle between the initial Langmuir and final EM wavevectors. Using this assumption we use the wavevector and frequency matching to calculate an emission probability.
Writing k1,k2 for the wavenumbers of the two coalescing Langmuir waves, ωk1,ωk2 the corresponding Langmuir wave frequencies, and 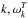 the wavenumber and frequency of the EM wave, we solve the energy and momentum conservation equations, given by ωk1 + ωk2 = ωkT and k1 + k2 = k, we then obtain
the wavenumber and frequency of the EM wave, we solve the energy and momentum conservation equations, given by ωk1 + ωk2 = ωkT and k1 + k2 = k, we then obtain 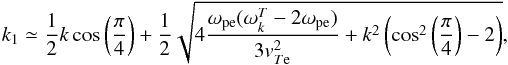 (15)and
(15)and 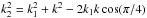 .
.
We then average the emission probability, given by the general expressions of e.g. Melrose (1980); Tsytovich (1995), over angles assuming the same geometry, and convert to brightness temperature using Eq. (13). The resulting source term for harmonic emission is, as in previous work (Ratcliffe & Kontar 2014): ![\begin{eqnarray} &&\mathrm{St}_{\rm harm}^{ll't}(T_T(k)) =\omega_{k}^T \frac{\pi \omega_{\rm pe}^2}{48 m_{\rm e} n_{\rm e} {v}_{T{\rm e}}^2} \int {\rm d} k_1 \frac{\left(k_2^2-k_1^2\right)^2}{4 k_2^2}\notag \\ && \quad \times \, \left[\frac{2\pi^2}{k_{\rm B} k_2^2 \Delta\Omega}\frac{W(k_1)}{\omega_{k_1^L}}\frac{W(k_2)}{\omega_{k_2}^L}-\frac{T_T(k)}{\omega_{k}^T} \left(\frac{W(k_1)}{\omega_{k_1}^L}+\frac{W(k_2)}{\omega_{k_2}^L}\right)\right] \notag \\&&\quad\times\, \delta\left(\omega_{k_1}+\omega_{k_2}-\omega_{k}^T\right). \end{eqnarray}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq101.png) (16)
(16)
2.7. Observed radiation fluxes
Because Langmuir waves are present over a range of wavenumbers, the emission at a given frequency arises from a range of spatial locations. Since the waves propagate at constant frequency, when they travel into lower density plasma their wavenumber increases. After a short distance, the wavenumber becomes too large to satisfy the momentum and energy matching conditions for interaction with Langmuir waves. We model the propagation of radiation using Eq. (11) through this interaction region.
After the radiation can no longer interact with Langmuir waves, we consider it as propagating directly from source to observer, along the ambient magnetic field, without angular scattering. Absorption due to inverse bremsstrahlung is included using Eq. (10), as this can be significant at the highest frequencies in the simulation. The resulting optical depth is given below. We assume the ambient magnetic field expands in a cone, and thus the cross sectional area of the electron beam expands similarly. We assume this cross section is circular and that emission is produced equally over the entire area. Thus we model the emission source as a circle subtending a solid angle πθ2 where θ is its half-angular size as seen by the remote observer. Furthermore, we currently assume the entire source is visible to the remote observer, and that emission directionality is unimportant.
The dependence of EM group velocity on wavenumber
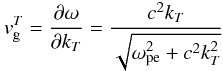 produces time delays between the arrival of the fundamental and harmonic components, and between radiation from different locations. These delays between the source at rSrc and observer at rObs are accounted for by integrating group velocity over distance
produces time delays between the arrival of the fundamental and harmonic components, and between radiation from different locations. These delays between the source at rSrc and observer at rObs are accounted for by integrating group velocity over distance
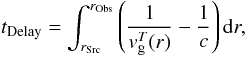 and are included in the dynamic spectra shown below.
and are included in the dynamic spectra shown below.
Changing Eq. (9) from intensity to flux as a function of frequency, defined by F(f) = I(f)πθ2, where θ is the source angular size, the observed flux density at the Earth for radiation with in-source brightness temperature TT is 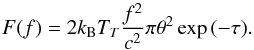 (17)Here τ is the optical depth for propagation from source to observer due to inverse bremsstrahlung absorption. We calculate this assuming a locally exponential background density profile with scale height H, i.e. ne(r) ∝ exp(−(r − rSrc) /H). The actual density used in the code is given by Eq. (25), but the locally exponential model suffices for this simple optical depth calculation. We obtain
(17)Here τ is the optical depth for propagation from source to observer due to inverse bremsstrahlung absorption. We calculate this assuming a locally exponential background density profile with scale height H, i.e. ne(r) ∝ exp(−(r − rSrc) /H). The actual density used in the code is given by Eq. (25), but the locally exponential model suffices for this simple optical depth calculation. We obtain 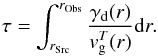 (18)Integration of Eq. (10) gives
(18)Integration of Eq. (10) gives ![\begin{eqnarray} \label{eqn:optDepFin} \tau&=&\sqrt{\frac{2}{\pi}}\frac{e^2 \ln\Lambda}{12 \pi^2 {v}_{T{\rm e}}^3 m_{\rm e}}\frac{H}{c} \notag\\ &&\times\left[ f_0^2 - \frac{1}{f_0}\sqrt{\left(f_0^2-f_{\rm pe}^2(0)\right)}\left(f_0^2 +0.5f_{\rm pe}^2(0) \right) \right], \end{eqnarray}](/articles/aa/full_html/2014/12/aa23731-14/aa23731-14-eq114.png) (19)where f0 is the frequency of the emission and fpe(r) the local plasma frequency at position r. In general exp(−τ) is of order unity for the frequencies considered here, although for fundamental emission near 500 MHz it falls as low as 0.1.
(19)where f0 is the frequency of the emission and fpe(r) the local plasma frequency at position r. In general exp(−τ) is of order unity for the frequencies considered here, although for fundamental emission near 500 MHz it falls as low as 0.1.
 |
Fig. 1 Dynamic spectrum of simulated type III radio burst emission (flux at 1 AU) for almost instantaneous injection of energetic electrons around 550 MHz. Differences in propagation time from the changing source position to the remote observer are included and the time axis is set such that emission from the injection region would appear at t = 0. |
3. Initial conditions
We model the injection of energetic electrons via the source term added to Eq. (1) with separate functions describing velocity, space and time dependencies 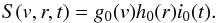 (20)Based on the simultaneous observations of energetic electrons at the Sun and near the Earth (e.g. Krucker et al. 2007) as well as the type III and X-ray emissions (e.g. Arzner & Benz 2005; Reid et al. 2011), we assume a power-law distribution in velocity
(20)Based on the simultaneous observations of energetic electrons at the Sun and near the Earth (e.g. Krucker et al. 2007) as well as the type III and X-ray emissions (e.g. Arzner & Benz 2005; Reid et al. 2011), we assume a power-law distribution in velocity 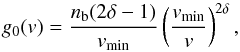 (21)where δ is the spectral index of the injected electrons in energy space (with δ = 3 for the simulations), and nb is time integrated beam number density. vmin is the minimum beam velocity which is set at 3 vTe, below which Langmuir waves are heavily Landau damped and can be safely neglected. The maximum velocity simulated is set to 2 × 1010 cm s-1 to avoid relativistic effects which are not accounted for. Because of the power-law form of the injected electron distribution, the number of electrons above this velocity is negligibly small. The injection time profile is assumed to be an asymmetric Gaussian
(21)where δ is the spectral index of the injected electrons in energy space (with δ = 3 for the simulations), and nb is time integrated beam number density. vmin is the minimum beam velocity which is set at 3 vTe, below which Langmuir waves are heavily Landau damped and can be safely neglected. The maximum velocity simulated is set to 2 × 1010 cm s-1 to avoid relativistic effects which are not accounted for. Because of the power-law form of the injected electron distribution, the number of electrons above this velocity is negligibly small. The injection time profile is assumed to be an asymmetric Gaussian 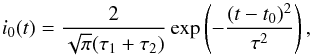 (22)with separate timescales, so that τ = τ1 during the rise at times t ≤ t0, and τ = τ2 during decay at t>t0. We set t0 = 4τ1, allowing time for the rise phase. In the simulations below we consider both almost instantaneous injection by setting τ1 = τ2 = 10-3 s, and slower injection with τ1 = 1 s and τ2 = 4 s. This value is sufficiently long to show the effects of injection on the observed emission, while being small enough that computational time is reasonable. Finally, the spatial distribution of the electron injection is also Gaussian, with
(22)with separate timescales, so that τ = τ1 during the rise at times t ≤ t0, and τ = τ2 during decay at t>t0. We set t0 = 4τ1, allowing time for the rise phase. In the simulations below we consider both almost instantaneous injection by setting τ1 = τ2 = 10-3 s, and slower injection with τ1 = 1 s and τ2 = 4 s. This value is sufficiently long to show the effects of injection on the observed emission, while being small enough that computational time is reasonable. Finally, the spatial distribution of the electron injection is also Gaussian, with 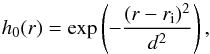 (23)where ri is the location of the injection region, and d its spatial size. We set ri = 2 × 109 cm, corresponding to a local plasma frequency of approximately 550 MHz, and d = 109 cm. The cross-sectional radius of the source in the injection region is taken as 2 × 109cm. Radial expansion of the magnetic field as the beam propagates will lead to a steadily increasing source size, giving angular sizes of 0.8′ at 432 MHz, 2.5′ at 169 MHz, and 6.3′ at 43 MHz, comparable to observed type III source sizes (e.g. McLean & Labrum 1985; Saint-Hilaire et al. 2013).
(23)where ri is the location of the injection region, and d its spatial size. We set ri = 2 × 109 cm, corresponding to a local plasma frequency of approximately 550 MHz, and d = 109 cm. The cross-sectional radius of the source in the injection region is taken as 2 × 109cm. Radial expansion of the magnetic field as the beam propagates will lead to a steadily increasing source size, giving angular sizes of 0.8′ at 432 MHz, 2.5′ at 169 MHz, and 6.3′ at 43 MHz, comparable to observed type III source sizes (e.g. McLean & Labrum 1985; Saint-Hilaire et al. 2013).
The initial Langmuir wave spectral energy density and radiation brightness temperatures are set to the thermal level 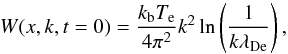 (24)with \begin{lxirformule}$\lambda_{\rm De}=1/k_{\rm De}={v}_{T{\rm e}}/\omega_{\rm pe}$\end{lxirformule} and TT = Te. The three-wave decay processes and ion-sound wave damping rapidly establish the level of ion-sound waves, and so we set the initial level of Ws to a small, non-zero value.
(24)with \begin{lxirformule}$\lambda_{\rm De}=1/k_{\rm De}={v}_{T{\rm e}}/\omega_{\rm pe}$\end{lxirformule} and TT = Te. The three-wave decay processes and ion-sound wave damping rapidly establish the level of ion-sound waves, and so we set the initial level of Ws to a small, non-zero value.
The background plasma is assumed to be isothermal at 1.5 MK, and the electron and ion temperatures are set everywhere equal. The plasma density profile is defined as in Reid & Kontar (2013), based on the model of Parker (1958) with normalisation as in Mann et al. (1999), as the solution of 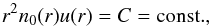 (25)where n0 is the plasma density, u(r) solar wind speed, and
(25)where n0 is the plasma density, u(r) solar wind speed, and 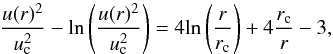 (26)where
(26)where 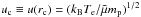 ,
, 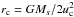 , Te is the electron temperature, Ms is the mass of the Sun, mp is the proton mass,
, Te is the electron temperature, Ms is the mass of the Sun, mp is the proton mass, 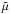 is the mean molecular weight, and the constant is C = 6.3 × 1034 s-1.
is the mean molecular weight, and the constant is C = 6.3 × 1034 s-1.
4. Numerical results
4.1. Instant electron injection
As an initial example, we consider electrons injected almost instantaneously (τ1 = τ2 = 10-3 s) at a height of 2 × 109 cm, with source function given by Eq. 20 with nb = 4 × 106 cm-3. The resulting dynamic spectrum is shown in Fig. 1. The injected power law of electrons is initially stable to Langmuir wave generation and so no emission is produced at the injection site. After a certain distance (e.g. Reid et al. 2011) the fast electrons outpace the slower ones and a reverse slope in velocity space is formed, leading to Langmuir wave generation and radio emission. The onset frequency therefore corresponds to a plasma frequency only slightly smaller than that of the injection site. The strong long-duration component in the spectrum in Fig. 1 is harmonic (2fp) emission, with the fundamental fluxes staying below 1 sfu. This emission therefore arises from a region where the plasma frequency is about half that of the emission itself. For comparison, the quiet Sun flux from the whole sun is, using average values from Benz (2009), around 27 sfu at 500 MHz, 8 sfu at 200 MHz and 0.07 sfu at 20 MHz.
Time profiles of the emission are shown in Fig. 2 for frequencies of 200, 150, 100, 75, 50 and 25 MHz. The timescale for Langmuir wave damping, originally thought to dictate the duration of Type III bursts, increases as frequency decreases. This is consistent with the observations by e.g. Aubier & Boischot (1972); Evans et al. (1973); Staehli & Benz (1987). These considered emission at frequencies from 100 s of MHz to the low kHz, and found an approximate 1 /f scaling of duration with frequency. Our results however suggest it is not in fact this damping time which dictates the duration: this is discussed further in Sect. 4.3 below.
The time profiles show a slight asymmetry, with faster rise and slower decay, and this asymmetry becomes stronger as frequency increases. For example, at 200 MHz the ratio of decay time (half-width half-maximum) and rise time is 1, while at 25 MHz it is approximately 1.6. This is because the excitation of Langmuir waves by fast electrons continues alongside their decay, as the exciter has a finite spatial length. Moreover, this length is seen to increase with as frequency decreases, leading to a corresponding increase in the duration of Langmuir wave excitation, and thus the increasing rise-time of the emission.
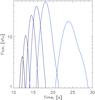 |
Fig. 2 Radio emission time profiles at the Earth for nearly instant electron injection, at frequencies of 200, 150, 100, 75, 50, and 25 MHz (from dark to light blue). |
 |
Fig. 3 Dynamic spectrum of a simulated type III radio burst for slow (τ1 = 1 s) injection of energetic electrons around 550 MHz. As in Fig. 1 the time axis is set such that emission from the injection site would appear at t = 0. |
4.2. Slow electron Injection
As noted in the previous section, the injected electrons have a power-law distribution in velocity space, which only becomes unstable to Langmuir wave generation due to time-of-flight effects (producing the bump-on-tail instability). For an electron injection function which is a function of time, the time-of-flight effects are altered and therefore so are the development of the bump-on-tail instability and consequently the radio emission. The faster electrons must now outpace both the slower electrons injected at the same time, and those injected earlier, before an unstable velocity space gradient can develop, leading to a decreased onset frequency of emission. For the remainder of this paper we consider electrons injected with τ1 = 1 s and τ2 = 4 s. We take a time-integrated beam density of nb = 5 × 106 cm-3. The total number of injected electrons above 50 keV, for cross-sectional source size 2 × 109 cm is then 1030 electrons. This is slightly below the lower limit of the observed densities (e.g. Krucker et al. 2007), but this is compensated for by the short injection time chosen here for computational purposes, which leads to larger instantaneous electron densities.
Figure 3 shows the dynamic spectrum for this case. The later onset of the emission is evident compared to Fig. 1, due to the slower development of the bump-on-tail instability. The fundamental component is again weak, in this case reaching only about 0.4 sfu. The fine structure in the dynamic spectrum is not a numerical effect, but probably related to the details of Langmuir wave scattering.
4.3. Burst duration, rise, and decay times at a given frequency
Figure 4 shows time profiles of the emission at frequencies of 200, 150, 100, 75, 50, 25, 10 and 5 MHz. The simulations show fast exponential rise and somewhat slower exponential decay. The characteristic duration of the burst at a given frequency is then the sum of these two times. In Fig. 4 we plot the half-width-half-maximum (HWHM) duration of the emission, calculated by finding the variance of the time profiles at each frequency. The profiles are very close to symmetric and so this is approximately equal to both the rise and decay times. For comparison, we plot the observationally derived empirical relationship of e.g. Alvarez & Haddock (1973a), which gives a decay time 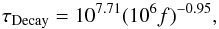 (27)where f is measured in MHz. Similar f-1 scalings were found by e.g. Aubier & Boischot (1972); Staehli & Benz (1987). We note that such empirical results are derived from a large number of bursts with varying exciter parameters, such as the injection timescale for accelerated electrons, injection region size, height etc. While our simulations use parameters within the inferred ranges, the typical values, and therefore those that would dominate the empirical result, are not known. Even the background plasma density profile chosen, while a reasonable assumption, may not fully reflect the real values. However, as is seen in Fig. 4, the simulated and empirical results agree well over the frequencies considered, always to within a factor of 2.
(27)where f is measured in MHz. Similar f-1 scalings were found by e.g. Aubier & Boischot (1972); Staehli & Benz (1987). We note that such empirical results are derived from a large number of bursts with varying exciter parameters, such as the injection timescale for accelerated electrons, injection region size, height etc. While our simulations use parameters within the inferred ranges, the typical values, and therefore those that would dominate the empirical result, are not known. Even the background plasma density profile chosen, while a reasonable assumption, may not fully reflect the real values. However, as is seen in Fig. 4, the simulated and empirical results agree well over the frequencies considered, always to within a factor of 2.
 |
Fig. 4 Top: radio emission time profiles at frequencies of 200, 150, 100, 75, 50, 25, 10, and 5 MHz (from dark to light blue) for a 1 s rise time of electron injection. Middle/Bottom: half-width-half-maximum of emission (black line), the collisional Langmuir wave decay time (Eq. (28), red dotted line), the timescale for Langmuir wave evolution due to plasma density inhomogeneity (Eq. (29), blue dot-dashed line) and the empirical result given by Eq. (27) (black dashed line), as a function of both background plasma frequency and distance from injection site. |
In order to discern the dominant physical factor in the decay time, in Fig. 4 we also plot the collisional decay timescale, 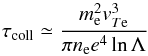 (28)and that for spectral evolution of Langmuir waves due to density inhomogeneities,
(28)and that for spectral evolution of Langmuir waves due to density inhomogeneities, 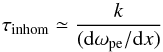 (29)for typical wavenumber k ~ 0.1kDe for beam-generated Langmuir waves.
(29)for typical wavenumber k ~ 0.1kDe for beam-generated Langmuir waves.
It was originally suggested that the decay of type III bursts was due to collisional damping of Langmuir waves (e.g. Hughes & Harkness 1963; Elgaroy & Lyngstad 1972). However, it is clear from this figure that the collisional decay of Langmuir waves is not the dominant factor. At high frequencies, it is far shorter than the decay time. The rise and decay times are similar (seen in the time profiles in Fig. 4) and the duration of excitation appears to be the main factor. At lower frequencies, the collisional time is far longer than the burst, and the burst decay time is longer than the rise time, although in this case only slightly. Here it appears the density inhomogeneity is responsible for the decay, as shown by the similar frequency scalings of the two. Finally we note that there is a region near 40 MHz (for these parameters) where the collisional timescale and the burst decay times are quantitatively similar. This may explain both the apparent successes and errors of previous attempts to use decay time to derive plasma temperature (e.g. Alvarez & Haddock 1973a; Bradford & Hughes 1974; Riddle 1974).
 |
Fig. 5 Top: full width at half maximum (FWHM) bandwidth of radio emission flux at a given time as a function of the peak emission frequency. Bottom: bandwidth divided by the peak frequency, as a function of the peak frequency. The red dashed lines are a linear fit, Δf = 0.57f. |
4.4. Instantaneous bandwidth
In Fig. 5 we plot the instantaneous bandwidth of the emission as a function of frequency, that is the FWHM bandwidth at a given time. The measured bandwidth is a significant fraction of the frequency, from 0.4 to 0.6 here. The frequency spread of Langmuir waves at a single location is small, with wavenumber spread kλDe ~ 0.2, varying very little with location, and corresponding to Δf/f = 0.06. To obtain a value of say Δf/f = 0.5 from a single location would require a much larger wavenumber range of kλDe ~ 0.6 as noted by Melnik et al. (2011). On the other hand, at a given instant Langmuir waves are present over a significant spatial length. This spread in space reflects the spatial extent of the fast electrons, which increases over time as the slower electrons are left behind by faster ones, and is easily able to explain the observed bandwidths.
4.5. Frequency drift
The frequency drift of the burst is related, although not straightforwardly, to the speed of the exciting electrons, and thus should show which electron energies are most important for emission. To find this, we first find the peak emission frequency as a function of time. This is plotted in the top panel of Fig. 6, along with a power law fit given by the red line. Using this fit, which gives f(t), we may analytically differentiate and rearrange to find df/dt as a function of f.
 |
Fig. 6 Top: peak emission frequency as a function of time. The red line is a single power-law fit of the form f = a(t − t0)b, where t0 accounts for the onset time of emission and we have a ≃ 150, b ≃ −0.6. Bottom: frequency drift rate, found by fitting power-laws to segments of the peak emission curve and differentiating these, as described in the text. |
Observationally, empirical fits to a large number of bursts across a wide frequency range give 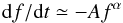 (30)for \begin{lxirformule}$f$\end{lxirformule} the frequency in MHz and df/dt the drift in MHz s-1, with A = 0.01,α = 1.84 (Alvarez & Haddock 1973b; McLean & Labrum 1985) for bursts between 550 MHz and 74 kHz, whereas a linear relationship of
(30)for \begin{lxirformule}$f$\end{lxirformule} the frequency in MHz and df/dt the drift in MHz s-1, with A = 0.01,α = 1.84 (Alvarez & Haddock 1973b; McLean & Labrum 1985) for bursts between 550 MHz and 74 kHz, whereas a linear relationship of 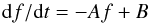 (31)with A ~ 0.1 and B ~ 1 MHz is found by Melnik et al. (2011) between 10 and 30 MHz similar to that found by Wild (1950) of
(31)with A ~ 0.1 and B ~ 1 MHz is found by Melnik et al. (2011) between 10 and 30 MHz similar to that found by Wild (1950) of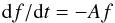 (32)with A = 0.14−0.5.
(32)with A = 0.14−0.5.
Fitting the frequency-time curve with a single power-law across all frequencies, as shown in Fig. 6 gives A = 0.015, α = 1.62. However, this fit does not work well across all frequencies. Instead, we can fit segments of the curve over small frequency ranges, giving a range of values for A and α, which vary with frequency within the following ranges: A ~ 0.005−0.1 and α ~ 1−2. The resulting df/dt is shown in the bottom panel of Fig. 6.
 |
Fig. 7 Exciter velocity derived from the frequency drift using Eq. (33), as a function of distance from the injection site. |
Now we can use this frequency drift to infer the source velocity, which is given by 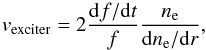 (33)where ne is the background electron density at the location of the exciter. In contrast to the estimates quoted above from e.g. Wild (1950), we know exactly the plasma density and its gradient from our simulations, and the code is able to resolve the dynamic spectra in frequency and time. Using the known density profile we obtain source velocities as plotted in Fig. 7. Because of the fitting involved, this derived velocity may have large errors. However, there is a clear trend of deceleration with frequency. The speeds are generally in the range of inferred values (e.g. Dulk et al. 1987) with a value for the exciter speed of about 0.12c near 10 MHz. The smaller values at lower frequency are closer to the Langmuir wave generating electrons inferred from in situ observations near 0.02 MHz (e.g. Lin et al. 1981). Robinson (1992) suggests that exciter speed should decrease to explain the empirical results (Alvarez & Haddock 1973b; McLean & Labrum 1985).
(33)where ne is the background electron density at the location of the exciter. In contrast to the estimates quoted above from e.g. Wild (1950), we know exactly the plasma density and its gradient from our simulations, and the code is able to resolve the dynamic spectra in frequency and time. Using the known density profile we obtain source velocities as plotted in Fig. 7. Because of the fitting involved, this derived velocity may have large errors. However, there is a clear trend of deceleration with frequency. The speeds are generally in the range of inferred values (e.g. Dulk et al. 1987) with a value for the exciter speed of about 0.12c near 10 MHz. The smaller values at lower frequency are closer to the Langmuir wave generating electrons inferred from in situ observations near 0.02 MHz (e.g. Lin et al. 1981). Robinson (1992) suggests that exciter speed should decrease to explain the empirical results (Alvarez & Haddock 1973b; McLean & Labrum 1985).
The exciter speed inferred from the peak of electromagnetic emission differs from that derived from the peak of Langmuir wave spectral energy density, and has different frequency dependency. This can be explained by the following. The harmonic emission arises from coalescence of waves from the forwards and backwards wave populations, and so the presence of an enhanced level of backscattered Langmuir waves is an essential condition for harmonic emission. Furthermore, there is significant spectral evolution of the Langmuir waves both due to transport effects on the generating electrons and to Langmuir wave back scattering. Thus the part of the beam which is most effective for generating emission does not correspond to the peak of Langmuir wave energy density and rather occurs where we have high levels of both forwards and backwards waves at appropriate wavenumbers.
In Fig. 8 we plot the snapshots of electron and Langmuir wave distributions at a few spatial locations. For a given local plasma frequency (100, 75, 25 and 5 MHz), we find the time at which the EM emission from this location is maximum, as shown in the top panel of Fig. 6, and plot the distributions at this location and time. The onset of emission is near 200 MHz, or local plasma frequency of 100 MHz as we observed the second-harmonic component, corresponding to the black line in the figure. At this time, the backscattered Langmuir wave level has reached several orders of magnitude over thermal, and peaks at wavenumber k/kDe ~ 0.1, corresponding to electrons at velocity 0.2c, or energy 12 keV. When the peak of the emission has reached 75 MHz we see a much higher level of backscattered Langmuir waves, extending to larger wavenumber, therefore resonant with slower electrons. In the next two curves, 25 and 5 MHz respectively, more Langmuir waves appear at larger, negative wavenumber, up to k/kDe ~ 0.2, corresponding to electrons at 0.1c. This trend is the origin of the decreasing exciter velocity seen in Fig. 7.
Additionally, in the 25 and 5 MHz curves in Fig. 8 we also see multiple backscatterings producing Langmuir waves at small positive wave numbers. These then interact with faster electrons, and produce the double plateau seen in the 5 MHz electron distribution cross-section.
 |
Fig. 8 Electron flux as a function of energy (top) and Langmuir wave spectral energy density as a function of wavenumber normalised by the Debye wavenumber kDe (bottom) at a local plasma frequency of 100 (black), 75 (blue), 25 (red) and 5 MHz (green) at the time of peak EM emission (as given by Fig. 6). |
5. Discussion and conclusions
In this work we have described a model simulating electron injection in the solar corona, and the subsequent evolution and wave production which leads to radio emission. To summarise, electrons are injected with a power-law distribution in velocity at a location corresponding to 550 MHz and propagate along the expanding magnetic field. The distribution of electrons evolves due to transport effects (where faster electrons outpace slower ones) to form a reverse slope in velocity space that is unstable to Langmuir wave generation. These Langmuir waves may then be re-absorbed by the beam, refracted, backscattered, and waves from the forwards and backwards populations can coalesce to produce radio emission at twice the local plasma frequency. Emission at the local plasma frequency, which can be due to scattering of Langmuir waves by ions or their interaction with ion-sound waves, is seen to be weak for the corona and beam parameters chosen.
Using the assumptions and simplifications outlined in Sect. 2, we have self-consistently treated all the steps in this process to produce simulated dynamic spectra of emission, and analysed the properties of the resulting radiation at the Earth. Our main findings are summarised here.
An observable level of harmonic plasma emission arises over wide range of Langmuir wave levels and different shapes of electron distribution function. A noticeable level of electromagnetic emission appears both when the flattening of the electron distribution function by quasilinear relaxation is weak near the starting frequency (~200 MHz) and when the distribution has a plateau-like shape at dekametre wavelengths (~10 MHz).
The simulations show that burst decay time is not, as previously suggested, due to collisional decay of Langmuir waves. The collisional decay time is too short at high frequencies and too long at low frequencies although for a small range around perhaps 30−100 MHz the decay time and the collisional time are coincidentally similar. Instead, at high frequencies the duration (and decay time) depends on the duration of excitation, which is itself a function of the injection characteristics of fast electrons. Further investigation of the effects of injection time on the emission is ongoing. On the other hand at lower frequencies it appears that plasma inhomogeneity plays a crucial role, by shifting Langmuir waves out of resonance with the fast electrons.
As discussed previously (e.g. Reid & Kontar 2013) we confirm that the time-injection profile of the electron beam alters the starting frequency of the radio emission, with a slower injection leading to lower starting frequency and vice versa.
The dominant factor in the instantaneous emission bandwidth is found to be the spatial extension of the emission source. At a given time, Langmuir waves are present over a large spatial extent, and therefore at a wide range of plasma frequencies. Backscattered Langmuir waves show a similar dispersion, and this is therefore mirrored in the harmonic emission. Again, this may be expected to depend on electron injection characteristics.
The frequency drift of the peak of emission can be used to infer the velocity of the emitting source if the background plasma density is known. However, the exciter of type III bursts cannot be uniquely associated with either electrons of a particular speed or with the peak of the Langmuir waves. There is a closer association of the derived exciter speed with the secondary (back-scattered) Langmuir waves, and the velocity of the exciter is better approximated by the speed of the peak of these secondary waves. The simulations suggest the rather slow deceleration of the exciter as frequency decreases. Indeed, the evolution of the electron distribution at the peak of the burst does show the distribution flattening between a few keV and around 15 keV. The overall deceleration of the beam-plasma structure is consistent with previous results (e.g. Kontar 2001a; Reid & Kontar 2013) and is due to evolution of Langmuir waves to larger wavenumbers (resonant with slower electrons) as the beam-plasma structure moves into the interplanetary space.
To conclude, we have investigated the several large-scale characteristics of type III radio bursts using large-scale simulations covering almost two orders in frequency. Due to the complex nature of the emission process such simulations are invaluable in order to determine which physical processes responsible for the particular features of the emission observed. Initial results have clarified several points regarding the burst excitation and duration, but there remains much to consider, especially regarding the influence of electron injection characteristics, and the time and frequency evolution of the emission processes.
Acknowledgments
We thank the referee for detailed comments on the manuscript. This work is supported by the European Research Council under the SeismoSun Research Project No. 321141 (H Ratcliffe), a Marie Curie International Research Staff Exchange Scheme “Radiosun” (PEOPLE-2011-IRSES-295272), an STFC consolidated grant (E.P. Kontar) and a SUPA LOFAR Advanced Fellowship (H.A.S. Reid). Additional thanks are due to ISSI (International Space Science Institute) for useful discussions during International Team meetings.
References
- Alvarez, H., & Haddock, F. T. 1973a, Sol. Phys., 30, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez, H., & Haddock, F. T. 1973b, Sol. Phys., 29, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Arzner, K., & Benz, A. O. 2005, Sol. Phys., 231, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Aubier, M., & Boischot, A. 1972, A&A, 19, 343 [NASA ADS] [Google Scholar]
- Bastian, T. S., Benz, A. O., & Gary, D. E. 1998, ARA&A, 36, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O. 2009, Radio emission of the quiet Sun, Landolt Börnstein (Berlin, Heidelberg: Springer), 103 [Google Scholar]
- Bradford, H. M., & Hughes, V. A. 1974, A&A, 31, 419 [NASA ADS] [Google Scholar]
- Cairns, I. H. 2000, Phys. Plasmas, 7, 4901 [NASA ADS] [CrossRef] [Google Scholar]
- Churaev, R. S., & Agapov, A. V. 1980, Sov. J. Plasma Phys., 6, 232 [NASA ADS] [Google Scholar]
- Daldorff, L. K. S., Pécseli, H. L., Trulsen, J. K., et al. 2011, Phys. Plasmas, 18, 052107 [NASA ADS] [CrossRef] [Google Scholar]
- Dennis, B. R. 1988, Sol. Phys., 118, 49 [NASA ADS] [CrossRef] [Google Scholar]
- D’Iachenko, A. I., Pushkarev, A. N., & Rubenchik, A. M. 1989, Fizika Plazmy, 15, 790 [NASA ADS] [Google Scholar]
- Drummond, W., & Pines, D. 1962, Ann. Phys. (NY), 28, 478 [Google Scholar]
- Dulk, G. A. 1985, ARA&A, 23, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Dulk, G. A., Goldman, M. V., Steinberg, J. L., & Hoang, S. 1987, A&A, 173, 366 [NASA ADS] [Google Scholar]
- Dum, C. T., & Nishikawa, K.-I. 1994, Phys. Plasmas, 1, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Elgaroy, O., & Lyngstad, E. 1972, A&A, 16, 1 [NASA ADS] [Google Scholar]
- Evans, L. G., Fainberg, J., & Stone, R. G. 1973, Sol. Phys., 31, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D., Kontar, E. P., Nita, G. M., & Gary, D. E. 2013, ApJ, 768, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, D. E., & Hurford, G. J. 1990, ApJ, 361, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Soviet Astron., 2, 653 [Google Scholar]
- Goldman, M. V., & Dubois, D. F. 1982, Phys. Fluids, 25, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, M. P., & Harkness, R. L. 1963, ApJ, 138, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P. 2001a, Sol. Phys., 202, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P. 2001b, A&A, 375, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., & Pécseli, H. L. 2002, Phys. Rev. E, 65, 066408 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., & Reid, H. A. S. 2009, ApJ, 695, L140 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Ratcliffe, H., & Bian, N. H. 2012, A&A, 539, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krucker, S., Kontar, E. P., Christe, S., & Lin, R. P. 2007, ApJ, 663, L109 [Google Scholar]
- Ledenev, V. G., Zverev, E. A., & Starygin, A. P. 2004, Sol. Phys., 222, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., & Cairns, I. H. 2013, J. Geophys. Res. (Space Physics), 118, 4748 [Google Scholar]
- Li, B., Robinson, P. A., & Cairns, I. H. 2006, Phys. Rev. Lett., 96, 145005 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, B., Cairns, I. H., & Robinson, P. A. 2008, J. Geophys. Res. (Space Physics), 113, 6104 [Google Scholar]
- Li, B., Cairns, I. H., Yan, Y. H., & Robinson, P. A. 2011, ApJ, 738, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lifshitz, E. M., & Pitaevskii, L. P. 1981, Physical kinetics (Oxford: Pergamon Press) [Google Scholar]
- Lin, R. P., Potter, D. W., Gurnett, D. A., & Scarf, F. L. 1981, ApJ, 251, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Magelssen, G. R., & Smith, D. F. 1977, Sol. Phys., 55, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, G., Jansen, F., MacDowall, R. J., Kaiser, M. L., & Stone, R. G. 1999, A&A, 348, 614 [NASA ADS] [Google Scholar]
- McLean, D. J., & Labrum, N. R. 1985, Solar radiophysics: Studies of emission from the sun at metre wavelengths (Cambridge: Cambridge University Press) [Google Scholar]
- Melnik, V. N., Konovalenko, A. A., Rucker, H. O., et al. 2011, Sol. Phys., 269, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Mel’Nik, V. N., Lapshin, V., & Kontar, E. 1999, Sol. Phys., 184, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Melnikov, V. F., Shibasaki, K., & Reznikova, V. E. 2002, ApJ, 580, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1980, Plasma astrophysics, Vols. 1 and 2 (New York: Gordon and Breach) [Google Scholar]
- Melrose, D. B. 1987, Sol. Phys., 111, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 2009, in IAU Symp. 257, eds. N. Gopalswamy, & D. F. Webb, 305 [Google Scholar]
- Melrose, D. B., & Stenhouse, J. E. 1979, A&A, 73, 151 [NASA ADS] [Google Scholar]
- Nindos, A., Aurass, H., Klein, K.-L., & Trottet, G. 2008, Sol. Phys., 253, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Ratcliffe, H., & Kontar, E. P. 2014, A&A, 562, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ratcliffe, H., Bian, N. H., & Kontar, E. P. 2012, ApJ, 761, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., & Kontar, E. P. 2010, ApJ, 721, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., & Kontar, E. P. 2013, Sol. Phys., 285, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., & Ratcliffe, H. 2014, RA&A, 14, 773 [Google Scholar]
- Reid, H. A. S., Vilmer, N., & Kontar, E. P. 2011, A&A, 529, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riddle, A. C. 1974, Sol. Phys., 34, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, P. A. 1992, Sol. Phys., 137, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Saint-Hilaire, P., Vilmer, N., & Kerdraon, A. 2013, ApJ, 762, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. F., & Sime, D. 1979, ApJ, 233, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Staehli, M., & Benz, A. O. 1987, A&A, 175, 271 [NASA ADS] [Google Scholar]
- Takakura, T., & Shibahashi, H. 1976, Sol. Phys., 46, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Tsytovich, V. N. 1995, Lectures on Non-linear Plasma Kinetics, Springer Series on Atoms and Plasmas (Berlin, Heidelberg, New York: Springer-Verlag), Vol. 17 [Google Scholar]
- Vedenov, A., Velikhov, E., & Sagdeev, R. 1962, Quasi-linear theory of plasma oscillations, Tech. Rep. [Google Scholar]
- Wild, J. P. 1950, Austr. J. Sci. Res. A Phys. Sci., 3, 541 [Google Scholar]
- Yoon, P. H., Rhee, T., & Ryu, C.-M. 2005, Phys. Rev. Lett., 95, 215003 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., Mityakov, N. A., & Rapoport, V. O. 1972, Sol. Phys., 24, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V. 1969, ApJ, 155, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V. 1996, Radiation in Astrophysical Plasmas, Astrophys. Space Sci. Lib., 204 [Google Scholar]
- Zheleznyakov, V. V., & Zaitsev, V. V. 1970a, Soviet Astron., 14, 47 [Google Scholar]
- Zheleznyakov, V. V., & Zaitsev, V. V. 1970b, Soviet Astron., 14, 250 [Google Scholar]
- Ziebell, L. F., Gaelzer, R., Pavan, J., & Yoon, P. H. 2008, Plasma Physics and Controlled Fusion, 50, 5011 [Google Scholar]
All Figures
 |
Fig. 1 Dynamic spectrum of simulated type III radio burst emission (flux at 1 AU) for almost instantaneous injection of energetic electrons around 550 MHz. Differences in propagation time from the changing source position to the remote observer are included and the time axis is set such that emission from the injection region would appear at t = 0. |
| In the text | |
 |
Fig. 2 Radio emission time profiles at the Earth for nearly instant electron injection, at frequencies of 200, 150, 100, 75, 50, and 25 MHz (from dark to light blue). |
| In the text | |
 |
Fig. 3 Dynamic spectrum of a simulated type III radio burst for slow (τ1 = 1 s) injection of energetic electrons around 550 MHz. As in Fig. 1 the time axis is set such that emission from the injection site would appear at t = 0. |
| In the text | |
 |
Fig. 4 Top: radio emission time profiles at frequencies of 200, 150, 100, 75, 50, 25, 10, and 5 MHz (from dark to light blue) for a 1 s rise time of electron injection. Middle/Bottom: half-width-half-maximum of emission (black line), the collisional Langmuir wave decay time (Eq. (28), red dotted line), the timescale for Langmuir wave evolution due to plasma density inhomogeneity (Eq. (29), blue dot-dashed line) and the empirical result given by Eq. (27) (black dashed line), as a function of both background plasma frequency and distance from injection site. |
| In the text | |
 |
Fig. 5 Top: full width at half maximum (FWHM) bandwidth of radio emission flux at a given time as a function of the peak emission frequency. Bottom: bandwidth divided by the peak frequency, as a function of the peak frequency. The red dashed lines are a linear fit, Δf = 0.57f. |
| In the text | |
 |
Fig. 6 Top: peak emission frequency as a function of time. The red line is a single power-law fit of the form f = a(t − t0)b, where t0 accounts for the onset time of emission and we have a ≃ 150, b ≃ −0.6. Bottom: frequency drift rate, found by fitting power-laws to segments of the peak emission curve and differentiating these, as described in the text. |
| In the text | |
 |
Fig. 7 Exciter velocity derived from the frequency drift using Eq. (33), as a function of distance from the injection site. |
| In the text | |
 |
Fig. 8 Electron flux as a function of energy (top) and Langmuir wave spectral energy density as a function of wavenumber normalised by the Debye wavenumber kDe (bottom) at a local plasma frequency of 100 (black), 75 (blue), 25 (red) and 5 MHz (green) at the time of peak EM emission (as given by Fig. 6). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


