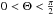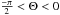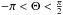| Issue |
A&A
Volume 571, November 2014
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201424436 | |
| Published online | 07 November 2014 | |
RRab Lyrae metallicity gradient in the Galactic bulge
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200 D,
3001
Leuven,
Belgium
e-mail:
Alejandra@ster.kuleuven.be
Received: 19 June 2014
Accepted: 12 September 2014
Aims. We revisit the presence and significance of the Galactic bulge metallicity gradients, using the OGlE-III RR Lyrae sample.
Methods. We implemented a Monte Carlo simulation to account for observational uncertainties and systematic errors to test the presence, significance, and spatial variation of RR Lyr photometric metallicity gradients within the Galactic bulge. Furthermore, we take special consideration to identify and account for possible observational and statistical biases, which may introduce an apparent metallicity gradient into the sample.
Results. We find a mean Galactic bulge RRab metallicity of −0.97 ± 0.29 dex, a global radial metallicity gradient of −0.016 ± 0.008 dex Kpc-1, and a global vertical metallicity gradient of −0.063 ± 0.013 dex Kpc-1. Furthermore, neither the global radial nor vertical gradients can be explained by random chance, unjustified extrapolation of the metallicity calibration law, or induced by a Malmquist bias.
Key words: stars: abundances / stars: variables: RR Lyrae / Galaxy: bulge / Galaxy: abundances / methods: statistical
© ESO, 2014
1. Introduction
The Galactic bulge consists of a rotating peanut-shaped structure made up largely of old stars (~10 Gyr; Wegg & Gerhard 2013; Martinez-Valpuesta & Gerhard 2013; Ness et al. 2013; Saito et al. 2011; Zoccali et al. 2003; Picaud & Robin 2004; Howard et al. 2009). General consensus has been reached that the Galactic bulge has a broad metallicity distribution due to a composite stellar population. Hill et al. (2011), using high resolution spectroscopic measurements of Fe and Mg for 219 red clump stars, find that the metallicity distribution for both Fe and Mg are best described by two super-imposed components: a young, broad metal-poor distribution centered at [Fe/H] = −0.30 dex and an old, narrow metal-rich component at [Fe/H] = + 0.32 dex. Taken alongside the kinematic work of Babusiaux et al. (2010), Hill et al. (2011) suggests that the chemical and kinematic evolution of the two components occurred at different timescales. More recently, Ness et al. (2012) and Ness et al. (2013) have shown that the Galactic bulge region, extending between | l | = 15 and | b | = 10, can be described by a global [Fe/H] distribution ranging from −2.5 to 1.0 dex. Fitting five Gaussian to the observed [Fe/H] distribution, Ness et al. (2012) and Ness et al. (2013), again show that at least two distinct populations (components A and B) make up the bulge, while the remaining three components are either disk or halo stars. Component A is found to be a kinematically hot population with a mean [Fe/H] ≈−0.25, while component B is a kinematically colder, more metal-rich population with mean [Fe/H] ≈ +0.15 (Ness et al. 2012, 2013); thereby reinforcing the composite stellar population hypothesis and indicating that the bulge is more complex than originally thought.
On the other hand, the heterogeneity in the quality of data between high and low resolution spectroscopic and photometric metallicity estimates makes reaching a general consensus on the presence and strength of metallicity gradients difficult. The works of Zoccali et al. (2008), Frogel et al. (1999), Minniti et al. (1995), Gonzalez et al. (2011), Johnson et al. (2013), Ness et al. (2013), Gonzalez et al. (2013) and Pietrukowicz et al. (2012) show that metallicity gradients depend on the galactic field coverage as well as data quality and methodology. The high resolution spectroscopic works of Zoccali et al. (2008), Johnson et al. (2013), and Ness et al. (2013), however, leave no doubt that radial and vertical metallicity gradients do exist in the Galactic bulge.
Zoccali et al. (2008), in a study of three different bulge fields (b = −4°, b = −6°, and b = −12°) using K-giants, found a vertical metallicity gradient of approximately −0.6 dex Kpc-1. Ness et al. (2013), using the ARGOS spectroscopic survey of the Galactic bulge, were able to detect metallicity gradients in both the vertical and radial directions in up to three of their components. In their components A and B, which correspond to the metal-rich boxy/peanut-bulge and the vertical thick bulge, they identify a metallicity gradient of −0.08 ± 0.05 dex Kpc-1 and −0.08 ± 0.04 dex Kpc-1 in the vertical direction between −5°<b< −10°. They also find a radial metallicity gradient of −0.02 ± 0.01 dex Kpc-1 in a range of galactocentric distances (RGCD) between 0 and 6 Kpc. Johnson et al. (2013) in a study of three off-axis Galactic fields ((l, b) = (−5.5, −7), (−4, −9), and (+8.5, +9)), using 264 red giants branch stars, estimated the off-axis vertical metallicity gradient to be −0.4 dex Kpc-1, while no strong gradient was found in the radial direction.
Moreover, a discontinuity in the presence and strength of the vertical gradient between low and high galactic latitudes is found (Zoccali et al. 2008; Frogel et al. 1999; Gonzalez et al. 2011, 2013; Minniti et al. 1995; Rich et al. 2012). The transition has been shown to occur at approximately b ≈ −4°, with a strong vertical metallicity gradient existing at higher latitudes (b< −4°), while closer to the plane (−4°<b< 0°) no vertical gradient has been detected.
The question now arises if multiple studies show a spatial metallicity gradient within the Galactic bulge, why does the OGLE-III Galactic bulge RR Lyr population seem uniformly distributed over the observed part of the Galactic bulge (Pietrukowicz et al. 2012)? Is the lack of such a gradient caused by the large uncertainties involved in the computation of photometric metallicities and spatial coordinates of the RR Lyrae stars, or is the RR Lyrae population indeed metal uniform and uniformly distributed across the observed volume? If so, what makes this population so distinct? In order to answer these questions, we carefully revisit the photometric metallicity and spatial distributions, associated uncertainties, and correlations for over 9400 RRab stars observed by OGLE-III, carefully taking into account the observational uncertainties and systematic errors. Using Monte Carlo (MC) simulations, we test the presence and significance of metallicity gradients within the Galactic bulge.
2. The dataset
In this work, we use the published RRab Lyr sample of the Optical Gravitational Lensing Experiment (OGLE-III) variable star catalog as presented by Soszyński et al. (2011). Within the regions −10°<l< 10° and 2°<| b | < 7°, the catalog contains good photometric time series in the I and V bands of more than 16 000 RR Lyrae stars, composed of 11 756 fundamental model pulsators (RRab) stars, 4989 overtone pulsators (RRc), and 91 double mode (RRd) stars (Soszyński et al. 2011; Udalski et al. 2008). Of these stars, 400 are likely members of the Sagittarius dwarf spheroidal galaxy (Sgr dSph; Soszyński et al. 2011; Pietrukowicz et al. 2012). Apart from the mean I (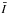 ) and the mean V (
) and the mean V (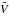 ) magnitudes, the catalog also contains the Fourier parameters of the time series, including the phase difference (Φ31) and the pulsation period (P), which were obtained by fitting the function:
) magnitudes, the catalog also contains the Fourier parameters of the time series, including the phase difference (Φ31) and the pulsation period (P), which were obtained by fitting the function: ![\begin{equation} f(t)=A_{0}+\sum\limits_{i=1}^8 A_{i}\cos\left[i\frac{2\pi}{P}\left(t-t_{0} \right)+\Phi_ {i} \right] \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq43.png) (1)to the I-band time series and defining Φ31 as
(1)to the I-band time series and defining Φ31 as 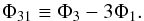 (2)The idea that the Fourier parameters (P and Φ31), describing the shape of the light curve, can be used to determine the RRab photometric metallicity will be key to the work presented here, as it provides a straightforward method to estimate metallicities for large scale photometric surveys (Soszyński et al. 2011; Jurcsik & Kovacs 1996; Jurcsik 1995; Kovacs & Zsoldos 1995; Smolec 2005; Nemec et al. 2013).
(2)The idea that the Fourier parameters (P and Φ31), describing the shape of the light curve, can be used to determine the RRab photometric metallicity will be key to the work presented here, as it provides a straightforward method to estimate metallicities for large scale photometric surveys (Soszyński et al. 2011; Jurcsik & Kovacs 1996; Jurcsik 1995; Kovacs & Zsoldos 1995; Smolec 2005; Nemec et al. 2013).
We will focus on the fundamental mode pulsators (RRab stars), with reliable values for the 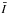 and
and 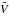 magnitudes and Φ31. For the latter, we restrict ourselves to RRab stars with an uncertainty σΦ31< 0.1. Higher values indicate that the amplitude of the third harmonic (A3) is too small to reliably determine the phase difference and hence Φ31 is not reliable enough to determine accurate metallicities. Following the work of Pietrukowicz et al. (2012), we also limit our sample of RRab stars to those with
magnitudes and Φ31. For the latter, we restrict ourselves to RRab stars with an uncertainty σΦ31< 0.1. Higher values indicate that the amplitude of the third harmonic (A3) is too small to reliably determine the phase difference and hence Φ31 is not reliable enough to determine accurate metallicities. Following the work of Pietrukowicz et al. (2012), we also limit our sample of RRab stars to those with 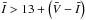 and
and 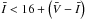 to limit the background contamination from the Sagittarius dwarf spheroidal galaxy. As a result of these primary selection criteria, we are left with 10 292 RRab stars. Furthermore, we excluded all stars with heliocentric distances R< 4 Kpc and R> 12 Kpc, avoiding targets that are unlikely to belong to the bulge. As a result of our selection criteria, we reduced the original Soszyński et al. (2011) sample from 11 756 to 9459 RRab stars.
to limit the background contamination from the Sagittarius dwarf spheroidal galaxy. As a result of these primary selection criteria, we are left with 10 292 RRab stars. Furthermore, we excluded all stars with heliocentric distances R< 4 Kpc and R> 12 Kpc, avoiding targets that are unlikely to belong to the bulge. As a result of our selection criteria, we reduced the original Soszyński et al. (2011) sample from 11 756 to 9459 RRab stars.
3. Methodology
3.1. Monte Carlo simulation setup
The strong correlations between most of the variables involved in the determination of photometric metallicity, absolute magnitudes, and galactocentric distances, and hence their uncertainty, could cause spurious gradients. In order to account for these correlations, we have set up a simple MC simulation to determine the photometric metallicities, the galactocentric coordinates, and their (co)-variances for our stars and Galactic bulge metallicity gradients.
Using 10 000 iterations, the probability distributions of our observables (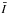 ,
, 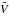 , P, Φ31, Ri, α and δ) are sampled, as described in the following sections. We account for sources of possible systematics, including correlations in fit coefficients and the uncertainty due to the scatter of the residuals of the calibration datasets. The proper determination of the uncertainty distributions of the observables will prove crucial in the accurate estimation of the metallicity and galactocentric distance distributions.
, P, Φ31, Ri, α and δ) are sampled, as described in the following sections. We account for sources of possible systematics, including correlations in fit coefficients and the uncertainty due to the scatter of the residuals of the calibration datasets. The proper determination of the uncertainty distributions of the observables will prove crucial in the accurate estimation of the metallicity and galactocentric distance distributions.
The procedure for each iteration is as follows: The photometric metallicities are estimated using the P-Φ31-[Fe/H] relation presented in Smolec (2005): ![\begin{equation} [{\rm Fe/H}]=\alpha_{1}+\alpha_{2}P+\alpha_{3}\left(\Phi_{31}+\pi\right) \label{eq:Metallicity_Refit} \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq54.png) (3)where a phase shift of π is necessary because of the sine/cosine fitting differences between Smolec (2005) and Soszyński et al. (2011). The heliocentric distances for each star are calculated, using a modified scheme similar to that presented in Pietrukowicz et al. (2012). The photometric metallicities are converted to metallicities using
(3)where a phase shift of π is necessary because of the sine/cosine fitting differences between Smolec (2005) and Soszyński et al. (2011). The heliocentric distances for each star are calculated, using a modified scheme similar to that presented in Pietrukowicz et al. (2012). The photometric metallicities are converted to metallicities using ![\begin{equation} \ \mathrm{log}\ Z =[{\rm Fe/H}]-1.765, \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq56.png) (4)and the absolute magnitudes in the V and I bands are computed with the calibration laws of Catelan et al. (2004):
(4)and the absolute magnitudes in the V and I bands are computed with the calibration laws of Catelan et al. (2004):
![\begin{eqnarray} \label{eq:M_V}&& M_{V}=\beta_{1}+\beta_{2}\ \mathrm{log}\ Z +\beta_{3}(\mathrm{log}\ Z)^{2}, \\[2mm] \label{eq:M_I}&&M_{I}=\gamma_{1}+\gamma_{2}\ \mathrm{log}\ P +\gamma_{3}\ \mathrm{log}\ Z. \end{eqnarray}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq57.png) Using the total to selective extinction ratio
Using the total to selective extinction ratio 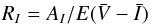 (7)we calculate the dereddened I0, and compute the heliocentric distance (R) with the distance modulus
(7)we calculate the dereddened I0, and compute the heliocentric distance (R) with the distance modulus 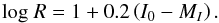 (8)Finally, the galactocentric polar cylindrical coordinates are computed: (RGCD, Θ, Z)1:
(8)Finally, the galactocentric polar cylindrical coordinates are computed: (RGCD, Θ, Z)1: ![\begin{eqnarray} &&R_{\rm GCD}=\sqrt{R_{0}^{2}+ R^2 \cos^2b-2RR_{0}\cos l \cos b} \\[2mm] \label{eq:theta} &&\Theta=\arccos\left(\frac{R_{0}^{2}+R_{\rm GCD}^{2}-R^2\cos^2b} { 2R_{ \rm GCD }R_{0} }\right) \\[2mm] && Z=R \sin l , \end{eqnarray}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq64.png) where R0 is the solar galactocentric distance (which we fixed to R0 = 8.5 Kpc), RGCD and R are the projected galactocentric and heliocentric distances of each star, and l and b are the galactic longitude and latitude. For each run of our MC, we calculate the projected radial metallicity gradient, where the radial gradient was computed using the projected galactocentric distance RGCD and the vertical metallicity gradient was computed using the distance Z above the galactic plane. Note that we use the projected radius RGCD rather than the radius R, unlike in some previous works (e.g. Zoccali et al. 2003, 2008; Minniti et al. 1995; Johnson et al. 2013). We use the symbol Z both for the metallicity of a star as well as for a polar cylindrical coordinate, but the context should clarify the meaning of the symbol.
where R0 is the solar galactocentric distance (which we fixed to R0 = 8.5 Kpc), RGCD and R are the projected galactocentric and heliocentric distances of each star, and l and b are the galactic longitude and latitude. For each run of our MC, we calculate the projected radial metallicity gradient, where the radial gradient was computed using the projected galactocentric distance RGCD and the vertical metallicity gradient was computed using the distance Z above the galactic plane. Note that we use the projected radius RGCD rather than the radius R, unlike in some previous works (e.g. Zoccali et al. 2003, 2008; Minniti et al. 1995; Johnson et al. 2013). We use the symbol Z both for the metallicity of a star as well as for a polar cylindrical coordinate, but the context should clarify the meaning of the symbol.
3.2. Probability distributions of the observables
3.2.1. I and V magnitudes (I, V):
From the OGLE-III time series (Ii ± σIi and Vi ± σVi), we compute the mean magnitudes (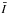 and
and 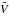 ) and estimate the corresponding uncertainties as
) and estimate the corresponding uncertainties as 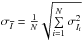 and
and 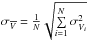 . During the MC sampling , we then draw from the distributions
. During the MC sampling , we then draw from the distributions 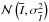 and
and 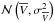 , where
, where 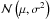 denotes a normal distribution with mean μ and variance σ2, a notation we use throughout this article.
denotes a normal distribution with mean μ and variance σ2, a notation we use throughout this article.
3.2.2. Right ascension and declination (α, δ):
The OGLE-III catalog derives its astrometric precision by a three-step comparison with the Two Micron All Sky Survey (2MASS) point source catalog as described by Udalski et al. (2008). To be conservative, we use the standard 2MASS astrometric precision of 0.01″ (Skrutskie et al. 2006) as the variance of the right ascension and declination for each of our objects.
The observational right ascension and declination probability distributions are defined as 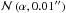 and
and 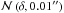 . During each MC iteration the right ascension and declination probability distributions are sampled and the values are converted to corresponding galactic longitude and latitude (l,b) in the J2000.00 epoch.
. During each MC iteration the right ascension and declination probability distributions are sampled and the values are converted to corresponding galactic longitude and latitude (l,b) in the J2000.00 epoch.
3.2.3. Pulsation period and phase difference (P,Φ31):
Uncertainty estimates of the pulsation period and Φ31 were obtained through private communication with Prof. Dr. Igor Soszyński, as the online catalog only contains the period uncertainties. Typical uncertainties are in the range 1−4 × 10-5 days for the pulsation period, and in the range 0.002−0.1 radians for the phase difference Φ31. The upper limit of the phase difference uncertainty was set as part of the selection process to ensure that all selected stars have a sufficiently precise photometric metallicity. The observational pulsation period and Φ31 probability distributions of each star are defined as 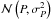 and
and 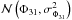 .
.
3.2.4. Extinction ratio (RI):
Instead of assuming a position independent ratio of total to selective extinction (RI = AI/E(V − I)), as was done by Pietrukowicz et al. (2012), we benefit from the extensive extinction tables recently published by Nataf et al. (2013). This extinction map shows that the reddening toward the Galactic bulge can be highly nonuniform, which in turn can have a significant impact on the distance estimates of the RR Lyr stars. The coordinates of each RR Lyr star are matched with the closest grid point in the extinction map, to estimate the corresponding value of RI. Although the formal uncertainty of RI can be determined from the Nataf et al. (2013) extinction map, this is likely a lower limit for our purposes. In some parts of the Galactic bulge the distribution of obscuring dust is so nonuniform that even their detailed reddening map, becuase of its finite-sized grid cells, gives only a crude approximation. To take this additional uncertainty into account, we compute for each RR Lyr star the total variance of RI as the sum of the intracell variance and the surrounding intercell variance: ![\begin{equation} {\rm Var}[R_I] = \sigma^2_{R_I} + \Sigma \label{eq:VarRi} \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq87.png) (12)where σRI is the formal uncertainty determined from Nataf et al. (2013) for a particular grid cell, and where Σ is the sample variance of the RI values of all surrounding grid cells (plus the grid cell containing the RR Lyr star itself) in the reddening map. In the case where neighboring cells have largely nonuniform values for RI, denoting a patchy part of the sky, the intercell variance Σ will dominate. In very patchy parts of the sky, the uncertainty due to inhomogeneity will therefore dominate the formal uncertainty on RI for a given cell. The adapted total to selective extinction ratio (RI) and total variance Var [ RI ] maps of the OGLE-III Galactic bulge sightlines are shown in Fig. 1.
(12)where σRI is the formal uncertainty determined from Nataf et al. (2013) for a particular grid cell, and where Σ is the sample variance of the RI values of all surrounding grid cells (plus the grid cell containing the RR Lyr star itself) in the reddening map. In the case where neighboring cells have largely nonuniform values for RI, denoting a patchy part of the sky, the intercell variance Σ will dominate. In very patchy parts of the sky, the uncertainty due to inhomogeneity will therefore dominate the formal uncertainty on RI for a given cell. The adapted total to selective extinction ratio (RI) and total variance Var [ RI ] maps of the OGLE-III Galactic bulge sightlines are shown in Fig. 1.
In the MC simulations described above, the probability density of RI for any particular line-of-sight is defined as ![\hbox{$\mathcal{N}\left(R_I,{\rm Var}[R_I] \right)$}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq92.png) .
.
 |
Fig. 1 Top panel: total to selective extinction ratio (RI) map of the OGLE-III Galactic bulge sightlines, adapted from Nataf et al. (2013). Bottom panel: total variance Var [ RI ] map, as defined in Eq. (12). Each RI and Var [ RI ] pair defines the normal distribution, which is sampled during our MC procedure to obtain the heliocentric distance of each star. |
3.3. Metallicity
Kovacs & Zsoldos (1995), Jurcsik (1995), and Jurcsik & Kovacs (1996) have shown that a linear relation exists between the iron abundance ([Fe/H]), the pulsation period (P) and the Fourier phase difference (Φ31) for V-band light curves. This relation has been recalibrated for a large number of photometric systems, which have been used to determine photometric metallicities for both globular and field RR Lyrae.
Since both the pulsation period (P) and the Fourier phase difference (Φ31) for the OGLE-III catalog have been defined in the I-band, we revisit the only available I-band calibrated relation presented by Smolec (2005). To account for the covariance of the coefficients in Eq. (3), we refitted the Smolec (2005) data using a two-dimensional linear regression. The resulting coefficients are: 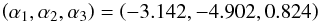 (13)with the corresponding covariance matrix:
(13)with the corresponding covariance matrix: ![\begin{equation} {\rm Cov}[\mathbf{\alpha}]= \begin{bmatrix} 0.416 & -0.082 & -0.064 \\[0.3em] -0.082 & 0.141 & 0.001 \\[0.3em] -0.064 & 0.001 & 0.011 \end{bmatrix} . \label{eq:FeHCoVarMatrix} \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq94.png) (14)During each iteration of the MC procedure, the coefficients for Eq. (3) are drawn from a multivariate Gaussian distribution with expectation values given be Eq. (13) and the covariances given by Eq. (14).
(14)During each iteration of the MC procedure, the coefficients for Eq. (3) are drawn from a multivariate Gaussian distribution with expectation values given be Eq. (13) and the covariances given by Eq. (14).
3.4. Mean absolute magnitudes
The theoretical period luminosity relations (Eqs. (5) and (6)) used in our MC procedure were first derived by Catelan et al. (2004) using a synthetic dataset of over 390 000 models with metallicity in the range of 0.0005 ≤ Z ≤ 0.006, covering our expected metallicity range nearly perfectly. The use of such a large dataset leads to formal fitting uncertainties in the derived mean value of coefficients to be extremely small ranging from 10-5 to 10-3. Consequently, we choose not to perturb the relational coefficients 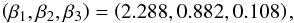 (15)for Eq. (5), and
(15)for Eq. (5), and 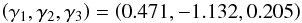 (16)for Eq. (6), during each iteration of the MC procedure.
(16)for Eq. (6), during each iteration of the MC procedure.
We do, however, take into account the uncertainty due to the scatter of the residuals, which are parameterized as the standard deviation of the residuals in each band. The resulting sigmas are σMV = 0.07 and σMI = 0.04. During each MC iteration the individual absolute magnitudes are determined as follows: 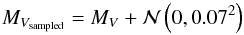 (17)and
(17)and 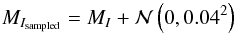 (18)where MV and MI are computed using Eqs. (5) and (6) with the coefficients given by Eqs. (15) and (16), and
(18)where MV and MI are computed using Eqs. (5) and (6) with the coefficients given by Eqs. (15) and (16), and 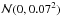 and
and 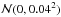 the normal distributions defined by the scatter of the residuals.
the normal distributions defined by the scatter of the residuals.
4. MC simulation results
Our MC sampling results in a 4-d spatial-metallicity probability distribution for each of our sample stars. As an example the resulting distributions for a single randomly chosen star have been projected onto the galactocentric polar cylindrical coordinates planes, shown in Fig. 2. The individual distributions of [Fe/H], RGCD, Θ, and Z depend on the observational values of I, V, P, Φ31, Ri, R0, α, and δ. As expected, the individual uncertainty distributions of each of our sample stars varies from star to star. In cases where large uncertainties in the observables are present, the proper propagation of errors through our MC sampling results in large errors for the individual distributions of [Fe/H], RGCD, Θ, and Z.
 |
Fig. 2 Result of the MC procedure for a randomly chosen star within our sample. Shown here are the projected 2D metallicity-spatial distributions for each of the galactocentric polar cylindrical coordinates. |
 |
Fig. 3 [Fe/H]-Rgcd (top panel) and [Fe/H]-Z (bottom panel) planes containg all stars in our sample. Each star is presented as a circle, where the size represents the uncertainty in the distance and the color represents the uncertainty in the metallicity. The red line represents our mean slope and the two green dashed lines represents the ±sigma region. |
Each of our sample stars are parameterized using the expectation values (E[Fe/H], E[RGCD], E[Θ], and E [ Z ]) and the corresponding variances (Var[Fe/H], Var [ RGCD ], Var [ Θ ], and Var [ Z ]), see Fig. 3 for a representation of the [Fe/H]-Rgcd and [Fe/H]-Z distributions. We determine, using the E[Fe/H] of each of our sample stars, the mean sample metallicity distribution, shown in Fig. 4. The mean of this distribution is −0.97 ± 0.29 dex, which is in good agreement with the value of −1.02 ± 0.25 dex of Pietrukowicz et al. (2012). Our larger dispersion arises as a result of including the scatter of the residuals in Eqs. (5) and (6).
Note the small asymmetry of the distribution in Fig. 4. This might be because of a small bias in the calibration of the photometric metallicity relation. Nemec (2004) showed that the calculated photometric metallicities of the most metal-poor stars within the very metal-poor globular cluster NGC 5053 were systematically higher by 0.3 dex than the metallicities derived from high resolution spectroscopy. The problem was identified originally by Jurcsik & Kovacs (1996) and further discussed in Smolec (2005), Nemec (2004), and Nemec et al. (2013).
 |
Fig. 4 Global OGLE-III sample photometric metallicity distribution, resulting from the MC procedure. The distribution peaks at [Fe/H] = −0.97 ± 0.29 dex, which is in good agreement with the [Fe/H] = −1.02 ± 0.25 dex determined by Pietrukowicz et al. (2012). |
5. Spatial metallicity gradients
5.1. Projected radial gradients
We test the projected radial metallicity gradients by fitting a linear relation to [Fe/H] as a function of the projected galactocentric distance RGCD for each of our 10 000 MC iterations. The resulting projected radial metallicity gradient distribution is shown in the top panel of Fig. 5. The distribution has a mean gradient value of −0.016 ± 0.008 dex Kpc-1, which is intrinsically connected to the observational uncertainty distributions. In a previous study of the OGLE-III Galactic bulge RRab stars, Pietrukowicz et al. (2012) qualitatively concludes that the bulge RR Lyrae seem more or less uniformly (in metallicity) distributed across the bulge area (see their Fig. 10). Here we quantify that the metallicity gradient is indeed very small, but we find that the value is statistically significant.
 |
Fig. 5 Top: probability density distribution of the projected radial (Rgcd) metallicity gradient, which peaks at −0.016 ± 0.008 dex Kpc-1. Bottom: probability density distribution of the vertical (|Z|) metallicity gradient, which peaks at −0.063 ± 0.0013 dex Kpc-1. |
5.2. Angular dependence of the radial gradient
We further investigate the angular dependence of the radial gradient. The sample generated in each iteration is subdivided based on galactocentric quadrants2. Fitting a linear relation to [Fe/H] as a function of RGCD for each quadrant, during our 10 000 samples, results in a metallicity gradient distribution per quadrant are shown in Fig. 6. The α-quadrant shows a significant radial metallicity gradient of −0.014 ± 0.008 dex Kpc-1, while the β-, γ, and δ-quadrants show gradients, −0.018 ± 0.009 dex Kpc-1, −0.029 ± 0.008 dex Kpc-1, and −0.005 ± 0.01 dex Kpc-1, respectively. The variation in the gradient values of the quadrant is likely because of the geometry of the sample where the α-quadrant contains 3407 (compared to the 2281, 1857, 1879, stars in the β-, δ-, and γ-quadrants), while the respective error bars depend on the 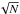 , the geometry of the sample, and the exact error distribution of the corresponding stars.
, the geometry of the sample, and the exact error distribution of the corresponding stars.
 |
Fig. 6 Radial [Fe/H] gradients for each of the galactic quadrants were the histograms present the same quantities as in Fig. 5. The most statistically significant gradient is apparent in the α-quadrant, with a value of −0.029 ± 0.008 dex Kpc-1. The β-, δ- and γ-quadrants show less significant gradients due to a decreased number of stars. |
5.3. Vertical gradients
To obtain the vertical metallicity gradient distribution, shown in the bottom panel of Fig. 5, we assume vertical symmetry with respect to the galactic plane (Z = 0), fold our data sample onto the | Z | and [Fe/H] plane and fit a linear regression to the | Z | and [Fe/H] plane during each iteration of the MC procedure. We determine the mean vertical metallicity gradient to be −0.063 ± 0.013 dex Kpc-1, see Fig. 5. Furthermore, we test both the ±Z directions independently, see Fig. 7 and compare these results with the global vertical metallicity gradient. As expected, the global vertical gradient is governed by the 8100 stars located below the galactic plane. Stars located below the galactic plane exhibit a metallicity gradient of −0.068 ± 0.012 dex Kpc-1, while the 1318 stars located above the galactic plane exhibit an insignificant gradient of −0.01 ± 0.02 dex Kpc-1. The apparent asymmetry in the ±Z direction should not be considered as a vertical asymmetry in the bulge region, as the insignificant gradient in the + Z direction is because of the relatively low star count.
6. Alternative gradient explanations
The gradients we detect are minute, but with relatively small errors thanks to the large sample size, making them statistically significant. Moreover, the values of the detected gradients are similar to some of the gradients reported in the literature (see Conclusions). In this section, we nevertheless investigate, if the observed gradients could possibly be explained by observational or systematic biases. We consider three possible alternative explanations: 1) the possibility that the observed gradients are so small that they could simply arise by chance; 2) the possibility that an unjustified extrapolation of the photometric metallicity law has introduced excess metal-poor/rich stars and therefore may have introduced a gradient; and 3) the possibility that the gradients are induced by a Malmquist bias.
 |
Fig. 7 Top: vertical [Fe/H] gradient distributions for the Z> 0 fields. Distribution peaks at −0.01 ± 0.02 dex Kpc-1 and consists of 1318 RRab stars. Bottom: vertical [Fe/H] gradient distributions for the Z< 0 fields. The distribution peaks at −0.068 ± 0.012 dex Kpc-1 and consists of 8100 RRab stars. |
 |
Fig. 8 Top: normalized histograms of the projected radial (Rgcd) metallicity gradient of original sample (red), and the normalized histograms of the projected radial gradient of the permuted samples (blue). Bottom: same as the top panel for the vertical (|Z|) metallicity gradient. The lack of overlap between the two (red and blue) histograms qualitatively indicates that neither the projected radial nor the vertical gradient can be explained by chance. Quantitatively, the two observed distribution means are at 3.2σ and 8.2σ from the permuted distribution means, reassuring that neither gradient is likely to have been reproduced by chance. |
6.1. Random chance
To investigate the random chance possibility, we test how likely it is that the population still shows a significant metallicity gradient if we randomly swap the galactic positions of the stars. For each MC iteration, we therefore perform 1000 permutations of our stellar sample, by randomly swapping the galactic positions of all stars. During each permutation we take care that the apparent magnitude of each of the stars always remain within the OGLE-III magnitude limits. Each time we fit a linear regression to the Rgcd-[Fe/H] and Z-[Fe/H] planes. The normalized histograms of our permuted projected radial and vertical metallicity gradients are shown in blue in Figs. 8–10.
 |
Fig. 9 Top: normalized histogram of the vertical metallicity gradient for Z> 0 fields (red), shown in Fig. 7, and corresponding histogram (blue) of the permuted sample. The near complete overlap (0.27σ) between the two distributions indicates that the vertical metallicity gradient in the Z> 0 might as well be obtained by pure chance. Bottom: same as the top panel for the Z< 0 fields. The mean value of the observed distribution (red) is located at 3.82σ from the mean of the permuted sample, indicating that it is unlikely that the vertical metallicity gradient for Z< 0 was obtained by chance. |
As expected, the majority of these permutations do not show an appreciable gradient because of the scrambling of the small gradient originally present. The distances between the mean of the red and the blue distributions of the gradients shown in Fig. 8 are 3.2σ and 8.2σ (σ of the blue distribution). The sigma distances for the separate vertical gradients (Z> 0, Z< 0) and for the radial quadrants (α, β, γ, δ) are stated in the captions of Figs. 9 and 10, respectively. Assuming a 3σ cutoff, neither the global projected radial nor the vertical metallicity gradients can be explained by chance. We see that only the gradients presented in the β −, γ −, and δ − quadrants, as well as the Z< 0 field fall within the 3σ cutoff indicating a larger possibility to be reproduced by chance.
6.2. Extrapolation of the metallicity calibration law
Part of our OGLE RR Lyr sample has pulsation periods that fall outside the period range of the data set that was used to calibrate the period-metallicity relation (Eq. (3)). Hence, we investigate if the extrapolation outside this range could cause or enhance the gradients by introducing excessively metal-rich and/or metal-poor stars into the sample. In order to test this we have restricted our sample to stars with P and Φ31 values within the range of 0.35 <P< 0.75 and 2.0 < Φ31< 3.4 as determined by the calibration set used in Smolec (2005). We have reduced our sample size to 7860 RRab stars for which we follow the same procedure, as described in Sect. 3, to determine the metallicity gradients.
We find that limiting our sample to the calibrated data has no major effect on the global vertical metallicity gradient and results in a similar radial metallicity gradient −0.018 ± 0.004 dex Kpc-1. Within the errors, the restricted radial metallicity gradient agrees well with the original global radial metallicity gradient of −0.016 ± 0.008 dex Kpc-1. However, the uncertainty value of the gradient decreases by a factor of two. Figure 11 shows the distribution of sigmas for [Fe/H] and Rgcd of the whole sample in blue and the restricted sample overplotted in red. As expected, the restricted sample [Fe/H] sigma distribution (red) is much narrower than the sigma distribution of the whole sample (blue), see Fig. 11, while the RGCD uncertainty distributions remains fairly constant between the two samples. The reason for this is twofold; the metallicity depends solely on the period and phase differences, while the RGCD depends on the absolute magnitude (MI), galactic position (l, b) and reddening making it only dependent on period and phase differences through MI. In Eqs. (6) and (16), we see that the dominate factor in the calculation of MI is the period, which is nearly equally covered in both samples3. As such the inclusion of stars with larger uncertainty values in [Fe/H], is the dominate factor for the increase of the uncertainty on the metallicity gradients. The dependence of Log Z in the calculation of MI, results in a dependence on [Fe/H]. The inclusion of the 1599 stars that fall outside of the calibration range, and therefore have large uncertainty values of [Fe/H] dominates the increase of the metallicity gradient uncertainty. We conclude that the extrapolation outside of the calibration range of Eq. (3) has an effect on the metallicity sigma distribution but no major influence on the presence or significance of the detected metallicity gradients.
 |
Fig. 10 Normalized histograms for each of the galactic coordinates in red, as shown in Fig. 6 and the corresponding histograms of the permuted sample in blue. The distances between the means of the red and the blue distributions in the the quadrants α, β, γ, and δ are 2.3σ, 2.5σ, 3.2σ, and 0.61σ, respectively. The α quadrant shows the most significant gradient. If we assume a 3σ cutoff, this gradient is the only one unlikely to be explained by chance. The varying significance is due to the corresponding stellar counts, see text for details. |
 |
Fig. 11 Distribution of sigmas for [Fe/H] (right pannel) and Rgcd (left panel) of the whole sample in blue and the sample restricted to the calibration parameters of Smolec (2005) overplotted in red. |
6.3. Malmquist bias
The classical Malmquist bias is a selection bias based on the preferential detection of intrinsically brighter objects at larger distances and affects almost every magnitude limited data sample to some degree. The presence of a Malmquist bias would cause an increasing absolute magnitude trend that could present itself by inducing a trend along the RGCD and Z coordinates. We therefore investigate if a Malmquist bias induced trend could be responsible for (or enhance) the observed radial and vertical metallicity gradients.
In order to avoid creating and fitting synthetic light curves, we have chosen to perform this investigation in the V-band alone, as the absolute V magnitude depends solely on the metallicity, see Eq. (5). We implemented a MC simulation in which we model the probability of finding a star in the bulge at the Cartesian coordinates (X,Y,Z) using a multivariate Gaussian with a mean E [ XYZ ] = (8.5,0,0), and a covariance matrix ![\begin{equation} {\rm Cov}[XYZ]= \begin{bmatrix} 1.00 & 0.00 & 0.00 \\[0.3em] 0.00 & 0.68 & 0.00 \\[0.3em] 0.00 & 0.00 & 0.31 \end{bmatrix} . \label{eq:COVXYZ} \end{equation}](/articles/aa/full_html/2014/11/aa24436-14/aa24436-14-eq144.png) (19)The covariance matrix presented above mimics the expected axisymmetric spheroidal distribution for RR Lyrae (Alcock et al. 1998; Dékány et al. 2013). Given that neither Dékány et al. (2013) nor Alcock et al. (1998) explicitly provide a quantitative description of the axisymmetric spheroid, we use the values of Vanhollebeke et al. (2009) to describe the extent of the bulge region.
(19)The covariance matrix presented above mimics the expected axisymmetric spheroidal distribution for RR Lyrae (Alcock et al. 1998; Dékány et al. 2013). Given that neither Dékány et al. (2013) nor Alcock et al. (1998) explicitly provide a quantitative description of the axisymmetric spheroid, we use the values of Vanhollebeke et al. (2009) to describe the extent of the bulge region.
 |
Fig. 12 Rhc-[Fe/H], RGCD-[Fe/H], and Z-[Fe/H] planes for the simulation used to test for the presence of a Malmquist bias induced gradient. Each panel consist of the three magnitude limited samples (16 <mv< 23 shown in blue, 16 <mv< 18 shown in green, and 16 <mv< 17 shown in red). Each sample has been fitted with a linear regression to test for the presence and strength of a Malmquist bias induced gradient. |
Furthermore, each star is assigned a [Fe/H] value drawn from the Gaussian 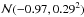 dex. The Cartesian (X,Y,Z) positions are converted to galactocentric polar cylindrical coordinates (RGCD, Θ, Z) and further converted to three dimensional heliocentric Galactic coordinates (Rhc, l, b). A selection based on the heliocentric Galactic coordinates is performed to simulate the spatial distribution of the OGLE-III data set. Each star is then assigned an absorption coefficient (Av) based on their positions in the Marshall et al. (2006) interstellar reddening map. The absolute V magnitude for each of our synthetic stars is calculated using Eq. (5) and finally, using the distance modulus, we calculate the apparent magnitude. Stars with an apparent V magnitude outside the OGLE-III magnitude range (16 <mv< 23) are discarded.
dex. The Cartesian (X,Y,Z) positions are converted to galactocentric polar cylindrical coordinates (RGCD, Θ, Z) and further converted to three dimensional heliocentric Galactic coordinates (Rhc, l, b). A selection based on the heliocentric Galactic coordinates is performed to simulate the spatial distribution of the OGLE-III data set. Each star is then assigned an absorption coefficient (Av) based on their positions in the Marshall et al. (2006) interstellar reddening map. The absolute V magnitude for each of our synthetic stars is calculated using Eq. (5) and finally, using the distance modulus, we calculate the apparent magnitude. Stars with an apparent V magnitude outside the OGLE-III magnitude range (16 <mv< 23) are discarded.
In Fig. 12, we show the Rhc-[Fe/H], RGCD-[Fe/H], and Z-[Fe/H] planes of our simulation with one million synthetic stars. Each panel consists of three different magnitude cuts, shown in different colors. Visual inspection shows the most prominent induced gradients within the Rhc-[Fe/H] plane when the sample is limited to 16 <mv< 17, shown in red. The sample shows a strong metallicity gradient because of the exclusion of instrinically fainter stars that are more metal-rich, due to Eq. (3). As a result, this sample exhibits a Malmquist bias induced gradient of −0.036 ± 0.002 dex Kpc-1. However, when converted to galactocentric coordinates, shown in the middle panel of Fig. 12 in red, the induced gradient changes sign and becomes 0.037 ± 0.003 dex Kpc-1. The change of sign occurs in all three samples and is due to the nonlinear dependence of l and b in the conversion from heliocentric to galactocentric coordinates. To determine if the observed OGLE-III gradients could be explained by a Malmquist bias induced gradient, we take a more detailed look at the simulated sample magnitude limited at 16 <mv< 23, shown in Fig. 12 in blue. Fitting a linear regression to the sample results in a Malmquist biased induced gradient of −0.0018 ± 0.0008 dex Kpc-1 in the heliocentric plane, while in the galactocentric plane a gradient of 0.0012 ± 0.0013 dex Kpc-1 is detected. Neither of these gradients would be detectable within the OGLE-III data sample as presented above, as they fall well within the noise of the OGLE-III simulations.
We perform a similar analysis in the vertical direction, assuming the Sun is located in the Galactic plane. The vertical distance (Z), drawn from the multivariate Gaussian described by Eq. (19), is equal in both the heliocentric and galactocentric coordinates systems. Our synthetic sample, magnitude limited between 16 <mv< 23, is shown in the right most panel of Fig. 12 in blue. Fitting a linear regression with respect to | Z |, leads to an insignificant gradient of −0.002 ± 0.005 dex Kpc-1. We conclude that neither the projected radial gradient nor the vertical gradient observed within the OGLE-III data sample can be explained by a Malmquist bias induced gradient.
7. Conclusion
We have shown that with the OGLE-III Galactic Bulge RR Lyrae catalog, the reddening maps presented by Nataf et al. (2013), and a MC simulation to carefully treat the uncertainty distributions of our observables, it is possible to detect small but significant metallicity gradients within the Galactic bulge. In the process, we have established uncertainty distributions for all of the required observables, accounted for systematics and residuals in the period-luminosity and metallicity-Fourier relations, and accounted for the inhomogeneity of the interstellar extinction toward the Galactic bulge. We find the following results:
-
a mean Galactic bulge RRab metallicity of −0.97 ± 0.29 dex,
-
a projected radial metallicity gradient of −0.016 ± 0.008 dex Kpc-1, and
-
a vertical metallicity gradient of −0.063 ± 0.013 dex Kpc-1.
We find that a decreasing vertical metallicity gradient is consistent with previous studies focusing primarily in the Baade windows and higher latitude regions as, for example, in the works presented by Zoccali et al. (2008), Frogel et al. (1999), and Minniti & Zoccali (2008).In particular, we directly compare our results to those of Ness et al. (2012, 2013), who determined a projected radial and vertical gradients using the same definition of galactocentric position as used here and find good agreement in both the observed projected radial and vertical gradients. In their work Ness et al. (2012, 2013), find that their components A and B, associated with the metal-rich boxy (A) and the vertically thick (B) components of the bulge, contain both projected radial and vertical gradients of −0.02 ± 0.01 dex Kpc-1 and the −0.08 ± 0.04 dex Kpc-1, respectively.
We have checked three possible alternative explanations (random chance, extrapolation of the metallicity calibration law, and a Malmquist induced gradient) of which none can be responsible for the observed gradients. We conclude that small but significant metallicity gradients exist in the RR Lyrae Galactic bulge population.
Acknowledgments
We thank the anonymous referee for a careful reading and insightful comments that led to the improvement of the article. The authors would like to thank Dr. Igor Soszynski and Dr. Marcio Catelan for providing necessary fit and calibrations errors. The authors also thank Dr. Jonas Debosscher for insightful and useful discussions regarding the methodology and procedures used in this work. This work was carried out, in whole or in part through the Gaia Research for European Astronomy Training (GREAT-ITN) network. The research leading to these results has received funding from the European Union Seventh Framework Programme ([FP7/2007-2013]) under grant agreement N° –264895.
References
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 1998, ApJ, 492, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M., Pritzl, B. J., & Smith, H. A. 2004, ApJS, 154, 633 [Google Scholar]
- Dékány, I., Minniti, D., Catelan, M., et al. 2013, ApJ, 776, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Frogel, J. A., Tiede, G. P., & Kuchinski, L. E. 1999, AJ, 117, 2296 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2013, A&A, 552, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., et al. 2013, ApJ, 765, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Jurcsik, J. 1995, Acta Astron., 45, 653 [NASA ADS] [Google Scholar]
- Jurcsik, J., & Kovacs, G. 1996, A&A, 312, 111 [NASA ADS] [Google Scholar]
- Kovacs, G., & Zsoldos, E. 1995, A&A, 293, L57 [NASA ADS] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2013, ApJ, 766, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D., & Zoccali, M. 2008, in IAU Symp. 245, eds. M. Bureau, E. Athanassoula, & B. Barbuy, 323 [Google Scholar]
- Minniti, D., Olszewski, E. W., Liebert, J., et al. 1995, MNRAS, 277, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M. 2004, AJ, 127, 2185 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Cohen, J. G., Ripepi, V., et al. 2013, ApJ, 773, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2012, ApJ, 756, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Picaud, S., & Robin, A. C. 2004, A&A, 428, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrukowicz, P., Udalski, A., Soszyński, I., et al. 2012, ApJ, 750, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2012, ApJ, 746, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smolec, R. 2005, Acta Astron., 55, 59 [NASA ADS] [Google Scholar]
- Soszyński, I., Dziembowski, W. A., Udalski, A., et al. 2011, Acta Astron., 61, 1 [NASA ADS] [Google Scholar]
- Udalski, A., Szymanski, M. K., Soszynski, I., & Poleski, R. 2008, Acta Astron., 58, 69 [NASA ADS] [Google Scholar]
- Vanhollebeke, E., Groenewegen, M. A. T., & Girardi, L. 2009, A&A, 498, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Top panel: total to selective extinction ratio (RI) map of the OGLE-III Galactic bulge sightlines, adapted from Nataf et al. (2013). Bottom panel: total variance Var [ RI ] map, as defined in Eq. (12). Each RI and Var [ RI ] pair defines the normal distribution, which is sampled during our MC procedure to obtain the heliocentric distance of each star. |
| In the text | |
 |
Fig. 2 Result of the MC procedure for a randomly chosen star within our sample. Shown here are the projected 2D metallicity-spatial distributions for each of the galactocentric polar cylindrical coordinates. |
| In the text | |
 |
Fig. 3 [Fe/H]-Rgcd (top panel) and [Fe/H]-Z (bottom panel) planes containg all stars in our sample. Each star is presented as a circle, where the size represents the uncertainty in the distance and the color represents the uncertainty in the metallicity. The red line represents our mean slope and the two green dashed lines represents the ±sigma region. |
| In the text | |
 |
Fig. 4 Global OGLE-III sample photometric metallicity distribution, resulting from the MC procedure. The distribution peaks at [Fe/H] = −0.97 ± 0.29 dex, which is in good agreement with the [Fe/H] = −1.02 ± 0.25 dex determined by Pietrukowicz et al. (2012). |
| In the text | |
 |
Fig. 5 Top: probability density distribution of the projected radial (Rgcd) metallicity gradient, which peaks at −0.016 ± 0.008 dex Kpc-1. Bottom: probability density distribution of the vertical (|Z|) metallicity gradient, which peaks at −0.063 ± 0.0013 dex Kpc-1. |
| In the text | |
 |
Fig. 6 Radial [Fe/H] gradients for each of the galactic quadrants were the histograms present the same quantities as in Fig. 5. The most statistically significant gradient is apparent in the α-quadrant, with a value of −0.029 ± 0.008 dex Kpc-1. The β-, δ- and γ-quadrants show less significant gradients due to a decreased number of stars. |
| In the text | |
 |
Fig. 7 Top: vertical [Fe/H] gradient distributions for the Z> 0 fields. Distribution peaks at −0.01 ± 0.02 dex Kpc-1 and consists of 1318 RRab stars. Bottom: vertical [Fe/H] gradient distributions for the Z< 0 fields. The distribution peaks at −0.068 ± 0.012 dex Kpc-1 and consists of 8100 RRab stars. |
| In the text | |
 |
Fig. 8 Top: normalized histograms of the projected radial (Rgcd) metallicity gradient of original sample (red), and the normalized histograms of the projected radial gradient of the permuted samples (blue). Bottom: same as the top panel for the vertical (|Z|) metallicity gradient. The lack of overlap between the two (red and blue) histograms qualitatively indicates that neither the projected radial nor the vertical gradient can be explained by chance. Quantitatively, the two observed distribution means are at 3.2σ and 8.2σ from the permuted distribution means, reassuring that neither gradient is likely to have been reproduced by chance. |
| In the text | |
 |
Fig. 9 Top: normalized histogram of the vertical metallicity gradient for Z> 0 fields (red), shown in Fig. 7, and corresponding histogram (blue) of the permuted sample. The near complete overlap (0.27σ) between the two distributions indicates that the vertical metallicity gradient in the Z> 0 might as well be obtained by pure chance. Bottom: same as the top panel for the Z< 0 fields. The mean value of the observed distribution (red) is located at 3.82σ from the mean of the permuted sample, indicating that it is unlikely that the vertical metallicity gradient for Z< 0 was obtained by chance. |
| In the text | |
 |
Fig. 10 Normalized histograms for each of the galactic coordinates in red, as shown in Fig. 6 and the corresponding histograms of the permuted sample in blue. The distances between the means of the red and the blue distributions in the the quadrants α, β, γ, and δ are 2.3σ, 2.5σ, 3.2σ, and 0.61σ, respectively. The α quadrant shows the most significant gradient. If we assume a 3σ cutoff, this gradient is the only one unlikely to be explained by chance. The varying significance is due to the corresponding stellar counts, see text for details. |
| In the text | |
 |
Fig. 11 Distribution of sigmas for [Fe/H] (right pannel) and Rgcd (left panel) of the whole sample in blue and the sample restricted to the calibration parameters of Smolec (2005) overplotted in red. |
| In the text | |
 |
Fig. 12 Rhc-[Fe/H], RGCD-[Fe/H], and Z-[Fe/H] planes for the simulation used to test for the presence of a Malmquist bias induced gradient. Each panel consist of the three magnitude limited samples (16 <mv< 23 shown in blue, 16 <mv< 18 shown in green, and 16 <mv< 17 shown in red). Each sample has been fitted with a linear regression to test for the presence and strength of a Malmquist bias induced gradient. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.