| Issue |
A&A
Volume 571, November 2014
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201424296 | |
| Published online | 14 November 2014 | |
Research Note
Probing the evolution of galaxy clusters with the SZ effect
1 Dip. Fisica, Univ. “Tor Vergata”, via Ricerca Scientifica 1, 00133 Roma, Italy
e-mail: lapi@roma2.infn.it
2 INAF, Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio, Italy
3 SISSA, via Bonomea 265, 34136 Trieste, Italy
4 INFN − Sezione di Trieste, via Valerio 2, 34127 Trieste, Italy
5 INAF − Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
Received: 28 May 2014
Accepted: 9 October 2014
In galaxy clusters the thermal Sunyaev-Zel’dovich (SZ) effect from the hot intracluster medium (ICM) provides a direct, self-contained measure of the pressure integrated over crossing lines of sight, that is intrinsically independent of redshift and well suited for evolutionary studies. We show in detail how the size of the effect and its pattern on the sky plane are directly related to the entropy levels in the ICM, and how they characterize the cluster cores and outskirts independently. We find that at redshifts z ≲ 0.3 the signals to be expected in the cores considerably exceed those detected at 10′ resolution with the Planck satellite. We propose that at 1′ resolutions as implemented on recent ground instrumentation for mapping features in individual clusters, the average patterns of the SZ signals can provide a direct and effective way to find and count cool, low-entropy cores and hot, high-entropy outskirts out to z ~ 2. Such counts will tell the timing and the mode of the processes that drive the evolution of the ICM from the distant to the local cluster population.
Key words: cosmic background radiation / galaxies: clusters: general / X-rays: galaxies: clusters / methods: analytical
© ESO, 2014
1. Introduction
The thermal SZ effect (Sunyaev & Zel’dovich 1972, 1980) from a galaxy cluster is produced when cold cosmic microwave background (CMB) photons are upscattered with Thomson cross section σT by the electrons in the hot electron-proton plasma constituting the intracluster medium (ICM). The resulting brightness is proportional to the Comptonization parameter 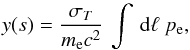 (1)given by the electron thermal pressure pe integrated along the line of sight (l.o.s.) ℓ crossing the cluster at the projected distance s from the center.
(1)given by the electron thermal pressure pe integrated along the line of sight (l.o.s.) ℓ crossing the cluster at the projected distance s from the center.
The effect carries a specific spectral signature, as the frequency-depending prefactor to y(s) goes from negative to positive through 217 GHz. Meanwhile, its 10-4 K amplitudes encase a wealth of information concerning the ICM. The SZ effect provides a self-contained probe of the ICM pressure, given by p ≃ 1.9 pe in the presence of thermal equilibrium and cosmic abundances. By its linear nature such a probe is insensitive to isobaric clumpiness; it is also intrinsically independent of the redshift z, and thus well suited for evolutionary studies.
The SZ effect is now providing comprehensive catalogues that comprise hundreds of clusters selected out to z ~ 1. So far, such selections have been mostly joined to X-ray analyses to describe the pressure profiles of the ICM through the cluster outskirts and within the cores at radii rc≲0.2 R5001. For example, McDonald et al. (2013, 2014) followed up with Chandra 80 clusters selected out to z ≃ 1.2 by the South Pole Telescope with SZ effects at high signal-to-noise S/N> 5 (see Reichardt et al. 2013). They combined highly resolved profiles of the number density n with temperatures T averaged within six ranges of z so as to gather sufficient counts for X-ray spectroscopy and to outline profiles of p ∝ nT. The focus was on profiles with a central temperature dip defining cool core clusters, as opposed to the extended plateau marking non-cool core clusters (CCs and NCCs; see Molendi & Pizzolato 2001; Hudson et al. 2010).
On the other hand, Planck Collaboration V (2013) analyzed their SZ data concerning 62 clusters mostly at z ≲ 0.3, and obtained the cluster signals through the procedure proposed and discussed by Melin et al. (2006). This included several steps: sky maps at several frequencies were cleaned of contaminating sources and deconvolved from the instrumental beam to high S/N, and patterns y(s) were extracted and finally deprojected to obtain radial pressure profiles p(r). The Planck resolution around 10′ can retrieve direct information concerning such profiles only at radii r ≳ 0.5R500, depending in detail on z. To reach inner regions, the observed profiles were matched to XMM-Newton X-ray information resolved on 1′ scales, with the help of fitting formulae of the generalized NFW kind that combine inverse power laws of r (Nagai et al. 2007; Arnaud et al. 2010; Bonamente et al. 2012).
Such a template is attractively simple. By the same token, it is constrained to the z dependence given by P500 ∝ h(z) 8/3, and to centrally diverging shapes p(r) ∝ r-0.3. In the outskirts, the pressure would always decline faster than p(r) ∝ r-3.5; there the signals would rapidly weaken, and noise combines with scatter introduced by deprojection to yield increasing uncertainties that blur physical information. Simplicity is paid for with wide dispersions.
Profiles and fits are best addressed in terms of the specific entropy 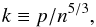 (2)the crucial quantity that controls the ICM sinking or rising (see Bower 1997; Voit 2005) in the gravitational potential well dominantly provided by the dark matter (DM) halo. We shall see how entropy also yields more and closer information concerning the physical processes that prevail at the inner and outer ends; their understanding is urged by everybody in the field, including Planck Collaboration V (2013) and XVI (2014), Eckert et al. (2013), McDonald et al. (2014).
(2)the crucial quantity that controls the ICM sinking or rising (see Bower 1997; Voit 2005) in the gravitational potential well dominantly provided by the dark matter (DM) halo. We shall see how entropy also yields more and closer information concerning the physical processes that prevail at the inner and outer ends; their understanding is urged by everybody in the field, including Planck Collaboration V (2013) and XVI (2014), Eckert et al. (2013), McDonald et al. (2014).
On the other hand, hundreds of SZ-detected clusters are still available, many with measured values of z ≳ 0.3, from Planck (see Planck Collaboration XXIX 2014) and from ground-based surveys (see Carlstrom et al. 2011; Hasselfield et al. 2013; Reichardt et al. 2013). Below we propose a fast way to scan and search such a large data body directly in terms of y(s) on arcmin scales, to retrieve information concerning the ICM evolution and its driving processes at increasing z.
Our aim warrants a detailed analysis as given in the next sections along the following layout. In Sect. 2 we make contact with previous work in showing how entropy governs the pressure profiles in the ICM. In Sect. 3 we detail how their inner and outer shapes independently relate to the entropy levels there. In Sect. 4 we propose and discuss our main point, centered on how such levels can be directly and separately probed with the use of simple scaling features marking the outer and inner SZ signals. In Sect. 5 we discuss how such features depend on the chemical composition of the ICM, on non-thermal contributions to pressure, and on the presence of multiple phases. Finally, Sect. 6 concludes with the specific information to be expected on the physical processes that shape the ICM.
2. Advanced pressure profiles
Our approach starts from the entropy reference run k(r) = kc + kR (r/R)a modulated by two intrinsic and independent parameters, namely, the core value kc and the slope a of the outer, rising ramp (see Voit 2005; Lapi et al. 2005; Cavagnolo et al. 2009). Both originate from gravitational processes during the closely self-similar formation process of the cluster DM halos (Zhao et al. 2003; Wang et al. 2011; Lapi & Cavaliere 2009; 2011).
In the ICM the initial entropy levels are expected to be high. Values kc ~ 102 keV cm2 are set at zt ~ 1 − 2 by the first collapse and virialization of the cores from an initial density perturbation, as the gas mass density nmp is raised by some 102 and the temperature to GM( <rc) mp/ 10 rc ~ a few keVs (see Kravtsov & Borgani 2012; and Cavaliere & Lapi 2013, hereafter CL13). Outer ramp slopes a ≃ 1 (Tozzi & Norman 2001) are built up during the inside-out cluster growth fed over several Gyrs by inflows of outer DM and gas through the virial boundary. The DM goes to increase the halo mass and the concentration C ≃ 3.5 (1 + zt)/(1 + z) (e.g., Zhao et al. 2003; Prada et al. 2012). The gas drives at r ~ R a layer of accretion shocks with Mach numbers given by 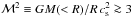 over the outer sound speed cs; the shocks promptly thermalize and stratify a share exceeding 60% of the gas infall energy (see CL13; also Vazza et al. 2009, Kravtsov & Borgani 2012). These processes concur to set an initial state of high entropy (HE) throughout the ICM.
over the outer sound speed cs; the shocks promptly thermalize and stratify a share exceeding 60% of the gas infall energy (see CL13; also Vazza et al. 2009, Kravtsov & Borgani 2012). These processes concur to set an initial state of high entropy (HE) throughout the ICM.
In the dense cores, however, the ICM radiates strongly in X-rays by optically thin thermal bremsstrahlung. Thus over times tc ≈ 0.3 (kc/ 10 keV cm2)1.2 Gyrs the ICM is expected to undergo accelerated cooling, and to gently settle down to a central state of lower entropy with kc ≃ a few keV cm2, until losses are roughly balanced by gains from bubbling or rekindled AGNs in the central member galaxies (see Fabian 2012). On the other hand, on comparable timescales (depending in detail on cluster age and environment richness, see Sect. 6 and CL13) outer inflows are expected to subside and drive diminishing entropy production, so that the outward ramp flattens out to slopes a ≲ 0.7. Thus conditions of low entropy (LE) tend to eventually prevail throughout the ICM; in particular, synchronous core cooling and diminishing outer entropy production would smoothly take the whole ICM from HE to LE overall conditions, and provide the simple picture we shall entertain first.
The actual conditions may be richer, however, and intermediate types will be discussed in Sect. 6. For example, initially many small mergers with their bound gas may keep the outer ICM cool; later massive mergers may hit and reheat the inner ICM for a while (see McCarthy et al. 2007), but pressure (when not sustained by dynamical stresses like that prevail in shocks) recovers from such perturbations over a few sound crossing times, so it is convenient to focus first on the condition for thermal, hydrostatic, and spherical equilibrium in the form 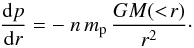 (3)This is governed by the specific gravitational force GM( <r) /r2 produced by the mass distribution in the DM halo (see Cavaliere et al. 2009, hereafter CLFF09) acting on the ICM mass density nmp.
(3)This is governed by the specific gravitational force GM( <r) /r2 produced by the mass distribution in the DM halo (see Cavaliere et al. 2009, hereafter CLFF09) acting on the ICM mass density nmp.
The entropy k as defined in Sect. 1 leads to expressing n ∝ (p/k)3/5. With that, Eq. (3) converts to an equality for dp2/5/ dr; the equality straightforwardly integrates to yield the pressure profile p(r) joining onto the value pR/p1 ≃ ℳ2/ 3, with the jump set by the boundary shocks above the outer value p1. The result writes ![\begin{equation} p(r)=\left[p_{\rm R}^{2/5}+{2\over 5}\,\int_r^R{\mathrm d}x~{m_{\rm p}\,G\, M(<\!\!x)\over x^2\, k^{3/5}(x)}~\right]^{5/2} , \end{equation}](/articles/aa/full_html/2014/11/aa24296-14/aa24296-14-eq61.png) (4)and shows how an entropy run k(r) provides the spine to the corresponding pressure profile p(r). Specifically, our reference run k(r) given at the beginning of this section yields the examples of p(r) illustrated in Fig. 1 for HE and for LE conditions throughout the ICM.
(4)and shows how an entropy run k(r) provides the spine to the corresponding pressure profile p(r). Specifically, our reference run k(r) given at the beginning of this section yields the examples of p(r) illustrated in Fig. 1 for HE and for LE conditions throughout the ICM.
3. Scaling laws
From Fig. 1 it may be also realized that the core profiles depend strongly on the central level kc while the outskirts are modulated by the outer slope a, with an independent role played by these parameters. For any specific cluster their values can be pinned down (using the Supermodel approach, see CLFF09) by choosing the parameters kc and a so that the model p(r) fits the observed shapes2.
Here we stress that before (or even instead of) fitting detailed pressure profiles, the HE/LE classification can be established simply by looking at scaling features of p(r) in terms of entropy. In the cores these read ![\begin{equation} p_{\rm c} \propto k_{\rm c}^{-5/8}~, ~~~~~{\rm and}~~~~\left[{\rm d}p/{\rm d}r\right]_{{r^*}} \propto k_{\rm c}^{-1} \propto p_{\rm c}^{8/5} , \end{equation}](/articles/aa/full_html/2014/11/aa24296-14/aa24296-14-eq63.png) (5)at radii r∗ ≲ 0.1 R500 (see Sect. 3, and CL13); the logarithmic slopes scale as
(5)at radii r∗ ≲ 0.1 R500 (see Sect. 3, and CL13); the logarithmic slopes scale as ![\begin{equation} \left[{{\rm d} \!\ln p \over {\rm d} \!\ln r}\right]_{{r^*}} \propto k_{\rm c}^{-1/3} \propto p_{\rm c}^{1/2} , \end{equation}](/articles/aa/full_html/2014/11/aa24296-14/aa24296-14-eq65.png) (6)yielding an indicator akin to the cuspiness defined for the density profiles by Vikhlinin et al. (2007). We note that the gradient dp/ dr in the cores is proportional to the force GM( <r) /r2 entering Eq. (3). Toward the center this vanishes for matter densities increasing less than r-1 (see data and discussion in Newman et al. 2013) and for a finite ICM entropy, as to yield a maximum of p(r). Then the value of pc does not depend strongly on the detailed choice of r⋆, nor on the presence of any central bright galaxy.
(6)yielding an indicator akin to the cuspiness defined for the density profiles by Vikhlinin et al. (2007). We note that the gradient dp/ dr in the cores is proportional to the force GM( <r) /r2 entering Eq. (3). Toward the center this vanishes for matter densities increasing less than r-1 (see data and discussion in Newman et al. 2013) and for a finite ICM entropy, as to yield a maximum of p(r). Then the value of pc does not depend strongly on the detailed choice of r⋆, nor on the presence of any central bright galaxy.
Thus we see how neatly steep gradients in the cores correlate with high central levels pc; both quantities are much larger for LEs than for HEs, and combine into a clear mark of the former condition. This means that, as kc lowers by a factor of 10, the central peak grows by a factor of 4, and the logarithmic slopes steepen by 2.
CLFF09 matched the boundary shock jumps to the adjoining hydrostatic equilibrium in the outskirts, and derived the scaling p(r) /pR ∝ (r/R)2a − 5. This yields 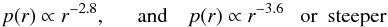 (7)for fully developed HE conditions with a ~ 1.1 and for aged LE conditions with a ≲ 0.7, respectively. How well all such features apply to HE and LE types can be checked in Fig. 1.
(7)for fully developed HE conditions with a ~ 1.1 and for aged LE conditions with a ≲ 0.7, respectively. How well all such features apply to HE and LE types can be checked in Fig. 1.
 |
Fig. 1 Pressure profiles we expect using Eq. (4) for a cluster in overall HE conditions with central entropy level kc = 100 keV cm2 and outer entropy slope a = 1.1 (red line), and for a cluster in overall LE conditions with kc = 10 keV cm2 and a = 0.7 (blue line); the outcome for a mixture of the two HE and LE templates in the 1:3 proportion (black line) is also presented. These profiles are compared with the SZ data from Planck, and with the X-ray observations from XMM-Newton (green squares, with the yellow shaded area illustrating the variance). All data are taken from Planck Collaboration V (2013), and are reproduced for the whole cluster sample (green circles with purple shaded area) and for the CC and NCC subsamples (open blue and red circles, respectively). |
 |
Fig. 2 Our predicted SZ patterns, corresponding to the pressure profiles marked with the same colors as in Fig. 1. The dashed lines refer to a resolution around 1′ (closely matching the unconvolved patterns), and the solid lines to a resolution around 10′ like Planck’s. The data are from SZ observations after Planck Collaboration V (2013; green squares, with yellow shaded area showing the associated variance). |
4. Direct use of SZ patterns
We now proceed toward our main aim, which is to see how direct use can be made of the SZ patterns y(s) on the sky plane; these constitute the primary observables, while the radial pressure profiles p(r) require delicate deprojections along the line of sight ℓ = (r2 − s2)1/2. In Fig. 2 we plot the patterns y(s) that we expect for a fully LE or HE cluster, corresponding to the profiles of p(r) given in Fig. 1.
In the cores, the pattern peaks are given by 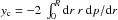 , once Eq. (1) is expressed in terms of r and integrated by parts. When the central pressure peak is as high as applies to LE conditions, its scaling in terms of central entropy dominates the result although in a mitigated fashion, to yield
, once Eq. (1) is expressed in terms of r and integrated by parts. When the central pressure peak is as high as applies to LE conditions, its scaling in terms of central entropy dominates the result although in a mitigated fashion, to yield 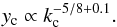 (8)This is derived from the approximation given by CLFF09 for p(r) in the cores that reads
(8)This is derived from the approximation given by CLFF09 for p(r) in the cores that reads ![\begin{equation} p(r) \simeq I^{5/2}(r) =\left [A_0\, {\rm e}^{- A_1\,r^{A_2}}\right]^{5/2} . \end{equation}](/articles/aa/full_html/2014/11/aa24296-14/aa24296-14-eq83.png) (9)The coefficient
(9)The coefficient 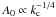 scales up with decreasing kc, as illustrated by the steep dotted line in Fig. 2 (bottom panel) of CLFF09. Meanwhile, A1 and A2 scale down slowly3, and contribute to the milder rise for small kc shown by the solid line in the same figure. In the present context,
scales up with decreasing kc, as illustrated by the steep dotted line in Fig. 2 (bottom panel) of CLFF09. Meanwhile, A1 and A2 scale down slowly3, and contribute to the milder rise for small kc shown by the solid line in the same figure. In the present context, 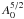 yields just the main scaling
yields just the main scaling 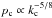 highlighted in Eq. (5); it also dominates yc. To a close approximation, the derivative dp/ dr (see the integration by parts spelled out above) implies that the factor A0 is multiplied by A1A2, which in turn mitigate the scaling as is shown in Eq. (8) and is borne out by comparing the peak ratios in Fig. 2 (dashed lines) with those in Fig. 1.
highlighted in Eq. (5); it also dominates yc. To a close approximation, the derivative dp/ dr (see the integration by parts spelled out above) implies that the factor A0 is multiplied by A1A2, which in turn mitigate the scaling as is shown in Eq. (8) and is borne out by comparing the peak ratios in Fig. 2 (dashed lines) with those in Fig. 1.
For a l.o.s. beyond the core, the integration in the form ![\hbox{$y(s) = 2\, \int_0^{\ell_{m}} {\rm d}\ell \, p[r(\ell)]$}](/articles/aa/full_html/2014/11/aa24296-14/aa24296-14-eq92.png) (with
(with 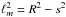 ) shows how the runs of p(r) are smoothed out to yield the slow (for HE), or the mild (for LE) pattern decline shown in Fig. 2.
) shows how the runs of p(r) are smoothed out to yield the slow (for HE), or the mild (for LE) pattern decline shown in Fig. 2.
In the outskirts the pressure profiles p(r) ∝ r2a − 5 with slopes ranging from a ≃ 1.1 to a ≲ 0.7 (see Eq. (7)) correspond to steeper and steeper declines of the patterns y(s), as borne out by Fig. 2 (from red to blue lines); at s = 1 (r = R) all plunge into the boundary value pR set by virial shocks. Specifically, we obtain 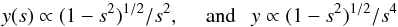 (10)for a = 1 (HE condition) and for a = 0 (low entropy condition), respectively. In brief, by l.o.s. integration the profiles p ∝ r2a − 5 are smoothed out into the patterns y(s) ∝ s2a − 4, before a final plunge at r ≃ R.
(10)for a = 1 (HE condition) and for a = 0 (low entropy condition), respectively. In brief, by l.o.s. integration the profiles p ∝ r2a − 5 are smoothed out into the patterns y(s) ∝ s2a − 4, before a final plunge at r ≃ R.
Thus the patterns corresponding to HE and LE conditions can be identified from their specific inner and outer scaling laws given above, and may be tested on stacked SZ observations as illustrated in Fig. 2. The solid lines show the representation provided by our patterns for the Planck data with their resolution around 10′. The dashed lines show the considerably larger signals to be expected at a resolution of 1′; they closely approach the unconvolved patterns, and vary with entropy just as expected from the scaling laws in Eqs. (8) and (10). A hint at the plunging behavior discussed above may be already discerned in the outer data (see green squares and solid red/black lines in Fig. 2).
We propose that individual patterns y(s) observed at resolutions substantially better than 10′ in the cores and in the outskirts be directly used for purposes of cluster classification and counts in terms of entropy, dispensing with deconvolutions and attendant uncertainties. We have shown that the classification can be pursued in terms of independent entropy levels in the cores and in the outskirts.
In a nutshell, we propose to directly relate the patterns y(s) observed with the SZ effect to entropy levels k(r), so as to produce independent and robust entropy maps in the ICM of the cores and of the outskirts.
5. Stability
How do the above patterns respond to variance in equilibrium conditions and chemical composition? Lapi et al. (2012a; see also references therein) have shown that the total pressure p supporting the equilibrium described by Eq. (3) may include – especially in the outer region of LEs – not only the thermal pressure p, but also a non-thermal, turbulent contribution δp, to yield 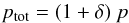 (11)with δ ≲ 40% slowly decaying inward of the shock layer. Such conditions imply correspondingly lower levels of the thermal component p(r) and of the related SZ signal y(s); so the outer shapes discussed in Sect. 4 constitute effective upper bounds. Likewise, pe is somewhat decreased (relative to the thermal equilibrium value given in Sect. 1) for electron temperatures still catching up with ions just downstream from the boundary shocks (see Wong & Sarazin 2009).
(11)with δ ≲ 40% slowly decaying inward of the shock layer. Such conditions imply correspondingly lower levels of the thermal component p(r) and of the related SZ signal y(s); so the outer shapes discussed in Sect. 4 constitute effective upper bounds. Likewise, pe is somewhat decreased (relative to the thermal equilibrium value given in Sect. 1) for electron temperatures still catching up with ions just downstream from the boundary shocks (see Wong & Sarazin 2009).
McDonald et al. (2014) show in their Fig. 6 that even for NCC clusters like SPT-CLJ0014-4952 where X-ray imaging emphasizes scars in the ICM from mergers and central features from sloshing, the SZ mapping is better at rendering centroid location and overall circularity on the sky plane. Along the l.o.s. the SZ signals will be anti-biased when ellipsoidal clusters are observed parallel to their minor axis; for the cluster RX J1347.5-1145 Plagge et al. (2013) find evidence of considerable compression, in line with Bonamente et al. (2012). From statistics of spherically averaged models, Buote & Humphrey (2012) find mean biases ~1% with scatter ≲10%, and less in the cores. So our LE characterization will be minimally affected, while HE outskirts will still provide valuable lower bounds to patterns y(s).
On the other hand, at the center of relaxed LEs some Helium sedimentation may occur (see discussions by Ettori & Fabian 2006 and Bulbul et al. 2011); this will decrease the hydrogen abundance X and increase the values of 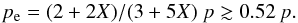 (12)So y will be enhanced, at least, in the core, though conceivably by less than the 4% level given by doubling the cosmic He abundance. On this account, the central values discussed in Sect. 4 constitute effective lower bounds. Thus the above considerations concur to widen the difference between LE and HE conditions both in the cores and in the outskirts.
(12)So y will be enhanced, at least, in the core, though conceivably by less than the 4% level given by doubling the cosmic He abundance. On this account, the central values discussed in Sect. 4 constitute effective lower bounds. Thus the above considerations concur to widen the difference between LE and HE conditions both in the cores and in the outskirts.
In a more radical vein, in LE cores the total entropy kc may be lowered to a few keV cm2 in low-z clusters by the settling of a cooled phase, as highlighted by finely resolved measurements of X-ray brightness (see Panagoulia et al. 2014). This condition will make the central arcmin peaks of y(s) even higher, and easier to recognize with the SZ effect than indicated by Eq. (8).
6. Discussion and conclusions
The SZ effect from galaxy clusters can directly probe the thermal pressure p in their ICM out to redshifts z ~ 1, where the X-ray brightness is so faint as to hinder measuring T and obtain p from p ∝ nT. We have shown in Sect. 3 how the pressure profiles p(r) differ in terms of entropy, the basic quantity that provides the key to characterizing the ICM thermal states in terms of low (LE) or high (HE) entropy conditions. To distinguish LEs from HEs it is enough to focus on a few basic profile features in the core (peak rise correlated with height) and in the outskirts (steep vs. shallow decline) as detailed in Sect. 3.
Even more directly, we have highlighted in Sect. 4 how such a cluster characterization can be carried out directly in terms of the primary SZ patterns y(s), focusing again on their core scaling and outer slopes. The task requires retrieving at resolutions ~1′ the considerable levels of SZ signals that went undetected in cores at resolutions ~10′. Thus efficient use can be made of larger samples, while deprojection uncertainties and template peculiarities are sidestepped. Then probing the ICM with the SZ effect can provide direct and fast statistical tests for redshift evolution of the ICM in cores and in outskirts.
The results may be compared with the simple picture anticipated in Sect. 2, where radiative cooling of cores and diminishing gravitational heating of outskirts − though independent − tend to proceed on comparable timescales of several Gyr. With growing lifetime the DM halo concentration C(z) increases, while radiative cooling and diminishing heating concur to drive the whole ICM away from its initial HE conditions marked by hot cores at kc ~ 102 keV cm2 and steep outer slopes a ≃ 1. Eventually, the ICM (coupled to its ambient by mass inflow and radiation outflow) would proceed toward overall LE states of lower entropy, with kc ≲ 10 keV cm2 and a ≲ 0.7.
At z ≲ 0.3 we expect that our LE core conditions largely superpose to the strong CC clusters (Hudson et al. 2010), as the HEs do with NCC ones. For increasing z, we expect the statistical LE/HE ratio to drift below the values around 1/2 prevailing locally (see Rossetti & Molendi 2010; Santos et al. 2010). We show in Figs. 1 and 2 and their captions a ratio LE/HE ≲1/3 to be more fitting for the SZ-selected sample in Planck Collaboration V (2013) than for its X-ray selected counterparts at lower z. Independent evidence of HE prevalence at high z emerges from observations at multipoles ℓ ~ 3000 of low levels of integrated SZ effect (Reichardt et al. 2011; Efsthathiou & Migliaccio 2012; Lapi et al. 2012a; Hinshaw et al. 2013).
On the other hand, intermediate types will occur even at z ≃ 0.5 when initial levels kc< 50 keV cm2 speed up the central cooling relative to flattening of the outer slope a, and allow a number of strong CCs to be already in place at z ≃ 0.5 (see Semler et al. 2012). In turn, the flattening is speeded up in long-lived clusters, especially at low z and/or in poor environments where the accretion feeds on the wings of the initial perturbation, while the ambient density is thinned out by the accelerating cosmic expansion (see Lapi et al. 2012a). On the other hand, cases with flat outer slope a have been discerned in X-rays also at intermediate z by Eckert et al. (2013), Walker et al. (2013), by Sato et al. (2014), and by McDonald et al. (2014). The feature has been discussed in terms of super-clumps, that is, low entropy gas loosely bound in small, early mergers. Alternatively, taking up from Sect. 2 one may think of it in terms of still incomplete outskirts formation, when low DM masses M( <R) drive slower inflows with lower Mach numbers ℳ2< 3 that cause meager entropy production.
In this complex context, where physical signals and prevailing processes are still to be sorted out, we have stressed the value of the SZ effect in the specific form of the patterns and scaling laws for y(s) as found in Sects. 3 and 4, separately for the cluster outskirts and cores. Here we add that the l.o.s. integrations yielding y(s) near the ends s ≃ 0 and s ≃ R are dominantly contributed by outskirts or cores, respectively. Thus such features of y(s) can also probe intermediate states arising from asynchronous evolutions of cores and outskirts.
In fact, the relative timing of inner and outer ICM processes constitutes a pressing physical issue to be directly addressed with SZ observations. The patterns y(s) can be pursued with developing ground instrumentation such as MUSTANG, BOLOCAM, and CARMA, that have already implemented sensitivities at sub-arcminute resolutions combined with a range of arc-minute fields of view, appropriate for mapping individual features or distant clusters in times from several to a few hours; see the discussions by Mroczkowski et al. (2012) with their S/N maps of MACS J0717.5+3745, by Plagge et al. (2013), and by Mantz et al. (2014) on XLSSU J0217-0345 at z = 1.9, aiming at S/N ~ 6 in 3 h for similar objects. We note that comparatively shorter observations per cluster are required for LE/HE classifications, while the independent core and outskirts patterns that we stress in Sects. 4 and 6 allow a separate census and alleviate requirements on field of view and resolution.
Such a strategy can be effective out to z ~ 2, where high-frequency SZ signals increasingly mix with the far-IR emissions from violent, dusty star formation in proto-spheroidal galaxies, often amplified by gravitational lensing (Lapi et al. 2012b). In fact, such emissions provide an effective probe for protoclusters, the first step toward cluster formation (see Davies et al. 2014; Clements et al. 2014). Other contaminations by (possibly lensed) background radiosources or by the CMB may be relevant at a single, low frequency, but can be cleaned out with standard procedures involving multifrequency observations, as discussed by Melin et al. (2006), Hasler et al. (2012), and Reichardt et al. (2013); see also Shirokoff et al. (2011).
Finally, we note that the z-depending physical conditions of the ICM discussed here are particularly relevant when clusters are used to probe cosmology in depth (see Vikhlinin et al. 2009). The use of reliable ICM templates (different from self-similar) as we propose for LE or HE types will help polish away the residual 10% scatter that still hinders relating strictly such homologous SZ and X-ray quantities as Y500 and YX (see McCarthy et al. 2003; Andreon 2014; Planck Collaboration XVI 2014). With nonthermal pressure included as recalled in Sect. 5, they will also help in pinning down cluster masses to closely constrain the values of cosmological parameters.
The radius R500 embraces a mean overdensity 500 times above the critical density at the epoch of cluster formation, and is related by R500 ≃ R/ 2 to the virial radius R. We adopt the flat, currently accelerating ΛCDM cosmology (see Hinshaw et al. 2013; Planck Collaboration XVI 2014) with round parameters: Hubble constant H0 = 70 km s-1 Mpc-1, matter density ΩM = 0.3 including a baryon density Ωb = 0.04; the Hubble function reads h(z) = [ΩM (1 + z)3 + ΩΛ] 1/2.
The procedure is detailed on http://people.sissa.it/~lapi/Supermodel/
Acknowledgments
We thank G. De Zotti, R. Fusco-Femiano, and K. Husband for helpful discussions. We acknowledge the comments from our referee that stimulated us to improve our presentation. Work supported in part by the MIUR PRIN 2010/2011 “The dark Universe and the cosmic evolution of baryons: from current surveys to Euclid”, and by the INAF PRIN 2012/2013 “Looking into the dust-obscured phase of galaxy formation through cosmic zoom lenses in the Herschel Astrophysical Terahertz Large Area Survey”. A.L. thanks SISSA for the warm hospitality.
References
- Andreon, S. 2014, A&A, 570, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonamente, M., Hasler, N., Bulbul, E., et al. 2012, New J. Phys., 14, 5010 [Google Scholar]
- Bower, R. G. 1997, MNRAS, 288, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, G. E., Hasler, N., Bonamente, M., et al. 2011, A&A, 533, A6 [Google Scholar]
- Buote, D. A., & Humphrey, P. J. 2012, MNRAS, 421, 1399 [NASA ADS] [CrossRef] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Lapi, A. 2013, Phys. Rep., 533, 69 (CL13) [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Lapi, A., & Fusco-Femiano, R. 2009, ApJ, 698, 580 (CLFF09) [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Lapi, A., & Fusco-Femiano, R. 2011, A&A, 525, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clements, D. L., Braglia, F. G., Hyde, A. K., et al. 2014, MNRAS, 439, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, L. J. M., Bremer, M. N., Stanway, E. R., et al. 2014, MNRAS, 438, 2732 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Molendi, S., Vazza, F., & Paltani, S. 2013, A&A, 551, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efstathiou, G., & Migliaccio, M. 2012, MNRAS, 423, 2492 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., & Fabian, A. C. 2006, MNRAS, 369, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Hasler, N., Bulbul, E., Bonamente, M., et al. 2012, ApJ, 748, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, JCAP, 07, 008 [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., & Cavaliere, A. 2009, ApJ, 692, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., & Cavaliere, A. 2011, ApJ, 743, 127 [Google Scholar]
- Lapi, A., Cavaliere, A., & Menci, N. 2005, ApJ, 619, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Cavaliere, A., & Fusco-Femiano, R. 2012a, ApJ, 745, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Negrello, M., González-Nuevo, J., et al. 2012b, ApJ, 755, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Abdulla, Z., Carlstrom, J. E., et al. 2014, ApJ, 794, 157 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Babul, A., Holder, G. P., & Balogh, M. 2003, ApJ, 591, 515 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Bower, R. G., Balogh, M. L., et al. 2007, MNRAS, 376, 497 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2013, ApJ, 774, 23 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2014, ApJ, 794, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Melin, J.-B., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molendi, S., & Pizzolato, F. 2001, ApJ, 560, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T., Dicker, S., Sayers, J., et al. 2012, 761, 47 [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007, ApJ, 668, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., & Sand, D. J. 2013, ApJ, 765, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Panagoulia, E. K., Fabian, A. C., & Sanders, J. S. 2013, MNRAS, 438, 2341 [Google Scholar]
- Plagge, T. J., Marrone, D. P., Abdulla, Z., et al. 2013, ApJ, 770, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. X. 2013, A&A, 554, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVI. 2014, A&A, 566, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Shaw, L., Zahn, O., et al., 2011, ApJ, 755, 70 [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Rossetti, M., & Molendi, S. 2010, A&A, 510, A83 [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., & Böhringer, H. 2010, A&A, 521, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, K., Matsushita, K., Yamasaki, N. Y., et al. 2014, PASJ, in press [arXiv:1406.1600] [Google Scholar]
- Semler, D. R., Suhada, R., Aird, K. A., et al. 2012, ApJ, 761, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Shirokoff, E., Reichardt, C. L., Shaw, L., et al. 2011, ApJ, 736, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Ya. B. 1972, CoASP, 4, 173 [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Ya. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., & Norman, C. 2001, ApJ, 546, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Brunetti, G., & Gheller, C. 2009, MNRAS, 395, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R., Forman, W. R., et al. 2007, in Heating versus Cooling in Galaxies and Clusters of Galaxies, ESO Astrophys. Symp. (Berlin, Heidelberg: Springer-Verlag), 48 [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al., 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, S. A., Fabian, A. C., Sanders, J. S., Simionescu, A., & Tawara, Y. 2013, MNRAS, 432, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Navarro, J. F., Frenk, C. S., et al. 2011, MNRAS, 413, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, K.-W., & Sarazin, C. L. 2009, ApJ, 707, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D. H., Mo, H. J., Jing, Y. P., & Börner, G. 2003, MNRAS, 339, 12 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Pressure profiles we expect using Eq. (4) for a cluster in overall HE conditions with central entropy level kc = 100 keV cm2 and outer entropy slope a = 1.1 (red line), and for a cluster in overall LE conditions with kc = 10 keV cm2 and a = 0.7 (blue line); the outcome for a mixture of the two HE and LE templates in the 1:3 proportion (black line) is also presented. These profiles are compared with the SZ data from Planck, and with the X-ray observations from XMM-Newton (green squares, with the yellow shaded area illustrating the variance). All data are taken from Planck Collaboration V (2013), and are reproduced for the whole cluster sample (green circles with purple shaded area) and for the CC and NCC subsamples (open blue and red circles, respectively). |
| In the text | |
 |
Fig. 2 Our predicted SZ patterns, corresponding to the pressure profiles marked with the same colors as in Fig. 1. The dashed lines refer to a resolution around 1′ (closely matching the unconvolved patterns), and the solid lines to a resolution around 10′ like Planck’s. The data are from SZ observations after Planck Collaboration V (2013; green squares, with yellow shaded area showing the associated variance). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


