| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424382 | |
| Published online | 27 August 2014 | |
HD 152246: a new high-mass triple system and its basic properties⋆
1 Astronomisches Institut, Ruhr–Universität Bochum, Universitätsstr. 150, 44801 Bochum, Germany
e-mail: chini@astro.rub.de
2 Instituto de Astronomía, Universidad Católica del Norte, Avenida Angamos 0610, Casilla 1280 Antofagasta, Chile
3 Astronomical Institute of the Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
4 Thüringer Landessternwarte Tautenburg, 07778 Tautenburg, Germany
5 ESA/Space Telescope Science Institute, 3700 San Martin drive, MD 21218, Baltimore, USA
6 Institut d’Astrophysique et de Planétologie de Grenoble, CNRS-UJF UMR 5571, 414 rue de la Piscine, 38400 St-Martin-d’Hères, France
Received: 12 June 2014
Accepted: 25 July 2014
Analyses of multi-epoch, high-resolution (R ~ 50 000) optical spectra of the O-type star HD 152246 (O9 IV according to the most recent classification), complemented by a limited number of earlier published radial velocities, led to the finding that the object is a hierarchical triple system, where a close inner pair (Ba–Bb) with a slightly eccentric orbit (e = 0.11) and a period of 6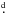 0049 revolves in a 470-day highly eccentric orbit (e = 0.865) with another massive and brighter component A. The mass ratio of the inner system must be low since we were unable to find any traces of the secondary spectrum. The mass ratio A/(Ba+Bb) is 0.89. The outer system has recently been resolved using long-baseline interferometry on three occasions. The interferometry confirms the spectroscopic results and specifies elements of the system. Our orbital solutions, including the combined radial-velocity and interferometric solution indicate an orbital inclination of the outer orbit of 112° and stellar masses of 20.4 and 22.8 M⊙. We also disentangled the spectra of components A and Ba and compare them to synthetic spectra from two independent programmes, TLUSTY and FASTWIND. In either case, the fit was not satisfactory and we postpone a better determination of the system properties for a future study, after obtaining observations during the periastron passage of the outer orbit (the nearest chance being March 2015). For the moment, we can only conclude that component A is an O9 IV star with v sin i = 210 ± 10 km s-1and effective temperature of 33 000 ± 500 K, while component Ba is an O9 V object with v sin i = 65 ± 3 km s-1and Teff = 33 600 ± 600 K.
0049 revolves in a 470-day highly eccentric orbit (e = 0.865) with another massive and brighter component A. The mass ratio of the inner system must be low since we were unable to find any traces of the secondary spectrum. The mass ratio A/(Ba+Bb) is 0.89. The outer system has recently been resolved using long-baseline interferometry on three occasions. The interferometry confirms the spectroscopic results and specifies elements of the system. Our orbital solutions, including the combined radial-velocity and interferometric solution indicate an orbital inclination of the outer orbit of 112° and stellar masses of 20.4 and 22.8 M⊙. We also disentangled the spectra of components A and Ba and compare them to synthetic spectra from two independent programmes, TLUSTY and FASTWIND. In either case, the fit was not satisfactory and we postpone a better determination of the system properties for a future study, after obtaining observations during the periastron passage of the outer orbit (the nearest chance being March 2015). For the moment, we can only conclude that component A is an O9 IV star with v sin i = 210 ± 10 km s-1and effective temperature of 33 000 ± 500 K, while component Ba is an O9 V object with v sin i = 65 ± 3 km s-1and Teff = 33 600 ± 600 K.
Key words: binaries: spectroscopic / stars: massive / stars: fundamental parameters / stars: individual: HD 152246
Based on data products from observations made with ESO telescopes at La Silla Paranal Observatory under programmes 68.D-0095(A), 71.D-0369(A), 073.D-0609(A), 075.D-0061(A), 076.D0294(A), 077.D-0146(A), 079.D-0718(A), 081.D-2008(B), 083.D-0589(B), 086.D-0997(B), 087.D-0946(A), and 089.D-0975(A), extracted from the ESO/ST-ECF Science Archive Facility, and on the BESO spectra.
© ESO, 2014
1. Introduction
The only stable configuration of a stellar triple system seems to consist of a close binary and a substantially more distant third component. These systems are important for testing theories of star formation and stellar evolution in the presence of nearby companions.
The source HD 152246 (HIP 82685) is a member of the Sco OB1 association at a distance of about 1.585 kpc (Sung et al. 2013). Although the star has been included in many photometric and spectroscopic surveys of O stars, the knowledge of its properties is quite limited.
The binary nature of HD 152246 was discovered by Thackeray et al. (1973) who published six radial velocities (RVs) from 1963−1967 showing a range of about 120 km s-1, but this finding has not received much attention. Conti et al. (1977) published one new RV and noted that the star is a RV variable. Penny (1996) suspected the presence of a weak secondary in the CCF peaks, but it was only Stickland & Lloyd (2001) who discovered the presence of sharp and wide lines in the IUE spectra and published two RVs for both components. They interpreted the two systems of lines as belonging to the primary and secondary in a binary system. Mason et al. (1998) observed the star with speckle interferometry, but could not detect any companion for the angular separation range 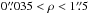 with Δm< 3.
with Δm< 3.
The HD 152246 system has been a part of our monitoring programme for stellar multiplicity (Chini et al. 2012) and attracted our attention because of its varying spectral line profiles. In our preliminary report based on an analysis of the He i 5876 Å line (Nasseri et al. 2013) we showed that HD 152246 must be a hierarchical triple system. What is actually observed is a combination of a broad-line O-type star (component A) and another O-type star with narrow lines, which itself is the primary component Ba of a close pair. The RVs of the narrow-line star follow the orbital motion with an invisible secondary Bb with a period of about 6 d and also a motion around the common centre of gravity with the component A. The RVs of the broad-lined component A follow only the orbital motion in the wide orbit (we had tentatively derived a period of 53 days for it; we revise the period here).
The combined spectral type of HD 152246 was first determined by Morgan et al. (1955) as O9: III:. Later, more accurate but fairly similar properties were found: Schild et al. (1969) and Garrison et al. (1977) classified the star as O9 III while Walborn (1973) and Thackeray et al. (1973) assigned spectral types of O9 III-IV(n) and O8.5 III, respectively. Several published measurements of the visual brightness of HD 152246 are mutually quite consistent (Thackeray et al. 1973; Klare & Neckel 1977; Dachs et al. 1982; Schild et al. 1983; Hog et al. 2000). Mermilliod & Mermilliod (1998) give the following weighted mean value V = 7.m308 ±0.m015. The only deviating value was reported by Heske & Wendker (1984): V = 8.m09, which we suspect could be a misidentification of the star. We also used all Hipparcos Hp observations with flags 0 and 1 (Perryman & ESA 1997) and transformed them to Johnson V following Harmanec (1998) to obtain V = 7.m330 ± 0.m008. The full range of individual values is 0.m05, so a future test for micro-variability would perhaps be useful. In any case it seems that no binary eclipses are observed.
Several – seemingly contradictory – determinations of the projected rotational velocity of HD 152246 were published (see Table 1). It seems clear now that Conti & Ebbets (1977) probably derived v sin i from the unresolved blend of lines of both stars, other investigators mainly measured the width of the narrow component Ba until Stickland & Lloyd (2001) resolved and measured the lines of both spectra.
In this paper we present the analysis of 49 high resolution spectra, obtain rather accurate orbital elements and estimate the basic physical properties of the system.
 |
Fig. 1 Two He i 5876 Å line profiles from different orbital phases. The observed profiles have been fitted by a narrow Gaussian and a wide rotationally broadened profile. The resulting fits are denoted by grey curves. |
Previously published determinations of the projected rotational velocity of HD 152246.
Published and new RVs of components A and Ba.
2. Observations and data reduction
2.1. Spectroscopy
We have secured 49 high resolution (R ~ 50 000) echelle spectra covering the wavelength range from 3620 to 8530 Å and the time interval from May 1999 to October 2013. Twenty-six spectra were taken at the ESO with the spectrograph FEROS (RJDs 51 327.9−56 098.8); the first two spectra from March and April 2002 stem from the ESO 1.52 m telescope, the remaining data come from the MPG/ESO 2.2 m telescope. Twenty-three spectra were obtained with BESO (RJDs 54 913.9−56 585.5)1 at the Universitätssternwarte Bochum on a side-hill of Cerro Armazones in Chile. BESO (Fuhrmann et al. 2011) is a clone of the ESO spectrograph FEROS on La Silla and has been attached to the 1.5 m Hexapod-Telescope. The identical spectrographs allowed a perfect combination of the two data sets. All spectra were reduced with a pipeline based on a MIDAS package adapted from FEROS. The signal-to-noise ratio of the reduced FEROS spectra ranges from 247 to 487; that of the BESO spectra from 65 to 177. For either instrument, the signal-to-noise ratio was measured in the neighbourhood of the He i line at 5876 Å.
At a later stage of the analysis, we also used 9 published RVs of component B and provided a few comments on 2 published RVs of component A (Table 2).
 |
Fig. 2 Visibilities (left panel), closure phase (middle panel) and χ2 map of the Feb 28 PIONIER observation of HD 152246. The best-fit binary model is overlaid. |
Interferometric best-fit measurements and 1σ error-bars.
2.2. Long-baseline interferometry
Interferometric measurements of HD 152246 were obtained on February 24, April 4 and May 8, 2014 using the PIONIER four-beam combiner (Le Bouquin et al. 2011) at the four Auxiliary Telescopes of the ESO Very Large Telescope Interferometer (VLTI, Haguenauer et al. 2008, 2010). The data were reduced with the pndrs package (Le Bouquin et al. 2011). Reduction steps and achieved calibration accuracy on the O-type stars were described earlier (Sana et al. 2013) and will not be repeated here. The data analysis closely follows the procedure used in the Southern Massive Star at High angular resolution survey (Sana et al. 2014), which uniformly analyses PIONIER observations of a sample of over 100 O-type stars.
HD 152246 was clearly resolved at three epochs with a separation of about 3.2−3.3 milli-arcsec (mas). A clear rotation of the binary axis could be detected over the 73 day baseline of our PIONIER observations. Table 3 provides the journal of the interferometric observations together with the parameters of the best fit binary model. Figure 2 shows and example of the measured data and the best fit binary model.
3. Line profiles, radial velocities and orbital periods
To have a guidance to a more sophisticated analysis, we first measured RVs of both components of the strong and usually well-exposed He i 5876 Å line, fitting the narrow component by a Gaussian and the broader one by a rotationally broadened profile. The examples of such fits are shown in Fig. 1 and all RVs, together with nine RVs from the literature, are in Table 2.
We note that Nasseri et al. (2013) originally reported a tentative value of 53 days for the longer period and 6 days for the shorter period. Meanwhile we could recover a number of old spectra from the epoch 1999−2003 which led to a substantial revision of the originally suggested long period.
The analysis of the RV variations soon showed that the RV of the component A varies with a single period, which turned out to be about 470 d. The RVs of component Ba are modulated also by this period (showing anti-phase variations with respect to those of component A), but they also varied with a shorter period of about 6 d. After deriving a more accurate value of the short period, treating data subsets as having individual systemic velocities (to allow for the changes with the 470 d orbit), we included all RVs and derived an orbital solution for the triple system. For this task the programme FOTEL (Hadrava 2004a, and references therein) is well suited. We also verified that the 6 d period is clearly seen in the RVs for the narrow component published by Thackeray et al. (1973), Conti et al. (1977), and Stickland & Lloyd (2001). The situation is a bit more complicated with the two RVs for component A as we shall discuss below.
 |
Fig. 3 Phase plots for both binary orbits. Top panel: RVs of component Ba, prewhitened for the variations in the 470 d orbit and plotted vs. phase for the 6 d period and periastron epoch from Table 4. Open circles denote RVs from the literature. Bottom panel: RV curves of components A and B in the wide orbit. Open circles denote component A, filled circles component B (smaller ones for RVs from the literature). We note that in both plots, RVs −γ are plotted. |
In a second step, we therefore derived a solution for the triple-star system with FOTEL, using all Gaussian RVs for both components measured in our new spectra and also all 9 RVs of component B from the literature, first with equal weights and then weighting the three data subsets by the weights inversely proportional to the square of root-mean-square residuals (rms) from the preliminary solution. This solution is presented in Table 4. The RV curve for the 6 d orbit is shown in Fig. 3 and corresponds to Table 4. The curve for the 470 d orbit is presented in Fig. 4; the parameters based also on the interferometric results as listed in Table 6 were used for its construction.
Stickland & Lloyd (2001) published two RVs for the component A (see Table 2): −109.4 km s-1 at RJD 44 995.7780, phase 0.7811, and −103.0 km s-1 at RJD 45 000.6090, phase 0.7913.
It is clear from Fig. 3 (bottom panel) that these RVs are for some −50 km s-1 too negative than our new RVs. The difference could be made smaller if the true value of the long period would be 474.3 d. However, this change in the period would increase the rms of the orbital solution of component B to 5.6 km s-1, and even then, a deviation of about 30 km s-1 would persist. One can conjecture that the reason for too negative RVs measured by Stickland & Lloyd (2001) lies in that our results (see below) show that v sin i of component A is about 200 km s-1, while they only derived 156 km s-1. As the relation between the narrow and broad profiles measured by Stickland & Lloyd (2001) was similar to that in Fig. 1 (bottom panel) here, the smaller v sin i means that the RVs of broad profiles as measured by them might be erroneously shifted by about one half of the v sin i difference, i.e. more than by 20 km s-1. Such a shift could explain the observed RV difference. The ultimate solution to this problem as well as the discrimination between a number of possible values of KA might come only with future dedicated observations, densely covering the phases of the periastron passage (the first chance being in March 2015). In any case, it is clear that the two RVs by Stickland & Lloyd (2001) provide additional support for the 470 d period.
FOTEL orbital solution for the triple system HD 152246.
4. RV orbital solutions with KOREL
The FOTEL orbital elements were eventually used as initial values for the solution with the spectral-disentangling programme KOREL (Hadrava 2004b). Apart from the He i 5876 Å line, we used five other suitable lines and spectral segments (He i 6678, He i 7065, He ii 5411, O iii 5592, and a longer segment 5670−5835 Å, which contains C iii 5695, C iv 5801, and C iv 5812 Å plus several stronger diffuse interstellar bands) to obtain six independent KOREL solutions.
In practice, we searched the parameter space and ran a number of trial solutions for each spectral region to find out a solution with the lowest sum of residuals. These final solutions and the resulting elements are summarised in Table 5 together with their mean values. We note that KOREL does not provide error estimates so the comparison of several independent solutions gives us some idea about the possible errors of the elements.
We carried out several attempts to detect also some weak lines of component Bb in KOREL solution but with no result. This means that we are unable to obtain the mass ratio between components Ba and Bb and conclude that the component Bb is much less massive than component Ba. This is similar to HD 165246 binary, for which Mayer et al. (2013) found a low mass ratio of 0.17.
5. Three-dimensional orbit of HD 152246 A, B
Having resolved the A,B pair and detected its orbital motion on the plane of the sky opens the possibility of computing the three-dimensional orbit of HD 152246. To this aim, we simultaneously fit the RV and astrometric measurements using the method described in Sana et al. (2013); we only used FEROS and BESO data. We corrected the RVs of component Ba listed in Table 2 from the orbital motion around the centre of mass of the Ba,Bb pair using the orbital solution given in Table 4. We adopted error bars on the A and B RV components given by the residual of the fit in Table 2, i.e. 5.66 and 4.29 km s-1 for component A and B, respectively. We also neglected the astrometric displacement of B attributable to its close companion in the VLTI data. This is a valid assumption given such displacement is likely of the order of 0.1 mas.
We used the averaged KOREL orbital solution as a starting point for our fit. We fixed the distance at 1585 kpc and we worked in the systemic velocity frame (i.e., γ = 0 km s-1 ). The obtained best-fit solution is given in Table 6 and shown in Fig. 4. As explained in Sana et al. (2013), we estimated the uncertainties on the best-fit parameters by Monte Carlo simulations. We randomly drew 1000 artificial RV and astrometric data sets. We preserved the observational time sampling. The data points were taken from Gaussian distributions centred on the best fit solution, using the observational error bars as the Gaussian standard deviations to draw. We then ran the fitting procedure on each of the synthetic data set and we estimated the uncertainties on the best-fit parameters from the distribution of retrieved parameters. The error intervals quoted in Table 6 correspond to the 68% confidence intervals. The intervals are taken as symmetric if the upper and lower error bars do not differ by more than 10%, asymmetric confidence intervals are otherwise provided.
Comparing the results of the three-dimensional orbit with the FOTEL and KOREL orbital solutions (Tables 4 and 5) reveal excellent agreement. The preference for a high eccentricity value is confirmed while we obtained slightly smaller RV semi-amplitudes. Importantly, the orbital inclination i is now constrained to 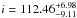 . This allows us to derive absolute masses for the A and B components to 20.35 ± 1.50 and 22.78 ± 1.82 M⊙, i.e. with a relative accuracy of 8%.
. This allows us to derive absolute masses for the A and B components to 20.35 ± 1.50 and 22.78 ± 1.82 M⊙, i.e. with a relative accuracy of 8%.
 |
Fig. 4 Astrometric orbital solution of the wide A, B pair (Table 6) and PIONIER interferometric measurements. The dashed line shows the line of nodes. |
KOREL solutions for the triple star, 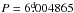 for the short orbit fixed.
for the short orbit fixed.
Best-fit simultaneous RV and interferometric orbital solution of the HD 152246 A,B system.
6. Spectral disentangling and preliminary physical properties of components A and Ba
Keeping the mean elements of Table 5 fixed, we used KOREL to disentangle the line profiles of components A and Ba in all six spectral regions. Synthetic spectra were then fitted to the disentangled profiles in order to estimate the effective temperatures Teff, gravitational acceleration g, projected rotational velocity v sin i , fractional luminosity LR, RV and metallicity Z of the resolved components of the system. We attempted two independent approaches.
6.1. TLUSTY model atmospheres and the OSTAR grid of synthetic spectra
One of us (JN) has developed a programme, which interpolates in a pre-calculated grid of synthetic stellar spectra in the effective temperature, gravitational acceleration, and metallicity. The programme starts with an initial estimate of all the parameters to be optimised. The interpolated spectrum of each component is shifted in RV, broadened to the projected rotational velocity with the programme ROTINS (written by Dr. I. Hubený) and multiplied by the fractional luminosity of the modelled component. The synthetic spectrum is compared to the disentangled one (normalised to the common continuum of the system) and the initial parameters are optimised by minimisation of χ2 (defined by Eq. (1) below) until best match is achieved: ![\begin{eqnarray} \chi^2 = \sum_{i=1}^{\rm N}w_{\rm i}\left[I_{\rm i}^{\rm disen} - I_{\rm i}^{\rm synt}\left(T_{\rm eff}, g, v_{\rm R}\sin i, L_{\rm R}, {\rm RV}, Z\right)\right]^2. \label{chisquare} \end{eqnarray}](/articles/aa/full_html/2014/08/aa24382-14/aa24382-14-eq186.png) (1)Here N is the number of disentangled components of the system,
(1)Here N is the number of disentangled components of the system, 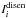 the disentangled spectrum,
the disentangled spectrum, 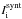 the synthetic spectrum and wi the weight of the i-th component. Fractional luminosities must satisfy the condition that
the synthetic spectrum and wi the weight of the i-th component. Fractional luminosities must satisfy the condition that 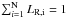 and metallicities must satisfy the condition Zi = Z1, for i = 1...N. The χ2 is minimised using the downhill simplex method (Nelder & Mead 1965).
and metallicities must satisfy the condition Zi = Z1, for i = 1...N. The χ2 is minimised using the downhill simplex method (Nelder & Mead 1965).
All the weights of the disentangled spectra were set to one and the interpolation was carried out in the OSTAR grid (Lanz & Hubeny 2003) based on TLUSTY model atmopspheres (Hubeny & Lanz 1995). Several short segments covering the neighbourhood of the spectral lines mentioned in Table 5 were optimised simultaneously and for both components at once, the C iii 5696 Å and the C iv 5801 and 5811 Å lines being treated as two separate data segments (not as one long segment as in KOREL). The results of minimisation of Eq. (1) are summarised in Table 7. To estimate uncertainties of all derived parameters, we repeated the optimisation of χ2 hundred times, each time starting the optimisation from a random point. The solutions having the final χ2 less than 1.06 times higher than the χ2 of the best solution were used to estimate the errors. The largest source of the error, uncertainty in the spectra (re)normalisation of the disentangled profiles, was not taken into account2. This means that the errors quoted in Table 7 should be taken as lower limits.
On modelling side, we note that TLUSTY models are static plane-parallel models with full non-LTE metal line blanketing. They are suitable for O stars that have weak stellar winds.
Results of the best fit of the OSTAR grid of synthetic spectra to the observed ones.
While the general fit of the disentangled by synthetic spectra resulting from the final solution of Table 7 was quite satisfactory, deviations up to several per cent of the continuum level were found in the cores of several investigated spectral lines.
There is a pronounced disagreement between the disentangled and synthetic spectra for the C iii 5696 Å line. The observed line is in emission in component Ba. According to the synthetic spectra, this line should be in emission only at low log g . When we tried to fit this line, and simultaneously also He ii and He i lines, we ended with a strong disagreement with reality. However, we note that the presence of the 5696 Å emission is common among main-sequence stars. The case of 15 Mon (O7 V) is known (Wilson 1955); see the ELODIE spectrum (Moultaka et al. 2004). By chance, we found that the line is in emission also in several O8 V stars: HD 161853 (FEROS spectrum) or in HD 49149 and HD 46966 (ELODIE spectra).
We also note that He i 6678 Å line, and the two C iv lines for both, A and Ba component are stronger than suggested by the synthetic model but this difference is only on the level of 1% of the continuum level only. Once again, at least for He i line, such a behaviour is not unusual and has been observed for two other O stars, SZ Cam (Lorenz et al. 1998), and V1331 Aql (Lorenz et al. 2005).
 |
Fig. 5 Disentangled spectrum of diffuse interstellar bands in the 5680−5820 Å. |
It would be worth of investigation whether the observed deviations are indicative of a temperature stratification in the extended atmospheres and/or winds around the objects in question. For those colleagues, who study the diffuse interstellar bands, we also plot in Fig. 5 the disentangled spectrum of diffuse interstellar bands in the region from 5680 to 5820 Å, normalised to the joint continuum of the system.
6.2. FASTWIND model spectra
We also attempted to adjust the disentangled spectra with the FASTWIND model atmosphere (Puls et al. 2005; Rivero González et al. 2012) using an automatic fitting method (Mokiem et al. 2005; Tramper et al. 2011). In contrast to TLUSTY this programme uses spherical model atmospheres, non-LTE with line blanketing and models also stellar wind lines. On the other hand, FASTWIND only computes H and He profiles, i.e. there is no information for the C iii 5696 Å line. The atmospheres are not truly hydrodynamic, however, as the programme does not solve for the wind structure but adopts a wind law. Accurate mass loss estimates from the optical require recombination lines, like Hα or He ii 4686 Å which have not yet been analysed in the current investigation. The results of the fit are summarised in Table 8. A detailed fit of some spectral line was not perfect in this case either.
Results of the best fit of the FASTWIND grid of synthetic spectra to the observed ones.
More generally, it is obvious that a really reliable line profile modelling awaits further improvements, both on the theoretical and observational side. For instance, Massey et al. (2013) compared FASTWIND and independent CMFGEN model spectra with observed spectra of 10 O stars and noted that the surface gravities of FASTWIND are systematically lower by 0.12 dex compared to CMFGEN and that both programmes have some problems to fit the He i lines for higher luminosity stars. Concerning the observed spectra, we believe that the spectral disentangling will provide better line profiles of both visible stellar components after we obtain good spectra during the periastron passage in the outer orbit.
6.3. Preliminary physical properties of components A and Ba
Considering the above exercises, we warn against taking the results of Tables 7 and 8 too seriously at the present stage of investigation and postpone a more accurate determination of the physical properties of the system for a future study. For the moment, we consider reasonable to adopt Teff = 33 000 ± 500 and v sin i = 210 ± 10 km s-1 for component A, and Teff = 33 600 ± 600 and v sin i = 65 ± 3 km s-1 for component Ba.
7. Physical properties of the system
According to Sota et al. (2014) the integrated spectral type of HD 152246 is O9 IV, and according to Mermilliod & Mermilliod (1998) V = 7.m308, = 0.m169. For that spectral type, the expected ()0 = −0.m30, therefore the excess E() = 0.m47. HD 152246 is close to NGC 6231 (angular separation of about 45′). Sung et al. (2013) gives for this cluster R = 3.m20 and a distance modulus of 11.0 (d = 1585 pc). The systemic velocity of NGC 6231 is −27.28 ± 2.98 as obtained from 10 high-mass stars (Sana et al. 2008); the scatter of individual RVs complies with the systemic velocity of HD 152246 as given in Table 6 corroborating its membership in Sco OB 1 association.
Moreover, Sana et al. (2005) derived basic physical properties of the massive spectroscopic and eclipsing binary CPD−41°7742, a member of NGC 6231 for which they were able to derive the distance modulus of 10.92 ± 0.16, in agreement with the above value. Applying the colour excess and a distance modulus of 11.0 to HD 152246, we obtain V0 = 5.m80 and MV = −5.m20.
The fitting of the disentangled spectra yields the monochromatic flux ratio between the narrow-lined component Ba and broad-lined component A as 0.429/0.571 = 0.751. This is close to the ratio 0.77 found in the H band by PIONIER (Table 3). However, we already noted that in this case the disentangling might not be reliable. Therefore, we prefer the value 0.77; the corresponding magnitude difference is 0.m284. Then the magnitude MV of the A component is −4.m58, of the B component −4.m30. Martins et al. (2005) has MV = −4.m05 for O9 V and −5.m25 for O9 III; the agreement with the expected magnitude of component A (O9 IV) is a very good one. Component Ba is then O9 V.
The typical expected mass for HD 152246 A, based on its spectral type, is ~20 M⊙ (Martins et al. 2005), in agreement with the derived dynamical mass. Since the expected mass for an O9 V star is 17.5 M⊙, the secondary Bb should contribute by about 6 M⊙; the mass ratio of 0.3 between Bb and Ba is quite acceptable given the SB1 nature of HD 152246B (the luminosity of the secondary can be neglected in the discussion made above).
 |
Fig. 6 Position of HD 152246 A and Ba in the HRD. Evolutionary tracks and isochrones of Brott et al. (2011) with initial rotation rate of 100 km s-1 are overlaid. |
8. Discussion
8.1. Evolutionary status
We used the BONNSAI3 Bayesian tool (Schneider et al. 2014) to compare the observational constraints and the single massive star evolutionary models of Brott et al. (2011). We used a Saltpeter IMF and flat priors for the age and initial rotational velocity.
For the A component, we provided the observed Teff, log Lbol/L⊙, log g, vsini and mass, together with their uncertainty. BONNSAI is able to find a set of models that perfectly reproduce the observed values. These correspond to initial masses of 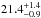 M⊙ and age of 4.7 ± 0.3 Myr.
M⊙ and age of 4.7 ± 0.3 Myr.
For the Ba component, we provided the same parameters with the exception of the stellar mass, that is not directly constrained by our observations owing to the uncertain mass of the Bb component. No model was able to reproduce all parameters. The main issue was that our derived log g is too low. We removed the observational constraint on the gravity and re-ran BONNSAI. The set of models able to reproduce our observations indicate log g = 4.03 ± 0.15, a present day mass of 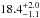 and an age of
and an age of 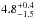 Myr. The agreement of the evolutionary mass of component Ba with the expected one based on its spectral properties is excellent. Similarly the evolutionary ages of both A and Ba component are identical, suggesting a coeval formation of the system. The location of both components in the Hertzsprung-Russell diagram (HRD) is displayed in Fig. 6. The derived age of HD 152246 agrees with that of other high-mass stars in NGC 6231 although the latter ones are model-dependent (Sung et al. 2013). If the rotating models of Ekström et al. (2012) are adopted the age is 4.0 − 7.0 Myr.
Myr. The agreement of the evolutionary mass of component Ba with the expected one based on its spectral properties is excellent. Similarly the evolutionary ages of both A and Ba component are identical, suggesting a coeval formation of the system. The location of both components in the Hertzsprung-Russell diagram (HRD) is displayed in Fig. 6. The derived age of HD 152246 agrees with that of other high-mass stars in NGC 6231 although the latter ones are model-dependent (Sung et al. 2013). If the rotating models of Ekström et al. (2012) are adopted the age is 4.0 − 7.0 Myr.
8.2. Rotational velocities and dynamical status
Intriguingly, the very similar A and Ba components in HD 152246 presents very different projected rotational velocities of 200 and 60 km s-1. Assuming the rotation and orbital spins of the wide binary are aligned, we would derive very similar values of 220 and 65 km s-1.
However, given the masses of the Ba, Bb system are relatively well constrained to about 18.4 and 4.4 M⊙, we can use the FOTEL orbital solution of Table 4 to estimate the orbital inclination of the Ba, Bb pair. We obtain iBa,Bb ≈ 32°. Assuming this time that rotation axis of the Ba component is aligned with the orbital spin of the short period system, we then obtain vrot,Ba ≈ 120 km s-1, i.e. still significantly lower that the one of the A component.
BONNSAI best models indicate a probable radius of 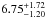 R⊙ for the Ba component. Tidal synchronisation of Ba in the Ba, Bb 6 d orbit would result in rotational velocity of
R⊙ for the Ba component. Tidal synchronisation of Ba in the Ba, Bb 6 d orbit would result in rotational velocity of 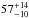 km s-1. Such velocity is in agreement with the measured projected rotational velocity and would suggest an inclination close to 90° for the spin axis of HD 152246 Ba. If this scenario is correct, then it would mean that the spin and orbital axis are not aligned in the Ba, Bb system. One might also speculate whether the star formation process had not allotted similar amounts of angular momentum to both components A and B. If so, this resulted in fast spin for A and the creation of a binary star in B.
km s-1. Such velocity is in agreement with the measured projected rotational velocity and would suggest an inclination close to 90° for the spin axis of HD 152246 Ba. If this scenario is correct, then it would mean that the spin and orbital axis are not aligned in the Ba, Bb system. One might also speculate whether the star formation process had not allotted similar amounts of angular momentum to both components A and B. If so, this resulted in fast spin for A and the creation of a binary star in B.
9. Conclusions
Several conclusions can be drawn here:
-
i.
the evolutionary ages of the O stars in HD 152246suggest a co-eval formation of the triple system;
-
ii.
with orbital inclination iA,B ≈ 112° and iBa,Bb ≈ 30 (or 150°) the two orbits are not co-aligned;
-
iii.
the components A and Ba likely have different rotational velocities;
-
iv.
the component Ba is possibly synchronised, but if this is correct the spin and orbital axis are not aligned;
-
v.
HD 152246 A,B pair has an eccentricity significantly higher than expected from the period-eccentricity diagram of other O-type systems (Sana et al. 2012).
It is possible that several of these properties result from the hierarchical nature and extreme eccentricity of the system. In this scenario, each close encounter of the Ba, Bb pair with the A component would perturb the Ba, Bb inclination and spin alignments. Even if the A and Ba components were born identical, the regular interactions between the three bodies may result in different rotation velocities. Alternatively, HD 152246 may be born as hierarchical quadruple systems formed by two close-binaries. The Aa, Ab initial binary may have been driven into coalescence because of stellar evolution (if the initial period was extremely short) or dynamical interaction with the Ba, Bb pair. This may have lead to a catastrophic event that may have pumped up the eccentricity of the wide system and left a rapidly rotating A component. Such event should however have happened early in the evolutionary life of HD 152246 as no rejuvenation effect is seen in the HRD. Future abundance determination of the HD 152246 components may help provide further constraints on these scenarios.
The BONNSAI web-service is available at http://www.astro.uni-bonn.de/stars/bonnsai
Acknowledgments
This publication is supported as a project of the Nordrhein-Westfälische Akademie der Wissenschaften und der Künste in the framework of the academy programme by the Federal Republic of Germany and the state Nordrhein-Westfalen. The research of P.H., P.M., and J.N. was supported by the grant P209/10/0715 of the Czech Science Foundation and from the research programme MSM0021620860. We are grateful for the help of A. Barr Domínguez, K. Fuhrmann, L. Kaderhandt and M. Ramolla during the observations and the reduction. We thank Universidad Católica del Norte in Antofagasta, Chile, for continuous support. The use of the NASA/ADS bibligraphical service and SIMBAD electronic database are gratefully acknowledged. PIONIER is funded by the Université Joseph Fourier (UJF), the Institut de Planétologie et d’Astrophysique de Grenoble (IPAG), the Agence Nationale pour la Recherche (ANR-06-BLAN-0421 and ANR-10-BLAN-0505), and the Institut National des Sciences de l’Univers (INSU PNPand PNPS).The integrated optics beam combiner result from a collaboration between IPAG and CEA=LETI based on CNRS R&T funding.
References
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., et al. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S., & Ebbets, D. 1977, ApJ, 213, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S., Leep, E. M., & Lorre, J. J. 1977, ApJ, 214, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Dachs, J., Kaiser, D., Nikolov, A., Sherwood, W. A. 1982, A&AS, 50, 261 [NASA ADS] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&AS, 537, 146 [Google Scholar]
- Fuhrmann, K., Chini, R., Hoffmeister, V. H., et al. 2011, MNRAS, 411, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Grigsby, J. A., Morrison, N. D., & Anderson, L. S. 1992, ApJS, 78, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Garrison, R. F., Schild, R. E., & Hiltner, W. A. 1977, ApJS, 35, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Hadrava, P. 2004a, Publ. Astron. Inst. Acad. Sci. Czech Rep., 92, 1 [Google Scholar]
- Hadrava, P. 2004b, Publ. Astron. Inst. Acad. Sci. Czech Rep., 92, 15 [Google Scholar]
- Haguenauer, P., Abuter, R., Alonso, J., et al. 2008, in SPIE Conf. Ser., 7013, 11 [Google Scholar]
- Haguenauer, P., Alonso, J., Bourget, P., et al. 2010, in SPIE Conf. Ser., 7734, 3 [Google Scholar]
- Harmanec, P. 1998, A&A, 335, 173 [NASA ADS] [Google Scholar]
- Heske, A., & Wendker, H. J. 1984, A&AS, 57, 205 [NASA ADS] [Google Scholar]
- Hog, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Howarth, I. D., Siebert, K. W., & Hussain, G. A. J. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Klare, G., & Neckel, T. 1977, A&AS, 27, 215 [NASA ADS] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bouquin, J.-B., Berger, J.-P., Lazareff, B., et al. 2011, A&A, 535, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenz, R., Mayer, P., & Drechsel, H. 1998, A&A, 332, 909 [NASA ADS] [Google Scholar]
- Lorenz, R., Mayer, P., & Drechsel, H. 2005, MNRAS, 360, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Neugent, F., Hillier, D. J., Puls, J. 2013, ApJ, 768, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P., Harmanec, P., & Pavlovski, K. 2013, A&A, 550, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.-C., & Mermilliod, M. 1998, Online catalogue of UBV photometry http://obswww.unige.ch/gcpd/cgi-bin/photoSys.cgi [Google Scholar]
- Mokiem, M. R., de Koter, A., Puls, J., et al. 2005, A&A, 441, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, A&A, 441, 711 [Google Scholar]
- Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Nasseri, A., Chini, R., Harmanec, P., et al. 2013, EAS Pub. Ser., 64, 411 [CrossRef] [EDP Sciences] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Penny, L. R. 1996, ApJ, 463, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues, ESA SP Ser. 1200 (Noordwijk: ESA Publ. Division) [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivero González, J. G., Puls, J., Najarro, F., Brott, I. 2012, A&A, 537, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Antokhina, E., Royer, P., et al. 2005, A&A, 441, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Gosset, E., Nazé, Y., et al. 2008, MNRAS, 386, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Mahy, L., et al. 2013, A&A, 553, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, submitted [Google Scholar]
- Schild, R. E., Hiltner, W. A., & Sanduleak, N. 1969, ApJ, 156, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, R. E., Garrison, R. F., & Hiltner, W. A. 1983, ApJS, 51, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, F. R. N., Langer, N., de Koter, A., et al. 2014, A&A, in press DOI: 10.1051/0004-6361/201424286 [Google Scholar]
- Sota, A., Maíz Apellániz, J., Morrell, N. I., et al. 2014, ApJS, 211, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Stickland, D. J., & Lloyd, C. 2001, The Observatory, 121, 1 [NASA ADS] [Google Scholar]
- Sung, H., Sana, H., & Bessell, M. S. 2013, AJ, 145, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Thackeray, A. D., Tritton, S. B., & Walker, E. N. 1973, Mem. Roy. Astron. Soc., 77, 199 [Google Scholar]
- Tramper, F., Sana, H., de Koter, A., & Kaper, L. 2011, ApJ, 741, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1973, AJ, 78, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. 1955, The Observatory, 75, 222 [NASA ADS] [Google Scholar]
All Tables
Previously published determinations of the projected rotational velocity of HD 152246.
Best-fit simultaneous RV and interferometric orbital solution of the HD 152246 A,B system.
Results of the best fit of the OSTAR grid of synthetic spectra to the observed ones.
Results of the best fit of the FASTWIND grid of synthetic spectra to the observed ones.
All Figures
 |
Fig. 1 Two He i 5876 Å line profiles from different orbital phases. The observed profiles have been fitted by a narrow Gaussian and a wide rotationally broadened profile. The resulting fits are denoted by grey curves. |
| In the text | |
 |
Fig. 2 Visibilities (left panel), closure phase (middle panel) and χ2 map of the Feb 28 PIONIER observation of HD 152246. The best-fit binary model is overlaid. |
| In the text | |
 |
Fig. 3 Phase plots for both binary orbits. Top panel: RVs of component Ba, prewhitened for the variations in the 470 d orbit and plotted vs. phase for the 6 d period and periastron epoch from Table 4. Open circles denote RVs from the literature. Bottom panel: RV curves of components A and B in the wide orbit. Open circles denote component A, filled circles component B (smaller ones for RVs from the literature). We note that in both plots, RVs −γ are plotted. |
| In the text | |
 |
Fig. 4 Astrometric orbital solution of the wide A, B pair (Table 6) and PIONIER interferometric measurements. The dashed line shows the line of nodes. |
| In the text | |
 |
Fig. 5 Disentangled spectrum of diffuse interstellar bands in the 5680−5820 Å. |
| In the text | |
 |
Fig. 6 Position of HD 152246 A and Ba in the HRD. Evolutionary tracks and isochrones of Brott et al. (2011) with initial rotation rate of 100 km s-1 are overlaid. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


