| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201423959 | |
| Published online | 05 August 2014 | |
Age, size, and position of H ii regions in the Galaxy
Expansion of ionized gas in turbulent molecular clouds
1
Astrophysics Group, University of Exeter,
EX4 4
QL Exeter,
UK
e-mail:
pascal.tremblin@cea.fr
2
Maison de la Simulation, CEA-CNRS-INRIA-UPS-UVSQ,
USR 3441, Centre d’étude de
Saclay, 91191
Gif-Sur-Yvette,
France
3
Nordita, KTH Royal Institute of Technology and Stockholm
University, Roslagstullsbacken
23, 10691
Stockholm,
Sweden
4
Department of Physics, West Virginia University,
Morgantown
WV
26506,
USA
5
Laboratoire AIM Paris-Saclay (CEA/Irfu – Uni. Paris Diderot –
CNRS/INSU), Centre d’études de
Saclay, 91191
Gif-Sur-Yvette,
France
6
Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de
México, Ap. 70-543,
04510
DF,
Mexico
7
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
8
Univ. Bordeaux, LAB, UMR 5804, 33270
Floirac,
France
9
CNRS, LAB, UMR 5804, 33270
Floirac,
France
Received:
8
April
2014
Accepted:
2
June
2014
Aims. This work aims to improve the current understanding of the interaction between H ii regions and turbulent molecular clouds. We propose a new method to determine the age of a large sample of OB associations by investigating the development of their associated H ii regions in the surrounding turbulent medium.
Methods. Using analytical solutions, one-dimensional (1D), and three-dimensional (3D) simulations, we constrained the expansion of the ionized bubble depending on the turbulence level of the parent molecular cloud. A grid of 1D simulations was then computed in order to build isochrone curves for H ii regions in a pressure–size diagram. This grid of models allowed us to date a large sample of OB associations that we obtained from the H ii Region Discovery Survey (HRDS).
Results. Analytical solutions and numerical simulations showed that the expansion of H ii regions is slowed down by the turbulence up to the point where the pressure of the ionized gas is in a quasi-equilibrium with the turbulent ram pressure. Based on this result, we built a grid of 1D models of the expansion of H ii regions in a profile based on Larson’s laws. We take the 3D turbulence into account with an effective 1D temperature profile. The ages estimated by the isochrones of this grid agree well with literature values of well known regions such as Rosette, RCW 36, RCW 79, and M 16. We thus propose that this method can be used to find ages of young OB associations through the Galaxy and also in nearby extra-galactic sources.
Key words: stars: formation / HII regions / methods: observational / methods: numerical / ISM: structure
© ESO, 2014
1. Introduction
The age of a star cluster can be derived using photometry or spectroscopy and evolutionary tracks in the Hertzsprung-Russell (HR) diagram (e.g. Meynet & Maeder 2003; Martins et al. 2010, 2012). To be precise, photometric methods require the analysis of a large statistic of stars, which can be tedious and is very difficult for a single object because of the uncertainties. Spectroscopic methods are more reliable but the analysis of many objects is also needed to derive an estimation of the cluster age. When the star cluster contains massive stars that ionize their environment, it is possible to use the size of the ionized gas bubble and infer the time needed for the expansion using an analytical solution such as that found by Spitzer (1978) and Dyson & Williams (1980). This method is commonly used (e.g. Zavagno et al. 2007) and yields a reasonable estimate, however, this solution is not exact and assumes a completely homogeneous medium. Therefore, the density variations and the turbulence of the gas are usually neglected. Indeed, Tremblin et al. (2012) showed that the size of the region can be influenced by the turbulence. In the present paper, we aim to quantify this effect to build a reliable method that can be used to date OB associations.
The paper is organized as follows. In Sect. 2, we quantify the interaction between the ionization of an OB association and the turbulence of the surrounding molecular gas using 1D and 3D simulations and comparisons with analytical solutions. In Sect. 3, we present our investigation of this interaction in observations by comparing the ionized gas pressure of a sample of H ii regions in the HRDS survey (Anderson et al. 2011) with the turbulent ram pressure that can be derived from Larson’s laws. In Sect. 4, we describe how we built a grid of 1D simulations that can be used to find an estimate of the dynamical age of these regions. The method is tested on four well known regions (Rosette, M 16, RCW 79, and RCW 36) for which we found photometric age estimations in the literature. Finally, in Sect. 5 we discuss the limitations and advantages of our approach.
2. Development of H ii regions in a turbulent medium
The expansion of 1D, spherical H ii regions in a homogeneous medium is a
theoretical exercise whose first solution was proposed by Spitzer (1978) and Dyson & Williams
(1980). Their solution can be written in terms of the initial Strömgren radius
rs: 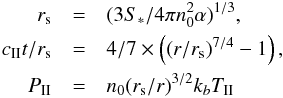 (1)where
S∗
is the production rate of ionizing photons, n0 the gas density of the initial
homogeneous medium, α the recombination rate, and cII and
TII the sound speed and temperature in the
ionized gas. Although this solution is accurate at early times, it is obviously wrong for
very long times since the radius of the ionized bubble would diverge to infinity. The radius
cannot increase indefinitely because the expansion is driven by the ionized gas pressure
that decreases similar to r−3/2 (see Eq. (1)), and the expansion will stop when this
pressure reaches the pressure of the external medium (neglected in the solution given by Eq.
(1)). A simulation of this phenomenon can
be found in Tremblin et al. (2011, Fig. 1).
(1)where
S∗
is the production rate of ionizing photons, n0 the gas density of the initial
homogeneous medium, α the recombination rate, and cII and
TII the sound speed and temperature in the
ionized gas. Although this solution is accurate at early times, it is obviously wrong for
very long times since the radius of the ionized bubble would diverge to infinity. The radius
cannot increase indefinitely because the expansion is driven by the ionized gas pressure
that decreases similar to r−3/2 (see Eq. (1)), and the expansion will stop when this
pressure reaches the pressure of the external medium (neglected in the solution given by Eq.
(1)). A simulation of this phenomenon can
be found in Tremblin et al. (2011, Fig. 1).
Recently, Raga et al. (2012) proposed a new 1D
spherical analytical solution of the expansion of H ii regions that takes into
account the post-shock material, and therefore the pressure of the external medium, in the
equation of motion of the ionization front: 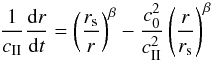 (2)where
c0
is the sound speed in the initial medium, and β is equal to 3/4 for a spherical geometry.
Neglecting the last term in Eq. (2) yields
the equation derived by Spitzer (1978) and Dyson & Williams (1980), for which no equilibrium
is possible. Equating Eq. (2) to zero
immediately yields an equilibrium radius req =
rs(cII/c0)4
/ 3, which corresponds to an ionization and
hydrostatic equilibrium for which the pressure of the ionized gas PII is equal to
the pressure of the surrounding medium P0. Raga
et al. (2012) compared this solution to 1D spherical simulations and they both
agree relatively well especially at late times. In the simulation, however, the region
overshoots the equilibrium radius before converging back to it. This effect is not present
in the analytical solution and could be a consequence of the inertia of the shell that is
neglected in the analytical derivation.
(2)where
c0
is the sound speed in the initial medium, and β is equal to 3/4 for a spherical geometry.
Neglecting the last term in Eq. (2) yields
the equation derived by Spitzer (1978) and Dyson & Williams (1980), for which no equilibrium
is possible. Equating Eq. (2) to zero
immediately yields an equilibrium radius req =
rs(cII/c0)4
/ 3, which corresponds to an ionization and
hydrostatic equilibrium for which the pressure of the ionized gas PII is equal to
the pressure of the surrounding medium P0. Raga
et al. (2012) compared this solution to 1D spherical simulations and they both
agree relatively well especially at late times. In the simulation, however, the region
overshoots the equilibrium radius before converging back to it. This effect is not present
in the analytical solution and could be a consequence of the inertia of the shell that is
neglected in the analytical derivation.
 |
Fig. 1 Top: position (relative to the top of the box) of the mean ionization front as a function of time for the 3D turbulent simulations (at Mach 1, 2, and 4 in solid blue) of Tremblin et al. (2012) and the corresponding analytical solutions (dotted red) and 1D simulations (dashed green) in which the turbulence is taken into account by an effective temperature/sound speed. Bottom: snapshots of the column density of the 3D simulations at a time of 1 Myr after the ionization is switched on at the top of the box. The blue-dashed lines show the mean position of the ionization front. |
It has been thought for a long time that this equilibrium cannot be reached in large and diffuse H ii regions, because it would take much longer than the lifetime of the ionizing sources to reach the balance of the two pressures. Although the thermal pressure of the initial medium cannot compensate the ionized gas pressure at early times, Tremblin et al. (2012) showed that the turbulent ram pressure can do the job. We recall this result in Fig. 1. The bottom panels show snapshots at 1 Myr of the column density of three different 3D simulations of the ionization of a turbulent medium with an initial turbulence of Mach 1, 2, and 4. All the simulations were performed with HERACLES1 (Audit et al. 2011). The box is 4 pc3 at a resolution of 4003, the ionizing flux at the top of the box is plane-parallel F∗ = 109 ph s-1 cm-1, the averaged density is n0 = 500 cm-3, and there is no gravity in these runs.
The turbulence investigated here is relatively moderate since one can expect a turbulence
up to Mach 10 from Larson’s laws at this scale (see Larson
1981). The dashed blue line in Fig. 1
represents the mean position of the ionization front in the simulations and it shows that
the ionization front is slowed down by the supersonic turbulence. To quantify this effect,
we adapted Eq. (2) to a plane-parallel
geometry (β is
equal to 1/4) and the equation still has an analytical solution:
![\begin{eqnarray} &&r_{\rm s} = F_*/n_0^2\alpha, \nonumber\\[3mm] &&c_{\rm II}t/r_{\rm s} = f\left(r/r_{\rm s},c_0^2/c_{\rm II}^2\right)-f\left(1,c_0^2/c_{\rm II}^2\right), \nonumber\\[3mm] &&f(x,a) = 4\tanh^{-1}\left(\sqrt{a}x^{1/4}\right)/a^{5/2}-4x^{1/4}/a^2-4x^{3/4}/3a. \end{eqnarray}](/articles/aa/full_html/2014/08/aa23959-14/aa23959-14-eq21.png) (3)To
take the turbulence into account, we replaced the initial temperature T0 in the sound
speed c0 by an effective turbulent temperature:
(3)To
take the turbulence into account, we replaced the initial temperature T0 in the sound
speed c0 by an effective turbulent temperature:
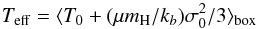 (4)where
μ is the mean
molecular weight, T0 and σ0 the temperature
and velocity field of the simulation before the ionization starts, and the rms average is
computed on the whole box. A discussion on the use of an effective turbulent
temperature/sound speed can be found in Mac Low &
Klessen (2004). Figure 1 shows the time
evolution of the mean position of the ionization front in the 3D simulations, the position
given by the analytical solution and the position of the front in 1D plane-parallel
simulations with the effective turbulent temperature. The analytical solution and the 1D
simulations capture quite well the slowing down of the ionization front caused by the
turbulence at late times. At early times, the ionization front in the 3D simulations
propagates faster with increasing turbulence levels. This is easy to understand: a larger
turbulence results in denser structures and since the total amount of material is fixed in
the box, this implies more low density parts. The average initial Strömgren radius computed
on the varying density field in the 3D runs increases with the turbulence level because
there are more and more low density parts for which the Strömgren radius will be large. In
the analytical solutions and 1D simulations, the initial Strömgren radius is computed on the
average density field, which is constant at n0 = 500 cm-3. Nevertheless, at later times,
the initial conditions do not matter so much, and the 3D simulations show a slowing down of
the propagation of the ionization front as the analytical solutions and the 1D simulations
point out.
(4)where
μ is the mean
molecular weight, T0 and σ0 the temperature
and velocity field of the simulation before the ionization starts, and the rms average is
computed on the whole box. A discussion on the use of an effective turbulent
temperature/sound speed can be found in Mac Low &
Klessen (2004). Figure 1 shows the time
evolution of the mean position of the ionization front in the 3D simulations, the position
given by the analytical solution and the position of the front in 1D plane-parallel
simulations with the effective turbulent temperature. The analytical solution and the 1D
simulations capture quite well the slowing down of the ionization front caused by the
turbulence at late times. At early times, the ionization front in the 3D simulations
propagates faster with increasing turbulence levels. This is easy to understand: a larger
turbulence results in denser structures and since the total amount of material is fixed in
the box, this implies more low density parts. The average initial Strömgren radius computed
on the varying density field in the 3D runs increases with the turbulence level because
there are more and more low density parts for which the Strömgren radius will be large. In
the analytical solutions and 1D simulations, the initial Strömgren radius is computed on the
average density field, which is constant at n0 = 500 cm-3. Nevertheless, at later times,
the initial conditions do not matter so much, and the 3D simulations show a slowing down of
the propagation of the ionization front as the analytical solutions and the 1D simulations
point out.
A direct consequence of this analysis is that an H ii region will be able to expand in a turbulent medium while PII ≥ Pturb until the point where the two pressures equilibrates. It can be seen with the effective temperatures in Fig. 1 that the turbulent ram pressure can easily be one order of magnitude bigger than the thermal pressure. Therefore, it is possible that some regions are in equilibrium with their turbulent environment before the ionizing stars explode.
3. HRDS survey and turbulent ram pressure from Larson’s laws
Using radio continuum surveys of H ii regions, it is possible to test that
PII ≥
Pturb and to see if the equilibrium is
reached for some regions. We used the HRDS Survey2
made with the Green Bank Telescope at 9 GHz whose beam size is 82′′ (see Anderson et al. 2011). The ionizing flux S∗ and the rms
electron density ⟨
nII ⟩ in a region can be computed by using
the radio continuum integrated flux (see Martín-Hernández et
al. 2005): ![\begin{eqnarray} \label{eq_flux} &&\langle n_{\rm II} \rangle = \frac{4.092\times 10^{5}\mathrm{ cm}^{-3}}{\sqrt{b(\nu,T_{\rm e})}} \left(\frac{S_\nu}{\mathrm{Jy}}\right)^{0.5}\nonumber\\[3mm] && \quad \quad \quad \times\left(\frac{T_{\rm e}}{10^4~\mathrm{ K}}\right)^{0.25}\left(\frac{D}{\mathrm{kpc}}\right)^{-0.5}\left(\frac{\theta_D}{''}\right)^{-1.5}, \\[3mm] &&S_* = \frac{7.603\times 10^{46}\mathrm{ s}^{-1}}{b(\nu,T_{\rm e})}\left(\frac{S_\nu}{\mathrm{Jy}}\right)\left(\frac{T_{\rm e}}{10^4~\mathrm{ K}}\right)^{-0.33}\left(\frac{D}{\mathrm{kpc}}\right)^{2}, \\[3mm] &&b(\nu,T_{\rm e}) = 1+0.3195\log\left(\frac{T_{\rm e}}{10^4~\mathrm{K}}\right)-0.2130\log\left(\frac{\nu}{\mathrm{GHz}}\right) \end{eqnarray}](/articles/aa/full_html/2014/08/aa23959-14/aa23959-14-eq30.png) where
Sν is the radio continuum
integrated flux at frequency ν, θD is the angular diameter of the source,
D the
distance from the Sun, and Te the electron temperature in the ionized
plasma.
where
Sν is the radio continuum
integrated flux at frequency ν, θD is the angular diameter of the source,
D the
distance from the Sun, and Te the electron temperature in the ionized
plasma.
 |
Fig. 2 Pressure of the H ii regions of the HRDS survey as a function of radius. The black line is the turbulent ram pressure evaluated from Larson’s laws at the scale of the radius of the region (Eq. (11)). The grey lines show the limits at ± 50% of this relation. The dashed coloured lines are 1D simulations performed in a density and temperature profile based on Larson’s laws at different Lyc fluxes given by the colour bar. The dashed black lines are isochrones (in Myr) built from these simulations, they are used to estimate the age of the H ii regions. To avoid a 3D plot, we assume an constant electron temperature of 8000 K for all of the regions and simulations (only for this plot). |
We deconvolved the beam size of the telescope (82′′) from the full width at half maximum (FWHM) of the flux given in the HRDS survey. The HRDS survey provides a complexity flag that indicates whether the region has a peaked well-defined emission or a complex multi-component emission. We exclude complex regions because the peak of the emission is not representative of the position of the ionizing sources, therefore the size of the region is likely to be wrong. These errors can be corrected with a careful look at the distribution of the radio emission (e.g. as for Rosette and RCW79 in Sect. 4, their emission has the shape of an annulus) but cannot be done automatically. This selection gives us a sample of 119 regions for which the ionizing flux and the rms electron density can be evaluated. Finally, we converted the FWHM into the 1/e2 width (FWHM × 1.7) to have the angular diameter of the region.
If not measured, Te can be inferred from the galacto-centric
distance of the source Rgal: 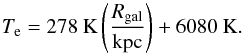 (8)This linear relation is
an average value of the two samples studied in Balser et al.
(2011) and the average value for the HRDS sample is 8000 K. The ionized gas
pressure is then given by:
(8)This linear relation is
an average value of the two samples studied in Balser et al.
(2011) and the average value for the HRDS sample is 8000 K. The ionized gas
pressure is then given by: 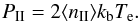 (9)We estimated the
turbulent ram pressure using Larson’s laws (see Larson
1981). Of course the result will be scale dependent, and one has to infer which
scale is going to matter when trying to compute this ram pressure. In Sect. 2, we used the scale of the box to compute the effective
sound speed. For the spherical H ii regions, we assume that the radius of the
region is the scale below which motions will act as an extra pressure against the expansion.
Therefore, taking the Larson’s relations:
(9)We estimated the
turbulent ram pressure using Larson’s laws (see Larson
1981). Of course the result will be scale dependent, and one has to infer which
scale is going to matter when trying to compute this ram pressure. In Sect. 2, we used the scale of the box to compute the effective
sound speed. For the spherical H ii regions, we assume that the radius of the
region is the scale below which motions will act as an extra pressure against the expansion.
Therefore, taking the Larson’s relations: ![\begin{eqnarray} \label{eq_larson} \langle \sigma \rangle &=& 1.1~\mathrm{km\,s^{-1}} \left(\frac{r}{\mathrm{pc}}\right)^{0.38} ,\nonumber\\[3mm] \langle n \rangle &=& 3400~\mathrm{cm}^{-3} \left(\frac{r}{\mathrm{pc}}\right)^{-1.1}, \end{eqnarray}](/articles/aa/full_html/2014/08/aa23959-14/aa23959-14-eq43.png) (10)we
evaluated the turbulent ram pressure at the scale of the radius of the region:
(10)we
evaluated the turbulent ram pressure at the scale of the radius of the region: 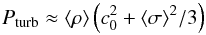 (11)with
⟨ ρ ⟩ the rms
density in g/cm3 and
c0
the sound speed (0.2 km s-1). This relation is plotted in Fig. 2 with the ionized gas pressure PII of the regions in the HRDS survey
evaluated from Eq. (9). There is of course a
large scatter around the Larson’s relations and uncertainties concerning the right scale
that should be used. Possible variations around these relations have been investigated in
Lombardi et al. (2010) (see also Hennebelle & Falgarone 2012). Therefore, we also
plot in Fig. 2 the ram pressure at ±50%. Overall, the pressure of the H ii
regions is greater than the turbulent ram pressure of the surrounding medium, meaning
that they are indeed able to expand in the turbulent medium. This is consistent with what we
infer from the numerical simulations in Sect. 2.
Furthermore, around 20% of our sample have pressures at ±50% of the turbulent ram pressure at the
scale of their radius. This suggests that contrary to the usual picture, these regions may
reach the limit of their expansion phase and may be in equilibrium with the surrounding
turbulent medium.
(11)with
⟨ ρ ⟩ the rms
density in g/cm3 and
c0
the sound speed (0.2 km s-1). This relation is plotted in Fig. 2 with the ionized gas pressure PII of the regions in the HRDS survey
evaluated from Eq. (9). There is of course a
large scatter around the Larson’s relations and uncertainties concerning the right scale
that should be used. Possible variations around these relations have been investigated in
Lombardi et al. (2010) (see also Hennebelle & Falgarone 2012). Therefore, we also
plot in Fig. 2 the ram pressure at ±50%. Overall, the pressure of the H ii
regions is greater than the turbulent ram pressure of the surrounding medium, meaning
that they are indeed able to expand in the turbulent medium. This is consistent with what we
infer from the numerical simulations in Sect. 2.
Furthermore, around 20% of our sample have pressures at ±50% of the turbulent ram pressure at the
scale of their radius. This suggests that contrary to the usual picture, these regions may
reach the limit of their expansion phase and may be in equilibrium with the surrounding
turbulent medium.
4. Age estimation of the H ii regions
Based on the comparison between the 3D turbulent simulations and the 1D models with an
effective turbulent temperature in Sect. 2, we are
confident about using 1D spherical simulations as a proxy to evaluate the age of the
H ii regions. The coupled system of equation for 1D-spherical hydrodynamics
coupled with ionization/recombination assuming the on-the-spot approximation is given by
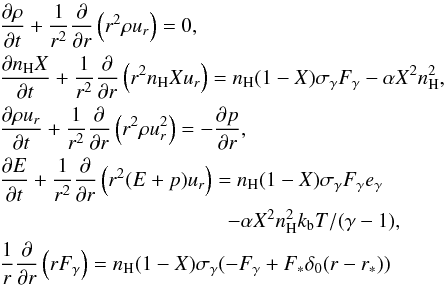 (12)where
ρ,
ur, P, T, are the density, velocity,
pressure, and temperature of the fluid, E is the total energy given by
(12)where
ρ,
ur, P, T, are the density, velocity,
pressure, and temperature of the fluid, E is the total energy given by
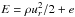 , X the ionization fraction
given by nH+/nH,
nH
the total hydrogen density nH+ +
nH0, Fγ the ionizing flux,
σγ the ionization cross
section, eγ the mean energy
given by an ionizing photon to the gas, α the recombination rate, and γ the adiabatic index. We
assume that an ideal gas links the internal energy e to the pressure:
p =
e(γ − 1). The system is split in a
hydrodynamic step solved explicitly by a Godunov exact solver and an
ionization/recombination step solved implicitly. We used a γ of 1.001 so that the gas is
locally isothermal in the absence of ionization/recombination processes.
, X the ionization fraction
given by nH+/nH,
nH
the total hydrogen density nH+ +
nH0, Fγ the ionizing flux,
σγ the ionization cross
section, eγ the mean energy
given by an ionizing photon to the gas, α the recombination rate, and γ the adiabatic index. We
assume that an ideal gas links the internal energy e to the pressure:
p =
e(γ − 1). The system is split in a
hydrodynamic step solved explicitly by a Godunov exact solver and an
ionization/recombination step solved implicitly. We used a γ of 1.001 so that the gas is
locally isothermal in the absence of ionization/recombination processes.
We performed 1D spherical models in a medium with a density and pressure profile given by
Eqs. (10) and (11). When the ionized bubble expands in such a density/pressure profile,
it will “feel” the turbulent ram pressure at a given radius acting against the expansion. A
grid of models was computed with different fluxes (log10(S∗) between 47. and 51. in steps of
0.25), electronic temperature (Te: 104 K ± 50% in steps of 1000 K), and density at 1 pc
(n(1pc): 3400
cm-3± 50% in steps of 340 cm-3). The simulation domain extends
up to 25 parsecs. We took a resolution of 2500 cells (uniformly spaced) and ran the
simulations during 12 Myr. These models are plotted in Fig. 2 for a fixed electron temperature Te = 8000 K and a density at 1 pc of
n(1 pc) =
3400 cm-3. We used a
fixed temperature in Fig. 2 to avoid a 3D plot for our
grid of simulations, however, we do take the electron temperature dependence for our final
age estimation into account. The regions from the HRDS survey fall exactly on the simulated
tracks at their ionizing fluxes. This is normal and a consequence of photon conservation
that is assumed in Eq. (5) to evaluate
S∗
from ⟨ nII
⟩ and is also assumed in the simulations. It can be shown using photon
conservation that 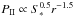 (see Eq. (1)), which gives the linear tracks
in log space for Fig. 5. The real
contribution of the simulations are the isochrone curves built out of them (dashed black
lines). We can then estimate the dynamical age of the different regions.
(see Eq. (1)), which gives the linear tracks
in log space for Fig. 5. The real
contribution of the simulations are the isochrone curves built out of them (dashed black
lines). We can then estimate the dynamical age of the different regions.
 |
Fig. 3 Left: diameter, age, and position of the H ii regions of the HRDS survey in the Galaxy. The dashed green lines show the limit of the survey, the thick black curves are the position of the spiral arms of our Galaxy based on Russeil (2003). The ages are estimated using the grid of 1D simulations at a fixed density at 1 pc (3400 cm-3) for the initial profile. The galactic electron temperature gradient is taken into account using Eq. (8). Right: age distribution of our sample, the ionizing flux of the regions is indicated by the colour scale. |
H ii regions used for comparison between photometric and dynamical age.
We tested this method on well known regions for which an independent age of the central massive OB stars is available from photometry and evolutionary tracks in the HR diagram. We took four regions: Rosette, M 16, RCW 79, and RCW 36, their parameters and the corresponding references are given in Table 1. We used Eq. (8) to estimate the electron temperature for all the regions. Our age estimations are in good agreement with the ages derived from photometry, however, some questions can be raised:
-
In the case of the Rosette Nebula, Martinset al. (2012) concluded thatthe age of the two most massive O stars inNGC 2244 is less than 2 Myr,however, they suggest that either there is a bias in their effec-tive temperature, or the two massive O starswere the last to form. For the second possibility, theH ii region would be powered first by theO stars with lower mass, and then by the twomost massive O stars that domi-nate the total ionizing flux. The ionizing flux is thus a function oftime in that case, and could change the dynamical age. The samemay also happen for the future development of RCW79 withthe appearance of a compact and younger H iiregion at the southeast of the region.
-
The dynamical age of RCW36 is at the lower end of the photometric range. This could mean that the ionizing O star is also the last to form, however contrary to the Rosette Nebula, we do not expect a two-stage expansion in this case because there is only one dominant ionizing source. Other physical phenomena at the early stages of the expansion could also delay the expansion by 0.1−0.2 Myr. (see Sect. 5.1).
In Sect. 5.2, we will discuss in further detail the possible biases of our approach, considering the uncertainties and the error bars of the age derived from evolutionary stages, the dynamical age agrees well. Besides, it has the advantage of being much simpler to compute and can be applied to a large sample of OB associations. We apply the method on the HRDS sample and give the age distribution in the right panel of Fig. 3. The average age of the 119 regions is 1.9 Myr ± 0.7 Myr. The distribution is plotted as a stacked histogram indicating the ionizing flux of the sources and we do not see any trend as a function of flux. There is a tail with older regions that is not very well sampled, probably because there are not many big and bright sources such as the Rosette Nebula in the survey. The average age of the sample is relatively small compared to the typical lifetime of a massive star (30 Myr for a typical B-type star of 10 M⊙). The left panel of Fig. 3 shows the size, age, and position of the regions in the Galaxy. The Scutum-Crux arm (dash-dotted spiral) has been extended beyond the distance constrained in Russeil (2003), this is probably why the most distant regions do not lie very well on the arm. At first sight, the regions in the Sagittarius-Carina arm (dashed spiral) seem younger than the regions in the other arms, however, most of these regions are also the closest to the Sun so the completeness and sensitivity limits of the survey have to be carefully studied before making any firm conclusion.
5. Discussion
5.1. What about gravity and magnetic fields?
Other physical phenomena could also affect the expansion of the ionization front and
balance the ionized gas pressure. Their associated pressure should be compared to the
turbulent pressure given by Eq. (11) and
with the ionized-gas pressure in Eq. (1).
The effect of self gravity is negligible on the expansion because of Gauss’s law for
gravity. Only the mass of the ionized gas will act at the ionization front, however, the
gas self gravity is an important effect to consider when studying the compression in the
shell. The gravity of the central cluster could play a role. If we assume that an
hydrostatic equilibrium is possible, we find the relation:
![\begin{eqnarray} && P_{\rm II}-P_0 = \int^\infty_r \frac{GM\rho(r')}{r'^2} {\rm d}r' \quad \mathrm{with} \quad \rho(r') = \rho(1~\mathrm{pc})\left(\frac{r'}{\mathrm{pc}}\right)^{-1.1} \nonumber\\[3mm] && P_{\rm II} \approx P_{\rm G} \approx\frac{GM\rho(1~\mathrm{pc})}{2.1\times(1~\mathrm{pc})} \left(\frac{r}{\mathrm{pc}}\right)^{-2.1} \end{eqnarray}](/articles/aa/full_html/2014/08/aa23959-14/aa23959-14-eq76.png) (13)where
M is the
mass of the central cluster. Assuming a cluster mass of 500 M⊙, we find a
gravitational pressure on the order of 1.62 ×
10-10 dyne cm-2 at one parsec, which is comparable to the turbulent
pressure at that scale (see Fig. 2). Nevertheless,
this pressure is dropping much faster than the turbulent pressure (≈r-2), therefore if expansion has happened at some point
with PII ≥
PG, the gravity of the central cluster
will never be able to stop large scale expansion in the future. Gravitational effects can
be important at small scales for compact and ultra-compact H ii regions (see
Keto 2007; Peters
et al. 2010), therefore we do not expect our model to apply for spatial scales
smaller than ≈0.1 pc (and ages
than 0.1−0.2 Myr).
(13)where
M is the
mass of the central cluster. Assuming a cluster mass of 500 M⊙, we find a
gravitational pressure on the order of 1.62 ×
10-10 dyne cm-2 at one parsec, which is comparable to the turbulent
pressure at that scale (see Fig. 2). Nevertheless,
this pressure is dropping much faster than the turbulent pressure (≈r-2), therefore if expansion has happened at some point
with PII ≥
PG, the gravity of the central cluster
will never be able to stop large scale expansion in the future. Gravitational effects can
be important at small scales for compact and ultra-compact H ii regions (see
Keto 2007; Peters
et al. 2010), therefore we do not expect our model to apply for spatial scales
smaller than ≈0.1 pc (and ages
than 0.1−0.2 Myr).
The magnetic pressure could also play a role. Assuming a constant mass to flux ratio in
molecular clouds and a typical magnetic field of 20 μG at one parsec (see Troland & Crutcher 2008; Lazarian et al. 2012), we can derive the scaling relation (for larger
scales): 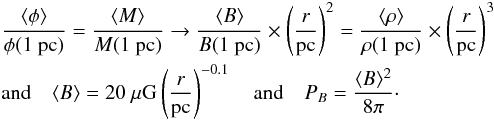 (14)At
one parsec, this magnetic field leads to a magnetic pressure on the order of
1.5 × 10-11
dyne cm-2, much
smaller than the turbulent pressure. Even if the magnetic pressure inside the
H ii region acts as a support, its strength is small compared to the
ionized-gas pressure. Therefore the magnetic field pressure does not have an important
effect for the large-scale evolution of H ii regions. Crutcher (2012) showed that the magnetic field can be on the order of
100−1000 μG for dense gas at small
scales, consequently the small-scale evolution of H ii regions could depend on
the magnetic field.
(14)At
one parsec, this magnetic field leads to a magnetic pressure on the order of
1.5 × 10-11
dyne cm-2, much
smaller than the turbulent pressure. Even if the magnetic pressure inside the
H ii region acts as a support, its strength is small compared to the
ionized-gas pressure. Therefore the magnetic field pressure does not have an important
effect for the large-scale evolution of H ii regions. Crutcher (2012) showed that the magnetic field can be on the order of
100−1000 μG for dense gas at small
scales, consequently the small-scale evolution of H ii regions could depend on
the magnetic field.
Both gravity and magnetic fields should be considered for the evolution of compact and ultra-compact H ii regions but should not affect the large-scale evolution of diffuse nebulae. The presence of dust can also have an important effect for small regions (see Inoue 2002; Arthur et al. 2004). As a consequence, we do not expect our models to be able to predict the ages for small regions at a scale of 0.1 pc and the error bars for regions around 1 pc are possibly larger because of the uncertainties in the small-scale evolution.
5.2. The effect of initial conditions
Environmental variations in the surrounding density can also be an issue. We managed to correct for the electron temperature but we did not take possible variations of the density profile around the profile given by Eq. (10) into account. Our grid of simulations can take such variations (up to ±50% around n(1 pc) = 3400 cm-3) into account, but we do not have observational constraints for the local density around the regions of the HRDS survey. To illustrate the effect of the density variations, we recomputed the age distribution of Fig. 3 for n(1 pc) = 1700 cm-3 and 5100 cm-3. The corresponding distributions are given in Fig. 4. For n(1 pc) = 1700 cm-3, the distribution is shifted at 1.4 Myr ± 0.8 Myr, and for n(1 pc) = 5100 cm-3 at 2.3 Myr ± 0.8 Myr. The changes are significant, but we do not expect the local variation in the density at one parsec to be systematically positive or negative for all regions so that we would have to shift the global Larson’s law accordingly. Therefore, the average age of the distribution should remain relatively constant and the variations around the density at one parsec may only increase the standard deviation. Furthermore, we do not expect the bias caused by density variations to be important for large regions. Indeed, large regions have a surrounding area big enough to recover an average density that should be relatively close to what can be inferred from Larson’s relation. For smaller regions (≈1 pc), the local density variations can be important and lead to different ages. If enough regions are included in the statistics however, the age distribution should be fairly good although the age estimation of a small particular region might be wrong.
 |
Fig. 4 Effect of changing by ±50% the density at 1 pc of the initial density profile on the total age distribution. Note that this effect is applied to all regions, in reality it should not be such a systematic positive or negative bias. |
5.3. Advantages of dynamical age determinations and perspectives
The dynamical evolution inferred from our grid of models is a good way to get an estimation of the age of the OB associations, especially when we consider how difficult and uncertain it is to get an age estimation from photometry and evolutionary tracks. In principle 3D simulations would be required to study the evolution in a turbulent medium, but they are currently too time consuming to allow for the computation of a full grid of models as a function of flux, temperature, and density. Thanks to the equivalent grid of 1D simulations, the method is relatively cheap and we can take the environmental dependences into account.
Although this method cannot be used for small regions for which magnetic fields and gravity have to be considered, we can easily date a large sample of diffuse H ii regions when they can be resolved and their Lyc flux estimated in observations. This method could also be applied to nearby extra-galactic H ii regions, thus allowing us to get age distributions of massive star-forming regions in other galaxies. These distributions could then be used to constrain galaxy-scale simulations of star formation.
Acknowledgments
We would like to acknowledge the Nordita program on Photo-Evaporation in Astrophysical Systems (June 2013) where part of the work for this paper was carried out. We also thank L. Deharveng, D. Russeil, J. Tigé, G. Chabrier, and E. Audit for valuable discussions. N.S. acknowledges support by the ANR-11-BS56-010 project “STARFICH”. This work is partly supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement No. 247060).
References
- Anderson, L. D., Bania, T. M., Balser, D. S., & Rood, R. T. 2011, ApJ, 194, 32 [NASA ADS] [Google Scholar]
- Arthur, S. J., Kurtz, S. E., Franco, J., & Albarrán, M. Y. 2004, ApJ, 608, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Audit, E., González, M., Vaytet, N., et al. 2011, Astrophysics Source Code Library, ascl:1102.016 [Google Scholar]
- Balser, D. S., Rood, R. T., Bania, T. M., & Anderson, L. D. 2011, ApJ, 738, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Celnik, W. E. 1985, A&A, 144, 171 [NASA ADS] [Google Scholar]
- Condon, J. J., Griffith, M. R., & Wright, A. E. 1993, AJ, 106, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dyson, J. E., & Williams, D. A. 1980, Physics of the interstellar medium (Manchester University Press) [Google Scholar]
- Ellerbroek, L. E., Bik, A., Kaper, L., et al. 2013, A&A, 558, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Prisinzano, L., Micela, G., et al. 2007, A&A, 462, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&AR, 20, 55 [Google Scholar]
- Hillenbrand, L. A., Massey, P., Strom, S. E., & Merrill, K. M. 1993, AJ, 106, 1906 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K. 2002, AJ, 570, 688 [Google Scholar]
- Keto, E. 2007, ApJ, 666, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., Esquivel, A., & Crutcher, R. 2012, ApJ, 757, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2010, A&A, 519, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Hernández, N. L., Vermeij, R., & van der Hulst, J. M. 2005, A&A, 433, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Pomarès, M., Deharveng, L., Zavagno, A., & Bouret, J. C. 2010, A&A, 510, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Mahy, L., Hillier, D. J., & Rauw, G. 2012, A&A, 538, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Mac Low, M.-M., Banerjee, R., Klessen, R. S., & Dullemond, C. P. 2010, ApJ, 719, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Raga, A. C., Canto, J., & Rodríguez, L. F. 2012, MNRAS, 419, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C. G., & Lada, E. A. 2008, Handbook of Star Forming Regions, Vol. I, ed. B. Reipurth (Northern Sky ASP Monograph Publ.), 4, 928 [Google Scholar]
- Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1978, Physical processes in the interstellar medium (New York: Wiley-Interscience) [Google Scholar]
- Tremblin, P., Audit, E., Minier, V., & Schneider, N. 2011, in Proc. 5th international conf. of numerical modeling of space plasma flows, Astronum 2010 (San Francisco: ASP), 87 [Google Scholar]
- Tremblin, P., Audit, E., Minier, V., Schmidt, W., & Schneider, N. 2012, A&A, 546, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Troland, T. H., & Crutcher, R. M. 2008, ApJ, 680, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, N., Mizuno, N., Saito, H., et al. 1999, PASJ, 51, 775 [NASA ADS] [Google Scholar]
- Zavagno, A., Pomarès, M., Deharveng, L., et al. 2007, A&A, 472, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: position (relative to the top of the box) of the mean ionization front as a function of time for the 3D turbulent simulations (at Mach 1, 2, and 4 in solid blue) of Tremblin et al. (2012) and the corresponding analytical solutions (dotted red) and 1D simulations (dashed green) in which the turbulence is taken into account by an effective temperature/sound speed. Bottom: snapshots of the column density of the 3D simulations at a time of 1 Myr after the ionization is switched on at the top of the box. The blue-dashed lines show the mean position of the ionization front. |
| In the text | |
 |
Fig. 2 Pressure of the H ii regions of the HRDS survey as a function of radius. The black line is the turbulent ram pressure evaluated from Larson’s laws at the scale of the radius of the region (Eq. (11)). The grey lines show the limits at ± 50% of this relation. The dashed coloured lines are 1D simulations performed in a density and temperature profile based on Larson’s laws at different Lyc fluxes given by the colour bar. The dashed black lines are isochrones (in Myr) built from these simulations, they are used to estimate the age of the H ii regions. To avoid a 3D plot, we assume an constant electron temperature of 8000 K for all of the regions and simulations (only for this plot). |
| In the text | |
 |
Fig. 3 Left: diameter, age, and position of the H ii regions of the HRDS survey in the Galaxy. The dashed green lines show the limit of the survey, the thick black curves are the position of the spiral arms of our Galaxy based on Russeil (2003). The ages are estimated using the grid of 1D simulations at a fixed density at 1 pc (3400 cm-3) for the initial profile. The galactic electron temperature gradient is taken into account using Eq. (8). Right: age distribution of our sample, the ionizing flux of the regions is indicated by the colour scale. |
| In the text | |
 |
Fig. 4 Effect of changing by ±50% the density at 1 pc of the initial density profile on the total age distribution. Note that this effect is applied to all regions, in reality it should not be such a systematic positive or negative bias. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


