| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201323202 | |
| Published online | 19 June 2014 | |
Collision avoidance in next-generation fiber positioner robotic systems for large survey spectrographs
1 Coordination and Interaction Systems Group (REACT), École Polytechnique Fédérale de Lausanne (EPFL), Switzerland
e-mail: laleh.makarem@epfl.ch
2 Laboratory of Astrophysics (LASTRO), École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
3 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
4 Laboratory of Robotic Systems (LSRO), École Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
5 Instituto de Astrofísica de Andalucía (CSIC), 18008 Granada, Spain
6 Instituto de Física Teórica, (UAM/CSIC), Universidad Autónoma de Madrid, Cantoblanco, 28049 Madrid, Spain
Received: 5 December 2013
Accepted: 14 February 2014
Some of the next-generation massive spectroscopic survey projects plan to use thousands of fiber positioner robots packed at a focal plane to quickly move the fiber ends in parallel from the previous to the next target points. The most direct trajectories are prone to collision that could damage the robots and have an impact on the survey operation. We thus present here a motion planning method based on a novel decentralized navigation function for collision-free coordination of fiber positioners. The navigation function takes into account the configuration of positioners as well as the actuator constraints. We provide details of the proof of convergence and collision avoidance. Decentralization results in linear complexity for the motion planning as well as no dependence of motion duration on the number of positioners. Therefore, the coordination method is scalable for large-scale spectrograph robots. The short in-motion duration of positioner robots will thus allow the time dedicated for observation to be maximized.
Key words: instrumentation: spectrographs / techniques: spectroscopic
© ESO, 2014
1. Introduction
After the discovery and confirmation of the accelerated expansion of the Universe (Riess et al. 1998; Perlmutter et al. 1999), one of the main challenges in cosmology is to discern the nature of the dark energy. In order to achieve this goal, different observational techniques have been proposed to tackle the geometry and evolution of the Universe. One of the most important techniques is the measurement of the baryonic acoustic oscillations (BAO) in massive spectroscopic surveys.
The very first large-scale spectroscopic survey (Huchra et al. 1983) revealed a cosmic web structure with filaments and voids, and soon after further investigations questioned the existence of a cosmological constant (Efstathiou et al. 1990). More recently, following the discovery of the imprint of the BAO in the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2005), massive spectroscopic surveys were developed to accurately measure the evolution of the distance–redshift relation using the BAO technique. In particular, 1) the WiggleZ redshift survey (Blake et al. 2011) completed a ~250 000 redshift survey of star-forming galaxies (at z< 0.8) at the 4m Anglo-Australian Telescope (AAT); 2) the Baryonic Oscillation Spectroscopic Survey (BOSS; Anderson et al. 2012) will complete in 2014 a major redshift survey of 1.4 million galaxy redshift quasars (at z< 0.7) and 160 000 high-redshift Lyman-α quasars using the SDSS telescope; and 3) the extended-BOSS survey (2014−2020) will complete the first BAO survey over the redshift range 0.7 <z< 2.2 using galaxies and quasars as well as the SDSS facility.
To go beyond the throughput limits of current surveys, new technologies are being developed to hasten the completion of the future spectroscopic facilities. The way forward is to use not only larger aperture telescopes, but also a larger multiplexing. Over the past few years two major projects have been approved for construction. First, the Primary Focus Spectrograph (PFS) is a Japanese lead project that aims to develop a 2400-fiber spectrograph on the 8.2 m Subaru telescope. Second, the Dark Energy Spectroscopic Instrument (DESI)1, a US department of energy (DOE) lead project, aims to develop a 5000-fiber spectrograph on the Mayall 4m telescope. Other less advanced projects are also being prepared such as 4MOST and WEAVE.
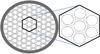 |
Fig. 1 Configuration of robot positioner on a focal plane. Positioners shown as black circles, form a hexagonal array in order to cover a patrol disk (shown in a dashed gray circle) as versatile as possible. |
Spectrographs fed by massive fiber bundles are one of the most advanced and proven methods compared to the multi-slit approach. Various technologies have been proposed for fiber positioning. For example, in the case of the SDSS spectrograph, fibers are placed manually into the holes drilled in an aluminum plate. This operation is done during the day prior to observations. In the case of the AAT spectrograph, a robot places fibers one at a time at the target points. This operation is done while another set of fiber is observing. In the case of the Chinese Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST; Cui et al. 2010) and the Japanese Fiber Multi-Object Spectrograph (FMOS; Kimura et al. 2003), robotic fiber positioners place in parallel the fibers at the target points just before the observations are conducted. The main advantage of using robotic positioners is that the fibers can be positioned simultaneously. So if the robotic system is fast, reconfiguration time can be executed during the observation overheads (readout time of the detectors and slewing of the telescope).
In the next-generation fiber-fed spectrographs such as the DESI and PFS projects, small robots are responsible for positioning the fiber ends. In order to improve the versatility of the system and to ensure the maximum number of observed galaxies, the robots share working spaces. Both project will use a robot with two degrees of freedom and eccentric rotary joints (the so-called θ − φ design). Our initial motivation for taking θ − φ design as an example for this paper, undertaken as part of the DESI project, is to solve the collision challenge in the motion planning of these robots. The proposed method could directly overcome the collision problem for any robot with two rotary joints that move a single fiber end such as for the DESI and PFS projects. This work presents a new motion planning method for the positioner robots based on decentralized navigation functions (DNF). The proposed trajectories guarantee collision-free path for all the fiber ends. The motion planning is decentralized in order to be able to extend the solution for large-scale positioner robots. In addition, the DNF method could be adopted for other fiber positioning systems with different geometry patterns where there is a potential risk of collision.
This paper is organized as follows. In Sect. 2 a description of the focal plane is given. In Sect. 3 we give the problem formulation for a collision-free trajectory planner. The solution to this problem, using DNF, is given in Sect. 4. Proof of convergence and constraints on parameter tuning is explained in Sect. 5. The simulation results corresponding to the proposed approach are presented and discussed in Sect. 6. Section 7 briefly explores some avenues for future research and concludes.
2. Description of focal plane
We describe a standard design for the focal plane, which can be extended to a number of future fiber-fed multi-object spectrograph instruments (and particularly designs explored for DESI and PFS). The main concept is a collection of identical positioners distributed over a hexagonal array (see Fig. 1). Each positioner robot is therefore assigned to a single target or if no target is accessible it will observe the sky. The positioner robots can cover the entire focal plane and each robot can move a fiber head toward a desired location within the patrol disk of the positioner. Because we require that any point in the focal plane be accessible by a fiber, there will be regions of the focal plane where the workspaces of adjacent positioners will overlap. In these overlap zones there is a risk of actuator collision. Target assignment and collision avoidance strategies will therefore be among the challenges in the design of such a massively parallel fiber-fed spectrograph.
2.1. Target assignment
Several strategies can be developed in order to assign targets (galaxies, quasars, or stars) to the end effectors (fiber ends) of the positioner robots. The simplest approach is to select randomly for each positioner any of the targets lying within the corresponding working space (patrol disk). To achieve an optimal solution, which means that the maximum number of targets is observed during a certain period of time, the drain algorithm was introduced (Morales et al. 2012). The method ensures observation of maximum number of targets in the first few sets of observations. Using both randomly distributed targets and mock galaxy catalogues, the authors showed that the number of observed galaxies could be increased by 2 percents in the first set of observations.
In this paper we assume that target assignment has been effectively done by one of the mentioned algorithms under three main assumptions. First, each target is assigned to one positioner only, and each positioner is assigned to only one target. Second, the target assigned to each positioner is always within its patrol disk and hence reachable by the positioner. The minimum distance between two assigned targets is d. Thus, the focus of the work presented here is on the coordination of positioners in motion to avoid collision. Third, we assume that the target of each positioner is fixed (not a quickly moving target) and known to the positioner robot.
3. Problem formulation
We consider a system composed of N positioner robots. The goal of each robot is to put its end effector (fiber end) on an assigned target point. Each positioner is a planar robot with two degrees of freedom, each moving via a rotational motor (Fig. 2).
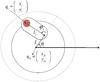 |
Fig. 2 A positioner robot with two degrees of freedom. The main disk (black circle) rotates along its central axis. Its angular position is shown as θi. The arm with the length of l2 rotates around an eccentric axis (with the distance of l1 from the center) fixed on the main disk and its angular position is shown as φi. qib is the position of the robot base fixed to the telescope structure in a global frame attached to the focal plane. qi is the position of the fiber attached to the robot i in that global frame. |
Each positioner robot covers the patrol area (workspace) through two correlated rotations: θ rotates around the actuator’s main axis, while φ moves the fiber arm tip from the peripheral circle to the central axis (Fig. 2). The optical fiber is attached to a ferrule at the arm tip, and passes through the center of the actuator and exits the rear side of the robot.
The forward kinematics of each positioner robot can be described as 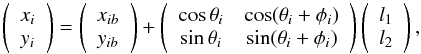 (1)where the end-effector position of positioner i is qi = (xi,yi) in a global frame attached to the focal plane; l1 and l2 are the first and second rotation links, respectively (Fig. 2); θ and φ are the angular positions of the two joints of the positioner i. Each positioner is controllable by its angular velocity, i.e., the speed of each of the two motors.
(1)where the end-effector position of positioner i is qi = (xi,yi) in a global frame attached to the focal plane; l1 and l2 are the first and second rotation links, respectively (Fig. 2); θ and φ are the angular positions of the two joints of the positioner i. Each positioner is controllable by its angular velocity, i.e., the speed of each of the two motors.
The main challenge is to coordinate the robots in motion to reach a predefined target point while avoiding collisions. The proposed approach should be expandable to larger scale problems. A centralized solution for such a problem would be impracticable and costly because of the presence of numerous positioners and constraints (Tanner & Kumar 2005). Therefore, among all the methods found in the literature for coordinating agents, decentralized and reactive control approaches seem promising.
4. Decentralized navigation function
Inspired by the emergent behaviors among swarms (insects, birds, fishes), methods based on local reactive control have received great interest (Ge et al. 2012). Therefore, artificial potential fields are often exploited for the coordination of autonomous agents. The main drawback of most potential field approaches is that convergence to the target is not guaranteed due to the presence of spurious local minima. In order to solve this problem and present a complete exact solution for the coordination problem, navigation functions have been introduced (Dimarogonas & Kyriakopoulos 2005).
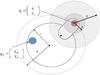 |
Fig. 3 The target point qiT is the destination of the robot end-effector. The collision detection envelope with radius D is the area where collision avoidance term in the navigation function is activated. This term ensures that the two positioner end-effectors will keep a distance larger than d. |
Navigation functions have been used in various robotic and control applications (Makarem & Gillet 2011, 2012; De Gennaro & Jadbabaie 2006). In these applications the actuation torque or other inputs (e.g., the acceleration, the velocity) is derived from some potential function that encode relevant information about the environment and the objective. In the framework of the problem presented in this paper, the use of navigation functions in a decentralized scheme is promising, as it can be implemented in realtime and it also shows good flexibility with regard to adding new robots and changing the problem constraints.
A navigation function is practically a smooth mapping which should be analytic in the workspace of every positioner robot and its gradient would be attractive to its destination and repulsive from other robots. So, an appropriate navigation function could be combined with a proper control law in order to obtain a trajectory for every motor of the robot leading to the destination and avoiding collisions.
Motion planning algorithm for all positioner robots.
We propose a navigation function ψi for the positioner i in Eq. (2) composed of two components. The first term, the attractive component, is the squared distance of the end-effector of positioner robot i from its target point. This term of the navigation function attains small values as the positioner brings the fiber closer to its target point (Fig. 3). The second term, the repulsive component, aims at avoiding collisions between positioner i and the six other positioners located in its vicinity. This term is activated when the two positioner robots are closer than a distance D, otherwise this term is zero. The value D defines the radius of a collision avoidance envelope and d<D defines the radius of the safety region. The closer the two robots get, the higher is the value this repulsive term attains. Moving toward the minimum point of this navigation function will guarantee the minimum distance of d between the positioners (Fig. 4). The values λ1 and λ2 are the two weighting parameters related to the two terms in the navigation function 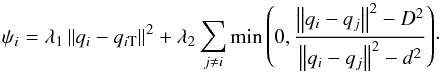 (2)According to the navigation function presented in Eq. (2) and the forward kinematics defined in Eq. (1), the following control law is proposed:
(2)According to the navigation function presented in Eq. (2) and the forward kinematics defined in Eq. (1), the following control law is proposed: 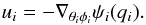 (3)At each step, the robot will move the fiber according to a gradient descent method. It is worth mentioning that the navigation function is a direct function of the end-effector positions. In order to obtain the angular velocities of each of the two motors, we calculate the gradient of the navigation function with respect to the angular positions of the links using the chain derivatives and the forward kinematics in Eq. (1) as
(3)At each step, the robot will move the fiber according to a gradient descent method. It is worth mentioning that the navigation function is a direct function of the end-effector positions. In order to obtain the angular velocities of each of the two motors, we calculate the gradient of the navigation function with respect to the angular positions of the links using the chain derivatives and the forward kinematics in Eq. (1) as 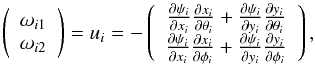 (4)where ωi1 and ωi2 are the angular velocity of the first and second motor of positioner robot i, respectively. There could be two final configurations that result in the same target point. However, when traveling from a known configuration, reaching one of these configurations is faster when considering no collision. In this work we assumed that the faster configuration is the goal configuration.
(4)where ωi1 and ωi2 are the angular velocity of the first and second motor of positioner robot i, respectively. There could be two final configurations that result in the same target point. However, when traveling from a known configuration, reaching one of these configurations is faster when considering no collision. In this work we assumed that the faster configuration is the goal configuration.
4.1. Algorithm complexity
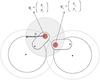 |
Fig. 4 A configuration in which there is a risk of collision between the end-effectors of two robots. In this configuration the collision avoidance term in the navigation functions of the two robots are active which means they take values more than zero. |
The main module of motion planning algorithm calls this module that calculates the gradient of the DNF.
Table 1 describes the motion planning algorithm. In each time step dt, each positioner robot computes the speed of its two motors knowing its current position and the target point as well as the position of adjacent robots. In each time step, each positioner calls the module that computes the gradient of decentralized navigation function (Table 2). So, the algorithm runs in a for-loop as many times as the number of positioner robots. On the other hand, the inner loop that calculates the gradient of the DNF runs constant times (number of adjacent positioners = 6). Therefore the complexity of the algorithm will remain O(N), where N is the number of positioner robots. Considering the fact that all the robots’ bases are fixed to the focal plane, collisions can occur locally and the chance of collision is only with the adjacent robots. Decentralizing motion planning and trajectory generation takes advantage of the limited number of adjacent robots and the locality of collisions and significantly reduces the complexity of the algorithm to a linear order. A low complexity of the algorithm guarantees its ease of use in mid-scale and large-scale robotic telescopes where there are thousands, or tens of thousands of positioners, respectively.
5. Collision-free motion toward equilibrium
The following theorem provides conditions under which DNF (2) in combination with control law (3) ensures convergence of all robots to their target points. Convergence of all robots means that using this method, practically no blocking will occur even if some complex maneuvers are needed in case of intricate initial configurations of the robots (see simulation example in Fig. 7).
Theorem 1.If the inequality 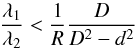 (5)is satisfied then function (2) is a Morse function (Milnor 1963) and there is no local minimum except the equilibrium in the target point.
(5)is satisfied then function (2) is a Morse function (Milnor 1963) and there is no local minimum except the equilibrium in the target point.
Proof. When ∇θiψ(qi) = 0.
It is either in the presence of no other positioner in the vicinity of positioner i, where 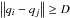 or there is a risk of collision
or there is a risk of collision  with at least one other positioner. The gradient of the navigation function for both cases is
with at least one other positioner. The gradient of the navigation function for both cases is 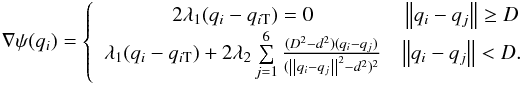 (6)In the case when there is no other positioner near the positioner i, ∇θiψ(qi) = 0 means 2λ1(qi − qiT) = 0, which directly indicates that the positioner robot is in its target point. Otherwise, there is at least one other positioner in the collision avoidance envelope (D):
(6)In the case when there is no other positioner near the positioner i, ∇θiψ(qi) = 0 means 2λ1(qi − qiT) = 0, which directly indicates that the positioner robot is in its target point. Otherwise, there is at least one other positioner in the collision avoidance envelope (D): 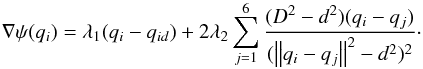 (7)The first term in the gradient of the potential field always satisfies the following inequality:
(7)The first term in the gradient of the potential field always satisfies the following inequality: 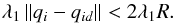 (8)in addition, the second term in the gradient of the potential field is:
(8)in addition, the second term in the gradient of the potential field is: 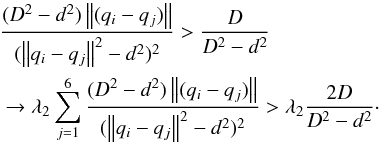 (9)So, if
(9)So, if 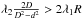 then there is no point where the gradient of the potential field could be zero except at the target point. It is worth noticing that there are two possibilities that have velocities equal to zero in angular coordination. One possibility is that the velocities are zero in the (x,y) coordination that is covered in the proof. The other possibility is that the positioner is in one of its singular configurations such as fully stretched or fully bent second arm. Technically we try to avoid singularities in any robotic manipulation, because the smoothness of motion and load on the motors are largely affected near singular points. So, we can assure that, in practice, the algorithm can guarantee deadlock-free motion.This guarantees that there will be no blocking (also called deadlock) in the method.
then there is no point where the gradient of the potential field could be zero except at the target point. It is worth noticing that there are two possibilities that have velocities equal to zero in angular coordination. One possibility is that the velocities are zero in the (x,y) coordination that is covered in the proof. The other possibility is that the positioner is in one of its singular configurations such as fully stretched or fully bent second arm. Technically we try to avoid singularities in any robotic manipulation, because the smoothness of motion and load on the motors are largely affected near singular points. So, we can assure that, in practice, the algorithm can guarantee deadlock-free motion.This guarantees that there will be no blocking (also called deadlock) in the method.
5.1. Parameter tuning
There are two weighting parameters that can be tuned in DNF (2): λ1 and λ2. Theorem 1 gives a condition for tuning these parameters which guarantees convergence of all positioners to their target points. In order to ensure the success of the motion planning algorithm, the maximum velocity generated should not exceed the maximum velocity feasible for motors. Lower values of λ1 and λ2 will result in lower values for the velocity of motors and will increase the convergence time. For an application in which fast convergence is desirable, the two parameters will be tuned to the highest values that still keep the maximum generated velocity in the feasible range. We soft-tuned these two parameters through simulations.
6. Simulation results
In order to study the performance of the motion planning algorithm, we conducted various sets of simulations for different numbers of positioners all in hexagonal configuration patterns. The size of positioners and the share volume between positioners are selected in a way to be compatible with next-generation spectrograph robots such as the one in DESI (Table 3). Therefore, the overlapping area of the robots are the fiber ends. In a scenario with different specifications, the robots may have collision risks with other parts of the adjacent positioners. In these scenarios, the collision avoidance envelope, D, should be modified in order to cover all collision risks.
For each set of simulations, we selected different numbers of positioners to verify our expectation on the complexity of the algorithm. In addition, we can extrapolate the simulation time and motion duration for other numbers of positioners for larger scales of robotic spectrographs. For each set we repeated the simulations 100 times. In all sets, the initial angular position of the two motors of each positioner robot and their target points are randomly generated. Table 4 shows the simulation parameters. The two weighting parameters in DNF (2) should satisfy the condition of Theorem 1. According to positioners’ specifications in Table 3, λ1 and λ2 should fit the inequality of 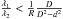 . This means λ1< 72λ2.
. This means λ1< 72λ2.
Simulation parameters used for all sets of simulations.
As expected, we observe no collision during all sets of simulations (4100 sets). Figures 5 and 6 show the simulation time and in-motion duration of robots, respectively. In-motion duration is the convergence time needed for all the positioner robots to arrive at their target points considering the constraints on actuator velocities listed in Table 4. The values for simulation times are calculated with a 3.33 GHz 6-Core Intel Xeon processor.
As expected , simulation time increases in a near linear manner with the number of positioners. This enables us to use this method for immediate motion planning for thousands of positioners. From the results, the amount of time needed to generate collision-free trajectories for 5000 positioners is less than 3 min (140 s) on today’s typical computers. This amount of time is very reasonable as it is smaller than the typical exposure time foreseen for the DESI and PFS experiment, thus allowing us to have an interactive planning of the observation. This would allow to modify in real time the target list in case of meteorological disturbances for example, or even the last minute discovered transient targets such as supernovae or gamma ray burst.
The main advantage of the method that derives from the idea of decentralization is that the motion duration does not change with the number of positioner robots. Decentralization benefits from the configuration of positioner robots and the fact that collisions could happen locally and they do not affect the motion of non-neighbor positioners. With realistic actuator constraints (Table 4) like those used in simulation sets, we can expect to accomplish the first run of motions for the positions of mid-scale robot positioners in less than 2.5 s. Such a short duration of time for coordination of all positioners will allow us to maximize the duration of observation and the survey efficiency.
In all sets of simulations, we have studied the performance of our motion planning algorithm for randomly distributed initial positions and randomly distributed target points. However, galaxies are not randomly distributed, but clustered. Therefore, in a realistic situation positioners will move toward very close targets and consequently start the next set of observation from a very close position toward other sets of target points. Therefore, it is expected that adjacent positioner robots will need sets of complex maneuvers in order to find a collision-free path toward their target points. Figure 7 shows snapshots of a simulation set where three positioners are engaged in a very close space. The motion planning algorithm succeeds in solving the conflict by directly executing the complex maneuvers from DNF and taking positioner robots to their target points. The main advantage of this method is that these types of conflicts could be solved in a decentralized manner which significantly decreases simulation time and motion duration. Therefore, the algorithm is reliable for large number of positioners.
 |
Fig. 5 Mean value simulation duration for sets with different numbers of positioners. Repeating sets of simulation, the simulation durations do not vary significantly. The lengths of the error bars are therefore chosen to be 10 times the standard deviation at each point. |
 |
Fig. 6 Mean value and standard deviation of convergence time (seconds) for simulation sets with different numbers of positioners. The scaling of the x-axis is not linear. |
 |
Fig. 7 Panels A)–F) show six snapshots of the simulation. 1*, 2*, and 3* are respectively the target positions for positioners 1, 2, and 3. These three positioners are engaged in a local conflict in which positioner 1 needs to make space for positioner 2 to pass. Positioner 2 cannot make room for positioner 1 because positioner 3 is blocking the way. Positioner 3 needs to pass both positioners to reach its target point. The small maneuver from positioner 1 that comes directly from DNF moves this positioner farther from its target point, but it makes room for positioner 2 to pass safely. When positioner 2 clears the way, positioner 1 starts moving toward its target point and this gives a safe way to positioner 3. |
 |
Fig. 8 Velocity profiles that correspond to the pairs of actuators for positioners 1, 2, and 3 in Fig. 7. Columns show the velocity profiles for each positioner. The first and second profiles of each column correspond to the first and second actuators of each positioner, respectively. Vertical lines indicate the moment at which the snapshots in Fig. 7 were taken. |
7. Conclusion
In the near future fiber-fed spectrograph robots such as the ones envisioned in DESI (5000 positioner robots) or PFS (2400 positioner robots) will provide a 3D map of a large portion of our Universe. The main concept common between the designs is the use of small mechanical robot positioners. These robot positioners are responsible for moving the fiber ends toward their target points where they can observe different sets of objects such as galaxies, quasars, or stars. As the robot positioners share work-space, the main challenge is designing a motion planning algorithm that guarantees collision avoidance. Our proposed decentralized method for coordination of positioners is a potential field that ensures collision avoidance as well as convergence of positioner robots (no blocking) to their target points. Simulation results show the feasibility of using this method for mid-scale and large-scale fiber-fed spectrograph robots. In-motion duration only lasts 2.5 s for any number of positioners. In addition, the massive spectroscopic projects could take advantage of short simulation times to compute trajectories and the ability of interactive motion planning of the robots to target recently discovered transient sources at the last minute. Given that the initial motivation of this work came from the collision challenge in the DESI project, the proposed method can be directly applied to the PFS project where number of robots is half that in DESI. From simulation results we can predict that the 4800 trajectories of 2400 robots could be generated with a typical computer in less than one minute and the motion duration would be less than 3 min. Moreover, this DNF could be adopted for other fiber positioning systems with different geometry patterns to avoid collisions.
Our future research directions include the discretization of velocity profiles in order to ensure the feasibility of a real-time coordination for a large number of positioner robots. In a framework where a centralized computer communicates with positioner robots, in order to minimize the communication time, the motor velocities should be discretized to fit in few bits. Moreover, we are exploring the connection between motion planning and target assignment in order to further minimize the in-motion duration of positioner robots.
Acknowledgments
L.M., J.P.K. and L.J. acknowledge support from the European Research Council (ERC) advanced grant “Light on the Dark” (LIDA). F.P. and J.S. are grateful for the support from the Spanish MINECO grants AYA10-21231 and MultiDark-CSD2009-0064.
References
- Anderson, La., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Blake, Ch., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cui, X., Wang, S.-G., Su, D.-Q., et al. 2010, in Proc. SPIE, 7733, 0B [Google Scholar]
- De Gennaro, M. C., & Jadbabaie, A. 2006, in Proc. American Control Conference (IEEE) available at www.seas.upenn.edu/~jadbabai/papers/2006ACC_1465_FI.pdf [Google Scholar]
- Dimarogonas, D. V., & Kyriakopoulos, K. J. 2005, Proc. American Control Conference (IEEE), 4667 [Google Scholar]
- Efstathiou, G., Sutherland, W. J., & Maddox, S. J. 1990, Nature, 348, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, F., Wei, Z., Lu, Y., Tian, Y., & Li, L. 2012, Nonlinear Dynamics, 70, 571 [CrossRef] [Google Scholar]
- Huchra, J., Davis, M., Latham, D., & Tonry, J. 1983, ApJS, 52, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, M., Maihara, T., Ohta, K., et al. 2003, In Astronomical Telescopes and Instrumentation, Proc. SPIE, 4841, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Makarem, L., & Gillet, D. 2011, In Proc. World Congress, 18, 13046 [Google Scholar]
- Makarem, L., & Gillet, D. 2012, In Proc. IEEE Int. Conf. on, Systems, Man, and Cybernetics (SMC), 2557 [Google Scholar]
- Milnor, J. 1963, Morse theory, Annals of Mathematics Studies (NJ, USA, Princeton), vol. 51 [Google Scholar]
- Morales, I., Montero-Dorta, A. D., Azzaro, M., et al. 2012, MNRAS, 419, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, ApJ, 116, 1009 [Google Scholar]
- Tanner, H. G., & Kumar, A. 2005, In Proc. IEEE Int. Conf., Robotics and Automation, ICRA 2005, 4132 [Google Scholar]
All Tables
The main module of motion planning algorithm calls this module that calculates the gradient of the DNF.
All Figures
 |
Fig. 1 Configuration of robot positioner on a focal plane. Positioners shown as black circles, form a hexagonal array in order to cover a patrol disk (shown in a dashed gray circle) as versatile as possible. |
| In the text | |
 |
Fig. 2 A positioner robot with two degrees of freedom. The main disk (black circle) rotates along its central axis. Its angular position is shown as θi. The arm with the length of l2 rotates around an eccentric axis (with the distance of l1 from the center) fixed on the main disk and its angular position is shown as φi. qib is the position of the robot base fixed to the telescope structure in a global frame attached to the focal plane. qi is the position of the fiber attached to the robot i in that global frame. |
| In the text | |
 |
Fig. 3 The target point qiT is the destination of the robot end-effector. The collision detection envelope with radius D is the area where collision avoidance term in the navigation function is activated. This term ensures that the two positioner end-effectors will keep a distance larger than d. |
| In the text | |
 |
Fig. 4 A configuration in which there is a risk of collision between the end-effectors of two robots. In this configuration the collision avoidance term in the navigation functions of the two robots are active which means they take values more than zero. |
| In the text | |
 |
Fig. 5 Mean value simulation duration for sets with different numbers of positioners. Repeating sets of simulation, the simulation durations do not vary significantly. The lengths of the error bars are therefore chosen to be 10 times the standard deviation at each point. |
| In the text | |
 |
Fig. 6 Mean value and standard deviation of convergence time (seconds) for simulation sets with different numbers of positioners. The scaling of the x-axis is not linear. |
| In the text | |
 |
Fig. 7 Panels A)–F) show six snapshots of the simulation. 1*, 2*, and 3* are respectively the target positions for positioners 1, 2, and 3. These three positioners are engaged in a local conflict in which positioner 1 needs to make space for positioner 2 to pass. Positioner 2 cannot make room for positioner 1 because positioner 3 is blocking the way. Positioner 3 needs to pass both positioners to reach its target point. The small maneuver from positioner 1 that comes directly from DNF moves this positioner farther from its target point, but it makes room for positioner 2 to pass safely. When positioner 2 clears the way, positioner 1 starts moving toward its target point and this gives a safe way to positioner 3. |
| In the text | |
 |
Fig. 8 Velocity profiles that correspond to the pairs of actuators for positioners 1, 2, and 3 in Fig. 7. Columns show the velocity profiles for each positioner. The first and second profiles of each column correspond to the first and second actuators of each positioner, respectively. Vertical lines indicate the moment at which the snapshots in Fig. 7 were taken. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


