| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322567 | |
| Published online | 12 May 2014 | |
On the steady state collisional evolution of debris disks around M dwarfs
1
Observatoire de Paris – LERMA, 61 Av. de l’Observatoire,
75014
Paris,
France
2
Observatoire de Paris – LERMA, CNRS, 61 Av. de l’Observatoire,
75014
Paris,
France
e-mail:
jean-francois.lestrade@obspm.fr
Received:
29
August
2013
Accepted:
21
February
2014
Debris disks have been found primarily around intermediate and solar mass stars (spectral types A-K), but rarely around low-mass M-type stars. This scarcity of detections in M star surveys can be confronted with the predictions of the steady state collisional evolution model. First, we determine the parameters of the disk population evolved with this model and fit to the distribution of the fractional dust luminosities measured in the surveys of A- and FGK-type stars observed by the infrared satellite Spitzer. Thus, in our approach, we stipulate that the initial disk mass distribution is bimodal and that only high-mass collisionally-dominated disks are detected. The best determined parameter is the diameter Dc of the largest planetesimals in the collisional cascade of the model, which ranges between 2 and 60 km, consistently for disks around both A- and FGK-type stars. Second, we assume that the same disk population surrounds the M dwarfs that have been the subjects of debris disk searches in the far-infrared with Spitzer and at submillimeter wavelengths with radiotelescopes. We find, in the framework of our study, that this disk population, which has been fit to the AFGK data, is still consistent with the observed lack of disks around M dwarfs with Spitzer.
Key words: Kuiper belt: general
© ESO, 2014
1. Introduction
A debris disk around a main sequence star is formed of planetesimals leftover from the planet formation process according to the core accretion theory. In our solar system, the asteroid belt and Edgeworth-Kuiper belt would be a debris disk to an hypothetical distant observer. Planetesimals are objects whose accretion was stymied by the formation and migration of giant planets in the system, or whose accretion simply occurred too slowly to grow larger. The relationship between debris disks and planetary systems is debated and should eventually place our solar system in context (Greaves & Wyatt 2010). The physical and observational properties of debris disks were defined by Lagrange et al. (2000), and their studies were reviewed by Wyatt (2008) and Krivov (2010).
It is thought that observed dust associated with debris disks must be replenished through continual collisional grinding or sublimation of planetesimals resulting either from a steady state or a stochastic process, or both. About 10−30% of mature stars from stellar type A to K harbor cold dust disks detected as excess emission above photospheric levels in the far-infrared at λ > 70 μm. The observed decay of these excesses with star ages is seen as evidence of evolution under a steady state collisional process (Dominik & Decin 2003; Rieke et al. 2005; Bryden et al. 2006; Wyatt et al. 2007a,b; Carpenter et al. 2009; Kains et al. 2011). The fact that debris disks are found around stars that have several orders of magnitude difference in stellar luminosities implies that planetesimal formation (a critical step in planet formation) is a robust process that can take place under a wide range of conditions.
In addition to searches targeted at A- to K-type stars, several large surveys have been conducted to search for cold debris disks around M dwarfs in the mid-infared by Plavchan et al. (2005, 2009), initially, and Avenhaus et al. (2012) with Wide Field Infrared Survey (WISE), as well as in the far-infrared with the satellites Spitzer and Herschel (Gautier et al. 2007; Matthews et al. 2010), and in the submillimeter domain with James Clerk Maxwell Telescope (JCMT) and 30-m Institut de Radioastronomie Millimétrique (IRAM; Lestrade et al. 2006, 2009). They have only yielded a bona fide disk around the mature M3 dwarf GJ581 (Lestrade et al. 2012), in addition to the disk around the young M0 dwarf AU Mic (12 Myr) (Liu et al. 2004; Kalas et al. 2004).
The fact that debris disks are less frequently detected among M-dwarfs than around higher-mass stars seems surprising at first, since stars of all spectral types have similar detection frequency of protoplanetary disks in the earlier stages of their evolution (e.g., Andrews & Williams 2005). It is also surprising in view of the recent observations showing that small, low-mass planets are more abundant among M-dwarfs than around stars of other types (Howard et al. 2012; Bonfils et al. 2013; Dressing & Charbonneau 2013; Kopparapu 2013), and in light of the prevalence of debris disks around G-type stars hosting low-mass planetary systems (Wyatt et al. 2012; Marshall et al., and Moro-Martín et al., in prep.). If the correlation between debris disks and low-mass planets for G stars applies to M dwarfs, then debris disks should be relatively common around M dwarfs, in contrast to recent observations.
In reality, current observations may simply not be sensitive enough because dust experiences significantly less heating around low-luminosity M dwarfs than around more massive stars. However, M dwarfs are usually closer and may have larger total dust-emitting surfaces because small grains are not blown out of the system by radiation pressure, unless a strong stellar wind is present.
In this paper, we show that under specific conditions (no stellar wind and high-mass collisionally-dominated disks), the disk population around M dwarfs is not different from the one around other types of stars, despite the lack of detected debris disks in surveys. In Sect. 2, we describe the steady state collisional evolution model developed in Wyatt et al. (2007a) and our adaptation for its use. In Sect. 3, we fit this model to the data of the Spitzer surveys of A stars and FGK stars with a novel fitting procedure, assuming a bimodal distribution for the masses of the debris disks. Interestingly, the best-fits of the two samples are shown to be consistent. Finally, in Sect. 4, we use this model and its assumptions to show that the observed lack of debris disks around M dwarfs found in the survey of Gautier et al. (2007) in the far-infared domain is consistent with the observations reported for A and FGK stars.
2. Model for the population of debris disks
2.1. Analytic steady state collisional evolution model
We assume that stars with detected debris disks are surrounded by a belt of planetesimals that is undergoing collisional cascades producing the dust observed. The long-term evolution of such a belt in steady state collisional equilibrium was originally developed analytically in Dominik & Decin (2003) and recast with slightly modified assumptions in Wyatt et al. (2007a). This model shows that debris disks decay at a constant rate proportional to t-1. An extension of this analytic model, which also includes the evolution of the star into the subgiant phase, is presented in Bonsor & Wyatt (2010), and yields a similar decay. Numerical models of single systems have shown that this decay is better described as a quasi-steady state with rates varying with time (Thébault et al. 2003; Löhne et al. 2008; Thébault & Augereau 2007; Gáspár et al. 2012).
In this study, we use the analytic model of Wyatt et al. (2007a) for its simplicity and overall accuracy in modelling collision-dominated disks that have been observed in surveys so far. In this model, the collisional equilibrium is described with a single power law for the size distribution defined by n(D) = KD2−3q between D and D + dD, and with q = 11/6 (Dohnanyi 1969). Such a collisional cascade implies infinity at both ends. But in debris disks, the cascade is truncated at the top end by the largest planetesimal of diameter Dc, and at the lower end by the blowout size if the stellar radiation pressure can blow out the smallest particles. In this model, the size distribution is independent of radial distance in the disk. The coefficient K can be related straightforwardly to the total mass or the total surface of the material. We recall that for index q = 11/6, most of the mass of the belt is in the largest planetesimals, while most of the emitting cross-sectional area is in the smallest particles.
In a collisional cascade, material within a given size range D to D + dD is
replaced by fragments from the destruction of larger objects at the same rate that it is
destroyed in collisions with other members of the cascade. The long timescale evolution is
thus determined by the removal of mass from the top end of the cascade, and, hence, by the
collisional lifetime tc(0) of the largest planetesimals of
size Dc at the initial epoch. In Wyatt et al. (2007a), planetesimals of size
Dc are destroyed by impacting
planetesimals down to size XcDc
(Xc < 1) making
collisional lifetimes shorter than in Dominik &
Decin (2003) where the large planetesimals feeding the cascade are less
realisticaly treated, as a population separate from the cascade. The ratio Xc =
Dcc/Dc,
where Dcc is the smallest planetesimal that has
enough energy to catastrophically destroy a planetesimal of size Dc, can be
expressed from the dispersal threshold 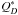 , i.e., the
specific incident energy required to catastrophically destroy a particle. Large bodies are
eventually ground to small particles generally expelled from the system by radiation or
wind pressure.
, i.e., the
specific incident energy required to catastrophically destroy a particle. Large bodies are
eventually ground to small particles generally expelled from the system by radiation or
wind pressure.
However, for low luminosity M dwarfs, the smallest grains cannot be expelled by radiation pressure, but by stellar wind if significantly above the solar value (Plavchan et al. 2005). This might be the case for very young M dwarfs, such as AU Mic, and possibly for fully convective stars later than the substellar spectral type M3 (Hawley et al. 2000; Wargelin & Drake 2001). The M dwarfs of unknown ages in the Spitzer sample of Gautier et al. (2007) are likely older than 1 Gyr, hence we have assumed no stellar wind to simplify their study and to test other parameters of the model, especially planetesimal size. We have set the smallest particle diameter Dmin for M dwarfs to 0.1 μm in our model because the absorption efficiency Qabs drops significantly below unity for smaller grains (Laor & Draine 1993) making their emission negligible.
In the model, the total mass Mtot(t) of the
planetesimals in the belt decays as: ![\begin{equation} M_{\rm tot}(t) = {{M_{\rm tot}(0)} \over {[1 + t/t_{\rm c}(0)]}} \label{eq:Mt} \end{equation}](/articles/aa/full_html/2014/05/aa22567-13/aa22567-13-eq20.png) (1)where
Mtot(0) is the initial total mass and
tc(0) is the collisional time scale at
that initial epoch. This solution is valid as long as the mass is the only time-variable
property of the disk. For the collisional lifetime tc(0), we used
Eq. (9) of Wyatt et al. (2007b) summarized here by:
(1)where
Mtot(0) is the initial total mass and
tc(0) is the collisional time scale at
that initial epoch. This solution is valid as long as the mass is the only time-variable
property of the disk. For the collisional lifetime tc(0), we used
Eq. (9) of Wyatt et al. (2007b) summarized here by:
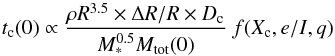 (2)and their expression
for the function f. The factor Xc has been
derived in Wyatt & Dent (2002):
(2)and their expression
for the function f. The factor Xc has been
derived in Wyatt & Dent (2002):
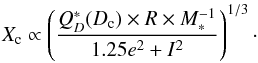 (3)These expressions
depend on the conditions in the disk (total mass Mtot(0) unless
t ≫
tc(0), mean radius R and width ΔR of the disk, diameter
Dc of the largest planetesimals) and on
the parameters controlling its subsequent collisional evolution (eccentricity and
inclination (e,I) of the perturbed planetesimals, material density
ρ, and the
star mass M∗).
(3)These expressions
depend on the conditions in the disk (total mass Mtot(0) unless
t ≫
tc(0), mean radius R and width ΔR of the disk, diameter
Dc of the largest planetesimals) and on
the parameters controlling its subsequent collisional evolution (eccentricity and
inclination (e,I) of the perturbed planetesimals, material density
ρ, and the
star mass M∗).
The specific energy threshold 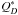 for
catastrophic disruption depends on the largest planetesimal Dc, and we use
the model of Benz & Asphaug (1999):
for
catastrophic disruption depends on the largest planetesimal Dc, and we use
the model of Benz & Asphaug (1999):
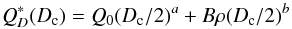 (4)where
Q0 ~ 1.6 ×
107−9 × 107 erg g-1, B ~ 0.3−2.1
erg cm-3 g-2, a ~ −0.4, and b ~ 1.20, as given in their
Table III for basalt and ice, and impact velocities 0.5, 3 and 5 km s-1. The assumptions that
(4)where
Q0 ~ 1.6 ×
107−9 × 107 erg g-1, B ~ 0.3−2.1
erg cm-3 g-2, a ~ −0.4, and b ~ 1.20, as given in their
Table III for basalt and ice, and impact velocities 0.5, 3 and 5 km s-1. The assumptions that
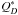 and
Dc are independent of stellar age and are
the same for all disks are limitations of the model.
and
Dc are independent of stellar age and are
the same for all disks are limitations of the model.
We synthesize a disk population by adopting distributions for the initial disk masses Mtot(0) and the mean disk radii. The distribution for Mtot(0) is based on the submillimeter study of protoplanetary disks of Andrews & Williams (2005) who derived a lognormal distribution of their dust masses centered on Mmid = 15 M⊕ (standard mass opacity of 0.1 cm2 g-1 at 1000 GHz and mass ratio of 100:1 between gas and dust) and with a 1σ width of 0.71 dex. As described later, we fit for Mmid but retained this 1σ width in our adjustment of the debris disk data. The distribution for the mean disk radii R is taken as the power-law n(R) ∝ Rγ between R and R + dR and is bound by the parameters R1 and R2. We fix γ to −0.5 based on the distributions found for the characteristic radii of the protoplanetary disks measured by the Submillimeter Array (SMA) in Andrews et al. (2011) and on the distribution of the mean radii of the nine resolved debris disks around A-stars of the Herschel program DEBRIS (Disc Emission via a Bias-free Reconnaissane in the Infrared/Submillimetre, Booth et al. 2013).
The total mass Mtot(t) of colliding
planetesimals at the age of the star can be converted into the total cross-sectional area
A(t) dominated by the dust with a
mass density ρ and the standard size distribution n(D) ∝
D-3.5 between D and D + dD for
spherical particles of diameter D from the largest value Dc to the
smallest Dmin taken as 0.1 μm (M dwarfs) or as the
blowout size if larger than 0.1 μm (i.e., most other stellar types). The total
cross-sectional area A(t) at the age of the star is:
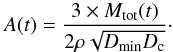 (5)Finally, the fractional
dust luminosity:
(5)Finally, the fractional
dust luminosity: 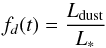 (6)is
calculated taking into account that the dust grains are spatially distributed according to
a radial profile taken as the power-law Σprα
between r and
r +
dr of the radial extent r from the inner radius
rin to the outer radius rout of the
disk. The term Σprα
is the emitting cross-sectional area of the grains per unit area of the disk surface. In
assuming that these grains absorb stellar light with 100% efficiency (Qabs = 1),
their total emission is proportional to
(6)is
calculated taking into account that the dust grains are spatially distributed according to
a radial profile taken as the power-law Σprα
between r and
r +
dr of the radial extent r from the inner radius
rin to the outer radius rout of the
disk. The term Σprα
is the emitting cross-sectional area of the grains per unit area of the disk surface. In
assuming that these grains absorb stellar light with 100% efficiency (Qabs = 1),
their total emission is proportional to 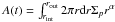 . Hence, if
α ≠ 0 and
using Eq. (3) of Lestrade et al. (2012) for
Σp, the fractional dust luminosity is:
. Hence, if
α ≠ 0 and
using Eq. (3) of Lestrade et al. (2012) for
Σp, the fractional dust luminosity is:
![\begin{eqnarray} {f_d(t)} & = & \int_{r_{\rm in}}^{r_{\rm out}} {{2 \pi r dr \Sigma_p r^{\alpha}} \over {4 \pi r^2}} \nonumber \\ & & {{1}\over {2 \pi}} {{A(t) \times (\alpha +2)} \over {\alpha}} \times \left[{{r_{\rm out}^{\alpha}-r_{\rm in}^{\alpha}} \over {r_{\rm out}^{\alpha+2}-r_{\rm in}^{\alpha+2}}}\right]\cdot \label{eq:fd2} \end{eqnarray}](/articles/aa/full_html/2014/05/aa22567-13/aa22567-13-eq64.png) (7)This
expression of the fractional dust luminosity accounts for the radial extent of the disk,
while it is usually estimated at its mean radius. The corresponding change is about 50%
for a disk width of ΔR =
R/2 and α = −1.5, as adopted in
this study. With these notations, the inner and outer radii in Eq. (7) above are rin = R −
ΔR/2 and rout = R +
ΔR/2, respectively. As mentioned
above, we adopt a power-law distribution for the mean disk radii R of the modeled disk
population extending between the lower and upper boundaries R1 and R2. These boundaries must
not be confused with rin and rout in Eq.
(7).
(7)This
expression of the fractional dust luminosity accounts for the radial extent of the disk,
while it is usually estimated at its mean radius. The corresponding change is about 50%
for a disk width of ΔR =
R/2 and α = −1.5, as adopted in
this study. With these notations, the inner and outer radii in Eq. (7) above are rin = R −
ΔR/2 and rout = R +
ΔR/2, respectively. As mentioned
above, we adopt a power-law distribution for the mean disk radii R of the modeled disk
population extending between the lower and upper boundaries R1 and R2. These boundaries must
not be confused with rin and rout in Eq.
(7).
2.2. Fitting procedure
The searches for debris disks around A stars (Su et al. 2006) and FGK stars (Trilling et al. 2008) at 24 and 70 μm with Spitzer are based on large samples of stars that are statistically not well defined because they are assembled from several programs based on various selection criteria and different integration times. Consequently, these surveys are neither volume-limited, nor flux-limited, and not representative of the stellar population in the solar neighborhood. For instance, the sample in Su et al. (2006) made of stars with spectral types ranging from B6 to A7 is highly biased toward A0 stars that constitute 27% of the selection while the A6 and A7 stars amount to less than 5%, unlike the actual stellar density in the solar neighborhood. The FGK star sample in Trilling et al. (2008) is biased toward F5-type stars representing 16% of this sample, while all K0 to K4 stars account for only 10%, unlike the stellar population in the solar neighborghood. In these conditions, it is debatable whether or not the detection frequency estimated from these samples are statistically representative of the population of cold outer debris disks as assumed in previous evolution studies.
In this work, we turn to the possibility that the distribution of their total masses is bimodal. High-mass cold disks are dense enough to be collisionally dominated and thus dusty enough to be detectable with Spitzer in the far-infrared and radiotelescopes at longer wavelengths. Instead, low mass cold disks are Poynting-Robertson-dominated and below detection level at these wavelengths, and they are possibly feeding exozodical regions detectable at much shorter wavelengths (Wyatt 2005). There are several reasons for this possible bimodal distribution. A fraction of outer debris disks can be stripped of their planetesimals during close stellar flybys while in the open cluster of their birth for the first 100 Myr of their lifetime if the stellar density is high (Lestrade et al. 2011). Also, planet-planet gravitational scattering can trigger dynamical instabilities that can eject planets and drastically remove planetesimals any time during the lifetime of the system. This scattering model is supported by several features of the observed giant exoplanets, notably their broad eccentricity distribution (Chatterjee et al. 2008; Jurić & Tremaine 2008; Raymond et al. 2010) and their clustering near the Hill stability limit (Raymond et al. 2009). Finally, giant planets, in crossing their mean motion resonances during migration, can destabilize the outer disk, triggering the late heavy bombardment and ejecting planetesimals as in the Nice model for the solar system (Gomes et al. 2005; Morbidelli et al. 2005; Tsiganis et al. 2005).
Hence, in this work, for each survey, we have only retained the stars with detected debris disks and made the hypothesis that this subsample is statistically representative of the population of high-mass cold disks. The nondetections are stars with low-mass disks that cannot be observed with our current capabilities in the far-infrared and submillimeter. Our statistical results hold within this framework.
For such a subsample, stellar distances, ages, and spectral types are known and only the parameters of the modeled debris disk population are unknown. In our study, this disk population is synthesized with the steady state collision model described in the previous section. This model is evolved using the known or adopted stellar ages and is fit to the distribution of observed fractional dust luminosities of the detected disks. The advantage of using the fractional dust luminosity rather than the photospheric excesses is that this quantity is distance-independent and combines both the 24 and 70 μm photometric measurements of the survey.
In our study, the stellar ages and spectral types, i.e., the masses and luminosities of the stars, are taken from Su et al. (2006) and Trilling et al. (2008). The initial total mass of planetesimals Mtot(0) and the mean disk radii R for the detected disks of the subsample were randomly drawn from their distributions. As justified in Sect. 2.1, we adopted a log-normal distribution for Mtot(0) centered on the median mass Mmid and having a 1σ width σMtot of 0.71 dex, and adopted the power-law distribution Rγ from R1 to R2, with γ = −0.5, for the mean disk radius R. In total, there are four independent parameters in our fit: Mmid, R1, R2, and the diameter Dc of the largest planetesimals. We have set fixed e = I = 0.05, ρ = 1000 kg m-3 (ice) or ρ = 2700 kg m-3 (basalt), ΔR = R/2, and q = 11/6 for all disks as in past studies of Wyatt et al. (2007b) and Kains et al. (2011). We have considered the effects of changing these parameters in Sect. 3.
The best-fit values of the four parameters Mmid, Dc, R1, and R2 of the model were searched numerically over a large grid using the Kolmogorov-Smirnov test (K-S test) to match the observed and modeled distributions of fractional dust luminosities. At each point of this 4D-parameter space, 100 simulations were carried out so that Mtot(0) and R take many randomly chosen values from their adopted distributions as in the Monte Carlo method. The best-fit values were those yielding the highest K-S test probability averaged over the 100 simulations.
The K-S test measures the largest absolute difference between the two distributions under consideration and estimates the probability of finding this difference larger than the observed value in the case of the null hypothesis (data drawn from the same distribution). Thus, this probability is an estimate of the significance level of the observed difference as a disproof of the null hypothesis; i.e., a small probability implies that the two distributions do not come from the same parent distribution. We have used the surbroutines in Press et al. (1992) which are reliable when the number of data points is larger than 20 and therefore appropriate for the subsamples of debris disks in our study. Figure 1 is an illustration of our fitting procedure.
 |
Fig. 1 Cumulative distributions of the fractional dust luminosities; the blue line corresponds to the observations and the red lines are eight independent simulations computed with the same parameters Mmid, R1, R2, and Dc, but with different random numbers to simulate the disk population around the A stars of the Su et al. (2006) survey. The statistical Kolmogorov-Smirnov test is used to match the observed and simulated distributions so they can be considered drawn from the same parent distribution. The maximum K-S probability is 75% in this example, averaged over 100 simulations. For clarity, only eight simulations are shown on this figure but 100 were actually computed at each point of the 4D parameter space (Mmid, R1, R2, Dc) for our numerical search. |
The values for Mtot(0) and R were drawn from the
log-normal and power-law distributions, respectively, using the reciprocal of a random
variable (Devroye 1986):
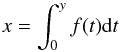 (8)where x is a random variable
drawn uniformly between 0 and 1 and y is an implicit variable that has the density
f(t) that can be set analytically or
as a binned distribution1.
(8)where x is a random variable
drawn uniformly between 0 and 1 and y is an implicit variable that has the density
f(t) that can be set analytically or
as a binned distribution1.
2.3. Tests of the fitting procedure
We have simulated fractional dust luminosities computed with the collisional equilibrium
evolution model of Wyatt et al. (2007a) described
above, including the relationship bewteen 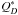 and
Dc of Benz
& Asphaug (1999). In addition, a uniformly distributed random noise of
±20% was added to each
modeled fractional dust luminosity. A first set of data was simulated with the a priori
values Mmid = 4
M⊕ and Dc = 10 km, and
a second with Mmid
= 40 M⊕ and Dc = 350 km, to
verify that these two disk populations, which are clearly distinct, can be distinguished
with our fitting procedure. We kept the other two fitted parameters set to the same a
prioiri values, R1 =
6.5 AU and R2 = 35 AU, for this verification. The
distributions of the stellar masses and ages were those of the sample of Su et al. (2006). In addition to the fitted parameters,
the disk population was controlled with the fixed parameters: e = I =
0.05, ΔR =
R/2, γ = −0.5, σMtot
= 0.71 dex and ice for the planetesimal material. The results of the
fits are in Fig. 2 where the contours of the K-S test
maximal probability indicate that the best-fit areas delineated with the 90% contours,
although large, do not ovelap for the two data sets of our tests. It is noticeable that
the peaks of these regions are close to the a priori values of the parameters
Mmid and Dc of the two
simulated data sets. Hence, the two disk populations can be distinguished. The impact of
modifying the fixed parameters are studied with the real data in Sect. 3.
and
Dc of Benz
& Asphaug (1999). In addition, a uniformly distributed random noise of
±20% was added to each
modeled fractional dust luminosity. A first set of data was simulated with the a priori
values Mmid = 4
M⊕ and Dc = 10 km, and
a second with Mmid
= 40 M⊕ and Dc = 350 km, to
verify that these two disk populations, which are clearly distinct, can be distinguished
with our fitting procedure. We kept the other two fitted parameters set to the same a
prioiri values, R1 =
6.5 AU and R2 = 35 AU, for this verification. The
distributions of the stellar masses and ages were those of the sample of Su et al. (2006). In addition to the fitted parameters,
the disk population was controlled with the fixed parameters: e = I =
0.05, ΔR =
R/2, γ = −0.5, σMtot
= 0.71 dex and ice for the planetesimal material. The results of the
fits are in Fig. 2 where the contours of the K-S test
maximal probability indicate that the best-fit areas delineated with the 90% contours,
although large, do not ovelap for the two data sets of our tests. It is noticeable that
the peaks of these regions are close to the a priori values of the parameters
Mmid and Dc of the two
simulated data sets. Hence, the two disk populations can be distinguished. The impact of
modifying the fixed parameters are studied with the real data in Sect. 3.
 |
Fig. 2 Tests of the fitting procedure with simulated data. Top: parameter search for data simulated with Mmid = 4 M⊕, Dc = 10 km, R1 = 6.5 AU, R2 = 35 AU. Bottom: parameter search for data simulated with Mmid = 40 M⊕, Dc = 350 km, and R1 and R2 as just mentioned. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green) and 10% (yellow). The two best-fit regions delineated by the 90% contour are clearly exclusive when comparing the two plots. Their peaks are close to the a priori values of Mmid and Dc. The two crossed circle symbols on each plot indicate the positions of the a priori values used for Mmid and Dc to simulate the two sets of data. |
 |
Fig. 3 Best-fit regions for the modeled disk population around the A-type stars of the Su et al. (2006) survey. Plots of the significance levels of the Kolmogorov-Smirnov test for the adjusted parameters Mmid, Dc, R1, and R2 of the model. The adopted values are e = I = 0.05, ΔR = R/2, γ = −0.5, σMtot = 0.71 dex and ice for the planetesimal material. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green), and 10% (yellow) of the peak K-S test probability (80.7%). The Mmid and Dc are on a log scale, while R1 and R2 are on linear scale. |
 |
Fig. 4 Best-fit regions for the sample of A-type stars with a model assuming narrow disks; width is ΔR = R/10 while it is ΔR = R/2 in Fig. 3. The peak K-S test probability is 77.6% in this new fit. See the legend of Fig. 3 for more details. Compare the 90% lower and upper limits for Mmid and Dc relative to Fig. 3. |
3. Determination of the parameters of the modeled debris disk population
3.1. Parameter search for the A-star survey of Su et al. (2006)
A total of 160 A stars with ages between 5 and 850 Myr and distances between 2.6 and 384 pc was surveyed at 24 and 70 μm with Spitzer (Su et al. 2006). We have fit the model to the distribution of the fractional dust luminosities of the sole 34 stars with detected disks at both 24 μm and 70 μm, and older than 9 Myr. We adopted the fractional dust luminosities fd of Table 3 (Group I) of Su et al. (2006) that are based on the observed [24]−[70] color temperature and on the assumption of blackbody emission for the dust. Since fractional dust luminosity is only ~8% overestimated between a blackbody and modified blackbody emission for A stars, this is irrelevent for our purpose. We did not retain the additional eight stars with only 70 μm excesses (Group II in Su et al. (2006)) which yield solely upper limits for fd.
The ranges of the model parameters tested were: Mmid of 0.1 to
100 M⊕; Dc of 1 to 500
km; R1 of 1
to 50 AU; and R2 of R1 + 10 AU to 150 AU. The grid was set up with 20
increments for each parameter. The fixed parameters are the mean planetesimal eccentricity
e = 0.05,
the disk width ΔR =
R/2, the exponent of the mean disk
radius power-law distribution γ = −0.5, the 1σ width of the log-normal
distribution of Mtot(0) taken to be 0.71 dex, and ice
for the planetesimal material ( ). We carried
out a numerical search in these conditions and plots of the significance levels based on
the K-S test probability for each pair of parameters are displayed in Fig. 3. These plots indicate that probabilities are equally
high over a broad region where the full ranges of the other two parameters are explored.
They are not the 2D projections of the 4D parameter space for the maximum K-S test
probability. Such projections provide “peaked” plots that are misleading because they
falsely convey the impression that the solution is unique.
). We carried
out a numerical search in these conditions and plots of the significance levels based on
the K-S test probability for each pair of parameters are displayed in Fig. 3. These plots indicate that probabilities are equally
high over a broad region where the full ranges of the other two parameters are explored.
They are not the 2D projections of the 4D parameter space for the maximum K-S test
probability. Such projections provide “peaked” plots that are misleading because they
falsely convey the impression that the solution is unique.
The most probable ranges for the parameters can be determined using the 90% significance
level in Fig. 3. For the median mass Mmid, the lower
and upper limits are 2 M⊕ and 20 M⊕; for
Dc, they are 2 km and 60 km; for
R1, they
are 2 AU and 20 AU. For R2, the range is from 30 AU to beyond >150 AU in Figs.
3, 4. Hence,
the upper boundary R2 of the distribution of the mean disk radii is
uncertain and can accommodate large disks, as a few have been observed; for instance, the
disk around HD 207129, which has also been modeled with a collisional cascade by Löhne et al. (2012). Based on the values given above
for Dc, the corresponding limits for
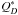 are between
62 J kg-1 and 895 J
kg-1 for ice and
are between 92 J kg-1 and 2277 J kg-1 for basalt using the model of Benz & Asphaug (1999).
are between
62 J kg-1 and 895 J
kg-1 for ice and
are between 92 J kg-1 and 2277 J kg-1 for basalt using the model of Benz & Asphaug (1999).
The parameters R1 and R2 are blackbody radii because the fractional dust luminosities used were estimated with this assumption for the grains. Hence, the true disk radii should be about twice these values in applying the factor Γ = 2 (ratio of the resolved radius to the blackbody radius) found for the resolved A star disks in the Herschel DEBRIS program (Booth et al. 2013).
The best-fit values in the determination of Wyatt et al.
(2007b), based on a fit to the disk detection frequencies binned in ages and
excess strengths, are Mmid = 10
M⊕, Dc = 60 km,
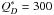 J/kg
(independent parameter in their study), R1 = 3 AU, and R2 = 120 AU. Additionally,
they fit γ = −0.8 ±
0.6 consistent with our adopted value of −0.5, and they assumed e = I =
0.05 and 1σ width of 1.14 dex for the log-normal distribution
of Mtot(0). Their solution is within the 75%
significance level region of our fit in Fig. 3.
J/kg
(independent parameter in their study), R1 = 3 AU, and R2 = 120 AU. Additionally,
they fit γ = −0.8 ±
0.6 consistent with our adopted value of −0.5, and they assumed e = I =
0.05 and 1σ width of 1.14 dex for the log-normal distribution
of Mtot(0). Their solution is within the 75%
significance level region of our fit in Fig. 3.
We have changed the fixed parameters of the model to test whether or not the best-fit regions are significantly modified. We changed the dynamical excitation of the disks e = I (0.05/2, 0.05 × 2, 0.05 × 4), we tested narrower disks with ΔR = R/10, as well as shallower and steeper distributions for the mean disk radii R with γ (0.0, −1.0), we modified the 1σ width of the log-normal distribution of Mtot(0) (σMtot = 0.25, 0.50, 1.14), and we tested the material of planetesimals (ice, basalt). The main structure and extent of the significance levels in the probability plots of Fig. 4 are very similar to those of our standard model (e = 0.05, ΔR = R/2, γ = −0.5, σMtot = 0.71 dex, ice) in Fig. 3. The most noticeable difference occured when changing from wide (ΔR = R/ 2) to narrow (ΔR = R/10) disks. Then, as shown in Fig. 4, the best-fit region is shifted upward, so that the lower and upper limits become ~1 M⊕ and 60 M⊕ for Mmid and 6 km and 100 km for Dc, respectively. This can be explained with Eq. (2) where it is clear that the collisional timescale tc(0) controlling disk evolution is proportional to ΔR/R × Dc, so narrower disks can be outweighed by increasing Dc.
Finally, we note that our optimum solution yields a slightly better K-S test probability (80.7%) than when we changed the fixed parameters to other values. For instance, changing σMtot to 0.25, 0.50, and 1.14 dex makes this probability becomes 77.7%, 78.1%, and 74.1%, respectively.
 |
Fig. 5 Best-fit for the FGK-type stars of the Trilling et al. (2008) survey. Plots of the significance levels of the K-S test for the adjusted parameters Mmid, Dc, R1, and R2 of the model. The adopted values are e = I = 0.05, ΔR = R/2, γ = −0.5, σMtot = 0.71 dex and ice for the planetesimal material. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green), and 10% (yellow) of the peak K-S test probability (87.1%). The Mmid and Dc are on a log scale, while R1 and R2 are on linear scale. |
3.2. Parameter search for the solar type star survey of Trilling et al. (2008)
Nearly 200 solar type stars (FGK) with ages between 290 Myr and 11.75 Gyr and distances between 4.7 and 148 pc were surveyed at 24 and 70 μm with Spitzer (Trilling et al. 2008). The sample was assembled from different programs. For the same reason as for the A star sample, we fit the model to the distribution of the fractional dust luminosities of the sole 28 stars with detected disks. The fractional dust luminosities of this subsample are taken from Tables 5 and 6 of Trilling et al. (2008). They are estimated from the [24]−[70] color temperature when excesses were measured at both bands (six disks). However, most excesses were detected at only 70 μm and so these authors set the 24 μm “excess” to be equal to three times the uncertainty at 24 μm and found the blackbody emission that best fit this excess and the 70 μm excess. Such a temperature is the maximum temperature for the excess yielding the maximum fractional dust luminosities that are consistent with the data.
The ranges of the parameters tested and the values adopted for the fixed parameters are the same as for the A stars in Sect. 3.1. Similarly, Fig. 5 shows also regions of maximum K-S test probabilities marginalized (not 2D projections of the 4D parameter space). Regions of highest K-S test probability shown by the 90% significance level in this figure are wider than for the A stars.
The FGK subsample is smaller and the fractional dust luminosities are mostly the maximum values from excesses detected at the single wavelength λ = 70 μm. This is a limitation of the analysis and is likely responsible for a somewhat degraded fit of this subsample compared to the A stars in the previous section. The 90% significance level in Fig. 5 yields only a lower limit of 0.8 M⊕ for Mmid and lower and upper limits of 2 km and 60 km for Dc, assuming ice for the material composition. The parameters R1 and R2 are not well determined.
The best-fit values in the determination of Kains et al.
(2011), based on a fit to the disk detection frequencies binned in ages and
excess strengths of FGK stars, are Mmid = 4 M⊕,
Dc =
450 km, 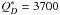 J/kg
(independent parameter in their study), R1 = 1 AU, and R2 = 160 AU. Additionally,
they fit γ = −0.60 ±
0.35 and this is consistent with our adopted value of −0.5, and they assumed e = I =
0.05 and a 1σ width of 0.8 dex for the log-normal distribution
of Mtot(0). This solution is within the 50%
significance level region in our Fig. 5.
J/kg
(independent parameter in their study), R1 = 1 AU, and R2 = 160 AU. Additionally,
they fit γ = −0.60 ±
0.35 and this is consistent with our adopted value of −0.5, and they assumed e = I =
0.05 and a 1σ width of 0.8 dex for the log-normal distribution
of Mtot(0). This solution is within the 50%
significance level region in our Fig. 5.
In a similar fashion as for the A stars discussed in the previous section, we changed the fixed parameters of the model to test whether or not the best-fit regions are significantly modified. No significant change is seen in the extent or shape of the highest K-S test probability regions in this case.
3.3. Comparison
The best-fit regions for the six pairs of parameters of the disk population model have been displayed and isoprobability coutours of the K-S test drawn. These regions are overlapping between the A- and FGK-type stars, indicating that there are best-fit values that are compatible with both Spitzer samples. The fit values found in previous studies for the A stars (Wyatt et al. 2007b) and for the FGK stars (Kains et al. 2011) differ significantly and may possibly be considered inconsistent. However, as is apparent in Figs. 3 and 5, they are specific solutions among an ensemble.
4. Steady state collisional evolution of debris disks around M dwarfs
Prior to Herschel, two searches for cold debris disks around M dwarfs were conducted in the far-infrared and at longer wavelengths. With Spitzer, Gautier et al. (2007) observed 41 M dwarfs at 70 μm with a 1σ sensitivity level of ~3 mJy. Their sample is made of the nearest stars at less than 5 pc, likely older than 1Gyr, and of spectral types between M0 and M6.5. With the IRAM 30-meter and JCMT radiotelescopes, Lestrade et al. (2006, 2009) observed 50 M dwarfs at λ = 850 μm and 1.2 mm with a 1σ sensitivity of 1−3 mJy. Half of this sample is made of nearby stars at less than 7.7 pc and likely older than 1 Gyr. The others are members of moving groups that have known ages of less than 600 Myr, but are located farther away.
We have investigated whether or not the lack of detected debris disks around these M dwarfs is consistent with the steady state collisional evolution model fit to the A and FGK data in the previous section. This model is based on the assumption that the initial disk mass distribution is bimodal; only the high-mass collisionally-dominated disks are detectable, representing ~25% of the AFGK star sample, the others are low-mass PR-dominated disks, which are undetected and not used in the fit.
Thus, in our simulation of the M stars now, we used the predicted flux density excesses from only 25% of the whole sample, just as we did for the AFGK stars. Hence, for the Gautier et al. (2007) survey, we picked 10-combinations out of the 35 stars with 70 μm measurements uncontaminated by cirrus or background galaxies, and tested 100 such combinations to establish the statistics of the flux density excesses.
We compute the optically thin dust emission of a disk by integrating over the radial
distribution of the grains: ![\begin{eqnarray} S_{\nu} & = & {2.5\,\times\,10^{11}} \times {{f_T^{-4}\times A(t_{\rm age}) \times (\alpha+2)} \over {d^2 \times (r_{\rm out}^{\alpha+2}-r_{\rm in}^{\alpha+2})}} \nonumber \\[-2mm] & & \times\, {\sum_{i=1}^{N} B_{\nu}(T(r_i)) \times r_i^{\alpha+1} \Delta r}, \label{S_nu} \end{eqnarray}](/articles/aa/full_html/2014/05/aa22567-13/aa22567-13-eq121.png) (9)where
Sν is in mJy, the distance
d to the star
is in pc, the emitting surface of the dust A(tage) is in
AU2. We assume that
small grains in these mostly old M dwarfs are not blown out by stellar wind and adopted the
minimum grain size of Dmin = 0.1 μm to estimate
this surface, as discussed above. The radial distance ri, ranges from the inner
radius rin to the outer radius rout, and is in
AU, as the increment Δr. The radial profile of the emitting cross-sectional
area of the grains per unit area of the disk surface is a power law with the standard index
α, as already
described for the fractional dust luminosity in Eq. (7). The Planck function Bν depends on the dust
temperature T(ri)
at radial distance ri. Several studies
have shown that this temperature is higher than the blackbody temperature TBB(ri)
when fitting simultaneously SED and images of resolved debris disks; this is due to
inefficient long wavelength emission of small grains, which become hotter than blackbodies
(e.g., Backman & Paresce 1993; Lebreton et al. 2012). A simplified model to account for
these properties is T(ri) =
fT ×
TBB(ri)
where
(9)where
Sν is in mJy, the distance
d to the star
is in pc, the emitting surface of the dust A(tage) is in
AU2. We assume that
small grains in these mostly old M dwarfs are not blown out by stellar wind and adopted the
minimum grain size of Dmin = 0.1 μm to estimate
this surface, as discussed above. The radial distance ri, ranges from the inner
radius rin to the outer radius rout, and is in
AU, as the increment Δr. The radial profile of the emitting cross-sectional
area of the grains per unit area of the disk surface is a power law with the standard index
α, as already
described for the fractional dust luminosity in Eq. (7). The Planck function Bν depends on the dust
temperature T(ri)
at radial distance ri. Several studies
have shown that this temperature is higher than the blackbody temperature TBB(ri)
when fitting simultaneously SED and images of resolved debris disks; this is due to
inefficient long wavelength emission of small grains, which become hotter than blackbodies
(e.g., Backman & Paresce 1993; Lebreton et al. 2012). A simplified model to account for
these properties is T(ri) =
fT ×
TBB(ri)
where 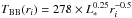 (L∗ in L⊙ and
ri in AU). The factor
fT is related to the grain
emission efficiency Q < 1 in a simple first-order
physical interpretation. This factor has only been determined in a few cases ;
(L∗ in L⊙ and
ri in AU). The factor
fT is related to the grain
emission efficiency Q < 1 in a simple first-order
physical interpretation. This factor has only been determined in a few cases ;
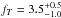 for the M3 star GJ581 (Lestrade et al. 2012),
fT
= 1.9 for the G star 61 Vir (Wyatt et al.
2012), and fT = 1.4 for A stars
(Bonsor & Wyatt 2010; Booth et al. 2013). This trend might be an indication that fT depends on the stellar
spectral type (higher fT for later type),
although this is a tentative conjecture given the limited observations. Note that the effect
of fT in Eq. (9) is double edges ; it makes the Planck function
peak toward shorter wavelengths, but at the same time the factor
for the M3 star GJ581 (Lestrade et al. 2012),
fT
= 1.9 for the G star 61 Vir (Wyatt et al.
2012), and fT = 1.4 for A stars
(Bonsor & Wyatt 2010; Booth et al. 2013). This trend might be an indication that fT depends on the stellar
spectral type (higher fT for later type),
although this is a tentative conjecture given the limited observations. Note that the effect
of fT in Eq. (9) is double edges ; it makes the Planck function
peak toward shorter wavelengths, but at the same time the factor
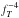 drasticly damps the flux density with fT>
1. The overall effect on the flux density can go both ways depending on
the Wien law maximum wavelength relative to the observing wavelength. We tested both
fT
= 1 and fT = 3.5 in this study
of M dwarfs.
drasticly damps the flux density with fT>
1. The overall effect on the flux density can go both ways depending on
the Wien law maximum wavelength relative to the observing wavelength. We tested both
fT
= 1 and fT = 3.5 in this study
of M dwarfs.
From the best-fit region of the A star disk population in Fig. 3, we adopt the smallest best-fit value for Dc, 2 km, the corresponding median mass, Mmid = 15 M⊕, and the lower limits, R1 = 2 AU, and R2 = 30 AU. These parameters make the shortest collisional timescale tc(0) (Eq. (2)), and therefore the lowest flux densities at the age of the star t (Eqs. (5), (9)), as hinted by the observations in Gautier et al. (2007).
With these parameters, we simulate total masses Mtot(tage) and
mean disk radii R for the population of disks around the M dwarfs
observed in the survey of Gautier et al. (2007) and
estimate their flux densities at λ = 70 μm with Eq. (9). Their distances are known and their ages,
which are undetermined but likely greater than 1 Gyr, were chosen randomly between 1 and 10
Gyr. In selecting one hundred 10-combinations among the 35 M dwarfs of the Gautier et al.’s
sample, and using the 3σ detection limit of their survey (9 mJy), the mean
disk frequency is 5 ± 3.5%
(fT = 1) or
6 ± 4% (fT =
3.5) with these simulations. These two frequencies can be compared to the
limit of 1% set by their survey in which no disk is detected. This limit is derived with the
binomial discrete probability distribution 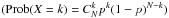 used to quantify the chance of
observing no disk (k =
0) in a sample of N = 35 stars when the mean detection rate is
p = 1% and
the probability Prob(X =
0) is 68% (equivalent to the 1σ Gaussian limit). The higher disk frequency
p ~ 5%, found
with our simulations above, corresponds to a probability Prob(X = 0) of 16% to find no
disk in a sample of N =
35 stars. This probability is still less than the 2σ limit used in Gaussian
statistics, and so the disk evolution model fit to the AFGK stars can be considered
consistent with the lack of disks detected around the M dwarfs of the Gautier’s sample.
used to quantify the chance of
observing no disk (k =
0) in a sample of N = 35 stars when the mean detection rate is
p = 1% and
the probability Prob(X =
0) is 68% (equivalent to the 1σ Gaussian limit). The higher disk frequency
p ~ 5%, found
with our simulations above, corresponds to a probability Prob(X = 0) of 16% to find no
disk in a sample of N =
35 stars. This probability is still less than the 2σ limit used in Gaussian
statistics, and so the disk evolution model fit to the AFGK stars can be considered
consistent with the lack of disks detected around the M dwarfs of the Gautier’s sample.
We treated the submillimeter survey of M dwarfs observed in Lestrade et al. (2006, 2009) the same way
after correcting the emission model by a factor (210 μm/λ)β and using
β = 1 to
account for the modified blackbody law at the longer observing wavelengths λ = 1200 μm
and 850 μm. The
3σ
sensitivity threshold is 3−9 mJy
for this survey. The optimum model parameters (Mmid = 15 M⊕,
Dc =
2 km, R1 =
2 AU, and R1
= 30 AU) yield simulated detection frequencies of 0% for fT =
3.5 and only ~ 2% ±
1.7 for fT = 1.0. Note,
surprisingly at first, that the frequency with fT = 1 is higher than the
frequency with fT = 3.5 because the
observing wavelength λ = 1200
μm is longer than the Wien law maximum wavelength for
the disk temperature: the increase of the Planck function when fT =
3.5 is counterbalanced by the factor
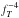 in the flux density estimation. Nonetheless, the disk evolution model found for the AFGK
stars is also consistent with the lack of disks detected around M dwarfs at 850 and 1200
μm in the
Lestrade et al. sample.
in the flux density estimation. Nonetheless, the disk evolution model found for the AFGK
stars is also consistent with the lack of disks detected around M dwarfs at 850 and 1200
μm in the
Lestrade et al. sample.
5. Discussion
5.1. Comparison between the Kuiper belt and the debris disks around A and FGK stars
The best-fit values for the diameter Dc of the largest planetesimals range from 2 to 60 km consistently for disks around both A- and FGK-type stars in Figs. 3 and 5, for our standard solution of broad disks (width ΔR = R/2). This range extends from 6 km to 100 km for narrow disks (ΔR = R/ 10) in Fig. 4. It is remarkable that the size of the largest bodies of the collisional cascade in our modeled disk population is close to the break found at around 30 km in the Kuiper belt objects size distribution (Fraser & Kavelaars 2009; Schlichting et al. 2009; Fuentes et al. 2010). This break is usually attributed to the erosion of planetesimals caused by the collisional evolution of bodies with size of <30 km over the age of the solar system while larger objects are primordial, i.e., not yet colliding (Schlichting et al. 2013). In the surveys used in our study, the mean age is 250 Myr for the A stars (about 1/3 of the lifetime for this stellar type) and is 4.3 Gyr for the FGK stars, i.e., close to the Sun age at about half of its lifetime. Although the Kuiper belt is presently a PR-dominated debris disk, it is thought that its mass was originally much higher than its present estimate of ~0.1 M⊕, possibly because of a catastrophic event in the meantime, such as the late heavy bombardment about 700 Myr after the birth of the Sun (Gomes et al. 2005; Morbidelli et al. 2005; Tsiganis et al. 2005). Hence, the break at 30 km seen today is a scar of the past high collisional activity of the Kuiper belt. We have found a new similarity between cold debris disks and the Kuiper belt, which might be rooted in their common formation and evolution mechanisms. It has been shown that the large KBO size distribution can be well matched by planet formation models of runaway growth where only a small fraction of the total mass is converted into large protoplanets and most of the initial mass remains in planetesimals that are 1−10 km rather than >100 km in radius (e.g., Kenyon & Luu 1999; Kenyon & Bromley 2004, 2012; Schlichting & Sari 2011). A caveat is that we assume in our model that all disks have the same Dc, and this is a limitation of our study.
The best-fit value for the median initial mass Mmid of debris disks around solar type stars is >0.8 M⊕ in our study and, hence, is about ten times larger than for the present Kuiper belt (Gladman et al. 2001). Consistently, Bryden et al. (2006) conclude that cold debris disks detected around FGK stars have a median fractional dust luminosity about ten times higher than the current solar value. These authors fit a theoretical Gaussian distribution in logarithmic space to the observed distribution of fractional dust luminosity frequencies by varying its median and standard deviation.
5.2. On the debris disks around M dwarfs within the framework of our study
We have shown that surveys have not been deep enough to conclude that the disk population found with the steady state evolution model for AFGK stars is not consistent with the lack of disks detected around the M dwarfs observed at far-infrared and submillimeter wavelengths. A more stringent test is expected with the DEBRIS Herschel survey because the sample is larger (N ~ 100 for M-dwarfs) and the images are at least three times deeper than the past surveys.
6. Conclusion
In our study, we have fit the steady state collisional evolution model of Wyatt et al. (2007a) to the fractional dust luminosity distributions measured with Spitzer for the A and FGK stars. Hence, we have postulated that these distrubutions correspond to the population of high-mass collisionally-dominated disks that are detectable in the current surveys and that can be analyzed per se. There is a distinct population of low-mass disks that are not considered in the study because they are undetectable. The results of our study must be understood in this framework.
The model parametrized with Mmid,Dc,R1, and R2 satisfactorily fits the observations and the two resulting best-fit regions for the samples of A and FGK stars are overlapping, indicating that there are solutions common to both samples.
We have applied this steady state collisional evolution model to potential high-mass collisionally-dominated disks around M dwarfs surveyed prior to the Herschel satellite in the far-infrared by Gautier et al. (2007) and in the submillimeter domain by Lestrade et al. (2006, 2009). Within the framework of this study, we have shown that the disk population fit to the AFGK stars is still consistent with the lack of disks detected around M-dwarfs in the far-infrared and submillimeter surveys.
In a future study, we shall apply our novel approach to study evolution of debris disks in the larger sample of M dwarfs in the unbiased Herschel DEBRIS survey.
Acknowledgments
Étienne Morey’s Ph.D. work is funded by a grant from the Fondation CFM-JP Aguilar. We are in debt to our referee for his/her incisive comments which have greatly benefited to the paper. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA.
References
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Avenhaus, H., Schmid, H. M., & Meyer, M. R. 2012, A&A, 548, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonsor, A., & Wyatt, M. 2010, MNRAS, 409, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Booth, M., Kennedy, G., Sibthorpe, B., et al. 2013, MNRAS, 428, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Bryden, G., Beichman, C. A., Trilling, D. E., et al. 2006, ApJ, 636, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Bouwman, J., Mamajek, E. E., et al. 2009, ApJS, 181, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Devroye, L. 1986, Non-Uniform Random Variate Generation (New York: Springer-Verlag) [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C., & Decin, G. 2003, ApJ, 598, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2013, ApJ, 767, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, W. C., & Kavelaars, J. J. 2009, AJ, 137, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes, C. I., Holman, M. J., Trilling, D. E., & Protopapas, P. 2010, ApJ, 722, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Gáspár, A., Psaltis, D., Özel, F., Rieke, G. H., & Cooney, A. 2012, ApJ, 749, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Gautier, III, T. N., Rieke, G. H., Stansberry, J., et al. 2007, ApJ, 667, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Kavelaars, J. J., Petit, J.-M., et al. 2001, AJ, 122, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greaves, J. S., & Wyatt, M. C. 2010, MNRAS, 404, 1944 [NASA ADS] [Google Scholar]
- Hawley, S., Reid, I. N., & Gizis, J. 2000, in From Giant Planets to Cool Stars, ed. C. A. Griffith, & M. S. Marley, ASP Conf. Ser., 212, 252 [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., & Tremaine, S. 2008, ApJ, 686, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kains, N., Wyatt, M. C., & Greaves, J. S. 2011, MNRAS, 414, 2486 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Liu, M. C., & Matthews, B. C. 2004, Science, 303, 1990 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2004, AJ, 128, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2012, AJ, 143, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Luu, J. X. 1999, AJ, 118, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K. 2013, ApJ, 767, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V. 2010, Res. Astron. Astrophys., 10, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Backman, D. E., & Artymowicz, P. 2000, in Protostars and Planets IV (Tucson: University of Arizona Press), 639 [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, J., Augereau, J.-C., Thi, W.-F., et al. 2012, A&A, 539, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Wyatt, M. C., Bertoldi, F., Dent, W. R. F., & Menten, K. M. 2006, A&A, 460, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Wyatt, M. C., Bertoldi, F., Menten, K. M., & Labaigt, G. 2009, A&A, 506, 1455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Morey, E., Lassus, A., & Phou, N. 2011, A&A, 532, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lestrade, J.-F., Matthews, B. C., Sibthorpe, B., et al. 2012, A&A, 548, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, M. C., Matthews, B. C., Williams, J. P., & Kalas, P. G. 2004, ApJ, 608, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Krivov, A. V., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, B. C., Sibthorpe, B., Kennedy, G., et al. 2010, A&A, 518, L135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Plavchan, P., Jura, M., & Lipscy, S. J. 2005, ApJ, 631, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Plavchan, P., Werner, M. W., Chen, C. H., et al. 2009, ApJ, 698, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing (Cambridge: University Press) [Google Scholar]
- Raymond, S. N., Barnes, R., Veras, D., et al. 2009, ApJ, 696, L98 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Raymond, S. N., Armitage, P. J., & Gorelick, N. 2010, ApJ, 711, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Su, K. Y. L., Stansberry, J. A., et al. 2005, ApJ, 620, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. E., & Sari, R. 2011, ApJ, 728, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. E., Ofek, E. O., Wenz, M., et al. 2009, Nature, 462, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. E., Fuentes, C. I., & Trilling, D. E. 2013, AJ, 146, 36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Stansberry, J. A., et al. 2006, ApJ, 653, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., & Augereau, J.-C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Augereau, J. C., & Beust, H. 2003, A&A, 408, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trilling, D. E., Bryden, G., Beichman, C. A., et al. 2008, ApJ, 674, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wargelin, B. J., & Drake, J. J. 2001, ApJ, 546, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C. 2005, A&A, 433, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., & Dent, W. R. F. 2002, MNRAS, 334, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Smith, R., Greaves, J. S., et al. 2007a, ApJ, 658, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Smith, R., Su, K. Y. L., et al. 2007b, ApJ, 663, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Kennedy, G., Sibthorpe, B., et al. 2012, MNRAS, 424, 1206 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Cumulative distributions of the fractional dust luminosities; the blue line corresponds to the observations and the red lines are eight independent simulations computed with the same parameters Mmid, R1, R2, and Dc, but with different random numbers to simulate the disk population around the A stars of the Su et al. (2006) survey. The statistical Kolmogorov-Smirnov test is used to match the observed and simulated distributions so they can be considered drawn from the same parent distribution. The maximum K-S probability is 75% in this example, averaged over 100 simulations. For clarity, only eight simulations are shown on this figure but 100 were actually computed at each point of the 4D parameter space (Mmid, R1, R2, Dc) for our numerical search. |
| In the text | |
 |
Fig. 2 Tests of the fitting procedure with simulated data. Top: parameter search for data simulated with Mmid = 4 M⊕, Dc = 10 km, R1 = 6.5 AU, R2 = 35 AU. Bottom: parameter search for data simulated with Mmid = 40 M⊕, Dc = 350 km, and R1 and R2 as just mentioned. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green) and 10% (yellow). The two best-fit regions delineated by the 90% contour are clearly exclusive when comparing the two plots. Their peaks are close to the a priori values of Mmid and Dc. The two crossed circle symbols on each plot indicate the positions of the a priori values used for Mmid and Dc to simulate the two sets of data. |
| In the text | |
 |
Fig. 3 Best-fit regions for the modeled disk population around the A-type stars of the Su et al. (2006) survey. Plots of the significance levels of the Kolmogorov-Smirnov test for the adjusted parameters Mmid, Dc, R1, and R2 of the model. The adopted values are e = I = 0.05, ΔR = R/2, γ = −0.5, σMtot = 0.71 dex and ice for the planetesimal material. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green), and 10% (yellow) of the peak K-S test probability (80.7%). The Mmid and Dc are on a log scale, while R1 and R2 are on linear scale. |
| In the text | |
 |
Fig. 4 Best-fit regions for the sample of A-type stars with a model assuming narrow disks; width is ΔR = R/10 while it is ΔR = R/2 in Fig. 3. The peak K-S test probability is 77.6% in this new fit. See the legend of Fig. 3 for more details. Compare the 90% lower and upper limits for Mmid and Dc relative to Fig. 3. |
| In the text | |
 |
Fig. 5 Best-fit for the FGK-type stars of the Trilling et al. (2008) survey. Plots of the significance levels of the K-S test for the adjusted parameters Mmid, Dc, R1, and R2 of the model. The adopted values are e = I = 0.05, ΔR = R/2, γ = −0.5, σMtot = 0.71 dex and ice for the planetesimal material. Levels are 99% (red), 90% (dark blue), 75% (light blue), 50% (green), and 10% (yellow) of the peak K-S test probability (87.1%). The Mmid and Dc are on a log scale, while R1 and R2 are on linear scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$y = [(b^{\gamma +1} - a^{\gamma +1}) x + a^{\gamma+1}]^{1 \over {\gamma +1}}$}](/articles/aa/full_html/2014/05/aa22567-13/aa22567-13-eq179.png)