| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201323226 | |
| Published online | 10 April 2014 | |
Proper motions of the optically visible open clusters based on the UCAC4 catalog⋆
1 UNIFEI, Instituto de Ciências Exatas, Universidade Federal de Itajubá, Av. BPS 1303 Pinheirinho, 37500-903 Itajubá, MG Brazil
e-mail: wiltonsdias@yahoo.com.br
2 Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, Cidade Universitária, São Paulo SP, Brazil
3 Observatório do Valongo, UFRJ, Ladeira Pedro Antonio 43, 20080-090 Rio de Janeiro, RJ, Brazil
Received: 10 December 2013
Accepted: 12 February 2014
We present a catalog of mean proper motions and membership probabilities of individual stars for optically visible open clusters, which have been determined using data from the UCAC4 catalog in a homogeneous way. The mean proper motion of the cluster and the membership probabilities of the stars in the region of each cluster were determined by applying the statistical method in a modified fashion. In this study, we applied a global optimization procedure to fit the observed distribution of proper motions with two overlapping normal bivariate frequency functions, which also take the individual proper motion errors into account. For 724 clusters, this is the first determination of proper motion, and for the whole sample, we present results with a much larger number of identified astrometric member stars. Furthermore, it was possible to estimate the mean radial velocity of 364 clusters (102 unpublished so far) with the stellar membership using published radial velocity catalogs. These results provide an increase of 30% and 19% in the sample of open clusters with a determined mean absolute proper motion and mean radial velocity, respectively.
Key words: open clusters and associations: general
Tables 2 to 1809 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A79
© ESO, 2014
1. Introduction
Open clusters are key objects used to study the structure of the Galaxy. Our group has been devoted to this field in the past few years, obtaining results, which includes the determination of the velocity of spiral pattern based on the integration of the orbits of known clusters and, consequently, the location of the co-rotation radius close to the solar radius (Dias & Lépine 2005). The open clusters have also provided constraints on the understanding of the step-like abrupt decrease in metallicity at 1 kpc from the Sun (Lépine et al. 2011).
We have dedicated special attention to the task of maintaining and improving the New catalog of Optically Visible Open Clusters and Candidates (Dias et al. (2002a), hereafter DAML02), which has been continuously updated with new data from the literature. Aside from updating the catalog, our group is actively producing new results, such as the determination of mean absolute proper motions and memberships of open clusters e.g. Dias et al. (2006) using the UCAC2 catalog. Recently, we developed a tool that performs isochrone fittings of open cluster photometric data with a global optimization algorithm, which avoids the need of performing fits visually and, thus, removes most of the related subjectivity, which allows us to obtain of error estimates of the fundamental parameters (Oliveira et al. 2013). These efforts improve the knowledge of the known population of open clusters in the Galaxy at optical wavelengths. The catalog has been used in hundreds of works, in a broad range of studies of both structure and dynamics of the Galaxy, and in other areas. In this context, the determination of homogeneous parameters is clearly desirable.
The determination of the mean radial velocity and metallicity of open clusters requires prior knowledge of the member stars due to the costly process of observing and reducing spectroscopic data on a large scale. In addition, the membership probability of the stars of the cluster’s field can weigh the stars in the color-magnitude diagram and contribute decisively in determining the distance and age of the objects by isochrone fitting. Therefore, it is essential to accurately determine the kinematic and fundamental parameters of the clusters, which are essential for studies of the Galactic dynamics, to identify the stars that compose the cluster.
After Sanders (1971), the statistical method for determining memberships using proper motions has been constantly improved: For instance, see the works of Slovak (1977), Cabrera-Cano & Alfaro (1990), Zhao & He (1990), Uribe & Brieva (1994), and Sánchez et al. (2010). Basically, the method adopts a parametric probability density function composed by the sum of the probability density function of the stars that belong to the cluster and of the probability density function of the field stars (details in Sect. 3). A nonparametric method was presented by Cabrera-Cano & Alfaro (1985). For a detailed discussion on the parametric and nonparametric method, see Balaguer-Núñez et al. (2004), which shows that the two approaches are similar and produces consistent results in the segregation of cluster and field populations.
In this, work we present further improvement of the statistical method by using large samples of stars from the UCAC4 catalog (Zacharias et al. 2013) and a global optimization technique to find the best combination of field and cluster probability distributions, which take the individual uncertainties of the proper motions into account.
This paper is organized as follows: in the next Section, we describe the data used. In Sect. 3, we present the method and the procedures adopted for determining the membership probabilities and mean proper motion of the clusters. The results are shown and discussed in Sect. 4, while we summarize the main results and give some concluding remarks in the last section.
2. Data used
2.1. The catalog of open clusters
We make use of the New catalog of Optically Visible Open Clusters and Candidates published by Dias et al. (2002a) and updated by Dias et al. (2013)1.
The present version of the catalog contains 2174 objects, of which 1620 (74.5%) have published distances and ages, 1190 (54.7%) have published proper motions (most of them determined by our group (Dias et al. (2001), Dias et al. (2002b) and Dias et al. (2006), hereafter DL06), and 543 (25.0%) have radial velocities.
In the present study, all 2164 catalogd open clusters with a diameter smaller than 300 arcmin were investigated and results were obtained for a sample of 1805 clusters. The main problems that affect clusters with large angular diameters are the excess of field stars compared to cluster stars and that the proper motions, which reflect the motion of the Sun, vary as the direction changes. For the remaining open clusters that were rejected, the quality of the solution was not compatible with the presence of two populations in the field and/or the final solution that provided parameters with numerical errors greater than 1.0 mas yr-1. The method used to determine the errors on the parameters is described in Sect. 3.
2.2. The proper motion data
The fourth United States Naval Observatory (USNO) CCD Astrograph catalog, UCAC4 (Zacharias et al. 2013) presents data for over 113 million objects covering entire sky complete from the brightest stars to those with a magnitude about R = 16. The accuracy in the position is about 15 to 100 mas per coordinate, depending on the magnitude, and the formal errors in proper motions of stars range from about 4 mas yr-1 to more than 10 mas yr-1, depending on the magnitude and observation history. The systematic errors in proper motions are estimated to be of 1 to 4 mas yr-1.
The extraction of the UCAC4 data was performed using the VizieR tool2 with the central coordinates and apparent diameters of the clusters taken from the DAML02 catalog.
3. Method
The field centered on the region of a cluster is analyzed from a purely kinematic point of view. The goal is to select the stars that belong to the clusters by determining their membership probability and mean proper motion of the cluster. We apply the statistical method proposed by Uribe & Brieva (1994) in a modified fashion, considering the existence of two elliptical bivariate populations in the region (cluster and field stars). We insert the proper motion’s errors in the frequency function as presented in Eq. (1) below, following Zhao & He (1990).
Let Φc and Φf be the cluster and the field probability density functions, respectively. As a simplification, we adopt henceforth the notation c and f subscripts for cluster and field parameters, respectively, x for the coordinate μαcosδ, and y for the coordinate μδ. Then, ![\begin{eqnarray} \Phi_{\rm c}(\mu_{x},\mu_{y}) &=& \frac{n_{c}}{2\pi\sqrt{\sigma_{x,{\rm c}}^2+\epsilon_{i}^2} \sqrt{\sigma_{y,{\rm c}}^2+\epsilon_{i}^2} \sqrt{1-\rho_{\rm c}^2}} . . \\[1mm] &&. . X \exp\left\{ -\frac{1}{2(1-\rho_{\rm c}^2)} \left[ \frac{(\mu_x - \mu_{x,{\rm c}})^2}{\sigma_{x,{\rm c}}^2+\epsilon_{i}^2} \right.\right. . . \nonumber \\[1mm] && \hspace*{-1cm} \left.\left. + . . \frac{(\mu_y - \mu_{y,{\rm c}})^2}{\sigma_{y,{\rm c}}^2+\epsilon_{i}^2} -2\rho_{c}\left(\frac{\mu_x-\mu_{x,{\rm c}}}{\sqrt{\sigma_{x,{\rm c}}^2+\epsilon_{i}^2}}\right) \left(\frac{\mu_y-\mu_{y,{\rm c}}}{\sqrt{\sigma_{y,{\rm c}}^2+\epsilon_{i}^2}}\right) \right] \right\} , \nonumber \end{eqnarray}](/articles/aa/full_html/2014/04/aa23226-13/aa23226-13-eq14.png) (1)and
(1)and ![\begin{eqnarray} \Phi_{\rm f}(\mu_x,\mu_y) &=& \frac{1-n_{c}}{2\pi\sqrt{\sigma_{x,{\rm f}}^2+\epsilon_{i}^2} \sqrt{\sigma_{y,{\rm f}}^2+\epsilon_{i}^2} \sqrt{1-\rho_{\rm f}^2}} . . \\[1mm] && . . X \exp\left\{ -\frac{1}{2(1-\rho_{f}^2)} \left[ \frac{(\mu_x - \mu_{x,{\rm f}})^2}{\sigma_{x,{\rm f}}^2+\epsilon_{i}^2} \right.\right. . . \nonumber \\[1mm] && \hspace*{-1cm} \left.\left. + . . \frac{(\mu_y - \mu_{y,{\rm f}})^2}{\sigma_{y,{\rm f}}^2+\epsilon_{i}^2} -2\rho_{\rm f}\left(\frac{\mu_x-\mu_{x,{\rm f}}}{\sqrt{\sigma_{x,{\rm f}}^2+\epsilon_{i}^2}}\right) \left(\frac{\mu_y-\mu_{y,{\rm f}}}{\sqrt{\sigma_{y,{\rm f}}^2+\epsilon_{i}^2}}\right) \right] \right\} , \nonumber \end{eqnarray}](/articles/aa/full_html/2014/04/aa23226-13/aa23226-13-eq15.png) (2)where Φ = Φc + Φf is the total probability distribution, (μx,c,μy,c) are the average of the cluster distribution with standard deviation σx,c and σy,c, (μx,f,μy,f) are the average of the field distribution with standard deviations σx,f and σy,f, and ρc and ρf are the correlation coefficients of cluster and field stars. The values (μx,μy) are the component of the stellar proper motion, and ϵi is the formal error in proper motion given by the catalog. The probability density function for the whole sample is simply
(2)where Φ = Φc + Φf is the total probability distribution, (μx,c,μy,c) are the average of the cluster distribution with standard deviation σx,c and σy,c, (μx,f,μy,f) are the average of the field distribution with standard deviations σx,f and σy,f, and ρc and ρf are the correlation coefficients of cluster and field stars. The values (μx,μy) are the component of the stellar proper motion, and ϵi is the formal error in proper motion given by the catalog. The probability density function for the whole sample is simply 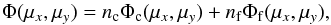 (3)where nc and nf are the number of cluster and field stars (non-members), respectively, normalized with respect to the total number of stars in the field.
(3)where nc and nf are the number of cluster and field stars (non-members), respectively, normalized with respect to the total number of stars in the field.
To obtain the unknown parameters (means, standard deviations, correlation coefficients, and numbers of members and non-members) in a non-subjective fashion, an automatic global optimization procedure was used by applying the maximum likelihood principle to the data by considering their individual formal errors, which is listed in the proper motion catalog.
3.1. The cross-entropy algorithm for the parameters estimation
In this work, we applied the global optimization technique based on the cross-entropy (CE) global optimization procedure to fit the observed distribution of proper motions and to obtain the unknown parameters simultaneously. We refer the reader to the papers of Rubinstein (1997), Rubinstein (1999), and Kroese & Rubinstein (2006) for their very complete discussion of the technique and the series of papers of our group (Monteiro et al. 2010; Monteiro & Dias 2011; Dias et al. 2012; and Oliveira et al. 2013) for an application of the method to the determine fundamental parameters of open clusters.
The main goal of the CE continuous multi-extremal optimization method is to find a set of parameters for which the model provides the best description of the data as per maximum likelihood definition. This is performed by randomly generating N independent sets of model parameters and minimizing the objective function S(X) used to transmit the quality of the fit during the run process. If the convergence to the exact solution is achieved, then S → 0.
We adopt the likelihood function given in the usual manner for the maximum likelihood problem as 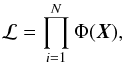 (4)where X is the vector of parameters (μx,c, μy,c, σx,c, σy,c, ρc, μx,f, μy,f, σx,f, σy,f, ρf, nc, nf) that define the maximum ℒ and the optimization is then done with respect to N.
(4)where X is the vector of parameters (μx,c, μy,c, σx,c, σy,c, ρc, μx,f, μy,f, σx,f, σy,f, ρf, nc, nf) that define the maximum ℒ and the optimization is then done with respect to N.
The likelihood above is used to define the objective function S(X) of the optimization algorithm as follows: 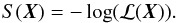 (5)The objective function is then minimized by the CE method described below to obtain the best solution.
(5)The objective function is then minimized by the CE method described below to obtain the best solution.
Briefly, the CE procedure provides a simple adaptive way of estimating the optimal reference parameters. Basically, the CE method involves an iterative statistical procedure where the following is done in each iteration:
-
1.
Random generation of the initial parameter sample, respectingpre-defined criteria;
-
2.
Selection of the best candidates based on some mathematical criterion;
-
3.
Random generation of updated parameter samples from the previous best candidates that are evaluated in the next iteration;
-
4.
Optimization process repeats steps (2) and (1) until a pre-specified stopping criterion is fulfilled.
In this work, a range of parameters were chosen based on our previous experience to contain all the possible cases. It was defined as follows
-
nc from 0.0005 to 1.0;
-
μx,c,μy,c from −50.0 to 50.0;
-
σx,c and σy,c from 0.1 to 50.0;
-
ρ from -0.99 to 0.99;
-
μx,f,μy,f from − 50.0 to 50.0;
-
σx,f and σy,f from 0.1 to 50.0;
The tuning parameters used that gave consistent convergence to the correct answer in all tested cases were α = 0.6, q = 0, Nelite = 50, and a sample of N = 100 trial solutions per iteration with a maximum number of 50 iterations. The parameter Nelite is the number of best solutions to take from the original sample that will be used to estimate the distribution parameters for the next iteration, and α is a smoothing factor that reduces the convergence speed of the algorithm. This parameter needs to be tuned depending on the type of problem being studied. We adopted 10-3 as the value of the tolerance for convergence. For more details, see the description of these parameters in Monteiro et al. (2010).
An advantage of this fitting procedure is that it allows the determination of the errors on the parameters through a Monte-Carlo technique. To accomplish this, we perform the fit for each data set NRun times; each time re-samples the original data set with a replacement to perform a bootstrap procedure. For each run, we also replace the stars chosen in the new bootstrap sample with the ones obtained by randomly generating values of X drawn from a normal distribution centered at the original data value. The final uncertainties of each parameter are obtained by calculating the standard deviation of the NRun fit, which are typically lower than 10-4.
In practice, we use the results of this procedure to verify the quality of the final fit and therefore, the quality of the parameters obtained. Only clusters whose final results have parameters errors smaller than 1.0 mas yr-1 were kept, and the results are provided in this work.
To minimize the effect of high proper motion field stars in the model (outliers), we follow the recipes adopted by DL06. We used all stars in the field and a Gaussian fit to estimate the average and standard deviation of the proper motions in each coordinate. The stars with proper motions that are different from the mean by more than three standard deviations were discarded before running the code. Basically, this is the same procedure suggested by Zhao et al. (1982).
Based on the obtained frequency function of parameters, the individual membership probability of each star (Pi) to the respective cluster is Pi = Φci/ Φi.
4. Results
The list of 1805 open clusters is given in the Table 2 in an online data file. For each cluster, a table is also given to provide all the UCAC4 original data plus the membership probability of each star. All Tables are given in electronic format at CDS and in the DAML02 website.
To check the quality of our mean proper motions, we compared the differences in the μαcosδ and μδ components for each cluster, weighted by the formal errors by computing the following quantity (D) 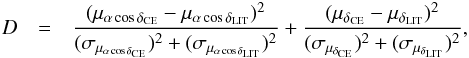 (6)where CE refers to the quantity obtained in this study from the global minimization method and LIT refers to the results obtained from literature.
(6)where CE refers to the quantity obtained in this study from the global minimization method and LIT refers to the results obtained from literature.
Comparison of our results with those from the literature, which contain a large number of open clusters and were published after the Hipparcos catalog.
The main results of mean proper motion published after the Hipparcos mission can briefly be described as follows:
-
Baumgardt et al. (2000)determined mean proper motions and parallaxes of 205 openclusters. The authors used stellar individual proper motion fromHipparcos catalog (ESA 1997), selectingmembers from ground-based information (photometry, radialvelocity, proper motion, and distance from the cluster center).
-
Dias et al. (2001) and Dias et al. (2002b) published mean proper motion of 205 open clusters using the Tycho-2 catalog (ESA 1997), applying the statistical method of Sanders (1971) to select members.
-
Dias et al. (2006) published mean proper motion of 430 open clusters using the UCAC2 catalog (Zacharias et al. 2004). The membership probabilities of the stars were obtained by applying the statistical method of Zhao & He (1990) to accommodate the individual stellar proper motion errors.
-
Loktin & Beshenov (2003) made use of the Tycho-2 catalog to determine mean proper motion for 167 open clusters. The authors considered a selection of the stars in the B − V vs. V diagram as cluster membership criteria and then applied a statistical method similar to that of Sanders (1971).
-
Beshenov & Loktin (2004), in a similar fashion of Loktin & Beshenov (2003), determined mean proper motions of 390 open clusters using the Tycho-2 catalog (ESA 1997).
-
Kharchenko et al. (2003) determined mean proper motion of 401 open clusters using the ASCC-2.5 all-sky catalog (Kharchenko 2001). The cluster’s members and probable members were identified using kinematic and photometric criteria.
-
Kharchenko et al. (2005) published mean proper motion of 520 open clusters also based on the ASCC-2.5 catalog (Kharchenko 2001). The membership determination was based on analysis of several diagrams such as a sky chart of the cluster, radial distribution of the projected stellar density, a vector point diagram of the proper motions, the magnitude dependence of the proper motion components, and a color-magnitude diagram.
-
Kharchenko et al. (2012) determined mean proper motion of 642 open clusters in the second quadrant of the Galaxy. The authors used the PPMXL catalog (Roeser et al. 2010) and multi-dimensional diagrams to determine kinematic and photometric membership probabilities for stars in a cluster region. The authors defined a combined probability considering all aspects of the membership selection procedure.
-
In the DAML02 database, 1190 objects (54.7% of the 2174 open clusters) have published proper motions in the Hipparcos system. This compilation presents the results commented above and those published by different authors for smaller numbers of open clusters.
Table 1 and Figs. 1 and 2 give the results of the comparison in μαcosδ and μδ, which confirm that the values of the literature are well reproduced and are not dominated by errors. The distribution of the quantity D, as described in the beginning of this section, for results obtained shows almost all values lying below 2.5 to 3.0. Thus, we can confidently state that there is no statistical distinction between the distributions of proper motion that are compared within the estimated errors.
 |
Fig. 1 Comparison of our results for mean proper motions with those provided in the literature post-Hipparcos catalog. The lines at 45° are the loci of equal proper motion. The right panels present the distribution of the proper motion differences for each comparison, taking into account the right ascension and declination components weighted by the formal errors (quantity D, see text). The mean and the standard deviation values are given in Table 1. The distribution of quantity D indicates that no statistical distinction exist between the compared proper motion distributions within the estimated errors. The literature codes are given in the Table 1, and details are given in the text. |
 |
Fig. 2 Comparison of our results for mean proper motions with those provided in the literature post-Hipparcos catalog. The lines at 45° are the loci of equal proper motion. The right panels present the distribution of the proper motion differences for each comparison, taking into account the right ascension and declination components weighted by the formal errors (quantity D, see text). The mean and the standard deviation values are given in Table 1. The distribution of quantity D indicates that no statistical distinction exits between the compared proper motion distributions within the estimated errors. The literature codes are given in the Table 1, and details are given in the text. |
 |
Fig. 3 Differences in the mean proper motion from this work minus DAML02 (left panel), and the values from this work minus DL06 (right panel) in μαcosδ and μδ. Circles show the regions of the one, two, and three standard deviations obtained in this study. The clusters outside of the circle of 3σ are discussed in the text. |
Despite the heterogeneity of the samples of mean proper motion of the DAML02 catalog, we point out that almost all D lie below 2.5 to 3.0, and the differences found are values compatible with our estimated errors. The differences are similar to those found when comparing the results with homogeneous samples (see Table 1), which indicates that the use of the mean proper motion from our catalog introduces the same error level as the use of averaged values from the literature.
4.1. Statistics and general comments
In this study, all 2164 cataloged open clusters with a diameter smaller than 300 arcmin were investigated, and the quality of the solution of each one was checked by verifying if the solution was compatible with the presence of two populations in the field. For that, we investigated the errors of the parameters (obtained by the bootstrap technique) to check if they were smaller than 1 mas yr-1 and if the cluster membership probability histogram showed two populations. For 355 open clusters of the sample, these criteria were not satisfied, and we opted to not include them in this work. The objects that met the quality criteria amounted to 1805 open clusters.
From this list, we present 724 clusters with previously unpublished proper motions in Table 3 in the online version. These are marked as follows in the DAML02 catalog: 145 were discovered in the infrared but are visible in the DSS images, 50 are considered doubtful based on the DSS images inspection, 5 are non-existent NGC (RNGC, Sulentic 1973), 32 were not found in the DSS images inspection, 2 are cluster remnants (Pavani & Bica 2007), and 9 are possible clusters. In the sample of clusters with unpublished mean proper motions, 373 objects have estimations of distance and age, of which 23 are within 1 kpc from the Sun and 17 are younger than 12 Myr. Only 12 clusters have radial velocities, and only 26 clusters have determinations of [Fe/H].
To check the occurrence of discrepant cases among the clusters that had previous measurements of proper motions, we compared the mean proper motions obtained in this work with those provided in DL06 and DAML02. These two works were chosen because a similar statistical method was used with data from the UCAC2 catalog in DL06, and DAML02 is being constantly updated. A considerable effort is made to examine critically the data included in the catalog.
 |
Fig. 4 Left panel: comparison of our results for mean radial velocity obtained with data from the CRVAD-2 catalog with those provided by Mermilliod et al. (2008). Central panel: the same but the mean radial velocity obtained from RAVE catalog. Right panel: final results for 292 open clusters of our mean radial velocity obtained from CRVAD-2 compared to those published in the DAML02 catalog. The lines at 45° are the loci of equal radial velocity. |
Considering the comparison between our results and those published in DAML02, Fig. 3 displays a diagram that simultaneously presents the differences in μαcosδ and μδ, showing 12 open clusters with differences exceeding 3σ (about 13 mas yr-1). For open clusters Danks 1 and Danks 2, the radius was small which did not allow a sufficient UCAC4 number of stars in the field for the application of statistical method. We prefer to keep the results obtained by Chené et al. (2012), although with large estimated errors, based on a selection of members using photometric (J, H, K) data, PPMXL proper motion and radial velocity. For the cluster Feigelson 1, our results were not satisfactory given the limitation of the method for nearby clusters, which typically have large proper motion and small number of member stars. For this cluster, we prefer the values from the literature (compiled in DAML02), since the members were selected from other data, which include proper motions (Feigelson et al. 2003). For the other 9 clusters with very different mean proper motion (Alessi 13, Melotte 20, Stock 2, ASCC 13, Platais 2, IC 2602, NGC 2541A, Mamajek 1, Platais 10), our analysis was unable to distinguish between members and background stars due to the large size of the clusters. For these cases, an analysis based on photometric and spectroscopic data becomes crucial, as presented by Curtis et al. (2013) for the open cluster Ruprecht 147.
Regarding the comparison between our results and those published in DL06, there are 7 open clusters with differences in μαcosδ and μδ, which exceed 3σ (about 7.5 mas yr-1) as presented in Fig. 3. The open clusters, NGC 2925, NGC 2395, and NGC 6649, have the same characteristic of being constituted by the majority of the stars of the field studied, which are mostly the brightest stars. In these cases, the statistical method fails to distinguish two populations by using the UCAC4 data. The object NGC 3603 is a distant open cluster in a region of massive star formation where our method is not efficient, because the region is not well sampled in the UCAC4 catalog. For cases like this one, we consider, that the most appropriate solution is to select the members based on high resolution spectroscopy and photometric data. Finally, for the relative small clusters Ruprecht 164 and Roslund 1, our method failed because the open clusters are practically not distinguishable from the field. Both clusters were studied by Kharchenko et al. (2005), who determined their fundamental parameters, member selection, and mean proper motion. For this reason, we chose to keep the mean proper motion provided by these authors.
Although the mean proper motions obtained in this work have been used successfully to determine memberships of stars, the results should be considered with caution. The analysis of discrepant cases indicates that the membership results were not adequate for a few cases. This happens mainly when it is not possible to distinguish two populations in the space of the proper motions. This can occur for very small clusters with fields that have a small number of stars and for very large open clusters for which it is not easy to distinguish between members and background stars.
5. Mean radial velocities
We used the results of membership probabilities that we determined to estimate the mean radial velocities of the open clusters. We searched for the individual radial velocities of the stars with membership probability greater than 50% in the second version of the catalog of radial velocities of Galactic Stars with High Precision Astrometric Data – CRVAD2 (Kharchenko et al. 2007) and in the third release of the Radial Velocity Experiment – RAVE (Siebert et al. 2011).
To accommodate different numbers of measurements and also measurements with different errors, the mean radial velocity of each open cluster was obtained by weigh the number of measurements stars and the mean error of a single measurement, according to Eqs. (4) and (5) by following (Barford 1967):
![\begin{eqnarray} &&{\rm weighted~RV} = \left( \frac{n_{1} {\rm RV}_{1} / s^{2}_{1} + n_{2} {\rm RV}_{2} +...+ n_{i} {\rm RV}_{i} / s^{2}_{i}}{n_{i} / s^{2}_{1} + n_{2} / s^{2}_{2}+...+n_{i} / s^{2}_{i}} \right), \\[4mm] && {\rm weighted~RVerror} = \left( \frac{n_{1} + n_{2}+...+n_{i}}{n_{1}/s^{2}_{1} + n_{2}/s^{2}_{2}+...+n_{i}/s^{2}_{i}} \right) ^{1/2}, \end{eqnarray}](/articles/aa/full_html/2014/04/aa23226-13/aa23226-13-eq72.png) where ni is the number of measurement, RVi is the individual radial velocity, and si is the mean error of a single measurement.
where ni is the number of measurement, RVi is the individual radial velocity, and si is the mean error of a single measurement.
We were able to obtain the mean radial velocity for 364 open clusters using CRVAD2 data with 72 of them having their radial velocity determined for the first time.
In the same way, we obtained the mean radial velocity for 90 open clusters using the data from the third release of RAVE, where 30 of them were the first determination. We compared both results to the radial velocities given by Mermilliod et al. (2008) and adopted in the DAML02 catalog because of their good accuracy and reliability. We found 44 values to agree with our results obtained with CRVAD-2 and the Mermilliod’s radial velocities and 10 values to agree with our results obtained with RAVE and the Mermilliod’s velocities. The comparisons are shown in Fig. 4.
The final mean RV presented in this work were based in the data of CRVAD-2 catalog. However, for 30 open clusters of the sample, the mean RV were estimated using data of the RAVE catalog. The list is given in Table 4 in an online data file.
Finally, to check the reliability of the new mean radial velocities, we compared the values obtained by our method to those that were already given in the DAML02 catalog. The Gaussian fit to the histogram of the differences gives a standard deviation of 11.2 km s-1. There is a mean velocity difference of 0.4 km s-1, which is small compared to the standard deviation. There is no indication of any systematic trend assuring that both sets of radial velocities agree, allowing the update of DAML02 catalog with 102 new determinations of the mean radial velocity.
6. Conclusions
In this paper, we present the mean proper motions and stellar membership probabilities for 1805 open clusters listed in the version 3.3 of The New Optically Visible Open Cluster catalog (Dias et al. 2002a). These results were obtained in a homogeneous and non-subjective manner by applying the statistical method of Uribe & Brieva (1994) in a modified approach, which takes into account the errors on proper motions in the frequency function. We applied the cross-entropy global optimization procedure to fit the observed distribution of proper motions and to obtain the unknown parameters (averages and standard deviations) simultaneously.
The comparison of our results with published ones confirms that the values of the literature are well reproduced, and our determinations are not affected by any systematic errors. Especially for the paper of Dias et al. (2006) and DAML02 catalog, we showed that both sets agree with the present results, making us confident that the mean proper motions that are derived for the first time are correct.
The stars considered as probable members were searched in radial velocity catalogs to estimate the mean radial velocity of the cluster. Hundreds of stars were found in common, which allowed the determination of new radial velocities for 102 clusters. As it has happened for the proper motions, the comparison of the open clusters that are in common with the DAML02 catalog and have measured radial velocities indicate that we can be confident in the quality of the new results.
The present results provide an increase of 30% for the sample of open clusters with a determined mean absolute proper motion and an increase of 19% of the sample of open clusters with a determined mean radial velocity. The membership lists can also be useful for determinations of distances and ages and for choosing targets for spectroscopy to obtain radial velocity and metallicity determinations of the clusters.
The latest version (3.3) can be accessed on line at http://www.astro.iag.usp.br/ocdb/
Acknowledgments
We thank the referee for his/her valuable suggestions which improved the text. We would like to thank Dr. Patrícia Cruz for her suggestions. W. S. Dias acknowledges the São Paulo State Agency FAPESP (fellowship 2013/01115-6). H. Monteiro would like to thank FAPEMIG grants APQ-02030-10 and CEX-PPM-00235-12. T. C. Caetano acknowledges CAPES. M. Assafin acknowledges CNPq for grants 478318/2007-3, 305420/2008-9 and 482080/2009-4.
References
- Balaguer-Núñez, L., Jordi, C., Galadí-Enríquez, D., & Zhao, J. L. 2004, A&A, 426, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barford, N. C. 1967, Experimental Measurements: Precision, Error, and Truth (Addison-Wesley) [Google Scholar]
- Baumgardt, H., Dettbarn, C., & Wielen, R. 2000, VizieR Online Data Catalog: J/A+A/414/251 [Google Scholar]
- Beshenov, G. V., & Loktin, A. V. 2004, Astron. Astrophys. Trans., 23, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Cano, J., & Alfaro, E. J. 1985, A&A, 150, 298 [NASA ADS] [Google Scholar]
- Cabrera-Cano, J., & Alfaro, E. J. 1990, A&A, 235, 94 [NASA ADS] [Google Scholar]
- Chené, A.-N., Borissova, J., Clarke, J. R. A., et al. 2012, A&A, 545, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curtis, J. L., Wolfgang, A., Wright, J. T., Brewer, J. M., & Johnson, J. A. 2013, AJ, 145, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., & Lépine, J. R. D. 2005, ApJ, 629, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Lépine, J. R. D., & Alessi, B. S. 2001, A&A, 376, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002a, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias, W. S., Lépine, J. R. D., & Alessi, B. S. 2002b, A&A, 388, 168 [Google Scholar]
- Dias, W. S., Assafin, M., Flório, V., Alessi, B. S., & Líbero, V. 2006, A&A, 446, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias, W. S., Monteiro, H., Caetano, T. C., & Oliveira, A. F. 2012, A&A, 539, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA 1997, The Hipparcos and TYCHO catalogues, ESA SP, 1200 [Google Scholar]
- Feigelson, E. D., Lawson, W. A., & Garmire, G. P. 2003, ApJ, 599, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Kharchenko, N. V., Pakulyak, L. K., & Piskunov, A. E. 2003, Astron. Rep., 47, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Kharchenko, N. V., Scholz, R.-D., Piskunov, A. E., Röser, S., & Schilbach, E. 2007, Astron. Nachr., 328, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2012, A&A, 543, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroese, D. P. P. S., & Rubinstein, R. Y. 2006, Methodol. Comput. Appl. Probab., 8, 383 [CrossRef] [Google Scholar]
- Lépine, J. R. D., Cruz, P., Scarano, Jr., S., et al. 2011, MNRAS, 417, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Loktin, A. V., & Beshenov, G. V. 2003, Astron. Rep., 47, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monteiro, H., & Dias, W. S. 2011, A&A, 530, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monteiro, H., Dias, W. S., & Caetano, T. C. 2010, A&A, 516, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliveira, A. F., Monteiro, H., Dias, W. S., & Caetano, T. C. 2013, A&A, 557, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavani, D. B., & Bica, E. 2007, A&A, 468, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Rubinstein, R. Y. 1997, Eur. J. Operat. Res., 99, 89 [Google Scholar]
- Rubinstein, R. Y. 1999, J. Method. Comp. Appl. Prob., 1, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, N., Vicente, B., & Alfaro, E. J. 2010, A&A, 510, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, W. L. 1971, A&A, 14, 226 [NASA ADS] [Google Scholar]
- Siebert, A., Williams, M. E. K., Siviero, A., et al. 2011, AJ, 141, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Slovak, M. H. 1977, AJ, 82, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., & Tifft, W. G. 1973, The Revised New General catalogue of Nonstellar Astronomical Objects (Tucson: U. of Arizona Press) [Google Scholar]
- Uribe, A., & Brieva, E. 1994, Ap&SS, 214, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J. L., & He, Y. P. 1990, A&A, 237, 54 [NASA ADS] [Google Scholar]
- Zhao, J.-l., Tian, K.-p., Xu, Z.-h., & Yin, M.-G. 1982, Chin. Astron. Astrophys., 6, 293 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of our results with those from the literature, which contain a large number of open clusters and were published after the Hipparcos catalog.
All Figures
 |
Fig. 1 Comparison of our results for mean proper motions with those provided in the literature post-Hipparcos catalog. The lines at 45° are the loci of equal proper motion. The right panels present the distribution of the proper motion differences for each comparison, taking into account the right ascension and declination components weighted by the formal errors (quantity D, see text). The mean and the standard deviation values are given in Table 1. The distribution of quantity D indicates that no statistical distinction exist between the compared proper motion distributions within the estimated errors. The literature codes are given in the Table 1, and details are given in the text. |
| In the text | |
 |
Fig. 2 Comparison of our results for mean proper motions with those provided in the literature post-Hipparcos catalog. The lines at 45° are the loci of equal proper motion. The right panels present the distribution of the proper motion differences for each comparison, taking into account the right ascension and declination components weighted by the formal errors (quantity D, see text). The mean and the standard deviation values are given in Table 1. The distribution of quantity D indicates that no statistical distinction exits between the compared proper motion distributions within the estimated errors. The literature codes are given in the Table 1, and details are given in the text. |
| In the text | |
 |
Fig. 3 Differences in the mean proper motion from this work minus DAML02 (left panel), and the values from this work minus DL06 (right panel) in μαcosδ and μδ. Circles show the regions of the one, two, and three standard deviations obtained in this study. The clusters outside of the circle of 3σ are discussed in the text. |
| In the text | |
 |
Fig. 4 Left panel: comparison of our results for mean radial velocity obtained with data from the CRVAD-2 catalog with those provided by Mermilliod et al. (2008). Central panel: the same but the mean radial velocity obtained from RAVE catalog. Right panel: final results for 292 open clusters of our mean radial velocity obtained from CRVAD-2 compared to those published in the DAML02 catalog. The lines at 45° are the loci of equal radial velocity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


