| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201323000 | |
| Published online | 28 March 2014 | |
Finding halo streams with a pencil-beam survey
New wraps in the Sagittarius stream
Leiden Observatory, Leiden University
Oort Building, Niels Bohrweg 2
2333 CA
Leiden
The Netherlands
e-mail: piladiez@strw.leidenuniv.nl;
kuijken@strw.leidenuniv.nl; jelte@strw.leidenuniv.nl;
hoekstra@strw.leidenuniv.nl; vdburg@strw.leidenuniv.nl
Received:
6
November
2013
Accepted:
18
February
2014
We use data from two CFHT-MegaCam photometric pencil-beam surveys in the g′ and the r′ bands to measure distances to the Sagittarius, the Palomar 5 and the Orphan stream. We show that, using a cross-correlation algorithm to detect the turnoff point of the main sequence, it is possible to overcome the main limitation of a two-bands pencil-beam survey, namely the lack of adjacent control-fields that can be used to subtract the foreground and background stars to enhance the signal on the colour−magnitude diagrams. We describe the cross-correlation algorithm and its implementation. We combine the resulting main sequence turnoff points with theoretical isochrones to derive photometric distances to the streams. Our results (31 detections on the Sagittarius stream and one each for the Palomar 5 and the Orphan streams) confirm the findings by previous studies, expand the distance trend for the Sagittarius faint southern branch and trace the Sagittarius faint branch of the northern-leading arm out to 56 kpc. In addition, they show evidence for nearby substructures. We argue that these detections trace the continuation of the Sagittarius northern-leading arm into the southern hemisphere, and the northern wrap of the Sagittarius trailing arm. We provide accurate distance measurements to these detections.
Key words: Galaxy: halo / Galaxy: structure
© ESO, 2014
1. Introduction
In the past decade our picture of the Milky Way’s stellar halo has dramatically changed thanks to the advent of several observational surveys, which have shown the richness and complexity of the substructure in the Galactic halo (Ibata et al. 2001; Newberg et al. 2002; Majewski et al. 2003; Yanny et al. 2003; Martin et al. 2004; Grillmair & Dionatos 2006b; Belokurov et al. 2006, 2007a,b). Our Galaxy is still undergoing an assembling process, where part of the infalling material has already been accreted and become dynamically relaxed (Helmi et al. 1999; Sheffield et al. 2012), part of it is still dynamically cold (Bell et al. 2008; Jurić et al. 2008) and another part is in the process of being dynamically stripped or even approaching its first dynamical encounter with our Galaxy (Kallivayalil et al. 2006b,a; Piatek et al. 2008; Besla et al. 2010; Rocha et al. 2012).
The most prominent example of a currently ongoing disruption is that of the Sagittarius stream (Sgr stream). Since its discovery in 1996 (Mateo et al. 1996), the stream has been mapped over roughly 2π radians on the sky, first through 2MASS (Majewski et al. 2003) and later through SDSS (Belokurov et al. 2006; Koposov et al. 2012). There is general agreement that it is the stellar debris of a disrupting satellite galaxy, the Sagittarius dwarf galaxy (Ibata et al. 1994), which is currently being accreted by the Milky Way (Velazquez & White 1995; Ibata et al. 1997; Niederste-Ostholt et al. 2010). The stream is composed of the leading and the trailing tails of this disruption event (Mateo et al. 1996; Ibata et al. 2001; Dohm-Palmer et al. 2001; Martínez-Delgado et al. 2001, 2004b; Majewski et al. 2003; Belokurov et al. 2006, 2014), which wrap at least once around the Galaxy but have been predicted to wrap more than once (Peñarrubia et al. 2010; Law & Majewski 2010). In addition, a bifurcation and what resembles an extra branch parallel to the main component of the Sgr stream have been discovered both in the northern hemisphere (Belokurov et al. 2006) and in the southern hemisphere (Koposov et al. 2012). The origin of this bifurcation and the meaning of the two branches are still debated: they could represent wraps of different age (Fellhauer et al. 2006), they could have arisen due to the internal dynamics of the progenitor (Peñarrubia et al. 2010, 2011) or they could indeed be due to different progenitors and a multiple accretion event (Koposov et al. 2012).
On the other hand, one of the simplest and neatest examples of a disrupting satellite is that of the Palomar 5 globular cluster (Sandage & Hartwick 1977; Odenkirchen et al. 2002; Dehnen et al. 2004) and its stream (Odenkirchen et al. 2001, 2003). This stream extends over 20° along its narrow leading and trailing tails. It displays an inhomogeneous stellar density in what resembles gaps or underdensities (Grillmair & Dionatos 2006a); the origin of this stellar distribution has been attributed both to interactions with dark satellites (Carlberg 2012) and to epicyclic motions of stars along the tails (Mastrobuono-Battisti et al. 2012).
Finally, there are also cases of streams with unknown progenitors, such as the so-called Orphan stream (Grillmair 2006a; Belokurov et al. 2006, 2007a; Newberg et al. 2010). This stream extends for 50° in the north galactic cap, and the chemical signatures from recent spectroscopic observations associate its progenitor with a dwarf galaxy (Casey et al. 2013b,a). A number of plausible progenitors have been suggested (Zucker et al. 2006; Fellhauer et al. 2007b; Jin & Lynden-Bell 2007; Sales et al. 2008), but it is still possible that the true progenitor remains undiscovered in the southern hemisphere (Casey et al. 2013b).
 |
Fig. 1 Equatorial map showing the position of all the fields from our survey (white hexagons) and highlighting the ones that lay on the Sagittarius stream (green circles for the faint branch and green squares for the bright branch), on the Palomar 5 stream and on the Orphan stream (orange diamonds). The background image is the SDSS-DR8 map of the Sgr stream from Koposov et al. (2012), where the location of the Sagittarius dwarf galaxy has been marked (red star). |
In general, the discovery of most of the substructures in the halo of the Milky Way has been possible thanks to photometric multi-colour wide area surveys. Such surveys pose several advantages for this kind of search. First, their multiple-band photometry allows for stellar population selections (halo or thick disk; red clump, main sequence turnoff point, etc.) based on colour-colour stellar loci. These selection criteria can be used to make stellar density maps that track the streams all through the survey’s coverage area (Majewski et al. 2003; Belokurov et al. 2006). Second, their continuous coverage of a large area allow the fields adjacent to the substructure to act as control fields. In this way, the colour−magnitude diagrams (CMDs) of the control fields can be used to statistically subtract the foreground and the background stars from the fields probing the substructure. This enhances the signature of the stellar population belonging to the stream or satellite (by removing the noise), and makes it possible to identify age and distance indicators such as the red clump or the main sequence turnoff point (Belokurov et al. 2006; Koposov et al. 2012; Slater et al. 2013).
In this paper we explore the possibilities of using deep two-band pencil-beam surveys instead of the usual wide-area multi-colour surveys in order to detect and characterize stellar streams of the halo and, in particular, we revisit the Sagittarius, the Palomar 5 and the Orphan streams. We derive photometric distances using purely the main sequence turnoff point and – unlike other works – regardless of the giant branch and its red clump.
2. Observations and data processing
2.1. Description of data set
We use deep photometric imaging from the MENeaCS and the CCCP surveys (Sand et al. 2012; Hoekstra et al. 2012; Bildfell et al. 2012) as well as several additional archival cluster fields, observed with the CFHT-MegaCam instrument. These surveys targeted pre-selected samples of galaxy clusters; therefore the surveys geometry takes the form of a beam-like survey where the pointings are distributed without prior knowledge of the halo substructure (blind survey).
Our pointings are one square degree wide and spread over the sky visible to CFHT. Each consists of several exposures through the g′ and r′ filters with image quality of sub-arcsecond seeing. After stacking the individual exposures, the limiting magnitudes reach ~25.0 at the 5.0σ level. Out of the 97 fields, at least 25 fall on the structure of the Sagittarius (Sgr) stream and show distinct signatures in their CMDs, one on the Orphan stream, one on the Palomar 5 stream and three to seven on the Virgo Overdensity and the Virgo Stellar Stream (Duffau et al. 2006; Jurić et al. 2008; Casetti-Dinescu et al. 2009; Prior et al. 2009; Bonaca et al. 2012b) (see Fig. 1). Further away from the plane of the Sgr stream, we also find three fields to be coincident with the Triangulum-Andromeda structure (Rocha-Pinto et al. 2004; Bonaca et al. 2012a), two to three with the Pisces Overdensity (Watkins et al. 2009; Sesar et al. 2010; Sharma et al. 2010), one transitional between the Triangulum-Andromeda and the Pisces Overdensity, four with the Anticenter Structure (Grillmair 2006b) and two to three with the NGC 5466 stream (Grillmair & Johnson 2006; Fellhauer et al. 2007a). We also find two fields on the Lethe stream (Grillmair 2009), four on the Styx stream (Grillmair 2009), one on a region apparently common to the Styx and Cocytos streams (Grillmair 2009) and two on the Canis Major overdensity (Martin et al. 2004).
In this paper we concentrate on the clearest structures (those where the contrast-to-noise in the CMD is higher) in order to test the capabilities of our method. In particular, we address the Sagittarius stream, the Palomar 5 stream and the Orphan stream.
2.2. Correction of the PSF distortion and implications for the star/galaxy separation
Before building catalogues and in order to perform an accurate star/galaxy separation, it is necessary to rectify the varying PSF across the fields of the CFHT images.
In order to correct for this effect, we make use of a “PSF-homogenizing” code (Kuijken et al., in prep.). The code uses the shapes of bright objects unambiguously classified as stars to map the point spread function (PSF) across the image, and then convolves it with an appropriate spatially variable kernel designed to render the PSF Gaussian everywhere. With a view to obtaining a PSF as homogeneous as possible, we treat the data as follows (van der Burg et al. 2013): i) we implement an accurate selection of sufficiently bright stars based on an initial catalogue; ii) we run the code on the individual exposures for each field; and iii) we reject bad exposures based on a seeing criterion1 before stacking them into one final image, on which we perform the final source extraction and photometry.
 |
Fig. 2 Brightness versus size diagram of all the sources in one of our pointings. The stellar locus prior to the PSF-homogenization (black) is wider and therefore subject to greater galaxy contamination at the faint end than the stellar locus posterior to the correction (blue) because the PSF initially varies across the field. The sources more compact than the stellar locus are artefacts from the source extraction; they hold no relevance for our analysis since they do not pass the star selection (see Fig. 3). |
The advantages of this procedure are twofold. First, because the resulting PSF for each exposure is gaussian, all the stars become round. Second, because the PSF anisotropy is removed from all exposures before stacking, the dispersion in size for the point-source objects becomes smaller, even if the average value increases after stacking the individual exposures (see Fig. 2). These two improvements significantly reduce the galaxy contamination when performing the star selection (illustrated in Fig. 3). Additionally, homogenizing the PSF also allows to measure colours in fixed apertures.
From the final images, we extract the sources and produce photometric catalogues using SExtractor (Bertin & Arnouts 1996). To derive the stellar catalogues, we use a code that filters the source catalogues as follows: i) finds the saturated stars and removes them from the stellar catalogue; ii) evaluates the distribution of bright sources (r′ = [18.0,20.0] mag) in the brightness-size parameter space, assumes a gaussian distribution in the size and in the ellipticity parameters (e1, e2)2 of stars, and uses this information to define the boundaries of the stellar locus along the bright range; iii) evaluates the dependence of the width of the stellar locus on brightness and extrapolates the relation to fainter magnitudes; iv) applies the extended stellar locus and an ellipticity criterion to drop galaxies from the stellar catalogue.
For the stars resulting from this selection (Fig. 3), we correct their photometry from galactic reddening by using the extinction maps from Schlegel et al. (1998). The final stellar catalogues are used to build the CMDs employed for our analysis. The PSF-corrected catalogues yield much cleaner CMDs than the catalogues with similar star/galaxy separation but no PSF-correction (Fig. 4).
 |
Fig. 3 Brightness versus size diagram showing all the PSF-corrected sources (blue) and the subset of sources selected as stars through our star/galaxy separation algorithm (red) for one of our pointings. Although the star selection may not be complete at the faint end due to increasing scatter, our algorithm minimizes the galaxy contamination, which otherwise would be the main obstacle for detecting faint structures in the CMD. |
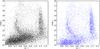 |
Fig. 4 Colour−magnitude diagram displaying the selection of sources considered stars (selected as explained in Sect. 2.2). The plume on the red side (g − r ≈ 1.2) is composed of the nearby M-dwarfs, whereas the main sequence on the bluer side (0.18 < g − r < 0.6) corresponds to a halo overdensity located at a particular well-defined distance. The cloud of sources at faint magnitudes are faint galaxies that enter the star selection. Left: CMD derived from an image that has not been PSF-corrected. Right: CMD derived from a PSF-corrected image. After homogenizing the PSF, the galaxy contamination decreases markedly below r ≈ 22. |
 |
Fig. 5 Left: dereddened CMD (black dots) with the search region (pink solid-line rectangle) for the cross-correlation and the template main sequence-shaped function (green solid line) at the position of maximum density (peak of the cross-correlation). Right: binned diagram representing the weighted density of stars resulting from the cross-correlation process. The density in each bin corresponds to the integral of the template main sequence-shaped function with top left corner in the position of the bin. |
2.3. Identification of the main sequence turnoff point
The photometric depth of our data allows us to detect a number of halo substructures several magnitudes below their main sequence turn-off point. However, because our survey is a pencil-beam survey lacking control fields adjacent to our target fields, we have no reference-CMDs representing a clean foreground plus a smooth halo, and thus a simple foreground subtraction is not possible. Instead the halo substructures in our survey can only be detected in those fields where the contrast in density between the main sequence stream stars and the foreground and background stars is significant in the CMD.
Thus, in order to search for main sequences in the CMDs, we build a cross-correlation algorithm that runs across a region of the CMD (the “search region”), focused on the colour range associated with the halo turnoff stars (0.18 ≤ g − r ≤ 0.30). Within the boundaries of this search region, we slide a template main sequence-shaped 2D function that operates over the number of stars and, for each step, yields an integral representing the weighted density of stars in such a main sequence-shaped area. When the template main sequence function coincides with a similarly shaped overdensity in the CMD, the value of the cross-correlation (the weighted density) is maximized, and a value for the turnoff point is assigned. This process is illustrated in Fig. 5.
In some cases a CMD presents more than one main sequence signature with sufficient contrast to noise. When this happens we use the detection of the primary main sequence (the position of its turnoff point and its characteristic width-function) to randomly subtract a percentage of the stars associated with it (lowering its density to the foreground level) and detect the next prominent main sequence feature. We name these main sequence detections as primary, secondary, etc., ranked by their signal to noise. We require the signal to noise to be >3.5σ for primary MSs and >4σ for the secondary or tertiary MSs after partially removing the primary one.
2.3.1. Shape of the template main sequence function
When constructing the template main sequence-shaped 2D function (from now on, “template-MS”), we use two ingredients. The first one is a theoretical isochrone3 of age t = 10 Gyr and metallicity [Fe/H] = −1.58, which is used to define the central spine of the template-MS. The position of this central spine is later shifted in magnitude and colour steps during the cross-correlation. Since we are only interested in the shape of this isochrone (its absolute values are irrelevant because it will be shifted) and since we are searching for halo substructures, we choose the above age and metallicity values because they yield an isochrone shape representative of old metal-poor stellar populations. The second ingredient is a magnitude-dependent colour-width, which is used to broaden the isochrone template as illustrated in the left panel of Fig. 5.
The width is in general directly derived from the width of the locus of nearby M-dwarfs (1.0 < g − r < 1.4). The width of this feature is calculated for a number of magnitude bins as three times the standard deviation in colour for each bin. Then a functional form dependent on magnitude is obtained through polynomial fitting. In a few cases, minor tweaking is needed to compensate for extremely large widths (colour shifts become insensitive to any substructure) or for extremely small widths (density values become meaningless due to the built-in weight (see below)). This way of defining the width of the template-MS accounts for the observational broadening of intrinsically well defined stellar loci due to increasing photometric uncertainties at faint magnitudes.
2.3.2. Weights within the template MS-function
In addition to a theoretically and observationally motivated shape for the template-MS, we also give a different weight to each region of the template. This means that, for each step of the cross-correlation, the stars contained within will contribute differently to the enclosed stellar density depending on how far they are from the spine of the template-MS.
The weight in colour (stars near the spine of the template-MS are more likely to belong to the main sequence than stars close to the boundaries) is assigned through the exponential term in a gaussian weight function. We match the standard deviation of the gaussian weight to the standard deviation of the template-MS width (3σ = ωMS) so that all the stars contained within the template-MS are assigned a weight. To guarantee that the weight does not favour bright features, we choose the amplitude of the gaussian function to be such that the integral of the weight function between the edges of the template-MS function is the same for all magnitudes.
The resulting weight function for a given star in the template-MS at a particular step
of the cross-correlation then follows:
![\begin{equation} W_{\ast}(mag,{\it colour})=\frac{A}{\sqrt{2\pi}\sigma(mag)}\cdot\exp\left\{-\frac{{\it colour}-\eta_{\rm CC}(mag)]^2}{2[\sigma(mag)]^2}\right\} \end{equation}](/articles/aa/full_html/2014/04/aa23000-13/aa23000-13-eq23.png) (1)where
mag and colour are the magnitude and colour of the
weighted star, ηCC(mag) represents
the theoretical isochrone at that particular step of the cross-correlation, and
(1)where
mag and colour are the magnitude and colour of the
weighted star, ηCC(mag) represents
the theoretical isochrone at that particular step of the cross-correlation, and
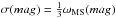 is
proportional to the width of the template-MS function for that particular CMD.
is
proportional to the width of the template-MS function for that particular CMD.
 |
Fig. 6 Absolute magnitude of the turnoff point in the r band as a function of metalllicity and age for metal poor populations (green circles). The values in this diagram meet the age/metallicity relation for the Sgr dwarf galaxy from Layden & Sarajedini (2000). The isochrone used in this paper to derive distances to the Sgr stream is represented with a yellow star, and its maximum difference to the other brightness values in this range is ΔM = ± 0.1mag. |
Position and distances to the Sgr stream, together with a tag for faint or bright branch membership, a tentative classification as leading or trailing arm and a number specifying the hierarchy of the detection in the CMD (primary, secondary, etc.).
2.4. Uncertainties in the turnoff point
The colour and magnitude values for the turnoff point of a given main sequence,
(cTO, magTO), are derived from
the position of the template at which the cross-correlation peaks. Therefore the
uncertainties for these turnoff point values derive from the contribution of individual
stars to the position and shape of the main sequence (the uncertainty from the CMD
itself). To evaluate this uncertainty, we carry out a bootstrapping process. In this
process first we generate re-sampled stellar catalogues by randomly withdrawing stars from
one of our true catalogues. Second we run the cross-correlation and obtain the turnoff
points for each of these re-samples. Third we consider the offsets between these turnoff
points and the original turnoff point and derive the standard deviation of the
distribution. The contribution of any CMD to the uncertainty of its turnoff point can then
be calculated as a function of a reference (bootstrapped) standard deviation,
s:
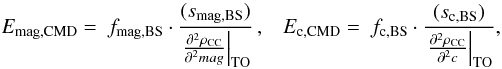 where,
in practice, smag,BS and
sc,BS are the standard
deviations calculated for a number of representative fields, fmag,BS and
fc,BS are scale factors
that allow to obtain the uncertainty for any field from the standard deviation of the
bootstrapped fields, and
where,
in practice, smag,BS and
sc,BS are the standard
deviations calculated for a number of representative fields, fmag,BS and
fc,BS are scale factors
that allow to obtain the uncertainty for any field from the standard deviation of the
bootstrapped fields, and 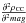 and
and 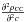 evaluate the prominence of the particular overdensity as a function of magnitude or as a
function of colour. In practice, Emag,CMD = smag,BS
and Ec,CMD = sc,BS
for the bootstrapped fields used as a reference.
evaluate the prominence of the particular overdensity as a function of magnitude or as a
function of colour. In practice, Emag,CMD = smag,BS
and Ec,CMD = sc,BS
for the bootstrapped fields used as a reference.
The photometric turnoff point distances are derived from the distance modulus. Therefore
the uncertainties in the distances can be calculated as a combination of two sources of
error: the uncertainty derived from the observed brightness of the turnoff point
(Emag,CMD, discussed
above) and the uncertainty derived from the absolute brightness of the turnoff point,
which depends on the choice of isochrone (and thus on the uncertainty in the age or in the
metallicity). 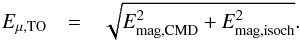 (2)
(2)
3. The Sagittarius stream
3.1. Turnoff point distances to the Sgr stream
The Sagittarius stream is clearly probed by at least 25 of our 97 fields (see the green and the orange markers in Fig. 1). They probe both the faint and the bright branches of the stream (the faint branch lying to the north of the bright one) and also two transitional areas, indicating that the transversal drop in stellar counts between both branches is not dramatic. Some of these fields present more than one main sequence in their CMDs; for those fields the secondary turnoff points are calculated by subtracting the primary MS and re-running the cross-correlation (as explained in Sect. 2.3).
 |
Fig. 7 Photometric main sequence turnoff point distances for the Sagittarius stream along right ascension (northern-leading tail and southern- trailing tail). The top panel shows results for the faint branch, whereas the bottom panel corresponds to the bright arm. Our data (blue circles for leading tails and red circles for trailing tails) are based on the theoretical isochrones by Marigo et al. (2008) and the corrections by Girardi et al. (2010), for a 10.2 Gyr old stellar population with [Fe/H] = −1.0. Other distance values correspond to Belokurov et al. (2006, green and grey triangles), Koposov et al. (2012, 2013, green asterisks), Belokurov et al. (2014, pink triangles) and Slater et al. (2013, yellow squares for >3σ detections and white squares for <3σ). White circles denote detections that can not be unambiguously tagged as leading or trailing. |
Based on the turnoff point values obtained from the cross-correlation, we calculate the distances to the Sagittarius stream in these 25 fields for 31 detections. For this calculation, we assume a single stellar population represented by a theoretical isochrone with age tage = 10.2 Gyr and metallicity [Fe/H] = −1.0 dex (for a detailed description on the set of isochrones see footnote 2 in Sect. 2.3). We choose these age and metallicity values because they match the age-metallicity relation for the Sgr dwarf galaxy (Layden & Sarajedini 2000) – which is also expected to hold for its debris – and are consistent with the range that characterizes old metal-poor populations. To account for the potential influence on our distance measurements of a possible metallicity gradient along the different Sgr arms (Chou et al. 2007; Shi et al. 2012; Vivas et al. 2005; Carlin et al. 2012), we analyse the dependency of the isochrones turnoff point absolute magnitude (MTO) with metallicity throughout the Sgr metal-poor range (see Fig. 6). We find that for − 1.53 dex < [Fe/H] < −0.8 dex the absolute brightness remains nearly constant in the r band, with a maximum variation of ΔM = ± 0.1 mag. We conclude that if we take this variation in absolute brightness as the isochrone uncertainty in the distance modulus (Emag,isoch = ΔM), we can use the tage = 10.2 Gyr and [Fe/H] = −1.0 dex isochrone to calculate distances to any region of the Sgr stream.
 |
Fig. 8 Our data compared to the predictions by the model from Peñarrubia et al. (2010). Top panel: equatorial map with the position of our fields plotted over the simulation. Bottom panel: distance vs. RA diagram with our results compared to the model predictions. Fields on the faint branch are denoted with circles, and fields on the bright branch are denoted with squares. Measurements matching the leading arm are denoted in pink, whereas those matching the trailing arm are denoted in light blue. White markers represent detections that can not be unambiguously tagged as leading or trailing; grey markers in the upper panel correspond to fields with more than one MS detection (they unfold in the bottom panel). The colour scales represent the time since the particles from the simulations became unbound. |
The resulting distances and distance uncertainties for these fields can be found in Table 1, together with the central position of each field (in equatorial coordinates), a “faint/bright branch” tag (derived from Fig. 1), a tentative classification as leading or trailing arm where posible (see below), a “primary/secondary detection” tag and the distance modulus (μ). In Fig. 7 we compare our results to values from the literature4, split in two diagrams (top panel for the faint branches and bottom panel for the bright branches in both hemispheres).
Remarkably our turnoff point distances are not only in agreement with previous distance measurements to known wraps, but also compatible with the distance predictions for nearby wraps by the models of Peñarrubia et al. (2010) and Law & Majewski (2010). In the following section we discuss in detail these findings.
 |
Fig. 9 Same as in Fig. 8 but for the model from Law & Majewski (2010). |
3.2. Comparison with models of the Sgr stream
Using the model predictions shown in Figs. 8 and 9, we classify each field as belonging to the leading or trailing arm, by matching the distance and the sky position. It is worth noting that the distance for a given particle in the models is sensitive not only to the right ascension but also to the declination of the particle. While we take into account both coordinates when classifying a detection as faint or bright branch, this may have some influence in the significance of the offsets between our distance measurement and the mean distance of the N-body particles of that particular branch when comparing them in Figs. 8 and 9 for a given RA.
Of these two models, the model by Peñarrubia et al. (2010) was designed to illustrate the effect of internal satellite rotation on the orbit of the Sgr debris, and it seems to recover better the northern bifurcation into faint and bright branches (Fig. 8, upper panel). On the other hand, the model by Law & Majewski (2010) was designed to reproduce the known observational properties of the stream (angular positions, distances, radial velocities), and it seems to reproduce better the projected 2MASS stellar density distribution (Fig. 9, upper panel). In relation to the southern region of the stream, although neither of the two models predicted the bifurcation in it, they succeed in reproducing the general distribution of the debris.
3.2.1. Northern leading arm
From our eighteen measurements on the bright and the faint branches of the northern-leading arm (branches A and B, in the terminology of Belokurov et al. 2006), nine (blue circles in Fig. 7) clearly reproduce the distance trends of Belokurov et al. (2006) and Belokurov et al. (2014) (green+grey and cyan triangles in Fig. 7, respectively) based on red giant and blue horizontal branch stars. For the faint branch, we extend westwards the distance measurements beyond those of SDSS, and we provide its most distant detections so far – out to 56 kpc at RA ~ 235°. Comparing these most distant detections to the distance trend of the models and to the bright branch at a similar right ascension, one can argue that these detections likely lie close to the apocenter of the faint branch (or represent the apocenter themselves), and therefore they are probably a good estimation for its distance.
For the other nine detections, we find that the derived distances are either in mild disagreement with the trends of the leading arm (four cases, white circles in Fig. 7) or incompatible with the leading arm (five cases, red and white circles in Fig. 7). In the single case of mild disagreement for the faint branch (A1185, RA ~ 168°) the distance is well below the trends of both this and previous work (offset ≈10 kpc); however its large uncertainty prevents us from ruling out that it belongs to the faint branch. We will discuss an alternative membership in Sect. 3.2.2. The three cases of mild disagreement for the bright branch (ZwCl1023, A795-2 and A763-1, RA ~150°) are slightly above the distance trend of this branch. Particularly, fields A795 and A763 also display two additional detections (primary and secondary, respectively) slightly under the expected distance trend. Fields A795 and A763 lie close in the sky (less than 4° apart) and both yield primary and secondary distance measurements very consistent with each other and with this dichotomy. We interpret this as possibly indicating a region of the sky where the bright branch runs broader in distance.
Out of the five detections incompatible with the distance trends of the leading arm, we will discuss three (RX J1524, A1413-2 and ZwCl1215-1) in Sect. 3.2.2, together with the above mentioned A1185. Regarding the other two (RX J1347 and ZwCl1215-3, RA ~205° and RA ~185° respectively), we have studied them individually and found the following. On the one hand, ZwCl1215-3 matches the distance to the Virgo Overdensity (Bonaca et al. 2012b) when using the appropriate age and metallicity values for the theoretical isochrone, so it is likely a detection of this cloud. On the other hand, RX J1347 matches the distance and position predicted by the model from Peñarrubia et al. (2010) for an older northern-wrap of the leading arm, but also the distances predicted by the two models for the northern-trailing wrap. However we can not draw conclusions regarding membership for an isolated detection and we lack kinematic data, so at the moment we can not discriminate between both options (or even a third one).
3.2.2. Northern trailing arm
In this subsection we revisit four detections in the galactic northern hemisphere which yield distances incompatible with (or off) the leading arm. These detections are RX J1524, A1413-2 (red circles in Fig. 7), A1185 (compatible with the faint leading branch thanks to its large error bars, but severely offset from the distance trend) and ZwCl1215-1 (white marker at RA ~185° on the bright branch). The three detections in the faint branch (RX J1524, A1413-2 and A1185) show distances strongly consistent with each other (~17 kpc). And the three of them are the fields most apart from the Sgr orbital plane in our northern sample, spreading 60° along the orbit.
Remarkably both their distances and their positions in the sky are in extremely good agreement with the predictions from the above mentioned models for the Sgr debris in the northern-trailing arm, and they are roughly comparable to the results in Correnti et al. (2010) and the suggestions in Martínez Delgado et al. (2004a). However they are at odds with the claim in Belokurov et al. (2014) that branch C (at lower declinations and more distant; see grey triangles in Fig. 7) is indeed a part of the northern-trailing arm and the continuation of the Gemini stream/arm (Newberg et al. 2003, Drake et al. 2013; see pink triangles from Belokurov et al. 2014 in Fig. 7).
Given the consistency of our distance measurements with each other and with the simulations, and given the distribution of the fields along the faint branch of the stream, we believe these detections are part of the Sgr stream, most likely a wrap of the northern trailing arm. However kinematic data or a spatially broader photometric coverage are needed to confirm this.
Additionally, ZwCl1215-1, which lies on the bright branch, yields a distance measurement compatible with the trend predicted for the northern-trailing arm. But its position on the sky (on the bright branch) can not be reconciled with the current models for the trailing tail, neither with the age, metallicity and distance values for the Virgo Overdensity. Thus, its membership and meaning in the puzzle of the halo remain an open question.
3.2.3. Southern trailing arm
Our measurements on the bright and the faint branches of the southern-trailing arm reproduce the distance trends of Koposov et al. (2012, 2013) and Slater et al. (2013) based on red clump and turnoff point stars. For the faint branch, we confirm the trend set by the <3σ detections in Slater et al. (2013), and we briefly extend westwards and eastwards the distance measurements. Contrary to Slater et al. (2013), we find no evidence for a difference in distance between the faint and the bright branches of the southern-trailing tail. However it is possible that such difference remains hidden in our distance uncertainties.
When comparing to the above mentioned models, we find that the measures are in general agreement with the predictions for both the faint and the bright branches. However the distance gradient in the faint branch seems to be less steep in the data than in the models, and the branch seems to be thinner in distance than predicted for any value of the probed RA range. In this sense it is worth noting that, in contrast to what happens to many of our northern hemisphere fields, only two of the CMDs in the southern galactic hemisphere show secondary MS detections (RX J0352 and RX J2344, at RA ~58° and RA ~356°, respectively). And the difference between the turnoff point brightness of these double detections does not favour a thick branch, but rather the detection of a previously unknown nearby wrap (see Sect. 3.2.4).
 |
Fig. 10 Left: dereddened CMD for the westernmost pointing probing the leading arm in the southern hemisphere; the template main sequence function and the turnoff point (green) are plotted for the maximum of the primary cross-correlation. Right: weighted-density diagram resulting from the primary cross- correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS at the position of the southern-leading arm main sequence, whereas the red overdensity at fainter magnitudes corresponds to the southern-trailing arm. |
 |
Fig. 11 Left: dereddened CMD for the easternmost pointing probing the leading arm in the southern hemisphere; the template main sequence function and the turnoff point (green) are plotted for the maximum of the secondary cross-correlation. We have randomly removed 50% of the stars contributing to the primary detection, which corresponds to the southern-trailing arm of the Sgr stream. Right: weighted-density diagram resulting from the secondary cross- correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the southern leading arm main sequence. The primary detection has been partially removed, and the remainings can be seen as a weak tail at fainter magnitudes and slightly bluer colour. |
 |
Fig. 12 Left: smoothed CMD for field RX J1524 containing the CFHT sources classified as stars in our work. Right: same diagram for the sources classified as stars in the SDSS database. The weaker features in the left figure are not detectable in the right figure due to photometric uncertainties and the different star/galaxy separations. The smoothing two-dimensional kernel is the standard bivariate normal density; the function mapping the density scale to the colour scale follows x0.25. |
3.2.4. Southern leading arm
In this subsection we revisit the double detections of 3.2.3, namely RX J0352-1 and RX J2344-2, (RA ~58° and RA ~356°, primary and secondary detections, respectively). We show their CMDs and their cross-correlation density diagrams in Figs. 10 and 11. We find that, using the same isochrone we have used to derive distances to all the Sgr fields, both yield a distance of ~13 kpc. These distances are in excellent agreement with the predictions from the two simulations for the leading arm in the south and also with the trend set by the leading-northern data. We thus claim that these two detections are part of the continuation of the northern-leading arm into the southern hemisphere (Chou et al. 2007). The positions of these fields, however, suggest that the leading arm dives into the southern hemisphere at higher declinations than predicted, overlapping in projection with the faint branch of the trailing arm.
If the detection of the southern-leading arm or the northern-trailing arm proposed in this paper are confirmed in future works (with kinematic measurements for membership or photometric follow-up for spatial coverage), our measurements will be part of the closest and the oldest debris of the Sgr stream. If so, this would mean that our method has succeeded in detecting nearby substructure in regions of the sky that had already been explored. The explanation to such a performance would lie on the fact that we use a sample of stars (a large part of the main sequence) to identify the overdensities in the CMD larger than the sample of the usual halo tracers (red clump, red giants or blue horizontal branch), and this could increase the contrast in regions of low concentration and thick disk contamination.
 |
Fig. 13 Left: dereddened CMD for the pointing containing the Palomar 5 stream as its primary feature; the template main sequence function and the turnoff point (green) are plotted for the maximum of the cross-correlation. The secondary main sequence at fainter magnitudes corresponds to the faint arm of the Sgr stream. Right: weighted-density diagram resulting from the cross-correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the Palomar 5 stream’s main sequence, whereas the cyan overdensity at fainter magnitudes corresponds to the Sgr stream. |
 |
Fig. 14 Left: dereddened CMD for the pointing containing the Orphan stream as its secondary feature; the template main sequence function and the turnoff point (green) are plotted for the maximum of the secondary cross-correlation. We have randomly removed 60% of the stars contributing to the primary detection, which corresponds to the bright arm of the Sgr stream. Right: weighted-density diagram resulting from the secondary cross-correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the Orphan stream’s main sequence. The primary detection has been removed, and thus it does not show in the density diagram. |
3.2.5. Presence of sparse nearby streams in SDSS
The lowest-contrast features we discuss have not been seen in previous analyses of the SDSS. Figure 12 shows this is not surprising: in the much shallower SDSS data the detected MS features are significantly smeared out by photometric uncertainties and poorer star/galaxy separation (see CMD comparison). As a consequence, sparsely populated main sequences would be more difficult to identify in SDSS (and their BHB or RC counterparts would be impossible to identify). This comparison nicely illustrates the complimentarity of our pencil beam survey to the large areal coverage of SDSS.
4. The Palomar 5 stream and the Orphan stream
4.1. Turnoff point distances to the Pal5 stream and the Orphan stream
The Palomar 5 stream and the Orphan stream are also probed by two of our fields (see orange diamonds in Fig. 1). Their CMDs and their corresponding turnoff points are shown in Figs. 13 and 14, together with their cross-correlation maps.
We use these turnoff point values to calculate photometric distances to each of the streams. Once again we assume single stellar populations characterized by theoretical isochrones but now with tage = 11.5 Gyr (Martell et al. 2002) and metallicity [Fe/H] = −1.43 (Harris 1996) in the case of the Pal5 stream, and tage = 10.0 Gyr and metallicity [Fe/H] = −1.63 in the case of the Orphan stream (Casey et al. 2013a). These values correspond to measurements for these particular streams, which are more metal-poor than the Sgr stream for similar ages. Since the absolute brightness of the turnoff point for a given stellar population depends on its age and metallicity, it is important to select representative values in order to derive the right photometric distances.
The resulting distances are collected in Table 2 and displayed in Figs. 15 and 16, respectively, where they are compared to previous findings by other groups. Both results show good agreement for the adopted age and metallicity values.
Position and distances to the Palomar 5 and Orphan stream.
4.2. Influence of the age/Z isochrone values on the distances
For the Palomar 5 stream and the Orphan stream, our pencil-beam survey returns only one
detection each. We compare their derived distance measurements (Table 2) to previous work (Figs. 15 and 16, respectively) and find
that our measurements are consistent and well within the values to be expected from
interpolations. We interpret this as an independent validation of the stellar population
parameters for these streams in the literature: 11.5 Gyr and [Fe/H] = −1.43 dex for the Pal5 stream
(Martell et al. 2002; Harris 1996), and 10.0 Gyr and [Fe/H] = −1.63 dex for the Orphan stream
(Casey et al. 2013a). Variations in the absolute
magnitude for the turnoff point of the theoretical isochrone assigned to a given stellar
population (characterized by a given age and metallicity) propagate into the distance
modulus, thus yielding variations in the distance. For the Pal5 stream, our distance
measurement can tolerate a relative variation of Δdrel ≈ ± 0.15
and still be in agreement with the previous distance measurements; this variation
threshold translates into an absolute magnitude variation threshold of ΔM ≈ ± 0.35. We find that
variations in 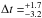 Gyr (limited by the formation time of the first stars) or in
Gyr (limited by the formation time of the first stars) or in
![\hbox{$\Delta \rm [Fe/H]=^{+0.72}_{-0.82} \mathrm{dex}$}](/articles/aa/full_html/2014/04/aa23000-13/aa23000-13-eq87.png) (limited by the minimum
metallicity available in the set of theoretical isochrones) for the age and metallicity of
the employed theoretical isochrones meet this tolerance criterion. For the Orphan stream,
our distance measurement can tolerate a relative variation of
(limited by the minimum
metallicity available in the set of theoretical isochrones) for the age and metallicity of
the employed theoretical isochrones meet this tolerance criterion. For the Orphan stream,
our distance measurement can tolerate a relative variation of
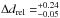 ,
which translates into
,
which translates into 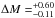 .
Variations in
.
Variations in 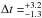 Gyr or in
Gyr or in ![\hbox{$\Delta\rm [Fe/H]=^{+0.83}_{-0.49} \mathrm{dex}$}](/articles/aa/full_html/2014/04/aa23000-13/aa23000-13-eq91.png) (same limitations as above)
for the age and metallicity of the theoretical isochrones respect this requirement.
(same limitations as above)
for the age and metallicity of the theoretical isochrones respect this requirement.
 |
Fig. 15 Photometric main sequence turnoff point distances along right ascension for the Palomar 5 stream. Our data point (blue circle) is based on a single stellar population of age 11.5 Gyr and metallicity [Fe/H] = −1.43. The other values correspond to Grillmair & Dionatos (2006a, green triangles) and Vivas & Zinn (2006, pink star). |
 |
Fig. 16 Photometric main sequence turnoff point distances along declination for the Orphan stream. Our data point (blue circle) is based on the theoretical isochrone for a 10.0 Gyr old stellar population with [Fe/H] = −1.63. The other values correspond to Belokurov et al. (2007a, green triangles), Newberg et al. (2010, orange diamonds) and Casey et al. (2006, cyan star). |
5. Conclusions
In this work we have used data from two deep cluster surveys, which provide randomly scattered photometric pencil-beams in g′ and r′, and a field of view of 1deg2 per pointing. We have used this data to characterize previously known substructure in the stellar halo of the Milky Way. We analysed these data using two novel ingredients: a PSF-homogenization for the images and a cross-correlation algorithm for the CMD. The PSF-homogenization algorithm corrects the inhomogeneous distortion of the sources across an image caused by the telescope’s optics. In this way, it recovers the true shapes and size distribution of the sources, improving the performance of any star/galaxy separation procedure, specially at the faint end. The cross-correlation algorithm explores the CMD of each field searching for an overdensity with the shape of a stellar main sequence, and returns the (colour, magnitude) coordinates of the corresponding turnoff point, from which distances can be derived. Through this method, we have shown that it is possible to exploit a two-filter pencil-beam survey to perform such a study of streams or satellites, provided that the contrast-to-noise ratio of the substructure’s main sequence is moderately significant. In this way our method bypasses the need for nearby control-fields that can be used to subtract a reference foreground from the target CMDs.
Using a set of theoretical isochrones (Marigo et al. 2008; Girardi et al. 2010), we have calculated the distances to different regions of the Sagittarius stream (faint and bright branches in both the northern and southern arms) and obtained results in good agreement with previous work (Belokurov et al. 2006; Koposov et al. 2012, 2013; Slater et al. 2013) (see Fig. 7).
We detect what seems to be the continuation of the northern-leading arm into the Southern hemisphere; we find that its distances are in excellent agreement with the predictions by the models in Peñarrubia et al. (2010) and Law & Majewski (2010), while the trajectory seems to be located at higher declinations. We also find evidence for a nearby branch of the northern-trailing arm at RA > 160°. Both the distances and the footprint on the sky are in good agreement with the predictions from the models, and are comparable to work by Correnti et al. (2010). It is also compatible with being the continuation of Gemini arm (claimed as part of a northern-trailing wrap in Belokurov et al. 2014) if it turns or broadens to higher latitudes as it evolves westwards, but it does not follow the same distance trend as branch C (Belokurov et al. 2006). The final interpretation of these different overdensities in the context of the Sgr stream will require kinematic data and more extensive photometric mapping.
We have also used age and metallicity measurements from previous work (Martell et al. 2002; Harris 1996; Casey et al. 2013a), to calculate distances to the Pal5 stream and the Orphan stream. These distances are in good agreement with the results in the literature (Grillmair & Dionatos 2006a; Vivas & Zinn 2006; Belokurov et al. 2007a; Newberg et al. 2010; Casey et al. 2013a), attesting – together with the results from the Sgr stream for previously known regions of the stream – the robustness and accuracy of the cross-correlation.
The methods presented in this paper open the possibility of using deeper existing pencil-beam surveys (maybe originally aimed for extragalactic studies) to measure accurate distances (or ages or metallicities, provided that two of the three parameters are known) to streams, globular clusters or dwarf galaxies. The existence of these pencil-beam surveys or the reduced requirements of prospective ones, allow for more complete maps of the Galactic halo substructure at reduced observational costs.
The rejection of exposures derives from trying to optimize the image quality while achieving the desired photometric depth. Thus our seeing criterion is a variable number dependent on the field itself, the seeing distribution for individual exposures and the individual plus total exposure time. In general it takes values 0.9 .
Through all this work we use a subset of theoretical isochrones from http://stev.oapd.inaf.it/cmd. The theoretical isochrones (Marigo et al. 2008; with the corrections from Case A in Girardi et al. 2010 and the bolometric corrections for Carbon stars from Loidl et al. 2001) are provided as observable quantities transformed into the CFHT photometric system.
The SDSS-DR8 measurements shown in this paper for the southern bright arm have been corrected for the difference in the calibration of the red clump absolute magnitude, as pointed out in Slater et al. (2013) and corrected in Koposov et al. (2013). And the SDSS-DR5 measurements have been decreased by 0.15 mag to match the BHB signal from SDSS, as prescribed in Belokurov et al. (2014).
Acknowledgments
We thank J. Peñarrubia for useful discussion and for the public availability of the data generated by his model; we also thank thank D.R. Law for the public availability of the data from his model and for his constructive comments as the referee; we thank K.V. Johnston for valuable discussion. Most of the data processing and analysis in this work has been carried out using the Python programming language and, in particular, the open source modules named Numpy, AstroAsciiData and Matplotlib. B.P.D. thanks support by NOVA, the Dutch Research School of Astronomy. H.H. and R.v.d.B. acknowledge support from the Netherlands Organisation for Scientific Research (NWO) grant number 639.042.814.
References
- Bell, E. F., Zucker, D. B., Belokurov, V., et al. 2008, ApJ, 680, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Evans, N. W., Irwin, M. J., et al. 2007a, ApJ, 658, 337 [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2007b, ApJ, 654, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Koposov, S. E., Evans, N. W., et al. 2014, MNRAS, 437, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2010, ApJ, 721, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Bildfell, C., Hoekstra, H., Babul, A., et al. 2012, MNRAS, 425, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Geha, M., & Kallivayalil, N. 2012a, ApJ, 760, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaca, A., Jurić, M., Ivezić, Ž., et al. 2012b, AJ, 143, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G. 2012, ApJ, 748, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, J. L., Majewski, S. R., Casetti-Dinescu, D. I., et al. 2012, ApJ, 744, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Casetti-Dinescu, D. I., Girard, T. M., Majewski, S. R., et al. 2009, ApJ, 701, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, A., Keller, S., Da Costa, G., Frebel, A., & Maunder, E. 2013a, ApJ, submitted [arXiv:1309.3563] [Google Scholar]
- Casey, A. R., Da Costa, G., Keller, S. C., & Maunder, E. 2013b, ApJ, 764, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, M.-Y., Majewski, S. R., Cunha, K., et al. 2007, ApJ, 670, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Correnti, M., Bellazzini, M., Ibata, R. A., Ferraro, F. R., & Varghese, A. 2010, ApJ, 721, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., Odenkirchen, M., Grebel, E. K., & Rix, H.-W. 2004, AJ, 127, 2753 [NASA ADS] [CrossRef] [Google Scholar]
- Dohm-Palmer, R. C., Helmi, A., Morrison, H., et al. 2001, ApJ, 555, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Catelan, M., Djorgovski, S. G., et al. 2013, ApJ, 765, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Duffau, S., Zinn, R., Vivas, A. K., et al. 2006, ApJ, 636, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Fellhauer, M., Belokurov, V., Evans, N. W., et al. 2006, ApJ, 651, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Fellhauer, M., Evans, N. W., Belokurov, V., Wilkinson, M. I., & Gilmore, G. 2007a, MNRAS, 380, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Fellhauer, M., Evans, N. W., Belokurov, V., et al. 2007b, MNRAS, 375, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Williams, B. F., Gilbert, K. M., et al. 2010, ApJ, 724, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J. 2006a, ApJ, 645, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J. 2006b, ApJ, 651, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J. 2009, ApJ, 693, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006a, ApJ, 641, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006b, ApJ, 643, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Johnson, R. 2006, ApJ, 639, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, in Formation of the Galactic Halo...Inside and Out, eds. H. L. Morrison, & A. Sarajedini, ASP Conf. Ser., 231 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Irwin, M., Lewis, G. F., & Stolte, A. 2001, ApJ, 547, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Wyse, R. F. G., Gilmore, G., Irwin, M. J., & Suntzeff, N. B. 1997, AJ, 113, 634 [Google Scholar]
- Jin, S., & Lynden-Bell, D. 2007, MNRAS, 378, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., & Alcock, C. 2006a, ApJ, 652, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., Alcock, C., et al. 2006b, ApJ, 638, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., Evans, N. W., et al. 2012, ApJ, 750, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., & Wyn Evans, N. 2013, ApJ, 765, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., & Majewski, S. R. 2010, ApJ, 714, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C., & Sarajedini, A. 2000, AJ, 119, 1760 [Google Scholar]
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., Smith, G. H., & Grillmair, C. J. 2002, BAAS, 34, 1103 [NASA ADS] [Google Scholar]
- Martin, N. F., Ibata, R. A., Bellazzini, M., et al. 2004, MNRAS, 348, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Aparicio, A., Gómez-Flechoso, M. Á., & Carrera, R. 2001, ApJ, 549, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Delgado, D., Dinescu, D. I., Zinn, R., et al. 2004a, in Satellites and Tidal Streams, eds. F. Prada, D. Martinez Delgado, & T. J. Mahoney, ASP Conf. Ser., 327, 255 [Google Scholar]
- Martínez-Delgado, D., Gómez-Flechoso, M. Á., Aparicio, A., & Carrera, R. 2004b, ApJ, 601, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Mastrobuono-Battisti, A., Di Matteo, P., Montuori, M., & Haywood, M. 2012, A&A, 546, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateo, M., Mirabal, N., Udalski, A., et al. 1996, ApJ, 458, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Newberg, H. J., Yanny, B., Grebel, E. K., et al. 2003, ApJ, 596, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Newberg, H. J., Willett, B. A., Yanny, B., & Xu, Y. 2010, ApJ, 711, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Niederste-Ostholt, M., Belokurov, V., Evans, N. W., & Peñarrubia, J. 2010, ApJ, 712, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., Rix, H.-W., & Cudworth, K. M. 2002, AJ, 124, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., et al. 2003, AJ, 126, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J., Belokurov, V., Evans, N. W., et al. 2010, MNRAS, 408, L26 [NASA ADS] [Google Scholar]
- Peñarrubia, J., Zucker, D. B., Irwin, M. J., et al. 2011, ApJ, 727, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Piatek, S., Pryor, C., & Olszewski, E. W. 2008, AJ, 135, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Prior, S. L., Da Costa, G. S., Keller, S. C., & Murphy, S. J. 2009, ApJ, 691, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha, M., Peter, A. H. G., & Bullock, J. 2012, MNRAS, 425, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha-Pinto, H. J., Majewski, S. R., Skrutskie, M. F., Crane, J. D., & Patterson, R. J. 2004, ApJ, 615, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Helmi, A., Starkenburg, E., et al. 2008, MNRAS, 389, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Graham, M. L., Bildfell, C., et al. 2012, ApJ, 746, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Hartwick, F. D. A. 1977, AJ, 82, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Vivas, A. K., Duffau, S., & Ivezić, Ž. 2010, ApJ, 717, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, S., Johnston, K. V., Majewski, S. R., et al. 2010, ApJ, 722, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffield, A. A., Majewski, S. R., Johnston, K. V., et al. 2012, ApJ, 761, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, W. B., Chen, Y. Q., Carrell, K., & Zhao, G. 2012, ApJ, 751, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Slater, C. T., Bell, E. F., Schlafly, E. F., et al. 2013, ApJ, 762, 6 [NASA ADS] [CrossRef] [Google Scholar]
- van der Burg, R. F. J., Muzzin, A., Hoekstra, H., et al. 2013, A&A, 557, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Velazquez, H., & White, S. D. M. 1995, MNRAS, 275, L23 [NASA ADS] [Google Scholar]
- Vivas, A. K., & Zinn, R. 2006, AJ, 132, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Vivas, A. K., Zinn, R., & Gallart, C. 2005, AJ, 129, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, L. L., Evans, N. W., Belokurov, V., et al. 2009, MNRAS, 398, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Newberg, H. J., Grebel, E. K., et al. 2003, ApJ, 588, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, D. B., Belokurov, V., Evans, N. W., et al. 2006, ApJ, 650, L41 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Position and distances to the Sgr stream, together with a tag for faint or bright branch membership, a tentative classification as leading or trailing arm and a number specifying the hierarchy of the detection in the CMD (primary, secondary, etc.).
All Figures
 |
Fig. 1 Equatorial map showing the position of all the fields from our survey (white hexagons) and highlighting the ones that lay on the Sagittarius stream (green circles for the faint branch and green squares for the bright branch), on the Palomar 5 stream and on the Orphan stream (orange diamonds). The background image is the SDSS-DR8 map of the Sgr stream from Koposov et al. (2012), where the location of the Sagittarius dwarf galaxy has been marked (red star). |
| In the text | |
 |
Fig. 2 Brightness versus size diagram of all the sources in one of our pointings. The stellar locus prior to the PSF-homogenization (black) is wider and therefore subject to greater galaxy contamination at the faint end than the stellar locus posterior to the correction (blue) because the PSF initially varies across the field. The sources more compact than the stellar locus are artefacts from the source extraction; they hold no relevance for our analysis since they do not pass the star selection (see Fig. 3). |
| In the text | |
 |
Fig. 3 Brightness versus size diagram showing all the PSF-corrected sources (blue) and the subset of sources selected as stars through our star/galaxy separation algorithm (red) for one of our pointings. Although the star selection may not be complete at the faint end due to increasing scatter, our algorithm minimizes the galaxy contamination, which otherwise would be the main obstacle for detecting faint structures in the CMD. |
| In the text | |
 |
Fig. 4 Colour−magnitude diagram displaying the selection of sources considered stars (selected as explained in Sect. 2.2). The plume on the red side (g − r ≈ 1.2) is composed of the nearby M-dwarfs, whereas the main sequence on the bluer side (0.18 < g − r < 0.6) corresponds to a halo overdensity located at a particular well-defined distance. The cloud of sources at faint magnitudes are faint galaxies that enter the star selection. Left: CMD derived from an image that has not been PSF-corrected. Right: CMD derived from a PSF-corrected image. After homogenizing the PSF, the galaxy contamination decreases markedly below r ≈ 22. |
| In the text | |
 |
Fig. 5 Left: dereddened CMD (black dots) with the search region (pink solid-line rectangle) for the cross-correlation and the template main sequence-shaped function (green solid line) at the position of maximum density (peak of the cross-correlation). Right: binned diagram representing the weighted density of stars resulting from the cross-correlation process. The density in each bin corresponds to the integral of the template main sequence-shaped function with top left corner in the position of the bin. |
| In the text | |
 |
Fig. 6 Absolute magnitude of the turnoff point in the r band as a function of metalllicity and age for metal poor populations (green circles). The values in this diagram meet the age/metallicity relation for the Sgr dwarf galaxy from Layden & Sarajedini (2000). The isochrone used in this paper to derive distances to the Sgr stream is represented with a yellow star, and its maximum difference to the other brightness values in this range is ΔM = ± 0.1mag. |
| In the text | |
 |
Fig. 7 Photometric main sequence turnoff point distances for the Sagittarius stream along right ascension (northern-leading tail and southern- trailing tail). The top panel shows results for the faint branch, whereas the bottom panel corresponds to the bright arm. Our data (blue circles for leading tails and red circles for trailing tails) are based on the theoretical isochrones by Marigo et al. (2008) and the corrections by Girardi et al. (2010), for a 10.2 Gyr old stellar population with [Fe/H] = −1.0. Other distance values correspond to Belokurov et al. (2006, green and grey triangles), Koposov et al. (2012, 2013, green asterisks), Belokurov et al. (2014, pink triangles) and Slater et al. (2013, yellow squares for >3σ detections and white squares for <3σ). White circles denote detections that can not be unambiguously tagged as leading or trailing. |
| In the text | |
 |
Fig. 8 Our data compared to the predictions by the model from Peñarrubia et al. (2010). Top panel: equatorial map with the position of our fields plotted over the simulation. Bottom panel: distance vs. RA diagram with our results compared to the model predictions. Fields on the faint branch are denoted with circles, and fields on the bright branch are denoted with squares. Measurements matching the leading arm are denoted in pink, whereas those matching the trailing arm are denoted in light blue. White markers represent detections that can not be unambiguously tagged as leading or trailing; grey markers in the upper panel correspond to fields with more than one MS detection (they unfold in the bottom panel). The colour scales represent the time since the particles from the simulations became unbound. |
| In the text | |
 |
Fig. 9 Same as in Fig. 8 but for the model from Law & Majewski (2010). |
| In the text | |
 |
Fig. 10 Left: dereddened CMD for the westernmost pointing probing the leading arm in the southern hemisphere; the template main sequence function and the turnoff point (green) are plotted for the maximum of the primary cross-correlation. Right: weighted-density diagram resulting from the primary cross- correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS at the position of the southern-leading arm main sequence, whereas the red overdensity at fainter magnitudes corresponds to the southern-trailing arm. |
| In the text | |
 |
Fig. 11 Left: dereddened CMD for the easternmost pointing probing the leading arm in the southern hemisphere; the template main sequence function and the turnoff point (green) are plotted for the maximum of the secondary cross-correlation. We have randomly removed 50% of the stars contributing to the primary detection, which corresponds to the southern-trailing arm of the Sgr stream. Right: weighted-density diagram resulting from the secondary cross- correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the southern leading arm main sequence. The primary detection has been partially removed, and the remainings can be seen as a weak tail at fainter magnitudes and slightly bluer colour. |
| In the text | |
 |
Fig. 12 Left: smoothed CMD for field RX J1524 containing the CFHT sources classified as stars in our work. Right: same diagram for the sources classified as stars in the SDSS database. The weaker features in the left figure are not detectable in the right figure due to photometric uncertainties and the different star/galaxy separations. The smoothing two-dimensional kernel is the standard bivariate normal density; the function mapping the density scale to the colour scale follows x0.25. |
| In the text | |
 |
Fig. 13 Left: dereddened CMD for the pointing containing the Palomar 5 stream as its primary feature; the template main sequence function and the turnoff point (green) are plotted for the maximum of the cross-correlation. The secondary main sequence at fainter magnitudes corresponds to the faint arm of the Sgr stream. Right: weighted-density diagram resulting from the cross-correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the Palomar 5 stream’s main sequence, whereas the cyan overdensity at fainter magnitudes corresponds to the Sgr stream. |
| In the text | |
 |
Fig. 14 Left: dereddened CMD for the pointing containing the Orphan stream as its secondary feature; the template main sequence function and the turnoff point (green) are plotted for the maximum of the secondary cross-correlation. We have randomly removed 60% of the stars contributing to the primary detection, which corresponds to the bright arm of the Sgr stream. Right: weighted-density diagram resulting from the secondary cross-correlation. The maximum (white bin, black cross) marks the top left corner of the template-MS function at the position of the Orphan stream’s main sequence. The primary detection has been removed, and thus it does not show in the density diagram. |
| In the text | |
 |
Fig. 15 Photometric main sequence turnoff point distances along right ascension for the Palomar 5 stream. Our data point (blue circle) is based on a single stellar population of age 11.5 Gyr and metallicity [Fe/H] = −1.43. The other values correspond to Grillmair & Dionatos (2006a, green triangles) and Vivas & Zinn (2006, pink star). |
| In the text | |
 |
Fig. 16 Photometric main sequence turnoff point distances along declination for the Orphan stream. Our data point (blue circle) is based on the theoretical isochrone for a 10.0 Gyr old stellar population with [Fe/H] = −1.63. The other values correspond to Belokurov et al. (2007a, green triangles), Newberg et al. (2010, orange diamonds) and Casey et al. (2006, cyan star). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


