| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322700 | |
| Published online | 14 April 2014 | |
Ionization compression impact on dense gas distribution and star formation
Probability density functions around H II regions as seen by Herschel⋆
1
Laboratoire AIM Paris-Saclay (CEA/Irfu – Univ. Paris Diderot –
CNRS/INSU),
Centre d’études de Saclay,
91191
Gif-Sur-Yvette,
France
e-mail:
pascal.tremblin@cea.fr
2
Astrophysics Group, University of Exeter,
EX4 4 QL Exeter, UK
3
Univ. Bordeaux, LAB, UMR 5804, 33270
Floirac,
France
4
CNRS, LAB, UMR 5804, 33270
Floirac,
France
5
Joint ALMA Observatory, Alonso de Cordova 3107, 7630355 Vitacura,
Santiago,
Chile
6
Department of Physics, West Virginia University,
Morgantown
WV
26506,
USA
7
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
8
IAS, CNRS (UMR 8617), Université Paris-Sud,
Bâtiment 121,
91400
Orsay,
France
9
Maison de la Simulation, CEA-CNRS-INRIA-UPS-UVSQ,
USR 3441, Centre d’étude de
Saclay, 91191
Gif-Sur-Yvette,
France
10
Istituto di Astrofisica e Planetologia Spaziali (INAF-IAPS), via
del Fosso del Cavaliere 100, 00133
Roma,
Italy
11
Max-Planck Institut für Radioastronomie,
Auf dem Hügel,
53121
Bonn,
Germany
12
National Research Council of Canada, Herzberg Institute of
Astrophysics, 5071 West Saanich
Road, Victoria, BC
V9E 2E7,
Canada
13
INAF Osservatorio Astronomico di Roma, via Frascati 33,
00040
Monte Porzio Catone,
Italy
14
Canadian Institute for Theoretical Astrophysics, University of
Toronto, 60 St. George Street,
Toronto, ON
M5S 3H8,
Canada
15
European Space Astronomy Centre, Urb. Villafranca del Castillo, PO
Box 50727, 28080
Madrid,
Spain
16
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The
Parade, Cardiff
CF24 3AA,
UK
17
Université de Toulouse, UPS-OMP, IRAP, 31400
Toulouse,
France
18
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
19
The Rutherford Appleton Laboratory, Chilton, Didcot, OX11
0NL, UK
20
Department of Physics and Astronomy, The Open
University, Milton
Keynes, UK
Received:
18
September
2013
Accepted:
28
January
2014
Aims. Ionization feedback should impact the probability distribution function (PDF) of the column density of cold dust around the ionized gas. We aim to quantify this effect and discuss its potential link to the core and initial mass function (CMF/IMF).
Methods. We used Herschel column density maps of several regions observed within the HOBYS key program in a systematic way: M 16, the Rosette and Vela C molecular clouds, and the RCW 120 H ii region. We computed the PDFs in concentric disks around the main ionizing sources, determined their properties, and discuss the effect of ionization pressure on the distribution of the column density.
Results. We fitted the column density PDFs of all clouds with two lognormal distributions, since they present a “double-peak” or an enlarged shape in the PDF. Our interpretation is that the lowest part of the column density distribution describes the turbulent molecular gas, while the second peak corresponds to a compression zone induced by the expansion of the ionized gas into the turbulent molecular cloud. Such a double peak is not visible for all clouds associated with ionization fronts, but it depends on the relative importance of ionization pressure and turbulent ram pressure. A power-law tail is present for higher column densities, which are generally ascribed to the effect of gravity. The condensations at the edge of the ionized gas have a steep compressed radial profile, sometimes recognizable in the flattening of the power-law tail. This could lead to an unambiguous criterion that is able to disentangle triggered star formation from pre-existing star formation.
Conclusions. In the context of the gravo-turbulent scenario for the origin of the CMF/IMF, the double-peaked or enlarged shape of the PDF may affect the formation of objects at both the low-mass and the high-mass ends of the CMF/IMF. In particular, a broader PDF is required by the gravo-turbulent scenario to fit the IMF properly with a reasonable initial Mach number for the molecular cloud. Since other physical processes (e.g., the equation of state and the variations among the core properties) have already been said to broaden the PDF, the relative importance of the different effects remains an open question.
Key words: stars: formation / HII regions / ISM: structure / methods: observational
© ESO, 2014
1. Introduction
The role of density compression by the expansion of ionized gas into a molecular cloud has been discussed since the pioneering theoretical work of Elmegreen & Lada (1977). Dense features are observed at the edge of H ii regions, i.e., condensations (e.g., Deharveng et al. 2009; Zavagno et al. 2010), globules (e.g., Schneider et al. 2012b), and pillars (e.g., Hester et al. 1996; Schneider et al. 2010b). Although many models and numerical simulations have been able to explain how small structures can form (see Bertoldi 1989; Lefloch & Lazareff 1994; Miao et al. 2006, 2009; Mackey & Lim 2010; Bisbas et al. 2011; Gritschneder et al. 2010; Haworth & Harries 2011; Tremblin et al. 2012a,b), the question remains whether they are triggered or pre-existing. Simulation on the molecular cloud scale has shown that the impact of high-mass stars on the molecular gas can enhance star formation (Dale et al. 2007) or that the impact is rather negligible (see Dale & Bonnell 2011), depending on the physical properties of the cloud. In Tremblin et al. (2012b), we showed that the key parameter to understanding the impact of a high-mass star on a molecular cloud is the ratio of the ionized-gas pressure to the ram pressure of the turbulence of the cloud. When the ionized-gas pressure dominates, compression from ionization is important, whereas the inverse leads to a compression dominated by the effect of turbulence.
Molecular cloud parameters.
Turbulent compression has been intensively studied in the past few years thanks to simulations of isothermal supersonic turbulence (see Vázquez-Semadeni 1994; Padoan et al. 1997; Kritsuk et al. 2007; Vázquez-Semadeni et al. 2008; Federrath et al. 2008, 2010). They show that the probability distribution function of the density (density PDF) is approximated well by a lognormal form. Deviations from the lognormal shape – mostly in the form of power-law tails – were seen in simulations of compressible turbulence of a nonisothermal gas distribution (Passot & Vázquez-Semadeni 1998) and/or in models including self-gravity (Klessen et al. 2000; Kritsuk et al. 2011; Federrath & Klessen 2013). The effect of magnetic fields on the density PDF was found to be less important, generally reducing the standard deviation (Molina et al. 2012; Federrath & Klessen 2012, 2013).
The impact of ionization on a turbulent velocity field was studied by Gritschneder et al. (2010) and the effect of ionization compression on the PDF in turbulent simulations has only recently been investigated by Tremblin et al. (2012b). They show that when the ionized-gas pressure is higher than the ram pressure of the turbulence, a second peak in the PDF forms at high densities in addition to the lognormal shape. Observationally, this second peak caused by the compression from the ionized-gas pressure has been identified in the Rosette nebula by Schneider et al. (2012a). But thanks to recent far-infrared (FIR) observations with the Herschel space telescope, it is now possible to study the column density PDF of the cold and warm molecular gas in high-mass star-forming regions, in which compression from ionization is likely to take place. Such regions are observed within the HOBYS1 key program (see Motte et al. 2010, 2012), and our study focuses on typical examples, i.e. the Rosette (Motte et al. 2010; Schneider et al. 2010b) and M 16 molecular clouds (Hill et al. 2012b), and the H ii regions RCW 120 (Zavagno et al. 2010; Anderson et al. 2010, 2012) and RCW 36 (in the Vela C molecular cloud, Hill et al. 2011; Minier et al. 2013).
We determined the PDFs in areas of four concentric disks around the H ii regions present in these clouds in order to study the large-scale effect of the ionization on the cold molecular gas. The first disk always contains the OB cluster region and includes the closest dense structures of the molecular cloud. The center of the disk is not the main ionizing source but corresponds to the approximate center of the Hα emission that is also approximately the center of the spherical column density structures seen at the edge of the cavity in the Herschel maps. For Rosette and M 16, the other disks are enlarged depending on the various dense structures present in the column density maps (37′′ angular resolution), up to the largest disks that contain most of the maps. This choice allows us to study the evolution of the shape of the PDF as a function of the column density structures that are included in the disks. For RCW 120 and RCW 36, less dense structures can be identified and the different radius are regularly spaced between the inner disk and the largest one reaching the edge of the observed map. Overall, the parameters of the fits of the PDFs depend only a little on the precise choice of the radii of the disks (given in Table 1) as long as they include the same dense column density structures that can be seen in the Herschel maps (see an example for Rosette in Appendix A). We first present and validate the method on the M 16 molecular cloud (Sect. 2), before showing the results on the Rosette nebula (Sect. 3). Both of these regions are relatively large, and their H ii region extended (≈10−20 pc). However, their mass and the incident UV-flux is fairly different (see Table 1). Finally, we study smaller scale H ii regions, RCW 120 and RCW 36 (Sects. 4 and 5), which are only ≈1 pc large and have lower masses. This approach allows us to explore the compression effect over one order of magnitude each of spatial scale, mass, and incident UV-flux.
2. M 16
M 16 is located in the constellation of Serpens at 1.8 kpc from the Sun (Bonatto et al. 2006). The young stellar cluster NGC 6611 is ionizing the molecular gas of this star-forming region. The principal ionizing sources are one O4 and one O5 stars whose combined ionizing flux is on the order of 2 × 1050 s-1 (Hester et al. 1996; White et al. 1999). The discovery of pillars of gas in M 16 by the Hubble Space Telescope (Hester et al. 1996) popularized this region by naming it “Pillars of Creation”. Many spectral line studies have been performed on the cloud (see Pound 1998; White et al. 1999; Allen et al. 1999; Urquhart et al. 2003, among others). The velocity of the CO line emission for the pillars is found between ∼20 and ∼30 km s-1 (White et al. 1999). These authors suggest that emission around 29 km s-1 is probably unrelated to the pillars. However with regard to the vicinity of the velocity to the cloud’s bulk emission and its spatial correlation (see their Fig. 8), a physical relation with the rest of the cloud is very likely. We thus do not expect the Herschel column density map to be strongly affected by line-of-sight (LOS) confusion.
Recently, Flagey et al. (2011) have measured dust spectral energy distributions (SEDs) thanks to Spitzer data. They show that the SED cannot be accounted for by interstellar-dust heating by UV radiation, but an additional source of radiation is needed to match the mid-infrared flux. They propose two explanations for this source of pressure: stellar winds or a supernova remnant. Herschel provides new observations on the region and Hill et al. (2012b) studied the impact of the ionizing source on the temperature of the molecular gas in detail. Heating is observed in regions with nH2 ≈ 105−106 cm-3, thus affecting the initial conditions of the star-forming sites. We use the same Herschel map to study the PDF of the cold molecular gas at the interface with the H ii region. The column density map of the M 16 molecular cloud (and of the other regions) was made by fitting the SED of a graybody pixel-by-pixel to the Herschel wavebands between 160 and 500 μm (at the same 37′′ resolution), assuming the dust opacity law of Hildebrand (1983) and a spectral index β of 2.
 |
Fig. 1 M 16 Herschel column density map (Hill et al. 2012b). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources. The limit of the Hα emission is inside region 1 + 2 + 3 showing approximately the limit of the H ii region (although the H ii region is not spherical in M 16). The blue circles indicate the position of the dense condensations identified in the power-law tail of the PDF of region 1. |
 |
Fig. 2 M 16 PDFs on the four regions indicated in Fig. 1. The multicomponent fit (green curve) is done using the sum of two lognormal distributions (red and blue dashed curves, see Eq. (1)) and a power law at high column densities (magenta line, see Eq. (2)). The error bars are computed assuming Poisson noise in each bin of the distribution. |
Figure 1 shows the different subregions in M 16 used for the PDFs plotted in Fig. 2. While the statistical Poisson error for the distribution is low (error bars are shown for the different PDFs) due to the large pixel statistics, there are systematic errors that influence the shape of the PDF. First, the assumption of isothermality along the LOS for fitting the pixel-to-pixel SED to derive the column density is not fully justified. Clouds with feedback due to radiation clearly show temperature variations. For M 16, a temperature gradient from ∼23 K to ∼16 K was found (Hill et al. 2012b). Second, the opacity increases towards higher column densities (Molina et al. 2012), which leads to a narrower PDF and a steeper slope of the power-law tail for high densities. It is important to exclude – or at least to quantify – possible LOS confusion that may result in a superposition of several PDFs from different clouds. This effect has already been proposed by Lombardi et al. (2006) for the Pipe molecular cloud. It is necessary to use complementary spectroscopic data (preferably atomic hydrogen or low-J CO) to define the velocity range of the cloud emission. Examples of how to estimate the contribution of foreground and background clouds in Herschel column density maps are given in Rivera-Ingraham et al. (2013) and Russeil et al. (2013). In the case of M 16, we do not expect the maps to be strongly affected by LOS confusion based on the CO line emission obtained by White et al. (1999).
Each disk contains the smaller ones, therefore Fig. 2 shows the evolution of the shape of the PDF while increasing the radius of the disk around the ionizing sources. The first disk (region 1) contains the ionizing sources and the dense column density structures up to the massive young stellar object west of the ionizing sources (blue circle in Fig. 1). The second disk (region 1 + 2) extends up to the base of the pillars of creation, the third disk (region 1 + 2 + 3) includes the whole dense structure at the northwest of the cavity (northern filament in Hill et al. 2012b), and the fourth disk (region 1 + 2 + 3 + 4) reaches the edge of the map.
In all the regions a double peak is clearly identified, especially in region 1 + 2 + 3. To locate the position of the compressed gas, we plot the PDF of region 1 + 2 + 3 and the PDF of region 4 in Fig. 3. This region is an annulus that represents the outward parts of the cloud that should not be too affected by the ionization. However a dense component is still present and corresponds to the eastern filament identified in Hill et al. (2012b). Apart from this filament, most of the compressed material in the second peak in the PDF in region 1 + 2 + 3 is not present in region 4, therefore the compression is likely to be linked with the ionized gas. To illustrate this point, we show the PDF obtained from the numerical simulation presented in Tremblin et al. (2012b) in Fig. 3. This simulation corresponds to the ionization of a turbulent cloud at Mach 1 (without self-gravity), in which the ionized-gas pressure is much greater than the turbulent ram pressure. The compression is therefore efficient and a second peak appears in the PDF of the column density of the gas. This simulation is not performed in the exact conditions of M 16, which are not exactly known because of projection effects, however, the double peak is a global property identified in both these observations and numerical simulations.
 |
Fig. 3 Left: M 16 column density PDFs on region 1 + 2 + 3 and region 4 in Fig. 1. Right: column density PDFs of the simulation of the ionization of a Mach-1 turbulent cloud (without self-gravity). The excess at high-density and the double-peaked distribution can be identified both in observations and numerical simulations. |
Because of this compressed peak, the PDFs are fitted using two lognormal distributions:
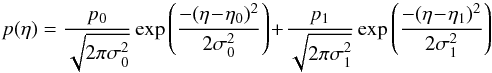 (1)where
η =
ln(NH2/ ⟨
NH2 ⟩). NH2 is
the column density and ⟨
NH2 ⟩ is the average of the
column density in the regions 1 + 2 + 3 +
4⟨
NH2 ⟩ = 6 × 1021
cm-2 for M 16.
(This value is different from the averaged value on the whole map) We used η with a natural logarithm to
ease comparisons with previous works (e.g., Federrath
& Klessen 2013). The variables ηi and σi are the peak value and
standard deviation of each component, and pi is the integral of
each component. The first lognormal component can be linked to the initial turbulent
molecular cloud, while the second lognormal component corresponds to a compression of the
turbulent cloud whose source can be either ionization compression, colliding flows, or even
winds, supernovas, etc. The high column-density part of the PDFs is fitted with a power law
of power m
which corresponds to an equivalent spherical density profile of power α (see Federrath & Klessen 2012; Schneider et al. 2013)
(1)where
η =
ln(NH2/ ⟨
NH2 ⟩). NH2 is
the column density and ⟨
NH2 ⟩ is the average of the
column density in the regions 1 + 2 + 3 +
4⟨
NH2 ⟩ = 6 × 1021
cm-2 for M 16.
(This value is different from the averaged value on the whole map) We used η with a natural logarithm to
ease comparisons with previous works (e.g., Federrath
& Klessen 2013). The variables ηi and σi are the peak value and
standard deviation of each component, and pi is the integral of
each component. The first lognormal component can be linked to the initial turbulent
molecular cloud, while the second lognormal component corresponds to a compression of the
turbulent cloud whose source can be either ionization compression, colliding flows, or even
winds, supernovas, etc. The high column-density part of the PDFs is fitted with a power law
of power m
which corresponds to an equivalent spherical density profile of power α (see Federrath & Klessen 2012; Schneider et al. 2013) 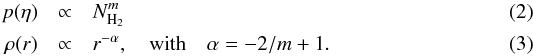 Assuming
spherical symmetry is a crude approximation for complex and large regions. However, if the
pixels contributing to the power-law tail do belong to a single condensation, this
approximation is relatively accurate. Therefore, we give the m values in the tables of
fitted parameters and only use the equivalent α values to discuss the results on single
condensations or compare with previous works that used this conversion. A spherical
self-gravitating cloud has an α value between 1.5 and 2, while higher values indicate
a steeper profile influenced by compression. We point out that, for some PDFs, it could be
argued that another choice of function (e.g., a lognormal and a two-step power law) could
also give a good fit to the data, especially in region 1 in the case of M 16. We will
discuss the differences and motivations for a two-lognormal plus one power-law fit or a
single lognormal plus a broken two-step power-law fit in more detail in Sect. 6.
Assuming
spherical symmetry is a crude approximation for complex and large regions. However, if the
pixels contributing to the power-law tail do belong to a single condensation, this
approximation is relatively accurate. Therefore, we give the m values in the tables of
fitted parameters and only use the equivalent α values to discuss the results on single
condensations or compare with previous works that used this conversion. A spherical
self-gravitating cloud has an α value between 1.5 and 2, while higher values indicate
a steeper profile influenced by compression. We point out that, for some PDFs, it could be
argued that another choice of function (e.g., a lognormal and a two-step power law) could
also give a good fit to the data, especially in region 1 in the case of M 16. We will
discuss the differences and motivations for a two-lognormal plus one power-law fit or a
single lognormal plus a broken two-step power-law fit in more detail in Sect. 6.
 |
Fig. 4 Top: zoom of the column density map on the western condensation. The magenta crosses indicate the pixels contributing to the power law of the PDF. The red dot is the position of the peak of the column density. The colormap is the color code used to show the orientation of the different profiles (e.g. green is north, yellow is east ...). Bottom: radial profiles of the column density of the western condensation. The color indicates the orientation of the profile. The power-law fits are performed around three different directions: north (180◦) in green, east (270◦) in yellow and south (360◦) in purple. Each fit includes all the points in ±40◦ around the main direction. |
Because of the number of parameters in Eq. (1), we fixed the peak values η0 and η1 based on the peak value of the low-density component seen in region 4 (Fig. 3) and the peak value of the compressed component seen in the concentric regions. After we have fixed these values, pi and σi are fitted to the observed distributions using a least-square method (Levenberg Marquardt algorithm). We point out that the exact values of the fitted parameters may depend on the choice of η0 and η1, however the general behavior deduced in our analysis is robust to this choice. The different parameters deduced from the fits are given in Table 2. In M 16, the lognormal fit of the low column density (Fig. 2) cannot account for the high column densities, and the double peak is clearly visible even at high radius (e.g., region 1 + 2 + 3). The integral of the low-density peak p0 increases with radius and the one of the compressed peak p1 decreases with distance. This behavior suggests that the compression effect is more important close to the ionizing source and is indeed linked to the ionization. Furthermore, the decrease in the compressed-peak gas quantity is rather small even for region 1 + 2 + 3 + 4: the impact of the H ii region is a large-scale compression.
In principle, a second compressed lognormal peak can be linked to shock compression around an H ii region. This shock is likely to be driven by the expansion of the ionized gas. Gravitational instabilities – assuming that these are the most important physical processes for shaping the PDF – lead to a power-law tail so could not account for the compressed peak visible in region 1 + 2 + 3. The power-law tail can still be identified at higher column densities (starting approximately for ln(NH2/ ⟨ NH2 ⟩ ) > 1.5) where the distribution starts to deviate from the second lognormal. The slope fit leads to α = 1.86 ± 0.05 in region 1 and decreases to α = 1.56 ± 0.02 in region 1 + 2 + 3 + 4. These values are similar to those obtained in other regions like Aquila and Polaris (Schneider et al. 2013). In region 1, the pixels that contribute to the power law are part of two dense clumps indicated in Fig. 1. Although the radial profiles of these clumps do show signs of compression, this effect is not reflected in the PDF, which mixes both condensations in the power-law tail. We give as an example the radial profiles of the massive western young stellar object (MYSO hereafter) in Fig. 4 as a function of the orientation. The profile is very steep on the side facing ionization (east side in yellow) with an α value of 2.3 (2.56 when the background column density is subtracted), while the profiles in the southern and northern directions (red and green) have an α value of 1.88 (1.99 when the background column density is subtracted), consistent with the influence of gravity. The average value is 2.25±0.02, suggesting that the compression on the MYSO is dominant. The same applies to the second condensation, although the average α value is α = 1.76 ± 0.02, suggesting that gravity is dominant. Thus, α values derived from the PDFs have to be taken with caution when different spherical structures are mixed in the same PDF. However, when the PDF is computed on separated areas for the two condensations, the deduced α values are compatible with their averaged fitted profiles. The use of steeper profiles to identified compressed cores will be discussed in Sect. 6.
3. Rosette nebula
The Rosette molecular cloud is located at 1.6 kpc from the Sun (Williams et al. 1994; Schneider et al. 1998a; Heyer et al. 2006) and is associated with a prominent H ii region, illuminated by the central cluster NGC 2244. The 17 OB stars of the cluster have a total Lyman-α luminosity of 3.8 × 105L⊙ (see Cox et al. 1990). The UV-flux is 100−200 G◦ (Habing-field) (Schneider et al. 1998b) at the interface zone between H ii region and molecular cloud and decreases to a few G◦ for the bulk emission deep (∼30 pc) into the cloud. Photon-dominated regions (PDRs) are found on the cloud surfaces where the UV-radiation shines directly onto the molecular cloud (see Schneider et al. 1998a,b). It is there where many pillars and globules are formed (see Schneider et al. 2010b; and Tremblin et al. 2013). Although the total UV-field is low (on average only ∼10 G◦, see Table 1) – compared to high-UV regions like Carina or Cygnus with up to 105 G◦ – the very clumpy and filamentary structure of the cloud enables a large penetration depth of UV-radiation so that PDRs are also found deep inside the cloud. The Rosette cloud contains several embedded infrared-clusters (see Poulton et al. 2008, and references therein), and is actively forming stars, as indicated by a larger reservoir of clumps (Di Francesco et al. 2010), a large population of protostars (Hennemann et al. 2010), molecular outflows (White et al., in prep.), and a few candidate massive dense cores (Motte et al. 2010). There is a long ongoing discussion about whether star formation is triggered in Rosette, with a possible increasing age gradient from the ionization front into the cloud (see Schneider et al. 2010b, for a detailed discussion). For Rosette, the bulk emission of the cloud is at ≈16 ± 6 km s-1 (Williams et al. 1994; Schneider et al. 1998a), and there is no significant emission in HI or CO outside this velocity range. Thus, the column density map is probably not very affected by LOS confusion.
Schneider et al. (2012a) has already shown that a double peak in the PDF was found for the gas close to the border of the shell (≈20 pc of radius). However, their distinctions into subregions are based mainly on morphology, so that here we study the evolution of the PDF as a function of radius around the H ii region in a more systematic way by taking the distribution in concentric disks around the bubble. In Fig. 5, we show the four different regions that are considered for the PDFs presented in Fig. 6. The first disk (region 1) contains the ionizing sources and the dense column density structures up to the massive young stellar object south of the ionizing sources. The second disk (region 1+2) extends up to the northern part of the main star-forming region of Rosette (see Schneider et al. 2012a), the third disk (region 1 + 2 + 3) includes this star-forming region, and the fourth disk (region 1 + 2 + 3 + 4) reaches the edge of the map. In Fig. 7, we show the PDF of the region 1 + 2 + 3 and the annular region 4 in order to compare the compressed part that is influenced by an effect localized near the ionizing sources.
 |
Fig. 5 Rosette Herschel column density map (Schneider et al. 2012a). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources, i.e. the most massive OB-stars from the NGC 2244 cluster. The extension of the Hα emission corresponds to region 1 + 2 but there is also a significant FUV radiation up to region 1 + 2 + 3 (see Schneider et al., in prep.). The blue circles indicate the position of the condensations identified in the PDFs of region 1 and of region 1 + 2. |
 |
Fig. 6 Rosette PDFs of the four regions indicated in Fig. 5. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). The black dotted line corresponds to a one-lognormal fit. |
 |
Fig. 7 Left: rosette column density PDFs on region 1 + 2 + 3 and region 4 in Fig. 5. Right: column density PDFs of the simulation of the ionization of a Mach-2 turbulent cloud. The excess at high density is still visible however the two peaks merge to form an enlarged distribution. The simulations are without self-gravity, therefore there are no power-law tails in the simulated PDFs while they are present in the observations. |
The PDF of region 1 + 2 + 3 is not double-peaked as was seen for M 16, and even the one of region 1 alone shows only a slight indication of a double peak, but less clearly than presented in Schneider et al. (2012a). Indeed, in Schneider et al. (2012a), the selection of regions focused explicitly on the interaction zone (only a small part of our region 1) and thus revealed the double peak. Taking a larger area adds more pixels that are not directly affected by the ionization front (towards the southwest in our region 1) and thus dilutes the double peak. For comparison we also show in Fig. 7 the PDFs of a simulated Mach-2 turbulent cloud exposed to ionization (Tremblin et al. 2012b). The PDF presents a similar shape where the two peaks merge to form an enlarged distribution. One could argue that these enlarged distributions can be fitted properly by a single lognormal component. We show in Fig. 6 such a fit and the corresponding parameters are given in Table 4 while the parameters of the two-lognormal fit are given in Table 3. The reduced χ2 values for both fits are computed assuming a Poisson noise in each bin. The corresponding error bars are plotted in Fig. 6, but the pixel statistic is so high that the error bars are small and barely visible in log-space. Such small error bars explain the large values of the χ2 for both fits. This means that these regions have complex structures and physics that are not well represented by the fitting models. We performed a F-test to check that the two-lognormal fit provides a significant improvement (see Bevington & Robinson 2003).
The F values for the different regions are respectively 3.3, 2.6, 6.8, and 15, and the critical value is 3 for a false-rejection probability of 5%. Therefore, the two-lognormal model gives a significantly better fit to the data, especially in regions 1 + 2 + 3 and 1 + 2 + 3 + 4. In all regions, there is an excess of compressed gas compared to the PDF in the annular region 4. The integral of the compressed component p1 in Table 3 decreases from 0.04 to 0.01 when the radius of the region increases. This behavior is expected: when the radius of the region increases, more and more unperturbed gas is added in the distribution while the compressed gas remains the same. Therefore the relative importance of the compressed gas decreases.
When this excess is taken into account by a second lognormal component in the fits in Fig. 6, a power-law deviation from the two-lognormal distribution is still visible and indicates the possible influence of gravity but at higher column densities. It is especially clear in regions 1 and 1 + 2 that the power-law deviation is occurring around η ≈ 1.5, indicating the regime in which gravity starts to dominate. Assuming an equivalent spherical density distribution (ρ ∝ r− α), a transition from an exponent α of 2.38±0.10 in regions 1 and 1 + 2 to a value of 1.62±0.08 in region 1 + 2 + 3 + 4 is derived from the power-law fits. This transition indicates that the ionization can even have an influence on the gravity-dominated regions that are in the PDR. Assuming spherical symmetry on a large scale (regions 1+2+3 and 1+2+3+4) is a very crude approximation in these complex regions and a detailed analysis taking the Mach numbers into account is needed to study the interplay between other different processes. In regions 1 and 1+2, the pixels that have a column density with η higher than 1.5 correspond to two nearly spherical dense condensations in the Monoceros Ridge and in dense southern region at the edge of the cavity (Fig. 5), which were already identified as regions of gas compression at the cloud-nebula interface (Román-Zúñiga & Lada 2008). As in M 16, these α values have to be taken with caution since they mix different structures. Nevertheless, the high alpha value observed in regions close to the ionizing sources has already been seen in other regions such as the central, dense, high-mass star-forming ridge in the cloud NGC 6334 (Russeil et al. 2013) and more recently in Palau et al. (2014) for the massive dense cores DR21-OH, AFGL 5142 and CB3. The transition from high values to low values typical of other clouds seems to indicate that the compression from ionization is also playing a role at high column densities where structures are expected to be gravitationally collapsing.
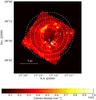 |
Fig. 8 RCW 120 Herschel column density map (Anderson et al. 2012). The circles indicate the different regions used for the PDFs. The white cross indicates the position of the main ionizing source (O8 star). The extension of the Hα emission and the limit of the H ii region is inside region 1. The blue circle indicates the position of the possible compressed core collapse identified in the PDFs. |
4. RCW 120
RCW 120 (Fig. 8) is an H ii region (see Rodgers et al. 1960; Zavagno et al. 2007) located at a distance of 1.3 kpc from the Sun that has been well studied by Spitzer (Deharveng et al. 2009) and Herschel (Zavagno et al. 2010; Anderson et al. 2010). Its circular shape led to its nickname as “the perfect bubble” (Deharveng et al. 2009), although the ionizing source, an O8 star (Martins et al. 2010), is not in the center of the ionized sphere. Since the ionizing source is very close to the southern part of the bubble, it is probable that the expansion is asymmetric. The molecular gas is denser in the south than in the north of the bubble, as indicated by the column density (see Fig. 8). Because of the asymmetry, the 1D model of collect and collapse is difficult to apply in the form presented in Elmegreen & Lada (1977). Among other regions, the dust properties of RCW 120 have recently been analyzed by Anderson et al. (2012) using Herschel observations. These authors find that the mass of the material in the PDR is compatible with the expected mass swept up during the expansion of the H ii region and that the FIR emission suggests that the bubble is a three-dimensional structure. We used the column density map derived by Anderson et al. (2012). We point out that the column density map of RCW 120 is done by a fit in linear space rather than log space (as for the other Herschel maps). However, we do not expect this inconsistency to influence our results.
 |
Fig. 9 RCW 120 PDFs of the four regions indicated in Fig. 8. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
In Fig. 8, we show the four different regions that are considered for the PDFs presented in Fig. 9. The parameters of the fits are listed in Table 5. The PDFs are well fit by a two-component lognormal, and the excess in the compressed component is clearly visible in regions 1 + 2 + 3 and 1 + 2 + 3 + 4. At high column densities, it is possible to identify the dense clump formed southwest of the ionizing source in the dense part of the PDF (Fig. 8). This clump is not part of the compressed component, and the PDF is well fit by a power law suggesting the role of gravity. In region 1, the power-law fit leads to an exponent α of 2.56±0.17 that may indicate the role of ionization compression in the formation of this condensation and its collapse to form stars. The radial profile of the condensation has an exponent α of 2.39±0.01, which is in good agreement with the value deduced from the PDF. If the gravitational collapse had happened before, we would expect the exponent to be close to 2 and to be only marginally affected by the ionization since the ionizing front did not overwhelm the condensation. Indeed, the numerical study in Minier et al. (2013) in the case of RCW 36 showed that the collapse of a condensation that is located in the shell is likely to be triggered. If the condensation had gravitationally collapsed prior to the passage of the ionization front, the condensation would already be dense enough to resist the ionization front expansion. It would, for example, trigger the formation of a pillar rather than a condensation remaining in the shell. Furthermore a statistical argument based on the study of Thompson et al. (2012) also suggests that the dense condensation is linked to the H ii region. Based on the numerical study of Minier et al. (2013), the triggering can be confirmed by comparing the velocities of the condensation and the nearby shell. If the velocities are the same, the formation of the condensation is dynamically linked to the shell and likely to be triggered.
The amplitude of the compressed lognormal decreases when the radius of the region increases (see Table 6). This is consistent with the picture we got from Rosette and M 16: the larger the region, the less important the peak, because more and more unperturbed gas is added to the distribution. However, the decrease in the amplitude of the compressed peak is more important in the case of RCW 120 (from 0.014 to 0.003). This can be explained by the H ii region occupying a smaller part of the image than the large ionized bubbles in the Eagle and Rosette nebula. The compression factor of the column density is typically on the order of 2 (given by exp(η1 − η0)). That is rather low compared to the factor 20−30 expected from the 1D simulations of Zavagno et al. (2007). However the difference could be a projection effect. Considering the size of the bubble, which has a radius of 1.8 pc, we can assume that the thickness along the LOS of the compressed layer is on the order of 1 pc. The cloud is at a column density of 1023 cm-2 and corresponds to a density of 3 × 103 cm-3 integrated over a LOS of 10 pc. The compressed layer has a column density of around 2 × 1023 cm-2, which corresponds to a density of 6 × 104 cm-3 integrated over 1 pc. We can therefore get a compression of ≈20 if the LOS thickness of the shell is ten times smaller than the thickness of the cloud. Therefore a factor of compression of 20−30 in density can result in a factor of compression of 2 in column density.
5. Vela C/RCW 36
At a distance of 700 pc from the Sun (Murphy & May 1991), RCW 36 has the shape of an hourglass. At the center, an embedded cluster, 2−3 Myr old, has 350 members with the most massive star being a type O8 or O9 (Baba et al. 2004). The cluster extends over a radius of 0.5 pc, with a stellar surface number density of 3000 stars pc-2 within the central 0.1 pc. FIR emission and radio continuum emission are reported to be consistent with the presence of an H ii region (Verma et al. 1994). The star cluster has probably inflated the G265.151+1.454 H ii region (Caswell & Haynes 1987) that is responsible for the Hα emission originally observed by Rodgers et al. (1960). Looking at larger scales, RCW 36 is located within the Vela C molecular cloud that consists of an apparent network of column density filaments (Hill et al. 2011). Such filaments are star formation sites. Herschel observations of low-mass star-forming molecular clouds (e.g., Arzoumanian et al. 2011) show that stars form in supercritical filaments, while Schneider et al. (2012a) propose that star-cluster formation sites correlate with filament network junctions. Among the networks of filaments in Vela C, there is a more prominent and elongated interstellar dust structure of ≈10 pc in length that is named the center-ridge by Hill et al. (2011). It encompasses RCW 36, which is at its southern end, a bipolar nebula surrounded by a dense ring of gas in the plane of the center-ridge (Minier et al. 2013).
 |
Fig. 10 RCW 36 Herschel column density map (Minier et al. 2013). The circles indicate the different regions used for the PDFs. The white cross indicates the position of the main ionizing source. The limit of the Hα emission and the limit of the H ii region are inside region 1. The blue circles indicate the positions of the condensations identified in the PDF of region 1. |
 |
Fig. 11 RCW 36 PDFs on the four regions indicated in Fig. 10. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
Figure 10 shows the Herschel column density map of RCW 36 inside the Vela C molecular cloud with the different regions for which we determined the PDFs (Fig. 11 and Table 6). The first region corresponds to the extension of the ionized gas. The PDF presents two components; however, unlike the other regions, the amplitude of the compressed peak does not decrease with increasing radius. In region 1, the high-density component consists of the dense ring close to the cluster (Minier et al. 2013), and the low-density one corresponds to the low-density medium that is present on each side of the bipolar nebula. The deviation at high densities (ln(NH2/⟨ NH2 ⟩ ) ≈ 2) corresponds to the dense condensations that are present in the ring and were also discussed in Minier et al. (2013). A power-law tail (although complex) for this range can be identified. Though the pixel statistic is small and the error larger, we tentatively determine a value of α = 2.80 ± 0.23 which is much higher than 2. This high value is also consistent with the filamentary profile measured by Hill et al. (2012a) (α = 2.70 ± 0.2). We checked the radial profiles of the densest and largest condensation and got an averaged fitted value of α = 2.30 ± 0.11. In some direction, the profile has an alpha value of 2.83.
We may have the same situation here as in RCW 120 where the PDF also shows a clear excess for the highest densities due to individual compressed core collapse. This supports the previous study in Minier et al. (2013) showing that, based on the morphology of the regions, the gravitational collapse of these condensations (Fig. 10) was likely to be triggered This is also confirmed by the recent age determination of the different stellar populations done by Ellerbroek et al. (2013). Furthermore, the exponent α decreases to a value of 1.54 ± 0.02 in region 1+2+3+4. The region is so large that the dense small clumps contribute to the probability distribution at less than 10-4 and therefore are not visible in the PDFs anymore. The dense compressed power-law tail is therefore only present in region 1 and probably linked to the ionization. In previous large-scale studies, such as of the Vela C cloud (Hill et al. 2011), Rosette (Schneider et al. 2012), and NGC 6334 (Russeil et al. 2013), it was not possible to distinguish whether the power-law tail arises from the collapse of many cores and/or the global collapse of clumps, filaments, or ridges since both processes play a role. In smaller regions, we are less perturbed by a large amount of bulk gas that constitutes the PDF, so global collapse may play a minor role. However, we emphasize that this finding remains slightly speculative and needs further detailed studies.
In any case, when the radius of the area increases, the low-density component remains the same and the amplitude of the high-density peak increases. This behavior is expected because the influence of the H ii region is limited to region 1, and in the other regions, the high-density component no longer consists of the compressed ring, but is dominated by the south-north elongated molecular cloud. When the radius is high, the area of the compressed ring around the H ii region is very small compared to the rest of the molecular cloud.
6. Discussion and interpretation
6.1. From large-scale to small-scale ionization compression
Based on the two-lognormal fits performed in the different regions, we define a compression parameter as the ratio of the number of pixels in the compressed component to the number of pixels in the low-density component. Figure 12 shows the evolution of this parameter as a function of radius for the four different clouds. For Rosette, M 16, and RCW 120, the compression impact decreases with increasing radius. Therefore, the compressed material is localized close to the ionizing sources and its relative volume decreases when the volume of the studied region increases.
At a first glance, it could be argued that dense gas is present close to ionizing sources
because they were born in a dense environment formed, say, by gravitational collapse or
colliding flows. This first possibility is ruled out by the comparison made in M 16 and
Rosette between the dense column density excess in region 1+2+3 compared to region 4
(Figs. 3 and 7).
This excess does not follow a power law as would be expected from gravitational collapse.
In the second case, it is much more difficult to distinguish dense gas formed from
colliding flows prior to the formation of the ionization sources and ionization
compression that will happen after that. However, the Vela C molecular cloud offers the
possibility to show how the difference can be inferred. For Vela C, the dense gas does not
seem to be related to the ionizing sources as shown by Fig. 12. The ratio of dense gas to low-density gas is relatively constant at 15% in
the whole region. From the column density map, we derive an average density in the Vela C
molecular ridge – assuming a thickness of the ridge of 1 pc – of 104 cm-3, while in the more extended
low-density medium (∼5 pc
thickness), the density is 102 cm-3. The lognormal shape of the high-density component
seen in regions 1 + 2 + 3 and
1 + 2 + 3 + 4 suggests that
the ridge is formed by shock compression rather than gravitational instabilities. The
ridge formation from shock compression caused by colliding flows was proposed in Vela
(Hill et al. 2011) and also, for example, in IRDC
G035.39-00.33 (Nguyen Luong et al. 2011) or W43
(Nguyen Luong et al. 2013). In this case, the
ridge could be the result of converging flows at a density of around 102 cm-3 that collided at a Mach number
∼10 to compress the gas by
two orders of magnitude, assuming isothermal gas. This estimation of the Mach number is
rather close to the Mach number expected for the cold interstellar medium (Tc ≈ 50–100 K
for the cold neutral medium, CNM) formed by the thermal instability inside the warm phase
of the interstellar medium (Tw ≈ 8000 K for the warm neutral medium,
WNM). Since the CNM has a typical velocity that is transonic relative to the sound speed
in the WNM (see Audit & Hennebelle 2010),
the Mach number of the CNM is given by 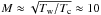 . Therefore it is possible that
the Vela C molecular ridge was formed by colliding flows, whereas the dense gas in the
three other regions M 16, Rosette and RCW 120 is formed by ionization compression since
its volume is inversely correlated with the distance from the ionizing sources.
. Therefore it is possible that
the Vela C molecular ridge was formed by colliding flows, whereas the dense gas in the
three other regions M 16, Rosette and RCW 120 is formed by ionization compression since
its volume is inversely correlated with the distance from the ionizing sources.
 |
Fig. 12 Radial evolution of the ratio of the number of pixels in the compressed peak to the number of pixel in the low-density peak p1/p0 for the four different clouds. |
On smaller scales, we have seen that in the inner regions with smaller pixel statistics, we can identify power-law tails that correspond to one or two dense condensations that have probably gravitationally collapsed. The PDF around these condensations and their radial profiles indicate α exponents higher than the free-fall value of 2. Therefore they could be examples of compressed core collapse triggered by the ionization compression. Although more studies are needed to confirm these results, this behavior could be the first unambiguous criterion that can define the difference between untriggered (free-fall) and triggered (forced-fall) core collapse around H ii regions. It could also be generalized to any type of external compression (winds, supernovas, etc.) whose source is identified.
6.2. The shape of double-peaked and broadened PDFs
The regions studied here – the Rosette and Eagle molecular clouds, and the RCW 36 and RCW 120 H ii regions – differ significantly in terms of mass (from ∼6 × 103M⊙ for RCW 120 to ∼4 × 105M⊙ for M 16), temperature and incident UV-flux (with a low G◦ cloud like Rosette in contrast to a bright cloud with a high G◦ like M 16), and size (a few pc for the small H ii regions up to ∼20 pc for the Rosette nebula). Nevertheless, they all show the same characteristic double-peaked and/or broadened PDFs. We argued that it is compression caused by the expansion of the ionized gas that causes a double peak in the column density PDF (in the case of the M 16 molecular cloud) or an enlarged distribution when the second peak is close to the first one (in the case of the Rosette molecular cloud and RCW 120). As explained in the previous section, the Vela C molecular cloud presents a dense component probably formed by colliding flows that also broaden the PDF. The difference between this scenario and that of ionization compression can be inferred from the evolution of the compression parameter with increasing radius (see Fig. 12).
For Rosette, M 16, and RCW 120, the compression parameter decreases when the radius of the region on which the PDF is computed increases. This is consistent with a compressed region localized at the edge of the ionized gas. When the radius increases, more and more unperturbed gas is added to the distribution. For more extended regions (Rosette and M 16), the H ii regions are relatively large compared to the molecular cloud, and the effect and the compression is important even on the large scale of the cloud (a few tens of parsecs). In contrast, RCW 120 is relatively small and the compression parameter is quite small compared to the other regions (see Fig. 12).
For these three ionization-compressed regions, we fitted the two-peaked and enlarged
distributions with two lognormals. A simple approach can qualitatively justify the choice
of a lognormal shape for the ionization-compressed component. The first component is
enlarged by the turbulence of the cloud, and its lognormal shape can be qualitatively
understood (see Vázquez-Semadeni 1994; Kevlahan & Pudritz 2009). If a region of
density ρ0 is compressed by a shock of Mach number
M1, the new density is then
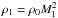 . When a second
shock compresses the region, the new density is
. When a second
shock compresses the region, the new density is 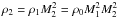 , and so on. This
process is additive with respect to ln(ρ), and if it is repetitive and random, we can
expect that the logarithm of the density is a Gaussian thanks to the central limit
theorem. The density should thus be lognormal, see also Federrath et al. (2010). There are some limits to this analysis (e.g., multiple
compressive forces, see Hennebelle & Falgarone
2012), but it is a straightforward way to understand the shape of the density
distribution.
, and so on. This
process is additive with respect to ln(ρ), and if it is repetitive and random, we can
expect that the logarithm of the density is a Gaussian thanks to the central limit
theorem. The density should thus be lognormal, see also Federrath et al. (2010). There are some limits to this analysis (e.g., multiple
compressive forces, see Hennebelle & Falgarone
2012), but it is a straightforward way to understand the shape of the density
distribution.
The same idea can be used to understand the shape of the double-peak distribution for the
surroundings of an H ii region. As explained in Tremblin et al. (2012b), there are two situations to consider, either the
ionized-gas pressure is much greater than the ram pressure of turbulence, or turbulence
dominates. In both cases, the Mach number of the shock driven by the H ii region
is approximated well by 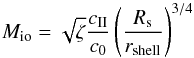 (4)where
cII and c0 are the sound
speed in the ionized and shocked region respectively, Rs is the
initial Strömgren radius (computed for the initial averaged density around the ionizing
source), rshell the radius of the H ii
region at the time considered, and ζ a parameter that is equal to two for a D-critical
front (Kahn 1954) and one for a weakly D-type front
(see Minier et al. 2013, for the detailed
calculation). At the beginning of the development of the H ii region, the
ionizing front is D-critical and rshell = Rs.
Therefore the Mach number is on the order of 40. Such a high level of turbulence is not
observed in molecular clouds, so there is always a period of time for which
Mio ≫
Mi where Mi are the Mach
numbers of the turbulent shocks in the molecular cloud. When the shock driven by the
ionized gas passes, the gas is compressed and the log-density increases by
(4)where
cII and c0 are the sound
speed in the ionized and shocked region respectively, Rs is the
initial Strömgren radius (computed for the initial averaged density around the ionizing
source), rshell the radius of the H ii
region at the time considered, and ζ a parameter that is equal to two for a D-critical
front (Kahn 1954) and one for a weakly D-type front
(see Minier et al. 2013, for the detailed
calculation). At the beginning of the development of the H ii region, the
ionizing front is D-critical and rshell = Rs.
Therefore the Mach number is on the order of 40. Such a high level of turbulence is not
observed in molecular clouds, so there is always a period of time for which
Mio ≫
Mi where Mi are the Mach
numbers of the turbulent shocks in the molecular cloud. When the shock driven by the
ionized gas passes, the gas is compressed and the log-density increases by
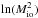 . In an initial turbulent
medium, the same analysis as Kevlahan & Pudritz
(2009) can be applied to
. In an initial turbulent
medium, the same analysis as Kevlahan & Pudritz
(2009) can be applied to 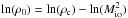 . Thanks to the central
limit theorem, ln(ρ0) is a Gaussian and ln(ρc) is a
Gaussian shifted by a compression factor
. Thanks to the central
limit theorem, ln(ρ0) is a Gaussian and ln(ρc) is a
Gaussian shifted by a compression factor 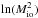 . Therefore, if enough material
is accumulated in the shell, two lognormal peaks appear in the PDF. When the turbulence is
high compared to the ionized-gas pressure, Mio ≈ Mi and
the term added to the log-density appears as one shock among others in the turbulent
medium. Therefore with the central limit theorem, the distribution of the log-density will
be unchanged by the ionization-driven shock. This is exactly what was observed in the
simulation of Tremblin et al. (2012b), the
lognormal double-peaked PDF appears when the ionized-gas pressure is high relative to the
turbulent ram pressure and at high turbulent level, the PDF is rather unchanged by the
ionization. This also explains why in some clouds, no second peak is observed but only
broadening by compression. A recent study of the Orion B molecular cloud (Schneider et al. 2013) has shown that the PDF has a
lognormal shape with a power-law tail but is a factor 1.5 broader than the one of a
similar region (Aquila) that has the same Mach number. The difference is that Orion B is
exposed to a large-scale compression from a nearby OB-cluster (also seen in asymmetric
column density profiles), while Aquila only contains a small internal H ii
region. Another example is the Auriga-California cloud (Harvey et al. 2013) that shows a double-peak in the PDF. But this cloud is a
low-mass star-forming region with only a B-star as ionizing source, so the total impact of
the ionization front is less than for a cloud that is impacted by a whole OB-cluster.
However – as outlined above – it is not the total energy contained in the
shock expansion that decides whether a compressed layer is formed and visible in the PDF,
but the interplay between ionized-gas pressure and turbulent ram pressure. We thus do not
expect a double-peaked PDF for all clouds associated with OB-clusters.
. Therefore, if enough material
is accumulated in the shell, two lognormal peaks appear in the PDF. When the turbulence is
high compared to the ionized-gas pressure, Mio ≈ Mi and
the term added to the log-density appears as one shock among others in the turbulent
medium. Therefore with the central limit theorem, the distribution of the log-density will
be unchanged by the ionization-driven shock. This is exactly what was observed in the
simulation of Tremblin et al. (2012b), the
lognormal double-peaked PDF appears when the ionized-gas pressure is high relative to the
turbulent ram pressure and at high turbulent level, the PDF is rather unchanged by the
ionization. This also explains why in some clouds, no second peak is observed but only
broadening by compression. A recent study of the Orion B molecular cloud (Schneider et al. 2013) has shown that the PDF has a
lognormal shape with a power-law tail but is a factor 1.5 broader than the one of a
similar region (Aquila) that has the same Mach number. The difference is that Orion B is
exposed to a large-scale compression from a nearby OB-cluster (also seen in asymmetric
column density profiles), while Aquila only contains a small internal H ii
region. Another example is the Auriga-California cloud (Harvey et al. 2013) that shows a double-peak in the PDF. But this cloud is a
low-mass star-forming region with only a B-star as ionizing source, so the total impact of
the ionization front is less than for a cloud that is impacted by a whole OB-cluster.
However – as outlined above – it is not the total energy contained in the
shock expansion that decides whether a compressed layer is formed and visible in the PDF,
but the interplay between ionized-gas pressure and turbulent ram pressure. We thus do not
expect a double-peaked PDF for all clouds associated with OB-clusters.
On the other hand, a second break in the PDF power law can be observed in some clouds and linked to the feedback (e.g., W3, Rivera-Ingraham et al., in prep.). These two breaks could mean that the PDFs can be fitted by a lognormal for the turbulent cloud, a first power law for the feedback compression, and a second power law for the influence of gravity. As mentioned in Sect. 2, the inner region in M 16 could also be well fit by such a model. Although our approach here is slightly different, we think that both methods are complementary. In the inner region, the scales are smaller and the compressed shell should be rather homogeneous. In this case, the statistic may not be sufficient to get a proper sampling of the turbulent compressed peak that is seen in the turbulent-ionized simulations. Therefore the column-density PDF of an homogeneous compressed shell could lead to a flat power law for the compressed component in column density, and the gravity to a power law with a steeper slope, hence a two-step power law. On a larger scale, a sufficiently large range of turbulent motions will be taken into account and a better statistic will lead to a compressed lognormal component as seen in the turbulent-ionized simulations. Thus, depending on the scale or turbulent state of the region, the compressed component may be approximated well by a power law or a lognormal. In both cases, the compression by ionization does have an impact and leads to a broadened PDF.
6.3. Possible consequences of external compression for the IMF
Recently, Hennebelle & Chabrier (2008, 2009, 2013) have proposed an analytical theory to derive the core/initial mass function (CMF/IMF) from the PDF of a gravo-turbulent molecular cloud. The central idea is that the shape of the IMF can be computed from any kind of PDF, assuming that the global properties of the cloud are the determinant factor to set the final IMF. Therefore the typical shape of the Chabrier IMF (lognormal at low mass and a Salpeter power law at high mass, see Chabrier 2003) could be determined from the global properties of the gravo-turbulent cloud by computing the gas volumes dense enough to collapse gravitationally. One direct implication of the present work is that the ionization compression affects the PDF around the ionized gas and consequently could also affect the CMF/IMF.
The H ii regions are present in a vast number of molecular clouds, even in low-mass star-forming regions: e.g., the Cocoon nebula in IC 5146 (Arzoumanian et al. 2011) and W40 in Aquila (Bontemps et al. 2010; Könyves et al. 2010). This type of feedback of high-mass stars is also thought to be one of the most important processes that disperse molecular clouds in our Galaxy (see Whitworth 1979; Matzner 2002). Considering the typical lifetime of molecular clouds (≈10 Myr) and the typical time of the development of H ii regions (≈1 Myr), the clouds should spend a large portion of their lifetime in a state where the ionized gas is present and compresses the cold gas to form a double-peaked or enlarged PDF (if the conditions outlined in Sect. 6.2 are fulfilled). It is therefore unlikely that the dispersion of the molecular gas by ionization is rapid enough to safely ignore its impact on the PDF of the gas that will form stars. It is also unlikely that other feedback processes, such as radiation pressure and stellar winds, are rapid enough to ignore the compression phase that will disperse the gas to get a gas-free cluster with a given IMF.
Multiple H ii regions may interact, but it is rather unlikely that the molecular clouds presented here would produce enough distinct H ii regions to restore a lognormal shape with the statistical argument of Kevlahan & Pudritz (2009). In all observations presented here, only one or two H ii regions are present in the cloud; however, it is sufficient to enlarge the PDF with a rather small initial Mach number for the cloud. For example, the width of the PDF of the ionized Mach-1 simulation in Tremblin et al. (2012b) is equivalent to the width of the Mach-4 simulation. Therefore we propose that the feedback processes, such as the ionization, could account for the relatively large PDFs that are needed in Hennebelle & Chabrier (2008) to have good agreement with the computed and observed IMF. Typically compressed gas could help form compressed dense and massive cores as seen in Rosette, RCW 120, and RCW 36 in the present study but also small and dense cores leading to the formation of brown dwarfs (see Padoan & Nordlund 2004). However high-resolution on large scales is needed to be able to have a full statistic of the cores around H ii regions. Since other processes could also enlarge the PDF (e.g., the equation of state and variations among the core properties, see Hennebelle & Chabrier 2009; Chabrier & Hennebelle 2010), the relative importance of the physical phenomena leading to these large PDF in molecular clouds remains a relatively open question although the present work observationally supports the role of ionization.
6.4. Pre-existing versus triggered dense structures
A number of recent Herschel studies showed the importance of gas accretion by filaments, both for low-mass (e.g., Arzoumanian et al. 2011; Peretto et al. 2012; Palmeirim et al. 2013) and high-mass (e.g., Schneider et al. 2012a; Hennemann et al. 2012; Nguyen Luong et al. 2013) star-forming regions, consistent with the accretion-driven turbulence scenario (Klessen & Hennebelle 2010). Filaments may form as a result of the dissipation of large-scale turbulence (Elmegreen & Scalo 2004; Federrath 2013) or by gravity (Bonnell et al. 2008). Because prestellar cores are found inside dense self-gravitating filaments (e.g., André et al. 2010), the general view is that the accumulation of matter leads to the formation of self-gravitating cores by gravitational fragmentation. These results suggest that the CMF from the filamentary structures resembles the stellar IMF which is consistent with the gravo-turbulent scenario (see Motte et al. 1998; André et al. 2010). However, because pre-stellar cores are primarily found inside dense self-gravitating filaments, the Herschel results on nearby clouds suggest that the peak of the pre-stellar CMF may result from the pure gravitational fragmentation of filaments, independently of the cloud PDF (see André et al. 2010, 2011). A detailed analysis of the data is therefore needed to fully characterize the CMF/IMF relationship (e.g., environmental effects on the M∗/Mcore conversion) and also to determine precisely the role of the turbulence, gravity, and feedback in the PDF/CMF relationship. In addition to individual core collapse, large-scale gravitational collapse across a length scale of several parsecs probably plays an important role as well, in particular for the formation of high-mass stars. Schneider et al. (2010a) showed that the global collapse of the DR21 filament and mass input by filaments would explain the formation of the proto-OB cluster region DR21(OH). A scenario that was confirmed by Herschel observations (Hennemann et al. 2012) and studies of other regions (e.g. Galván-Madrid et al. 2010; Peretto et al. 2013).
The effect of the ionizing compression on these pre-existing massive filaments and gravitationally-bound clumps could be marginal since these structures are already quite dense. One could expect, for example, that the ionization only erodes the structures and that they keep radial profiles dominated by gravity, i.e., ∝r−α with α between 1.5 and 2. However this effect is still relatively unknown. Furthermore, the relative importance of triggered and pre-existing dense structures is strongly debated. While statistical observations (Thompson et al. 2012) show that massive young stellar objects are mainly found at the edge of H ii regions, numerical studies (Dale et al. 2013) shows that it is very difficult to separate the pre-existing and triggered star formation even at the edge of ionized regions. Observationally, only on the closest regions like RCW 36 in Vela C is a detailed study of the link between compression and the dense clumps possible thanks to velocity information (Minier et al. 2013). In this region it was shown that the dense cores are associated with the dense shell around the ionized gas and were formed by the compression effect caused by ionization before becoming gravitationally unstable. Furthermore, the forced-fall collapses with steep radial profiles confirm this analysis.
Based on this work and the large-scale compression highlighted in the present paper, we postulate that the feedback helps to form denser cores and consequently a possible broader CMF. A systematic comparison of the shape of the CMF between isolated regions and regions influenced by the feedback is needed to confirm this hypothesis. Large-scale mapping at a very high angular resolution will help for computing PDFs with a large pixel statistic. These PDFs and the radial profiles of the cores could be used to distinguish between free-fall and compressed core collapse with the criterion used in the present paper. Since most of the high-mass star-forming regions are located at more than 1000 pc from the solar system, this systematic comparison is beyond reach with the present observatories and could only be done thanks to a high-resolution (typically 1′′ at 100 μm) and to a wide-field submillimeter instrument with high sensitivity.
7. Conclusions and perspectives
With the help of the recent Herschel observations, we analyzed of the column-density structure of four molecular clouds around H ii regions, namely M 16, the Rosette and Vela C molecular cloud, and the RCW 120 H ii region. The compression induced by the expansion of the ionized gas leads to PDFs that are enlarged (as in Rosette, and the RCW 120) or double peaked (as in M 16). The form is determined by the relative importance between the initial turbulence of the molecular cloud and the compression. This result was also predicted by turbulent-ionized numerical simulations. If the PDF of the molecular cloud is lognormal, the peak induced by the compression can be qualitatively understood to also be a lognormal, shifted to higher densities. The difference between a dense lognormal induced by colliding flows and the ionization compression can be made by studying the evolution of the PDFs around the ionizing sources (i.e., Vela C versus other regions in the present paper). In addition to that, a power-law tail can be identified for the highest column density range and can be attributed to the effect of the gravitational force. There are especially good candidates of single core collapse in some of the regions that can be identified thanks to the PDFs and localized by looking at the spatial distribution of the contributing pixels. Furthermore, a criterion based on the power law and the radial profiles can be derived to distinguish between free-fall and compressed core collapse. This criterion could be used to unambiguously tell the difference between triggered and pre-existing star formation (free-fall core collapse with a radial profile ∝r-2 and forced-fall core collapse with a steeper profile). In this paper, the triggering mechanism is the ionization, but this criterion could also be generalized to other types of external compression.
The enlarged PDFs are important since they may lead to an IMF that matches the observations while keeping a relatively low Mach number for the initial cloud. Since ionization is thought to be one of the primary effects for the dispersion of molecular clouds, its compression effect during the lifetime of the cloud could be a key ingredient for explaining the relatively large PDF that are needed by a gravo-turbulent scenario to get a reasonable IMF. A detailed theoretical study of the passage between these ionized-enlarged PDFs to the final IMF has to be done in order to confirm this link. Such a study, in particular, could tell what is the relative importance of the different effects, the compression observed in this paper, the equation of state, or the variations among the core properties. Furthermore, a detailed observational study of the cores around H ii regions and in feedback-isolated regions is needed to complete our understanding of the effect of the compression on the CMF. Since the PDF is observed to be affected by the ionization compression, such a study could also help determine the nature of the link between the PDF and the CMF. A submillimeter space observatory with high sensitivity, wide field, and very high resolution will produce the data needed to fulfill this task.
Acknowledgments
SPIRE was developed by a consortium of institutes led by Cardiff Univ. (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development was supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). Part of this work was supported by the ANR-11-BS56-010 project “STARFICH”.
References
- Allen, L. E.,Burton, M. G.,Ryder, S. D.,Ashley, M. C. B., &Storey, J. W. V. 1999, MNRAS, 304, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L. D.,Zavagno, A.,Rodón, J. A., et al. 2010, A&A, 518, L99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, L. D.,Zavagno, A.,Deharveng, L., et al. 2012, A&A, 542, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Könyves, V., &Arzoumanian, D. 2011, Computational Star Formation, Proc. IAU Symp., 270, 255 [NASA ADS] [Google Scholar]
- Arzoumanian, D.,André, P.,Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Audit, E., &Hennebelle, P. 2010, A&A, 511, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baba, D.,Nagata, T.,Nagayama, T., et al. 2004, ApJ, 614, 818 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F. 1989, ApJ, 346, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences (Boston: McGraw-Hill) [Google Scholar]
- Bisbas, T. G.,Wünsch, R.,Whitworth, A. P.,Hubber, D. A., &Walch, S. 2011, ApJ, 736, 142 [Google Scholar]
- Bohlin, R. C.,Savage, B. D., &Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C.,Santos, J. F. C. J., &Bica, E. 2006, A&A, 445, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnell, I. A.,Clark, P., &Bate, M. R. 2008, MNRAS, 389, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Bontemps, S.,André, P.,Könyves, V., et al. 2010, A&A, 518, L85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caswell, J. L., &Haynes, R. F. 1987, A&A, 171, 261 [NASA ADS] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., &Hennebelle, P. 2010, ApJ, 725, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, P.,Deharveng, L., &Leene, A. 1990, A&A, 230, 181 [NASA ADS] [Google Scholar]
- Dale, J. E., &Bonnell, I. 2011, MNRAS, 414, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E.,Clark, P. C., &Bonnell, I. A. 2007, MNRAS, 377, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E.,Ercolano, B., &Bonnell, I. A. 2013, MNRAS, 431, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L.,Zavagno, A.,Schuller, F., et al. 2009, A&A, 496, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Francesco, J.,Sadavoy, S.,Motte, F., et al. 2010, A&A, 518, L91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellerbroek, L. E.,Bik, A.,Kaper, L., et al. 2013, A&A, 558, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G., &Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., &Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C. 2013, MNRAS, 436, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., &Klessen, R. S. 2012, ApJ, 761, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., &Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C.,Klessen, R. S., &Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flagey, N.,Boulanger, F.,Noriega-Crespo, A., et al. 2011, A&A, 531, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galván-Madrid, R.,Zhang, Q.,Keto, E., et al. 2010, ApJ, 725, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gritschneder, M.,Burkert, A.,Naab, T., &Walch, S. 2010, ApJ, 723, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M.,Fallscheer, C.,Ginsburg, A., et al. 2013, ApJ, 764, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Haworth, T. J., &Harries, T. J. 2011, MNRAS, 420, 562 [Google Scholar]
- Hennebelle, P., &Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., &Chabrier, G. 2009, ApJ, 702, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., &Chabrier, G. 2013, ApJ, 770, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., &Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M.,Motte, F.,Bontemps, S., et al. 2010, A&A, 518, L84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennemann, M.,Motte, F.,Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hester, J. J.,Scowen, P. A.,Sankrit, R., et al. 1996, AJ, 111, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H.,Williams, J. P., &Brunt, C. M. 2006, ApJ, 643, 956 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hill, T.,Motte, F.,Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, T.,André, P.,Arzoumanian, D., et al. 2012a, A&A, 548, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, T.,Motte, F.,Didelon, P., et al. 2012b, A&A, 542, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahn, F. D. 1954, Bull. Astron. Inst. Netherlands, 12, 187 [NASA ADS] [Google Scholar]
- Kevlahan, N., &Pudritz, R. E. 2009, ApJ, 702, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., &Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kritsuk, A. G.,Norman, M. L.,Padoan, P., &Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G.,Norman, M. L., &Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., &Lazareff, B. 1994, A&A, 289, 559 [NASA ADS] [Google Scholar]
- Lombardi, M.,Alves, J., &Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, J., &Lim, A. J. 2010, MNRAS, 403, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F.,Pomarès, M.,Deharveng, L.,Zavagno, A., &Bouret, J. C. 2010, A&A, 510, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matzner, C. D. 2002, ApJ, 566, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Miao, J.,White, G. J.,Nelson, R.,Thompson, M., &Morgan, L. 2006, MNRAS, 369, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Miao, J.,White, G. J.,Thompson, M. A., &Nelson, R. P. 2009, ApJ, 692, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Minier, V.,Tremblin, P.,Hill, T., et al. 2013, A&A, 550, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molina, F. Z.,Glover, S. C. O.,Federrath, C., &Klessen, R. S. 2012, MNRAS, 423, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F.,André, P., &Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Motte, F.,Zavagno, A.,Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Bontemps, S., Hennemann, M., et al. 2012, in SF2A-2012: Proc. of the Annual meeting of the French Society of Astronomy and Astrophysics, ed. S. Boissier, 45 [Google Scholar]
- Murphy, D. C., &May, J. 1991, A&A, 247, 202 [NASA ADS] [Google Scholar]
- Nguyen Luong, Q.,Motte, F.,Hennemann, M., et al. 2011, A&A, 535, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nguyen Luong, Q.,Motte, F.,Carlhoff, P., et al. 2013, ApJ, 775, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., &Nordlund, A. 2004, ApJ, 617, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P.,Nordlund, A., &Jones, B. J. T. 1997, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Palau, A.,Estalella, R.,Girart, J. M., et al. 2014, ApJ, 785, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P.,André, P.,Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Passot, T., &Vázquez-Semadeni, E. 1998, Phys. Rev. E (Statistical Physics), 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N.,André, P.,Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N.,Fuller, G. A.,Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poulton, C. J.,Robitaille, T. P.,Greaves, J. S., et al. 2008, MNRAS, 384, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Pound, M. W. 1998, ApJ, 493, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Ingraham, A.,Martin, P. G.,Polychroni, D., et al. 2013, ApJ, 766, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Roccatagliata, V.,Preibisch, T.,Ratzka, T., &Gaczkowski, B. 2013, A&A, 554, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodgers, A. W.,Campbell, C. T., &Whiteoak, J. B. 1960, MNRAS, 121, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C. G., & Lada, E. A. 2008, in Handbook of Star Forming Regions, Vol. I, 928 [Google Scholar]
- Russeil, D.,Schneider, N.,Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N.,Stutzki, J.,Winnewisser, G., &Block, D. 1998a, A&A, 335, 1049 [NASA ADS] [Google Scholar]
- Schneider, N.,Stutzki, J.,Winnewisser, G.,Poglitsch, A., &Madden, S. 1998b, A&A, 338, 262 [NASA ADS] [Google Scholar]
- Schneider, N.,Csengeri, T.,Bontemps, S., et al. 2010a, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N.,Motte, F.,Bontemps, S., et al. 2010b, A&A, 518, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N.,Csengeri, T.,Hennemann, M., et al. 2012a, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N.,Güsten, R.,Tremblin, P., et al. 2012b, A&A, 542, L18 [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, accepted [Google Scholar]
- Thompson, M. A.,Urquhart, J. S.,Moore, T. J. T., &Morgan, L. K. 2012, MNRAS, 421, 408 [NASA ADS] [Google Scholar]
- Tremblin, P.,Audit, E.,Minier, V., &Schneider, N. 2012a, A&A, 538, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblin, P.,Audit, E.,Minier, V.,Schmidt, W., &Schneider, N. 2012b, A&A, 546, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblin, P.,Minier, V.,Schneider, N., et al. 2013, A&A, 560, A19 [Google Scholar]
- Urquhart, J. S.,White, G. J.,Pilbratt, G. L., &Fridlund, C. V. M. 2003, A&A, 409, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vázquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E.,González, R. F.,Ballesteros-Paredes, J.,Gazol, A., &Kim, J. 2008, MNRAS, 390, 769 [NASA ADS] [Google Scholar]
- Verma, R. P.,Bisht, R. S.,Ghosh, S. K., et al. 1994, A&A, 284, 936 [NASA ADS] [Google Scholar]
- White, G.,Nelson, R. P.,Holland, W. S., et al. 1999, A&A, 342, 233 [NASA ADS] [Google Scholar]
- Whitworth, A. P. 1979, MNRAS, 186, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., &Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Zavagno, A.,Pomarès, M.,Deharveng, L., et al. 2007, A&A, 472, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zavagno, A.,Russeil, D.,Motte, F., et al. 2010, A&A, 518, L81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Concentric PDFs of Rosette with a regular increase in radius
We show in this Appendix the concentric PDFs of Rosette for another choice of radius, regularly spaced between the inner and outer disks.
 |
Fig. A.1 Rosette Herschel column density map (Schneider et al. 2012a). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources, i.e. the most massive OB-stars from the NGC 2244 cluster. The radius of the disks are regularly spaced between the inner and outer disks. |
 |
Fig. A.2 Rosette PDFs of the four regions indicated in Fig. 5. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
The shape of the PDF in region 1 + 2, 1 + 2 + 3, and 1 + 2 + 3 + 4 is relatively similar. They all include the central star-forming region, therefore this region is indeed the important structure that shapes the power-law tail of the three distributions. The compression parameter p1/p0 still decreases from 0.58 in region 1 down to 0.09 in region 1 + 2 + 3 + 4.
All Tables
All Figures
 |
Fig. 1 M 16 Herschel column density map (Hill et al. 2012b). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources. The limit of the Hα emission is inside region 1 + 2 + 3 showing approximately the limit of the H ii region (although the H ii region is not spherical in M 16). The blue circles indicate the position of the dense condensations identified in the power-law tail of the PDF of region 1. |
| In the text | |
 |
Fig. 2 M 16 PDFs on the four regions indicated in Fig. 1. The multicomponent fit (green curve) is done using the sum of two lognormal distributions (red and blue dashed curves, see Eq. (1)) and a power law at high column densities (magenta line, see Eq. (2)). The error bars are computed assuming Poisson noise in each bin of the distribution. |
| In the text | |
 |
Fig. 3 Left: M 16 column density PDFs on region 1 + 2 + 3 and region 4 in Fig. 1. Right: column density PDFs of the simulation of the ionization of a Mach-1 turbulent cloud (without self-gravity). The excess at high-density and the double-peaked distribution can be identified both in observations and numerical simulations. |
| In the text | |
 |
Fig. 4 Top: zoom of the column density map on the western condensation. The magenta crosses indicate the pixels contributing to the power law of the PDF. The red dot is the position of the peak of the column density. The colormap is the color code used to show the orientation of the different profiles (e.g. green is north, yellow is east ...). Bottom: radial profiles of the column density of the western condensation. The color indicates the orientation of the profile. The power-law fits are performed around three different directions: north (180◦) in green, east (270◦) in yellow and south (360◦) in purple. Each fit includes all the points in ±40◦ around the main direction. |
| In the text | |
 |
Fig. 5 Rosette Herschel column density map (Schneider et al. 2012a). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources, i.e. the most massive OB-stars from the NGC 2244 cluster. The extension of the Hα emission corresponds to region 1 + 2 but there is also a significant FUV radiation up to region 1 + 2 + 3 (see Schneider et al., in prep.). The blue circles indicate the position of the condensations identified in the PDFs of region 1 and of region 1 + 2. |
| In the text | |
 |
Fig. 6 Rosette PDFs of the four regions indicated in Fig. 5. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). The black dotted line corresponds to a one-lognormal fit. |
| In the text | |
 |
Fig. 7 Left: rosette column density PDFs on region 1 + 2 + 3 and region 4 in Fig. 5. Right: column density PDFs of the simulation of the ionization of a Mach-2 turbulent cloud. The excess at high density is still visible however the two peaks merge to form an enlarged distribution. The simulations are without self-gravity, therefore there are no power-law tails in the simulated PDFs while they are present in the observations. |
| In the text | |
 |
Fig. 8 RCW 120 Herschel column density map (Anderson et al. 2012). The circles indicate the different regions used for the PDFs. The white cross indicates the position of the main ionizing source (O8 star). The extension of the Hα emission and the limit of the H ii region is inside region 1. The blue circle indicates the position of the possible compressed core collapse identified in the PDFs. |
| In the text | |
 |
Fig. 9 RCW 120 PDFs of the four regions indicated in Fig. 8. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
| In the text | |
 |
Fig. 10 RCW 36 Herschel column density map (Minier et al. 2013). The circles indicate the different regions used for the PDFs. The white cross indicates the position of the main ionizing source. The limit of the Hα emission and the limit of the H ii region are inside region 1. The blue circles indicate the positions of the condensations identified in the PDF of region 1. |
| In the text | |
 |
Fig. 11 RCW 36 PDFs on the four regions indicated in Fig. 10. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
| In the text | |
 |
Fig. 12 Radial evolution of the ratio of the number of pixels in the compressed peak to the number of pixel in the low-density peak p1/p0 for the four different clouds. |
| In the text | |
 |
Fig. A.1 Rosette Herschel column density map (Schneider et al. 2012a). The circles indicate the different regions used for the PDFs. The white crosses indicate the position of the main ionizing sources, i.e. the most massive OB-stars from the NGC 2244 cluster. The radius of the disks are regularly spaced between the inner and outer disks. |
| In the text | |
 |
Fig. A.2 Rosette PDFs of the four regions indicated in Fig. 5. The multicomponent fit is done using lognormal distributions (see Eq. (1)) and a power law at high column densities (see Eq. (2)). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


