| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201323288 | |
| Published online | 14 March 2014 | |
The Gaia-ESO Survey: Kinematic structure in the Gamma Velorum cluster⋆,⋆⋆
1
Astrophysics Group, Keele University,
Keele,
ST5 5BG,
UK
e-mail:
r.d.jeffries@keele.ac.uk
2
Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27,
8093
Zurich,
Switzerland
3
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
4
Dipartimento di Fisica e Astronomia, Sezione Astrofisica,
Università di Catania, via S. Sofia
78, 95123
Catania,
Italy
5
INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento
1, 90134
Palermo,
Italy
6
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5,
50125
Florence,
Italy
7
INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78,
95123
Catania,
Italy
8
Instituto de Astrofísica de Andalucía-CSIC,
Apdo. 3004,
18080
Granada,
Spain
9
Lund Observatory, Department of Astronomy and Theoretical
Physics, Box 43,
221 00
Lund,
Sweden
10
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
11
Laboratoire Lagrange (UMR7293), Université de Nice Sophia
Antipolis, CNRS, Observatoire de la Côte d’Azur, BP 4229, 06304
Nice Cedex 4,
France
Received:
18
December
2013
Accepted:
20
January
2014
Context. A key science goal of the Gaia-ESO survey (GES) at the VLT is to use the kinematics of low-mass stars in young clusters and star forming regions to probe their dynamical histories and how they populate the field as they become unbound. The clustering of low-mass stars around the massive Wolf-Rayet binary system γ2 Velorum was one of the first GES targets.
Aims. We empirically determine the radial velocity precision of GES data, construct a kinematically unbiased sample of cluster members and characterise their dynamical state.
Methods. Targets were selected from colour–magnitude diagrams and intermediate resolution spectroscopy was used to derive radial velocities and assess membership from the strength of the Li i 6708 Å line. The radial velocity distribution was analysed using a maximum likelihood technique that accounts for unresolved binaries.
Results. The GES radial velocity precision is about 0.25 km s-1 and sufficient to resolve velocity structure in the low-mass population around γ2 Vel. The structure is well fitted by two kinematic components with roughly equal numbers of stars; the first has an intrinsic dispersion of 0.34 ± 0.16 km s-1, consistent with virial equilibrium. The second has a broader dispersion of 1.60 ± 0.37 km s-1 and is offset from the first by ≃2 km s-1. The first population is older by 1–2 Myr based on a greater level of Li depletion seen among its M-type stars and is probably more centrally concentrated around γ2 Vel.
Conclusions. We consider several formation scenarios, concluding that the two kinematic components are a bound remnant of the original, denser cluster that formed γ2 Vel, and a dispersed population from the wider Vela OB2 association, of which γ2 Vel is the most massive member. The apparent youth of γ2 Vel compared to the older (≥10 Myr) low-mass population surrounding it suggests a scenario in which the massive binary formed in a clustered environment after the formation of the bulk of the low-mass stars.
Key words: stars: pre-main sequence / stars: kinematics and dynamics / open clusters and associations: individual: gamma2 Velorum / stars: formation
Based on observations collected with the FLAMES spectrograph at VLT/UT2 telescope (Paranal Observatory, ESO, Chile), for the Gaia- ESO Large Public Survey (188.B-3002).
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/563/A94
© ESO, 2014
1. Introduction
The Gaia-ESO survey (GES) is employing the FLAMES multi-object spectrograph (Pasquini et al. 2002) on the VLT UT-2 (Kueyen) telescope to obtain high quality, uniformly calibrated spectroscopy of >105 stars in the Milky Way (Gilmore et al. 2012; Randich & Gilmore 2013). The survey covers stars in the halo, bulge, thick and thin discs, as well as in star forming regions and clusters of all ages. Samples are chosen from photometric surveys with the overarching aim of characterizing the chemical and kinematic evolution of these populations. The survey will provide a rich dataset which, when combined with proper motions and parallaxes from the forthcoming Gaia mission (Perryman et al. 2001), will simultaneously yield 3D spatial distributions, 3D kinematics, chemical abundances and astrophysical parameters for large numbers of representative stars.
One of the key science drivers of the survey is probing the formation and subsequent dissolution of young clusters and associations using the kinematics of their constituent low-mass stars. It is often claimed that most stars form in clusters, but a comparison of the observed number of clusters embedded in their natal gas with older, gas-free open clusters suggests that 90 per cent of clusters must either start in an unbound state or become unbound during this transition (Carpenter 2000; Lada & Lada 2003). The heating and subsequent expulsion of gas by ionising radiation, winds or supernovae in clusters containing high-mass stars, but with relatively low star forming efficiency, is likely to unbind a significant fraction of their stars and possibly disrupt the whole cluster (Tutukov 1978; Hills 1980; Goodwin & Bastian 2006; Baumgardt & Kroupa 2007; Bastian 2011). OB associations have a similar stellar content to young clusters but are of much lower density and may be the unbound remnants or halos of clusters after the gas expulsion phase (Kroupa et al. 2001; Clark et al. 2005). Alternatively, it is possible that the importance of clustered star formation has been overestimated and that stars are formed hierarchically in environments with a wide range of initial densities; bound clusters are formed from the densest regions whilst associations formed at low densities and were possibly never bound to begin with (e.g. Bressert et al. 2010; Bonnell et al. 2011; Kruijssen et al. 2012).
The key to understanding the past and future evolution of clusters and associations lies in careful measurements of the positions and velocities of their constituent stars. Gaia will ultimately yield very precise tangential motions, but observations of radial velocities (RVs) and RV distributions in cluster and association populations can be used to assess membership, probe the current dynamical state, search for and parametrise binary populations, and investigate spatially coherent velocity gradients or substructure that might give clues to the initial conditions or reveal multiple populations (e.g. Jeffries et al. 2006; Fűrész et al. 2006, 2008; Briceño et al. 2007; Sacco et al. 2008; Maxted et al. 2008; Tobin et al. 2009; Cottaar et al. 2012a).
The GES began on 31 December 2011 and will be completed over the course of ≃5 years. Many important results regarding the
issues discussed above will emerge from a homogeneous analysis of the ≃30 young (<1 Gyr) clusters that
will eventually be targeted, but significant progress can be made before then because the
data for individual clusters are usually collected in one observing season, and these
datasets can serve to refine and test analysis techniques. The first “cluster” target was
the collection of young, low-mass stars around the massive WC8/O8III binary system,
γ2
Velorum (HD 68273, WR11; Smith 1968; Schaerer et al.
1997). This binary, with a 78.5-day period and
eccentricity of 0.33 (North et al. 2007), is the most
massive member of the common proper motion Vela OB2 association, consisting of 93 early-type
candidate members spread over 100 square degrees (de Zeeuw et al. 1999). The Wolf-Rayet and O-star components have current masses of
9 M⊙ + 30 M⊙
(de Marco & Schmutz 1999), but initial masses
of about 35 M⊙ + 31.5 M⊙
(Eldridge 2009). A further common proper motion
component of the system, γ1 Vel (HD 68243), is separated by 41
arcsecs to the south-west and is itself a multiple system containing a close SB1 binary with
a B2III primary (Hernández & Sahade 1980) and
a tertiary at 0.037 arcsecs that is 1.8 mag fainter (Tokovinin et al. 2010). A surrounding association of low-mass pre-main-sequence (PMS)
stars was first identified by Pozzo et al. (2000) by
virtue of their strong X-ray emission. A consideration of the colour-magnitude diagram of
the X-ray sources and their concentration around γ2 Vel, led Pozzo et al. to conclude that
the PMS stars were coeval with the massive binary at an age of ~4 Myr, and at a distance of 350–400 pc. This
distance is approximately consistent with the revised Hipparcos parallax-based
distance to γ2 Vel of
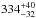 pc
(van Leeuwen 2007) and with interferometric
determinations of
pc
(van Leeuwen 2007) and with interferometric
determinations of 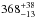 pc
and
pc
and 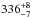 pc
by Millour et al. (2007) and North et al. (2007) respectively.
pc
by Millour et al. (2007) and North et al. (2007) respectively.
Jeffries et al. (2009, hereafter J09) made a further study of the relationship between γ2 Vel, Vela OB2 and the X-ray-active PMS stars using a 0.9 square degree BVI photometric survey centred on γ2 Vel, supported by XMM-Newton X-ray observations and some fibre spectroscopy of solar-type candidate association members. They confirmed that the PMS stars are strong X-ray emitters and are spatially concentrated around γ2 Vel. The PMS stars also have proper motions and RVs consistent with γ2 Vel and Vela OB2, and main-sequence fitting to stars in the wider Vela OB2 association gives a distance that coincides with the distance to γ2 Vel and the main-sequence fitting distance to the early-type stars immediately surrounding it. Using PMS isochrones and a handful of observations of lithium in K-type kinematic members, J09 claimed an age of 5–10 Myr for the low-mass PMS stars. A Spitzer survey for circumstellar material around the low-mass association members reported by Hernández et al. (2008) revealed a very low disc frequency that may be consistent with this age estimate given the short disc half-life of ≃3 Myr found from Spitzer observations of many other young clusters. On the basis of a 3–4 Myr age estimate for γ2 Vel made by de Marco & Schmutz (1999) and North et al. (2007), J09 suggested a cluster formation scenario in which the massive binary formed last, heating and evaporating the remaining gas, unbinding the cluster and terminating star formation – a scenario similar to the gas expulsion model for the unbinding and expansion of OB associations (e.g. Lada & Lada 2003; Goodwin & Bastian 2006). However, Eldridge (2009) updated the age of γ2 Vel to 5.5 ± 1 Myr using models that take account of rotation and previous mass transfer between its binary components, weakening the evidence that it is younger than the surrounding low-mass stars.
The RVs obtained by J09 had comparatively low precision and could not resolve the association kinematics. The observed RV dispersion of 2.5 km s-1 was interpreted as mostly due to measurement uncertainties. Any intrinsic RV dispersion would be unable to explain the presence of stars over the full 10 degree diameter of Vela OB2 if they were intially in a much more compact configuration. Instead it was proposed that γ2 Vel and its surrounding low-mass siblings are a subcluster within a larger star forming region responsible for Vela OB2.
In this paper we present initial results from GES for the Gamma Vel cluster, focused on the kinematics of its low-mass members. In Sect. 2 we describe the spectroscopic observations and the measurement of RVs. Included in this is an empirical estimate of the RV precision obtained by GES. In Sect. 3 we describe how we select a kinematically unbiased sample of cluster members and in Sect. 4 we present an analysis of the RV and spatial distribution of these members. In Sect. 5 we discuss our results in the context of the formation and evolution of the Gamma Vel cluster and its relationship with Vela OB2.
2. Gaia-ESO survey spectroscopy
2.1. Target selection and observations
 |
Fig. 1 Colour–magnitude diagram for unflagged objects with good photometry (uncertainties <0.1 mag in V and V − I) in a 0.9 deg2 area around γ2 Vel (from Jeffries et al. 2009). Objects with larger red symbols were observed in the GES. The lines shows theoretical 10 Myr PMS isochrones (from Siess et al. 2000; and Baraffe et al. 1998, using a colour–Teff relation tuned to match the Pleiades) at an intrinsic distance modulus of 7.76, and with a reddening and extinction of E(V − I) = 0.055 and AV = 0.131. |
The GES strategy for target selection within clusters is described in detail by Bragaglia et al. (in prep.). Low-mass targets in the direction of the Gamma Vel cluster were chosen primarily by their location in the V − I/V and B − V/V colour–magnitude diagrams (CMDs) using the 0.9 deg2 photometric survey of J09. Targets with 12 < V < 19 mag, corresponding to a mass range of 1.5 > M/M⊙ > 0.2 (based on an intrinsic distance modulus of 7.76 ± 0.07, E(B − V) = 0.038 ± 0.016, AV = 0.131 from J09, an assumed age of 10 Myr and the evolutionary models of Siess et al. 2000), were selected from the region of the CMDs surrounding the known spectroscopic and X-ray selected members in J09. A very wide surrounding margin was considered to ensure that selection is not biased by these properties. The V − I/V CMD of all stars is shown in Fig. 1, with the objects actually observed (see below) indicated.
The targets were observed with the FLAMES fibre-fed spectrographs at the VLT UT-2 (Kueyen) on the nights of 31 December 2011, 01-02 January 2012, and 14 February 2012. Both the UVES high-resolution and GIRAFFE intermediate-resolution spectrographs were used. More than 90 per cent of the spectra were obtained with GIRAFFE and we deal only with these data here. GIRAFFE was used in conjunction with the Medusa fibre system and the HR15n order-sorting filter, which gave spectra with a resolving power of 17 000 covering a common wavelength range of 6444–6816 Å.
A log of the VLT/Flames observations.
Targets were grouped according to their V magnitude and configured for multi-fibre spectroscopy in 18 fields that covered the area of the photometric survey with significant overlap between fields. Depending on target brightness, these fields were observed in “observation blocks” (OBs) of 2 × 600 s or 2 × 1500 s. The two exposures were interleaved with a 60 s exposure in which 5 dedicated fibres were illuminated by a bright (compared with the stellar spectra) thorium-argon (ThAr) lamp. These short exposures, known as “simcal” observations, combined with much longer day-time ThAr lamp exposures that illuminated all the instrument fibres, formed the basis of a precise wavelength calibration. Approximately 20 fibres in each configuration were placed on blank sky regions and used during the analysis to subtract the sky contribution from each target spectrum. The times of observation, central positions, exposure times and number of targets for each OB are listed in Table 1.
A total of 1802 observations of 1242 unique targets were obtained. The overlap between fields meant that 353 targets were observed twice, 59 were observed 3 times, 23 were observed 4 times and 4 objects were observed on 6 occasions. These multiple observations were used to empirically judge the precision of the RV measurements. The survey covered 85 per cent of possible targets selected from the photometric survey; the majority of the unobserved targets have 12 < V < 16 mag.
2.2. Data reduction
Full details of the GES GIRAFFE data reduction will be given in a forthcoming paper (Lewis et al., in prep.). In brief, the raw data frames were corrected for a bias level using zero exposure bias frames and the images were divided by normalised daytime tungsten lamp exposures to remove pixel-to-pixel sensitivity variations. The multiple spectra on each frame were also traced using the tungsten lamp exposures and then extracted using the optimal algorithm described by Horne (1986). This algorithm also yields the estimated signal-to-noise ratio (S/N) in the extracted spectral pixels, given the readout noise and gain of the CCD, and it is this estimate that is propagated through subsequent analysis steps leading to the final reported S/N of the spectra. The extracted tungsten lamp spectra were used to correct the overall shape of the spectrum and calibrate the individual transmission efficiencies of each fibre.
The wavelength calibration proceeded in two stages. Deep exposures of a daytime ThAr arc lamp were used to define a polynomial relationship between extracted spectral pixel and wavelength, which typically returned an rms difference from the fit of 0.005 Å for about 20 lines used in each calibration. This relationship was subsequently modified by an offset determined from the positions of the most prominent arc lines in the short “simcal” exposures and by a barycentric correction. Spectra were rebinned into 0.05 Å pixels using this wavelength solution and sky was subtracted using a median of the sky spectra corrected for the differing responses of each fibre.
Several iterations of the data reduction were made including consistency checks between parallel but independent GIRAFFE reduction pipelines operated at the Cambridge Astronomical Survey Unit (CASU) and at Keele University. The analyses in this paper are based on the first internal data released by CASU to the GES consortium in July 2013 (GESviDR1Final) and placed in the GES archive at the Wide Field Astronomy Unit at Edinburgh University1.
2.3. Radial velocities
RVs were determined using two techniques that will be fully described in a forthcoming paper (Koposov et al., in prep.). A first pass used a standard cross-correlation method with a grid of synthetic template spectra at a range of temperatures, metallicities and gravities (Munari et al. 2005) to give an initial RV estimate. The second pass used a direct modelling approach that fits each spectrum with a low-order polynomial multiplied by a template spectrum, with the RV, projected equatorial velocity (vsini), temperature, gravity, metallicity and polynomial coefficients as free parameters. An automated emission-line detection procedure excluded emission lines from the fitting process – predominantly the Hα line in young members of the Gamma Vel cluster. The best-fit was found by chi-squared minimisation, but the formal RV uncertainties estimated with this technique were found to be too small, chiefly due to systematic uncertainties in wavelength calibration.
2.3.1. Radial velocity precision
 |
Fig. 2 Empirically determined RV precision. Upper panel: rms of the empirically estimated RV uncertainties (see text) from pairs of observations within an OB, binned by S/N. A separate set of points is calculated for stars that have an estimated vsini > 30 km s-1 to demonstrate their larger empirical uncertainties. The lines on the plot are loci determined from Eq. (1) using the coefficients A = 0.09 ± 0.01, B = 3.52 ± 0.23, C = 38 ± 8 for several labelled vsini values. The fit is poorly constrained for large vsini and there are some indications that the semi-empirical model underestimates the uncertainties for such stars at high S/N. Lower panel: frequency distribution of empirical RV uncertainties determined from repeated observations within an OB and from repeated observations from separate OBs. The increase in the width of the latter distribution indicates additional uncertainties associated with wavelength calibration between OBs. |
An accurate assessment of RV precision is key to the dynamical analysis of clusters. The format of the Gamma Vel observations lend themselves to a semi-empirical determination of the RV uncertainties. Repeated observations of a target in the same and different fibre configurations allow us to identify and assess various sources of error.
A series of simulations (see also Jackson & Jeffries 2010) suggest that the RV uncertainty, σ, has the following
functional form ![\begin{equation} \sigma^2 = A^2 + B^2\left[ \frac{1 + (v\sin i/C)^2}{{S/N}}\right]^2 , \label{rverr} \end{equation}](/articles/aa/full_html/2014/03/aa23288-13/aa23288-13-eq47.png) (1)where
A,
B and
C are
constants to be determined, vsini is measured from the
spectrum during the chi-squared fitting process (Koposov et al., in prep.) and S/N is
the median signal-to-noise ratio per pixel of the spectrum derived during the extraction
process. This formula allows for the expected decrease in precision with decreasing S/N
and increasing vsini, but the A term also accounts for
any systematic uncertainty associated with the wavelength calibration. We determine
A,
B and
C in two
stages.
(1)where
A,
B and
C are
constants to be determined, vsini is measured from the
spectrum during the chi-squared fitting process (Koposov et al., in prep.) and S/N is
the median signal-to-noise ratio per pixel of the spectrum derived during the extraction
process. This formula allows for the expected decrease in precision with decreasing S/N
and increasing vsini, but the A term also accounts for
any systematic uncertainty associated with the wavelength calibration. We determine
A,
B and
C in two
stages.
(i) We consider 1770 pairs of exposures of the same object, taken within the same OB
and where the combined spectrum has a S/N > 5.
An estimate of the RV precision in the combined spectrum is given by
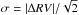 ,
where ΔRV
is the change in RV between the two exposures. We clip out 53 pairs with | ΔRV| > 2 km s-1. Figure 2 shows the rms value of σ as a function of S/N for the remaining pairs.
A,
B and
C are
estimated by fitting Eq. (1) to a surface
of σ in the
S/N vs vsini plane. This yields
A = 0.09 ± 0.01, B = 3.52 ± 0.23,
C = 38 ± 8 (all in units of km s-1). This means that within a
single OB, the repeatability of RV measurements is 90 m s-1 for stars with high S/N and
small vsini. Several loci determined
using Eq. (1) with these coefficients are
shown in Fig. 2 where the uncertainty is plotted
versus S/N for binned data points with vsini above and below
30 km s-1.
Although the model is poorly constrained at high vsini
values where there is little data (95 per cent of the targets used have vsini < 30 km s-1), it appears that rotational
broadening has little effect below 30 km s-1, but uncertainties increase rapidly thereafter, with
some indication that Eq. (1)
underestimates the uncertainties for high vsini and S/N by about 30 per
cent.
,
where ΔRV
is the change in RV between the two exposures. We clip out 53 pairs with | ΔRV| > 2 km s-1. Figure 2 shows the rms value of σ as a function of S/N for the remaining pairs.
A,
B and
C are
estimated by fitting Eq. (1) to a surface
of σ in the
S/N vs vsini plane. This yields
A = 0.09 ± 0.01, B = 3.52 ± 0.23,
C = 38 ± 8 (all in units of km s-1). This means that within a
single OB, the repeatability of RV measurements is 90 m s-1 for stars with high S/N and
small vsini. Several loci determined
using Eq. (1) with these coefficients are
shown in Fig. 2 where the uncertainty is plotted
versus S/N for binned data points with vsini above and below
30 km s-1.
Although the model is poorly constrained at high vsini
values where there is little data (95 per cent of the targets used have vsini < 30 km s-1), it appears that rotational
broadening has little effect below 30 km s-1, but uncertainties increase rapidly thereafter, with
some indication that Eq. (1)
underestimates the uncertainties for high vsini and S/N by about 30 per
cent.
(ii) The coefficients do not yet account for uncertainties in the wavelength calibration because an identical calibration is applied to each set of spectra within an OB. We assume that B and C are properties of the observed stars and the fitting process alone and can be applied to any spectrum. To estimate a value of A that takes account of wavelength calibration uncertainties we fix B and C and fit Eq. (1) to the RV differences from 329 pairs of observations2 in different OBs, and where each contributing spectrum has a S/N > 5 and the OBs were taken within 3 days of each other. This latter condition minimises any variations caused by the motion of unresolved binary systems. Using a model binary distribution (see Sect. 4.1) we estimate that only one per cent of our targets are expected to be in unresolved binaries that have an RV that varies by between 0.5 km s-1 and 2 km s-1 (beyond which they are clipped in any case) on 3-day timescales. The bottom panel of Fig. 2 shows that the distribution of empirically estimated uncertainties becomes broader when considering repeat measurement from different OBs and we find A = (0.246 ± 0.029) km s-1. The rms uncertainty increases from about 0.10 km s-1 for repeats within an OB to 0.28 km s-1 for repeats between OBs, though in both cases, a Gaussian distribution is not a good representation. There is a narrower core and longer tails, presumably because of stars with low S/N and/or high vsini. This is accounted for by our model and is why in our subsequent modelling we assign an individual RV uncertainty to each star, based on Eq. (1), rather than using a single average value.
The B and C coefficients derived here will be specific to the wavelength range and types of star observed. However, we anticipate that in most cases the GES RV precision will be dominated by the A coefficient and so the estimates provided here are likely to be widely applicable to late-type stars observed in GES with the same instrumental configuration. Early-type stars with fewer spectral features and often rapid rotation will have less precise RVs that are determined by their own particular B and C coefficients.
2.4. Lithium equivalent widths
The GESviDR1Final spectra include the Li i 6708Å feature that can be used as a membership indicator (see Sect. 3). The GES analysis (described in more detail in a forthcoming paper; Lanzafame et al., in prep.) uses three independent methods for deriving the equivalent width of this feature in the GIRAFFE spectra (hereafter referred to as EW(Li)): direct profile integration as implemented in splot as part of the iraf package3, daospec (Stetson & Pancino 2008) and an ad hoc procedure written in idl (E. Franciosini, priv. comm.). The latter automatically derives EW(Li) and its uncertainty by a direct profile integration taking into account the star’s RV, vsini, and S/N. The analyses were performed on the summed spectra of each object.
The results obtained by the three different methods were first compared to check for systematic differences before combining them to produce the final results. Above 300 mÅ the daospec results were discarded because they systematically underestimated EW(Li) in FGK stars and overestimated it in M stars and fast rotators with respect to the results obtained using iraf (probably because the strong line is non-Gaussian – see Pancino & Stetson 2008). In this range the final EW(Li) is given as the average between the iraf value and idl procedure. Below 300 mÅ the results obtained by the three methods were averaged, eventually discarding one of the three values if it deviated by more than one standard deviation. The uncertainty on the final EW(Li) is given conservatively as the larger of the standard deviation or the average uncertainty from the independent measurements. The median uncertainty of a detected Li line is 14 mÅ with a median S/N of 36. Where no significant EW(Li) can be found, an upper limit is estimated using the approach suggested by Cayrel (1988). As each of the three EW estimation procedures uses an independent approach to establishing a continuum level, the quoted uncertainties automatically contain some allowance for uncertain continuum placement and this is the dominant source of uncertainty even at the median S/N.
The standard GES analysis of EW(Li) also makes an attempt to account, where necessary, for blending with a nearby weak Fe i line (Soderblom et al. 1993) and, in only 14 cases, the presence of a veiling continuum that is presumably due to accretion and diminishes the measured EW(Li). We ignore both of these corrections in the present analysis, using only the “raw”, blended EW(Li) that is reported in the GESviDR1Final tables, but have confirmed that their inclusion would have made no difference to the selection of members described below.
3. Membership selection
 |
Fig. 3 Equivalent width of the Li i 6708 Å feature (EW(Li)) versus V − I. Objects selected as candidate members are marked with blue diamonds; red circles mark objects that are potential members based on their photospheric Li content, but fall outside the sequence of members in the colour–magnitude diagram (see Fig. 4). Triangles mark upper limits. The solid red lines show theoretical isochrones at 10 Myr and 20 Myr from the models of Baraffe et al. (1998, see text), reddened with E(V − I) = 0.055. The dashed line marks the upper envelope of EW(Li) for IC 2391 and IC 2602 at ages ≃50 Myr. |
Coordinates, photometry and measurements of RV, EW(Li), vsini and estimated masses for 208 targets selected as Gamma Vel members.
For this paper, our aim is to select a sample of association members as free from any kinematic bias as possible. The initial selection of candidate members therefore did not use the RV results. Instead we rely on the presence and strength of the Li i 6708 Å feature and the position of candidates in the V − I/V CMD.
Lithium is a well-known age indicator for young PMS stars because it is rapidly depleted if the temperature at the base of the convection zone, or core of a fully convective star, exceeds ≃3 × 106 K (e.g. Soderblom 2010). Theoretical isochrones of Li depletion have been calculated (e.g. Baraffe et al. 1998; Siess et al. 2000), but are subject to significant uncertainties regarding convective efficiency and atmospheric opacities. The models match the broad picture that has emerged from observations of Li abundances in young clusters, but do not agree with each other and cannot explain the significant scatter in Li abundance often seen in stars with similar age and Teff. Here we adopt an empirical approach and use a large EW(Li) as the principal criterion for selecting cluster members. The timescale for significant Li depletion ranges from ~10–20 Myr in mid-M stars, ~100 Myr in K-type stars, to ~1 Gyr in G-type stars. Thus, the presence of Li will exclude the vast majority of field K- and M-dwarfs, but will not be as effective at excluding contaminating field G dwarfs.
Figure 3 shows EW(Li) plotted against V − I colour compared with 10 and 20 Myr isochrones calculated from the evolutionary models of Baraffe et al. (1998 – with mixing length of 1.0 pressure scale heights). The model Li abundances are folded through the NLTE curves of growth described in Jeffries et al. (2003), based on atlas9 models for warmer stars (Teff > 4000 K, Kurucz 1993) and from Zapatero-Osorio et al. (2002) for Teff ≤ 4000 K. The relationship between Teff and V − I is also that used in Jeffries et al. (2003 – see their Fig. 6) and we redden the models by E(V − I) = 0.055. The 20 Myr isochrone is a guide to the lowest EW(Li) we might expect from Gamma Vel cluster members, but must be used with caution given the sensitivity of such models to convective efficiency and the details of the atmosphere and curves of growth. A further empirical locus marks the observed upper envelope of EW(Li) in the clusters IC 2391 and IC 2602 (Randich et al. 1997, 2001), that have ages of about 50 Myr and which we expect more definitely define a lower boundary for association members. E(V − I) values of 0.01 and 0.04 were assumed for these clusters (Patten & Simon 1996). Caution is still warranted in stars with V − I < 1.5, where any small systematic differences in the EW(Li) measurements between our work and the literature samples (e.g due to the continuum definition, or how rapid rotation is dealt with) could be comparable to the Li depletion expected between 10 and 50 Myr.
The larger symbols (both blue diamonds and red circles) in Fig. 3 show those objects we initially select as Gamma Vel cluster members on the basis of EW(Li) and the loci discussed above. A significant detection of the Li line with EW(Li) > 100 mÅ was taken as an absolute criterion. Contamination by Li-rich field giants is still possible, but is ignored because only ~1 per cent of G/K giants might exhibit photospheric Li at a level that meets our threshold (Brown et al. 1989). The Li-selected targets are then passed through a further filter in the V − I/V CMD (shown in Fig. 4). Here, the purpose is to exclude Li-rich objects that appear to lie well away from the locus defined by most cluster members. Figure 4 shows that, as expected, the presence of Li in G stars is not a reliable indication of cluster membership and most of these have been excluded by the CMD filtering. Few stars at cooler spectral types are excluded in the CMD because field stars at these temperatures are rarely expected to retain Li at the levels we demanded in Fig. 3.
 |
Fig. 4 Colour–magnitude diagram for the Gamma Vel targets. Blue diamonds show the Li-rich targets we select as members (see Fig. 3); red circles are Li-rich targets that do not follow the sequence defined by the bulk of cluster members and are excluded. Solid red lines show isochrones from the Baraffe et al. (1998) evolutionary models (see text), shifted to a distance modulus of 7.76 mag, with reddening E(V − I) = 0.055 and extinction AV = 0.131 applied. |
The definition of these two filters is to some extent arbitrary, our concern is mainly to avoid contamination by field stars. We note that it is possible that we have excluded a few genuine cluster members. These might be objects that are displaced in the CMD by variability or their photometric uncertainties, but our filter should not exclude unresolved binaries. It is also possible we have excluded a few objects that have an apparently weak Li line due to very rapid rotation or, particularly around V − I ~ 2.7, have actually depleted Li beyond the limits we have accepted. On the basis of the RVs of excluded objects and the small fraction of objects showing evidence for rapid rotation in our sample, the numbers of excluded genuine members is unlikely to amount to more than a few per cent of the accepted sample.
4. Results and analysis
All the data for all the targets observed in the Gamma Vel OBs listed in Table 1, including the EW(Li) values, photometry (from J09) and RVs (including RVs determined from individual exposures and from OBs) can be obtained from the Gaia-ESO archive hosted by the Edinburgh University Wide Field Astronomy Unit. Results for the 208 Gamma Vel members selected in Sect. 3 are reported in Table 2 (available in electronic format). For each cluster member we report the weighted mean RV (weighted by the uncertainties calculated from Eq. (1) for each contributing OB) and its total calculated uncertainty, the mean rotational broadening and the total S/N (across multiple OBs where appropriate) and the mean EW(Li) and its uncertainty obtained as described in Sect. 2.4. Figure 5 shows the distribution of calculated RV uncertainties for the Gamma Vel members. The median uncertainty is 0.26 km s-1. The obvious bimodality arises from the 80 objects with more than one independent observation and consequently smaller final RV uncertainties.
4.1. Modelling the radial velocity distribution
 |
Fig. 5 Distribution of RV uncertainties for the selected Gamma Vel members, calculated using Eq. (1). Where objects were observed in more than one OB, the uncertainty in the weighted mean RV is correspondingly smaller. |
 |
Fig. 6 Binned RV histogram for the Gamma Vel members (note that fitting was carried out on unbinned data). Upper panel: the best fit for a model consisting of a single Gaussian population with a fraction fbin = 0.46 of unresolved binaries (see text). The fit is poor. Lower panel: the best fit for a population represented by two Gaussian components, each with an unresolved binary population. |
A histogram of the mean RVs for stars selected as members is shown in Fig. 6 and is modelled using a maximum likelihood technique. We implicitly assume that our membership selection procedure has excluded unassociated field stars. A complication is that some fraction of these objects will be unresolved binary systems. The procedure we adopt is described in detail by Cottaar et al. (2012b) but is summarised here with some minor differences highlighted.
We assume that the observed RVs are drawn from an intrinsic distribution that is
broadened by measurement uncertanties and the possibility of binary motion. Single stars
and the centres of mass for binaries are assumed to share the same intrinsic RV
distribution. The likelihood of a star’s observed RV, vi, given an intrinsic RV
distribution and the estimated RV uncertainty, σi is 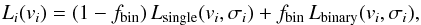 (2)where
fbin is the fraction of observed objects
that are unresolved binaries; Lsingle is the convolution of a model
intrinsic RV distribution with a Gaussian of dispersion σi; and Lbinary is the
equivalent likelihood distribution for binary systems, but is calculated after convolving
the model intrinsic RV distribution with an uncertainty and the
distribution of velocity offsets expected from a set of randomly oriented SB1 binary
systems, with a specified distribution of orbital periods and eccentricities.
(2)where
fbin is the fraction of observed objects
that are unresolved binaries; Lsingle is the convolution of a model
intrinsic RV distribution with a Gaussian of dispersion σi; and Lbinary is the
equivalent likelihood distribution for binary systems, but is calculated after convolving
the model intrinsic RV distribution with an uncertainty and the
distribution of velocity offsets expected from a set of randomly oriented SB1 binary
systems, with a specified distribution of orbital periods and eccentricities.
For binaries, we assume fbin = 0.46, a lognormal period distribution, a mean log P = 5.03 (in days) and dispersion 2.28 dex, with a flat mass ratio distribution for 0.1 < q < 1 (Raghavan et al. 2010). For ease of computation we consider only circular orbits; tests using an eccentricity distribution showed that it has no significant effect on the results. The binaries are assumed to have a random orientation in space and to be observed at a random phase of their orbits. Monte Carlo simulations give a distribution of observed RV offsets for the primary star with respect to the binary centre of mass. The calculation was performed separately for each target, assuming a primary mass (given in Table 2) approximated by interpolating its V − I colour along a 10 Myr Baraffe et al. (1998) isochrone and a system mass a factor of (1 + q) larger4.
Given a model intrinsic RV distribution described by a number of free parameters (see below), the best-fitting model is found by calculating the likelihood for each star (from Eq. (2)) and then maximising the summed log likelihood for all stars by varying the parameters over a grid of possible values. Uncertainties in a parameter are calculated from the distribution of maximum log likelihoods for that parameter evaluated after optimisation with respect to all other model parameters.
4.1.1. A single Gaussian population
Results of the maximum likelihood RV modelling.
We begin by considering an intrinsic RV distribution modelled with a single Gaussian of width σA and centre RVA. The fit was made only to data with weighted mean RV between 8 and 26 km s-1. There are 18 objects that lie outside this range. All must be considered candidate binary systems. Only four have multiple measurements, but these do not show evidence of RV variability at the 1 km s-1 level. The most likely fit to the remaining 190 objects has σA = 1.63 ± 0.13 km s-1 and RVA = 17.71 ± 0.14 km s-1. An approximation5 to this model is shown in Fig. 6, where the intrinsic distribution has been broadened by the mean uncertainty profile (note that this is not the same as a Gaussian with a dispersion equal to the mean RV uncertainty) and a fraction (fbin = 0.46) of the model realisations are broadened due to binary motion as described earlier. The fit looks poor, but maximum likelihood fitting does not yield a “goodness of fit” parameter. Instead we have compared the cumulative RV distributions of data and model using a Kolmogorov-Smirnov (KS) test, which rejects the hypothesis that the data are drawn from the model distribution with 99.4 per cent confidence.
4.1.2. A two-component model
The data suggest the addition of a second Gaussian component. We refer to the two
components, or populations, as A and B. With the binary parameters fixed, this model has
5 free parameters: the central RV of one population, RVA, the
difference in central RV of the two components ΔRVAB, the Gaussian
dispersions of the two components σA and σB and the
fraction of stars that belong to the first component fA. It is
assumed that the stars belong to one component or the other so that fB = 1 − fA.
The likelihood of observing a given RV is now 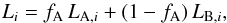 (3)where LA and
LB are likelihoods calculated using Eq.
(2), but with the appropriate intrinsic
model RV distributions for components A and B respectively.
(3)where LA and
LB are likelihoods calculated using Eq.
(2), but with the appropriate intrinsic
model RV distributions for components A and B respectively.
The values of the parameters at the maximum likelihood fit are given in Table 3 along with symmetric 68 per cent confidence intervals for a single parameter of interest. An approximation to the best-fitting model (calculated using the mean uncertainty profile) is shown in the lower panel of Fig. 6 and consists of roughly equal numbers of stars in each component, one with a very narrow intrinsic dispersion and the other much broader and offset by 2.15 km s-1. The maximum log likelihood increases by 21 with this more complex model at the cost of three additional degrees of freedom. Using the Wilk’s theorem approximation, the two component model is preferred over the single component model with 99.99 per cent confidence. The two component model is also preferred according to the Bayesian information criterion. A KS test yields PKS = 0.994, suggesting the data and model are consistent and that searching for more complex structure is unlikely to yield further significant improvement.
Whilst there are roughly equal numbers of stars belonging to each of the two components (fA = 0.48 ± 0.11), their RV dispersions are quite different. To test whether correlations between the various parameters might affect this conclusion Fig. 7 shows the maximum likelihood space in the σA versus σB plane. Confidence contours are calculated according to the usual increments in log likelihood for two parameters of interest. We find there is no strong correlation and that σB > σA with a high degree of confidence. Similarly, we find that the two components have different RV centroids with a high degree of confidence; i.e. ΔRVAB > 0.
 |
Fig. 7 Likelihood space for σA versus σB for the two-Gaussian fit to the RV distribution. Confidence contours are shown for two parameters of interest. σB > σA with a high degree of confidence. |
The binary parameters we have used in our models come from a study of solar-type field stars. About half our sample has lower masses and there is some evidence that the binary frequency is smaller for such objects – perhaps 30 per cent (Duchêne & Kraus 2013). In any case, there may also be some difference in binary parameters associated with birth environment, so it is prudent to investigate the sensitivity of our results to this. We repeated the analysis with a binary frequency of 30 per cent. The main difference is that σB increases from 1.60 km s-1 to 1.89 km s-1, a change that is less than the original uncertainty estimate. All other parameters change by much less than the uncertainties listed in Table 3, so we conclude that the results are quite insensitive to plausible uncertainties in the binary parameters.
4.2. Two populations in the Gamma Vel cluster?
 |
Fig. 8 Probability that each Gamma Vel member belongs to population A in the two-component kinematic model described in Sect. 4.1.2. Relatively secure members of population A (PA > 0.75) and B (PA < 0.25) and objects that cannot be confidently assigned to either population are identified with different symbols in this and subsequent plots. |
Having established (at least) two kinematic components in the RV distribution of Gamma
Vel members, we can ask whether there are any other properties that might distinguish
these populations. We consider the CMD, the spatial distribution, the lithium depletion,
rotational broadening and proper motions. In each case it is necessary to distinguish
between members of the two populations, but this can only be done in a probabilistic way.
For our two-component model we can calculate, for each star, the probability that it
belongs to either populations A or B as
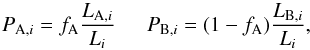 (4)where the terms
are as defined in Eq. (3). This could be
calculated for the maximum likelihood model, but we obtain a more accurate estimate by
integrating this probability over the full 5D parameter space and then PA,i is found from the
expectation value of the total probability distribution function. PB,i is given by
1 − PA,i. The results
of this calculation are illustrated in Fig. 8 and
listed in Table 2 for each star. Stars outside the
range 8 < RV < 26
km s-1 are not
considered and given PA = −1. PA depends
mainly on the RV of the star but also to a lesser extent on the RV uncertainty. To test
for differences in properties between the two populations we adopt two approaches. (i)
Where appropriate, we use PA and PB as
statistical weights in determining mean properties; (ii) for plotting purposes and also as
a way of more carefully cleaning the samples of contamination, we divide the sample into a
population of 73 objects having PA > 0.75, which
we will call population A, though we understand it will still have ≃19 per cent contamination by stars in the
other population, and 66 stars with PA < 0.25 that
we call population B, but will have ≃9 per cent contamination from the other population (see Fig. 8). The remaining 69 objects cannot be assigned to either
population with great confidence and are plotted with different symbols.
(4)where the terms
are as defined in Eq. (3). This could be
calculated for the maximum likelihood model, but we obtain a more accurate estimate by
integrating this probability over the full 5D parameter space and then PA,i is found from the
expectation value of the total probability distribution function. PB,i is given by
1 − PA,i. The results
of this calculation are illustrated in Fig. 8 and
listed in Table 2 for each star. Stars outside the
range 8 < RV < 26
km s-1 are not
considered and given PA = −1. PA depends
mainly on the RV of the star but also to a lesser extent on the RV uncertainty. To test
for differences in properties between the two populations we adopt two approaches. (i)
Where appropriate, we use PA and PB as
statistical weights in determining mean properties; (ii) for plotting purposes and also as
a way of more carefully cleaning the samples of contamination, we divide the sample into a
population of 73 objects having PA > 0.75, which
we will call population A, though we understand it will still have ≃19 per cent contamination by stars in the
other population, and 66 stars with PA < 0.25 that
we call population B, but will have ≃9 per cent contamination from the other population (see Fig. 8). The remaining 69 objects cannot be assigned to either
population with great confidence and are plotted with different symbols.
4.2.1. The colour–magnitude diagram
 |
Fig. 9 Colour–magnitude diagram for the two kinematic populations around γ2 Vel. The populations are distinguished here by a simple probability criterion (see Sect. 4.2) into population A (with a narrow RV distribution) or population B (with a broader RV distribution). The other cluster members cannot be assigned to either population with great confidence. |
Figure 9 shows the V − I/V CMD for members, coded for populations A or B according to the probabilistic criterion described above. The unassigned objects and objects with RV outside the range 8 < RV < 26 km s-1 are also shown for completeness. We fit the distribution of points with a quadratic in V − I for V − I > 1.5 mag, as the few points bluer than this define a kink in the diagram that is poorly reproduced by a polynomial. Fixing the linear and quadratic terms, we then fit populations A and B separately, allowing a constant offset. If the division is carried out as in Fig. 9, the difference in offsets for the two populations is a marginal 0.06 ± 0.07 mag in the sense that population A is brighter. If instead we perform fits weighted according to the probability of membership of populations A or B, this difference becomes 0.02 ± 0.03 mag. At an age of about 10 Myr the latter result and the Baraffe et al. (1998) isochrones plotted in Fig. 9 imply that population A is younger than population B by about 0.4 ± 0.6 Myr if they are at the same distance and have the same unresolved binary frequency. Alternatively, if they both have the same age, then population A is closer by 4 ± 5 pc.
A KS test of the mass distributions of the two populations resolved according to the probability criteria, reveals no significant difference (PKS = 0.84). There are 8 higher mass objects in population B with V − I < 1.5, and only 2 in population A. This difference is not regarded as significant by a KS test though it is marginally significant (at the 95 per cent level) using a two-tailed Fisher test.
4.2.2. The spatial distribution
 |
Fig. 10 Spatial distribution of populations A and B, defined according to the probability criterion described in Sect. 4.2. In the main panel these populations and the set of cluster members that cannot be confidently assigned to either are shown. Symbols are as defined in Fig. 9. The cross marks the position of γ2 Vel. In the top and side panels we show the distribution of RV with right ascension and declination respectively. The solid (red) lines and the dashed (blue) lines show best-fitting linear relationships for populations A and B respectively. |
Figure 10 examines the projected spatial distributions of the two populations, with different symbols corresponding to the populations as in Fig. 9. The position of γ2 Vel is marked. The most obvious difference between the populations is their centroid. Population A has a centroid of (RA = 122.413 ± 0.034, Dec = −47.378 ± 0.027), whilst the centroid of population B is at (RA = 122.305 ± 0.038, Dec = −47.381 ± 0.032). The distributions of the two populations are different in RA according to a KS test (PKS = 0.03), but not in Dec (PKS = 0.64). Accompanying this shift there appears to be an increase in RV of ~2 km s-1 for population B towards the south-west. A weighted linear fit of RV versus position for the population B objects gives a slope of −0.28 ± 0.60 km s-1 deg-1 in the RA direction and −1.80 ± 0.68 km s-1 deg-1 in the Dec direction. No drifts are apparent for population A. The best fitting lines are shown in Fig. 10.
 |
Fig. 11 Projected space density of members of populations A and B, along with that of all the (non-members of the Gamma Vel cluster) targets observed. Population A is more centrally concentrated than population B, though the significance of this is low (see Sect. 4.2.2). |
There is a hint that population A is more centrally concentrated than population B. The centroid of population A is consistent with the position of γ2 Vel, whilst the centroid of population B is separated from γ2 Vel by 4.1 ± 2.3 arc minutes. A KS test of the distributions of radial distance from γ2 Vel reveals only a marginal difference with PKS = 0.15. A central concentration in either population might be due to biases in the target selection. To check this we examined the spatial distribution of targeted objects not considered to be Gamma Vel members in Sect. 3, because these should be subject to a similar spatial bias in target selection, but should have an approximately uniform intrinsic spatial distribution. The normalised distributions of spatial density with radius for populations A, B and the targeted non-members are shown in Fig. 11. Population A is more centrally concentrated than the target population, with a significantly different radial distribution (PKS < 10-5). Population B is also more centrally concentrated than the targets, but less so than population A (PKS = 0.02). Given that it is still contaminated with ≃6 stars from population A, it is conceivable that population B has a quite similar spatial distribution to the general field population and that population A, which has ~13 contaminants from population B, is even more centrally concentrated. If we use PA and PB to weight the contributions from all stars, we find the mean radial distances from γ2 Vel are 15.2 ± 0.6, 18.8 ± 1.0 and 21.8 ± 0.2 arcminutes for populations A, B and the targeted non-members respectively.
In summary then, Population A has a centroid consistent with the position of γ2 Vel, is definitely more centrally concentrated than the observed targets and probably more centrally concentrated than population B. The centroid of Population B is offset from population A by 4.4 ± 3.0 arcminutes and has a spatial distribution that is marginally consistent with either population A or the observed targets. Population B shows significant evidence for a spatial gradient in RV in the declination direction.
4.2.3. Lithium depletion
 |
Fig. 12 Equivalent width of the Li i 6708 Å line versus colour, with different symbols corresponding to the populations as in Fig. 9. The solid lines are isochrones calculated according to the evolutionary models of Baraffe et al. (1998, with mixing length of 1.0 pressure scale heights) at 10, 15 and 20 Myr, transformed into the observational plane as described in Sect. 3. |
Figure 12 shows the EW(Li) versus colour plot, with the Gamma Vel members separated by population as described in Sect. 4.2. There is a suggestion in this plot that population A is more Li-depleted than population B, especially in the range 2.5 < V − I < 2.8 where age-dependent Li-depletion is expected to be strongest.
The statistics bear this conclusion out. The weighted mean EW(Li) for stars with 2.5 < V − I < 2.8 is 269 ± 21 mÅ for population A and 433 ± 19 mÅ for population B. If we use the whole sample, but apply a further weighting according to the probability of membership of populations A or B, the results for the mean EW(Li) in this colour range are 303 ± 17 mÅ for population A and 413 ± 15 mÅ, a smaller difference, but still significant at the 5-sigma level. Hence this result is quite robust to the details of how membership of the two populations is assigned.
The difference in Li-depletion implies a difference in age. Population A would need to be older (on average) by an amount which is dependent on the the way that EW(Li) is translated into a Li abundance. Because the Li i 6708 Å line is in the saturated part of the curve of growth, a small change in EW(Li) corresponds to a large change in Li abundance (Palla et al. 2007), but Li-depletion is also very rapid at these masses, so a large change in abundance is expected in a small amount of time. Adopting the models of Baraffe et al. (1998) and the isochrones shown in Fig. 12, which at least match the colour of dip in Li abundance quite well, we see that rapid depletion commences at ~10 Myr and the small EW(Li) difference we have found could correspond to only ~1–2 Myr in mean age. The absolute age at which rapid Li depletion commences is model dependent and begins earlier (but at bluer colours) for models with higher convective efficiencies, but the implied age difference of ~1–2 Myr is reasonably robust to choice of model. That there are examples of Li-depleted and undepleted stars in both populations with 2.5 < V − I < 3 might suggest that age spreads are larger than any age difference. Alternatively it might simply reflect that the samples identified in Fig. 12 are still cross-contaminated by the other population.
Another possibility is that the differences in photospheric Li are due to composition rather than age differences. Li depletion is predicted to be very sensitive to interior opacity and if Population A were even only 0.1 dex more metal-rich than Population B this might explain the observed difference (e.g. Piau & Turck-Chièze 2002). A detailed compositional analysis of the Gamma Vel cluster GES UVES data is underway (Spina et al., in prep.). A detailed discussion of the Li abundances and comparison with models is deferred to Franciosini et al. (in prep.); the important point here is that there is a difference between populations A and B.
4.2.4. Rotation rates
 |
Fig. 13 Projected rotational velocities as a function of colour. The different symbols correspond to the various populations as described in Fig. 9. Objects with vsini < 10 km s-1 are marked as upper limits (triangles). |
Figure 13 shows the projected equatorial velocities of the sample as a function of colour. Values of vsini < 10 km s-1 are unlikely to be accurate, given the resolution of the spectra, and are regarded as limits of <10 km s-1. There is a hint that members of population B are more rapidly rotating, on average, especially for V − I < 2.5 mag, but the numbers are small. A two-tailed KS test of the cumulative vsini distributions reveals a marginal difference (PKS = 0.12). Even if the two populations had different ages, it is unlikely that this comparison would be diagnostic, because the timescale of rotation spindown with age is too slow (~50 Myr) at the masses of the sample we consider. Any differences are more likely to reflect different birth conditions.
4.2.5. Proper motions
 |
Fig. 14 UCAC4 proper motions (in milli-arcseconds per year) for our selected Gamma Vel members. The different symbols correspond to the various populations as described in Fig. 9. The proper motion of γ2 Vel itself is shown with a cross. There are 6 objects that lie beyond the borders of the plot. These and the other very discrepant objects show evidence of binarity or lie very close to γ2 Vel and are likely to have unreliable proper motions. |
The catalogue of Gamma Vel members was matched with the Fourth US Naval Observatory CCD Astrograph Catalog (UCAC4, Zacharias et al. 2013). There were 92 matches within 1 arcsecond, most members brighter than V ~ 17 had a match. Figure 14 shows the vector point diagram with population A and B indicated. There are a number of very discrepant points. We have examined these stars individually and there are reasons to be suspicious about all of them; either they appear as blended, unresolved binaries on photographic plates or they are very close to γ2 Vel itself. Clipping the sample between −20 < PM(RA) < 5 mas/yr and −10 < PM(Dec) < 25 mas/yr we obtain mean proper motions of (−5.9 ± 0.8, +8.6 ± 1.0) and (−4.5 ± 1.0, +8.7 ± 0.9) mas/yr for populations A and B respectively. The standard deviations for populations A and B are both ≃4.5 mas/yr in each coordinate, corresponding to ≃7 km s-1 at the distance of γ2 Vel. This is only slightly larger than the respective mean proper motion uncertainties and incapable of resolving differences in tangential velocity dispersion comparable to that seen in the RV dispersions. If the proper motions are weighted by the probability of population membership, the mean proper motions of populations A and B are (−5.9 ± 0.8, +8.5±1.0) and (−4.6 ± 1.0, + 8.7 ± 0.9) mas/yr respectively.
These mean proper motions are similar to each other and also similar to the proper motion of γ2 Vel (−5.9 ± 0.4, + 9.9 ± 0.4 mas/yr; from Hipparcos) and the mean proper motion of early type stars in Vela OB2 (−6.6 ± 1.3, + 8.1 ± 1.4 mas/yr; Tycho proper motions compiled by J09).
5. Discussion
The RV distribution of the young, low-mass stars surrounding γ2 Vel clearly exhibits structure that has a bearing on the current dynamical state and the star formation history of the region. The evidence at hand can be summarised as follows.
-
The RV distribution must be modelled with more thanone component. A good fit is obtained by dividing theyoung stars into two, roughly equal, kinematic popu-lations A and B, one with a narrow intrinsic dispersion(σA = 0.34 ± 0.16 km s-1) and the other much broader (σB = 1.60 ± 0.37 km s-1). The populations are significantly offset from each other by 2.15 ± 0.48 km s-1.
-
Pozzo et al. (2000) and J09 showed that the young, low-mass stars have a spatial density distribution that is concentrated towards γ2 Vel. Here, we have shown that this concentration is mostly evident in population A, which has a centroid consistent with the position of γ2 Vel. Population B appears less spatially concentrated and may be consistent with a uniform distribution across our surveyed area. The lack of a clean kinematic separation between the populations prevents us being more definitive.
-
The two populations are not clearly distinguished from each other in the V − I/V CMD or by their rotational properties. Their proper motions are similar and consistent with the proper motions of γ2 Vel and the wider Vela OB2 association that extends well beyond the spatial extent of the GES data.
-
The mid M-type objects in Population A do show significantly more Li depletion than those in Population B. This difference is robust to how the populations are separated kinematically and suggests that population A could be older on average by perhaps 1–2 Myr. The presence of stars that appear undepleted and depleted in both populations implies that their age distributions may overlap, though this latter conclusion is again weakened by the lack of clear kinematic separation of the populations.
We can hypothesize a number of scenarios for the origin of these two populations: (i) γ2 Vel formed in an originally more massive, gas-rich cluster. Population A is the bound remnant of the cluster after gas expulsion and population B is an unbound halo of escaping stars. We refer to this as the “core-halo scenario”; (ii) γ2 Vel formed in an isolated way but has attracted a retinue of low-mass stars from the dispersed Vela OB2 association. Population A would be the “captured” stars whilst population B is the dispersed low-mass component of Vela OB2. We refer to this as the “captured cluster” scenario; (iii) γ2 Vel formed in a denser sub-clustering of the Vela OB2 association. At least part of this subcluster survived any gas expulsion to form population A, while population B consists of the dispersed low-mass component of the Vela OB2 association. We refer to this as the “cluster plus association” scenario. We consider each of these possibilities in turn with reference to the evidence listed above.
5.1. The core-halo scenario
It would be very rare for a star as massive as γ2 Vel (with initial mass ≃35 M⊙ + 31.5 M⊙; Eldridge 2009) to form in a cluster with total mass ~100 M⊙. The cluster would be the most distant outlier from the relationship between cluster mass and mass of the most massive star proposed by Weidner et al. (2010), where instead the expected initial cluster mass would be ~1000 M⊙. Gas expulsion might solve this problem (and is the reason that Weidner et al. excluded γ2 Vel from their sample). The fraction of stars lost after gas expulsion depends on the (local) star forming efficiency, ratio of half-mass radius to tidal radius, how quickly the gas is lost and the initial clumpiness of the gas and stars (e.g. Gieles 2010; Bastian 2011). Many simulations show (e.g. Baumgardt & Kroupa 2007; Fellhauer et al. 2009; Moeckel & Bate 2011) that gas removal on less than a dynamical timescale or a low star formation efficiency can lead to the loss of most of the original cluster, leaving a bound remnant (Population A), that may be orders of magnitude less dense than the original embedded cluster, surrounded by an expanding halo (Population B).
The dynamics of this scenario can be checked using the velocity dispersions of the two
populations. Clusters in virial equilibrium have RV dispersions (σv) that are related to
their total dynamical masses (Mdyn) and projected half mass radii
(rm) by 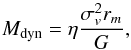 (5)where
η is a
numerical constant related to the density profile and is approximately 10 for a Plummer
density distribution (Spitzer 1987; Portegies Zwart
et al. 2010).
(5)where
η is a
numerical constant related to the density profile and is approximately 10 for a Plummer
density distribution (Spitzer 1987; Portegies Zwart
et al. 2010).
If we sum up the Gamma Vel members in our survey, weighted according to their probability of belonging to population A, and assuming that those that lie outside 8 < RV < 26 km s-1 have PA = fA = 0.48, then the total mass of population A (among the GES survey objects) is 58 M⊙. This mass estimate should be increased by a factor 1/0.85 to reflect that GES spectroscopy was obtained for 85 per cent of cluster candidates and by another factor of 1.25 to account for an assumed binary fraction of 0.46 with a flat mass ratio distribution between 0.1 and 1 (see Sect. 4.1). If we further assume that our survey covers the full extent of population A and that it is centred on γ2 Vel, then the half mass radius of this distributed population is rm = 0.225 degrees, equivalent to 1.37 pc at the distance of the cluster.
To these low-mass stars we can add the more massive stars that are not included in GES. These are obtained from the Tycho catalogue and filtered on proper motion and their position in the V versus B − V CMD to obtain a list of secure association members (see J09). We assign masses to these based on their V magnitudes and a Z = 0.02 10 Myr isochrone from the Siess et al. (2000) models. There are 13 stars which are likely association members and within the area surveyed by GES, with a total mass of 32 M⊙. However, we do not know if these belong to populations A or B, so assign a fraction fA of the mass to population A. The total mass of distributed stars in population A is therefore (58 × 1.25/0.85) + (32 × 0.48) = 101 M⊙, where we neglect the contribution of any stars below 0.2 M⊙. We also neglect the contribution from any residual gas. The low and uniform extinction towards the early type stars of the Gamma Vel cluster suggests this is justified.
The central concentration of population A and the positional coincidence between its centroid and the position of γ2 Vel, suggest that γ Vel belongs to population A. If so, the total mass of that system is 39 M⊙ (for γ2 Vel; de Marco & Schmutz 1999) and a further 12 M⊙ for its proper motion companion γ1 Vel, which is a resolved multiple with components for which we estimate masses of 7 M⊙ and 5 M⊙ respectively. The addition of this mass alone to the population A “cluster” would increase σv, but as it is all added to the centre, it also decreases η to ≃6.3 and the final expected virial velocity from Eq. (5) is σv = 0.28 km s-1 (or about 0.18 km s-1 if γ Vel were not part of population A). The measured RV dispersion is σA = 0.34 ± 0.16 km s-1, so population A appears consistent with virial equilibrium and currently bound. If population B were also spatially centred on γ2 Vel it would roughly double the total mass, but its velocity dispersion of σB = 1.60 ± 0.37 km s-1 would clearly make it unbound.
Although this scenario is consistent with the velocity dispersions, there is no simple explanation for why population B would have a mean velocity that is significantly different to population A or why there should be a gradient in the mean RV of population B. It is also unclear why there would be any difference in the mean ages of the populations manifested as the differences seen in Li depletion. For these reasons we think this scenario is unlikely.
5.2. Captured cluster scenario
If γ2 Vel formed as part of an initially
supervirial OB association. Then, despite the global expansion, it may have captured a
retinue of lower mass stars in its local potential well (e.g. Parker et al. 2014). In this scenario population A would be captured
low-mass stars and population B would be expanding remnants of the original association.
Stars in the original association would have a (supervirial) velocity dispersion, but the
captured stars would settle into a new equilibrium roughly centred on the peculiar
velocity of the γ Vel system. This might explain why the two
populations have discrepant, but overlapping velocity distributions. The evolution of such
a substructure within an expanding association could occur on a dynamical timescale
≃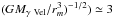 Myr.
Myr.
Given that γ2 Vel has an age of ≥5 Myr (see below) there appears to be time for this process to have occurred. Furthermore, because the captured stars are most likely to have similar velocities to γ2 Vel, this can explain the small velocity dispersion of population A. However, there is no simple explanation for any age or composition difference between the populations as suggested by the difference in photospheric Li among their M-dwarfs.
5.3. Cluster plus association scenario
A hybrid of these two models is that γ Vel formed near the centre of a locally dense region, whilst less dense regions formed stars with lower efficiency which became the wider Vela OB2 association (e.g. see the numerical simulations by Bonnell et al. 2011). Following gas expulsion, this dense region expanded and lost some fraction of its members. With an escape velocity of ~1 km s-1, this halo of lost stars has expanded to of order 5 pc radius and been diluted into the general background of objects in Vela OB2. Population A is then the bound remnant of the originally dense region and population B is mostly formed of a general background of young objects in the wider Vela OB2 association. If population A is older by 1–2 Myr, then the very small difference in the loci of the two populations in the CMD would mean that population A would need to be closer (on average) than B by about 10–20 pc. In such an extended region of star formation, it is hardly surprising that age differences of 1–2 Myr or RV differences of ~2 km s-1 exist. A similar situation applies on similar scales in other star forming regions. Tobin et al. (2009) finds RV gradients of ≃0.3 km s-1 pc-1 on ≃10 pc scales in Orion A, very similar in magnitude to what is found here in population B.
The “cluster” defined by population A is barely bound. Its current crossing time of a few Myr is similar to the age of γ2 Vel and so it falls on the cusp of the tcross /age ~1 criterion that can be used to separate bound clusters from unbound associations (see Gieles & Portegies Zwart 2011), an outcome predicted by models that assume a reasonably high star forming efficiency (≥30 per cent; Pelupessy & Portegies Zwart 2012). It seems unlikely that it will remain as a bound entity for very long. The tidal radius of the cluster in the gravitational field of the Galaxy, is approximately rt ≃ 1.4(M/M⊙)1/3 at the solar Galactocentric radius, so rt/rm ≃ 5. The relaxation time is only a few times the crossing time, so significant evaporation should take place on timescales of 10 Myr, and this will be exacerbated by the significant mass loss expected within the next few Myr from γ2 Vel through winds and supernovae.
These first kinematic results for a young cluster in the Gaia-ESO survey demonstrate their power in deciphering the histories and predicting the futures of star forming regions. The RVs and kinematically unbiased membership determination offered by the GES data will be complementary to proper motions and parallaxes from the Gaia spacecraft. Gaia should give the distances to individual stars at the distance of γ2 Vel (at V ~ 16) to about ± 3 pc, and tangential velocities to <0.2 km s-1 for stars with V ≤ 20. Such precision will allow searches for radially anisotropic velocity distributions associated with rapid gas expulsion (e.g. Baumgardt & Kroupa 2007) and precisely test whether population A is indeed closer on average than population B.
5.4. Age puzzle
A lingering mystery is that the γ2 Vel system appears to be younger than the cluster (population A) that surrounds it. This issue was extensively discussed in J09, but in brief it was claimed that the age of γ2 Vel, citing work by North et al. (2007), was 3.5 Myr and that this was younger than the low-mass PMS population around it on the basis of (i) comparison with theoretical isochrones in the V − I/V CMD; (ii) empirical comparison of the locus of PMS stars in the CMD with those in other star forming regions of known (or assumed to be known) age. These considerations along with the lack of Li depletion among the G/K-type stars led to an age estimate of 5–10 Myr and to an inferred star forming history where the most massive object (γ2 Vel) forms last in accordance with the “sorted sampling” hypothesis of Weidner & Kroupa (2006).
Using evolutionary models that incorporated binary interactions and rotation, Eldridge (2009) revised the age of γ2 Vel upwards to 5.5 ± 1 Myr, weakening the case for any age discrepancy with the low-mass cluster. However it is now worth revisiting the age of the low-mass cluster too, because the new Li data we present here are more constraining and also because the overall age scale of young clusters, and in particular the ages of the clusters to which the Gamma Vel cluster was compared have been revised.
The absolute age determined by comparison to low-mass isochrones is unchanged with respect to the situation described in J09 and illustrated in their Fig. 13 and in Figs. 4 and 9 in this paper. The results are highly model dependent (models vary because of different assumptions about atmospheres, convective efficiency and opacities), and also depend on how luminosities and temperatures are converted into the observational plane, but currently suggest an age somewhere between 10 and 20 Myr.
In J09 (their Fig. 15), the empirical locus of the low-mass stars in the V − I/V CMD was found to be older than that of σ Ori, λ Ori and NGC 2362, and similar to the 25 Ori cluster. The ages of the three younger clusters have been homogeneously reanalysed using their high-mass populations and revised upwards to 6, 10 and 12 Myr respectively by Bell et al. (2013). Less model-dependence and systematic error is expected from ages determined by stars on the upper part of the main-sequence. On the same age scale the low-mass stars in the Gamma Vel cluster would have empirical isochronal ages >10 Myr.
An older age for the low-mass stars is also consistent with the Li depletion seen among the M-dwarfs (Fig. 12). Ages from Li depletion are also quite model dependent, but the models of Baraffe et al. (1998) predict little depletion for ages less than about 10 Myr (and unlike the CMD isochrones this is independent of the assumed distance). Models with higher convective efficiency can deplete Li faster, but also predict the depletion to occur in somewhat warmer stars first. A full investigation of the Li depletion pattern and comparison with models is deferred to a subsequent GES paper (Franciosini et al., in prep.). An empirical comparison is also possible; for instance Dahm (2005) shows that stars with V − I ~ 2.7 in NGC 2362 (age 12 Myr; Bell et al. 2013) show no evidence for significant Li depletion, whereas the β Pic association (age 21 ± 4 Myr; Binks & Jeffries 2014) has many M-dwarfs where Li cannot be detected (Mentuch et al. 2008). Hence this comparison also suggests that population A is older than 10 Myr (but younger than 20 Myr).
This issue is yet to be resolved conclusively, mainly due to the uncertainties in estimating the absolute ages of low-mass stars and the model-dependence of isochrones in the CMD and of Li depletion. The evidence as it stands still suggests that γ2 Vel formed in a clustered environment and is significantly younger, by at least a few Myr, than the bulk of the surrounding low-mass population. This is qualitatively in agreemement with massive star formation scenarios involving competitive accretion and mergers (e.g. Bonnell & Bate 2005; Bonnell et al. 2011). Perhaps an alternative explanation that might be explored is whether additional mass transfer between the components of γ2 Vel could make them appear younger or whether the system was initially a triple and the present Wolf-Rayet component is the rejuvenated remnant of a merged close binary (e.g. de Mink et al. 2013), although the small separation of the current components may make the latter unlikely.
6. Summary
One of the main goals of GES is to characterise the current dynamical state of young clusters and star forming regions and attempt to infer their histories and predict their futures. A key part of this task is to deliver precision RV for young stars. The work in Sect. 2.3.1 shows that in the best cases (vsini < 30 km s-1 and S/N > 30) that GES RVs have uncertainties of 0.25 km s-1 for a single observation and that this is dominated by systematic uncertainties associated with instrumental calibration.
The excellent RV precision has enabled us to uncover significant velocity structure in the low-mass stars surrounding the massive binary system γ2 Vel. The RV distribution is reasonably modelled with two Gaussian components (populations A and B) with roughly equal numbers in each, one with a very narrow intrinsic width of 0.34 ± 0.16 km s-1 and the other much broader, with a dispersion of 1.60 ± 0.37 km s-1 and offset by 2 km s-1 from the first component. We have searched for other differences in the two overlapping kinematic populations, finding that population A is probably more centrally concentrated around γ2 Vel than population B, and is about 1–2 Myr older from the evidence of significantly more photospheric Li depletion among its mid M-type members.
The velocity dispersion and estimated mass of population A indicate that it is roughly in virial equilibrium, but only tenuously bound, thanks to a short relaxation time and a half-mass radius that is only five times smaller than its tidal radius in the Galactic potential. It seems likely that population A is the bound remnant of an initially larger cluster, formed in a denser region of the Vela OB2 association, that has been partially disrupted by gas expulsion. Population B consists of a scattered population of unbound stars born in less dense regions of Vela OB2. γ2 Vel appears to be younger by at least a few Myr than the bulk of the low-mass population surrounding it, suggesting a formation scenario in which γ2 Vel forms after the low-mass stars, possibly terminating star formation and expelling gas.
Acknowledgments
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. The results presented here benefited from discussions in three Gaia-ESO workshops supported by the ESF (European Science Foundation) through the GREAT (Gaia Research for European Astronomy Training) Research Network Program (Science meetings 3855, 4127 and 4415) This work was partially supported by the Gaia Research for European Astronomy Training (GREAT-ITN) Marie Curie network, funded through the European Union Seventh Framework Programme [FP7/2007-2013] under grant agreement 264895 and supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. RJJ acknowledges financial support from the UK Science and Technology Facilities Council.
References
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Bastian, N. 2011, in Proc. Stellar Clusters and Associations: A RIA Workshop on Gaia, 85 [Google Scholar]
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Binks, A. S., & Jeffries, R. D. 2014, MNRAS, 438, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2005, MNRAS, 362, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Smith, R. J., Clark, P. C., & Bate, M. R. 2011, MNRAS, 410, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Bressert, E., Bastian, N., Gutermuth, R., et al. 2010, MNRAS, 409, L54 [NASA ADS] [Google Scholar]
- Briceño, C., Hartmann, L., Hernández, J., et al. 2007, ApJ, 661, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. A., Sneden, C., Lambert, D. L., & Dutchover, Jr., E. 1989, ApJS, 71, 293 [CrossRef] [Google Scholar]
- Carpenter, J. M. 2000, AJ, 120, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
- Clark, P. C., Bonnell, I. A., Zinnecker, H., & Bate, M. R. 2005, MNRAS, 359, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Cottaar, M., Meyer, M. R., Andersen, M., & Espinoza, P. 2012a, A&A, 539, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cottaar, M., Meyer, M. R., & Parker, R. J. 2012b, A&A, 547, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dahm, S. E. 2005, AJ, 130, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- De Marco, O., & Schmutz, W. 1999, A&A, 345, 163 [NASA ADS] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2013, ApJ, submitted [arXiv:1312.3650] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Eldridge, J. J. 2009, MNRAS, 400, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Fellhauer, M., Wilkinson, M. I., & Kroupa, P. 2009, MNRAS, 397, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Fűrész, G., Hartmann, L. W., Szentgyorgyi, A. H., et al. 2006, ApJ, 648, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Fűrész, G., Hartmann, L. W., Megeath, S. T., Szentgyorgyi, A. H., & Hamden, E. T. 2008, ApJ, 676, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M. 2010, in IAU Symp. 266, eds. R. de Grijs, & J. R. D. Lépine, 69 [Google Scholar]
- Gieles, M., & Portegies Zwart, S. F. 2011, MNRAS, 410, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, C. A., & Sahade, J. 1980, PASP, 92, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Calvet, N., et al. 2008, ApJ, 686, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1980, ApJ, 235, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, R. J., & Jeffries, R. D. 2010, MNRAS, 407, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Oliveira, J. M., Barrado y Navascués, D., & Stauffer, J. R. 2003, MNRAS, 343, 1271 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jeffries, R. D., Maxted, P. F. L., Oliveira, J. M., & Naylor, T. 2006, MNRAS, 371, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Naylor, T., Walter, F. M., Pozzo, M. P., & Devey, C. R. 2009, MNRAS, 393, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Maschberger, T., Moeckel, N., et al. 2012, MNRAS, 419, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Jeffries, R. D., Oliveira, J. M., Naylor, T., & Jackson, R. J. 2008, MNRAS, 385, 2210 [NASA ADS] [CrossRef] [Google Scholar]
- Mentuch, E., Brandeker, A., van Kerkwijk, M. H., Jayawardhana, R., & Hauschildt, P. H. 2008, ApJ, 689, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Millour, F., Petrov, R. G., Chesneau, O., et al. 2007, A&A, 464, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- North, J. R., Tuthill, P. G., Tango, W. J., & Davis, J. 2007, MNRAS, 377, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., Randich, S., Pavlenko, Y. V., Flaccomio, E., & Pallavicini, R. 2007, ApJ, 659, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., Wright, N. J., Goodwin, S. P., & Meyer, M. R. 2014, MNRAS, 438, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Patten, B. M., & Simon, T. 1996, ApJS, 106, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Pelupessy, F. I., & Portegies Zwart, S. 2012, MNRAS, 420, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piau, L., & Turck-Chièze, S. 2002, ApJ, 566, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzo, M., Jeffries, R. D., Naylor, T., et al. 2000, MNRAS, 313, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., & Gilmore, G. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Randich, S., Aharpour, N., Pallavicini, R., Prosser, C. F., & Stauffer, J. R. 1997, A&A, 323, 86 [NASA ADS] [Google Scholar]
- Randich, S., Pallavicini, R., Meola, G., Stauffer, J. R., & Balachandran, S. C. 2001, A&A, 372, 862 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Franciosini, E., Randich, S., & Pallavicini, R. 2008, A&A, 488, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Schmutz, W., & Grenon, M. 1997, ApJ, 484, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Smith, L. F. 1968, MNRAS, 138, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R. 2010, ARA&A, 48, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Jones, B. F., Balachandran, S., et al. 1993, AJ, 106, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1987, Dynamical evolution of globular clusters (Princeton University Press) [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Tobin, J. J., Hartmann, L., Furesz, G., Mateo, M., & Megeath, S. T. 2009, ApJ, 697, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Cantarutti, R., Tighe, R., et al. 2010, PASP, 122, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V. 1978, A&A, 70, 57 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Bonnell, I. A. D. 2010, MNRAS, 401, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zapatero Osorio, M. R., Béjar, V. J. S., Pavlenko, Y., et al. 2002, A&A, 384, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Coordinates, photometry and measurements of RV, EW(Li), vsini and estimated masses for 208 targets selected as Gamma Vel members.
All Figures
 |
Fig. 1 Colour–magnitude diagram for unflagged objects with good photometry (uncertainties <0.1 mag in V and V − I) in a 0.9 deg2 area around γ2 Vel (from Jeffries et al. 2009). Objects with larger red symbols were observed in the GES. The lines shows theoretical 10 Myr PMS isochrones (from Siess et al. 2000; and Baraffe et al. 1998, using a colour–Teff relation tuned to match the Pleiades) at an intrinsic distance modulus of 7.76, and with a reddening and extinction of E(V − I) = 0.055 and AV = 0.131. |
| In the text | |
 |
Fig. 2 Empirically determined RV precision. Upper panel: rms of the empirically estimated RV uncertainties (see text) from pairs of observations within an OB, binned by S/N. A separate set of points is calculated for stars that have an estimated vsini > 30 km s-1 to demonstrate their larger empirical uncertainties. The lines on the plot are loci determined from Eq. (1) using the coefficients A = 0.09 ± 0.01, B = 3.52 ± 0.23, C = 38 ± 8 for several labelled vsini values. The fit is poorly constrained for large vsini and there are some indications that the semi-empirical model underestimates the uncertainties for such stars at high S/N. Lower panel: frequency distribution of empirical RV uncertainties determined from repeated observations within an OB and from repeated observations from separate OBs. The increase in the width of the latter distribution indicates additional uncertainties associated with wavelength calibration between OBs. |
| In the text | |
 |
Fig. 3 Equivalent width of the Li i 6708 Å feature (EW(Li)) versus V − I. Objects selected as candidate members are marked with blue diamonds; red circles mark objects that are potential members based on their photospheric Li content, but fall outside the sequence of members in the colour–magnitude diagram (see Fig. 4). Triangles mark upper limits. The solid red lines show theoretical isochrones at 10 Myr and 20 Myr from the models of Baraffe et al. (1998, see text), reddened with E(V − I) = 0.055. The dashed line marks the upper envelope of EW(Li) for IC 2391 and IC 2602 at ages ≃50 Myr. |
| In the text | |
 |
Fig. 4 Colour–magnitude diagram for the Gamma Vel targets. Blue diamonds show the Li-rich targets we select as members (see Fig. 3); red circles are Li-rich targets that do not follow the sequence defined by the bulk of cluster members and are excluded. Solid red lines show isochrones from the Baraffe et al. (1998) evolutionary models (see text), shifted to a distance modulus of 7.76 mag, with reddening E(V − I) = 0.055 and extinction AV = 0.131 applied. |
| In the text | |
 |
Fig. 5 Distribution of RV uncertainties for the selected Gamma Vel members, calculated using Eq. (1). Where objects were observed in more than one OB, the uncertainty in the weighted mean RV is correspondingly smaller. |
| In the text | |
 |
Fig. 6 Binned RV histogram for the Gamma Vel members (note that fitting was carried out on unbinned data). Upper panel: the best fit for a model consisting of a single Gaussian population with a fraction fbin = 0.46 of unresolved binaries (see text). The fit is poor. Lower panel: the best fit for a population represented by two Gaussian components, each with an unresolved binary population. |
| In the text | |
 |
Fig. 7 Likelihood space for σA versus σB for the two-Gaussian fit to the RV distribution. Confidence contours are shown for two parameters of interest. σB > σA with a high degree of confidence. |
| In the text | |
 |
Fig. 8 Probability that each Gamma Vel member belongs to population A in the two-component kinematic model described in Sect. 4.1.2. Relatively secure members of population A (PA > 0.75) and B (PA < 0.25) and objects that cannot be confidently assigned to either population are identified with different symbols in this and subsequent plots. |
| In the text | |
 |
Fig. 9 Colour–magnitude diagram for the two kinematic populations around γ2 Vel. The populations are distinguished here by a simple probability criterion (see Sect. 4.2) into population A (with a narrow RV distribution) or population B (with a broader RV distribution). The other cluster members cannot be assigned to either population with great confidence. |
| In the text | |
 |
Fig. 10 Spatial distribution of populations A and B, defined according to the probability criterion described in Sect. 4.2. In the main panel these populations and the set of cluster members that cannot be confidently assigned to either are shown. Symbols are as defined in Fig. 9. The cross marks the position of γ2 Vel. In the top and side panels we show the distribution of RV with right ascension and declination respectively. The solid (red) lines and the dashed (blue) lines show best-fitting linear relationships for populations A and B respectively. |
| In the text | |
 |
Fig. 11 Projected space density of members of populations A and B, along with that of all the (non-members of the Gamma Vel cluster) targets observed. Population A is more centrally concentrated than population B, though the significance of this is low (see Sect. 4.2.2). |
| In the text | |
 |
Fig. 12 Equivalent width of the Li i 6708 Å line versus colour, with different symbols corresponding to the populations as in Fig. 9. The solid lines are isochrones calculated according to the evolutionary models of Baraffe et al. (1998, with mixing length of 1.0 pressure scale heights) at 10, 15 and 20 Myr, transformed into the observational plane as described in Sect. 3. |
| In the text | |
 |
Fig. 13 Projected rotational velocities as a function of colour. The different symbols correspond to the various populations as described in Fig. 9. Objects with vsini < 10 km s-1 are marked as upper limits (triangles). |
| In the text | |
 |
Fig. 14 UCAC4 proper motions (in milli-arcseconds per year) for our selected Gamma Vel members. The different symbols correspond to the various populations as described in Fig. 9. The proper motion of γ2 Vel itself is shown with a cross. There are 6 objects that lie beyond the borders of the plot. These and the other very discrepant objects show evidence of binarity or lie very close to γ2 Vel and are likely to have unreliable proper motions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


