| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201323059 | |
| Published online | 17 March 2014 | |
A new fitting-function to describe the time evolution of a galaxy’s gravitational potential
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV
Groningen,
The Netherlands
e-mail:
buist@astro.rug.nl
Received:
15
November
2013
Accepted:
19
January
2014
We present a new simple functional form to model the evolution of a spherical mass distribution in a cosmological context. Two parameters control the growth of the system and this is modelled using a redshift-dependent exponential for the scale mass and scale radius. In this new model, systems form inside out and the mass of a given shell can be made never to decrease, as generally expected. This feature makes it more suitable for studying the smooth growth of galactic potentials or cosmological halos than other parametrizations often used in the literature. This is further confirmed through a comparison to the growth of dark matter halos in the Aquarius simulations.
Key words: galaxies: evolution / dark matter
© ESO, 2014
1. Introduction
The cosmological model predicts significant evolution in the mass content of galaxies and of their dark matter halos through cosmic time. This evolution may be directly measurable using stellar streams, as these are typically sensitive probes of the gravitational potential in which they are embedded (Eyre & Binney 2009; Gómez & Helmi 2010). Clearly, to properly model this dynamical evolution it is critical to use a physically motivated representation of the time-dependency of the host’s gravitational potential.
In the literature the time evolution of a galactic potential is often parametrized through the evolution of its characteristic parameters, such as total mass and scale radius. In the case of dark matter halos, the most often used parameters are its virial mass Mvir and concentration c. The virial mass is defined as the mass enclosed within the virial radius rvir, and at this radius the density of the halo ρ(rvir) = Δ × ρcrit, where ρcrit is the critical density of the Universe, and the exact value of Δ depends on cosmology (Navarro et al. 1996, 1997). The evolution of Mvir and c has been thoroughly studied in cosmological numerical simulations (Bullock et al. 2001; Wechsler et al. 2002; Zhao et al. 2003b,a, 2009; Tasitsiomi et al. 2004; Boylan-Kolchin et al. 2010). It has been found that the evolution of the virial mass is well fitted with an exponential in redshift (but see also Tasitsiomi et al. 2004 and Boylan-Kolchin et al. 2010 for more complex functions), while the concentration appears to depend linearly on the expansion factor (Bullock et al. 2001; Wechsler et al. 2002; but see also Zhao et al. 2003b,a, 2009). These relations work well in a statistical sense for an ensemble of halos, but do not always guarantee that the evolution of an individual system is well represented and physical as we discuss below. Furthermore, it has recently been pointed out that part of the evolution in mass, especially at late times, is driven by the definition of virial mass (through its connection to the background cosmology) rather than to a true increase in the mass bound to the system (Diemer et al. 2013).
In this paper, we revisit the most widely used model for the time evolution of dark matter halos (Sect. 2) and show that for certain choices of the characteristic parameters, mass growth does not proceed inside out in this model. In Sect. 3 we develop a new prescription for the time evolution of a general spherical mass distribution that does have that property. In Sect. 4 we compare this model to the growth of dark halos in cosmological simulations and we summarize in Sect. 5.
2. Wechsler’s model of the evolution of NFW halos
 |
Fig. 1 Evolution in time of a halo with virial mass Mvir = 1012 M⊙ and formation epoch ac = 0.15 (for a cosmology with h = 0.7, Ωm = 0.28, and ΩΛ = 0.72) using the Wechsler model. The left panel shows that the mass growth rate reaches a minimum for all shells between t = 1 and t = 7 Gyr, and is negative for the innermost shells, which implies they decrease in mass. The central panel shows the mass history for all shells. The shells show a temporary stall in their growth, or even a decrease in mass, between t = 1 and t = 7 Gyr, before resuming growth again at later times. The right panel shows the mass profile at different epochs. |
The most commonly used approach to model the evolution of dark matter halos is that of
Wechsler et al. (2002). Cosmological simulations
show that halos follow characteristic density profiles known as NFW after the seminal work
of Navarro et al. (1996). Generally, a two-parameter
mass-profile may be expressed as 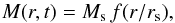 (1)with rs(t) the scale radius,
Ms(t) the mass contained
within the scale radius, and f(x) the functional form of the mass
profile, with f(1) = 1. The relative mass growth rate Ṁ/M is
(1)with rs(t) the scale radius,
Ms(t) the mass contained
within the scale radius, and f(x) the functional form of the mass
profile, with f(1) = 1. The relative mass growth rate Ṁ/M is
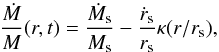 (2)where κ(x) is the
logarithmic slope of the mass profile
(2)where κ(x) is the
logarithmic slope of the mass profile
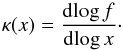 (3)Typically
κ(x) is a positive monotonically
decreasing function of radius. For the NFW profile, f(x) is
given by
(3)Typically
κ(x) is a positive monotonically
decreasing function of radius. For the NFW profile, f(x) is
given by 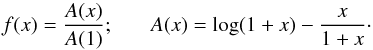 (4)The relation
between Ms and virial mass Mvir(t) for an NFW profile
is
(4)The relation
between Ms and virial mass Mvir(t) for an NFW profile
is 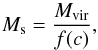 (5)where the
concentration c ≡ rvir/rs.
As discussed in the Introduction, the virial radius is defined as the radius at which the
spherically averaged density reaches a certain threshold value ρc. For a given
choice of ρc, the virial radius and the virial mass
are related through
(5)where the
concentration c ≡ rvir/rs.
As discussed in the Introduction, the virial radius is defined as the radius at which the
spherically averaged density reaches a certain threshold value ρc. For a given
choice of ρc, the virial radius and the virial mass
are related through 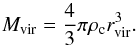 (6)Therefore, only two
parameters from the set {Ms, rs,
Mvir, c} are needed to fully
specify the profile. According to Wechsler et al.
(2002) the virial mass evolves as
(6)Therefore, only two
parameters from the set {Ms, rs,
Mvir, c} are needed to fully
specify the profile. According to Wechsler et al.
(2002) the virial mass evolves as
![\begin{equation} M_\text{vir}(z) = M_{\rm O} \exp{\left[-2 a_{\rm c} (z - z_{\rm O})\right]} , \end{equation}](/articles/aa/full_html/2014/03/aa23059-13/aa23059-13-eq31.png) (7)with MO = Mvir(zO)
and zO the epoch where the halo is “observed”.
The formation epoch ac is arbitrarily defined to be the
expansion factor at which dlog M/dlog a = 2. Wechsler
et al. (2002) found the concentration to evolve on average as
(7)with MO = Mvir(zO)
and zO the epoch where the halo is “observed”.
The formation epoch ac is arbitrarily defined to be the
expansion factor at which dlog M/dlog a = 2. Wechsler
et al. (2002) found the concentration to evolve on average as
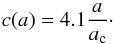 (8)Halos with more quiescent
histories are best described by these relations, while violent mergers can lead to
significant departures from these smooth functions.
(8)Halos with more quiescent
histories are best described by these relations, while violent mergers can lead to
significant departures from these smooth functions.
The Wechsler model can give realistic trajectories in Mvir(t) and c(t) for many individual halos. However, Fig. 1 shows a problem case. In this figure we have plotted the behaviour predicted for a halo of 1012 M⊙ and ac = 0.15. The left panel shows the mass growth rate Ṁ/M as a function of time for different shells in the halo. We note that the mass growth rate of a given shell decreases with time, as expected, but that for inner shells it becomes negative, indicating that the mass in the shell has decreased. At later times, the mass growth for the inner shells seems to increase and even exceeds the growth rate at larger radii.
This behaviour is unexpected in the ΛCDM cosmology, as halos tend to form inside out (Helmi et al. 2003; Wang et al. 2011), implying that the inner shells collapse first and should not grow further at late times by smooth accretion; usually a redistribution of mass is only expected during major mergers. Let us now look in more detail at what causes this odd unphysical behaviour.
From Eq. (2), the condition that leads to a
violation of Ṁ/M > 0
at a given radius is 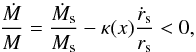 (9)which we can express in
terms of Mvir(t) and
c(t) using that
(9)which we can express in
terms of Mvir(t) and
c(t) using that
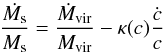 (10)and
(10)and
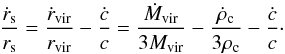 (11)This leads to
(11)This leads to
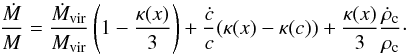 (12)Since for an NFW it can be
shown that κ(x) ≤ 2, for the Wechsler model, the
first term is
(12)Since for an NFW it can be
shown that κ(x) ≤ 2, for the Wechsler model, the
first term is 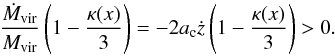 (13)On the other hand,
since κ(x) is a monotonically decreasing
function, the second term is
(13)On the other hand,
since κ(x) is a monotonically decreasing
function, the second term is 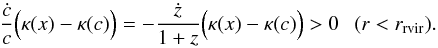 (14)Finally, the last term in
Eq. (12) is always negative as
(14)Finally, the last term in
Eq. (12) is always negative as
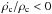 . This implies that there may be
times and radii for which the combination of the various terms is negative, leading to a
decrease in the mass contained within a given shell. The above analysis shows that the
Wechsler model has this behaviour because of pseudo-evolution: the virial mass is defined
with respect to the cosmological background density and this background density evolves in
time.
. This implies that there may be
times and radii for which the combination of the various terms is negative, leading to a
decrease in the mass contained within a given shell. The above analysis shows that the
Wechsler model has this behaviour because of pseudo-evolution: the virial mass is defined
with respect to the cosmological background density and this background density evolves in
time.
3. Alternative model
 |
Fig. 2 Evolution in time of the same final halo of Fig. 1, but using our new model with ag = 0.04 and γ = 2. Left panel: the relative growth rate does not reach a minimum, nor does it reach negative values. This implies that the shells grow at all times, but as the central panel shows, the mass growth history for the shells flattens out towards the end. The behaviour at the virial radius follows closely (but not exactly) the Wechsler model, as shown by the dash-dotted curve. Right panel: mass profile at different epochs. |
We have explored a different way of modelling the evolution of a mass profile, by directly
focusing on the growth of the scale radius rs(t) and the scale mass
Ms(t). We require our
model to have non-negative mass growth at all times and at every radius
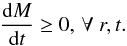 (15)In addition, we require
that the mass grows inside out, which means that the relative mass growth rate should
increase with radius
(15)In addition, we require
that the mass grows inside out, which means that the relative mass growth rate should
increase with radius 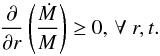 (16)The logarithmic slope
κ(x) in Eq. (2) is essential in the determination of whether
these conditions are satisfied. Because κ(x) is a monotonically decreasing
positive function, we can set a lower limit on the mass growth
(16)The logarithmic slope
κ(x) in Eq. (2) is essential in the determination of whether
these conditions are satisfied. Because κ(x) is a monotonically decreasing
positive function, we can set a lower limit on the mass growth
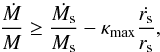 (17)where
κmax is the maximum value of κ(x). For
NFW and Hernquist profiles κmax = 2, for Jaffe profiles
κmax = 1, while for the Plummer and
isochrone potentials κmax = 3. The condition Ṁ/M = 0 would lead
to a solution of the form
(17)where
κmax is the maximum value of κ(x). For
NFW and Hernquist profiles κmax = 2, for Jaffe profiles
κmax = 1, while for the Plummer and
isochrone potentials κmax = 3. The condition Ṁ/M = 0 would lead
to a solution of the form 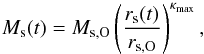 (18)with rs,O and Ms,O the scale mass and
scale radius at some epoch zO. Motivated by this we propose that in
general, a solution of Eq. (2) should be of
the form
(18)with rs,O and Ms,O the scale mass and
scale radius at some epoch zO. Motivated by this we propose that in
general, a solution of Eq. (2) should be of
the form 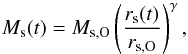 (19)where
γ > 0 is a constant. This
functional form is also supported by the work of Zhao et al.
(2003a,b), who used N-body cosmological
simulations to show that a strong correlation between rs and
Ms
exists. This correlation may be modelled as a power law with exponent 3α (so γ = 3α) for
NFW profiles. The growth equation is then given by
(19)where
γ > 0 is a constant. This
functional form is also supported by the work of Zhao et al.
(2003a,b), who used N-body cosmological
simulations to show that a strong correlation between rs and
Ms
exists. This correlation may be modelled as a power law with exponent 3α (so γ = 3α) for
NFW profiles. The growth equation is then given by
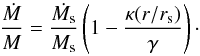 (20)Assuming that
Ṁs ≥ 0, the mass growth rate is positive at
every radius for γ ≥ κmax, while for
γ < κmax
the mass will decrease at radii where γ < κ(r/rs).
The critical radius rcrit occurs where γ = κ(rcrit/rs).
Since at early times rs ≪ 1, all radii are beyond the critical
radius and the mass increases everywhere. As the scale radius grows, eventually some radii
move inside the critical radius. When this occurs, the mass at those radii would actually
decrease according to this model, but this can be avoided with a proper choice of
γ.
(20)Assuming that
Ṁs ≥ 0, the mass growth rate is positive at
every radius for γ ≥ κmax, while for
γ < κmax
the mass will decrease at radii where γ < κ(r/rs).
The critical radius rcrit occurs where γ = κ(rcrit/rs).
Since at early times rs ≪ 1, all radii are beyond the critical
radius and the mass increases everywhere. As the scale radius grows, eventually some radii
move inside the critical radius. When this occurs, the mass at those radii would actually
decrease according to this model, but this can be avoided with a proper choice of
γ.
This model also ensures that the mass grows inside out since
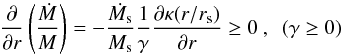 (21)and the gradient of
the logarithmic slope of κ(x) is negative.
(21)and the gradient of
the logarithmic slope of κ(x) is negative.
For the evolution of the parameters Ms(t) and rs(t) we propose an
exponential behaviour similar to that used by Wechsler et
al. (2002), i.e. ![\begin{equation} M_{\rm s}(z) = M_{\rm s,O} \exp{\left[-2 a_{\rm g} (z - z_{\rm O})\right]} , \label{eq:mass_z} \end{equation}](/articles/aa/full_html/2014/03/aa23059-13/aa23059-13-eq80.png) (22)with ag the growth
parameter of the halo. Using Eq. (19), the
evolution of rs is given by
(22)with ag the growth
parameter of the halo. Using Eq. (19), the
evolution of rs is given by ![\begin{equation} r_{\rm s}(z) = r_{\rm s,O} \exp{\left[-2 \frac{a_{\rm g}}{\gamma} (z - z_{\rm O})\right]} . \label{eq:rs_z} \end{equation}](/articles/aa/full_html/2014/03/aa23059-13/aa23059-13-eq82.png) (23)This model has two free
parameters (after one has fixed zO), namely ag which
determines the growth of Ms, and γ, which is related to the
growth rate of the scale radius through ag/γ.
Figure 2 shows the evolution of a 1012 M⊙ halo that has the same
final mass and scale radius as that in Fig. 1, taking
ag = 0.04 and γ = 2 to produce a similar
growth history. The evolution of the halo is as desired: the mass growth rate (left panel)
is always positive and slows down as time goes by, and this slowing down is more pronounced
for the innermost shells. The halo thus forms inside out as expected (central panel), and
there is no mass exchange/decrease between neighbouring shells. In this figure we have also
plotted the behaviour of Mvir(t), determined using
Eqs. (1) and (6). We note with satisfaction that the evolution of the virial mass for
our model is very similar to that of Wechsler et al.
(2002).
(23)This model has two free
parameters (after one has fixed zO), namely ag which
determines the growth of Ms, and γ, which is related to the
growth rate of the scale radius through ag/γ.
Figure 2 shows the evolution of a 1012 M⊙ halo that has the same
final mass and scale radius as that in Fig. 1, taking
ag = 0.04 and γ = 2 to produce a similar
growth history. The evolution of the halo is as desired: the mass growth rate (left panel)
is always positive and slows down as time goes by, and this slowing down is more pronounced
for the innermost shells. The halo thus forms inside out as expected (central panel), and
there is no mass exchange/decrease between neighbouring shells. In this figure we have also
plotted the behaviour of Mvir(t), determined using
Eqs. (1) and (6). We note with satisfaction that the evolution of the virial mass for
our model is very similar to that of Wechsler et al.
(2002).
 |
Fig. 3 Mass growth history for various radial shells, normalised to the final value as in Fig. 2, for different values of ag and γ. The formation epoch ag changes the growth of the individual shells and the overall growth pattern of the halo. This can also be seen in the half-mass time of the shells indicated with a plus on every curve. The parameter γ mostly influences how individual shells grow. This is seen as we change γ from 2 to 4 (left vs. right panels): only a small effect is seen in the overall growth of the halo, but the inner shells grow on much shorter timescales than the outer shells. |
In Fig. 3 we show the effect of changing the slope γ and the formation epoch ag. For example, for smaller ag (bottom panels) the mass growth occurs earlier, and the growth rate today is lower. The parameter γ does not alter the overall evolution of the halo very much, but changes the (relative) growth pattern for the individual radial shells. For example, for γ = 2 (left panels) the inner shells grow much faster than the outer shells, while for γ = 4 (right panels) the difference in mass growth between the different shells is much smaller.
4. Comparison with simulations
 |
Fig. 4 Mass growth history of the Milky Way-like Aquarius halos at different radii compared to the fit obtained using our model for rs and Ms (colour dashed curves) and fitted for z < 6 to avoid the epoch of significant mergers. The dashed orange line indicates the evolution of the scale mass Ms. Setting γ = 2 also gives a reasonable fit as indicated by the dotted grey curve for each halo. |
To further justify our model, we have studied how well it describes the behaviour of the Milky Way-like dark matter halos from the Aquarius project simulations (Springel et al. 2008). This is a suite of six cosmological dark matter N-body simulations that were run at a variety of resolutions. We used an intermediate resolution level, in which the Aquarius Milky Way-like (or main) halos have ~5 × 106 particles, and we focused on the behaviour of halos Aq-A-4 to Aq-E-4 (the sixth halo, Aq-F, experiences a major merger at low redshift and so is not considered in our analysis). For each main halo, we computed the spherically averaged density profile at each output redshift and fitted the NFW functional form with parameters Ms and rs. We only used snapshots with z < 6 to avoid the epoch of major merger activity. In this way we determine the behaviour of Ms and rs with redshift for each halo, to which we then fit our model to determine ag and γ/ag in Eqs. (22) and (23).
The mass growth history of the halos and the results of our fitting procedure are shown in Fig. 4. The values of ag for halos Aq-A and Aq-C are low (0.05 and 0.04, respectively), implying an early formation, while Aq-B, Aq-D, and Aq-E having formed later, have larger ag (0.14, 0.10, and 0.09, respectively). This is consistent with the results of Boylan-Kolchin et al. (2010), who studied the mass accretion history of Milky Way-mass halos in the Millenium-II cosmological simulations. These authors found that halos D and E follow the median history, while halos A and C form earlier. Halo B was found to catch up with the median growth around z ≈ 2. In view of this, we may argue that a value ag ~ 0.1 roughly corresponds to the median mass accretion history of Milky Way-mass halos.
The values of the slope γ determined in our fits are close to 2, the κmax for the NFW potential, but generally tend to be slightly smaller, which would imply a mass decrease for some shells. Figure 4 shows that halo Aq-A depicts this behaviour early in its history. Nonetheless, we find that for all halos, setting γ = 2 also produces a reasonable fit to the evolution history in Ms and rs, as can be seen from the grey dotted line in this figure.
In order to relate our results more closely to the Wechsler et al. (2002) model, we determined the ac values for halos Aq-A to Aq-E, and found these to be in the range 0.1 to 0.2, therefore appearing at the lower end of the distribution given by Wechsler et al. in their Fig. 8. This could be due to the more quiescent merger history of the Aq-halos.
5. Summary and conclusions
We have studied the evolution of a spherical mass distribution in a cosmological context. Since we expect galaxies (and their halos) to grow inside out, inner shells should form earlier than outer ones, and in the smooth accretion regime, their mass should not decrease with time. Motivated by violations of these conditions found in some models often used in the literature for certain regions of parameter space, we have presented an alternative way of modelling the mass evolution of a spherical potential. In our model, we let the scale radius and the mass at the scale radius grow exponentially with redshift, but relate them in such a way that the condition of no mass decrease at any radius can always be satisfied. The setup is quite general, and can be applied to any spherical density profile. The model has two parameters that can be chosen to obtain a variety of growth histories, providing more control over the growth rate of shells at different radii.
In comparison to previous work, our model does not differ greatly from that presented by Zhao et al. (2003b,a, 2009) who also use a power-law relation between scale mass and scale radius to describe the growth of dark matter halos in cosmological simulations, except that we have found a general condition under which a system following a given density profile will grow inside out. Tasitsiomi et al. (2004) found that some accretion histories were better fitted using a power law of the scale factor a, instead of an exponential in redshift z, and proposed a mass accretion history that combines both the power-law relation and the exponential behaviour. Boylan-Kolchin et al. (2010) proposed a slight modification to this model, which gives even better fits to the MS-II simulations. Their addition of an extra parameter allows the halos to grow earlier and to reach a much lower growth rate at later times.
However, given that the comparison to the growth of dark matter halos in the Aquarius simulations shows that our model works quite well, we believe it is worthwhile to keep its simplicity, particularly in applications that model the behaviour of streams in time-dependent Galactic potentials (Bullock & Johnston 2005; Gómez & Helmi 2010; Gómez et al. 2010).
Acknowledgments
We are grateful to Volker Springel, Simon White, and Carlos Frenk for generously allowing us to use the Aquarius simulations. Carlos Vera-Ciro is acknowledged for his help in the analysis of these simulations. H.J.T.B. and A.H. gratefully acknowledge financial support from ERC-Starting Grant GALACTICA-240271.
References
- Boylan-Kolchin, M., Springel, V., White, S. D. M., & Jenkins, A. 2010, MNRAS, 406, 896 [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Diemer, B., More, S., & Kravtsov, A. V. 2013, ApJ, 766, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Eyre, A., & Binney, J. 2009, MNRAS, 400, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, F. A., & Helmi, A. 2010, MNRAS, 401, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, F. A., Helmi, A., Brown, A. G. A., & Li, Y.-S. 2010, MNRAS, 408, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., White, S. D. M., & Springel, V. 2003, MNRAS, 339, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Tasitsiomi, A., Kravtsov, A. V., Gottlöber, S., & Klypin, A. A. 2004, ApJ, 607, 125 [Google Scholar]
- Wang, J., Navarro, J. F., Frenk, C. S., et al. 2011, MNRAS, 413, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2003a, ApJ, 597, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D. H., Mo, H. J., Jing, Y. P., & Börner, G. 2003b, MNRAS, 339, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2009, ApJ, 707, 354 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Evolution in time of a halo with virial mass Mvir = 1012 M⊙ and formation epoch ac = 0.15 (for a cosmology with h = 0.7, Ωm = 0.28, and ΩΛ = 0.72) using the Wechsler model. The left panel shows that the mass growth rate reaches a minimum for all shells between t = 1 and t = 7 Gyr, and is negative for the innermost shells, which implies they decrease in mass. The central panel shows the mass history for all shells. The shells show a temporary stall in their growth, or even a decrease in mass, between t = 1 and t = 7 Gyr, before resuming growth again at later times. The right panel shows the mass profile at different epochs. |
| In the text | |
 |
Fig. 2 Evolution in time of the same final halo of Fig. 1, but using our new model with ag = 0.04 and γ = 2. Left panel: the relative growth rate does not reach a minimum, nor does it reach negative values. This implies that the shells grow at all times, but as the central panel shows, the mass growth history for the shells flattens out towards the end. The behaviour at the virial radius follows closely (but not exactly) the Wechsler model, as shown by the dash-dotted curve. Right panel: mass profile at different epochs. |
| In the text | |
 |
Fig. 3 Mass growth history for various radial shells, normalised to the final value as in Fig. 2, for different values of ag and γ. The formation epoch ag changes the growth of the individual shells and the overall growth pattern of the halo. This can also be seen in the half-mass time of the shells indicated with a plus on every curve. The parameter γ mostly influences how individual shells grow. This is seen as we change γ from 2 to 4 (left vs. right panels): only a small effect is seen in the overall growth of the halo, but the inner shells grow on much shorter timescales than the outer shells. |
| In the text | |
 |
Fig. 4 Mass growth history of the Milky Way-like Aquarius halos at different radii compared to the fit obtained using our model for rs and Ms (colour dashed curves) and fitted for z < 6 to avoid the epoch of significant mergers. The dashed orange line indicates the evolution of the scale mass Ms. Setting γ = 2 also gives a reasonable fit as indicated by the dotted grey curve for each halo. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


