| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 28 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322867 | |
| Published online | 27 February 2014 | |
Classifying orbits in galaxy models with a prolate or an oblate dark matter halo component⋆
Department of PhysicsSchool of Science, Aristotle University of
Thessaloniki,
541 24
Thessaloniki,
Greece
e-mail:
evzotos@physics.auth.gr
Received:
17
October
2013
Accepted:
3
January
2014
Aims. The distinction between regular and chaotic motion in galaxies is undoubtedly an issue of paramount importance. We explore the nature of orbits of stars moving in the meridional plane (R,z) of an axially symmetric galactic model with a disk, a spherical nucleus, and a flat biaxial dark matter halo component. In particular, we study the influence of all the involved parameters of the dynamical system by computing both the percentage of chaotic orbits and the percentages of orbits of the main regular resonant families in each case.
Methods. To distinguish between ordered and chaotic motion, we use the smaller alignment index (SALI) method to extensive samples of orbits by numerically integrating the equations of motion as well as the variational equations. Moreover, a method based on the concept of spectral dynamics that utilizes the Fourier transform of the time series of each coordinate is used to identify the various families of regular orbits and also to recognize the secondary resonances that bifurcate from them. Two cases are studied for every parameter: (i) the case where the halo component is prolate and (ii) the case where an oblate dark halo is present.
Results. Our numerical investigation indicates that all the dynamical quantities affect, more or less, the overall orbital structure. It was observed that the mass of the nucleus, the halo flattening parameter, the scale length of the halo, the angular momentum, and the orbital energy are the most influential quantities, while the effect of all the other parameters is much weaker. It was also found that all the parameters corresponding to the disk only have a minor influence on the nature of orbits. Furthermore, some other quantities, such as the minimum distance to the origin, the horizontal, and the vertical force, were tested as potential chaos detectors. Our analysis revealed that only general information can be obtained from these quantities. We also compared our results with early related work.
Key words: Galaxy: kinematics and dynamics / galaxies: halos / galaxies: structure
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
One of the most controversial topics in astronomy is that of dark matter, which was introduced by Zwicky (1933) about a century ago. In his pioneer work, he discovered that the mass-to-light ratio (M/L) of the Coma cluster had larger value than those known from luminous parts of nearby galaxies. Therefore, in an attempt to explain and justify this phenomenon, he claimed the existence of an invisible (dark) matter. About forty years later, Ostriker et al. (1974) proposed that dark matter should be concentrated in extended galactic haloes. Hot X-ray emitting haloes have been used to estimate the total mass of galaxies (e.g., McLaughlin 1999). Computing the values of M/L in several galaxies shows that it always exceeds the maximum values of stellar populations and, therefore, only the presence of dark matter can explain the missing mass. Another solid indication for the presence of dark matter in galaxies is the flattened rotation curves at large galactocentric distances (Rubin et al. 1980). Analysis of rotation curves of spiral galaxies (e.g., Bosma 1981; Rubin & Burstein 1988) denotes that their profiles cannot be explained without the presence of non-radiating (invisible) dark matter.
Furthermore, the presence of dark matter haloes in galaxies is indeed expected by the standard cold dark matter (CDM) cosmology models regarding formation of galaxies. The most well-known model for CDM haloes is the flattened cuspy Navarro Frenk White (NFW) model (Navarro et al. 1996, 1997), which is simplified to be spherical. Most CDM models, however, take considerable deviations from the standard spherically symmetric dark matter halo distributions into account. For instance, the model of formation of dark matter haloes in a universe dominated by CDM by Frenk et al. (1988) produced triaxial haloes with a preference for prolate configurations. In addition, numerical simulations of dark matter halo formation conducted by Dubinski & Carlberg (1991) are consistent with haloes that are triaxial and flat. There are roughly equal numbers of dark halos with oblate and prolate forms.
Observational data indicate that disk galaxies are often surrounded by massive and extended dark matter haloes. The best tool to study dark matter haloes in galaxies, as explained earlier, is the galactic rotation curve derived from neutral hydrogen HI (e.g., Clemens 1985; Persic & Salucci 1995; Honma & Sofue 1997). However, the determination of the exact shape of a dark matter halo is a challenging task. Numerical simulations suggest that dark matter galactic haloes are not only spherical, but may also be oblate, prolate, or even triaxial (e.g., Merritt & Fridman 1996; Cooray 2000; Kunihito et al. 2000; Olling & Merrifield 2000; Jing & Suto 2002; Wechsler et al. 2002; Kasun & Evrard 2005; Allgood et al. 2006; Capuzzo-Dolcetta et al. 2007; Wang et al. 2009; Evans & Bridle 2009; Caranicolas & Zotos 2009, 2010, 2011). The variety of the shapes of galactic haloes points out that the structure of these objects plays an important role in the orbital behavior and, generally, in the dynamics of a galaxy.
Knowing the regular or chaotic nature of orbits in galaxies is an issue of great importance. This is true because this knowledge allow us to understand and interpret the formation and also predict the evolution of galaxies. In addition, families of regular orbits are often used as the basic tool in constructing a dynamical model for describing the main properties of galaxies. Over the last several decades, a huge amount of research work has been devoted to understanding the orbital structure in different types of galaxy models (e.g., Pfenniger 1984; Contopoulos & Grosbøl 1989; Sellwood & Wilkinson 1993; Pfenniger 1996; Ollé & Pfenniger 1998; Pichardo et al. 2004). However, the vast majority of the existing literature deals only either with the distinction between regular and chaotic motion (e.g., Manos & Athanassoula 2011; Bountis et al. 2012; Manos et al. 2013) or the detection of periodic orbits and the analysis of their stability (e.g., Skokos et al. 2002a,b; Kaufmann & Patsis 2005). We would like to note that all the above-mentioned references on the dynamics of galaxies are exemplary rather than exhaustive. In the present paper, on the other hand, we proceed one step further contributing to this active field by classifying ordered orbits into different regular families.
In Caranicolas & Zotos (2009), a three-dimensional galactic model consisting of a disk, a spherical nucleus, and a logarithmic asymmetric dark matter halo component was used. For simplicity, we chose a nearly spherical dark matter halo with an internal, small deviation from spherical symmetry described by the term −λx3. The results of this work suggest that even small asymmetries in the galactic halo play a significant role in the nature of three-dimensional orbits stars, mainly by depopulating the box family; the box orbits become chaotic as the value of the internal perturbation increases. In the same vein, a similar three-dimensional composite galaxy model was utilized in Caranicolas & Zotos (2011), however, in this case the dark mater halo was modeled by a mass Plummer potential. The mass of the halo was found to be an important physical quantity, acting as a chaos controller in galaxies. In particular, the percentage of chaotic orbits reduces rapidly as the mass of the spherical dark halo increases. Moreover, it was found that the amount of chaos is higher in asymmetric triaxial galaxies when they are surrounded by less concentrated spherical dark halo components.
In two earlier papers (Caranicolas 1997; Papadopoulos & Caranicolas 2006), two-dimensional, axially symmetric or non-axially symmetric active galaxy models with an additional spherical halo component were studied. In both cases it was observed that the presence of a spherical halo resulted in reduced area in the phase space occupied by the chaotic orbits. Moreover, the behavior of orbits in an active galaxy with a biaxial (prolate or oblate) dark matter halo was investigated recently in Caranicolas & Zotos (2010, hereafter Paper I). In this work, we studied how the regular or chaotic nature of orbits is influenced by some important quantities of the system, such as the flattening parameter of the halo, the scale length of the halo component, and the conserved component of the angular momentum. It was found that when a biaxial halo component is present there is a linear relationship between the chaotic percentage in the phase plane and the flattening parameter. In contrast, the relation between chaos and the scale length of the halo was found to be not linear but exponential. A similar model was used in Helmi (2004) for numerical simulations of the evolution of a system like the Sagittarius dSph in a variety of galactic potentials varying the flattening parameter. In the current research, we use the results of Paper I as a starting point and we try to explore how all the involved parameters influence the overall orbital structure, not only distinguishing between order and chaos, but taking a step further by classifying and distributing all regular orbits into different families (e.g., Zotos & Carpintero 2013; Caranicolas & Zotos 2013; Zotos & Caranicolas 2013a,b).
The present article is organized as follows. In Sect. 2, we present in detail the structure and the properties of our gravitational galactic model. In Sect. 3, we describe the computational methods we used in order to determine the character of orbits. In the following section, we investigate how the involved parameters of the dynamical system influence the nature of the orbits when a prolate or an oblate dark halo component is present. In Sect. 5, we present some heuristic arguments in an attempt to support and explain the numerically obtained outcomes of the previous Section. Our paper ends with Sect. 6, where the discussion and the conclusions of this research are presented.
2. Presentation and properties of the galactic model
In the present work, we investigate the character of motion in the meridional plane of an axially symmetric galaxy model with a disk, a spherical nucleus, and a flat biaxial dark halo component. For this purpose, we use the usual cylindrical coordinates (R,φ,z), where z is the axis of symmetry.
The total potential V(R,z) in our model consists of
three components: (i) the disk potential Vd; (ii) the central spherical component
Vn; and (iii) the dark matter halo component
Vh. The first one is represented by a
generalization of the Miyamoto & Nagai (1975)
potential (see also Carlberg & Innanen 1987;
Caranicolas & Innanen 1991) 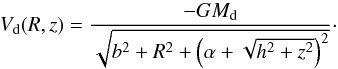 (1)Here G is the gravitational
constant, Md is the mass of the disk, b is the core radius of the
disk-halo, α is
the scale length of the disk, while h corresponds to the disk’s scale height. Here we
should note that potential (1) is very
similar to the potential introduced by Satoh (Satoh
1980). On the other hand, a new gravitational model, which is a combination of the
standard logarithmic and the Miyamoto-Nagai model, was proposed by Zotos (2011) to describe the motion of stars both in elliptical and disk
galaxies. For the description of the spherically symmetric nucleus, we use a Plummer
potential (e.g., Binney & Tremaine 2008)
(1)Here G is the gravitational
constant, Md is the mass of the disk, b is the core radius of the
disk-halo, α is
the scale length of the disk, while h corresponds to the disk’s scale height. Here we
should note that potential (1) is very
similar to the potential introduced by Satoh (Satoh
1980). On the other hand, a new gravitational model, which is a combination of the
standard logarithmic and the Miyamoto-Nagai model, was proposed by Zotos (2011) to describe the motion of stars both in elliptical and disk
galaxies. For the description of the spherically symmetric nucleus, we use a Plummer
potential (e.g., Binney & Tremaine 2008)
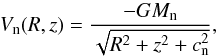 (2)where Mn and
cn
are the mass and the scale length of the nucleus, respectively. This potential has been used
successfully in the past to model and, therefore, interpret the effects of the central mass
component in a galaxy (see, e.g., Hasan & Norman
1990; Hasan et al. 1993; Zotos 2012). At this point, we must clarify that we do
not include any relativistic effects, because the nucleus represents a bulge rather than a
black hole or any other compact object. The potential of the dark matter halo is modeled by
the flattened axisymmetric logarithmic potential
(2)where Mn and
cn
are the mass and the scale length of the nucleus, respectively. This potential has been used
successfully in the past to model and, therefore, interpret the effects of the central mass
component in a galaxy (see, e.g., Hasan & Norman
1990; Hasan et al. 1993; Zotos 2012). At this point, we must clarify that we do
not include any relativistic effects, because the nucleus represents a bulge rather than a
black hole or any other compact object. The potential of the dark matter halo is modeled by
the flattened axisymmetric logarithmic potential 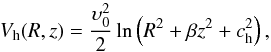 (3)where β is the flattening parameter
and ch stands for the scale length of the dark
halo component. The parameter υ0 is used for the consistency of the
galactic units. The choice for the logarithmic potential was motivated for several reasons:
(i) it can model a wide variety of shapes of galactic haloes by suitably choosing the
parameter β. In
particular, when 0.1 ≤ β < 1 the dark matter
halo is prolate, when β = 1 is spherical, while when 1 < β < 2
is oblate; (ii) it is appropriate for the description of motion in a dark matter halo as it
produces a flat rotation curve at large radii (see Fig. 1); (iii) it allows for the investigation of flattened configurations of the
galactic halo at low computational costs; (iv) the relatively small number of input
parameters of Eq. (3) is an advantage
concerning the performance and speed of the numerical model; and (v) the flattened
logarithmic potential was utilized successfully in previous works to model a dark matter
halo component (see, e.g. Helmi 2004; Ružička et al. 2007).
(3)where β is the flattening parameter
and ch stands for the scale length of the dark
halo component. The parameter υ0 is used for the consistency of the
galactic units. The choice for the logarithmic potential was motivated for several reasons:
(i) it can model a wide variety of shapes of galactic haloes by suitably choosing the
parameter β. In
particular, when 0.1 ≤ β < 1 the dark matter
halo is prolate, when β = 1 is spherical, while when 1 < β < 2
is oblate; (ii) it is appropriate for the description of motion in a dark matter halo as it
produces a flat rotation curve at large radii (see Fig. 1); (iii) it allows for the investigation of flattened configurations of the
galactic halo at low computational costs; (iv) the relatively small number of input
parameters of Eq. (3) is an advantage
concerning the performance and speed of the numerical model; and (v) the flattened
logarithmic potential was utilized successfully in previous works to model a dark matter
halo component (see, e.g. Helmi 2004; Ružička et al. 2007).
In this work, we use a system of galactic units where the unit of length is 1 kpc, the unit of velocity is 10 km s-1, and G = 1. Thus, the unit of mass is 2.325 × 107 M⊙, that of time is 0.9778 × 108 yr, the unit of angular momentum (per unit mass) is 10 km kpc-1 s-1, and the unit of energy (per unit mass) is 100 km2 s-2. Our main objective is to investigate the regular or chaotic nature of orbits in two different cases: that is when the dark matter halo component is (i) prolate (PH model) and (ii) oblate (OH model). Our models have the following standard values of the parameters: Md = 7000 (corresponding to 1.63 × 1011 M⊙, i.e., a normal disk galaxy mass), b = 6, α = 3, h = 0.2, Mn = 250 (corresponding to 5.8 × 109 M⊙), cn = 0.25, υ0 = 20 and ch = 8.5, while β = 0.5 for the PH model and β = 1.5 for the OH model. The values of the disk and the nucleus were chosen with a Milky Way-type galaxy in mind (e.g., Allen & Santillán 1991). In the case of the prolate dark halo, the set of the values of the parameters define the standard prolate model (SPM), while when the dark halo is oblate we use the standard oblate model (SOM). The values of the parameters of the standard models secure positive density everywhere.
 |
Fig. 1 Plot of the rotation curve in our galactic model. We distinguish the total circular velocity (black) and also the contributions from the spherical nucleus (red), the disk (blue) and that of the dark matter halo (green). |
It is well known that in disk galaxies the circular velocity in the galactic plane
z = 0,
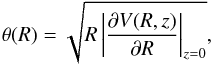 (4)is a very important
physical quantity. A plot of θ(R) for our galactic model1 is presented in Fig. 1 as a black curve. Moreover, in the same plot, the red line shows the
contribution from the spherical nucleus, the blue curve is the contribution from the disk,
while the green line corresponds to the contribution form the dark halo. It is seen that
each contribution prevails in different distances form the galactic center. In particular,
at small distances when R ≤ 2 kpc, the contribution from the spherical nucleus
dominates, while at mediocre distances, 2 < R < 18
kpc, the disk contribution is the dominant factor. On the other hand, at large
galactocentric distances, R > 18 kpc, we see that the
contribution from the dark halo prevails, thus forcing the rotation curve to remain flat
with increasing distance from the center. We also observe the characteristic local minimum
of the rotation curve due to the massive nucleus, which appears when fitting observed data
to a galactic model (e.g., Gómez et al. 2010; Irrgang et al. 2013).
(4)is a very important
physical quantity. A plot of θ(R) for our galactic model1 is presented in Fig. 1 as a black curve. Moreover, in the same plot, the red line shows the
contribution from the spherical nucleus, the blue curve is the contribution from the disk,
while the green line corresponds to the contribution form the dark halo. It is seen that
each contribution prevails in different distances form the galactic center. In particular,
at small distances when R ≤ 2 kpc, the contribution from the spherical nucleus
dominates, while at mediocre distances, 2 < R < 18
kpc, the disk contribution is the dominant factor. On the other hand, at large
galactocentric distances, R > 18 kpc, we see that the
contribution from the dark halo prevails, thus forcing the rotation curve to remain flat
with increasing distance from the center. We also observe the characteristic local minimum
of the rotation curve due to the massive nucleus, which appears when fitting observed data
to a galactic model (e.g., Gómez et al. 2010; Irrgang et al. 2013).
 |
Fig. 2 Iso-density contours for our galactic model when the dark matter halo is a) left: prolate (PH model) and b) right: oblate (OH model). |
It is very useful to compute the mass density ρ(R,z) derived from the total
potential V(R,z) using the Poisson’s equation
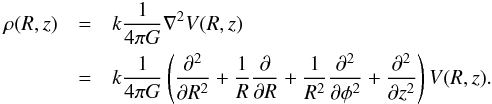 (5)Recall,
that due to the axial symmetry the third term in Eq. (5) is zero. In the same equation, we observe the presence of an
additional parameter k = 2.325 × 10-2, which is simply a
numerical coefficient dictated by the current system of galactic units to obtain the density
in units of M⊙/pc3. Figures 2a,b shows the iso-density contours ρ(R,z) = const.,
for the PH and OH galaxy models, respectively. In Fig. 3, the evolution of the total mass density ρ(R,z = 0)
in the galactic plane for SPM, as a function of the radius R from the galactic center is
shown as the black curve. In the same diagram, the red line shows the contribution from the
spherical nucleus, the blue curve is the contribution from the disk, while the green line
corresponds to the contribution form the dark matter halo. It is evident that the density of
the nucleus decreases rapidly obtaining very low values, while on the other hand, the
density of both the disk and the halo continues to hold significantly larger values. We also
see that when R > 1 kpc, the total mass
density coincides with the density of the disk. Therefore, at large galactocentric
distances, the mass density should vary like 1/R3 (to be more
precise, from the nonlinear fit, we derived that the exact power of the 1/Rn
decrease law of the total mass density is n = 2.847). This means that the total mass
M(R), enclosed in a sphere of radius
R, increases
with the distance. This fact explains why the circular velocity profile shown in Fig. 1 remains flat. Things are quite similar for the SOM. Here,
we must point out that our gravitational potential is truncated ar Rmax = 50 kpc,
otherwise the total mass of the galaxy modeled by this potential would be infinite, which is
obviously not physical.
(5)Recall,
that due to the axial symmetry the third term in Eq. (5) is zero. In the same equation, we observe the presence of an
additional parameter k = 2.325 × 10-2, which is simply a
numerical coefficient dictated by the current system of galactic units to obtain the density
in units of M⊙/pc3. Figures 2a,b shows the iso-density contours ρ(R,z) = const.,
for the PH and OH galaxy models, respectively. In Fig. 3, the evolution of the total mass density ρ(R,z = 0)
in the galactic plane for SPM, as a function of the radius R from the galactic center is
shown as the black curve. In the same diagram, the red line shows the contribution from the
spherical nucleus, the blue curve is the contribution from the disk, while the green line
corresponds to the contribution form the dark matter halo. It is evident that the density of
the nucleus decreases rapidly obtaining very low values, while on the other hand, the
density of both the disk and the halo continues to hold significantly larger values. We also
see that when R > 1 kpc, the total mass
density coincides with the density of the disk. Therefore, at large galactocentric
distances, the mass density should vary like 1/R3 (to be more
precise, from the nonlinear fit, we derived that the exact power of the 1/Rn
decrease law of the total mass density is n = 2.847). This means that the total mass
M(R), enclosed in a sphere of radius
R, increases
with the distance. This fact explains why the circular velocity profile shown in Fig. 1 remains flat. Things are quite similar for the SOM. Here,
we must point out that our gravitational potential is truncated ar Rmax = 50 kpc,
otherwise the total mass of the galaxy modeled by this potential would be infinite, which is
obviously not physical.
 |
Fig. 3 Evolution of the mass density ρ(R) in the galactic plane (z = 0), as a function of the distance R from the center for SPM. The total mass density is shown in black, while we distinguish the three different contributions: the spherical nucleus (red), the disk (blue), and the dark matter halo (green). |
Taking into account that the total potential V(R,z) is axisymmetric, the
z-component
of the angular momentum Lz is conserved. With
this restriction, orbits can be described by means of the effective potential (e.g., Binney & Tremaine 2008) 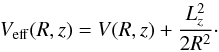 (6)The equations of motion on
the meridional plane are
(6)The equations of motion on
the meridional plane are 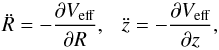 (7)while the equations
governing the evolution of a deviation vector w = (δR,δz,δṘ,δż),
which joins the corresponding phase space points of two initially nearby orbits, needed for
the calculation of the standard indicators of chaos (the SALI in our case), are given by the
variational equations
(7)while the equations
governing the evolution of a deviation vector w = (δR,δz,δṘ,δż),
which joins the corresponding phase space points of two initially nearby orbits, needed for
the calculation of the standard indicators of chaos (the SALI in our case), are given by the
variational equations
![\begin{eqnarray} &&\dot{(\delta R)} = \delta \dot{R}, \ \ \ \dot{(\delta z)} = \delta \dot{z}, \nonumber \\[1mm] &&(\dot{\delta \dot{R}}) = - \frac{\partial^2 V_{\rm eff}}{\partial R^2} \delta R - \frac{\partial^2 V_{\rm eff}}{\partial R \partial z}\delta z, \nonumber \\[1mm] &&(\dot{\delta \dot{z}}) = - \frac{\partial^2 V_{\rm eff}}{\partial z \partial R} \delta R - \frac{\partial^2 V_{\rm eff}}{\partial z^2}\delta z \cdot \label{vareq} \end{eqnarray}](/articles/aa/full_html/2014/03/aa22867-13/aa22867-13-eq69.png) (8)Consequently,
the corresponding Hamiltonian to the effective potential given in Eq. (6) can be written as
(8)Consequently,
the corresponding Hamiltonian to the effective potential given in Eq. (6) can be written as 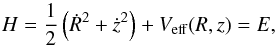 (9)where Ṙ and ż are momenta per unit mass,
and conjugate to R and z, respectively, while E is the numerical value of
the Hamiltonian, which is conserved. Therefore, an orbit is restricted to the area in the
meridional plane satisfying E ≥ Veff.
(9)where Ṙ and ż are momenta per unit mass,
and conjugate to R and z, respectively, while E is the numerical value of
the Hamiltonian, which is conserved. Therefore, an orbit is restricted to the area in the
meridional plane satisfying E ≥ Veff.
3. Computational methods
In our study, we seek to determine whether an orbit is regular or chaotic. Several indicators of chaos are available in the literature; we chose the SALI indicator (Skokos 2001). We use the usual method in which we check after a certain and predefined time interval of numerical integration whether the value of SALI is less than a very small threshold value, in order to decide whether an orbit is ordered or chaotic. In our current research, we define this value to be equal to 10-8. However, depending on the particular location of each orbit, this threshold value can be reached more or less quickly, as there are phenomena that can hold off the final classification of the orbit (i.e., there are special orbits called “sticky” orbits, which behave regularly for long time periods before they finally drift away from the regular regions and start to wander in the chaotic domain, revealing their true chaotic nature fully.
To determine the chaoticity of our models, we chose, for each set of values of the
parameters of the potential, a dense grid of initial conditions in the (R,Ṙ) plane,
regularly distributed in the area allowed by the value of the energy E. In cases, z0 = 0, while
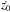 is found from the energy integral (Eq. (9)).
The points of the grid were separated 0.1 units in R and 0.5 units in
Ṙ direction.
For each initial condition, we integrated the equations of motion (7) as well as the variational Eqs. (8) with a double precision Bulirsch-Stoer
algorithm (e.g., Press et al. 1992) with a small time
step of the order of 10-2, which is sufficient enough for the desired accuracy of
our computations (i.e., our results practically do not change by halving the time step). In
all cases, the energy integral (Eq. (9)) was
conserved better than one part in 10-10, although for most orbits it was better than one part
in 10-11.
is found from the energy integral (Eq. (9)).
The points of the grid were separated 0.1 units in R and 0.5 units in
Ṙ direction.
For each initial condition, we integrated the equations of motion (7) as well as the variational Eqs. (8) with a double precision Bulirsch-Stoer
algorithm (e.g., Press et al. 1992) with a small time
step of the order of 10-2, which is sufficient enough for the desired accuracy of
our computations (i.e., our results practically do not change by halving the time step). In
all cases, the energy integral (Eq. (9)) was
conserved better than one part in 10-10, although for most orbits it was better than one part
in 10-11.
 |
Fig. 4 The (R,Ṙ)z = 0, ż > 0 Poincaré surface of section (PSS) for the a) left: standard prolate model (SPM) and b) right: standard oblate model (SOM). |
Each orbit was integrated numerically for a time interval of 104 time units (1012 yr), which corresponds to a time span of the order of hundreds of orbital periods. The particular choice of the total integration time is an element of great importance, especially in the case of the sticky orbits. A sticky orbit could be easily misclassified as regular by any chaos indicator2, if the total integration interval is too small, so that the orbit does not have enough time to reveal its true chaotic character. Thus, all the initial conditions of the orbits of a given grid were integrated, as we already said, for 104 time units, thus avoiding sticky orbits with a stickiness at least of the order of 102 Hubble time. All the sticky orbits that do not show any signs of chaoticity for 104 time units are counted as regular orbits since such vast sticky periods are completely out of the scope of our research.
A first step toward the understanding of the overall behavior of our system is knowing whether the orbits in the galactic model are regular or chaotic. Also of particular interest is the distribution of regular orbits into different families. Therefore, once the orbits have been characterized as regular or chaotic, we then further classified the regular orbits into different families by using a frequency analysis method (Carpintero & Aguilar 1998; Muzzio et al. 2005). Initially, Binney & Spergel (1982, 1984) proposed a technique, dubbed spectral dynamics, for this particular purpose. Later on, this method has been extended and improved by Carpintero & Aguilar (1998) and Šidlichovský and Nesvorný (1996). In a recent work, (Zotos & Carpintero 2013) the algorithm was refined even further so it can be used to classify orbits in the meridional plane. In general terms, this method computes the Fourier transform of the coordinates of an orbit, identifies its peaks, extracts the corresponding frequencies, and searches for the fundamental frequencies and their possible resonances. Thus, we can easily identify the various families of regular orbits and also recognize the secondary resonances that bifurcate from them.
 |
Fig. 5 Grid of initial conditions revealing the orbital structure of the (R,Ṙ) phase plane for the a) left: PH model and b) right: OH model. |
 |
Fig. 6 Orbit collection of the eight basic types in the PH galactic model: a) box orbit; b) 2:1 banana-type orbit; c) 1:1 linear orbit; d) 4:3 boxlet orbit; e) 6:3 boxlet orbit; f) 10:5 boxlet orbit; g) 12:7 boxlet orbit; h) chaotic orbit. |
 |
Fig. 7 Orbit collection of the eight basic types in the OH galactic model: a) box orbit; b) 2:1 banana-type orbit; c) 1:1 linear orbit; d) 3:2 boxlet orbit; e) 4:3 boxlet orbit; f) 8:5 boxlet orbit; g) 13:8 boxlet orbit, one of our “orbits with higher resonance”; h) chaotic orbit. |
Before closing this section, we would like to make a clarification about the nomenclature of orbits. All the orbits of an axisymmetric potential are in fact three-dimensional (3D) loop orbits, i.e., orbits that always rotate around the axis of symmetry in the same direction. However, in dealing with the meridional plane, the rotational motion is lost, so the path that the orbit follows onto this plane can take any shape, depending on the nature of the orbit. Following the same approach of the previous papers of this series, we characterize an orbit according to its behavior in the meridional plane. If, for example, an orbit is a rosette lying in the equatorial plane of the axisymmetric potential, it will be a linear orbit in the meridional plane, a tube orbit it will be a 2:1 orbit, etc. We should emphasize that we use the term “box orbit” for an orbit that conserves circulation, but this refers only to the meridional plane. Because of their boxlike shape in the meridional plane, such orbits were originally called “boxes” (e.g., Ollongren 1962), even though their three-dimensional shapes are more similar to doughnuts (see the review of Merritt 1999). Nevertheless, we kept this formalism to maintain continuity with all the previous papers of this series.
4. Numerical results – orbit classification
In this section, we will numerically integrate several sets of orbits to distinguish the
regular or chaotic nature of motion. We use the initial conditions mentioned in the previous
section to construct the respective grids, always adopting values inside the zero velocity
curve (ZVC) defined by 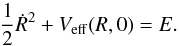 (10)In all cases, the
energy was set to 600 and the
angular momentum of the orbits is Lz = 10. We chose, for
both PH and OH models, the particular energy level, which yields Rmax ≃ 15 kpc,
where Rmax is the maximum possible value of
R on the
(R,Ṙ) phase plane. Once the values of
the parameters were chosen, we computed a set of initial conditions as described in Sect.
3 and integrated the corresponding orbits calculating
the value of SALI and then classifying the regular orbits into different families. Each grid
contains roughly a total of 20 000 initial conditions
(10)In all cases, the
energy was set to 600 and the
angular momentum of the orbits is Lz = 10. We chose, for
both PH and OH models, the particular energy level, which yields Rmax ≃ 15 kpc,
where Rmax is the maximum possible value of
R on the
(R,Ṙ) phase plane. Once the values of
the parameters were chosen, we computed a set of initial conditions as described in Sect.
3 and integrated the corresponding orbits calculating
the value of SALI and then classifying the regular orbits into different families. Each grid
contains roughly a total of 20 000 initial conditions
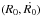 of orbits
with, z0 = 0, while
of orbits
with, z0 = 0, while
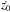 is always obtained from the energy integral (Eq. (9)). In every case, we let one quantity vary in a predefined range, while fixing
the values of all the other parameters, according to SPM and SOM. Color-coded grids of
initial conditions
is always obtained from the energy integral (Eq. (9)). In every case, we let one quantity vary in a predefined range, while fixing
the values of all the other parameters, according to SPM and SOM. Color-coded grids of
initial conditions 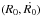 ,
equivalent to surfaces of section, that allow us to determine what types of orbits occupy
specific areas in the phase plane are presented in Appendix A.
,
equivalent to surfaces of section, that allow us to determine what types of orbits occupy
specific areas in the phase plane are presented in Appendix A.
Figure 4a depicts the (R,Ṙ), z = 0, ż > 0 Poincaré surface of section (PSS) of the PH model. We observe that majority of the phase plane is covered by different types of regular orbits, while there is also a unified chaotic domain separating the areas of regularity. The outermost black thick curve is the ZVC. In Fig. 4b, we present the phase plane of the OH model. It is evident that when the dark matter halo has an oblate shape, the observed amount of chaos is considerably higher than that in the case where we have a prolate dark halo component.
To identify all the different regular families belonging to each of the islands seen in the PSSs, we present, in Fig. 5a and b, grids of orbits that we have classified on the PSSs of Fig. 4a and b, respectively. In Fig. 5a, we distinguish eight main families of regular orbits: (i) 2:1 banana-type orbits correspond mainly to the invariant curves surrounding the central periodic point in the PSS; (ii) box orbits are situated mainly outside of the 2:1 resonant orbits; (iii) 1:1 open linear orbits form the double set of elongated islands in the PSS; (iv) 4:3 resonant orbits form the outer triple set of small islands of the PSS; (v) 6:3 resonant orbits correspond to the middle triple set of islands in the PSS; (vi) 10:5 resonant orbits form the chain of five islands of the PSS inside the 2:1 area; (vii) 12:7 resonant orbits produce the set of seven islands of invariant curves of the PSS; and (viii) other types of resonances produce extremely small islands, embedded in the chaotic layers. The outermost black thick curve is the ZVC. In the OH model shown in Fig. 5b the box orbits, 2:1 resonant orbits, 1:1 linear open orbits, 4:3 resonant orbits. Other types of orbits are also observed. However, two new families of orbits are introduced: (i) 3:2 resonant orbits correspond to the middle double set of islands in the PSS; and (ii) 8:5 resonant orbits form the chain of five islands of the PSS outside the box orbits. Note that every resonance n:m is expressed in such a way that m is equal to the total number of islands of invariant curves produced in the (R,Ṙ) phase plane by the corresponding orbit.
The basic types of regular orbits, plus an example of a chaotic one, for both PH and OH models are shown in Fig. 6a–h and Fig. 7a–h, respectively. The box and chaotic orbits were computed up to t = 100 time units, while all the rest of the parent3 periodic orbits were computed until one period was completed. The curve circumscribing each orbit is the limiting curve in the meridional plane defined as Veff(R,z) = E. Table 1 shows the type and the initial conditions for each of the depicted orbits; for the resonant cases, the initial conditions and the period Tper correspond to the parent periodic orbit. We observe that the orbits in the PH model obtain larger values of the z coordinate (zmax ≃ 13 kpc), while the orbits of the OH model shown in Fig. 7a–h stay closer to the galactic plane (zmax ≃ 10 kpc). Here we note that in the PH model two of the basic types of orbits (the 6:3 orbits and the 10:5 orbits), are in fact subfamilies of the main 2:1 family. An orbit with an improper ratio of frequencies (i.e., a ratio that is a reducible fraction) is a member of a subfamily of the orbits with a ratio of frequencies that is the irreducible corresponding fraction. For instance, a 6:3 orbit torus always surrounds a 2:1 torus; a 6:3 entire subfamily (as opposed to a single, invisible 6:3 orbit) appears when the parent 6:3 is stable and so it spawns its own subfamily. The 6:3 family has a parent closed periodic orbit the torus of which surrounds the 2:1 parent torus. All of this is beautifully seen in the PSS plot shown in Fig. 4a and better viewed in the corresponding grid of Fig. 5a. So, in one sense, 6:3 orbits are the same as the 2:1 ones (they are members of the same family), but in another sense they are not the same (6:3 is a separated subfamily). In our research, we consider that both 6:3 and 10:5 orbits form separate families of orbits.
Here we should note that the 1:1 resonance is usually the hallmark of the loop orbits and both coordinates oscillate with the same frequency in their main motion. Their mother orbit is a closed loop orbit. Moreover, when the oscillations are in phase, the 1:1 orbit degenerates into a linear orbit (the same as in Lissajous figures made with two oscillators). In our meridional plane, however, 1:1 orbits do not have the shape of a loop. In fact, their mother orbit is linear (as in Figs. 6c and 7c), and thus they do not have a hollow (in the meridional plane), but fill a region around the linear mother, always oscillating along the R and z directions with the same frequency. We designate these orbits “1:1 linear open orbits” to differentiate them from true meridional plane loop orbits, which have a hollow and also always rotate in the same direction.
4.1. Influence of the mass of the nucleus
 |
Fig. 8 Evolution of the different kinds of orbits, varying Mn for a) left: PH models and b)right: OH models. |
 |
Fig. 9 Evolution of the different kinds of orbits, varying cn for a) left: PH models and b)right: OH models. |
To study how the mass of the nucleus Mn influences the level of chaos, we let it vary while fixing all the other parameters of our model, and integrate orbits in the meridional plane for the set Mn = {0, 50, 100, ..., 500}. In all cases, the energy was set to 600 and the angular momentum of the orbits Lz = 10. Once the values of the parameters were chosen, we computed a set of initial conditions as described in Sect. 3, and integrated the corresponding orbits computing the SALI of the orbits and then classified regular orbits into different families.
The evolution of the resulting percentages of the chaotic orbits and of the mean families of regular orbits as Mn varies for the PH model is shown in Fig. 8a. It can be seen that when the nucleus is absent, the amount of chaos is low and the majority of orbits is 2:1 banana-type orbits. In fact, the 2:1 orbits are reduced as the nucleus gains mass, but the 2:1 family always remains the dominant one. Moreover, the evolution of box and chaotic orbits is very similar, while all the rest of the resonant families continue to have low percentages (less that 10%) with increasing Mn. Thus, we could argue that in galaxy models with prolate dark halo, the mass of the nucleus influences mainly the box, the 2:1 banana-type, and the chaotic orbits. In Fig. 8b, we present a similar figure regarding the OH models. We observe that when the central nucleus is not present there is no chaos whatsoever and almost all orbits are box orbits. However, even a small nucleus is enough to trigger chaotic phenomena, whereas the box orbits are gradually depleted. This trend continues, although at a lower rate, as the nucleus grows in mass, i.e., the percentage of box orbits is reduced, and at the same time that of chaotic orbits is increased. The remaining orbits change very little; the meridional bananas, in fact, are almost unperturbed by the shifting of the mass of the nucleus. From this figure, one may conclude that Mn affects mostly the box and chaotic orbits in oblate dark halo galactic models.
4.2. Influence of the scale length of the nucleus
Now we proceed to investigate how the scale length of the nucleus cn influences the amount of chaos in our PH and OH models. Again, we let it vary while fixing all the other parameters of our galactic model and integrating orbits in the meridional plane for the set cn = {0.05, 0.10, 0.15, ..., 0.50 }.
The resulting percentages of chaotic and regular orbits for the PH models as the scale length of the nucleus cn varies are shown in Fig. 9a. It is evident that the 2:1 banana-type orbits exhibit an almost monotone evolution as the nucleus become less dense, but nevertheless this family always prevails over all other regular families. In contrast, box and chaotic orbits are the most affected types of orbits, especially when the nucleus is fairly concentrated (cn < 0.25). All the rest of the resonant families raise their percentages with increasing cn, but with a significant smaller rate, being always less than 5%. Therefore, we could say that in prolate dark halo models, the box and chaotic orbits are most affected by the scale length of the nucleus. In Fig. 9b, we present the evolution of the percentages of orbits for the OH galaxy models. We observe that there is a strong correlation between the percentage of chaotic orbits and the value of cn. However, chaotic orbits ate always the dominant type of orbits. At the same time, as the nucleus become less concentrated, there is a gradual increase in the percentage of almost all of the regular families, most noticeably the box and the high resonant boxlets. Once again, the meridional 2:1 bananas and the 8:5 resonant orbits are immune to changes of the value of the scale length of the nucleus. Thus, decreasing the scale length of the nucleus (in other words, the nucleus becomes more concentrated and dense) in oblate dark halo models turns box and high resonant orbits into chaotic orbits, while those with low resonances are less affected.
4.3. Influence of the mass of the disk
 |
Fig. 10 Evolution of the different kinds of orbits, varying Md for a) left: PH models and b)right: OH models. |
 |
Fig. 11 Evolution of the different kinds of orbits, varying b for a) left: PH models and b)right: OH models. |
Our next step is to reveal how the overall orbital structure in our PH and OH models is affected by the mass of the disk Md. As usual, we let this quantity vary while fixing the values of all the other parameters of our galactic model and integrating orbits in the meridional plane for the set Md = {4500, 5000, 5500, ..., 9000}.
In Fig. 10a,b, we present the resulting percentages of chaotic and regular orbits for both PH, and OH models as the mass of the disk Md varies. In Fig. 10a, we observe that in galaxy models with prolate dark matter haloes the 2:1 meridional bananas are always the dominant type of orbits. As the disk gains mass there is a continuous and similar variation at the percentage of box and chaotic orbits. At the higher value of the mass of the disk studied, the percentages of chaotic and box orbits tend to a common value (around 20%), thus sharing four-tenths of the entire phase plane. Moreover, it is evident that all the other types of regular orbits remain almost unperturbed and with very low percentages throughout (less than 5%). Therefore, one may reasonably conclude that in prolate dark matter halo models the chaotic, box and the 2:1 orbits are mostly affected by the mass of the disk. The evolution of the resulting percentages of the types of orbits in the OH models is shown in Fig. 10b. In the case of OH models the motion of stars is highly chaotic throughout the range of the values of Md. However, our numerical experiments suggest that the mass of disk plays an important role on the amount of chaos. In particular, the percentage of chaos decreases following an almost linear trend with increasing Md. At the same time, the 2:1 banana-type orbits exhibit a perfect linear increase, while all the other types of regular orbits change very little when Md varies. Thus, we may say that the change in the mass of the disk in oblate dark matter halo galaxy models affects mostly chaotic and 2:1 resonant orbits.
 |
Fig. 12 Evolution of the different kinds of orbits, varying α for a) left: PH models and b)right: OH models. |
4.4. Influence of the core radius of the disk-halo
The next parameter under investigation is the core radius of the disk-halo b. We will try to understand how the overall orbital structure in our PH and OH galaxy models is influenced by b. Again, we let this quantity vary while fixing the values of all the other parameters of our galactic model and integrating orbits in the meridional plane for the set b = {4, 4.5, 5, ..., 8 }.
Figures 11a,b shows the resulting percentages of chaotic and regular orbits for both PH and OH galaxy models as the core radius of the disk-halo b varies. Looking at Fig. 11a, it becomes evident that once more, the meridional 2:1 banana-type orbit is the dominant type of star orbits when the dark matter halo has a prolate shape. We also observe that the core radius parameter has no influence to the box orbits whose rate always remains at about 15%. On the other hand, we see that the chaotic orbits are affected by b and their percentage exhibits a decrease as we proceed in models with larger values of the core radius parameter. All the other resonant families hold small percentages (less than 10%) and varying the value of b only shuffles the orbital content among them. Hence, we argue that in galaxy models with prolate dark matter haloes the core radius of the disk halo b mainly influences the portion of chaotic and 2:1 banana-type orbits. Interestingly, the same parameter (b) affects the families of orbits in the case of oblate dark matter haloes completely differently, as we can see in Fig. 11b. Here, chaotic motion prevails throughout the range of b. In fact, the percentage of chaotic orbits increases constantly as the value of b grows, thus suppressing the rates of almost all the regular families. It seems that only box orbits are able to sustain their percentage, which hovers around 20%. At the same time, however, the percentages of the 2:1, 1:1, 3:2, and 4:3 resonant orbits are being reduced. Therefore, increasing the core radius of the disk-halo in OH galaxy models turns the majority of different kinds of low resonant orbits into chaotic orbits, while those with high resonances are considerably less affected.
 |
Fig. 13 Evolution of the different kinds of orbits, varying h for a) left: PH models and b)right: OH models. |
4.5. Influence of the scale length of the disk
We continue our quest of trying to understand how the scale length of galaxy α influences the overall orbital structure in our PH and OH galaxy models. As usual, we let this parameter vary while fixing the values of all the other quantities of our galactic model and integrating orbits in the meridional plane for the set α = {2.5, 2.75, 3, ..., 5}.
The evolution of the resulting percentages of both the chaotic orbits and the different families of regular orbits for both the PH and OH galaxy models, as the scale length of the disk α varies is shown in Fig. 12a,b. As Fig. 12a clearly indicates, in galaxy models with prolate dark matter haloes the motion of stars is highly regular since the 2:1 meridional banana-type orbits account for the largest proportion throughout. However, we observe that as we proceed to larger values of α, the percentage of the 2:1 resonant orbits declines linearly, although such resonances still dominate the distribution of orbits. At the same time, the percentages of box and chaotic orbits are elevated, while all the other resonant families are only marginally affected by the change in the value of α. Furthermore, with a much closer look at the diagram, we see that the 12:7 family disappears when α > 3.75. Therefore, taking all the above into account, we may conclude that in galaxy models with prolate dark matter haloes the scale length of the disk halo α affects mainly the chaotic, box, and 2:1 banana-type orbits. In galaxy models with an oblate dark matter halo on the other hand, the vast majority of stars move in chaotic orbits. We see in Fig. 12b that the percentages of the chaotic and the 1:1 resonant orbits increase almost linearly at the expense of box, 2:1, 3:2 orbits. Only higher resonant orbits (i.e., 4:3, 8.5) are able to maintain their rates. Thus, increasing the scale length of the disk in OH galaxy models turns different kinds of low resonant orbits either into chaotic orbits or 1:1 resonant orbits, while high resonant families are practically unaffected.
4.6. Influence of the scale height of the disk
The next stop of our investigation is to determine how the overall orbital structure of our PH and OH galaxy models is affected by the scale height of disk h. Following the usual procedure, we let this parameter vary while fixing the values of all the other quantities of our galactic models and integrating orbits in the meridional plane for the set h = {0.1, 0.2, 0.3, ..., 1}.
Figures 13a,b demonstrates the influence of the scale height of disk h to the percentages both of the chaotic orbits and the different families of regular orbits for both the PH and OH galaxy models. Based on both diagrams, we observe that h is the least influential parameter we encountered so far. In galaxy models with prolate dark matter haloes, only the chaotic and the box orbits are affected by the variation of the value of h, while the percentages of all the other families of orbits present a monotone evolution as h varies. In particular, we see that as the scale height of the disk is amplified, the rates of chaotic and box orbits are reduced and increased, respectively, following a linear trend. Specifically, at the higher value of h studied, the percentages of the chaotic and box orbits tend to a common value of around 20%, thus sharing two fifths of the entire phase plane. Figure 13b shows the evolution of the resulting percentages of the chaotic orbits, as well as the different families of regular orbits for the OH galaxy models, as the scale height of the disk h varies. Again, except for the chaotic and 1:1 resonant orbits, all the other families of orbits are completely unperturbed by h, exhibiting a monotone evolution. Specifically, the percentage of the 1:1 resonant orbits starts to arise as soon as the percentage of the chaotic orbits begins to deteriorate. Therefore, we conclude that in galaxy models with oblate dark matter haloes, the scale height of the disk h affects only the chaotic and 1:1 resonant orbits.
4.7. Influence of the halo flattening parameter
 |
Fig. 14 Evolution of the different kinds of orbits, varying β for a) left: PH models and b)right: OH models. |
The exact shape (prolate, spherical, or oblate) of the dark matter halo is determined by the flattening parameter β. So, it would be of particular interest to define how this parameter influences the overall orbital structure of our PH and OH galaxy models. Once more, we let this parameter vary while fixing the values of all the other parameters of our galactic models and integrating orbits in the meridional plane for the set β = {0.1, 0.2, 0.3, ..., 1.9}.
We see that the flattening parameter β significantly influences the orbital structure in the phase plane. In Fig. 14a,b, we observe exactly how the flattening parameter affects both the percentages of the chaotic orbits and the different families of regular orbits for both PH and OH galaxy models. Here we should mention that if all the types of orbits were the same for both PH and OH models, we could merge these two plots. We demonstrate in Fig. 14a that when 0.1 ≤ β ≤ 0.9, which is a prolate dark matter halo, the majority of stars perform regular 2:1 banana-type orbits. The percentage of the 2:1 resonant orbits increases sharply for small values of β, while this tendency is reversed at higher values of the flattening parameter (β > 0.4). The rate of the chaotic orbits is reduced to β = 0.7, while for higher values it increases. On the other hand, the percentage of box orbits grows steadily when 0.4 < β < 0.7 and then begins to diminish. When β = 0.9 the rates of chaotic and 2:1 resonant orbits tend to a common value (around 30%), thus sharing about the two thirds of the entire phase plane. The rest of the families of orbits change little, always having small percentages (less than 10%). To summarize, in prolate dark matter halo models, the box, 2:1, and chaotic orbits are mostly affected by the flattening parameter. In Fig. 14b, we see that the downward trend of the resonant 2:1 and box orbits continues to exist in the case of an oblate halo. At the same time, the percentage of the chaotic orbits keeps growing throughout the range of β. At extreme flattened oblate halo models (β > 1.8) almost half of the phase plane is occupied by chaotic orbits. Moreover, the rates of 1:1, 3:2, and 4:3 resonant orbits rise with increasing β, while the rates of all the other regular families remain unperturbed. However, when β = 1.7, we observe a sudden increase at the percentage of higher resonances (in this case, the 13:8 resonance) accompanied by another sudden drop of the box orbits. Once more, the box, 2:1, and chaotic orbits are the types of orbits that are influenced greatly by the flattening parameter in oblate dark halo models. Here we should point out that our initial estimate suggested that the greater amount of chaos should exist at highly flattened halo models (prolate or oblate), while the lower amount should be observed when the dark matter halo is spherically symmetric (β = 1). However, our numerical experiments only confirm the first part of our assumptions regarding the most chaotic model. Indeed, in Fig. 14a,b, the greater rate of chaos (around 50%) occurs at the two opposite, extreme values of the flattening parameter (0.1 and 1.9). In contrast, and surprisingly enough, the smallest portion of chaotic orbits is observed when β = 0.7 thus dispelling our initial assumption.
 |
Fig. 15 Evolution of the different kinds of orbits, varying ch for a) left: PH models and b)right: OH models. |
4.8. Influence of the scale length of the halo
The concentration of the logarithmic, flattened dark matter halo is controlled by its scale length ch. In the following, we try to reveal how the scale length of the dark halo influences the overall orbital structure of our PH and OH galaxy models. As usual, we let this parameter vary while fixing the values of all the other parameters of our galactic models and integrating orbits in the meridional plane for the set ch = {7, 8.5, 10, ..., 22}.
The evolution of both the resulting percentages of the chaotic orbits and the different families of regular orbits for both PH and OH galaxy models, as the scale length of the halo ch varies, is presented in Fig. 15a,b. In prolate dark matter halo galaxy models, Fig. 15a shows that, as ch increases, the percentage of the 2:1 meridional banana-type orbits decreases following almost a linear drop, while that of the chaotic orbits grows steadily when ch > 13. In fact, when ch > 14 chaotic orbits are the all-dominant types of orbits. Furthermore, the rate of box orbits increases until ch = 13, while for higher values of the scale length of the halo it decreases. On the other hand, the percentage of the 1:1 resonant family exhibits a small, but constant growth. The remaining families of orbits change insignificantly. Thus, taking all of the above into account, we conclude that in galaxy models with prolate dark matter haloes, the scale length of the halo affects mostly the box, the 2:1 banana-type, 1:1 resonant and chaotic orbits. As Fig. 15b indicates, things are very different when the halo has an oblate shape. Here, the bulk of the stars move in chaotic orbits. Specifically, as we move on to less concentrated oblate halo models (larger value of ch) the percentage of the chaotic orbits increases, and at the higher value of the scale length of the halo studied (ch = 22), around two thirds of the total orbits are chaotic. The meridional 2:1 banana-type orbits exhibit a linear decrease, while the percentage of the 1:1 resonant orbits grows when ch > 13. The rates of the remaining families of orbits perform small fluctuations and change little. Therefore, our calculations suggest that ch influences mostly the chaotic, 2:1, and 1:1 resonant orbits in oblate dark halo galaxy models. In Fig. 15a,b, we also observe that when ch = 22 (the maximum studied value of the scale length of the dark halo), the percentages of box, 2:1, and 1:1 resonant orbits tend to a common value (around 10%), thus sharing three tens of the entire phase plane, while the rate of the chaotic orbits is about 60%. This evidence supports the conclusion derived from the above grids (see Fig. A.8b and d), where we claimed that the overall orbital structure in high values of ch is totally independent of the particular shape of the dark halo.
 |
Fig. 16 Evolution of the different kinds of orbits, varying Lz for a) left: PH models and b)right: OH models. |
4.9. Influence of the angular momentum
One of the most important quantities, which plays a vital role in the nature of star orbits in the meridional plane (R,z), is the angular momentum Lz. Therefore, it is of paramount significance to investigate how the angular momentum affects the overall orbital structure of our PH and OH galaxy models. Using the same technique as in all previous cases, we let this quantity vary while fixing the values of all the other parameters of our galactic models and integrating orbits in the meridional plane for the set Lz = {1, 5, 10, ..., 50}.
The following Fig. 16a,b shows the evolution of the resulting percentages of both the chaotic orbits and the different families of regular orbits for both PH and OH galaxy models as the value of the angular momentum Lz varies. We see in Fig. 16a that when the dark matter halo is prolate, the vast majority of low angular momentum stars move in regular orbits; 2:1 banana-type orbits to be exact. We note that the percentages of the 2:1 resonant and chaotic orbits is reduced as the value of the angular momentum increases. The rate of the box orbits, on the other hand, exhibits a rapid increase when Lz > 25 and, in high angular momentum models, is the dominant type of orbits. We also observe that the percentage of the high resonant orbits grows significantly when Lz > 25 reaches just over 10% at the height studied value of the angular momentum (Lz = 50). The percentages of the remaining families of orbits are practically unperturbed by the shifting of the Lz. To summarize, the angular momentum in prolate dark halo models affects mostly the chaotic, box, 2:1, and higher resonant orbits. Figure 16b presents the evolution of the percentages of orbits, as Lz varies when the dark halo is oblate. One may observe that the percentage of chaotic orbits decreases almost linearly, while that of box orbits raises steadily when Lz > 10. In particular, when Lz > 20, box orbits are the dominant types of orbits. The rest of the families of orbits change less. In fact, the percentage of the meridional 2:1 banana-type orbits is minimally affected by the increase of the angular momentum, unlike in the previous case. We also note that when Lz = 50 the percentages of 1:1, 4:3, and other types of resonant orbits tend to a common value of around 8%. Thus, one may conclude that the angular momentum influences mostly box and chaotic orbits in galaxy models with an oblate dark matter halo.
4.10. Influence of the orbital energy
 |
Fig. 17 Evolution of the different kinds of orbits, varying E for a) left: PH models and b)right: OH models. |
The last parameter under investigation is the total orbital energy E. To explore how the energy level affects the overall orbital structure of our PH and OH galaxy models, we use the normal procedure according to which we let the energy vary while fixing the values of all the other parameters of our galactic models and integrating orbits in the meridional plane for the set E = {−300, −200, −100, 0, 100, ..., 700}. At this point we should point out that the particular value of the energy determines the maximum possible value of the R coordinate (Rmax) on the (R,Ṙ) phase plane. The energy values in the above interval result in 1.4 ≲ Rmax ≲ 15.
The evolution of the resulting percentages of both the chaotic orbits and the different families of regular orbits for both PH and OH galaxy models, as the value of the orbital energy E varies, is presented in Fig. 17a,b. In Fig. 17a, we show that in low energy prolate dark halo models the motion is entirely regular. However, when E > −300 the percentage of chaotic orbits increases sharply and reaches its maximum value, of around 65% when E = 0, while for all positive energy values it decreases almost linearly. The rate of the box orbits, on the other hand, fluctuates when −300 < E < 300, while for lager energies it decreases. Furthermore, we see that for low energy models, 1:1 and higher resonant orbits possess high rates, which, however, decrease when E > 0. At the same time, the percentage of the meridional 2:1 banana-type orbits grows rapidly for positive energy levels and when E > 400, the 2:1 resonant orbit is the most populated family. All the other resonant families remain completely unperturbed having infinitesimal rates throughout. Thus, one may reasonably conclude that in prolate dark halo models the energy mostly affects the chaotic, box, 1:1, 2:1, and higher resonant orbits. Figure 17b shows the resulting percentages of chaotic and regular orbits for the oblate halo models when E varies. We can identify many similarities regarding the evolution of the percentages between prolate and oblate dark halo models. To begin with, the rate of chaotic orbits follows a similar pattern, increasing rapidly for negative energies and maximizing its value when E = 0, while dropping for negative energy levels, although chaotic orbits remain by far the dominant type of orbits. Furthermore, the 1:1, 2:1, and higher resonant orbits evolve similarly. In contrast the percentages of box and 4:3 resonant orbits seem to change little, fluctuating around 15% and 10% respectively, while that of the 3:2 and 8:5 resonant families are very low (less than 10%). Therefore, our numerical experiments reveal that in oblate dark halo models, varying the value of the energy mainly shuffles the orbital content among the families of regular orbits and only chaotic orbits suffer the most.
5. Analysis of the results
 |
Fig. 18 Forces acting at every time step of the numerical integration along the path of a regular 2:1 banana-type orbit (purple color), a 4:3 resonant orbit (red color), and a chaotic orbit (blue color) in the Mn = 250 OH galaxy model. a) Left: horizontal force FR and b) right: vertical force Fz. |
The dynamical origin of the onset of chaos has proven very elusive so far. A promising line of investigation, namely the curvature of the phase space, although theoretically sound, came up against many experimental counterexamples (e.g., Szydlowski 1994). Therefore, we will not attempt to explain which dynamical factors are responsible for the onset and growth of chaos, but we will try to isolate any behavior that may be correlated with that.
Almost 30 years ago, Gerhard & Binney (1985)
demonstrated that stars that pass near a density cusp, thus experiencing strong horizontal
or vertical forces, may depopulate the family of box orbits that supports the triaxial
figure of a galaxy. Thus, regions in which strong forces act, should be responsible for the
onset of chaos. Since our potential is nowhere divergent, we do not have any cusps.
Nevertheless, the centrifugal term 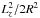 creates a cusp at the
origin of the effective potential on the meridional plane4. Therefore, we seek to understand whether there is a relationship between chaos
and a star passing near the origin. In Fig. 18a,b, we
present how the horizontal force FR and the vertical force
Fz act at every time step
of the numerical integration on the path of two regulars orbits and one chaotic orbit. All
three orbits were chosen randomly and integrated for a time interval of 500 time units, so
that there is enough time for both forces to act on them. The regular 2:1 banana-type orbit
shown in purple has initial conditions: R0 = 5.8,
creates a cusp at the
origin of the effective potential on the meridional plane4. Therefore, we seek to understand whether there is a relationship between chaos
and a star passing near the origin. In Fig. 18a,b, we
present how the horizontal force FR and the vertical force
Fz act at every time step
of the numerical integration on the path of two regulars orbits and one chaotic orbit. All
three orbits were chosen randomly and integrated for a time interval of 500 time units, so
that there is enough time for both forces to act on them. The regular 2:1 banana-type orbit
shown in purple has initial conditions: R0 = 5.8,
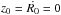 , the 4:3 resonant orbit shown in
red has initial conditions: R0 = 11.6,
, the 4:3 resonant orbit shown in
red has initial conditions: R0 = 11.6,
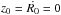 , while the initial conditions of
the chaotic orbit (blue) are: R0 = 0.18,
, while the initial conditions of
the chaotic orbit (blue) are: R0 = 0.18,
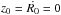 . The initial value of
. The initial value of
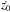 was obtained from the energy integral (9) and
all orbits belong to the Mn = 250 OH galaxy model. At every time
step of the numerical integration we recorded both forces, and their values are given in the
vertical axis of the plots. It is evident that stars moving either in regular (i.e., the 4:3
resonant orbit) or chaotic orbits suffer from strong horizontal and vertical forces upon
approaching the center of the galaxy. On the other hand, there are other types of regular
orbits, such as the box, 2:1, and 8:5 resonances, which do not pass close to the center and
therefore, the acting forces are immaterial along their entire orbital path. We found that
the minimum distance of chaotic orbits to the origin
was obtained from the energy integral (9) and
all orbits belong to the Mn = 250 OH galaxy model. At every time
step of the numerical integration we recorded both forces, and their values are given in the
vertical axis of the plots. It is evident that stars moving either in regular (i.e., the 4:3
resonant orbit) or chaotic orbits suffer from strong horizontal and vertical forces upon
approaching the center of the galaxy. On the other hand, there are other types of regular
orbits, such as the box, 2:1, and 8:5 resonances, which do not pass close to the center and
therefore, the acting forces are immaterial along their entire orbital path. We found that
the minimum distance of chaotic orbits to the origin 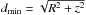 ,
is very small and in many cases it coincides with the minimum allowed R value as it is defined by
the corresponding ZVC. Moreover, we also observe that the maximum value of the horizontal
force FR is about twice that of
the vertical force Fz. Extensive numerical
experiments indicate that the fundamental criterion that distinguishes ordered from chaotic
orbits is how close to the center of the potential an orbit passes.
,
is very small and in many cases it coincides with the minimum allowed R value as it is defined by
the corresponding ZVC. Moreover, we also observe that the maximum value of the horizontal
force FR is about twice that of
the vertical force Fz. Extensive numerical
experiments indicate that the fundamental criterion that distinguishes ordered from chaotic
orbits is how close to the center of the potential an orbit passes.
 |
Fig. 19 Grids of initial conditions |
 |
Fig. 20 a)Left: minimum distance of orbits to the origin versus SALI. The horizontal, blue line shows the limit separating ordered from chaotic orbits. All the orbits between the two horizontal lines (orange and blue) are probably sticky orbits, which require more than 104 time units of integration time, so as to reveal their true chaotic nature. b)Right: minimum distances of orbits to the origin versus minimum distances to the minimum of the effective potential, located at (Rg,0). Green color corresponds to regular motion, while red corresponds to chaotic. |
 |
Fig. 21 a)Left: Minimum distances of orbits to the origin versus a) left: maximum force at the R direction, b) right: maximum force in the z direction. Green color corresponds to regular motion, while red corresponds to chaotic. |
So far, we discussed three different quantities (the minimum distance to the origin
dmin, the FR, and the Fz force) that somehow act
differently on regular and chaotic orbits. Therefore, a question of great importance that
arises is the following: can these quantities be used to safely distinguish between ordered
and chaotic motion? The answer to this question is given in Fig. 19a,d. To test the efficiency of these quantities, we chose the
Mn = 250 OH galaxy model as a test field in
our investigation. In Fig. 19b, we reconstructed the
grid of the initial conditions 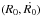 in which
each point is colored according to the minimum to the origin distance dmin of the
orbits. In this plot, the reddish colors correspond to large values of dmin, while the
blue/purple colors adhere to low values of dmin. The same philosophy is used in Fig.
19c,d where each point is colored according to the
maximum value of the forces FR and Fz that act on the orbits.
We observe that although these plots reveal the rough characteristics of the phase plane and
we can indeed distinguish the different sets of islands corresponding to several resonant
families. However, it is very difficult, or even impossible, to define numerical threshold
values, thus separating safely between regular and chaotic motion. This is true because
there will always be regular types of orbits, such as the 1:1 and 4:3 in our case, that
approach very close to the center of the galaxy experiencing strong forces. On the other
hand, we observe in Fig. 19a the distinction between
regular and chaotic motion is absolutely clear and beyond any doubt when using the SALI
value as a criterion. Here we must note that in Fig. 19a,d we actually reproduced the OH grid shown in Fig. 5b with four different methods.
in which
each point is colored according to the minimum to the origin distance dmin of the
orbits. In this plot, the reddish colors correspond to large values of dmin, while the
blue/purple colors adhere to low values of dmin. The same philosophy is used in Fig.
19c,d where each point is colored according to the
maximum value of the forces FR and Fz that act on the orbits.
We observe that although these plots reveal the rough characteristics of the phase plane and
we can indeed distinguish the different sets of islands corresponding to several resonant
families. However, it is very difficult, or even impossible, to define numerical threshold
values, thus separating safely between regular and chaotic motion. This is true because
there will always be regular types of orbits, such as the 1:1 and 4:3 in our case, that
approach very close to the center of the galaxy experiencing strong forces. On the other
hand, we observe in Fig. 19a the distinction between
regular and chaotic motion is absolutely clear and beyond any doubt when using the SALI
value as a criterion. Here we must note that in Fig. 19a,d we actually reproduced the OH grid shown in Fig. 5b with four different methods.
In order to have a more complete view of the situation, we let Mn vary, and them we computed the following, for each star in our OH models: the minimum distance dmin (in the meridional plane) to the origin of coordinates; the minimum distance to the minimum of the effective potential Rgmin; and the maximum values of the forces FR and Fz. Then, we tried to see if there is a correlation between these quantities. Figure 20a shows these minimum distances for all the orbits used to study the influence of the mass of the nucleus Mn of all the OH models, versus the value of their respective SALIs, while the horizontal, blue line indicates the threshold between ordered and chaotic orbits. In the same diagram, there is a dashed orange line at SALI = 10-5. We have strong numerical evidence that all the orbits between the two horizontal lines (orange and blue) are probably sticky orbits that require larger integration time so as to expose their true chaotic character. We show that all the chaotic orbits pass near the center, thus suffering at one time or another some sudden acceleration due to the strong centrifugal force. However, this is not a sufficient condition to be chaotic: regular orbits can also pass near the center. Exactly the same behavior was found when using orbits from all the other PH and OH models analyzed in Sect. 4. Therefore, we may draw the following conclusion: in the meridional plane of our galactic model, a necessary condition for an orbit to be chaotic is to pass near the center of the potential; a sufficient condition for an orbit to be regular is not to pass near the center of the potential.
The analysis we conducted in the previous section revealed that almost all the studied parameters significantly influence the percentage of chaos in the meridional plane. For instance, the chaotic percentage grows with the increment of the mass of the nucleus (see Fig. 8), the decrement of the scale length of it (see Fig. 9), the increment of the scale length of the disk (see Fig. 12), the increment of the scale length of the halo (see Fig. 15), the decrement of the angular momentum (see Fig. 16), etc. Our numerical calculations indicate that in all the cases the position Rg of the minimum of the effective potential, which is always located on the R axis (e.g., Binney & Tremaine 2008), nears the origin of coordinates whenever the percentage of chaos rises. Figure 20b shows the minimum distance to the origin for all the orbits shown in Fig. 20a, versus their minimum distances to Rg. We can see a consistent correlation between those quantities, hinting that the position of the minimum of the effective potential might influence the degree of chaos, although we were not be able to find an analytic proof of this. Green dots correspond to regular orbits, while red dots correspond to chaotic orbits.
In Fig. 21a,b, we present diagrams connecting the maximum value of FR and Fz forces respectively with the corresponding minimum distance of the orbits. In all cases, we observe a common behavior: the value of dmin of the chaotic orbits is always low (≲1 kpc) exhibiting at the same time high maximum values of the forces. The picture described above is consistent with the rising of the percentage of the chaotic orbits with Mn (see Fig. 8b), since both forces grow with the mass of the nucleus. Also, it is consistent with the behavior of the chaotic percentage seen in Fig. 9b, considering that the more concentrated the nucleus, the more acceleration it causes near the center. It also explains why the percentage of chaotic motion diminishes when the angular momentum increases (Fig. 16b), given that a low angular momentum allows the star to approach the center of the potential. On the other hand, Fig. 8b shows that when the nucleus is absent, there is no chaotic motion at all. Whereas this proves that the onset of chaos is driven mainly by the presence of dark matter, it also poses a question about the above-mentioned role of the centrifugal force, since this force is at work even in this completely regular case.
6. Discussion
In the present work, we used an analytic, axially symmetric galactic gravitational model that embraces the general features of a disk galaxy with a dense, massive nucleus and a biaxial prolate or oblate dark matter halo component. To simplify our study, we chose to work in the meridional plane (R,z), thus reducing three-dimensional to two-dimensional motion. Varying the values of all the involved parameters of the dynamical system, as well as the two global isolating integrals of the orbits, namely the angular momentum and the energy, we found that the level of chaos and the distribution in regular families is indeed very dependent on all of these parameters. Here we must point out that the present article belongs to a series of papers (Zotos & Carpintero 2013; Caranicolas & Zotos 2013; Zotos & Caranicolas 2013a,b) that have as their main objective the orbit classification (not only regular versus chaotic, but also separating regular orbits into different regular families) in different galactic gravitational potentials. Thus, we decided to follow a similar structure and the same numerical approach in all of them.
We found that in our PH and OH galaxy models several types of regular orbits exist, while there is also a unified chaotic domain separating the areas of regularity. In particular, most types of regular orbits, such as the box, 1:1, 2:1, 4:3, higher resonant, and chaotic orbits are common in both prolate and oblate dark halo models. Here we must clarify that by the term “higher resonant orbits” we refer to resonant orbits with a rational quotient of frequencies made from integers >5, which of course do not belong to the main families. However, each model type (PH or OH) has its own private families of regular orbits. Specifically, in prolate halo models we encountered subfamilies of the basic 2:1 family (i.e., the 6:3 and the 10:5 family) and resonant orbits of higher multiplicity, such as the 12:7 family. In the oblate halo models, on the other hand, the special families of orbits were the 3:2 and the 8:5. Our numerical calculations indicate that when the dark matter halo has a prolate shape with the vast majority of stars move in regular orbits, the 2:1 resonant family being the most populated one, while in the case of oblate dark halo chaos prevails, thus chaotic orbits are the all-dominant type.
Our investigation reveals that all the parameters of the dynamical system affect, more or less, the overall orbital structure of our PH and OH models. It was observed that the mass of the nucleus, the halo flattening parameter, the scale length of the halo, the angular momentum and the orbital energy are the most influential quantities, while the effect of all the other parameters is much weaker. In fact, we should point out that all the parameters corresponding to the disk potential have a minor influence on the nature of orbits, therefore we can conclude that of the three components of the model, the disk is the one that causes the least disturbance to the percentages of the orbits. In more precise terms, the influence of all the parameters can be summarized as follows:
-
1.
In PH galaxy models, the mass of the nucleusMn mainly influences the box, the 2:1 banana-type, and the chaotic orbits. However, in OH models the mass of the nucleus although spherically symmetric and, therefore, maintaining the axial symmetry of the whole galaxy, generates chaos in the meridional plane as soon as it is above zero. As the mass increases, this chaotic motion grows in percentage at the expense of the box orbits. The chaotic percentage approached ≃55% once Mn has reached some ≃7% of the Md.
-
2.
The box and the chaotic orbits are the types of orbits mostly influenced by the concentration of the nucleus cn in PH models. Moreover, in OH models, the percentage of chaotic motion depends almost linearly on this parameter. Once more, box orbits and high resonant orbits are the ones that give way to the chaotic orbits, while those with low resonances are less affected. The amount of chaos decreases as we proceed to OH models with less concentrated nuclei, corresponding between about 30%−50% of the total orbits.
-
3.
The mass of the disk Md mostly affects the percentages of the chaotic, box, and the 2:1 banana-type orbits in PH models, while in OH models only the chaotic and 2:1 resonant orbits are influenced by Md. In fact, the rate of chaotic orbits decreases linearly, while that of 2:1 resonant orbits increases linearly with increasing Md. In OH models, Md acts as chaos regulator; the more massive is the disk, the less chaos is observed.
-
4.
The core radius of the disk-halo b plays a similar role in the case of a prolate dark matter halo: the percentage of 2:1 resonant orbits depends almost linearly on this parameter. On the other hand, increasing the core radius of the disk-halo in OH galaxy models turns the majority of different types of low resonant orbits into chaotic orbits, while higher resonant orbits are considerably less affected. In all cases, chaotic orbits occupy between around one and two thirds of the total orbits.
-
5.
In galaxy models with prolate dark matter haloes, the scale length of the disk α affects mainly the chaotic, box, and 2:1 banana-type orbits. In contrast, increasing the scale length of the disk in OH galaxy models turns different kinds of low resonant orbits either into chaotic orbits or 1:1 resonant orbits, while high resonant families are practically unaffected. In the case of an oblate dark halo, the percentage of chaotic orbits seems to saturate at ≃55% of the orbits, when α > 4.5.
-
6.
The scale height of disk h is the least influential parameter of all that were studied. Nevertheless, in PH galaxy models only the chaotic and box orbits are affected by the variation of the value of h (sharing about 20% of the total orbits when h = 1), while the percentages of all the other families of orbits present a monotone evolution as h varies. Moreover, chaotic and 1:1 resonant orbits are the orbits mostly influenced by h in OH models.
-
7.
One of the most influential quantities is the halo flattening parameter β. In both PH and OH models the percentages of box, 2:1 resonant, and chaotic orbits are those mostly affected. The maximum percentage of regular orbits (around 65%) was observed when β = 0.4, while that of the chaotic orbits (around 50%) occurs at the extreme opposite values of β, that is when β = 0.1 (highly prolate halo), and β = 1.9 (highly oblate halo). Interestingly enough, the minimum amount of chaos (around 20%) takes place at β = 0.7, thus rejecting our initial assumption according to which a spherical (β = 1) dark matter halo should be the least chaotic.
-
8.
The scale length of the dark halo ch is another parameter with a vital role on the orbital structure. We found that the percentage of chaos quickly grows as ch increases, by collapsing the rates of regular orbits. In particular, the box, the 2:1 banana-type and 1:1 resonant orbits suffer the most in both PH and OH models. It was also observed, that at high values of ch, when the dark halo is much less concentrated, chaotic orbits is the most populated family holding high rates (around 60%) and the overall orbital structure of the phase plane is the same, regardless of the particular type (prolate or oblate) of the dark halo.
-
9.
Our experiments suggest that the angular momentum of the orbits Lz greatly influences the level of chaos: orbits with low angular momenta have higher chances of being chaotic, especially in OH models, than those with high values of angular momentum. The relationship between chaos and angular momentum is close to linear in both cases and again, box and 2:1 banana-type orbits are the most affected by the percentage of chaos. At extreme high values of the angular momentum Lz ≃ 50, box orbits are the all-dominant type of orbits possessing rates around 45% and 65% in PH and OH models, respectively.
-
10.
In models with very low negative values of the orbital energy E the motion of stars is almost entirely regular. However, the percentage of chaotic orbits grows rapidly with increasing energy showing the maximum value when E = 0, while for all positive energies it decreases following an almost linear trend. In prolate dark halo models, the energy mostly affects the chaotic, box, 1:1, 2:1, and higher resonant orbits. When E > 350, 2:1 banana-type orbits take the field heavily increasing their rates covering about the two thirds of the phase plane. In contrast, in OH models, varying the value of the energy mainly shuffles the orbital content among the families of regular orbits and only chaotic orbits suffer the most, however, being the most populated family.
When we take the fact that the effective potential in the meridional plane has a cusp caused by the centrifugal acceleration into account, all these behaviors turn out to be consistent with the analysis we made in Sect. 5, where we arrived at the conclusion that a necessary condition for an orbit to be chaotic is to pass near the center of the potential, while a sufficient condition for an orbit to be regular is not to pass near the center of the potential. In the same vein, we tested some dynamical quantities such as the minimum distance to the origin and the horizontal and vertical forces acting on stars, to determine if they can be used as chaos detectors. Unfortunately, our numerical experiments indicate that for all these quantities, even though they provide some general results, we cannot establish numerical threshold values that allow us to distinguish safely between ordered and chaotic motion. However, if we combine in pairs the outcomes of these quantities, we can extract useful information regarding the dynamical origin of the onset and the degree of chaos in our galaxy models.
We consider the results of the present research as an initial effort and also a promising step in the task of exploring the orbital structure of disk galaxies with dark matter haloes. Taking our encouraging outcomes into account, it is in our future plans to modify our dynamical model properly to expand our investigation into three dimensions. This will allow us to unveil how the parameters of the system influence the nature of three-dimensional orbits. Also, we would be particularly interested in obtaining the entire network of periodic orbits, revealing the evolution of the periodic points as well as their stability when varying the different parameters of our model.
Online material
Appendix A: Orbital structure
To show how the dynamical parameters of our galactic model influence the orbital
structure of the system, we present for each case, color-coded grids of initial
conditions 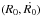 , equivalent to surfaces
of section, which allow us to visualize what types of orbits occupy specific areas in
the phase-space.
, equivalent to surfaces
of section, which allow us to visualize what types of orbits occupy specific areas in
the phase-space.
Figure A.1a depicts the phase plane of the PH model when Mn = 0. One can observe that most of the phase space is covered by 2:1 resonant orbits, while there is also a weak chaotic layer that separates the areas of regularity. The outermost thick curve is the ZVC. In Fig. A.1b, we present a grid on the phase plane when Mn = 500, i.e., a model with a more massive central nucleus. It is evident that there are many differences with respect to Fig. A.1a, being the most visible: (i) the growth of the region occupied by chaotic orbits; (ii) an increase in the allowed radial velocity Ṙ of the stars near the center of the galaxy; and (iii) the absence of several families of resonant orbits (i.e., 1:1, 4:3, and 6:3 resonant orbits). In Fig. A.1c, we can see the structure of the phase plane of the OH model when Mn = 0. In this case, we observe that the phase plane is flooded with box orbits due to the absence of the central nucleus. On the other hand, in Fig. A.1d, where we have an OH model with a massive nucleus (Mn = 500), the portion of box orbits is confined considerably as a vast unified chaotic sea emerges surrounding several islands of secondary resonances.
 |
Fig. A.1 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Mn = 0 and b) upper right: Mn = 500 and for the OH model when c) lower left: Mn = 0 and d) lower right: Mn = 500. |
The grid structure of the (R,Ṙ) phase plane for the PH model when cn = 0.05 is presented in Fig. A.2a. We see that when the concentration of the spherical nucleus is very high, a solid chaotic sea exists at the outer parts of the phase plane, resulting in the complete absence of secondary resonances. On the other hand, when cn = 0.50, we observe in Fig. A.2b that the area on the phase plane occupied by chaotic orbits has shrunk, thus leaving space for several resonant families (i.e., 1:1, 4:3 and other resonances) to increase their rates. Furthermore, the 12:7 chain of islands emerges inside the box domain. A similar comparison between lower and higher concentrated nucleus for the OH models is made in Fig. A.2c and d. We show that when cn = 0.05 (Fig. A.2c) all the different resonant families are present and are surrounded by a unified chaotic sea. In the case where cn = 0.50 (Fig. A.2d), the structure of the phase plane remains almost the same and the most prominent difference lies in the increasing rates of all of the regular families, which of course entails a reduction of the chaotic region.
 |
Fig. A.2 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: cn = 0.05 and b) upper right: cn = 0.50 and for the OH model when c) lower left: cn = 0.05 and d) lower right: cn = 0.50. |
A grid of initial conditions 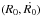 for the PH model when the
disk has the minimum possible value (Md = 4500) is given in Fig. A.3a. We observe that almost all of the resonant
families are present forming well-defined sets of islands. It is interesting to note,
the presence of a set of three islands corresponding to the so-called other resonances.
In fact, this is the 5:3 resonance which, however, appears itself only in some isolated
cases, so we do not feel it is necessary to include it in the list containing all the
main resonant families under investigation. Figure A.3b shows a similar grid when Md = 9000 (i.e., the maximum possible
value of the mass of the disk). It is evident that the structure of the phase plane has
several differences with respect to the Fig. A.3a
which are: (i) the reduction of the region occupied by chaotic orbits; (ii) the
approximately 40% increase in the allowed radial velocity Ṙ of the stars near the
central region of the galaxy; and (iii) the appearance of a second smaller area near the
center occupied by 2:1 banana-type orbit. In Fig. A.3c and d, we present two similar grids of initial conditions for the same
values of Md as in Fig. A.3a and b, respectively, but applied to the OH models this time.
Once more, as the disk becomes more massive the extent of the chaotic sea decreases,
thus amplifying the rates of all the regular families.
for the PH model when the
disk has the minimum possible value (Md = 4500) is given in Fig. A.3a. We observe that almost all of the resonant
families are present forming well-defined sets of islands. It is interesting to note,
the presence of a set of three islands corresponding to the so-called other resonances.
In fact, this is the 5:3 resonance which, however, appears itself only in some isolated
cases, so we do not feel it is necessary to include it in the list containing all the
main resonant families under investigation. Figure A.3b shows a similar grid when Md = 9000 (i.e., the maximum possible
value of the mass of the disk). It is evident that the structure of the phase plane has
several differences with respect to the Fig. A.3a
which are: (i) the reduction of the region occupied by chaotic orbits; (ii) the
approximately 40% increase in the allowed radial velocity Ṙ of the stars near the
central region of the galaxy; and (iii) the appearance of a second smaller area near the
center occupied by 2:1 banana-type orbit. In Fig. A.3c and d, we present two similar grids of initial conditions for the same
values of Md as in Fig. A.3a and b, respectively, but applied to the OH models this time.
Once more, as the disk becomes more massive the extent of the chaotic sea decreases,
thus amplifying the rates of all the regular families.
 |
Fig. A.3 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Md = 4500 and b) upper right: Md = 9000 and for the OH model when c) lower left: Md = 4500 and d) lower right: Md = 9000. |
In Fig. A.4a, we present the orbital structure of
a grid of initial conditions 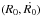 for the PH model when
b = 4. We
show that almost all resonant families are present, forming different sets of islands.
Here we have to point out the existence of an additional resonant family, that of the
5:3 resonant orbits, which correspond to the so-called “other resonances” and produce
the set of the well-defined purple triple islands at the phase plane. Figure A.4b shows a similar grid of initial conditions when
the core radius of the disk-halo possess its maximum possible value (b = 8). One may
distinguish several differences in the structure of the phase plane with respect to that
shown in Fig. A.4a. The main differences are the
following: (i) the area occupied by chaotic orbits has been reduced significantly and it
is confined to the very outer parts of the phase plane; (ii) the bifurcated 10:5 family
has been adsorbed by the main 2:1 family; (iii) the presence of higher resonances such
as the 12:7 family is much stronger; and (iv) the 4:3 resonance is depopulated and the
corresponding islands are so tiny that they appear as isolated points in the grid.
Similar grids of initial conditions for the same values of b as in Fig. A.4a and b, respectively, but for the OH models, are
shown in Fig. A.4c and d. We observe that at
highest value of b (Fig. A.4d)
the amount of initial conditions corresponding to chaotic orbits is significantly
greater with respect to Fig. A.4c, thus limiting
the extent of all the different areas of stability. Furthermore, higher resonant orbits
(i.e., the 8:5 family) appear only in models with large values of b.
for the PH model when
b = 4. We
show that almost all resonant families are present, forming different sets of islands.
Here we have to point out the existence of an additional resonant family, that of the
5:3 resonant orbits, which correspond to the so-called “other resonances” and produce
the set of the well-defined purple triple islands at the phase plane. Figure A.4b shows a similar grid of initial conditions when
the core radius of the disk-halo possess its maximum possible value (b = 8). One may
distinguish several differences in the structure of the phase plane with respect to that
shown in Fig. A.4a. The main differences are the
following: (i) the area occupied by chaotic orbits has been reduced significantly and it
is confined to the very outer parts of the phase plane; (ii) the bifurcated 10:5 family
has been adsorbed by the main 2:1 family; (iii) the presence of higher resonances such
as the 12:7 family is much stronger; and (iv) the 4:3 resonance is depopulated and the
corresponding islands are so tiny that they appear as isolated points in the grid.
Similar grids of initial conditions for the same values of b as in Fig. A.4a and b, respectively, but for the OH models, are
shown in Fig. A.4c and d. We observe that at
highest value of b (Fig. A.4d)
the amount of initial conditions corresponding to chaotic orbits is significantly
greater with respect to Fig. A.4c, thus limiting
the extent of all the different areas of stability. Furthermore, higher resonant orbits
(i.e., the 8:5 family) appear only in models with large values of b.
 |
Fig. A.4 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: b = 4 and b) upper right: b = 8 and for the OH model when c) lower left: b = 4 and d) lower right: b = 8. |
The orbital structure of a grid of initial conditions
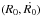 for the PH model when
α = 2.5
is presented in Fig. A.5a. We observe that the
vast majority of the phase plane is covered by resonant 2:1 banana-type orbits.
Specifically, there are two regions corresponding to 2:1 resonant orbits. It should be
emphasized that the 1:1 resonant family, which is a basic family, is absent in PH galaxy
models with sufficient small values of the scale length of the disk. A similar grid of
initial conditions when α = 5 is given in Fig. A.5b. This grid has many similarities with respect to that shown in
Fig. A.5a, but it also has several important
differences. The most visible differences are the growth of the area corresponding to
chaotic orbits, the appearance of the main 1:1 family, the absence of the second small
region occupied by 2:1 resonant orbits, and the disappearance of secondary resonances
such as the 4:3 and the 12:7. In Fig. A.5c and d
we present grids of initial conditions for the same values of α as in Fig. A.5a and b, respectively, but for the OH galaxy
models. It is evident, that in the case of the highest value of α, that is in Fig. A.5d, the portion of the chaotic and the 1:1 resonant
orbits is considerably larger, while at the same time, all the other regions of
stability have been reduced (i.e., regions corresponding to box, 2:1, and 3:2 resonant
orbits). Moreover, we should point out that in both cases, several higher, secondary
resonant orbits (i.e., 11:7, 13:8, 14:9) emerge mainly inside the area of the box
orbits.
for the PH model when
α = 2.5
is presented in Fig. A.5a. We observe that the
vast majority of the phase plane is covered by resonant 2:1 banana-type orbits.
Specifically, there are two regions corresponding to 2:1 resonant orbits. It should be
emphasized that the 1:1 resonant family, which is a basic family, is absent in PH galaxy
models with sufficient small values of the scale length of the disk. A similar grid of
initial conditions when α = 5 is given in Fig. A.5b. This grid has many similarities with respect to that shown in
Fig. A.5a, but it also has several important
differences. The most visible differences are the growth of the area corresponding to
chaotic orbits, the appearance of the main 1:1 family, the absence of the second small
region occupied by 2:1 resonant orbits, and the disappearance of secondary resonances
such as the 4:3 and the 12:7. In Fig. A.5c and d
we present grids of initial conditions for the same values of α as in Fig. A.5a and b, respectively, but for the OH galaxy
models. It is evident, that in the case of the highest value of α, that is in Fig. A.5d, the portion of the chaotic and the 1:1 resonant
orbits is considerably larger, while at the same time, all the other regions of
stability have been reduced (i.e., regions corresponding to box, 2:1, and 3:2 resonant
orbits). Moreover, we should point out that in both cases, several higher, secondary
resonant orbits (i.e., 11:7, 13:8, 14:9) emerge mainly inside the area of the box
orbits.
 |
Fig. A.5 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: α = 2.5 and b) upper right: α = 5 and for the OH model when c) lower left: α = 2.5 and d) lower right: α = 5. |
Figure A.6a depicts the orbital structure of a
grid of initial conditions 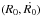 for the prolate dark
matter halo (PH) model when h = 0.1. As in all previous cases, more than half
the phase plane is covered by 2:1 banana-type orbits. A unified chaotic layer exists at
the outer parts of the phase plane and surrounds most of the different stability
islands. However, the islands produced by the 4:3 resonant orbits are so small that they
appear as lonely points in the gird. Things are quite similar in Fig. A.6b where h = 1. We see that the overall grid structure is
maintained and the observed differences are minor. In fact, the most noticeable
differences are the following: (i) the extent of the chaotic layer is smaller, giving
space to box orbits; (ii) the portion of the 4:3 resonant orbits looks more prominent;
and (iii) the extent of the 12:7 resonant orbits has been reduced. Similar grids of
initial conditions for the same values of h exist, as in Fig. A.6a and b, but for the OH galaxy models are shown in Fig. A.6c and d, respectively. Once more, we note that the
change of the value of the scale height of the disk does not cause significant influence
on the structure of the phase plane. All it does is to shrink the area occupied by
chaotic orbits thus, allowing mainly the 1:1 resonant orbits to enlarge their rate.
for the prolate dark
matter halo (PH) model when h = 0.1. As in all previous cases, more than half
the phase plane is covered by 2:1 banana-type orbits. A unified chaotic layer exists at
the outer parts of the phase plane and surrounds most of the different stability
islands. However, the islands produced by the 4:3 resonant orbits are so small that they
appear as lonely points in the gird. Things are quite similar in Fig. A.6b where h = 1. We see that the overall grid structure is
maintained and the observed differences are minor. In fact, the most noticeable
differences are the following: (i) the extent of the chaotic layer is smaller, giving
space to box orbits; (ii) the portion of the 4:3 resonant orbits looks more prominent;
and (iii) the extent of the 12:7 resonant orbits has been reduced. Similar grids of
initial conditions for the same values of h exist, as in Fig. A.6a and b, but for the OH galaxy models are shown in Fig. A.6c and d, respectively. Once more, we note that the
change of the value of the scale height of the disk does not cause significant influence
on the structure of the phase plane. All it does is to shrink the area occupied by
chaotic orbits thus, allowing mainly the 1:1 resonant orbits to enlarge their rate.
 |
Fig. A.6 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: h = 0.1 and b) upper right: h = 1 and for the OH model when c) lower left: h = 0.1 and d) lower right: h = 1. |
In Fig. A.7a, we present the orbital structure of
a grid of initial conditions 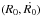 for the prolate dark
matter halo (PH) model when β = 0.1. Undoubtedly, this is a very interesting
phase plane that is very different from what we have seen so far. We observe the
existence of a vast chaotic sea that embraces many islands of stability formed by
different regular families of orbits. The meridional 2:1 banana-type and the linear 1:1
resonant orbits form two different islands on the grid, while box orbits have an anemic
presence. Moreover, we distinguish several purple regions corresponding to other types
of resonances. Here we have to point out that is the first time we have encountered such
an intense presence of that type of orbits. Our numerical calculations suggest that
these regions are produced by two different types of orbits. The set of the triple
islands inside the region of the 10:5 orbits correspond to the 10:3 resonance, while the
double set of islands inside the large 2:1 region and also above the box orbits is
produced by the 8:4 resonance. The grid shown in Fig. A.7b corresponds to the case where β = 0.9. We see that everything is now back to
normal and the previous complicated structure has vanished. Again, we can distinguish
many sets of islands formed by miscellaneous resonances. The small islands inside the
region of box orbits correspond to the 13:8 resonance, the set right above the box
orbits corresponds to the 8:5 resonance, while the set of the double islands embedded in
the chaotic sea corresponds to the 3:2 resonant family. The orbital structure of the
grid in the case of the spherical dark halo (β = 1) is presented in Fig. A.7c. Considering the previous analysis of the “other resonances”
shows that the orbital structure has remained almost unperturbed. Finally, Fig. A.7d, shows the case of a highly flattened halo where
β = 1.9.
Here, the increase of several types of orbits (i.e., 1:1, 3:2, 4:3, chaotic) spurred
both box and 2:1 orbits to reduce their rates and to be limited to the center of the
phase plane.
for the prolate dark
matter halo (PH) model when β = 0.1. Undoubtedly, this is a very interesting
phase plane that is very different from what we have seen so far. We observe the
existence of a vast chaotic sea that embraces many islands of stability formed by
different regular families of orbits. The meridional 2:1 banana-type and the linear 1:1
resonant orbits form two different islands on the grid, while box orbits have an anemic
presence. Moreover, we distinguish several purple regions corresponding to other types
of resonances. Here we have to point out that is the first time we have encountered such
an intense presence of that type of orbits. Our numerical calculations suggest that
these regions are produced by two different types of orbits. The set of the triple
islands inside the region of the 10:5 orbits correspond to the 10:3 resonance, while the
double set of islands inside the large 2:1 region and also above the box orbits is
produced by the 8:4 resonance. The grid shown in Fig. A.7b corresponds to the case where β = 0.9. We see that everything is now back to
normal and the previous complicated structure has vanished. Again, we can distinguish
many sets of islands formed by miscellaneous resonances. The small islands inside the
region of box orbits correspond to the 13:8 resonance, the set right above the box
orbits corresponds to the 8:5 resonance, while the set of the double islands embedded in
the chaotic sea corresponds to the 3:2 resonant family. The orbital structure of the
grid in the case of the spherical dark halo (β = 1) is presented in Fig. A.7c. Considering the previous analysis of the “other resonances”
shows that the orbital structure has remained almost unperturbed. Finally, Fig. A.7d, shows the case of a highly flattened halo where
β = 1.9.
Here, the increase of several types of orbits (i.e., 1:1, 3:2, 4:3, chaotic) spurred
both box and 2:1 orbits to reduce their rates and to be limited to the center of the
phase plane.
 |
Fig. A.7 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: β = 0.1 and b) upper right: β = 0.9 and for the OH model when c) lower left: β = 1 and d) lower right: β = 1.9. |
The orbital structure of a grid of initial conditions
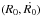 for the prolate dark
matter halo (PH) model when ch = 7 is shown in Fig. A.8a. One may observe that the vast majority of the
phase plane is covered by initial conditions corresponding to 2:1 banana-type orbits. In
fact, there are two distinct regions formed by these orbits. At the outer parts of the
phase plane, a chaotic layer is present that contains small stability islands. In
particular, we can distinguish a tiny region formed by the 1:1 resonant orbits, while
the points on the grid corresponding to the 4:3 resonant orbits are hardly visible.
Figure A.8b shows a similar grid of initial
conditions for a prolate galaxy model when ch = 22. It is evident that the
orbital structure has many significant differences with respect to that presented in
Fig. A.8a. The most noticeable differences are:
(i) the amount of chaos has increased considerably leading to a vast chaotic sea; (ii)
box orbits have been greatly depopulated and now are confined only to the center of the
grid; (iii) all the bifurcated resonances (i.e., 6:3 and 12:5) have disappeared, while
new resonant families such as the 3:2 family appear; and (iv) the total area of the
phase plane is reduced. In Fig. A.8c, we present
another grid of initial conditions for an oblate dark halo galaxy model when
ch = 7. In this case, all the expected
types of orbits are present forming well-defined regions in the phase plane. The purple
dots correspond to resonant orbits of higher multiplicity (i.e., 11:7 and 13:8 resonant
orbits). A similar oblate dark halo grid when ch = 22 is shown in Fig. A.8d. We show that the extent of chaos is
significantly larger than that observed in Fig. A.8c. Moreover, the higher resonant 8:5 family is completely absent. With a
closer look at the overall orbital structure, we realize that the grid of Fig. A.8d is very similar to that shown in Fig. A.8b. Those two grids correspond to the same value of
scale length of the halo ch = 22, but to different shapes of
the halo (prolate and oblate, respectively). Therefore, we may conclude that in high
values of ch, or in other words, when the halo is
much less concentrated, the orbital structure is the same, regardless of the particular
shape of the halo (prolate or oblate).
for the prolate dark
matter halo (PH) model when ch = 7 is shown in Fig. A.8a. One may observe that the vast majority of the
phase plane is covered by initial conditions corresponding to 2:1 banana-type orbits. In
fact, there are two distinct regions formed by these orbits. At the outer parts of the
phase plane, a chaotic layer is present that contains small stability islands. In
particular, we can distinguish a tiny region formed by the 1:1 resonant orbits, while
the points on the grid corresponding to the 4:3 resonant orbits are hardly visible.
Figure A.8b shows a similar grid of initial
conditions for a prolate galaxy model when ch = 22. It is evident that the
orbital structure has many significant differences with respect to that presented in
Fig. A.8a. The most noticeable differences are:
(i) the amount of chaos has increased considerably leading to a vast chaotic sea; (ii)
box orbits have been greatly depopulated and now are confined only to the center of the
grid; (iii) all the bifurcated resonances (i.e., 6:3 and 12:5) have disappeared, while
new resonant families such as the 3:2 family appear; and (iv) the total area of the
phase plane is reduced. In Fig. A.8c, we present
another grid of initial conditions for an oblate dark halo galaxy model when
ch = 7. In this case, all the expected
types of orbits are present forming well-defined regions in the phase plane. The purple
dots correspond to resonant orbits of higher multiplicity (i.e., 11:7 and 13:8 resonant
orbits). A similar oblate dark halo grid when ch = 22 is shown in Fig. A.8d. We show that the extent of chaos is
significantly larger than that observed in Fig. A.8c. Moreover, the higher resonant 8:5 family is completely absent. With a
closer look at the overall orbital structure, we realize that the grid of Fig. A.8d is very similar to that shown in Fig. A.8b. Those two grids correspond to the same value of
scale length of the halo ch = 22, but to different shapes of
the halo (prolate and oblate, respectively). Therefore, we may conclude that in high
values of ch, or in other words, when the halo is
much less concentrated, the orbital structure is the same, regardless of the particular
shape of the halo (prolate or oblate).
 |
Fig. A.8 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: ch = 7 and b) upper right: ch = 22 and for the OH model when c) lower left: ch = 7 and d) lower right: ch = 22. |
A grid of initial conditions 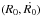 showing the orbital
structure of the prolate dark matter halo model when Lz = 1 is presented in
Fig. A.9a. We observe the existence of a dense and
unified chaotic sea, while the majority of the regular domains are located near the
central region of the phase plane, although there are important stability islands
surrounding them. Moreover, we should notice the complete absence of 4:3 or higher
resonant orbits. Figure A.9b shows a similar grid
of initial conditions corresponding to the Lz = 50 prolate halo
model. It is evident that the structure of this phase plane differs greatly from the
previous one. The most significant differences are: (i) the entire phase plane is
covered by regular orbits therefore chaotic motion, if any, is negligible; (ii) numerous
types of miscellaneous resonant orbits belonging to the “other resonances” class are
spread all over the phase plane (3:2, 5:3, 4:5, 8:5, 5:7, 6:7, 10:7, 11:7, 13:8, 14:9
resonant orbits, mentioning most of them); (iii) the allowed radial velocity
Ṙ of
stars passing near the center of the galaxy is almost decreased by half; and (iv) the
permissible area on the (R,Ṙ) plane is reduced. In Fig.
A.9c, we present another grid of initial
conditions for the Lz = 1 oblate halo
model. A vast chaotic sea is observed surrounding all the different stability islands.
Furthermore, we should note, a lack of higher resonant orbits, while the 8:5 resonant
orbits appear as extreme isolated points on the grid. Things are very different in Fig.
A.9d where the grid of the Lz = 50 oblate halo
model is depicted. The main differences with respect to the structure of the grid shown
in Fig. A.9c are very similar to those described
earlier in the prolate dark halo case. Again, the 8:5 resonant orbits are hardly
visible. However, we should point out that in this case, the number of the “other
resonances” orbits (4:5, 6:5, 7:5, 6:7, 8:7, 10:7, 8:9, 12:11, 13:11, mentioning the
most important of them) is lower.
showing the orbital
structure of the prolate dark matter halo model when Lz = 1 is presented in
Fig. A.9a. We observe the existence of a dense and
unified chaotic sea, while the majority of the regular domains are located near the
central region of the phase plane, although there are important stability islands
surrounding them. Moreover, we should notice the complete absence of 4:3 or higher
resonant orbits. Figure A.9b shows a similar grid
of initial conditions corresponding to the Lz = 50 prolate halo
model. It is evident that the structure of this phase plane differs greatly from the
previous one. The most significant differences are: (i) the entire phase plane is
covered by regular orbits therefore chaotic motion, if any, is negligible; (ii) numerous
types of miscellaneous resonant orbits belonging to the “other resonances” class are
spread all over the phase plane (3:2, 5:3, 4:5, 8:5, 5:7, 6:7, 10:7, 11:7, 13:8, 14:9
resonant orbits, mentioning most of them); (iii) the allowed radial velocity
Ṙ of
stars passing near the center of the galaxy is almost decreased by half; and (iv) the
permissible area on the (R,Ṙ) plane is reduced. In Fig.
A.9c, we present another grid of initial
conditions for the Lz = 1 oblate halo
model. A vast chaotic sea is observed surrounding all the different stability islands.
Furthermore, we should note, a lack of higher resonant orbits, while the 8:5 resonant
orbits appear as extreme isolated points on the grid. Things are very different in Fig.
A.9d where the grid of the Lz = 50 oblate halo
model is depicted. The main differences with respect to the structure of the grid shown
in Fig. A.9c are very similar to those described
earlier in the prolate dark halo case. Again, the 8:5 resonant orbits are hardly
visible. However, we should point out that in this case, the number of the “other
resonances” orbits (4:5, 6:5, 7:5, 6:7, 8:7, 10:7, 8:9, 12:11, 13:11, mentioning the
most important of them) is lower.
 |
Fig. A.9 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Lz = 1 and b) upper right: Lz = 50 and for the OH model when c) lower left: Lz = 1 and d) lower right: Lz = 50. |
 |
Fig. A.10 Orbital structure of the (R,Ṙ) phase plane for a) left: the PH model and b) right: the OH model when E = 700. |
The orbital structure of a grid of initial conditions
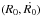 of the prolate dark
matter halo model when E = 700 (the maximum energy level studied) is
presented in Fig. A.10a. It is clearly seen that
the vast majority (about 60%) of the phase plane is covered by initial conditions
corresponding to the 2:1 banana-type orbits. As in many previous prolate halo grids, the
2:1 resonant orbits form two separate islands of stability on the phase plane. In Fig.
A.10a, we note a complete lack of 4:3 and 12:7
boxlet orbits, while we can identify the presence of “other resonant” orbits. Inside the
main 2:1 region, there is a thin ribbon of initial conditions produced by the 8:4
resonance, which is a bifurcated subfamily of the main 2:1 family (like the 6:3 and the
10:5 families of orbits). Moreover, just outside the box orbits we see a set of five
islands of initial conditions corresponding to
of the prolate dark
matter halo model when E = 700 (the maximum energy level studied) is
presented in Fig. A.10a. It is clearly seen that
the vast majority (about 60%) of the phase plane is covered by initial conditions
corresponding to the 2:1 banana-type orbits. As in many previous prolate halo grids, the
2:1 resonant orbits form two separate islands of stability on the phase plane. In Fig.
A.10a, we note a complete lack of 4:3 and 12:7
boxlet orbits, while we can identify the presence of “other resonant” orbits. Inside the
main 2:1 region, there is a thin ribbon of initial conditions produced by the 8:4
resonance, which is a bifurcated subfamily of the main 2:1 family (like the 6:3 and the
10:5 families of orbits). Moreover, just outside the box orbits we see a set of five
islands of initial conditions corresponding to
the 12:5 resonance. In Fig. A.10b, a similar grid of initial conditions for the same value of the energy (E = 700), but for the oblate case, is given. We observe that all the orbit families are present forming distinct well-defined stability islands, which are embraced by a unified chaotic sea. We should mention, that there is a strong presence of resonant orbits of higher multiplicity inside the area occupied by box orbits. Our numerical calculations indicate that these initial conditions correspond either to 10:7 or 13:8 resonant orbits.
Generally, dynamical methods are broadly split into two types: (i) those based on the evolution of sets of deviation vectors to characterize an orbit and (ii) those based on the frequencies of the orbits that extract information about the nature of motion only through the basic orbital elements without the use of deviation vectors.
For every orbital family there is a parent (or mother) periodic orbit, that is, an orbit that describes a closed figure. Perturbing the initial conditions which define the exact position of a periodic orbit we generate quasi-periodic orbits that belong to the same orbital family and librate around their closed parent periodic orbit.
Acknowledgments
I would like to express my warmest thanks to Dr. D.D. Carpintero for all the illuminating and creative discussions during this research and also for his substantial contribution to our efforts to refine and improve further the orbit classification code. My thanks also go to the anonymous referee for the careful reading of the manuscript and for all the apt suggestions and comments that allowed us to improve both the quality and the clarity of the paper.
References
- Allen, C., & Santillán, A. 1991, Rev. Mex. Astron. Astrofís., 22, 255 [Google Scholar]
- Allgood, B., Flores, R. A., Primack, J. R., et al. 2006, MNRAS, 367, 1781 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Spergel, D. 1982, ApJ, 252, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Spergel, D. 1984, MNRAS, 206, 159 [NASA ADS] [Google Scholar]
- Binney J., & Tremaine S. 2008, Galactic Dynamics (Princeton, USA: Princeton Univ. Press) [Google Scholar]
- Bosma, A. 1981, AJ, 86, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Bountis, T., Manos, T., & Antonopoulos, Ch. 2012, Celest. Mech. Dyn. Astron., 113, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Capuzzo-Dolcetta, R., Leccese, L., Merritt, D., & Vicari, A. 2007, ApJ, 666, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Caranicolas, N. D. 1997, Ap&SS, 246, 15 [Google Scholar]
- Caranicolas, N. D., & Innanen, K. A. 1991, AJ, 102, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Caranicolas, N. D., & Zotos, E. E. 2009, Baltic Astron., 18, 205 [NASA ADS] [Google Scholar]
- Caranicolas, N. D., & Zotos, E. E. 2010, Astron. Nachr., 331, 330 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Caranicolas, N. D., & Zotos, E. E. 2011, Res. Astron. Astrophys., 11, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Caranicolas, N. D., & Zotos, E. E. 2013, PASA, 30, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., & Innanen, K. A. 1987, AJ, 94, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Carpintero, D. D., & Aguilar, L. A. 1998, MNRAS, 298, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, D. P. 1985, ApJ, 295, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G., & Grosbøol, P. 1989, A&AR, 1, 261 [Google Scholar]
- Cooray, A. R. 2000, MNRAS, 313, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496 [Google Scholar]
- Evans, A. K. D., & Bridle, S. 2009, ApJ, 695, 1446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frenk, C. S., White, S. D. M., Davis, M., & Efstathiou, G. 1988, ApJ, 327, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., & Binney, J. 1985, MNRAS, 216, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, F., Helmi, A., Brown, A. G. A., & Li, Y. S. 2010, MNRAS, 408, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Hasan, H., & Norman, C. A. 1990, ApJ, 361, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Hasan, H., Pfenniger, D., & Norman, C. 1993, ApJ, 409, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2004, PASA, 21, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Honma, M., & Sofue, Y. 1997, PASJ, 49, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Irrgang, A., Wilcox, B., Tucker, E., & Schiefelbein, L. 2013, A&A, 549, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Kasun, S. F., & Evrard, A. E. 2005, ApJ, 629, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, D., & Patsis, P. 2005, ApJ, 624, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Kunihito, I., Takahiro, T., & Takashi, N. 2000, ApJ, 528, 51 [CrossRef] [Google Scholar]
- Manos, T., & Athansssoula, E. 2011, MNRAS, 415, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Manos, T., Bountis, T., & Skokos, Ch. 2013, J. Phys. A: Math. Theor. 46, 254017 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E. 1999, ApJ, 512, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. PASP, 111, 129 [Google Scholar]
- Merritt, D., & Fridman, T. 1996, ApJ, 460, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, W., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Muzzio, J. C., Carpintero, D. D., & Wachlin, F. C. 2005, Celest. Mech. Dyn. Astron., 91, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Ollé, M., & Pfenniger, D. 1998, A&A, 334, 829 [NASA ADS] [Google Scholar]
- Olling, R. P., & Merrifield, M. R. 2000, MNRAS, 311, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Ollongren, A. 1962, Bulletin of the Astronomical Institutes of the Netherlands, 16, 241 [Google Scholar]
- Ostriker, J. P., Peebles, P. J. E., & Yahil, A. 1974, ApJ, 193, 2, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, N. J., & Caranicolas, N. D. 2006, New Astron., 12, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., & Salucci, P. 1995, ApJS, 99, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Pfenniger, D. 1984, A&A, 134, 373 [NASA ADS] [Google Scholar]
- Pfenniger, D. 1996, in Proc. Barred Galaxies, eds. R. Buta, D. A. Crocker, & B. G. Elmegreen, ASP Conf. Ser., 91, 273 [Google Scholar]
- Pichardo, B., Martos, M., & Moreno, E. 2004, ApJ, 609, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Press, H. P., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN 77, 2nd edn. (Cambridge, USA: Cambridge Univ. Press) [Google Scholar]
- Rubin, V. C., & Burstein, D. 1985, ApJ, 297, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C., Ford, W. K., & Thonnard, N. 1980, ApJ, 238, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Ružička, A., Palouš, J., & Theis, C. 2007, A&A, 461, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Satoh, C. 1980, PASJ, 32, 41 [NASA ADS] [Google Scholar]
- Sellwood, J., & Wilkinson, A. 1993, Rep. Prog. Phys., 56, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Šidlichovský, M., & Nesvorný, D. 1996, Celest. Mech. Dyn. Astron., 65, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Skokos, C. 2001, J. Phys. A: Math. Gen., 34, 10029 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Skokos, Ch., Patsis, P. A., & Athanassoula, E. 2002a, MNRAS, 333 847 [Google Scholar]
- Skokos, Ch., Patsis, P. A., & Athanassoula, E. 2002b, MNRAS, 333, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Kollmeier, J. A., Shapley, A. E., et al. 2002, ApJ, 570, 526 [Google Scholar]
- Szydlowski, M. 1994, J. Math. Phys., 35, 1850 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Jing, Y. P., et al. 2009, MNRAS, 394, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Zotos, E. E. 2011, New Astron., 16, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Zotos, E. E. 2012, New Astron., 17, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Zotos, E. E., & Caranicolas, N. D. 2013, A&A, 560, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zotos, E. E., & Caranicolas, N. D. 2014, Nonlinear Dynamics, in press DOI: 10.1007/s11071-013-1129-8 [Google Scholar]
- Zotos, E. E., & Carpintero, D. D. 2013, Celest. Mech. Dyn. Astron., 116, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helvetica Physica Acta, 6, 110 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Plot of the rotation curve in our galactic model. We distinguish the total circular velocity (black) and also the contributions from the spherical nucleus (red), the disk (blue) and that of the dark matter halo (green). |
| In the text | |
 |
Fig. 2 Iso-density contours for our galactic model when the dark matter halo is a) left: prolate (PH model) and b) right: oblate (OH model). |
| In the text | |
 |
Fig. 3 Evolution of the mass density ρ(R) in the galactic plane (z = 0), as a function of the distance R from the center for SPM. The total mass density is shown in black, while we distinguish the three different contributions: the spherical nucleus (red), the disk (blue), and the dark matter halo (green). |
| In the text | |
 |
Fig. 4 The (R,Ṙ)z = 0, ż > 0 Poincaré surface of section (PSS) for the a) left: standard prolate model (SPM) and b) right: standard oblate model (SOM). |
| In the text | |
 |
Fig. 5 Grid of initial conditions revealing the orbital structure of the (R,Ṙ) phase plane for the a) left: PH model and b) right: OH model. |
| In the text | |
 |
Fig. 6 Orbit collection of the eight basic types in the PH galactic model: a) box orbit; b) 2:1 banana-type orbit; c) 1:1 linear orbit; d) 4:3 boxlet orbit; e) 6:3 boxlet orbit; f) 10:5 boxlet orbit; g) 12:7 boxlet orbit; h) chaotic orbit. |
| In the text | |
 |
Fig. 7 Orbit collection of the eight basic types in the OH galactic model: a) box orbit; b) 2:1 banana-type orbit; c) 1:1 linear orbit; d) 3:2 boxlet orbit; e) 4:3 boxlet orbit; f) 8:5 boxlet orbit; g) 13:8 boxlet orbit, one of our “orbits with higher resonance”; h) chaotic orbit. |
| In the text | |
 |
Fig. 8 Evolution of the different kinds of orbits, varying Mn for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 9 Evolution of the different kinds of orbits, varying cn for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 10 Evolution of the different kinds of orbits, varying Md for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 11 Evolution of the different kinds of orbits, varying b for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 12 Evolution of the different kinds of orbits, varying α for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 13 Evolution of the different kinds of orbits, varying h for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 14 Evolution of the different kinds of orbits, varying β for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 15 Evolution of the different kinds of orbits, varying ch for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 16 Evolution of the different kinds of orbits, varying Lz for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 17 Evolution of the different kinds of orbits, varying E for a) left: PH models and b)right: OH models. |
| In the text | |
 |
Fig. 18 Forces acting at every time step of the numerical integration along the path of a regular 2:1 banana-type orbit (purple color), a 4:3 resonant orbit (red color), and a chaotic orbit (blue color) in the Mn = 250 OH galaxy model. a) Left: horizontal force FR and b) right: vertical force Fz. |
| In the text | |
 |
Fig. 19 Grids of initial conditions |
| In the text | |
 |
Fig. 20 a)Left: minimum distance of orbits to the origin versus SALI. The horizontal, blue line shows the limit separating ordered from chaotic orbits. All the orbits between the two horizontal lines (orange and blue) are probably sticky orbits, which require more than 104 time units of integration time, so as to reveal their true chaotic nature. b)Right: minimum distances of orbits to the origin versus minimum distances to the minimum of the effective potential, located at (Rg,0). Green color corresponds to regular motion, while red corresponds to chaotic. |
| In the text | |
 |
Fig. 21 a)Left: Minimum distances of orbits to the origin versus a) left: maximum force at the R direction, b) right: maximum force in the z direction. Green color corresponds to regular motion, while red corresponds to chaotic. |
| In the text | |
 |
Fig. A.1 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Mn = 0 and b) upper right: Mn = 500 and for the OH model when c) lower left: Mn = 0 and d) lower right: Mn = 500. |
| In the text | |
 |
Fig. A.2 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: cn = 0.05 and b) upper right: cn = 0.50 and for the OH model when c) lower left: cn = 0.05 and d) lower right: cn = 0.50. |
| In the text | |
 |
Fig. A.3 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Md = 4500 and b) upper right: Md = 9000 and for the OH model when c) lower left: Md = 4500 and d) lower right: Md = 9000. |
| In the text | |
 |
Fig. A.4 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: b = 4 and b) upper right: b = 8 and for the OH model when c) lower left: b = 4 and d) lower right: b = 8. |
| In the text | |
 |
Fig. A.5 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: α = 2.5 and b) upper right: α = 5 and for the OH model when c) lower left: α = 2.5 and d) lower right: α = 5. |
| In the text | |
 |
Fig. A.6 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: h = 0.1 and b) upper right: h = 1 and for the OH model when c) lower left: h = 0.1 and d) lower right: h = 1. |
| In the text | |
 |
Fig. A.7 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: β = 0.1 and b) upper right: β = 0.9 and for the OH model when c) lower left: β = 1 and d) lower right: β = 1.9. |
| In the text | |
 |
Fig. A.8 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: ch = 7 and b) upper right: ch = 22 and for the OH model when c) lower left: ch = 7 and d) lower right: ch = 22. |
| In the text | |
 |
Fig. A.9 Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Lz = 1 and b) upper right: Lz = 50 and for the OH model when c) lower left: Lz = 1 and d) lower right: Lz = 50. |
| In the text | |
 |
Fig. A.10 Orbital structure of the (R,Ṙ) phase plane for a) left: the PH model and b) right: the OH model when E = 700. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


