| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 28 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322867 | |
| Published online | 27 February 2014 | |
Online material
Appendix A: Orbital structure
To show how the dynamical parameters of our galactic model influence the orbital
structure of the system, we present for each case, color-coded grids of initial
conditions 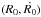 , equivalent to surfaces
of section, which allow us to visualize what types of orbits occupy specific areas in
the phase-space.
, equivalent to surfaces
of section, which allow us to visualize what types of orbits occupy specific areas in
the phase-space.
Figure A.1a depicts the phase plane of the PH model when Mn = 0. One can observe that most of the phase space is covered by 2:1 resonant orbits, while there is also a weak chaotic layer that separates the areas of regularity. The outermost thick curve is the ZVC. In Fig. A.1b, we present a grid on the phase plane when Mn = 500, i.e., a model with a more massive central nucleus. It is evident that there are many differences with respect to Fig. A.1a, being the most visible: (i) the growth of the region occupied by chaotic orbits; (ii) an increase in the allowed radial velocity Ṙ of the stars near the center of the galaxy; and (iii) the absence of several families of resonant orbits (i.e., 1:1, 4:3, and 6:3 resonant orbits). In Fig. A.1c, we can see the structure of the phase plane of the OH model when Mn = 0. In this case, we observe that the phase plane is flooded with box orbits due to the absence of the central nucleus. On the other hand, in Fig. A.1d, where we have an OH model with a massive nucleus (Mn = 500), the portion of box orbits is confined considerably as a vast unified chaotic sea emerges surrounding several islands of secondary resonances.
 |
Fig. A.1
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Mn = 0 and b) upper right: Mn = 500 and for the OH model when c) lower left: Mn = 0 and d) lower right: Mn = 500. |
| Open with DEXTER | |
The grid structure of the (R,Ṙ) phase plane for the PH model when cn = 0.05 is presented in Fig. A.2a. We see that when the concentration of the spherical nucleus is very high, a solid chaotic sea exists at the outer parts of the phase plane, resulting in the complete absence of secondary resonances. On the other hand, when cn = 0.50, we observe in Fig. A.2b that the area on the phase plane occupied by chaotic orbits has shrunk, thus leaving space for several resonant families (i.e., 1:1, 4:3 and other resonances) to increase their rates. Furthermore, the 12:7 chain of islands emerges inside the box domain. A similar comparison between lower and higher concentrated nucleus for the OH models is made in Fig. A.2c and d. We show that when cn = 0.05 (Fig. A.2c) all the different resonant families are present and are surrounded by a unified chaotic sea. In the case where cn = 0.50 (Fig. A.2d), the structure of the phase plane remains almost the same and the most prominent difference lies in the increasing rates of all of the regular families, which of course entails a reduction of the chaotic region.
 |
Fig. A.2
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: cn = 0.05 and b) upper right: cn = 0.50 and for the OH model when c) lower left: cn = 0.05 and d) lower right: cn = 0.50. |
| Open with DEXTER | |
A grid of initial conditions 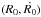 for the PH model when the
disk has the minimum possible value (Md = 4500) is given in Fig. A.3a. We observe that almost all of the resonant
families are present forming well-defined sets of islands. It is interesting to note,
the presence of a set of three islands corresponding to the so-called other resonances.
In fact, this is the 5:3 resonance which, however, appears itself only in some isolated
cases, so we do not feel it is necessary to include it in the list containing all the
main resonant families under investigation. Figure A.3b shows a similar grid when Md = 9000 (i.e., the maximum possible
value of the mass of the disk). It is evident that the structure of the phase plane has
several differences with respect to the Fig. A.3a
which are: (i) the reduction of the region occupied by chaotic orbits; (ii) the
approximately 40% increase in the allowed radial velocity Ṙ of the stars near the
central region of the galaxy; and (iii) the appearance of a second smaller area near the
center occupied by 2:1 banana-type orbit. In Fig. A.3c and d, we present two similar grids of initial conditions for the same
values of Md as in Fig. A.3a and b, respectively, but applied to the OH models this time.
Once more, as the disk becomes more massive the extent of the chaotic sea decreases,
thus amplifying the rates of all the regular families.
for the PH model when the
disk has the minimum possible value (Md = 4500) is given in Fig. A.3a. We observe that almost all of the resonant
families are present forming well-defined sets of islands. It is interesting to note,
the presence of a set of three islands corresponding to the so-called other resonances.
In fact, this is the 5:3 resonance which, however, appears itself only in some isolated
cases, so we do not feel it is necessary to include it in the list containing all the
main resonant families under investigation. Figure A.3b shows a similar grid when Md = 9000 (i.e., the maximum possible
value of the mass of the disk). It is evident that the structure of the phase plane has
several differences with respect to the Fig. A.3a
which are: (i) the reduction of the region occupied by chaotic orbits; (ii) the
approximately 40% increase in the allowed radial velocity Ṙ of the stars near the
central region of the galaxy; and (iii) the appearance of a second smaller area near the
center occupied by 2:1 banana-type orbit. In Fig. A.3c and d, we present two similar grids of initial conditions for the same
values of Md as in Fig. A.3a and b, respectively, but applied to the OH models this time.
Once more, as the disk becomes more massive the extent of the chaotic sea decreases,
thus amplifying the rates of all the regular families.
 |
Fig. A.3
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Md = 4500 and b) upper right: Md = 9000 and for the OH model when c) lower left: Md = 4500 and d) lower right: Md = 9000. |
| Open with DEXTER | |
In Fig. A.4a, we present the orbital structure of
a grid of initial conditions 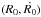 for the PH model when
b = 4. We
show that almost all resonant families are present, forming different sets of islands.
Here we have to point out the existence of an additional resonant family, that of the
5:3 resonant orbits, which correspond to the so-called “other resonances” and produce
the set of the well-defined purple triple islands at the phase plane. Figure A.4b shows a similar grid of initial conditions when
the core radius of the disk-halo possess its maximum possible value (b = 8). One may
distinguish several differences in the structure of the phase plane with respect to that
shown in Fig. A.4a. The main differences are the
following: (i) the area occupied by chaotic orbits has been reduced significantly and it
is confined to the very outer parts of the phase plane; (ii) the bifurcated 10:5 family
has been adsorbed by the main 2:1 family; (iii) the presence of higher resonances such
as the 12:7 family is much stronger; and (iv) the 4:3 resonance is depopulated and the
corresponding islands are so tiny that they appear as isolated points in the grid.
Similar grids of initial conditions for the same values of b as in Fig. A.4a and b, respectively, but for the OH models, are
shown in Fig. A.4c and d. We observe that at
highest value of b (Fig. A.4d)
the amount of initial conditions corresponding to chaotic orbits is significantly
greater with respect to Fig. A.4c, thus limiting
the extent of all the different areas of stability. Furthermore, higher resonant orbits
(i.e., the 8:5 family) appear only in models with large values of b.
for the PH model when
b = 4. We
show that almost all resonant families are present, forming different sets of islands.
Here we have to point out the existence of an additional resonant family, that of the
5:3 resonant orbits, which correspond to the so-called “other resonances” and produce
the set of the well-defined purple triple islands at the phase plane. Figure A.4b shows a similar grid of initial conditions when
the core radius of the disk-halo possess its maximum possible value (b = 8). One may
distinguish several differences in the structure of the phase plane with respect to that
shown in Fig. A.4a. The main differences are the
following: (i) the area occupied by chaotic orbits has been reduced significantly and it
is confined to the very outer parts of the phase plane; (ii) the bifurcated 10:5 family
has been adsorbed by the main 2:1 family; (iii) the presence of higher resonances such
as the 12:7 family is much stronger; and (iv) the 4:3 resonance is depopulated and the
corresponding islands are so tiny that they appear as isolated points in the grid.
Similar grids of initial conditions for the same values of b as in Fig. A.4a and b, respectively, but for the OH models, are
shown in Fig. A.4c and d. We observe that at
highest value of b (Fig. A.4d)
the amount of initial conditions corresponding to chaotic orbits is significantly
greater with respect to Fig. A.4c, thus limiting
the extent of all the different areas of stability. Furthermore, higher resonant orbits
(i.e., the 8:5 family) appear only in models with large values of b.
 |
Fig. A.4
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: b = 4 and b) upper right: b = 8 and for the OH model when c) lower left: b = 4 and d) lower right: b = 8. |
| Open with DEXTER | |
The orbital structure of a grid of initial conditions
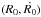 for the PH model when
α = 2.5
is presented in Fig. A.5a. We observe that the
vast majority of the phase plane is covered by resonant 2:1 banana-type orbits.
Specifically, there are two regions corresponding to 2:1 resonant orbits. It should be
emphasized that the 1:1 resonant family, which is a basic family, is absent in PH galaxy
models with sufficient small values of the scale length of the disk. A similar grid of
initial conditions when α = 5 is given in Fig. A.5b. This grid has many similarities with respect to that shown in
Fig. A.5a, but it also has several important
differences. The most visible differences are the growth of the area corresponding to
chaotic orbits, the appearance of the main 1:1 family, the absence of the second small
region occupied by 2:1 resonant orbits, and the disappearance of secondary resonances
such as the 4:3 and the 12:7. In Fig. A.5c and d
we present grids of initial conditions for the same values of α as in Fig. A.5a and b, respectively, but for the OH galaxy
models. It is evident, that in the case of the highest value of α, that is in Fig. A.5d, the portion of the chaotic and the 1:1 resonant
orbits is considerably larger, while at the same time, all the other regions of
stability have been reduced (i.e., regions corresponding to box, 2:1, and 3:2 resonant
orbits). Moreover, we should point out that in both cases, several higher, secondary
resonant orbits (i.e., 11:7, 13:8, 14:9) emerge mainly inside the area of the box
orbits.
for the PH model when
α = 2.5
is presented in Fig. A.5a. We observe that the
vast majority of the phase plane is covered by resonant 2:1 banana-type orbits.
Specifically, there are two regions corresponding to 2:1 resonant orbits. It should be
emphasized that the 1:1 resonant family, which is a basic family, is absent in PH galaxy
models with sufficient small values of the scale length of the disk. A similar grid of
initial conditions when α = 5 is given in Fig. A.5b. This grid has many similarities with respect to that shown in
Fig. A.5a, but it also has several important
differences. The most visible differences are the growth of the area corresponding to
chaotic orbits, the appearance of the main 1:1 family, the absence of the second small
region occupied by 2:1 resonant orbits, and the disappearance of secondary resonances
such as the 4:3 and the 12:7. In Fig. A.5c and d
we present grids of initial conditions for the same values of α as in Fig. A.5a and b, respectively, but for the OH galaxy
models. It is evident, that in the case of the highest value of α, that is in Fig. A.5d, the portion of the chaotic and the 1:1 resonant
orbits is considerably larger, while at the same time, all the other regions of
stability have been reduced (i.e., regions corresponding to box, 2:1, and 3:2 resonant
orbits). Moreover, we should point out that in both cases, several higher, secondary
resonant orbits (i.e., 11:7, 13:8, 14:9) emerge mainly inside the area of the box
orbits.
 |
Fig. A.5
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: α = 2.5 and b) upper right: α = 5 and for the OH model when c) lower left: α = 2.5 and d) lower right: α = 5. |
| Open with DEXTER | |
Figure A.6a depicts the orbital structure of a
grid of initial conditions 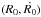 for the prolate dark
matter halo (PH) model when h = 0.1. As in all previous cases, more than half
the phase plane is covered by 2:1 banana-type orbits. A unified chaotic layer exists at
the outer parts of the phase plane and surrounds most of the different stability
islands. However, the islands produced by the 4:3 resonant orbits are so small that they
appear as lonely points in the gird. Things are quite similar in Fig. A.6b where h = 1. We see that the overall grid structure is
maintained and the observed differences are minor. In fact, the most noticeable
differences are the following: (i) the extent of the chaotic layer is smaller, giving
space to box orbits; (ii) the portion of the 4:3 resonant orbits looks more prominent;
and (iii) the extent of the 12:7 resonant orbits has been reduced. Similar grids of
initial conditions for the same values of h exist, as in Fig. A.6a and b, but for the OH galaxy models are shown in Fig. A.6c and d, respectively. Once more, we note that the
change of the value of the scale height of the disk does not cause significant influence
on the structure of the phase plane. All it does is to shrink the area occupied by
chaotic orbits thus, allowing mainly the 1:1 resonant orbits to enlarge their rate.
for the prolate dark
matter halo (PH) model when h = 0.1. As in all previous cases, more than half
the phase plane is covered by 2:1 banana-type orbits. A unified chaotic layer exists at
the outer parts of the phase plane and surrounds most of the different stability
islands. However, the islands produced by the 4:3 resonant orbits are so small that they
appear as lonely points in the gird. Things are quite similar in Fig. A.6b where h = 1. We see that the overall grid structure is
maintained and the observed differences are minor. In fact, the most noticeable
differences are the following: (i) the extent of the chaotic layer is smaller, giving
space to box orbits; (ii) the portion of the 4:3 resonant orbits looks more prominent;
and (iii) the extent of the 12:7 resonant orbits has been reduced. Similar grids of
initial conditions for the same values of h exist, as in Fig. A.6a and b, but for the OH galaxy models are shown in Fig. A.6c and d, respectively. Once more, we note that the
change of the value of the scale height of the disk does not cause significant influence
on the structure of the phase plane. All it does is to shrink the area occupied by
chaotic orbits thus, allowing mainly the 1:1 resonant orbits to enlarge their rate.
 |
Fig. A.6
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: h = 0.1 and b) upper right: h = 1 and for the OH model when c) lower left: h = 0.1 and d) lower right: h = 1. |
| Open with DEXTER | |
In Fig. A.7a, we present the orbital structure of
a grid of initial conditions 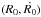 for the prolate dark
matter halo (PH) model when β = 0.1. Undoubtedly, this is a very interesting
phase plane that is very different from what we have seen so far. We observe the
existence of a vast chaotic sea that embraces many islands of stability formed by
different regular families of orbits. The meridional 2:1 banana-type and the linear 1:1
resonant orbits form two different islands on the grid, while box orbits have an anemic
presence. Moreover, we distinguish several purple regions corresponding to other types
of resonances. Here we have to point out that is the first time we have encountered such
an intense presence of that type of orbits. Our numerical calculations suggest that
these regions are produced by two different types of orbits. The set of the triple
islands inside the region of the 10:5 orbits correspond to the 10:3 resonance, while the
double set of islands inside the large 2:1 region and also above the box orbits is
produced by the 8:4 resonance. The grid shown in Fig. A.7b corresponds to the case where β = 0.9. We see that everything is now back to
normal and the previous complicated structure has vanished. Again, we can distinguish
many sets of islands formed by miscellaneous resonances. The small islands inside the
region of box orbits correspond to the 13:8 resonance, the set right above the box
orbits corresponds to the 8:5 resonance, while the set of the double islands embedded in
the chaotic sea corresponds to the 3:2 resonant family. The orbital structure of the
grid in the case of the spherical dark halo (β = 1) is presented in Fig. A.7c. Considering the previous analysis of the “other resonances”
shows that the orbital structure has remained almost unperturbed. Finally, Fig. A.7d, shows the case of a highly flattened halo where
β = 1.9.
Here, the increase of several types of orbits (i.e., 1:1, 3:2, 4:3, chaotic) spurred
both box and 2:1 orbits to reduce their rates and to be limited to the center of the
phase plane.
for the prolate dark
matter halo (PH) model when β = 0.1. Undoubtedly, this is a very interesting
phase plane that is very different from what we have seen so far. We observe the
existence of a vast chaotic sea that embraces many islands of stability formed by
different regular families of orbits. The meridional 2:1 banana-type and the linear 1:1
resonant orbits form two different islands on the grid, while box orbits have an anemic
presence. Moreover, we distinguish several purple regions corresponding to other types
of resonances. Here we have to point out that is the first time we have encountered such
an intense presence of that type of orbits. Our numerical calculations suggest that
these regions are produced by two different types of orbits. The set of the triple
islands inside the region of the 10:5 orbits correspond to the 10:3 resonance, while the
double set of islands inside the large 2:1 region and also above the box orbits is
produced by the 8:4 resonance. The grid shown in Fig. A.7b corresponds to the case where β = 0.9. We see that everything is now back to
normal and the previous complicated structure has vanished. Again, we can distinguish
many sets of islands formed by miscellaneous resonances. The small islands inside the
region of box orbits correspond to the 13:8 resonance, the set right above the box
orbits corresponds to the 8:5 resonance, while the set of the double islands embedded in
the chaotic sea corresponds to the 3:2 resonant family. The orbital structure of the
grid in the case of the spherical dark halo (β = 1) is presented in Fig. A.7c. Considering the previous analysis of the “other resonances”
shows that the orbital structure has remained almost unperturbed. Finally, Fig. A.7d, shows the case of a highly flattened halo where
β = 1.9.
Here, the increase of several types of orbits (i.e., 1:1, 3:2, 4:3, chaotic) spurred
both box and 2:1 orbits to reduce their rates and to be limited to the center of the
phase plane.
 |
Fig. A.7
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: β = 0.1 and b) upper right: β = 0.9 and for the OH model when c) lower left: β = 1 and d) lower right: β = 1.9. |
| Open with DEXTER | |
The orbital structure of a grid of initial conditions
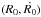 for the prolate dark
matter halo (PH) model when ch = 7 is shown in Fig. A.8a. One may observe that the vast majority of the
phase plane is covered by initial conditions corresponding to 2:1 banana-type orbits. In
fact, there are two distinct regions formed by these orbits. At the outer parts of the
phase plane, a chaotic layer is present that contains small stability islands. In
particular, we can distinguish a tiny region formed by the 1:1 resonant orbits, while
the points on the grid corresponding to the 4:3 resonant orbits are hardly visible.
Figure A.8b shows a similar grid of initial
conditions for a prolate galaxy model when ch = 22. It is evident that the
orbital structure has many significant differences with respect to that presented in
Fig. A.8a. The most noticeable differences are:
(i) the amount of chaos has increased considerably leading to a vast chaotic sea; (ii)
box orbits have been greatly depopulated and now are confined only to the center of the
grid; (iii) all the bifurcated resonances (i.e., 6:3 and 12:5) have disappeared, while
new resonant families such as the 3:2 family appear; and (iv) the total area of the
phase plane is reduced. In Fig. A.8c, we present
another grid of initial conditions for an oblate dark halo galaxy model when
ch = 7. In this case, all the expected
types of orbits are present forming well-defined regions in the phase plane. The purple
dots correspond to resonant orbits of higher multiplicity (i.e., 11:7 and 13:8 resonant
orbits). A similar oblate dark halo grid when ch = 22 is shown in Fig. A.8d. We show that the extent of chaos is
significantly larger than that observed in Fig. A.8c. Moreover, the higher resonant 8:5 family is completely absent. With a
closer look at the overall orbital structure, we realize that the grid of Fig. A.8d is very similar to that shown in Fig. A.8b. Those two grids correspond to the same value of
scale length of the halo ch = 22, but to different shapes of
the halo (prolate and oblate, respectively). Therefore, we may conclude that in high
values of ch, or in other words, when the halo is
much less concentrated, the orbital structure is the same, regardless of the particular
shape of the halo (prolate or oblate).
for the prolate dark
matter halo (PH) model when ch = 7 is shown in Fig. A.8a. One may observe that the vast majority of the
phase plane is covered by initial conditions corresponding to 2:1 banana-type orbits. In
fact, there are two distinct regions formed by these orbits. At the outer parts of the
phase plane, a chaotic layer is present that contains small stability islands. In
particular, we can distinguish a tiny region formed by the 1:1 resonant orbits, while
the points on the grid corresponding to the 4:3 resonant orbits are hardly visible.
Figure A.8b shows a similar grid of initial
conditions for a prolate galaxy model when ch = 22. It is evident that the
orbital structure has many significant differences with respect to that presented in
Fig. A.8a. The most noticeable differences are:
(i) the amount of chaos has increased considerably leading to a vast chaotic sea; (ii)
box orbits have been greatly depopulated and now are confined only to the center of the
grid; (iii) all the bifurcated resonances (i.e., 6:3 and 12:5) have disappeared, while
new resonant families such as the 3:2 family appear; and (iv) the total area of the
phase plane is reduced. In Fig. A.8c, we present
another grid of initial conditions for an oblate dark halo galaxy model when
ch = 7. In this case, all the expected
types of orbits are present forming well-defined regions in the phase plane. The purple
dots correspond to resonant orbits of higher multiplicity (i.e., 11:7 and 13:8 resonant
orbits). A similar oblate dark halo grid when ch = 22 is shown in Fig. A.8d. We show that the extent of chaos is
significantly larger than that observed in Fig. A.8c. Moreover, the higher resonant 8:5 family is completely absent. With a
closer look at the overall orbital structure, we realize that the grid of Fig. A.8d is very similar to that shown in Fig. A.8b. Those two grids correspond to the same value of
scale length of the halo ch = 22, but to different shapes of
the halo (prolate and oblate, respectively). Therefore, we may conclude that in high
values of ch, or in other words, when the halo is
much less concentrated, the orbital structure is the same, regardless of the particular
shape of the halo (prolate or oblate).
 |
Fig. A.8
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: ch = 7 and b) upper right: ch = 22 and for the OH model when c) lower left: ch = 7 and d) lower right: ch = 22. |
| Open with DEXTER | |
A grid of initial conditions 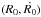 showing the orbital
structure of the prolate dark matter halo model when Lz = 1 is presented in
Fig. A.9a. We observe the existence of a dense and
unified chaotic sea, while the majority of the regular domains are located near the
central region of the phase plane, although there are important stability islands
surrounding them. Moreover, we should notice the complete absence of 4:3 or higher
resonant orbits. Figure A.9b shows a similar grid
of initial conditions corresponding to the Lz = 50 prolate halo
model. It is evident that the structure of this phase plane differs greatly from the
previous one. The most significant differences are: (i) the entire phase plane is
covered by regular orbits therefore chaotic motion, if any, is negligible; (ii) numerous
types of miscellaneous resonant orbits belonging to the “other resonances” class are
spread all over the phase plane (3:2, 5:3, 4:5, 8:5, 5:7, 6:7, 10:7, 11:7, 13:8, 14:9
resonant orbits, mentioning most of them); (iii) the allowed radial velocity
Ṙ of
stars passing near the center of the galaxy is almost decreased by half; and (iv) the
permissible area on the (R,Ṙ) plane is reduced. In Fig.
A.9c, we present another grid of initial
conditions for the Lz = 1 oblate halo
model. A vast chaotic sea is observed surrounding all the different stability islands.
Furthermore, we should note, a lack of higher resonant orbits, while the 8:5 resonant
orbits appear as extreme isolated points on the grid. Things are very different in Fig.
A.9d where the grid of the Lz = 50 oblate halo
model is depicted. The main differences with respect to the structure of the grid shown
in Fig. A.9c are very similar to those described
earlier in the prolate dark halo case. Again, the 8:5 resonant orbits are hardly
visible. However, we should point out that in this case, the number of the “other
resonances” orbits (4:5, 6:5, 7:5, 6:7, 8:7, 10:7, 8:9, 12:11, 13:11, mentioning the
most important of them) is lower.
showing the orbital
structure of the prolate dark matter halo model when Lz = 1 is presented in
Fig. A.9a. We observe the existence of a dense and
unified chaotic sea, while the majority of the regular domains are located near the
central region of the phase plane, although there are important stability islands
surrounding them. Moreover, we should notice the complete absence of 4:3 or higher
resonant orbits. Figure A.9b shows a similar grid
of initial conditions corresponding to the Lz = 50 prolate halo
model. It is evident that the structure of this phase plane differs greatly from the
previous one. The most significant differences are: (i) the entire phase plane is
covered by regular orbits therefore chaotic motion, if any, is negligible; (ii) numerous
types of miscellaneous resonant orbits belonging to the “other resonances” class are
spread all over the phase plane (3:2, 5:3, 4:5, 8:5, 5:7, 6:7, 10:7, 11:7, 13:8, 14:9
resonant orbits, mentioning most of them); (iii) the allowed radial velocity
Ṙ of
stars passing near the center of the galaxy is almost decreased by half; and (iv) the
permissible area on the (R,Ṙ) plane is reduced. In Fig.
A.9c, we present another grid of initial
conditions for the Lz = 1 oblate halo
model. A vast chaotic sea is observed surrounding all the different stability islands.
Furthermore, we should note, a lack of higher resonant orbits, while the 8:5 resonant
orbits appear as extreme isolated points on the grid. Things are very different in Fig.
A.9d where the grid of the Lz = 50 oblate halo
model is depicted. The main differences with respect to the structure of the grid shown
in Fig. A.9c are very similar to those described
earlier in the prolate dark halo case. Again, the 8:5 resonant orbits are hardly
visible. However, we should point out that in this case, the number of the “other
resonances” orbits (4:5, 6:5, 7:5, 6:7, 8:7, 10:7, 8:9, 12:11, 13:11, mentioning the
most important of them) is lower.
 |
Fig. A.9
Orbital structure of the (R,Ṙ) phase plane for the PH model when a) upper left: Lz = 1 and b) upper right: Lz = 50 and for the OH model when c) lower left: Lz = 1 and d) lower right: Lz = 50. |
| Open with DEXTER | |
 |
Fig. A.10
Orbital structure of the (R,Ṙ) phase plane for a) left: the PH model and b) right: the OH model when E = 700. |
| Open with DEXTER | |
The orbital structure of a grid of initial conditions
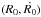 of the prolate dark
matter halo model when E = 700 (the maximum energy level studied) is
presented in Fig. A.10a. It is clearly seen that
the vast majority (about 60%) of the phase plane is covered by initial conditions
corresponding to the 2:1 banana-type orbits. As in many previous prolate halo grids, the
2:1 resonant orbits form two separate islands of stability on the phase plane. In Fig.
A.10a, we note a complete lack of 4:3 and 12:7
boxlet orbits, while we can identify the presence of “other resonant” orbits. Inside the
main 2:1 region, there is a thin ribbon of initial conditions produced by the 8:4
resonance, which is a bifurcated subfamily of the main 2:1 family (like the 6:3 and the
10:5 families of orbits). Moreover, just outside the box orbits we see a set of five
islands of initial conditions corresponding to
of the prolate dark
matter halo model when E = 700 (the maximum energy level studied) is
presented in Fig. A.10a. It is clearly seen that
the vast majority (about 60%) of the phase plane is covered by initial conditions
corresponding to the 2:1 banana-type orbits. As in many previous prolate halo grids, the
2:1 resonant orbits form two separate islands of stability on the phase plane. In Fig.
A.10a, we note a complete lack of 4:3 and 12:7
boxlet orbits, while we can identify the presence of “other resonant” orbits. Inside the
main 2:1 region, there is a thin ribbon of initial conditions produced by the 8:4
resonance, which is a bifurcated subfamily of the main 2:1 family (like the 6:3 and the
10:5 families of orbits). Moreover, just outside the box orbits we see a set of five
islands of initial conditions corresponding to
the 12:5 resonance. In Fig. A.10b, a similar grid of initial conditions for the same value of the energy (E = 700), but for the oblate case, is given. We observe that all the orbit families are present forming distinct well-defined stability islands, which are embraced by a unified chaotic sea. We should mention, that there is a strong presence of resonant orbits of higher multiplicity inside the area occupied by box orbits. Our numerical calculations indicate that these initial conditions correspond either to 10:7 or 13:8 resonant orbits.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


