| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 8 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201322625 | |
| Published online | 26 February 2014 | |
Improving cross-identification of galaxies using their photometry
1
UNED, Dpto. de Inteligencia Artificial, ETSI Informática, Juan del Rosal,
16,
28040
Madrid,
Spain
e-mail:
mmarquez92@alumno.uned.es
2
Johns Hopkins University, Baltimore
MD
21218,
USA
Received:
8
September
2013
Accepted:
13
December
2013
The identification of the same astronomical objects in different exposures taken with different instruments is a fundamental but difficult problem, which has long been studied for its statistical and computational complexity. We typically consider the celestial coordinates of detections to decide whether they belong to the same object, but crowded areas often yield degenerate cases when multiple matching configurations have similar likelihoods. We applied Bayesian inference to alleviate the problem by including photometric measurements. The spectral energy distribution of a candidate association is compared with models to test whether the photometric evidence points toward a good match or not. We discuss our preliminary results from simulated data and the COSMOS catalog.
Key words: surveys / catalogs / techniques: photometric / galaxies: photometry
© ESO, 2014
1. Introduction
Most astronomical studies today use data from a number of observations. Variability analysis uses repeated observations, which are then combined into time-series data. At other times we combine photometric measurements from separate instruments to understand the properties of the objects based on a wider wavelength coverage. All these projects rely on a fundamental preprocessing step that creates the associations called crossmatching. The apparently simple problem of identifying the same astronomical object in separate observations becomes most challenging in crowded regions. When the uncertainties of the celestial coordinates are similar to the separation of the sources, the directional data will not be sufficient to distinguish between competing associations. For the large datasets today, manually sorting through the possible candidates is too time consuming, and we need to find a better solution. Additional measurements are needed to fully resolve these problems, and photometry is the first choice because it is readily available in most cases. Our goal is to design and implement an automatic pipeline capable of including measured fluxes to improve the quality of crossmatches. We applied Bayesian hypotheses testing to the problem, which provides a clear framework for combining different measurements in the decision-making process. Budavári & Szalay (2008) introduced the methodology and calculated the relevant Bayes factor for the astrometric measurements. In this paper we explore the power of the method when applied to photometry and illustrate its power on synthetic and observed galaxies. In Sect. 2 we discuss the methodology and show that the calculations in fact involve the same formulas as are routinely used for spectral energy distribution (SED) fitting and photometric redshift estimation. Section 3 describes the impact of uncertainties and priors on the framework. Section 4 focuses on the experimental setup and our preliminary results. Sections 5 analyzes the results from simulated catalogs and the COSMOS dataset, and Sect. 6 concludes our study.
2. Methodology
In Budavári & Szalay (2008) an astrometric
crossmatching problem was addressed by comparing the likelihood of two complementary
hypotheses: hypothesis H represents the case in which the astrometric positions of a group
of detections correspond to the same object, and hypothesis K stands for the case in which
the detections do not belong to the same object. For Gaussian (or Fisher) uncertainties, the
astrometric Bayes factor can be analytically calculated and efficiently implemented for the
N-way case
using recursions. In this paper we consider candidate associations from astrometric matches
and compare H to K in light of photometric measurements. The photometric Bayes factor
Bph compares the likelihood of the two
hypotheses p(D|H) and p(D|K),
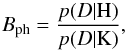 (1)where the datum
D is the
observed fluxes { gi }. When the Bayes
factor is larger than unity, the data have supporting evidence for a true association, but
low values argue for no match. When the Bayes factor is 1, the data do not provide
information with which we can decide for one of the hypotheses. To evaluate this ratio we
marginalize over a familiar likelihood function.
(1)where the datum
D is the
observed fluxes { gi }. When the Bayes
factor is larger than unity, the data have supporting evidence for a true association, but
low values argue for no match. When the Bayes factor is 1, the data do not provide
information with which we can decide for one of the hypotheses. To evaluate this ratio we
marginalize over a familiar likelihood function.
The problem to be considered here is similar to photometric redshift estimation Benítez (2000) and in general the SED fitting; for a
recent review see Walcher et al. (2011). Fitting the
SED of galaxies uses semi-analytic models, for instance that of Bruzual & Charlot (2003), or empirical template spectra such as
those reported in Coleman et al. (1980). In the
simplest case, a discrete number of templates are used that are scaled and redshifted to
match the measured broadband fluxes. Formally, this is built upon the normalized convolution
of the galaxy spectrum templates with the response function of the measurement systems,
which includes the filter transmission, quantum efficiency, optical effect of the
instrument, etc. that correspond to the bands under consideration. The spectrum of the
galaxy is defined in terms of a restframe at different redshifts. For a given
T template,
z redshift,
and α
brightness we can evaluate the simulated fluxes in any photometric system, which can then be
compared with the { gi } observations.
Typically ![\begin{equation} \chi^2(\alpha,T,z) = \sum_{i}^{n} \frac{1}{ \sigma_i^2} \Big[ {g_i}-\alpha\,{f_i}(T,z) \Big]^2 \end{equation}](/articles/aa/full_html/2014/03/aa22625-13/aa22625-13-eq11.png) (2)is minimized to
find the best-fitting model, which is equivalent to the maximum-likelihood estimation (MLE)
with a Gaussian,
(2)is minimized to
find the best-fitting model, which is equivalent to the maximum-likelihood estimation (MLE)
with a Gaussian, ![\begin{equation} \label{eq3} L(\alpha,T,z) \equiv p\left(\{g_i\}\, |\, \alpha,T,z\right) = \frac{1}{Z}\exp\left[-\frac{\chi^2(\alpha,T,z)}{2}\right], \end{equation}](/articles/aa/full_html/2014/03/aa22625-13/aa22625-13-eq12.png) (3)where Z is the normalization
constant that depends on the covariance matrix, or in this case, the { σi } diagonal elements.
As shown in Fig. 1, the models used fit real COSMOS catalog data considerably well, whereas
for artificially nonmatched data the fit to the models is clearly poor.
(3)where Z is the normalization
constant that depends on the covariance matrix, or in this case, the { σi } diagonal elements.
As shown in Fig. 1, the models used fit real COSMOS catalog data considerably well, whereas
for artificially nonmatched data the fit to the models is clearly poor.
 |
Fig. 1 a) Real data. Best SED fit for a matched tuple of a COSMOS galaxy of type Ell3A0, redshift of 1.4, color index B − V of 1.2567. b) Best SED fit for a matched tuple of a COSMOS galaxy of type ScA2, redshift of 3.15, color index B − V of − 0.0653. c) Best SED fit for a shuffled tuple of a COSMOS galaxy of type Ell6A0, redshift of 0.6, color index B − V of 1.7867. d) Best SED fit for a shuffled tuple of a COSMOS galaxy of type S0A0, redshift of 2.48, color index B − V of − 0.5123. This figure shows that our models reasonably fit real COSMOS galaxies. This is not true for random associations. |
After computing the probability of the data given the model (for all models), the one with the lowest χ2 yields the best SED for fitting the data.
We evaluated however the likelihoods of the hypotheses by integrating them over the entire
parameter space. We call Φ the
parameter vector of the model H, which is just a shorthand for writing (α,T,z), o, similarly, we can
consider (m,T,z) by applying a simple coordinate change between
the brightness scale α, and the magnitude m in our model. These are the
unknown model properties of the common object behind the observations. The numerator of
Bph is
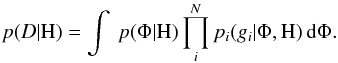 (4)With the likelihood
function at hand, this can be numerically evaluated for a choice of any prior, see below for
details.
(4)With the likelihood
function at hand, this can be numerically evaluated for a choice of any prior, see below for
details.
On the other hand, we considered the possibility of separate objects that correspond to the
observations, hence the denominator of Bph is a product of N integrals because separate
sets of { Φi } parameters are required to
accommodate this hypothesis: 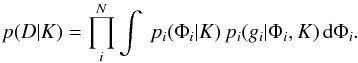 (5)
(5)
2.1. Matching with multiband measurements
Previously we only considered separate detections with their own measurements. When
matching across surveys or instruments, one is often given multiple fluxes in each
catalog. A good example is matching the catalogs of the Sloan Digital Sky Survey (SDSS;
Shimasaku et al. 2001) and the Galaxy Evolution
Explorer (GALEX; Martin et al. 2005). The former
provides ugriz magnitudes, while the latter has near and far
ultraviolet fluxes (NUV and FUV for near- and far-ultravoilet). This can be considered as
a two-way crossmatch problem with 5+2 measurements. If, however, the GALEX band-merging
algorithm were suspect due to its large astrometric uncertainties, one could consider this
a three-way matching problem of SDSS, NUV and FUV catalogs with 5+1+1 fluxes so that the
joint analysis could improve the quality of the associations. Our statistical methodology
can naturally deal with these scenarios and any other combination. The H hypothesis does
not change, but the competing hypothesis K now has { Gk } groups of
measurements, hence its likelihood becomes
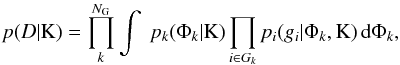 (6)where
NG is the number of groups. For
N groups
with an individual data point in each one, this becomes Eq. (5). Also, formally, when all observations are in the same group, it
becomes H, but would not correspond to a matching problem.
(6)where
NG is the number of groups. For
N groups
with an individual data point in each one, this becomes Eq. (5). Also, formally, when all observations are in the same group, it
becomes H, but would not correspond to a matching problem.
 |
Fig. 2 Simulated data. 2-way matches (named l-way approach in the figure) created from two groups of four bands: one group encompasses the Subaru bands U, B, R, I and the other group encompasses the Spitzer bands IRAC36, IRAC45, IRAC58, and IRAC80, and eight-way matches (named n-way approach in the figure) created from Subaru bands U, B, R, I and Spitzer IRAC bands IRAC36, IRAC45, IRAC58 and IRAC80 without grouping them per instrument. The samples are created from a specific elliptic, Ell5, and SWIRE SED templates of redshift 2.68, adding measurement errors to simulate real measurements. |
3. Discussion
3.1. Influence of uncertainties in the photometric Bayes factor
Uncertainties are always a topic of interest in the field of data analysis. Every piece of quantitative information in science is linked to a certain degree of uncertainty that needs to be analyzed to provide a realistic interpretation of the results. Uncertainties associated with the data (measured error), with the model (softening factor), and systematic uncertainties associated with the computational limit and efficiency of the algorithms proposed were assessed to evaluate their impact on our problem.
Similarly as for astrometric uncertainties, the photometry of sources in a catalog is calibrated by comparing data values with the photometric values of model SED templates from an adequate library. Today we can find an appropriate SED template library as a reference for the true values for almost every survey. It is important to understand the effects of uncertainties in the Bayes factor result, which in turn means understanding the role of uncertainty in the Bayesian inference. The magnitude uncertainty dm is approximately dm ≈ df/f, f being the flux and df the uncertainties in terms of flux.
The SED templates do not come with uncertainties; a possible work around used sometimes
is to soften the measurement errors to account for this. A typical softening factor is a
few percent of the measured flux added in quadrature. Thus, in addition to the above
df, a
softening factor, named smooth factor η, which accounts for the template uncertainties,
was introduced to simulate the error in the model. Therefore, we can write
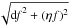 for the flux error to be considered.
for the flux error to be considered.
It is very important to find an appropriate range of values for the smooth factor; if we have a very large smooth factor, the values of the Bayes factor for the match samples will shrink toward zero and there will not be much evidence from the data; if the value of the Smooth factor is low but still realistic, the range of Bayes factor values will be wider and therefore we will gain more useful information from the data. For our problem, a Smooth factor of 0.03 was adopted.
A set of repeated software executions were run and results assessed to determine whether there were significant systematic errors. The results of these executions showed a random slight scatter around the expected values; therefore we conclude that there are no significant systematic errors affecting the results of the algorithms presented here.
In Fig. 2, the log 10BFph is represented versus measurement error. Here different values of measurement errors are analyzed to study their influence on the overall approach; it can be observed that the increase of measurement errors yields no constraint from the data, thus we cannot learn much from the data, and the values of Bayes factors are low.
 |
Fig. 3 Histogram of a ten-way matching of real data from the Cosmos catalog with a uniform prior. |
Figure 7 shows the log 10BFph for different values of uncertainties. It can be seen that the larger the uncertainty, the more the range of log 10BFph decreases, which means that the evidence offered by the data is weaker; on the other hand, the smaller the uncertainty, the wider the range of log 10BFph will be and this means that the data offer increasingly useful information in the plausible scenarios presented here.
3.2. Influence of priors on the photometric Bayes factor
Assuming enough knowledge to describe the problem, different prior probability distribution functions are proposed and analyzed to obtain preliminary results for their impacts on the problem of hypotheses decision. The quality of the approach presented here was measured in terms of the level of discrimination between matches and no matches, which is linked to the variability of the results from the photometric Bayes factor for the different prior pdfs exercised.
3.2.1. Uniform priors
Considering no information a priori about the model proposed, we assumed a 3D uniform
distribution. This means separate uniform priors for each of the model parameters
indicated in Sect. 2; therefore the prior pdf can
be expressed as follows: 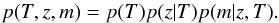 (7)The functional form of
these pdfs is a constant value for each of the relevant parameters – T, z and m – in a defined
range of values and such that the integral is one.
(7)The functional form of
these pdfs is a constant value for each of the relevant parameters – T, z and m – in a defined
range of values and such that the integral is one.
The ten-way and two-way histograms of the Bayes factor for matches and no matches represented in Figs. 3 and 4 show, as expected, that real associations have a larger Bayes factor than the random associations.
 |
Fig. 4 Histogram of a two-way matching of real data from the Cosmos catalog with a uniform prior. |
3.2.2. Non-uniform prior: surface brightness
Following Trotta (2008), we propose a new
nonuniform prior by using the concept of galaxy surface brightness; its dimming is
proportional to (1 + z)-4 in conventional cosmology,
therefore it can be used as a prior in our problem. The use of surface brightness as
prior intends to break the redshift degeneracy, as indicated in Xia et al. (2009). Therefore for a source with magnitude
m
extending over an area A square arcseconds, we propose the following
dependency: 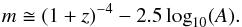 (8)Then we introduce the
following prior into our problem: p(T,m,z) = p(m|z,T)p(z|T)p(T),
where we eliminated the influence of parameter A in Eq. (7) by marginalizing as follows:
(8)Then we introduce the
following prior into our problem: p(T,m,z) = p(m|z,T)p(z|T)p(T),
where we eliminated the influence of parameter A in Eq. (7) by marginalizing as follows: 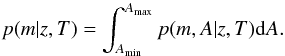 (9)A step further would
be to consider the 2D prior, p(T,m) = p(T)p(m|T),
by marginalizing over the area A and the redshift z:
(9)A step further would
be to consider the 2D prior, p(T,m) = p(T)p(m|T),
by marginalizing over the area A and the redshift z: 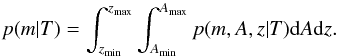 (10)The functional form
of this pdf belongs to the family of power functions, and again the value of the
integral over the parameter range is one.
(10)The functional form
of this pdf belongs to the family of power functions, and again the value of the
integral over the parameter range is one.
The histogram of ten-way matching for the prior based on the surface brightness, shown in Fig. 5, is very similar to the one corresponding to the uniform prior, shown in Fig. 3. Therefore using a surface brightness prior for the data set used here slightly improves the computational aspect, but it does not greatly improve the classification compared with using uniform prior. We therefore conclude that the sensitivity of our approach to different priors is very low, which proves the robustness of the approach.
 |
Fig. 5 Histogram of a ten-way matching of real data from the Cosmos catalog with a flux prior. |
3.2.3. Prior based on data fluxes: flux prior
This paragraph describes the prior proposed in Fadely
et al. (2012) adapted to our problem of a multiband galaxies crossmatch. We
used a set of hyper-parameters to parametrize the prior probability density
distributions; these hyper-parameters were chosen such that their sum was equal to one.
The benefit of this approach compared with others, such as those presented in the above
paragraphs of this section, is that the full data sample provides information about the
prior probabilities for each individual source, therefore the prior probability
distribution contains information from all the data values. For the parameters presented
in Sect. 2 – T,z,α – uniform
distributions were considered for the priors on template type T and on redshift
z, and
similarly as in Fadely et al. (2012), we
marginalized over the fitting for the scale brightness parameter within a range of
±3σ. Thus the prior
probability density distribution for the scale brightness was approximated by a Gaussian
distribution where the mean and deviation were obtained by computing the weighted
average and variance for each model SED-fitting with the complete data set or a
representative subset of it, because the hyper-parameters β parametrize the scale
brightness prior distribution. This implementation improves the computational cost
considerably compared with the implementations described in the two previous paragraphs.
We here reduced the 3D uniform prior defined above by a 2D uniform prior in type
T and
redshift z.
The reason for this is that here we marginalized the likelihood over the uncertainties
of the scale brightness for the best fitting, therefore, the likelihood can be written
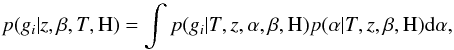 (11)where α is the overall scale
brightness factor, as indicated in Sect. 2, and
β
represents the hyper-parameters used when marginalizing over the scale brightness
fitting-uncertainty. The value resulting from computing this indefinite integral was
approximated here by computing a definite integral in the range of ±3σα uncertainty.
d are the
data values for this problem, this means, the tuples Nd of
Nb bands, and e are the uncertainties
in the data; the size of d is NdxNb,
where Nd is the number of tuples that
encompass the dataset, and Nb is the number of bands in each
tuple for the multiband problem under consideration; accordingly, for each SED template
SEDi,
where i
denotes a specific type and redshift, the two hyper-parameters for the prior of scale
brightness are, as indicated above, the weighted mean
(11)where α is the overall scale
brightness factor, as indicated in Sect. 2, and
β
represents the hyper-parameters used when marginalizing over the scale brightness
fitting-uncertainty. The value resulting from computing this indefinite integral was
approximated here by computing a definite integral in the range of ±3σα uncertainty.
d are the
data values for this problem, this means, the tuples Nd of
Nb bands, and e are the uncertainties
in the data; the size of d is NdxNb,
where Nd is the number of tuples that
encompass the dataset, and Nb is the number of bands in each
tuple for the multiband problem under consideration; accordingly, for each SED template
SEDi,
where i
denotes a specific type and redshift, the two hyper-parameters for the prior of scale
brightness are, as indicated above, the weighted mean
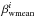 and the weighted
deviation
and the weighted
deviation 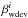 of the fitting of
the data set against the SEDi
template. For the sake of readability, the super-index i was suppressed because
it is clear that the following expressions refer to a specific SED template
SEDi.
The size of the hyper-parameters βi, for each specific
SED template, SEDi
is NdxNb.
We write the prior for the overall scale brightness factor as follows:
of the fitting of
the data set against the SEDi
template. For the sake of readability, the super-index i was suppressed because
it is clear that the following expressions refer to a specific SED template
SEDi.
The size of the hyper-parameters βi, for each specific
SED template, SEDi
is NdxNb.
We write the prior for the overall scale brightness factor as follows: 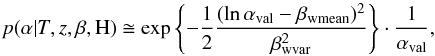 (12)where a
log-normal distribution was chosen to represent the probability density distribution of
the scale brightness factor.
(12)where a
log-normal distribution was chosen to represent the probability density distribution of
the scale brightness factor.
 |
Fig. 6 Real data. Histogram of a two-way matching of real data from the Cosmos catalog with a flux prior. |
Figures 3 to 6 show the result of computing the photometric Bayes factor for the above priors for a total of 2656 tuples of ten different bands: CFHT u*, Subaru B, Subaru V, Subaru g+, Subaru r+, Subaru i+, Subaru z+, CFHT i‘, UKIRT J, and CFHT K. These figures represent the histograms, associated with the distributions of matches and no matches of a COSMOS photometric catalog. In all these three cases, the model – SED templates convolved with the relevant filters – was softened by a smooth factor of 0.03 included in the error as defined in Sect. 3. In general, these figures show that the real associations have a larger Bayes factor than the random associations.
Figures 3 and 4 show the Bayes factor histogram of matches and no matches when using the uniform prior for two configurations, the ten-way in Fig. 3 and the two-way in Fig. 4 (Subaru B, V, g+ as one group and Subaru r‘+, i+, z+ as another group). In Fig. 3, the values of the Bayes factor of the matches are concentrated around positive values, whereas the Bayes factor for no matches are dispersed along negative values except for a considerably high number of results that are beyond the computational precision range and are not shown here. A reduced number of expected no matches are misclassified because they have a value of the Bayes factor ≫1; a considerable number of low values of the Bayes factor are also present in the expected match group, which might be due to the existence of rare galaxies with an SED out of the SED template library. Compared with Fig. 3, the average values of Bayes factor in Fig. 4 are lower and this may be due to the boost effect between two-way versus ten-way matching. The results shown in Fig. 4 offer a similar result as observed in Fig. 3 with a slight increase in the number of expected no matches misclassified as matches. Similarly, there is a slight reduction in the misclassification of matches as non matches. This may be due to the boost effect in terms of the overall Bayes factor values, but in general, similar conclusions can be derived as from Fig. 3. Figures 5 and 6 show the Bayes factor histogram of matches and no matches when using the flux prior and for two configurations, the ten-way in Fig. 5 and the two-way in Fig. 6 (Subaru B, V, g+ as one group and Subaru r‘+, i+, z+ as another group). With the configuration of Fig. 5 we observe that compared with Fig. 3 the distribution of no matches is less dispersed and concentrated around more specific Bayes factor negative values, and similarly, the values of Bayes factor for the matches are higher on average. We also observe that the area of apparent false classification is somewhat more extended than in Fig. 3. Compared with Fig. 5, the results shown in Fig. 6 remain similar and have on average lower values of Bayes factor due to the boost effect between the ten-way and two-way.
4. Experimental setup
The data are composed of tuples of fluxes measured in different bands, from the ultraviolet to the infrared, and the photometric uncertainties associated to those measurements. This type of data is typically used in the so-called photometric catalogs, which are extensively used in the photometric redshift estimation problem. Details on the model are provided in Sect. 2. Two sets of data were used here: simulated samples, that were created artificially from a specific SED model, and real samples that were extracted from existing calibrated catalogs. The main purpose of the simulated samples is to validate the approach proposed for the SED-fitting and for the photometric crossmatching; while the main objective of the real samples is to extract valid statistics and connected conclusions from the implementation of the framework presented here.
The selection of an appropriate model for each dataset is the key for a correct development of a framework as the one presented in this paper; therefore, we were very careful in selecting an appropriate SED templates library from which the SED models were derived.
4.1. Simulated samples
The SWIRE SED template library from Polletta et al. (2007) was the basis for our construction of simulated samples. It contains 25 templates, including shapes such as elliptical, spiral, starburst, and quasi-stellar object (QSO), and a redshift up to 4.02 for which we considered steps of 0.04 in convoluting the SED templates with the band transmission filter. The following bands and associated transmission filters were considered: Subaru U, Subaru B, Subaru R, Subaru I, IRAC36, IRAC45, IRAC58, and IRAC80, with an effective wavelength range from 3574.45 to 78 720 Å.
The simulated matched tuples were created by selecting a specific galaxy from the SED library and adding a random error (from a gaussian distribution) to simulate the deviation from a perfect match between data and model, as in a real measurement.
An assessment of the MATLAB code, which is based on Mersenne Twister, was used to generate random numbers from a gaussian distribution, showing that it is in line with the generation of random bits described in Press et al. (2007). A bench-marking of the execution of this algorithm in C++ and MATLAB environments was made obtaining very similar results. Therefore we conclude that the algorithm used by MATLAB for generating random numbers is adequate for our purposes.
4.2. Real samples
The COSMOS multiwavelength survey is suitable for use in the multiwavelength crossmatching problem indicated here. We used the photometric catalog from COSMOS survey obtained from Capak et al. (2008) via the NASA/IPAC Infrared Science Archive web site1 as a good candidate for real data because it offers relatively recent information with proper calibration. This photometric catalog has a well-defined SED template library that contains 31 templates, including shapes such as elliptical and spiral and a range of redshift up to 6. The following bands and associated transmission filters were considered: CFHT u*, Subaru B, Subaru V, Subaru g+, Subaru r+, Subaru i+, Subaru z+, CFHT i’, UKIRT J, and CFHT K, with an effective wavelength range from 3798 to 21 460 Å.
The cases of non-crossmatched tuples were created with artificial data obtained from the real COSMOS tuples by randomly shuffling the tuples from each band along the catalog. If we consider that the full catalog is a table where each of the m-rows is a tuple of n-columns, one for each band, the algorithm of building tuples by randomly shuffling n-columns along the m-rows is immediate. The resulting catalog is by default a nonmatched one, which allows us to complete the assessment of the results of the algorithm implemented for this approach.
 |
Fig. 7 Simulated data. Eight-way cross-matching (from the Subaru and IRAC bands enumerated in Sect. 2.1) log 10BFph versus a range of magnitude error values simulating real data for the different priors considered in this paper – uniform, flux, and surface brightness. |
Regarding the model, the SED template library corresponding with this dataset is well-known and can be easily extracted from Arnouts et al. (1999) and Ilbert et al. (2006) by applying the convolution procedure described in Sect. 2. Two main groups of SED templates, associated with inclusion or exclusion of dust in the SED templates, are part of this library.
5. Results
A validation step with simulated data was executed prior to the run of the algorithms with real data. The simulated matched test samples were created by using the same values as those from galaxies of the SWIRE SED template library from Polletta et al. (2007), incorporating different values of dm to simulate the typical measurement error. In addition to this, different values of the model smooth factor ηf were explored. Figure 1 shows a few examples of SED-fitting for different photometric matching results; Fig. 2 shows the results of computing a crossmatching Bayes factor for a two-way approach (named generically l-way in the figure) and for an eight-way approach (named generically n-way in the figure). Here the boost factor can be clearly seen; Fig. 2 shows the result of computing the photometric Bayes factor for simulated data created from an elliptical SWIRE SED template using different values of photometric uncertainties to simulate real measurements with different degrees of error; clearly, as expected, high values of uncertainties in the data produce poor results in terms of best fit and of matches, and small uncertainties in the data produce a good-quality fit and high values of the photometric Bayes factor for simulated matched samples.
The two-way approach was executed on a subset of COSMOS data composed of the six bands of Subaru (U, B, V, g, r, i) split into two subsets (the three redder and the three bluer sources of the six-tuple), therefore it is named in the figures as two-way approach, whereas the ten-way approach used the ten bands from the COSMOS photometric catalog used considering the flux measured in each band independent of the others. These two approaches are represented in Figs. 3 to 6. When comparing the results from the two-way versus ten-way approach, we observe a boost of the Bayes factor values that is related to the number of bands of the data set under consideration.
Figure 7 allows one to assess the impact of magnitude errors in the Bayes factor for the three different priors proposed here. This was implemented using simulated data sets from the SWIRE library as described above.
 |
Fig. 8 Real data. Ratio of matches and no matches for a ten-way crossmatching (ten bands from the COSMOS photometric catalog). Bayesian inference approach and the uniform prior. The red line represents the ratio of no matches for the different Bayes factor thresholds and the blue line corresponds to the ratio of matches. |
 |
Fig. 9 Real data. Ratio of matches and no matches for a ten-way crossmatching (ten bands from the COSMOS photometric catalog). Bayesian inference approach with the flux prior. The red line represents the ratio of no matches for the different Bayes factor thresholds and the blue line corresponds to ratio of matches. |
A fundamental question to be answered at this stage is how well the Bayes factor discriminates between matches and no matches. To evaluate how good a discriminator the Bayes factor is, we selected different thresholds and obtained the fraction of true positive matches and of false positive matches found. Figures 8 to 10 show the ratio of true and false positive matches for a range of Bayes factor thresholds defined, under different configurations – two-way and ten-way – and with different priors – uniform, surface brightness and flux. Results from surface brightness and uniform priors are very similar to each other. All these results offer an interesting assessment of the method. In general, we observe that the results from the ten-way approach show a better quality of the Bayes factor in its capability of match discriminator than the 2-way approach. This proves that the Bayesian inference allows for a progressive improvement based on ingesting additional information into the framework. We observe in Fig. 8 (ten-way, a configuration with uniform prior) and in Fig. 9 (ten-way, a configuration with flux prior) that for a positive realistic value of the log 10(Bph) threshold of ten the ratio of matches for a real COSMOS-matched catalog is very high, whereas the ratio of no matches in Fig. 8 is very low, and moderately low in Fig. 9. This result demonstrates a good capability of this approach to classify photometric matches.
The comparison of the ratio of true and false matches against the log 10BFph is shown in Fig. 11 for the three priors presented in this paper – uniform, flux, and surface brightness prior. From these results we observe that a smooth factor of 0.03 yields an acceptable and balanced compromise in terms of the model and data uncertainties and their influence on the classification.
 |
Fig. 10 Real data. The three figures are the result of using a ten-way cross-matching approach for the ten bands of the COSMOS photometric real catalog. The upper panel represents the ratio of true positive matches (in blue) and false positive matches (in red) when using the surface brightness prior, as detailed in Sect. 3. This result is very similar to that of the middle panel, which corresponds to the ratio of true and false positive matches (same color code) when using a uniform prior. The bottom panel shows the corresponding results when using the flux prior. In this last case for a value of log 10Bph higher than 2 the ratio of false positive matches is higher than in the two other cases. |
Regarding the different priors tested and considering the two-way approach as an implicit prior, we see in Fig. 11 that the three ten-way approaches produce results of better quality than the equivalent two-way approach; then within the ten-way approach, that with the uniform prior seems to reach a better quality, followed by the surface brightness prior and then the flux prior. It seems that the reduction in computation proposed by the approach with the flux prior is slightly penalizing the quality of the discrimination between true positive cross-matches and false positive cross-matches.
Two main observations can be made from these results: the influence of the different sources of uncertainties plays a key role in the result of valid method extracting information from measured data; therefore a detailed consideration of the uncertainties of the data and of the model is very relevant to obtain realistic outcomes when using a Bayesian inference framework in data analysis. Another observation is that different priors yield slightly different results, but the overall balance of the Bayes factor between quality of the fit and complexity of the model is retained, and when combined with the astrometric Bayes factor numerical value, these differences are expected to be mitigated, which improves the sensitivity of the Bayes factor to different priors.
In terms of computational cost the solutions with a 3D uniform prior are more demanding because the number of integrals to be considered is higher than in the flux prior solution.
The following figures, referred to in the above sections, show different aspects of the implementation of the crossmatching problem with different priors from the COSMOS photometric catalog : astrometry.cosmos zphot mag2512985.tbl.
 |
Fig. 11 Real data. Receiver operating characteristic (ROC) curve for the different priors in the photometric matching problem. This curve shows the true positive match ratio versus false positive match ratio. The area below the curve varies with the different priors; the larger the area, the better the performance: uniform prior (red), flux prior (blue), surface brightness prior (green), two-way uniform prior (magenta), two-way flux prior(cyan). |
6. Conclusions
We have described the implementation of a Bayesian framework prototype that we used to study how much the photometric measurements can contribute to the problem of identifying and classifying multiband matched galaxies. This is mostly relevant where the astrometry is not decisive. In principle, we can create multiple matched catalogs based on just astrometry or based on both astrometry and photometry, which can become particularly interesting when the results of crossmatching based only on astrometric data are too poor to yield robust conclusions, which could lead to missing or incorrect matches. For the prototype created here we studied the influence of different sources of uncertainties and different priors, leading to a good understanding of how much we can learn from the data, how good the model is, and with that, how good the quality of the photometric Bayes factor is for classifying cross-matched versus non cross-matched galaxies. We reached the following main conclusions from this study:
-
1.
A sound consistency between cross-matched sources, highBayes factor, and good fitting with the relevant SED template wasfound.
-
2.
In the process of validating the prototype with nominal cases where the matches/no matches were clear and known, we found that the astro-photometric crossmatching approach yields consistent results with the astrometric crossmatching approach.
-
3.
The photometric crossmatching Bayesian framework implemented on astrometric matches can increase the level of confidence on crossmatch results of multiwavelength tuples, which has a particular importance when the astrometric Bayes factor cannot help in determining whether there is a match or not.
-
4.
When only astronometry was used to identify matches, the photometric cross-match approach performed a refined discrimination of matches from no matches. An astrometric match where photometry is not considered at all may lead to identifying galaxies with different values in terms of redshift and/or shapes as the same source. Therefore using photometric information as implemented in this approach improves the identification of matches in crowded areas where the precision in the astrometric positions may be compromised. The SED-fitting derived from the implementation proposed here can then resolve the astrometric degeneracy. When faint sources are part of the data under consideration, the combined astrometric and photometric Bayes factor allows a further refinement in the identification of matches and no matches. Cases, such as overlapping sources that belong to different redshifts can be identified as astrometric matches, whereas the photometric Bayesian inference described here will discriminate this as a no match with poor SED-fitting
-
5.
For the way the different priors affect the model decision problem, we observed that the uniform prior, where no previous knowledge is assumed, retains the best results in terms of discrimination between matches and no matches. On the other hand, the knowledge introduced by the prior based on the flux does not always yield the best model decision results in this case. We conclude here that the data used to compute the flux prior in this case might create a slight bias in the overall computation; however, this deserves a further detailed study. In conclusion, the influence of the different priors is very weak because the overall result in terms of Bayes factor magnitude is generally kept. Therefore we consider that the robustness of the approach presented here is supported by the fact that different priors do not substantially change the results.
-
6.
From an implementation point of view, the correctness and validity of the SED template library is the key to reach reliable and useful results, therefore it is important to consider a step in validating the SED template to be used as described here.
-
7.
The correctness and validity of the uncertainties described here is on the one hand a complex topic of current active research, and on the other hand, the values used in this prototype, validated through artificial and real data sets, yield a well-balanced level of quality in the results obtained.
-
8.
Another implementation aspect to consider is the computational cost, which mainly depends on the integral dimension and also on the complexity of the prior probability distribution. Therefore, we recommend studying the precision range of the computational system that is used in order to minimize computational lack of precision in the results.
Acknowledgments
The extensive computation required to compile some of the results illustrated here has been possible thanks to the good support obtained from the virtual MATLAB environment offered by Johns Hopkins University.
References
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Budavári, T., & Szalay, A. S. 2008, ApJ, 679, 301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Budding, E., & Demircan, O. 2007, Introduction to astronomical photometry, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2008, VizieR Online Data Catalog: II/284 [Google Scholar]
- Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- D’Agostini, G. 2003, Rep. Prog. Phys., 66, 1383 [Google Scholar]
- Fadely, R., Hogg, D. W., & Willman, B. 2012, ApJ, 760, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D. 2014, StatProb: The Encyclopedia Sponsored by Statistics and Probability Societies. Available at http://statprob.com/encyclopedia/Astrostatistics.html [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Galadi-Enriquez, D. 1998, Manual Practico de Astronomia con CCD (Barcelona: Ediciones Omega) [Google Scholar]
- Gregory, P. 2010, Bayesian Logical Data Analysis for the Physical Sciences (Cambridge University Press) [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lahav, O. 2006 [arXiv:astro-ph/0610713] [Google Scholar]
- Marquez, M. J., & Sarro, L. M. 2013, International Journal of Soft Computing and Software Engineering, 3, 644 [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes. The Art of Scientific Computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Romanishin, W. 2000, An Introduction to Astronomical Photometry Using CCDs (University of Oklahoma) [Google Scholar]
- Sarro, L. M., Eyer, L., O’Mullane, W., & De Ridder, J. 2012, Astrostatistics and Data Mining (Springer) [Google Scholar]
- Schneider, P. 2006, Extragalactic Astronomy and Cosmology. Introduction (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Shimasaku, K., Fukugita, M., Doi, M., et al. 2001, AJ, 122, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Sivia, D. S., & Skilling, J. 2011, Data Analysis. A Bayesian Tutorial, 2nd edn. (Oxford University Press) [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, L., Cohen, S., Malhotra, S., et al. 2009, AJ, 138, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 a) Real data. Best SED fit for a matched tuple of a COSMOS galaxy of type Ell3A0, redshift of 1.4, color index B − V of 1.2567. b) Best SED fit for a matched tuple of a COSMOS galaxy of type ScA2, redshift of 3.15, color index B − V of − 0.0653. c) Best SED fit for a shuffled tuple of a COSMOS galaxy of type Ell6A0, redshift of 0.6, color index B − V of 1.7867. d) Best SED fit for a shuffled tuple of a COSMOS galaxy of type S0A0, redshift of 2.48, color index B − V of − 0.5123. This figure shows that our models reasonably fit real COSMOS galaxies. This is not true for random associations. |
| In the text | |
 |
Fig. 2 Simulated data. 2-way matches (named l-way approach in the figure) created from two groups of four bands: one group encompasses the Subaru bands U, B, R, I and the other group encompasses the Spitzer bands IRAC36, IRAC45, IRAC58, and IRAC80, and eight-way matches (named n-way approach in the figure) created from Subaru bands U, B, R, I and Spitzer IRAC bands IRAC36, IRAC45, IRAC58 and IRAC80 without grouping them per instrument. The samples are created from a specific elliptic, Ell5, and SWIRE SED templates of redshift 2.68, adding measurement errors to simulate real measurements. |
| In the text | |
 |
Fig. 3 Histogram of a ten-way matching of real data from the Cosmos catalog with a uniform prior. |
| In the text | |
 |
Fig. 4 Histogram of a two-way matching of real data from the Cosmos catalog with a uniform prior. |
| In the text | |
 |
Fig. 5 Histogram of a ten-way matching of real data from the Cosmos catalog with a flux prior. |
| In the text | |
 |
Fig. 6 Real data. Histogram of a two-way matching of real data from the Cosmos catalog with a flux prior. |
| In the text | |
 |
Fig. 7 Simulated data. Eight-way cross-matching (from the Subaru and IRAC bands enumerated in Sect. 2.1) log 10BFph versus a range of magnitude error values simulating real data for the different priors considered in this paper – uniform, flux, and surface brightness. |
| In the text | |
 |
Fig. 8 Real data. Ratio of matches and no matches for a ten-way crossmatching (ten bands from the COSMOS photometric catalog). Bayesian inference approach and the uniform prior. The red line represents the ratio of no matches for the different Bayes factor thresholds and the blue line corresponds to the ratio of matches. |
| In the text | |
 |
Fig. 9 Real data. Ratio of matches and no matches for a ten-way crossmatching (ten bands from the COSMOS photometric catalog). Bayesian inference approach with the flux prior. The red line represents the ratio of no matches for the different Bayes factor thresholds and the blue line corresponds to ratio of matches. |
| In the text | |
 |
Fig. 10 Real data. The three figures are the result of using a ten-way cross-matching approach for the ten bands of the COSMOS photometric real catalog. The upper panel represents the ratio of true positive matches (in blue) and false positive matches (in red) when using the surface brightness prior, as detailed in Sect. 3. This result is very similar to that of the middle panel, which corresponds to the ratio of true and false positive matches (same color code) when using a uniform prior. The bottom panel shows the corresponding results when using the flux prior. In this last case for a value of log 10Bph higher than 2 the ratio of false positive matches is higher than in the two other cases. |
| In the text | |
 |
Fig. 11 Real data. Receiver operating characteristic (ROC) curve for the different priors in the photometric matching problem. This curve shows the true positive match ratio versus false positive match ratio. The area below the curve varies with the different priors; the larger the area, the better the performance: uniform prior (red), flux prior (blue), surface brightness prior (green), two-way uniform prior (magenta), two-way flux prior(cyan). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


