| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322469 | |
| Published online | 12 March 2014 | |
Can eccentric debris disks be long-lived?
A first numerical investigation and application to ζ2 Reticuli⋆,⋆⋆
1 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: Virginie.Faramaz@obs.ujf-grenoble.fr
2 LESIA, Observatoire de Paris, 92195 Meudon, France
3 Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro 1, Sta. Ma. Tonantzintla, Puebla, Mexico
4 Universidad Autónoma de Madrid, Dpto. Física Teórica, Módulo 15, Facultad de Ciencias, Campus de Cantoblanco, 28049 Madrid, Spain
5 European Southern Observatory, Casilla 19001, Santiago 19, Chile
6 Dpt de Astrofísica, Centro de Astrobiología (INTA-CSIC), ESAC Campus, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
7 Aurora Technology B.V., ESA-ESAC, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
8 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove drive, Pasadena CA 91109, USA
9 NASA Goddard Space Flight Center, Exoplanets and Stellar Astrophysics, Code 667, Greenbelt MD 20771, USA
10 Rutherford Appleton Laboratory, Chilton OX11 0QX, UK
11 Department of Physics and Astrophysics, Open University, Walton Hall, Milton Keynes MK7 6AA, UK
12 Christian-Albrechts-Universität zu Kiel, Institut für Theoretische Physik und Astrophysik, Leibnizstr. 15, 24098 Kiel, Germany
Received: 9 August 2013
Accepted: 13 December 2013
Context. Imaging of debris disks has found evidence for both eccentric and offset disks. One hypothesis is that they provide evidence for massive perturbers, for example, planets or binary companions, which sculpt the observed structures. One such disk was recently observed in the far-IR by the Herschel Space Observatory around ζ2 Reticuli. In contrast with previously reported systems, the disk is significantly eccentric, and the system is several Gyr old.
Aims. We aim to investigate the long-term evolution of eccentric structures in debris disks caused by a perturber on an eccentric orbit around the star. We hypothesise that the observed eccentric disk around ζ2 Reticuli might be evidence of such a scenario. If so, we are able to constrain the mass and orbit of a potential perturber, either a giant planet or a binary companion.
Methods. Analytical techniques were used to predict the effects of a perturber on a debris disk. Numerical N-body simulations were used to verify these results and further investigate the observable structures that may be produced by eccentric perturbers. The long-term evolution of the disk geometry was examined, with particular application to the ζ2 Reticuli system. In addition, synthetic images of the disk were produced for direct comparison with Herschel observations.
Results. We show that an eccentric companion can produce both the observed offsets and eccentric disks. These effects are not immediate, and we characterise the timescale required for the disk to develop to an eccentric state (and any spirals to vanish). For ζ2 Reticuli, we derive limits on the mass and orbit of the companion required to produce the observations. Synthetic images show that the pattern observed around ζ2 Reticuli can be produced by an eccentric disk seen close to edge-on, and allow us to bring additional constraints on the disk parameters of our model (disk flux and extent).
Conclusions. We conclude that eccentric planets or stellar companions can induce long-lived eccentric structures in debris disks. Observations of such eccentric structures thus provide potential evidence of the presence of such a companion in a planetary system. We considered the specific example of ζ2 Reticuli, whose observed eccentric disk can be explained by a distant companion (at tens of AU) on an eccentric orbit (ep ≳ 0.3).
Key words: circumstellar matter / methods: numerical / planetary systems / stars: individual:ζ2Reticuli / celestial mechanics
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The first debris disk was discovered in 1984, when the Infrared Astronomical Satellite (IRAS) found a strong IR excess around Vega, revealing the presence of micron-sized dust grains (Aumann et al. 1984). For most debris disks, these grains have a limited lifetime, which is shorter than the system’s age because of Poynting Robertson drag and collisions. Therefore, this dust is assumed to be replenished by collisional grinding of much larger parent bodies, which are at least kilometre-sized for this collisional cascade to be sustained over the system’s age (Backman & Paresce 1993; Löhne et al. 2008). Consequently, debris disks provide evidence for the existence of solid bodies that have reached km-size, and potentially the planetary-size level.
Spatially resolved structures in debris disks can provide clues to the invisible planetary component of those systems. Such planets may be responsible for sculpting these disks and may leave their signature through various asymmetries such as wing asymmetries, resonant clumpy structures, warps, spirals, gaps, or eccentric ring structures (see, e.g., Wyatt 1999). This diversity is to be compared with the variety of exoplanetary systems1 discovered around main sequence stars since 1995 (51 Peg b, Mayor & Queloz 1995). Dynamical modelling of such asymmetries is the only method to place constraints on the masses and orbital parameters of planets in systems where direct observations are not possible (see, e.g., Mouillet et al. 1997; Wyatt et al. 1999, 2004; Augereau et al. 2001; Moro-Martín & Malhotra 2002; Kalas et al. 2005; Quillen 2006; Stark & Kuchner 2008; Chiang et al. 2009; Ertel et al. 2011; Boley et al. 2012; Ertel et al. 2012; Thebault et al. 2012).
We focus here on cases of eccentric patterns in debris disks. The modelling of this type of asymmetry and its possible link with the dynamical influence of eccentric companions has been investigated in several previous studies: authoritative work was carried out by Wyatt et al. (1999, 2000) for HR 4796. Another case of interest is the debris disk of Fomalhaut (Stapelfeldt et al. 2004; Kalas et al. 2005, 2013; Quillen 2006; Chiang et al. 2009; Boley et al. 2012; Kalas et al. 2013; Beust et al. 2014).
This pioneering work showed that these large-scale structures arise in systems where debris disks are perturbed by an eccentric companion on a low-inclination orbit relative to the disk (Wyatt et al. 1999). The disk centre of symmetry is offset from the star, which may be measured explicitly in high-resolution images (e.g., HST scattered light). Furthermore, its periastron is closer to the star and thus hotter and brighter, which results in a two-sided brightness asymmetry.
However, it is important to emphasize that previous studies considered low-eccentricity rings (e ≳ 0.02 for HR4796 and e = 0.11 ± 0.01 for Fomalhaut), and were limited to timescales shorter than the typical ages of mature disks (≤10 Myr for HR4796 simulations and ≤100 Myr for Fomalhaut). The question of whether highly eccentric ring structures could be sustained over very long timescales has not been addressed thus far in the literature. This question has become very topical because of the discovery of at least two several Gyr old and significantly eccentric debris disks: one around ζ2 Reticuli (e ≳ 0.3, Eiroa et al. 2010), which is used as a reference case in this paper, and another one around HD 202628 (e ~ 0.18, Stapelfeldt et al. 2012; Krist et al. 2012). These systems are older than either Fomalhaut or HR 4796, and their disks are also much more eccentric.
In the present work, we investigate the long-term evolution of highly eccentric structures in debris disks and their relation to planetary or stellar perturbers by investigating their evolution over Gyr timescales. One of the questions we address is whether these structures are indeed several Gyr old, or if they might have originated from a more recent event, either a flyby or the late excitement of a sherpherding planet’s eccentricity. We also summarise a general modelling method, based on complementary analytical and numerical tools, which we apply to the specific case of ζ2 Reticuli.
This paper is structured as follows: Sect. 2 presents how a perturber can generate an eccentric ring structure. Useful analytical expressions are derived to study under which conditions such a pattern can be created. We also show that these predictions can be complemented by numerical studies. Section 3 describes the debris disk of ζ2 Reticuli, along with newly reduced Herschel/PACS images. This debris disk is used as a proxy to determine a numerical set-up. Then, in Sect. 4, the numerical investigation is carried out. From N-body simulations, we examine both the onset and suvival of an eccentric pattern and explore their dependencies on the perturber’s characteristics. This modelling approach allows one to put constraints on a perturber at work in shaping a debris disk into an eccentric ring over Gyr timescales, and it is applied to the debris disk of ζ2 Reticuli. Section 5 shows synthetic images on which we perform a full comparison with observations of ζ2 Reticuli, and retrieve additional constraints on this disk. Finally, Sect. 6 is devoted to conclusions, discussions, and propositions for future work.
2. Footprints of eccentric companions on debris disks
We have developed a dynamical model to investigate the shaping of a debris disk into an eccentric ring, and the timescales associated with its onset and survival. More specifically, we seek to determine whether perturbers are able to shape and maintain a disk into a significantly eccentric ring structure on Gyr timescales, and whether the asymmetry relaxes or not.
Before presenting our model and our results in detail for this as yet unexplored case, we present the current understanding on how eccentric ring structures arise as a result of the dynamical effect of an eccentric perturber.
2.1. Basic principle
For a disk to be shaped into an eccentric ring, it must be perturbed in such a way that the eccentricity of its components are forced to higher values, and that the orbits of these components are more or less oriented in a common direction. These conditions are both fulfilled if the disk is under the gravitational influence of a perturber, namely a planetary or a stellar companion (nearly) coplanar to the disk and on an eccentric orbit. The eccentricity of the ring causes the disk centre of symmetry to be offset from the star, and the disk pericentre to be brighter than the apocentre, since it is closer to the star and thus hotter. This feature was studied by Wyatt et al. (1999) for a planetary companion, and was called the pericentre glow phenomenon.
Spatially resolved imaging is required to determine the structure of debris disks, and therefore renewed efforts have been made to image as many debris disks as possible2. Most images of resolved debris disks have been obtained so far in the visible or near-IR. At these wavelengths, the emission is dominated by small grains close to the blow-out limit imposed by stellar radiation (sub-micron to micron, depending on stellar luminosity). These grains exhibit a complex evolution because of the coupled effects of collisions and radiation pressure (see, e.g., Thébault & Augereau 2007). This may strongly alter or even mask the dynamical structures imparted by a massive perturber. Observations at longer wavelengths detect larger grains that are less affected by stellar radiation (a few tens to a few hundreds of micron in size, depending on the observing wavelength). These directly trace the distribution of larger parent bodies and thus more directly reflect the dynamical effect of a perturber (see, e.g., Krivov 2010; Moro-Martín 2013, for exhaustive reviews).
Since the origin of an eccentric pattern is gravitational, we can reasonably assume that large-scale asymmetries among an observed dust population already exist amongst the parent planetesimal population that produces it and result from pure gravitational perturbations. This assumption allows us to study the influence of different eccentric perturbers in a simplified way, neglecting the effect of radiation pressure and considering parent planetesimals as mass-less and collision-less particles in orbit around their host star and perturbed by a companion, either stellar or planetary.
We assumed that at the end of the protoplanetary phase, the planetesimals start from almost circular orbits because of orbital eccentricity-damping by primordial gas. We furthermore assumed that any perturbing planet in the system is fully formed by the time the gas disappears, and evolves on a significantly eccentric orbit, because of a major perturbing event such as planet-planet scattering. Thus, we can consider the disappearance of the gas as time zero for the onset of planetesimal perturbations by an eccentric companion. From this moment, the planetesimal eccentricities start to increase and their lines of apsides tend to align with this of the planet. Under these assumptions, the forced elliptic ring structure takes some time to settle in, and it is preceded by the appearance and disappearance of transient spiral features. These are due to differential precession within the disk: all the planetesimals in the disk have different precession rates (because of their different orbital distances), such that these spiral structures are expected to wind up and finally generate an eccentric ring, as shown by Augereau & Papaloizou (2004) and Wyatt (2005). The characteristic time for reaching this state is of the order of a few precession timescales at the considered distance (Wyatt 2005). Consequently, the onset of an eccentric ring structure is a matter of timescales, while the value of the disk global eccentricity is to be linked with the planetesimals’ forced eccentricity, and thus to the companion’s eccentricity.
2.2. Analytical approach
We show here how the onset of these structures can be understood from analytical considerations. Planetesimals are considered to be mass-less particles. We focus on the secular response of a debris disk to a coplanar perturbing body, either a planet or a star. More specifically, both the forced secular eccentricity ef and the apsidal precession rate dϖ/dt of test planetesimals are examined, where ϖ is the longitude of periastron with respect to the direction of the perturber’s periastron, that is, the planet and planetesimal have their periastra aligned when ϖ = 0 and anti-aligned when ϖ = π.
When secularly perturbed, the eccentricity of a planetesimal evolves cyclically; its period is related to the rate of orbital precession. This holds in particular when we consider a dynamically cold disk of planetesimals as an initial condition, which is a reasonable and classical assumption considering the damping effect of the gas during the protoplanetary phase. In that case, the secular behaviour of a planetesimal can be understood considering the analytical solution for its eccentricity. In the Laplace-Lagrange theory, the complex eccentricity of a planetesimal, z(t), can be written  (1)where I2 = −1, and
(1)where I2 = −1, and 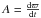 is the secular precession rate.
is the secular precession rate.
One can see from this expression that the maximum induced eccentricity for a planetesimal is twice the forced eccentricity, that is, ef,max = 2ef. This occurs when At = π [2π], that is, when the longitudes of periastra of the planetesimal and the perturber are equal (ϖ = 0, see Fig. 1 and, for more details, see e.g., Wyatt 2005; Beust et al. 2014).
 |
Fig. 1 Co-evolution of a planetesimal eccentricity and orbital precession when acted upon by an eccentric perturber. Since the planetesimal orbit precesses, its periastron will eventually be aligned with that of the perturber on the same side of the massive central body, that is, the longitudes of periastra of the planetesimal and the perturber are equal (ϖ = 0). In this configuration, the planetesimal eccentricity is maximum. |
There are several ways to analytically derive ef and dϖ/dt. The most classical one is to apply the linear Laplace-Lagrange theory, which is an expansion of the interaction Hamiltonian to second order in ascending powers of the eccentricities of the two bodies and an averaging over the two orbits (see, e.g., Eq. (6) of Mustill & Wyatt 2009). However, this approach is valid only for low eccentricities, but the perturber’s orbital eccentricity ep is not necessarily low. Therefore, restricting our analytical study to small ep may not be appropriate.
Another way to proceed is to expand the interaction Hamiltonian in spherical harmonics and truncate it at some order in α, where α is the ratio3 between a and ap, the planetesimal and the perturber’s semi-major axis, respectively, and to average after over the two orbits. This permits us to perform an analysis without any restriction on the eccentricities. The resulting Hamiltonian is given by Krymolowski & Mazeh (1999), Ford et al. (2000), or Beust & Dutrey (2006).
To the lowest order in α (second order, quadrupolar), it yields a forced eccentricity ef: 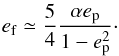 (2)This expression is given by Augereau & Papaloizou (2004) and Mustill & Wyatt (Eq. (8) of 2009). Note that this approach is only valid for low enough values of α to ensure a fast convergence of the expansion, that is, for orbits with significantly different sizes. It is also only valid far from mean-motion resonances. However, these resonances’ spatial extension along the semi-major axis (of the order of ~0.1 AU) is typically two orders of magnitude smaller than the extent of the observed structures (of the order of ~10 AU), although when the particles are on eccentric orbits, these resonances may span much wider ranges in terms of radial distance to the star than their span in semi-major axis may have hinted at. But in any case, the amount of material trapped in resonance can reasonably be assumed to be much smaller than the amount of non-resonant material, all the more so because we did not assume here that the planet has migrated, and thus excluded resonant capture during migration. Therefore, these structures are assumed to result from non-resonant material, and our approach is appropriate. Moreover, resonances were be treated in our N-body integrations, and were confirmed to be only important for limited parameter combinations (see Sect. 4).
(2)This expression is given by Augereau & Papaloizou (2004) and Mustill & Wyatt (Eq. (8) of 2009). Note that this approach is only valid for low enough values of α to ensure a fast convergence of the expansion, that is, for orbits with significantly different sizes. It is also only valid far from mean-motion resonances. However, these resonances’ spatial extension along the semi-major axis (of the order of ~0.1 AU) is typically two orders of magnitude smaller than the extent of the observed structures (of the order of ~10 AU), although when the particles are on eccentric orbits, these resonances may span much wider ranges in terms of radial distance to the star than their span in semi-major axis may have hinted at. But in any case, the amount of material trapped in resonance can reasonably be assumed to be much smaller than the amount of non-resonant material, all the more so because we did not assume here that the planet has migrated, and thus excluded resonant capture during migration. Therefore, these structures are assumed to result from non-resonant material, and our approach is appropriate. Moreover, resonances were be treated in our N-body integrations, and were confirmed to be only important for limited parameter combinations (see Sect. 4).
To derive the precession rate in the spherical harmonic expansion case, we followed the method given by Mardling & Lin (2002). The variation rate for the Runge-Lenz vector of the orbit was computed, expanded to any given order, and integrated over one orbital period.
After the numerical tests, there were fewer than two orders of magnitude between terms of the second and the fourth order (the third-order terms cancel out), therefore we retained terms up to fourth order in the spherical harmonic expansion, and averaged the resulting precession rate over the longitude of periastron. The precession rate is 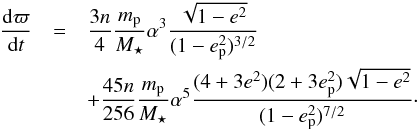 (3)We then followed Wyatt et al. (1999) and assumed that the precession timescale, tprec, corresponds to the lower limit of the typical dynamical timescale for setting a dynamical steady state:
(3)We then followed Wyatt et al. (1999) and assumed that the precession timescale, tprec, corresponds to the lower limit of the typical dynamical timescale for setting a dynamical steady state: 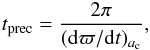 (4)where ac is the typical semi-major axis of a particle in the ring.
(4)where ac is the typical semi-major axis of a particle in the ring.
With this we analytically predict the effect of a perturber on a debris disk, that is, for a given set of values of ep and of the planet periastron qp, one can derive the precession rate (dϖ/dt)ac corresponding to planetesimals that orbit at this distance. Conversely, one can set this dynamical timescale and the forced eccentricity for a particle with semi-major axis ac to correspond to those derived from observations of an eccentric debris disk, and thus initially estimate the perturber’s characteristics (see Fig. 2).
 |
Fig. 2 Example colour map of the maximum induced eccentricity 2ef imposed by a planetary perturber on a particle with semi-major axis 100 AU and eccentricity e = 0 as a function of its periastron and eccentricity, as estimated from Eq. (2). The black line corresponds to a 2ef = 0.3 condition, which was set to mimic the condition for the disk of ζ2 Reticuli. Note that it does not depend on the mass of the planet. The white lines show the parameters for which the typical timescale to reach a steady state at 100 AU is tprec = 1 Gyr, using Eq. (4). This timescale depends on the mass: mp = 0.1 MJup (solid line), 1 MJup (dashed line) and 2 MJup (dotted line). For example, a perturber of mass 0.1 MJup, periastron qp = 150 AU and eccentricity ep = 0.4 is expected to produce a significantly eccentric ring in shorter than 1 Gyr, although spiral patterns may remain since it can take several precession timescales for them to vanish, as was shown by Wyatt (2005). |
However, the problem is more complex for real disks, which have a finite spatial extension, since these estimates depend on radial locations. To first order, it can be seen from Eqs. (2), to (4) that the forced eccentricity and the secular timescale scale as 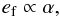 (5)and
(5)and 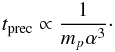 (6)We now define ain and aout as the inner and outer limits of the disk in the semi-major axis and define ef,min and ef,max as the minimum and maximum eccentricities induced across the disk4. The minimum and maximum precession timescales, tprec,min and tprec,max, are defined in the same manner. Then, using Eqs. (5) and (6), one obtains
(6)We now define ain and aout as the inner and outer limits of the disk in the semi-major axis and define ef,min and ef,max as the minimum and maximum eccentricities induced across the disk4. The minimum and maximum precession timescales, tprec,min and tprec,max, are defined in the same manner. Then, using Eqs. (5) and (6), one obtains 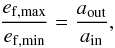 (7)and
(7)and  (8)It is easy to see from these equations that the secular precession timescale spans a wide range of values across the disk. This means that making analytical predictions by setting the desired values for the forced eccentricity and the secular precession timescale for a particle with semi-major axis at the centre of the distribution suffers limitations when applied to an extended disk, especially concerning the timescale.
(8)It is easy to see from these equations that the secular precession timescale spans a wide range of values across the disk. This means that making analytical predictions by setting the desired values for the forced eccentricity and the secular precession timescale for a particle with semi-major axis at the centre of the distribution suffers limitations when applied to an extended disk, especially concerning the timescale.
 |
Fig. 3 Herschel/PACS images of ζ2 Reticuli at 70, 100 and 160 microns from left to right. North is up and east is to the left. The insets in the bottom-left corners show the PSF. The north-west lobe is noted N-W, while the south-east lobe is noted S-E. |
Equations (7) and (8) can be rewritten using Δa, the half width of the disk extent, along with ef,c and tprec,c, the forced eccentricity and secular precession timescale at ac, respectively:  (9)and
(9)and 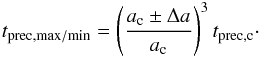 (10)As an example, we set ac = 100 AU, Δa = 25 AU, 2ec = 0.3 and tprec,c = 1 Gyr. These values are close to those derived for the disk of ζ2 Reticuli (e ≳ 0.3 and extent 70–120 AU: Eiroa et al. 2010,and Sect. 3 of the present work). One obtains
(10)As an example, we set ac = 100 AU, Δa = 25 AU, 2ec = 0.3 and tprec,c = 1 Gyr. These values are close to those derived for the disk of ζ2 Reticuli (e ≳ 0.3 and extent 70–120 AU: Eiroa et al. 2010,and Sect. 3 of the present work). One obtains 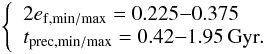 (11)In these conditions, the extent of the disk is not expected to affect the global eccentricity of the disk too much, that is, we expect to recover on average a global eccentricity corresponding to the forced eccentricity at ac after the steady state is reached. But the problem is that the extent of the disk strongly affects the timescale to reach this steady state. This is a limitation of the analytic approach that can be overcome by the use of numerical simulations.
(11)In these conditions, the extent of the disk is not expected to affect the global eccentricity of the disk too much, that is, we expect to recover on average a global eccentricity corresponding to the forced eccentricity at ac after the steady state is reached. But the problem is that the extent of the disk strongly affects the timescale to reach this steady state. This is a limitation of the analytic approach that can be overcome by the use of numerical simulations.
3. Numerical investigation: a typical set-up, the highly eccentric, old disk of ζ2 Reticuli
To move beyond the simplified analytical approach and explore the high-eccentricity case on Gyr timescales, we resorted to numerical tools. We placed ourselves in the frame of the restricted three-body problem, thatb is, one central star, a planet, and a mass-less planetesimal. The symplectic N-body code SWIFT-RMVS of Levison & Duncan (1994) was used to integrate the evolution of a ring of planetesimals around a solar-mass star, over 1 Gyr. We used a typical timestep of ~1/20 of the shortest orbital period and ensured a conservation of energy with a typical error of ~10-6 on relative energy. This code has a crucial advantage over an analytical approach: it is able to handle close encounters and scattering processes, along with the short-term variations of the planetesimals orbital elements, whereas these effects were ignored in the analytical approach, for which orbits were averaged, short-term variations were los,t and the approach is valid only for α ≪ 1, that is, far from close encounters. As we show in Sect. 4, the scattering events play a crucial role in the system’s evolution.
For the sake of clarity, the ζ2 Reticuli system was considered as a proxy for a typical mature and significantly eccentric debris ring. We explore different planet-disk configurations, and produce synthetic images for comparison with Herschel/PACS observations. We show that the hypothesis of an eccentric debris disk around ζ2 Reticuli is fully consistent with the observations.
3.1. The ζ2 Reticuli system
The G1V solar-type star ζ2 Reticuli (HR 1010, HIP 15371) (Eiroa et al. 2013) is located at 12 pc (van Leeuwen 2007), has a luminosity L⋆ = 0.97 L⊙, log g = 4.51, and is ~2–3 Gyr old (Eiroa et al. 2013). It has a binary companion ζ1Reticuli, a G2–4V (Gray et al. 2006; Torres et al. 2006) star located at a projected distance of 3713 AU from ζ2 Reticuli (Mason et al. 2001). Bayesian analysis by Shaya & Olling (2011) of the proper motions of these stars indicates a very high (near 100%) probability that the pair are physically connected.
The presence of dust around ζ2 Reticuli has been probed with Spitzer (Trilling et al. 2008); the results suggest a ~150 K emission at ~4.3 AU. However, the angular resolution of Spitzer is limited, and the dust spatial distribution remained unconstrained. New observations with Herschel/PACS completed the spectral energy distribution (SED), providing the suggestion of an optically thin, ~40 K, emission at ~100 AU, with fractional luminosity Ldust/L⋆ ≈ 10-5 (Eiroa et al. 2010). Moreover, Herschel/PACS provided spatially resolved images of the dust thermal emission surrounding ζ2 Reticuli at 70 μm and 100 μm (Eiroa et al. 2010). We present here newly reduced Herschel/PACS images (see Fig. 3). The images show a double-lobe feature, asymmetric both in position and brightness. Note that at 70 μm, the probability for alignment with a background source within 10′′ is extremely low, namely 10-3 (Eiroa et al. 2010). The disk is not resolved at Herschel/SPIRE wavelengths: newly reduced images and star-disk flux measurements are presented in Appendix A.
As suggested by Eiroa et al. (2010), the asymmetry revealed by Herschel/PACS in the disk of ζ2 Reticuli can be interpreted as a ring-like elliptical structure with e ≳ 0.3 seen close to edge-on and extending from ~70 to ~120 AU, which is fully consistent with the information derived from the SED (Eiroa et al. 2010). Alternatively, it might also be interpreted as two clumps from an over-density of dust and planetesimals. In Appendix B, we investigate the system inclination on the line of sight, a crucial parameter required for correctly interpreting the observed structures. More precisely, we determined the star inclination and assumed that the disk and the star are coplanar. The 50% probability value is i = 65.5°, meaning that the system is highly inclined to the line of sight, which tends to support the eccentric-ring scenario.
Without a doubt, this asymmetric structure provides evidence that “something” is dynamically sculpting the disk. This may be the stellar companion ζ1Reticuli or a (as yet undetected) planet. The latter hypothesis is fully compatible with radial velocity measurements of ζ2 Reticuli, which suggest there is no Jupiter-mass (or larger) planet interior to ~5–10 AU (Mayor et al. 2003), but which put no contraints on a small planet or a Jupiter-like planet at larger radii. It is also compatible with growing observational evidence for planets at large orbital separation, that is, several tens to a few hundreds of AU from their host star (see, e.g., Luhman et al. 2007; Kalas et al. 2008; Marois et al. 2008, 2010).
Constraints from direct imaging are presented in Fig. 4 using the two evolutionary models COND 2003 (Baraffe et al. 2003) or BT-settl 2011 (Allard et al. 2011). Details of the reduction procedure are presented in Appendix C. These constraints were obtained from VLT/NaCo archival data taken in November 2010 in the Ks band. These data do not provide constraints on companions beyond a projected distance of ~30 AU. The presence of a brown dwarf within ~20 AU is still compatible with observations.
3.2. Numerical set-up
We considered a ring of 150 000 mass-less planetesimals uniformly distributed between 70 and 140 AU (except when specified otherwise) around a solar-mass host star, with initial eccentricities randomly distributed between 0 and 0.05, and initial inclinations between ± 3°, while the remaining angles (longitudes of nodes and periastra) were randomly distributed between 0 and 2π. These values are summarised in Table 1. This reasonably well mimics the low eccentricities and inclinations expected at the end of the protoplanetary phase. The radial extent of the model disk was configured to closely match the observed properties of the disk around ζ2 Reticuli.
 |
Fig. 4 Detection limits set by direct imaging on the presence of brown dwarf/close binary between 1′′ and 2.5′′ in projected separation. |
Using mass-less test particles removes self-gravity in the disk, as well as a back-reaction of the disk on the planet. In general, both of these phenomena are significant when the planet mass is similar to the disk mass. We have no mass estimate for the debris disk of ζ2 Reticuli. However, a well studied case is the debris disk of Fomalhaut, whose mass was estimated to be ~3–20 M⊕ (Wyatt & Dent 2002; Chiang et al. 2009). Since a debris disk loses material over time due to the combined effects of collisional evolution, Poynting-Robertson drag, and radiation pressure, and since ζ2 Reticuli is much older than Fomalhaut (440 Myr; Mamajek 2012), it is reasonable to assume that the debris disk surrounding ζ2 Reticuli does not contain more than a few Earth masses. In this case, it is also reasonable to assume that the disk self-gravity and back-reaction are negligible, and the planet will still be able to imprint on the disk structure if its mass is at least 0.1 MJup ~ 32 M⊕.
Initial parameters for the planetesimals used in our N-body simulations.
We considered two planet-disk configurations, inside and outside the planetesimal belt, and performing parametrically explored their influent orbital elements.
3.2.1. Inner perturber
The first case is that of a planet interior to the initial ring. In this case, we considered that the inner edge of the disk is located at 70 AU, and made the classical assumption that it is truncated by the chaotic zone generated by a coplanar planet (see, e.g., the approach used by Chiang et al. 2009). The chaotic zone is defined as the region where mean-motion resonances overlap. The width of this zone depends on the mass ratio between the central star and the perturber,  (12)where μ = mplanet/m∗ (Wisdom 1980; Duncan et al. 1989). Consequently, one can deduce the semi-major axis of a planet of a given mass that generates a disk inner edge at 70 AU:
(12)where μ = mplanet/m∗ (Wisdom 1980; Duncan et al. 1989). Consequently, one can deduce the semi-major axis of a planet of a given mass that generates a disk inner edge at 70 AU: 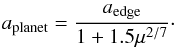 (13)We chose to perform a parametric exploration of the mass and eccentricity of the perturber, fixing its semi-major axis to the value deduced from the formula above. The values explored were 0.1 MJup, 0.5 MJup, and 1 MJup for the mass and 0.2, 0.4 and 0.6 for the eccentricity (see Table 2). Here the disk initial inner edge was fixed halfway between 70 AU and the planet semi-major axis.
(13)We chose to perform a parametric exploration of the mass and eccentricity of the perturber, fixing its semi-major axis to the value deduced from the formula above. The values explored were 0.1 MJup, 0.5 MJup, and 1 MJup for the mass and 0.2, 0.4 and 0.6 for the eccentricity (see Table 2). Here the disk initial inner edge was fixed halfway between 70 AU and the planet semi-major axis.
In addition, we also considered a more massive perturber such as a brown dwarf, located farther inside the system. This was motivated by the observation of a suspicious point source on observations in Ks-band data from the ESO archive (ID 086.C-0732(A); PI: Löhne, 71574), which disappeared after re-reduction of the data, and consequently, since its existence is controversial, we chose not to show these images. However, if it were confirmed, this point source was showing a 42 MJup brown dwarf located at a projected distance of 17.5 AU from the star. Therefore, we investigated the possibility for the presence of a brown dwarf in the inner parts of the system. For an inner edge to be produced at 70 AU, the planet’s semi-major axis need to be 43.8 AU. Since this constraint is less relevant for very eccentric inner perturbers (see Sect. 4), we chose here to set this value to the perturber’s apastron and not its semi-major axis. We fixed its periastron to 17.5 AU, which led to an orbital eccentricity of 0.43 and a semi-major axis of 30.6 AU. With this orbit, analytical predictions indicate that the perturberexcites planetesimals eccentricities up to 0.4. Therefore, this orbit was chosen for numerical tests (see Table 2).
3.2.2. Outer perturber
The second case considered is that of a planet exterior to the ring. There is indeed growing evidence for planets at large orbital separations, that is, several tens to a few hundreds of AU away from their host star (see e.g. Luhman et al. 2007; Kalas et al. 2008; Marois et al. 2008, 2010), and the mass constraints set by direct imaging are loose given the age of the system (see Sect. 4.1.3). Therefore, we also investigated the ability of an external perturber to shape a disk.
We considered coplanar outer planetary companions and explored the impact of the eccentricity, mass, and periastron on the disk asymmetry. While an inner edge is in general considered as a clue for the presence of inner perturbers, it is obviously more of a conjecture to assume that an outer edge is formed in the same manner, since a disk instrinsically has an outer limit. Therefore, the outer edge was not assumed here to be formed because of resonance overlap, and the planet periastron was fixed instead, to ensure that it does not cross the disk. To explore a great variety of situations despite the CPU-time limitations, we considered a rough parameter space consisting of all the possible combinations between masses mp = 0.1 − 1 − 2 MJup, periastra qp = 150 − 200 − 250 AU, and eccentricities ep = 0.2 − 0.4 − 0.6 (see Table 2).
Summary of numerical experiments with an inner and outer perturber, and for a brown dwarf and the stellar binary companion ζ1 Reticuli.
Note that the perturbers were set on an initially eccentric orbit, which requires an explanation, because we assumed that the disk is initally symmetric. Indeed, this pictures a situation where the process that sets the perturber on its eccentric orbit leaves the disk unperturbed. This may seem rather unrealistic, even though some scenarios can be envisaged. For instance, an inner perturber might acquire its eccentricity via a planet-planet scattering event. However, this event should be such that a single perturber remains in the system. Otherwise, additional perturbations of a second planet would generate an orbital precession of the eccentric perturber, which in turn would not be able to sculpt the disk into an eccentric shape. This is compatible with observational constraints, since as previously mentioned radial velocity measurements rule out a massive perturber in the inner system. For an outer perturber, an eccentric outer binary companion may be able to generate these initial conditions (see Sect. 6). In summary, retrieving realistic initial conditions relies on a complete study of the perturbations induced on the disk for multiple scenarios and, most probably, an extensive parameter space exploration. This is beyond the scope of the present paper, and will be the subject of future work; this motivated us to choose simple initial conditions.
4. Numerical investigation: results
We present here results obtained for the two disk-planet set-ups we considered: an inner and outer planet, and when the perturber is the stellar companion ζ1 Ret. For each case, we aimed to find the result that gives an eccentric disk compatible with observational constraints.
Eiroa et al. (2010) derived a lower limit for the eccentricity of the disk in ζ2 Reticuli of 0.3. Therefore, given the uncertainties in the estimation of the disk global eccentricity we computed from our simulations, a disk global eccentricity lower than 0.2 was discarded in our analysis. This global eccentricity was evaluated considering the geometry of an ellipse: the offset δ of the centre of symmetry from one of the foci of an ellipse is simply the product of its semi-major axis a by its eccentricity e, that is, δ = ae. For a disk from our simulations, δ can be obtained by calculating the centre of symmetry of the disk, using the positions of the test particles in the heliocentric frame: δ is the distance of this centre of symmetry to the star. The disk semi-major axis a was determined as follows: the disk was divided into superimposed angular sectors of 3°. For each of these sectors, the radial distribution of the particles was fitted to a Gaussian. This provided the radial position of the maximum density for each angular sector, and thus a set of points defining the global shape of the disk. It is then straightforward to retrieve a from this set of points by seeking for the major axis, that is, the maximum distance between two opposite points. Finally, the disk eccentricity is simply e = δ/a.
4.1. Inner perturber
We chose four illustrative results (see Table 2). For each, we show pole-on projections of the system at 1 Gyr in Fig. 7. We also summarise the results of our simulations in Table 2.
The best candidates needed a significant orbital eccentricity of ~0.4. The example of Case B is shown in Fig. 7 (upper-right panel). However, scattering processes may be important, and studying them allowed us to place constraints on the mass of the perturber.
4.1.1. Scattered disks
 |
Fig. 5 Semi-major axis versus eccentricity diagram of the disk at 1 Gyr for the Case C perturber. Overdensities of planetesimals at ~79 and ~95 AU correspond to planetesimals in 3:2 and 2:1 mean-motion resonance with the perturber. |
Inner perturbers may lead to very significant scattering processes. Namely, they can fill the inner parts of the disk instead of producing a well-defined ring. Such effects are presented with Case A in Fig. 7 (upper-left panel).
This effect appears for low-mass perturbers. These perturbers do not scatter material efficiently enough. This material then tends to populate the inner parts of the system.
As a consequence, there is a lower mass limit for inner perturbers, and in the specific case of the ζ2 Reticuli system, this lower limit is between 0.1 and 0.5 MJup. However, one cannot exclude that another more massive planet produces scattering of the material, blowing it out and leaving an inner hole, therefore a more correct way to express this constraint would be that perturbers with masses as low as 0.1 MJup should be accompanied by another more massive planet to create this pattern. But this scenario presents difficulties: while this second planet must be massive enough to clear the inner parts of the system of its material, it also must have a limited dynamical effect on the first planet that sculpts the disk: this second planet must be distant and not too massive for the orbit of the first planet to remain unperturbed. Otherwise, this orbit would precess and no longer lead to an eccentric pattern. It is not our purpose here to investigate this scenario, but based on the previous arguments, it would most probably work in a very limited parameter space.
4.1.2. Resonant patterns
Remarkably, for very eccentric (ep = 0.6) inner perturbers of mass between 0.5 and 1 MJup, resonant clumpy structures may arise. An example is Case C, shown in Fig. 7 (bottom-left panel). In Fig. 5, we show a semi-major axis vs eccentricity diagram of the disk: it reveals two populations in resonance with the planet, namely the 3:2 and 2:1 mean-motion resonances, at ~79 AU and ~95 AU, respectively. These resonant populations are shown in Fig. 6. Typically, a population in 3:2 resonance is associated with capture during outward planetary migration, as is the case in our own solar system (Malhotra 1993, 1995). But here, these structures is most probably appear because we used the chaotic-zone formula (Eq. (13)) to determine the perturber semi-major axis, which was derived for perturbers on circular orbits. Therefore, it is expected that this formula works less efficiently with increasing orbital eccentricity of the perturber: the result is that the planet digs into the disk, and consequently, planetesimals unprotected against close encounters by mean-motion resonance are scattered out, leaving the resonant structures apparent. This is supported by the fact that these resonant structures disappear when the constraint given by the chaotic-zone formula is applied to the perturber’s apastron instead of its semi-major axis, as for an inner brown-dwarf-type companion. Interestingly, the observation of these resonant structures in a system may provide other clues on the dynamical history of a perturber than an outward migration: it may mean that the planet was originally shaping the inner edge of the disk before it was set on an eccentric orbit. However, these are thin structures, and when the disk is seen close to edge-on, as is the case for ζ2 Reticuli, they would most probably be hidden by the non-resonant population.
4.1.3. Brown dwarf
Additionally, we investigated the possibility for the presence of a brown dwarf in the inner parts of the system, on an orbit such that the perturber excites planetesimal eccentricities up to 0.4. The disk at 1 Gyr is shown in Fig. 7 (bottom-right panel). Its global eccentricity is ~0.2–0.25, which shows that very massive perturbers in the inner parts of the system can create the desired pattern.
 |
Fig. 6 Views from above the plane of disks at 1 Gyr in Case C, i.e., where resonant patterns appear. Planetesimals in 3:2 (left) and 2:1 (right) mean-motion resonance with the perturber are shown in red. |
 |
Fig. 7 Example views from above the plane of disks at 1 Gyr, under the influence of inner perturbers. Top left: the perturber scatters material in the inner parts of the system (Case A). Right: one of the best candidates (Case B). Bottom left: resonant patterns appear (Case C). Right: a brown-dwarf perturber can be a good candidate. |
4.2. Outer perturber
We chose four illustrative results (see Table 2) and show pole-on projections of the system at 1 Gyr in Fig. 8 for each, along with the evolution of the disk offset on 1 Gyr in Fig. 9. The results of our simulations are summarised in Table 2.
4.2.1. Good candidates
Case D is shown in Fig. 8 (upper left panel). The corresponding evolution of the offset clearly shows that the disk is at steady state and significantly eccentric (see Fig. 9). The best candidates must have significant eccentricities: none of our 0.2 eccentric perturbers creates the desired eccentric structure, even in the limit case predicted analytically, where a 0.1 MJup perturber has a pericentre qp = 150 AU and eccentricity ep = 0.2 (see Fig. 2). As a consequence, the best outer candidates have eccentricities ~0.4–0.6.
 |
Fig. 8 Example views from above the disk plane at 1 Gyr, under the influence of outer perturbers. Top left: one of the best candidates (Case D). Right: spirals are still apparent (Case E). Bottom left: one might question the contribution of the scattered material to the disk emission (Case F). Right: scattering processes tend to destroy the structure (Case G). |
4.2.2. Spiral patterns
Case E is shown in Fig. 8 (upper-right panel). The system shows a spiral pattern at 1 Gyr, which, according to analytical predictions, corresponds to one precession timescale (see Fig. 2). Thus, our N-body integrations confirm what was noted by Wyatt (2005): the analytical formula appears to be a lower limit and several precession timescales are sometimes necessary for spiral patterns to vanish. The effect of spirals can also be seen in the evolution of the disk offset, which oscillates (see Fig. 9).
If we had observational proof that the disk of ζ2 Reticuli has reached steady state and contains no spiral pattern, the results of our numerical investigation would allow us to place a lower mass limit of 0.1 MJup on an outer perturber in a range of periastra from 150 to 250 AU, based on a dynamical timescales criterion, otherwise it takes longer than 1 Gyr to generate a steady-state eccentric disk. This limit still holds for larger periastra than the range explored, since dynamical timescales increase with distance. But because of the slightly edge-on orientation of the disk and the resolution of the Herschel/PACS images, it is extremely difficult to discard a possible spiral pattern in this disk, and no lower mass limit can be clearly defined for an outer perturber.
4.2.3. Scattered disks
Outer perturbers may lead to very significant scattering processes. We present such effects in Fig. 8 (lower panels), where Case F and Case G are considered.
These processes are even more significant when the mass of the perturber increases. Indeed, as physically expected, more massive perturbers tend to scatter small bodies more efficiently. The distance to the disk plays a major part in this effect too, since close perturbers also tend to scatter more material. Additionally, when a perturber is on an eccentric orbit, it approaches even closer to the disk. In the most dramatic cases, the disk is completely destroyed. Consequently, for a given distance to the disk, there is an upper limit to the mass of an outer companion.
For Case F, one might question the contribution of the scattered inner material to the emission of the disk, and whether it would be visible on resolved images. In this case, the potential visibility of material on real observations relies on the sensitivity and resolution of the instrument used for these observations, as well as on the distance of the object, the radiative properties of the material itself and the quantity of light it receives, that is, on the host star properties. Therefore, only the production of synthetic images for direct comparison with observations can reveal whether this material is apparent or not, and refine constraints on the potential perturbers at work in the system. Additionally, the evolution of the offset clearly suggests that the asymmetry relaxes asymptotically to a low but non-zero value, and indeed, the apparent ring structure shows little eccentricity.
More specifically, our results allow us to place an upper mass limit of 2 MJup on an outer perturber in a range of periastra from 150 to 250 AU for the ζ2 Reticuli system. However, this upper mass limit is expected to increase for periastra higher than those explored, since scattering processes are expected to be less efficient for a given mass when the companion is farther away from the disk.
 |
Fig. 9 Example of the time evolution on 1 Gyr of the disk offset coordinates (X (solid line) and Y (dashed line)) for outer perturbers. Top left: one of the best candidates (Case D). Because of the orientation of the perturber orbit, where its semi-major axis is along the X-axis with positive periastron, this corresponds to a negative X-offset ΔX ~ − 30 AU and a zero Y-offset for a disk located at ac ~ 100 AU. Top right: the oscillations of the offset coordinates reveal the spiral-winding regime (Case E). Bottom: the offset seems to relax; left: case F; right: case G. |
 |
Fig. 10 Semi-major axis vs. eccentricity diagram (left) and pole-on projection (right) of a disk of planetesimals after 2 Gyr under the influence of a one-solar-mass star of semi-major axis 2046 AU on an orbit of eccentricity 0.815. The disk is truncated at ~80 AU and nearly circular. It has no clear offset: its centre of symmetry is offset by ~6 AU from the star along the perturber major axis. With a disk mean semi-major axis of ~70 AU, this gives a global eccentricity of ~0.08. |
4.3. Stellar binary companion
We investigated the influence of the binary companion ζ1 Reticuli on the debris disk surrounding ζ2 Reticuli. The aim was to determine whether it alone could generate the observed asymmetry. If this were to be the case, the companion must be on an eccentric orbit. The only observational constraint available so far on the relative orbit of the binary system is the projected distance between the two stars, namely 3713 AU (Mason et al. 2001). Consequently, we cannot exclude the possibility that its orbit is eccentric, with a present-day location near apastron. We investigated whether a binary companion on an eccentric orbit at this distance might account alone for the observed structure of the disk, which would mean an elliptic ring with a minimum global eccentricity of 0.3, without any constraint on the binary eccentricity. We used analytical and numerical methods.
We first examined the forced secular eccentricity applied to the planetesimals by an eccentric binary companion, which was assumed to be coplanar. The debris disk surrounding ζ2 Reticuli is approximately centred on a = 100 AU, and the binary perturber is at 3713 AU from ζ2 Reticuli. This is only a projected distance, not a semi-major axis. We assumed that the binary companion is currently located at a distance r⋆ from ζ2 Reticuli. The equation of its orbit around ζ2 Reticuli reads 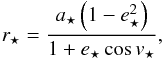 (14)where v⋆, a⋆ and e⋆ are the binary companion current true anomaly, semi-major axis, and orbital eccentricity, respectively. The observed distance d = 3713 AU is related to r⋆ by d = r⋆cosψ, where ψ is a projection angle. This gives
(14)where v⋆, a⋆ and e⋆ are the binary companion current true anomaly, semi-major axis, and orbital eccentricity, respectively. The observed distance d = 3713 AU is related to r⋆ by d = r⋆cosψ, where ψ is a projection angle. This gives 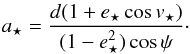 (15)From this result Eqs. (15) and (2), where ap and ep are substituted by a⋆ and e⋆,
(15)From this result Eqs. (15) and (2), where ap and ep are substituted by a⋆ and e⋆, 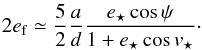 (16)It is clear from this equation that the highest possible ef values ware obtained for cosv⋆ = −1 (binary currently at apastron) and cosψ = 1 (no projection factor). With these assumptions, one derives
(16)It is clear from this equation that the highest possible ef values ware obtained for cosv⋆ = −1 (binary currently at apastron) and cosψ = 1 (no projection factor). With these assumptions, one derives 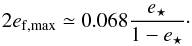 (17)For 2ef,max to reach at least 0.3, e⋆ ≥ 0.815 is required.
(17)For 2ef,max to reach at least 0.3, e⋆ ≥ 0.815 is required.
This seems highly eccentric and very unlikely at first sight. Yet, Duquennoy & Mayor (1991, see their Fig. 6b) have shown that almost 25% of binaries with orbital periods longer than 103 days have orbital eccentrities e⋆ = 0.825 ± 0.075. In the present case, d = 3713 AU and e⋆ = 0.815 lead to a⋆ = 2046 AU and an orbital period T⋆ ~ 105 yr. Therefore it is possible that ζ1 Reticuli is on an eccentric orbit, if not a highly eccentric one. However, the derived orbit should also have an apoastron value of q⋆ = 379 AU and one might question the disk survival at ~70–120 AU with a stellar-type perturber approaching so close to the system.
Equation (1) of Holman & Wiegert (1999) gives the critical semi-major axis acrit for orbital stability around a star perturbed by a binary. This is ![\begin{eqnarray} a_\mathrm{crit} & = & [(0.464\pm 0.006)+(-0.380\pm 0.010)\mu \nonumber\\ & & +(-0.631\pm 0.034)e_\star + (0.586 \pm 0.061)\mu e_\star \nonumber\\ & & +(0.150\pm 0.041)e_\star^2+ (-0.198\pm 0.074)\mu e_\star^2]a_\star, \end{eqnarray}](/articles/aa/full_html/2014/03/aa22469-13/aa22469-13-eq157.png) (18)where μ = m⋆/(mζ2 Reticuli + m⋆) is the star mass ratio of value 1/2 if we assume here m⋆ = mζ2 Reticuli = 1 M⊙. Material with a ≥ acrit will be on an unstable orbit, and most probably scattered out of the system.
(18)where μ = m⋆/(mζ2 Reticuli + m⋆) is the star mass ratio of value 1/2 if we assume here m⋆ = mζ2 Reticuli = 1 M⊙. Material with a ≥ acrit will be on an unstable orbit, and most probably scattered out of the system.
Applying this to our case leads to 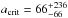 AU. Uncertainties on acrit are very large, and this result shows that within uncertainties, the disk could exist at the observed distances, or, in contrast, not exist at all. Therefore, this orbit was tested numerically. We considered a ring of 150 000 mass-less planetesimals uniformly distributed between 70 and 140 AU from their solar-mass host star, with proper initial eccentricities randomly distributed between 0 and 0.05, and initial inclinations between ± 3°.
AU. Uncertainties on acrit are very large, and this result shows that within uncertainties, the disk could exist at the observed distances, or, in contrast, not exist at all. Therefore, this orbit was tested numerically. We considered a ring of 150 000 mass-less planetesimals uniformly distributed between 70 and 140 AU from their solar-mass host star, with proper initial eccentricities randomly distributed between 0 and 0.05, and initial inclinations between ± 3°.
The test particles are perturbed by another solar-mass star in orbit around the primary with a semi-major axis 2046 AU and eccentricity 0.815, coplanar to the disk. We used the SWIFT-RMVS N-body symplectic code of Levison & Duncan (1994) to compute their orbital evolution for 2 Gyr.
Our results are consistent with the predictions of Holman & Wiegert (1999): the disk is truncated at ~80 AU (see Fig. 10, left panel), which is incompatible with observational constraints of the debris disk of ζ2 Reticuli, since it radially extends up to ~120 AU.
Moreover, at 2 Gyr, the disk has a highly symmetric shape and no clear offset from the star (see Fig. 10, right panel). These results suggest that the binary companion on an eccentric orbit can not account for the disk structure, and that an unseen eccentric companion is more likely responsible for shaping the disk.
Another possible way for a stellar binary companion to generate high-eccentricity orbiting bodies around a primary is the Kozai mechanism (Kozai 1962). This would occur if the disk and the binary orbit were mutually inclined by more than ~39°. In that case, the orbit of a particle in the disk would suffer coupled modulations in inclination and eccentricity, that is, a particle would periodically switch from a highly eccentric orbit, coplanar with the binary companion’s orbit, to a circular orbit, highly inclined with respect to the orbit of the binary companion. However, we can discard this mechanism as a possible explanation for the eccentric global structure of the disk of ζ2 Reticuli: indeed, the Kozai Hamiltonian is invariant by rotation, meaning that, if this mechanism is able to excite planetesimal eccentricities to high values, their longitudes of periastra remain uniformely distributed, while they should be preferentially aligned for an eccentric and offset disk to be generated.
5. Synthetic images
In this section, we use the results of our best-fit N-body simulations to produce a realistic dust population and synthetic images for comparison with Herschel/PACS observations. The procedure followed to create synthetic images is straightforward: a population of dust was created from the position of the parent planetesimals.
The main difference between dust particles and planetesimals is that the former are small enough to be affected by stellar radiation pressure. Radiation pressure is usually described for a particle by its constant ratio β to stellar gravity. The dust particles are assumed to be released by planetesimals, which feel no radiation pressure. Hence the daugther particles assume an orbit that is very different from that of their parent bodies. It is well known that if the parent bodies move on circular orbits, the dust particles are unbound from the star as soon as β ≥ 0.5. In our case, however, dust particles may be released by planetesimals orbiting on more or less eccentric orbits, which may slightly change this threshold. Because planetesimal eccentricities are expected to be moderate on average, β = 0.5 can nevertheless be considered as a reasonable approximation.
Small grains are released from seed planetesimal positions at the planetesimal velocity, and are then spread along the orbits determined by these initial conditions and their β value. We are aware that this simple procedure cannot accurately evaluate the spatial distribution of the smallest grains. To do this, complex models such as the DyCoSS code of Thébault (2012), the CGA of Stark & Kuchner (2009), or the LIDT-DD ode by Kral et al. (2013) have to be used to evaluate the complex interplay between the rate at which grains are collisionally produced from parent planetesimals, the time they spend (because of their highly eccentric orbits) in empty collisionally inactive regions and the rate at which they can be affected or even ejected by close encounters with the perturbing planet (see Sect. 4 of Thebault et al. 2012), not to mention the Poynting-Robertson drag these small grains are subject to.
However, this caveat is acceptable for the present problem, because the role played by small micron-sized grains close to the blow-out size is very minor at wavelengths >70 μm, so that our synthetic images are not strongly affected by errors in their spatial distribution.
We set the dust grain sizes range from 0.5 μm to 1 mm, with a classical Dohnanyi (1969) power-law distribution (index −3.5), which covers the β distribution from 0 to 0.5 well, since this parameter depends on grain size.
Their emission was computed using the radiative transfer code GRaTeR (see, e.g., Lebreton et al. 2012). To do this, the following parameters are required: distance of the star (12 pc), magnitude in band V (V = 5.24), and total luminosity 0.96 L⊙.
Stellar and disk fluxes at 70, 100, and 160 μm (Eiroa et al. 2010).
Because the disk is optically thin, its mass is linearly linked to the flux emission intensity, and it can be easily scaled to fit the observed intensity (see Table 3). The mass needed for the disk to produce a flux as observed on Herschel/PACS will vary with the dust grain composition, and thus its density. But because we have no constraints on the dust composition, astrosilicate grains were used (Draine 2003), and the mass of the disk was simply scaled to obtain intensities compatible with observational constraints for a given wavelength.
Thermal emission images were produced with a resolution of 1′′/pixel at 70 and 100 μm and 2′′/pixel at 160 μm. Before convolving these images with the point spread function (PSF), the star was added at the central pixel with a flux intensity matching the predicted stellar photosphere flux density in each waveband. The position angles of the disk observed with Herschel/PACS and of the disk in our synthetic images, as well as the orientation of the telescope during the observations were taken into account (see Table 4). Our purpose was to match the observations.
Disk position angle observed with Herschel/PACS, disk position angle in our synthetic images, and telescope orientation during Herschel/PACS observations and PSF.
We chose the simulation that led to a clear and significantly eccentric disk at 1 Gyr, namely our Case A (see Table 2, and upper-left panels of Figs. 8 and 9) to reproduce the Herschel/PACS image at 100 μm. The mass of the disk was scaled so that a total flux of 13.5 mJy as observed with Herschel/PACS at 100 μm was spread all over the disk. The last parameter needed is the system inclination. Our best fit gives 65.5° (see Appendix B).
 |
Fig. 11 Synthetic images at λ = 100 μm, unconvolved disk (no star) (left) and convolved disk and star image with the PSF (right). Disk at 1 Gyr in Case A (see Table 2), seen with inclination 65°. The star is at the centre of the image, and in the convolved image, the flux scale is set to match that in the Herschel/PACS image. |
We present an unconvolved and convolved image of this disk in Fig. 11. The disk offset is clearly visible in unconvolved images. However, there seem to be no difference between the symmetric and asymmetric state after the images are convolved because of the contrast between the star and the disk emission. Moreover, the disk flux per pixel is one order of magnitude lower than the fluxes observed in Herschel/PACS images.
This is not surprising, however: to estimate the total disk flux, the flux was measured in a small region of the disk before applying aperture correction. Even if the correct aperture correction for a point source were used, it would always be a lower limit, and the total disk flux would be underestimated. The parent ring may also be narrower, which would increase the flux per pixel.
Therefore, we investigated the impact of the width and of the total flux of the disk on the features visible with PACS and produced convolved images of a dusty disk produced by an asymmetric eccentric parent ring of diverse total fluxes (1, 2, and 5 times the flux measured by Herschel/PACS) and of diverse widths (semi-major axis centred on 100 AU, widths 5, 10, and 20 AU). To do this, particles from a range of semi-major axes from our N-body simulation output were selected. An inclination angle of 65° was chosen, which is the most probable inclination derived for the system.
The fluxes per pixel recovered in convolved images with a disk five times more massive than the mass initially derived from observations match the observations better. This provides a better constraint on the disk mass and total flux. We show this example in Fig. 12 (left panel): the asymmetric double-lobe structure now appears clearly.
It is worth noting that the width of the parent ring has a more limited influence on the flux per pixel than the mass of the disk. But it has an influence on the appearance of the disk: a narrow parent ring (<10 AU) leads to a resolved apastron lobe, which is more consistent with Herschel/PACS images, although this lobe does not seem to be located as far from the star as it is in the Herschel/PACS images.
Therefore, we also investigated the location of the disk by producing convolved images of a ring of dust produced by a narrow eccentric parent ring of width 5 AU and semi-major axis centred on 120, 130, and 140 AU. The disk total flux was set to be five times the flux derived from observations. The inclination angle was here again set to 65°. As expected, the farther away the disk is located, the clearer the lobes appear (see Fig. 12).
 |
Fig. 12 Synthetic images of Case A (see Table 2) at 100 μm and convolved with the PSF. The parent ring is centred on 100 AU (left) and 130 AU (right), has a width of 5 AU and is seen with an inclination of 65°. The disk total flux is five times the flux measured by Herschel/PACS. The star is at the centre of the image and the flux scale is set to match that of Herschel/PACS image. |
Finally, with all these insights, we conclude that the hypothesis of an eccentric dusty disk around ζ2 Reticuli is indeed compatible with Herschel/PACS images, provided that the dust is produced by a narrow parent ring with width less than 10 AU and located slightly farther away than derived by Eiroa et al. (2010), such that its a semi-major axis distribution is centred between 120 and 140 AU.
This slightly changes the constraints derived on potential perturbers, but the forced eccentricity only depends on the ratio between the planet and planetesimal semi-major axis, and in a linear way at lowest-order approximation. This means that in this approximation the constraints can be completely scaled in a linear way, that is, the potential semi-major axis for planets must also be increased by 20–40% and the disk needs to be centred on 120–140 AU, while the constraint on the perturber eccentricity (e ≳ 0.3) remains identical.
6. Discussion and conclusion
We used ζ2 Reticuli as an example to discuss the shaping of a disk into an eccentric ring on Gyr timescales.
We showed that eccentric patterns in debris disks can be maintained on Gyr timescales, but also that eccentric perturbers can produce patterns other than eccentric rings.
The general results of our simulations show that both inner and outer perturbers can generate extremely significant scattering processes. They can cause a disk to adopt structures that show no clear elliptic ring: the inner part of the disk is either filled or the structure is destroyed. These scattering processes endanger the survival of an eccentric ring, and investigating these processes with numerical experiments allowed us to put constraints on potential perturbers. From these constraints, we derived an upper-mass limit for outer perturbers in a certain range of periastra and a lower-mass limit for inner perturbers.
Moreover, the timescale for spiral structures to vanish is longer with smaller-mass perturbers, and thus, investigating this timescale with numerical experiments permitted us to place a lower-mass limit on perturbers, provided that spiral structures in a disk can definitely be ruled out from observations. The role of numerical experiments is crucial here, since the analytical timescale at the disk centre of distribution underestimates the effective timescale in a real extended disk.
The offset of the disk centre with respect to the star is mostly stable; however, we note that it seems to relax very slowly in rare cases. While the former evolution is characteristic for pericentre glow dynamics, the latter one is surprising. The relaxation of the eccentric structure is not expected in the first-order secular analysis described by Wyatt et al. (1999) and Wyatt (2005). It may be the result of higher-order terms that have been neglected in the analytical study, and is more probably caused by erratic short-term variations of the planetesimals’ semi-major axes due to moderately distant approaches to the planet. These effects, which can lead to scattering of the planetesimals, are eliminated in the analytical averaging process of the perturbations, and thus cannot be predicted analytically in the secular approximations used here. A more detailed study of this relaxation phenomenon of pericentre glow structures is nevertheless beyond the scope of the present paper and will be the purpose of future work.
Transient spiral structures, filled inner holes, sparsely populated scattered disks, and resonant clumpy structures are all possible results when an eccentric perturber acts on a debris disk. They can be shown with numerical simulations, but more importantly, used to derive constraints on a perturber in a system (mass and eccentricity). Therefore, we provided a method for investigating and modelling eccentric ring structures based on a complementary analytic and numerical approach, where one can derive potential orbits from analytics and test them numerically using N-body codes. This method can be easily applied to other systems and is expected to be useful in the near future.
Indeed, Kaib et al. (2013) have pointed out that wide binary star systems, that is, systems with separations greater than 1000 AU, can produce eccentric planets around a primary star on Gyr timescales. This is due to Galactic tides and passing star perturbations, which are able, sooner or later, to set the secondary star on a highly eccentric orbit. The proportion of wide binary systems is by no means negligible (~50%, Duquennoy & Mayor 1991), and although debris disks which are several Gyr old are faint and difficult to detect, this will be overcome with the unique capabilities of ALMA, JWST, and SPICA. Therefore, old eccentric patterns in debris disks are expected to be commonly observed in the future.
The ζ2 Reticuli disk is one such example of such a Gyr-old eccentric debris disk. Moreover, ζ2 Reticuli is part of a wide binary star system, which may provide an explanation for the presence of an eccentric perturber around ζ2 Reticuli. We showed that the binary companion cannot be directly responsible for the eccentric ring structure, and also that the asymmetry is instead caused by a closer companion, either interior or exterior to the disk. In all cases, the eccentric companion is expected to have an eccentricity e ≳ 0.3 to produce this pattern.
Investigation of the disk structure generated by the scattering processes provided an upper-mass limit of 2 MJup for an outer perturber located in a range of periastra 150–250 AU, whereas a lower-mass limit of 0.1 MJup is associated with inner perturbers in the ζ2 Reticuli system.
By producing synthetic images, we showed that the original interpretation of the double-lobed feature around ζ2 Reticuli, that is, the observed eccentric ring e ≳ 0.3, is clearly supported, although the disk is located slightly farther away (20–40%) than originally derived. Moreover, we found that the dusty disk is probably created by a narrow parent ring (width <10 AU), which should have a slight inclination with the line of sight, compatible with the most probable inclination derived for the system, and it also has a significantly higher flux than that estimated from the Herschel/PACS measurements (at least five times).
Online material
Appendix C: Constraints on ζ2 Ret set by direct imaging
VLT/NaCo (Lenzen et al. 2003; Rousset et al. 2003) Ks-band data were retrieved from the ESO archive (ID 086.C-0732(A); PI: Löhne, 71574). Two epochs were available in August 2010 and November 2010, the former missing photometric calibration therefore only the latter was used to set detection limits on the presence of bound companions. Nevertheless, both data sets were reduced and no companion was detected. The data from November 11, 2010 were obtained in field stabilized-mode with five manual offsets of the derotator to simulate field rotation, with the S27 camera providing a pixel scale of 27 mas/pixel. Twenty image cubes with a DITxNDIT of 1.5 s × 42 were obtained for a total observing time on target of 21 min. The semi-transparent mask C_0.7_sep_10 with a diameter of 0.7′′ and a central transmission of 3.5 × 10-3 was used. Each individual image was bad pixel-corrected and flat-fielded. Background subtraction was made for each cube using the closest sky images. The images were rencentred using a Gaussian fit of the attenuated central star. The data were selected within each data cube using criteria based on the attenuated central star flux and the encircled energy between 0.4′′ and 0.55′′. The images were then binned every 6 s and derotated into a reference frame where the pupil was stabilized in order to simulate angular differential imaging (ADI, Marois et al. 2006). In this reference frame, the total field rotation provided by the manual offsets plus the natural pupi/field rotation is 17°. This data cube was then reduced using principal components analysis (PCA, Soummer et al. 2012), retaining four components out of 105.
The noise in the final reduced image was estimated using a sliding nine pixel-wide box to obtain a preliminary map of detection limits in magnitude. We corrected this map by computing the flux losses due to the PCA reduction. They were estimated by injecting fake planets into the data cube at a 10-σ level and processing the data again. Last, these detection limits in magnitude were converted into detection limits in masses, using the COND (Baraffe et al. 2003) or BT-settl models (Allard et al. 2011), assuming an age of 2 Gyr. The 2D-detection limits derived with the COND evolutionary models are presented in Fig. C.1.
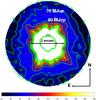 |
Fig. C.1 Map of the detection limits in Jupiter masses set by the COND evolutionary models. The contours range from 60 to 150 MJup with a step of 10 MJup. |
See, e.g., http://www.circumstellardisks.org
Acknowledgments
We thank the referee, A. Mustill, for very useful comments that contributed to the clarity of this paper. Computations presented in this paper were performed at the Service Commun de Calcul Intensif de l’Observatoire de Grenoble (SCCI), France, on the super-computer funded by the Agence Nationale pour la Recherche under contracts ANR-07-BLAN-0221, ANR-2010-JCJC-0504-01 and ANR-2010-JCJC-0501-01. B. Montesinos, C. Eiroa and J.P. Marshall are supported by Spanish grant AYA 2011-26202. A. Bonsor and S. Ertel acknowledge support from the ANR-2010 BLAN-0505- 01 (EXOZODI). The authors wish to thank the PNP/CNES for their financial support. This work has also greatly benefited from the software resulting from Thomas Tintillier’s training project.
References
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Augereau, J. C., & Papaloizou, J. C. B. 2004, A&A, 414, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Augereau, J. C., Nelson, R. P., Lagrange, A. M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumann, H. H., Beichman, C. A., Gillett, F. C., et al. 1984, ApJ, 278, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beust, H., & Dutrey, A. 2006, A&A, 446, 137 [Google Scholar]
- Beust, H., Augereau, J.-C., Bonsor, A., et al. 2014, A&A, 561, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boley, A. C., Payne, M. J., Corder, S., et al. 2012, ApJ, 750, L21 [Google Scholar]
- Chiang, E., Kite, E., Kalas, P., Graham, J. R., & Clampin, M. 2009, ApJ, 693, 734 [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1989, Icarus, 82, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eiroa, C., Fedele, D., Maldonado, J., et al. 2010, A&A, 518, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eiroa, C., Marshall, J. P., Mora, A., et al. 2013, A&A, 555, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ertel, S., Wolf, S., Eiroa, C., et al. 2011, in EPSC-DPS Joint Meeting 2011, 678, available at http://meetings.copernicus.org/epsc-dps2001 [Google Scholar]
- Ertel, S., Wolf, S., & Rodmann, J. 2012, A&A, 544, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B., Kozinsky, B., & Rasio, F. A. 2000, ApJ, 535, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, T. J., Soderblom, D. R., Donahue, R. A., & Baliunas, S. L. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Mitchell, R. I., Iriarte, B., & Wisniewski, W. Z. 1966, Communications of the Lunar and Planetary Laboratory, 4, 99 [Google Scholar]
- Kaib, N. A., Raymond, S. N., & Duncan, M. 2013, Nature, 493, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Graham, J. R., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Fitzgerald, M. P., & Clampin, M. 2013, ApJ, 775, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kral, Q., Thébault, P., & Charnoz, S. 2013, A&A, 558, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krist, J. E., Stapelfeldt, K. R., Bryden, G., & Plavchan, P. 2012, AJ, 144, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V. 2010, Res. Astron. Astrophys., 10, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Krymolowski, Y., & Mazeh, T. 1999, MNRAS, 304, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, J., Augereau, J.-C., Thi, W.-F., et al. 2012, A&A, 539, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in Proc. SPIE 4841, eds. M. Iye, & A. F. M. Moorwood, 944 [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Krivov, A. V., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Patten, B. M., Marengo, M., et al. 2007, ApJ, 654, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1993, Nature, 365, 819 [CrossRef] [Google Scholar]
- Malhotra, R. 1995, AJ, 110, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E. 2012, ApJ, 754, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Mardling, R. A., & Lin, D. N. C. 2002, ApJ, 573, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Moro-Martín, A. 2013, in Planets, Stars and Stellar Systems, eds. T. D. Oswalt, L. M. French, & P. Kalas (Dordrecht: Springer Science and Business Media), 431 [Google Scholar]
- Moro-Martín, A., & Malhotra, R. 2002, AJ, 124, 2305 [NASA ADS] [CrossRef] [Google Scholar]
- Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A. M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mustill, A. J., & Wyatt, M. C. 2009, MNRAS, 399, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C. 2006, MNRAS, 372, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Reche, R., Beust, H., Augereau, J.-C., & Absil, O. 2008, A&A, 480, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., & Schmitt, J. H. M. M. 2003, A&A, 398, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in Proc. SPIE 4839, eds. P. L. Wizinowich, & D. Bonaccini, 140 [Google Scholar]
- Shaya, E. J., & Olling, R. P. 2011, ApJS, 192, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Stapelfeldt, K. R., Holmes, E. K., Chen, C., et al. 2004, ApJS, 154, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Stapelfeldt, K. R., Krist, J. E., Bryden, G. C., & Plavchan, P. 2012, in Am. Astron. Soc. Meet. Abstract, 220, 506.03 [Google Scholar]
- Stark, C. C., & Kuchner, M. J. 2008, ApJ, 686, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, C. C., & Kuchner, M. J. 2009, ApJ, 707, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P. 2012, A&A, 537, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., & Augereau, J.-C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., Kral, Q., & Ertel, S. 2012, A&A, 547, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trilling, D. E., Bryden, G., Beichman, C. A., et al. 2008, ApJ, 674, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, C. A., Littlefair, S. P., Diamond, C., et al. 2011, MNRAS, 413, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J. 1980, AJ, 85, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C. 1999, Ph.D. Thesis, Royal Observatory, Edinburgh, UK [Google Scholar]
- Wyatt, M. C. 2004, in The Search for Other Worlds, eds. S. S. Holt, & D. Deming, AIP Conf. Ser., 713, 93 [Google Scholar]
- Wyatt, M. C. 2005, A&A, 440, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C., & Dent, W. R. F. 2002, MNRAS, 334, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Dermott, S. F., Telesco, C. M., et al. 1999, ApJ, 527, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Dermott, S. F., & Telesco, C. M. 2000, in Disks, Planetesimals, and Planets, eds. G. Garzón, C. Eiroa, D. de Winter, & T. J. Mahoney, ASP Conf. Ser., 219, 289 [Google Scholar]
All Tables
Summary of numerical experiments with an inner and outer perturber, and for a brown dwarf and the stellar binary companion ζ1 Reticuli.
Disk position angle observed with Herschel/PACS, disk position angle in our synthetic images, and telescope orientation during Herschel/PACS observations and PSF.
All Figures
 |
Fig. 1 Co-evolution of a planetesimal eccentricity and orbital precession when acted upon by an eccentric perturber. Since the planetesimal orbit precesses, its periastron will eventually be aligned with that of the perturber on the same side of the massive central body, that is, the longitudes of periastra of the planetesimal and the perturber are equal (ϖ = 0). In this configuration, the planetesimal eccentricity is maximum. |
| In the text | |
 |
Fig. 2 Example colour map of the maximum induced eccentricity 2ef imposed by a planetary perturber on a particle with semi-major axis 100 AU and eccentricity e = 0 as a function of its periastron and eccentricity, as estimated from Eq. (2). The black line corresponds to a 2ef = 0.3 condition, which was set to mimic the condition for the disk of ζ2 Reticuli. Note that it does not depend on the mass of the planet. The white lines show the parameters for which the typical timescale to reach a steady state at 100 AU is tprec = 1 Gyr, using Eq. (4). This timescale depends on the mass: mp = 0.1 MJup (solid line), 1 MJup (dashed line) and 2 MJup (dotted line). For example, a perturber of mass 0.1 MJup, periastron qp = 150 AU and eccentricity ep = 0.4 is expected to produce a significantly eccentric ring in shorter than 1 Gyr, although spiral patterns may remain since it can take several precession timescales for them to vanish, as was shown by Wyatt (2005). |
| In the text | |
 |
Fig. 3 Herschel/PACS images of ζ2 Reticuli at 70, 100 and 160 microns from left to right. North is up and east is to the left. The insets in the bottom-left corners show the PSF. The north-west lobe is noted N-W, while the south-east lobe is noted S-E. |
| In the text | |
 |
Fig. 4 Detection limits set by direct imaging on the presence of brown dwarf/close binary between 1′′ and 2.5′′ in projected separation. |
| In the text | |
 |
Fig. 5 Semi-major axis versus eccentricity diagram of the disk at 1 Gyr for the Case C perturber. Overdensities of planetesimals at ~79 and ~95 AU correspond to planetesimals in 3:2 and 2:1 mean-motion resonance with the perturber. |
| In the text | |
 |
Fig. 6 Views from above the plane of disks at 1 Gyr in Case C, i.e., where resonant patterns appear. Planetesimals in 3:2 (left) and 2:1 (right) mean-motion resonance with the perturber are shown in red. |
| In the text | |
 |
Fig. 7 Example views from above the plane of disks at 1 Gyr, under the influence of inner perturbers. Top left: the perturber scatters material in the inner parts of the system (Case A). Right: one of the best candidates (Case B). Bottom left: resonant patterns appear (Case C). Right: a brown-dwarf perturber can be a good candidate. |
| In the text | |
 |
Fig. 8 Example views from above the disk plane at 1 Gyr, under the influence of outer perturbers. Top left: one of the best candidates (Case D). Right: spirals are still apparent (Case E). Bottom left: one might question the contribution of the scattered material to the disk emission (Case F). Right: scattering processes tend to destroy the structure (Case G). |
| In the text | |
 |
Fig. 9 Example of the time evolution on 1 Gyr of the disk offset coordinates (X (solid line) and Y (dashed line)) for outer perturbers. Top left: one of the best candidates (Case D). Because of the orientation of the perturber orbit, where its semi-major axis is along the X-axis with positive periastron, this corresponds to a negative X-offset ΔX ~ − 30 AU and a zero Y-offset for a disk located at ac ~ 100 AU. Top right: the oscillations of the offset coordinates reveal the spiral-winding regime (Case E). Bottom: the offset seems to relax; left: case F; right: case G. |
| In the text | |
 |
Fig. 10 Semi-major axis vs. eccentricity diagram (left) and pole-on projection (right) of a disk of planetesimals after 2 Gyr under the influence of a one-solar-mass star of semi-major axis 2046 AU on an orbit of eccentricity 0.815. The disk is truncated at ~80 AU and nearly circular. It has no clear offset: its centre of symmetry is offset by ~6 AU from the star along the perturber major axis. With a disk mean semi-major axis of ~70 AU, this gives a global eccentricity of ~0.08. |
| In the text | |
 |
Fig. 11 Synthetic images at λ = 100 μm, unconvolved disk (no star) (left) and convolved disk and star image with the PSF (right). Disk at 1 Gyr in Case A (see Table 2), seen with inclination 65°. The star is at the centre of the image, and in the convolved image, the flux scale is set to match that in the Herschel/PACS image. |
| In the text | |
 |
Fig. 12 Synthetic images of Case A (see Table 2) at 100 μm and convolved with the PSF. The parent ring is centred on 100 AU (left) and 130 AU (right), has a width of 5 AU and is seen with an inclination of 65°. The disk total flux is five times the flux measured by Herschel/PACS. The star is at the centre of the image and the flux scale is set to match that of Herschel/PACS image. |
| In the text | |
 |
Fig. C.1 Map of the detection limits in Jupiter masses set by the COND evolutionary models. The contours range from 60 to 150 MJup with a step of 10 MJup. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


