| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322408 | |
| Published online | 13 February 2014 | |
The dynamical behaviour of a jet in an on-disk coronal hole observed with AIA/SDO⋆
1
Indian Institute of Astrophysics,
Koramangala, 560034
Bangalore,
Karnataka,
India
2
Mathematics and Information Science, Pandon Building, Camden
Street, Northumbria University, Newcastle Upon Tyne
NE1 8ST,
UK
e-mail:
richard.morton@northumbria.ac.uk
3
Max-Plank-Institut für Sonnensystemforschung (MPS),
37191
Katlenburg-Lindau,
Germany
Received:
31
July
2013
Accepted:
28
October
2013
Aims. Extreme ultraviolet (EUV) jets situated in coronal holes are thought to play an important role in supplying heated material to the corona and solar wind. The multi-wavelength capabilities and high signal-to-noise ratio of detectors on board the Solar Dynamic Observatory (SDO) allow for detailed study of these jets’ evolution. We aim to exploit SDO’s capabilities to reveal information on the jet dynamics and to obtain estimates for plasma properties associated with the jets.
Methods. We studied the dynamics of an EUV jet with SDO at a coronal hole boundary. The details of the jet evolution are discussed and measurements of the jet’s parameters, e.g. length, width, life time, and outward speed, are obtained. Furthermore, automated emission measure analysis is exploited to determine estimates for the temperature and density of the jet. A propagating transverse wave supported by the jet spire is also observed. Measurements of the wave properties are exploited for magneto-seismology and are used in conjunction with the emission measure results to estimate the magnetic field strength of the jet.
Results. We present a detailed description of the jet’s evolution, with new evidence of plasma flows, prior to the jet’s initiation, along the loops at the base of the jet and also find further evidence that flows along the jet spire consist of multiple, quasi-periodic small-scale plasma ejection events. In addition, spectroscopic analysis reveal that the jet has temperatures of log 5.89 ± 0.08 K and electron densities of log 8.75 ± 0.05 cm-3. Measured properties of the transverse wave provide evidence that a strong damping of the wave occurs as it propagates along the jet spire with speeds of ~110 km s-1. The magneto-seismological inversion of the wave parameters provides values of B = 1.21 ± 0.2 G along the jet spire, which is in line with previous estimates for open fields in coronal holes.
Key words: Sun: corona / Sun: magnetic fields / Sun: oscillations / magnetohydrodynamics (MHD) / Sun: activity
Movies are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Over the last two decades it has become evident that large-scale ejections of collimated plasma from the lower solar atmosphere into the corona occurs on a regular basis (e.g. Shibata et al. 1992; Shimojo et al. 1996; Cirtain et al. 2007). These events, referred to as extreme ultraviolet (EUV), X-ray, or coronal plasma jets, are common in coronal holes and at the coronal hole boundaries (Savcheva et al. 2007). These jets are often considered a potential mechanism for supplying the corona with heated plasma and maintaining the solar wind (e.g. Subramanian et al. 2010; Moore et al. 2011).
Recent high-resolution and high-cadence multi-wavelength observations using Hinode, STEREO, and the Solar Dynamic Observatory (SDO), for example, have allowed the detailed study of coronal hole jets, providing information on their inherent dynamic behaviour (e.g. Kamio et al. 2007, 2010; Patsourakos et al. 2008; Nisticò et al. 2009; Filippov et al. 2009; Liu et al. 2009, 2011; Shen et al. 2011; Yang et al. 2011; Morton et al. 2012a; Chen et al. 2012) and estimates for the plasma parameters (Culhane et al. 2007; Doschek et al. 2010; He et al. 2010a; Madjarska 2011; Nisticò et al. 2011). In brief, the observations tend to show the jets as an inverted-Y shape, consisting of a collimated ejection that forms the spire and with a number of heated loop structures seen at the base. Measured plasma outflow velocities along the spire display a range of speeds, some showing impulsive (and occasionally quasi-periodic) phases with Alfvénic speeds (200−600 km s-1) and others with continuous outflow velocities of the order of the sound speed (30−100 km s-1). The jets also seem to demonstrate two distinct subclasses of behaviour allowing observations to be separated into standard or blow-out jet categories (e.g. Moore et al. 2010). The standard jets consist of hot EUV and soft X-ray components, while the blow-out jets also have the additional emission of a cool plasma component (sometimes referred to as the plasma curtain) that is visible in spectral lines that typically correspond to chromospheric and transition region emission.
In conjunction with the observations, advanced numerical modelling of jet formation has also been undertaken (e.g. Moreno-Insertis et al. 2008; Pariat et al. 2009; Moreno-Insertis & Galsgaard 2013). The formation mechanism of the coronal jets is typically assumed to be due to reconnection of emerging flux with pre-existing flux (Yokoyama & Shibata 1995). Magnetic energy release(s) due to the reconnection is diverted to the heating of the plasma, wave excitation, or kinetic energy (i.e. bulk plasma motions). The simulations of the emerging flux scenario seem to provide a good qualitative agreement with observations.
As mentioned, magnetohydrodynamic (MHD) waves are excited during magnetic reconnection and are an effective mechanism for the transport of energy. This feature is highlighted in observations (Kamio et al. 2010; Shen et al. 2011; Morton et al. 2012a; Chen et al. 2012) and simulations (Pariat et al. 2009), where non-linear torsional motions are seen to drive magnetic field and plasma away from the reconnection site. The presence of MHD waves in and around magnetic null- points can also lead to periodic reconnection (e.g. Murray et al. 2009; McLaughlin et al. 2009, 2012a,b; Heggland et al. 2009). Evidence of periodic reconnection has been noted by Morton et al. (2012a), who observe the periodic (~50 s) ejection of small-scale jets that appear to supply the main jet spire with heated plasma. The presence of wave phenomenon in these jet events provides a unique opportunity for magneto-seismology, i.e. the inversion of measured wave parameters to reveal information on the local magnetised plasma. The potential for these studies has been demonstrated in Morton et al. (2012c), where the plasma temperature, magnetic field gradients, and plasma density gradients were determined for a cool loop that had erupted from an arcade at the base of a jet.
Magneto-seismology has previously been used to infer magnetic field strengths and gradients in a number of other magnetic structures, such as coronal loops (e.g. Verwichte et al. 2013a; or for reviews see, e.g. Ruderman & Erdélyi 2009; Andries et al. 2009; Erdélyi & Goossens 2011), EUV jets (Morton et al. 2012c), and spicules (Verth et al. 2011). However, the real key to determining the plasma parameters will be a combination of spectroscopic techniques with magneto-seismology. In this paper, we study the properties of a coronal jet using data from multiple channels of the Atmospheric Imaging Assembly (AIA) on board SDO. The temperature and density of the jet are determined using differential emission measure (DEM) analysis and provide comparable results to previous measurements. Furthermore, the presence of transverse perturbations of the jet spire are observed and the wave amplitude, period and phase speed are measured. The diagnostic potential from the union of spectroscopic and magneto-seismological techniques is demonstrated and an estimate of the magnetic field along the jet spire is obtained.
2. Observations
The Solar Dynamic Observatory is the first mission of NASA’s Living With a Star Program. It was launched on 11 February 2010, and allows nearly continuous observations of the Sun. The AIA instrument on board SDO provides an unprecedented view of the solar corona at a high cadence in multiple EUV wavelengths nearly simultaneously. The high spatial and temporal resolutions of AIA are 0.6 arcsec per pixel and 12 s respectively (Lemen et al. 2011) and this allows the detailed study of transient solar events. AIA provides narrow-band imaging in seven EUV bandpasses which are centred on Fe xviii (94 Å), Fe vii, xxi (131 Å), Fe ix (171 Å), Fe xii, xxiv (193 Å), Fe xiv (211 Å), He ii (304 Å), and Fe xvi (335 Å) spectral lines.
For this study, we have used data taken with SDO during a period from 21:00 to 22:00 UT 31 May 2011. The data set is of a region containing the boundary of an on-disk coronal hole situated in the northern hemisphere. The level 1.0 data were processed to remove bad pixels, to remove spikes due to radiation effects, and to correct the image flat-field. Level 1.0 data were then converted to level 1.5 using the aia_prep.pro procedure in Solar Soft (SSW). This procedure also adjusts the different filter images to a common 0.6″ plate-scale. To correct for rotation and achieve subpixel alignment accuracy of the time-series, we applied cross-correlation techniques. Figure 1 shows images of the jet at its maximum activity in the different AIA channels. The boundary of the coronal hole can be identified in 193 Å, 211 Å, and 94 Å, where the closed corona is identified by the bright emission in the lower-left corner.
The SDO data is supplemented with data from SECCHI/ STEREO (Howard et al. 2008), using the 304 Å and 195 Å channels. The STEREO data were processed using the standard software. The jet is only visible in the 304 Å of both A and B space-crafts and its signature is conspicuously absent in 195 Å images. The STEREO images (Fig. 1) reveal that the jet makes an angle almost normal to the surface, hence, it is inclined to the projected view of SDO. The angle between the jet and the SDO projection is ~36°, which is in line with the jet’s latitude of 37° in SDO images.
 |
Fig. 1 Top panels: SDO/AIA images of the polar coronal hole jet. The wavelength corresponding to each channel is given in the panels. The rectangular box in each frame marks the location of the pixels used to generate the light curves in Fig. 4. Bottom panels: STEREO/SECCHI EUVI images of the same jet. The position of the jet is not obvious in the 195 Å bandpass but can be seen clearly above the limb in 304 Å. |
 |
Fig. 2 Evolution of the jet in 171 Å. The left-hand column of each block shows log intensity and the right-hand column the unsharp masked log intensities. Top left set of panels: enhanced emission at arcade foot points and observed outflow. Middle left: apparent reconfiguration of the magnetic field and increased emission along the base arcade. Bottom left: rise phase of a loop overlying the base arcade. Top right: formation of jet spire and the rising loop apparently connects with unseen open field. Middle right: initiation of outflowing plasma along the jet spire. Bottom right: elongated jet structure with overplotted cross-cuts used for anlaysis of the kink motion (Online movie). |
3. Dynamical evolution of the jet
In this section, we describe the jet evolution and highlight some of its more interesting aspects. The onset of dynamic behaviour begins with the appearance of a pair of bright points (Fig. 2 first panel) that mark the foot-points of a loop arcade (the arcade becomes conspicuous at a later time).
On viewing co-temporal magneto-grams taken with Helioseismic and Magnetic Imager (HMI), the region shows only weak magnetic flux elements present in this region. A popular mechanism for the initiation of coronal jets is the interaction between an emerging bipolar region of magnetic flux and an existing unipolar field in the coronal holes (Yokoyama & Shibata 1995). The emergence of a bipolar region or the injection of twisted flux into an existing bipolar region eventually leads to reconnection between the bipolar and unipolar fields. The weak nature of the signal in the magnetograms means we cannot use them to confirm this hypothesis.
The injection of new magnetic flux into the region can lead to the build-up of currents (e.g. Pariat et al. 2009), which could potentially be dissipated and heat the plasma in the lower atmosphere. We suggest that the observed brightenings are potential signatures of the injection of new flux into the region and the subsequent heating. The increase in pressure at the foot-points due to the heating would lead to a pressure gradient and drive flows of heated plasma away from the region. These outflows from the bright points are indeed visible (see online movie 1 of Fig. 2) and the flow is highlighted in Fig. 2 first panel. The flow of heated plasma highlights an existing loop structure and the the arrow demonstrates the flow direction.
At approximately 250 s later, there is an apparent initial reconfiguration of the magnetic field where a loop structure(s) begin to open up (Fig. 2 second panel), which could possibly be due to reconnection. This is coupled with increased emission and the loop arcade becomes increasingly more visible. Drawing from the findings of simulations (e.g. Moreno-Insertis & Galsgaard 2013), the increased visibility of the loop arcade is a potential signature that a current sheet has formed. This would occur if new flux has emerged and is impinging on the pre-existing field, and would also lead to reconnection between the two fields. The enhanced emission may come from plasma heating due to the dissipation of the current or be related to the presence of dense, warm material.
It is possible to observe outflowing plasma along the newly opened field lines. Co-temporal 304 Å images (online movies 2–4) show that a significant amount of cool material is ejected at this stage, making up a portion of the outflowing material. Again, with reference to simulations, the ejection of the cool dense material can be associated with flux emergence. The emerging flux would bring dense material with it as it rises into the atmosphere. Reconnection of the emerging flux with the ambient open field leads to dense material being ejected along the reconnected field lines.
In conjunction with the outflow, an extended low-lying loop, almost perpendicular to the arcade, becomes visible. The loop structure appears to have one foot-point rooted in the left-hand side of the arcade and the other in a region at least 10 Mm from the arcade. In time, the loop expands upwards into the atmosphere, but with no apparent horizontal expansion. The loop is deformed into a semi-elliptical shape during the expansion and the structure is highlighted by the dashed line in Fig. 2 panel three. It is unclear whether the loop begins to rise because of the upward pressure from the outflowing plasma; however, when the loop becomes noticeable it appears at the leading edge of the outflow (clearly seen in 304 Å) and continues to rise with the outflowing plasma. The measured rise speed of the loop in the plane is 25 ± 5 km s-1; however, this value is probably subject to effects of projection and is, in reality, larger than the measured value.
In Fig. 2 panel four, the loop is now clearly visible. Overlying open fields give the appearance of barbs in the direction perpendicular to the magnetic field of the loop. Careful study of the movie implies that these features are not related to the rising loop, they just become visible at a similar time. Observed movement of these features away from the arcade may point towards them being additional field lines that have reconnected. Just after this frame, the loop opens up in the middle and connects to a non-visible, presumably pre-existing field, forming a funnel shape (Fig. 2 panel five) which eventually becomes the main spire of the jet (Fig. 2 panel six). Soon after the funnel is formed, the ejection of plasma begins and there is visible evidence of torsional/helical motions during the first phase of ejection (see Fig. 6 and online movie 1).
 |
Fig. 3 Time-distance diagrams for the jet as seen in the 171 Å channel. The diamond symbols indicate the two points selected for producing the slope and the dashed line indicates the fit obtained. |
Plasma is seen to flow out along the spire for at least 10 min, with the intensity of the outflowing plasma decreasing over time. The outward speed of the plasma is estimated in the different channels by plotting time-distance maps (Fig. 3). The time-distance maps are produced by plotting intensity along the length of the jet versus time, with the slope of the line fitted to the bright region giving the speed of the jet. Fitting for the time-distance map is done as follows. First, we selected two points well separated along the left side of the bright emission in the time-distance map. From the time-distance map data we produced light curves at the various heights along the jet spire. Peaks in the light curves are assumed to correspond to the time at which outflowing plasma reaches each particular height. Figure 3 shows time-distance maps for the jet as seen in the 171 Å channel. The diamond symbols indicate the two points selected for producing the light curves and the dashed line indicates the fit obtained. The speeds measured from the slopes in different channels are as follows: AIA 131 Å (334 km s-1), AIA 171 Å (308 km s-1), AIA 193 Å (360 km s-1), AIA 211 Å (312 km s-1), and AIA 335 Å (312 km s-1). The errors in the estimated speeds are ± 36 km s-1 guided by the pixel size and cadence of observation. However, the jet is at an angle to the AIA projection, so the true speeds are given by dividing by cosθ, hence the corrected outflow speeds are 412 km s-1, 381 km s-1, 445 km s-1, 386 km s-1, and 386 km s-1.
Figure 4 shows the light curves of the different channels in AIA corresponding to a small region shown as a rectangular box in Fig. 1. The initial eruptive phase of the jet is seen to begin around 21:37 UT. Additional enhancements in emission occur at 21:45 UT, except in the 304 Å line, indicating that a second eruptive stage occurs with the emission of hot plasma only. The 131 Å and 335 Å display clear evidence of multiple peaks. This behaviour is not as evident in the other light curves, but it can be clearly seen in Fig. 3 that there are multiple outflows events.
A 3 × 5 pixel2 box is placed along the main axis of the jet in 171 Å, the data is averaged over the box to obtain a light curve. The running average of 12 frames is subtracted from the curve and the de-trended data (top panel in Fig. 5) is subject to wavelet analysis (bottom panel in Fig. 5). Details of the wavelet analysis are described in Torrence & Compo (1998). In the wavelet spectrum, the cross-hatched regions are locations where estimates of the oscillation period become unreliable. The global wavelet plots are obtained by taking the mean over the wavelet time domain which makes it very similar to the Fourier transform (oscillatory power distribution with respect to period). The periods with the strongest oscillatory power peaks in the global wavelet spectrum are labelled above the global wavelet spectrum. The wavelet power spectra demonstrate the quasi-periodic behaviour of the outflow events, which has a period of about ~150 s. The presence of quasi-periodic outflows has previously been noted in Morton et al. (2012a) for EUV jets and Morton (2012) for chromospheric jets.
 |
Fig. 4 Light curves corresponding to the rectangular box region shown in Fig. 1. The different colours correspond to the different channels as labelled in the figure, along with the peak formation temperatures of the dominant ions in parentheses. |
 |
Fig. 5 Wavelet result for the quasi-periodic behaviour of the jet outflow events as observed from the AIA 171 Å channel. The top panel shows the background trend removed (12-point running average) intensity variation with time. The bottom-left panel shows the wavelet power spectrum with 99% confidence-level contours, whereas the bottom-right panel shows the global wavelet power spectrum with 99% global confidence level. The periods P1 and P2 at the locations of the first two maxima in the global wavelet spectrum are also shown above the global wavelet spectrum. |
4. Transverse oscillations on jet
The jet shows signs of apparent wave motion in the fine-scale structure, which we now describe. The observed motion is a transverse displacement of the jet’s axis. The 171 Å data is further processed for wave studies. Firstly, the data is aligned using cross-correlation to achieve subpixel accuracy, with an apparent root mean squared frame-to-frame shift of 0.03 pixels remaining. The signal-to-noise ratio in the coronal hole is relatively low, so the data is smoothed with a 3 × 3 boxcar function to increase the signal-to- noise ratio. We then apply the unsharp mask technique to reveal the fine-structure of the jet. The data noise is calculated using the formulae given in Yuan & Nakariakov (2012); however, the boxcar smoothing reduces the data noise by a factor of a third.
From the filtered data, time-distance diagrams are created which reveal the transverse wave motion. Figure 6 shows the cross-cut taken close to the foot-point of the jet. There are two readily identifiable features in the given time-distance diagrams. Upon studying the data it is apparent that the longer duration event is a signature of the magnetic field untwisting as it rises into the solar atmosphere. The motion in the time-distance diagram looks distinctly like transverse wave motion, but is probably best described by a torsional motion. The shorter duration event is a transverse wave and has a large enough total displacement that it can be identified by eye in movies of the event. It should be pointed out that the second transverse waves occurs at a time (~21:42) when the intensity of the jet event has decreased significantly (see Fig. 4), hence the main violent and eruptive phase has finished, although the periodic out-flows are still occurring. The lower values of intensities would imply that the plasma along the jet spire is cooler and/or less dense when the wave phenomena occurs than during the first phase of plasma ejection.
 |
Fig. 6 Upper-left panel: time-distance diagram created using unsharp masked data. The time is in seconds from 21:34:00 UT. Two neighbouring threads of the jet are clearly visible. The observed motion in the lower thread is due to the field line untwisting, while the upper thread supports a transverse MHD wave. Upper-right panel: results from the fitting process. The data points are obtained from a Gaussian fit and the error bars show the total error. The solid line shows the sinusoidal fit to the data points. The data points have been de-trended by subtracting the G(t) term (see Eq. (2)). Lower-left panel: de-trended fits in all slits: slit 1 is solid black, slit 2 is dotted purple, slit 3 is dashed blue, slit 4 is dash-dotted green and slit 5 is triple-dot-dashed red. Bottom-right panel: decrease in amplitude as a function of slit. The amplitudes and sigma errors are plotted along with the exponential fits (lines) for the first minimum (black crosses and solid lines), first maximum (blue stars and dashed line), second minimum (green diamonds and dash-dotted line) and second maximum (red triangles and triple-dot-dashed line). |
Measured parameters of the transverse waves.
The identification of the wave mode is aided by the observation of the physical
displacement of the jet’s axis. Magnetohydrodynamic wave theory demonstrates that in a
cylindrical flux tube the fast magnetoacoustic kink mode is the only wave mode that perturbs
the flux tube in this manner. In the long wavelength limit, the kink mode has a phase speed
equal to the kink speed (Edwin & Roberts
1983) 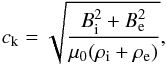 (1)where B is the magnetic field
strength, μ0 is the magnetic permeability of free
space, ρ is the
density; the subscripts i and e refer to the jet and ambient plasma quantities,
respectively.
(1)where B is the magnetic field
strength, μ0 is the magnetic permeability of free
space, ρ is the
density; the subscripts i and e refer to the jet and ambient plasma quantities,
respectively.
The transverse wave is measured by fitting a Gaussian function to the cross-sectional flux
profile of the jet axis in each time slice (see, e.g. Morton
et al. 2012b), providing the data noise as errors for the fitting. The Gaussian
centroid is taken as the central position of the jets axis, and to the associated errors
from the fit we add the estimated remaining displacement error. These data points are then
fitted with a damped sinusoidal function of the form 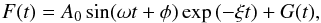 (2)where A0 is the
amplitude of the transverse displacement, ω = 2π/P
is the frequency, and P is the period; ξ = 1/τ where
τ is the
damping timescale and G(t) is a linear function. The
results of the wave fitting are shown in Fig. 6. The
velocity amplitude is calculated using v = 2πA0/P.
(2)where A0 is the
amplitude of the transverse displacement, ω = 2π/P
is the frequency, and P is the period; ξ = 1/τ where
τ is the
damping timescale and G(t) is a linear function. The
results of the wave fitting are shown in Fig. 6. The
velocity amplitude is calculated using v = 2πA0/P.
We fitted the wave in five cross-cuts which are separated by approximately one pixel. The results for the wave fitting in each cross-cut are given in Table 1. It is apparent that the wave propagates as there is a delay between observing the wave in each of the cross-cuts (see, Fig.6, lower left panel). The arrival times of the maximum and minimum displacements were used to calculate the phase speed averaged across the five cross-cuts, which gives vph = 88 ± 7 km s-1. Here, the ± 7 km s-1 corresponds to the standard deviation of the measured velocities. Correcting for the jet’s inclination the phase speed is vph = 110 ± 10 km s-1.
The wave is seen to be heavily damped as it propagates along the jet. The damping time-scale given from the fit parameters is not the damping time. Because the wave is propagating along the structure, the wave damping is a function distance, i.e. a damping length, LD.
The damping length is calculated from the decrease in amplitude of the wave in each slit and the fitting of an exponential profile gives LD = 1990 ± 170 km, 3740 ± 770 km, 3.6 × 105 ± 90 × 105 km and −4610 ± 1910 km for the first minimum, first maximum, second minimum, and second maximum, respectively. Correcting for the inclination of the jet with respect to the SDO projection gives LD = 2470 ± 210 km, 4620 ± 950 km, 4.4 × 105 ± 1 × 106 km, and −5700 ± 2360 km. The increase in damping length is clear and there is even the suggestion of a slight amplification of the wave.
For damped oscillators, the size of the quality factor (ξE) determines
whether the oscillation is under damped, critically damped or over damped (e.g. French 1971). The relation for the quality factor for
propagating waves is 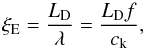 (3)where
λ is the
wavelength of the oscillation and f = 1/P is the
frequency. The values of ξE are then determined using the
observationally derived values of phase speed, frequency, and damping length, where it is
found that ξE = 0.10 ± 0.09 and 0.19 ± 0.04 for LD = 2470 ± 170 km and 4620 ± 770 km, respectively.
(3)where
λ is the
wavelength of the oscillation and f = 1/P is the
frequency. The values of ξE are then determined using the
observationally derived values of phase speed, frequency, and damping length, where it is
found that ξE = 0.10 ± 0.09 and 0.19 ± 0.04 for LD = 2470 ± 170 km and 4620 ± 770 km, respectively.
Critical damping occurs when ξE = 1/2π ≈ 0.16, hence the results suggest that the first wave front is classed to lie in the over damped regime (ξE < 1/2π). The consequence of this is that the first hundred seconds of the wave motion is evanescent in nature (French 1971). For the remaining wave fronts, ξE > 1/2π and the wave motion is under damped and oscillatory.
Observations of kink motions in coronal loops typically show a quality factor
>0.16
and appear to be under damped oscillators (e.g. Verwichte et
al. 2013b). Often, resonant absorption (Ruderman
& Roberts 2002; Goossens et al.
2002) is cited as the mechanism behind the observed damping, with the theoretical
predictions providing a good agreement with the observations (e.g. Verth et al. 2010). If we assume that the observed damping is due to
resonant absorption, then the quality factor is given by the TGV relationship derived by
Terradas et al. (2010), i.e. 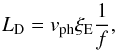 (4)which is identical to
Eq. (3). The magnitude of the quality factor
is dependent on the thickness of the inhomogeneous layer l between an over-dense flux
tube and its environment, and the gradient of the density contrast, i.e.
(4)which is identical to
Eq. (3). The magnitude of the quality factor
is dependent on the thickness of the inhomogeneous layer l between an over-dense flux
tube and its environment, and the gradient of the density contrast, i.e. 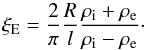 (5)Here, R is the radius of the flux
tube supporting the oscillation. Note that Eq. (5) is derived for weakly damped wave motion.
(5)Here, R is the radius of the flux
tube supporting the oscillation. Note that Eq. (5) is derived for weakly damped wave motion.
If resonant absorption is responsible for the observed damping, then the over damped motion suggests that the density contrast is large, such that ρe/ρi ≪ 1, or the inhomogeneous layer is thick. It is still unclear why the damping length changes for different cycles of the wave. It may be that as the jet develops, the internal density of the plasma along the jet spire tends towards the background coronal hole value. This would lead to a change in density ratio, i.e. ρi/ρe → 1, hence the damping length would increase. However, it may well be that other mechanisms are acting on the system, working together or individually, to bring about the enhanced damping, e.g. mode conversion/coupling, non-linearity (Ofman 2009; Ruderman et al. 2010).
We note that, the damping timescale τ represents the change in amplitude of the wave packet that propagates through the slit, hence it demonstrates that the driver of the wave decreases with amplitude in time. The increase in the damping timescale with distance along the jet axis is probably due to combination of decrease in driving amplitude with time, the wave being damped as a function of distance, and the change in the jet parameters over time.
5. DEM analysis
Now, the density and temperature of the jet plasma are estimated from the emission measure of the jet using the automated DEM tool described in Aschwanden et al. (2011). The DEM method assumes that the plasma is isothermal, in ionisation equilibrium, and has Maxwellian velocities. It is unclear whether all these conditions are satisfied by the jet plasma. We discuss the potential influence of these effects at the end of this section.
 |
Fig. 7 Example result from DEM analysis. Top panel shows the selected section of the jet plasma as seen in the 171 Å line used for the emission-measure and temperature analysis (axes are in solar radii units). The middle panel is the estimated electron temperature along the jet, with the horizontal axis corresponding to bin number along the jet. Bottom panel shows the variation of electron number density along the length of the jet. |
In Fig. 7 we show the results of the DEM analysis. The top panel shows a zoomed portion of the jet plasma with the axes in units of solar radii. The jet length is divided into 45 spatial bins for the calculation of the DEM. The bottom three panels show the electron temperature, number densities and width along the length of the jet. We estimated the electron density and temperature of the jet material for the time sequence starting from 21:39:12 UT to 21:40:36 UT, for nine consecutive frames in order to assess how rapidly plasma parameters evolve in the jet. Averaged values of the electron number density and temperature corresponding to each time sequence selected is given in Table 2. In general, the DEM shows relatively consistent values of ne and T. Electron number density and temperature of the plasma outside the jet cannot be calculated since the method is not suitable for DEM measurements for uniform density background plasma. For calculations in the following section we take a value of log (ne) = 8.1, as a reference value for the number density corresponding to the ambient coronal hole (Banerjee et al. 1998; Cranmer 2009). In Banerjee et al. (1998), the electron density was estimated from the intensity line ratios of forbidden spectral lines of Si viii and using the CHIANTI database. The spectra were obtained with the Solar Ultraviolet Measurements of Emitted Radiation spectrometer (SUMER) flown on the Solar and Heliospheric Observatory spacecraft. The relative measuring error in deriving ne is estimated to be 12% to 15%, similar to the expected absolute error (see Laming et al. 1997). Doyle et al. (1998) measured electron densities at the equatorial limb, again using the Si viii line ratio. Comparing their Table 1 with Banerjee et al. (1998), the densities in the coronal holes are lower than the quiet Sun, by approximately a factor of two, as also noted by Doschek et al. (1977).
Estimates of the average electron number density along the length of the jet.
The temperatures given in Table 2 suggest that the jet is relatively cool when compared to jets emitting in X-ray wavelengths (T ~2 MK). However, we believe the measured value is supported by the STEREO data. In particular, the jet is seen clearly in 304 Å, but is not distinguishable in 195 Å from the emission along the line of sight. This can be explained as follows. The jet is clearly visible in SDO 193 Å which has a temperature coverage similar to STEREO 195 Å (e.g. Howard et al. 2008). However, SDO is able to view the jet in the coronal hole with little surrounding hot (T > 1 MK) plasma. In contrast, there are closed coronal structures along the line of sight between the jet and STEREO A/B viewpoints which strongly contribute to the observed emission in 193/195 Å passbands. Hence, the relatively cooler temperature (in comparison to the closed corona) and approximate coronal densities of the jet means the jet’s emission is not strong enough to stand out amongst the general coronal emission (as viewed by STEREO).
It is worth discussing the potential fragilities associated with the DEM results. Rapid injections of heat can drive the plasma into a state of non-equilibrium ionisation (e.g. Bradshaw & Mason 2003; Bradshaw et al. 2004), leading to ions of relatively low charge existing at higher temperatures than usual. The temperature estimate obtained from the DEM, T ≈ 105.89 K, suggests that the plasma temperature is close to the peak formation temperature of Fe ix (i.e. T ~ 105.8 K), a dominant contributor to the observed emission in 171 Å. If the jet plasma has been heated rapidly from a cooler temperature, it will lead to delay in ionisation rates and have influence on emission in 171 Å. Hence, in this scenario, the DEM technique would underestimate the plasma temperature. Furthermore, the electron density, which is calculated from the derived value of EM, would also be underestimated, along with the plasma density (if using the typical coronal assumption that the plasma is fully ionised, i.e. ne ≈ ni).
The timescales for ionisation equilibrium are dependent on the heating rate and it is calculated that equilibrium is reached in a matter of seconds to minutes (e.g. Bradshaw & Mason 2003; Bradshaw et al. 2004). De Moortel & Bradshaw (2008) also demonstrate the quasi-periodic heating events (e.g. periodic reconnection) could lead to the plasma to a state of constant non-equilibrium. For this to occur, the timescales for heating would have to be of a relatively high-frequency. If the multiple, periodic ejections observed in the jet do correspond to heating events, the large periodicity (~150 s) means the jet plasma has time to reach ionisation equilibrium.
Impulsive heating events may also accelerate particles to non-thermal (i.e. non-Maxwellian) velocities, which can influence ionisation rates (e.g. Dzifčáková 2006; Dzifčáková et al. 2011). It is still unclear whether these situations occur in jet events, but they should be kept in mind when interpreting the DEM results.
6. Magneto-seismology
Next, the results from the wave fitting and the DEM analysis area combined to estimate the
magnetic field strength along the jet spire. The average magnetic field in the jet material
is estimated from the definition of the kink speed and is given by
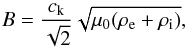 (6)where B is the average magnetic
field given by
(6)where B is the average magnetic
field given by 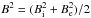 . First, the plasma density from
the electron number density is estimated. Taking a typical value for the electron density
from Table 2, i.e. log 8.8 ± 0.1
cm-3, the plasma
density for a fully ionized plasma can be estimated using
. First, the plasma density from
the electron number density is estimated. Taking a typical value for the electron density
from Table 2, i.e. log 8.8 ± 0.1
cm-3, the plasma
density for a fully ionized plasma can be estimated using
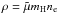 , where
mH = 1.67 × 10-27 kg is the
mass of hydrogen and
, where
mH = 1.67 × 10-27 kg is the
mass of hydrogen and 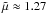 is the mean molecular weight
per atom. Hence, the internal and external plasma densities are ρi = 1.69 ± 0.43 × 10-12
kg m-3 and
ρe = 2.5 ± 0.4 × 10-13
kg m-3. Using the
measured value of kink speed (ck = 110 ± 10 km s-1), the magnetic field of the jet
spire is estimated to be B = 1.21 ± 0.2 G (corrected for inclination). To
calculate the error in the magnetic field strength we used the following formula
is the mean molecular weight
per atom. Hence, the internal and external plasma densities are ρi = 1.69 ± 0.43 × 10-12
kg m-3 and
ρe = 2.5 ± 0.4 × 10-13
kg m-3. Using the
measured value of kink speed (ck = 110 ± 10 km s-1), the magnetic field of the jet
spire is estimated to be B = 1.21 ± 0.2 G (corrected for inclination). To
calculate the error in the magnetic field strength we used the following formula
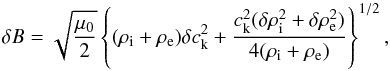 (7)and it is assumed that the
error in the external density value is equal to the error in the internal density value. The
δx
corresponds to the associated error in the parameter x.
(7)and it is assumed that the
error in the external density value is equal to the error in the internal density value. The
δx
corresponds to the associated error in the parameter x.
In order to compare these derived values of field strength to previous measurements and expectations of coronal hole magnetic fields, it is necessary to discuss the typical magnetic geometry of coronal holes. From the correlation of Doppler velocities in a number of different spectral lines (Tu et al. 2005a; Tian et al. 2008) that are assumed to be formed at various heights in the atmosphere, the results appears to show that coronal holes are composed of rapidly expanding magnetic funnels. To date, the majority of measurements of magnetic field strength in coronal holes have been of the underlying, photospheric field and then extrapolations have provided coronal values (Tu et al. 2005b,a; Wang 2010; He et al. 2010b). Magnetic field strengths at the photosphere of coronal holes are measured to be | B| < 200 G (e.g. Wang 2010) with average values of unsigned flux ⟨ |B| ⟩ ~ 1−40 G (see, e.g. Wiegelmann & Solanki 2004, and references therein).
Using HMI data from a 50′′ × 40′′ region centred on the jet, the
largest value of field strength reaches ~−250 G (line-of-sight value ~200 G) with an average unsigned value of
~11 G (line-of-sight value
~9 G). To compare this to our
estimated coronal value, we follow He et al. (2008)
and assume the variation of magnetic field strength with height for the magnetic funnels is
exponential, i.e. 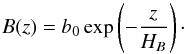 (8)Here, b0 is the
photospheric field value and HB is the magnetic
scale height, which we take to be 3.57 Mm (Tu et al. 2005a). Using
the average value of unsigned magnetic flux a value of B(z) ~ 1.2 G
at a height of z ≈ 7.9 Mm is obtained. Hence, this value is consistent
with the height of the base of the corona at which the transverse wave is measured.
(8)Here, b0 is the
photospheric field value and HB is the magnetic
scale height, which we take to be 3.57 Mm (Tu et al. 2005a). Using
the average value of unsigned magnetic flux a value of B(z) ~ 1.2 G
at a height of z ≈ 7.9 Mm is obtained. Hence, this value is consistent
with the height of the base of the corona at which the transverse wave is measured.
Recently, Chen et al. (2012) also estimated the magnetic field strength of a solar jet in polar coronal hole, obtaining a field strength of 15 G at 11 Mm that decreased to around 3 G at 28 Mm. However, the authors use a mean photospheric value of magnetic flux density from active region observations (i.e. ~500 G). If they had used typical measured coronal hole values for the average field strength, ~10 G, the value of field strength at 11 Mm would be 0.3 G, which is consistent with the estimate of weak magnetic field strength obtained here.
In different (possibly open-field) regions of the solar atmosphere, West et al. (2011) performed a seismological study using an EIT waves and estimated coronal magnetic field strength to be relatively weak (0.7 ± 0.7 G) in the quiet Sun.
7. Conclusion
We present here the observation and analysis of a jet in a solar coronal hole, close to the hole’s boundary. The observed features during the evolution of the jet are discussed in light of numerical simulations of jet formation from (e.g. Moreno-Insertis & Galsgaard 2013). We interpret enhanced emission in multiple AIA bandpasses as evidence of the jet being initiated by the emergence of new flux into the region and the formation of current sheets and sites of heating during the initial stage of the jet’s formation. However, the HMI data does not appear to contain evidence of emerging flux. We can only suggest that the emerging flux is relatively weak.
Following the initial phase, the jet spire is formed and is associated with fast outflowing plasma (>360 km s-1). After an initial ejection, there is a delay before multiple smaller, quasi-periodic (~150 s) outflows occur along the spire. This may be related to oscillatory reconnection events or to multiple eruptive phases due to various instabilities of the system (see, e.g. Moreno-Insertis & Galsgaard 2013).
During the later stages of the jet’s evolution, we are able to identify a transverse oscillatory motion of the jet’s spire. Using an advanced fitting technique we are able to measure the properties of the transverse displacement with a high degree of accuracy. The wave is found to propagate along the spire with speeds of 110 km s-1. In addition, the latest differential emission measure techniques are exploited to estimate the temperature and electron density along the jet spire, obtaining values of log T ~ 5.8 K and log ne ~ 8.8 cm-3. These values are in agreement with previous measured values using a variety of techniques (e.g. Doschek et al. 2010; Nisticò et al. 2011). It is then demonstrated that, using the measured values of the observed transverse wave and the density estimates from the DEM, we are able to obtain an estimate for the magnetic field strength (B = 1.21 ± 0.2 G ) of the section of the jet structure that supports the wave.
In conclusion, we demonstrate the potential of combining magneto-seismology with spectroscopic techniques for obtaining insights into local plasma parameters. This work provides support for previous measurements of density and temperature using spectrometers. However, by combining the two techniques we are able to reveal additional information on the magnetic field in the coronal hole. Future studies that obtain detailed information on the plasma parameters of particular jet events will provide valuable constraints for future modelling efforts.
Online material
Movie of Fig. 2 Access here
Movie of Fig. A.1 Access here
Movie of Fig. A.2 Access here
Movie of FIg. A.3 Access here
Acknowledgments
The authors thank M. Aschwanden and G. Verth for enlightening discussions and the anonymous referee for comments that improved the manuscript. The authors would also like to thank the Royal Society for support that made this work possible. This work is supported by the UK Science and Technology Facilities Council (STFC), with RM grateful to the Northumbria University for the award of the Anniversary Fellowship.
References
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Boerner, P., Schrijver, C. J., & Malanushenko, A. 2011, Sol. Phys., 384 [Google Scholar]
- Banerjee, D., Teriaca, L., Doyle, J. G., & Wilhelm, K. 1998, A&A, 339, 208 [NASA ADS] [Google Scholar]
- Bradshaw, S. J., & Mason, H. E. 2003, A&A, 407, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., Del Zanna, G., & Mason, H. E. 2004, A&A, 425, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, H.-D., Zhang, J., & Ma, S.-L. 2012, RA&A, 12, 573 [Google Scholar]
- Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cranmer, S. R. 2009, Liv. Rev. Sol. Phys., 6, 3 [Google Scholar]
- Culhane, L., Harra, L. K., Baker, D., et al. 2007, PASJ, 59, 751 [Google Scholar]
- De Moortel, I., & Bradshaw, S. J. 2008, Sol. Phys., 252, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Doschek, G. A., Cohen, L., & Feldman, U. 1977, ApJS, 33, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Doschek, G. A., Landi, E., Warren, H. P., & Harra, L. K. 2010, ApJ, 710, 1806 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doyle, J. G., Banerjee, D., & Perez, M. E. 1998, Sol. Phys., 181, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E. 2006, Sol. Phys., 234, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E., Homola, M., & Dudík, J. 2011, A&A, 531, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Erdélyi, R., & Goossens, M. 2011, Space Sci. Rev., 158, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Filippov, B., Golub, L., & Koutchmy, S. 2009, Sol. Phys., 254, 259 [NASA ADS] [CrossRef] [Google Scholar]
- French, A. P. 1971, Vibrations and waves (Van Nostrand Reinhold co. Ltd, UK) [Google Scholar]
- Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- He, J.-S., Tu, C.-Y., & Marsch, E. 2008, Sol. Phys., 250, 147 [NASA ADS] [CrossRef] [Google Scholar]
- He, J.-S., Marsch, E., Curdt, W., et al. 2010a, A&A, 519, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- He, J.-S., Tu, C.-Y., Tian, H., & Marsch, E. 2010b, Adv. Space Res., 45, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Heggland, L., De Pontieu, B., & Hansteen, V. H. 2009, ApJ, 702, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kamio, S., Hara, H., Watanabe, T., et al. 2007, PASJ, 59, 757 [Google Scholar]
- Kamio, S., Curdt, W., Teriaca, L., Inhester, B., & Solanki, S. K. 2010, A&A, 510, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laming, J. M., Feldman, U., Schuehle, U., et al. 1997, ApJ, 485, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2011, Sol. Phys., 172 [Google Scholar]
- Liu, W., Berger, T. E., Title, A. M., & Tarbell, T. D. 2009, ApJ, 707, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., Title, A. M., Tarbell, T. D., & Low, B. C. 2011, ApJ, 728, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Madjarska, M. S. 2011, A&A, 526, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., De Moortel, I., Hood, A. W., & Brady, C. S. 2009, A&A, 493, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Thurgood, J. O., & MacTaggart, D. 2012a, A&A, 548, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Verth, G., Fedun, V., & Erdélyi, R. 2012b, ApJ, 749, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, R. L., Cirtain, J. W., Sterling, A. C., & Falconer, D. A. 2010, ApJ, 720, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, R. L., Sterling, A. C., Cirtain, J. W., & Falconer, D. A. 2011, ApJ, 731, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., & Galsgaard, K. 2013, ApJ, 771, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., Galsgaard, K., & Ugarte-Urra, I. 2008, ApJ, 673, L211 [Google Scholar]
- Morton, R. J. 2012, A&A, 543, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Srivastava, A. K., & Erdélyi, R. 2012a, A&A, 542, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Verth, G., Jess, D. B., et al. 2012b, Nat. Comm., 3, 1315 [Google Scholar]
- Morton, R. J., Verth, G., McLaughlin, J. A., & Erdélyi, R. 2012c, ApJ, 744, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, M. J., van Driel-Gesztelyi, L., & Baker, D. 2009, A&A, 494, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Bothmer, V., Patsourakos, S., & Zimbardo, G. 2009, Sol. Phys., 259, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Nisticò, G., Patsourakos, S., Bothmer, V., & Zimbardo, G. 2011, Adv. Space Res., 48, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L. 2009, Space Sci. Rev., 149, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., Pariat, E., Vourlidas, A., Antiochos, S. K., & Wuelser, J. P. 2008, ApJ, 680, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space Sci. Rev., 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Goossens, M., & Andries, J. 2010, Phys. Plasmas, 17, 8 [Google Scholar]
- Savcheva, A., Cirtain, J., Deluca, E. E., et al. 2007, PASJ, 59, 771 [NASA ADS] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., & Ibrahim, A. 2011, ApJ, 735, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Ishido, Y., Acton, L. W., Strong, K. T., & Hirayama, T. E. 1992, PASJ, 44, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Shimojo, M., Hashimoto, S., Shibata, K., et al. 1996, PASJ, 48, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., Madjarska, M. S., & Doyle, J. G. 2010, A&A, 516, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Goossens, M., & Verth, G. 2010, A&A, 524, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, H., Marsch, E., Tu, C.-Y., Xia, L.-D., & He, J.-S. 2008, A&A, 482, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc, 79, 61 [Google Scholar]
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005a, in Solar Wind 11/SOHO 16, Connecting Sun and Heliosphere, eds. B. Fleck, T. H. Zurbuchen, & H. Lacoste, ESA SP, 592, 131 [Google Scholar]
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005b, Science, 308, 519 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verth, G., Terradas, J., & Goossens, M. 2010, ApJ, 718, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., Goossens, M., & He, J.-S. 2011, ApJ, 733, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Van Doorsselaere, T., Foullon, C., & White, R. S. 2013a, ApJ, 767, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Van Doorsselaere, T., White, R. S., & Antolin, P. 2013b, A&A, 552, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y.-M. 2010, ApJ, 715, L121 [Google Scholar]
- West, M. J., Zhukov, A. N., Dolla, L., & Rodriguez, L. 2011, ApJ, 730, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Solanki, S. K. 2004, Sol. Phys., 225, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, S., Zhang, J., Li, T., & Liu, Y. 2011, ApJ, 732, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Yokoyama, T., & Shibata, K. 1995, Nature, 375, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., & Nakariakov, V. M. 2012, A&A, 543, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Online movies
Movie 1: shows the evolution of the jet in 171 Å depicted in Fig. 2. The left-hand panel shows the log of intensity and the right panel displays the unsharp masked version of the same image.
 |
Fig. A.1 A still from Movie 2. Evolution of the jet in both 304 Å (left panel) and 171 Å (right panel). The time is given in seconds from 21:20 UT (Online movie). |
 |
Fig. A.2 A still from Movie 3. Similar to Movie 2 but showing the unsharp masked images of both channels (Online movie). |
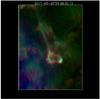 |
Fig. A.3 A still from Movie 4. Composite movie of the jet showing 304 Å in red, 171 Å in green, and 193 Å in blue (Online movie). |
All Tables
All Figures
 |
Fig. 1 Top panels: SDO/AIA images of the polar coronal hole jet. The wavelength corresponding to each channel is given in the panels. The rectangular box in each frame marks the location of the pixels used to generate the light curves in Fig. 4. Bottom panels: STEREO/SECCHI EUVI images of the same jet. The position of the jet is not obvious in the 195 Å bandpass but can be seen clearly above the limb in 304 Å. |
| In the text | |
 |
Fig. 2 Evolution of the jet in 171 Å. The left-hand column of each block shows log intensity and the right-hand column the unsharp masked log intensities. Top left set of panels: enhanced emission at arcade foot points and observed outflow. Middle left: apparent reconfiguration of the magnetic field and increased emission along the base arcade. Bottom left: rise phase of a loop overlying the base arcade. Top right: formation of jet spire and the rising loop apparently connects with unseen open field. Middle right: initiation of outflowing plasma along the jet spire. Bottom right: elongated jet structure with overplotted cross-cuts used for anlaysis of the kink motion (Online movie). |
| In the text | |
 |
Fig. 3 Time-distance diagrams for the jet as seen in the 171 Å channel. The diamond symbols indicate the two points selected for producing the slope and the dashed line indicates the fit obtained. |
| In the text | |
 |
Fig. 4 Light curves corresponding to the rectangular box region shown in Fig. 1. The different colours correspond to the different channels as labelled in the figure, along with the peak formation temperatures of the dominant ions in parentheses. |
| In the text | |
 |
Fig. 5 Wavelet result for the quasi-periodic behaviour of the jet outflow events as observed from the AIA 171 Å channel. The top panel shows the background trend removed (12-point running average) intensity variation with time. The bottom-left panel shows the wavelet power spectrum with 99% confidence-level contours, whereas the bottom-right panel shows the global wavelet power spectrum with 99% global confidence level. The periods P1 and P2 at the locations of the first two maxima in the global wavelet spectrum are also shown above the global wavelet spectrum. |
| In the text | |
 |
Fig. 6 Upper-left panel: time-distance diagram created using unsharp masked data. The time is in seconds from 21:34:00 UT. Two neighbouring threads of the jet are clearly visible. The observed motion in the lower thread is due to the field line untwisting, while the upper thread supports a transverse MHD wave. Upper-right panel: results from the fitting process. The data points are obtained from a Gaussian fit and the error bars show the total error. The solid line shows the sinusoidal fit to the data points. The data points have been de-trended by subtracting the G(t) term (see Eq. (2)). Lower-left panel: de-trended fits in all slits: slit 1 is solid black, slit 2 is dotted purple, slit 3 is dashed blue, slit 4 is dash-dotted green and slit 5 is triple-dot-dashed red. Bottom-right panel: decrease in amplitude as a function of slit. The amplitudes and sigma errors are plotted along with the exponential fits (lines) for the first minimum (black crosses and solid lines), first maximum (blue stars and dashed line), second minimum (green diamonds and dash-dotted line) and second maximum (red triangles and triple-dot-dashed line). |
| In the text | |
 |
Fig. 7 Example result from DEM analysis. Top panel shows the selected section of the jet plasma as seen in the 171 Å line used for the emission-measure and temperature analysis (axes are in solar radii units). The middle panel is the estimated electron temperature along the jet, with the horizontal axis corresponding to bin number along the jet. Bottom panel shows the variation of electron number density along the length of the jet. |
| In the text | |
 |
Fig. A.1 A still from Movie 2. Evolution of the jet in both 304 Å (left panel) and 171 Å (right panel). The time is given in seconds from 21:20 UT (Online movie). |
| In the text | |
 |
Fig. A.2 A still from Movie 3. Similar to Movie 2 but showing the unsharp masked images of both channels (Online movie). |
| In the text | |
 |
Fig. A.3 A still from Movie 4. Composite movie of the jet showing 304 Å in red, 171 Å in green, and 193 Å in blue (Online movie). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


