| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201322140 | |
| Published online | 18 February 2014 | |
Vacuum-UV spectroscopy of interstellar ice analogs
I. Absorption cross-sections of polar-ice molecules⋆
1
Centro de Astrobiología, INTA-CSIC, Carretera de Ajalvir,
km 4, Torrejón de Ardoz,
28850
Madrid, Spain
e-mail: cruzdga@cab.inta-csic.es;
munozcg@cab.inta-csic.es
2
Space Sciences Center and Department of Physics and Astronomy,
University of Southern California, Los Angeles, CA
90089-1341,
USA
3
Department of Physics, National Central University,
Jhongli City, 32054
Taoyuan Country,
Taiwan
Received:
25
June
2013
Accepted:
15
December
2013
Context. The vacuum-UV (VUV) absorption cross sections of most molecular solids present in interstellar ice mantles with the exception of H2O, NH3, and CO2 have not been reported yet. Models of ice photoprocessing depend on the VUV absorption cross section of the ice to estimate the penetration depth and radiation dose, and in the past, gas phase cross section values were used as an approximation.
Aims. We aim to estimate the VUV absorption cross section of molecular ice components.
Methods. Pure ices composed of CO, H2O, CH3OH, NH3, or H2S were deposited at 8 K. The column density of the ice samples was measured in situ by infrared spectroscopy in transmittance. VUV spectra of the ice samples were collected in the 120–160 nm (10.33–7.74 eV) range using a commercial microwave-discharged hydrogen flow lamp.
Results. We provide VUV absorption cross sections of the reported molecular ices. Our results agree with those previously reported for H2O and NH3 ices. Vacuum-UV absorption cross section of CH3OH, CO, and H2S in solid phase are reported for the first time. H2S presents the highest absorption in the 120–160 nm range.
Conclusions. Our method allows fast and readily available VUV spectroscopy of ices without the need to use a synchrotron beamline. We found that the ice absorption cross sections can be very different from the gas-phase values, and therefore, our data will significantly improve models that simulate the VUV photoprocessing and photodesorption of ice mantles. Photodesorption rates of pure ices, expressed in molecules per absorbed photon, can be derived from our data.
Key words: astrochemistry / ultraviolet: ISM / ISM: molecules / instrumentation: spectrographs / methods: laboratory / techniques: photometric
Data can be found at http://ghosst.osug.fr/
© ESO, 2014
1. Introduction
Ice mantles in dense cloud interiors and cold circumstellar environments are composed mainly of H2O and other species such as CO2, CO, CH4, CH3OH, and NH3 (Mumma & Charnley 2011, and references therein). Some species with no permanent or induced dipole moment, such as O2 and N2, cannot be easily observed in the infrared, but are also expected to be present in the solid phase (e.g., Ehrenfreund & van Dishoeck 1998). The relative to water abundances of the polar species CO, CH3OH, and NH3 are between 0–100%, 1–30%, and 2–15%. In comets the abundances are 0.4–30%, 0.2–7%, 0.2–7%, and ~0.12–1.4% for CO, CH3OH, NH3, and H2S (Mumma & Charnley 2011, and references therein). We therefore included H2S in this study because this reduced species was detected in comets and is expected to form in ice mantles (Jiménez-Escobar & Muñoz Caro 2011). In the coldest regions where ice mantles form, thermally induced reactions are inhibited. Therefore, irradiation processes by UV-photons or cosmic rays may play an important role in the formation of new species in the ice and contribute to the desorption of ice species to the gas phase. Cosmic rays penetrate deeper into the cloud interior than UV-photons, generating secondary UV-photons by excitation of H2 molecules. This secondary UV-field will interact more intensively with the grain mantles than direct impact by cosmic rays (Cecchi-Pestellini & Aiello 1992; Chen et al. 2004). VUV photons have the power to excite or dissociate molecules, leading to a complex chemistry in the grains. The VUV-region encloses wavelengths from 200 nm to about 100 nm, since the term extreme-ultraviolet (EUV) is often used for shorter wavelengths.
The estimation of the VUV-absorption cross sections of molecular ice components allows one to calculate the photon absorption of icy grains in that range. In addition, the VUV-absorption spectrum as a function of photon wavelength is required to study the photodesorption processes over the full photon emission energy range. Photoabsorption cross-section measurements in the VUV-region were performed for many gas phase molecules. Results for small molecules in the gas phase were summarized by Okabe (1978), but most of these cross-section measurements for molecular bands with fine structure are severely distorted by the instrumental bandwidths (Hudson & Carter 1968). The integrated cross sections are less affected by the instrumental widths, and approach the true cross sections as optical depth approaches zero. Therefore, the true integrated cross section can be obtained from series of data taken with different column densities (Samson & Ederer 2000).
The lack of cross-section measurements in solids has led to the assumption that the cross sections of molecules in ice mantles were similar to the gas phase values. In recent years the VUV-absorption spectra of solid H2O, CH3OH, NH3, CO2, O2, N2, and CH4 were reported by Mason et al. (2006), Kuo et al. (2007), and Lu et al. (2008). But the VUV-absorption cross sections were only estimated for solid H2O, NH3, and CO2 (Mason et al. 2006). Furthermore, all previous works have been performed using synchrotron monochromatic light as the VUV-source, scanning the measured spectral range.
 |
Fig. 1 Scheme of the main chamber of ISAC. The VUV-light intersects three MgF2 windows before it enters the UV-spectrometer, but the emission spectrum that the ice experiences corresponds to only one MgF2 window absorption, the one between the VUV-lamp and the ISAC main chamber. FTIR denotes the source and the detector used to perform infrared spectroscopy. QMS is the quadrupole mass spectrometer used to detect gas-phase species. PMT is the photomultiplier tube that makes the ultraviolet spectroscopy possible. |
In the present work, we aim to provide accurate measurements of the VUV-absorption cross sections of interstellar ice polar components including H2O, CH3OH, NH3, CO, and H2S. The use of a hydrogen VUV-lamp, commonly used in ice irradiation experiments, limits the spectroscopy to the emission range between 120 and 160 nm, but this has several advantages: the measurements are easy to perform and can be made regularly in the laboratory, without the need to use synchrotron beam time. A second paper will be dedicated to the nonpolar molecular ice components including CO2, CH4, N2, and O2. In Sect. 2 the experimental protocol is described. Section 3 provides the determination of VUV-absorption cross sections for the different ice samples. The astrophysical implications are presented in Sect. 4. The conclusions are summarized in Sect. 5.
2. Experimental protocol
The experiments were performed using the interstellar astrochemistry chamber (ISAC), see Fig. 1. This set-up and the standard experimental protocol were described in Muñoz Caro et al. (2010). ISAC mainly consists of an ultra-high-vacuum (UHV) chamber, with pressure typically in the range P = 3−4.0 × 10-11 mbar, where an ice layer made by deposition of a gas species onto a cold finger at 8 K, achieved by means of a closed-cycle helium cryostat, can be UV-irradiated. The evolution of the solid sample was monitored with in situ transmittance FTIR spectroscopy and VUV-spectroscopy. The chemical components used for the experiments described in this paper were H2O(liquid), triply distilled; CH3OH(liquid), Panreac Química S. A. 99.9%; CO(gas), Praxair 99.998%; NH3(gas), Praxair 99.999%; and H2S(gas), Praxair 99.8%. The deposited ice layer was photoprocessed with an F-type microwave-discharged hydrogen flow lamp (MDHL), from Opthos Instruments. The source has a VUV-flux of ≈2 × 1014 cm-2 s-1 at the sample position, measured by CO2→ CO actinometry, see Muñoz Caro et al. (2010). The Evenson cavity of the lamp is refrigerated with air. The VUV-spectrum is measured routinely in situ during the irradiation experiments with the use of a McPherson 0.2 m focal length VUV monochromator (model 234/302) with a photomultiplier tube (PMT) detector equipped with a sodium salicylate window, optimized to operate from 100–500 nm (11.27–2.47 eV), with a resolution of 0.4 nm. The characterization of the MDHL spectrum has been studied before by Chen et al. (2010) and will be discussed in more detail by Chen et al. (2013).
The interface between the MDHL and the vacuum chamber is a MgF2 window. The monochromator is located at the rear end of the chamber, separated by another MgF2 window. This means that the measured background spectra, that is without an ice sample intersecting the VUV-light cone, are the result of the radiation that intersects two MgF2 windows.
Grating corrections were made for the VUV-spectra in the range of 110–180 nm (11.27–6.88 eV). The mean photon energy was calculated for the spectrum corresponding to only one MgF2 window intersecting the VUV-lamp emission, since that is the mean photon energy that the ice sample experiences. This one-window spectrum, displayed in Fig. 2, was measured by directly coupling the VUV-lamp to the spectrometer with a MgF2 window acting as the interface. The proportion of Ly-α in 110–180 nm range is 5.8%, lower than the 8.4% value estimated by Chen et al. (2013). This difference could be due to the lower transmittance of the MgF2 window used as interface between the MDHL and the UHV-chamber, although the different position of the pressure gauge measuring the H2 flow in the MDHL may also play a role.
 |
Fig. 2 UV-photon flux as a function of wavelength of the MDHL in the 110 to 170 nm range estimated with the total photon flux calculated using actinometry. The spectrum corresponds to a measurement with one MgF2 window intersecting the emitted VUV-light cone. This spectrum is the one experienced by the ice sample. The VUV-emission is dominated by the Ly-α peak (121.6 nm) and the Lyman band system. |
It was observed that most of the energy emitted by the VUV-lamp lies below 183 nm (6.77 eV) and the MgF2 window cutoff occurs at 114 nm (10.87 eV). The mean photon energy in the 114–180 nm (10.87–6.88 eV) range is Ephoton = 8.6 eV. The main emission bands are Ly-α at 121.6 nm (10.20 eV) and the molecular hydrogen bands centered on 157.8 nm (7.85 eV) and 160.8 nm (7.71 eV) for a hydrogen pressure of 0.4 mbar, see Fig. 2.
3. VUV-absorption cross section of interstellar polar ice analogs
We recorded VUV-absorption spectra of pure ices composed of CO, H2O, CH3OH, NH3, and H2S. For each ice spectrum a series
of three measurements was performed: i) the emission spectrum of the VUV-lamp was measured
to monitor the intensity of the main emission bands; ii) the emission spectrum transmitted
by the MgF2 substrate
window was measured to monitor its transmittance; and iii) the emission spectrum transmitted
by the substrate window with the deposited ice on top was measured. The absorption spectrum
of the ice corresponds to the spectrum of the substrate with the ice after subtracting the
bare MgF2 substrate
spectrum. In addition, the column density of the ice sample was measured by FTIR in
transmittance. The VUV-spectrum and the column density of the ice were therefore monitored
in a single experiment for the same ice sample. This improvement allowed us to estimate the
VUV-absorption cross section of the ice more accurately. The column density of the deposited
ice obtained by FTIR was calculated according to the formula 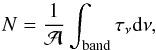 (1)where N is the column density of
the ice, τν the optical depth of
the band, dν
the wavenumber differential, in cm-1, and
(1)where N is the column density of
the ice, τν the optical depth of
the band, dν
the wavenumber differential, in cm-1, and 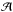 is the band strength in cm molecule-1. The integrated absorbance is equal to 0.43
×τ, where τ is the integrated optical
depth of the band. The VUV-absorption cross section was estimated according to the
Beer-Lambert law,
is the band strength in cm molecule-1. The integrated absorbance is equal to 0.43
×τ, where τ is the integrated optical
depth of the band. The VUV-absorption cross section was estimated according to the
Beer-Lambert law, 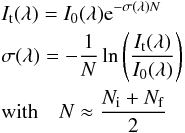 (2)where It(λ) is
the transmitted intensity for a given wavelength λ, I0(λ) the incident
intensity, N is
an average ice column density before (Ni) and after (Nf) irradiation in
cm-2, and
σ is the
cross section in cm2.
It is important to notice that the total VUV-flux value emitted by the lamp does not affect
the VUV-absorption spectrum of the ice sample, since it is obtained by substracting two
spectra to obtain the absorbance in the VUV.
(2)where It(λ) is
the transmitted intensity for a given wavelength λ, I0(λ) the incident
intensity, N is
an average ice column density before (Ni) and after (Nf) irradiation in
cm-2, and
σ is the
cross section in cm2.
It is important to notice that the total VUV-flux value emitted by the lamp does not affect
the VUV-absorption spectrum of the ice sample, since it is obtained by substracting two
spectra to obtain the absorbance in the VUV.
A priori, the VUV-absorption cross section of the ice was not known. Therefore, several measurements for different values of the ice column density were performed to improve the spectroscopy. Table 1 provides the infrared-band position and the band strength used to obtain the column density of each ice component, along with the molecular dipole moment, since the latter has an effect on the intermolecular forces that operate in the ice that distinguish solid spectroscopy from gas phase spectroscopy in the IR and VUV ranges. The gas-phase cross sections published in the literature were also represented for comparison. We note that the majority of the gas-phase cross sections were performed at room temperature. The gas-phase spectrum can vary significantly when the gas sample is cooled to cryogenic temperatures, but it will still differ from the solid-phase spectrum, see Yoshino et al. (1996) and Cheng et al. (2011).
Infrared-band positions and strengths (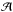 ),
deposited column density (N in 1015 molec/cm2) and molecular dipole
moment (μ) of the samples used in this work.
),
deposited column density (N in 1015 molec/cm2) and molecular dipole
moment (μ) of the samples used in this work.
The performance of VUV-spectroscopy inevitably leads to exposure of the sample to irradiation, often causing photodestruction or photodesorption of the ice molecules to some extent during spectral acquisition (e.g., d’Hendecourt et al. 1985, 1986; Bernstein et al. 1995; Gerakines et al. 1995, 1996; Schutte 1996; Sandford 1996; Muñoz Caro et al. 2003, 2010; Dartois 2009; Öberg et al. 2009a,b; Fillion et al. 2012; Fayolle et al. 2011, 2013, and references therein). Photoproduction of new compounds and the decrease of the starting ice column density was monitored by IR spectroscopy. Photodesorption was less intense for the reported species except for CO, in line with the previous works mentioned above; it will also contribute to the decrease of the column density of the ice during irradiation. Photoproduct formation of new compounds is different for each molecule. No photoproducts were detected after the 9 min VUV exposure required for VUV-spectroscopy, except for CH3OH ice, where product formation was 2%, 6%, 7%, and 8% for CO2, CH4, CO, and H2CO relative to the initial CH3OH column density estimated by IR spectroscopy. But the VUV-absorption spectrum of CH3OH was not significantly affected, cf Kuo et al. (2007). Indeed, we show below that the discrete bands of the CO photoproduced in the CH3OH ice matrix, with an intrinsic absorption higher than methanol in the VUV, are absent from the VUV-absorption spectrum.
Error values for the column density in Table 1
result mainly from the selection of the baseline for integration of the IR absorption band
and the decrease of the ice column density due to VUV-irradiation during spectral
acquisition. The band strengths were adapted from the literature, and their error estimates
are no more than 10% of the reported values (Richey & Gerakines 2012). The solid H2O band strength in Table 1 was estimated by us using interference fringes in the infrared spectrum for a
density of 0.94 g cm-3 and a refractive index of 1.3. This estimation gives a
value of 1.7 ± 0.2 × 10-16 cm molec-1, different from the Hagen et al.
(1985) value (2 × 10-16 cm molec-1). The errors in the column density determined by IR
spectroscopy were 16%, 15%, 23%, 19 %, and 32% for solid CO, H2O, CH3OH, NH3, and H2S ices. The MDHL, photomultiplier
tube (PMT), and multimeter stabilities lead to an estimated error of about 6% in the values
of the VUV-absorption cross sections of the ices. The largest error corresponds to
H2S ice, the most
VUV photoactive molecule studied in this work. It presents a high photodestruction
(Jiménez-Escobar & Muñoz Caro 2011), which leads
to a fast decrease in its IR feature. Therefore, VUV-absorption cross-section errors result
from the error values estimated above, using the expression
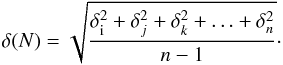 (3)The VUV-absorption cross-section spectra of CO,
H2O,
CH3OH, and
NH3 ices were
fitted with Gaussian profiles using the band positions reported in the literature (Lu et al.
2005, 2008;
Kuo et al. 2007) as a starting point, see the red
traces in Figs. 3–6. Table 2 summarizes the Gaussian profile
parameters used to fit the spectra of these ices, deposited at 8 K. H2S ice displays only a slightly
decreasing absorption at longer wavelengths, and Gaussian deconvolution is thus not
pertinent. Gaussian fits of the reported molecules were made with an in-house IDL code. The
fits reproduce the VUV-absorption cross-section spectra well.
(3)The VUV-absorption cross-section spectra of CO,
H2O,
CH3OH, and
NH3 ices were
fitted with Gaussian profiles using the band positions reported in the literature (Lu et al.
2005, 2008;
Kuo et al. 2007) as a starting point, see the red
traces in Figs. 3–6. Table 2 summarizes the Gaussian profile
parameters used to fit the spectra of these ices, deposited at 8 K. H2S ice displays only a slightly
decreasing absorption at longer wavelengths, and Gaussian deconvolution is thus not
pertinent. Gaussian fits of the reported molecules were made with an in-house IDL code. The
fits reproduce the VUV-absorption cross-section spectra well.
Parameter values used to fit the spectra of Gaussian profiles of the different molecular pure ices deposited at 8 K.
3.1. Solid carbon monoxide
The ground state of CO is X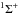 and its bond energy is Eb(C−O) = 11.09
eV (Okabe 1978).
and its bond energy is Eb(C−O) = 11.09
eV (Okabe 1978).
Figure 3 displays the CO fourth positive band
system; it is attributed to the A 1Π ← X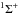 system. Table 3 summarizes the transition, band position, and area of each feature at
8 K. We were able to observe twelve bands identified as (0, 0) to (11, 0) where the (0,
0), (1, 0), and (2, 0) bands present a Davydov splitting, in agreement with Mason et al.
(2006), Lu et al. (2005), and Brith & Schnepp (1965). Like Mason et al. (2006), we were
unable to observe the (12, 0) transition reported by Brith & Schnepp (1965) and Lu et al. (2005), because of the low intensity of this feature. We detected part of the
transitions to the excited Rydberg states, B
system. Table 3 summarizes the transition, band position, and area of each feature at
8 K. We were able to observe twelve bands identified as (0, 0) to (11, 0) where the (0,
0), (1, 0), and (2, 0) bands present a Davydov splitting, in agreement with Mason et al.
(2006), Lu et al. (2005), and Brith & Schnepp (1965). Like Mason et al. (2006), we were
unable to observe the (12, 0) transition reported by Brith & Schnepp (1965) and Lu et al. (2005), because of the low intensity of this feature. We detected part of the
transitions to the excited Rydberg states, B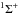 , C
, C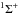 , and E1Π measured by Lu et al. (2005) as a broad band in the 116–121 nm (10.68–10.25
eV) region, despite the decreasing VUV-flux in this region.
, and E1Π measured by Lu et al. (2005) as a broad band in the 116–121 nm (10.68–10.25
eV) region, despite the decreasing VUV-flux in this region.
 |
Fig. 3 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure CO ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of CO gas (divided by a factor of 40 to compare it with CO ice) adapted from Lee & Guest (1981). The fit, red trace, is the sum of 15 Gaussians, dashed trace. It has been vertically offset for clarity. |
 |
Fig. 4 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure H2O ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase H2O taken from Mota et al. (2005). The gray area is the measurement error zone. The fit, red trace, is the sum of three Gaussians, dashed trace. It has been vertically offset for clarity. |
 |
Fig. 5 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure CH3OH ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase CH3OH adapted from Nee et al. (1985). The fit, red trace, is the sum of two Gaussians, dashed trace. It has been vertically offset for clarity. |
 |
Fig. 6 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure NH3 ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase NH3 adapted from Cheng et al. (2006) and Wu et al. (2007). The fit, red trace, is the sum of two Gaussians, dashed trace. It has been vertically offset for clarity. |
The average VUV-absorption cross section has a value of
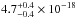 cm2. This value is not very
different from the one roughly estimated by Muñoz Caro et al. (2010), 3.8 × 10-18 cm2 in the 115–170 nm range based on Lu et al. (2005). The total integrated VUV-absorption cross
section has a value of
cm2. This value is not very
different from the one roughly estimated by Muñoz Caro et al. (2010), 3.8 × 10-18 cm2 in the 115–170 nm range based on Lu et al. (2005). The total integrated VUV-absorption cross
section has a value of 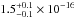 cm2 nm
(
cm2 nm
(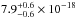 cm2 eV) in the 116–163 nm
(10.68–7.60 eV) spectral region. The VUV-absorption of CO ice at 121.6 nm is very low, an
upper limit of ≤
cm2 eV) in the 116–163 nm
(10.68–7.60 eV) spectral region. The VUV-absorption of CO ice at 121.6 nm is very low, an
upper limit of ≤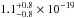 cm2 was estimated, while at 157.8
and 160.8 nm the VUV-absorption cross sections are
cm2 was estimated, while at 157.8
and 160.8 nm the VUV-absorption cross sections are 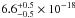 cm2 and
cm2 and
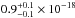 cm2. The VUV-absorption spectrum of
solid CO presents a maximum at 153.0 nm (8.10 eV) with a value of
cm2. The VUV-absorption spectrum of
solid CO presents a maximum at 153.0 nm (8.10 eV) with a value of
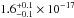 cm2. Table 4 summarizes the transition, band position, and area of each feature
present in the CO gas-phase spectrum (blue trace in Fig. 3) adapted from Lee & Guest (1981).
The VUV-absorption cross section of CO in the gas phase has an average value of
20.7 × 10-18 cm2. Based on Lee & Guest
(1981), the estimated total integrated
VUV-absorption cross section, 2.3 × 10-16 cm2 nm, is larger than the CO ice value, 1.5 ± 0.1 × 10-16
cm2 nm. Similar
to solid CO, the VUV-absorption cross section of CO gas is very low at 121.6 nm. There are
no data available at 157.8 and 160.8 nm, but the absorption is expected to be very low or
zero because the first transition (ν0) is centered on 154.5 nm.
cm2. Table 4 summarizes the transition, band position, and area of each feature
present in the CO gas-phase spectrum (blue trace in Fig. 3) adapted from Lee & Guest (1981).
The VUV-absorption cross section of CO in the gas phase has an average value of
20.7 × 10-18 cm2. Based on Lee & Guest
(1981), the estimated total integrated
VUV-absorption cross section, 2.3 × 10-16 cm2 nm, is larger than the CO ice value, 1.5 ± 0.1 × 10-16
cm2 nm. Similar
to solid CO, the VUV-absorption cross section of CO gas is very low at 121.6 nm. There are
no data available at 157.8 and 160.8 nm, but the absorption is expected to be very low or
zero because the first transition (ν0) is centered on 154.5 nm.
Transitions observed in the VUV-absorption cross-section spectrum of pure CO ice, deposited at 8 K, in the 115–170 nm range.
3.2. Solid water
The ground state and bond energy of H2O are 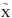 1A1 and Eb(H–OH) = 5.1 eV (Okabe 1978).
1A1 and Eb(H–OH) = 5.1 eV (Okabe 1978).
The VUV-absorption cross-section spectrum of H2O ice is displayed in Fig. 4. The spectral profile is similar to those reported by Lu et al. (2008) and Mason et al. (2006). The band between 132–163 nm is centered on 142 nm (8.73 eV), in agreement
with Lu et al. (2008) and Mason et al. (2006). This band is attributed to the 4a1:Ã1B1 ← 1b1: 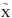 1A
1
transition. The VUV-absorption cross section reaches a value of
1A
1
transition. The VUV-absorption cross section reaches a value of
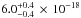 cm-2 at this peak, which coincides
with the spectrum displayed in Fig. 3 of Mason et al. (2006). The H2O ice spectrum of Lu et al. (2008) presents a local minimum at 132 nm, also visible in Fig. 4. This minimum is not observed in the Mason et al.
(2006) data, which is most likely due to the
larger scale of their plot. The portion of the band in the 120–132 nm range is attributed
to the transition
cm-2 at this peak, which coincides
with the spectrum displayed in Fig. 3 of Mason et al. (2006). The H2O ice spectrum of Lu et al. (2008) presents a local minimum at 132 nm, also visible in Fig. 4. This minimum is not observed in the Mason et al.
(2006) data, which is most likely due to the
larger scale of their plot. The portion of the band in the 120–132 nm range is attributed
to the transition 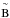 1A1←
1A1←
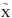 1A1, according to Lu et al. (2008).
1A1, according to Lu et al. (2008).
The average and the total integrated VUV-absorption cross sections of H2O ice are
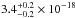 cm2 and
cm2 and
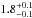 × 10-16 cm2 nm (
× 10-16 cm2 nm (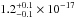 cm2 eV) in the 120–165 nm
(10.33–7.51 eV) spectral region. The VUV-absorption cross sections of H2O ice at 121.6, 157.8, and 160.8
nm are
cm2 eV) in the 120–165 nm
(10.33–7.51 eV) spectral region. The VUV-absorption cross sections of H2O ice at 121.6, 157.8, and 160.8
nm are 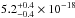 cm2,
cm2,
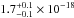 cm2, and
cm2, and
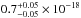 cm2. Gas-phase data from Mota et
al. (2005) were adapted for comparison with our
solid-phase data, see Fig. 4. Gas and ice data were
previously compared by Mason et al. (2006). The
VUV-absorption cross section of H2O in the gas phase has an average value of 3.1 × 10-18 cm2. H2O gas data were integrated in
the 120–182 nm range, giving a value for the VUV-absorption cross section of
2.3 × 10-16
cm2 nm
(1.4 × 10-17
cm2 eV), which is
higher than the VUV-absorption cross section of solid H2O. The VUV-absorption cross
sections of H2O gas
at 121.6, 157.8, and 160.8 nm are 13.6 × 10-18 cm2, 3.2 × 10-18 cm2, and 4.1 × 10-18 cm2, which is also higher than the solid-phase
measurements.
cm2. Gas-phase data from Mota et
al. (2005) were adapted for comparison with our
solid-phase data, see Fig. 4. Gas and ice data were
previously compared by Mason et al. (2006). The
VUV-absorption cross section of H2O in the gas phase has an average value of 3.1 × 10-18 cm2. H2O gas data were integrated in
the 120–182 nm range, giving a value for the VUV-absorption cross section of
2.3 × 10-16
cm2 nm
(1.4 × 10-17
cm2 eV), which is
higher than the VUV-absorption cross section of solid H2O. The VUV-absorption cross
sections of H2O gas
at 121.6, 157.8, and 160.8 nm are 13.6 × 10-18 cm2, 3.2 × 10-18 cm2, and 4.1 × 10-18 cm2, which is also higher than the solid-phase
measurements.
3.3. Solid methanol
The ground state and bond energy of CH3OH are X1A′ and Eb(H–CH2OH) = 4.0 eV (Darwent 1970).
Figure 5 shows the VUV-absorption cross section of CH3OH as a function of wavelength and photon energy. The spectrum profile is similar to the one reported by Kuo et al. (2007), a decreasing continuum for longer wavelengths without distinct local maximum. These authors found three possible broad bands centered on 147 nm (8.43 eV), 118 nm (10.50 eV), and 106 nm (11.68 eV), the latter is beyond our spectral range. We observed the 147 nm peak (associated to the 21A′′ ← X1A′ molecular transition) as well as part of the 118 nm band (corresponding to the 31A′′ ← X1A′ molecular transition), but due to the decreasing VUV-flux below 120 nm it was not possible to confirm the exact position of this peak.
The average and the total integrated VUV-absorption cross sections of solid
CH3OH are
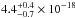 cm2 and
cm2 and
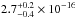 cm2 nm
(
cm2 nm
(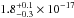 cm2 eV) in the 120–173 nm
(10.33–7.16 eV) spectral region. The VUV-absorption cross sections of CH3OH ice at 121.6 nm, 157.8 and
160.8 nm are
cm2 eV) in the 120–173 nm
(10.33–7.16 eV) spectral region. The VUV-absorption cross sections of CH3OH ice at 121.6 nm, 157.8 and
160.8 nm are 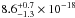 cm2,
cm2,
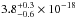 cm2, and
cm2, and
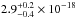 cm2. Gas phase data from Nee et al.
(1985) were used for comparison with our
solid-phase spectrum, see Fig. 5. Pure gas and solid
CH3OH, and
CH3OH in Ar or Kr
matrices were compared by Kuo et al. (2007).
CH3OH gas has a
vibrational peak profile throughtout the 120–173 nm range, which is absent from in
CH3OH ice. The
VUV-absorption cross section of CH3OH in the gas phase has an average value of
8.9 × 10-18
cm2.
CH3OH gas data
were integrated in the 120–173 nm range, giving a value for the VUV-absorption cross
section of 3.7 × 10-16 cm2 nm (2.5 × 10-17 cm2 eV), which is higher than the VUV-absorption cross
section (
cm2. Gas phase data from Nee et al.
(1985) were used for comparison with our
solid-phase spectrum, see Fig. 5. Pure gas and solid
CH3OH, and
CH3OH in Ar or Kr
matrices were compared by Kuo et al. (2007).
CH3OH gas has a
vibrational peak profile throughtout the 120–173 nm range, which is absent from in
CH3OH ice. The
VUV-absorption cross section of CH3OH in the gas phase has an average value of
8.9 × 10-18
cm2.
CH3OH gas data
were integrated in the 120–173 nm range, giving a value for the VUV-absorption cross
section of 3.7 × 10-16 cm2 nm (2.5 × 10-17 cm2 eV), which is higher than the VUV-absorption cross
section (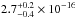 cm2 nm) for solid CH3OH. The VUV-absorption cross
sections of CH3OH
gas at 121.6 nm, 157.8, and 160.8 nm are 13.2 × 10-18 cm2, 9.9 × 10-18 cm2, and 8.6 × 10-18 cm2, which are also higher than the ice-phase measurements.
cm2 nm) for solid CH3OH. The VUV-absorption cross
sections of CH3OH
gas at 121.6 nm, 157.8, and 160.8 nm are 13.2 × 10-18 cm2, 9.9 × 10-18 cm2, and 8.6 × 10-18 cm2, which are also higher than the ice-phase measurements.
3.4. Solid ammonia
The ground state of NH3 is 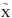 1A1 and its bond energy is Eb(H–NH2) = 4.4 eV (Okabe 1978).
1A1 and its bond energy is Eb(H–NH2) = 4.4 eV (Okabe 1978).
Figure 6 displays the VUV-absorption cross section
of NH3 as a
function of the photon wavelength and photon energy. It presents a continuum with two
broad absorption bands between 120–151 nm (10.33–8.21 eV) and 151–163 nm (8.21–7.60 eV) in
this wavelength region, without narrow bands associated to vibrational structure. Mason et
al. (2006) found a broad band centered on 177 nm
(7.00 eV) in the 146–225 nm (5.50–8.50 eV) spectral range. Lu et al. (2008) observed the same feature centered on 179 nm
(6.94 eV). We observed only a portion of this feature because of the low VUV-flux of the
MDHL in the 163–180 nm (7.60–6.88 eV) spectral range. This band is associated to the Ã1A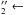
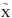 1
A1
molecular transition. The minimum we observed at 151 nm (8.21 eV) is the same as in the
above-cited works. At this minimum, the VUV-absorption cross section reaches a value of
3.3 ± 0.2 × 10-18 cm2, higher than the
1.9 × 10-18
cm2 value
reported in Fig. 10 of Mason et al. (2006). We also
obtained a higher value at 128.4 nm (9.65 eV), 8.1 ±0.5 × 10-18 cm2 compared with 3.8 × 10-18 cm2 by Mason et al. (2006). This difference is most likely due to the
different method employed to estimate the ice column density, infrared spectroscopy or
laser interferometry. In addition, a broad band centered on 121.2 nm (10.23 eV) was
observed, in agreement with Lu et al. (2008),
probably associated to the
1
A1
molecular transition. The minimum we observed at 151 nm (8.21 eV) is the same as in the
above-cited works. At this minimum, the VUV-absorption cross section reaches a value of
3.3 ± 0.2 × 10-18 cm2, higher than the
1.9 × 10-18
cm2 value
reported in Fig. 10 of Mason et al. (2006). We also
obtained a higher value at 128.4 nm (9.65 eV), 8.1 ±0.5 × 10-18 cm2 compared with 3.8 × 10-18 cm2 by Mason et al. (2006). This difference is most likely due to the
different method employed to estimate the ice column density, infrared spectroscopy or
laser interferometry. In addition, a broad band centered on 121.2 nm (10.23 eV) was
observed, in agreement with Lu et al. (2008),
probably associated to the 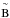 ←
←
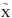 molecular transition.
molecular transition.
The average and the total integrated VUV-absorption cross sections of solid
NH3 are
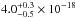 cm2 and
cm2 and
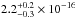 cm2 nm
(
cm2 nm
(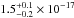 cm2 eV) in the 120–161 nm
(10.33–7.70 eV) spectral region. The VUV-absorption cross sections of NH3 ice at 121.6 nm, 157.8 and
160.8 nm are
cm2 eV) in the 120–161 nm
(10.33–7.70 eV) spectral region. The VUV-absorption cross sections of NH3 ice at 121.6 nm, 157.8 and
160.8 nm are 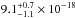 cm2,
cm2,
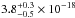 cm2, and
cm2, and
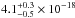 cm2. Gas-phase data from Cheng et
al. (2006) and Wu et al. (2007) were adapted, see Fig. 5. At
least qualitatively, our result is compatible with Mason et al. (2006). The VUV-absorption cross section of NH3 in the gas phase has an average
value of 6.1 × 10-18 cm2. NH3 gas data were integrated in the 120–161 nm range,
giving a value of 2.5 × 10-16 cm2 nm (1.8 × 10-17 cm2 eV), slightly higher than the VUV-absorption cross
section of solid NH3 (
cm2. Gas-phase data from Cheng et
al. (2006) and Wu et al. (2007) were adapted, see Fig. 5. At
least qualitatively, our result is compatible with Mason et al. (2006). The VUV-absorption cross section of NH3 in the gas phase has an average
value of 6.1 × 10-18 cm2. NH3 gas data were integrated in the 120–161 nm range,
giving a value of 2.5 × 10-16 cm2 nm (1.8 × 10-17 cm2 eV), slightly higher than the VUV-absorption cross
section of solid NH3 (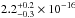 cm2 nm). The VUV-absorption cross
sections of NH3 gas
at 121.6, 157.8 and 160.8 nm are 9.8 × 10-18 cm2, 0.1 × 10-18 cm2, and 0.3 × 10-18 cm2; these values are lower than the ice-phase
measurements, except for the Ly-α photon wavelength (121.6 nm).
cm2 nm). The VUV-absorption cross
sections of NH3 gas
at 121.6, 157.8 and 160.8 nm are 9.8 × 10-18 cm2, 0.1 × 10-18 cm2, and 0.3 × 10-18 cm2; these values are lower than the ice-phase
measurements, except for the Ly-α photon wavelength (121.6 nm).
3.5. Solid hydrogen sulfide
The ground state and bond energy of H2S are 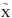 1A1 and Eb(H–SH) = 3.91 eV (Okabe 1978).
1A1 and Eb(H–SH) = 3.91 eV (Okabe 1978).
Figure 7 shows the VUV-absorption cross section of H2S as a function of the wavelength and photon energy. Owing to the high VUV-absorption of solid H2S, very thin ice samples were deposited to obtain a proper VUV-spectrum. H2S gas has a nearly constant VUV-absorption cross section in the 120–150 nm (10.33–8.26 eV) range, between 150–180 nm (8.26–6.88 eV) it decreases, and in the 180–250 nm (6.88–4.95 eV) region it presents a maximum at 187 nm (6.63 eV), see Okabe (1978). The VUV-absorption cross section of H2S is almost constant in the 120–143 nm (10.33–8.67 eV) range and decreases in the 143–173 nm (8.67–7.16 eV) range, with a maximum at 200 nm (6.19 eV) according to Feng et al. (1999). The 1B1←1A1 molecular transition was identified at 139.1 nm (8.91 eV) by Price & Simpson (1938) and confirmed by Gallo & Innes (1975).
 |
Fig. 7 VUV-absorption cross section as a function of wavelength (bottom X-axis) and photon energy (top X-axis) of pure H2S ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase H2S adapted from Feng et al. (1999). |
The total integrated VUV-absorption cross section of H2S ice has a value of
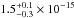 cm2 nm
(
cm2 nm
(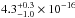 cm2 eV) in the 120–160 nm
(10.33–7.74 eV) spectral region. The VUV-absorption cross sections of the same ice at
121.6, 157.8, and 160.8 nm are
cm2 eV) in the 120–160 nm
(10.33–7.74 eV) spectral region. The VUV-absorption cross sections of the same ice at
121.6, 157.8, and 160.8 nm are 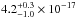 cm2,
cm2,
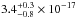 cm2, and
cm2, and
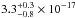 cm2. Gas-phase data from Feng et
al. (1999) were adapted, see Fig. 7. The spectrum of the solid is almost constant, only a
slight decrease is observed as the wavelength increases. The gas-phase spectrum presents
an abrupt decrease in the cross section starting near 140 nm, according to Feng et al.
(1999). In contrast to the Okabe (1978) data, this spectrum of the gas shows no
vibrational structure, probably because of its low resolution. The average VUV-absorption
cross section of H2S gas reported by Feng et al. (1999), 3.1 × 10-17 cm2, disagrees by one order of magnitude with the
3−4 × 10-18
cm2 value of
Okabe (1978). We estimated a value of
cm2. Gas-phase data from Feng et
al. (1999) were adapted, see Fig. 7. The spectrum of the solid is almost constant, only a
slight decrease is observed as the wavelength increases. The gas-phase spectrum presents
an abrupt decrease in the cross section starting near 140 nm, according to Feng et al.
(1999). In contrast to the Okabe (1978) data, this spectrum of the gas shows no
vibrational structure, probably because of its low resolution. The average VUV-absorption
cross section of H2S gas reported by Feng et al. (1999), 3.1 × 10-17 cm2, disagrees by one order of magnitude with the
3−4 × 10-18
cm2 value of
Okabe (1978). We estimated a value of
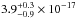 cm2 for the solid in the same
range, which is close to the Feng et al. (1999)
gas-phase value.
cm2 for the solid in the same
range, which is close to the Feng et al. (1999)
gas-phase value.
H2S gas data were integrated in the 120–160 nm range, giving a value of 10.2 × 10-16 cm2 nm (8.0 × 10-17 cm2 eV), which is lower than the VUV-absorption cross section of solid H2S. The VUV-absorption cross sections of H2S gas at 121.6, 157.8, and 160.8 nm are 31.0 × 10-18 cm2, 7.9 × 10-18 cm2, and 4.9 × 10-18 cm2, which are also lower than the solid-phase values reported above.
3.6. Comparison between all the ice species
Figure 8 shows a comparison of the VUV-absorption cross section for all the ice species deposited at 8 K, represented in the same linear scale. The most absorbing molecule is H2S. H2O has the lowest average absorption in this range. All the represented species absorb VUV-light significantly in the 120–163 nm (10.33–7.60 eV) range, only the CO absorption is negligible at the Ly-α wavelength. Except for CO, the absorption of the reported ice species in the H2 molecular emission region between 157–161 nm is lower than the Ly-α absorption. Table 5 summarizes the comparison between the VUV-absorption cross sections of all the species in the gas and solid phase.
Comparison between the VUV-absorption cross sections in the 120–160 nm range of all the pure species in the gas and solid (deposited at 8 K) phase.
 |
Fig. 8 VUV-absorption cross section as a function of wavelength (bottom x-axis) and photon energy (top x-axis) of all the pure ice species studied in this work, deposited at 8 K. |
4. Astrophysical implications
Far-ultraviolet observations of IC 63, an emission/reflection nebula illuminated by the B0.5 IV star γCas, with the Hopkins Ultraviolet Telescope (HUT) on the central nebular position, have revealed a VUV-emission spectrum very similar to the spectrum of our VUV-lamp, see Fig. 4 of France et al. (2005), which means that the VUV-spectrum that interacts with the ice sample mimicks the molecular hydrogen photoexcitation observed toward this photodissociation region (PDR) in the local interstellar medium. This spectrum is similar to that emitted by the MDHL with a H2 pressure of 0.2 mbar.
Ice mantle build-up takes place in cold environments such as dark cloud interiors, where the radiation acting on dust grains is the secondary UV field produced by cosmic ray ionization of H2. These are the conditions mimicked in our experiments: low density and low temperature, and UV photons impinging on ice mantles. The secondary UV field calculated by Gredel et al. (1989) is very similar to the emission spectrum of our lamp, see Fig. 9, except for photons with wavelengths shorter than about 114 nm, which are not transmitted by the MgF2 window used as interface between the MDHL and the ISAC set-up.
 |
Fig. 9 Calculated spectrum of ultraviolet photons created in the interior of dense molecular clouds by impact excitation of molecular hydrogen by cosmic ray ionization, adapted from Gredel et al. (1989), in the background. VUV-emission spectrum of the MDHL used in this work, red foreground trace. |
The reported VUV-absorption cross sections allow a more quantitative study of photon absorption in ice mantles. Based on our data, the VUV-light reaching an interstellar ice mantle must have an energy higher than 7.00, 7.60, and 7.08 eV, to be absorbed by solid CO, H2O, and CH3OH, respectively. The full absorption spectrum in the VUV measured by other authors provides an absorption threshold above 6.20 and 5.16 eV for NH3 and H2S, respectively, see Mason et al. (2006) and Feng et al. (1999).
The ice penetration depth of photons with a given wavelength, or the equivalent absorbing ice column density of a species in the solid phase, can be calculated from the VUV-absorption cross section following Eq. (2). Table 6 summarizes the penetration depth of the ice species for an absorbed photon flux of 95% and 99% using the cross section value at Ly-α, the average value of the cross section in the 120–160 nm range, and the maximum value of the cross section in the same range.
Penetration depth, expressed as absorbing column density, of the different pure ice species deposited at 8 K, corresponding to an absorbed photon flux of 95% and 99%.
The VUV-absorption of ice mantles is low compared with that of the dust grain cores, and therefore difficult to observe directly, but it is an essential parameter quantitatively for studing the photoprocessing and photodesorption of molecular species in the ice mantle. The desorbing photoproducts can be detected in observations of the gas phase. The reported measurements of the cross sections are thus needed to estimate the absorption of icy grain mantles in the photon range where molecules are photodissociated or photodesorbed, which often leads to the formation of photoproducts. These results can be used as input in models that predict the processing of ice mantles that are exposed to an interstellar VUV-field. They can be used, for instance, to predict the gas phase abundances of molecules photodesorbed from the ice mantles, as we discuss below.
There is a clear correspondence between the photodesorption rates of CO ice measured at
different photon energies (Fayolle et al. 2011) and
the VUV-absorption spectrum of CO ice (Lu et al. 2009, this work) for the same photon
energies. This indicates that photodesorption of some ice species like CO and
N2 is mainly driven
by a desorption induced by electronic transition (DIET) process (Fayolle et al. 2011, 2013). The
lowest photodesorption reported by Fayolle et al. (2011) at the Ly-α wavelength (121.6 nm) is <6 × 10-3 molecules per incident photon, coinciding with the low
VUV-absorption at this wavelength in Fig. 3, and the
maximum in the photodesorption occurs approximately at ~151.2 nm, near the most intense
VUV-absorption band, see Fig. 3. The photodesorption
rate per absorbed photon in the [λi, λf] wavelength
range, 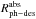 , can differ significantly from the
photodesorption rate per incident photon,
, can differ significantly from the
photodesorption rate per incident photon, 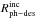 . It can be estimated as follows:
. It can be estimated as follows:
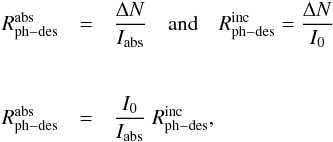 (4)where
(4)where 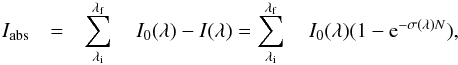 and ΔN is the column density decrease for a given
irradiation time in molecules cm-2 s-1, I0 is the total photon flux emitted
(Fayolle et al. 2011 reports ~1.7 × 1014
photons cm-2
s-1, in our
experiments ~2.0 × 1014 photons cm-2 s-1), Iabs is the total
photon flux absorbed by the ice, I0(λ) is the photon flux
emitted at wavelength λ, σ(λ) is the VUV absorption cross
section at the same wavelength, and N is the column density of the ice sample.
and ΔN is the column density decrease for a given
irradiation time in molecules cm-2 s-1, I0 is the total photon flux emitted
(Fayolle et al. 2011 reports ~1.7 × 1014
photons cm-2
s-1, in our
experiments ~2.0 × 1014 photons cm-2 s-1), Iabs is the total
photon flux absorbed by the ice, I0(λ) is the photon flux
emitted at wavelength λ, σ(λ) is the VUV absorption cross
section at the same wavelength, and N is the column density of the ice sample.
Fayolle et al. (2011) reported
 = 5 × 10-2 molecules per incident photon for monochromatic
~8.2 eV light irradiation
of a 9–10 ML ice column density of CO. We also estimated the value of
= 5 × 10-2 molecules per incident photon for monochromatic
~8.2 eV light irradiation
of a 9–10 ML ice column density of CO. We also estimated the value of
 in our CO irradiation experiment using the
MDHL continuum emission source with an average photon energy of 8.6 eV; this gave a value of
5.1 ±0.2 × 10-2 for an ice column
density of 223 ML, in agreement with Muñoz Caro et al. (2010). Therefore, similar values of
in our CO irradiation experiment using the
MDHL continuum emission source with an average photon energy of 8.6 eV; this gave a value of
5.1 ±0.2 × 10-2 for an ice column
density of 223 ML, in agreement with Muñoz Caro et al. (2010). Therefore, similar values of  are obtained using either, monochromatic or
continuum emission sources, provided that the photon energy of the former is near the
average photon energy of the latter, this is discussed below. Using Eq. (4), we estimated the
are obtained using either, monochromatic or
continuum emission sources, provided that the photon energy of the former is near the
average photon energy of the latter, this is discussed below. Using Eq. (4), we estimated the
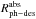 values in both experiments; they are
summarized in Table 7 for a column density of 5 ML
(only the photons absorbed in the top 5 ± 1 ML participate in the photodesorption) for three monochromatic
photon energies in the Fayolle et al. (2011) work,
selected to coincide with Lyman-α (10.2 eV), the maximum cross section (9.2 eV
energy), and the monochromatic energy of 8.2 eV, that is, the one closer to the average
photon energy of the MDHL at 8.6 eV.
values in both experiments; they are
summarized in Table 7 for a column density of 5 ML
(only the photons absorbed in the top 5 ± 1 ML participate in the photodesorption) for three monochromatic
photon energies in the Fayolle et al. (2011) work,
selected to coincide with Lyman-α (10.2 eV), the maximum cross section (9.2 eV
energy), and the monochromatic energy of 8.2 eV, that is, the one closer to the average
photon energy of the MDHL at 8.6 eV.
VUV-absorption cross sections for different irradiation energies.
Irradiation of CO ice using our VUV-lamp, with a broad-band energy distribution and mean
energy of ~8.6 eV, gives
similar 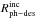 values, but different
values, but different
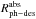 values than irradiation with a
~8.2 eV energy
monochromatic light source (Fayolle et al. 2011).
This suggests that in this particular case, the photodesorption rate per incident photon
does not depend much on the photon energy distribution, but this coincidence is only by
chance, since the corresponding
values than irradiation with a
~8.2 eV energy
monochromatic light source (Fayolle et al. 2011).
This suggests that in this particular case, the photodesorption rate per incident photon
does not depend much on the photon energy distribution, but this coincidence is only by
chance, since the corresponding 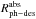 values differ significantly.
values differ significantly.
The properties of individual molecular componentes of interstellar ice analogs have been studied over the years (e.g., Sandford et al. 1988; Sandford & Allamandola 1990; Gerakines et al. 1996; Escribano et al. 2013). Our VUV-absorption spectra can be directly applied to astrophysical icy environments practically made of a single compound, for example, either CO2 or H2O largely dominate the composition of different regions at the south pole of Mars (Bibring et al. 2004). Nevertheless, interstellar ice mantles are either thought to be a mixture of different species or to present a layered structure (e.g., Gerakines et al. 1995; Dartois et al. 1999; Pontoppidan et al. 2008; Boogert et al. 2011; Öberg et al. 2011; Kim et al. 2012). Our study on pure ices can be used to estimate the absorption of multilayered ice mantles, but a priori, it cannot be extrapolated to ice mixtures. A follow-up of this work will include ice mixtures and VUV-spectroscopy at ice temperatures above 8 K.
5. Conclusions
Several conclusions can be drawn from our experimental work; they are summarized as follows:
-
The combination of infrared (FTIR) spectroscopy in transmission for measuring the deposited ice column density and VUV-spectroscopy allowed us to determine more accurate VUV-absorption cross-section values of interstellar ice analogs with an error within 16%, 15%, 23%, 19%, and 32% for CO, H2O, CH3OH, NH3, and H2S. The errors are mainly caused by the ice column density decrease due to VUV-irradiation during VUV spectral acquisition.
-
For the first time, the VUV-absorption cross sections of CO, CH3OH and H2S were measured for the solid phase, with average VUV-absorption cross sections of
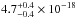 cm2,
cm2,
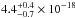 cm2, and
cm2, and
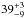 × 10-18 cm2. The total integrated
VUV-absorption cross sections are
× 10-18 cm2. The total integrated
VUV-absorption cross sections are 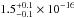 cm2 nm,
cm2 nm,
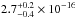 cm2 nm, and
cm2 nm, and
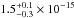 cm2 nm. Our estimated values of
the average VUV-absorption cross sections of H2O and NH3 ices
cm2 nm. Our estimated values of
the average VUV-absorption cross sections of H2O and NH3 ices
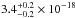 cm2 and
cm2 and
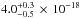 cm2, are comparable with those
reported by Mason et al. (2006), which were
measured using a synchrotron as the emission source.
cm2, are comparable with those
reported by Mason et al. (2006), which were
measured using a synchrotron as the emission source.
-
The ice samples made of molecules such as H2O, CH3OH, and NH3 present broad absorption bands and similar average VUV-absorption cross sections between
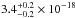 cm2 and
cm2 and
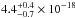 cm2, see Fig. 8. But H2S ice, which also displays a continuum spectrum,
presents about four times more absorption than the other molecules in the same VUV
range.
cm2, see Fig. 8. But H2S ice, which also displays a continuum spectrum,
presents about four times more absorption than the other molecules in the same VUV
range.
-
Solid CO displays discrete VUV-absorption bands and very low absorption at the Ly-α wavelength. But the other solid samples present high absorption at the Ly-α wavelength.
-
For the H2O, CH3OH, and NH3 species, the VUV-absorption range and the total integrated VUV-absorption cross section in the gas phase is larger than the solid phase. An exception is H2S.
-
The main emission peaks of the MDHL occur at 121.6 nm (Lyman-α), 157.8 nm and 160.8 nm (molecular H2 bands), see Fig. 2. It is still a common mistake in the molecular astrophysics community to consider the MDHL as a pure Ly-α photon source. As we mentioned, the lamp VUV-spectrum affects the photochemistry but not the VUV-spectroscopy in a direct way, since the VUV-emission spectrum was subtracted to measure the ice absorption in the same energy range.
-
Monitoring of the photon energy distribution and the stability of the irradiation source is important for studing ice photoprocesses.
-
The results are satisfactory and demonstrate the viability of the MDHL, which commonly used in irradiation experiments, as a source for VUV spectroscopy of solid samples. This method to perform VUV-spectroscopy does not require a synchrotron facility and can be used routinely in the laboratory.
-
Our estimates of the VUV-absorption cross sections of polar ice molecules can be used as input in models that simulate the photoprocessing of ice mantles present in cold environments, such as dense cloud interiors and circumstellar regions. The data reported in this paper can be applied to estimate the absorption of layered ice mantles, but not to ices built up with different species that are intimately mixed.
Acknowledgments
This research was financed by the Spanish MICINN under projects AYA2011–29375 and CONSOLIDER grant CSD2009–00038. This work was partially supported by NSC grants NSC99–2112-M-008–011-MY3 and NSC99–2923-M-008–011-MY3, and the NSF Planetary Astronomy Program under Grant AST-1108898.
References
- Bibring, J.-P., Langevin, Y., Poulet, F., et al. 2004, Nature, 428, 627 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boursey, E., Chandrasekharan, V., Gürtler, P., et al. 1978, Phys. Rev. Lett., 41, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Huard, T. L., Cook, A. M., et al. 2011, ApJ, 729, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Brith, M., & Schnepp, O. 1965, Molecular Phys., 9, 473 [Google Scholar]
- Cecchi-Pestellini, C., & Aiello, S. 1992, MNRAS, 258, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-J., Chu, C.-C, Lin, Y.-C, et al. 2010, Adv. Geosci., 25, 259 [Google Scholar]
- Chen, Y.-J., Chuang, K.-Y., & Muñoz Caro, G. M. 2013, ApJ, in press [Google Scholar]
- Cheng, B.-M., Lu, H.-C., Chen, H.-K., et al. 2006, ApJ, 647, 1535 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, B.-M., Chen, H.-F., Lu, H.-C., et al. 2011, ApJS, 196, 6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collings, M.P., Anderson, M.A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., & Stephens, T. L. 1970, ApJ, 160, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Darwent, B. de B. 1970, Bond Dissociation Energies in Simple Molecules, National Standard Reference Data System, 31, 70–602101 [Google Scholar]
- Dartois, E. 2009, ASP Conf. Ser., 414, 411 [Google Scholar]
- Dartois, E., Demyk, K., d’Hendecourt, L., & Ehrenfreund, P. 1999, A&A, 351, 1066 [NASA ADS] [Google Scholar]
- Dartois, E., Pontoppidan, K., Thi, W.-F., & Muñoz Caro, G. M. 2005, A&A, 444, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawes, A., Mukerji, R. J., Davis, M. P., et al. 2007, J. Chem. Phys., 126, 244711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- d’Hendecourt, L. B., Allamandola, L. J., & Greenberg, J. M., 1985. A&A, 152, 130 [NASA ADS] [Google Scholar]
- d’Hendecourt, L. B., Allamandola, L. J., Grim, R. J. A., & Greenberg, J. M. 1986. A&A, 158, 119 [NASA ADS] [Google Scholar]
- Ehrenfreund, P., & van Dishoeck, E. F. 1998, Adv. Space Res., 21, 15 [Google Scholar]
- Escribano, R., Muñoz Caro, G. M., Cruz-Diaz, G. A., Rodríguez-Lazcano, Y., & Maté, B. 2013, PNAS, 110, 12899 [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2011, ApJ, 739, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Fayolle, E. C., Bertin, M., Romanzin, C., et al. 2013, A&A, 556, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, R., Cooper, G., & Brion, C. E. 1999, Chem. Phys., 244, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Fillion, J.-H., Bertin, M., Lekic, A., et al. 2012, EAS Publ. Ser., 58, 307 [CrossRef] [EDP Sciences] [Google Scholar]
- France, K., Andersson, B.-G., McCandliss, S. R., & Feldman, P. D. 2005, ApJ, 628, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Gallo, A. R., & Innes, K. K. 1975, J. Mol. Spectrosc., 54, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., Greenberg, J. M., & van Dishoeck, E. F. 1995. A&A, 296, 810 [NASA ADS] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJ, 151, 35 [NASA ADS] [Google Scholar]
- Gredel, R., Lepp, S., & Dalgarno, A. 1989, ApJ, 347, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. D., & Carter, V. L. 1968, J. Opt. Soc. Am., 58, 227 [Google Scholar]
- Inn, E. C. Y. 1954, Spectrochimica Acta, 7, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G. J., Person, W. B., & Brown, K. G. 1975, J. Chem. Phys., 75, 4198 [Google Scholar]
- Jiménez-Escobar, A., & Muñoz Caro, G. M. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, H. J., Evans II, N. J., Dunham, M. M., Lee, J. -E., & Pontoppidan, K. M. 2012, ApJ, 758, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Knez, C., Boogert, A. C. A., Pontoppidan, K. M., et al. 2005, ApJ, 635, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Kuo, Y.-P., Lu, H.-C., Wu, Y.-J., Cheng, B.-M., & Ogilvie, J. F. 2007, Chem. Phys. Lett., 447, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, L. C., & Guest, J. A. 1981, J. Phys. B: At. Mol. Phys., 14, 3415 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, H.-C., Chen, H.-K., Cheng, B.-M., Kuo, Y.-P., & Ogilvie, J. F. 2005, J. Phys. B: At. Mol. Opt. Phys., 38, 3693 [CrossRef] [Google Scholar]
- Lu, H.-C., Chen, H.-K., Cheng, B.-M., & Ogilvie, J. F. 2008, Spectrochimica Acta Part A, 71, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, N. J., Dawes, A., Holton, P. D., et al. 2006, Faraday Discussions, 133, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Monahan, K. M., & Walker, W. C. 1974, J. Chem. Phys., 61, 3886 [NASA ADS] [CrossRef] [Google Scholar]
- Mota, R., Parafita, R., Giuliani, A., et al. 2005, Chem. Phys. Lett., 416, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, Annu. Rev. Astro. Astrophys., 49, 471 [Google Scholar]
- Muñoz Caro, G. M., Jiménez-Escobar, A., Martín-Gago, J.Á., et al. 2010, A&A, 522, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nee, J. B., Suto, M., & Lee, L. C. 1985, Chem. Phys., 98, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009a. A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009b. ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, H. 1978, Photochemistry of small molecules (New York: John Wiley & Sons) [Google Scholar]
- Pontoppidan, K. M., Boogert, A. C. A., Fraser, H. J., et al. 2008, ApJ, 678, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Price, W. C., & Simpson, D. M. 1938, Proc. Roy. Soc. London A, 165, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Richey, C. R., & Gerakines, P. A. 2012, ApJ, 759, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, J. A. R., & Ederer, D. L. 2000, Vacuum Ultaviolet Spectroscopy (Elsevier Inc.) [Google Scholar]
- Sandford, S. A. 1996, ASP Conf. Ser., 97, 29 [NASA ADS] [Google Scholar]
- Sandford, S. A., & Allamandola, L. J. 1990, ApJ, 355, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, S. A., Allamandola, L. J., Tielens, A. G. G. M., & Valero, G. J. 1988, ApJ, 329, 498 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schutte, W. A. 1996, Molecules in Astrophysics: Probes and Processes, IAU Symp., 178, 1 [Google Scholar]
- Smith, P. L., Rufus, L., Yoshino, K., & Parkinson, W. H. 2002, in NASA Laboratory Astrophysics Workshop, NASA/CP-2002–21186, ed. F. Salama, 158 [Google Scholar]
- Sternberg, A. 1989, ApJ, 347, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y.-J., Lu, H.-C., Chen, H.-K., & Cheng, B.-M. 2007, J. Chem. Phys., 127, 154311 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y.-J., Wu, C. Y. R., Chou, S.-L., et al. 2012, ApJ, 746, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, K., Esmond, J. R., Sun, Y., et al. 1996, J. Quant. Spectrosc. Radiat. Transf., 55, 53 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Infrared-band positions and strengths (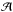 ),
deposited column density (N in 1015 molec/cm2) and molecular dipole
moment (μ) of the samples used in this work.
),
deposited column density (N in 1015 molec/cm2) and molecular dipole
moment (μ) of the samples used in this work.
Parameter values used to fit the spectra of Gaussian profiles of the different molecular pure ices deposited at 8 K.
Transitions observed in the VUV-absorption cross-section spectrum of pure CO ice, deposited at 8 K, in the 115–170 nm range.
Comparison between the VUV-absorption cross sections in the 120–160 nm range of all the pure species in the gas and solid (deposited at 8 K) phase.
Penetration depth, expressed as absorbing column density, of the different pure ice species deposited at 8 K, corresponding to an absorbed photon flux of 95% and 99%.
All Figures
 |
Fig. 1 Scheme of the main chamber of ISAC. The VUV-light intersects three MgF2 windows before it enters the UV-spectrometer, but the emission spectrum that the ice experiences corresponds to only one MgF2 window absorption, the one between the VUV-lamp and the ISAC main chamber. FTIR denotes the source and the detector used to perform infrared spectroscopy. QMS is the quadrupole mass spectrometer used to detect gas-phase species. PMT is the photomultiplier tube that makes the ultraviolet spectroscopy possible. |
| In the text | |
 |
Fig. 2 UV-photon flux as a function of wavelength of the MDHL in the 110 to 170 nm range estimated with the total photon flux calculated using actinometry. The spectrum corresponds to a measurement with one MgF2 window intersecting the emitted VUV-light cone. This spectrum is the one experienced by the ice sample. The VUV-emission is dominated by the Ly-α peak (121.6 nm) and the Lyman band system. |
| In the text | |
 |
Fig. 3 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure CO ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of CO gas (divided by a factor of 40 to compare it with CO ice) adapted from Lee & Guest (1981). The fit, red trace, is the sum of 15 Gaussians, dashed trace. It has been vertically offset for clarity. |
| In the text | |
 |
Fig. 4 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure H2O ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase H2O taken from Mota et al. (2005). The gray area is the measurement error zone. The fit, red trace, is the sum of three Gaussians, dashed trace. It has been vertically offset for clarity. |
| In the text | |
 |
Fig. 5 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure CH3OH ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase CH3OH adapted from Nee et al. (1985). The fit, red trace, is the sum of two Gaussians, dashed trace. It has been vertically offset for clarity. |
| In the text | |
 |
Fig. 6 VUV-absorption cross section as a function of photon wavelength (bottom X-axis) and VUV-photon energy (top X-axis) of pure NH3 ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase NH3 adapted from Cheng et al. (2006) and Wu et al. (2007). The fit, red trace, is the sum of two Gaussians, dashed trace. It has been vertically offset for clarity. |
| In the text | |
 |
Fig. 7 VUV-absorption cross section as a function of wavelength (bottom X-axis) and photon energy (top X-axis) of pure H2S ice deposited at 8 K, black trace. The blue trace is the VUV-absorption cross-section spectrum of gas phase H2S adapted from Feng et al. (1999). |
| In the text | |
 |
Fig. 8 VUV-absorption cross section as a function of wavelength (bottom x-axis) and photon energy (top x-axis) of all the pure ice species studied in this work, deposited at 8 K. |
| In the text | |
 |
Fig. 9 Calculated spectrum of ultraviolet photons created in the interior of dense molecular clouds by impact excitation of molecular hydrogen by cosmic ray ionization, adapted from Gredel et al. (1989), in the background. VUV-emission spectrum of the MDHL used in this work, red foreground trace. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


