EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 561 (January 2014) A&A, 561 (2014) A70 Full HTML
Free Access
Issue
A&A
Volume 561, January 2014
Article Number A70
Number of page(s) 10
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201322774
Published online 03 January 2014

© ESO, 2014

1. Introduction

Understanding the size distribution of supernova remnants (SNRs) can be useful to study the physics and astrophysics of these objects themselves as well as the interstellar medium (ISM) of the galaxy where their evolution takes place. The form of the size distribution of SNRs is determined by the properties of their exploding parent stars, the mechanism of supernova (SN) events, and the properties of the ISM where SNRs are evolving. The majority of the observed SNRs consists of older, evolved SNRs, but they still retain information on the energy released by their exploding progenitors. Although SNe are divided into two large groups, SNI and SNII, which are quite different in the properties of parent stars and the mechanisms of explosion, they deposit a similar amount (~1051 erg) of kinetic energy into the surrounding medium, therefore we did not distinguish between types of SNe in this study. Other factors affecting the size distribution of SNRs are the physical properties of the ISM, mainly the density and, in the final stages of the evolution, the total pressure of the ISM. The pressure in the ISM is the main factor that determines the final fate of the SNR.

Mathewson et al. (1983) were among the first to report on the size distribution of SNRs in the Magellanic Clouds, and from the approximately linear cumulative size distribution the authors have concluded that a majority of SNRs in the Magellanic Clouds are in a “free expansion” phase of evolution, with shocks propagating at a constant velocity into a tenuous ambient medium. This conclusion was in apparent contradiction with the observational evidence that a large portion of observed SNRs in the Magellanic Clouds are in an adiabatic phase. The effect of the various selection effects and the nonuniformity of the ISM density distribution on the size distributions are considered in a number of works (e.g., Hughes et al. 1984; Berkhuijsen 1986, 1987; Fusco-Femiano & Preite-Martinez 1984; Badenes et al. 2010).

Obviously, the detected and cataloged SNRs constitute only a small fraction of the real number of objects. This fraction depends on various factors – the waveband of observations, the characteristics of the instrument with which the object is observed, on the site where the remnants are located, etc. Since the observed sample of SNRs consists of objects with different and uncorrelated parameters, and because they evolve in environments with different properties, the use of Monte Carlo methods is justified and can be very effective in statistical studies of SNRs. Using the real bands of variation of the physical parameters that characterize the remnant and the ISM, we generated a set of SNRs that can be compared with the homogenous subset of observed SNRs with known parameters. The realization of this scheme became possible thanks to the recently published results by Long et al. (2010, hereafter L10), which present very rich and high-quality Chandra X-ray observational data on the SNRs in the nearby galaxy M 33 from the deepest Chandra ACIS survey of M 33 (ChASeM33).

The main aim of the present study is to improve our understanding of the problem of the evolution of SNRs in real conditions of the ISM. This complex problem consists of a number of aspects – the law of expansion, the evolution of emission in various bands of the electromagnetic spectrum, the interrelation of the observational characteristics of SNRs with the properties of the ISM where the objects are located, etc.

The paper is organized as follows: in Sect. 2 we consider the evolution of the SNR, where we derive the equations describing the dependence of the shock Mach number on the radius of the remnant with and without cooling. In Sect. 3 we present the observational X-ray data of SNRs in M 33. In this section we also discuss the thermal X-ray emission from evolved SNRs. From the catalog of SNRs in M 33, we have identified an ensemble of objects that can be considered as a statistically complete set, which is then used in Sect. 4 for comparison with the Monte Carlo modeled SNRs. In Sect. 4 we also present an analysis of the results. The final section contains our main conclusions.

2. Expansion of SNRs

The problem of expansion of the SN blast wave in general is well understood and described in number of detailed studies (e.g., Zel’dovich & Raizer 1966; Bisnovatyi-Kogan & Silich 1995; Ostriker & McKee 1988). In the course of evolution with time, the SNR evolves through several phases. The first, free expansion phase lasts up to the moment when the swept-up mass equals the ejecta mass. Since the duration of this phase is relatively short, fewer than ~103 years, this period of life of the remnant plays only a minor role in the overall statistics of SNRs. By the time the swept-up mass equals the ejecta mass a smooth transition from this stage to the adiabatic Sedov-Taylor phase begins (Truelove & McKee 1999). This phase is believed to play very important role in the life of the remnant because at this stage SNR intensively emits practically in all wavelengths of the electromagnetic spectrum from radio to gamma. The structure of the remnant is described by the exact self-similar Sedov’ solution. The transition to this phase is smooth and asymptotic (Cioffi et al. 1988); depending on the real conditions, the duration and applicability of this solution to real SNR may vary within broad limits. In all cases, the sudden liberation of a large amount of energy in a small volume would result in generation of strong shock wave with the structure asymptotically approaching to the self-similar Sedov solution (Landau & Lifshic 1986; Zel’dovich & Raizer 1966). The radius of the spherical blast wave that evolves in the homogeneous and stationary ISM changes according to the expansion law (Sedov 1977) 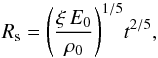(1)where Rs is the radius of the shock front, E0 is total (thermal plus kinetic) energy of the blast wave, ρ0 is the mass density in the ISM where the shock front evolves, ξ is the dimensionless numerical constant, which depends on the adiabatic index of the plasma γ: ξ = 2.026 for γ = 5/3.

To ensure a smooth transition from free expansion to the expansion law (1) we used the condition of constancy of the kinetic energy of the shell with an ejected mass of Mej: 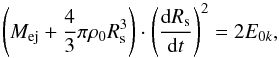which gives for the shock wave velocity 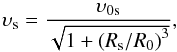(2)where 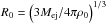, and 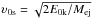, from which it follows that when Rs ≪ R0, υs = υ0s = const. (free expansion) and at Rs ≫ R0, υs = υ0s·(Rs/R0)− 3/2 in accordance with the Sedov expansion law (Eq. (1)).

In Eq. (2) the evolution of the SNR is described with the help of the dependence of the forward shock velocity on the radius instead of the standard radius – time (age) relation as in Eq. (1). The evolution of the remnant can also be described with the help of other dependences, for instance, velocity – age (time), velocity-radius relationships. The Mach number of the SNR shock wave can be used as another parameter to describe the evolution of the SNR. This quantity allows us to include the parameters of the ISM into the expansion equation. We determine the Mach number as the ratio of the shock velocity υs = dRs/dt to the maximal speed of propagation of small disturbances in the magnetized ISM, (magneto-) sound speed, cms0: 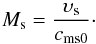(3)The (magneto-) sound speed in the ISM is determined as 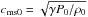, where P0 is the total pressure (the sum of thermal and nonthermal particles and magnetic field pressures) in the ISM. Note that including the relativistic gas component and the magnetic fields leads to a softening the equation of state of the plasma, and the adiabatic index γ is expected to be in the range 4/3–5/3.

The applicability of the Sedov self-similar solution to real SNR is determined by two main conditions: 1) the pressure of the ambient medium is negligible and 2) the condition of adiabaticity of the matter inside the remnant holds. Violation of any of these conditions leads to a violation of the applicability of the Sedov solution. In very tenuous environments the adiabaticity is retained up to the very large diameters at which the pressure of the ISM becomes important. It is important to note that the law of motion (Eq. (1)) gives relatively good results up to values of the shock Mach numbers of 2, although the internal structure of the shell begins to depart from the Sedov self-similar solution much earlier, when Ms ≤ 10 (Sedov 1977; Cox & Anderson 1982). In relatively dense medium the decrease of the post-shock plasma temperature with time increases the radiative losses of the matter in the shell of the remnant. According to Cox (1972), at some time during the evolution (moment tsg, sag time), radiative cooling begins to affect the temperature distribution downstream and initiates the deviation from the self-similar nature of the flow. For an SNR evolving in a homogeneous ISM, Cioffi et al. (1988) found that the time taken to cool an element of mass to 0 temperature, that is, to form the shell, is 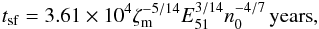(4)where E51 is the SN energy in units of 1051 erg, n0 is the number density of the gas in the ISM, ζm is the metallicity factor (=1 for solar abundances). After about this time the shock can be described by the radiative pressure-driven snowplow (PDS) model. In a number of papers the problem of transition from the adiabatic to the radiative phase of evolution is discussed. Practically the same expression as Eq. (4) for the transition time is derived in Cox & Anderson (1982), although they used slightly different methods. In Franco et al. (1994) the same time is derived with the same functional form, but with a slightly different value of the coefficient. A more detailed analysis of the problem of transition of the SNR from the adiabatic phase to the radiative phase is given by Petruk (2006).

Assuming that the remnant evolves according to the Sedov solution up to the very moment when the shell formation finishes, tsf, we have for the radius and velocity at tsf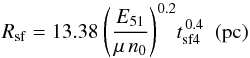(5)and 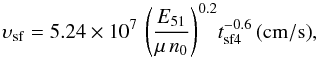(6)where tsf4 is tsf in 104yr, μ is the mean ISM molecular weight in units of the proton mass. At the moment tsf the formation of cool thin shell ends, and the following expansion of this shell takes place due to the pressure of the hot interior gas. Because we are interested mainly in the SNRs in Sedov and radiative phases, we consider here the evolution of these shells in detail, taking into account the pressure of the ISM. Unlike the adiabatic case, where the expansion rate of the gas immediately behind the shock front lags behind the shock velocity, for a cold isothermal shell these speeds are the same. The system of equations governing the expansion of this snow-plowing shell includes the equation of mass conservation (Bisnovatyi-Kogan & Silich 1995), 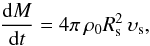(7)the equation of momentum conservation, 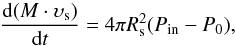(8)and the equation of energy conservation, 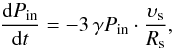(9)where 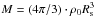is the mass accumulated in the thin shell,   υs = dRs/dt is the velocity of the shell, which is equal to the shock velocity; Pin and P0 are the total pressures inside the shell and in the ISM. With a little manipulation the system of Eqs. (7) and (8) can be transformed to an equation linear in 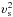, 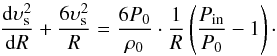(10)By using Eq. (3), the general solution of the Eq. (10) can be written as 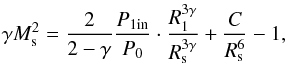(11)where C is the integration constant, P1in is the pressure inside of the shell at arbitrary radius Rs1 of the radiative remnant. For this radius we take the radius Rsf. According to the exact Sedov solution, the ratio of the central almost uniform pressure to the pressure immediately behind the shock front is constant, and for γ = 5/3 this ratio is α ≈ 0.31 (Sedov 1977). Therefore, for the initial pressure inside the remnant, which in the course of evolution will change according to Eq. (9) and push the dense shell forward, we hav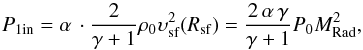e where 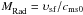is the shock Mach number at the time tsf. Numerical calculations show (Cioffi et al. 1988; Mansfield & Salpeter 1974) that at the transition between Sedov and radiative phases a sudden ~20% decrease in shock velocity occurs. Therefore the initial velocity of the shell at the moment tsf, when the snow-plow phase just begins to act, is υ1 = θ·υsf, with θ ≈ 0.8 (Draine & Woods 1991).

After substituting these last expressions into Eq. (11), we have (12)Finally, we rewrite the Eq. (11) as the dependence of the shock Mach number on the normalized shock radius x ≡ Rs/Rsf in the form 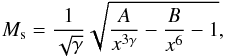(13)where 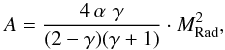and 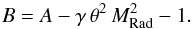Equation (13) can be used to describe the evolution of SNR. The dependences Ms(Rs) and υs(Rs) can be numerically converted into time dependences with the help of integrals: 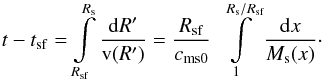(14)In principle, Eq. (13) can be analyzed analytically, but since there are no physically meaningful asymptotes, we used it in numerical calculations. Assuming a power-law dependence for the expansion law as Rs ∝ tm, the dependence of 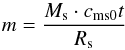on time is presented in Fig. 1. This parameter is called the expansion parameter and it measures the shell deceleration.

thumbnail Fig. 1

Dependence of the expansion parameter m on time for an SNR with E0 = 1051  erg,   n0 = 0.5  cm-3 and P04 = 4 × 104   K cm-3. The solid line corresponds to the case of evolution with the effect of pressure of the ISM, the dashed line for the case without pressure. The vertical lines denote the moments when the shock Mach number Ms = 2 (left) and Ms = 1 (right).

The figure shows that m ~ 0.4 in the Sedov phase, at the end of which it suddenly drops to a slowly varying value of 0.3 − 0.33 during the remaining active life of the SNR (Ms > 2) in accordance with detailed numerical results (e.g Chevalier 1974). However, our solution does not show the value m = 2/7 ≈ 0.29 following from the pressure-driven snowplow solutions (McKee & Ostriker 1977; Blinnikov et al. 1982). The late-time behavior of the SNRs is mainly determined by the conditions in the ISM, where the remnant evolves. For a more detailed analysis, it is desirable to determine the lifetime of the remnant by using the shock Mach number. This parameter shows how strong the shock wave is, which in turn determines the visibility of the remnant in any waveband of the electromagnetic spectrum. We define the lifetime of the remnant as the moment when the shock Mach number becomes equal to 2. Indeed, an SNR with Ms < 2 is unlikely to be detected in any wavelength range, and such SNRs can be considered as dead SNRs. When we take the effect of the interstellar pressure into account, the occurrence of the so-called momentum-conserving snowplow with Rs ∝ t1/4, known as the Oort phase, becomes problematical. The late-time evolution problem was studied in detail by Cioffi et al. (1988), who also discussed whether an evolution of the remnant without the radiative phase is at all possible. In our case this situation occurs when Mrad ≤ 2, which can be expressed as 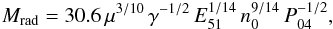from which the condition on the density can be obtained (for γ = 5/3;  μ ≈ 0.61) 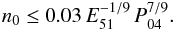In these equations P04 is the total pressure in the ambient ISM in units of 104   K cm-3. As we noted, at these densities the evolution of the shock radius can be described by the Sedov law of expansion Rs ~ t2/5 up to values of the Mach number of Ms ~ 2, although at these values of Ms the internal structure strongly deviates from the self-similar exact solution (Sedov 1977; Cox & Anderson 1982).

It is important to note that in the evolution of old and evolved SNRs the external pressure of the ISM becomes a dominant factor that determines the lifetime and maximum achievable size of the SNR. In general, the total pressure is the sum of contributions of thermal particles, cosmic rays, and magnetic fields at various scales. It is well known that the thermal pressure in disk galaxies is only a small part of the total pressure in the gas; in particular, Boulares & Cox (1990) have shown that the turbulent pressure is considerably higher than the thermal pressure.They have estimated the total pressure (with thermal plus turbulent contributions) of the ISM to be on the order of 104   K cm-3. For the subsequent analysis, it is important to note that it follows from the general theoretical analysis that the spatial variation of the total pressure in the plane of the galaxy is about an order of magnitude or less (e.g. Wolfire et al. 2003), while the contrast in other physical characteristics of the ISM (density, temperature) can reach 4–5 orders of magnitude. Therefore, it is reasonable to assume that the total pressure of the ISM is in the range of (1 − 5) × 104   K cm-3.

In Fig. 2 some curves describing the evolution of the shock Mach number with the diameter are shown, which demonstrate the role of the interstellar pressure on the evolution of the SNR. The pressure also affects the evolution of SNR through the definition of the shock Mach number, the parameter that serves as the measure of the blast wave intensity. The pressure effect becomes noticeable at the very end of the SNR life and, in general, the including the interstellar pressure results in a considerable reduction of the highest values of the SNR diameter and lifetime.

thumbnail Fig. 2

Dependence of the Mach number on the diameter of the SNR for E0 = 1051  erg and n0 = 0.5  cm-3 for the two values of pressure P04 = 2.17 (thick lines) and P04 = 8.6 (thin lines). The solid and dotted curves describe the solution of the system of Eqs. (6)–(8) with and without the pressure of the ISM, and the dashed curves describe the Sedov solution without radiative cooling. The horizontal dash-dotted line corresponds to the point Ms = 2.

As we have proposed above, the active life of the SNR ends when its Mach number reaches the value of 2. We adopted the diameter and age of the remnant at this moment as the largest size Dmax and longest lifetime of the SNR. Obviously, this choice is arbitrary, but at this value of Ms, in specific conditions of the ISM, the SNR can preserve its integrity more or less, but its ability to generate detectable emission in any of the energy bands is strongly reduced. As can be seen in Fig. 2 the value of largest diameter of the SNR in real conditions of the ISM is much larger than the observational values of 30–50 pc. This fact implies that either we do not see a large portion of real existing objects, or that in real conditions of the ISM SNRs do not expand to large diameters, that is, our model is incorrect.

Using the above solution for an SNR evolving in the ISM with n0 = 1 cm-3 and P0 = 2.2 × 104 K cm-3, we estimate the largest diameter and longest lifetime to be 90 pc and 4.5 × 105 yr, respectively. These values are reduced to 68 pc and 1.75 × 105 yr, respectively, when the pressure is increased to P0 = 8.6 × 104 K cm-3. If we take for the density n0 = 0.1 cm-3, which is typical for the warm phase of the ISM, the largest diameter and longest lifetime of the SNR are 126 pc and 2.11 × 105 yr at P0 = 2.2 × 104  K cm-3 and 102 pc and 1.11 × 105 yr when the interstellar pressure is P0 = 8.6 × 104 K cm-3. From these numerical estimations we can also see that the effect of the ambient interstellar pressure on the active lifetime of the SNR is more prominent than on the value of its largest size.

3. X-ray SNRs

Supernova remnants are studied practically in all bands of the electromagnetic emission, but the most extensive observational information is available in radio, X-ray, and optical wavebands. For the present study the main advantage of the X-ray band over others is that the nature of X-ray emission of evolved SNRs is clearly established, which we cannot say about the nature of the emission in other wavebands. The thermal nature of the SNR X-ray emission is often used as one of the main properties of shell-type SNRs - to identify the X-ray sources as SNRs, they should be extended objects and sources of thermal emission. Indeed, the majority of detected shell-like SNRs exhibits thermal X-ray emission. The exception is the small number of young SNRs with power-law X-ray spectra that are generally believed to originate from synchrotron emission, although bremsstrahlung emission of electrons with a non-Maxwellian distribution function (Asvarov et al. 1990) cannot be excluded.

Supernova remnants are relatively well studied in X-ray wavebands, though the details of this emission are somewhat complicated because the X-ray spectrum in the 0.1–2 keV range is formed by a variety of line and continuum processes that depend on the details of the temperature and density structure and on the physical conditions in the hot gas, and on the interstellar absorption as well. Another difficulty is the inhomogeneity of data from different data sets of X-ray SNRs. In this sense, for statistical studies of SNRs the radio observations are favorable, as is the case with our Galaxy and the Magellanic Clouds. Unfortunately, because we lack a reliable theory of the origin of the SNR radio emission, we cannot simulate their evolution in the present study. For the same reason we cannot use the rich data of optical observations of SNRs that are located mostly in neighboring galaxies.

3.1. Data

With regard to the above discussion, the recent work of L10, devoted to a statistical study of SNRs in optical and X-ray ranges in the nearby galaxy M 33, is of great value for the present study. The SNRs in M 33, as is typically the case for nearby galaxies, are mainly detected in the optical waveband. The previously published list of SNRs (Gordon et al. 1998, 1999), which consisted of 99 optical SNRs, has been expanded to 137 SNRs and SNR candidates in L10.

Using Chandra data from the ChASeM33 survey, 82 of 137 SNR candidates were detected as X-ray sources. According to the authors, the catalog includes all the SNRs in the portions of M 33 covered by the ChASeM33 survey with 0.35–2 keV X-ray luminosity higher than ~4 × 1034 erg  s-1, and the sample in L10 provides the largest sample of remnants detected at optical and X-ray wavelengths in any galaxy, including the Milky Way. For uniformity of the statistics it is desirable to have results of relatively simultaneous observations conducted with the help of the same instrument. Fortunately, the catalog of SNRs in M 33 from L10 satisfies these conditions. Importantly, the X-ray data in this catalog were obtained with the help of the Chandra observatory between 2005 September and 2006 November (L10). We also used the recent ChASeM33 point-source catalog of M 33 (Tüllmann et al. 2011, T11 hereafter), in which only 45 SNRs of the 82 SNRs from L10 are detected as point sources. These SNRs are expected to be less contaminated with background emission, which makes this sample of SNRs much more statistically uniform.

We note that the ChASeM33 survey only covers the inner region of M 33 to a radius of about 4.3 kpc, which is about 70% of the area of the galaxy (Plucinsky et al. 2008).

3.2. X-ray emission from SNRs

For a Maxwellian energy distribution of the electrons, which we assume is the case for the SNRs discussed here, the emissivity of the thermal continuum X-ray emission at photon energy Ex is given (Vink 2012) (in units of erg s-1 cm-3 Hz-1) 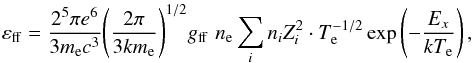(15)where with gff ≈ 1, the gaunt-factor, which depends weakly on the electron temperature Te and photon energy Ex, ne and ni are the densities of electrons and ions with charge Z, respectively, and the remaining variables have standard meanings. Due to the factor 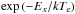in this formula, the X-ray flux from the SNR is very sensitive to the temperature of the post-shock plasma and the range of photon energies at which the X-ray detector operates. The temperature of the post-shock electrons is determined by the evolutionary status of the remnant’s shock wave, namely, by the shock velocity. If we assume a strong shock in a fully ionized gas with complete temperature equilibration between ions and electrons, then the X-ray temperature implies a shock velocity (McKee & Hollenbach 1980) 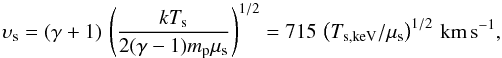where Ts,keV is the post-shock temperature in keV and μs is the post-shock mean mass per free particle in proton masses mp. If the temperature of the plasma falls below the lower energy limit of the X-ray detector (in the present analysis this is 0.35 keV), the flux of X-ray photons will decrease exponentially as the radius of the remnant increases and the remnant disappears as an X-ray source. So, the SNRs in our list are the remnants with υs ≥ 715(0.35/μs)1/2  km s-1 ≈ 530 km s-1. We did not consider the complicated behavior of the electron temperature behind the shock front (see e.g., Ghavamian et al. 2013) or the role of radiation in the lines at low energies of the observed band. We assumed that SNRs emit in X-rays according to Eq. (15), although at energies ~0.1 keV the contribution of the line emission to the total emission may be very substantial.

The X-ray detector counts the photons within specific instrument energy channels. To convert these data into physically important information (photon flux, energy spectrum, luminosity, etc.), we have to perform a number of intermediate steps and make assumptions about the spectra of the electrons that emit in the X-ray waveband. All these make the obtained information less reliable. Therefore, we used the raw count rates given in the list of SNRs in L10 and made no assumptions about the spectra of the sources other than the assumption that the emissivity has a thermal nature of the form (Eq. (15)). We calculated one of the important characteristics of the X-ray emission of the remnant – the count rate of X-ray photons in the range of energies [Ex1;Ex2], as 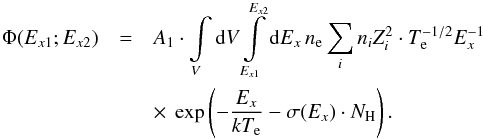(16)To calculate this quantity, we used the approximation 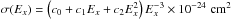for the cross-section per hydrogen atom from Zombeck (2007), where Ex is given in keV and the coefficients c0, c1 and c2 are tabulated. For the radial dependences of the densities and the temperature in this formula we have used the exact Sedov self-similar solution when the shock wave was strong (Ms ≥ 10), but for Ms < 10 we used the approximate solution of Cox & Anderson (1982). The evolution of the X-ray count rates with the SNR diameter is shown in Fig. 3. This figure also illustrates how the observed values of the X-ray emission depend on the characteristics of the energy band at which the emission is detected. The analysis of Eq. (16) shows that the highest X-ray count rate of the SNR is reached when the temperature of the X-ray emitting electrons corresponds to the energy band of the observations. Applying this picture to the SNRs in M 33, we used for the distance and column density the values of 817 kpc and NH = 1021 cm-2 (L10), respectively.

To reduce the effect of the poorly determined normalizing coefficient A1 in Eq. (16), it is useful to employ the hardness ratio (HR), which is commonly calculated as the normalized difference of the exposure-corrected counts in two energy bands. The dependence of the HR on the energy of photons directly indicates the nature of the X-ray emission – thermal, power-law, or some other. In L10 this parameter was defined as the ratio HR =  [Φ(1.2;2.6) − Φ(0.35;1.2)] /Φ(0.35;8.0) where Φ(0.35;1.2),  Φ(1.2;2.6), and Φ(0.35;8.0) are the numbers of counts correspondingly in the 0.35 − 1.2 keV, 1.2–2.6 keV and 0.35–8.0 keV bands, and for all the sources detected in X-rays the values of HR hardness ratios are given. To select the SNRs from other Chandra sources, L10 used the criterion that HR < 0. This directly reflects the thermal nature of the X-ray emission of detected SNRs. The evolution of HR with diameter is determined mainly by the behavior of the exponential factor ~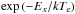, therefore the distribution of this parameter can be used to estimate the evolutionary status of the objects in the list.

thumbnail Fig. 3

Evolution of the [0.35 − 1.1] keV (thick curves) and [1.1 − 2.6] keV (thin curves) X-ray photon count rates as a function of SNR diameter for the ambient particle densities 1, 0.1, and 0.01 cm-3, as denoted near the corresponding curves, and E0 = 1051 erg, NH = 1021 cm-2 as in the case of M 33.

We also calculated the HRs using the recently published catalog of X-ray sources in M 33 T11, where the count rates in different energy bands are given. The hardness ratios calculated from these data are well correlated with the HRs given in L10, with the exception of the source L10-096 (G98-73) (source number in the catalog T11 is 426), for which we obtained HR = 0.34, but L10 found HR =  −0.6. The only SNR with a high positive value of HR ~ 0.4 in both catalogs is the object L10-119 (Scr. No in T11 is 493). In Fig. 4 the evolution of HR with D is shown together with 44 observational points calculated using the data from T11; for the SNR L10-096 we adopted HR =  −0.6 as in L10, and L10-119 is not shown in this figure. The hardness ratio histogram is shown in Fig. 5, where HRs for 45 SNRs from T11 and HRs of 82 SNR from L10 are presented. In both cases it can be seen that there is a higher concentration of SNRs around HR ~  −0.5. The mean values of the HR are −0.44 for both calculations. It is important to note that at HR ~  −0.5 the SNR reach the highest X-ray luminosity, which is why we assume that the population of observed SNRs with HR around −0.5 forms the uniform set of objects that are unaffected by selection effects.

thumbnail Fig. 4

Hardness ratio (HR, see text for definition) evolution with diameter of SNR for E0 = 1051  erg and n0 = 0.01, 0.1,  and  1.0  cm-3. Filled circles correspond to the 44 SNRs from the T11 catalog.

thumbnail Fig. 5

Hardness ratio distribution of SNRs in M 33. The solid line histogram corresponds to 82 SNRs from L10, the histogram for 45 SNRs with HRs calculated by using the data from T11 is drawn with dashed lines.

4. Model: results and discussion

Observations show that SNRs have very different characteristics. This is partly due to the scatter in the properties of parent SNe (mainly, SN energies in case of evolved sources), partly due to the broad spread of the ISM properties (density, pressure, chemical abundances, etc.) where SNRs expand.

To separate the effects of these factors on the statistics of SNRs, we built a simple evolution model of SNRs with different initial birth parameters and evolving in sites with different ambient conditions. We generated a set of SNR as follows: every ΔT year an SN occurs, the initial parameters of which are randomly distributed in intervals: 1) the explosion energy (kinetic) E0 = (0.2 ÷ 5) × 1051 erg; 2) the ejecta mass Mej = (1 ÷ 5) M⊙. The parameters of the ISM, the total pressure and the density, where the SN occurs, also were chosen in a random manner: 3) the total pressure in the range P0 = (1 ÷ 5) × 104 K cm-3; 4) for the density we considered a three-phase model in which for the hot, warm and cold phases the values of the density are taken randomly from the intervals nh =  [0.005 ÷ 0.1) cm-3, nw =  [0.1 ÷ 1)  cm-3, and nc =  [1 ÷ 10]   cm-3 with volume-filling factors φh, φw, and φc, respectively. For the cold phase we adopted the constant value φc = 0.01, but φh or φw (φh + φw = 0.99) was the main varying input parameter of the model.

In this way, both populations of SNRs, the observed and the modeled, are sets of SNRs with different birth characteristics, and these SNRs are evolving in different conditions of the ISM and are at a different stage of evolution, but there is one main difference between them – the modeled SNRs are free from any selection effects.

We assumed that the shock of radius Rs expands in accordance with Eqs. (2) and (13) into a fully ionized gas with a ratio of specific heats γ = 5/3 and with a helium abundance relative to hydrogen as nHe = 0.1 nH. The number density and electron density were n = nHe + nH = 1.1 nH and ne = nH + 2 nHe = 1.2 nH, respectively.

thumbnail Fig. 6

Size distribution of observed SNRs in M 33 and Monte Carlo simulated SNRs for various values of the warm phase filling-factor (indicated in the panels). In simulations ΔT = 250 yr, the lifetime is determined as t = t(Ms = 2) and the largest dimension of simulated SNRs is D = D(Ms = 2). The bin size is 7 pc.

As an example, we show in Fig. 6 the size distributions of SNRs modeled for different values of the filling factor of the warm phase of the ISM. This figure illustrates the general behavior of the size distribution of SNRs: with the decrease of the warm-phase filling factor the size distribution broadens and the fraction of the large diameter SNRs increase. The distribution of 137 real SNRs in M 33 is also shown in Fig. 6. However, from this comparison of modeled and observed distributions we are unable to obtain useful information either on the SNR evolution or about the ISM in M 33. This is because the sample of simulated SNRs is free from selection effects but the experimental SNRs are the objects detected in a certain electromagnetic waveband and suffer from various selection effects. In general, a selection effect occurs when we cannot see a weak point source or when we overlook a weak, extended source because of background emission. Typically, an object bright in some waveband may be dim in other waveband, therefore observations at different wavebands are of great importance for statistical consideration. Accordingly, to compare the modeled size distribution with the observed distribution in a given waveband we need to model the evolution of the SNR emissivity in this waveband.

As we showed, SNRs with HR ~  −0.5 constitute a more or less uniform group of SNRs, therefore we selected SNRs with these values of HR among the observed as well as the modeled SNRs. In Table 4 of L10, of the 82 X-ray SNRs and SNR candidates the HR lies in the interval −0.7 ≤ HR ≤  −0.3 for 48 objects. This subset of SNRs have diameters ranging from 8 to 111 pc; the mean diameter is 40 pc, the median diameter is 36 pc. The statistics of these SNRs is given in Table 1. In this table Dm, Dmin, and Dmax are the mean, minimum, and maximum diameters of SNRs in each sample, respectively. In the last column we list the ratio of highest to lowest values of the (0.35–2.6) keV count rates, which were determined as the ratio of the count rates averaged over the three brightest SNRs to the count rates averaged over the three weakest sources in the list of each sets of SNRs.

Table 1

Parameters of observed and modeled SNRs, selected according to the criterion of − 0.7 ≤ HR ≤  −0.3.

Returning to our model, for each SNR along with kinematic parameters such as the velocity, radius, Mach number, etc., we calculated the (0.35–2.6) keV photon counts with the help of Eq. (16) and thermal X-ray luminosity in the same energy range with arbitrary normalization. Initially, for the birthrate, (ΔT)-1, we took higher values to reduce the statistical fluctuations, and the generation of new SNRs stops when the birth and death rates become equal. As discussed above, the moment when the shock Mach number drops to 2 was adopted as the SNR death point. The main input parameter of each run was the filling-factor of the hot (or warm) phase of the ISM. In the generated set of SNRs we selected the subset of SNRs with HR in − 0.7 ≤ HR ≤  − 0.3, which then we compared with the selected subset of observed SNRs. As initial fitting parameters we used the mean value of the diameters and the ratios of highest to lowest count rates and X-ray luminosities. To take the influence of statistical fluctuations into account, which are inherent in the Monte Carlo method, the same model was repeated on the fit procedure with different statistical realizations of the model with the same input parameters. Results of several runs with φw = 0.90, differing only by the value of the random seed, are presented in Table 1, and in Fig. 7 the diameter distribution histogram is shown for comparative purposes.

The observed count rates for detected SNRs vary by a factor of 430, which we used as the parameter in fitting the modeled and observed SNRs. In the modeled SNR sample the ratio 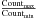is very close to the observed value (Table 1). This indicates that the observed SNR sample with HR ~  −0.5 constitutes a statistically complete set of objects, that is, there are no missing low-luminosity SNRs. The best agreement between the simulated and observed distributions was reached at a filling-factor of the warm phase of 90%. From the comparison of the number of observed and modeled SNRs with HR in − 0.7 ≤ HR ≤  − 0.3 we obtain the value ΔT ~ (140−150) yr for SNRs in M 33. This value agrees well with the estimate of Tammann et al. (1994) for a birthrate of 147 years between SN events in M 33 and is consistent with the fact that for the past 100 years of observations no SN event has been detected.

thumbnail Fig. 7

Diameter distribution of SNRs with −0.7 ≤ HR ≤  −0.3 in M 33 (dashed lines) and modeled SNRs (solid lines). The data for 48 SNRs in M 33 are taken from L10, the 49 modeled SNRs represent the scenario of 90% warm gas filling-factor and a birthrate of 150 yr. The size of the bins is 10 pc.

Knowing the birthrate of SNRs allows us to estimate their total number, the volume of the galaxy occupied by them, and other very important characteristics of the galaxy. To estimate the full number of SNRs in M 33 it is important to know the lifetime of the SNR in dependence on the initial and environmental conditions. As was discussed above, if we assume that the end of the SNR life occurs when the shock Mach number reaches 2, then the total number of SNRs will be dependent on the total pressure in the ISM. In M 33 the total number of SNRs with Ms ≥ 2 lies in the interval (1000−1600) SNRs when we adopt a pressure in the range (2−8) × 104   K  cm-3. In Fig. 8 the distribution of all modeled SNRs with Ms ≥ 2 for 8 × 104  K cm-3 is shown together with the distributions of observed and modeled SNRs selected according to the criteria −0.7 ≤ HR ≤  −0.3 shown in Fig. 7. Here we have taken the highest attainable ambient pressure in the ISM of M 33 to obtain the minimum possible number of active SNRs. It is important to emphasize that neither the birth rate of SNRs nor the volume-filling factor is dependent on the ambient pressure. At higher ambient interstellar pressure the lifetime of the SNR decreases significantly, which results in a decrease of the number of active SNRs. At the same time, the increase of the pressure results in an insignificant decrease of the maximum size of the remnant (see Sect. 2). Therefore, the effect of the interstellar ambient pressure on the size distribution is negligibly small.

As can be seen in Fig. 8, the diameter distribution of the SNRs that are predicted by the model but that are undetected peaks at 70 − 80 pc, which is almost twice the mean diameter of observed X-ray active SNRs. They cover up to 5% of the surface of the Galaxy, and assuming the volume of the observed part of M 33 is V = 4·π·R2 × h = 4·π·4.32 × 1  (kpc3) = 6.86 × 1066  cm3, SNRs with Ms ≥ 2 occupy less than 1% of the total volume of the galaxy.

thumbnail Fig. 8

Diameter distribution of 1050 modeled SNRs with Ms ≥ 2 together with the distributions shown in Fig. 7. For the modeled SNRs the filling-factor of the warm phase of the ISM is 90%, the birthrate is 1/150 yr-1, and P0 = 8.6 × 104 K cm-3.

thumbnail Fig. 9

Normalized cumulative N − D distribution for X-ray SNRs with − 0.7 ≤ HR ≤  − 0.3 in M 33 (filled squares) and two representative (run 1-open squares, run 3-open diamonds) modeled SNR subsets. The data for 48 SNRs in M 33 are taken from L10; for the modeled SNRs the filling-factor of the warm phase of the ISM is 90%.

With the aim of comparing of the modeled and observed statistics of SNRs with −0.7 ≤ HR ≤  −0.3, we show in Fig. 9 their normalized cumulative number − diameter (N − D) distributions. As can be seen from this comparison, the correspondence between observed and modeled distributions is very good. For remnants with D < 60  pc the cumulative N − D relation for both SNR subsets (observed and modeled) is approximated by the form N(D) ~ Dη, with η = 1.2−1.6, though for the Sedov expansion in the uniform ISM the expected value is η = 2.5. This long-known discrepancy (Mathewson et al. 1983, 1984) is now explained by the strong variations in ambient density (Berkhuijsen 1987) and partly by the selection effects (Hughes et al. 1984), but our analysis shows that the selection effects play a minor role.

thumbnail Fig. 10

Dependence of 0.35−2 keV photon count rates of M 33 SNRs on the diameters. The 48 SNRs with −0.7 ≤ HR ≤  −0.3 are denoted with filled circles, open circles denote the remaining 34 SNRs. All the data are taken from the list in L10.

thumbnail Fig. 11

Dependence of (0.35−2) keV photon count rates on the diameter for modeled SNRs. The normalization is arbitrary. In this run for the 90% warm-phase filling-factor and the mean total pressure 4 × 104 K cm-3 the number of SNRs with Ms ≥ 2 is 1530, of which 53 SNRs with −0.7 ≤ HR ≤  −0.3 are presented in this figure.

We considered the dependence of SNR X-ray luminosity on diameter. Fig. 10 displays the relation between the count rates (in place of X-ray luminosity) and the SNR diameters. Obviously, there is practically no correlation between these parameters. Almost the same relationship holds for the simulated SNRs (see Fig. 11). The lack of correlation between count rates and the diameters can be easily explained by the fact that the observed set of SNRs consists of objects evolving in very different initial and environmental conditions, although every individual SNR has a count rate – diameter relation as shown in Fig. 3. It is important to note that the subset of considered remnants constitutes a homogeneous statistical set of objects free from selection effects, which means that the lack of an Lx − D dependence is the common picture for the shell-like SNRs, and can be used as a strong evidence in favor of the considered picture of SNR evolution in the real conditions of the ISM.

The modeled SNR sample, which agrees very well with the observed X-ray SNRs, also exhibits the well-known correlation of apparent density n0 with SNR diameter. This correlation, to the author’s knowledge, was first noticed by McKee & Ostriker (1977) for a small sample of galactic SNRs. Although they used this correlation to support a multiphase model of the ISM, we now know that this relationship has a statistical nature (Berkhuijsen 1987). The statistical relation D − n0 for the modeled sample has the form D ~ n0-0.33 with the correlation coefficient ~0.77, which does not contradict the result of Berkhuijsen (1986) of D ~ n0− 0.39  ± 0.04.

5. Conclusions

We have modeled the statistics of the SNRs evolving in the three-phase ISM. The evolution of SNRs in various conditions of the ISM was considered, taking into account the effect of the total interstellar pressure. We assumed that the X-ray emission from the SNRs is thermal. Using the Monte Carlo method, we then modeled the set of SNRs by varying the values of the initial (explosion energy and ejected mass of the SN) and environmental parameters (conditions in the ISM), which control the evolution and final fate of the SNR. Among many other statistical relations, the size distribution of SNRs is very sensitive to the density distribution in the ISM. In the three-phase ISM the shape of this relation strongly depends on the filling factor of phases of the ISM.

This simple method is only effective for a statistically complete and homogeneous sample of observed SNRs. Fortunately, the recently published detailed catalog of SNRs in the nearby galaxy M 33 by L10 contains all the information needed for our analysis.

We showed that the population of SNRs with an X-ray hardness ratio of about − 0.5 yields the statistically most complete sample of objects that is free from various selection effects. We selected 48 such SNRs from the total numbers of 82 X-ray SNRs in the list of L10 for a comparison with the modeled SNRs with the same HR values. From the comparison of these two sets of SNRs we obtained the following results:

  • the volume-filling factor of the warm phase of the ISM ofM 33 is ~90%;

  • the birthrate of SNRs in M 33 is 6.7−7.1 SNRs per millennium for the inner 4.3 kpc.

The estimate of the total number of SNRs in M 33 depends on the total interstellar pressure of the galaxy and, also, on the definition of the SNR lifetime. The SNR was considered to exist when the shock Mach number was equal to or higher than 2. Our model predicts the existence of at least 1000 such alive SNRs in M 33, which occupy less than 1% of the galaxy volume within R < 4.3 kpc.

The modeled set of SNRs shows several statistical relations that also exist in the observed populations of SNRs, such as the shape of the relation N − D, the negative correlation between the apparent ambient density n0 and diameter D, and the lack of a statistical correlation between X-ray luminosity and diameter.

Acknowledgments

This work was supported by the Science Development Foundation under the President of the Republic of Azerbaijan – Grant No. EIF-2010-1(1)-40/05. The author is grateful to the referee, Elly Berkhuijsen, for her careful reading and invaluable comments and suggestions, which greatly improved this paper.

References

  1. Asvarov, A. I., Guseinov, O. H., Kasumov, F. K., & Dogel’, V. A. 1990, A&A, 229, 196 [NASA ADS] [Google Scholar]
  2. Badenes, C., Maoz, D., & Draine, B. T. 2010, MNRAS, 407, 1301 [NASA ADS] [CrossRef] [Google Scholar]
  3. Berkhuijsen, E. M. 1986, A&A, 166, 257 [NASA ADS] [Google Scholar]
  4. Berkhuijsen, E. M. 1987, A&A, 181, 398 [NASA ADS] [Google Scholar]
  5. Bisnovatyi-Kogan, G. S., & Silich, S. A. 1995, Rev. Mod. Phys., 67, 661 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blinnikov, S. I., Imshennik, V. S., & Utrobin, V. P. 1982, SvA Lett., 8, 361 [Google Scholar]
  7. Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chevalier, R. A. 1974, ApJ, 188, 501 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cioffi, D. F., McKee, C. F., & Bertschinger, E. 1988, ApJ, 334, 252 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cox, D. P. 1972, ApJ, 178, 159 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cox, D. P., & Anderson, P. R. 1982, ApJ, 253, 268 [NASA ADS] [CrossRef] [Google Scholar]
  12. Draine, B. T., & Woods, D. T. 1991, ApJ, 383, 621 [NASA ADS] [CrossRef] [Google Scholar]
  13. Franco, J., Miller, III, W. W., Arthur, S. J., Tenorio-Tagle, G., & Terlevich, R. 1994, ApJ, 435, 805 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fusco-Femiano, R., & Preite-Martinez, A. 1984, ApJ, 281, 593 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ghavamian, P., Schwartz, S. J., Mitchell, J., Masters, A., & Laming, J. M. 2013, Space Sci. Rev. [Google Scholar]
  16. Gordon, S. M., Kirshner, R. P., Long, K. S., et al. 1998, ApJS, 117, 89 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gordon, S. M., Duric, N., Kirshner, R. P., Goss, W. M., & Viallefond, F. 1999, ApJS, 120, 247 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hughes, J. P., Helfand, D. J., & Kahn, S. M. 1984, ApJ, 281, L25 [NASA ADS] [CrossRef] [Google Scholar]
  19. Landau, L. D., & Lifshic, E. M. 1986, Gidrodinamika (in Russian) (Moscow: Nauka) [Google Scholar]
  20. Long, K. S., Blair, W. P., Winkler, P. F., et al. 2010, ApJS, 187, 495 (L10) [NASA ADS] [CrossRef] [Google Scholar]
  21. Mansfield, V. N., & Salpeter, E. E. 1974, ApJ, 190, 305 [NASA ADS] [CrossRef] [Google Scholar]
  22. Mathewson, D. S., Ford, V. L., Dopita, M. A., et al. 1983, ApJS, 51, 345 [NASA ADS] [CrossRef] [Google Scholar]
  23. Mathewson, D. S., Ford, V. L., Dopita, M. A., et al. 1984, ApJS, 55, 189 [NASA ADS] [CrossRef] [Google Scholar]
  24. McKee, C. F., & Hollenbach, D. J. 1980, ARA&A, 18, 219 [NASA ADS] [CrossRef] [Google Scholar]
  25. McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ostriker, J. P., & McKee, C. F. 1988, Rev. Mod. Phys., 60, 1 [NASA ADS] [CrossRef] [Google Scholar]
  27. Petruk, O. 2006 [arXiv:astro-ph/0604057] [Google Scholar]
  28. Plucinsky, P. P., Williams, B., Long, K. S., et al. 2008, ApJS, 174, 366 [NASA ADS] [CrossRef] [Google Scholar]
  29. Sedov, L. I. 1977, Similarity methods and dimensional analysis in mechanics (Moscow: Nauka) [Google Scholar]
  30. Tammann, G. A., Loeffler, W., & Schroeder, A. 1994, ApJS, 92, 487 [NASA ADS] [CrossRef] [Google Scholar]
  31. Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
  32. Tüllmann, R., Gaetz, T. J., Plucinsky, P. P., et al. 2011, ApJS, 193, 31 (T11) [NASA ADS] [CrossRef] [Google Scholar]
  33. Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
  34. Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
  35. Zel’dovich, Y. B., & Raizer, Y. P. 1966, Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena (Moscow: Nauka) [Google Scholar]
  36. Zombeck, M. 2007, Handbook of Space Astronomy and Astrophysics, 3nd edn. (Cambridge University Press) [Google Scholar]

All Tables

Table 1

Parameters of observed and modeled SNRs, selected according to the criterion of − 0.7 ≤ HR ≤  −0.3.

In the text

All Figures

thumbnail Fig. 1

Dependence of the expansion parameter m on time for an SNR with E0 = 1051  erg,   n0 = 0.5  cm-3 and P04 = 4 × 104   K cm-3. The solid line corresponds to the case of evolution with the effect of pressure of the ISM, the dashed line for the case without pressure. The vertical lines denote the moments when the shock Mach number Ms = 2 (left) and Ms = 1 (right).
In the text
thumbnail Fig. 2

Dependence of the Mach number on the diameter of the SNR for E0 = 1051  erg and n0 = 0.5  cm-3 for the two values of pressure P04 = 2.17 (thick lines) and P04 = 8.6 (thin lines). The solid and dotted curves describe the solution of the system of Eqs. (6)–(8) with and without the pressure of the ISM, and the dashed curves describe the Sedov solution without radiative cooling. The horizontal dash-dotted line corresponds to the point Ms = 2.
In the text
thumbnail Fig. 3

Evolution of the [0.35 − 1.1] keV (thick curves) and [1.1 − 2.6] keV (thin curves) X-ray photon count rates as a function of SNR diameter for the ambient particle densities 1, 0.1, and 0.01 cm-3, as denoted near the corresponding curves, and E0 = 1051 erg, NH = 1021 cm-2 as in the case of M 33.
In the text
thumbnail Fig. 4

Hardness ratio (HR, see text for definition) evolution with diameter of SNR for E0 = 1051  erg and n0 = 0.01, 0.1,  and  1.0  cm-3. Filled circles correspond to the 44 SNRs from the T11 catalog.
In the text
thumbnail Fig. 5

Hardness ratio distribution of SNRs in M 33. The solid line histogram corresponds to 82 SNRs from L10, the histogram for 45 SNRs with HRs calculated by using the data from T11 is drawn with dashed lines.
In the text
thumbnail Fig. 6

Size distribution of observed SNRs in M 33 and Monte Carlo simulated SNRs for various values of the warm phase filling-factor (indicated in the panels). In simulations ΔT = 250 yr, the lifetime is determined as t = t(Ms = 2) and the largest dimension of simulated SNRs is D = D(Ms = 2). The bin size is 7 pc.
In the text
thumbnail Fig. 7

Diameter distribution of SNRs with −0.7 ≤ HR ≤  −0.3 in M 33 (dashed lines) and modeled SNRs (solid lines). The data for 48 SNRs in M 33 are taken from L10, the 49 modeled SNRs represent the scenario of 90% warm gas filling-factor and a birthrate of 150 yr. The size of the bins is 10 pc.
In the text
thumbnail Fig. 8

Diameter distribution of 1050 modeled SNRs with Ms ≥ 2 together with the distributions shown in Fig. 7. For the modeled SNRs the filling-factor of the warm phase of the ISM is 90%, the birthrate is 1/150 yr-1, and P0 = 8.6 × 104 K cm-3.

In the text
thumbnail Fig. 9

Normalized cumulative N − D distribution for X-ray SNRs with − 0.7 ≤ HR ≤  − 0.3 in M 33 (filled squares) and two representative (run 1-open squares, run 3-open diamonds) modeled SNR subsets. The data for 48 SNRs in M 33 are taken from L10; for the modeled SNRs the filling-factor of the warm phase of the ISM is 90%.

In the text
thumbnail Fig. 10

Dependence of 0.35−2 keV photon count rates of M 33 SNRs on the diameters. The 48 SNRs with −0.7 ≤ HR ≤  −0.3 are denoted with filled circles, open circles denote the remaining 34 SNRs. All the data are taken from the list in L10.
In the text
thumbnail Fig. 11

Dependence of (0.35−2) keV photon count rates on the diameter for modeled SNRs. The normalization is arbitrary. In this run for the 90% warm-phase filling-factor and the mean total pressure 4 × 104 K cm-3 the number of SNRs with Ms ≥ 2 is 1530, of which 53 SNRs with −0.7 ≤ HR ≤  −0.3 are presented in this figure.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.