| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322428 | |
| Published online | 23 December 2013 | |
Radial velocity variations in the young eruptive star EX Lupi⋆,⋆⋆
1 European Space Agency (ESA-ESTEC, SRE-S), PO Box 299, 2200 AG Noordwijk, The Netherlands
e-mail: akospal@rssd.esa.int
2 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
3 Departamento de Física Teórica, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Cantoblanco, Madrid, Spain
4 Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences, PO Box 67, 1525 Budapest, Hungary
5 Departamento de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, Av. Gran Bretaña 1111, 5030 Casilla, Valparaíso, Chile
6 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
Received: 1 August 2013
Accepted: 21 October 2013
Context. EX Lup-type objects (EXors) are low-mass pre-main sequence objects characterized by optical and near-infrared outbursts attributed to highly enhanced accretion from the circumstellar disk onto the star.
Aims. The trigger mechanism of EXor outbursts is still debated. One type of theory requires a close (sub)stellar companion that perturbs the inner part of the disk and triggers the onset of the enhanced accretion. Here, we study the radial velocity (RV) variations of EX Lup, the prototype of the EXor class, and test whether they can be related to a close companion.
Methods. We conducted a five-year RV survey, collecting 54 observations with HARPS and FEROS. We analyzed the activity of EX Lup by checking the bisector, the equivalent width of the Ca 8662 Å line, the asymmetry of the Ca II K line, the activity indicator SFEROS, the asymmetry of the cross-correlation function, the line depth ratio of the VI/FeI lines, and the TiO, CaH 2, CaH 3, CaOH, and Hα indices. We complemented the RV measurements with a 14-day optical/infrared photometric monitoring to look for signatures of activity or varying accretion.
Results. We found that the RV of EX Lup is periodic (P = 7.417 d), with stable period, semi-amplitude (2.2 km s-1), and phase over at least four years of observations. This period is not present in any of the above-mentioned activity indicators. However, the RVs of narrow metallic emission lines suggest the same period, but with an anti-correlating phase. The observed absorption line RVs can be fitted with a Keplerian solution around a 0.6 M⊙ central star with msini = (14.7 ± 0.7) MJup and eccentricity of e = 0.24. Alternatively, we attempted to model the observations with a cold or hot stellar spot as well. We found that in our simple model, the spot parameters needed to reproduce the RV semi-amplitude are in contradiction with the photometric variability, making the spot scenario unlikely.
Conclusions. We qualitatively discuss two possibilities to explain the RV data: a geometry with two accretion columns rotating with the star, and a single accretion flow synchronized with the orbital motion of the hypothetical companion; the second scenario is more consistent with the observed properties of EX Lup. In this scenario, the companion’s mass would fall into the brown dwarf desert, which, together with the unusually small separation of 0.06 au would make EX Lup a unique binary system. The companion also has interesting implications on the physical mechanisms responsible for triggering the outburst.
Key words: stars: formation / circumstellar matter / infrared: stars / techniques: radial velocities / stars: individual: EX Lupi
This work is based in part on observations made with ESO Telescopes at the La Silla Paranal Observatory under program IDs 079.A-9017, 081.A-9005, 081.A-9023, 081.C-0779, 082.C-0390, 082.C-0427, 083.A-9011, 083.A-9017, 084.A-9011, 085.A-9027, 086.A-9006, 086.A-9012, 087.A-9013, 087.A-9029, and 089.A-9007.
Tables 2 and 3 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
EX Lup-type objects (EXors) form a spectacular group of low-mass pre-main sequence (PMS) objects, characterized by repetitive optical outbursts of 1–5 mag, lasting from a few months to a few years. The outburst is usually attributed to enhanced accretion from the inner circumstellar disk (within ~0.1 au) to the stellar surface, caused by an instability in the disk (Herbig 1977, 2008). In quiescence, EXors typically accrete at a rate of 10-10 to 10-7 M⊙ yr-1, while in outburst, accretion rates are about an order of magnitude higher (Lorenzetti et al. 2012). The brief episodes of highly increased accretion may significantly contribute to the build-up of the final stellar mass. Moreover, the outbursts have a substantial effect on the circumstellar material. The importance of the outburst phase on early stellar/disk evolution was demonstrated by Ábrahám et al. (2009), for example, who discovered episodic crystallization of silicate grains in the disk surface due to the increased luminosity and temperature during the 2008 outburst of EX Lup, resulting in material that forms the building blocks of primitive comets.
The origin of these accretion outbursts is still highly debated. One type of explanation includes viscous-thermal instabilities in the disk (Bell & Lin 1994), a combination of gravitational and magneto-rotational instability (Armitage et al. 2001), or accretion of clumps in a gravitationally unstable disk (Vorobyov & Basu 2005, 2006). Another model proposes that accretion onto a strongly magnetic protostar is inherently episodic if the disk is truncated close to the corotation radius (D’Angelo & Spruit 2010). Yet another type of theory involves a close stellar or sub-stellar companion that perturbs the disk and triggers the onset of the enhanced accretion. The actual physical process could be thermal instability induced by density perturbations due to a massive planet in the disk (Lodato & Clarke 2004), for example, or tidal effects from close companions (Bonnell & Bastien 1992). Such explanations are especially favored in cases where the accretion rate increases by several orders of magnitude in just a few weeks or few months, because these rapid rise times are difficult to explain without external perturbations.
It is an open question whether all young eruptive stars have companions. Among the FU Orionis-type objects, which are young stars producing even more powerful and longer lasting outbursts than EXors, binarity is not unheard of. For instance, a companion to the prototype object FU Ori was found with the direct imaging technique at a projected distance of 225 au (Wang et al. 2004). Some EXors are also in binaries, such as the spectroscopic binary system UZ Tau E (Jensen et al. 2007), or the visual binaries V1118 Ori (separation 0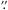 18; Reipurth et al. 2007) and VY Tau (separation 0
18; Reipurth et al. 2007) and VY Tau (separation 0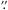 66; Leinert et al. 1993). Since the triggering mechanism requires a companion that perturbs the inner part of the disk, typically at a few tenths of an au, radial velocity (RV) methods could be suitable to find such companions. However, many of the young eruptive stars have never been searched for close companions with RV methods, mostly because of the difficulty of measuring the RV in young, chromospherically active and/or actively accreting stars.
66; Leinert et al. 1993). Since the triggering mechanism requires a companion that perturbs the inner part of the disk, typically at a few tenths of an au, radial velocity (RV) methods could be suitable to find such companions. However, many of the young eruptive stars have never been searched for close companions with RV methods, mostly because of the difficulty of measuring the RV in young, chromospherically active and/or actively accreting stars.
In this paper we present a spectroscopic and photometric monitoring of EX Lup, the prototypical EXor object, focusing on the possible existence of a close companion and on the accretion process. EX Lup is an M0.5-type young star situated not far from the Lupus 3 star-forming region, at a distance of 155 pc (Lombardi et al. 2008). Over the last six decades, EX Lup has exhibited two large eruptions (ΔV ≳ 5 mag), and several smaller (ΔV = 1 − 3 mag) outbursts. The latest outburst happened in 2008. Since then, the system has been mostly quiescent, with minor fluctuations around V = 12 − 13 mag. Several authors have searched for a companion to EX Lup with different methods without any success. Ghez et al. (1997) used K-band direct imaging and were able to exclude the presence of a companion between about 150 au and 1800 au. Bailey (1998) used spectro-astrometry, but found no companion down to 15 au. A few sporadic RV measurements with different instruments (two values in Melo 2003, three values in Guenther et al. 2007, and four values in Herbig 2007) were inconclusive in terms of a companion.
This study is the continuation of a series of papers by our group investigating the quiescent state and the extreme outburst of EX Lup in 2008 (Sipos et al. 2009; Ábrahám et al. 2009; Goto et al. 2011; Kóspál et al. 2011; Juhász et al. 2012; Sicilia-Aguilar et al. 2012). In Sect. 2 we summarize the observations and describe the steps of data reduction. In Sect. 3 we analyze the RV data and different stellar activity indicators, present our spot model, and study the photometric light curves. In Sect. 4 we discuss the implications of our results in the broader context of young eruptive stars.
2. Observations and data reduction
2.1. Radial velocity measurements
FEROS.
We obtained 57 spectra of EX Lup between 2007 July and 2012 July with FEROS, the Fiber-fed Extended Range Optical Spectrograph (Kaufer et al. 1999), which is an échelle spectrograph mounted at the MPG/ESO 2.2 m telescope at La Silla Observatory, Chile. The spectra cover the 3500–9200 Å wavelength range with high resolution (R = 48 000), distributed in 39 different échelle orders. The wavelength calibration was done with a thorium-argon (ThAr) lamp and spectra were obtained in object-cal (simultaneous exposure to the ThAr lamp during the target observation) and in object-sky mode (simultaneous sky exposure). Exposure times were typically 1200–1500 s, but in some cases were increased to 3000 s because of bad weather conditions. The spectra were reduced using the online Data Reduction System (DRS) on site, which included the following steps: detection of spectral orders, wavelength calibration, background subtraction, flatfield correction, and order extraction. Finally, the DRS rebinned the reduced spectra to constant wavelength steps and merged the individual orders. The signal-to-noise ratio in the final spectra is between 5 and 80. Given the known problem with the barycentric correction provided by the FEROS pipeline (Müller et al. 2013), we recalculated the barycentric correction by using the IDL routine baryvel.pro1. The necessary corrections were in the range of 0–70 m/s, with a seasonal variation.
HARPS.
We obtained ten spectra of EX Lup between 2008 May and 2009 March with HARPS, the High Accuracy Radial velocity Planet Searcher (Mayor et al. 2003), which is a fiber-fed high-resolution (R = 115 000) spectrograph mounted at the 3.6 m telescope at La Silla Observatory, Chile. The instrument is able to obtain target and ThAr calibration spectra simultaneously, as well as target and sky spectra at once. The spectra cover the 3780–6910 Å wavelength range, distributed over the échelle orders 89–161. Exposure times were between 600 s and 1200 s. The reduced data were obtained from the ESO archive pipeline processed data query2. The spectra have similar signal-to-noise ratios to the FEROS spectra.
RV determination.
Because EX Lup is a highly active star, special care had to be taken when determining its RV. During the 2008 outburst, except for a very veiled Li 6708 Å line, no photospheric absorption lines were visible in the optical and near-infrared spectra of EX Lup (Sicilia-Aguilar et al. 2012; Kóspál et al. 2011). Thus RV determination was not possible from those spectra. Before the outburst in 2007, and after the outburst in 2009–2012, however, several photospheric absorption lines were present. We used the list of emission lines detected by Sicilia-Aguilar et al. (2012, see their Table 2), and checked whether we see emission at these wavelengths, either as pure emission lines, or as little narrow emission peaks superimposed on broader absorption lines. The affected absorption lines were discarded from the RV analysis.
To obtain RV from the absorption lines (i.e., the RV of the central star), we cross-correlated the object spectra with a synthetic template spectrum. We chose a synthetic template with an effective temperature of Teff = 3750 K, surface gravity of log g = 4.0, and solar metallicity, because EX Lup is an M0.5-type star with an estimated stellar mass of M∗ = 0.6 M⊙ and stellar radius of R∗ = 1.6 R⊙ (Gras-Velázquez & Ray 2005; Sipos et al. 2009; Aspin et al. 2010). We synthesized the template spectrum using the SPECTRUM software3 by Gray & Corbally (1994). Following the method of Reiners et al. (2012), we broadened the synthetic spectrum to account for the line broadening due to the stellar rotation in the object spectrum. Owing to the finite spectral resolution of FEROS (and the resulting instrumental broadening of about 2−3 km s-1), we could only determine an upper limit of vsini < 3 km s-1 for EX Lup. We obtained the same upper limit for vsini from the HARPS spectra, which is consistent with the detection limit of HARPS without observing a large sample of M dwarfs (cf. Houdebine 2010; Reiners et al. 2012).
We used similar RV determination procedures for both FEROS and HARPS. In the case of FEROS, we used 10 échelle orders between 5580 Å and 7875 Å, and discarded shorter wavelengths because the signal-to-noise ratio was too low. We avoided regions contaminated by telluric absorption features. We calculated the cross-correlation function (CCF) of the observed and the synthetic spectrum for each individual order separately. By fitting a Gaussian to the CCF, we determined the RV shift for each order. We checked whether there is any systematic difference in the RV values obtained for bluer or redder orders, but detected no difference. Thus, we calculated a weighted average of the RVs from all orders. The errors for the average values were calculated using the relation derived in Setiawan et al. (2003). In the case of HARPS, we used nine different orders between 5450 Å and 6865 Å, again avoiding telluric absorption lines, and determined the RV and its uncertainty the same way as for FEROS, using the same CCF template. In total we obtained 45 FEROS and 9 HARPS RV values. Five FEROS spectra were unusable because of very low signal-to-noise ratio caused by bad weather or high airmass, while seven FEROS spectra and one HARPS spectrum had to be discarded because they were taken in 2008 when EX Lup was in outburst. The results are listed in Table 2.
The quiescence spectra of EX Lup are very rich in emission lines. Such lines are assumed to form in the hot gas within the accretion columns (e.g., Beristain et al. 1998), and given that they appear at near-zero velocity, they probably originate from hot gas not far from the stellar photosphere. To understand the causes of the EX Lup RV variations, we also measured separate RVs for the emission lines. For this purpose, we selected a number of strong, narrow (FWHM typically around 10−20 km s-1) emission lines in the quiescent spectra of EX Lup. We tested three different sets of lines: (a) 60 emission lines identified in the one quiescent spectrum with the best signal-to-noise ratio; (b) 133 emission lines identified by Sicilia-Aguilar et al. (2012) in the outburst spectra; and (c) 25 Fe II lines, the strongest ones among the emission lines visible in the quiescent spectra (a subset of the 133 lines in point b). We used the RVSAO/EMSAO package in IRAF to determine RV from the emission lines by fitting Gaussians to the detected narrow emission lines. We found that the RVs obtained with the different sets of lines were consistent within the measurement uncertainties, although there is a hint of small systematic differences between the ionized and the neutral lines. In the following, we will use the emission line RVs detemined in point (b) because these have the smallest uncertainties. These results are also listed in Table 2.
2.2. Optical and infrared light curves
Spitzer.
We obtained 3.6 μm and 4.5 μm observations of EX Lup with IRAC, the infrared camera on-board the Spitzer Space Telescope, as part of a post-He program aimed at monitoring low- and intermediate-mass young stellar objects (PID: 60167, PI: P. Ábrahám). Observations were taken between 2010 April 24 and May 7 with an approximately one-day cadence. On each day, images were taken in full array mode, using an exposure time of 0.2 s and a 5-point dithering. We downloaded corrected basic calibrated data (CBCD) produced by the pipeline version S18.18 from the Spitzer Archive. Photometry was made on individual CBCD frames that were corrected for array location dependence. We performed aperture photometry with an aperture radius of 2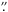 4 (2 pixels), and sky annulus between 14
4 (2 pixels), and sky annulus between 14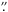 4 and 24′′ (12 and 20 pixels). For the sky estimates, we used an iterative sigma-clipping method with a clipping threshold of 3σ. We applied pixel phase correction to the 3.6 μm data. Aperture corrections were 1.205 at 3.6 μm and 1.221 at 4.5 μm (IRAC Instrument Handbook v2.0). Finally, we computed the average and rms of the individual flux values measured in the different dither positions (at each band). The obtained fluxes and their uncertainties can be found in Table 3.
4 and 24′′ (12 and 20 pixels). For the sky estimates, we used an iterative sigma-clipping method with a clipping threshold of 3σ. We applied pixel phase correction to the 3.6 μm data. Aperture corrections were 1.205 at 3.6 μm and 1.221 at 4.5 μm (IRAC Instrument Handbook v2.0). Finally, we computed the average and rms of the individual flux values measured in the different dither positions (at each band). The obtained fluxes and their uncertainties can be found in Table 3.
REM.
Ground-based optical and near-infrared observations were obtained with the 60 cm diameter Rapid Eye Mount (REM) telescope located in La Silla, Chile (Covino et al. 2004). The telescope is equipped with two cameras that are operated simultaneously. Optical images using the V filter were taken with the ROSS instrument, while infrared images using the J, H, and K′ filters were taken with the REMIR instrument: ROSS has an 1024 × 1024 pixel Apogee Alta CCD camera with a pixel scale of 0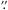 575 and REMIR has a 512 × 512 Rockwell Hawaii detector with a pixel scale of 1
575 and REMIR has a 512 × 512 Rockwell Hawaii detector with a pixel scale of 1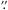 2. Both cameras have a field of view of about 10′ × 10′. Observations were executed in service mode during 14 nights between 2010 April 24 and May 9, in most cases simultaneously with the Spitzer observations.
2. Both cameras have a field of view of about 10′ × 10′. Observations were executed in service mode during 14 nights between 2010 April 24 and May 9, in most cases simultaneously with the Spitzer observations.
Nine V-band images were obtained on each night with an exposure time of 60 s. We corrected the images for bias, dark, and flatfield in the usual way. Then, we shifted and co-added the nine frames in order to increase the signal-to-noise ratio. We obtained aperture photometry on the co-added frames using an aperture radius of 4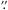 6 (8 pixels) and a sky annulus between 17
6 (8 pixels) and a sky annulus between 17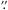 25 and 23′′ (30 and 40 pixels). We calculated instrumental magnitudes for the science target and four other stars in the field, to be used as comparison stars in differential photometry. For absolute calibration of the magnitude scale, V magnitudes of four comparison stars (NOMAD 0496-0417325, 0496-0417355, 0496-0417185, and 0496-0417090) were taken from the NOMAD catalog (Zacharias et al. 2005).
25 and 23′′ (30 and 40 pixels). We calculated instrumental magnitudes for the science target and four other stars in the field, to be used as comparison stars in differential photometry. For absolute calibration of the magnitude scale, V magnitudes of four comparison stars (NOMAD 0496-0417325, 0496-0417355, 0496-0417185, and 0496-0417090) were taken from the NOMAD catalog (Zacharias et al. 2005).
The near-infrared images were obtained with exposure time of 5 s (in the H and K′ filters) or 10 s (in the J filter). Each observation was taken at five dither positions, which were combined to eliminate the sky signal and correct for flatfield differences. We performed aperture photometry on the individual dither frames, with a radius of 3 6 (3 pixels) and a sky annulus between 12′′ and 16′′ (10 and 13 pixels). For the photometric calibration, we used the Two Micron All Sky Survey (2MASS) catalog (Cutri et al. 2003). To avoid any remaining flatfield inhomogeneities within the image, we used the two closest bright 2MASS stars with AAA quality flag (2MASS16031144-4018178, and 2MASS 16030056-4018290) as comparison stars. We determined the offset between the instrumental and the 2MASS magnitudes by combining the five dither measurements of both comparison stars using an outlier-resistant algorithm. No color term was needed in this transformation. The uncertainty of the final photometry is the quadratic sum of the formal uncertainty of the aperture photometry, the scatter of the photometry of the individual dither frames, and photometric calibration. The resulting photometry is listed in Table 3.
6 (3 pixels) and a sky annulus between 12′′ and 16′′ (10 and 13 pixels). For the photometric calibration, we used the Two Micron All Sky Survey (2MASS) catalog (Cutri et al. 2003). To avoid any remaining flatfield inhomogeneities within the image, we used the two closest bright 2MASS stars with AAA quality flag (2MASS16031144-4018178, and 2MASS 16030056-4018290) as comparison stars. We determined the offset between the instrumental and the 2MASS magnitudes by combining the five dither measurements of both comparison stars using an outlier-resistant algorithm. No color term was needed in this transformation. The uncertainty of the final photometry is the quadratic sum of the formal uncertainty of the aperture photometry, the scatter of the photometry of the individual dither frames, and photometric calibration. The resulting photometry is listed in Table 3.
 |
Fig. 1 Top: GLS periodogram of the FEROS RV values, showing the best period of 7.417 days. The horizontal dashed line indicates the FAP level of 10-4. Bottom: window function. |
3. Results and analysis
3.1. Period analysis of the RV data and orbital solution
To search for periodicities in the RV values measured from the absorption lines, we used the generalized Lomb-Scargle (GLS) method (Zechmeister & Kürster 2009). Since the number of available HARPS points is not sufficient to carry out an independent RV period determination, we first considered the FEROS data only, and afterwards we combined the FEROS and HARPS data points, and repeated our analysis. The data points were weighted with the inverse square of their uncertainties. Figure 1 shows the GLS periodogram calculated for the 45 FEROS points. Two significant periods with false alarm probability (FAP) of <10-4 are visible, one at around 1 day, which is an alias caused by the sampling (see the window function in the bottom panel of Fig. 1), and another one at 7.417 days. The RV curve phase-folded with the 7.417 day period is plotted in Fig. 2.
Figure 2 exhibits a clear periodic signal with an RV semi-amplitude of ≈2.2 km s-1. The shape of the curve is asymmetric, with the increasing part approximately 1.7 times longer than the decreasing part. In the figure, we color-coded the different observing seasons during our five-year monitoring program. No systematic differences can be seen between the different seasons, which suggests that the period, phase, and amplitude of the RV variations were stable for at least four years, between 2009 and 2012. The three data points from 2007 are also consistent with the later observations, implying that the RV variations were largely unaffected by the largest outburst of EX Lup ever observed which occurred in 2008.
 |
Fig. 2 Top: best Keplerian fit to the absorption line RVs for the combined FEROS and HARPS RV data set (with RVlin). The different colors indicate different observing seasons (-1 stands for the first half of the year, -2 for the second half). Circles represent FEROS and squares HARPS data points. Middle: residua with the same color and shape coding. Bottom: emission line RVs with the same color and shape coding. |
Best-fitting parameters of the Keplerian solution fitted to the RV measurements of EX Lup (with RVlin, using the combined FEROS and HARPS dataset).
The shape of the phase-folded RV curve suggests the possible existence of a companion on an eccentric orbit around EX Lup. We fitted a Keplerian solution to the FEROS RVs using both GLS and the idl code RVlin4 (Wright & Howard 2009). The RVlin code can handle data from different instruments by fitting parameters to correct for the relative offset between them, thus, we used it to fit the combined FEROS+HARPS data sets, and determined an offset of 0.291 km s-1 between the two instruments. The code also calculates uncertainties for the fitted parameters using a bootstrapping algorithm (Xuesong Wang et al. 2012). The orbital parameters determined from the fit for the combined data sets are listed in Table 1. The values derived for the different data sets using different methods are all consistent within the uncertainties.
To calculate msini and the semi-major axis a, we assumed a stellar mass of M∗ = 0.6 M⊙ for EX Lup (Gras-Velázquez & Ray 2005). Figure 2 shows the best fit for the combined data set, which has a FAP of 6.7 × 10-27. After subtracting the 7.417 day period Keplerian fit from the RV data, we searched for sine periodicities in the RV residuals, but found no significant periods with FAP < 10-4.
As described in Sect. 2.1, we calculated RVs from those narrow emission lines that are isolated and not superimposed on broader absorption features. Similar but weaker emission lines may distort the absorption lines and might introduce artificial RV signals, despite our best efforts to discard the affected absorption lines from our analysis. To make sure that this is not the case, we performed a period analysis on the RVs of the emission lines. The algorithm found no significant periods, although a small peak is present at about 7 days with FAP of 10-2. In Fig. 2, we plotted the RVs of the emission lines phase folded with the 7.417 d period. The data points have a large scatter compared to the RVs determined from the absorption lines, and they show instead a sinusoidal variation with a semi-amplitude of about 0.8 km s-1. From this exercise, it is clear that emission components moving at this velocity cannot cause the RV signal observed in the absorption lines.
3.2. Analysis of the stellar activity
The presence of a companion is not the only possible explanation for periodic RV changes. Photospheric stellar activity, i.e., dark (cold) or bright (hot) spots, are known to result in periodic RV variations (e.g., Lanza et al. 2011, and references therein). For instance, a cool spot on the stellar surface would produce a deficit of emission at the spot’s velocity within the line profile, and the rotation of the star then leads to an RV signal which is periodic with the rotational period. Additionally, RV measurements from lines with different temperature sensitivities would yield different RV amplitudes (e.g., Hatzes 1999). Thus, by analyzing the distortion of the spectral lines and their correlation with the RV, or by analyzing line ratios sensitive to the effective temperature, it is possible to verify the presence of stellar spots. In addition to the photospheric spots, cool stars, especially the rapidly rotating younger ones, have very active chromospheres (Montes et al. 2004). The chromospheric spectrum is dominated by emission lines, which again can distort the photospheric absorption line profiles, or in extreme cases can even fill them up or turn them into emission lines. Chromospheric activity may increase the noise of RV measurements, but it may also produce periodic RV signals over a few rotational periods (Santos et al. 2003). In the following, we check whether the RV variations and their periodicity observed for EX Lup can be due to stellar activity.
Bisector analysis.
The CCF represents the mean absorption line profile of the star. We computed the CCF for each spectrum by combining the individual CCFs of the different orders into a master CCF using a robust averaging method that assigns less weight to the deviating orders. One way to analyze its distortion is to compute the bisector (e.g., Queloz et al. 2001; Gray 2005), as illustrated in Fig. 3. Following Dall et al. (2006), we computed the mean bisector velocities for different regions in the CCF, and estimated the formal uncertainty of the mean values from the dispersion of the bisector points within that region. Following Povich et al. (2001), we defined three regions: v1 for 0.4 ≤ CCF ≤ 0.55, v2 for 0.55 ≤ CCF ≤ 0.7, and v3 for 0.7 ≤ CCF ≤ 0.9 (Fig. 3). These CCF ranges were suitable for most spectra; however, in a few cases the continuum level was high and affected the lowest bisector points in the v1 range. These measurements were discarded from further analysis. In the next step, we calculated the bisector velocity span (BVS = v3 − v1), the bisector curvature (BC = (v3 − v2) − (v2 − v1)), and the bisector velocity displacement (BVD = (v1 + v2 + v3)/3 − λc, where λc is the observed central wavelength).
We checked whether the BVSs correlate with the RV, which is expected if the RV variations are caused by rotational modulation due to starspots (e.g., Queloz et al. 2001). Figure 4 shows the BVS plotted as a function of the RV and the RV residua (after the subtraction of the Keplerian solution). The linear Pearson correlation coefficients (Pearson 1920) for the two graphs are 0.08 and 0.27, respectively, indicating no correlation between the quantities. As an independent check, we also performed a bisector analysis on carefully selected individual absorption lines in the FEROS spectra. Similarly to our previous results, no correlation between the BVS and the RV was found. We calculated GLS periodograms for the BVS, BC, and BVD (Fig. 5), but found no significant period with FAP smaller than 10-4. As indicated by the arrows in the figure, no peak is present at a period of 7.417 days.
 |
Fig. 3 Bisector of the CCF computed from the FEROS spectrum of EX Lup observed on 2010 July 23. |
 |
Fig. 4 BVS values plotted against the RV (left) and against the RV residua (right). |
 |
Fig. 5 GLS periodograms of the BVS, BC, BVD, CCF asymmetry, and the LDR of V I and F I. The arrows mark the 7.417 day RV period. The horizontal dashed lines indicate a FAP level of 10-4. |
Asymmetry of the CCF.
Distortions of the CCF profile can also be analyzed by first plotting the slope of the CCF at each velocity, then by integrating over the velocity axis with positive and negative slopes, respectively, and calculating the ratio of the positive and negative areas. For a perfectly symmetric Gaussian, this ratio would be 1, while for a distorted Gaussian, it would be below or over 1. We determined this measure of the CCF asymmetry for each order separately, then took their weighted average. Finally, we calculated the GLS periodogram (Fig. 5), but again found no significant periods, and no peak at a period of 7.417 days.
Temperature-sensitive spectral features.
A cool spot on the stellar surface, rotating in and out of view, changes the effective temperature of the visible stellar hemisphere. This has an influence on the strength of temperature-sensitive absorption lines or bands. For instance, Catalano et al. (2002) showed that both the 6268.87 Å V I line and the 6270.23 Å Fe I line become stronger with decreasing temperature, but the variation of the line depth of the low-excitation V I line is more pronounced than that of Fe I. For this reason, the line depth ratio (LDR) is a good tracer of changes in the effective surface temperature. We calculated the GLS periodogram of the LDR of V I and Fe I (Fig. 5), but found no significant period, and no peak at 7.417 days.
In the presence of a cool spot, bands like TiO, CaH, and CaOH may appear or strengthen (see Reid et al. 1995, who measured these bands in a large number of M dwarfs). Using our FEROS spectra, we determined the TiO 1, TiO 2, TiO 3, TiO 4, TiO 5, CaH 2, CaH 3, CaOH, and Hα indices as defined by Reid et al. (1995), and looked for periodic changes due to spots on the stellar surface. Similarly to the other stellar spot indicators discussed above, we found no significant period in the GLS periodograms of these spectral indices, and no peak at a period of 7.417 days.
 |
Fig. 6 Illustration of the calculation method of the CCF asymmetry. The quantity of asymmetry is determined by obtaining the quotient of the area of positive slope (red) and of negative slope (blue). The CCF displayed here was computed from the FEROS spectrum of EX Lup observed on 2010 July 23. |
Analysis of the Ca lines.
Larson et al. (1993) have shown that calcium lines in the stellar spectrum, such as the Ca II H and K lines at 3968 Å and 3933 Å and the Ca II infrared triplet at 8498 Å, 8542 Å, and 8662 Å are good indicators of stellar chromospheric activity. Since the Ca II H line is possibly blended with Hϵ, and the Ca II 8498 Å and 8542 Å lines are contaminated by terrestrial water vapor lines, we discarded them from further analysis and concentrated on the Ca II K line at 3933 Å and on the Ca II line at 8662 Å. For Caλ3933 Å we calculated the chromospheric activity index SFEROS and monitored its variation over time. SFEROS is defined as follows: 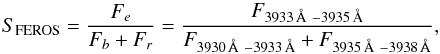 (1)where Fe, Fb, and Fr are the fluxes integrated over the wavelength ranges indicated in the equation above. These S-indices for the Ca II H and K lines were first defined by Vaughan et al. (1978), and they measure the strength of the line emission relative to the adjacent continuum, an established chromospheric activity indicator (e.g., Mittag et al. 2013). Additionally we calculated the equivalent width (EW) of Caλ8662 Å, and applied the method of the asymmetry analysis of the CCF to the emission core of the Ca II K line. We calculated GLS periodograms for all three indicators, but found no significant peak at the RV period of 7.417 d. The SFEROS index and the Caλ8662 Å line EW show a peak around 1.0 d with a FAP smaller than 10-5, which we interpret as a feature of the sampling effect. The Caλ8662 Å line EW reveals a strong peak at a FAP smaller than 10-5 at about 25 d. However, by looking at the window function of the EW values, it is apparent that this is a result of the sampling as well. The Ca II K asymmetry does not exhibit any significant peaks between 1 and 1000 d. We note that the Ca II infrared triplet is often considered a good accretion tracer (e.g., Muzerolle et al. 1998). EX Lup has a non-negligible accretion rate even in quiescence, and the broad wings of the Ca II lines (Fig. 3 in Sicilia-Aguilar et al. 2012) suggest that part of the line flux is related to accretion rather than to chromospheric activity.
(1)where Fe, Fb, and Fr are the fluxes integrated over the wavelength ranges indicated in the equation above. These S-indices for the Ca II H and K lines were first defined by Vaughan et al. (1978), and they measure the strength of the line emission relative to the adjacent continuum, an established chromospheric activity indicator (e.g., Mittag et al. 2013). Additionally we calculated the equivalent width (EW) of Caλ8662 Å, and applied the method of the asymmetry analysis of the CCF to the emission core of the Ca II K line. We calculated GLS periodograms for all three indicators, but found no significant peak at the RV period of 7.417 d. The SFEROS index and the Caλ8662 Å line EW show a peak around 1.0 d with a FAP smaller than 10-5, which we interpret as a feature of the sampling effect. The Caλ8662 Å line EW reveals a strong peak at a FAP smaller than 10-5 at about 25 d. However, by looking at the window function of the EW values, it is apparent that this is a result of the sampling as well. The Ca II K asymmetry does not exhibit any significant peaks between 1 and 1000 d. We note that the Ca II infrared triplet is often considered a good accretion tracer (e.g., Muzerolle et al. 1998). EX Lup has a non-negligible accretion rate even in quiescence, and the broad wings of the Ca II lines (Fig. 3 in Sicilia-Aguilar et al. 2012) suggest that part of the line flux is related to accretion rather than to chromospheric activity.
3.3. Spot model
In all our previous analyses we found no evidence of periodic stellar activity. Nevertheless, in the following we will assume that the 7.417 d period we found in the RVs is in fact due to stellar rotation, and we will try to find a spot model that can reproduce the observed ≈2.2 km s-1 semi-amplitude of the RV curve. Since there is no flat section in the RV curve, the spot should practically always be visible to a certain extent. Given the large RV semi-amplitude compared to the small vsini < 3 km s-1, we expect spots with large filling factors. We constructed a simple spot model and simulated a grid of single spots with different temperatures, sizes, and latitudes on the photosphere of EX Lup with different stellar inclinations. The results showed that typical cold or hot spots, covering a few per cent of the stellar surface and having a temperature difference of a few hundred K, are unable to reproduce the measured RV semi-amplitude. Thus, we had to explore more extreme parameters in our modeling. We found that a large cold spot covering practically a whole hemisphere, with a filling factor between 80% and 100%, with a temperature of 1500−2500 K cooler than the stellar photosphere at low latitudes (within 30° of the equator), and with low stellar inclinations (the angle between the line of sight and the stellar equator being between 0 and 30°) reproduced the observed RV semi-amplitude. Similarly, even if it is unrealistic, the only hot spot that produced an adequate fit to the RV semi-amplitude covered a whole hemisphere with a temperature of 10 500 K hotter than the photosphere at a latitude of 0°, and an inclination of 0°.
 |
Fig. 7 Light curves and RV curves of EX Lup. For clarity, the light curves were shifted along the y-axis by the amounts indicated on the right side. Dashed and dotted lines mark when the RV equals the systemic velocity. |
To test if any of these spot models could reproduce the observed photometric behavior, we plotted in Fig. 7 the light curves of EX Lup between 0.55 and 4.5 μm covering about two weeks in 2010 with an approximately daily cadence. We observed significant brightness changes in this period at all wavelengths. The curves between V and H exhibit similar shapes with a decreasing amplitude towards longer wavelengths. The peak-to-peak amplitude of the variability is ΔV = 0.33 mag, ΔJ = 0.18 mag, and ΔH = 0.14 mag. The curves seem to be periodic with minima around MJD = 55 316 and MJD = 55 323, which is consistent with the rotation period of our spot model. This periodicity is observable also between K and [4.5], but superimposed on a rising trend. There is a hint of a phase lag in the maxima towards longer wavelengths. The peak-to-peak variability amplitudes here are ΔK = 0.16 mag, Δ [3.6] = 0.24 mag, and Δ [4.5] = 0.25 mag, as measured directly on the light curves, and ΔK = 0.14 mag, Δ [3.6] = 0.17 mag, and Δ [4.5] = 0.13 mag if we subtract a linearly increasing trend.
We calculated the photometric variability amplitudes from our spot models using the limb darkening coefficients from John Southworth’s JKTLD code5 (0.787 for the V band, 0.470 for the J band, 0.439 for the H band, 0.366 for the K band, 0.190 at 3.550 μm, and 0.142 at 4.493 μm). The obtained values (the median of several models that were all consistent with the observed RV amplitude, with the standard deviation as error bars) are plotted in Fig. 8. It is evident that the amplitudes for the spot models exceed the observed ones by several magnitudes. In the case of a cold spot, the phase when the spot faces towards the observer corresponds to the lowest photometric brightness and the point in the RV curve when it becomes smaller than the systemic velocity (dotted lines in Fig. 7). Conversely, in the case of a hot spot, the phase when the spot faces towards the observer corresponds to the highest photometric brightness and the point in the RV curve when it becomes larger than the systemic velocity (dashed lines in Fig. 7). While this is approximately consistent with our observations, the extremely large variability amplitudes predicted by the spot models still make it improbable that spots are wholly responsible for the observed RV variations.
In case spots cause the RV variations of EX Lup, the observed RV semi-amplitude should depend on the wavelength. As the contrast between the spot and the unspotted stellar photosphere decreases with increasing wavelength, we expect gradually smaller RV amplitudes. For our large cold spot model, the difference between 5580 Å and 7875 Å (roughly corresponding to the bluest and reddest FEROS orders we used) would be 0.05 km s-1 in the RV semi-amplitude. For our large hot spot model, the value would be 0.28 km s-1. As we briefly mentioned in Sect. 2.1, we found no significant difference in the RVs obtained from bluer or redder orders. Our RV data allowed us to determine the RV semi-amplitude to a precision of about 0.1 km s-1 (Table 1). Thus, while we cannot exclude the cold spot scenario based on these arguments alone, the hot spot scenario seems to be unlikely.
Finally, we checked whether we can find a spot model (either cold or hot) that would reproduce the observed photometric variability amplitudes and calculated the expected RV semi-amplitudes. We found that a cold spot with a temperature of 1500 K cooler than the photosphere and covering 11% of a hemisphere would give ΔV = 0.33 mag (both the latitude of the spot and the inclination of the star was taken to be 0°). The same ΔV can also be the result of a hot spot with a temperature of 525 K hotter than the photosphere (covering factor, latitude, and inclination are the same as before). However, these relatively small spots would only cause an approximately 0.3 km s-1 RV semi-amplitude, much smaller than the observed 2.2 km s-1. Thus, we can conclude that the observed photometric and RV variations cannot be reproduced at the same time with cold or hot spots on the stellar surface.
 |
Fig. 8 Variability amplitudes as measured on the light curves of EX Lup and as obtained from the spot models made to reproduce the observed RV semi-amplitude (for details, see Sect. 3.3). |
4. Discussion
4.1. EX Lup: a spotted or an active star?
In Sects. 3.2 and 3.3 we investigated in detail whether the observed RV signal could be caused by cold or hot spots on the stellar surface. We verified that spot indicators like the BVS, BC, and CCF asymmetry do not exhibit any periodicity. Nor do we see any dependence of the observed RV on wavelength within the range covered by the FEROS spectra. We constructed a simple spot model to reproduce the observed RV semi-amplitude. Our modeling suggests that the spot would have to cover a complete hemisphere, which is an extreme and atypical solution. Moreover, the temperature of this extended spot deviates from that of the photosphere by several thousand K. Thus, unless it cools mainly through line emission (c.f. Dodin & Lamzin 2013), it would cause periodic photometric changes of 4−8 mag in the V band, which is not seen in our observations. A spot model that reproduces the observed V band variability amplitude fails to reproduce the large RV semi-amplitude. We note that in the middle of our observing campaign (2008) EX Lup produced its historically largest outburst when the accretion rate increased by a factor of 30. This event probably did not leave unchanged the size and location of the spots; however this rearrangement is not evident from the data.
In the stellar spot scenario, the 7.4 d period of the RV curve would represent the rotational period of the star. The true stellar rotational period of EX Lup is unknown. However, considering our upper limit of 3 km s-1 for vsini, EX Lup is probably not a very fast rotator, except if the inclination of the star’s equator is sufficiently low. A rotation period of 7.4 d would limit the inclination below 16° (Fig. 9). If the planes of the circumstellar disk and the star’s equator are not very different, modeling the circumstellar disk geometry also provides information on the inclination. Sipos et al. (2009) fitted the broad-band spectral energy distribution of the quiescent EX Lup system, and were able to constrain the disk inclination to be between 0° and 40°. The lower part of this range is thus consistent with the 7.4 d rotation (Fig. 9). Goto et al. (2011), however, found that a disk inclination between 40° and 50° is needed to fit the fundamental vibrational lines of CO observed in the 4.5–5 μm range during the 2008 outburst. The combination of the two constraints give a most probable inclination of 40°, which, combined with our upper limit on vsini, indicates a rotation period of at least 17 d, inconsistent with the spot scenario. We conclude that the explanation of the measured RV curve with photospheric spots is an unlikely hypothesis.
 |
Fig. 9 Inclination vs. vsini. The solid lines indicate the period of 7.4 d (obtained from the RV analysis) and 17 d (a lower limit obtained from the inclination constraint). The hatched area marks the vsini constraint from the FEROS and HARPS spectra; the orange and red areas mark the constraints for disk inclination from Sipos et al. (2009) and Goto et al. (2011), respectively. |
We also checked in Sect. 3.2 whether flows and inhomogeneities on the stellar surface or in the chromosphere could produce the measured RV variations. In this scenario the RV period again would be identical to the stellar rotation period. EX Lup, as an M-type star, is probably chromospherically active. However, the phenomena responsible for the distortions of the line profiles and thus for the RV variations are not expected to survive more than a few rotation periods, while our measured RV curve, its phase, period, and amplitude, was stable for at least four years. Moreover, our frequency analysis revealed no periodic signal in the behavior of activity indicators derived from the Ca II K line and from the Ca II infrared triplet. Thus, although chromospheric activity might be present in EX Lup and might add some random noise to the RV measurements, the periodic signal is very unlikely to be due to the activity.
4.2. Accretion scenarios in the quiescent EX Lup system
As we briefly discussed in Sect. 3.2, EX Lup displays a number of narrow emission lines whose RV, phase-folded with a period of 7.417 d (Fig. 7, bottom), reveal slight sinusoidal variations. Although the peak-to-peak amplitude is small and the scatter is large, there seems to be an anti-correlation (or 180° phase shift) between the RV of the emission lines and the RV of the absorption lines. EX Lup is not the first object where an anti-correlation of this kind has been observed: Gahm et al. (1999) discovered that RW Aur A shows photospheric RV variations with an amplitude of 5.7 km s-1 and period of 2.77 d, while the RV of the narrow emission components of the He I and He II lines vary in anti-phase with the photospheric lines. Petrov et al. (2001) proposed two possible interpretations. One possibility is that RW Aur A is a single star whose rotational and magnetic axes are misaligned and the magnetic poles are associated with the footprints of accretion flows. The star in this model rotates with a period of 5.5 d, and the two active regions give rise to the observed 2.77 d periodicity in the RV of both the absorption and the emission lines (see also Dodin et al. 2012). The other scenario is that RW Aur A is a binary with a brown dwarf companion on a 2.77 d orbit. This companion may induce a flow of material from one side of the inner disk to the primary. The accretion flow could be generated either via gravitational perturbations by the secondary, or by magnetospheric interactions between the two components.
Our results in Sect. 3 suggest a possible analogy between RW Aur A and EX Lup. Thus, in the following we will check whether the explanations proposed by Petrov et al. (2001) for RW Aur A can be applied to EX Lup as well. By analysing optical spectra taken during the 2008 outburst, Sicilia-Aguilar et al. (2012) concluded that there is a hot and non-axisymmetric accretion flow or column(s) in the EX Lup system, where clumps of gas are accreted onto the star. Based on the rapid recovery of the system after the outburst and the similarity between the pre-outburst and post-outburst spectra, they also suggest that the accretion channels are stable formations, and only the accretion rate varies between the quiescent and outburst periods.
Following Petrov et al. (2001), it is possible that EX Lup is a single star with stable, rotating accretion column(s). A single column would imply a 7.4 d rotational period, while two opposite columns would allow for a 14.8 d period, which is more consistent with our constraints on vsini and inclination (Fig. 9). The structure of the accretion columns may resemble the one outlined by Dupree et al. (2012), where the emission lines originate from an accretion shock above the stellar surface. This picture could explain the kinematics of the emission lines, and may cause photometric variations as was observed in Fig. 7. The accretion columns would distort the photospheric line profiles and cause an apparent RV signal in the absorption lines. However, our observations show no clear signature of line distortions (see Figs. 3, 4, and 6).
In the alternative scenario, Petrov et al. (2001) postulates a companion that maintains an accretion column in the system. Our Keplerian fit to the absorption line RVs in Sect. 3.1 suggests that EX Lup has a close companion on an eccentric orbit with 7.4 d period. In the Artymowicz & Lubow (1996) model, this companion may cause pulsed accretion by periodically channeling material from the inner disk onto the binary components with the same period as the binary orbital period. In this picture, the accretion channel follows the orbital motion of the companion, which would explain the RV curve of the emission lines, while the absorption lines would wobble because of the orbital motion of the binary. We note, however, that the situation may actually be more complex. The typical magnetospheric truncation radius of a T Tauri star is about 7 R∗ (Bouvier et al. 2007). The binary components orbit each other between 6.5 R∗ and 10.4 R∗, which means that their magnetospheres partially overlap and may create a complicated field for the accreting material (see Fig. 23 in Petrov et al. 2001).
In conclusion, both of the outlined pictures could work qualitatively for EX Lup, but the binary scenario accounts for more observed properties. Further observations are necessary to prove the existence of EX Lup’s companion. Nevertheless, in the following, we will examine the properties of the hypothetical companion, and briefly discuss its possible effect on the disk and the outbursts.
4.3. The companion candidate of EX Lup
According to our Keplerian fit (Table 1), the msini of the companion candidate is approximately 15 MJup. Taking 50° as an upper limit for the inclination, this gives a lower limit of 0.018 M⊙ for the mass of the companion, putting it into the mass range of high-mass planets, brown dwarfs, or very low-mass stars. According to the evolutionary models of Baraffe et al. (2002), a brown dwarf with a mass of 0.02 M⊙ has an effective temperature of about 2500 K (or higher if it is more massive) for the first few million years of its life. This means a spectral type of L0 or earlier and an absolute magnitude of MJ = 11 mag or brighter (corresponding to J = 17 mag at a distance of 155 pc), based on the results of Dahn et al. (2002). Since EX Lup has an average J = 9.8 mag, this is a brightness contrast of less than a factor of 800.
The companion orbits EX Lup between 0.049 au and 0.078 au (or 6.5 R∗ and 10.4 R∗). Interestingly, Sipos et al. (2009) found that the inner radius of the dust disk around EX Lup in quiescence is 0.2 au, which is larger than the dust sublimation radius, and they speculate that binarity may be responsible for clearing up the inner circumstellar region. Simulations of binary-disk interactions indicate that the inner radius of a circumbinary disk is typically 1.8–4 times the semi-major axis of the binary for different eccentricities, mass ratios, and disk viscosities (Artymowicz & Lubow 1994). For the EX Lup system, this value is 2.6, well within the range predicted by the simulations. Recent theoretical and observational results also support the idea that companions can create an inner hole in the dust distribution by trapping dust particles depending on grain size (Rice et al. 2006; van der Marel et al. 2013). Thus, if the existence of the hypothetical companion proves to be true, it may have caused the opening of the dust-free hole in the disk of EX Lup.
Considering its small mass and separation, the companion candidate of EX Lup might be a unique object. The distribution of binary separations peaks at 2–16 au for main sequence M dwarfs (Fischer & Marcy 1992; Gizis et al. 2003), at 30–50 au for main sequence solar-type stars (Duquennoy & Mayor 1991; Raghavan et al. 2010), and at even larger separations for PMS binaries (Mathieu 1994). Thus, the EX Lup binary with its ~7 d orbit and ~0.06 au separation may indeed be a very atypical system. Considering companion masses, Grether & Lineweaver (2006) found a deficit of companions to Sun-like stars at around 30−40 MJupiter, the so-called brown dwarf desert. Their results show that 11% of the solar-type stars have stellar companions and 5% of them have planetary companions, but less than 1% of them have brown dwarf companions. Sahlmann et al. (2011) put an even more stringent upper limit of 0.6% for the frequency of brown dwarf companions around Sun-like stars. Endl et al. (2006) found that planets around M dwarfs are even less frequent (<1.3%) than around FGK-type stars. Depending on the inclination and the exact mass of the primary, the companion of EX Lup may fall in the brown dwarf desert, towards the lower end of the brown dwarf mass range. It is interesting to speculate about the companion being a deuterium-burning planet (e.g., Mordasini et al. 2009; Spiegel et al. 2011).
The existence of a companion around EX Lup might be related to the episodic accretion behavior of this star. Close companions are known to affect the short-term variability of the accretion rate in some PMS binaries. DQ Tau and UZ Tau E, for example, show signs of pulsed accretion, a process where the companion periodically modulates the mass infall from the disk (Mathieu et al. 1997; Jensen et al. 2007). The detailed analysis of the accretion process in the quiescent EX Lup system will be analyzed in a later paper (Sicilia-Aguilar et al., in prep.). It is tempting to speculate that the companion may also have a role in the large outbursts of EX Lup, like the ones in 1955−1956, and in 2008. It may slow down the accretion onto the star causing the pile-up of such a large amount of material that it will eventually result in an extreme accretion outburst via some kind of instability.
5. Summary and outlook
In this paper we presented a five-year RV monitoring study of EX Lup. We discovered periodic variations in the RVs of the photospheric absorption lines. We checked that none of the usual activity indicators shows periodicity. However, the RV of the narrow emission lines seem to show slight variations in anti-phase with the absorption line RVs, if phase-folded with the same period. Based on our simple modeling, and considering the low vsini < 3 km s-1 and large RV semi-amplitude of 2.2 km s-1, we suggest that a cold or hot spot on the stellar surface is unlikely to explain the observed absorption line RVs and photometric variations. The RV signal could be fitted with a companion of msini = 14.7 MJup in a 7.417 d period eccentric orbit around EX Lup. Following the analogy with RW Aur A, we qualitatively discussed two scenarios to explain the observed spectral variations in EX Lup: a geometry with two accretion columns rotating with the star, and a single accretion flow synchronized with the orbital motion of the hypothetical companion. Taking 40–50° as the most likely value for the inclination, the mass of this hypothetical companion is probably in the brown dwarf range. The small separation and large mass ratio make EX Lup a very atypical binary system. The companion candidate may be responsible for the smaller or larger accretion outbursts of EX Lup, supporting those theories that assume a companion as the triggering mechanism for the eruptions of certain EXors.
Online material
FEROS and HARPS observations of EX Lup.
Optical and infrared photometry of EX Lup in magnitudes.
The barycentric correction in the FEROS pipeline was found to be inaccurate, which introduces an artificial one-year period with a semi-amplitude of 62 m s-1. The algorithm used in baryvel.pro is accurate to ~1 m s-1. For details, see Müller et al. (2013).
Acknowledgments
The authors thank the referee, D. Lorenzetti, for his comments that helped to improve the manuscript. The authors also thank V. Roccatagliata, and M. Fang for their help with the FEROS barycentric correction and A. Simon for his help with the bisector analysis. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. A.S.A. acknowledges support of the Spanish MICINN/MINECO “Ramón y Cajal” program, grant number RYC-2010-06164, and the action “Proyectos de Investigación fundamental no orientada”, grant number AYA2012-35008. This work was partly supported by the grant OTKA K101393 of the Hungarian Scientific Research Fund.
References
- Ábrahám, P., Juhász, A., Dullemond, C. P., et al. 2009, Nature, 459, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Armitage, P. J., Livio, M., & Pringle, J. E. 2001, MNRAS, 324, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Aspin, C., Reipurth, B., Herczeg, G. J., & Capak, P. 2010, ApJ, 719, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J. 1998, MNRAS, 301, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 2002, A&A, 382, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Beristain, G., Edwards, S., & Kwan, J. 1998, ApJ, 499, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I., & Bastien, P. 1992, ApJ, 401, L31 [Google Scholar]
- Bouvier, J., Alencar, S. H. P., Harries, T. J., Johns-Krull, C. M., & Romanova, M. M. 2007, Protostars and Planets V (Tucson: Unitersity of Arizona Press), 479 [Google Scholar]
- Catalano, S., Biazzo, K., Frasca, A., & Marilli, E. 2002, A&A, 394, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covino, S., Zerbi, F. M., Chincarini, G., et al. 2004, Astron. Nachr., 325, 543 [Google Scholar]
- Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources, Vizier online Data Catalog: II/246 [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2010, MNRAS, 406, 1208 [NASA ADS] [Google Scholar]
- Dahn, C. C., Harris, H. C., Vrba, F. J., et al. 2002, AJ, 124, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Dall, T. H., Santos, N. C., Arentoft, T., Bedding, T. R., & Kjeldsen, H. 2006, A&A, 454, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dodin, A. V., & Lamzin, S. A. 2013, Astron. Lett., 39, 389 [Google Scholar]
- Dodin, A. V., Lamzin, S. A., & Chuntonov, G. A. 2012, Astron. Lett., 38, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Brickhouse, N. S., Cranmer, S. R., et al. 2012, ApJ, 750, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
- Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Gahm, G. F., Petrov, P. P., Duemmler, R., Gameiro, J. F., & Lago, M. T. V. T. 1999, A&A, 352, L95 [NASA ADS] [Google Scholar]
- Ghez, A. M., McCarthy, D. W., Patience, J. L., & Beck, T. L. 1997, ApJ, 481, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Gizis, J. E., Reid, I. N., Knapp, G. R., et al. 2003, AJ, 125, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, M., Regály, Z., Dullemond, C. P., et al. 2011, ApJ, 728, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Gras-Velázquez, À., & Ray, T. P. 2005, A&A, 443, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, PASP, 117, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., & Corbally, C. J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, E. W., Esposito, M., Mundt, R., et al. 2007, A&A, 467, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P. 1999, in IAU Colloq. 170: Precise Stellar Radial Velocities, eds. J. B. Hearnshaw, & C. D. Scarfe, ASP Conf. Ser., 185, 259 [Google Scholar]
- Herbig, G. H. 1977, ApJ, 217, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 2007, AJ, 133, 2679 [Google Scholar]
- Herbig, G. H. 2008, AJ, 135, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R. 2010, MNRAS, 407, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, E. L. N., Dhital, S., Stassun, K. G., et al. 2007, AJ, 134, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Juhász, A., Dullemond, C. P., van Boekel, R., et al. 2012, ApJ, 744, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kóspál, Á., Ábrahám, P., Goto, M., et al. 2011, ApJ, 736, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Boisse, I., Bouchy, F., Bonomo, A. S., & Moutou, C. 2011, A&A, 533, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, A. M., Irwin, A. W., Yang, S. L. S., et al. 1993, PASP, 105, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Lodato, G., & Clarke, C. J. 2004, MNRAS, 353, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2008, A&A, 480, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenzetti, D., Antoniucci, S., Giannini, T., et al. 2012, ApJ, 749, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D. 1994, ARA&A, 32, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Stassun, K., Basri, G., et al. 1997, AJ, 113, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Melo, C. H. F. 2003, A&A, 410, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mittag, M., Schmitt, J. H. M. M., & Schröder, K.-P. 2013, A&A, 549, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montes, D., Crespo-Chacón, I., Gálvez, M. C., et al. 2004, Lecture Notes and Essays in Astrophysics, 1, 119 [NASA ADS] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, A., Roccatagliata, V., Henning, T., et al. 2013, A&A, 556, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998, AJ, 116, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, K. 1920, Biometrica Trust, 13, 25 [CrossRef] [Google Scholar]
- Petrov, P. P., Gahm, G. F., Gameiro, J. F., et al. 2001, A&A, 369, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Joshi, N., & Goldman, B. 2012, AJ, 143, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Guimarães, M. M., Connelley, M. S., & Bally, J. 2007, AJ, 134, 2272 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Udry, S., Mayor, M., et al. 2003, A&A, 406, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Setiawan, J., Pasquini, L., da Silva, L., von der Lühe, O., & Hatzes, A. 2003, A&A, 397, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicilia-Aguilar, A., Kóspál, Á., Setiawan, J., et al. 2012, A&A, 544, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipos, N., Ábrahám, P., Acosta-Pulido, J., et al. 2009, A&A, 507, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, D. S., Burrows, A., & Milsom, J. A. 2011, ApJ, 727, 57 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, ApJ, 633, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2006, ApJ, 650, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Apai, D., Henning, T., & Pascucci, I. 2004, ApJ, 601, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., & Howard, A. W. 2009, ApJS, 182, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Xuesong Wang, S., Wright, J. T., Cochran, W., et al. 2012, ApJ, 761, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, VizieR Online Data Catalog: I/297 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Best-fitting parameters of the Keplerian solution fitted to the RV measurements of EX Lup (with RVlin, using the combined FEROS and HARPS dataset).
All Figures
 |
Fig. 1 Top: GLS periodogram of the FEROS RV values, showing the best period of 7.417 days. The horizontal dashed line indicates the FAP level of 10-4. Bottom: window function. |
| In the text | |
 |
Fig. 2 Top: best Keplerian fit to the absorption line RVs for the combined FEROS and HARPS RV data set (with RVlin). The different colors indicate different observing seasons (-1 stands for the first half of the year, -2 for the second half). Circles represent FEROS and squares HARPS data points. Middle: residua with the same color and shape coding. Bottom: emission line RVs with the same color and shape coding. |
| In the text | |
 |
Fig. 3 Bisector of the CCF computed from the FEROS spectrum of EX Lup observed on 2010 July 23. |
| In the text | |
 |
Fig. 4 BVS values plotted against the RV (left) and against the RV residua (right). |
| In the text | |
 |
Fig. 5 GLS periodograms of the BVS, BC, BVD, CCF asymmetry, and the LDR of V I and F I. The arrows mark the 7.417 day RV period. The horizontal dashed lines indicate a FAP level of 10-4. |
| In the text | |
 |
Fig. 6 Illustration of the calculation method of the CCF asymmetry. The quantity of asymmetry is determined by obtaining the quotient of the area of positive slope (red) and of negative slope (blue). The CCF displayed here was computed from the FEROS spectrum of EX Lup observed on 2010 July 23. |
| In the text | |
 |
Fig. 7 Light curves and RV curves of EX Lup. For clarity, the light curves were shifted along the y-axis by the amounts indicated on the right side. Dashed and dotted lines mark when the RV equals the systemic velocity. |
| In the text | |
 |
Fig. 8 Variability amplitudes as measured on the light curves of EX Lup and as obtained from the spot models made to reproduce the observed RV semi-amplitude (for details, see Sect. 3.3). |
| In the text | |
 |
Fig. 9 Inclination vs. vsini. The solid lines indicate the period of 7.4 d (obtained from the RV analysis) and 17 d (a lower limit obtained from the inclination constraint). The hatched area marks the vsini constraint from the FEROS and HARPS spectra; the orange and red areas mark the constraints for disk inclination from Sipos et al. (2009) and Goto et al. (2011), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


