| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322398 | |
| Published online | 17 December 2013 | |
Analysis and interpretation of 15 quarters of Kepler data of the disintegrating planet KIC 12557548 b
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: werkhoven@strw.leidenuniv.nl
Received: 30 July 2013
Accepted: 7 November 2013
Context. The Kepler object KIC 12557548 shows irregular eclipsing behaviour with a constant 15.685 h period, but strongly varying transit depth. The object responsible for this is believed to be a disintegrating planet forming a trailing dust cloud transiting the star. A 1D model of an exponentially decaying dust tail was found to reproduce the average eclipse in intricate detail. Based on radiative hydrodynamic modelling, the upper limit for the planet mass was found to be twice the mass of the Moon.
Aims. In this paper we fit individual eclipses, in addition to fitting binned light curves, to learn more about the process underlying the eclipse depth variation. Additionally, we put forward observational constraints that any model of this planet-star system will have to match.
Methods. We manually de-correlated and de-trended 15 quarters of Kepler data, three of which were observed in short cadence mode. We determined the transit depth, egress depth, and stellar intensity for each orbit and search for dependencies between these parameters. We investigated the full orbit by comparing the flux distribution of a moving phase window of interest versus the out-of-eclipse flux distribution. We fit short cadence data on a per-orbit basis using a two-parameter tail model, allowing us to investigate potential dust tail property variations.
Results. We find two quiescent spells of ~30 orbital periods each where the transit depth is <0.1%, followed by relatively deep transits. Additionally, we find periods of on-off behaviour where >0.5% deep transits are followed by apparently no transit at all. Apart from these isolated events we find neither significant correlation between consecutive transit depths nor a correlation between transit depth and stellar intensity. We find a three-sigma upper limit for the secondary eclipse of 4.9 × 10-5, consistent with a planet candidate with a radius of less than 4600 km. Using the short cadence data we find that a 1D exponential dust tail model is insufficient to explain the data. We improved our model to a 2D, two-component dust model with an opaque core and an exponential tail. Using this model we fit individual eclipses observed in short cadence mode. We find an improved fit of the data, quantifying earlier suggestions by Budaj (2013, A&A, 557, A72) of the necessity of at least two components. We find that deep transits have most absorption in the tail, and not in a disk-shaped, opaque coma, but the transit depth and the total absorption show no correlation with the tail length.
Key words: eclipses / occultations / planet-star interactions / planets and satellites: general
© ESO, 2013
1. Introduction
Rappaport et al. (2012) discovered the peculiar target KIC 12557548 in the Kepler database, which shows dips in the light curve with a period of about 15.7 h (constant to within 10-5), but a depth varying from less than 0.2% to up to 1.3%. The phase-folded light curve shows no signs of ellipsoidal light variations, which limits the mass of planet candidate KIC 12557548 b1 to <3 MJ.
Rappaport et al. (2012) exclude several other scenarios for this target, including a dual-planet system and a low-mass eclipsing stellar binary. The authors argue for a disintegrating planet as the most likely scenario in which the close proximity to the host star causes parts of the planet’s surface to evaporate. The evaporated gas drags dust along, which subsequently eclipses parts of the star. Because of the stochastic nature of this process, transits have variable depth. The authors also find evidence of forward scattering due to this dust cloud, which creates a slight increase in intensity just before ingress. This scenario puts an upper limit on the planet’s escape velocity, such that a Mercury-mass planet is the most likely candidate. The authors qualitatively investigate the likeliness of this scenario and find it to be consistent with observations.
Subsequently, Brogi et al. (2012) quantitatively investigated the planet hypothesis using a 1D model to constrain the transit parameters, the shape of the dust cloud, and the average particle size. They find that a dust cloud with ~0.1 μm-sized particles best matches the observed, average eclipse light curve. The authors also find different system parameters for subsets of the transits consisting of relatively shallow (0.2% to 0.5%) and deep (>0.8%) eclipses.
Perez-Becker & Chiang (2013) investigate the evaporation dynamics of this planet candidate and, through radiative hydrodynamic modelling, argue that it is losing mass at a rate of Ṁ ≳ 0.1 M⊕ Gyr. They conclude that the planet candidate has a mass of less than 0.02 M⊕, or twice the mass of the Moon. According to the authors, KIC 1255b may have lost up to 70% of its initial mass, with only the inner iron core left. Budaj (2013) investigates the dust tail properties in more detail and argues that the particle size changes along the tail, where micron-sized particles best explain ingress while 0.1 to 0.01-micron sized particles fit egress best.
Here we investigate the shape of individual eclipses and provide statistical constraints on the system. We extend the previous model from Brogi et al. (2012) to a pseudo 2D variant where the vertical extent of the cloud of dust is not neglected, and an opaque core is included as a disk centred on the planet candidate. The short cadence data for quarters 13 through 15 allow us to fit the model on a per-transit basis to compare individual transits. Using the 15-quarter coverage of the target we investigate correlations between the transit depth, the depth at egress, and the stellar activity as well as variations of these parameters. Additionally, we derive a three-sigma upper limit for the secondary eclipse of 4.9 × 10-5, which is consistent with an object radius smaller than 4600 km for an albedo of 1.
The data reduction is explained in Sect. 2, and the light curve analysis is presented in Sect. 3. Section 4 describes the improved model with which we investigate per-orbit properties for the short cadence data as well as an analysis and interpretation of those results.
2. Data reduction
Kepler is a 0.95 m-aperture Schmidt telescope with a 16° diameter field of view, observing 156 453 stars with a 95 megapixel, 42 science CCD focal plane (Koch et al. 2010). The telescope was launched on 6 March 2009 and started observing on 2 May 2009. Unfortunately, in May 2013 Kepler went into safe mode due to a second reaction wheel failing.
At the basic level, frames are recorded by integrating for 6.02 s, followed by a 0.52 s readout. Data is then stored in short cadence (SC) mode by co-adding 9 frames, giving a cadence of 58.86 s with a 54.18 s exposure time (Gilliland et al. 2010) or in long cadence (LC) mode by co-adding 270 frames resulting in a cadence of 29.4244 mn and an exposure time of 27.1 mn (Jenkins et al. 2010b). Because of the limited telemetry bandwidth, Kepler observes no more than 512 targets – about 0.3% of the total – in SC mode.
At the time of writing, 15 quarters of Kepler data are publicly available at the Multi-Mission Archive (MAST2) at the Space Telescope Science Institute. KIC 12557548 was observed in LC mode for quarters 1 to 12, and in SC mode during the last quarters (13 to 15). The latter data have a 30 times shorter exposure time, resulting in a factor of 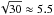 lower signal-to-noise ratio, assuming pure Poisson noise.
lower signal-to-noise ratio, assuming pure Poisson noise.
The Kepler pipeline (Jenkins et al. 2010a) delivers the light curve as simple aperture photometry flux (SAP_FLUX), as well as an automatically reduced presearch data conditioning (PDC) flux (PDCSAP_FLUX). The PDC aims to remove systematic errors from the raw flux time series. Since KIC 1255 exhibits a very peculiar light curve, the pipeline may have difficulty in automatically reducing the data. Indeed, we find that for the LC data, deep transit data are flagged as outliers. The automatically reduced SC data has a noise level approximately 1.5 times higher than our manually reduced data. Because of this, we started the data reduction from the raw SAP_FLUX and manually de-correlate the data.
The data reduction is explained in more detail below. First we selected usable data and filtered out bad data. For SAP_FLUX only, we manually de-correlated the signal using linear co-trending basis vectors supplied by the Kepler pipeline to remove systematics from the signal. Finally, we removed the stellar signal by de-trending the flux.
2.1. Data selection
We used all LC data from Kepler quarters 1 through 15, and all SC data, which were taken during quarters 13 to 15. We ignored non-finite data and most non-zero SAP_QUALITY flagged data. The Kepler pipeline erroneously marks some data with flag 2048 (“Impulsive outlier removed after cotrending”, (Fraquelli & Thompson 2012, p. 20) for transits deeper than ~0.8%. Considering that this is a highly variable target, it is not unlikely that the automated Kepler pipeline has some difficulties, and indeed the Kepler archive manual warns of these cases (kepcotrend documentation3). Ignoring these data points would not correctly sample deep transits, and we therefore included these flagged data. We have not found any other SAP_QUALITY flags that correlate with the orbital phase, and we therefore removed all other flagged data from our analysis.
 |
Fig. 1 De-trending fit for the de-correlated, long cadence SAP_FLUX, showing the stellar variability during quarters 1 through 15. Odd quarters are shaded. |
2.2. De-correlating systematics
To remove systematics from the light curve, the Kepler archive provides a set of 16 linear co-trending basis vectors (LCBV) for each detector, which are derived from a subset of highly correlated and quiet stars and are meant to remove satellite systematics from the data (Fraquelli & Thompson 2012, p. 21). The pipeline automatically de-correlates the light curve for all targets against these LCBVs, but the Kepler archive manual recommends to manually de-correlate signals that are highly variable.
Linear co-trending basis vectors are only available for LC data and cannot be constructed manually for the SC data because not enough targets are observed in SC to generate a set of LCBVs. To de-correlate the SC data, we linearly interpolated the LCBVs on the SC time points before de-correlation. We successfully used this technique to minimise the out-of-eclipse residual variance of the SC data of quarters 13 to 15. We note that this approach is unable to correct for systematics occurring on timescales significantly shorter than 29 mn (i.e. that of the long cadence).
We de-correlated the flux as follows. First we interpolated the Kepler LCBVs on SAP_FLUX exposure times for the SC data. Then we excluded the primary eclipse at orbital phase φ ∈ [−0.15,0.20] from the fitting process. We least-squares fit all 16 vectors to the remaining data and selected the first n vectors that reduce the out-of-eclipse variance significantly (see Fig. 2). In our case, we used n = 2 vectors for the SC data and n = 2 to 5 for the each of the LC data quarters.
 |
Fig. 2 Ratio of long cadence SAP_FLUX over PDCSAP_FLUX standard deviation during the out-of-eclipse part of the orbit (phase φ ∈ [−0.4, −0.1] ; [0.2,0.4]). Odd quarters are shaded. The flux variance differs per quarter. |
2.3. Removing stellar variability
When the de-correlation is performed correctly, it must preserve all astrophysical signal. This includes stellar variability, which has to be removed to analyse the eclipse behaviour. Since the data has jumps in both time and flux due to gaps in the data, we de-trended the data piece-wise per block, where a block is delimited by either a jump in time or flux. A time jump is defined as a gap in data of more than twice the data cadence, a flux jump is defined as a change of flux of more than 0.5% (LC) and 2% (SC) difference between two consecutive data points, and if the difference in the median of the 20 data points around the jump differs by more than 3.5 times the standard deviation of those points. These parameters were chosen on trial and error basis.
For each block, we masked out the transits during orbital phase φ ∈ [− 0.15,0.20] when fitting. For blocks up to 10 data points or spanning a single orbit, we normalised the data by the median. For blocks up to 200 data points we normalised using a second-order polynomial fit, and for larger blocks we fit a cubic spline to the data with a knot at each orbit at φ = 0.5, exactly opposite to the transit. We flagged data that are near the edge of a block: within one orbital period of the edge, or data outside the outer knots of a spline fit. Both of these flags are excluded in subsequent analyses since these data are poorly fitted and may introduce unwanted errors in subsequent steps. By removing the stellar variation with only one degree of freedom per orbit (i.e. a spline knot), we keep the transit signal intact.
Figure 1 shows the de-trending fit by which we divided the de-correlated SAP_FLUX to remove the stellar signal. The variability in this plot is caused by star spots coming in and out of view due to the stellar rotation. We find a period for the stellar rotation of 22.65(5) d by auto-correlating the signal, which is consistent with the findings of Kawahara et al. (2013).
2.4. Orbital parameters
Once the signal is de-correlated and the stellar variability is removed, we computed the orbital period of the planet candidate by minimising the difference between the phase-folded LC data and the best-fitting model from Brogi et al. (2012) in a least-squares sense. This method is similar to phase dispersion minimisation (Stellingwerf 1978) with the exception that we use a model instead of smoothed data. For these analyses, we used barycentric Julian days expressed in barycentric dynamical time, as given by the Kepler pipeline (Eastman et al. 2010). The values for the period with one-sigma uncertainties are listed in Table 1. We do not find significantly different values for the period for PDCSAP_FLUX and SAP_FLUX reduced data. Additionally, we fitted the 1D model parameters described in Brogi et al. (2012) using 15 quarters of data (see Sects. 4.1 and 4.3 for more details). Likewise, we calculated these parameters for deep (more than 0.8%) and shallow transits (0.2% to 0.5%) as well as all transits. The results are shown in Table 2.
Comparison between the literature values of the orbital period of KIC 1255b and the value determined through our analysis.
Best-fit 1D model parameters and their one-sigma uncertainties, as derived from the Markov chain Monte Carlo analysis.
3. KIC 1255b analysis
After reducing all available data, we investigated them on a per-orbit basis. We numbered the orbits sequentially; orbit 1 is the first orbit observed by Kepler and 2050 is the last orbit in these data. We used light curves for 1773 orbits in total, excluding bad data as identified by the Kepler pipeline (i.e. SAP_QUALITY) as well as data that was poorly de-trended. As an example orbit 1700 is shown in Fig. 3 for both the long cadence (LC) and short cadence (SC) data.
 |
Fig. 3 Orbit 1700 of KIC 1255b in long- (top) and short cadence (bottom) data. The short cadence data has a 30× higher temporal resolution, but correspondingly higher noise. We overplot the best-fitting 1D model in the upper panels. |
3.1. Primary eclipse
Since the LC data has a cadence of 29.4 mn, we have an average of 31.984 data points per 15.6854 h orbit and are limited to about 31.984 × 0.1 ≈ 3 data points per individual transit (see for example Fig. 3, top panel). Hence we only fit the depth of the transits using the 1D model with the best-fitting parameters of Brogi et al. (2012). To measure the depth, we performed a least-squares fit using a scaled best-fitting model to the data at φ ∈ [− 0.1,0.2].
For LC data, we convolved the model data with the Kepler exposure time before fitting, as explained in Brogi et al. (2012). For the SC data we did not convolve the data with the Kepler exposure time, and there is sufficient temporal resolution to additionally fit the onset of the transit. The transit onset is determined by shifting the best-fitting model in time. A least-squares fit yields both onset and depth simultaneously for each transit.
A histogram of all LC transit depths is shown in Fig. 4. Figure 5 shows the normalised, binned, phase-folded light curve for short cadence and long cadence data of transits of depth 0.8% to 1.0%, with the residuals between the model and the data shown below. The model deviates from the data during egress, showing that the simple, exponential tail model cannot explain the light curve in full detail.
 |
Fig. 4 All long cadence transit depths obtained from scaling the best-fitting model to SAP_FLUX data. Here we plot the depth at the minimum of those scaled models. The few negative eclipse depths are due to noise in the data. |
 |
Fig. 5 Phase-folded, normalised flux binned in 192 bins for long cadence (top) and short cadence (bottom) data for transits with depths from 0.8% to 1.0%. The number of data points in each bin is indicated with horizontal bars according to the right y-axis. The model is based on the parameters from the “deep” column in Table 2. The best-fitting model deviates from the short cadence data during both ingress and egress. The vertical bar indicates the median three-sigma error of the binned flux. The residual rms for these data in the phase displayed are 2.0 × 10-4 and 3.7 × 10-4 respectively, showing a greater mismatch between the short cadence data and the 1D model. |
In Fig. 6 we plot the transit depth as a function of orbit, with a 30-orbit (approximately one stellar rotation) moving average plotted as a solid black line. There are two quiet regions around orbit 50 and 1950 (MBJD 55 000 and 56 250) during which the average transit depth is on the order of 0.1%, the former is plotted in Fig. 7. The quiet periods are followed by periods during which the moving-average depths are 0.8% and 0.7%, approximately 0.1% to 0.2% deeper than the average. Additionally, we find times at which the transits appear in an on-off-pattern where >0.5% deep transits are followed by apparently no transit signal at all for up to 11 orbits. This occurs for example around orbit 1076 and to a lesser extent around orbit 940 (MBJD 55 667 and 55 578). In Fig. 8 we show the period around orbit 1076.
 |
Fig. 6 Transit depth as a function of orbit for long cadence data. The solid line is a 30-orbit moving average. There are two quiet regions around orbit 50 and 1950. Odd quarters are shaded. |
 |
Fig. 7 Transit depth as a function of orbit, showing the first quiet period around orbit 50 in Fig. 6 in more detail. |
 |
Fig. 8 Long cadence flux as a function of time where KIC 1255b shows on-off-like behaviour in the transit depth. The triangles indicate the midpoint of the transits. |
3.1.1. Transit depth correlation
Rappaport et al. (2012) argue that the dust has a sublimation lifetime of 3 × 104 s, or 8 h, such that it does not survive one orbit. To test this, we investigated the correlation between consecutive transit depths, as well as transit depth and consecutive egress depth, defined as the depth during φ ∈ [0.055,0.15]. In the former case we expect a correlation if the dust generation lasts longer than one orbit, such that subsequent transits are correlated. When investigating the transit and consecutive egress depths, we quantified the longevity of a dust cloud, such that deep transit clouds survive as an elongated tail in the next transit, which would lead to a particularly long egress signature. In this scenario, we would observe a deep transit as caused by a recent outburst where the dust is close to the planet candidate, eclipsing a large part of the star. Under the influence of gravity and the stellar radiation pressure this cloud would deform into a comet-like tail during the orbit, such that a more tenuous dust tail would eclipse the star during the following orbit.
For this analysis we selected all pairs of sequential orbits. We plot the depth versus the depth and egress depth for consecutive orbits in the LC data in Figs. 9 and 10, respectively.
 |
Fig. 9 Transit depth plotted against the following transit depth, showing no correlation (R2 = 0.026). This constrains the dynamic processes that underlie the dust cloud generation. The lower-left corner is slightly overpopulated due to two quiet periods of KIC 1255b as explained in Sect. 3.1. The cross indicates the median error for the depth estimate. |
 |
Fig. 10 Transit depth versus egress intensity for consecutive orbits for the long cadence data. We observe no significant correlation (R2 = 0.0019). |
There is no obvious correlation between the depth of consecutive transits (Pearson’s R2 = 0.026) nor between depth and consecutive egress depth (R2 = 0.0019). The absence of a correlation between consecutive transit depths indicates that the process underlying the dust generation is erratic and occurs on time scales shorter than one orbit. Furthermore, the lack of correlation between transit and consecutive egress depths is consistent with earlier findings by Rappaport et al. (2012) and puts an upper limit on the dynamical time scale of the dust tail dissipation at one orbit, i.e. 15.7 h. This is consistent with Perez-Becker & Chiang (2013), who calculated the dynamical timescale of the dust tail and found it to be approximately 14 h.
We also investigated the correlation between the stellar intensity in the Kepler band and the transit depth. The intensity is a proxy for the stellar activity, and a correlation might reveal the influence of stellar activity on the transit depth and thus gas and dust generation, as observed for Mercury (Potter & Morgan 1990). As we observe the rotational modulation of the stellar intensity due to star spots, and not the absolute intensity, the amplitude of the cyclical intensity variations is also influenced by the spatial and size distributions of the star spots. As is observed on the Sun, we assume that there is a positive correlation between the amplitude of the cyclical intensity variations and the magnetospheric effects affecting the planet and its dust tail.
 |
Fig. 11 Transit depth versus stellar activity, as determined by the peak-to-peak value of the stellar intensity in a 24 d moving window centred at the time of the transit. |
We measured the stellar variability as a by-product of our data de-trending, as described in Sect. 2.3. From the stellar variability we computed the peak-to-peak value in a moving 24 d window (about one stellar rotation period) to obtain a proxy for the stellar activity, where we assume that a higher amplitude corresponds to a more active star. We show the transit depth versus the stellar activity at each orbit in Fig. 11. We observe no significant correlation between transit depth and our stellar activity proxy (R2 = 0.0011). Kawahara et al. (2013) performed a time-series analysis of the transit depth evolution and found a periodicity close to the rotation period of the star, which they interpret as an influence of stellar activity on the atmospheric escape of the planet candidate. We have not found any evidence for this using our method.
3.2. Secondary eclipse
We divided the LC flux during the expected secondary eclipse (φ ∈ [0.45,0.55]) by the out-of-eclipse flux. Using this ratio ensures that any residual deviations from unity in the flux due to inaccuracies in the de-trending will not be mistaken for a real signal at the time of the secondary eclipse. This ratio is plotted in Fig. 12, with the mean error of the data points shown on the left. The weighted average and the error of all data give a three-sigma upper limit for the secondary eclipse of 4.9 × 10-5. Using simple geometry we find that a planet candidate with radius smaller than 4600 km, or an Earth-sized object with an albedo of ~0.5 is consistent with this finding. Furthermore, we find no correlation (R2 = -0.012) between the depth of the primary eclipse and the secondary eclipse, indicating that even deep primary eclipses do not leave any significant, back-scattering dust after half an orbit.
 |
Fig. 12 Long cadence flux during the secondary eclipse divided by flux during out-of-eclipse periods as a function of orbit. The weighted-average three-sigma upper limit is 4.9 × 10-5. The black error bar is the mean error of the individual data points. |
3.3. Full orbit
To investigate features at phases other than the transit, we compared the flux distribution at different phases against the distribution of the out-of-eclipse flux. Since we expect a flat light curve during the out-of-eclipse phase, significant deviations from zero in the differences between these distributions are indications of potential features due to the dust. We plot the difference between the out-of-eclipse distribution and a distribution of the flux in a moving phase bin as histograms in Fig. 13. We used 100 intensity bins, and we oversampled the phase bin direction four times, resulting in 320 overlapping phase bins each 0.0125 wide in phase. There is larger spread in the SC data, and both the forward scattering peak as well as the egress are less visible than in the LC data. As expected from the analysis in Sect. 3.2, there are no signs of a secondary eclipse in either plot. Besides features already investigated above, we see no features apart from those explained by the 1D model.
 |
Fig. 13 2D differential histogram comparing the flux distribution at a certain phase against the out-of-eclipse flux distribution for all long- (top) and short cadence (bottom) data. Excess flux compared to the out-of-eclipse histogram shows up as bright areas. We use 100 intensity bins and 320 phase bins of width 0.0125 such that the phase bins are 4 × oversampled. Note the excess flux around phase φ = -0.1 in the long cadence data indicating the forward scattering, which is not visible in the SC data. |
4. Cloud model
4.1. Model for the LC data
The Kepler long cadence (LC) data are fitted by employing the one-dimensional model of Brogi et al. (2012). Since the LC data have an insufficient number of points per transit, it is unrealistic to fit individual eclipses; we therefore only fit phase-folded and binned LC data with this model, realising that we may average events that differ by more than just the transit depth.
Because of the improved data reduction and the much larger dataset available, we also compared the best-fit values and uncertainties derived here with those of our previous work.
4.2. Model for the LC data
The analysis of the morphology of the short cadence data (SC) (see Sect. 3.1 and Fig. 5) reveals residual structures after subtracting a properly scaled 1D model. This suggests that this model is not sufficient to describe the full morphology of the KIC 1255 light curve, when observed with a higher time resolution.
In an attempt to better fit the KeplerSC data, we developed an improved cloud model by accounting for the vertical extent of the cloud, and by splitting the cloud structure into an opaque component for the dust around the planet, and an optically thin, exponentially-decaying cloud of dust following it. When not accounting for the vertical extent of the cloud, the impact parameter derived from fitting the data is an effective impact parameter, meaning that it is averaged over the non-uniform brightness of the stellar disk occulted by the cloud of dust. This could partially explain why the impact parameters for deep and shallow data differ (see Table 2). In addition, it is plausible that – at least for the strongest outbursts – the amount of dust ejected from the planet is sufficient to create an opaque envelope of material, which could also explain why the maximum transit depth seems to be limited to 1.2% to 1.4%. Indeed, it has been pointed out that the cloud should consist of at least two component with different properties for the dust (Budaj 2013).
As a trade-off for the higher number of free parameters, we neglected the scattering component in this new model. This is justified by the much lower photometric precision (by a factor of ~45) of the KeplerSC, unfolded and unbinned data, with respect to the phase-folded and binned LC data. The scattering properties are almost exclusively constrained by the small peak just before ingress, which is completely buried in the noise in these data, as shown in Fig. 13. The egress part of the light curve is also affected by scattering, but it is degenerate with the properties of the tail, meaning that by changing the exponential decay of the tail we could mimic the effects of a forward-scattering component. Therefore, although this model may miss some of the physics involved, our aim is not to derive physical parameters or to compare them to the previous study, but to better understand the basic geometry of the cloud, and therefore we only focus on its structure.
 |
Fig. 14 Geometry of the two-component, 2D model. x is along the planet candidate orbit, y is perpendicular to that. rth is the radius of the opaque core. |
The 2D model shares the mathematical background of the previous 1D code, i.e. it generates the light curve by convolving the profiles of the dust cloud and the stellar disk. The vertical extent of the cloud is described by 2n slices centred on the position of the planet candidate. The model is parametrised via the radius of the opaque, circular cloud of dust (rth), the scale-length of the exponentially-decaying, optically thin tail of dust (λtail), and the impact parameter of the transit (b). All these quantities are expressed in units of the stellar radius (RS), and both vertical and horizontal directions are quantised with the same step size Δr. This is defined by subdividing the total length of the orbit into m steps. For a semi-major axis of a = 4.31, we have Δr = 2πa/m ≈ 27.1/m. We denote the vertical direction with y (i.e. perpendicular to the orbit) and the horizontal direction with x (i.e. along the orbit). The curved path of the planet across the stellar disk for b ≠ 0 is approximated with a straight line.
Figure 14 shows the geometry and the main quantities involved in this new 2D model. The position along the orbit is traced through the vector x = [x1,x2,··· ,xm], in the interval (−πa,πa), which is related to the orbital phase φ via φ = x/a. The zero point for the orbital phase coincides with the centre of the star and – for j = 1 in Eq. (6) – with the position of KIC 1255b. At any time, the centre of the planet candidate, which also coincides with the centre of the opaque part of the cloud, is placed at x = xj and y = b. The vertical position of the slices is defined by the vector ycloud = [y1,y2,··· ,y2n], which is centred on y = b and in the interval (b − rth,b + rth). For each slice i, the absorption properties of the cloud are defined by 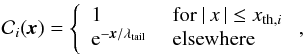 (1)where
(1)where 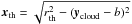 denotes the intersections of the orbital vector x with the opaque disk of dust, for each of the 2n slices.
denotes the intersections of the orbital vector x with the opaque disk of dust, for each of the 2n slices.
The stellar profile is computed by assuming a quadratic limb-darkening law, meaning that the intensity of the stellar disk is expressed as 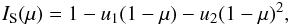 (2)where u1,u2 are the quadratic limb-darkening coefficients for a star of similar properties as KIC 12557548 (Claret & Bloemen 2011), while μ is the cosine of the angle between the line of sight of the observer and the normal to the stellar surface. Therefore, μ is a function of two variables (the x,y coordinates), and it is meaningful only for points inside the stellar disk. For a given slice i, the intersection between the orbital vector x and the stellar disk (i.e. the edge of the star) is given by
(2)where u1,u2 are the quadratic limb-darkening coefficients for a star of similar properties as KIC 12557548 (Claret & Bloemen 2011), while μ is the cosine of the angle between the line of sight of the observer and the normal to the stellar surface. Therefore, μ is a function of two variables (the x,y coordinates), and it is meaningful only for points inside the stellar disk. For a given slice i, the intersection between the orbital vector x and the stellar disk (i.e. the edge of the star) is given by 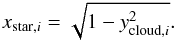 (3)The stellar brightness profile is therefore
(3)The stellar brightness profile is therefore 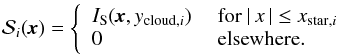 (4)The previous relation can be expressed explicitly by substituting
(4)The previous relation can be expressed explicitly by substituting 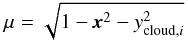 (5)in Eq. (2). The total light curve is finally given by convolving the stellar and the cloud profiles for each slice, which is
(5)in Eq. (2). The total light curve is finally given by convolving the stellar and the cloud profiles for each slice, which is 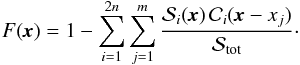 (6)The normalisation factor
(6)The normalisation factor 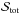 (the total flux from the star) is precomputed by discretising the full limb-darkened stellar disk with the same step size as for the model, and summing over all pixels of the matrix. It is therefore a much more straightforward normalisation than in our previous 1D model, where the stellar profile for b = 0 had to be normalised such that the sum of its elements was equal to unity.
(the total flux from the star) is precomputed by discretising the full limb-darkened stellar disk with the same step size as for the model, and summing over all pixels of the matrix. It is therefore a much more straightforward normalisation than in our previous 1D model, where the stellar profile for b = 0 had to be normalised such that the sum of its elements was equal to unity.
In this two-dimensional model, fractional pixel coverage is also taken into account via a linear approximation. This is particularly important for very small rth, or when b approaches (1 + rth), and prevents us from using a too-small (and computationally demanding) Δr. We validated our model with the Mandel & Agol (2002) transit code by choosing a very small value for λtail, which is equivalent to neglecting the optically thin part of the cloud. For an optimal value of m = 3000, found via trial and error, the two models differ by less than 10-5, which is at least two orders of magnitude better than the accuracy of the Kepler short cadence data.
4.3. Fitting of LC data
The updated parameters of KIC 1255b, as derived from the fitting of 15 quarters of KeplerLC data, are listed in Table 2. For deep and shallow transits, we observe a better mixing of the Markov chain Monte Carlo (MCMC) chains (quantified following Gelman & Rubin 1992) than in the previous work, which is expected from the much larger amount of data used. This also results in more symmetric posterior distributions and less correlation between the parameters.
4.4. Fitting of SC data
To compare our 2D model with the 1D model, we fit it to the subset of deep transits (see Table 2), and perform a similar analysis as in Sect. 3.1. Even though we excluded the forward scattering from the 2D model, the residuals are reduced as compared to the 1D model, as shown in Fig. 15, indicating a better match to the data.
 |
Fig. 15 Phase-folded, normalised flux binned in 192 bins for short cadence data for transits with depths from 0.8% to 1.0%, as in Fig. 5, but instead using the 2D model to fit the data. Even though the 2D model does not include forward scattering, we observe an improved fit and reduced residuals, with a 16% lower residual rms of 3.1 × 10-4. |
Subsequently, we selected 213 light curves sampled in SC mode with transit depths greater than 0.5%, no discontinuities in the data and sufficient photometric precision to fit the 2D model to the individual transits to be used for a per-orbit analysis. Each individual orbit contains 447 points.
We fit the geometry of the dust cloud individually for each light curve by first performing a least-squares fit with a grid of widely spaced parameter values. The set of parameters corresponding to the minimum χ2 is then used as input for a single MCMC chain of 50 000 steps. This assures that the chain is already started in the proximity of the global χ2 minimum, and does not get stuck in a local minimum.
By performing the analysis with all free parameters, we notice that a large fraction of the MCMC chains fail to converge. However, by investigating those chains that do converge, we observe that all transits are consistent with the same impact parameter (b = 0.6 ± 0.1). This suggests that our two-component, two-dimensional model is a better approximation for the cloud of dust, and does measure a true impact parameter, as opposed to the previous one-dimensional model. Therefore, we fixed the impact parameter to 0.6 and recomputed the MCMC chains.
To verify that the model parameters are not degenerate, we computed artificial light curves by:
-
1.
Assuming a small tail (λ = 0.3) and only varying the opaque part;
-
2.
Fixing rth = 0.01 and only varying the exponential tail.
We added noise based on the photometric precision of the KeplerSC data, and fit these simulated data with the method described above. In both cases the retrieved parameters are compatible with the single-parameter distributions given as input, and we do not obtain a mixing between the two model components, as is observed in the real data. This suggests that the two components are indeed present in the data.
In our model the size of the opaque part also drives the vertical extent of the cloud. This means that, if the tail covers a certain effective area (integrated over the x and y direction), its specific length λ has to change as a function of the size of the opaque core. Larger rth means a wider cloud, which requires a faster decay in order to maintain approximately the same effective area. Simply plotting rth versus λ therefore shows a correlation due to the model, and tells little about the system itself (see Fig. 16). For this reason we plot the absorption by the core as 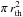 and of the tail as 2 rth λtail.
and of the tail as 2 rth λtail.
 |
Fig. 16 Deep (>0.5%) short cadence transit Kepler data fitted with the two-component 2D model. The point surface scales with the transit depth squared (for clarity) as determined in Sect. 3.1. The top plot shows the best-fitting model parameters rth and λ for each individual SC transit. The correlation in this plot is largely due to the model (see text). We show the effective area of the tail versus the size of the opaque core (middle), and the tail length versus total absorption (bottom). We observe no clear relation between the tail or the core absorption, while the transit depth scales with the total absorption. Very deep transits seem to require a strong tail component, as is evident by the cluster of points in the bottom-right corner of the middle panel. The void in the triangular lower-left corner in the middle panel is due to the exclusion of shallow transits, where iso-transit depth lines run diagonally. |
The results of the short cadence transit analysis are shown in Fig. 16. Besides plotting the model parameters, we also show the absorption of the core versus the absorption of the tail and the tail length versus the total absorption since these better describe the physics of the system. The total absorption is highly correlated with transit depth (bottom panel; as determined in Sect. 3.1) which is expected: more material will yield a deeper minimum. We find no relation between the tail length and the transit depth or total absorption (bottom panel). Although shallow transits are evenly distributed between the core and tail absorption, deeper eclipses appear to have most absorption in the tail, and not in a disk-shaped, opaque coma (bottom-right corner of middle panel).
Our model is certainly not the only possible geometric description of KIC 1255b, and it is unclear whether the two components we propose are an accurate physical description of the system. One could, for example, fix the vertical extent of the cloud to allow for a variable optical depth for the core with an exponentially decreasing tail. The main point is that the data suggest the necessity of at least two independent components for the cloud, in agreement with Budaj (2013).
5. Conclusions
We have manually de-correlated and de-trended 15 quarters of Kepler data, of which three quarters were observed in short cadence mode for KIC 12557548, and investigated statistical constraints on system dynamics as well as a per-orbit analysis using three quarters of SC data.
We find two quiescent spells of KIC 1255b of ~30 orbits each around orbit 50 and 1950 where the average transit depth is 0.1%. These two periods appear to be followed by periods where the transit depth is 0.1% to 0.2% deeper than the average transit depth. Additionally, we find times at which the transits show on-off-like behaviour, where >0.5% deep eclipses are followed by hardly any eclipse at all. Aside from these isolated events, we find no significant overall correlation between consecutive transit depths, nor between transit depth and consecutive egress depth. This implies that the majority of the dust does not survive a single orbit, and that the process underlying the dust generation occurs erratically. The independence of transit depth and consecutive egress depth implies that an opaque dust cloud yielding a deep transit does not survive to form part of a more tenuous and stretched-out dust cloud during the next eclipse, in agreement with (Perez-Becker & Chiang 2013).
Furthermore, we put an upper limit of 4.9 × 10-5 on the secondary eclipse. This constrains the radius of a planet candidate to less than 4600 km, or one Earth radius for an albedo of ~0.5.
We find a significant discrepancy when fitting our previous 1D model to the SC data around egress. Our improved model adds a second dimension and represents the dust tail with two components, which better fits individual SC transits than the old 1D model. We verified that the two components are not degenerate in the model and are data-driven.
Our results suggest that a 1D, exponentially decaying dust tail is insufficient to represent the data. We find that deep transits have most absorption in the tail, and not in a disk-shaped, opaque coma, but the transit depth or total absorption show no correlation with the tail length. Although our model is only one possible interpretation of the cloud structure, there is also qualitative evidence (Budaj 2013) of the need of at least two components. We anticipate that models including realistic physics and geometry are required to fully understand this peculiar system.
Acknowledgments
The authors would like to thank Ernst de Mooij for his constructive discussion concerning the modelling of this object. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate. All of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts.
References
- Brogi, M., Keller, C. U., de Juan, Ovelar, et al. 2012, A&A, 545, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Budaj, J. 2013, A&A, 557, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fraquelli, D., & Thompson, S. E. 2012, Kepler Archive Manual (KDMC-10008-004), Tech. Rep., Space Telescope Science Institute [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010a, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010b, ApJ, 713, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Kawahara, H., Hirano, T., Kurosaki, K., Ito, Y., & Ikoma, M. 2013, ApJ, 776, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, L171 [Google Scholar]
- Perez-Becker, D., & Chiang, E. 2013, MNRAS, 433, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, A. E., & Morgan, T. H. 1990, Science, 248, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Levine, A., Chiang, E., et al. 2012, ApJ, 752, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between the literature values of the orbital period of KIC 1255b and the value determined through our analysis.
Best-fit 1D model parameters and their one-sigma uncertainties, as derived from the Markov chain Monte Carlo analysis.
All Figures
 |
Fig. 1 De-trending fit for the de-correlated, long cadence SAP_FLUX, showing the stellar variability during quarters 1 through 15. Odd quarters are shaded. |
| In the text | |
 |
Fig. 2 Ratio of long cadence SAP_FLUX over PDCSAP_FLUX standard deviation during the out-of-eclipse part of the orbit (phase φ ∈ [−0.4, −0.1] ; [0.2,0.4]). Odd quarters are shaded. The flux variance differs per quarter. |
| In the text | |
 |
Fig. 3 Orbit 1700 of KIC 1255b in long- (top) and short cadence (bottom) data. The short cadence data has a 30× higher temporal resolution, but correspondingly higher noise. We overplot the best-fitting 1D model in the upper panels. |
| In the text | |
 |
Fig. 4 All long cadence transit depths obtained from scaling the best-fitting model to SAP_FLUX data. Here we plot the depth at the minimum of those scaled models. The few negative eclipse depths are due to noise in the data. |
| In the text | |
 |
Fig. 5 Phase-folded, normalised flux binned in 192 bins for long cadence (top) and short cadence (bottom) data for transits with depths from 0.8% to 1.0%. The number of data points in each bin is indicated with horizontal bars according to the right y-axis. The model is based on the parameters from the “deep” column in Table 2. The best-fitting model deviates from the short cadence data during both ingress and egress. The vertical bar indicates the median three-sigma error of the binned flux. The residual rms for these data in the phase displayed are 2.0 × 10-4 and 3.7 × 10-4 respectively, showing a greater mismatch between the short cadence data and the 1D model. |
| In the text | |
 |
Fig. 6 Transit depth as a function of orbit for long cadence data. The solid line is a 30-orbit moving average. There are two quiet regions around orbit 50 and 1950. Odd quarters are shaded. |
| In the text | |
 |
Fig. 7 Transit depth as a function of orbit, showing the first quiet period around orbit 50 in Fig. 6 in more detail. |
| In the text | |
 |
Fig. 8 Long cadence flux as a function of time where KIC 1255b shows on-off-like behaviour in the transit depth. The triangles indicate the midpoint of the transits. |
| In the text | |
 |
Fig. 9 Transit depth plotted against the following transit depth, showing no correlation (R2 = 0.026). This constrains the dynamic processes that underlie the dust cloud generation. The lower-left corner is slightly overpopulated due to two quiet periods of KIC 1255b as explained in Sect. 3.1. The cross indicates the median error for the depth estimate. |
| In the text | |
 |
Fig. 10 Transit depth versus egress intensity for consecutive orbits for the long cadence data. We observe no significant correlation (R2 = 0.0019). |
| In the text | |
 |
Fig. 11 Transit depth versus stellar activity, as determined by the peak-to-peak value of the stellar intensity in a 24 d moving window centred at the time of the transit. |
| In the text | |
 |
Fig. 12 Long cadence flux during the secondary eclipse divided by flux during out-of-eclipse periods as a function of orbit. The weighted-average three-sigma upper limit is 4.9 × 10-5. The black error bar is the mean error of the individual data points. |
| In the text | |
 |
Fig. 13 2D differential histogram comparing the flux distribution at a certain phase against the out-of-eclipse flux distribution for all long- (top) and short cadence (bottom) data. Excess flux compared to the out-of-eclipse histogram shows up as bright areas. We use 100 intensity bins and 320 phase bins of width 0.0125 such that the phase bins are 4 × oversampled. Note the excess flux around phase φ = -0.1 in the long cadence data indicating the forward scattering, which is not visible in the SC data. |
| In the text | |
 |
Fig. 14 Geometry of the two-component, 2D model. x is along the planet candidate orbit, y is perpendicular to that. rth is the radius of the opaque core. |
| In the text | |
 |
Fig. 15 Phase-folded, normalised flux binned in 192 bins for short cadence data for transits with depths from 0.8% to 1.0%, as in Fig. 5, but instead using the 2D model to fit the data. Even though the 2D model does not include forward scattering, we observe an improved fit and reduced residuals, with a 16% lower residual rms of 3.1 × 10-4. |
| In the text | |
 |
Fig. 16 Deep (>0.5%) short cadence transit Kepler data fitted with the two-component 2D model. The point surface scales with the transit depth squared (for clarity) as determined in Sect. 3.1. The top plot shows the best-fitting model parameters rth and λ for each individual SC transit. The correlation in this plot is largely due to the model (see text). We show the effective area of the tail versus the size of the opaque core (middle), and the tail length versus total absorption (bottom). We observe no clear relation between the tail or the core absorption, while the transit depth scales with the total absorption. Very deep transits seem to require a strong tail component, as is evident by the cluster of points in the bottom-right corner of the middle panel. The void in the triangular lower-left corner in the middle panel is due to the exclusion of shallow transits, where iso-transit depth lines run diagonally. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


