| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 15 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201322256 | |
| Published online | 19 December 2013 | |
The spectral catalogue of INTEGRAL gamma-ray bursts
results of the joint IBIS/SPI spectral analysis
1
AIM (UMR 7158 CEA/DSM-CNRS-Université Paris Diderot) Irfu/Service
d’Astrophysique, Saclay,
91191
Gif-sur-Yvette Cedex
France
e-mail:
zeljka.bosnjak@cea.fr
2
Department of Physics, University of Rijeka,
51000
Rijeka,
Croatia
3
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse,
France
4
CNRS, IRAP, 9
Av. Colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
Received:
10
July
2013
Accepted:
10
September
2013
We present the updated INTEGRAL catalogue of gamma-ray bursts (GRBs) observed between December 2002 and February 2012. The catalogue contains the spectral parameters for 59 GRBs localized by the INTEGRAL Burst Alert System (IBAS). We used the data from the two main instruments on board the INTEGRAL satellite: the spectrometer SPI (SPectrometer on INTEGRAL) nominally covering the energy range 20 keV−8 MeV, and the imager IBIS (the Imager on Board the INTEGRAL Satellite) operating in the range from 15 keV to 10 MeV. For the spectral analysis we applied a new data extraction technique, developed to explore the energy regions of highest sensitivity for both instruments, SPI and IBIS. It allowed us to analyse the GRB spectra over a broad energy range and to determine the bursts’ spectral peak energies. The spectral analysis was performed on the whole sample of GRBs triggered by IBAS, including all the events observed in the period December 2002 to February 2012. The catalogue contains the trigger times, burst coordinates, positional errors, durations, and peak fluxes for 28 unpublished GRBs observed between September 2008 and February 2012. The light curves in the 20−200 keV energy band of these events were derived using IBIS data. We compare the prompt emission properties of the INTEGRAL GRB sample with the BATSE and Fermi samples.
Key words: methods: data analysis / gamma-ray burst: general / catalogs
© ESO, 2013
1. Introduction
Over the past two decades gamma-ray bursts (GRBs) have been observed by several missions, providing a wealth of spectral and temporal data. The properties of the prompt gamma-ray emission have been studied over a broad energy range from keV to GeV energies. Prompt GRB spectra are commonly described by two power laws smoothly connected around the spectral peak energy typically observed at a few hundred keV (Band et al. 1993; Preece et al. 2000). The values of the spectral parameters, i.e. the slopes of the low- and high-energy power laws and the peak energy, are associated with the radiative mechanisms governing the emission and with the energy dissipation processes within the relativistic jet, so that they impose important constraints on the theoretical models for prompt GRB emission. To date, the most complete catalogues of spectral GRB properties comprise the events observed by the Burst And Transient Source Experiment (BATSE) on board the Compton Gamma-Ray Observatory in operation from 1991 to 2000 (Fishman et al. 1989; Gehrels et al. 1994), by the Swift satellite launched in 2004 (Gehrels et al. 2004), and by the Fermi satellite launched in 2008 (Meegan et al. 2009; Gehrels & Razzaque 2013).
INTEGRAL has contributed important discoveries to the GRB field, including the detection and observation of GRB 031203 associated with SN 2003lw (Malesani et al. 2004), the polarization measurements from GRB 041219 (Götz et al. 2009) and GRB 061122 (Götz et al. 2013), and the discovery of the (inferred) population of low-luminosity GRBs (Foley et al. 2008). In this paper we present a catalogue of GRBs detected by the INTEGRAL satellite. In the period between December 2002 and February 2012, INTEGRAL observed 83 GRBs (the low number of events compared to other GRB missions, e.g. 2704 GRBs observed by BATSE in a nine-year period, is mainly due to the small field of view of the IBIS instrument, ~0.1 sr). We report the results of spectral analysis of 59 out of 83 GRBs. The spectral parameters were derived by combining the data from the two main instruments on board INTEGRAL, the spectrometer SPI nominally covering the energy range 20 keV−8 MeV and the imager IBIS with spectral sensitivity in the range 15 keV−10 MeV. To date, the systematic spectral analysis of INTEGRAL GRBs has been performed in a limited energy range using only the data from the IBIS instrument (Vianello et al. 2009; Foley et al. 2008; Tierney et al. 2010). Foley et al. (2008) report the results of the spectral analysis using SPI data for nine GRBs, but, with one exception, the analysis of the IBIS data and the SPI data has been performed independently. In addition to the spectral analysis performed over a broad energy range for the complete sample of INTEGRAL GRBs, we have derived the IBIS light curves and durations for the previously unpublished 28 events observed between September 2008 and February 2012.
The paper is organized as follows. In Sect. 2 we discuss the catalogues of GRBs detected by BATSE, Fermi, and Swift, and the possible biases in the results due to the instrumental differences. We compare the instrumental properties of different missions with those of the INTEGRAL instruments. The timing analysis and the spectral extraction technique we developed are presented in Sect. 3. The basic properties of the INTEGRAL GRB sample are discussed in Sect. 4. We compare the basic properties of our sample with the large GRB samples obtained by CGRO BATSE, Fermi Gamma-Ray Burst Monitor (GBM) and Swift Burst Alert Telescope (BAT) instruments. We report the results of the spectral analysis in Sect. 5, and make a statistical comparison of our results with respect to BATSE and Fermi/GBM samples. The summary of our results is presented in Sect. 6.
2. GRB samples
A systematic spectral analysis of a subsample of 350 bright GRBs selected from the complete set of 2704 BATSE GRBs, in the energy range ~30 keV−2 MeV observed by BATSE was performed by Kaneko et al. (2006; see also Preece et al. 2000). Five percent of the bursts in this sample are short GRBs (with durations less than 2 s). Kaneko et al. (2006) find that the most common value for the low-energy slope of the photon spectra is α ~ −1, and therefore the distribution of the low-energy indices is not consistent with the value predicted by the standard synchrotron emission model in fast cooling regime, –3/2 (Sari et al. 1998). The distribution of the peak energies of the time-integrated spectra of long BATSE GRBs has a maximum at ~250 keV and a very narrow width ≲100 keV. Ghirlanda et al. (2004) find that the time-integrated spectra of a sample of short GRBs observed by BATSE are harder than those of long GRBs spectra, mainly due to a harder low-energy spectral component (~−0.6). Goldstein et al. (2012; see also Bissaldi et al. 2011; Nava et al. 2011) report the results of the spectral analysis of 487 GRBs detected by Fermi/GBM operating in the energy band ~8 keV−40 MeV, during its first two years of operation. They find that the distribution of spectral peak energies has a maximum at ~200 keV for the time-integrated spectra and also report several GRBs with time-integrated peak energies greater than 1 MeV. The properties of the sample of 476 GRBs observed by Swift/BAT on 15−150 keV energy range were reported by Sakamoto et al. (2011). They distinguish the classes of long duration GRBs (89%), short duration GRBs (8%), and short-duration GRBs with extended emission (2%). Their GRB sample was found to be significantly softer than the BATSE bright GRBs, with time-integrated peak energies around ~80 keV.
To test the emission models using the observed spectral parameters or to deduce some global properties of a GRB sample, it is necessary to take the possible biases in the results of the spectral analysis into account:
-
1.
When we consider the low-energy portion of the spectrum, the data may not approach a low energy asymptotic power law within the energy band of the instrument (Preece et al. 1998; Kaneko et al. 2006): e.g. if the spectral peak energy is close to the lower edge of the instrumental energy band, lower values of α are determined. Preece et al. (1998) introduced as a better measure of the low-energy spectral index the effective value of α, defined as the slope of the power-law tangent to the GRB spectrum at some chosen energy (25 keV for BATSE data).
-
2.
There may be biases in the results when the analysis is performed on a sample of the brightest events, since there is a tendency for bright GRBs (having higher photon fluxes) to have higher spectral peak energies than faint GRBs (Borgonovo & Ryde 2001; Mallozzi et al. 1995). For example, Kaneko et al. (2006) burst selection criteria required a peak photon flux on the energy range 50−300 keV greater than 10 photons s-1 cm-2 or a total energy fluence in 20−2000 keV energy range larger than 2.0 × 10-5 erg cm-2. Nava et al. (2008) have extended the spectral analysis of BATSE GRBs to the fainter bursts (down to fluences ~10-6 erg cm-2) and find a lower value for the average spectral peak energy, ~160 keV, compared to the Kaneko et al. (2006) results.
-
3.
The instrumental selection effects (e.g. the integration time scale for the burst trigger) may also affect the properties of the GRB samples obtained by different gamma-ray experiments. For example, Sakamoto et al. (2011; see Qin et al. 2013 for Fermi/GBM results) found that the distribution of long GRB durations from Swift/BAT sample is shifted towards longer times (~70 s) than for BATSE (~25 s, Kouveliotou et al. 1993), coherently with the longer BAT triggering time scales. The lack of short GRBs in imaging instruments (such as Swift/BAT) with respect to non-imaging instruments (such as BATSE and GBM), on the other hand, is attributed to the requirement of a minimum number of photons needed to build an image with a coded-mask instrument.
2.1. INTEGRAL instruments
INTEGRAL (Winkler et al. 2003) is an ESA mission launched on October 17, 2002 and dedicated to high-resolution imaging and spectroscopy in the hard X-/soft γ-ray domain. It carries two main coded-mask instruments, SPI (Vedrenne et al. 2003) and IBIS (Ubertini et al. 2003).
SPI is made of 19 Ge detectors1, working in the 20 keV−8 MeV energy range, and it is optimized for high-resolution spectroscopy (~2 keV at 1 MeV), in spite of a relatively poor spatial resolving power of ~2°. IBIS is made of two pixellated detection planes: the upper plane, ISGRI−INTEGRAL Soft Gamma-Ray Imager (Lebrun et al. 2003), is made of 128 × 128 CdTe detectors and operates in the 15 keV–1 MeV energy range. ISGRI has an unprecedented point spread function (PSF) in the soft γ-ray domain of 12 arcmin FWHM. The lower detection plane, PICsIT (PIxellated CsI Telescope; Di Cocco et al. 2003), consists of 64 × 64 pixels of CsI and is sensitive between 150 keV and 10 MeV. For our analysis we used only ISGRI data from IBIS. Owing to satellite telemetry limitations, PICsIT spectral-imaging data are temporally binned over the duration of an INTEGRAL pointing (lasting typically 30−45 min), so they are not suited to studies of short transients like GRBs. On the other hand, PICsIT spectral-timing data cannot be used in our analysis due to the lack of a proper response matrix.
Despite being a non GRB-oriented mission, INTEGRAL can be used as a GRB experiment: the GRBs presented in this paper have all been detected in (near-)real time by the INTEGRAL Burst Alert System (IBAS; Mereghetti et al. 2003). IBAS is running on ground at the INTEGRAL Science Data Centre (ISDC; Courvoisier et al. 2003) thanks to the continuous downlink of the INTEGRAL telemetry. As soon as the IBIS/ISGRI data are received at ISDC, they are analysed in real time by several triggering processes running in parallel. The triggering algorithms are of two kinds: one is continuously comparing the current sky image with a reference image to look for new sources, and the second one examines the global count rate of ISGRI. In the latter case, once a significant excess is found, imaging is used to check that it corresponds to a new point source or if it has a different origin (e.g. cosmic rays or solar flares). The nominal triggering energy band for IBAS is 15−200 keV, and different time scales are explored from 2 ms up to 100 s.
As a comparison, in Fig. 1 we show the sensitivity of some past and current GRB triggering experiments2, as a function of the GRB peak energy. The sensitivity is presented as the threshold peak photon flux (in 1−1000 keV energy band) detected at a 5.5σ signal-to-noise ratio, during accumulation time Δt = 1 s (cf. Band 2003). It can be seen that the IBAS system is expected to be the most sensitive experiment provided that the peak energy is larger than ~50 keV. This has allowed us to investigate the GRB spectral properties for faint (down to fluences of a few 10-8 erg cm-2) GRBs, see Fig. 5.
 |
Fig. 1 Sensitivity of past and present GRB experiments as a function of the GRB peak energy. For Fermi/GBM NaI detectors, BeppoSAX/WFC, BeppoSAX/GRBM, HETE-2/Fregate, HETE-2/ WXM, and CGRO/BATSE LAD detectors the data are taken from Band (2003); for Swift/BAT the data are taken from Band (2006); for INTEGRAL/IBAS the data are taken from the IBAS web site4. |
3. Data analysis
Owing to their short durations, GRBs usually do not provide a large number of counts, especially above ~200 keV where the IBIS/ISGRI effective area starts to decline rapidly. To provide broader energy coverage and better sensitivity for the INTEGRAL GRB spectra, we combined the data from the IBIS/ISGRI and the SPI instruments.
The previously published catalogue of INTEGRAL GRBs (Vianello et al. 2009) comprises the analysis of only the IBIS/ISGRI data, providing the GRB spectra on 18−300 keV band. Most of the spectra were fitted with a single power-law model over this limited energy range. The spectral energy peak was determined for only 9 out of 56 bursts in their sample. Foley et al. (2008) used SPI and IBIS/ISGRI data to analyse 9 out of 45 GRBs. They performed the spectral analysis using the data from each of the two instruments independently, and in four cases the spectrum was fitted by a different model for IBIS and for SPI data.
We combined the data from both instruments, SPI and IBIS/ISGRI3: in this way the low-energy portion (≲200 keV) of the GRB spectrum is explored by ISGRI where its sensitivity is highest, while the high-energy portion of the spectrum (≳200 keV) is better investigated by the SPI data. Joint spectral analysis, using the data from both instruments (see Fig. 2), allows us to analyse the spectra consistently and to exploit the maximum potential of each instrument. The SPI data can provide better spectral information at energies where IBIS/ISGRI effective area becomes low, and therefore are suitable for determining the GRB spectral peak energy (typically at ~a few 100 keV).
 |
Fig. 2 Spectral model and data for GRB 061122. The violet triangles are the 20−200 keV ISGRI data points used for the fit. The coloured dots covering the energy range 40−1000 keV are the data from the 11 SPI detectors with the highest signal-to-noise ratio selected for the spectral analysis (cf. McGlynn et al. 2009). We fitted the cut-off power-law model in this case, with α = −1.3 and E0 = 263 keV (see Sect. 5 on spectral analysis). |
The spectra were analysed using the C-statistic (Cash 1979), which is commonly used for experiments with a low number of counts. To fit the spectra of both instruments simultaneously, we used the XPSEC 12.7.1 fitting package (Arnaud 2010). For the C-statistic to be applied, we needed to provide on-burst spectra and background spectra separately for every GRB. This cannot be obtained by the INTEGRAL standard Off-line Scientifc Analysis (OSA) software, and therefore we developed additional tools to extract the spectra in the required format.
To maximize the sensitivity of both instruments, SPI and ISGRI spectra were extracted in the range (40 keV−1 MeV) and (20−200 keV), respectively, because outside this energy range, the effective areas of the corresponding instruments decrease very rapidly (see Ubertini et al. 2003; Vedrenne et al. 2003). First, we computed the ISGRI light curves for each GRB (Fig. A.1). To enhance the signal-to-noise ratio, we selected only the events that were recorded by the pixels having more than 60% of their surface illuminated by the GRB.
Based on these light curves we selected on-burst intervals for spectral analysis (see dashed lines in Fig. A.1). The off-burst intervals for the spectral analysis were determined by selecting the times before and after the GRB, excluding intervals of ≳10 s close to the event in order to ensure that the off-burst intervals were not contaminated by the GRB counts. For the SPI instrument, a spectrum for each of the 19 Ge detectors was computed (where applicable). The net individual GRB spectra (i.e. on-burst – off-burst spectra) have the advantage (over the global spectra produced by OSA software) of being more accurate, since the background spectra were computed for each GRB and each detector, taking the local spectral and temporal background evolution into account. The OSA software, in contrast, computes the SPI background from a model template and the net spectrum is derived from the sky deconvolution process, which introduces more uncertainties than a simple subtraction of the number of background counts per detector. For each SPI detector an individual response function was calculated, considering the GRB direction (either as determined by IBIS/ISGRI or by more precise X-ray or optical follow-up observations). The response function takes the exposed fraction of each detector given the GRB direction into account. This means that for detectors that are completely shadowed by the SPI mask, the corresponding net spectrum is consistent with zero (see e.g. McGlynn et al. 2009), and it is automatically neglected in the analysis since the effective area is also consistent with zero.
For the IBIS/ISGRI spectra, the large number of detectors led us to decide not to compute individual pixel spectra. We selected only the pixels that were fully illuminated by the GRB, in order to compute the off-burst and on-burst spectra. A corresponding ancillary response function (ARF) was computed, taking the reduced (~30%) area of the detector plane we used into account. For each GRB we computed and fitted the time-integrated spectrum, using all the available SPI spectra and one ISGRI spectrum. In order to account for SPI/IBIS inter-calibration and especially for IBIS count losses due to telemetry limitations (see e.g. Fig. A.1 last panel), we allowed a constant normalization factor between ISGRI and SPI. On the other hand, we assumed that the differences among the individual SPI detectors are all accounted for by the ad-hoc generated response matrices. An example of a simultaneous fit is shown in Fig. 2.
 |
Fig. 3 Example of T90 calculation using the time-integrated IBIS/ISGRI light curve of GRB 081003B. The vertical dashed lines represent the times when the GRB integrated counts exceed 5% (S5) and 95% (S95) of the maximal integrated flux value, respectively. |
We determined the T90 duration for sample of GRBs observed after September 2008 (Table 1). The T90 duration of prompt emission measures the duration of the time interval during which 90% of the observed counts are accumulated (Kouveliotou et al. 1993). The start and the end of this interval are defined by the time at which 5% and 95% of the counts are accumulated, respectively (see Fig. 3).
The GRB durations were determined using the IBIS/ISGRI lightcurves (see Fig. A.1) obtained
for 20−200 keV energy band. The background rate was determined by fitting a linear or
constant function to the data, in the time intervals before and after the burst. The time
intervals for background fitting typically lasted for ≳100 s, and they were separated by ~10
s from the burst. We show the background-subtracted lightcurves for GRBs detected between
September 2008 and February 2012 in Figs. A.1. The errors on T90
were calculated using the method developed by Koshut et al.
(1996). They define the total net (i.e. background-subtracted) source counts
observed for a single event as 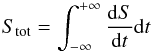 (1)where
dS/dt is the source count rate
history. The time τf during which a given
fraction f of the total counts is accumulated is defined as the time at
which
(1)where
dS/dt is the source count rate
history. The time τf during which a given
fraction f of the total counts is accumulated is defined as the time at
which 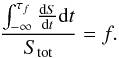 (2)As a result,
T90 is defined as
τ95 − τ5, see Fig. 3.
(2)As a result,
T90 is defined as
τ95 − τ5, see Fig. 3. 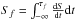 represents the value of the
integrated counts S(t) when f of the
total counts have been detected. The uncertainties on
Sf consist of two contributions:
(dSf)cnt, due to the uncertainty
in the integrated counts S(t) at any time
t (see Eq. (12) in Koshut et al.
1996), and (dSf)fluc, due
to the statistical fluctuations (see Eq. (14) in Koshut et
al. 1996) with respect to the smooth background model:
represents the value of the
integrated counts S(t) when f of the
total counts have been detected. The uncertainties on
Sf consist of two contributions:
(dSf)cnt, due to the uncertainty
in the integrated counts S(t) at any time
t (see Eq. (12) in Koshut et al.
1996), and (dSf)fluc, due
to the statistical fluctuations (see Eq. (14) in Koshut et
al. 1996) with respect to the smooth background model:
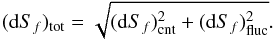 (3)The times
τf − and
τf + are the times at which
Sf − (dSf)tot
and
Sf + (dSf)tot
counts have been reached respectively. In this case, one can define
(3)The times
τf − and
τf + are the times at which
Sf − (dSf)tot
and
Sf + (dSf)tot
counts have been reached respectively. In this case, one can define
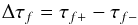 (4)and
the statistical uncertainty in T90 is given by
(4)and
the statistical uncertainty in T90 is given by
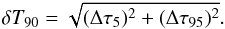 (5)In Table 1, we also report the peak fluxes of the GRBs. They were
calculated over 1 s for long GRBs, using only the standard OSA v10.0 software and IBIS/ISGRI
data. We did not use our new spectral extraction method since the low statistics over such a
short time interval meant the spectral fitting does not require more sophisticated models
than a simple power law to estimate the peak flux. In this case, the large IBIS/ISGRI
effective area was adapted to provide a fair measure of the peak flux. We also used the
latest available calibration files to recalculate the positions and the associated 90% c.l.
errors. They were computed using ISGRI alone, thanks to its higher positional accuracy with
respect to SPI.
(5)In Table 1, we also report the peak fluxes of the GRBs. They were
calculated over 1 s for long GRBs, using only the standard OSA v10.0 software and IBIS/ISGRI
data. We did not use our new spectral extraction method since the low statistics over such a
short time interval meant the spectral fitting does not require more sophisticated models
than a simple power law to estimate the peak flux. In this case, the large IBIS/ISGRI
effective area was adapted to provide a fair measure of the peak flux. We also used the
latest available calibration files to recalculate the positions and the associated 90% c.l.
errors. They were computed using ISGRI alone, thanks to its higher positional accuracy with
respect to SPI.
 |
Fig. 4 Distribution of the duration T90. Top: distribution of durations derived from BATSE (violet) and Fermi/GBM (red) light curves in the 50−300 keV band (c.f. Kouveliotou et al. 1993; Paciesas et al. 2012). Middle: T90 durations derived using Swift/BAT instrument on 15−150 keV (c.f. Sakamoto et al. 2011). Bottom: distribution of durations for 20−200 keV light curves obtained from IBIS/ISGRI. |
 |
Fig. 5 Distribution of fluences. Left: the distributions represent the fluences corresponding to the 50−300 keV energy range for the three instruments: BATSE (blue), Fermi GBM (red), and INTEGRAL (black). Right: the distribution of fluences in 15−150 keV energy range for Swift (green) and INTEGRAL GRB sample (black). |
 |
Fig. 6 Distribution of the spectral peak energies (left) and the low-energy spectral power-law indices (right). The sample of INTEGRAL GRBs is shown in black; BATSE results (violet) and Fermi/GBM results (red) of the time-integrated spectral analysis were used for comparison. Only long events were selected, fitted with the Band or cut-off power-law model, and having a fluence in the same range as INTEGRAL GRBs. |
4. INTEGRAL GRB sample: basic properties
We present an updated version of the currently published INTEGRAL GRB catalogues in Table 1 (for the previous versions, see Vianello et al. 2009; Foley et al. 2008). The basic properties of the 28 events observed in the period September 2008 to February 2012 are reported. The information on the counterpart observations are adopted from INTEGRAL GRB archive4. The histogram of the duration T90 is shown in the bottom panel of Fig. 4. For comparison, we also present the distributions of T90 for GRB samples from BATSE5 catalogue, as well as Fermi/GBM6 and Swift/BAT7 GRBs observed to date. The durations T90 of BATSE and Fermi/GBM bursts were determined using the light curves in the 50−300 keV energy band, while Swift GRB durations were determined using light curves obtained in the 15−150 keV energy band. The maximum of the T90 distribution for INTEGRAL GRB sample is at ~30 s, which is comparable to the samples obtained by BATSE and Fermi/GBM. The distinct property of the distribution of T90 durations of INTEGRAL GRBs is the very low number of short GRBs with respect to the total number of observed events: only 6% of the GRBs in the sample have durations <2 s, compared to 24%, 17% and 9% of short bursts observed by BATSE, Fermi/GBM, and Swift/BAT, respectively. The paucity of the short events is expected for the imaging instruments, such as the Swift/BAT, where a minimum number of counts is required to localize an excess in the derived image, making confirmation of real bursts with fewer counts (like the short ones) difficult or impossible even if they are detected by count-rate-increase algorithms.
To compare with the results from the other GRB missions, we present the cumulative fluence distributions for different instruments in Fig. 5. We calculated the fluences for the INTEGRAL set of bursts in two different energy bands, 50−300 keV and 15−150 keV, to compare with the data published for the BATSE and Fermi/GBM GRB samples and with the Swift/BAT GRB sample, respectively. We applied the Kolmogorov-Smirnov (KS) test (Press et al. 1992) and found that the fluence sample of GRBs observed by INTEGRAL is consistent with the distributions of fluences observed by Swift/BAT and Fermi/GBM, with the respective significance probabilities PKS = 0.76 and 0.27. A larger difference is found when the INTEGRAL GRB sample is compared with the distribution corresponding to BATSE sample (PKS = 0.02). Owing to the larger sensitivity of the IBIS instrument, one would expected that the larger number of faint GRBs are observed with respect to the Swift/BAT and Fermi/GBM missions; however, since INTEGRAL points for 67% of its time at low Galactic latitude (|b| < 20°) targets, its sensitivity is affected by the background induced by the Galactic sources.
INTEGRAL gamma-ray bursts detected between September 2008 and February 2012.
5. Spectral analysis
We performed spectral analysis on the whole sample of bursts observed between December 2002
and February 2012. Out of 83 GRBs in the initial sample, we report the results for 59
bursts: for 23 GRBs the data do not provide sufficient signal above the background for
accurate spectral analysis (three of these events, GRB 021219, GRB 040624, and GRB 050129,
were analysed using only IBIS/ISGRI data by Vianello et al.
2009). One GRB was only observed during part of its duration (GRB 080603). The
photon spectra were fitted with three models: a single power law, the empirical model for
prompt GRB spectra proposed by Band et al. (1993), and
a cutoff power-law model. The count spectrum, N(E), is
given in photons s-1 cm-2 keV-1, and E is
in units of keV. The power-law model is described by
N(E) = AEλ,
and it usually characterizes the spectra for which the break energy of the two component
spectrum lies outside the instrument energy band, or the spectra for which the signal at
high energies is weak and the break energy could not be accurately determined. The other two
models we tested allow determination of the spectral peak energy: the empirical model
introduced by Band et al. (1993),
![\begin{eqnarray} N(E) & = & A (E/100)^\alpha \exp \left( - {E \over E_0} \right); \quad {\rm for} \ E \leq \left( \alpha - \beta \right) E_{0} \nonumber \\ & = & A (E/100)^{\beta} [(\alpha-\beta)(E_0/100)]^{\alpha-\beta} \exp(\beta-\alpha); \nonumber \\ & & {\rm for} \;\; E \geq \left( \alpha - \beta \right) E_{0} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22256-13/aa22256-13-eq95.png) (6)and
power-law model with a high-energy exponential cutoff:
(6)and
power-law model with a high-energy exponential cutoff:
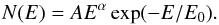 (7)Here,
E0 is the break energy in the Band model; in cutoff power-law
model it denotes the e-folding energy. The cutoff power-law model is often
used for GRB spectra for which the high-energy power-law slope β in Band
model is not well defined due to the low number of high-energy photon counts. Using this
notation, the peak of the νFν
spectrum for the spectra described by Band or cutoff power-law model is given by
Epeak = (α + 2)E0.
In Table 2 we report the results of the spectral
analysis (the best-fit spectral model) of the time-integrated spectra. The fluences in
(20−200) keV energy band reported in the table were calculated using the best-fit spectral
model. We also report the value of C-statistic and the number of degrees of freedom for the
XSPEC spectral analysis.
(7)Here,
E0 is the break energy in the Band model; in cutoff power-law
model it denotes the e-folding energy. The cutoff power-law model is often
used for GRB spectra for which the high-energy power-law slope β in Band
model is not well defined due to the low number of high-energy photon counts. Using this
notation, the peak of the νFν
spectrum for the spectra described by Band or cutoff power-law model is given by
Epeak = (α + 2)E0.
In Table 2 we report the results of the spectral
analysis (the best-fit spectral model) of the time-integrated spectra. The fluences in
(20−200) keV energy band reported in the table were calculated using the best-fit spectral
model. We also report the value of C-statistic and the number of degrees of freedom for the
XSPEC spectral analysis.
Results of the spectral fitting: best-fit spectral parameters, the associated 90% c.l. errors, the value of C-statistic for given d.o.f., and the fluence in 20−200 keV range.
Distribution of Epeak. We show the histogram of the observed values of the spectral peak energy in the left-hand panel of Fig. 6. It contains the results obtained by fitting the Band or the cut-off power-law model to the time-integrated spectra of the INTEGRAL bursts. There were 30 GRBs that were fitted with the cut-off power-law model and 2 GRBs fitted with the Band model in our sample. We compared these results with those from Fermi/GBM and BATSE detectors. It was shown by various authors that the observed Epeak correlates with the burst brightness (e.g. Mallozzi et al. 1995; Lloyd et al. 2000; Kaneko et al. 2006; Nava et al. 2008); in order to account for the possible biases in the distribution of the spectral parameters, we made a comparison of the GRBs within the same fluence range (see also Nava et al. 2011 for the comparison between the spectral properties of Fermi/GBM and BATSE GRBs). We selected from the Fermi/GBM6 and BATSE5 databases the results of the analysis obtained for: (i) GRBs within same fluence range as INTEGRAL GRBs (i.e. fluence in 50−300 keV energy range <8.7 × 10-5 erg cm-2). The lower fluence limit is approximately the same for all three samples (~10-8 erg cm-2). Only the condition on the fluence limit was imposed since the peak fluxes were determined on 20−200 keV energy band for INTEGRAL GRBs, while the Fermi/GBM and BATSE databases contain the values of peak fluxes determined on 50–300 keV; (ii) GRBs with durations of T90 > 2 s; (iii) GRBs for which the model that best fitted the time-integrated spectrum was the Band or the cutoff power-law model. We did not apply any additional condition based on the quality of the spectral fit (cf. Goldstein et al. 2012; Kaneko et al. 2006). The histograms for Fermi/GBM bursts and BATSE bursts are shown in Fig. 6. We used the Kolmogorov-Smirnov test to establish the probability whether the distribution of the spectral parameters of the INTEGRAL GRBs can be derived from the same parent distribution as Fermi/GBM or BATSE bursts. For the distribution of spectral peak energies, we found that our distribution is consistent with the distribution of the spectral peak energies of GRBs observed by Fermi/GBM (KS probability =0.55) and not consistent with the distribution of BATSE GRBs (KS probability =6 × 10-3) in a given fluence range.
Distribution of α. The distribution of the low-energy spectral slopes for INTEGRAL GRBs is shown in the right-hand panel of Fig. 6. We compared this distribution with the parameters of the Fermi/GBM and BATSE GRB samples. The selection of GRBs from Fermi/GBM and BATSE samples was done in the same way as in the case of Epeak distribution. The distribution of the low-energy power-law slopes obtained for ISGRI/SPI GRBs is consistent with both Fermi/GBM (KS probability =0.23) and BATSE (KS probability =0.92) GRB samples.
Distribution of λ. In the INTEGRAL sample there were 27 GRBs for which the model that best fitted the data was a single power law with the slope λ (see Table 2). Figure 7 shows the distribution of λ for our sample. For the comparison we plotted the results obtained for the BATSE and Fermi/GBM sample of GRBs for which the best fitted model was a single power law. We selected only the long bursts within the same fluences range as the INTEGRAL GRBs. We find that the distribution obtained for the INTEGRAL GRBs is not consistent with the distribution corresponding to Fermi/GBM population (KS probability =5 × 10-6), and is consistent with the distribution of BATSE GRBs (KS probability =0.05).
 |
Fig. 7 Distribution of the power law indices for the subsample of INTEGRAL GRBs that were fitted with the single power law model on the energy range 20−1000 keV (black line). BATSE results (violet) and Fermi GBM results (red) are shown for the GRBs for which the best spectral model was a single power law. The results for the analysis of the time-integrated spectra are shown, using GRBs within the same fluence range as INTEGRAL GRBs. |
 |
Fig. 8 Correlations between spectral parameters. Energy fluence in 20−200 keV vs. spectral peak energy Epeak. |
Correlations among spectral parameters. The empirical correlations among time-resolved spectral parameters were examined for BATSE and Fermi/GBM samples (Crider et al. 1997; Preece et al. 1998; Lloyd-Ronning & Petrosian 2002; Kaneko et al. 2006; Goldstein et al. 2012). The most significant correlation is found between Epeak and low-energy spectral index for the time-resolved spectra of individual bursts. The correlations between the time-integrated parameters Epeak and α,β and energy or photon flux/fluence were also investigated (Kaneko et al. 2006; Goldstein et al. 2012). We show in Figs. 8 and 9 energy fluence in 20−200 keV vs. Epeak and the scatter plots α vs. Epeak, α vs. E0. For reference, we show the parameters resulting from the spectral analysis of time-integrated spectra for Fermi/GBM and BATSE GRB samples. The general trend is that lower measured spectral peak energies (close to the lower end of the instrument energy band) increase the uncertainty of the low-energy power-law index (cf. Goldstein et al. 2012 for the sample of Fermi/GBM GRBs). We calculated the Spearman rank-order correlation coefficient (rs) and the corresponding significance probability Prs to test for correlations among pairs of the time-integrated parameters, low-energy spectral index−Epeak and low-energy spectral index−E0. We found no significant correlation in the first case, while for the second there is a marginal negative correlation (rs = −0.44) with the associated significance probability Prs = 1.15 × 10-2. Among the energy fluence−Epeak, see Fig. 8, we found a weak positive correlation (rs = 0.50) with the associated significance probability Prs = 1.88 × 10-2. Examining the correlations among time-integrated parameters Kaneko et al. (2006) also found only one significant correlation, namely between Epeak and total energy fluence.
 |
Fig. 9 Correlations between spectral parameters. Low-energy spectral index α vs. spectral peak energy Epeak (left) and low-energy spectral index α vs. break energy E0 (right). For reference, we also show the parameters of the time-integrated spectral analysis for Fermi (red) and BATSE (violet) GRBs. |
6. Summary
We have presented a spectral catalogue of the GRBs observed by the INTEGRAL instruments in the period December 2002−February 2012. We developed a new spectral extraction method especially suited for short transients where total number of counts is small. We were nevertheless able to probe the high spectral end of the INTEGRAL instruments’ energy range thanks to the use of the Cash statistic. This new method has been applied in a coherent way to the already published GRBs, as well as to the unpublished ones. It allowed us to measure the time integrated GRB peak energy in about 54% of the GRBs of our sample, while for the most complete INTEGRAL GRB sample published to date (Vianello et al. 2009), this fraction was just 16%. For BAT data, this fraction corresponds to 17% (Sakamoto et al. 2011). This allowed us for the first time to fully compare the INTEGRAL sample to previous and current GRB dedicated experiments’ results in the spectral and temporal domain.
Median parameter values and dispersion (quartile) of the distributions obtained for time-integrated spectra fitted with Band or cutoff power-law model.
Our temporal analysis showed that the T90 duration distribution of INTEGRAL GRBs is comparable to the one of BAT bursts, showing the paucity of the short GRBs with respect to the GRB samples detected by Fermi/GBM and BATSE. The maximum of the distribution of T90 durations is at ~30 s, which on the other hand, makes it similar to the Fermi/GBM sample. The reason for that lies in the triggering time scales of the two instruments: in the case of IBAS, Fermi/GBM, and BATSE it is tens of seconds, while Swift/BAT triggering time scales can be as long as tens of minutes.
Concerning the GRB fluence distribution of our sample, we found it statistically compatible with the Swift/BAT and Fermi/GBM ones. While the IBAS system is expected to be intrinsically more sensitive than Swift/BAT or Fermi/GBM (see Fig. 1), the fact that INTEGRAL spends most of its observing time pointing Galactic sources implies a diminished sensitivity due to the increased background induced by these sources.
In Table 3 we report the median spectral parameter values and the dispersions for the distributions obtained for INTEGRAL GRB time-integrated spectra. The peak energy values we could determine are compatible with the ones obtained by the Fermi/GBM experiment and not with the ones measured by BATSE, being systematically softer.
This can be explained by the similar triggering threshold of the two former instruments (15 keV vs. 8 keV), which are both significantly lower than the nominal BATSE low energy threshold of 50 keV. The median of the peak energy distribution is at ~180 keV, with a dispersion of ~100 keV. The slopes of the low-energy photon spectra are found to be consistent with both samples, Fermi/GBM and BATSE, having the median of the distribution at α = −1 and a spread ≲0.3. When a single power law was fitted to the spectra, we found that the distribution of power-law indices has its median at λ = −1.4 and a spread ≲0.3. INTEGRAL GRBs that are fitted with a single power-law are therefore harder than Fermi/GBM sample, and consistent with the BATSE GRB sample. The correlations among the spectral properties (e.g. low-energy spectral index vs. spectral peak energy) were investigated for the time-resolved spectra of the individual GRBs and were not tested in this work due to the insufficient count number. We confirm that the analogous correlation among the time-integrated spectral properties does not hold for the INTEGRAL GRB sample, as it was also found for the BATSE data by Kaneko et al. (2006). Weak correlations were found for low-energy spectral index α vs. break energy E0, and energy fluence vs. the observed spectral peak energy.
The GRB catalogue we presented contains a limited number of events compared to other missions’ databases. Our results allow however an important insight into the possible instrumental biases in spectral and temporal parameter distributions, and also provide the spectral analysis for a sample of faint GRBs with good statistics.
For updated sensitivity of Fermi/GBM, see Bissaldi et al. (2009) and Meegan et al. (2009).
To access the reduced spectra, see http://ibas.iasf-milano.inaf.it/spectral_catalogue/spectra.html
Acknowledgments
The authors thank Jochen Greiner for careful reading of the manuscript and for valuable comments on this work. The authors thank Thomas Maccarone, Patrick Sizun, and Fabio Mattana for discussions on data analysis. ZB acknowledges financial support from the French Space Agency (CNES). ISGRI has been realized and maintained in flight by CEA-Saclay/Irfu with the support of the CNES. Based on observations with INTEGRAL, an ESA project with the instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain), the Czech Republic, and Poland, and with the participation of Russia and the USA.
References
- Arnaud, K. A. 2010, in AAS/High Energy Astrophysics Division #11, BAAS, 41, 668 [Google Scholar]
- Band, D. L. 2003, ApJ, 588, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D. L. 2006, ApJ, 644, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Bissaldi, E., von Kienlin, A., Lichti, G., et al. 2009, Exp. Astron., 24, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Bissaldi, E., von Kienlin, A., Kouveliotou, C., et al. 2011, ApJ, 733, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Borgonovo, L., & Ryde, F. 2001, ApJ, 548, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crider, A., Liang, E. P., Smith, I. A., et al. 1997, ApJ, 479, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cocco, G., Caroli, E., Celesti, E., et al. 2003, A&A, 411, L189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fishman, G. J., Meegan, C. A., Wilson, R. B., et al. 1989, in BAAS, 21, 860 [Google Scholar]
- Foley, S., McGlynn, S., Hanlon, L., McBreen, S., & McBreen, B. 2008, A&A, 484, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, N., & Razzaque, S. 2013, in Frontiers of Physics (Springer-Verlag) [Google Scholar]
- Gehrels, N., Chipman, E., & Kniffen, D. 1994, ApJS, 92, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Ghisellini, G., & Celotti, A. 2004, A&A, 422, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldstein, A., Burgess, J. M., Preece, R. D., et al. 2012, ApJS, 199, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Götz, D., Laurent, P., Lebrun, F., Daigne, F., & Bošnjak, Ž. 2009, ApJ, 695, L208 [NASA ADS] [CrossRef] [Google Scholar]
- Götz, D., Covino, S., Fernández-Soto, A., Laurent, P., & Bošnjak, Ž. 2013, MNRAS, 431, 3550 [NASA ADS] [CrossRef] [Google Scholar]
- Kaneko, Y., Preece, R. D., Briggs, M. S., et al. 2006, ApJS, 166, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Koshut, T. M., Paciesas, W. S., Kouveliotou, C., et al. 1996, ApJ, 463, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lloyd, N. M., Petrosian, V., & Mallozzi, R. S. 2000, ApJ, 534, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd-Ronning, N. M., & Petrosian, V. 2002, ApJ, 565, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, D., Tagliaferri, G., Chincarini, G., et al. 2004, ApJ, 609, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Mallozzi, R. S., Paciesas, W. S., Pendleton, G. N., et al. 1995, ApJ, 454, 597 [NASA ADS] [CrossRef] [Google Scholar]
- McGlynn, S., Foley, S., McBreen, B., et al. 2009, A&A, 499, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Götz, D., Borkowski, J., Walter, R., & Pedersen, H. 2003, A&A, 411, L291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, MNRAS, 415, 3153 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Firmani, C. 2008, MNRAS, 391, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Paciesas, W. S., Meegan, C. A., von Kienlin, A., et al. 2012, ApJS, 199, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 1998, ApJ, 506, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 2000, ApJS, 126, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN: the art of scientific computing (Cambridge University press) [Google Scholar]
- Qin, Y., Liang, E.-W., Liang, Y.-F., et al. 2013, ApJ, 763, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Baumgartner, W. H., et al. 2011, ApJS, 195, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Tierney, D., McBreen, S., Fermi Gbm Team, et al. 2010, in Proc. Eighth Integral Workshop. The Restless Gamma-ray Universe (INTEGRAL 2010), 103 [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vedrenne, G., Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vianello, G., Götz, D., & Mereghetti, S. 2009, A&A, 495, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: IBIS/ISGRI light curves of INTEGRAL GRBs
 |
Fig. A.1 Light curves of INTEGRAL GRBs observed in the period September 2008−February 2012. The dashed lines show the interval in which the spectral information was extracted. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
All Tables
Results of the spectral fitting: best-fit spectral parameters, the associated 90% c.l. errors, the value of C-statistic for given d.o.f., and the fluence in 20−200 keV range.
Median parameter values and dispersion (quartile) of the distributions obtained for time-integrated spectra fitted with Band or cutoff power-law model.
All Figures
 |
Fig. 1 Sensitivity of past and present GRB experiments as a function of the GRB peak energy. For Fermi/GBM NaI detectors, BeppoSAX/WFC, BeppoSAX/GRBM, HETE-2/Fregate, HETE-2/ WXM, and CGRO/BATSE LAD detectors the data are taken from Band (2003); for Swift/BAT the data are taken from Band (2006); for INTEGRAL/IBAS the data are taken from the IBAS web site4. |
| In the text | |
 |
Fig. 2 Spectral model and data for GRB 061122. The violet triangles are the 20−200 keV ISGRI data points used for the fit. The coloured dots covering the energy range 40−1000 keV are the data from the 11 SPI detectors with the highest signal-to-noise ratio selected for the spectral analysis (cf. McGlynn et al. 2009). We fitted the cut-off power-law model in this case, with α = −1.3 and E0 = 263 keV (see Sect. 5 on spectral analysis). |
| In the text | |
 |
Fig. 3 Example of T90 calculation using the time-integrated IBIS/ISGRI light curve of GRB 081003B. The vertical dashed lines represent the times when the GRB integrated counts exceed 5% (S5) and 95% (S95) of the maximal integrated flux value, respectively. |
| In the text | |
 |
Fig. 4 Distribution of the duration T90. Top: distribution of durations derived from BATSE (violet) and Fermi/GBM (red) light curves in the 50−300 keV band (c.f. Kouveliotou et al. 1993; Paciesas et al. 2012). Middle: T90 durations derived using Swift/BAT instrument on 15−150 keV (c.f. Sakamoto et al. 2011). Bottom: distribution of durations for 20−200 keV light curves obtained from IBIS/ISGRI. |
| In the text | |
 |
Fig. 5 Distribution of fluences. Left: the distributions represent the fluences corresponding to the 50−300 keV energy range for the three instruments: BATSE (blue), Fermi GBM (red), and INTEGRAL (black). Right: the distribution of fluences in 15−150 keV energy range for Swift (green) and INTEGRAL GRB sample (black). |
| In the text | |
 |
Fig. 6 Distribution of the spectral peak energies (left) and the low-energy spectral power-law indices (right). The sample of INTEGRAL GRBs is shown in black; BATSE results (violet) and Fermi/GBM results (red) of the time-integrated spectral analysis were used for comparison. Only long events were selected, fitted with the Band or cut-off power-law model, and having a fluence in the same range as INTEGRAL GRBs. |
| In the text | |
 |
Fig. 7 Distribution of the power law indices for the subsample of INTEGRAL GRBs that were fitted with the single power law model on the energy range 20−1000 keV (black line). BATSE results (violet) and Fermi GBM results (red) are shown for the GRBs for which the best spectral model was a single power law. The results for the analysis of the time-integrated spectra are shown, using GRBs within the same fluence range as INTEGRAL GRBs. |
| In the text | |
 |
Fig. 8 Correlations between spectral parameters. Energy fluence in 20−200 keV vs. spectral peak energy Epeak. |
| In the text | |
 |
Fig. 9 Correlations between spectral parameters. Low-energy spectral index α vs. spectral peak energy Epeak (left) and low-energy spectral index α vs. break energy E0 (right). For reference, we also show the parameters of the time-integrated spectral analysis for Fermi (red) and BATSE (violet) GRBs. |
| In the text | |
 |
Fig. A.1 Light curves of INTEGRAL GRBs observed in the period September 2008−February 2012. The dashed lines show the interval in which the spectral information was extracted. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


