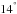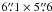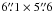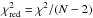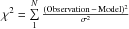| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322460 | |
| Published online | 06 December 2013 | |
The IRAM-30 m line survey of the Horsehead PDR
IV. Comparative chemistry of H2CO and CH3OH⋆,⋆⋆
1 Institut de Radioastronomie Millimétrique (IRAM), 300 rue de la Piscine, 38406 Saint-Martin-d’Hères France
e-mail: guzman@iram.fr; pety@iram.fr; gratier@iram.fr
2 Departamento de Astrofísica, Centro de Astrobiología, CSIC-INTA, Carretera de Ajalvir, Km 4. Torrejón de Ardoz, 28850 Madrid, Spain
e-mail: jr.goicoechea@cab.inta-csic.es
3 LERMA – LRA, UMR 8112, Observatoire de Paris and École Normale Supérieure, 24 rue Lhomond, 75231 Paris, France
e-mail: maryvonne.gerin@lra.ens.fr
4 LUTH UMR 8102, CNRS and Observatoire de Paris, Place J. Janssen, 92195 Meudon Cedex, France
e-mail: evelyne.roueff@obspm.fr; franck.lepetit@obspm.fr; jacques.lebourlot@obspm.fr
5 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: alexandre.faure@obs.ujf-grenoble.fr
Received: 7 August 2013
Accepted: 21 October 2013
Context. Theoretical models and laboratory experiments show that CH3OH is efficiently formed on cold grain surfaces through the successive hydrogenation of CO, forming HCO and H2CO as intermediate species. In cold cores and low UV-field illumination photo-dissociation regions (PDRs) the ices can be released into the gas-phase through nonthermal processes such as photodesorption, which considerably increases their gas-phase abundances.
Aims. We investigate the dominant formation mechanism of H2CO and CH3OH in the Horsehead PDR and its associated dense core.
Methods. We performed deep integrations of several H2CO and CH3OH lines at two positions in the Horsehead, namely the PDR and dense core, with the IRAM-30 m telescope. In addition, we observed one H2CO higher-frequency line with the CSO telescope at both positions. We determined the H2CO and CH3OH column densities and abundances from the single-dish observations complemented with IRAM-PdBI high-angular resolution maps (6′′) of both species. We compared the observed abundances with PDR models including either pure gas-phase chemistry or both gas-phase and grain surface chemistry.
Results. We derived CH3OH abundances relative to total number of hydrogen atoms of ~1.2 × 10-10 and ~2.3 × 10-10 in the PDR and dense-core positions, respectively. These abundances are similar to the inferred H2CO abundance in both positions (~2 × 10-10). We find an abundance ratio H2CO/CH3OH of ~2 in the PDR and ~1 in the dense core. Pure gas-phase models cannot reproduce the observed abundances of either H2CO or CH3OH at the PDR position. The two species are therefore formed on the surface of dust grains and are subsequently photodesorbed into the gas-phase at this position. At the dense core, on the other hand, photodesorption of ices is needed to explain the observed abundance of CH3OH, while a pure gas-phase model can reproduce the observed H2CO abundance. The high-resolution observations show that CH3OH is depleted onto grains at the dense core. CH3OH is thus present in an envelope around this position, while H2CO is present in both the envelope and the dense core itself.
Conclusions. Photodesorption is an efficient mechanism to release complex molecules in low-FUV-illuminated PDRs, where thermal desorption of ice mantles is ineffective.
Key words: astrochemistry / ISM: clouds / ISM: molecules / photon-dominated region (PDR) / radiative transfer / radio lines: ISM
Based on observations obtained with the IRAM Plateau de Bure interferometer and 30 m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
The reduced datacubes (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A73
© ESO, 2013
1. Introduction
Formaldehyde (H2CO) and methanol (CH3OH) are key species in the synthesis of more complex organic molecules, such as amino acids and other prebiotic molecules (Bernstein et al. 2002; Muñoz Caro et al. 2002; Garrod et al. 2008), that might finally arrive in proto-planetary disks, and hence in new planetary systems. It is therefore of great interest to understand how these molecules are formed. Both species have been detected in a wide range of interstellar environments, with typical gas-phase abundances relative to H2 of ~10-7 in hot cores (e.g., Sutton et al. 1995; Ceccarelli et al. 2000) and ~10-9 in cold dark clouds (e.g., Bergman et al. 2011). They are also observed in shocked regions, caused by an impact of molecular outflows on the surrounding molecular clouds (e.g., Sakai et al. 2012; Codella et al. 2012; Tafalla et al. 2010). Because they are slightly asymmetric rotors, H2CO and CH3OH are good tracers of the physical conditions in Galactic and extragalactic molecular clouds (Mangum & Wootten 1993; Leurini et al. 2004; Mangum et al. 2013).
Unlike H2CO, which can be formed both in the gas-phase and on the surface of dust grains, CH3OH is thought to be formed entirely on the surfaces of dust grains, because classical ion-neutral chemistry in the gas-phase alone cannot account for the observed CH3OH abundances (Garrod et al. 2006; Geppert et al. 2006). The mechanism to form CH3OH on ices is thought to be the successive hydrogenation of CO, forming H2CO as an intermediate product, ![\begin{equation} \mathrm{CO} \xrightarrow[\h]{E_{\rm b}} \mathrm{HCO} \xrightarrow[\h]{} \hhco \xrightarrow[\h]{E_{\rm b}} \mathrm{CH}_2\mathrm{OH},\mathrm{CH}_3\mathrm{O} \xrightarrow[\h]{} \chhhoh, \label{eq:path} \end{equation}](/articles/aa/full_html/2013/12/aa22460-13/aa22460-13-eq27.png) (1)
where Eb are activation energy barries (Tielens & Whittet 1997; Watanabe & Kouchi 2002). Indeed, laboratory experiments have succeeded to efficiently form both H2CO and CH3OH through this mechanism (Watanabe et al. 2004; Fuchs et al. 2009). Moreover, observations by the Infrared Space Observatory (ISO) and Spitzer have shown that dust grains are covered by ice mantles in the cold envelopes surrounding high-mass protostars (Gibb et al. 2000, 2004), low-mass protostars (Boogert et al. 2008; Pontoppidan et al. 2008; Öberg et al. 2008; Bottinelli et al. 2010), and in isolated dense cores (Boogert et al. 2011). These studies revealed that the ice mantles consist mostly of H2O, CO2 and CO, with smaller amounts of CH3OH, CH4, NH3, and H2CO. HCO ice has not been detected in the interstellar medium (ISM), probably because its formation on the ices is slower than its subsequent hydrogenation to form H2CO. Indeed, the reactions starting with CO and H2CO in the hydrogenation path (1) have activation energy barriers (Fuchs et al. 2009).
(1)
where Eb are activation energy barries (Tielens & Whittet 1997; Watanabe & Kouchi 2002). Indeed, laboratory experiments have succeeded to efficiently form both H2CO and CH3OH through this mechanism (Watanabe et al. 2004; Fuchs et al. 2009). Moreover, observations by the Infrared Space Observatory (ISO) and Spitzer have shown that dust grains are covered by ice mantles in the cold envelopes surrounding high-mass protostars (Gibb et al. 2000, 2004), low-mass protostars (Boogert et al. 2008; Pontoppidan et al. 2008; Öberg et al. 2008; Bottinelli et al. 2010), and in isolated dense cores (Boogert et al. 2011). These studies revealed that the ice mantles consist mostly of H2O, CO2 and CO, with smaller amounts of CH3OH, CH4, NH3, and H2CO. HCO ice has not been detected in the interstellar medium (ISM), probably because its formation on the ices is slower than its subsequent hydrogenation to form H2CO. Indeed, the reactions starting with CO and H2CO in the hydrogenation path (1) have activation energy barriers (Fuchs et al. 2009).
Once these species are formed on the ices, they can be desorbed into the gas-phase either through thermal or nonthermal processes. Thermal desorption dominates in regions where dust grains reach temperatures of at least 45 K for formaldehyde (Tielens & Allamandola 1987) and 80 K for methanol (Brown & Bolina 2007; Green et al. 2009). This occurs in hot cores and hot corinos (e.g., Jørgensen et al. 2005; Bisschop et al. 2007; Bottinelli et al. 2007), but also in highly far-ultraviolet (FUV) illuminated photo-dissociation regions (PDRs), such as the Orion bar (Leurini et al. 2010). Nonthermal desorption by FUV photons can also be efficient, as shown by laboratory experiments (Öberg et al. 2009b,c). Nonthermal desorption dominates in colder regions, either UV-shielded dense cores where secondary UV photons are produced by the interaction between cosmic rays and H2 molecules (e.g., Caselli et al. 2012), or in low-UV-field illumination photo-dissociation regions, where dust grains are too cold to sublimate their ices. This is the case of the Horsehead, where the combination of a moderate-radiation field (χ = 60 relative to the Draine field; Draine 1978), and high density (nH ~ 104 − 105 cm-3) implies low dust grain temperatures, from Tdust ~ 30 K in the outer PDR to Tdust ~ 20 K slightly deeper inside the cloud (Goicoechea et al. 2009a). Guzmán et al. (2011) compared single-dish observations of H2CO with PDR models including grain-surface chemistry. They showed that the observed H2CO abundance in the UV-illuminated edge of the Horsehead nebula can only be explained by the formation of H2CO on the grains followed by its photo-desorption into the gas-phase. Pure gas-phase chemistry was enough to explain the H2CO abundance in the colder and UV-shielded gas. The assignments of different formation routes were strengthened by the different measured ortho-to-para ratio of H2CO: the dense core displays an equilibrium value of ~3, while the PDR displays an out-of-equilibrium value of ~2. The PDR model predicted that H2CO will be one order of magnitude more abundant in the PDR than the IRAM-30 m beam-averaged measurements.
To further constrain the chemistry of complex organic molecules and investigate the high abundance in the PDR position predicted by the model, we here present high-resolution interferometric maps of H2CO and CH3OH in addition to single-dish deep integrations of the low-lying rotational lines of CH3OH toward two particular positions in the Horsehead: the warm PDR and its associated cold dense core. The observations and data reduction are presented in Sect. 2. The resulting single-dish and interferometric data are described in Sect. 3. In Sect. 4, we compute the CH3OH column densities and abundances. We compare these results with PDR models in Sect. 5. A discussion is presented in Sect. 6. We summarize and conclude in Sect. 7.
Observation parameters of the deep integrations of the CH3OH lines detected with the 30 m and the H2CO line detected with the CSO toward the PDR and the dense core.
2. Observations and data reduction
In this section, we describe the observations and data reduction of the newly acquired H2CO and CH3OH data. A detailed description of the HCO, 218.222 GHz H2CO, DCO+, and 1.2 mm continuum observations and data reduction can be found in Gerin et al. (2009), Guzmán et al. (2011), Pety et al. (2007), and Hily-Blant et al. (2005), respectively. Tables 1–3 summarize the observation parameters of the data obtained with the IRAM-30 m, PdBI, and CSO telescopes.
2.1. PdBI maps
We used the Plateau de Bure Interferometer (PdBI) to obtain 6′′ resolution maps of the emission of the H2CO 202 − 101 line at 146.603 GHz, the CH3OH − E 3-1 − 2-1 line at 145.097 GHz, and the CH3OH − A 30 − 20 line at 145.103 GHz. These observations were carried out in August and October 2011 with five antennas in the D configuration and six antennas in the C configuration. The baseline lengths ranged between 24 and 176 m. We observed a 19-field mosaic in a hexagonal pattern covering an almost circular field-of-view of 80′′ in diameter. The observations used about 19 h of telescope time. The on-source time scaled to a six antenna array is 5.3 h after filtering out low-quality visibilities. Two correlator windows of 20 MHz (yielding a spectral resolution of 39 kHz) were concatenated to cover both CH3OH lines. Another 20 MHz window was centered on the targeted H2CO line. During the observations, the typical precipitable water vapor amounted to 6 mm and the typical system temperature was 145 K. The median noise level achieved over the mosaic is 0.24 K and 0.12 K (Tmb, in channels of 0.2 km s-1 width) for H2CO and CH3OH, respectively.
We used the standard algorithms implemented in the GILDAS1/CLIC software to calibrate the PdBI data. The radio-frequency bandpass was calibrated by observing the bright quasar 3C 454.3. Phase and amplitude temporal variations where calibrated by fitting spline polynomials through regular mesurements of two nearby quasars (0420−014 and 0528+134). The PdBI secondary flux calibrator MWC 349 was observed once during every track, which allowed us to derive the flux scale of the interferometric data. The absolute flux accuracy is ~10%.
2.2. 30 m maps
 |
Fig. 1 Detected CH3OH lines toward the dense-core (left) and PDR (right) positions. The green curves are Gaussian fits. The line frequency in GHz is given in each box. For each line, the same scale is used at both positions to facilitate the comparison. |
A multiplicative interferometer filters out the low spatial frequencies, that is, spatially extended emission. We therefore observed the same region with the IRAM-30 m single-dish telescope to recover the low spatial frequency (short- and zero-spacing) information filtered out by the PdBI. The H2CO 202 − 101 (145.603 GHz) line was observed simultaneously with the CH3OH − E 3-1 − 2-1 (145.097 GHz) and CH3OH − A 30 − 20 (145.103 GHz) lines during ~13 h of average summer weather in August and September 2012. We used the two polarizations of the EMIR receivers and the FTS backends at 49 kHz spectral resolution. We used the position-switching, on-the-fly observing mode. The off-position offsets were (δRA,δDec) = (100′′,0′′), that is, the H ii region ionized by σOri and free of molecular emission. We completed the observations of the 146.097 GHz and 146.103 GHz CH3OH lines with older but higher-quality observations obtained in January 2007. We used one polarization of the C150 receiver and one 20 MHz window of the VESPA correlator, yielding a spectral resolution of 20 kHz. In this case, we used the frequency-switched, on-the-fly observing mode, with a frequency throw of 7.9 MHz. In both observations, we observed along and perpendicular to the direction of the exciting star in zigzags (i.e., ± the lambda and beta scanning direction). From our knowledge of the IRAM-30 m telescope, we estimate the absolute position accuracy to be 3′′.
The IRAM-30 m data were processed with the GILDAS/ CLASS software. The data were first calibrated to the  scale using the chopper-wheel method (Penzias & Burrus 1973). The mixer tuning tables were incorrect for the frequency tuned in 2012. This basically turned the single sideband mixers into double-sideband ones. Because the actual rejection was unknown, we were unable to recompute an accurate
scale using the chopper-wheel method (Penzias & Burrus 1973). The mixer tuning tables were incorrect for the frequency tuned in 2012. This basically turned the single sideband mixers into double-sideband ones. Because the actual rejection was unknown, we were unable to recompute an accurate  scale. Instead, we fixed the 2012
scale. Instead, we fixed the 2012  scale according to the 2007 scale, which was correct. To do this, we correlated the 2007 and 2012 CH3OH data sets, which allowed us to determine the multiplicative factors needed to fix the 2012 data (1.9 and 2.4 for the vertical and horizontal polarizations, respectively). We applied the same factors for the H2CO data that were acquired with the same tuning. The data were converted to main-beam temperatures (Tmb) using the forward and main-beam efficiencies (Feff and Beff). The resulting amplitude accuracy is 10%. We then computed the experimental noise by subtracting a zeroth-order baseline from every spectra. A systematic comparison of this noise value with the theoretical noise computed from the system temperature, the integration time, and the channel width allowed us to filter out outlier spectra. The spectra where then gridded to a data cube through a convolution with a Gaussian kernel. Finally, we fitted another baseline of order 3 through each spectra of the cube.
scale according to the 2007 scale, which was correct. To do this, we correlated the 2007 and 2012 CH3OH data sets, which allowed us to determine the multiplicative factors needed to fix the 2012 data (1.9 and 2.4 for the vertical and horizontal polarizations, respectively). We applied the same factors for the H2CO data that were acquired with the same tuning. The data were converted to main-beam temperatures (Tmb) using the forward and main-beam efficiencies (Feff and Beff). The resulting amplitude accuracy is 10%. We then computed the experimental noise by subtracting a zeroth-order baseline from every spectra. A systematic comparison of this noise value with the theoretical noise computed from the system temperature, the integration time, and the channel width allowed us to filter out outlier spectra. The spectra where then gridded to a data cube through a convolution with a Gaussian kernel. Finally, we fitted another baseline of order 3 through each spectra of the cube.
2.3. Joint imaging and deconvolving of the interferometric and single-dish data
Following Rodriguez-Fernandez et al. (2008), the GILDAS/ MAPPING software and the single-dish map from the IRAM-30 m were used to create the short-spacing visibilities not sampled by the Plateau de Bure interferometer. In short, the maps were deconvolved from the IRAM-30 m beam in the Fourier plane before multiplication by the PdBI primary beam in the image plane. After a last Fourier transform, pseudo-visibilities were sampled between 0 and 15 m (the diameter of the PdBI antenna). These visibilities were then merged with the interferometric observations. Each mosaic field was imaged and a dirty mosaic was built by combining these fields in the following best way in terms of signal-to-noise ratio (Pety & Rodríguez-Fernández 2010). The resulting data cubes were then scaled from Jy/beam to Tmb temperature scale using the synthesized beam size (see Table 2).
2.4. Deep pointed integrations with the 30 m
These observations are part of the Horsehead WHISPER project (Wideband High-resolution Iram-30 m Surveys at two Positions with Emir Receivers, PI: J. Pety), a complete and unbiased line survey at 1, 2, and 3 mm, carried out with the IRAM-30 m telescope. Two positions were observed: 1) the HCO peak, which is characteristic of the photo-dissociation region at the surface of the Horsehead nebula (Gerin et al. 2009); and 2) the DCO+ peak, which belongs to a cold condensation located less than 40′′ away from the PDR edge, where HCO+ and other species are highly deuterated (Pety et al. 2007). Hereafter we refer to these two positions as the PDR and dense core, respectively. The combination of the new EMIR receivers at the IRAM-30 m telescope and the Fourier transform spectrometers (FTS) yields a spectral survey with unprecedented combination of bandwidth (36 GHz at 3 mm, 25 GHz at 2 mm and 76 GHz at 1 mm), spectral resolution (49 kHz at 3 and 2 mm; and 195 kHz at 1 mm), and sensitivity (median noise 8.1 mK, 18.5 mK and 8.3 mK, respectively). A detailed presentation of the observing strategy and data reduction process will be given in a forthcoming paper. In short, all frequencies were observed with two different frequency tunings and the Horsehead PDR and dense-core positions were alternatively observed every 15 min in position-switching mode with a common fixed off-position. This observing strategy allows us to remove potential ghost lines that are incompletely rejected from a strong line in the image sideband (the typical rejection of the EMIR sideband-separating mixers is only 13dB).
2.5. Deep pointed integrations with the CSO
We also report the detection of a new H2CO line in the Horsehead. The H2CO 413 − 312 at line at 300.836 GHz was observed at the Caltech Submillimeter Observatory (CSO) telescope in October 2012. We used the Barney receiver and the FFTS2 backends at 269 kHz spectral resolution. We used the position-switching mode with the same off-position as was used in the 30 m observations, that is, (δRA,δDec) = (100′′,0′′). The data were processed with the GILDAS/CLASS software. A fourth-order baseline was fit and subtracted from the spectra. The data were converted to Tmb using a beam efficiency of 0.68 measured towards Jupiter.
3. Observational results
3.1. Deep pointed integrations
Figure 1 presents the CH3OH lines detected in the Horsehead. A diagram with the lower-energy rotational levels of E- and A-type methanol is shown in Fig. 2, with color arrows indicating the detected lines. We detected 9 and 16 lines at the PDR and dense-core positions, respectively. Of these lines, at each position, three arise from A-type methanol and the rest arise from E-type methanol. The brightest CH3OH lines are those arising from A-type symmetry species. All lines are brighter in the dense core than in the PDR. The same behavior was found for H2CO (Guzmán et al. 2011). Gaussian fits of the CH3OH lines at the PDR in general result in broader line widths than at the dense core, although a few lines have similar linewidths toward both positions.
 |
Fig. 2 Lower-energy rotational levels of CH3OH − E (left) and CH3OH − A (right). The arrows indicate the lines detected in the PDR (red) and the core (blue). |
3.2. 30m maps
Figure 3 displays the single-dish maps of the 1.2 mm dust continuum emission and the line-integrated emission of the DCO+(3 − 2) (216 GHz) line, the p − H2CO 303 − 202 (218 GHz) and 202 − 101 (146 GHz) lines, the CH3OH − E 3-1 − 2-1 (146 GHz) line, and the CH3OH − A 30 − 20 (146 GHz) line. The formaldehyde and methanol emission to first order resembles the dust continuum spatial distribution. It first follows the photo-dissociation front, that is, the top of the Horsehead nebula from its front to its mane. It then forms two filaments almost perpendicular to the photo-dissociation front, one of them delineating the Horsehead throat. The E- and A-type methanol emission shows similar spatial distributions.
 |
Fig. 3 IRAM-30 m maps of the Horsehead edge. Maps were rotated by |
 |
Fig. 4 IRAM-PdBI maps of the Horsehead edge. The field of view is smaller than in Fig. 3. The angular resolution is |
In contrast to the DCO+ emission, which delineates a narrow filament, formaldehyde and methanol emission is extended. The impression that the formaldehyde emission is slightly more extended than the methanol emission is an artifact related to the different signal-to-noise ratio of these maps. Indeed, the 146 GHz E-type methanol map has by far the lowest signal-to-noise ratio. The highest signal-to-noise ratio map (i.e., the 146 GHz formaldehyde one) thus indicates that both formaldehyde and methanol emit in the PDR region (green cross).
Although the methanol emission in general correlates well with the formaldehyde emission, there are a few differences. First, formaldehyde peaks on the right side (closest to the photo-dissociation front) of the dense core as traced by the DCO+ emission, while methanol peaks on its left side. Second, the 146 GHz formaldehyde line peaks at the DCO+ emission peak (blue cross), where the gas is cold (Tkin ≃ 20 K) and dense (nH ~ 105 cm-3), while CH3OH presents a local minimum at the same position.
3.3. PdBI maps
Figure 4 displays the HCO 1013/2,2 − 0001/2,1 (86.670 GHz), H2CO 202 − 101 (145.602 GHz), CH3OH − E 3-1 − 2-1 (145.097 GHz), and CH3OH − A 30 − 20 (145.103 GHz) integrated intensity maps obtained with the PdBI. In contrast to the case of HCO, which peaks in the PDR, the H2CO and CH3OH lines are brighter in the more UV-shielded layers of the nebula. However, the filament traced by the HCO emission is clearly seen in the H2CO map at the PDR edge. The exact spatial distribution of the CH3OH emission near the PDR position is difficult to infer due to the low signal-to-noise ratio at this position.
The minimum seen in the methanol 30 m maps near the dense-core position (blue cross) is present in both methanol lines and is preserved in the higher angular resolution map. On the other hand, H2CO, which was observed simultaneously with CH3OH, peaks at the dense core. This suggests that 1) the methanol gap is real and not an artifact of the deconvolution; and 2) methanol and formaldehyde emission show opposite behavior at the DCO+ peak.
In contrast with HCO data, the maps of H2CO and CH3OH emission obtained with the PdBI only data (i.e., without the short-spacings from the IRAM-30 m telescope) looks like noise with a typical noise level of 0.15 K. Indeed, the spectra extracted from the hybrid synthesis (PdBI + 30 m) cube at the position of the dense core and of the PDR have an integrated area compatible, within the noise level, with the 30 m spectra at the same positions. This implies that the beam dilution of the single-dish observations of H2CO and CH3OH is marginal. We therefore used the higher signal-to-noise ratio 30 m spectra to infer the column densities at the PDR and dense-core positions.
 |
Fig. 5 New o - H2CO line detected toward the PDR (left) and dense-core (right) positions. The three color lines plot the radiative-transfer models from Guzmán et al. (2011), where the column density was varied around the best match (red curve) by a factor of 1.5 (blue curve) and 1/1.5 (green curve). The column density used for the best fit is given in Table 6. The line frequency in GHz is given in each box. |
4. Column densities and abundances
4.1. H2CO
Figure 5 shows the new o - H2CO 413 − 312 line detected in the Horsehead. Guzmán et al. (2011) reported the detection of four o - H2CO lines at lower frequencies. They used a nonlocal excitation and radiative transfer model from Goicoechea et al. (2006) adapted to the Horsehead geometry to model the observed H2CO line intensities. The parameters they used are Tkin = 60 K and n(H2) = 6 × 104 cm-3 at the PDR position and Tkin = 20 K and n(H2) = 105 cm-3 at the dense-core position. The column density that best reproduced the observations is given in Table 6 and the modeled line profile is shown in red in Fig. 5. The line profiles for two other models are also shown. The new detected H2CO line agrees with the predictions of our previous model and thus corroborates the H2CO column density derived by Guzmán et al. (2011).
4.2. CH3OH
Typical densities in the Horsehead (nH = 104 − 105 cm-3) are lower than the critical densities of the observed transitions of methanol (see Table 4). We therefore expect the lines to be subthermally excited (Tex ≪ Tkin), and a non-LTE approach is needed to compute the CH3OH column densities. E and A symmetries of CH3OH were treated as different species because radiative transitions between them occur on timescales too long compared with the lifetime of the molecules. We did not correct for beam-dilution factors because the interferometric maps indicate that beam dilution is marginal for these molecules. The spectroscopic parameters for the detected transitions are given in Table 5.
Critical densitiesa ( cm-3) for the CH3OH lines detected in this work with p - H2 and o - H2 as colliding partners computed for two kinetic temperatures.
Spectroscopic parameters of the detected lines obtained from the CDMS data base (Müller et al. 2001).
We performed non-LTE radiative-transfer modeling using the RADEX LVG model (van der Tak et al. 2007), which computes the line intensities of a species for a given column density, kinetic temperature, and density of H2. We included 100 rotational levels for CH3OH − E and CH3OH − A, where the highest energy level lies at ~155 cm-1 for both species. We considered p - H2 and o - H2 as collision partners with collisional excitation rates from Rabli & Flower (2010). An H2 ortho-to-para ratio of 3 (high-temperature limit) was assumed in the models. Lower H2 ortho-to-para ratios were also tested, and we found that the difference is negligible. We also investigated the importance of electrons in the excitation at the PDR. The electron fraction is 10-4 relative to H2 in the PDR position, while in the dense core the electron fraction is ~10-9 (Goicoechea et al. 2009b). We computed the CH3OH − E −electron and CH3OH − A −electron collisional coefficients within the dipolar Born approximation (e.g., Itikawa 1971). Owing to the relatively large dipole of methanol (1.7 D), dipole-allowed cross sections are expected to be dominant and mostly determined by the long-range electron-dipole interaction. Thus, for the water molecule, which has a similar dipole (1.8 D), Faure et al. (2004) have shown that the Born approximation is accurate down to typically 1 eV. At lower energy, short-range forces can become important, and these effects were found to reduce the low-energy cross-sections by up to a factor of ~1.5. In the case of methanol, the Born treatment probably overestimates the rotational cross-sections by a factor of 2–3, as suggested by the measurements of the total elastic cross-section (see Vinodkumar et al. 2013, and references therein). In the Born approximation, cross-sections are proportional to line strengths and the square of the dipole and therefore strictly obey the dipolar selection rule. In this work, line strengths and dipoles were taken from the JPL catalog (Pickett et al. 1998). Excitation cross-sections were computed in the energy range 0.1 meV–1 eV and rate coefficients were deduced in the range 10–1000 K, for the lowest 256 levels of CH3OH − A (1853 transitions) and the lowest 256 levels of CH3OH − E (2324 transitions).
We first constrained the column density of CH3OH − E because we detected more lines of this species. The density profile across the PDR in the Horsehead is well constrained (Habart et al. 2005). Several efforts have been made to compute the thermal profile, but it remains less well constrained than the density. We therefore decided to fix the H2 density and vary the temperature in our models. For this, we ran grids of models for kinetic temperatures of 10–100 K and CH3OH − E column densities between 1011 and 1015 cm-2. The density of H2 was kept constant to the well-known values of nH = 6 × 104 cm-3 in the PDR and nH = 1 × 105 cm-3 in the dense core. Then, the χ2 was computed2 at each point of the grid to determine the best-fit parameters. Figure 6 shows the 1, 2, and 3σ confidence levels for the PDR (red) and dense core (blue) for models without electron excitation. The best fits are for kinetic temperatures of 60 K (PDR) and 30 K (core), which agrees well with previous determinations. The CH3OH − E column densities are well constrained. The best fits are for CH3OH − E column densities of (2.7 ± 0.5) × 1012 cm-2 and (6.5 ± 0.8) × 1012 cm-2 for the PDR and dense core, respectively. We also ran models for a fixed kinetic temperature instead of a fixed gas density. These models resulted in similar CH3OH column densities, but in a H2 gas density of nH = 6 × 104 cm-3 at the dense-core position, which is lower than expected (nH ~ 105 cm-3).
 |
Fig. 6 χ2 as a function of N(CH3OH − E) and Tkin for the PDR (red) and dense-core (blue) positions. The H2 density was kept constant to n(H2) = 6 × 104 cm-3 (PDR) and n(H2) = 1 × 105 cm-3 (dense core). The contours indicate the 1, 2, and 3σ confidence levels for the models. The reduced χ2, defined as |
We found that the change in the CH3OH − E column density is negligible in these models when we included the electron excitation. However, for a grid of models with the three parameters (Tkin,nH and N(CH3OH)) free and no electron excitation, we found a low kinetic temperature (Tkin = 40 K) and a high density (nH = 105) at the PDR. When we included the electron excitation, on the other hand, we obtained Tkin ~ 65 K and nH ~ 5 × 104 cm-3, which agrees much better with previous estimates. The inferred CH3OH column density is the same for both models (N = 2.7 × 1012 cm-2). Hence, collisions with electrons are not important for determining the CH3OH column density, but they are important for determining the kinetic temperature and density of the gas. The electron excitation was found to be important for determining the column density of CH3CN in the PDR (Gratier et al. 2013).
The determination of the CH3OH − A column density is more difficult because only three lines were detected, which provides fewer constrains to the model. We therefore fixed the kinetic temperature to the best-fit values found for CH3OH − E, in addition to keeping the density of H2 constant, and ran models varying the column density only. The best fits are obtained for CH3OH − A column densities of (2.0 ± 0.3) × 1012 cm-2 and (8.1 ± 1.0) × 1012 cm-2 for the PDR and dense core, respectively.
Table 6 summarizes the derived column densities and abundances relative to the total number of atomic hydrogen atoms for HCO, H2CO, and CH3OH. The E/A methanol ratio is 1.3 ± 0.3 and 0.8 ± 0.1 for the PDR and dense core, respectively. The total CH3OH abundance is similar in the PDR and dense core, being only a factor ~ 1.9 larger in the dense core. Similar abundances were also found for H2CO in both positions. The H2CO/CH3OH abundance ratio is ~2.3 ± 0.4 in the PDR and ~0.9 ± 0.1 in the dense core.
Column densities and abundances.
 |
Fig. 7 Photochemical model of the Horsehead PDR. The left column shows the full-resolution model and the right column shows the model convolved with a Gaussian of 6′′ FWHM. Upper panel: PDR density profile (nH = n(H)+ 2n(H2) in cm-3). Middle panel: predicted abundance (relative to nH) of HCO (red), H2CO (blue) and CH3OH (green). Lower panel: predicted H2CO/CH3OH abundance ratio. Models shown as dashed lines include pure gas-phase chemistry and models shown as solid lines include both gas-phase and grain surface chemistry. The CH3OH abundance predicted by the pure gas-phase model has been multiplied by 103 in the middle panel so that it could fit in the figure. |
4.3. Deuterated CH3OH
Guzmán et al. (2011) detected single and doubly deuterated formaldehyde in the Horsehead and derived [HDCO]/ [H2CO] = 0.11 and [D2CO]/[H2CO] = 0.04 in the dense core. We now searched for deuterated methanol at this position. We did not detect transitions from deuterated methanol, but we computed an upper limit for the CH2DOH column density toward the dense core. The low-energy transitions 2K − 2K of CH2DOH lie at 89 GHz. The rms noise at this frequency is 6.43 mK with 0.17 km s-1 spectral resolution. Assuming a linewidth of 0.5 km s-1, we obtain an upper limit for the integrated line intensity of 6 mK km s-1. This translates into a 1σ upper limit for the column density of 1.4 × 1012 cm-2 and a fractionation ratio [CH2DOH/CH3OH] ≤ 0.26 at the dense-core position. Assuming that methanol has fractionation levels similar to those of H2CO, we conclude that our data are not sensitive enough to detect lines from deuterated methanol molecules. For reference, singly, doubly, and even triply deuterated methanol species such as CH2DOH, CHD2OH, and CD3OH have been detected toward low-mass protostars with abundance ratios of 37–65% (CH2DOH), 20% (CHD2OH), and 1.4% (CD3OH) compared to their non-deuterated isotopologue (Parise et al. 2004, 2006).
5. Comparison with models
In this section we study the HCO, H2CO, and CH3OH chemistry in the Horsehead. We used an updated version of the one-dimensional, steady-state photochemical model (Le Petit et al. 2006) used in the study of H2CO by Guzmán et al. (2011). We include the density profile displayed in the upper panel of Fig. 7, a radiation field χ = 60 (relative to the Draine field; Draine 1978), the elemental gas-phase abundances from Goicoechea et al. (2009b; see their Table 5), and a cosmic-ray ionization rate ζ = 5 × 10-17 s-1 per H2 molecule.
We compare the results of a pure gas-phase chemical network with one that also includes grain surface reactions. Figure 7 displays the results for the photochemical models. The left column presents the results computed by the code, which samples the UV-illuminated gas on a finer spatial grid than the UV-shielded gas to correctly represent the steep physical and chemical gradients. The right column presents the results convolved with a Gaussian of 6′′ (FWHM) to facilitate the comparison with the abundances inferred from the PdBI observations at 6′′ angular resolution. The predicted H2CO and CH3OH abundance profiles are shown in the middle panel. The H2CO/CH3OH abundance ratio is shown in the lower panel. The horizontal bars show the results inferred from observations. Results for the pure gas-phase model are shown as dashed lines and results for the model including grain surface chemistry are shown as solid lines.
5.1. Pure gas-phase models
We used a modified version of the pure gas-phase chemical network of the Ohio State University (OSU). Our network includes the photodissociation of HCO and of H2CO (leading to CO and H2), and the atomic oxygen reaction with the methylene radical (CH2) to explain the high abundance of HCO in the PDR (Gerin et al. 2009). The H2CO photodissociation channel that leads to HCO + H is also included.
As previously shown by Guzmán et al. (2011), the pure-gas phase model satisfactorily reproduces the observed H2CO abundance in the dense core (δx ~ 35′′), but it underestimates the abundance in the PDR (δx ~ 15′′) by at least one order of magnitude. In this model the formation of H2CO is dominated by reactions between oxygen atoms and the methyl radical (CH3) in both the PDR and dense core. The destruction of H2CO in the PDR is dominated by reactions with S+ and by photodissociation, while it is dominated by reactions with ions (mainly H3O+, HCO+ and S+) in the dense core.
In the gas phase, methanol is mainly produced by the dissociative recombination of CH3OH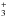 , which is formed by reactions between CH
, which is formed by reactions between CH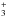 and water. It is now well established that this reaction is not efficient enough to explain the observed CH3OH abundances (Garrod et al. 2006; Geppert et al. 2006). Indeed, the pure gas-phase model underestimates the CH3OH abundance by ~5 orders of magnitude in both the PDR and dense core. Note that the CH3OH abundance predicted by the pure gas-phase model has been multiplied by 1000 in Fig. 7.
and water. It is now well established that this reaction is not efficient enough to explain the observed CH3OH abundances (Garrod et al. 2006; Geppert et al. 2006). Indeed, the pure gas-phase model underestimates the CH3OH abundance by ~5 orders of magnitude in both the PDR and dense core. Note that the CH3OH abundance predicted by the pure gas-phase model has been multiplied by 1000 in Fig. 7.
5.2. Grain surface chemistry models
We included the reactions on the surface of dust grains to the gas-phase chemical network described in Sect. 5.1. A detailed description of the implementation of grain surface chemistry in the Meudon PDR code will be given in a subsequent paper (Le Bourlot et al., in prep.). The model includes the adsorption, desorption, and diffusive reactions on grains, where the sequence to form formaldehyde and methanol is the one shown in the hydrogenation path (1). We also introduce water formation via hydrogenation reactions of O, OH until H2O. The hydrogenation of formaldehyde can lead to CH3O and/or CH2OH. Gas-phase methoxy radical (CH3O) was recently detected in the cold dense core B1-b (Cernicharo et al. 2012). We do not distinguish between these two isomers, that is, CH3O and CH2OH, in our network. The energy barriers associated with the H + CO (200 K) and H + H2CO (300 K) reactions have been modified with respect to Guzmán et al. (2011). As shown by laboratory studies (Öberg et al. 2009b,a; Muñoz Caro et al. 2010), photodesorption can be an efficient mechanism to release molecules into the gas phase in regions exposed to radiation fields. We included photodesorption yields of 10-3 and 2 × 10-4 molecules per incident UV photon, for H2CO and CH3OH, respectively. These values are close to those measured in the laboratory for CO, CO2, H2O, and CH3OH (Öberg et al. 2007, 2009a–c). Photodesorption of adsorbed CH3OH can produce both methanol and formaldehyde in the gas-phase with a 50/50 branching ratio. This channel was not included in the model of Guzmán et al. (2011), where photodesorption of adsorbed CH3OH produced only gas-phase methanol. We checked that the use of steady-state chemistry in the model is a valid assumption for the physical conditions prevailing in the Horsehead PDR and dense core. Indeed, the formation and destruction timescales of H2CO and CH3OH are <30 yr and <5000 yr at the PDR and dense core, respectively, while the estimated age of the Horsehead is ~5 × 105 yr (Pound et al. 2003).
The new results are shown as solid lines in Fig. 7. The dust temperatures in this model are 20 K. The model predicts two abundance peaks at the edge of the nebula (δx ~ 15 and δx ~ 20), with CH3OH peaking deeper inside the cloud than HCO and H2CO, and an abundance plateau at the inner layers of the cloud. This way, HCO and H2CO dominate at the outer layers of the cloud, while CH3OH dominates in the inner layers. At the dense-core position (δx ~ 35′′), the modeled H2CO abundance is similar to the one predicted by the pure gas-phase model. The CH3OH abundance, on the other hand, increases by ~5 orders of magnitude with respect to the pure gas-phase model. The observed H2CO and CH3OH abundances in the dense core are well reproduced by the model that includes both gas-phase and grain surface chemistry. In the PDR, this model also agrees well with the observed HCO and CH3OH abundances, but the predicted H2CO abundance is higher than observed.
In this model, CH3OH is produced by photodesorption of CH3OH ices everywhere in the cloud. At the dense core, the FUV photons that photodesorb the CH3OH ices are secondary photons produced by the interaction between cosmic rays and H2 molecules. Gas-phase CH3OH is mainly destroyed by photodissociation in the PDR and by freeze-out in the dense core. H2CO is produced mainly by direct photodesorption of H2CO ices in the PDR position. In the model of Guzmán et al. (2011), we found that the dominant formation path for H2CO in the dense core was the gas-phase route that involved CH3 and O. With this new model, we find that at the dense core H2CO is produced mainly by photodissociation of CH3OH ices. This difference is the result of the several modifications made to the model, of which the most important is the inclusion of the channel that leads to H2CO in the photodesorption of CH3OH ice. H2CO is mainly destroyed by photodissociation in the PDR and by reactions with ions (mainly N2H+ and H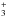 ) in the dense core3.
) in the dense core3.
It is important to remember that models that include complex grain surface processes use numerous physical parameters, such as the adsorption energy, diffusion energy of absorbed species, the activation energy of the different hydrogenation reactions, and the desorption yield, which have large uncertainties. The results predicted by these models are highly dependent on the values used for these parameters. Providing observational results is crucial to constrain these parameters and benchmark the models.
6. Discussion
6.1. Observational evidence of different H2CO formation mechanisms
The observations suggest that H2CO is formed on the surface of dust grains at the PDR and is mostly formed in the gas-phase at the dense core. First, we found a different ortho-to-para ratio in each position: an equilibrium value of 3 was found at the dense core, while a lower out-of-equilibrium value of 2 was found at the PDR. Second, if H2CO is formed on the grains, its spatial distribution is expected to resemble the spatial distribution of CH3OH. However, the high-resolution PdBI maps show that the CH3OH emission presents a minimum at the dense-core position, while H2CO peaks at this position. The easiest interpretation is that 1) the photodesorption of both H2CO and CH3OH is inefficient at the dense core, therefore the ices remain depleted onto grains; and that 2) H2CO is formed in the gas phase at this position. Indeed, the pure gas-phase model reproduces the H2CO abundance at the dense core well. Moreover, fewer photons can photodesorb species at the dense core than are available at the PDR position. This way, gas-phase CH3OH is present in an envelope around the dense core, while H2CO is present in both the envelope and the dense core itself. This is consistent with the lower gas-density inferred from the radiative-transfer analysis of CH3OH at the dense-core position.
Depletion of CH3OH has also been observed in other dense cores. Tafalla et al. (2006) found that CH3OH shows a dip in its emission at the center of the dense cores L1498 and L1517B. They concluded that the drop in emission corresponds to a real drop in column density, suggesting that CH3OH freeze out onto grains at the center of these dense cores.
6.2. Comparison with other environments
H2CO and CH3OH have been detected in the Orion Bar, which is a more extreme case of a PDR (higher χ, Tkin and Tdust). Leurini et al. (2010) estimated an abundance ratio H2CO/ CH3OH = 14 − 1400 in the interclump medium (nH ~ 104 cm-3) and H2CO/CH3OH = 0.9 − 2.5 in the denser clumps (nH ~ 106 cm-3). Despite the large uncertainties and the fact that the clumpy medium was not resolved, they concluded that the abundance of methanol relative to formaldehyde decreases by at least one order of magnitude in the interclump medium in comparison to the dense clumps. Unlike the situation at the Orion Bar, we only found a small difference in the H2CO/CH3OH abundance ratio between the PDR and dense core in the Horsehead (H2CO/CH3OH is only twice as high in the PDR). This is probably due to the difference in the radiation field between the two sources (χ ≃ 104 in the Orion Bar; χ = 60 in the Horsehead). Hence, photodissociation of CH3OH (which produces H2CO) is more efficient in the Orion Bar, especially in the interclump medium, and the ratio of H2CO/CH3OH is thus higher. The H2CO/CH3OH abundance ratio we derive in the Horshead (0.9–2.3) is very similar to the one found in the dense clumps of the Orion Bar. These clumps are more protected from the FUV photons and thus resemble more closely the conditions prevailing in the Horsehead. Indeed, χ/n ~ 100/104 in the Horsehead, which is similar to the ratio found in the dense clumps of the Orion Bar (χ/n ~ 104/106).
Maret et al. (2004, 2005) measured the formaldehyde and methanol abundances toward a sample of low-mass protostars. From these studies, an abundance ratio H2CO/CH3OH = 0.7 − 4.3 was found for the hot-corino region. In the low-mass starless cores, L1498 and L1517B, Tafalla et al. (2006) found H2CO/CH3OH = 1.1 − 2.2. These values are similar to the abundance ratio derived in the Horsehead. A lower abundance ratio was found in hot cores (H2CO/CH3OH = 0.13 − 0.28; Bisschop et al. 2007), and an even lower ratio was found in shocked gas in Galactic center clouds (H2CO/CH3OH ~ 0.01; Requena-Torres et al. 2006). In the diffuse medium, H2CO is widely detected (e.g., Liszt et al. 2006), but methanol has not been detected, although it has been searched for by Liszt et al. (2008). They derived an upper limit for the CH3OH column density, which translates into a lower limit for the abundance ratio of H2CO/CH3OH ≥ 12.
6.3. Thermal and nonthermal desorption
In hot cores, hot corinos, and shocked regions the ices that were formed in the cold gas in the prestellar stage are completely sublimated into the gas-phase through thermal desorption and sputtering. The observed H2CO and CH3OH gas-phase abundances in these regions should therefore resemble the original ice composition. Observations of ices in the envelopes of low-mass protostars show strong variations of the CH3OH ice abundance with respect to water ice (1%–30%; Boogert et al. 2008). In cold cores, a methanol ice abundance of 5%–12% relative to water has been found (Boogert et al. 2011). The variations in the CH3OH ice abundance are caused by the different local physical conditions and thus reflect the variations in the evolutionary stages of these sources (Cuppen et al. 2009). The abundance of H2CO ice has been more difficult to determine because it has been detected in just a few sources, and its stronger ice feature at 6 μm is blended with that of HCOOH (Öberg et al. 2011). A relatively constant H2CO ice abundance of ~6% relative to water was found in low-mass protostars (Gibb et al. 2004; Boogert et al. 2008). This value seems to be independent of the CH3OH ice abundance. From these detections, an ice abundance ratio H2CO/CH3OH ≃ 0.2 − 6.0 is obtained in low-mass protostars, which is consistent with the gas-phase abundance ratio found in hot corinos by Maret et al. (2004, 2005).
In cold cores and low-UV illumination PDRs, the ices are released through nonthermal processes, such as photodesorption. The H2CO/CH3OH ratio will therefore depend on the dust temperature and on the number of UV photons that will desorb the ices into the gas-phase. The CH3OH photodesorption yield has been previously found to be ~10-3 molecules per incident UV photon, similar to other species such as CO, CO2, and H2O (Öberg et al. 2009a–c). Although the CH3OH photodesorption yield is uncertain, the one adopted in our model gives a CH3OH abundance that is consistent with the observations. As discussed in Sect. 5.2, the predictions of chemical models including grain surface chemistry are highly dependent on the different physical parameters. Future laboratory studies, using different ice mixtures (similar to those observed in the ISM), will help to better understand the nonthermal desorption of ices into the gas phase and will hopefully provide precise values for the photodesorption yields and other parameters needed in the models.
7. Summary and conclusions
We have presented deep observations of CH3OH lines toward the Horsehead PDR and its associated dense core, together with single-dish and interferometric observations of H2CO and CH3OH. In general, formaldehyde and methanol emission is extended, although there are a few differences. The CH3OH emission presents a minimum at the dense-core position that is also seen in the lower angular resolution 30 m map, while H2CO peaks at this position. From the high-resolution maps, we concluded that beam dilution of the single-dish deep integrations is marginal. This is in contrast with the model prediction of an abundance peak at the PDR position. We therefore confirm the H2CO abundances inferred by Guzmán et al. (2011) and derived a similar CH3OH abundance with respect to H (~10-10) in the PDR and dense-core position that is also similar to the observed abundance of H2CO. We found that collisions with electrons are not important in determining the CH3OH column density when the physical conditions of the gas are known. However, to determine the kinetic temperature and density of the gas, electron excitation should be taken into account. The inferred methanol E/A ratio is close to one in both the PDR and the dense-core position. The H2CO/CH3OH abundance ratio is 2.3 ± 0.4 in the PDR and 0.9 ± 0.1 in the dense core.
At the PDR, observations suggest that both H2CO and CH3OH are formed on the surface of dust grains and are subsequently released into the gas phase through photodesorption. Indeed, pure gas-phase chemical models predict H2CO and CH3OH abundances that are too low compared with what is inferred from the observations. At the dense core, on the other hand, the dominant formation mechanism differs for H2CO and CH3OH. H2CO is mostly formed in the gas phase, while CH3OH is formed on the grains. Indeed, a pure gas-phase model can reproduce the observed H2CO abundance at this position, while it fails by ~5 orders of magnitude for CH3OH. Moreover, the high-resolution PdBI maps show that CH3OH is present in an envelope around the dense core, while H2CO is present in both the envelope and the dense core itself. The result of different H2CO formation mechanisms in the PDR and dense core are strengthened by the different ortho-to-para ratio inferred from the observations (o/p ~ 2 in the PDR and the equilibrium value o/p ~ 3 in the dense core).
See http://www.iram.fr/IRAMFR/GILDAS for more information about the GILDAS softwares (Pety 2005).
We first ran models assuming the solar sulfur abundance (S/H = 1.38 × 10-5). With this S abundance and including the grain surface chemistry, the destruction of H2CO is dominated by reactions with S+ in both the PDR and dense core. We then ran models using a lower sulfur abundance (S/H = 3.5 × 10-6), which reproduces the observed CS and HCS+ abundances (Goicoechea et al. 2006). In this model, which is the one adopted in this paper, S+ is not important in the destruction of H2CO. As a result, the predicted H2CO abundance at the dense core is three times higher in the low-S abundance model and the agreement between model and observations is better. We conclude that a sulfur abundance of S/H = 3.5 × 10-6 can reproduce the observed abundance of CS, HCS+, and H2CO.
Acknowledgments
We thank the IRAM PdBI and 30 m staff for their support during the observations. We thank Simon Radford for his help during the CSO observations and data reduction. VG thanks support from the Chilean Government through the Becas Chile scholarship program. This work was also funded by grant ANR-09-BLAN-0231-01 from the French Agence Nationale de la Recherche as part of the SCHISM project. J.R.G. thanks the Spanish MINECO for funding support from grants AYA2012-32032, AYA2009-07304 and CSD2009-00038. J.R.G. is supported by a Ramón y Cajal research contract.
References
- Bergman, P., Parise, B., Liseau, R., & Larsson, B. 2011, A&A, 527, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernstein, M. P., Dworkin, J. P., Sandford, S. A., Cooper, G. W., & Allamandola, L. J. 2002, Nature, 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Huard, T. L., Cook, A. M., et al. 2011, ApJ, 729, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Williams, J. P., & Lefloch, B. 2007, A&A, 463, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottinelli, S., Boogert, A. C. A., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. A., & Bolina, A. S. 2007, MNRAS, 374, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., Tielens, A. G. G. M., & Caux, E. 2000, A&A, 357, L9 [NASA ADS] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Codella, C., Ceccarelli, C., Lefloch, B., et al. 2012, ApJ, 757, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., van Dishoeck, E. F., Herbst, E., & Tielens, A. G. G. M. 2009, A&A, 508, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Gorfinkiel, J. D., & Tennyson, J. 2004, MNRAS, 347, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Faraday Discuss., 133, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garrod, R. T., Weaver, S. L. W., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, W. D., Hamberg, M., Thomas, R. D., et al. 2006, Faraday Discuss., 133, 177 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gerin, M., Goicoechea, J. R., Pety, J., & Hily-Blant, P. 2009, A&A, 494, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Compiègne, M., & Habart, E. 2009a, ApJ, 699, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., Hily-Blant, P., & Le Bourlot, J. 2009b, A&A, 498, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratier, P., Pety, J., Guzmán, V., et al. 2013, A&A, 557, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, S. D., Bolina, A. S., Chen, R., et al. 2009, MNRAS, 398, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, V., Pety, J., Goicoechea, J. R., Gerin, M., & Roueff, E. 2011, A&A, 534, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Abergel, A., Walmsley, C. M., Teyssier, D., & Pety, J. 2005, A&A, 437, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Teyssier, D., Philipp, S., & Güsten, R. 2005, A&A, 440, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Itikawa, Y. 1971, J. Phys. Soc. Jpn., 30, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2005, A&A, 437, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Schilke, P., Menten, K. M., et al. 2004, A&A, 422, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Parise, B., Schilke, P., Pety, J., & Rolffs, R. 2010, A&A, 511, A82 [Google Scholar]
- Liszt, H. S., Lucas, R., & Pety, J. 2006, A&A, 448, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., Pety, J., & Lucas, R. 2008, A&A, 486, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mangum, J. G., & Wootten, A. 1993, ApJS, 89, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G., Darling, J., Henkel, C., & Menten, K. M. 2013, ApJ, 766, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maret, S., Ceccarelli, C., Tielens, A. G. G. M., et al. 2005, A&A, 442, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz Caro, G. M., Meierhenrich, U. J., Schutte, W. A., et al. 2002, Nature, 416, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Muñoz Caro, G. M., Jiménez-Escobar, A., Martín-Gago, J. Á., et al. 2010, A&A, 522, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Fuchs, G. W., Awad, Z., et al. 2007, ApJ, 662, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2008, ApJ, 678, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009a, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009b, ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009c, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Parise, B., Castets, A., Herbst, E., et al. 2004, A&A, 416, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2006, A&A, 453, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penzias, A. A., & Burrus, C. A. 1973, ARA&A, 11, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Française, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
- Pety, J., & Rodríguez-Fernández, N. 2010, A&A, 517, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Goicoechea, J. R., Hily-Blant, P., Gerin, M., & Teyssier, D. 2007, A&A, 464, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Rad. Transf., 60, 883 [Google Scholar]
- Pontoppidan, K. M., Boogert, A. C. A., Fraser, H. J., et al. 2008, ApJ, 678, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Pound, M. W., Reipurth, B., & Bally, J. 2003, AJ, 125, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Rabli, D., & Flower, D. R. 2010, MNRAS, 406, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Requena-Torres, M. A., Martín-Pintado, J., Rodríguez-Franco, A., et al. 2006, A&A, 455, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez-Fernandez, N., Pety, J., & Gueth, F. 2008, Single-dish observation and processing to produce the short-spacing information for a millimeter interferometer, Tech. Rep., IRAM Memo 2008-2 [Google Scholar]
- Sakai, N., Ceccarelli, C., Bottinelli, S., Sakai, T., & Yamamoto, S. 2012, ApJ, 754, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, A&A, 455, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Santiago-García, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Allamandola, L. J. 1987, in Interstellar Processes, eds. D. J. Hollenbach, & H. A. Thronson, Jr., Astrophys. Space Sci. Lib., 134, 397 [Google Scholar]
- Tielens, A. G. G. M., & Whittet, D. C. B. 1997, in IAU Symp. 178, ed. E. F. van Dishoeck, 45 [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinodkumar, M., Limbachiya, C., Barot, A., & Mason, N. 2013, Phys. Rev. A, 87, 012702 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., Nagaoka, A., Shiraki, T., & Kouchi, A. 2004, ApJ, 616, 638 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observation parameters of the deep integrations of the CH3OH lines detected with the 30 m and the H2CO line detected with the CSO toward the PDR and the dense core.
Critical densitiesa ( cm-3) for the CH3OH lines detected in this work with p - H2 and o - H2 as colliding partners computed for two kinetic temperatures.
Spectroscopic parameters of the detected lines obtained from the CDMS data base (Müller et al. 2001).
All Figures
 |
Fig. 1 Detected CH3OH lines toward the dense-core (left) and PDR (right) positions. The green curves are Gaussian fits. The line frequency in GHz is given in each box. For each line, the same scale is used at both positions to facilitate the comparison. |
| In the text | |
 |
Fig. 2 Lower-energy rotational levels of CH3OH − E (left) and CH3OH − A (right). The arrows indicate the lines detected in the PDR (red) and the core (blue). |
| In the text | |
 |
Fig. 3 IRAM-30 m maps of the Horsehead edge. Maps were rotated by |
| In the text | |
 |
Fig. 4 IRAM-PdBI maps of the Horsehead edge. The field of view is smaller than in Fig. 3. The angular resolution is |
| In the text | |
 |
Fig. 5 New o - H2CO line detected toward the PDR (left) and dense-core (right) positions. The three color lines plot the radiative-transfer models from Guzmán et al. (2011), where the column density was varied around the best match (red curve) by a factor of 1.5 (blue curve) and 1/1.5 (green curve). The column density used for the best fit is given in Table 6. The line frequency in GHz is given in each box. |
| In the text | |
 |
Fig. 6 χ2 as a function of N(CH3OH − E) and Tkin for the PDR (red) and dense-core (blue) positions. The H2 density was kept constant to n(H2) = 6 × 104 cm-3 (PDR) and n(H2) = 1 × 105 cm-3 (dense core). The contours indicate the 1, 2, and 3σ confidence levels for the models. The reduced χ2, defined as |
| In the text | |
 |
Fig. 7 Photochemical model of the Horsehead PDR. The left column shows the full-resolution model and the right column shows the model convolved with a Gaussian of 6′′ FWHM. Upper panel: PDR density profile (nH = n(H)+ 2n(H2) in cm-3). Middle panel: predicted abundance (relative to nH) of HCO (red), H2CO (blue) and CH3OH (green). Lower panel: predicted H2CO/CH3OH abundance ratio. Models shown as dashed lines include pure gas-phase chemistry and models shown as solid lines include both gas-phase and grain surface chemistry. The CH3OH abundance predicted by the pure gas-phase model has been multiplied by 103 in the middle panel so that it could fit in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.