| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 20 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322376 | |
| Published online | 09 December 2013 | |
New insights into the dust formation of oxygen-rich AGB stars ⋆,⋆⋆
1
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
e-mail: ikarovic@mpia.de
2
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching bei München,
Germany
3
Max-Planck-Institut für Radioastronomie,
auf dem Hügel 69, 53121
Bonn,
Germany
4
United States Naval Observatory, 3450 Massachusetts Avenue,
Washington DC 20392-5420, NW, USA Present address: National Science
Foundation, 4201 Wilson
Boulevard, Arlington, VA
22230,
USA
5
Laboratoire Lagrange, UMR7293, Université de Nice
Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300
Nice,
France
6
Zentrum für Astronomie der Universität Heidelberg (ZAH), Institut
für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120
Heidelberg,
Germany
7
Sydney Institute for Astronomy, School of Physics, University of
Sydney, NSW, 2006
Sydney,
Australia
Received:
26
July
2013
Accepted:
30
September
2013
Context. Asymptotic giant branch (AGB) stars are one of the major sources of dust in the universe. The formation of molecules and dust grains and their subsequent expulsion into the interstellar medium via strong stellar winds is under intense investigation. This is in particular true for oxygen-rich stars, for which the path of dust formation has remained unclear.
Aims. We conducted spatially and spectrally resolved mid-infrared multi-epoch interferometric observations to investigate the dust formation process in the extended atmospheres of oxygen-rich AGB stars.
Methods. We observed the Mira variable AGB stars S Ori, GX Mon, and R Cnc between February 2006 and March 2009 with the MIDI instrument at the VLT interferometer. We compared the data to radiative transfer models of the dust shells, where the central stellar intensity profiles were described by dust-free dynamic model atmospheres. We used Al2O3 and warm silicate grains, following earlier studies in the literature.
Results. Our S Ori and R Cnc data could be well described by an Al2O3 dust shell alone, and our GX Mon data by a mix of an Al2O3 and a silicate shell. The best-fit parameters for S Ori and R Cnc included photospheric angular diameters ΘPhot of 9.7 ± 1.0 mas and 12.3 ± 1.0 mas, optical depths τV(Al2O3) of 1.5 ± 0.5 and 1.35 ± 0.2, and inner radii Rin of 1.9 ± 0.3 RPhot and 2.2 ± 0.3 RPhot, respectively. Best-fit parameters for GX Mon were ΘPhot = 8.7 ± 1.3 mas, τV(Al2O3) = 1.9 ± 0.6, Rin(Al2O3) = 2.1 ± 0.3 RPhot, τV(silicate)= 3.2 ± 0.5, and Rin(silicate)= 4.6 ± 0.2 RPhot. Our data did not show evidence of intra-cycle and cycle-to-cycle variability or of asymmetries within the error-bars and within the limits of our baseline and phase coverage.
Conclusions. Our model fits constrain the chemical composition and the inner boundary radii of the dust shells, as well as the photospheric angular diameters. Our interferometric results are consistent with Al2O3 grains condensing close to the stellar surface at about 2 stellar radii, co-located with the extended atmosphere and SiO maser emission, and warm silicate grains at larger distances of about 4–5 stellar radii. We verified that the number densities of aluminum can match that of the best-fit Al2O3 dust shell near the inner dust radius in sufficiently extended atmospheres, confirming that Al2O3 grains can be seed particles for the further dust condensation. Together with literature data of the mass-loss rates, our sample is consistent with a hypothesis that stars with low mass-loss rates form primarily dust that preserves the spectral properties of Al2O3, and stars with higher mass-loss rate form dust with properties of warm silicates.
Key words: stars: AGB and post-AGB / stars: atmospheres / stars: mass-loss / techniques: interferometric
Based on observations made with the Very Large Telescope Interferometer (VLTI) at the Paranal Observatory under program IDs 073.D-0711, 075.D-0097, 077.D-0630, 079.D-0172, and 082.D-0723.
Tables 1–3, 8, 9 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Stars on the asymptotic giant branch (AGB) are low and intermediate mass stars at the end of their stellar lives, rapidly loosing mass via strong stellar winds. These winds from AGB stars are one of the major sources of dust in the Universe. The mass loss and the related processes are currently under extensive investigation. Mira variables are AGB stars which pulsate with long periods around several hundreds days and large amplitudes up to several magnitudes (Habing & Olofsson 2003). It is widely accepted that pulsations and dynamic effects, including shock waves propagating through the stellar atmosphere, lift the upper parts of the atmosphere and create a dense and cool environment suitable for the formation of molecules and dust grains by condensation from the gas phase. Due to its large opacity, the dust absorbs the radiation pressure from the star and drags along the surrounding gas as it is pushed away (Höfner 2009). The mass is expelled via a dense and dusty outflow from an extended stellar atmosphere with rates of up to 10-4 M⊙/year (Matsuura et al. 2009), and expansion velocities of 5–30 km s-1 (Höfner 2005). However, the corresponding key molecules as well as the detailed nucleation mechanisms are different for oxygen-rich and carbon-rich stars. While carbon grain formation in winds of carbon-rich stars is rather well defined with various forms of carbon or hydrocarbons evolving and finally resulting in macroscopic carbon grains, the dust formation process in oxygen-rich outflows is not as clear (Woitke 2006; Höfner & Andersen 2007). Although several condensation calculations and observations were recently performed in order to explain the observed dust components and to predict the presence of as yet unidentified dust species (Höfner 2008; Goumans & Bromley 2012; Bladh & Höfner 2012; Bladh et al. 2013; Sacuto et al. 2013; Gail et al. 2013), the formation and growth of dust grains in oxygen-rich stars is still a widely unsolved problem.
The spectral energy distributions (SEDs) of oxygen-rich AGB stars are known to show a diversity of characteristic shapes. Based on IRAS data, Little-Marenin & Little (1990) classified AGB stars into several groups depending on different features of the SED. Lorenz-Martins & Pompeia (2000) were successful to describe the SEDs of a number of oxygen-rich Mira variable AGB stars using Al2O3 dust shells, silicate dust shells, or a mix thereof, where the Al2O3 dust reproduces a characteristic broad feature from 9 μm to 15 μm, and the silicate dust reproduces characteristic features (the “silicate features”) near 9.7 μm and 18 μm. This approach is supported by theoretical thermodynamic calculations where Al2O3 condenses at relatively high temperatures of ~1400 K and different kinds of silicates at lower temperatures below ~1200 K (e.g., Tielens et al. 1998; Gail 2010).
Interferometry in the mid-infrared domain was shown to be well suited to probe the atmospheres and dust shells around AGB stars since it is sensitive to the chemical composition and geometry of dust shells, their temperature, inner radii, radial distribution, and the mass-loss rate (for oxygen-rich stars, e.g., Danchi et al. 1994; Monnier et al. 1997, 2000; Lopez et al. 1997; Tuthill et al. 2000; Tevousjan et al. 2004; Ohnaka et al. 2005; Weiner et al. 2006; Wishnow et al. 2010; Zhao-Geisler et al. 2011, 2012).
Using optical and near-infrared interferometric polarimetry, Ireland et al. (2005) and Norris et al. (2012) confirmed the presence of dust with large grain sizes of ~0.3 μm at small radii below three and below two stellar radii, respectively. These radii correspond to condensation temperatures above that of the usual warm silicates. They suggest that their observations may be consistent with scattering iron-poor magnesium-rich silicates (forsterite) or with Al2O3 dust, both of which are transparent at wavelengths of 1–4 μm.
Höfner (2008); Bladh & Höfner (2012); Bladh et al. (2013) also suggested micron-sized iron-free silicates as wind-driving grains via scattering, motivated by an insufficient radiation pressure of usual silicates to drive the winds of oxygen-rich AGB stars (Woitke 2006; Höfner & Andersen 2007) and the low abundance of aluminum. Sacuto et al. (2013) compared dynamic model atmospheres including such dust grains to mid-infrared interferometry of the M-type AGB star RT Vir, and succeeded to model the observed interferometric visibility data in an ad-hoc manner only by adding a substantial amount of Al2O3 grains.
An alternative scenario was proposed by Gail et al. (2013) based on cluster formation of SiO as seed particles for silicate dust together with revised (lower) calculated condensation temperatures of silicate dust. Goumans & Bromley (2012) favor the nucleation of magnesium-rich iron-free silicates via heteromolecular condensation based on Mg, SiO, and H2O.
It is also not yet understood whether there is a relation between dust formation and stellar pulsation, i.e. whether dust formation occurs preferentially at certain phases, or only during some cycles. Lopez et al. (1997); Tevousjan et al. (2004); Wittkowski et al. (2007) reported temporal variations of the dust located close to the photosphere for oxygen-rich sources. Monitoring observations by Karovicova et al. (2011) did not show an indication of flux and variability variations and confirmed that the expected variations are below their measurement uncertainties.
Various infrared interferometric observations revealed deviations from spherical symmetry already in the AGB phase (Lopez et al. 1997; Monnier et al. 2004; Ragland et al. 2006; Wittkowski et al. 2011; Paladini et al. 2012). Non-spherical structures in the molecular and dust shells are theoretically predicted by three dimensional radiation hydrodynamic simulations of the convective interior and the stellar atmosphere of AGB stars (Freytag & Höfner 2008), as well as by pulsation- and shock-induced weak chaotic motion in the extended atmosphere (Icke et al. 1992; Ireland et al. 2008; Wittkowski et al. 2011). Ohnaka et al. (2012) detected asymmetry in the M7 giant BK Vir in the 2.3 μm CO line-forming region using the AMBER instrument at the VLTI. The asymmetry manifests itself as non-zero/non-π differential and closure phases. Sacuto et al. (2013) reported on the deviation from spherical symmetry in the atmosphere of the M-type semi-regular variable RT Vir. Interferometric measurements of non-zero differential phases (up to 90°) using MIDI at the VLTI originated most likely from the presence of one or several clumpy structures in the vicinity of the star.
The main goal of the present study was to investigate the dust formation process in the atmospheres of oxygen-rich AGB stars using multi-epoch spatially and spectrally resolved mid-infrared interferometric observations. First results from our project were reported by Wittkowski et al. (2007) who presented MIDI observations at 4 epochs of the oxygen-rich AGB star S Ori and by Karovicova et al. (2011) who presented MIDI observations at 13 epochs of the oxygen-rich AGB star RR Aql. These observations were successfully compared to a radiative transfer model of the dust shell, where the central stellar intensity profile was described by a series of dust-free dynamic model atmospheres based on self-excited pulsation models. Following the successful comparison to IRAS SEDs by Lorenz-Martins & Pompeia (2000), Al2O3 and warm silicate grains were used in these studies. In this paper we present further multi-epoch observations of additional phases of S Ori, and of the oxygen-rich AGB stars GX Mon and R Cnc. These observations were coordinated with VLBA measurements of SiO masers toward these sources, providing additional constraints on the conditions and kinematics within the extended atmosphere where the dust forms. These VLBA measurements will be described in a forthcoming paper. Using all results form this project, we discuss the dust condensation sequence as a function of the distance from the stellar surface and as a function of the mass-loss rate.
2. Characteristics of S ORI, GX Mon, and R Cnc
S Ori:
S Ori is an oxygen-rich Mira variable star with spectral type M6.5e-M9.5e and V magnitude 7.2–14.0 (Samus et al. 2009). We adopted a period of P ~ 430 days and a Julian date of last maximum brightness T0 = 2 453 190 days derived from the AAVSO1 and AFOEV2 data for the cycles of our observations. Wittkowski et al. (2007) presented the first multi-epoch study of mid-infrared observations using the MIDI instrument at the VLTI and concurrent radio interferometric observations using the VLBA, and reported on a phase-dependence of photospheric radii and dust shell parameters. They showed that Al2O3 dust grains and SiO maser spots form at relatively small radii of ~1.8–2.4 photospheric radii. The results suggested increased mass loss with dust formation close to the surface near the minimum visual phase, when Al2O3 dust grains were co-located with the molecular gas and the SiO maser shells, and a more expanded dust shell after visual maximum. van Belle et al. (1996), Millan-Gabet et al. (2005), and Boboltz & Wittkowski (2005) measured the near-infrared K-band uniform-disk (UD) angular diameter 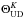 of S Ori to values between 9.6 mas and 10.5 mas at different phases. The distance toward S Ori is not precisely known, and we adopted the distance estimated by van Belle et al. (2002) of 480 pc ± 120 pc based on a calibration of the period-luminosity relationship by Feast et al. (1989). Young (1995) estimated a mass loss rate of 2.2 × 10-7M⊙/year.
of S Ori to values between 9.6 mas and 10.5 mas at different phases. The distance toward S Ori is not precisely known, and we adopted the distance estimated by van Belle et al. (2002) of 480 pc ± 120 pc based on a calibration of the period-luminosity relationship by Feast et al. (1989). Young (1995) estimated a mass loss rate of 2.2 × 10-7M⊙/year.
GX Mon:
the oxygen-rich Mira variable GX Mon is not very well investigated. Due to the relatively faint V magnitude, the light curve of GX Mon is not monitored, and therefore the visual phase of GX Mon is not well known. GX Mon is a star with spectral type M9 and V magnitude 13.2–17.0. The mean pulsation period P is uncertain, estimated to 527 days (Samus et al. 2009). The distance toward GX Mon is also not well known. Olivier et al. (2001) estimated a distance of 700 pc based on the period-luminosity relationship by Feast et al. (1989) and Justtanont et al. (1994) derived a distance of 740 pc from modeling the CO J = 1–0 and 2–1 lines. In our study, we adopt a mean value, and estimate the uncertainty to 25%, i.e. we use a distance of 720 ± 185 pc. Diameter measurements of GX Mon have so far not been reported. Based an an empirical calibration by van Belle (1999), we estimated the angular photospheric diameter of GX Mon of 6.0 mas to 7.5 mas. A mass loss rate of 5.4 × 10-6M⊙/year was estimated by Loup et al. (1993). Justtanont et al. (1994) estimated a mass-loss rate of 7.2 × 10-6M⊙/year assuming a luminosity of 104L⊙.
R Cnc:
R Cnc is a Mira variable star with spectral type M6e–M9e, a V magnitude of 6.1–11.8 and a period of 362 days (Samus et al. 2009). Wittkowski et al. (2011) studied the photospheric and molecular layers of R Cnc using near-infrared interferometry and derived a photospheric angular diameter of 11.8 ± 0.7 mas at phase 0.3. We adopt their distance of d = 280 ± 28 pc, which is based on the period-luminosity relation by Whitelock et al. (2000). Young (1995) estimated a mass loss rate of 2 × 10-8M⊙/year.
3. VLTI/MIDI observations and data reduction
We obtained a total of 97 spectrally-dispersed mid-infrared interferometric observations, 48 for S Ori, 40 for GX Mon, and 9 for R Cnc. The observations were conducted using the mid-infrared interferometric instrument MIDI (Leinert et al. 2004). MIDI combines the beams from two telescopes of the VLTI (Glindemann et al. 2003) and provides spectrally resolved visibilities in the N-band (8–13 μm). We used the PRISM as a dispersive element with a spectral resolution R = λ/Δλ ~ 30. For most observations, the beams were combined in Sci_Phot (SP) mode, complemented by several observations in the High_Sens (HS) mode. In the Sci_Phot mode beam splitters record the interferograms and the photometric spectra simultaneously, while in the High_Sens mode the photometric signal is observed after the interferometric signal.
The details of the observations and the instrumental settings are summarized in Tables 1–3. The Tables list the epoch, the date, the time, the Julian date (JD), the visual pulsation phase Φvis, the baseline configuration, the ground length of the configuration, the dispersive element, the beam combiner BC, the projected baseline length Bp, the position angle on the sky PA (° east of north), the DIMM seeing (at 500 nm), and the coherence time τ0 (at 500 nm). All observations were executed in service mode and employed different configurations of the auxiliary telescopes (ATs, 1.8 m diameter). Figure 1 shows the uv coverage of our new S Ori, GX Mon, and R Cnc observations.
 |
Fig. 1 Coverage of the uv-plane of our MIDI observations of S Ori, GX Mon, and R Cnc. Each line represents one AT observation over the wavelength range from 8 μm to 13 μm. The color of each point corresponds to the wavelength of the observations, as indicated by the color bar. |
The new observations of S Ori were obtained between Feb. 16, 2006 and Mar. 14, 2009 and represent a follow-up of 7 MIDI observations obtained between Dec. 31, 2004 and Dec. 30, 2005 by Wittkowski et al. (2007). The new observations covered 4 pulsation cycles and were merged into 14 epochs with a maximum time-lag between individual observations of 8 days for each epoch (1.9% of the pulsation period). For technical problems we had to eliminate 6 observations. Our new observations of S Ori cover half a pulsation cycle from pre-maximum (0.9) to pre-minimum (1.4) phases, but where most observations were obtained at near-maximum phases of 0.9–1.2. The four previous S Ori observations by Wittkowski et al. (2007) covered near-minimum and post-maximum phases 0.42, 0.55, 1.16, and 1.27.
The GX Mon observations were obtained between Feb. 16, 2006 and Apr. 1, 2008 and were merged into 12 epochs with a maximum time-lag between individual observations of 11 days (~2% of the pulsation period). We had to eliminate 5 observations for technical reasons. We did not assign variability phases to these observations, because the light-curve is not well known.
The observations of R Cnc were obtained at 2 epochs between Dec. 25 and Dec. 31, 2008 and between Feb. 26 and Mar. 4 2009, corresponding to near-maximum phases of 0.95 and 1.10.
For the data reduction we used the MIA+EWS software package, version 1.63. This package includes two different methods, an incoherent method (MPIA software package MIA) that analyzes the power spectrum of the observed fringe signal and a coherent integration method (EWS), which first compensates for optical path differences, including both instrumental and atmospheric delays in each scan, and then coherently adds the fringes. We applied both methods to independently verify the data reduction results. The detector masks were calculated by the procedure of MIA, and were used for both the MIA and the EWS analysis. The obtained data reduction values correspond to each other, and we chose to use the results derived from the EWS analysis, which offer error estimations.
In order to estimate the instrumental visibility losses and to determine the absolute flux values, we observed immediately before or after the science target calibrator stars close on sky and with known diameter and absolute flux values. Our main calibrators were Sirius (S Ori, GX Mon), HD 81797 (S Ori, GX Mon, R Cnc), and HD 25025 (S Ori, GX Mon). We adopted a uniform-disk diameter of ΘUD = 6.09 ± 0.03 and a 12 μm IRAS flux (Beichman et al. 1988) of 193 Jy for Sirius, ΘUD = 9.14 ± 0.05 and 158 Jy for HD 81797, and ΘUD = 8.74 ± 0.09 and 109 Jy for HD 25025. The angular diameters are from the calibrator list of the MIDI instrument consortium4.
Calibrated science target visibility spectra were calculated using the instrumental transfer function derived from all calibrator data sets taken during the same night with the same baseline and instrumental mode as our scientific target. The number of available transfer function measurements is related to the number of calibrator stars observed per specific night including those calibrators observed by other programs. The standard deviation of all transfer function measurements per night was used as the uncertainty of the transfer functions. When only one calibrator was available, we estimated the uncertainty of the transfer function based on typical values when many calibrator stars were observed. The final errors on the observed visibilities are mostly systematic, and include the error of the coherence factor of the science target and the calibrators, the adopted diameter errors, and the standard deviation of the transfer function over the night.
For most calibrator stars, absolutely calibrated spectra are available in Cohen et al. (1999). If the absolutely calibrated spectrum was not directly available, we instead used a spectrum of a calibrator with a similar spectral type and similar effective temperature. The spectra of such calibrators were scaled with the IRAS flux at 12 μm to the level of our calibrator. In a few cases, when the atmospheric absorption was strongly affecting the spectra around 9.5 μm, we used another similar calibrator instead of the main calibrator observed in the same night with the same level of flux. The ambient conditions for all the observations were monitored, and in case of problems with clouds, constraints due to wind, significant differences in seeing, humidity, coherence time, and airmass between the science target and the corresponding calibrator, the photometry was omitted from the analysis.
4. Modeling of the MIDI data
The data were modeled using our established approach, which was successful to describe the shape and features of the flux and visibility spectra of the oxygen-rich Mira variables S Ori (Wittkowski et al. 2007) and RR Aql (Karovicova et al. 2011). The modeling approach consisted of a radiative transfer model of the dust shell using the Monte-Carlo radiative transfer code mcsim_mpi (Ohnaka et al. 2006), which allows us to use two dust shells with different parameters. The central stellar source was described by the dust-free dynamic model atmosphere P and M series by Ireland et al. (2004a,b). The P and M series differ with respect to the mass of the so-called “parent star”, which is the hypothetical non-pulsating equivalent of the pulsating Mira variable. The model series have been constructed to match the prototype oxygen-rich Mira stars o Cet and R Leo (for more details see Wittkowski et al. 2007). Following the successful description of IRAS data of a number of Mira stars by Lorenz-Martins & Pompeia (2000), we used one dust shell of Al2O3 grains and one of silicate grains. As in our previous studies, we used the optical properties of alumina Al2O3 grains from Koike et al. (1995) for λ < 8 μm and porous amorphous Al2O3 from Begemann et al. (1997) for λ > 8 μm. For the silicate shell, we used the warm oxygen-deficient astronomical silicates by Ossenkopf et al. (1992), representative of circumstellar silicate dust, which include inclusions of metallic iron and iron oxides. The size of dust grains was set to 0.1 μm for all grains.
As outlined in the introduction (Sect. 1), the dust contents and the dust condensation process of oxygen-rich AGB stars is currently being heavily debated and is not yet understood. It is likely that other grain species and other grain sizes than those included in our modeling approach are present in the circumstellar environments of Mira variables (e.g. Gail & Sedlmayr 1999). However, since this mix of Al2O3 and silicate grains was successful to describe both the IRAS spectra (Lorenz-Martins & Pompeia 2000) and the MIDI flux and visibility spectra (Wittkowski et al. 2007; Karovicova et al. 2011) of a number of Mira variables, we continued to use this modeling approach for the purpose of a characterization of the dust shell geometry and optical depth. In order to minimize the (already plentiful) number of fit parameters, we refrained from adding additional grain properties in the fit procedure. A few first attempts were recently made to include dust formation in dynamic model atmosphere calculations in a self-consistent way for oxygen-rich AGB stars (Ireland & Scholz 2006; Ireland et al. 2008, 2011; Sacuto et al. 2013). However, as the description of the dust formation is not yet definite, we also refrained from a direct comparison of our MIDI data to such dynamic model atmospheres with dust formation included. A more detailed discussion on the dust condensation process follows below in Sect. 6.
Best-fit model parameters for each epoch of our S Ori observations.
Best-fit model parameters for each epoch of our R Cnc observations.
Our fit procedure was the same as described by Karovicova et al. (2011). We used ten dynamic atmosphere models from the M series that are expected to be better-suited to describe our stars. The models cover one complete cycle of the M series by Ireland et al. (2004a,b): M16n (model visual phase Φmodel = 0.60), M18 (0.75), M18n (0.84), M19n (0.90), M20 (0.05), M21n (0.10), M22 (0.25), M23n (0.30), M24n (0.40), and M25n (0.50). For each of these models, we computed a grid of radiative transfer models of the dust shell. The radiative transfer model included variations of 6 parameters, 3 for each of the independent Al2O3 and silicate shells, the optical depths τV (Al2O3) and τV(silicate), the inner boundary radii Rin/RPhot (Al2O3) and Rin/RPhot (silicate), and the density gradients pA (Al2O3) and pB (silicate). The first grid included all combinations of optical depths τV (Al2O3) = 1.0, 1.3, 1.6, 1.9, 2.1, 2.4, 2.7, 3.1; τV (silicate)= 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0; Rin/RPhot (Al2O3) = 2.0, 2.5, 3.0; Rin/RPhot (silicate)= 2.5, 3.5, 4.5, 5.5, 6.5; pA (Al2O3) = 2.0, 2.5, 3.0, 3.5; and pB (silicate)= 2.0, 2.5, 3.0, 3.5. In a following step, a grid with finer steps around the parameters with lowest χ2 value was computed. For each individual fit, the angular diameter of the atmosphere model ΘPhot was the only free fit parameter. Here, the photospheric radius RPhot is defined as the 1.04 μm continuum radius of the P/M model atmospheres. We remind the reader that we weighted down the part of the photometric spectra around 9.5 μm, which is strongly affected by telluric absorption. The weight of all other data points was given by the corresponding uncertainty. From all fits, we selected the results with the best χ2 values. It should be mentioned that with the available accuracy, a few models of the final selection fit equally well.
Best-fit model parameters for each epoch of our GX Mon observations.
 |
Fig. 2 VLTI/MIDI interferometry at 8–13 μm of S Ori for the example of epoch B (stellar phase 0.89, see Table 1). The panels show (upper left) the flux, (upper right) the visibility amplitude, (lower left) the corresponding UD diameter, and (lower right) the visibility amplitude as a function of spatial frequency for three averaged band passes of 8–9 μm, 10–11 μm, and 12–13 μm. The gray shade indicates the wavelength region around 9.5 μm that is affected by atmospheric absorption. The crosses with error bars denote the measured values. The solid lines indicate our best-fit model. The contributions of the stellar and dust components alone are indicated by the dotted and the dashed line, respectively. |
S Ori and R Cnc were a part of the study by Lorenz-Martins & Pompeia (2000) and were modeled using Al2O3 alone. Consistently, our MIDI spectra of S Ori and R Cnc do not exhibit any prominent silicate feature. GX Mon was not a part of their study. Our MIDI spectra of GX Mon show a pronounced silicate feature, indicating that silicate is one of the components of the dust shell. Independent of this information, we considered the full grid of models, including Al2O3 and silicate shells, for all targets.
5. Results
5.1. Best-fit model parameters
The best-fit results for S Ori and R Cnc were obtained with an Al2O3 shell without a contribution by silicate dust, consistent with Lorenz-Martins & Pompeia (2000). The best-fit results for GX Mon were obtained with a silicate shell together with a contribution by an Al2O3 shell. Tables 4– 6 list the best-fit parameters for each epoch of our S Ori, R Cnc, and GX Mon observations separately. The tables lists the epoch, the variability phase, the atmosphere model and its model phase, the optical depth τV, the inner boundary radius Rin/RPhot, the density distribution p, and the continuum photospheric angular diameter ΘPhot. Since the best-fit models for S Ori and R Cnc were obtained without a contribution by a silicate shell, only the parameters of the Al2O3 dust shell are listed for these targets.
The agreement between the best-fit models and the observed data is satisfactory for all targets and epochs. Figures 2–4 show for each source one example of the observed and synthetic flux and visibility spectra. The general shape of the S Ori and R Cnc spectra are similar and were discussed in more detail by Wittkowski et al. (2007). The spectra of GX Mon are similar to those of RR Aql as discussed by Karovicova et al. (2011).
The model fit results obtained at the individual epochs did not indicate any significant dependence of the dust formation on phase or cycle within the phase coverage of our observations. In addition, a direct comparison of the flux and visibility spectra (cf. Sect. 5.5 below) obtained at different phases and cycles showed a good agreement and no variability within our measurement uncertainties. As a result, we concentrate in the following on the average best-fit dust shell parameters. Table 7 lists these averaged dust shell parameters together with the averaged observational phases. Note that we do not cover a full cycle, therefore we indicate the average observational phase and the most frequent model. The averaged model parameters belong to a certain averaged phase, and may be different for a different phase. Figure 5 shows the stratification of the gas and dust temperatures for the example of the average GX Mon model, which consists of an Al2O3 and a silicate dust shell. The dust temperatures at the inner radii are given in the paragraphs on the individual sources below.
S Ori:
our S Ori observations had an average visual phase of 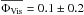 (post-maximum phase). The average model phase was
(post-maximum phase). The average model phase was 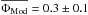 , corresponding to model M22/M23n. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.5 ± 0.5 at λ = 0.55 μm (corresponding to 0.04 at λ = 8 μm, 0.29 at λ = 12 μm, and a maximum within 8–12 μm of 0.30 at λ = 11.8 μm). The inner radius of the Al2O3 dust shell was Rin = 1.9 ± 0.3 RPhot, and the power-law index of the density distribution was p = 2.9 ± 0.4. The dust temperature at Rin was 1340 K, close to the condensation temperature of Al2O3 of ~1400 K (Gail 2010). The average photospheric angular diameter resulted in ΘPhot = 9.7 ± 1.0 mas. This value is consistent with the K-band (λ = 2.2 μm, Δλ = 0.4 μm) UD diameter values measured to be between 9.6 mas and 10.5 mas by van Belle et al. (1996); Millan-Gabet et al. (2005); and Boboltz & Wittkowski (2005). The best-fit parameters for S Ori are also consistent with those derived from the earlier VLTI/MIDI observations by Wittkowski et al. (2007), who derived at near-minimum and post-maximum phases Al2O3 dust shells with inner boundary radii between 1.8 RPhot and 2.4 RPhot and optical depths between τV(Al2O3) = 1.5 (post-maximum) and τV(Al2O3) = 2.5 (near minimum). Our average photospheric angular diameter at an average post-maximum visual phase is also consistent with the post-maximum diameter derived from the previous VLTI/MIDI S Ori observations (Wittkowski et al. 2007) of 9.7 mas at visual phase 0.16. Our value for ΘPhot corresponds to a photospheric radius of
, corresponding to model M22/M23n. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.5 ± 0.5 at λ = 0.55 μm (corresponding to 0.04 at λ = 8 μm, 0.29 at λ = 12 μm, and a maximum within 8–12 μm of 0.30 at λ = 11.8 μm). The inner radius of the Al2O3 dust shell was Rin = 1.9 ± 0.3 RPhot, and the power-law index of the density distribution was p = 2.9 ± 0.4. The dust temperature at Rin was 1340 K, close to the condensation temperature of Al2O3 of ~1400 K (Gail 2010). The average photospheric angular diameter resulted in ΘPhot = 9.7 ± 1.0 mas. This value is consistent with the K-band (λ = 2.2 μm, Δλ = 0.4 μm) UD diameter values measured to be between 9.6 mas and 10.5 mas by van Belle et al. (1996); Millan-Gabet et al. (2005); and Boboltz & Wittkowski (2005). The best-fit parameters for S Ori are also consistent with those derived from the earlier VLTI/MIDI observations by Wittkowski et al. (2007), who derived at near-minimum and post-maximum phases Al2O3 dust shells with inner boundary radii between 1.8 RPhot and 2.4 RPhot and optical depths between τV(Al2O3) = 1.5 (post-maximum) and τV(Al2O3) = 2.5 (near minimum). Our average photospheric angular diameter at an average post-maximum visual phase is also consistent with the post-maximum diameter derived from the previous VLTI/MIDI S Ori observations (Wittkowski et al. 2007) of 9.7 mas at visual phase 0.16. Our value for ΘPhot corresponds to a photospheric radius of 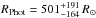 . With the bolometric magnitude of S Ori of mbol = 3.08 and Δmbol = 0.49 from Whitelock et al. (2000), we derived an effective temperature of Teff ~ 2627 ± 300 K.
. With the bolometric magnitude of S Ori of mbol = 3.08 and Δmbol = 0.49 from Whitelock et al. (2000), we derived an effective temperature of Teff ~ 2627 ± 300 K.
R Cnc:
our R Cnc observations had an average visual phase of 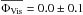 (near-maximum phase). The average model phase was
(near-maximum phase). The average model phase was 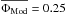 , corresponding to model M22. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.35 ± 0.2 at λ = 0.55 μm (corresponding to 0.03 at λ = 8 μm, 0.27 at λ = 12 μm, and a maximum within 8–12 μm of 0.27 at λ = 11.8 μm). The inner radius of the dust shell was Rin = 2.2 ± 0.3 RPhot, and the power-law index of the density distribution was p = 2.5. The dust temperature at Rin was 1210 K, below the condensation temperature of Al2O3 of ~1400 K. The average photospheric angular diameter resulted in ΘPhot = 12.3 mas, which is consistent with the value of 11.8 mas ± 0.7 mas derived from near-infrared VLTI/AMBER observations by Wittkowski et al. (2011) at phase 0.3. Our value for ΘPhot corresponds to a photospheric radius of RPhot = 371 ± 37 R⊙. Together with the bolometric magnitude of mbol = 2.60 and Δmbol = 1.05 from Whitelock et al. (2000), we derived an effective temperature of Teff ~ 2604 ± 300 K.
, corresponding to model M22. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.35 ± 0.2 at λ = 0.55 μm (corresponding to 0.03 at λ = 8 μm, 0.27 at λ = 12 μm, and a maximum within 8–12 μm of 0.27 at λ = 11.8 μm). The inner radius of the dust shell was Rin = 2.2 ± 0.3 RPhot, and the power-law index of the density distribution was p = 2.5. The dust temperature at Rin was 1210 K, below the condensation temperature of Al2O3 of ~1400 K. The average photospheric angular diameter resulted in ΘPhot = 12.3 mas, which is consistent with the value of 11.8 mas ± 0.7 mas derived from near-infrared VLTI/AMBER observations by Wittkowski et al. (2011) at phase 0.3. Our value for ΘPhot corresponds to a photospheric radius of RPhot = 371 ± 37 R⊙. Together with the bolometric magnitude of mbol = 2.60 and Δmbol = 1.05 from Whitelock et al. (2000), we derived an effective temperature of Teff ~ 2604 ± 300 K.
Average dust shell parameters.
 |
Fig. 5 Stratification of the gas temperature and dust temperature (Al2O3 and silicate dust) for the example of our GX Mon model. The solid line shows the gas temperature (model M21n), the dotted line the dust temperature of the Al2O3 dust shell, and the dashed line the dust temperature of the silicate dust shell. The vertical line indicates RPhot = 2.19 × 1013 cm. For the model parameters, see Table 7. |
GX Mon:
the visual phase of our GX Mon observations is unknown. The average model phase was 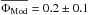 , corresponding to model M21n/M22. An Al2O3 dust shell in combination with a silicate dust shell provided the best agreement with our data. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.9 ± 0.6 and the average optical depth of the silicate dust was τV(silicate)= 3.2 ± 0.5 at λ = 0.55 μm corresponding to 0.05 at λ = 8 μm (Al2O3) and 0.03 at λ = 8 μm (silicate), 0.38 at λ = 12 μm (Al2O3) and 0.09 at λ = 12 μm (silicate). The inner radius of the Al2O3 dust shell was Rin(Al2O3) = 2.1 ± 0.3 RPhot and the inner radius of the silicate dust shell was Rin(silicate)= 4.6 ± 0.2 RPhot. The power-law indices of the density distribution were p(Al2O3) = 2.8 ± 0.4 and p(silicate)= 2.5 ± 0.0. The dust temperatures at the inner radii of the Al2O3 and silicate shells were 1350 K and 1070 K, respectively, consistent with the typical condensation temperatures of ~1400 K and ~1000 K (Gail 2010). The average photospheric angular diameter resulted in ΘPhot = 8.7 ± 1.3 mas. A previous direct diameter measurement for GX Mon is not available. However, our best-fit angular diameter is consistent with the estimate based on the surface brightness calibration by van Belle (1999) of 6–7.5 mas. For our value for ΘPhot we derived a photospheric radius of
, corresponding to model M21n/M22. An Al2O3 dust shell in combination with a silicate dust shell provided the best agreement with our data. The average optical depth of the Al2O3 dust shell was τV(Al2O3) = 1.9 ± 0.6 and the average optical depth of the silicate dust was τV(silicate)= 3.2 ± 0.5 at λ = 0.55 μm corresponding to 0.05 at λ = 8 μm (Al2O3) and 0.03 at λ = 8 μm (silicate), 0.38 at λ = 12 μm (Al2O3) and 0.09 at λ = 12 μm (silicate). The inner radius of the Al2O3 dust shell was Rin(Al2O3) = 2.1 ± 0.3 RPhot and the inner radius of the silicate dust shell was Rin(silicate)= 4.6 ± 0.2 RPhot. The power-law indices of the density distribution were p(Al2O3) = 2.8 ± 0.4 and p(silicate)= 2.5 ± 0.0. The dust temperatures at the inner radii of the Al2O3 and silicate shells were 1350 K and 1070 K, respectively, consistent with the typical condensation temperatures of ~1400 K and ~1000 K (Gail 2010). The average photospheric angular diameter resulted in ΘPhot = 8.7 ± 1.3 mas. A previous direct diameter measurement for GX Mon is not available. However, our best-fit angular diameter is consistent with the estimate based on the surface brightness calibration by van Belle (1999) of 6–7.5 mas. For our value for ΘPhot we derived a photospheric radius of 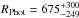 R⊙. A bolometric magnitude of mbol = 4.09 and Mbol = −5.19 was adopted from Olivier et al. (2001). These values correspond to an effective temperature of Teff ~ 2173 ± 300 K.
R⊙. A bolometric magnitude of mbol = 4.09 and Mbol = −5.19 was adopted from Olivier et al. (2001). These values correspond to an effective temperature of Teff ~ 2173 ± 300 K.
RR Aql:
the dust shell parameters for RR Aql were already reported by Karovicova et al. (2011). We repeat the average best-fit parameters, because we will discuss the general dust shell properties based on all 4 targets in the following. RR Aql could best be described with a silicate dust shell alone, consistent with Lorenz-Martins & Pompeia (2000). The average visual phase was 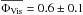 (near-minimum phase). The average optical depth of the silicate dust shell was τV(silicate)= 2.8 ± 0.8 at λ = 0.55 μm (corresponding to 0.03 at λ = 8 μm, 0.06 at λ = 12 μm, and a maximum of 0.22 at λ = 9.8 μm), The inner radius was Rin = 4.1 ± 0.7 RPhot, and the power-law index of the density distribution was p = 2.6. The dust temperature at the inner radius was 1130 K, consistent with typical silicate condensation temperatures. The angular diameter corresponds to a photospheric radius of
(near-minimum phase). The average optical depth of the silicate dust shell was τV(silicate)= 2.8 ± 0.8 at λ = 0.55 μm (corresponding to 0.03 at λ = 8 μm, 0.06 at λ = 12 μm, and a maximum of 0.22 at λ = 9.8 μm), The inner radius was Rin = 4.1 ± 0.7 RPhot, and the power-law index of the density distribution was p = 2.6. The dust temperature at the inner radius was 1130 K, consistent with typical silicate condensation temperatures. The angular diameter corresponds to a photospheric radius of 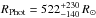 and an effective temperature of Teff = 2420 ± 200 K.
and an effective temperature of Teff = 2420 ± 200 K.
Summary:
the results show that the shape of both the visibility and the photometry spectra for the Mira variables S Ori, GX Mon, R Cnc and RR Aql, can be well reproduced by the radiative transfer model of the circumstellar dust shell using Al2O3 and silicate dust grains with different inner radii, where the central source was described by dynamic model atmospheres. The same approach has already been successful to describe IRAS spectra of a number of Mira variables (Lorenz-Martins & Pompeia 2000). S Ori and R Cnc could best be described by only an Al2O3 dust shell, RR Aql by only a silicate dust shell, and GX Mon by a combination of an Al2O3 and a silicate dust shell. The Al2O3 shells have inner radii between 1.9 and 2.2 stellar photospheric radii, and the silicate shells have inner radii between 4.1 and 4.6 stellar photospheric radii. The best-fit photospheric angular diameters are consistent with independent estimates. The model dust temperatures at the inner radii of 1.9–2.2 stellar radii and 4.1–4.6 stellar radii are consistent with dust condensation temperatures of Al2O3 and silicates, respectively.
5.2. Aluminum abundance
We used an ad-hoc radiative transfer model of the dust shell that did not self-consistently include the dust formation process based on the available elements in the extended atmosphere. However, we investigated whether a sufficient amount of aluminum is available in the extended atmospheres to match the required number density of Al2O3 dust grains of our best-fit radiative transfer models. We calculated the aluminum abundances in the gas and the dust based on our models. We used as an example the best-fit model for S Ori consisting of the M22 model atmosphere and an Al2O3 dust shell with parameters as listed in Table 7. M22 shows a relatively compact atmospheric extension, so that we used in addition model P20 as an example of a more extended atmosphere.
Aluminum number density in the dust component:
the number density of the dust grains as a function of radius is an output of our radiative transfer model, based on the chosen optical depth, the inner radius, and the power-law index of the density distribution. We converted the Al2O3 grain number density (N) into the mass density (g cm-3) by 4/3 × π × a3 × ϱbulk × N, where a is the grain radius, and ϱbulk is the bulk density of the grain. Århammar et al. (2011) give bulk densities of amorphous Al2O3 between 2.1 g cm-3 and 3.6 g cm-3. We used a mean value of 2.85 g cm-3. The mass of a single Al2O3 molecule is 102 amu, where amu is the atomic mass unit. From the mass density and this mass of a single Al2O3 molecule we computed the number density of Al2O3 molecules and thus of aluminum atoms in the dust shell.
 |
Fig. 6 Number density of available aluminum atoms in the dust-free extended model atmospheres M22 (top) and P20 (bottom) compared to the number density of aluminum in the dust shell. Shown is the overlapping radial range between the inner radius of the dust shell model and the maximum radius of the atmosphere model. The vertical line indicates RPhot = 1.99 × 1013 cm (M22) and RPhot = 1.74 × 1013 cm (P20). |
Aluminum number density in the extended atmosphere (gas component):
we calculated the molecular and atomic abundances in chemical equilibrium for the given temperature and gas stratification of the (dust free) atmosphere model based on solar abundances. The total number density of available aluminum atoms was computed as the sum of all molecules, atoms, and ions containing aluminum.
Comparison of the aluminum number density in the dust and the gas:
Fig. 6 shows the comparison of the aluminum atoms in the dust shell to the number of available aluminum atoms in the gas. Compared to model M22, the number density of aluminum in our dust shell matches that of the atmosphere at the inner dust shell radius Rin ~ 4 × 1013 cm. At larger radii more aluminum atoms are needed for the best-fit dust shell than available in the atmosphere. This discrepancy gets wider for larger radii. Compared to the more extended model P20, a sufficient number of aluminum atoms is available up to about two times the inner dust shell radius, or about 4 times the photospheric radius. It has to be noted that our best-fit power-law density profile for the dust shell corresponds to material that is outflowing, while the gas density is based on a dynamical model without mass loss. This results in a steeper density for the gas, while the dust density falls off more gradually. Assuming that the dust grains are accelerated and drag along the gas, the gas density would have a smaller gradient as well, and the number density of aluminum atoms in the gas may match the required numbers of the dust shell over a larger radial range.
Overall abundance of aluminum:
overall, the mass-loss rate at the outer boundary radius of the dust shell must equal the mass-loss rate just inside the inner boundary. Just inside Rin, where no dust particles have yet formed, the mass-loss fraction of aluminum of the gas component is based on the chemical composition of the gas. Assuming solar metallicity, and using the number densities by Asplund et al. (2009), the mass fraction of aluminum is fAl (<Rin) = 5.5 × 10-5. The chemical composition may be altered by hot-bottom-burning and thermal pulses, but the abundance of aluminum is not expected to change significantly and to essentially equal solar system abundances (Gail 2010). In our best-fit models of R Cnc and S Ori, the dust shells consisted only of Al2O3. We thus assumed that at the outer boundary radius of the dust shell (Rout) all aluminum is bound in Al2O3, and that this is the only contributor to the dust component. Then, the mass fraction of aluminum of the total mass-loss rate is the mass fraction of aluminum in Al2O3 (53%) divided by the gas-to-dust ratio. Knapp (1985) gave a typical gas-to-dust ratio of 160 for oxygen-rich Mira variables. Norris et al. (2012) give a larger gas-to-dust ratio of ~600 for W Hya. With these values, we obtain an aluminum mass fraction at the outer shell radius fAl (>Rout) between 3.3 × 10-3 and 8.8 × 10-4, i.e. larger than fAl (<Rin) by a factor between 60 and 16. This means that the abundance of aluminum is too small to explain typical observed gas-to-dust ratios with an Al2O3 dust shell alone. As a result, it is likely that additional dust species contribute to the dust shells of these types of Mira variables. Because the Al2O3 shell is successful to describe both the IRAS spectra as well as the MIDI photometry and visibility of these sources, the additional species should have similar properties as Al2O3, in particular preserve the broad feature at 9–15 μm that is attributed to Al2O3 and not add additional features that are not observed in the spectra of these stars, such as the “silicate features” near 9.7 μm and 18 μm. We have shown above that the number density of aluminum can be high enough in an extended atmosphere to match the required number density of Al2O3 dust up to about 4 stellar radii, so that Al2O3 grains can be seed particles for additional dust condensation at larger radii. Candidates for such grains or inclusions are Fe (metallic iron) or (Fe,Mg)O (magnesiowüstite), (cf. e.g., Ferrarotti & Gail 2006; McDonald et al. 2010; Posch et al. 2002). Another possibility may be scattering iron-free silicates (Mg2SiO4, forsterite), which may also not have a significant silicate signature in the mid-IR if distributed in certain geometries, such as a geometrically thin shell (Ireland et al. 2005). Sacuto et al. (2013) could explain VLTI/MIDI spectra of RT Vir, which have a similar shape as those of S Ori and R Cnc, by a combination of forsterite grains and Al2O3 grains.
5.3. Coordinated SiO maser observations
The VLTI/MIDI observations of our project were coordinated with VLBA observations of the v = 1, J = 1–0 (43.1 GHz) and v = 2, J = 1–0 (42.8 GHz) SiO maser emission toward the same sources. Wittkowski et al. (2007) discussed the relationships between the photosphere, molecular layer, dust shell, and SiO maser shell at 4 epochs of S Ori. The SiO maser ring radii were found to be between 1.9 and 2.4 photospheric radii and to be co-located with the extended molecular layers and the inner Al2O3 dust shell radii. Unpublished SiO maser ring radii for GX Mon, RR Aql, and R Cnc (Boboltz et al, in prep.) are on average approximately 9.6 mas, 8.8 mas, and 12.0 mas, respectively, putting them as well between 1.9 and 2.3 photospheric radii using the average photospheric angular diameters of Table 7. These SiO maser ring radii of about 2 photospheric radii, possibly related to a shock front position, are consistent with other independent measurements of Mira variables (Cotton et al. 2010) and with theoretical models (Gray et al. 2009). The co-location of our inner Al2O3 dust shell radii between 1.9 and 2.2 photospheric radii (Table 7) with the SiO maser ring radii between 1.9 and 2.3 photospheric radii suggests that at these radii silicon is mostly available as SiO in the gas phase, and that the dust grains at these small inner dust radii are thus unlikely to be related to SiO nucleation or to silicate dust. If for some reason such dust could form at these radii despite the high temperature, the dust would deplete Si so that there would not be enough SiO gas left for the maser emission. Our following paper will be dedicated to a more detailed study on this topic.
5.4. Effect of small amounts if silicate grains added to an Al2O3 dust shell
Karovicova et al. (2011, their simulation 4) demonstrated that the addition of small amounts (10%) of amorphous Al2O3 grains to a silicate dust shell are not detectable within the uncertainties of our MIDI visibility and photometry measurements (differences < 2%). Here, we investigate the opposite case, whether the addition of warm silicate grains to an Al2O3 dust shell significantly affects the shape and features of the mid-infrared visibility and photometry spectra.
For a given inner radius and density distribution, the amount of dust grains of each compound was characterized by the optical depths at a wavelength of 0.55 μm. For our simulation we used typical model parameters from Sect. 5.1. We used model M21n at a post-maximum phase (0.1). The inner boundary radii were set to 2.4 (Al2O3), and 4.0 (silicate), the power law index to 3.0 (Al2O3) and 2.5 (silicate), the angular photospheric diameter to 9.4, and the projected baseline length to 35 m. We considered models with the following combinations of optical depths:
-
τV (Al2O3) = 3.0 and τV (silicate) = 0.0;
-
τV (Al2O3) = 3.0 and τV (silicate) = 0.7;
-
τV (Al2O3) = 3.0 and τV (silicate) = 1.5;
-
τV (Al2O3) = 3.0 and τV (silicate) = 3.0.
Figure 7 shows the synthetic visibility and flux spectra based on the model parameters above. The addition of a silicate dust shell with τV (silicate) = 0.7 leads to an increase of the flux at the wavelength of the silicate feature at 9.8 μ by 68%, and to a decrease of the visibility by 75%. These differences are significant compared to our observational uncertainties of 30–50% for the flux and of 5–20% for the visibilities. We conclude that the addition of a silicate dust shell with fairly low optical depth (τV (silicate) = 0.7 at a wavelength of 0.55 μm) to the Al2O3 dust shell strongly affects the shape and features of the photometry and visibility spectra.
5.5. Variability
 |
Fig. 7 Synthetic flux spectra (top) and visibility amplitude (bottom) based on the model parameters from Sec. 5.1 The simulation compares four different sets of dust shell parameters where only the optical depth of the silicate dust shell varies. The optical depth of an Al2O3 dust shell τV (Al2O3) is set to 3.0 and the optical depth of a silicate dust shell τV (silicate) is set to 0.0 (red), 0.7 (green), 1.5 (blue) and 3.0 (light blue). The full set of parameters can be found in the text. |
 |
Fig. 8 Example of a test for intra-cycle visibility (top) and photometry (bottom) variability of S Ori. The red lines denote a pre-minimum phase of 1.39 and the green lines a pre-maximum phase of 1.94. The visibility observations were obtained at similar projected baseline lengths of ~15 m and similar position angles of ~71 °. Both lines were computed as an average of data obtained at the respective phase (±0.15), and for the visibility data at the respective projected baseline length (Bp ± 10%) and position angle (PA ± 10%) (see Table 8). |
 |
Fig. 9 Example of a test for cycle-to-cycle visibility (top) and photometry (bottom) variability of S Ori. The red lines denote a post-maximum phase of 2.12 and the green lines denote a similar phase of 3.14 of the next cycle. The visibility observations were obtained at a similar projected baseline length of ~30 m and at a similar position angle of ~73° (see Table 8). |
We investigated whether our visibility and photometry data exhibit a sign of intra-cycle or cycle-to-cycle variability. Such a variability could be caused by dust formation that occurs preferentially at certain variability phases or only during some cycles. Variability at mid-infrared wavelengths has previously been noted by Lopez et al. (1997); Tevousjan et al. (2004); Ohnaka et al. (2007); Zhao-Geisler et al. (2012).
Our observations of S Ori included 13 epochs of several phases between a pre-maximum phase of 0.9 and a pre-minimum phase of 0.4 (see Sect. 3), and some of these phases were obtained at several cycles. Likewise, the GX Mon observations were obtained at 11 different epochs, but for which we could not assign certain phases to the epochs because of the unknown lightcurve of GX Mon. The R Cnc observations were obtained at only 2 epochs, both at near-maximum phases, so that R Cnc could not be probed for variability.
We directly compared visibility data that were obtained at similar projected baseline length and position angles, which is important for a meaningful comparison. Visibility observations obtained at different baseline lengths show different values, so that a direct comparison is not possible. Visibility observations obtained at the same baseline length but at different position angles could also be caused by an asymmetric intensity distribution, which could be confused with variability. Our direct intra-cycle and cycle-to-cycle comparisons follow the investigations by Karovicova et al. (2011) of RR Aql. Tables 8–9 detail for our comparisons of S Ori and GX Mon the combinations of projected baseline lengths, position angles, and variability phases. Our direct visibility comparisons did not exhibit any significant variability for S Ori and GX Mon within our visibility accuracies of ~5–20%, and within the limits of the phase coverage and the available baseline lengths. Our MIDI photometry data showed large uncertainties at some epochs of up to 50%. The data of GX Mon showed a variability, both intra-cycle and cycle-to-cycle, at the level of ~2–3 σ (tests 7 and 9 of Table 9), which was most pronounced near the silicate emission feature at 9.8 μm. However, because of the large uncertainties of our MIDI photometry, this variability is not conclusive, and follow-up observations with a higher photometric accuracy, for example employing the instrument VISIR at the VLT, are needed to confirm a photometric variability. As an illustration, Fig. 8 shows an example of a test for intra-cycle variability of S Ori (phases 0.4 and 0.9, observed with a projected baseline length of ~15 m at position angle ~71°.), and Fig. 9 shows an example of a test for cycle-to-cycle variability of S Ori (phases ~0.1 observed at a baseline length of ~30 m and position angle ~73°.).
It has to be noted that our direct comparisons of the visibility and photometry spectra had some limitations. As mentioned above, the phase coverage of our observations was not complete. Most observations of S Ori and all observations of R Cnc were obtained at near-maximum phases, and we could not assign variability phases to the epochs of GX Mon. In addition, Karovicova et al. (2011) showed that the expected variability is small at mid-infrared wavelengths, and is difficult to detect within the uncertainties of the MIDI data. In addition, they showed that differences of the visibility spectra can best be detected using certain baseline lengths so that the dust shells are neither unresolved nor over-resolved. As a result, we can not exclude that intra-cycle or cycle-to-cycle variability of our sources could be detected with a more complete coverage of phases and baseline lengths or with a higher precision.
5.6. Asymmetries
Asymmetric intensity distributions can be probed in two different ways using VLTI/MIDI data. Asymmetries can be investigated either by comparing visibility data obtained at the same projected baseline length, but different position angles, or by analyzing the differential phases that are computed as a part of the EWS data reduction. The latter method was previously used by Ohnaka et al. (2008); Paladini et al. (2012); Sacuto et al. (2013) to detect asymmetric intensity distributions of the environments of AGB stars.
Our data of S Ori were mostly obtained at position angles around 70°. Only 4 observations were obtained at a different position angle of ~125°, but also at a different baseline length (different by at least 10 m). Our GX Mon observations were all obtained at similar position angles between ~60° and ~80°. Our R Cnc observations were obtained at two different position angles, but these also correspond to clearly different baseline lengths. This means that we could not probe our sources for asymmetries using a direct comparison of visibility amplitudes.
The differential phases show deviations from zero by less then 5° for S Ori and R Cnc, and less than 10° for GX Mon. These values are of the order of typical instrumental and atmospheric differential phases (Ohnaka et al. 2008). This means that our data do not show an indication of asymmetric intensity distributions. Figure 10 shows one example of a differential phase of S Ori, obtained with one of the longest available projected baseline lengths of ~64 m. The differential phase probes scales corresponding to the projected baseline length. We can not exclude that asymmetries of our sources might be detectable with longer projected baseline lengths.
6. Discussion of the dust condensation process
In our project we focused on an investigation of the dust condensation process based on spatially and spectrally resolved mid-infrared interferometry. In the following we discuss our results in the context of the scenarios on the formation of seed particles and on the dust condensation sequence that have been discussed in the literature.
 |
Fig. 10 Calibrated differential phase [°] of one of the observations of S Ori obtained on 10/02/2007 with a projected baseline length of ~64 m. |
6.1. Seed particles
It is known that the candidates for the first kind of grains forming from the gas phase in the environment of oxygen rich stars should condense out of abundant species, the reactions should not be blocked by high bond energies, and the condensation temperature should be high enough to allow the dust to survive in the hostile environment (Gail & Sedlmayr 1999). The dust temperatures at the inner edge of dust shells were observed to be at least around 1000 K (Gail et al. 2013). However, the smallest observed dust radii of 1.5–3 stellar radii (Ireland et al. 2005; Wittkowski et al. 2007; Norris et al. 2012) correspond to higher dust temperatures of 1300–1400 K. Generally, three options for the condensation of seed particles are being discussed in the recent literature.
(I) SiO is one of the most abundant species, but its efficient condensation takes place only below 600 K. However, new measurements seem to indicate higher SiO condensation temperatures, so that silicate dust formation triggered by cluster formation of SiO may be compatible with observed dust temperatures around 1000 K (Gail et al. 2013).
(II) Magnesium oxide can be ruled out as seed particle due to its low stability. All other species are less abundant. According to Gail & Sedlmayr (1999) aluminum oxides and titanium oxides remain as potentially possible primary condensing species. A possibility is that dust formation starts with the formation of TiO clusters, which serve as growth centers both for aluminum oxides and silicates. However, aluminum can also condense in circumstellar shells of its own due to the temperature gap between the formation of TiO seed nuclei and the growth of silicate dust (Gail & Sedlmayr 1999). The high condensation temperature of aluminum oxide (Al2O3) of ~1400 K in circumstellar environments allows these refractory grains to exist relatively close to the star. In addition, Al2O3 grains can condense before silicate grains, not only because of the higher condensation temperature, but also due to the greater affinity of oxygen for aluminum compared to silicon (Stencel et al. 1990), together making it a good candidate as a seed particle. Note that Gail et al. (2013) also discussed that Al2O3 grains and SiO clustering are mutually exclusive as seed particles. Many studies suggested that Al2O3 grains can become coated with silicates at larger radii where the dust temperature is lower and can serve as seed nuclei for the subsequent silicate formation (e.g.: Deguchi 1980; Vardya et al. 1986; Kozasa & Sogawa 1997a,b). Aluminum dust as well as for instance alloys of iron and nickel are difficult to detect because of the lack of diagnostically useful emission bands (McDonald et al. 2010). Amorphous Al2O3 is associated to a broad spectral feature at wavelengths between 9 μm to 15 μm (Koike et al. 1995; Begemann et al. 1997) due to a broad Al-O vibrational band. The origin of the 13 μm feature is still under debate (DePew et al. 2006). Vardya et al. (1986); Clayton & Nittler (2004) assign it to crystalline Al2O3. On the other hand, Speck (1998) attribute it to silica SiO2, and Posch et al. (1999); Smolders et al. (2012) to spinel MgAl2O4. A detailed investigation is still required. However, crystalline oxides are expected to be a minor component of most oxygen-rich dust shells.
(III) Ireland et al. (2005) and Norris et al. (2012) discussed that large (~300 nm) scattering iron-free, magnesium-rich silicate (forsterite) grains can be stable at small radii down to observed radii of 1.5 stellar radii. Similarly, Höfner (2008); Bladh & Höfner (2012); Bladh et al. (2013) proposed micron-sized iron-free silicates as wind-driving grains. However, both teams also mention Al2O3 grains as an alternative (Ireland et al. 2005; Norris et al. 2012) or additional (Sacuto et al. 2013) dust species. Goumans & Bromley (2012) favor the formation of magnesium-rich iron-free silicates via heteromolecular condensation based on Mg, SiO, and H2O.
The small observed dust radii of 1.9–2.2 stellar radii based on our models of S Ori, R Cnc, and GX Mon, and the corresponding high dust temperatures of 1200–1350 K support a scenario where Al2O3 grains serve as seed particles for the dust formation (scenario II) of these targets. This scenario is further supported by the good agreement of the MIDI spectra and the models including Al2O3 grains, in particular regarding the broad spectral feature at ~9–15 μm that is attributed to Al2O3. In addition, we have shown that the aluminum number density in an extended stellar atmosphere can be sufficiently high to match the number densities of Al2O3 grains of our dust shell model between ~2 and up to ~4 stellar radii (Sect. 5.2). The co-location of SiO maser emission and the inner dust radii at about 2 stellar radii for the same sources (Sect. 5.3) show that silicon is available as SiO in the gas phase at these radii, indicating that SiO clustering (scenario I) and the formation of silicates at these small radii (scenario III) are unlikely. It is not clear if Al2O3 grains also play a role in the case of RR Aql, where our best-fit dust model consisted only of silicate grains with a larger inner radius of about 4 stellar radii (Karovicova et al. 2011). It is possible that also in this case Al2O3 grains serve as seed particles at smaller inner radii, but that they are not visible behind the silicate grains in the model comparison. Indeed, model simulations have shown that the 8–13 μm visibility and flux values are not sensitive to the addition of an Al2O3 dust shell with low optical depth (10–20%) to a silicate dust shell within the VLTI/MIDI uncertainties (Karovicova et al. 2011). However, RR Aql may also be an example of another route of direct silicate dust formation at larger radii via scenarios I/III.
6.2. Dust condensation sequence
Our results were consistent with the approach by Little-Marenin & Little (1990) to classify Mira variable AGB stars into three groups that can be described by Al2O3 shells, silicate shells, or a mix thereof. Our targets S Ori and R Cnc could be well described by Al2O3 shells with small inner radii of 1.9–2.2 photospheric radii. GX Mon could be well described with a mix of an Al2O3 shell with an inner radius of 2.1 photospheric radii, and a silicate shell with an inner radius of 4.6 photospheric radii. RR Aql could be well described by a silicate dust shell alone with an inner radius of 4.1 photospheric radii.
Little-Marenin & Little (1990) suggested that these three groups of sources follow an evolutionary sequence in the spectral features. This sequence starts with a featureless continuum, then develops toward strong silicate features. This is in accordance with a theoretical dust condensation sequence by Lattimer & Grossman (1978) that predicts primary condensation of refractory oxides. If in the cooler regions, further out in the circumstellar shell, the densities are still high enough, the formation of silicate dust can occur. In cases where the densities are not high enough for the formation of the silicate dust, the dust condensation sequence can “freeze-out”. This would imply that stars with low mass-loss rates will predominantly exhibit an oxide mineralogy while stars with high mass-loss rates will form substantial amounts of silicate dust. This scenario was confirmed e.g. by Stencel et al. (1990); Blommaert et al. (2006); Posch et al. (1999); Heras & Hony (2005); Smolders et al. (2012); Zeidler et al. (2013) showing that for low mass-loss rate stars the dust content is dominated by Al2O3 grains.
A second scenario was suggested by Sloan & Price (1998). According to these authors, the chemistry of the dust (i.e. the condensation sequence) is driven by the C/O abundance of the out-flowing gas. In this scenario, less evolved stars – stars with low C/O ratio – produce larger amounts of silicate grains compared to alumina grains due to the abundance of oxygen atoms, and therefore we should see strong silicate features. For more evolved stars – stars with C/O ratio close to the unity – most of the oxygen will be bound up in CO molecules and in-sufficient oxygen will remain for grain condensation in order to form silicate grains. Al2O3 grains will therefore dominate in the dust shell. The second scenario suggests an increasing oxide dust content with an increasing mass-loss rate during the evolution of the star along the AGB.
Dust condensation sequence.
Table 10 lists for our targets the dust chemistry and the optical depth together with the mass loss rates adopted from the literature. These results point in the direction of the hypothesis by Little-Marenin & Little (1990) and Blommaert et al. (2006) that the dust content of stars with low mass-loss rates is dominated by Al2O3 and other oxide grains while the dust content of stars with higher mass-loss rates predominantly exhibits substantial amounts of silicates.
However, as outlined in Sect. 5.2, it is unlikely that in those sources that can be described by only an Al2O3 shell (S Ori and R Cnc in our sample), Al2O3 grains can indeed alone explain the observed gas-to-dust ratios of the stellar outflows, owing to the relatively low abundance of aluminum. This means that it is unlikely that the dust condensation sequence already freezes out directly after the formation of Al2O3 grains. It is more likely that Al2O3 grains form at small inner radii (about 2 stellar radii), see above, and serve as seed particles for grains at larger radii (from about 4 stellar radii). For those sources that do not show the typical silicate features in the spectra and that can be well described by Al2O3 shells alone, the additional dust species need to have properties that preserve the spectral signature of Al2O3, in particular the broad feature at ~9–15 μm, and that do not add the typical silicate features at 9.7 μm and 18 μm, which is not seen in the spectra of these sources. As shown in Sect. 5.4, already a small amount of additional warm silicate grains would significantly affect the shape and features of the visibility and photometry spectra.
The class of sources that can be well described by a combination of an Al2O3 shell with an inner radius around 2 photospheric radii and a silicate shell with an inner radius around 4–5 photospheric radii (GX Mon in our sample), as well as those that can be described by a silicate shell alone (RR Aql in our sample) show the typical silicate emission features at roughly 9.7 μm and 18 μm. These sources also show larger mass-loss rates and larger overall optical depths of the dust shell (cf. Table 10). For these sources, the dust condensation sequence continues beyond that described above. The silicate emission features are generally believed to be associated with silicate condensates or more precisely to amorphous silicates known as glasses. The features are associated with vibrational modes of the fundamental SiO4 tetrahedron in silicate condensates of a largely disordered lattice structure (Gail & Sedlmayr 1999). The main dust components responsible for most of the dust opacity and the emission of infrared radiation are olivine and pyroxene (Vollmer et al. 2007), non-stoichiometric varieties, with random ratios between the Fe/Mg, Si, together with oxygen. The condensation of amorphous silicates proceeds at temperatures below the glass temperature. An amorphous structure is formed by molecules that stick to the surface of the grain, and immediately freeze out without having sufficient energy to find energetically more favorable lattice positions. The spectrometers on board of ISO showed that in addition to amorphous silicates also the crystalline silicates were found in the circumstellar environment of evolved star (Waters et al. 1996). It is under debate how both crystalline and amorphous silicates can be formed in the outflow of evolved stars. It is believed that crystalline silicates are not present in the dust shells around low mass-loss rate AGB stars with optically thin dust shells. However, Kemper et al. (2001) showed that due to a temperature difference between amorphous and crystalline silicates it is possible to include up to 40% of crystalline silicate material in the circumstellar dust shell, without the spectra showing the characteristic spectral features.
7. Summary and conclusions
We presented multi-epoch spectrally and spatially resolved mid-infrared interferometric observations of the oxygen-rich Mira variables S Ori, GX Mon, and R Cnc obtained with the MIDI instrument at the Very Large Telescope Interferometer (VLTI). This study represents a continuation of previous results by Wittkowski et al. (2007) and Karovicova et al. (2011), who compared multi-epoch VLTI/MIDI data of the Mira variables S Ori and RR Aql to radiative transfer models of the dust shell. The main goal of this project was to trace the dust formation process as a function of mass-loss rate, distance from the photosphere, and pulsation phase and cycle.
Our data did not show significant signs of variability or asymmetry within their uncertainties, and within our limited baseline coverage and phase coverage. Intra-cycle and cycle-to-cycle photometry variations may be present at the level of ~2−3σ for GX Mon. However, because of the large uncertainties, this photometric variability is not conclusive, and observations with a higher photometric accuracy (e.g. VISIR at the VLT) are needed for a confirmation. A variability of the visibility may be expected with mid-infrared interferometric observations that cover more phases and use optimized baseline lengths, such that the dust shells are neither barely resolved nor over-resolved (cf. Karovicova et al. 2011).
We modeled the observed data with an ad-hoc radiative transfer model of the dust shell using the radiative transfer code mcsim_mpi (Ohnaka et al. 2006). We used a series of dust-free dynamic model atmospheres based on self-excited pulsation models (M series, Ireland et al. 2004a,b) to describe the intensity profile of the central source. Following the successful description of IRAS data of a number of Mira stars by Lorenz-Martins & Pompeia (2000), we used two dust shells that can have different parameters, one using amorphous Al2O3 grains (Koike et al. 1995; Begemann et al. 1997) and one using warm “astronomical” silicate grains (Ossenkopf et al. 1992).
We showed that the photometric and visibility spectra of all our sources can be well described by our modeling approach. We found for all epochs the best-fit dust shell parameters including the optical depths of the dust shells, the inner boundary radii, the power-law indexes of the density distributions, as well as the photospheric angular diameter.
The parameters of our best-fit models were listed in Table 7 and were described in Sect. 5.1.
In summary, our Mira variable sources can be classified in three groups, as suggested by Lorenz-Martins & Pompeia (2000), where the dust shell can be characterized by (I) an Al2O3 shell alone (S Ori and R Cnc); (II) a silicate shell alone (RR Aql); and (III) a combination of an Al2O3 shell and a silicate shell (GX Mon). Hereby, the inner dust shell radii of Al2O3 are located closer to the star at distances of 1.9–2.2 photospheric radii, and the inner dust shell radii of the silicates are farther away at distances of 4–5 photospheric radii. The best-fit photospheric radii are consistent with independent estimates. The derived absolute photospheric radii of ~350–675 R⊙ and effective temperatures of ~2200–2600 K are consistent with typical values of Mira variables. The dust temperatures at the inner radii of 1200–1350 K (Al2O3) and ~1100 K (silicates) are consistent with the condensation temperatures of Al2O3 and silicate grains, respectively. This increases the confidence in our modeling approach. The inner dust shell radii of the Al2O3 grains are co-located with the extended atmospheres and with SiO maser emission for all our sources. Our results combined with mass loss rates adopted from the literature support the hypothesis that stars with low mass-loss rates are those that can be described with Al2O3 grains alone (group I), and stars with higher mass-loss contain significant amounts of warm silicates displaying the prominent silicate features (groups II and III). It should be noted that even tough the results are very interesting, there are, due to the rather small sample size (four stars), still relatively far from reaching solid conclusions.
For group (I), sources which are characterized by only an Al2O3 shell, we confirmed that the number density of aluminum in a sufficiently extended atmosphere can match the required number density of Al2O3 grains of the best-fit dust shell models up to roughly 2 × the inner dust shell radius, or 4 × the photospheric radius. However, we also showed that it is unlikely that Al2O3 grains alone can explain typical observed dust-to-gas ratios of the outflows of Mira variables, owing to the relatively low abundance of aluminum. It is more likely that Al2O3 grains are present at close radii of ~2–4 stellar radii and can serve as seed particles for further dust formation at larger radii and lower dust temperatures. In the case of group (I), these additional grains need to preserve the spectral signature of Al2O3, in particular the broad feature at 9–15 μm, without adding features that are not observed for these targets, such as the silicate features at 9.8 μm. We demonstrated that already the addition of small amounts of warm silicates to an Al2O3 shell has a strong effect on the photometry and visibility spectra, and would have been detected by our VLTI/MIDI observations. Candidates for such additional grains metallic iron or (Fe,Mg)O (magnesiowüstite), (e.g., Ferrarotti & Gail 2006; McDonald et al. 2010; Posch et al. 2002). Also scattering iron-free magnesium-rich silicates (Mg2SiO4, forsterite) may not have a significant silicate signature in the mid-IR if distributed in certain geometries, such as a geometrically thin shell (Ireland et al. 2005). Sacuto et al. (2013) could explain VLTI/MIDI spectra of RT Vir, which have a similar shape as those of S Ori and R Cnc, by a combination of forsterite grains and Al2O3 grains. The presence of dust grains at small radii of ~2 stellar radii and below have also been observationally confirmed by interferometric polarimetry and been attributed to forsterite or Al2O3 grains (Ireland et al. 2005; Norris et al. 2012). Dust grains at close radii of ~2 stellar radii are co-located with SiO maser emission for all our sources, so that SiO nucleation and silicate dust formation are unlikely at these radii. Sources of group (I) are consistent with relatively low mass-loss rates, so that the dust condensation sequence may freeze out for these sources before the formation of silicates that display the typical silicate features at 9.7 μm and 18 μm.
Sources of group (III), which can be described by a mix of an Al2O3 shell and a silicate shell, are consistent to be associated with higher mass-loss rates and higher optical depths of the dust shells. For these sources, the density at larger radii may be sufficiently high so that the dust condensation sequence described above may continue to the formation of amorphous silicates such as olivine and pyroxene, which add the typical silicate emission features to the spectra of these sources.
Sources of group (II), which can be described by a silicate dust shell alone, may be of the same kind as sources of group (III), but where the signature of Al2O3 grains is not detected. Alternatively, these sources may be an example of direct silicate formation at larger radii via SiO nucleation (Gail et al. 2013) or heteromolecular condensation (Goumans & Bromley 2012).
The results from the project will allow refinements and enhancements of state-of-the-art dynamic model atmospheres and radiative transfer modeling codes, as well as new models describing the mass-loss process and the wind driving mechanism. Future observations aiming at characterizing and constraining such new models would benefit from obtaining additional concurrent spectrally resolved near-infrared interferometry bringing stronger constraints on atmospheric molecular layers located close to the photosphere.
Online material
VLTI/MIDI observation of S Ori.
VLTI/MIDI observation of GX Mon.
VLTI/MIDI observation of R Cnc.
Details of our tests to search for variability of S Ori.
Details of our tests to search for variability of GX Mon.
Acknowledgments
We would like to thank Prof. H.-P. Gail for his scientific advice and his suggestions, and we would also like to thank the referee for the comments that helped to improve our manuscript. We used the AAVSO International Database along with the AFOEV and SIMBAD databases, operated at the CDS, France. We acknowledge star observers providing active data support in the observations of the variable stars. The authors would also like to acknowledge all who are involved in developing the publicly accessible MIDI data reduction software packages and tools EWS and MIA. This work is based on service mode observations made with the MIDI instrument, which is operated by the ESO. We would like to thank the operating team at the Paranal Observatory for their careful execution of the observations. Any findings or conclusions expressed by DAB in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
- Århammar, C., Pietzsch, A., Bock, N., et al. 2011, Proc. Natl. Acad. Sci. USA, 108, 6355 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, Explanatory supplement, 1 [Google Scholar]
- Bladh, S., & Höfner, S. 2012, A&A, 546, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bladh, S., Höfner, S., Nowotny, W., Aringer, B., & Eriksson, K. 2013, A&A, 553, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blommaert, J. A. D. L., Groenewegen, M. A. T., Okumura, K., et al. 2006, A&A, 460, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boboltz, D. A., & Wittkowski, M. 2005, ApJ, 618, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Nittler, L. R. 2004, ARA&A, 42, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D., Ragland, S., Pluzhnik, E. A., et al. 2010, ApJS, 188, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Danchi, W. C., Bester, M., Degiacomi, C. G., Greenhill, L. J., & Townes, C. H. 1994, AJ, 107, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S. 1980, ApJ, 236, 567 [NASA ADS] [CrossRef] [Google Scholar]
- DePew, K., Speck, A., & Dijkstra, C. 2006, ApJ, 640, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W., Glass, I. S., Whitelock, P. A., & Catchpole, R. M. 1989, MNRAS, 241, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarotti, A. S., & Gail, H.-P. 2006, A&A, 447, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., & Höfner, S. 2008, A&A, 483, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gail, H.-P. 2010, in Lect. Notes Phys. 815, ed. T. Henning (Berlin: Springer Verlag), 61 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1999, A&A, 347, 594 [NASA ADS] [Google Scholar]
- Gail, H.-P., Wetzel, S., Pucci, A., & Tamanai, A. 2013, A&A, 555, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glindemann, A., Algomedo, J., Amestica, R., et al. 2003, in Proc. SPIE, 4838, ed. W. A. Traub, 89 [Google Scholar]
- Goumans, T. P. M., & Bromley, S. T. 2012, MNRAS, 420, 3344 [NASA ADS] [Google Scholar]
- Gray, M. D., Wittkowski, M., Scholz, M., et al. 2009, MNRAS, 394, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., & Olofsson, H. 2003, Asymptotic giant branch stars (New York, Berlin: Springer) [Google Scholar]
- Heras, A. M., & Hony, S. 2005, A&A, 439, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höfner, S. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 335 [Google Scholar]
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höfner, S. 2009, in Cosmic dust – near and far, eds. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 3 [Google Scholar]
- Höfner, S., & Andersen, A. C. 2007, A&A, 465, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Icke, V., Frank, A., & Heske, A. 1992, A&A, 258, 341 [NASA ADS] [Google Scholar]
- Ireland, M. J., & Scholz, M. 2006, MNRAS, 367, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., Tuthill, P. G., & Wood, P. R. 2004a, MNRAS, 355, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., & Wood, P. R. 2004b, MNRAS, 352, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Tuthill, P. G., Davis, J., & Tango, W. 2005, MNRAS, 361, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., & Wood, P. R. 2008, MNRAS, 391, 1994 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Scholz, M., & Wood, P. R. 2011, MNRAS, 418, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Justtanont, K., Skinner, C. J., & Tielens, A. G. G. M. 1994, ApJ, 435, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Karovicova, I., Wittkowski, M., Boboltz, D. A., et al. 2011, A&A, 532, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemper, F., Waters, L. B. F. M., de Koter, A., & Tielens, A. G. G. M. 2001, A&A, 369, 132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knapp, G. R. 1985, ApJ, 293, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Koike, C., Kaito, C., Yamamoto, T., et al. 1995, Icarus, 114, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Kozasa, T., & Sogawa, H. 1997a, Ap&SS, 255, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Kozasa, T., & Sogawa, H. 1997b, Ap&SS, 251, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Grossman, L. 1978, Moon and Planets, 19, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Little-Marenin, I. R., & Little, S. J. 1990, AJ, 99, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, B., Danchi, W. C., Bester, M., et al. 1997, ApJ, 488, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenz-Martins, S., & Pompeia, L. 2000, MNRAS, 315, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Loup, C., Forveille, T., Omont, A., & Paul, J. F. 1993, A&AS, 99, 291 [NASA ADS] [Google Scholar]
- Matsuura, M., Barlow, M. J., Zijlstra, A. A., et al. 2009, MNRAS, 396, 918 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, I., Sloan, G. C., Zijlstra, A. A., et al. 2010, ApJ, 717, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Millan-Gabet, R., Pedretti, E., Monnier, J. D., et al. 2005, ApJ, 620, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Bester, M., Danchi, W. C., et al. 1997, ApJ, 481, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Danchi, W. C., Hale, D. S., et al. 2000, ApJ, 543, 861 [Google Scholar]
- Monnier, J. D., Millan-Gabet, R., Tuthill, P. G., et al. 2004, ApJ, 605, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, B. R. M., Tuthill, P. G., Ireland, M. J., et al. 2012, Nature, 484, 220 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ohnaka, K., Bergeat, J., Driebe, T., et al. 2005, A&A, 429, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Driebe, T., Hofmann, K., et al. 2006, A&A, 445, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Driebe, T., Weigelt, G., & Wittkowski, M. 2007, A&A, 466, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Izumiura, H., Leinert, C., et al. 2008, A&A, 490, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Schertl, D., et al. 2012, A&A, 537, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olivier, E. A., Whitelock, P., & Marang, F. 2001, MNRAS, 326, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., Henning, T., & Mathis, J. S. 1992, A&A, 261, 567 [NASA ADS] [Google Scholar]
- Paladini, C., Sacuto, S., Klotz, D., et al. 2012, A&A, 544, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posch, T., Kerschbaum, F., Mutschke, H., et al. 1999, A&A, 352, 609 [NASA ADS] [Google Scholar]
- Posch, T., Kerschbaum, F., Mutschke, H., Dorschner, J., & Jäger, C. 2002, A&A, 393, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragland, S., Traub, W. A., Berger, J.-P., et al. 2006, ApJ, 652, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Sacuto, S., Ramstedt, S., Höfner, S., et al. 2013, A&A, 551, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samus, N. N., Durlevich, O. V., & et al. 2009, VizieR Online Data Catalog: II/250 [Google Scholar]
- Sloan, G. C., & Price, S. D. 1998, ApJS, 119, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Smolders, K., Neyskens, P., Blommaert, J. A. D. L., et al. 2012, A&A, 540, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speck, A. K. 1998, Ph.D. Thesis, University College London, UK [Google Scholar]
- Stencel, R. E., Nuth, III, J. A., Little-Marenin, I. R., & Little, S. J. 1990, ApJ, 350, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Tevousjan, S., Abdeli, K., Weiner, J., Hale, D. D. S., & Townes, C. H. 2004, ApJ, 611, 466 [Google Scholar]
- Tielens, A. G. G. M., Waters, L. B. F. M., Molster, F. J., & Justtanont, K. 1998, Ap&SS, 255, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Tuthill, P. G., Danchi, W. C., Hale, D. S., Monnier, J. D., & Townes, C. H. 2000, ApJ, 534, 907 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T. 1999, PASP, 111, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Dyck, H. M., Benson, J. A., & Lacasse, M. G. 1996, AJ, 112, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Thompson, R. R., & Creech-Eakman, M. J. 2002, AJ, 124, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Vardya, M. S., de Jong, T., & Willems, F. J. 1986, ApJ, 304, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, C., Stadermann, F. J., Bose, M., et al. 2007, Meteoritics and Planetary Science Supplement, 42, 5107 [NASA ADS] [Google Scholar]
- Waters, L. B. F. M., Molster, F. J., de Jong, T., et al. 1996, A&A, 315, L361 [NASA ADS] [Google Scholar]
- Weiner, J., Tatebe, K., Hale, D. D. S., et al. 2006, ApJ, 636, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Whitelock, P., Marang, F., & Feast, M. 2000, MNRAS, 319, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Wishnow, E. H., Townes, C. H., Walp, B., & Lockwood, S. 2010, ApJ, 712, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ohnaka, K., Driebe, T., & Scholz, M. 2007, A&A, 470, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ireland, M., et al. 2011, A&A, 532, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P. 2006, A&A, 460, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Young, K. 1995, ApJ, 445, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Zeidler, S., Posch, T., & Mutschke, H. 2013, A&A, 553, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao-Geisler, R., Quirrenbach, A., Köhler, R., Lopez, B., & Leinert, C. 2011, A&A, 530, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao-Geisler, R., Quirrenbach, A., Köhler, R., & Lopez, B. 2012, A&A, 545, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Coverage of the uv-plane of our MIDI observations of S Ori, GX Mon, and R Cnc. Each line represents one AT observation over the wavelength range from 8 μm to 13 μm. The color of each point corresponds to the wavelength of the observations, as indicated by the color bar. |
| In the text | |
 |
Fig. 2 VLTI/MIDI interferometry at 8–13 μm of S Ori for the example of epoch B (stellar phase 0.89, see Table 1). The panels show (upper left) the flux, (upper right) the visibility amplitude, (lower left) the corresponding UD diameter, and (lower right) the visibility amplitude as a function of spatial frequency for three averaged band passes of 8–9 μm, 10–11 μm, and 12–13 μm. The gray shade indicates the wavelength region around 9.5 μm that is affected by atmospheric absorption. The crosses with error bars denote the measured values. The solid lines indicate our best-fit model. The contributions of the stellar and dust components alone are indicated by the dotted and the dashed line, respectively. |
| In the text | |
 |
Fig. 3 As Fig. 2, but for the example of epoch E of GX Mon (see Table 2). |
| In the text | |
 |
Fig. 4 As Fig. 2, but for the example of epoch A of R Cnc (see Table 3). |
| In the text | |
 |
Fig. 5 Stratification of the gas temperature and dust temperature (Al2O3 and silicate dust) for the example of our GX Mon model. The solid line shows the gas temperature (model M21n), the dotted line the dust temperature of the Al2O3 dust shell, and the dashed line the dust temperature of the silicate dust shell. The vertical line indicates RPhot = 2.19 × 1013 cm. For the model parameters, see Table 7. |
| In the text | |
 |
Fig. 6 Number density of available aluminum atoms in the dust-free extended model atmospheres M22 (top) and P20 (bottom) compared to the number density of aluminum in the dust shell. Shown is the overlapping radial range between the inner radius of the dust shell model and the maximum radius of the atmosphere model. The vertical line indicates RPhot = 1.99 × 1013 cm (M22) and RPhot = 1.74 × 1013 cm (P20). |
| In the text | |
 |
Fig. 7 Synthetic flux spectra (top) and visibility amplitude (bottom) based on the model parameters from Sec. 5.1 The simulation compares four different sets of dust shell parameters where only the optical depth of the silicate dust shell varies. The optical depth of an Al2O3 dust shell τV (Al2O3) is set to 3.0 and the optical depth of a silicate dust shell τV (silicate) is set to 0.0 (red), 0.7 (green), 1.5 (blue) and 3.0 (light blue). The full set of parameters can be found in the text. |
| In the text | |
 |
Fig. 8 Example of a test for intra-cycle visibility (top) and photometry (bottom) variability of S Ori. The red lines denote a pre-minimum phase of 1.39 and the green lines a pre-maximum phase of 1.94. The visibility observations were obtained at similar projected baseline lengths of ~15 m and similar position angles of ~71 °. Both lines were computed as an average of data obtained at the respective phase (±0.15), and for the visibility data at the respective projected baseline length (Bp ± 10%) and position angle (PA ± 10%) (see Table 8). |
| In the text | |
 |
Fig. 9 Example of a test for cycle-to-cycle visibility (top) and photometry (bottom) variability of S Ori. The red lines denote a post-maximum phase of 2.12 and the green lines denote a similar phase of 3.14 of the next cycle. The visibility observations were obtained at a similar projected baseline length of ~30 m and at a similar position angle of ~73° (see Table 8). |
| In the text | |
 |
Fig. 10 Calibrated differential phase [°] of one of the observations of S Ori obtained on 10/02/2007 with a projected baseline length of ~64 m. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


