| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322365 | |
| Published online | 29 November 2013 | |
Multiple spiral patterns in the transitional disk of HD 100546⋆
1 LESIA, Observatoire de Paris, CNRS, University Pierre et Marie Curie Paris 6 and University Denis Diderot Paris 7, 5 place Jules Janssen, 92195 Meudon, France
e-mail: anthony.boccaletti@obspm.fr
2 Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
3 Institut de Planétologie et d’Astrophysique de Grenoble, Université Joseph Fourier, CNRS, BP 53, 38041 Grenoble, France
4 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
Received: 25 July 2013
Accepted: 23 October 2013
Context. Protoplanetary disks around young stars harbor many structures related to planetary formation. Of particular interest, spiral patterns were discovered among several of these disks and are expected to be the sign of gravitational instabilities leading to giant planet formation or gravitational perturbations caused by already existing planets. In this context, the star HD 100546 presents some specific characteristics with a complex gaseous and dusty disk that includes spirals, as well as a possible planet in formation.
Aims. The objective of this study is to analyze high-contrast and high angular resolution images of this emblematic system to shed light on critical steps in planet formation.
Methods. We retrieved archival images obtained at Gemini in the near IR (Ks band) with the instrument NICI and processed the data using an advanced high contrast imaging technique that takes advantage of the angular differential imaging.
Results. These new images reveal the spiral pattern previously identified with Hubble Space Telescope (HST) with an unprecedented resolution, while the large-scale structure of the disk is mostly cancelled by the data processing. The single pattern to the southeast in HST images is now resolved into a multi-armed spiral pattern. Using two models of a gravitational perturber orbiting in a gaseous disk, we attempted to constrain the characteristics of this perturber, assuming that each spiral is independent, and drew qualitative conclusions. The non-detection of the northeast spiral pattern observed in HST allows putting a lower limit on the intensity ratio between the two sides of the disk, which if interpreted as forward scattering, yields a larger anisotropic scattering than is derived in the visible. Also, we find that the spirals are likely to be spatially resolved with a thickness of about 5–10 AU. Finally, we did not detect the candidate planet in formation recently discovered in the Lp band, with a mass upper limit of 16–18 MJ.
Key words: stars: individual: HD 100546 / protoplanetary disks / planet-disk interactions / stars: early-type / techniques: image processing / techniques: high angular resolution
© ESO, 2013
1. Introduction
Understanding planetary formation requires identiying and describing the many steps in this complex process and in particular, the moment they start to form in circumstellar disks. At least two formation mechanisms have been proposed to explain the diversity of giant exoplanets as observed today. The so-called core accretion model (Pollack et al. 1996) is able to account for the presence of most of the exoplanets discovered by radial velocity and located in the first ten AU from the star. At the same time, direct imaging has provided detections of young (>10 Myr) and massive planets at much larger separations (>50 AU, e.g. Chauvin et al. 2005) and, of which the vast majority presumably require gravitational instabilities to form (Boss 1998). So far, β Pictoris b (Lagrange et al. 2010) could be the only imaged exoplanet that may have formed in the core-accretion regime (Rameau et al. 2013). This peculiar object also indicates that the timescale for formation can be very short (≤10 Myr). However, it is difficult to rely solely on astrometric and photometric measurements in direct images to determine which formation model is at work in a given planetary system. Therefore, the observation of younger (<10 Myr) protoplanetary disks is of prime importance for detecting any signs of planetary formation and ideally for catching a planet in formation. In particular, imaging in scattered light allows the spatial distribution of the dust to be mapped on the disk surface, and can complement the information collected from unresolved photometric or spectroscopic observations, as well as from mid-infrared and sub-mm imaging.
Among the protoplanetary disks in the solar vicinity for which the spatial resolution is fine enough to probe the regions of planetary formation, the system HD 100546 has recently been the focus of a lot of attention with the announcement by Quanz et al. (2013) of a candidate planet in formation. The star is young (5–10 Myr, Guimarães et al. 2006) and belongs to the class of Herbig Ae/Be star. However, the large amount of gas observed in absorption and emission (Panić et al. 2010; Goto et al. 2012) may suggest an age closer to the lower limit of 5 Myr. The presence of a circumstellar disk has been suspected since IRAS observations, and its spectral energy distribution suggests both warm and a cold grain populations. Silicate emission features a comet-like spectrum (Malfait et al. 1998). Resolved images in the near-IR were first obtained from ground-based adaptive optics by Pantin et al. (2000) and then with HST/NICMOS (Augereau et al. 2001). The disk was seen as an elliptical featureless extended source, which extends far from the star (~380 AU) with an inclination of about 51° from the line of sight. An asymmetry along the minor axis was marginally detected. To account for the near-IR scattered light emission the grains must be larger than 0.1–0.5 μm (Mulders et al. 2013a).
Observations in the visible with STIS (Grady et al. 2001) and ACS (Ardila et al. 2007) have provided an improved angular resolution and sensitivity with respect to near IR and revealed a much more complex morphology. The environment of the star includes nebulosity that extends beyond 8′′ from the star and a mid disk (3′′–8′′) where the minor axis asymmetry is interpreted as scattering anisotropy (g = 0.15 − 0.2). These HST images revealed two trailing spiral arms in the disk region between 1.5′′ and 3′′, which develop towards the southeast and the northwest respectively (150 ~ 300 AU). Moreover, the most detailed images obtained so far show some hints of additional spiral patterns (Ardila et al. 2007).
The innermost part of the disk, intensively studied by Benisty et al. (2010) and Tatulli et al. (2011) with VLTI/AMBER, shows an inner hole between 4 AU and 13 AU. While the location of the outer rim is confirmed by VLTI/MIDI, Panić et al. (2012) observed that the inner boundary of the gap might be located at 0.7 AU instead of 4 AU. The rim at 13 AU was marginally detected with polarimetric imaging in the near-IR (Quanz et al. 2011). Both the spirals and the hole suggest that planetary formation has already occurred in different places of the HD 100546 environment and, interestingly, that the two alternative formation mechanisms may coexist in the same system. Since then, spiral patterns have been observed in other protoplanetary disks (Fukagawa et al. 2004, 2006; Muto et al. 2012; Grady et al. 2013; Rameau et al. 2012) and are suspected to be the signs of self-gravity or planets that trigger spiral wave densities in massive regions of a disk.
In this paper, we report the observation of HD 100546 with NICI using public data retrieved from the Gemini archive. The images reveal a set of multiple spiral patterns in the southeastern region. Section 2 presents the observation and the data reduction procedure. The sensitivity to point sources is analyzed in Sect. 3, and the morphology of the spirals is described in Sect. 4. Finally, possible origins of the spirals are discussed in Sect. 5.
2. Observation and data reduction
We retrieved archival data obtained with the Near Infrared Coronagraphic Imager (NICI; Toomey & Ftaclas 2003), installed at the 8-m telescope, Gemini South. The instrument is based on a near-IR (1–5 μm) dual-band imager in which two images are formed simultaneously (owing to a beam splitter) on two separate detectors. NICI was designed for high-contrast imaging and, in particular, for an optimum the search for young planetary mass objects as companion to stars (Liu et al. 2010). In turn, these capacities make NICI suitable for direct imaging of protoplanetary and debris disks as it combines an adaptive optics system, a Lyot coronagraph and angular differential imaging capability (Marois et al. 2006).
The observation was done on March 6, 2010 (Table 1) using a single-channel configuration in the Ks band (2.15 μm) with the 0.32′′ flat-topped Gaussian Lyot coronagraphic mask and the 95% undersized stop. The pixel scale is 18 mas per pixel. The data set consists of 53 files of 1.9 s × 22 coadds = 41.8 s each. The star itself is used for the wavefront sensing. HD 100546 is a Be star (B9Ve, V = 6.7, K = 5.42) located at a distance of 97 ± 4 pc according to van Leeuwen (2007).
Log of observations.
 |
Fig. 1 Images of the environment of the star HD100546 as seen in the Ks band with NICI and with several ADI-algorithms: cADI (left), KLIP (middle), and LOCI (right). The field is 8′′ large and the central area (<1.25′′) is masked out numerically. A 2-pixel smoothing is applied. Pixel intensities are coded in contrast with respect to the star. The point source at the south corresponds to the object labeled B7 in Fig. 2. |
We followed the data reduction procedure described in Boccaletti et al. (2013). The images are dark-subtracted and flat-fielded. The stability of this observing sequence in terms of AO correction is good enough to retain all the available frames corresponding to a total integration time of 2215.4 s. The registration of coronagraphic images was obtained in two steps, first with a rough estimation of the star position with a Gaussian fit of the images that were typically thresholded at a few percent of the maximum flux (Boccaletti et al. 2012). Thus, frames are registered at one-pixel precision. Then, we performed a more precise determination of the star location with Moffat fitting of the central attenuated spot behind the semi-transparent Lyot mask, which is known to move linearly with the actual star position (Lloyd & Sivaramakrishnan 2005). A precision of ~0.2 pixel is achieved for the frame registration.
Out-of-mask unsaturated images of the star used to determine the PSF shape and intensity are not available in the archive. For photometric purpose, we therefore measured the coronagraph attenuation factor separately on a binary star observed with the same settings on May 2010 and derived a value of 180 (~5.6 ± 0.14 mag), in agreement with Wahhaj et al. (2011) and Boccaletti et al. (2012). The angular resolution measured on a field star is FWHM ≈ 65 mas.
Then, we processed the data with a set of ADI algorithms: cADI (Marois et al. 2006), LOCI (Lafrenière et al. 2007), and also KLIP, which makes use of a principal component analysis (Soummer et al. 2012). For a brief description of these algorithms and relevant control parameters, see Lagrange et al. (2012) and Boccaletti et al. (2012). Several parameters for these algorithms were tested to achieve the best detection performance. The KLIP analysis is applied on an annular region between 20 (the radius of the coronagraphic mask) and 225 pixels (4′′ in radius), and we retain 1, 2, 3, 4, and 5 modes (out of 53) in estimating the stellar contribution. In the LOCI approach, we used the geometry defined by Lafrenière et al. (2007) with NA = 300, g = 1, and Nδ = 0.5,1.0,1.5,2.0 in the central 4′′ region. To produce the final images, the frames are mean-combined for cADI and KLIP and median-combined for LOCI. The images presented in Fig. 1 are scaled in contrast with respect to the star maximum intensity measured in the central spot behind the mask in a single pixel. To even further reinforce the speckle attenuation, the KLIP and LOCI images are obtained from the averaging of several reductions with the parameters indicated above.
LOCI produces the sharpest view. A complex set of spiral patterns is detected in the southern part of the field in the region where Ardila et al. (2007) reported detecting a single spiral (see Sect. 4 for a description). We note that the range of the parallactic angle along the sequence is relatively small (17.15°), which is not particularly favorable for detecting extended objects like circumstellar disks (Milli et al. 2012).
 |
Fig. 2 A large 15′′ field of view image processed with cADI. The central 3′′ region is masked. The detected point sources are indicated with labels (B1 to B9). Pixel intensities are coded in contrast with respect to the star. |
3. Point sources
3.1. Background stars
The 15′′ field of view displayed in Fig. 2 shows many point sources, most of them (B1 to B7) already identified as background stars by Ardila et al. (2007) based on BVI photometry. A comparison of the NICI image with HST/ACS images in F606W and F814W taken six to seven years apart unambiguously confirms that HD 100546 has moved with respect to all other sources B1 to B9, as expected from its proper motion (μα = −38.9 mas/yr, μδ = 0.3 mas/yr).
3.2. Detection limits
We measured the detection limits in the closer-in region (<4′′) using fake planets injected at known positions/fluxes with respect to the central star. Twenty fake planets are distributed between 0.3′′ and 3.9′′ from the star (separated by at least 0.1′′) in the direction1 of the companion candidate reported by Quanz et al. (2013, ρ = 0.48′′, PA = 8.9°. We scanned the contrast ratio of these fake objects from 10-3 to 10-7 (sampled with 13 values) with respect to the star maximum intensity and calculated the resulting signal-to-noise ratio (S/N) of each fake planet. The signal is taken from the maximum intensity of a fake planet, while the noise is the standard deviation of pixels contained on a ring centered on the star with ±1 FWHM width and excluding the fake planet. Then, the S/N is interpolated as a function of contrast (for each fake planet’s separations) to determine the detection limit. To account for the departure from Gaussian noise in high-contrast imaging (Marois et al. 2008), which here is particularly important since the field rotation is small, we considered a seven-sigma threshold at separations closer than 1.5′′, while we keep the standard five-sigma limit farther out. These values were determined from a visual inspection of images with fake planets. The resulting detection limits are shown in Fig. 3 for cADI and LOCI and were corrected for the coronagraphic mask attenuation as explained in Boccaletti et al. (2013). There is no planet more massive than 10 MJ (10 Myr, BT-SETTL) at projected separations greater than ~60 AU (0.62′′). LOCI marginally produces a better starlight suppression than cADI in the inner 0.7′′ region, while the gain becomes significant farther out to approximately 3.5′′ (about the boundary of the stellar halo). We overlaid the expected contrast in Ks of the putative forming planet discovered by Quanz et al. (2013) with NaCo/VLT assuming a magnitude difference in Lp of 9.0 ± 0.5 mag that translates to an absolute magnitude MLp = 7.6 − 8.6 mag. We considered several evolutionary models, COND, DUSTY, and BT-SETTL (Chabrier et al. 2000; Baraffe et al. 2003; Allard et al. 2011), to convert absolute magnitudes to masses from which we derived the expected absolute magnitudes, and then the difference of magnitude in Ks (Table 2). Overall, the planet/star achieved contrast ratio ranges between 2.6 × 10-4 and 8.7 × 10-4 (Δ Ks = 7.7 − 9.0 mag) rather independently of the age. As a result, the contrast achieved in the NICI data at a separation of 0.48′′ allows a self-luminous planet more massive than 16 − 18 MJ to be ruled out according to the age and regardless of the evolutionary model. Quanz et al. (2013) suggested that if the planet is still forming the flux measured in Lp may not come entirely from its photosphere, so that we cannot expect the planet’s intensity to follow the evolutionary models. Our non-detection, as presented here, is still important for setting a lower limit, assuming no absorption, on the Ks–Lp color of 1.07 ± 0.50 mag. More observations will be required to decide about the companionship of this candidate forming planet (in particular a third epoch) and to compare its spectral energy distribution with evolutionary models.
 |
Fig. 3 Limit of detection calculated for cADI and LOCI. The red bar shows the expected position in the contrast/separation diagram of the Quanz et al. (2013) candidate planet for which the Ks contrasts are extrapolated from the Lp photometry. The contrast of a few particular masses (2, 5, and 10 MJ) provided by the BT-SETTL model are plotted for an age of 10 Myr (dashed lines). The red diamond gives the contrast of a candidate companion suspected from the NICI data and located at ρ = 0.44′′, PA = 194.1°. The top-right subpanel shows a zoom-in version of the same plot. |
Masses (in units of Jupiter mass), absolute magnitudes, and contrast in the Ks band corresponding to the candidate planet or several models (COND, DUSTY, BT-SETTL) and two ages (5 and 10 Myr), and assuming all the Lp band flux comes from the planet’s photosphere.
 |
Fig. 4 Environment of the star HD 100546 as seen in the Ks band with NICI processed with LOCI. The field is 3′′ large, and the central area (<0.39′′) is masked out numerically. |
3.3. Additional point sources of interest
Since planetary formation has presumably started inside the HD 100546 protoplanetary disk, we searched for other low-mass candidates in the field, focusing on point-like objects in the star’s proximity (<1′′). In Fig. 4 we identified two potential objects, one in the north (ρ = 0.51 ± 0.01′′, PA = 4.3 ± 0.7°) and one in the south (ρ = 0.44 ± 0.01′′, PA = 194.1 ± 0.7°). The northern one is separated by Δα = −0.036′′, Δδ = 0.037 (about two NICI pixels in both axis) from the Quanz et al. (2013) candidate. However, we checked that, given the temporal difference of about 15 months, this offset is not consistent with either the proper motion of the star or an orbital motion. Moreover, this northern candidate falls right in a region of the very bright speckles identified in raw images. Therefore, it is most likely an artifact.
The southern candidate is seen in the LOCI image but also in cADI and KLIP as a more or less extended pattern and at a lower significance. We measured a contrast (corrected from LOCI attenuation) of about 6.8 × 10-4 (ΔKs ≈ 7.9 mag) after correcting by the mask transmission, which is about 40% at this separation (due to the flat-topped Gaussian profile of the mask). It lies at about our limit of detection so, seven sigma (Fig. 3), and was not identified by Quanz et al. (2013). The current data do not allow us to conclude anything about the likelihood of this candidate, so more observations will be needed. The relationship between this candidate and the spiral pattern is discussed in the next section.
 |
Fig. 5 Southern spiral patterns in the LOCI image, with each pieces labeled (left), and the corresponding fits with a Muto et al. (2012) model calculated in the deprojected image (right). The positions of the Quanz et al. (2013) candidate forming planet and the southern point-source candidate identified in Sect. 3 are indicated by two white crosses in the deprojected image. |
 |
Fig. 6 Left: S/N map measured in the LOCI image. S4 and S6 have a higher S/N in the cADI image as seen in Fig. 1. Right: LOCI image as in Fig. 5 together with the contour of the F606W ACS image superimposed. |
4. Spiral patterns
4.1. Description
The disk around HD 100546 is a complex system with a extended nebulosity and an inner dusty and gaseous, optically thick disk (in the 13–80 AU region), including some spirals. Here, the observing mode, combined with a very small field rotation, mostly erases the low-frequency spatial structures in the disk and leaves only a set of spiral patterns in the southeastern region. We can identify six spiral structures from Fig. 1, and the cADI process, which is less aggressive than LOCI or KLIP, also shows an extended feature to the southwest (ρ = 2 ~ 3′′, PA = 200 ~ 225° from the north) with a counterpart in HST images. The most obvious features are labeled S1, S2 and S3 in Fig. 5. The sharpest view of the main spiral patterns is obtained with the LOCI image. The brightest and longest spiral, S1, starts from ρ = 1.40′′, PA = 150° to ρ = 2.27′′, PA = 190°. The equivalent projected length is about 155 AU. No pattern is detected closer in owing to the large stellar residuals. Both S1 and S2 are seen in the HST/ACS image as a single broken spiral2 but here are identified as two separate features. The inner part of S1, at a radius smaller than 1.8′′, is not seen in the HST image. S3 is similar to S1 and both are nearly parallel. Three additional patterns S4, S5, and S6 are marginally visible in the LOCI image with S5 lying in between S1 and S3, possibly on a different track. Both S4 and S6 are identified well in the cADI image in Fig. 1, while they are more attenuated by LOCI. The S/N map is shown in Fig. 6 (left) for the LOCI process where the noise is the azimuthal standard deviation for each radius. All spirals have S/N > 3, locally. This must be considered as a minimum value since the spirals themselves contribute to the azimuthal variations, and then to the noise. A comparison of NICI and HST images obtained six to seven years apart did not reveal any significant orbital motion of the spirals (Fig. 6, right). There might be a small offset of S2, but it is unrealistic to decide on a motion as long as the star positions match at the one-pixel-level precision, and the field orientation is known to be only a few tenths of a degree. All spirals appear clumpy, but it remains delicate to determine the impact of the speckle noise and the reduction process in these data, so the surface brightness inhomogeneities along the spirals might just be an artifact. We do not detect any spirals in the northern region, while S1 clearly has a centro-symmetrical counterpart in the HST data (Ardila et al. 2007) where it appears fainter and thicker. Gas observations indicate that the disk rotates counterclockwise and so the spirals would be trailing the rotation (Acke & van den Ancker 2006). If assuming that photometric asymmetries are due to forward scattering, then the southwest part is the closest to us (Ardila et al. 2007).
4.2. Spiral fitting
Determining the morphology of the spirals is of prime importance for understanding their dynamics and origins. Among the various mechanisms that can produce spirals in a protoplanetary disk containing a significant amount of gas (see Sect. 5), we considered models with gravitational perturbers where each single perturber produces a single spiral. As an important assumption, we supposed that the dust we observe in scattered light follows the distribution of the gas. The dynamical models used hereafter are applicable to face-on geometries, so the disk image must be deprojected. However, the geometrical parameters of the HD 100546 disk are poorly constrained with near-IR images providing PAnir = 161 ± 5°, inir = 51 ± 3° (Augereau et al. 2001), and visible images yielding PAvis = 145 ± 5°, ivis = 42 ± 5° (Ardila et al. 2007). These two sets of values were tested. Qualitatively, the results are similar but we present those obtained using [ PAvis, ivis ] since they provide a slightly better match between models and data.
We started to fit the traces of these spirals with Archimedean relations as suggested by the theoretical work by Kim (2011) where a planet orbits in a gaseous disk. In such a case, the radius ρ is directly proportional to the azimuth θ according to the relation ρ = aθ + b in which a = rp/ℳp, and b is a constant, with rp and ℳp the orbital distance and Mach number of the hypothetical planet launching the spiral. Each spiral (S1 to S5) was isolated with a mask in the image and a Gaussian profile is fitted at each PA (relative to the star position) along the spiral to determine its spine. This profile is not locally orthogonal to the spiral so there is a small projection effect. From the measured coordinates (ρ, θ) of these spines, we fitted the linear relation of Kim (2011) to derive the parameters (a, b). We found that the slopes (a) vary from 0.51 to 1.24 depending on spiral, so rather close to unity. S1 and S3, the more extended spirals, provide the best fits with a = −0.51 ± 0.01 and a = −1.04 ± 0.07, respectively. Interestingly, if the Archimedean spirals, except for S1, are extended inward, they lead to the central star and cross the location of the southern point-like source (ρ = 0.44′′, PA = 194.1°) identified in Sect. 3. Moreover, if they are extended outward to the northwest, they appear at larger physical separations than the northern spirals identified in HST images, which would mean that the southern and northern spirals are not connected. This simple analytical study shows morphological similarities between the different spirals and could suggest a common origin for some of them at least (perturbers).
Another mathematical framework based on spiral density wave theory is proposed by Muto et al. (2012) to also model the effect of a gravitational perturber. For a circular planet orbit, the shape of the density wave is given by ![\begin{eqnarray} \theta(r) &=& \theta_0-\frac{\text{sgn}(r-r_{\rm c})}{h_{\rm c}} \nonumber \\ &&\times \left[ \left(\frac{r}{r_{\rm c}}\right)^{1\,+\,\beta} \left\{ \frac{1}{1+\beta}-\frac{1}{1-\alpha+\beta} \left(\frac{r}{r_{\rm c}}\right)^{-\alpha} \right\} \right. \nonumber\\ && \left. -\left( \frac{1}{1+\beta} - \frac{1}{1-\alpha+\beta} \right)\right] \label{eq:muto} \end{eqnarray}](/articles/aa/full_html/2013/12/aa22365-13/aa22365-13-eq76.png) (1)with rc, θ0 the approximate planet location, and hc the disk aspect ratio at radius rc. It assumes that the disk angular frequency (Ω) and sound speed (cs) vary as power laws with the radius according to Ω ∝ r− α and cs ∝ r− β. To restrain the parameter space we set α = 1.5 assuming a Keplerian rotation, and β = 0.25 following the temperature profile (T) measured in the outer disk by Panić et al. (2012) and assuming T ∝ r− 2β. We still considered the spirals independently and fit Eq. (1) to each of them (S1 to S5). The parameters of this model are highly degenerated as indicated by Muto et al. (2012) and Grady et al. (2013). Table 3 summarizes the values of rc, θ0, and hc measured for each spiral. The fits of each spiral yield comparable values, which is to be expected from the image since all spirals nearly point in the same direction. On average, we obtained rc = 0.23 ± 0.04′′, θ0 = 230 ± 55°, and hc = 0.13 ± 0.04, where the error bars corresponds to the one-sigma dispersion of parameters taken from Table 3. Changing the initial conditions of the fit or the way the measures are performed (for instance the shape of the mask to extract each single spiral) yields more dispersion. If one or several perturbers are responsible for these spirals, the model of Muto et al. (2012) derives a physical separation of 20–30 AU, which is outside of the gap detected from interferometry data (Benisty et al. 2010). Moreover, we reached similar conclusions to those of the former model when the spirals are extended inward and outward. Interestingly, the fit to S1 appears on a different track than the other fitted spirals. Whether or not it suggests an additional perturber is difficult to conclude, especially given the important degeneracy in between parameters of this model. Finally, with the same model, we tried to fit several spirals simultaneously or to force the fit to S1 to cross the position of the potential planet reported by Quanz et al. (2013), but with no success.
(1)with rc, θ0 the approximate planet location, and hc the disk aspect ratio at radius rc. It assumes that the disk angular frequency (Ω) and sound speed (cs) vary as power laws with the radius according to Ω ∝ r− α and cs ∝ r− β. To restrain the parameter space we set α = 1.5 assuming a Keplerian rotation, and β = 0.25 following the temperature profile (T) measured in the outer disk by Panić et al. (2012) and assuming T ∝ r− 2β. We still considered the spirals independently and fit Eq. (1) to each of them (S1 to S5). The parameters of this model are highly degenerated as indicated by Muto et al. (2012) and Grady et al. (2013). Table 3 summarizes the values of rc, θ0, and hc measured for each spiral. The fits of each spiral yield comparable values, which is to be expected from the image since all spirals nearly point in the same direction. On average, we obtained rc = 0.23 ± 0.04′′, θ0 = 230 ± 55°, and hc = 0.13 ± 0.04, where the error bars corresponds to the one-sigma dispersion of parameters taken from Table 3. Changing the initial conditions of the fit or the way the measures are performed (for instance the shape of the mask to extract each single spiral) yields more dispersion. If one or several perturbers are responsible for these spirals, the model of Muto et al. (2012) derives a physical separation of 20–30 AU, which is outside of the gap detected from interferometry data (Benisty et al. 2010). Moreover, we reached similar conclusions to those of the former model when the spirals are extended inward and outward. Interestingly, the fit to S1 appears on a different track than the other fitted spirals. Whether or not it suggests an additional perturber is difficult to conclude, especially given the important degeneracy in between parameters of this model. Finally, with the same model, we tried to fit several spirals simultaneously or to force the fit to S1 to cross the position of the potential planet reported by Quanz et al. (2013), but with no success.
We note that a perturber located at ~20 AU, have a period of about 50 years as will the spiral wave, as expected from Eq. (1). In such conditions, the spiral pattern in the NICI image should feature a noticeable offset (on the order of 1′′) with respect to the HST image. Since this is not what we observe, the perturber might actually be farther away (on the order of 100 AU). This inconsistency again illustrates the degeneracies in the model. Indeed, Muto et al. (2012) and Grady et al. (2013) have shown that a family of values (rc, θ0) can match the spiral shape in a protoplanetary disk.
 |
Fig. 7 Width ratios (without/with cADI) measured on the fake spirals (left plot), and apparent width (right plot) measured on S1 (dark line with diamonds) and compared to fake spirals of different sizes (colored lines). |
4.3. Characteristics of the brightest spiral
4.3.1. Spatial extension
To investigate the morphology and photometry of the brightest spiral S1 we generated a fake spiral. We used the coordinates of the fitted Muto et al. (2012) model to the spiral S1 to obtain a trace of the fake spiral. Convolution with a two-dimensional Gaussian function produces several fake spirals of different sizes, the FWHM of which is 3.5, 7.0, 10.5, and 14.0 pixels (~65, 125, 190, 250 mas). The fake spirals, once convolved with the PSF, were implanted symmetrically in the raw data, at 180° from the real one, at a contrast of 2 × 10-6 with respect to the star.
We reprocessed the data with the cADI algorithm using an averaged combination of frames in order to preserve the photometric information better. In addition, the fake spiral is also implanted in an empty data cube (no signal, no noise), and the frames are simply derotated and stacked. This provides a reference spiral not affected by any ADI subtraction. The fake spiral is detected well in the processed image and demonstrates that the narrow range of parallactic angle quoted in Sect. 2 is not a limitation, in fact.
The resulting width was measured in a perpendicular direction with respect to the spine of the spiral. To avoid contamination by other spirals and starlight residuals, S1 was isolated in an annular mask that is ten-pixel wide (~0.18′′). The spiral profile was fitted with a one-dimensional Gaussian for each position angle (spanning 40°) and from a curvature radius located, roughly, at [ − 1.06′′;0.23′′ ] with respect to the star position. The width of fake spiral located to the northwest was measured the same way.
We first compared the resulting width of the fake spiral measured in the cADI image with respect to that in the empty data cube to assess the ADI-induced geometrical effect. Figure 7 (left) shows this width ratio as a function of radius (from the star) for several initial sizes of the spiral (3.5 to 14 pix, with 0 corresponding to the unresolved case). The width ratio features a small slope in the 1.6–2.0′′ range corresponding to a downsizing of 10% to 20% with respect to the initial width. The apparent width of the spiral S1 is plotted in Fig. 7 (right) against the separation. The net effect of ADI on the spiral width is not proportional to its width. The width profile does not decrease monotonically but has a large bump peaking at 1.85′′. Actually, this radius corresponds to the position where S5 meets S1, so that the width measurement is affected, inevitably. In addition, the spiral has a dip at about 1.65′′ which reinforces the appearance of a bump farther out. It would not be reliable with the current data to gauge the significance of these features as they might be just artifacts. Nevertheless, from the comparison with fake spirals, we can conclude that S1 is angularly resolved in the direction perpendicular to the spine since it is not coincident with the zero-pixel unresolved case (dark blue line in Fig. 7). Still, we can determine that the apparent width is about 3.5 to 7 pixels, which converts to ~6–12 AU at the distance of HD 100546.
4.3.2. Surface brightness
In the following, we considered a 3-pixel wide fake spiral to correct for the ADI photometric artifacts. The surface brightness of S1 is measured in the annular mask (ten pixels wide) as defined in the previous section. For each position along the spiral, we extracted the averaged intensity and standard deviation perpendicularly to the spiral. The same is performed on the fake spiral with and without the ADI process to calibrate for the flux losses. This correcting factor varies non linearly from about one at the inner edge of the spiral (near 1.5′′) to about two at the outer edge (near 2.2′′). In addition, the averaged intensity of the background is measured at +/–90° from the spiral and averaged. Intensities are converted to magnitude/arcsec2 (using the 2MASS star magnitude and the total flux of the observed PSF), and plotted in Fig. 8. As a result, the surface brightness of S1 features a linear decreasing with radius at a rate of ~1 mag/arcsec2/arcsec. Finally, we compared these measurements to the surface brightness obtained by Augereau et al. (2001) with HST/NICMOS at 1.6 μm in the region that encompasses the spiral S1. At the first order, and assuming a scattered light regime, the surface brightness from NICMOS is scaled to 2.2 μm using the star color (H − Ks = 0.54). As expected from ADI, the surface brightness of the spirals is less steep than that of the outer disk (which goes as r-2.9) as most of the low-frequency components in the image were certainly removed/attenuated by the ADI process. At least, the levels of intensities are consistent with this hypothesis. However, it is difficult to claim the spiral photometry to be accurate here, especially given the small amount of field rotation, but our measurement sets an order of magnitude.
4.3.3. Anisotropy
As long as the northern counterpart of the spiral is not detected, this provides a lower limit on the intensity ratio between the southeast and northwest. As a result, the scattering properties of the spiral S1 can be inferred comparing its intensity with the background. As explained in the previous section, we fitted with straight lines the surface brightness (in intensity unit rather than mag/arcsec2) of the spiral S1 (before correction by the ADI attenuation) and that of the background. The intensity ratio varies from 2.7 at the closest separation (~1.5′′) to 3.3 at the edge of the spiral (~2.2′′). We assumed PAnir = 161 ± 5°, i = 51nir ± 3° because it corresponds to the same spectral range as our data and hence traces the same dust grains. We also assumed that the brightest southwest side of the disk is the closest to us (Ardila et al. 2007). In such conditions, the major axis of the disk corresponds of 90° phase angles, while the phase angles of the minor axis are respectively 40° in the front (southwest) and 140° in the back (northeast). The spiral S1 is located in between the forefront minor and major axes and so spans a range of phase angles. To simplify the calculation, we supposed that S1 is at a median phase angle of 65°, while that of its symmetrical undetected counterpart would be at 115°. Assuming a Henyey-Greenstein phase function, we derived g, the anisotropy scattering factor, which reproduces the measured intensity ratio lower limits. We found a lower limit of 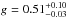 , which is higher than the anisotropy scattering factor derived from ACS observations, but our measurement is only obtained inside the spirals. At visible wavelengths, in the disk, Ardila et al. (2007) report g = 0.15 − 0.23. The two observations might not be directly comparable since we are referring to different phase angles, and our measurement is certainly affected by an uncalibrated ADI attenuation on the low-frequency components of the disk. Still, the numbers are different enough to hypothesize a modification in the scattering properties of the grains from the visible to the near IR. A higher value of g may imply larger grains. In that respect, Mulders et al. (2013a) has calculated the asymmetry parameter as a function of grain size and shows that g = 0.15 − 0.23 in the visible would correspond to particles of about 0.1 μm. But for g > 0.5, a second set of solutions exists that instead corresponds to a grain size of about 2.5 μm (at λ = 0.6 μm). Since the particle size scales linearly with wavelength, our measurement of g in the Ks band yields a particle size of about 10 μm so a hundred times larger than what is inferred from visible images, but measured in a different location. This can be consistent, qualitatively speaking, with the hypothesis that regions of higher pressure, like a spiral (precisely, where we measured g), tend to favor grain growth (Rice et al. 2006).
, which is higher than the anisotropy scattering factor derived from ACS observations, but our measurement is only obtained inside the spirals. At visible wavelengths, in the disk, Ardila et al. (2007) report g = 0.15 − 0.23. The two observations might not be directly comparable since we are referring to different phase angles, and our measurement is certainly affected by an uncalibrated ADI attenuation on the low-frequency components of the disk. Still, the numbers are different enough to hypothesize a modification in the scattering properties of the grains from the visible to the near IR. A higher value of g may imply larger grains. In that respect, Mulders et al. (2013a) has calculated the asymmetry parameter as a function of grain size and shows that g = 0.15 − 0.23 in the visible would correspond to particles of about 0.1 μm. But for g > 0.5, a second set of solutions exists that instead corresponds to a grain size of about 2.5 μm (at λ = 0.6 μm). Since the particle size scales linearly with wavelength, our measurement of g in the Ks band yields a particle size of about 10 μm so a hundred times larger than what is inferred from visible images, but measured in a different location. This can be consistent, qualitatively speaking, with the hypothesis that regions of higher pressure, like a spiral (precisely, where we measured g), tend to favor grain growth (Rice et al. 2006).
 |
Fig. 8 Surface brightness measured in Ks (red line) along S1 and corrected by the ADI attenuation (blue line). The NICMOS surface brightness is taken from Augereau et al. (2001) and scaled in intensity from H to Ks. Dotted lines correspond to the intensity dispersion, while the dashed line is measured in the background where no spiral is detected. |
4.3.4. Scale height
The fit to spirals in Sect. 4.2 yields a disk aspect ratio hc = 0.09 − 0.18. Assuming spherical particles, composed of silicates (Draine & Lee 1984), with a size distribution following a power law with –3.5 index, and radii between 1 and 1000 μm, the dust extinction coefficients can be computed using the Mie theory. Using the disk model parameters obtained by Benisty et al. (2010), one can estimate the normal optical thickness at a distance of 150 AU from the star, where the spirals start to emerge from the noise. At wavelengths between 0.4 μm and 0.8 μm, i.e. in the HST/ACS observing wavelength range, the normal optical thickness is around ~0.6. At the NICI observing wavelength (2.12 μm), this value remains almost the same. Therefore, the disk is at the limit between the optically thin/thick cases at these wavelengths and distance from the star. We then suppose that the disk is optically thick and can thus apply the ellipse-fitting method developed in Lagage et al. (2006) to measure the disk height. This method fits elliptical contours using a chi-square minimization based on a Levenberg-Marquardt algorithm. At a given radial distance of 150 AU (1.5′′) from the star, the isophote fit to Ardila et al. (2007) ACS images (and the corresponding offset between the star position and the ellipse center) implies an estimated scale height of 10 ± 12 AU. The error on the scale height is estimated from the standard deviation of the offsets in the direction along the ellipse main axis (that in principle should be formally equal to 0.0). Given this relatively large error, only an upper scale height of 22 AU at 150 AU from the star can be deduced from this measurement. This upper limit is compatible with the scale height estimated from spiral-shape fitting (h = 0.13). On the other hand, the difficulty of measuring an effective scale height may favor an optically thin case, which we consider in the next section.
5. Discussion
The multiple spirals detected with NICI around HD 100546 are remarkable because they are probably the first examples of this pattern in a transitional disk (depleted in gas compared to proto-planetary disks). However, it is beyond the scope of this paper to propose a unique explanation to account for these spirals since it will require a strong modeling effort and certainly more observations to disentangle different scenarios. Our objective in this section is simply to present some hypotheses that may eventually guide more careful theoretical works.
Any large perturbation in a disk of gas tends to launch sound waves resulting in a spiral shape due to the differential rotation of the disk. This shape is given by the rotation and sound speed profiles in the disk. Spirals tend to concentrate the solids that are loosely coupled to the gas. The coupling between gas and solids depend on the size of the solids and on the density and velocity of the gas. With a size of 0.1 μm measured in the disk of HD 100546 (Pantin et al. 2000; Ardila et al. 2007), these particles should be strongly coupled to the gas and follow the gas density structure, except for the dust situated in the low-density region, high above the disk midplane, that will tend to be more concentrated than the gas in the pressure bumps. The dust grains seen in near-IR are situated in the upper part of the disk, partially coupled to the gas, and we can consider that the observed spiral structures are also present in the gas disk. In the following we discuss some plausible scenarios, without affirming which one is the most likely, although we can exclude some.
-
Self gravity: a massive disk can be unstable against gravitationalinstability that forms large amplitude spirals in the gas. Themultiple spirals formed by this instability are also distributedaround the disk. We assume that the Toomre parameter, whichmeasures the degree of instability, can be approximated byQ ≈ (M∗/Md) × h, where M∗ and Md are the mass of the star and the disk, respectively,and h is the aspect ratio (Meru & Bate 2011).Given the mass of dust (5 × 10-4 M⊙, Benistyet al. 2010) and gas (1 × 10-3 M⊙,[en-tity!#x20!]Thi et al. 2011)reported in previous studies for the outer disk (13–350 AU) and the aspect ratio we measured in ourwork (h = 0.13), we find Q = 217 ≫ 1. We therefore reach the conclusion that the disk isnot likely to undergo gravitational instabilities as already noticedearlier by Quillen et al. (2005).However, we also note that the mass of the gas and the coolingrate are not well constrained while it is fundamental for deter-mining of the Q parameter. In particular, Panićet al. (2010) find a significant massof gas at 400 AU.
-
Warp: based on the former conclusion, Quillen (2006) propose an alternative scenario involving a planet on an inclined orbit (6 to 15°) causing surface brightness variations in the form of a two-armed spiral, provided that the outer disk is optically thin. In this framework, the spirals will be leading instead of trailing features. Quillen (2006) find that a Jovian-mass planet orbiting in the gap cannot be responsible for this warp. On the other hand, the possible planet detected by Quanz et al. (2013) would satisfy the constraint to produce a tilted warp. However, we note that the simulations presented by Quillen (2006) produce two symmetrical arms that were compliant with the HST images presented in Ardila et al. (2007) but no longer agree with the NICI data. In particular, the multiplicity of spirals is not reproduced in this model.
-
Rossby instability: if there is a pressure bump in the disk such as the one expected at the border of a planet gap, the disk can become unstable to the Rossby wave instability. This instability has the appealing effect of lifting large solid grains to the upper part of the disk, limiting the dust settling as observed in the outer disk of HD 100546 (Mulders et al. 2013a). However, the spiral density waves formed by this instability should also be distributed thoughout the gas disk.
-
External perturber/fly-by: Quillen et al. (2005) present hydrodynamic simulations that allow for the formation of spirals caused by the influence of a bound external perturber (planetary to substellar mass range) on a non-self-gravitating gaseous disk. A qualitative matching with HST images is achieved when tuning the relevant parameters (star/perturber mass ratio, disk aspect ratio, perturber eccentricity). However, they point out that no corresponding bound low-mass object is detected in any of the HST data (Augereau et al. 2001; Ardila et al. 2007). Our limit of detection clearly confirms this result, thereby improving the minimal mass from ~10 MJ (HST) to ~2 MJ (NICI) nonetheless, in a narrow field of view. In addition, Quillen et al. (2005) searched the USNO-B catalog for stellar encounters and found none. As a conclusion, if an external perturber is responsible for the spiral structures, it should be a very low-mass object like a brown dwarf that encountered the HD 100546 system a few dynamical timescales earlier.
-
Inner planetary mass perturber: a planet located inside a disk launches a set of sound waves, and owing to interference between the waves, a unique spiral forms with a large amplitude. Up to a few spirals of different amplitudes can be formed by a unique companion, but again those would be distributed throughout the disk (Kley 1999). In this paper, we modeled the spirals using two independent theories accounting for the presence of a perturber inside a gaseous disk (Kim 2011; Muto et al. 2012). Although the agreement is acceptable for each spiral individually, this exercise does not allow the origin of the multiplicity to be determined and is not accurate enough to firmly conclude on the perturber properties in a mass/separation parameter space. To explain the presence of the multiple spiral pattern in close proximity with this approach, one would have to assume the presence of multiple objects that givie rise to multiple and independent wakes. Signs of planetary mass objects have already been reported in the HD 100546 system: the presence of a gap within 13 AU (Bouwman et al. 2003), or a planet in formation at 68 AU, or for explaining the radial structure of the disk (Mulders et al. 2013b). But in this scenario, there is no connection between the spiral patterns, and the grouping of up to five spirals in the same region of the disk is unlikely.
-
Two-face spiral: assuming that the disk is marginally optically thin as hypothesized in Sect. 4.3.4, there is the interesting possibility that two observed spirals features actually correspond to the same 3D spiral wave entity. Indeed, in this case, one can detect spiral-wave scattered light from both disk sides. The projected offset (at a given distance from the star) between these two spiral emissions gives a direct measurement of the disk thickness (t = o/sini, where t is the disk thickness in AU, o the geometrical offset in AU and i the disk inclination assumed to be 42°). Applying this method to spirals features S1 and S3 (which are very similar in shape/opening angle), one gets a thickness of ~44 AU that corresponds to a disk aspect ratio of h = 0.10 − 0.15 in agreement with Sect. 4.2. Ardila et al. (2007) suggest, based on disk angularly resolved colors and asymmetry factor, that the disk frontside has a PA around 235°. In that case, and in a simple scenario, one would expect S3 to be brighter than S1 because of dust absorption. We observe the opposite. However, there is no guarantee that the spiral pattern on both disk sides have exactly the same surface brightness. This surface brightness inversion could proceed from structural inhomogeneities between the two sides.
-
Gas and planetesimals coupling: if the disk has experienced a self-gravitating phase with formation of spirals in the past, the solids preceding the formation of planetesimals are expected to migrate towards the region of higher pressure and then follow the morphology of the gaseous disk. Simulations presented in Rice et al. (2006) show that the planetesimals (and then dust) tend to concentrate in narrow multiple spirals, some as broken patterns. To some extent, these results are qualitatively in accordance with what we observed in the disk of HD 100546. Whether the solids can stay in the same spatial distribution long after the disk has stopped being self-gravitating remains to be investigated.
6. Conclusion
We have presented high-contrast images of the environment of HD 100546 obtained with NICI/Gemini. The planetary mass object detected by Quanz et al. (2013) in the Lp band, and proposed to be a planet in formation, was not detected again at shorter wavelengths in the Ks band, while the sensitivity we obtained allows ruling out objects that are more massive than 16–18 MJ. This confirms that a part of the Lp band flux does not come from the photosphere of this object. The data reach a contrast limit of ~10-5 and 10-6 at about ~1′′ and 2′′ respectively, corresponding to about five and two masses of Jupiter for the oldest age estimate of 10 Myr. We also identified a possible point-source to the south, close to the detection limit, which still needs to be followed to determine whether it is a physical object or an artifact.
More important, our data processing revealed the spiral pattern of HD 100546 with more contrast and clarity than ever before owing to the observing strategy used in NICI, and resolved this structure, formerly identified with HST in the visible, into a set of multiple spirals southeast of the star. The brightest spiral is located at 130–220 AU from the star and traceable on a projected distance of 155 AU. We attempted to fit the traces of these spirals individually, assuming that they were launched by a planet perturber in a disk of gas. For that, we used two models to derive some constraints on the perturbing bodies, but we note that these parameters are degenerate. More observations and modeling will definitely be needed to derive more quantitative information on potential perturbers and possible links between the spirals. In addition, the non-detection of the northern spiral observed in HST images is peculiar and led us to derive constraints on grain properties.
Finally, we draw several hypotheses to account for the presence of these spirals. A self-gravitating disk or the presence of a warp appears unlikely, although the amount of gas in the system is not well constrained. Gravitational perturbations by inner bodies could be the most likely scenario, but they require several perturbers. Providing the disk is optically thin, an attractive solution would be that a single spiral appears two-folded owing to the disk inclination and the reflection of the starlight on each disk surface. All these scenarios are to be worked out to identify the most likely. A modeling effort based on the various available data will be presented in a forthcoming paper. Ultimately, the origin of the spiral could be understood when the subsequent high-contrast facilities will offer higher contrasts at closer separations.
S1 and S2 are noted 3a in Fig. 7 of Ardila et al. (2007).
Acknowledgments
We would like to thank S. Fromang, S. Charnoz, P. Thébault., F. Meru, R. R. Rafikov, and R. Nelson for helpful discussions. In addition, we are grateful to the referee for providing useful comments.
References
- Acke, B., & van den Ancker, M. E. 2006, A&A, 449, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in ASP Conf. Ser. 448, eds. C. Johns-Krull, M. K. Browning, & A. A. West, 91 [Google Scholar]
- Ardila, D. R., Golimowski, D. A., Krist, J. E., et al. 2007, ApJ, 665, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Augereau, J. C., Lagrange, A. M., Mouillet, D., & Ménard, F. 2001, A&A, 365, 78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benisty, M., Tatulli, E., Menard, F., & Swain, M. R. 2010, A&A, 511, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Augereau, J. C., Lagrange, A. M., et al. 2012, A&A, 544, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Lagrange, A. M., Bonnefoy, M., Galicher, R., & Chauvin, G. 2013, A&A, 551, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 1998, ApJ, 503, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, J., de Koter, A., Dominik, C., & Waters, L. B. F. M. 2003, A&A, 401, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A. M., Dumas, C., et al. 2005, A&A, 438, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Fukagawa, M., Hayashi, M., Tamura, M., et al. 2004, ApJ, 605, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, M., van der Plas, G., van den Ancker, M., et al. 2012, A&A, 539, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Polomski, E. F., Henning, T., et al. 2001, AJ, 122, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Guimarães, M. M., Alencar, S. H. P., Corradi, W. J. B., & Vieira, S. L. A. 2006, A&A, 457, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, H. 2011, ApJ, 739, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lagage, P.-O., Doucet, C., Pantin, E., et al. 2006, Science, 314, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A. M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A.-M., Boccaletti, A., Milli, J., et al. 2012, A&A, 542, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, M. C., Wahhaj, Z., Biller, B. A., et al. 2010, Adaptive Optics Systems I, eds. B. L. Ellerbroek, M. Hart, N. Hubin, & P. L. Wizinowich, Proc. SPIE, 7736, 53 [Google Scholar]
- Lloyd, J. P., & Sivaramakrishnan, A. 2005, ApJ, 621, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Malfait, K., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 332, L25 [NASA ADS] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2008, ApJ, 673, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Meru, F., & Bate, M. R. 2011, MNRAS, 410, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Milli, J., Mouillet, D., Lagrange, A. M., et al. 2012, A&A, 545, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Min, M., Dominik, C., Debes, J. H., & Schneider, G. 2013a, A&A, 549, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Paardekooper, S.-J., Dominik, C., van Boekel, R., & Ratzka, T. 2013b, A&A, 557, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Panić, O., Ratzka, T., Mulders, G. D., et al. 2012, A&A, submitted [arXiv:1203.6265] [Google Scholar]
- Panić, O., van Dishoeck, E. F., Hogerheijde, M. R., et al. 2010, A&A, 519, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pantin, E., Waelkens, C., & Lagage, P. O. 2000, A&A, 361, L9 [NASA ADS] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2013, ApJ, 766, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C. 2006, ApJ, 640, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Varnière, P., Minchev, I., & Frank, A. 2005, AJ, 129, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2012, A&A, 546, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013, A&A, 553, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., Lodato, G., Pringle, J. E., Armitage, P. J., & Bonnell, I. A. 2006, MNRAS, 372, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., benisty, M., Menard, F., et al. 2011, A&A, 531, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W.-F., Ménard, F., Meeus, G., et al. 2011, A&A, 530, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toomey, D. W., & Ftaclas, C. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. I. Masanori, & A. F. M. Moorwood, Proc. SPIE, 4841, 889 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2011, ApJ, 729, 139 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Masses (in units of Jupiter mass), absolute magnitudes, and contrast in the Ks band corresponding to the candidate planet or several models (COND, DUSTY, BT-SETTL) and two ages (5 and 10 Myr), and assuming all the Lp band flux comes from the planet’s photosphere.
All Figures
 |
Fig. 1 Images of the environment of the star HD100546 as seen in the Ks band with NICI and with several ADI-algorithms: cADI (left), KLIP (middle), and LOCI (right). The field is 8′′ large and the central area (<1.25′′) is masked out numerically. A 2-pixel smoothing is applied. Pixel intensities are coded in contrast with respect to the star. The point source at the south corresponds to the object labeled B7 in Fig. 2. |
| In the text | |
 |
Fig. 2 A large 15′′ field of view image processed with cADI. The central 3′′ region is masked. The detected point sources are indicated with labels (B1 to B9). Pixel intensities are coded in contrast with respect to the star. |
| In the text | |
 |
Fig. 3 Limit of detection calculated for cADI and LOCI. The red bar shows the expected position in the contrast/separation diagram of the Quanz et al. (2013) candidate planet for which the Ks contrasts are extrapolated from the Lp photometry. The contrast of a few particular masses (2, 5, and 10 MJ) provided by the BT-SETTL model are plotted for an age of 10 Myr (dashed lines). The red diamond gives the contrast of a candidate companion suspected from the NICI data and located at ρ = 0.44′′, PA = 194.1°. The top-right subpanel shows a zoom-in version of the same plot. |
| In the text | |
 |
Fig. 4 Environment of the star HD 100546 as seen in the Ks band with NICI processed with LOCI. The field is 3′′ large, and the central area (<0.39′′) is masked out numerically. |
| In the text | |
 |
Fig. 5 Southern spiral patterns in the LOCI image, with each pieces labeled (left), and the corresponding fits with a Muto et al. (2012) model calculated in the deprojected image (right). The positions of the Quanz et al. (2013) candidate forming planet and the southern point-source candidate identified in Sect. 3 are indicated by two white crosses in the deprojected image. |
| In the text | |
 |
Fig. 6 Left: S/N map measured in the LOCI image. S4 and S6 have a higher S/N in the cADI image as seen in Fig. 1. Right: LOCI image as in Fig. 5 together with the contour of the F606W ACS image superimposed. |
| In the text | |
 |
Fig. 7 Width ratios (without/with cADI) measured on the fake spirals (left plot), and apparent width (right plot) measured on S1 (dark line with diamonds) and compared to fake spirals of different sizes (colored lines). |
| In the text | |
 |
Fig. 8 Surface brightness measured in Ks (red line) along S1 and corrected by the ADI attenuation (blue line). The NICMOS surface brightness is taken from Augereau et al. (2001) and scaled in intensity from H to Ks. Dotted lines correspond to the intensity dispersion, while the dashed line is measured in the background where no spiral is detected. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


