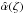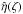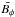| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322349 | |
| Published online | 11 December 2013 | |
Towards a hybrid dynamo model for the Milky Way
1
NORDITA, KTH Royal Institute of Technology and Stockholm
University,
Roslagstullsbacken 23,
106 91
Stockholm,
Sweden
e-mail:
gressel@kth.se
2
Leibniz-Institut für Astrophysik Potsdam (AIP),
an der Sternwarte
16, 14482
Potsdam,
Germany
Received:
23
July
2013
Accepted:
21
October
2013
Context. Based on the rapidly increasing all-sky data of Faraday rotation measures and polarised synchrotron radiation, the Milky Way’s magnetic field can now be modelled with an unprecedented level of detail and complexity.
Aims. We aim to complement this phenomenological approach with a physically motivated, quantitative dynamo model – a model that moreover allows for the evolution of the system as a whole, instead of just solving the induction equation for a fixed static disc.
Methods. Building on the framework of mean-field magnetohydrodynamics and extending it to the realm of a hybrid evolution, we performed three-dimensional global simulations of the Galactic disc. To eliminate free parameters, closure coefficients embodying the mean-field dynamo were calibrated against resolved local simulations of supernova-driven interstellar turbulence.
Results. The emerging dynamo solutions comprise a mixture of the dominant axisymmetric S0 mode with even parity, and a subdominant A0 mode with odd parity. Notably, this superposition of modes creates a strong localised vertical field on one side of the Galactic disc. Moreover, we found significant radial pitch angles that decay with radius, which can be explained by flaring of the disc. In accordance with previous work, magnetic instabilities appear to be restricted to the calmer outer Galactic disc. Their main effect is to create strong fields at large radii such that the radial scale length of the magnetic field increases from 4 kpc (for a mean-field dynamo alone) to about 10 kpc in the hybrid models – the latter being in much better agreement with observations.
Conclusions. There remain aspects (e.g., spiral arms, X-shaped halo fields, fluctuating fields) that are not captured by the current model and that will require further development towards a fully dynamical evolution. Nevertheless, we demonstrate that a hybrid modelling of the Galactic dynamo is feasible and can serve as a foundation for future efforts.
Key words: dynamo / Galaxy: disk / Galaxy: evolution / magnetic fields / magnetohydrodynamics (MHD)
© ESO, 2013
1. Introduction
The Galactic magnetic field (GMF) can now be modelled with an ever increasing level of detail (see e.g. Brown et al. 2007; Jaffe et al. 2010, 2011; Fauvet et al. 2011; Van Eck et al. 2011; Jansson & Farrar 2012a,b; Mao et al. 2012). This becomes possible with the availability of all-sky data of Faraday rotation measures (Oppermann et al. 2012) and polarised synchrotron emission obtained by space missions such as WMAP or Planck (see Fauvet et al. 2012). The typical approach uses χ2 minimisation for fitting a large number of free parameters.
Theoretical models for the GMF are largely heuristic and are guided by existing knowledge, derived from external galaxies, for example. Modelling assumptions such as the winding angle of the spiral arms and its variation with radius (and near reversals) remain under debate (see e.g. the discussion in Brown 2010). From a theoretician’s point of view, these models still provide a convenient link to observations and can serve as a benchmark for dynamo models in the framework of mean-field magnetohydrodynamics (MHD; Beck et al. 1996; Brandenburg et al. 2012b). Despite the success of the heuristic description, a thorough understanding of the underlying field amplification mechanism appears desirable.
Different flavours of mean-field models have been studied for typical galaxies, but under many simplifying assumptions. Concerning models specifically designed for the GMF, the most prominent difference of the Milky Way magnetic field in comparison with external galaxies is the reversal of the mean magnetic field in the radial direction. Whereas observationally now well-supported for our own Galaxy (see e.g. the discussion in Kronberg & Newton-McGee 2011), such a reversal has never yet been observed in other galaxies1. Mean-field models allow such field reversals in principle, depending on the seeding of the dynamo process (Moss & Sokoloff 2012). Alternative explanations include oscillating solutions due to a vertical dependence of differential rotation (Ferrière & Schmitt 2000) or, as we propose here, a vertical undulation of the Galactic midplane combined with an antisymmetric vertical parity of the disc field, which leads to apparent reversals. Yet another possibility, investigated here for the first time, is the mode interface between the dynamo-dominated inner region and the instability-dominated outer region of the Galaxy.
Another peculiarity of the GMF is the relatively small pitch angle (≲10°) compared to many other galaxies with similarly strong differential rotation and pitch angles of up to ~45° as are observed in M94 and M33, for instance (Chyży & Buta 2008; Tabatabaei et al. 2008). This dominance of the azimuthal field appears to agree better with mean-field models than with the large pitch angles observed in external galaxies. The magnetic field of mean-field dynamos is typically a stationary axisymmetric quadrupole. But for some cases such as weak differential rotation or cases where the halo is included in the dynamo process, dipolar and/or oscillatory solutions may occur (Elstner et al. 1992; Brandenburg et al. 1992; Moss et al. 2010). The flaring of the Galactic disc was usually ignored in the modelling, but has been considered in some recent publications (Moss et al. 2013; Chamandy et al. 2013a,b). This is despite observations seem to favour a non-flaring disc, at least in HII – see Lazio & Cordes (1998), and the discussion in Moss et al. (2013). Our own model is guided by more recent observations (Kalberla & Dedes 2008) of the HI distribution, which is indeed found to be flared.
A notable exception to dynamo models with constant scale height is the work by Poezd et al. (1993), who assumed a flared gas distribution and applied mean-field models in the thin-disc approximation to the Milky Way, relying on an observed rotation curve, and estimates for disc height, turbulent velocity, correlation length, and gas density. They derived radial profiles of the final magnetic field for regular and chaotic seed fields with α quenching due to magnetic helicity. The maximum field strength of the regular field appeared at about 6 kpc. For a strong enough seed field (0.001 to 0.1 μG) they found reversals.
While these models have provided us with a wealth of qualitative understanding of the expected mode structure that appears in αΩ-type disc dynamos, they lack a rigorous foundation for the actual amplitude and spatial distribution of the imposed mean-field effects. Recently, a quantitative measurement of the transport coefficients has become possible by applying the so-called test-field (TF) method (Schrinner et al. 2005) to realistic local simulations of interstellar turbulence (Gressel et al. 2008b). This also includes the determination of quenching functions (Gressel et al. 2013), which are required to evolve the mean-field models into the saturated regime. Based on this previous work, we here present a quantitative mean-field dynamo model. By doing so, we aim to provide a comprehensive description of the GMF that is supported by observable properties of the Galaxy.
An additional improvement over existing work is the combined evolution of the induction and momentum equations. While there exist global 3D MHD simulations of galactic gaseous discs (e.g. Dziourkevitch et al. 2004; Hanasz et al. 2009; Kulpa-Dybeł et al. 2011; Machida et al. 2013), these simulations typically do not account for the effects caused by the vigorous supernova turbulence on scales unresolved on the global mesh. On the other hand, in classical mean-field models, the velocity field is kept fixed at its initially prescribed state. In contrast to this, including the momentum equation allows the underlying disc model to evolve in time. At the same time, solving the full MHD equations (subject to parametrised enhanced dissipation) permits the emergence of magnetic instabilities such as the magnetorotational instability (MRI) and buoyancy instabilities.
Clearly, our model still lacks important aspects of the evolution of the Galactic disc: it currently ignores a self-consistent prescription, for example, of self-regulatory star formation (SF), formation of spiral arms via self-gravity, emergence of a Galactic wind driven by a cosmic-ray (CR) component, or the multi-phase nature of the interstellar medium (ISM). Nevertheless, the presented framework can be regarded as a first step towards less “static” dynamo models.
2. Methods
As outlined above, we aim to derive a quantitative model for the Galactic dynamo that is
based, as directly as possible, on observable quantities. Instead of solving the induction
equation with a given stationary velocity field, 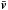 ,
we perform simulations of the full mean-field MHD equations
,
we perform simulations of the full mean-field MHD equations 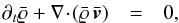 (1)
(1)![\begin{eqnarray} \label{eq:mom} \partial_t(\mrho\,\V) +\nabla\cdot \left[\;\mrho\,\V\,\V+\bar{p}^{\star}I-\B\B \;\right] & = & - \mrho\,\nabla\Phi + \nabla\cdt\visfl, \end{eqnarray}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq14.png) (2)
(2)![\begin{eqnarray} \label{eq:ind} \partial_t \B - \nabla \times \left[\;\V\tms\B + \EMF - \etat \nabla\tms\B \;\right] & = & 0, \end{eqnarray}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq15.png) (3)where
the viscous stress tensor is given by
(3)where
the viscous stress tensor is given by ![\hbox{$\visfl = \mrho\,\vist \, [\nabla\V + (\nabla\V)^{\top} -2/3\,(\nabla\cdt\V)\,I ]$}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq16.png) with kinematic viscosity νt, and
with kinematic viscosity νt, and
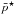 denotes the total pressure
denotes the total pressure 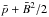 .
As made explicit by writing vertical bars over the constituent variables, Eqs. (1)−(3) are mean-field equations governing the evolution of large-scale
quantities. We emphasise that the given set of equations still neglects a number of
additional “micro-physics” that will be important to consider in the future (see Sect. 2.2.1 for a discussion). As justified by the immense
Reynolds numbers within the ISM, we furthermore ignored contributions to the dissipation
coefficients stemming from molecular effects. In this sense, ηt
and νt represent the turbulent diffusivity and kinematic
viscosity, respectively. Induction effects stemming from unresolved scales are included in
Eq. (3) in the form of a mean electromotive
force,
.
As made explicit by writing vertical bars over the constituent variables, Eqs. (1)−(3) are mean-field equations governing the evolution of large-scale
quantities. We emphasise that the given set of equations still neglects a number of
additional “micro-physics” that will be important to consider in the future (see Sect. 2.2.1 for a discussion). As justified by the immense
Reynolds numbers within the ISM, we furthermore ignored contributions to the dissipation
coefficients stemming from molecular effects. In this sense, ηt
and νt represent the turbulent diffusivity and kinematic
viscosity, respectively. Induction effects stemming from unresolved scales are included in
Eq. (3) in the form of a mean electromotive
force, 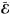 ,
which we specify in Sect. 2.2.2. We modified the
publicly available nirvana-iii code (Ziegler
2004, 2011) to include this additional EMF
and have verified our implementation against the benchmark described in Jouve et al. (2008).
,
which we specify in Sect. 2.2.2. We modified the
publicly available nirvana-iii code (Ziegler
2004, 2011) to include this additional EMF
and have verified our implementation against the benchmark described in Jouve et al. (2008).
For the simulations presented here, we chose a domain size of r ∈ [1.5,21.5] kpc, θ ∈ [0.415,0.585] π, and φ ∈ [0,2] π. Note that, owing to the use of polar coordinates, the central region of the disc is excluded for reasons of computational expedience. We typically employed a resolution of 256 × 48 × 64 grid points in the radial, latitudinal, and azimuthal directions, respectively. For the static 2D simulations, we also checked convergence when increasing the resolution to 512 × 96 grid points. For the fully dynamic 3D simulations we ran simulations up to 384 × 72 × 96. The hydrodynamic boundary conditions (BCs) are of the standard outflow type; as an example, for the lower θ boundary this implies setting ∂θvθ = 0 if vθ < 0, and enforcing vθ = 0 otherwise. We furthermore solved for hydrostatic/dynamic balance in the vertical and radial directions, respectively, and imposed the equilibrium rotation profile at the inner radial boundary. For the magnetic field we employed both pseudo-vacuum (i.e., B∥ = E⊥ = 0) and perfect-conductor (B⊥ = E∥ = 0) boundary conditions. We moreover imposed the initial net-vertical field on the boundaries, if present.
In the following, we begin our formulation by specifying a complete disc model. We then prescribe turbulent closure coefficients subsuming effects due to the turbulence driven by supernovae (SNe).
2.1. Equilibrium-disc model
The initial density profile and rotation curve were constructed to be in a stationary hydrodynamic equilibrium with a given gravitational potential, consisting of a standard Navarro, Frenk, & White (NFW) dark-matter halo, a component due to a stellar disc (Miyamoto & Nagai 1975), and a central bulge. We chose these simplified prescriptions because they are commonly used for fitting observational data, allowing a reasonable constraint of the shape parameters. For simplicity, we ignored the contributions from the central bar and the self-gravity of the gaseous disc.
2.1.1. External gravity
The gravitational potential due to the Galactic dark-matter halo can be approximated by
(Navarro et al. 1997)
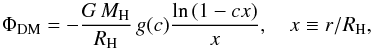 (4)with
r the spherical radius, g(c) the
NFW shape function, and where we have chosen a concentration parameter of
c = 13, and RH = 213 kpc, and
MH = 1012 M⊙ are
the assumed virial radius and the virial mass of the Milky Way dark-matter halo (cf.
Xue et al. 2008), respectively. For the stellar
disc, we assumed a parametrisation according to Miyamoto
& Nagai (1975), with
(4)with
r the spherical radius, g(c) the
NFW shape function, and where we have chosen a concentration parameter of
c = 13, and RH = 213 kpc, and
MH = 1012 M⊙ are
the assumed virial radius and the virial mass of the Milky Way dark-matter halo (cf.
Xue et al. 2008), respectively. For the stellar
disc, we assumed a parametrisation according to Miyamoto
& Nagai (1975), with ![\begin{equation} \Phi_{\rm \star} = \frac{G\,M_{\star}} {\sqrt{R^2+\left[a+\sqrt{z^2+b^2}\right]^2}}, \label{eq:MiyNag} \end{equation}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq41.png) (5)where
R ≡ r sin(θ) is now the
cylindrical radius and z ≡ r cos(θ)
is the vertical coordinate. We adopted a total mass of
Mdisc = 7 × 1010 M⊙
and shape parameters a = 3.5 kpc and b = 0.18 kpc
in accordance with the potential used in our local-box simulations situated at
R = 8.5 kpc (cf. Gressel et al.
2008b). For a simplified representation of the Galactic bulge (Flynn et al. 1996) with an assumed mass
Mbulge = 1.6 × 1010 M⊙,
we again used expression (5), but now
with a = 0 kpc and b = 0.42 kpc, resulting in a
spherically symmetric potential. Ignoring the self-gravity of the gas, the effective
gravitational potential we used is given by
Φ(R,z) ≡ ΦDM + Φdisc + Φbulge.
(5)where
R ≡ r sin(θ) is now the
cylindrical radius and z ≡ r cos(θ)
is the vertical coordinate. We adopted a total mass of
Mdisc = 7 × 1010 M⊙
and shape parameters a = 3.5 kpc and b = 0.18 kpc
in accordance with the potential used in our local-box simulations situated at
R = 8.5 kpc (cf. Gressel et al.
2008b). For a simplified representation of the Galactic bulge (Flynn et al. 1996) with an assumed mass
Mbulge = 1.6 × 1010 M⊙,
we again used expression (5), but now
with a = 0 kpc and b = 0.42 kpc, resulting in a
spherically symmetric potential. Ignoring the self-gravity of the gas, the effective
gravitational potential we used is given by
Φ(R,z) ≡ ΦDM + Φdisc + Φbulge.
2.1.2. Disc model and rotation curve
Our hydrodynamic model is based on the flaring HI disc of the Milky Way, which has
recently been constrained observationally by Kalberla
& Dedes (2008). Improving their simple exponential fit for the radial
profile of the surface density, we propose a split profile with a radial break,
yielding2![\begin{equation} \mrho(R,z) = \mrho(R_{\rm br},0)\;{\rm e}^{-\Phi_z/c_{\rm s}^2}\;\times\; \begin{cases} \;\exp ( -\frac{R-R_{\rm br}}{R_{\rm exp}} ) & \text{for }R<R_{\rm br} \\[4pt] \;\left(\frac{R}{R_{\rm br}}\right)^p & \text{for }R\ge R_{\rm br} \end{cases} \label{eq:rho_mid} \end{equation}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq52.png) (6)for
the initial density distribution in hydrostatic equilibrium. Here the vertical disc
structure is given by
(6)for
the initial density distribution in hydrostatic equilibrium. Here the vertical disc
structure is given by 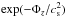 , that is, by setting the
thermal pressure in balance with the function
, that is, by setting the
thermal pressure in balance with the function
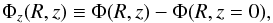 (7)expressing the vertical
potential difference (cf. Wang et al. 2010).
Furthermore, the reference density
(7)expressing the vertical
potential difference (cf. Wang et al. 2010).
Furthermore, the reference density 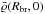 is specified at the break radius Rbr = 13 kpc, and we used
Rexp = 4 kpc, which is somewhat less steep than the
3.75 kpc proposed by Kalberla & Dedes.
For our fiducial model, we chose an exponent p = −6.5, and we note
that the power-law closely reproduces the upward curvature seen in Figs. 3−6 of Kalberla & Dedes (2008), which cannot be
matched by a single exponential. The disc surface density of our model is shown in Fig.
1, where we also plot the flaring scale height,
h(R), of the disc. The flaring of the disc is
controlled by prescribing a radial temperature profile such that
is specified at the break radius Rbr = 13 kpc, and we used
Rexp = 4 kpc, which is somewhat less steep than the
3.75 kpc proposed by Kalberla & Dedes.
For our fiducial model, we chose an exponent p = −6.5, and we note
that the power-law closely reproduces the upward curvature seen in Figs. 3−6 of Kalberla & Dedes (2008), which cannot be
matched by a single exponential. The disc surface density of our model is shown in Fig.
1, where we also plot the flaring scale height,
h(R), of the disc. The flaring of the disc is
controlled by prescribing a radial temperature profile such that
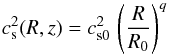 (8)is
a power-law function of R. To be more specific, a value
q = −1 would produce a disc with constant opening angle, whereas
q ≃ 0 would lead to a globally isothermal, flaring disc. Limited by
numerical feasibility, we here chose q = −0.5 and
h/R = 0.15 (at
R0 = 10 kpc), which leads to a more inflated disc (see
inset Fig. 1), but still provides a reasonable fit
to the observed h(R) – also cf. Fig. 7 in Kalberla & Dedes (2008). A discussion of the
effect of a radially non-uniform scale height on the dynamo can be found in Sect. VII.6
of Ruzmaikin et al. (1988).
(8)is
a power-law function of R. To be more specific, a value
q = −1 would produce a disc with constant opening angle, whereas
q ≃ 0 would lead to a globally isothermal, flaring disc. Limited by
numerical feasibility, we here chose q = −0.5 and
h/R = 0.15 (at
R0 = 10 kpc), which leads to a more inflated disc (see
inset Fig. 1), but still provides a reasonable fit
to the observed h(R) – also cf. Fig. 7 in Kalberla & Dedes (2008). A discussion of the
effect of a radially non-uniform scale height on the dynamo can be found in Sect. VII.6
of Ruzmaikin et al. (1988).
 |
Fig. 1 Midplane rotation curve (dotted line = 220 km s-1) and disc surface density. The inset shows the flaring scale-height of the HI gas disc. Dashed lines indicate observational approximations suggested by Kalberla & Dedes (2008). |
The functional form of (6) is not
differentiable at Rbr, which implies a slight jump in the
azimuthal velocity, which we derive as 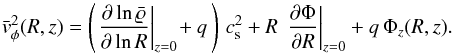 (9)For
q ≠ 0, the last term will lead to a vertical variation of the rotation
profile. Because the prescribed gravitational potential has been designed as a fit to
the Galactic rotation curve, it suffices to say that Eq. (9) reproduces the classical Brandt-type curve with a plateau at
(9)For
q ≠ 0, the last term will lead to a vertical variation of the rotation
profile. Because the prescribed gravitational potential has been designed as a fit to
the Galactic rotation curve, it suffices to say that Eq. (9) reproduces the classical Brandt-type curve with a plateau at
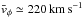 ,
as also shown in Fig. 1, where we plot the rotation
curve in the disc midplane. This completes the description of our hydrodynamic disc
model. We verified that the inviscid model can be evolved stably for times exceeding the
age of the universe. When including turbulent viscosity, the disc evolves viscously on a
secular time scale.
,
as also shown in Fig. 1, where we plot the rotation
curve in the disc midplane. This completes the description of our hydrodynamic disc
model. We verified that the inviscid model can be evolved stably for times exceeding the
age of the universe. When including turbulent viscosity, the disc evolves viscously on a
secular time scale.
2.2. Turbulent closure parameters
Using a mean-field approach, we aimed to simulate the common evolution of the regular magnetic field and the large-scale flow of the Galactic gas disc. Conceptually, this implies that we solve the full MHD equations subject to turbulent transport coefficients, that is, we prescribe a turbulent diffusivity in the induction equation along with a corresponding turbulent viscosity in the momentum equation. These turbulent dissipation coefficients, as well as the prescribed α effect (see Sect. 2.2.2), were derived from a series of resolved direct numerical simulations (DNS). The basic setup, which assumes a local-box geometry and uses realistic driving of interstellar turbulence via injection of localised supernova explosions, is described in detail in Gressel (2009). Scaling relations for mean-field effects were derived from a set of models with box size 0.8 kpc × 0.8 kpc × ± 2.1 kpc, and more accurate vertical shapes were obtained using a larger 1.6 kpc × 1.6 kpc × ± 6.4 kpc domain (Gressel et al. 2011). The requirement to resolve individual explosions demands grid resolutions below 10 pc, which is met in the box simulations, but will remain unaffordable in global simulations for some time.
Since in the DNS we only measure ηt, but not νt, we had to assume a turbulent magnetic Prandtl number, Pmt = νt/ηt of unity. This assumption is backed by recent numerical investigations that found very little deviation from this value (Guan & Gammie 2009; Fromang & Stone 2009). Note that unlike for a classical α viscosity, we prescribed νt(R,z) directly as a function of space, that is, independent of the gas pressure. This is because (for consistency with the mean induction equation) we assumed the turbulent velocity field to be given a priori as a consequence of the underlying SNe distribution. To avoid restrictive time-step constraints arising from high values of the diffusion coefficients, we implemented the super-time-stepping scheme, introduced by Alexiades, Amiez, & Gremaud (1996), for the viscous and diffusive updates.
 |
Fig. 2 Vertical profiles of TF coefficients
αφφ (left),
γz (centre), and
ηt (right panel) measured from DNS
(light colours); shaded areas indicate 1σ fluctuations. Black
curves show model profiles |
2.2.1. Neglected effects
Turbulent viscosity is by no means the only mean-field effect in the momentum equation but, in fact, is a crude oversimplification. For reasons of tractability, we had to ignore more involved contributions, however, such as the turbulent kinetic pressure or the turbulent contribution to the Lorentz force in our current considerations. A rudimentary attempt to allow the former effect to self-consistently launch a Galactic wind (driven by the gradient in the turbulence intensity) led to unacceptable mass-loss rates. This is because in our mean-field model, the single-phase density field cannot properly capture the multi-phase nature of the ISM: ultimately, what we described as a wind really is a fountain flow, that is, tenuous gas being blown out of the Galaxy, while high-density clumps raining down compensate the overall mass balance. Ultimately, it will be of great interest to study related effects. We speculate that the suppression of the turbulent magnetic pressure by mean fields (Kleeorin et al. 1989; Brandenburg et al. 2012a) may also be of importance in a Galactic context, potentially leading to an increased heterogeneity of the observed field (but see also Fletcher et al. 2009).
To be able to use periodic boundary conditions, an important simplification of our local box simulations was to ignore any large-scale radial structure, for example, in the gas density or supernova rate. Even though we were able to vary quantities like the midplane density, rotation rate, or shearing rate for each of the individual runs (i.e. to adjust to the situation at different locations within the Galaxy), we could not obtain contributions in the dynamo tensor due to radial gradients.
2.2.2. Dynamo tensor
We here focus on a well-studied effect appearing in the mean induction equation, that
is, the turbulent electromotive force 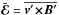 ,
where primes denote fluctuating quantities. We implemented this term by means of the
classic tensor prescription
,
where primes denote fluctuating quantities. We implemented this term by means of the
classic tensor prescription ![\begin{equation} \EMF_i = \alpha_{ij}\,\bar{B}_j\, \qquad i,j\,\in\left[r,\theta,\phi\right] , \end{equation}](/articles/aa/full_html/2013/12/aa22349-13/aa22349-13-eq86.png) (10)that is, with an
α tensor locally relating the mean EMF to the mean magnetic field. We
argue that the good quantitative agreement between DNS and 1D mean-field simulations
(Gressel 2009) warrants the neglect of
non-local (Brandenburg et al. 2008) as well as
non-instantaneous (Hubbard & Brandenburg
2009) contributions to the closure. As laid out below,
αij is parametrised according to
coefficients measured within a comprehensive set of DNS of SN-driven ISM turbulence by
means of the TF method (Schrinner et al. 2005,
2007).
(10)that is, with an
α tensor locally relating the mean EMF to the mean magnetic field. We
argue that the good quantitative agreement between DNS and 1D mean-field simulations
(Gressel 2009) warrants the neglect of
non-local (Brandenburg et al. 2008) as well as
non-instantaneous (Hubbard & Brandenburg
2009) contributions to the closure. As laid out below,
αij is parametrised according to
coefficients measured within a comprehensive set of DNS of SN-driven ISM turbulence by
means of the TF method (Schrinner et al. 2005,
2007).
Because of our flaring disc model and for reasons of simplicity, we identified the x, y, and z direction in these local Cartesian box simulations (Gressel et al. 2008a, 2009) with spherical polar coordinates r, φ (azimuth), and θ (co-latitude), respectively. To reflect the geometry of the disc, shape functions were defined with respect to a flaring coordinate ζ ≡ z/h(r) such as to follow the local scale-height of the HI gas disc. At a spherical radius, r, the latitudinal variation was approximated by the profiles shown in Fig. 2. In accordance with our box model, the aspect ratio, h(R)/R, for the vertical profiles of the dynamo tensor is about a factor of two larger than that for the HI disc shown in the inset of Fig. 2, resulting in a scale height of ~1 kpc at R ≃ 10 kpc.
Scaling exponents for the dynamo α tensor, the turbulent
diffusivity and viscosity, and vertical fountain flow,
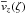 .
.
The tensor components
αrr ≃ αφφ ≃ 5 αθθ,
and
αrφ ≃ −αφr,
which we directly measured in the DNS, were parametrised according to their inferred
dependence on the supernova rate
σ/σ0, rotation rate
Ω/Ω0, and disc midplane density
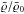 .
To additionally reduce the number of free parameters, we identified
σ/σ0 with the star
formation rate and linked it to the local surface density by means of a
Kennicutt-Schmidt law
.
To additionally reduce the number of free parameters, we identified
σ/σ0 with the star
formation rate and linked it to the local surface density by means of a
Kennicutt-Schmidt law 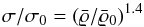 (11)(Kennicutt 1998). Scaling exponents are listed for
reference in Table 1. For reasons of
completeness, we include the radial and vertical diagonal elements of the tensor, even
though we found these terms to be negligible compared to the αΩ
mechanism driven via3αφφ.
(11)(Kennicutt 1998). Scaling exponents are listed for
reference in Table 1. For reasons of
completeness, we include the radial and vertical diagonal elements of the tensor, even
though we found these terms to be negligible compared to the αΩ
mechanism driven via3αφφ.
Another important result from our local simulations was the existence of a vertical
fountain flow, 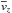 , which was
discerned to balance the effect of the turbulent pumping. The vertical profile
, which was
discerned to balance the effect of the turbulent pumping. The vertical profile
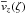 we adopted in our
mean-field prescription consists of two parts: a contribution linear in
ζ, and a characteristic modulation (cf. Fig. 2 in Gressel et al. 2009), that roughly coincides with
αrφ(ζ). It is important
to note that the mean flow
we adopted in our
mean-field prescription consists of two parts: a contribution linear in
ζ, and a characteristic modulation (cf. Fig. 2 in Gressel et al. 2009), that roughly coincides with
αrφ(ζ). It is important
to note that the mean flow 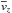 – for reasons
discussed in Sect. 2.2.1 – only contributes to the
induction equation, but is not included in the momentum equation.
– for reasons
discussed in Sect. 2.2.1 – only contributes to the
induction equation, but is not included in the momentum equation.
2.2.3. Quenching functions
Avoiding a more complex description relating to the (approximate) conservation of
magnetic helicity (see e.g. discussion in Moss &
Sokoloff 2011), we here resorted to a simple algebraic expression for the
α quenching as justified by our recent analysis (Gressel et al. 2013). Unlike in many previous
studies, we explicitly included a quenching for the ηt (and
νt) coefficient (see also Yousef et al. 2003). Adopting an isotropic quenching for the
α tensor, we used 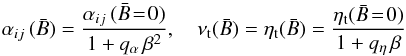 (12)with
(12)with
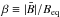 ,
and coefficients qα = 10, and
qη = 5 approximating the results from
direct simulations (Gressel et al. 2013). Because
of the close correspondence of αrφ and the
characteristic modulation seen in the mean flow (cf. Fig. 3b in Gressel et al. 2013), we chose to apply quenching only to the
modulation in
,
and coefficients qα = 10, and
qη = 5 approximating the results from
direct simulations (Gressel et al. 2013). Because
of the close correspondence of αrφ and the
characteristic modulation seen in the mean flow (cf. Fig. 3b in Gressel et al. 2013), we chose to apply quenching only to the
modulation in 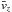 and left the underlying linear profile unquenched.
and left the underlying linear profile unquenched.
For consistency, we moreover computed the equipartition field strength
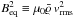 from a turbulent
velocity profile vrms(ζ) that was itself
derived from the (unquenched) ηt(ζ)
profile, assuming the classical relation
from a turbulent
velocity profile vrms(ζ) that was itself
derived from the (unquenched) ηt(ζ)
profile, assuming the classical relation 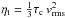 , and where we
have used a constant τc = 3.5 Myr in consistence with DNS.
, and where we
have used a constant τc = 3.5 Myr in consistence with DNS.
It is essential that the α effect and the turbulent diffusion are
quenched differently. This becomes obvious by evaluating
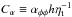 ,
and
,
and 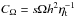 (with s ≡ d lnΩ/d lnr).
Curiously, the resulting dynamo number
D ≡ CαCΩ
is asymptotically independent of
(with s ≡ d lnΩ/d lnr).
Curiously, the resulting dynamo number
D ≡ CαCΩ
is asymptotically independent of 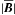 . In
practice, however, we have
qα > qη,
which implies that α is quenched earlier. Estimating
. In
practice, however, we have
qα > qη,
which implies that α is quenched earlier. Estimating
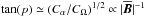 ,
we see that a quenched αΩ dynamo is dominated by differential rotation,
leading to a vanishing radial pitch angle. The loss of pitch angle in the saturated
state can be circumvented if the dynamo is saturated at high
Cα – for instance, via the vertical
wind (see Elstner et al. 2009).
,
we see that a quenched αΩ dynamo is dominated by differential rotation,
leading to a vanishing radial pitch angle. The loss of pitch angle in the saturated
state can be circumvented if the dynamo is saturated at high
Cα – for instance, via the vertical
wind (see Elstner et al. 2009).
3. Results
In the following, we present results from a comprehensive suite of simulations. After we have attempted to eliminate as many free parameters from our model as possible, there remain only two major aspects that require testing: (i) the disc mass, which represents the central input parameter governing the SF rate; and (ii) the initial topology of the magnetic field. Moreover, we aim to study non-axisymmetric modes, and whether the inclusion of the Navier-Stokes (NS) equation has an effect on the evolution of the Galaxy as a whole. In particular, we are interested in whether the MRI or convective instabilities can emerge on scales long enough not to be immediately affected by turbulent diffusion.
 |
Fig. 3 Saturated regular magnetic field for model X1s-0.5; colour-coded toroidal field,
|
A compilation of the main results can be found in Table 2, where we also list the input parameters of our setup. Models labelled “s” are what we refer to as static, which means that the density and velocity field were kept fixed during the evolution of the model. This is commonly assumed for the kinematic dynamo problem, albeit one of course includes a back-reaction of the field to obtain saturation of the dynamo. For some of the 3D models, we furthermore evolved the full MHD equations including the density and velocity field; these simulations are labelled “d” for dynamic. For our fiducial axisymmetric (“X”) model X1s, we varied the disc mass in steps of 0.5 times the fiducial mass of 1.14 × 1010 M⊙ (see first four rows of Table 2). With models X2s-halo and X3s-VF, we studied the influence of a halo dynamo and vertical-field seeding, respectively. The fiducial non-axisymmetric (“N”) models N1s and N1d probed the effects of various seed-field geometries. With the exception of the two models N2d-noD (without any α effect, but including turbulent diffusion) and N2d-MRI (without any prescribed turbulence effects), all simulations include mean-field (MF) effects as described in Sect. 2.2 above. Generally, the MF dynamo remains dominant for these models, but subtle differences arise, for example, due to the long-term evolution of the density distribution, which indirectly enters the MF prescription.
Simulation parameters and results.
To be as unrestrictive as possible on the emerging dynamo mode, we generally applied a white-noise (WN) initial field, resulting in approximately equal amounts of energy in all permissive modes. Moreover, for the 2D models, we alternatively applied a net-vertical field (VF), which might be hypothesised as a plausible seed topology. Finally, in the 3D case, it furthermore becomes possible to test a configuration with an initially horizontal field (HF); even though this topology is generally found to be impractical because of the winding-up effect of the differential rotation (Moss & Sokoloff 2012).
3.1. Vertical parity and growth rates
In agreement with many previous studies (see e.g. Beck et al. 1996), we found the axisymmetric (i.e., m = 0, hence “0”) mode with symmetric vertical parity (“S”) to be the fastest-growing dynamo mode (see column 8 in Table 2). Notably, in the low-density part of the disc (beyond R ≃ 10 kpc), a weak anti-symmetric (“A”) mode emerges. This is illustrated in Fig. 3, which shows the saturated magnetic field for model X1s-0.5 (with lower disc mass), where the A0 mode is seen to be most pronounced. Possible reasons for this may be a combination of pumping and wind, as well as the disc flaring. In most models, the A0 contribution remains subdominant, but appears during a transitional phase in the case of a vertical-field initial condition (e.g. model X3s-VF). Note that the mixed S0+A0 leads to a radially confined, strong vertical field on only one side of the Galactic disc. This is consistent with radio observations of extragalactic Faraday rotation at high Galactic latitude by Mao et al. (2010), who found a vertical field consistent with (0.00 ± 0.02) μG towards the north, and (0.31 ± 0.03) μG towards the south Galactic pole, respectively.
Exponential growth times of the mean-field dynamo are presented in Col. 11 of Table 2. Generally, we found τe to be of the order of half a Gyr, which is sufficient to explain the present-day field strength of the Galaxy based on reasonable assumptions on the initial seed field. Neronov & Vovk (2010) estimated from Fermi observations a lower bound of 3 × 10-16 G for the intergalactic field on Mpc scales. A possible explanation of the generation process was recently given by Schlickeiser (2012). The formation of the protogalaxy leads to a further amplification to 3 × 10-12 G (Lesch & Chiba 1995), such that after ~7 Gyr the dynamo has reached its equipartition field strength of several μG. Prior to the epoch of star formation, the MRI may grow unhindered by turbulence from SNe and hence serve as a seed-field mechanism, as suggested by Kitchatinov & Rüdiger (2004).
For the fiducial model X1s, we found a trend to faster growth for lighter-disc models. This is presumably due to the reduced turbulent diffusivity at lower SF activity. For lighter disc models we also expect the wind to dominate the vertical pumping, resulting in weaker saturated fields and larger magnetic pitch angles. The fastest growth of τe = 0.358 Gyr was found in model X2s-halo, including a non-zero α effect at high Galactic latitude (cf. dashed line in Fig. 2). Compared with the standard model X1s, which is seeded from white noise, model X3s-VF with a vertical-field initial condition shows a slightly slower growth rate of τe = 0.539, which can be identified with the A0 eigenmode. Faster growth can be obtained if one starts with the S0 mode directly – cf. model N1s-VF, where a combined vertical and azimuthal field is applied.
3.2. Radial structure
The amount of quantitative information that can be confidently extracted from radio observations of the Milky Way or nearby galaxies is very limited. In particular, reliable positional information is restricted to considering the radial variation of azimuthally and vertically averaged quantities. In the interest of direct quantitative comparison with observations, we here discuss the magnetic field strength and its inclination with respect to the toroidal direction.
3.2.1. Magnetic pitch angle
One major observable derived from radio polarisation maps is the radial pitch angle,
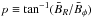 of the mean magnetic field. Because values of
of the mean magnetic field. Because values of 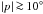 are hard to
explain in the presence of differential rotation alone, large pitch angles are generally
interpreted as the hallmark of an α-effect dynamo. Our models generally
show moderately large pitch angles close to −10° (see Col. 9 of Table 2) in the inner region of the Galactic disc, that is,
where the magnetic energy is highest. The models N1d-HF/VF, including evolution of the
disc, show somewhat reduced pitch angles. This may be related to the long-term viscous
evolution of the radial gas density profile, which reduces the SF rate that enters our
dynamo prescription, and hence the strength of the MF dynamo near the Galactic centre.
It is interesting to note that we did not see a significant change of pitch angle during
the simulation – implying a saturation at high
Cα, most likely caused by the action of
the vertical fountain flow (cf. Elstner et al.
2009).
are hard to
explain in the presence of differential rotation alone, large pitch angles are generally
interpreted as the hallmark of an α-effect dynamo. Our models generally
show moderately large pitch angles close to −10° (see Col. 9 of Table 2) in the inner region of the Galactic disc, that is,
where the magnetic energy is highest. The models N1d-HF/VF, including evolution of the
disc, show somewhat reduced pitch angles. This may be related to the long-term viscous
evolution of the radial gas density profile, which reduces the SF rate that enters our
dynamo prescription, and hence the strength of the MF dynamo near the Galactic centre.
It is interesting to note that we did not see a significant change of pitch angle during
the simulation – implying a saturation at high
Cα, most likely caused by the action of
the vertical fountain flow (cf. Elstner et al.
2009).
 |
Fig. 4 Radial pitch angle |
Fletcher (2010) pointed out the systematic
variation of the magnetic pitch angle with radius, which he ascribed to the flaring of
the disc. Similarly, Rae & Brown (2010)
observed a vanishingly small pitch angle for the outer Galaxy. In Fig. 4, we plot the radial profile of the pitch angle (in
the disc midplane) for the fiducial model X1s. The large angles of the order of −30° in
the inner part should be ignored since the mean field is significantly lower than the
equipartition value there (cf. Fig. 5), which makes
them very hard to detect in polarised synchrotron emission. Consistent with observations
(see e.g. Fig. 4 in Fletcher 2010), the pitch
angle in our simulations decreases roughly like R-1. Crudely
estimating
p ≃ l0 h-1,
with a correlation length, l0, of the turbulence, this
behaviour can conveniently be explained by the flaring of the gas disc (cf. Fig. 1). The good match is somewhat deceiving because the
allegedly more accurate estimate 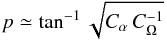 (13)in
fact provides a much poorer description of the actual result. Whereas Fig. 4 shows the pitch angle in the Galactic midplane, the
peculiar shape of the dynamo A0 mode in the outer Galaxy (seen in Fig. 3) suggests that one should look at latitudinal slices
away from the midplane – and, in fact, the pitch angle of the A0 mode follows Eq. (13) more closely. Concluding this section,
we point out that the two models N2d-noD and N2d-MRI without prescribed dynamo action
produce vanishingly small pitch angles. This may be because the initial magnetic field
is comparatively weak and accordingly the unstable modes lie close to the diffusive
border of the unstable region. In this case, the unstable mode is characterised by a
dominant toroidal field (Kitchatinov & Rüdiger
2004). The pitch angle is larger for model N3d-VF with the stronger initial
field of 0.1 μG, however.
(13)in
fact provides a much poorer description of the actual result. Whereas Fig. 4 shows the pitch angle in the Galactic midplane, the
peculiar shape of the dynamo A0 mode in the outer Galaxy (seen in Fig. 3) suggests that one should look at latitudinal slices
away from the midplane – and, in fact, the pitch angle of the A0 mode follows Eq. (13) more closely. Concluding this section,
we point out that the two models N2d-noD and N2d-MRI without prescribed dynamo action
produce vanishingly small pitch angles. This may be because the initial magnetic field
is comparatively weak and accordingly the unstable modes lie close to the diffusive
border of the unstable region. In this case, the unstable mode is characterised by a
dominant toroidal field (Kitchatinov & Rüdiger
2004). The pitch angle is larger for model N3d-VF with the stronger initial
field of 0.1 μG, however.
 |
Fig. 5 Saturated regular magnetic field for model X1s for various cuts of constant co-latitude. The midplane field peaks at about 4 μG. Dashed lines show exponentials with scale lengths of 3 and 4 kpc, respectively. |
3.2.2. Saturated field strength
Most of the nearby spiral galaxies are believed to be observed in the saturated state of the dynamo (Beck et al. 1996). With increasingly detailed observations, it becomes possible to determine the radial profile of the field strength (see e.g. Beck 2007). Based on this, one can then estimate the relative importance of magnetic forces on the overall rotational balance within the Galactic disc (see Sánchez-Salcedo & Santillán 2013). Because we started from a quantitative disc model, we can hope to make meaningful predictions about the radial distribution of the magnetic field. Accordingly, in Fig. 5 we present radial profiles of the fiducial model X1s in the saturated state. As one can see in Fig. 3 above, the dominant dynamo mode has a characteristic V-shape, which makes it instructive to plot radial cuts at various angles θ away from the midplane. The different curves are within 0−15° below the midplane (in steps of δθ = 2.5°) and cuts farther away from the midplane are shown in increasingly lighter colour. The positions of the cuts are also indicated in Fig. 3 by short line segments. The profiles are steepest near the midplane, and roughly follow exponential curves with scale lengths between 3−4 kpc, as indicated by dashed lines in Fig. 5. This scale appears to be partly inherited from the equipartition profile, which is itself a consequence of the disc model and the scaling relations entering via ηt(r,θ). Owing to the rather restrictive quenching factor of qα = 10, our dynamo solutions remain well below equipartition strength (dark line), but peak values of a few μG are obtained nevertheless (see Col. 12 in Table 2). The final field strength shows substantial variation, illustrating the dependence on the disc model. The highest absolute value (i.e., 9 μG) of the mean field is found in the high disc-mass case – with a trend to weaker fields for less-massive gas discs. This trend also explains the lower saturated field strength of ≃2.5 μG in model N1d-HF (and similarly N1d-VF) compared to ≃3.8 μG in N1s-HF (and N1s-VF), which does not include the evolution of the disc’s surface density.
3.3. Role of dynamical instabilities
One key aspect of the simulations presented in this paper is the inclusion of the Navier-Stokes equations in the modelling, which enabled us to capture dynamical instabilities occurring on large length scales. It has been suggested by Sellwood & Balbus (1999) that turbulence created via MRI may play a role in the outer Galactic disc, that is, in the absence of significant star-formation activity and the associated enhanced diffusion. In view of this, it is interesting to study the hypothetical case of a Galactic disc without any star-formation activity, for which one can perform simple MHD simulations without any prescribed mean-field effects from unresolved scales (see e.g. Dziourkevitch et al. 2004; Machida et al. 2013). Such simulations should be interpreted with care, however, since they neglect the dominant source of energy input to the system, namely that from SNe.
 |
Fig. 6 Vertical-field Alfvén speed for the initial configuration of model N3d-VF (with Bz = 0.1 μG), along with marginal stability lines according to the diffusive limit (solid) and strong-field limit (dashed line), represented by the left- and right-hand sides of Eq. (14), respectively. |
The occurrence of MRI – subject to pre-existing turbulence from SNe – can easily be
gauged from linear theory. According to the local criterion derived in Appendix A of Kitchatinov & Rüdiger (2004), who studied the
linear stability of MRI in a global cylindrical disc of semi-thickness H,
instability is obtained within a range 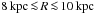 (14)where
vA ≡ |Bz| ρ−1/2
is with respect to the vertical field. For a flat rotation curve with
s = 1, this yields
ηt H-1 < vA < 1.4HΩ,
implying that already for CΩ > 1,
there exists a magnetic field unstable to MRI. This is illustrated in Fig. 6, where we show the marginal stability lines for our
model N3d-VF with a moderately strong initial field of 0.1 μG. For
(14)where
vA ≡ |Bz| ρ−1/2
is with respect to the vertical field. For a flat rotation curve with
s = 1, this yields
ηt H-1 < vA < 1.4HΩ,
implying that already for CΩ > 1,
there exists a magnetic field unstable to MRI. This is illustrated in Fig. 6, where we show the marginal stability lines for our
model N3d-VF with a moderately strong initial field of 0.1 μG. For
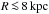 , the region of possible
MRI activity is significantly restricted, while the outer disc clearly shows the potential
to develop the instability.
, the region of possible
MRI activity is significantly restricted, while the outer disc clearly shows the potential
to develop the instability.
 |
Fig. 7 Same as Fig. 5, but for different dynamical
models. Top panel: model N2d-MRI without prescribed MF effects; the
radial scale length of the magnetic field is ≃10 kpc. Middle
panel: model N2d-noD without α effect, but including
turbulent diffusion (which suppresses the MRI for
|
In the three panels of Fig. 7, we aim to illustrate the interplay of prescribed small-scale effects with dynamical instabilities. In the upper panel of that figure, we present model N2d-MRI, where no dynamo-effects or turbulent diffusivity have been prescribed and where dynamo activity is caused by magnetic instabilities such as the MRI and convection. This case corresponds to the MHD simulations of Machida et al. (2013). In contrast to the static dynamo simulation discussed earlier (see Fig. 5), it is worth mentioning that in this case one obtains a much flatter radial dependence of the mean magnetic field strength, which agrees better with observations (see e.g. Beck 2007, who investigated the external galaxy NGC 6946, however).
Because isolated MRI is a highly idealised scenario, we now turn to the more realistic case where the MRI is affected by turbulence resulting from SNe. In a general context, the effect of Ohmic diffusion on growing MRI modes has been studied in the framework of linear perturbation (Jin 1996), and based on this, Gressel et al. (2008b) have argued that the turbulent diffusion from SNe should be sufficient to damp the MRI at the solar radius (also cf. Fig. 6). Whether the simple picture of “enhanced” diffusion is viable needs to be scrutinised. Simulations combining hydrodynamic forcing with the non-linear evolution of the MRI (Workman & Armitage 2008), produce a rather varied picture. However, for moderately strong small-scale forcing, the authors indeed concluded that MRI may be suppressed by preexisting turbulence. A similar conclusion was reached by Korpi et al. (2010), who ran shearing-box simulations with finite Ohmic resistivity and, alternatively, with small-scale forcing. The authors demonstrated that, assuming a typical ηt(R), MRI turbulence can be sustained inside the Galactic disc outside R ≃ 14 kpc. This finding turns out to be in excellent agreement with our model N2d-noD, where we applied turbulent diffusion (and viscosity), but disabled the mean-field dynamo. The resulting radial field profiles are plotted in the middle panel of Fig. 7.
As an aside, we note that in MRI turbulence, the velocity dispersion is typically found to be linked to the Alfvén speed (Dziourkevitch et al. 2004). As can be seen in Fig. 7, outside ≃15 kpc the MRI indeed leads to super-equipartition field strengths with respect to the turbulent kinetic energy input from SNe4. Furthermore, in agreement with the profiles obtained for NGC 6946 (Beck 2007), the radial scale length of the regular field exceeds the scale length of the turbulence – this is unlikely for the dynamo-only case (cf. Fig. 5).
Regarding the general field morphology (also see Sect. 3.4 below), we found that anti-symmetric parity of the emerging mean field
prevails. This is despite linear theory predicts quadrupolar-like (i.e., S0) parity (Kitchatinov & Rüdiger 2004) for MRI – albeit
for a non-flaring disc of constant thickness. Because of the dominance of the A0 mode, the
peak value of approximately 1 μG is reached away from the disc
midplane. Returning to the importance of pre-existing turbulence, we emphasise that for
model N2d-noD, turbulent diffusion dominates in the inner disc (i.e., for
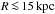 ); there the mean magnetic
field remains at the initial seed-field level. Away from the disc midplane, where the
prescribed turbulent diffusion is stronger, the field is diffused-in from the MRI-active
outer region.
); there the mean magnetic
field remains at the initial seed-field level. Away from the disc midplane, where the
prescribed turbulent diffusion is stronger, the field is diffused-in from the MRI-active
outer region.
 |
Fig. 8 Alfvén velocity based on the azimuthal field,
|
Both of the two previously described scenarios only tell part of the story. The models
without any explicit mean-field effects (upper panel of Fig. 7) and without an α effect (middle panel) instead should be
contrasted with the case of a combined evolution of mean-field effects
and dynamical instabilities on large scales – this is shown in the
lower panel of the same figure. In the inner disc (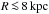 ), the S0 dynamo mode
prevails, with strong fields near the midplane. In the range
), the S0 dynamo mode
prevails, with strong fields near the midplane. In the range
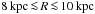 , the A0 dynamo mode
results in weak fields near z = 0, whereas for
, the A0 dynamo mode
results in weak fields near z = 0, whereas for
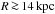 the magnetic field is
mostly caused by MRI activity. Unlike in the case without prescribed dynamo effects, at
late times, that is, after t = 3.9 Gyr, the MRI now reaches in to about
the magnetic field is
mostly caused by MRI activity. Unlike in the case without prescribed dynamo effects, at
late times, that is, after t = 3.9 Gyr, the MRI now reaches in to about
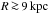 – probably assisted by
field-amplification via the α-effect dynamo. Observationally, the
resulting radial scale length would most likely appear considerably larger than for a pure
dynamo field (cf. Fig. 5).
– probably assisted by
field-amplification via the α-effect dynamo. Observationally, the
resulting radial scale length would most likely appear considerably larger than for a pure
dynamo field (cf. Fig. 5).
Returning to the question concerning effects of the regular magnetic field on the Galactic rotation curve (see Sánchez-Salcedo & Santillán 2013), we point out that the relative importance of magnetic fields in the overall force balance can be roughly estimated by considering the strength of the field with respect to the gas density. Accordingly, in Fig. 8, we plot the azimuthal-field Alfvén velocity for the third case discussed above. Most notably, vA is very uniform throughout the outer Galactic disc. With values of several tens of km s-1, the effect of the Lorentz force on the rotation curve can be predicted to remain low and within current observational uncertainties. Near the magnetic reversal at R ≃ 10 kpc, a minor deviation of ≃+10 km s-1 is seen in the rotational velocity at intermediate Galactic latitude. This potential correlation between a field reversal and a peak in the rotation curve may be a promising future target for combined optical and radio-polarimetric observations.
3.4. Morphology of fully dynamical discs
 |
Fig. 9 Poloidal cuts through model N3d-VF, with colour-coded
|
The emergence of the MRI in our simulations is limited by various factors. Weak seed
fields, for example, imply that the plasma parameter
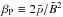 falls into a range where MRI only appears at high wavenumbers and only far up in the disc
where the gas pressure is low. To circumvent limitations due to insufficient numerical
resolution, we ran an additional scenario N3d-VF, which is identical to N1d-VF, but has a
higher initial net-vertical magnetic field of
Bz = 0.1 μG, and adopts
a higher resolution of 384 × 72 × 96 grid cells. With this model, we aim to study the
combined effects of the mean-field dynamo and secondary instabilities, as illustrated in
the previous section.
falls into a range where MRI only appears at high wavenumbers and only far up in the disc
where the gas pressure is low. To circumvent limitations due to insufficient numerical
resolution, we ran an additional scenario N3d-VF, which is identical to N1d-VF, but has a
higher initial net-vertical magnetic field of
Bz = 0.1 μG, and adopts
a higher resolution of 384 × 72 × 96 grid cells. With this model, we aim to study the
combined effects of the mean-field dynamo and secondary instabilities, as illustrated in
the previous section.
A more detailed evolution of this model is presented in Fig. 9, where we show vertical cuts through the domain. The
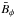 field created by the MRI (visible in the outer disc) has the opposite polarity from the A0
dynamo mode (seen between
field created by the MRI (visible in the outer disc) has the opposite polarity from the A0
dynamo mode (seen between 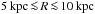 ). This leads to a
distinct radius where the field is zero (which is also clearly visible in the derived
polarisation map – see Fig. 12). While this would
provide a natural explanation for the observed field reversal in our own Galaxy, it is
currently unclear whether the antagonism between the MRI mode and the dynamo mode is
random or systematic in our model. A careful study of what determines the prevalent mode
structure in the presence of combined MRI and mean-field effects is certainly called for.
). This leads to a
distinct radius where the field is zero (which is also clearly visible in the derived
polarisation map – see Fig. 12). While this would
provide a natural explanation for the observed field reversal in our own Galaxy, it is
currently unclear whether the antagonism between the MRI mode and the dynamo mode is
random or systematic in our model. A careful study of what determines the prevalent mode
structure in the presence of combined MRI and mean-field effects is certainly called for.
Owing to the lower βP, the MRI develops closer to the disc
midplane. There the density is strongly stratified, which in turn seems to lead to a
Parker-type convective instability (Newcomb 1961;
Foglizzo & Tagger 1994, 1995) visible in the form of field arcs. As a
consequence, the vertical undulation of the antisymmetric
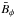 creates apparent radial reversals of the field direction in the disc
midplane. It would be interesting to investigate whether such a field distribution is
consistent with all-sky data of Faraday rotation and polarised emission (see e.g. Jaffe et al. 2010). Clearly, this type of reversal
would be very difficult to observe in external galaxies – which may conveniently explain
why the Milky Way appears unusual in this regard.
creates apparent radial reversals of the field direction in the disc
midplane. It would be interesting to investigate whether such a field distribution is
consistent with all-sky data of Faraday rotation and polarised emission (see e.g. Jaffe et al. 2010). Clearly, this type of reversal
would be very difficult to observe in external galaxies – which may conveniently explain
why the Milky Way appears unusual in this regard.
 |
Fig. 10 Projected θ-φ-slice of the azimuthal magnetic field at r = 16 kpc. The dominant wavelength along the field lines is on the order of 30 kpc. |
Our claim that a Parker-like buoyant instability is operating in the regions of strong
field creation has so far largely been guided by visual appearance. In the following we
therefore try to assess in a semi-quantitative manner the requirements for buoyancy
instabilities to occur. It is well established that the convective instability (Newcomb 1961) works to interchange neighbouring
segments of field lines. Because magnetic tension forces oppose line bending, the
interchange will preferably occur on long segments. With dominant
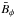 fields, one would thus expect perturbations that have higher wave numbers in the radial
direction compared to the azimuthal direction. This is illustrated for model N3d-VF in
Fig. 10, where we show a
θ-φ slice of the
fields, one would thus expect perturbations that have higher wave numbers in the radial
direction compared to the azimuthal direction. This is illustrated for model N3d-VF in
Fig. 10, where we show a
θ-φ slice of the
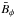 field component (for the same point in time as for panel a in Fig. 9). Note that Fig. 10 does not
preserve the aspect ratio and the azimuthal coordinate y′ is
strongly compressed compared to the poloidal slice in the previous figure. The dominant
azimuthal mode appears to be m = 3, which corresponds to a wavelength of
λy ≃ 30 kpc. In agreement with local
simulations by Johansen & Levin (2008),
this is about a factor of 10−20 larger than the radial wavelength
λx ≃ 2 kpc. By order of magnitude
(Newcomb 1961), one would expect
2πL/λy ~ 1,
where L is the scale height of the total pressure
field component (for the same point in time as for panel a in Fig. 9). Note that Fig. 10 does not
preserve the aspect ratio and the azimuthal coordinate y′ is
strongly compressed compared to the poloidal slice in the previous figure. The dominant
azimuthal mode appears to be m = 3, which corresponds to a wavelength of
λy ≃ 30 kpc. In agreement with local
simulations by Johansen & Levin (2008),
this is about a factor of 10−20 larger than the radial wavelength
λx ≃ 2 kpc. By order of magnitude
(Newcomb 1961), one would expect
2πL/λy ~ 1,
where L is the scale height of the total pressure
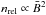 .
In agreement with this estimate, we inferred a value of L ≃ 5 kpc.
Based on our simulation data, we moreover evaluated the basic stability criterion for
convective stability (assuming γ = 1), the fastest-growing wave number
(λy ~ 10 kpc), and growth rates
(τe ~ 100 Myr). While a quantitative comparison is
hampered by the fact that we cannot isolate the unperturbed background state, the overall
numbers support the notion that convective perturbations in the disc are indeed created by
magnetic buoyancy. We point out that including a non-isothermal equation of state may have
a stabilising effect on the system, which means that our current models may overestimate
related effects. On the other hand, this type of instability has been argued to be
enhanced by the presence of a cosmic-ray component (Parker
1992; Hanasz et al. 2004). As a concluding
remark, we note that observational support for such buoyant arcs remains largely
unavailable – although claims have been made for magnetic loops in the inner Galactic disc
(Fukui et al. 2006).
.
In agreement with this estimate, we inferred a value of L ≃ 5 kpc.
Based on our simulation data, we moreover evaluated the basic stability criterion for
convective stability (assuming γ = 1), the fastest-growing wave number
(λy ~ 10 kpc), and growth rates
(τe ~ 100 Myr). While a quantitative comparison is
hampered by the fact that we cannot isolate the unperturbed background state, the overall
numbers support the notion that convective perturbations in the disc are indeed created by
magnetic buoyancy. We point out that including a non-isothermal equation of state may have
a stabilising effect on the system, which means that our current models may overestimate
related effects. On the other hand, this type of instability has been argued to be
enhanced by the presence of a cosmic-ray component (Parker
1992; Hanasz et al. 2004). As a concluding
remark, we note that observational support for such buoyant arcs remains largely
unavailable – although claims have been made for magnetic loops in the inner Galactic disc
(Fukui et al. 2006).
 |
Fig. 11 Logarithmic power spectrum of |
To illustrate the very distinctive character of the dynamo-generated field on one hand and the field resulting from dynamical magnetic instabilities on the other hand, we show in Fig. 11 the vertically averaged azimuthal power spectrum of the magnetic field. The spectrum is taken from model N3d-VF at time t = 3.9 Gyr and was normalised to a maximum of one. The logarithmic colour-coding spans the available dynamic range of the double-precision floating point numbers used in the simulation, ranging from essentially zero (blue) to maximum (dark red). The dynamo field is characterised by a perfectly axisymmetric m = 0 mode. Outside R ≃ 9 kpc, we find significant non-axisymmetric modes, but without any particular mode number dominating. In the transition region between the αΩ dynamo and the MRI-dominated region, we see power at odd overtones as well as a peak at m = 2.
 |
Fig. 12 Synthetic polarisation maps for model N3d-VF at t = 3.9 Gyr, i.e., corresponding to the lower panel in Fig. 9. Colour-coding shows the Stokes-I parameter, and compass needles indicate the direction of polarisation (rotated by 90°). |
This feature is also seen in Fig. 12, where we show
a very basic polarisation map created from the saturated state of model N3d-VF. This
synthetic radio map integrates polarised synchrotron emission along the line of sight,
ignoring effects of Faraday-rotation and -depolarisation, and assuming a flaring disc (of
scale height hrel = 1.5 kpc at
R = 10 kpc) for the density nrel of
relativistic electrons. In the edge-on projection, we inferred a radial scale length of
the total intensity of about 5 kpc if we assume a radially constant
nrel. If we assume a correlation
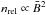 ,
this is naturally reduced to 2.5 kpc. Needless to say, both results are consistent with
the radial scale length of 10 kpc seen for the magnetic field in Fig. 7. We remark that these estimates refer to the strong
fields created in the outer disc by the MRI in combination with buoyancy and the
mean-field dynamo. We conclude that a potential field reversal at a mode interface will
make it difficult to infer a meaningful global scale length from observations. This is in
any case difficult for the Milky Way itself, but slightly higher values have been obtained
for NGC 6946 (Beck 2007), for example, where a scale
length of 14 kpc has been found for the total magnetic field.
,
this is naturally reduced to 2.5 kpc. Needless to say, both results are consistent with
the radial scale length of 10 kpc seen for the magnetic field in Fig. 7. We remark that these estimates refer to the strong
fields created in the outer disc by the MRI in combination with buoyancy and the
mean-field dynamo. We conclude that a potential field reversal at a mode interface will
make it difficult to infer a meaningful global scale length from observations. This is in
any case difficult for the Milky Way itself, but slightly higher values have been obtained
for NGC 6946 (Beck 2007), for example, where a scale
length of 14 kpc has been found for the total magnetic field.
Ultimately, we aim to compare polarisation maps such as in Fig. 12 to observation-based models for the GMF, such as the face-on view (top panel) of the heuristic model derived by Jansson & Farrar (2012a, their Fig. 9). We see that our dynamo field is less centrally-confined than the best-fit to the all-sky polarisation maps, and obviously lacks the precise spiral features. More significantly, in the edge-on view (see lower panel of Fig. 12), we do not see any X-shaped field topology. Even though our dynamo models do produce significant vertical field, these are always dominated by stronger radial and azimuthal fields. In the edge-on projection, the polarisation vectors are accordingly aligned with the horizontal direction.
4. Summary of results
With mean-field coefficients calibrated from direct SN simulations (see Table 1), and with quenching functions determined quantitatively (Gressel et al. 2013), we are left with essentially no free input parameters other than the initial geometry of the magnetic seed field. This of course precludes the possibility of deriving a bifurcation diagram for dynamo modes or critical dynamo numbers (Brandenburg et al. 1992). On the other hand, it is satisfying that without tuning of any parameters, the outcome of our simulations indeed agrees well with observational constraints.
-
In all our models, we found a dominant S0 mode for the dynamo, but with a subdominant A0 mode situated in the outer disc. In the case of a low disc mass, the A0 mode is most pronounced. Moreover, we found antisymmetric parity (notably of the opposite sign) for the dominant MRI mode.
-
The mixed S0+A0 dynamo mode leads to a localised region of strong vertical field, which is enforced by the requirement of a zero divergence. Because of the mixed parity, the vertical field only appears on one side of the disc, as is consistent with recent observations by Mao et al. (2010).
-
Consistent with a topical compilation of observations by Fletcher (2010), the radial profile of the magnetic pitch angle emerging from our model decreases with inverse radius. This is very well approximated by p ≃ l0h-1, with h the local scale-height of the flaring disc.
-
Vertical undulations caused by magnetic instabilities, in connection with an anti-symmetric vertical parity, can create apparent radial reversals near the disc midplane. The resulting field topology needs to be tested against available data of rotation measures in the Galactic plane. A reversal is also seen at the interface between the dynamo and MRI modes.
-
The most pronounced effect of allowing magnetic instabilities is to significantly enhance the radial scale length of the magnetic energy in the outer disc. Such shallow profiles, where the scale length of the field exceeds that of the turbulence, have been observed in NGC 6946 (Beck 2007).
-
There has been renewed interest in the radial dependence of the magnetic-field strength and its influence on the rotation curve (Sánchez-Salcedo & Santillán 2013). In our dynamo models, we found exponential scale lengths of ~3−4 kpc, which is somewhat shorter than expected. A shallower radial profile is seen in the disc halo, as well as in cases where the MRI leads to strong fields in the outer disc. Even there, deviations from the initial rotation curve stay well below current observational uncertainties.
5. Conclusions
We have described a new, comprehensive modelling approach for global mean-field simulations of the Galactic dynamo. To be able to make quantitative predictions, we aimed to constrain all relevant input parameters in a rigorous way. Our model for the gaseous disc was derived in a self-consistent way, based on the observed gravitational potential of the Galaxy, and its measured HI distribution. The prescription of mean-field effects (stemming from spatial scales unresolved in the global simulation) was parametrised from a comprehensive set of resolved shearing-box simulations including the treatment of the multi-phase ISM and energy input from SNe.
In a further step towards improving the generality of our mean-field models, we moreover solved the complete MHD equations instead of keeping the flow field fixed. This was necessary to capture magnetic instabilities such as the MRI and convective instabilities. These arise on scales that are large compared to the outer scale of the SN-driven turbulence, where turbulent diffusion is less and less efficient. Another prospect of solving the MHD equations is the future extension of the model towards a self-consistent galaxy evolution model. Such a model could potentially include spiral arm features (via self-gravity of a stellar N-body population or the gas disc itself), effects from accretion of material onto the galaxy, from galaxy encounters, or ram-pressure stripping. For all of these, including mean-field effects appears to be mandatory, as has recently been demonstrated for the latter case by Moss et al. (2012).
We stress that our model should only be regarded as a very first step towards a fully comprehensive approach. Clearly there remain discrepancies with respect to observations. For example, the only way to produce X-shaped polarisation vectors in edge-on polarisation maps is to start with a strong vertical field that is already present (and to prescribe a differential wind in the radial direction). This is because in the edge-on projection the horizontal disc field always dominates. We hence conjecture that the X-shaped fields seen in edge-on galaxies are possibly not the result of a disc dynamo. In contrast, dynamo simulations that show X-like field configurations typically include the polar regions of the spherical domain – something that is currently lacking in our own description. Examples include the work by Brandenburg et al. (1993), who also assumed a much stronger wind. More recently, Moss et al. (2010) have obtained X-shaped topologies in simulations including an α effect in the halo itself (cf. also Moss & Sokoloff 2008). Such a spherical halo dynamo has originally been proposed by Sokoloff & Shukurov (1990). In the absence of such an effect, a strong outflow (such as seen in NGC 253, Heesen et al. 2009, 2011) is probably required to explain these field geometries. One way to explore this in more detail will be global MHD simulations that incorporate both mean-field effects from small-scale turbulence and the effect of CRs and SNe in form of a nuclear star-burst (Melioli et al. 2013) and super-bubbles. However, such simulations must account for the multi-phase nature of the ISM (via an appropriate cooling function), and are highly demanding in terms of CPU resources.
Also note that Gressel et al. (2008a) found the α2 dynamo to be only marginally excited for the coefficients measured in DNS.
Acknowledgments
We thank the referee, David Moss, for useful comments that led to an improvement of the paper. This project is part of DFG research unit 1254. Computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the High Performance Computing Center North (HPC2N) in Umeå.
References
- Alexiades, V., Amiez, G., & Gremaud, P.-A. 1996, Communications in Numerical Methods in Engineering, 12, 31 [CrossRef] [Google Scholar]
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Donner, K. J., Moss, D., et al. 1992, A&A, 259, 453 [NASA ADS] [Google Scholar]
- Brandenburg, A., Donner, K. J., Moss, D., et al. 1993, A&A, 271, 36 [NASA ADS] [Google Scholar]
- Brandenburg, A., Rädler, K.-H., & Schrinner, M. 2008, A&A, 482, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., & Rogachevskii, I. 2012a, ApJ, 749, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Sokoloff, D., & Subramanian, K. 2012b, Space Sci. Rev., 57 [Google Scholar]
- Brown, J. C. 2010, in The dynamic interstellar medium: a celebration of the Canadian Galactic Plane Survey, eds. R. Kothes, T. L. Landecker, & A. G. Willis, ASP Conf. Ser., 438, 216 [Google Scholar]
- Brown, J. C., Haverkorn, M., Gaensler, B. M., et al. 2007, ApJ, 663, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013a, MNRAS, 428, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013b, MNRAS, 433, 3274 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., & Buta, R. J. 2008, ApJ, 677, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Dziourkevitch, N., Elstner, D., & Rüdiger, G. 2004, A&A, 423, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elstner, D., Meinel, R., & Beck, R. 1992, A&AS, 94, 587 [Google Scholar]
- Elstner, D., Gressel, O., & Rüdiger, G. 2009, in IAU Symp., 259, 467 [Google Scholar]
- Fauvet, L., Macías-Pérez, J. F., Aumont, J., et al. 2011, A&A, 526, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fauvet, L., Macías-Pérez, J. F., Jaffe, T. R., et al. 2012, A&A, 540, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K., & Schmitt, D. 2000, A&A, 358, 125 [NASA ADS] [Google Scholar]
- Fletcher, A. 2010, in The dynamic interstellar medium: a celebration of the Canadian Galactic Plane Survey, eds. R. Kothes, T. L. Landecker, & A. G. Willis, ASP Conf. Ser., 438, 197 [Google Scholar]
- Fletcher, A., Korpi, M., & Shukurov, A. 2009, in IAU Symp., 259, 87 [Google Scholar]
- Flynn, C., Sommer-Larsen, J., & Christensen, P. R. 1996, MNRAS, 281, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Foglizzo, T., & Tagger, M. 1994, A&A, 287, 297 [NASA ADS] [Google Scholar]
- Foglizzo, T., & Tagger, M. 1995, A&A, 301, 293 [NASA ADS] [Google Scholar]
- Fromang, S., & Stone, J. M. 2009, A&A, 507, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukui, Y., Yamamoto, H., Fujishita, M., et al. 2006, Science, 314, 106 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gressel, O. 2009, Ph.D. Thesis, University of Potsdam, Germany [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008a, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gressel, O., Ziegler, U., Elstner, D., & Rüdiger, G. 2008b, Astron. Nachr., 329, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Ziegler, U., Elstner, D., & Rüdiger, G. 2009, in IAU Symp., 259, 81 [Google Scholar]
- Gressel, O., Elstner, D., & Rüdiger, G. 2011, in IAU Symp. 274, eds. A. Bonanno, E. de Gouveia Dal Pino, & A. G. Kosovichev, 348 [Google Scholar]
- Gressel, O., Bendre, A., & Elstner, D. 2013, MNRAS, 429, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Guan, X., & Gammie, C. F. 2009, ApJ, 697, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Kowal, G., Otmianowska-Mazur, K., & Lesch, H. 2004, ApJ, 605, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Wóltański, D., & Kowalik, K. 2009, ApJ, 706, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Krause, M., Beck, R., & Dettmar, R.-J. 2009, A&A, 506, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2011, A&A, 535, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubbard, A., & Brandenburg, A. 2009, ApJ, 706, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, T. R., Leahy, J. P., Banday, A. J., et al. 2010, MNRAS, 401, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, T. R., Banday, A. J., Leahy, J. P., Leach, S., & Strong, A. W. 2011, MNRAS, 416, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012a, ApJ, 757, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2012b, ApJ, 761, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, L. 1996, ApJ, 457, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Levin, Y. 2008, A&A, 490, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., Brun, A. S., Arlt, R., et al. 2008, A&A, 483, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C.1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 2004, A&A, 424, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1989, Sov. Astron. Lett., 15, 274 [NASA ADS] [Google Scholar]
- Korpi, M. J., Käpylä, P. J., & Väisälä, M. S. 2010, Astron. Nachr., 331, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberg, P. P., & Newton-McGee, K. J. 2011, PASA, 28, 171 [NASA ADS] [Google Scholar]
- Kulpa-Dybeł, K., Otmianowska-Mazur, K., Kulesza-Żydzik, B., et al. 2011, ApJ, 733, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Lazio, T. J. W., & Cordes, J. M. 1998, ApJ, 497, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Lesch, H., & Chiba, M. 1995, A&A, 297, 305 [NASA ADS] [Google Scholar]
- Machida, M., Nakamura, K. E., Kudoh, T., et al. 2013, ApJ, 764, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Haverkorn, M., et al. 2010, ApJ, 714, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., McClure-Griffiths, N. M., Gaensler, B. M., et al. 2012, ApJ, 755, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Melioli, C., de Gouveia Dal Pino, E. M., & Geraissate, F. G. 2013, MNRAS, 430, 3235 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Moss, D., & Sokoloff, D. 2008, A&A, 487, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., & Sokoloff, D. 2011, Astron. Nachr., 332, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., & Sokoloff, D. 2012, Astron. Astrophys. Trans., 27, 319 [NASA ADS] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2010, A&A, 512, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., & Beck, R. 2012, A&A, 544, A5 [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Vovk, I. 2010, Science, 328, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Newcomb, W. A. 1961, Phys. Fluids, 4, 391 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Oppermann, N., Junklewitz, H., Robbers, G., et al. 2012, A&A, 542, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1992, ApJ, 401, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Poezd, A., Shukurov, A., & Sokoloff, D. 1993, MNRAS, 264, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Rae, K. M., & Brown, J. C. 2010, in The dynamic interstellar medium: a celebration of the Canadian Galactic Plane Survey, eds. R. Kothes, T. L. Landecker, & A. G. Willis, 438, 229 [Google Scholar]
- Ruzmaikin, A. A., Sokolov, D. D., & Shukurov, A. M. 1988, Magnetic fields of galaxies (Astrophys. Space Sci. Lib.), 133 [Google Scholar]
- Sánchez-Salcedo, F. J., & Santillán, A. 2013, MNRAS [Google Scholar]
- Schlickeiser, R. 2012, Phys. Rev. Lett., 109, 261101 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. 2005, Astron. Nachr., 326, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. R. 2007, GApFD, 101, 81 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Balbus, S. A. 1999, ApJ, 511, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloff, D., & Shukurov, A. 1990, Nature, 347, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Krause, M., Fletcher, A., & Beck, R. 2008, A&A, 490, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eck, C. L., Brown, J. C., Stil, J. M., et al. 2011, ApJ, 728, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H.-H., Klessen, R. S., Dullemond, C. P., van den Bosch, F. C., & Fuchs, B. 2010, MNRAS, 407, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Workman, J. C., & Armitage, P. J. 2008, ApJ, 685, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Yousef, T. A., Brandenburg, A., & Rüdiger, G. 2003, A&A, 411, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ziegler, U. 2004, J. Comput. Phys., 196, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, U. 2011, J. Comput. Phys., 230, 1035 [Google Scholar]
All Tables
Scaling exponents for the dynamo α tensor, the turbulent
diffusivity and viscosity, and vertical fountain flow,
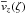 .
.
All Figures
 |
Fig. 1 Midplane rotation curve (dotted line = 220 km s-1) and disc surface density. The inset shows the flaring scale-height of the HI gas disc. Dashed lines indicate observational approximations suggested by Kalberla & Dedes (2008). |
| In the text | |
 |
Fig. 2 Vertical profiles of TF coefficients
αφφ (left),
γz (centre), and
ηt (right panel) measured from DNS
(light colours); shaded areas indicate 1σ fluctuations. Black
curves show model profiles |
| In the text | |
 |
Fig. 3 Saturated regular magnetic field for model X1s-0.5; colour-coded toroidal field,
|
| In the text | |
 |
Fig. 4 Radial pitch angle |
| In the text | |
 |
Fig. 5 Saturated regular magnetic field for model X1s for various cuts of constant co-latitude. The midplane field peaks at about 4 μG. Dashed lines show exponentials with scale lengths of 3 and 4 kpc, respectively. |
| In the text | |
 |
Fig. 6 Vertical-field Alfvén speed for the initial configuration of model N3d-VF (with Bz = 0.1 μG), along with marginal stability lines according to the diffusive limit (solid) and strong-field limit (dashed line), represented by the left- and right-hand sides of Eq. (14), respectively. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, but for different dynamical
models. Top panel: model N2d-MRI without prescribed MF effects; the
radial scale length of the magnetic field is ≃10 kpc. Middle
panel: model N2d-noD without α effect, but including
turbulent diffusion (which suppresses the MRI for
|
| In the text | |
 |
Fig. 8 Alfvén velocity based on the azimuthal field,
|
| In the text | |
 |
Fig. 9 Poloidal cuts through model N3d-VF, with colour-coded
|
| In the text | |
 |
Fig. 10 Projected θ-φ-slice of the azimuthal magnetic field at r = 16 kpc. The dominant wavelength along the field lines is on the order of 30 kpc. |
| In the text | |
 |
Fig. 11 Logarithmic power spectrum of |
| In the text | |
 |
Fig. 12 Synthetic polarisation maps for model N3d-VF at t = 3.9 Gyr, i.e., corresponding to the lower panel in Fig. 9. Colour-coding shows the Stokes-I parameter, and compass needles indicate the direction of polarisation (rotated by 90°). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.