| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321917 | |
| Published online | 06 December 2013 | |
A new scenario for the origin of the 3/2 resonant system HD 45364
1
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, USP,
Rua do
Matão 1226,
05508-090
São Paulo,
Brazil
e-mail:
jorge9895@usp.br
2
Instituto de Astronomía Teórica y Experimental, Observatorio
Astronómico, Universidad Nacional de Córdoba, Laprida 854, (X5000BGR)
Córdoba,
Argentina
Received:
17
May
2013
Accepted:
4
October
2013
We revise the model for the origin of the HD 45364 exoplanetary system proposed by Rein et al. (2010, A&A, 510, A4), which is currently known to host two planets close to the 3/2 mean-motion resonance (MMR). We show that due to the high surface density of the protoplanetary disk needed for type III migration, this model can only lead to planets in a quasi-resonant regime of motion and thus is not consistent with the resonant configuration obtained by Correia et al. (2009, A&A, 496, 521). Although both resonant and quasi-resonant solutions are statistically indistinguishable with respect to radial velocity measurements, their distinct dynamical behavior is intriguing. We used the semi-analytical model to confirm the quantitative difference between two configurations. To form a system that evolves inside the 3/2 resonance, we developed a different model. Our scenario includes an interaction between different (but slower) planetary migration types, planet growth, and gap formation in the protoplanetary disk. The evolutionary path was chosen due to a detailed analysis of the phase space structure in the vicinity of the 3/2 MMR that employed dynamical mapping techniques. The outcomes of our simulations are able to very closely reproduce the 3/2 resonant dynamics obtained from the best fit presented by Correia et al. In addition, by varying the strength of the eccentricity damping, we can also simulate the quasi-resonant configuration similar to that reported in Rein et al. We furthermore show that our scenario is reliable with respect to the physical parameters involved in the resonance-trapping process. However, our scenario can only be confirmed with additional radial velocities measurements.
Key words: celestial mechanics / planets and satellites: formation / planets and satellites: dynamical evolution and stability / methods: numerical
© ESO, 2013
1. Introduction
HD 45364 is the first discovered system with two planets that evolve inside or near the 3/2 mean-motion resonance (MMR; Correia et al. 2009). Recently, the HD 204313 system was also suggested as a candidate for this resonance (Robertson et al. 2012), but the stability of the proposed configuration still needs to be confirmed. There are also several Kepler systems located near the 3/2 resonance, but it is uncertain whether they are connected with this resonance because we lack information on their eccentricities. The long-term survivance of the HD 45364 system in the 3/2 MMR that corresponds to the best fit of Correia et al. (2009) was tested and confirmed through numerical integrations of the exact equations of motion (Correia et al. 2009).
The semimajor axes of planets b and c of HD 45364 are equal to 0.682 AU and 0.898 AU, respectively. A study of the origin of this compact planetary configuration was first carried out by Rein et al. (2010). To form this resonant pair, the authors initially tested the standard scenario of a convergent migration of two planets embedded in a protoplanetary disk. They noted, however, that a type II migration most likely leads to a capture inside the strong 2/1 MMR, which formed a dynamical barrier that blocked the road to the 3/2 MMR. To overcome this problem, the authors suggested an alternative scenario, introducing a nonconventional type III migration. Due to the assumed high density of the disk, this type of migration produces a very rapid orbital decay of the planets, allowing them to by-pass the 2/1 resonance and capture in the 3/2 MMR.
However, one fact, already noted by Rein et al. (2010), attracted our attention: the discrepancy in the dynamical behavior of the simulated solution and that obtained from the best fit of Correia et al. (2009). The difference lies mainly in the magnitudes of the planet eccentricities (it was explained by the authors as caused by possible errors in the radial velocity data). Moreover, other discrepancies appear when the dynamics of the Rein et al. (2010) solution is analyzed in detail. An N-body simulation shows that the proposed solution does not lie within the libration zone of the 3/2 MMR, but exhibits a quasi-resonant behavior. In addition, some characteristic dynamical quantities, such as the frequencies and oscillation amplitudes of orbital elements, differ by orders in magnitude compared with those of the best fit solution.
It should be noted that, notwithstanding the distinct dynamical behavior of the two solutions, both solutions lead to practically the same radial velocity measurements; thus from an observational point of view, the two solutions are statistically indistinguishable. Only additional radial velocity measurements will allow us to unambiguously determine the resonant state of the system. HD 45364 is therefore an ideal test case for planet formation scenarios.
To form a pair of planets that evolve inside the 3/2 resonance, we consider a different scenario in this paper. Although we also suggest resonance-trapping following planetary migration from disk-planet interactions, there are some important differences: (i) we assume a slower migration rate than predicted by either type I or type II migration modes; (ii) we adopt different disk parameters, especially a lower surface density; (iii) we introduce mass growth during both the migration and the resonance-trapping processes; and (iv) we assume that the migration process begins when the planets are in the embryonic stage (~0.1 M⊕) and thus much smaller than the present-day Saturn-size planets.
We show that depending on just one parameter, our scenario is able to reproduce the averaged magnitudes of the orbital elements and the resonant behavior of the best fits of Correia et al. (2009), also for the solution given in Rein et al. (2010). In addition, we study the phase space of the 3/2 MMR using a semi-analytical model originally developed by Michtchenko et al. (2008a). This analysis allows us to compare the dynamical behavior of the best-fit solution of Correia et al. (2010) and the solution obtained by Rein et al. (2010), and identify the most significant differences between them.
This paper is organized as follows. In Sect. 2, we briefly describe the scenario proposed in Rein et al. (2010) and compare the dynamics of the simulated orbit with the best-fit solution from Correia et al. (2009). In this section we also present the phase-space portraits of the 3/2 MMR configuration of the system and the quasi-resonant configuration. In Sect. 3, we present dynamical maps for the region between 2/1 and 3/2 MMRs. In Sect. 4, we describe the two stages of formation of HD 45364 proposed by our scenario. The capture process in the 3/2 MMR is described in Sect. 5. The conclusions are presented in the last section.
2. Scenario 1 (Rein et al. 2010)
Gravitational interactions between the protoplanetary disk and fully formed planets drive the bodies towards the central star (Lin & Papaloizou 1979; Goldreich & Tremaine 1979, 1980). If the planet migration is convergent (i.e., the mutual distance is decreasing), two planets can be captured into a mean-motion commensurability and continue to migrate in the resonance lock (e.g., Lee & Peale 2002; Ferraz-Mello et al. 2003; Beaugé et al. 2003, 2006). This mechanism is generally accepted to explain the existence of several extrasolar systems inside mean-motion resonances. The most populated one is the 2/1 MMR, which is a very strong first-order resonance with an extensive domain of stable motion. Because of this, it acts as a natural dynamical barrier that prevents most planets, formed far apart, to migrate to other commensurabilities, such as the 3/2 MMR.
To understand the existence of the HD 45364 system, Rein et al. (2010) proposed a scenario based on type III planet migration (Masset & Papaloizou 2003). This mode of inward migration is characterized by the very fast decay that allows the planets to overshoot the 2/1 MMR and to be captured in the 3/2 MMR. N-body and hydrodynamic simulations showed that this is indeed possible, although it seems to require a surface density for the protoplanetary disk at least five times higher than the minimum mass solar nebula (MMSN, Hayashi 1981). The authors concluded that this might be the first direct evidence for type III planet migration.
However, comparing the dynamics of the solution simulated in Rein et al. (2010, hereafter, R10) with that given by the best fit solution in Correia et al. (2009, hereafter C09), we note substantial differences. Figures 1 and 2 show the time evolution of both orbits, averaged over high-frequency terms on the order of the orbital periods. The initial orbital parameters used in the integrations are listed in Cols. 3 and 4 of Table 1.
 |
Fig. 1 Time evolution of the semimajor axes of the inner planet (top panel), of the outer planet (middle panel), and the mean-motion ratio (bottom panel). The black curves correspond to the best fit C09 of Correia et al. (2009), while the red curves correspond to the solution R10 of Rein et al. (2010) |
The two figures show that the orbital elements of the simulated R10 system (red curves) oscillate with very small amplitudes, in contrast with the fitted C09 system (black curves). The mean-motion ratio n1/n2 of R10 oscillates around 1.52, while for C09, this occurs around 1.50. The periods of the resonant oscillations estimated from the semimajor axes are Tres ~ 19 years for C09 and Tres ~ 17 years for R10. A higher discrepancy is noted in the secular period, as estimated from the eccentricity variations, giving Tsec ~ 400 years for C09 and only Tsec ~ 50 years for R10. The bottom panel of Fig. 2 shows the evolution of the characteristic angles of the system, the resonant angle σ1 = 2λ1 − 3λ2 + ϖ1 and the secular angle Δϖ = ϖ1 − ϖ2, where λi are the mean longitudes and ϖi are the longitudes of pericenter; hereafter, the subscript 1 is used for the inner planet, while 2 is reserved for the outer body. We can see that for R10, σ1 oscillates with a very small amplitude compared with its behavior in C09 and the amplitude of the secular component of Δϖ tends to 0.
 |
Fig. 2 Same as in Fig. 1, except for the planet eccentricities (top panel) and the characteristic angles σ1 and Δϖ (bottom panel). |
2.1. Topology of the phase space of the C09 and R10 systems
A simple comparison of the evolution of the orbital elements is insufficient to
understand why the two solutions are so different. For this task, we need to visualize the
phase space of the 3/2 MMR by plotting energy levels of the system on the
(e1,e2)-plane
of the initial eccentricities. The energy 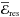 , together
with two integrals of motion, the total angular momentum
, together
with two integrals of motion, the total angular momentum
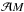 ,
and the spacing parameter
,
and the spacing parameter 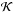 are given by the expressions (Michtchenko et al. 2008a,b)
are given by the expressions (Michtchenko et al. 2008a,b) 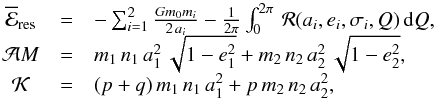 (1)where
the orbital elements, including the semimajor axes
ai and eccentricities
ei
(i = 1,2), are canonical astrocentric variables
(Ferraz-Mello et al. 2006). We averaged the
disturbing function ℛ with respect to the synodic angle
Q = λ2 − λ1,
where λi are the mean longitudes of the
planets. We fixed the initial values of the resonant angles σ1
and σ2 at 0 or 1800 and calculated the values of
the semimajor axes of the planets (required to calculate energy levels) using the
expressions for the constants of motion
(1)where
the orbital elements, including the semimajor axes
ai and eccentricities
ei
(i = 1,2), are canonical astrocentric variables
(Ferraz-Mello et al. 2006). We averaged the
disturbing function ℛ with respect to the synodic angle
Q = λ2 − λ1,
where λi are the mean longitudes of the
planets. We fixed the initial values of the resonant angles σ1
and σ2 at 0 or 1800 and calculated the values of
the semimajor axes of the planets (required to calculate energy levels) using the
expressions for the constants of motion  and
and  (Eqs. (1)).
(Eqs. (1)).
 |
Fig. 3 Energy levels of the 3/2 resonant Hamiltonian (1) on the (e1, e2)-plane for the C09 (top) and the R10 solution (bottom). The dashed green lines show the true separatrix (top) and the kinematic transition from oscillations to circulations (bottom). The ACR of each solution is presented with a red symbol, while the corresponding energy level is plotted as a continuous green curve. |
Two (e1, e2)-planes are shown in Fig. 3: the top graph was constructed with the parameter set of the best fit C09 configuration, while the bottom graph corresponds to the simulated R10 system. In both graphs, the positive (negative) values on the ei-axis correspond to σi fixed at 0 (180°). The stable stationary solutions corresponding to the highest energy of the system (frequently referred to as ACR-solutions) are shown as red dots in the two planes.
The comparison of dynamical structures of two planes allows us to understand the different behavior of the simulated system R10 (Rein et al. 2010) and the best fit solution C09 (Correia et al. 2009). Indeed, although the resonant angles are oscillating in both cases, these oscillations are topologically different. In the case of R10 (bottom panel), the oscillations are merely kinematic since all levels, even that passing through the origin (dashed green curve), belong to a same structurally stable family. In other words, there is no topological difference between oscillations and circulations. In this case, we say that the system is in a quasi-resonant regime of motion.
In contrast, for the C09 solution (top panel), the transition from oscillation of the resonant angle to circulation occurs through true bifurcations of the solutions, along the separatrix that contains a saddle-like point (dashed green curve). In other words, the two regimes of motions, oscillations and circulations, are topologically distinct. In this case, we say that the resonant angle librates and the system is in a true resonance state.
 |
Fig. 4 Comparison of different orbital solutions: radial velocity measurements (blue dots), the best fit solution C09 (green line), the R10 simulation (yellow line), and our two solutions with K3 (black line) and K100 (red line). See text for details. |
2.2. Radial velocity curves
It is worth noting that notwithstanding the distinct dynamical behavior of the two solutions C09 and R10, both lead to practically the same radial velocity curve. This is illustrated in Fig. 4, where the observational data are shown as dots and the solutions C09 and R10 are shown as green and yellow lines, respectively. As has been noted in Rein et al. (2010), it is very difficult to see any difference in the quality of the two fits; moreover, the similar χ2-values (see Table 1) suggest that the two solutions are statistically indistinguishable.
 |
Fig. 5 Dynamical maps of the domain between the 2/1 and 3/2 MMRs, for two fictitious systems composed of a solar-mass star and two planets with masses m1 = m2 = 1.0 MJ (top panel) and m1 = m2 = 0.1 MJ (bottom panel). The initial conditions are e1 = 0 and σ1 = 0; Δϖ is fixed at 0 (positive values on the e2-axis) or 180° (negative values on the e2-axis). The location of several MMRs are shown as vertical dashed lines. The light-gray tones correspond to regions of regular motion, while the hatched red regions correspond to strongly chaotic motion. |
3. Dynamical maps of the region between the 2/1 and 3/2 resonances
To investigate the possible migration routes of the HD 45364 system toward the 3/2 MMR, we analyzed the dynamics in the region between the 2/1 and 3/2 MMRs. This was made using dynamical maps drawn in the (n2/n1,e2) representative plane. Here we only briefly describe their construction; details can be found in (Michtchenko et al. 2002; Ferraz-Mello et al. 2005). The (n2/n1,e2)-plane was covered with a rectangular grid of initial conditions with spacings Δ(n2/n1) = 0.002 and Δe2 = 0.002. The semimajor axis and the eccentricity of the inner planet were fixed at a1 = 1 AU and e1 = 0.001, respectively. The initial values of the mean longitudes were fixed at λ1 = λ2 = 0, while the secular angle was fixed at Δϖ = 0 (positive values on the e2-axis in Fig. 5) or 180° (negative values on the e2-axis in Fig. 5). The maps were constructed for two values for the planetary masses; the top graph shows results for m1 = m2 = 1.0 MJ, while in the bottom graph we used m1 = m2 = 0.1 MJ. These values were chosen to understand qualitatively the dependence of the dynamical features on the individual planetary masses.
Each point of the grid was numerically integrated over 1.3 × 105 years, and the output was Fourier-analyzed to obtain the spectral number N. This quantity is defined as the number of peaks in the power spectrum of the eccentricity of the inner planet and is used to qualify the chaoticity of planetary motion (see Michtchenko et al. 2002): low values of N (light shades) correspond to regular motion, while the high values (darker tones) indicate the onset of chaos.
The map obtained for m1 = m2 = 1.0 MJ is shown in the top panel in Fig. 5. The regions of regular motion are presented in light-gray tones and the hatched red regions correspond to strongly chaotic motion that leads to collisions between the planets. The domain of the 2/1 MMR is located around n2/n1 = 0.5; it is bounded by the chaotic layers, which correspond to the separatrix of the resonance. The robust structure of the resonance indicates that the smooth passage of the system during converging type II migration must be interrupted either by capture inside the resonance domain (at low eccentricities) or by ejection of the planets (at high eccentricities). There are also other mean-motion resonances between 2/1 and 3/2 MMR: they are 7/4, 5/3, and 8/5 commensurabilities located at n2/n1 ~ 0.57, 0.6, and 0.625, respectively. Of these, the second-order 5/3 MMR is also strong enough to capture or disrupt the system during slow migration.
 |
Fig. 6 Resonance capture of a Jupiter-mass planet evolving assuming type II migration. Starting at n1/n2 > 2, the planet is ultimately trapped in the 2/1 MMR (top panel). Starting at 1.67 < n1/n2 < 2, the planet is trapped in the 5/3 MMR (middle panel), and starting at n1/n2 < 1.67, in the 3/2 MMR (bottom panel). |
We tested the possibility of trapping inside each of these resonances, by performing three N-body simulations. Results are shown in Fig. 6. In all cases we considered a system of two equal-mass planets (m1 = m2 = 1.0 MJ) orbiting a solar-mass star. The inner planet was placed at 1 AU, while the position of the outer planet was defined by three different values of the mean-motion ratio. The initial values of the eccentricities and the angular variables of both planets were fixed at zero. The migration was simulated using a fictitious non-conservative force, leading to an orbital decay of the outer planet with a characteristic timescale of τa2 = 105 years (Beaugé et al. 2006).
The first simulation was made with the outer planet starting at n1/n2 = 2.5, beyond the 2/1 MMR. The time evolution of the mean-motion ratio of this system (top panel in Fig. 6) shows a capture in the 2/1 MMR at ~1.3 × 105 years. The system starting between 2/1 and 5/3 MMR, at n1/n2 = 1.8, was captured in the 5/3 MMR at ~3 × 104 years (middle panel). The capture in the 3/2 MMR was only possible for the systems starting between 5/3 and 3/2 MMRs, for instance, at n1/n2 = 1.61 (bottom panel).
It is worth noting that the captures shown in Fig. 6 are fairly robust when considering a slow (type II) migration. Therefore, to explain the existence of the HD 45364 system in the context of the type II migration, the two planets are expected to form very close to each other, in a small region located practically on top of the 3/2 MMR. This hypothesis seems very unlikely, however.
4. Scenario 2 for the origin of the 3/2 resonance for the HD 45364 system
We introduce an alternative scenario that describes the trapping in the 3/2 MMR of the embryo-size planets that are still in the initial stage of the planetary formation. It is worth noting that this possibility has been mentioned previously (but has not be studied) in Rein et al. (2010).
Our main idea is well illustrated in the bottom panel of Fig. 5, where we present a dynamical map analogous to that in the top panel, except that the individual planetary masses were chosen to be ten times smaller. Since the mutual perturbations are weaker in this case, the size of the resonant domains and their chaotic layers decreases (Michtchenko et al. 2008a,b). This is clearly seen in the case of the 5/3 and 2/1 MMRs located at n2/n1 = 0.6 and 0.5, respectively. As a consequence, two small planets undergoing the type I migration process are able to by-pass the 2/1 and 5/3 MMRs toward the 3/2 MMR.
According to current theories, tidal interactions between planets and a gas disk cause a migration process that is categorized as type I for planetary embryos and small core-planets ( ≤10.0 M⊕), and as type II for massive giant planets. The precise delimitation between the two types is defined by many factors, such as the viscosity of the disk and its scale height (Armitage 2010; Crida & Morbidelli 2007). The migration types are qualitatively different: the type I timescale is inversely proportional to the planetary masses, while the type II timescale is mainly determined by the physical properties of the disk. The most rapid migration is predicted to occur for masses between 0.03 MJ and 1.0 MJ (Armitage 2010).
The giant-planet formation scenario provides a formation timescale on the order of 8 × 106 years (Armitage 2010). The mass growth is separated into three stages (for more details see Pollack et al. 1996; Rice & Armitage 2003): core formation, hydrostatic growth, and runaway growth. The formation timescale of a giant planet is almost entirely determined by the second stage, which ends when the mass of the planet envelope becomes equal to the mass of the planet core. However, the duration of the hydrostatic growth is revealed to be much longer than the typical timescales of planet migration. To overcome this problem, Alibert et al. (2005) suggested including the migration effects in the formation model. This scenario shortens the formation timescale to a few 106 years. It also considers only two stages of mass growth: the first stage is core formation that ceases when the planets reach the critical mass (mass of the envelope equal to mass of the core). The second stage is runaway growth that starts when the planet masses exceed the critical mass value. The duration of the first stage of core formation is about 1 × 106 years (Alibert et al. 2005), and the second stage of runaway mass growth last for about 1 × 105 years (Armitage 2010); in this way, the process of planet formation is completed after ~1.1 × 106 years.
We adopted the Alibert et al. (2005) scenario to explain the existence of the HD 45364 system. We propose that the approach of the planet pair to the 3/2 MMR occurred during the first phase of the planet growth, when the planet migration toward the 3/2 MMR was favored by the small masses and the fast type I migration. After the planets had been trapped in this resonance, they continued to grow in the stage 1, until their masses reached ~10 M⊕ (a typical critical mass value), when they evolved to the stage 2 (runaway growth) and a slower type II migration. In our experiments, this process is separated schematically into two phases that are described below.
4.1. Stage I: core formation, type I migration and capture into the 3/2 MMR
In the first stage of the evolution, the system is composed initially of the two planetary embryos of equal masses (0.1 M⊕) that orbit a central star of mass 0.82 M⊙ (HD 45364). The planetary embryos are embedded in the protoplanetary disk (we considered a vertically isothermal and laminar disk); the interactions of the planets with the disk produce their type I converging migration toward the central star. This stage lasts over 1 × 106 years and the planets grow up to 10.0 M⊕.
We modeled the evolution of the system at this stage as follows: the mass growth was approximated with an exponential law m(t) = m° expt/τ, with equal initial masses m° = 0.1 M⊕ and a timescale τ = 2 × 105 years for both planets. This e-folding time provides the planet growth up to ~10 M⊕ after 1.0 × 106 years. Although there is no widely accepted expression for the mass growth at this stage of planet formation, the exponential law seems to be a good approximation (Alibert et al. 2005, see Figs. 5 and 8 in that paper); on the other hand, other authors considered different expressions, for instance, sin2t (Lega et al. 2013). The chosen parameters correspond to sufficiently small planets to experiment initially type I migration, but also to sufficiently large planets to yield migration timescales on the order of some 105 years (see Armitage 2010). It is worth noting that in our case, the type I migration is still much slower than that of type III considered in Rein et al. (2010).
To simulate the migration during the first stage, we applied the semi-analytical models
of Tanaka et al. (2002) and Tanaka & Ward
(2004), which provide the decay and damping rates
of a planet, with mass m, semimajor axis a, and
eccentricity e, orbiting a star of mass m∗
and embedded in a laminar disk, ![\begin{eqnarray} \label{form1} \dot{a} &\simeq& - \frac{2.7 + 1.1 q}{h^2} \frac{ m }{ m_*^{1.5}} \sqrt{{\mathcal G}} \Sigma_0 a^{(1.5-q)}, \notag \\[-1mm] \dot{e} &\simeq& \frac{e}{h^2} \frac{0.78}{(2.7+1.1 q)} \frac{\dot{a}}{a}, \end{eqnarray}](/articles/aa/full_html/2013/12/aa21917-13/aa21917-13-eq99.png) (2)where
(2)where
 is the gravitational constant, and h, q and
Σ0 are the scale height, the shape of the surface density profile and the
surface density of the disk at 1 AU, respectively. It is worth mentioning that the model
is valid only for low eccentricities (e ≲ 0.05) and small planetary
masses (≲13 M⊕). In the case of a smooth density profile,
explicit expressions for the forces acting on the planetary masses can be found in Ogihara
& Ida (2009) and Ogihara et al. (2010), while model applications can be found in
Giuppone et al. (2012). In our simulation, we
assumed a scale height
h = H/r = 0.05 and
a constant surface density profile
Σ(r) = Σ0(r/1 AU)− q
with q = 0 and Σ0 = 150 g/cm2, which corresponds
to the minimum mass solar nebula at 5 AU (MMSN, Hayashi 1981). Rein et al. (2010) assumed a more
massive protoplanetary disk, with a surface density five times higher than the MMSN. From
Eq. (2), we estimate that for the chosen
disk parameters, the e-damping is ~100 times faster that the
a-decay.
is the gravitational constant, and h, q and
Σ0 are the scale height, the shape of the surface density profile and the
surface density of the disk at 1 AU, respectively. It is worth mentioning that the model
is valid only for low eccentricities (e ≲ 0.05) and small planetary
masses (≲13 M⊕). In the case of a smooth density profile,
explicit expressions for the forces acting on the planetary masses can be found in Ogihara
& Ida (2009) and Ogihara et al. (2010), while model applications can be found in
Giuppone et al. (2012). In our simulation, we
assumed a scale height
h = H/r = 0.05 and
a constant surface density profile
Σ(r) = Σ0(r/1 AU)− q
with q = 0 and Σ0 = 150 g/cm2, which corresponds
to the minimum mass solar nebula at 5 AU (MMSN, Hayashi 1981). Rein et al. (2010) assumed a more
massive protoplanetary disk, with a surface density five times higher than the MMSN. From
Eq. (2), we estimate that for the chosen
disk parameters, the e-damping is ~100 times faster that the
a-decay.
The inner planet was placed initially on an orbit similar to that of Jupiter, at a1 = 5.2 AU, while the outer planet was located on the Saturn orbit at a2 = 9.5 AU, yielding the initial configuration beyond the 2/1 MMR, at n1/n2 ~ 2.46 (or n2/n1 ~ 0.4). The initial eccentricities of the planets were e1 = e2 = 0.02, and the values of their angular elements were chosen to be equal to zero. The set of disk parameters and the initial configurations are referred to hereafter as the standard configuration; it is summarized in Table 2 (first row). The results of the planet growth simulation based on the standard configuration are shown in Figs. 7−9.
 |
Fig. 7 Two stages of the mass growth of the HD 45364 planets (in logarithmic scale). During the first stage (blue line) which lasts 106 yr, the equal-mass planets grow with the same rate, from 0.1 M⊕ to ~10.0 M⊕. During the second stage, the runaway growth occurs with different rates in such a way that the inner planet (black line) reaches 0.187 MJ and the outer planet (red line) 0.658 MJ after ~ 1.5 × 105 years. |
The blue line in Fig. 7 shows the mass evolution (identical for both planets) during the first phase of formation. Figure 8 shows the decay both of the semimajor axes (top graph) and of the mean-motion ratio (bottom graph). The smooth evolution of the system, even during the passages through the 2/1 and 5/3 MMRs, is noticeable. The system approaches the 3/2 MMR in about 8 × 105 years.
 |
Fig. 8 Orbital decay of the HD 45364 planets during the first stage of the mass growth. The top panel shows the evolution of the two semimajor axes, while the bottom panel shows the mean-motion ratio as a function of time. The system approaches the 3/2 MMR at ~ 8 × 105 years. |
 |
Fig. 9 Evolution of the eccentricities (top panel) and the angles σ1 and Δϖ (bottom panel) during the first stage of the mass growth. The locations of the 2/1 and 5/3 MMRs are shown with vertical lines. |
The time evolution of the planet eccentricities is shown at the top of Fig. 9. Due to the strong damping provoked by interactions with the disk, both eccentricities drop rapidly to 0. The passage through the 2/1 MMR, at ~5.7 × 105 years, provokes some visible excitations of both eccentricities, which are damped again as soon as the system leaves the 2/1 MMR. When the planets cross the strong 2/1 MMR, their masses are still small, ~1.2 M⊕, the eccentricity excitation is weak, and no resonant capture is observed.
Approaching the very strong 3/2 MMR after ~8 × 105 years of evolution, the two planets have masses of ~6 M⊕. The excitation of the planet eccentricities (Fig. 9 top) and the characteristic behavior of the resonant angle σ1 and the secular angle Δϖ (Fig. 9 bottom) confirm that the system evolves close to the 3/2 MMR.
The first stage ceases after 106 years, with two planets locked near the 3/2 MMR. The masses of the inner and outer planets have grown up to to 10.0 M⊕ (~0.03 MJ). This value corresponds to the critical value for which the envelope mass of the planets is nearly equal to their core mass (Alibert et al. 2005; Armitage 2010) and runaway growth begins (Pollack et al. 1996; Rice & Armitage 2003; Ikoma et al. 2000).
4.2. Probability of the trapping in the 3/2 MMR during stage I
We tested different parameter sets of the disk and the initial planet configurations. Some of these sets are present in Table 2, where the first row shows the parameters of the standard configuration and the other rows show one-by-one (systematic) parameter changes of this configuration. The last column shows the final configurations of the system at the end of stage I of the evolution. We detected three possible final configurations: the trapping in the 3/2 MMR, the capture in the 2/1 MMR, and the non-resonant configuration caused by the diverging evolution of the planet orbits.
From Table 2, we observe that the 3/2 trapping of the standard configuration of the HD 45364 system is not sensitive to the variations of the initial conditions (runs #1–#4). This result may be easily understood by analyzing the evolution of the orbital elements in Figs. 8 and 9. Indeed, due to the continuous decay of the planets, the different initial positions from the central star will only accelerate/decelerate the trapping in the 3/2 MMR. The non-zero initial eccentricities are rapidly damped to zero-values by the disk-planet interactions, and consequently have no effect on the capture into a mean-motion resonance. Finally, for nearly circular orbits, the angular variables σ1 and Δϖ are high-frequency circulating angles that can acquire any value in the range of 0 and 360°.
This changes when we consider different disk properties (runs #5–#9 in Table 2), specially the different values of the shape of the surface density profile q. Indeed, from Eq. (2), we have that ȧ ∝ a(1.5 − q). For low q-values (in our runs, <0.25), the decay of the outer planet is much faster than that of the inner planet (ȧ2 ≫ ȧ1), which causes a rapid convergence of the planetary orbits and the non-capture passage through the 2/1 MMR.
For higher q-values (run # 6, with q = 0.5), the orbits converge more slowly (ȧ2 > ȧ1) and the capture inside the 2/1 MMR becomes possible, which reduces the probability of trapping in the 3/2 MMR. This result agree with the investigations of the capture probability inside the first-order resonances as a function of the rate of the orbital convergence present in Mustill & Wyatt (2011). Finally, for q = 1.5 (run # 7), ȧ2 = ȧ1 and the two orbits diverge, that is, the planet distance increases during the orbital decay.
We can conclude that for sufficiently low q-values (q ≤ 0.25), that is in a disk with a smooth surface density profile, the trapping inside the 3/2 MMR is robust during the first stage of the planet formation/migration.
4.3. Stage II: runaway mass growth and type II migration
The second stage of the evolution begins when the envelope mass of the planet becomes equal to or larger than the core mass of the planet; as a consequence, the accretion rate is accelerated dramatically and the runaway growth is initiated (Pollack et al. 1996; Ikoma et al. 2000; Armitage 2010). This phase lasts on average approximately ~1 × 105 years (Alibert et al. 2005; Armitage 2010; Hasegawa & Pudritz 2012). During this stage, the mass growth of the planets is approximated by an exponential law m(t) = miexpt/τi, where mi are the initial masses of the planets and τi are the e-folding times of the planet growth (i = 1,2). The values of mi come from stage I and are 10.0 M⊕, for both planets. The values of τi were chosen to be 5.6 × 104 years and 3.5 × 104 years for the inner and outer planets, respectively, such that the planets reach their current masses (0.1872 MJ and 0.6579 MJ) after 1 × 105 years.
Figure 7 shows the exponential accretion of the planet masses during the second phase: the rapid growth of the outer planet is plotted as a red line and the slower growth of the inner planet as a black line. The growth process is stopped after ~1.1 × 106 years, and the final values of the planetary masses are compatible with those of the C09 and R10 solutions.
As the planets become more massive, the structure of the disk in their neighborhood is
modified and gaps begin to form. From this stage onward we assume a type II of migration
of the two planets that already locked near the 3/2 MMR resonance. To simulate this
migration, we applied a Stokes-like non-conservative force (Beaugé et al. 2006). The effects of the Stokes force on the semimajor
axis and eccentricity evolution are decay and damping, respectively, given as
 (3)where
a0 and e0 are the initial values
of the semimajor axis and the eccentricity, respectively, and
τa and
τe are the e-folding times of the
corresponding orbital elements (Beaugé & Ferraz-Mello 1993; Gomes 1995). The planet
configurations at the end of stage I of the evolution were used as input of the second
stage.
(3)where
a0 and e0 are the initial values
of the semimajor axis and the eccentricity, respectively, and
τa and
τe are the e-folding times of the
corresponding orbital elements (Beaugé & Ferraz-Mello 1993; Gomes 1995). The planet
configurations at the end of stage I of the evolution were used as input of the second
stage.
 |
Fig. 10 Orbital decay of the HD 45364 planets during the second stage of the planet formation. The top panel shows the evolution of the two semimajor axes, while the bottom panel shows the mean-motion ratio as a function of time. The black dots correspond to the K3 solution and the red dots to the K100 solution. |
The loss of the orbital energy during the migration of the planets toward the central star defines the choice of the values of the e-folding times τa. They are typically obtained through adjustment between the migration duration and the final planet positions, which, in the case of the HD 45364 system, are roughly a1 ~ 0.68 AU and a2 ~ 0.90 AU (Table 1). If we assume that the second stage lasted 1.5 × 105 years, we obtain τa1 = 6 × 105 and τa2 = 3 × 105 years.
Choosing the e-folding times of the eccentricity damping is more complicated. This is because the exchange of the angular momentum between the planets and the disk is very sensitive to the disk properties and the processes involved. In the simplified simulations based on the Stokes-like forces, it is common to introduce the factor K = τa/τe, which is the ratio of the e-folding times of the orbital decay and the eccentricity damping, and use it as a free parameter (Lee & Peale 2002; Beaugé et al. 2006; Kley et al. 2005). The typical values of the factor K lie in the range of 1 and 100 (Lee & Peale 2002). We tested several values of K from this interval and chose two specific values; they are same for both planets and are 3 and 100. Hereafter, we refer to these solutions as K3 and K100. The values of the masses and the orbital configurations are given in the two last columns in Table 1.
The stability of the two solutions was tested and confirmed using the stochasticity indicator MEGNO (Cincotta & Simó 2000). We found that both systems achieve ⟨ Y ⟩ = 2 in ~3000 years. The two simulations also agree well with the observation data. The corresponding radial velocity fits are shown in Fig. 4 as black and red lines for K3 and K100. The χ2-values shown in Table 1 confirm the statistical equivalence of our solutions with the solutions C09 (green line) and R10 (yellow line). We stress that no effort was made to minimize the χ2-value by fine-tuning the parameters of the problem.
The dynamics of the K3 solution is similar to the best fit C09 solution, while the K100 solution reproduces solution R10 well. The time evolution of solutions K3 and K100 is shown in Figs. 10 and 11 as black and red lines. The migration process characterized by decay of the planetary semimajor axes is shown at the top of Fig. 10: the time-span of the decay, defined by the value of τa1 and τa2, is extended to ~1.15 × 106 years. We can see that the averaged magnitudes of the semimajor axes of K3 at the end of migration are compatible with those of the best fit of Correia et al. (2009) and of K100 with the F5 simulation of Rein et al. (2010) (see Table 1). Although the top graph in Fig. 10 seems to show no difference between the values of the semimajor axes of the two solutions, in the enlarged scale we can observe a small but important difference (see Table 1), which implies that for K = 100, the mean-motion ratio n1/n2 ~ 1.52 (close to the R10 solution); for K = 3, n1/n2 ~ 1.5 (close to the C09 solution).
 |
Fig. 11 Evolution of the eccentricities (top panel) and the angles σ1 and Δϖ (bottom panel) during the second stage of planet formation, when the planets increase their masses from 10.0 M⊕ to the current values. The black dots correspond to the K3 solution and the red dots to the K100 solution. |
The behavior of the eccentricities and the characteristic angles σ1 and Δϖ during the second stage of migration is shown in Fig. 11, again with a red line for K = 100 and a black line for K = 3. Because the migration is enough slow the evolution of the eccentricities (top panel) closely follows the family of stationary solutions of the conservative 3/2 resonant problem, the ACR-family (Beaugé et al. 2003, Michtchenko et al. 2006). The different rates of the mass accretion, when the outer planet grows more rapidly, are responsible for the excitation and the continuous increase of the eccentricity of the less massive inner planet (the evolutionary paths are discussed in Sect. 5). We can see that the results obtained for K = 3 reproduce the high eccentricities of C09, while the results obtained with K = 100 reproduce the low-eccentricity solution R10.
The evolution of the characteristic angles σ1 and Δϖ (bottom panel in Fig. 11) shows low-amplitude oscillations around 0 and 180°, respectively, for both solutions. Despite the apparently similar behavior of the characteristic angles in both cases, the dynamical analysis shows that solution K3 is involved deeply inside the 3/2 MMR during this stage, while solution K100 is in a quasi-resonant state, similar to the system R10 (see Sect. 2.1).
During the last 5 × 104 years of the process, the gas disk is dissipated, while the pair of previously formed planets, trapped in the 3/2 MMR (see Fig. 10), continues to decay slowly (since the characteristic frequencies of the system evolution are, at least, one order higher, this process can still be considered to be adiabatic). The disk is dissipated completely after 1.15 × 106 years and the planets begin to evolve solely due to their mutual gravitational perturbations (the last 104 years in our simulation). The time-span of 1.15 × 106 years is compatible with the lifetime of protoplanetary disks, which is estimated to lie between 1−10 Myr (Armitage 2010; Haisch et al. 2001).
5. Evolutionary paths during capture in the 3/2 MMR
Figure 12 shows the projections of the
high-eccentricity C09 solution and the low-eccentricity R10 solution (green dots) on the
(e1,e2) – plane.
We plot two ACR-families parameterized by the ratios of the initially equal masses
m2/m1 = 1.0 and
of the actual planet masses
m2/m1 = 3.51
(continued curves). The motion of solutions C09 and R10 on this plane is an oscillation
around an ACR defined by the total angular momentum  and the scaling parameter
and the scaling parameter 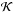 (see Eq. (1)). Since the planet masses and the semimajor axes are
similar, the
(see Eq. (1)). Since the planet masses and the semimajor axes are
similar, the 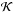 -parameter
is the same for both solutions, and the difference in the positions of the corresponding ACR
is due to distinct values of the angular momentum
-parameter
is the same for both solutions, and the difference in the positions of the corresponding ACR
is due to distinct values of the angular momentum 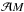 (or eccentricities). It must be kept in mind that the difference between the two solution is
qualitative: the solution C09 is resonant, while the solution R10 is quasi-resonant (Sect.
2.1).
(or eccentricities). It must be kept in mind that the difference between the two solution is
qualitative: the solution C09 is resonant, while the solution R10 is quasi-resonant (Sect.
2.1).
 |
Fig. 12 Projections of the C09 and R10 oscillations (green dots) and the K3 and K100 evolutionary paths during the two stages of planet formation/migration on the (e1,e2)-plane. The first stage of accretion includes the passage through the 2/1 MMR and the capture into the 3/2 MMR (blue points). The evolution during the second stage of the runaway mass growth and the type II migration is shown as black dots for the K3 solution and as red dots for the K100 solution. The ACR-families are shown by continuous lines; one is parameterized by m2/m1 = 1, the other by m2/m1 = 3.51. The black cross shows the initial configuration of the planet pair. |
The same (e1,e2)-plane can also visualize the capture process of the system inside the 3/2 MMR. We show the projections of the two evolutionary paths, K3 and K100, during the two stages described in Sect.4.
The first stage is the fast type I migration of the initially equal-mass planetary embryos (0.1 M⊕) that grow with the same rate until ~10.0 M⊕ during 106 years; the evolution of the system during this stage is similar for both simulations. The initial planet configuration is shown as a black cross at e1 = e2 = 0.02. Blue dots show first the rapid eccentricity-damping to the circular orbits, then the passages through 2/1 MMR, with a slight excitation of the planet eccentricities, and finally the approach to the 3/2 MMR. Since the planet masses are still equal during this stage, the evolution occurs along the ACR-family parameterized by m2/m1 = 1.
In the second stage of the slow type II migration and the fast runaway mass accretion, the evolution of two solutions becomes distinct due to the different rates of the mass growth. Both solutions diffuse in the direction of the ACR-family parameterized by the actual ratio m2/m1 = 3.51, but the path on the (e1,e2) taken by the K100 solution (red dots) is much shorter than that taken by the K3 solution (black dots). This is because the value K = 100 implies a strong damping of the eccentricities during the second stage of the evolution and the consequent formation of the system in the quasi-resonant state, similar to that proposed by Rein et al. (2010). Thus, our scenario is able to reproduce the R10 solution well, without invoking type III migration and high disk density.
The solution obtained with K = 3 exhibits a resonant dynamical behavior similar to that of the C09 configuration of the HD 45364 system (Correia et al. 2009). Moreover, the magnitudes of the orbital elements agree with the averaged values of solution C09, also as the resonant and secular frequencies. The discrepancy with C09 we have noted lies in the amplitudes of the orbital elements oscillation around the corresponding ACR solution of the maximal energy. This may be explained by simplifications introduced in our model, which, for instance, do not account for stochastic processes during the planet formation/migration. The stochastic forces can be responsible for weak energy fluctuations and a consequent deviation of the system from the highest energy equilibrium configuration. This would imply increasing oscillation amplitudes of the orbital elements of the planets observable in the best fit solution of Correia et al. (2009).
6. Conclusions
We have presented a new scenario for the origin of HD 45364, which, depending on the free parameter K, reproduces both the resonant and quasi-resonant configurations of the system. The former is associated to the best fit solution by Correia et al. (2009), the other is the simulation of Rein et al. (2010). We considered that the migration process of the planets began during the first stages of mass growth. The initial planetary masses were chosen to be on the order of planetary embryos and, at the end of the formation process, they achieved giant planet masses. The system formation involved both type I and type II migration sets. The total time-span of simultaneous accretion and migration was assumed to have lasted ~106 years, which is compatible with the lifetimes observed for protoplanetary disks.
Our scenario presents several differences with respect to that proposed by Rein et al. (2010). The first one concerns the type of migration assumed to have dominated the resonance trapping: instead of the non-conventional type III migration, we considered the combined effects of type I and the type II migration processes, depending on the planetary masses. We found that the passage across the 2/1 and 5/3 MMRs, without capture inside them, is possible during the type I migration assuming small planetary masses instead of Jupiter-like masses. We showed that this process remains the same when we considered the vertically isothermal and laminar disk with a nearly constant surface density profile.
The other difference between two scenarios concerns the disk properties. To simulate type III migration, Rein et al. (2010) needed to consider a massive protoplanetary disk, with a surface density five times higher than the MMSN. On the other hand, the observational data indicate a correlation between the mass of the disk and that of the central star: the median disk-to-star mass ratio is ~0.5% (Andrews & Williams 2005). Therefore, for the HD 45364 star of 0.82 M⊙, the assumption of a disk with 5 MMSN seems to be unreasonable. Moreover, the massive disk implies extremely short times-pans of planet formation, order of 103 years. In contrast, our scenario assumes the typical MMSN for the disk in the first stage of the planet formation/migration and a duration of the planet formation on the order of 106 years, compatible with the lifetimes observed for the protoplanetary disks.
We also explored the different features of the disk during the second stage of the runaway planet formation and the slow type II migration. This was made by introducing a free parameter K = τa/τe, defined as the ratio between the e-folding times of the orbital decay and the eccentricity damping (Lee & Peale 2002; Beaugé et al. 2006; Kley et al. 2005). We found that for high values of K, the intense eccentricity damping prevents the resonant capture of the planets; in this way, the pair remains close to the 3/2 MMR, in a quasi-resonant state. It is interesting to note that this feature might explain the abundance of the low-eccentricity Kepler objects close to the strong first-order MMRs. Our simulation run with K = 100 produced a quasi-resonant pair of the HD 45364 planets, similar to the F5 simulation of Rein et al. (2010).
For low values of K, the interactions with the protoplanetary disk allow an effective locking of the planetary motions in the 3/2 MMR, inside the resonant domain. Our simulation run with K = 3 produced a resonant pair of the HD 45364 planets, similar to the best fit simulation of Correia et al. (2009). Thus, the quasi-resonant or resonant configurations of the HD 45364 system have been shown to be a direct consequence of the properties of the assumed gas disk. The additional radial velocity measurements can confirm the real configuration of the HD 45364 system, allowing to assess the physical properties of the primordial protoplanetary disk of this system.
Finally, we emphasize that the formation and capture model of the HD 45364 system in the 3/2 MMR presented here suffers from several simplifications and limitations; for instance, the exponential law for the mass growth was assumed arbitrarily, and the complex processes produced by interactions between the gas/dust disk and the growing planets were schematized assuming simple analytical expressions for the orbital decay and eccentricity damping. On the other hand, it should be noted that i) these expressions are provided by solid theories on the formation and early evolution of the planets; ii) the values of physical and orbital parameters used in the simulations are consistent with observed and widely accepted values; and iii) the final solutions are robust in the range of the typical input parameters of the model. Therefore, we consider our model as a plausible mechanism to explain the possible near 3/2 resonance configuration of the HD 45364 system.
Acknowledgments
This work was supported by the São Paulo State Science Foundation, FAPESP, the Brazilian National Research Council, CNPq, and the Argentinean Research Council, CONICET. This work has made use of the facilities of the Computation Center of the University of São Paulo (LCCA-USP) and of the Laboratory of Astroinformatics (IAG/USP, NAT/Unicsul), whose purchase was made possible by the Brazilian agency FAPESP (grant 2009/54006-4) and the INCT-A. The authors are grateful to Hanno Rein for numerous suggestions and correction to this paper.
References
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Bate, M. R., Lubow, S. H., Ogilvie, G. I., & Miller, K. A. 2003, MNRAS, 341, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., & Ferraz-Mello, S. 1993, Icarus, 103, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., & Michtchenko, T. A. 2003, MNRAS, 341, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., Ferraz-Mello, S., & Michtchenko, T. A. 2003, ApJ, 593, 1124 [Google Scholar]
- Beaugé, C., Michtchenko, T. A., & Ferraz-Mello, S. 2006, MNRAS, 365, 1160 [Google Scholar]
- Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2009, A&A, 496, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., & Morbidelli, A. 2007, MNRAS, 377, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S., Beaugé, C., & Michtchenko, T. A. 2003, CeMDA, 87, 99 [Google Scholar]
- Ferraz-Mello, S., Michtchenko, T. A., Beaugé, C., & Callegari, N. 2005, Lect. Not. Phys., 683, 219 [Google Scholar]
- Ferraz-Mello, S., Michtchenko, T. A., & Beaugé, C. 2006, in Chaotic Worlds: From Order to Disorder in Gravitational N-body Systems, NATO Science Series II, eds. B. A. Steves, A. J. Maciejewski, & M. Hendry (Berlin: Springer), 255 [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gomes, R. 1995, Icarus, 115, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Giuppone, C. A., Benítez-Llambay, P., & Beaugé, C. 2012, MNRAS, 421, 356 [NASA ADS] [Google Scholar]
- Hadjidemetriou, J. D., & Psychoyos, D. 2003, Lect. Not. Phys., 626, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, 153 [Google Scholar]
- Hasegawa, Y., & Pudritz, R. E. 2012, ApJ, 760, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., Lee, M. H., Murray, N., & Peale, S. J. 2005, A&A, 437, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H. 2004, ApJ, 611, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Morbidelli, A., & Nesvorný, D. 2013, MNRAS, 431, 3494 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1979, MNRAS, 186, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., & Papaloizou, J. C. B. 2003, ApJ, 588, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Lazzaro, D., Ferraz-Mello, S., & Roig, F. 2002, Icarus, 158, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Ferraz-Mello, S. 2006, CeMDA, 94, 411 [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Ferraz-Mello, S. 2008a, MNRAS, 387, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Ferraz-Mello, S. 2008b, MNRAS, 391, 227 [Google Scholar]
- Mustill, A. J., & Wyatt, M. C. 2011, MNRAS, 413, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., & Papaloizou, J. C. B. 2004, MNRAS, 350, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., Duncan, M. J., & Ida, S. 2010, ApJ, 721, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., Papaloizou, J. C. B., & Kley, W. 2010, A&A, 510, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W. K. M., & Armitage, P. J. 2003, ApJ, 598, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Horner, J., Wittenmyer, R. A., et al. 2012, ApJ, 754, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Sándor, Zs., Kley, W., & Klagyivik, P. 2007, A&A, 472, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Voyatzis, G., & Hadjidemetriou, J. D. 2006, CeMDA, 95, 259 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time evolution of the semimajor axes of the inner planet (top panel), of the outer planet (middle panel), and the mean-motion ratio (bottom panel). The black curves correspond to the best fit C09 of Correia et al. (2009), while the red curves correspond to the solution R10 of Rein et al. (2010) |
| In the text | |
 |
Fig. 2 Same as in Fig. 1, except for the planet eccentricities (top panel) and the characteristic angles σ1 and Δϖ (bottom panel). |
| In the text | |
 |
Fig. 3 Energy levels of the 3/2 resonant Hamiltonian (1) on the (e1, e2)-plane for the C09 (top) and the R10 solution (bottom). The dashed green lines show the true separatrix (top) and the kinematic transition from oscillations to circulations (bottom). The ACR of each solution is presented with a red symbol, while the corresponding energy level is plotted as a continuous green curve. |
| In the text | |
 |
Fig. 4 Comparison of different orbital solutions: radial velocity measurements (blue dots), the best fit solution C09 (green line), the R10 simulation (yellow line), and our two solutions with K3 (black line) and K100 (red line). See text for details. |
| In the text | |
 |
Fig. 5 Dynamical maps of the domain between the 2/1 and 3/2 MMRs, for two fictitious systems composed of a solar-mass star and two planets with masses m1 = m2 = 1.0 MJ (top panel) and m1 = m2 = 0.1 MJ (bottom panel). The initial conditions are e1 = 0 and σ1 = 0; Δϖ is fixed at 0 (positive values on the e2-axis) or 180° (negative values on the e2-axis). The location of several MMRs are shown as vertical dashed lines. The light-gray tones correspond to regions of regular motion, while the hatched red regions correspond to strongly chaotic motion. |
| In the text | |
 |
Fig. 6 Resonance capture of a Jupiter-mass planet evolving assuming type II migration. Starting at n1/n2 > 2, the planet is ultimately trapped in the 2/1 MMR (top panel). Starting at 1.67 < n1/n2 < 2, the planet is trapped in the 5/3 MMR (middle panel), and starting at n1/n2 < 1.67, in the 3/2 MMR (bottom panel). |
| In the text | |
 |
Fig. 7 Two stages of the mass growth of the HD 45364 planets (in logarithmic scale). During the first stage (blue line) which lasts 106 yr, the equal-mass planets grow with the same rate, from 0.1 M⊕ to ~10.0 M⊕. During the second stage, the runaway growth occurs with different rates in such a way that the inner planet (black line) reaches 0.187 MJ and the outer planet (red line) 0.658 MJ after ~ 1.5 × 105 years. |
| In the text | |
 |
Fig. 8 Orbital decay of the HD 45364 planets during the first stage of the mass growth. The top panel shows the evolution of the two semimajor axes, while the bottom panel shows the mean-motion ratio as a function of time. The system approaches the 3/2 MMR at ~ 8 × 105 years. |
| In the text | |
 |
Fig. 9 Evolution of the eccentricities (top panel) and the angles σ1 and Δϖ (bottom panel) during the first stage of the mass growth. The locations of the 2/1 and 5/3 MMRs are shown with vertical lines. |
| In the text | |
 |
Fig. 10 Orbital decay of the HD 45364 planets during the second stage of the planet formation. The top panel shows the evolution of the two semimajor axes, while the bottom panel shows the mean-motion ratio as a function of time. The black dots correspond to the K3 solution and the red dots to the K100 solution. |
| In the text | |
 |
Fig. 11 Evolution of the eccentricities (top panel) and the angles σ1 and Δϖ (bottom panel) during the second stage of planet formation, when the planets increase their masses from 10.0 M⊕ to the current values. The black dots correspond to the K3 solution and the red dots to the K100 solution. |
| In the text | |
 |
Fig. 12 Projections of the C09 and R10 oscillations (green dots) and the K3 and K100 evolutionary paths during the two stages of planet formation/migration on the (e1,e2)-plane. The first stage of accretion includes the passage through the 2/1 MMR and the capture into the 3/2 MMR (blue points). The evolution during the second stage of the runaway mass growth and the type II migration is shown as black dots for the K3 solution and as red dots for the K100 solution. The ACR-families are shown by continuous lines; one is parameterized by m2/m1 = 1, the other by m2/m1 = 3.51. The black cross shows the initial configuration of the planet pair. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


