| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 27 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201321814 | |
| Published online | 11 December 2013 | |
On-sky characterisation of the VISTA NB118 narrow-band filters at 1.19 μm⋆
1 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
e-mail: milvang@dark-cosmology.dk
2 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3 TERAPIX/Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
4 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
5 Scottish Universities Physics Alliance (SUPA), Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh EH9 3HJ, UK
6 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
Received: 1 May 2013
Accepted: 18 October 2013
Observations of the high redshift Universe through narrow-band filters have proven very successful in the last decade. The 4-m VISTA telescope, equipped with the wide-field camera VIRCAM, offers a major step forward in wide-field near-infrared imaging, and in order to utilise VISTA’s large field-of-view and sensitivity, the Dark Cosmology Centre provided a set of 16 narrow-band filters for VIRCAM. These NB118 filters are centered at a wavelength near 1.19 μm in a region with few airglow emission lines. The filters allow the detection of Hα emitters at z = 0.8, Hβ and [O iii] emitters at z ≈ 1.4, [O ii] emitters at z = 2.2, and Lyα emitters at z = 8.8. Based on guaranteed time observations of the COSMOS field we here present a detailed description and characterization of the filters and their performance. In particular we provide sky-brightness levels and depths for each of the 16 detector/filter sets and find that some of the filters show signs of some red-leak. We identify a sample of 2 × 103 candidate emission-line objects in the data. Cross-correlating this sample with a large set of galaxies with known spectroscopic redshifts we determine the “in situ” passbands of the filters and find that they are shifted by about 3.5 − 4 nm (corresponding to 30% of the filter width) to the red compared to the expectation based on the laboratory measurements. Finally, we present an algorithm to mask out persistence in VIRCAM data. Scientific results extracted from the data will be presented separately.
Key words: techniques: photometric / instrumentation: photometers / methods: observational / galaxies: photometry / galaxies: high-redshift
© ESO, 2013
1. Introduction
The potential of narrow-band searches for redshifted emission lines from star-forming galaxies has been discussed in the literature for more than two decades (e.g., Pritchet & Hartwick 1987; Smith et al. 1989; Møller & Warren 1993). With the advent of sensitive detectors on large telescopes, large samples of e.g. Lyman-α (Lyα) emitting objects have been collected (e.g., Hu et al. 1998; Kudritzki et al. 2000; Steidel et al. 2000; Fynbo et al. 2001, 2003; Malhotra & Rhoads 2002; Hayashino et al. 2004; Venemans et al. 2005; Kashikawa et al. 2006; Grove et al. 2009; Ouchi et al. 2009, 2010). This selection method combines narrow-band imaging with observations in one or more broad-band filters. Objects that show excess emission in the narrow-band image compared to the broad-band images are selected as candidates. The result is a list of candidate emission-line galaxies within a narrow redshift range, typically Δz = 0.02 − 0.05. Multi-band photometry can be used to determine the approximate redshift of the emission line, allowing one to distinguish e.g. between Hα+[N ii] on the one hand and Hβ+[O iii] on the other, while spectroscopic follow-up is often necessary to establish the exact nature of the emission line source and to measure the precise redshifts.
Of particular interest is the search for Lyα emitters at very high redshift as a probe of the epoch of reionization (Partridge & Peebles 1967; Barton et al. 2004; Nilsson et al. 2007). At redshifts z > 7, this search requires narrow-band imaging in the near-infrared (NIR) as the emission line moves out of the sensitivity range of classical CCDs. Searches for emission line galaxies based on NIR narrow-band imaging are already maturing (e.g., Willis & Courbin 2005; Finn et al. 2005; Cuby et al. 2007; Geach et al. 2008; Villar et al. 2008; Sobral et al. 2009, 2012, 2013; Bayliss et al. 2011; Ly et al. 2011; Lee et al. 2012) but so far we lack any detections of narrow-band selected Lyα emitters at z ≳ 7.5 (see Shibuya et al. 2012; Rhoads et al. 2012; Clément et al. 2012, and references therein).
The advent of the VISTA telescope (e.g. Emerson et al. 2006; Emerson & Sutherland 2010a,b) and its wide-field camera VIRCAM (Dalton et al. 2006, 2010) provides a new opportunity to undertake a deep, wide-field search for emission-line galaxies. To take advantage of this opportunity, we acquired a set of narrow-band filters (named NB118) for the VISTA telescope. The filters were designed to be about 10 nm wide and centred at around 1185 nm where there is a prominent gap in the night sky OH forest (Barton et al. 2004).
The NB118 filters allow a search for a number of line emitters at various redshifts. The most prominent are Hα emitters at z = 0.8, Hβ and [OIII] emitters at z ≈ 1.4 and [OII] emitters at z = 2.2. The forbidden oxygen lines are metallicity dependent, but also affected by active galactic nuclei (AGN). Nevertheless, in particular [OII] is still a good tracer of star formation and hence we will have an interesting handle on the star formation density at z = 2.2 (e.g., Sobral et al. 2012; Ly et al. 2012; Hayashi et al. 2013), which is complementary to broad- or narrow-band surveys targeting similar redshifts (Adelberger et al. 2004; Nilsson et al. 2009). Follow-up spectroscopy of these candidates can provide insight into the metallicity evolution of star forming galaxies with redshift (Kewley & Ellison 2008). If sufficient sensitivity can be reached, the filters will also allow a search for Lyα emitters at z = 8.8. This type of survey is currently being undertaken as part of the ongoing UltraVISTA survey (McCracken et al. 2012)1.
In return for providing ESO with the set of 16 NB118 filters (one per detector), we were awarded 3 nights of guaranteed time observations (GTO) on VISTA (PI: Fynbo), cf. Sect. 2.2. This paper is the first to report results obtained with the NB118 filters on VISTA. Therefore, the primary purpose of the paper is to describe the NB118 filters, to characterize the data obtained with them, and to describe how best to reduce the narrow-band images. In order to quantify the performance of the filters we report on some preliminary results, but the final scientific exploitation of the NB118 GTO data will be the subject of a separate paper.
This paper is organised as follows: in Sects. 2 and 3 we describe our observations and data reduction. In Sect. 4 we describe the NB118 filters and predict their filter curves based on laboratory measurements. In Sect. 5 we select objects with narrow-band excess, cross correlate with spectroscopic redshift catalogues, and infer the on-sky filter curves. In Sect. 6 we analyse the NB118 sky brightness based on observations, and we investigate indications of red-leaks. In Sect. 7 we use models of the sky background to investigate both the absolute sky brightness and the changes resulting from a shift of the wavelengths of the filters. In Sect. 8 we summarize the main findings. In Appendix A we describe the persistence masking algorithm we developed.
The photometry is on the AB system (Oke & Gunn 1983) and the wavelengths are in vacuum, unless stated otherwise.
2. Field selection and observations
2.1. Field selection
 |
Fig. 1 Schematic sky coverage. Blue hatched columns: stripes observed in this GTO work. Red filled columns: UltraVISTA ultra-deep stripes. Blue outline: UltraVISTA contiguous region. Green outline: HST/ACS region. |
For the GTO programme described in this paper we targeted part of the COSMOS field (Scoville et al. 2007b) due to its wealth of multi-wavelength data, including data from the UltraVISTA survey (McCracken et al. 2012). We selected our subfield within the COSMOS field in coordination with UltraVISTA as illustrated by Fig. 1. The outer blue rectangle of size ≈ 1.5° × 1.2° is the UltraVISTA contiguous region, where UltraVISTA provides imaging in Y, J, H and Ks to varying depths (referred to as either “deep” or “ultra-deep”). The 4 filled stripes are the UltraVISTA ultra-deep stripes, where UltraVISTA additionally provides imaging in NB118. The 4 hatched stripes are the stripes observed in this GTO programme in NB118 (and to a smaller extent also in J); these stripes have imaging in Y, J, H and Ks but not NB118 from UltraVISTA. The area of the stripes is 1 deg2 (see Sect. 3.7). The green, jagged outline shows the HST/ACS imaging (Scoville et al. 2007a), which covers almost the full GTO area.
2.2. Observations
Observations using VIRCAM on VISTA were obtained in visitor mode during 6 half-nights (second half of the night), starting on the night beginning 2010 January 17. In the first 4 half-nights about 3 h were spent on NB118 observations followed by about 1.5 h on J-band observations, while in the last 2 half-nights all time was spent on NB118 observations. This is illustrated by Fig. 11 below, which shows sky level in the two filters versus time. The moon was below the horizon all the time. The seeing in the obtained NB118 images, as computed by the QualityFITS tool, had a median value of 0.83′′ and a mean value of 0.89′′. The mean airmass of the NB118 observations was 1.19.
The sky coverage of VIRCAM in a single exposure, the so-called pawprint, is illustrated in panels (a) − (c) of Fig. 2. A pawprint covers 0.6 deg2 on the sky (16 detectors each 20482 pixels with a scale of 0.34′′ px-1). The 16 detectors are widely spaced, with gaps that are slightly less than a full detector in X and half a detector in Y. The 3 particular positions on the sky shown by the pawprints in panels (a) − (c) are named paw6, paw5 and paw4 within the UltraVISTA project. They are spaced in Y (here Dec) by 5.5′, and by combining exposures taken at these 3 positions, one gets a set of 4 stripes or columns (see Fig. 2d) in which each pixel typically receives data from 2 of the 3 pawprints.
 |
Fig. 2 a) − c) Individual VIRCAM NB118 exposures obtained at the positions named paw6, paw5 and paw4, respectively. d) The NB118 stack. In panel a) the detector numbers are given. North is up and east is to the left. |
The observing strategy employed in this project was to obtain a single exposure at each pawprint position and then move to the next, in the sequence paw6, paw5, paw4; paw6, paw5, paw4; etc. The moves paw6 → paw5 and paw5 → paw4 were always 5.5′ in Dec, i.e. with no random component, and only in the paw4 → paw6 move a random component (jitter), drawn from a box of size 122′′ × 122′′ in RA × Dec, was added2. The lack of a random component in some of the telescope moves meant that fake sources (so-called persistent images) were present when we first stacked the data, despite combining the individual images using sigma clipping. Only after developing a method to mask the fake sources in the individual images (see Sect. 3.3), the resulting stack was free of such fake sources.
The exposure times of the individual images were 280 s in NB118 (NDIT = 1, DIT = 280 s) and 120 s in J (NDIT = 4, DIT = 30 s). The total exposure time obtained is listed in Table 1.
Total usable exposure time from the GTO programme.
2.3. Additional imaging
In addition to the NB118 and J-band VISTA data obtained in this programme, we used Y and J-band VISTA data from the UltraVISTA DR1 dataset (McCracken et al. 2012). Specifically, for Y we directly use the stack and weight map from McCracken et al. (2012), although we add 0.04 mag to the zeropoint to reproduce the effect of the latest photometric calibration (colour equation) from CASU (Sect. 3.2). For J, we use the individual images and weight maps (which McCracken et al. 2012 used to make their stack) and combine them with the individual images and weight maps from our programme (Sect. 3.4). This combined J-band stack has a typical exposure time per pixel of 17.2 h in the stripes of interest here, of which 13.8 h come from UltraVISTA (Table 2 in McCracken et al. 2012) and 3.4 h come from our programme (Table 1). We use the NB118, J and Y photometry to select candidate emission line objects (Sect. 5.1).
3. Data reduction
3.1. Processing in the Data Acquisition System
VIRCAM uses correlated double sample (CDS) readout mode, also known as Fowler-1 sampling (Fowler & Gatley 1991; McMurtry et al. 2005) and as a reset-read-read sequence. This means that if the user requests a single 280 s exposure (DIT = 280 s, NDIT = 1), the Data Acquisition System (DAS) will (a) reset the detectors, (b) integrate on sky for 1 s and read, (c) integrate on sky for 281 s and read, and (d) write the difference between the second and the first readout to disk. (For NDIT > 1 the above procedure is carried out NDIT times, and the delivered FITS file contains the sum of the NDIT image differences.) This process is transparent to the user, but it has implications for the appearance of saturated objects (Sect. 3.3), as well as for estimating the linearity of the detectors (Sect. 3.2 and Lewis et al. 2010). It also means that the pedestal (bias) level set by the readout electronics has already been subtracted by the DAS, removing the need for such a reset correction in the subsequent reduction pipeline (Sect. 3.2). The effective readout noise resulting from this readout mode is about 23 e − on average over the 16 detectors (see e.g. the VIRCAM/VISTA user manual). No other readout modes are offered.
3.2. Processing at CASU
All VISTA data are processed by the VISTA Data Flow System (VDFS) (e.g. Emerson et al. 2004), which consists of quality control pipelines at ESO Paranal and Garching (e.g. Hummel et al. 2010, and the VIRCAM/VISTA user manual), a science reduction pipeline at the Cambridge Astronomy Survey Unit (CASU) (e.g. Irwin et al. 2004; Lewis et al. 2010, and the CASU web site3), and a generation of futher data products and archiving at the VISTA Science Archive (VSA) at the Wide-Field Astronomy Unit (WFAU) in Edinburgh (e.g. Hambly et al. 2004; Cross et al. 2012). For the present work, only the CASU processing is relevant. The “raw” (as coming from the DAS, see Sect. 3.1) individual images, i.e. the set of 16 detector images for a single exposure, undergo the following processing steps in the CASU science pipeline:
-
Dark correction, performed by subtracting a combined darkimage based on individual dark images with the same DIT andNDIT as the science image in question; this corrects both for thethermal dark current and for the effect termed “reset anomaly”(e.g. Irwinet al. 2004, and theVIRCAM/VISTA user manual).
-
Nonlinearity correction, derived from screen flats (dome flats) of different exposure times, taken under a constant light level.
-
Flat field correction, performed by division by a normalised, combined twilight sky flat field image. This step corrects for small-scale variations in the quantum efficiency within each detector as well as for the vignetting of the camera. This step also corrects for more effects by virtue of the normalisation: all 16 detector images of the flat field are normalised by the same number, namely the mean (over the 16 detectors) of the median level in each detector. The resulting flat does not have a level near 1 in each detector; rather, it has a level of about 1.15 in detector 1 and 0.70 in detector 2, for example (this value is recorded in the GAINCOR header keyword for the given detector). This means that the combined effect of detector-to-detector differences in gain (in e− ADU-1) [ADU: analogue-to-digital unit] and in overall quantum efficiency (QE) are removed. The unit of the counts in the flat-fielded science images is termed “gain-normalised ADU”. If QE differences are ignored, these counts can indeed be converted to electrons using a single gain valid for all detectors; this gain is about 4.2 electrons per gain-normalised ADU.
-
Sky background correction or sky subtraction, performed by subtracting a sky image. The sky images are made by splitting the time sequence of science images into blocks; for this dataset blocks of 6 images were used. The objects in the images are masked (for this dataset using a mask we provided, which was based on existing Ks and i-band data), and then these 6 object-masked images are combined to form the sky frame. This single sky frame is normalised by subtracting its median level and then subtracted from the 6 science images.
-
Destriping, which removes stripes caused by the readout electronics. The stripes are horisontal in the detector x,y coordinate system contained in the raw FITS files. For our data taken with a position angle of 0°, the stripes are vertical in our astrometrically calibrated images having north up and east left.
-
Astrometric calibration, based on the 2MASS catalogue (Skrutskie et al. 2006).
The VIRCAM data show no evidence of detector crosstalk or sky fringing, so the pipeline does not need to correct for these effects (Lewis et al. 2010).
The reduced individual images for each OB and each pawprint are stacked (hereafter referred to as the _st stacks). For example, our NB118 data resulted in 18 _st stacks, since our OBs obtained data at 3 pawprint positions and since one OB was executed per night for 6 nights. In these stacks, a photometric calibration onto the VISTA photometric system is performed, see the CASU web site4, the presentation by S. Hodgkin5, and the paper by Hodgkin et al. (2009) describing the analogous calibration for the UKIRT/WFCAM photometric system. The calibration works as follows. On the one hand instrumental total magnitudes for stars in the image are calculated from the flux (in units of gain-normalised ADU per second), corrected for the radially changing pixel size. On the other hand magnitudes in the VISTA photometric system (Vega) are predicted based on the 2MASS J, H and Ks (Vega) magnitudes for stars in the image using colour equations, which for Y, NB118 and J are 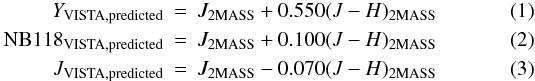 and where the stated coefficients refer to version 1.0 of the CASU VIRCAM pipeline6 which applies to the data used here; from CASU version 1.1, the coefficient for Y was changed to 0.610 and for J to − 0.077. The advantage of using standard stars (here the 2MASS stars) located in the image itself is that a zeropoint can be calculated simply by comparing the predicted magnitudes with the instrumental magnitudes − the actual atmospheric extinction for the given image (even including possible clouds) is automatically included. However, the CASU pipeline calculates a zeropoint “corrected” to airmass unity, which makes it easier to monitor e.g. the instrument throughput, but which necessitates a reverse correction when users want to transform instrumental magnitudes into magnitudes on the VISTA photometric system (cf. appendix C in Hodgkin et al. 2009). The equation for the CASU zeropoint, here for the Y band, reads
and where the stated coefficients refer to version 1.0 of the CASU VIRCAM pipeline6 which applies to the data used here; from CASU version 1.1, the coefficient for Y was changed to 0.610 and for J to − 0.077. The advantage of using standard stars (here the 2MASS stars) located in the image itself is that a zeropoint can be calculated simply by comparing the predicted magnitudes with the instrumental magnitudes − the actual atmospheric extinction for the given image (even including possible clouds) is automatically included. However, the CASU pipeline calculates a zeropoint “corrected” to airmass unity, which makes it easier to monitor e.g. the instrument throughput, but which necessitates a reverse correction when users want to transform instrumental magnitudes into magnitudes on the VISTA photometric system (cf. appendix C in Hodgkin et al. 2009). The equation for the CASU zeropoint, here for the Y band, reads 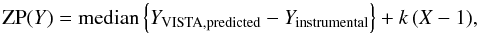 (4)where the median is taken over the used stars (typically 380 stars per image for our NB118 data), X is the airmass, and k is the atmospheric extinction coefficient, which seems to be 0.05 mag/airmass for all bands (listed in header keyword EXTINCT). This zeropoint at airmass unity is written to the header (keyword MAGZPT). For our NB118 and J-band data, the value of this keyword was the same for all 16 detectors. It makes sense that the zeropoint is almost the same for all detectors since the flat fielding has removed detector-to-detector differences in both gain and in QE; however, the colour of the twilight sky (used in the flat fielding) and of the astronomical objects of interest may differ, and filter-to-filter differences (since each detector has its own filter) could also be relevant. A robust estimate of the standard deviation of the differences between predicted and instrumental magnitudes over the used stars is written to keyword MAGZRR, which typically was 0.018 mag for our NB118 data.
(4)where the median is taken over the used stars (typically 380 stars per image for our NB118 data), X is the airmass, and k is the atmospheric extinction coefficient, which seems to be 0.05 mag/airmass for all bands (listed in header keyword EXTINCT). This zeropoint at airmass unity is written to the header (keyword MAGZPT). For our NB118 and J-band data, the value of this keyword was the same for all 16 detectors. It makes sense that the zeropoint is almost the same for all detectors since the flat fielding has removed detector-to-detector differences in both gain and in QE; however, the colour of the twilight sky (used in the flat fielding) and of the astronomical objects of interest may differ, and filter-to-filter differences (since each detector has its own filter) could also be relevant. A robust estimate of the standard deviation of the differences between predicted and instrumental magnitudes over the used stars is written to keyword MAGZRR, which typically was 0.018 mag for our NB118 data.
For completeness it should be mentioned that, as written here, the equations for the predicted magnitudes (Eq. (1) − (3)), or equivalently the equation for the zeropoint (Eq. (4)), miss a term of the form − c E(B − V)′, where E(B − V)′ is calculated from the Galactic reddening E(B − V) from Schlegel et al. (1998) using Eq. (1) in Bonifacio et al. (2000). This term corrects for the different stellar population mix found in highly reddened parts of the sky. The constant c is generally small, e.g. 0.14 for Y, and it is very small for bands within the JHKs wavelength domain of 2MASS, e.g. 0.01 for J. The term does not correct for Galactic extinction as such.
Processed data were made available to us by CASU on 2010 July 21. This included reduced individual images, calibration frames (darks, flats and sky frames) and _st stacks. We process these data further, as described in Sect. 3.4. The essence is that we undo the CASU sky subtraction in the individual images, apply our own sky subtraction and stack these images, masking fake sources (“persistent images”, see Sect. 3.3) at the same time. We do not use the _st stacks, except that we use the photometric calibration contained in their headers.
Reduced individual images were provided for all 258 obtained NB118 exposures, but only for 152 of the 164 obtained J-band exposures. The latter problem seems to be due to the J-band OBs being interrupted and restarted at two points due to minor technical (software) problems, which due to an unfortunate interplay between ESO’s automatic image grading and the CASU pipeline made some images be rejected. Since plenty of additional J-band data subsequently became available from UltraVISTA, this minor loss of data was not a problem.
3.3. Creation of persistence masks
The VIRCAM detectors do have some persistence, in which a somewhat bright star (down to say J ≈ 16) leaves a faint fake source at the same position on the detector in the next 1 or 2 images. For our observing pattern (nesting) such faint fake sources would add up in the stack, and it was therefore necessary to deal with this problem. We developed a masking algorithm that masks the affected pixels in the individual images, thus excluding those pixels when stacking the data. This algorithm is described in Appendix A. An illustration of persistence in individual VIRCAM images is given in the top row of Fig. A.1. The effect of persistence in the stack of our data without and with our persistence masking is illustrated in Fig. A.2.
3.4. Processing at TERAPIX
We used the TERAPIX (Traitement Élémentaire, Réduction et Analyse des PIXels) facility to process the individual reduced images from CASU (Sect. 3.2). This processing was similar to that done for the UltraVISTA DR1 data, and we refer to McCracken et al. (2012) for details. Here we will mention the main points.
The 410 individual reduced images (×16 detectors) from CASU (258 NB118 and 152 J-band images) and a number of diagnostic plots based on these were visually inspected within the Youpi7 environment (Monnerville & Sémah 2010). One NB118 image, namely the very first taken for this project, was found to contain a strange diagonal stripe, and was therefore flagged for exclusion from the stacking. Unlike for UltraVISTA DR1, we did not additionally reject images based on the PSF size or ellipticity.
For each image, a weight map was constructed as a copy of the flat field from CASU. Pixels in the bad pixel mask from CASU were set to zero. At this point all the weight maps would be identical and resemble the confidence map from CASU, which we do not use. For each weight map, a value of zero was assigned to the pixels in the computed persistence mask (Sect. 3.3) for the given image, enabling persistence-free stacks to be made. The weight maps were generated using the WeightWatcher tool (Marmo & Bertin 2008). The weight maps are used in the sky subtraction and in the stacking.
As the first step in the two-step sky-subtraction procedure, the individual images from CASU were stacked to produce a first-pass stack. From this, an object mask was generated and subsequently transformed (resampled) to create an object mask for each individual image.
As the second step, we apply our own sky subtraction. We first undo the CASU sky subtraction. Specifically, to each individual reduced image from CASU we add the sky frame from CASU for that image. A new sky subtraction was performed with the following three key features: (1) masking of objects was based on the above-mentioned first-pass stack of all the data plus a mask generated from the objects detected in the image itself (thus including artefacts not found in the stack, e.g. satellite trails and cosmics). For comparison, the CASU sky subtraction for this dataset used masking based on a mask we provided, which was based on existing Ks and i-band data. (2) For each image a sky frame was constructed from the images (excluding the image itself) in a window of ± 20 min centered on the image in question (also known as running sky or sliding sky). Since the NB118 images typically are spaced by 4.9 min, typically 8 images were used to create the sky frame, namely 4 images before and 4 after. For the images at the start or end of a sequence (an OB), the window was made asymmetric so that it would still contain 8 images (this differs from the UltraVISTA DR1 processing). For comparison, the CASU sky subtraction for this dataset consisted of creating a sky frame based on fixed groups of 6 NB118 images (corresponding to a time span of about 30 min) and using that sky frame to sky-subtract all 6 images. When inspecting the individual images as sky subtracted by CASU, we noted that the large-scale sky background was less flat for the images at the ends of such a 6-image sequence than for the images in the middle of the sequence. (3) Large-scale gradients were fitted and subtracted using SExtractor8 (Bertin & Arnouts 1996), with the objects being masked using the object masks also used in the sky subtraction process. Finally an additional destriping was done. After the sky subraction, the weight maps were updated, assigning a value of zero to pixels where no sky frame could be computed; this happens when the given pixel is masked in all the images used to create the sky frame. Also the catalogues needed for SCAMP (see below) were remade.
We note in passing that an earlier version of the TERAPIX sky-subtraction code had a bug involving images sometimes are shifted by 1 pixel. That bug has been fixed in this work. The bug affected the NB118 UltraVISTA DR1 stack.
For each image the astrometric and photometric solutions were computed using SCAMP9 (Bertin 2006). The photometric calibration is based on that provided by CASU. As described in Sect. 3.2, a photometric zeropoint is only derived for the _st stacks, of which there are 18 for the NB118 data. The zeropoint is listed as corrected to airmass unity, and we undo this correction, making the zeropoint applicable to the actual airmass. As the intial guess of the zeropoint for a given individual image we use the zeropoint of the _st stack in which the image is part. Using a catalogue for each image, SCAMP then compares the object fluxes between images and for each image computes a flux scale factor that will bring all images to agree. The absolute zeropoint is computed as the average over all the initial zeropoints: in the language of SCAMP all images were classified as photometric. While not all images may be photometric, the CASU zeropoints were computed from stacks of all the images, and therefore all images should be used to derive overall zeropoint. A conversion from Vega to AB was also included, using the same offsets as McCracken et al. (2012). The astrometric calibration was computed using the COSMOS CFHT i-band astrometric reference catalogue (Capak et al. 2007; McCracken et al. 2010, 2012). For the NB118 data, the internal astrometric scatter was 0.043′′ in RA and 0.062′′ in Dec for about 30 000 high S/N objects. The external astrometric scatter was 0.075′′ in RA and 0.077′′ in Dec for about 400 high S/N objects.
The individual images were regridded and stacked using SWarp10 (Bertin et al. 2002). The regridding (interpolation) was done to the same tangent point and pixel scale of 0.15′′ px-1 used in UltraVISTA and in most available images for the COSMOS field. For reference, the native pixel of VIRCAM is 0.34′′ px-1. The stacking was done using sigma clipping (at 2.8σ); a modified version of SWarp was used to accomplish this. The output files from SCAMP were used to define the astrometry and the photometric zeropoint of the stack. We created two stacks: an NB118 stack based on the GTO data, and a J-band stack based on both the GTO and the UltraVISTA DR1 data (McCracken et al. 2012).
3.5. Test using the CASU sky subtraction
As a test, we stacked the individual NB118 images as sky subtracted by CASU. This was done in almost the same way as for the individual images as sky subtracted by TERAPIX. Specifically, SWarp was run with the same parameters and the same individual SCAMP files (containing the astrometric and photometric solutions) were used. The only difference was that we let SWarp fit and subtract large-scale gradients in the individual images, since such gradients were clearly present.
Compared visually to the TERAPIX stack, the CASU-based stack had slightly more cosmetic problems on large scales. On small scales, the CASU-based stack sometimes showed stripes, but otherwise this stack appeared at least as deep as the TERAPIX stack. The result from empty aperture measurements is given in Sect. 3.8.
 |
Fig. 3 Empty aperture noise measurements for the GTO NB118 data. The rectangles in panel a) show the regions used to analyse the empty aperture measurements. The detector(s) contributing data in the given region are listed, and parentheses indicate regions that have half the exposure time of the other regions. Panels b) and c) give the 2′′ diameter 5σ AB mag values for the NB118 TERAPIX stack (Sect. 3.4) and our NB118 test stack based on the CASU sky subtraction (which has about 0.1 mag lower noise, but which still may not be the best possible version of our data; Sect. 3.5), respectively. The aperture correction to total magnitude of 0.34 mag has not been subtracted. |
Note that in the above test, we stacked the 257 individual NB118 images as sky subtracted by CASU (and we first removed the large-scale gradients), not the 18 _st stacks made by CASU (at the native pixel scale). We expect that (a) only stacking once, i.e. going from the individual images to the stack, and (b) using a finer pixel scale to (marginally) recover spatial resolution is the better procedure.
3.6. Photometry
Photometry was performed using SExtractor version 2.8.6. Objects were detected/defined in the NB118 image, and fluxes in identical apertures were measured in the NB118, J and Y-band images.
Isolated bright but unsaturated stars were located in a FWHM versus magnitude plot. The typical seeing (FWHM, as measured by SExtractor), was 0.89′′ for NB118, 0.87′′ for J, and 0.88′′ for Y. Using circular apertures of 2.0′′ and 7.1′′ diameter (following McCracken et al. 2012), the aperture correction between these two apertures was found to be 0.34 mag for NB118, 0.32 mag for J, and 0.35 mag for Y. Typically, 1000 stars were used and the standard deviation was 0.01 mag. The 2.0′′ diameter aperture magnitudes with these aperture corrections subtracted are used throughout this paper. It should be noted that the used aperture corrections only are correct for unresolved objects. Conversely, it should be noted that the different bands have almost the same seeing, so the aperture corrections are not critical for the derived colours.
The errors on the aperture magnitudes computed by SExtractor are too small due to, among other things, correlated errors introduced by the resampling. We used the empty aperture measurements (Sect. 3.8) to derive a typical correction factor of 2.7 to the SExtractor flux (i.e. counts) errors. This method is similar to the simulations done by McCracken et al. (2010).
3.7. Masking of bad regions of the stacks
In the analysis we mask certain regions of the stack where it is difficult to extract correct photometry. In a zone of width 122′′ around the edges of the 4 stripes the exposure time linearly decreases due to the jittering (Sect. 2.2). This is mostly not a problem since the weight map of the stack tracks this, but very close to the edge the photometry is unreliable, as seen by objects being detected in NB118 but not in J, and objects showing narrow-band excess but having a spectroscopic redshift that does not match known strong emission lines. We therefore mask typically 15′′ around the edges. We also mask regions contaminated by reflections from bright stars, also based on a visual inspection. The area of the stack containing data, defined as pixels with a positive value in the weight map, is 1.08 deg2 before masking. This area includes the regions of height ≈ 5.5′ at the top and bottom of the stack where the exposure time is only half of that in the main part of the stack, and it includes the 122′′ around the edges where the exposure time is lower due to the jittering. After the masking the area containing data is 0.98 deg2.
3.8. Depth of the obtained stacks
To measure the depth in the stacks we proceed as follows. We first run SExtractor in the given stack to detect the objects. This produces a so-called segmentation image, which identifies all the pixels that contain signal from objects. We then place as many non-overlapping circles of 5′′ diameter as possible in the image in such a way that the circles do not contain any object pixels. At the centre of these circles we force SExtractor to perform aperture photometry in circular apertures with a range of sizes; here we will report the results for the 2′′ diameter apertures.
To accurately track the depth as function of detector (or as function of each of the 16 NB118 filters), we identify regions in the stack that are fully covered by exactly 2 of the 3 pawprints. These regions are shown in Fig. 3(a). On the figure the detector number(s) contributing data to the given region are given. A label such as “2” indicate that the region only contains data from detector 2. There are two such regions: the top one gets data from paw4 and paw5, and the bottom one from paw5 and paw6. The area between these two regions is covered either by 2 or 3 pawprints (the average is 2.2 pawprints) and hence has a 10% larger exposure time per pixel. These areas are not analysed in the following depth analysis. The regions with the detector number given in parenthesis are special cases: they are fully covered by exactly 1 pawprint and thus have half the exposure time per pixel of the other regions.
For detector 16 the regions take into account that our weight maps for the individual images remove 3.3′ on the south side and 5.5′ on the east side as this part of the detector is deemed unreliable. For detector 4 we remove 1′ on the west side.
Each region contains typically 2500 empty aperture flux measurements. The standard deviation σ of these values is calculated and turned into a 5σ AB magnitude. The results for our TERAPIX stack (Sect. 3.4) are shown in Fig. 3b and for our test stack of the individual images as sky subtracted by CASU (Sect. 3.5) in Fig. 3c. It is seen that the 5σ AB noise typically is about 0.1 mag worse in our TERAPIX stack than in the CASU-based stack. The reason for this is unknown. It indicates that the reduction can be marginally improved. A difference in depth at this level does not affect the conclusions in this paper.
For both stacks there is a substantial variation in the noise within the stack. Using the numbers from Fig. 3(c), the lowest noise (ca. 23.9 mag) is found for detectors 1, 6 and 10, and the highest noise (ca. 23.2 mag) is found for detectors 2, 3, 13 and 14. This difference strongly tracks the difference in sky brightness, as will be discussed in Sect. 6.1 − see e.g. Table 3.
Over the 44 regions with full exposure (cf. Fig. 3a), the median 5σ noise is 23.54 mag for the TERAPIX stack and 23.67 mag for the CASU-based stack. Subtracting the point source aperture correction of 0.34 mag (Sect. 3.6) we obtain the corresponding median 5σ detection limits of 23.20 mag and 23.33 mag, respectively. These values can be converted into median 5σ detection limits in line flux of 5.0 × 10-17 erg s-1 cm-2 and 4.4 × 10-17 erg s-1 cm-2, respectively, via 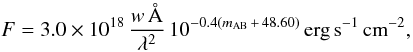 (5)using typical values of the filter width w = 123 Å and wavelength λ = 11 910 Å (Sect. 4). However, since the filters are not tophats, the detection limit in line flux will vary with wavelength across the filter.
(5)using typical values of the filter width w = 123 Å and wavelength λ = 11 910 Å (Sect. 4). However, since the filters are not tophats, the detection limit in line flux will vary with wavelength across the filter.
4. The NB118 filter curves based on laboratory measurements
Searches for emission lines in the J band are difficult due to the many strong telluric emission lines (mainly due to hydroxyl, Rousselot et al. 2000) at that wavelength band. Only a limited number of wavelength intervals are suitable (e.g. Nilsson et al. 2007). Among these is the window at 1185 nm, which corresponds to a Lyα redshift of z = 8.8. This specific window is free from strong skylines within the wavelength range from 1179 nm to 1196 nm and is the target of the NB118 VIRCAM filters. These narrow-band interference filters were specified to have a central vacuum wavelength of 1185 ± 2 nm and a FWHM of 10 ± 2 nm at an operating temperature of 100 K and in a convergent f/3.3 beam, which was to be approximated as a collimated beam at an angle of incidence of 7°. In addition, the specifications placed limits on the out-of-passband leaks: the average transmission between 700 nm and 1140 nm should be below 0.1%, and the average transmission between 1250 nm and 3000 nm should be below 0.01%.
 |
Fig. 4 Four different steps in the determination of transmittance curves shown for each of the 16 individual copies of the NB118 filter in VIRCAM. First row: collimated beam measurement at room temperature as provided by the manufacturer NDC. Second row: shift as expected due to the temperature difference. Third row: theoretical conversion to the convergent beam. Fourth row: response function including all theoretical filter transmittance, mirror reflectivity, detector QE, and atmospheric transmission (PWV = 1 mm, airmass = 1). In the plot, the 16 filters are separated into subsets of four filters corresponding to the four columns or stripes of the combined image (cf. Fig. 2d). In addition, the other 12 filters are shown in every panel in light gray. Positions and relative strengths of the sky emission lines are also included. |
A total of 20 individual filters (of size 54 mm × 54 mm) were delivered in 2007 by NDC Infrared Engineering11, of which 16 were installed in VIRCAM (one filter in front of each of the 16 detectors) and four were kept as spares. With the delivery of the filters, the manufacturer provided measurements of the transmittance in the collimated beam at normal incidence at room temperature over the wavelength range 1100 − 1300 nm with a sampling of 1 nm. The wavelength type was not specified; we have assumed it to be air. The manufacturer stated that the central wavelength of the filters would move down 7 nm with cooling and cone angle, and that the bandwidth at 10% would increase by 0.9 nm.
NDC has in April 2013 provided additional information about the filters based on recent measurements done by NDC on filter parts still in their possession, using more accurate equipment than was available originally. NDC now predicts that the central wavelength of the filters would move down 5.2 nm with cooling and cone angle.
We will now derive this shift in wavelength for the 16 NB118 filters installed in VIRCAM. When using narrow-band interference filters in fast convergent beams under cryogenic temperature, several considerations have to be taken into account (e.g. Reitmeyer 1967; Parker & Bland-Hawthorn 1998; Morelli 1991). First, the passband of the filters is temperature dependent. In VIRCAM there is no temperature sensor on the filters, only on the filter wheel hub. This latter temperature is reported in the headers of the individual images, and for this dataset the median value is 101.4 K, with a range of 101.1−101.7 K. Paranal Science Operations estimate that (a) the typical filter temperature is 90 K ± 5 K, and (b) the filters typically are 5 − 10 K colder than the filter wheel hub, which for this dataset would imply a filter temperature of 91−96 K. We will assume a filter temperature of 90 K in our calculations. The temperature difference between room temperature (295 K) and operating temperature (90 K) gives rise to a blueward shift of the passband of 3.8 nm, based on a linear relation of 0.0186 nm/K measured by NDC in 2013.
Second, VIRCAM has no collimated beam and the filter wheel is located in the fast convergent beam (f/3.25 at the Cassegrain focus, Dalton et al. 2006) of VISTA. This means that effectively a superposition of rays with various incidence angles is passing the filter. A ray with incidence angle away from the normal will experience a blue-shifted passband, due to the decreased optical path difference of interfering rays (e.g. Morelli 1991). Therefore, the effect of a convergent beam is a further shift of the passband to shorter wavelengths compared to the normal incidence collimated curve. This is accompanied by a transformation of the passband, which is mainly a broadening (e.g. Lissberger 1970; Bland-Hawthorn et al. 2001). The shift and transformation depends slightly on the position of the filter in the focal plane. Our calculation uses an effective refractive index of 2.2, as quoted by NDC in 2013. We also assume that the incidence angle of the chief-ray can be estimated from the position of the object as 7.15° per degree distance from the centre of the FOV (Findlay 2012).
Based on the first principles described above, we calculated the expected transmittance for each of the 16 NB118 filters according to their position in the cryogenic convergent beam of VIRCAM from the available collimated beam measurements (more details will be given in Zabl et al., in prep.). In the calculation we assume that both a change of temperature and a change of incidence angle (still for a collimated beam) only shifts the filter curve and does not change the shape. However, measurements of filter curves in the literature at different incidence angles show different extents of deviations from this assumption (e.g. Vanzi et al. 1998; Ghinassi et al. 2002). Therefore, the calculated curves must be understood as an approximation.
 |
Fig. 5 Filter curves for the 4 spare filters. These filters are relevant since they are the only ones that have two sets of measurements available: by NDC over 1100 − 1300 nm (dashed lines) and by ESO over 800 − 3000 nm (solid lines). Each colour represents one of the four filters. The left panel shows the full wavelength range covered by our measurements from the ESO laboratory. The grey line is a sky emission spectrum (see text), and the dotted line represents detector QE and mirror reflectivity (see text), but not atmospheric absorption. The right panel shows a zoom near the passband of the filters; here both NDC and ESO measurements are available. The 16 grey curves in the background show the 16 filters installed in VIRCAM (these are the filter curves shown in the top row of Fig. 4). All curves have been transformed from air to vacuum, but no further transformations have been applied. |
In Fig. 4, all the original collimated beam measurements performed at room temperature are shown in the first row of panels, while the same curves shifted to 90 K are shown in the second row. The convergent beam transformed curves, including the temperature shift, are shown in the third row. Additionally, the complete response function including detector QE, primary and secondary mirror reflectivity, and an atmosphere of airmass 1.0 and a precipitable water vapour (PWV) of 1.0 mm is plotted in the fourth row, using data from ESO12.
The total blueshift from the measurements at room temperature in a collimated beam (Fig. 4, top row) to our calculation representing cryogenic temperature in the convergent beam, with atmosphere, mirror reflectivity and detector QE (Fig. 4, bottom row) is 6.0 nm on average over the 16 filters (detectors), where 3.8 nm comes from temperature and 2.2 nm comes from the convergent beam. The temperature shift is the same for all filters, whereas the shift due to the convergent beam is larger for the filters further from the optical axis. The total predicted blueshift is 6.3 nm for the outermost filters (1, 4, 13 and 16), and 5.6 nm for the innermost filters (6, 7, 10, 11).
The 16 final cryogenic convergent beam curves, T(λ), at their respective positions within the beam have an average mean wavelength λ0 of 1187.9 nm, with a minimum of 1184.8 nm (filter 2) and a maximum of 1189.6 nm (filter 9), where the mean wavelength of the given filter is calculated as 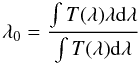 (6)(e.g. Pascual et al. 2007). The FWHM of these curves is 12.3 nm on average over the 16 filters, and ranges from 11.5 nm (filter 15) to 12.9 nm (filter 4).
(6)(e.g. Pascual et al. 2007). The FWHM of these curves is 12.3 nm on average over the 16 filters, and ranges from 11.5 nm (filter 15) to 12.9 nm (filter 4).
Due to inevitable production differences, the individual NB118 filters differ slightly from each other. The 20 filters manufactured were carefully inspected for obvious production problems (Nilsson 2007). One filter had a problem and was designated as spare. The 3 filters with the most blue central wavelengths were also designated as spare. The remaining 16 filters were installed in VIRCAM in such a way that the 4 filters in a given column of filters/detectors were as identical as possible. In the “stripe” observing pattern used both here and in UltraVISTA for the NB118 observations, data from different filters/detectors are only mixed within a column (cf. Sect. 2.2 and Fig. 2). By this arrangement of the filters, the effect of an effective bandpass broadening on the reachable line depth and the minimum detectable equivalent width is minimised.
In this work (Sects. 5.3 and 6) we conclude that the 16 NB118 filters in VIRCAM have some problems: the passband is shifted to the red, and some filters show signs of red-leaks. For this reason the 4 spare filters become important. For logistical reasons it was not possible to obtain an independent measurement of the 16 filters that were installed in VIRCAM, so for these only the NDC measurements over 1100−1300 nm are available. However, we had the 4 spare filters re-measured at ESO, allowing a check of the NDC curves. Furthermore, the ESO measurements were performed over the wide wavelength range of 800−3000 nm, allowing a check of possible red-leaks in these filters. The comparison of the NDC and ESO measurements is shown in the right panel of Fig. 5. Both sets of measurements agree reasonably well in shape. However, the central wavelengths measured by NDC are about 0.7 nm shorter than those measured at ESO. The uncertainty in the ESO measurements is estimated to be 0.4 nm.
The full wavelength range of the ESO measurements is shown in the left panel of Fig. 5. In addition to some smaller leaks spread over the complete wavelength range, substantial leaks exist near 2675 nm for three out of the four spare filters. According to NDC, a leak at this wavelength would be where the coated blocking meets the absorption on the BK7 substrate. The average transmission in the range 1250−3000 nm for the four spare filters is 0.022%, 0.019%, 0.020%, and 0.012%, where the main contribution in the first three cases is coming from the 2675 nm leak. A level of 0.020% violates the specifications by a factor of two.
Although the 2675 nm leaks are mainly outside the efficiency range of the detectors, thermal sky light passing through these leaks might significantly increase the background level for these filters (had they been used in the instrument). We estimated the contribution from the leaks to the sky-background based on the Gemini Observatory theoretical sky spectrum13 calculated using Lord (1992) for an airmass of 1.0, a PWV of 2.3 mm and at an atmospheric temperature of 280 K. For the calculation, we have shifted the measured transmittance curves by 6.0 nm towards the blue to account for the expected passband shift. The sky spectrum is shown in the left panel of Fig. 5.
Then, we calculated the fraction of detected sky photons passing the filters both in and out of the main passband. Here, we define the filter passband by the wavelength range 1165 − 1210 nm, where by specification the transmittance outside these interval boundaries was required to be below 1%. We found that if the spare filters were used in VIRCAM, sky light passing through the out of passband leaks would contribute 38%, 31%, 39%, and 26% to the total sky background, respectively. We further note that the wavelength range 2500−2770 nm alone would contribute 24%, 21%, 24%, and 8%, respectively. These calculations should be considered as crude estimates for several reasons. First, the used sky spectrum seems to overpredict the inter-line telluric background. Second, we do not have estimates for the accuracy of most of the used data. Third, we are using the quantum efficiency (QE) curve as used in the ESO exposure time calculator. However, the QE is probably varying at some level from detector to detector, which could have strong consequences on the impact of the 2675 nm leak (cf. Sect. 6.2). Fourth, we are simply assuming that the leaks are shifted due to convergent beam and temperature by the same amount as the main passband. However, a slightly different shift of the main red-leak would give different results.
For the 16 filters installed in VIRCAM we do not have the required filter curve measurements to predict the effect of possible red-leaks. However, we can study these indirectly, as done in Sect. 6.
The above-mentioned sky spectrum has very high spectral resolution, i.e. has very narrow emission lines. For aesthetic reasons we have convolved the spectrum by a Gaussian kernel with a FWHM of 0.2 nm (and down-sampled from 0.02 nm to 0.1 nm) to reach a spectral resolution similar to that of X-shooter and used that for the plots (Figs. 4, 5 and 10). In Fig. 5 this procedure affects how strong the skylines appear relative to the continuum near 2675 nm.
In Sect. 5.3 we make a first attempt at comparing our predicted filter curves (Fig. 4, bottom row) to the narrow-band excess as function of wavelength as inferred from spectroscopic redshifts. We find that the filter curves need to be shifted approximately 3.5 − 4 nm to the red to match the data, while the FWHM values appear correct. Such a shift implies that the average mean wavelength λ0 of the 16 filters probably is about 1191 − 1192 nm. It could be argued that the filters should be renamed NB119, but we have kept the name NB118 for consistency with the current documentation and processing setup at ESO and CASU.
5. The NB118 filter curves based on observations
5.1. Selection of candidate emission line objects
NB118 is located inside the J band, so the simplest selection of candidate emission line objects would use only the (J − NB118) colour. NB118 is not located at the centre of the J band, so objects with a non-flat continuum in Fν would have a non-zero (J − NB118) colour just from the continuum slope. Since NB118 is located near the blue edge of the J band, see Fig. 6, it is natural to additionally use the Y-band data to select candidate emission line objects.
 |
Fig. 6 Filter curves for Y, NB118 and J. |
Figure 7 shows (J − NB118) vs. (Y − J) for all objects that are detected at 5σ in NB118 and at 2σ in Y and J. A bright cut in all 3 bands of 18 mag has been imposed. The objects that are candidate emission line objects according to the criteria discussed below are shown in blue and the rest in grey.
We want to determine the typical locus of galaxies in this diagram. We illustrate this by the contours, which show the density of objects after excluding likely stars, defined as objects with FWHM less than 1′′ in the NB118 stack; this mainly means that the contours exclude the clump of objects (i.e. stars) with colours (−0.1,0.0) in the figure. For objects with (Y − J) below about 0.5 the trend is clear, and we model this with a line with slope − 0.34, as shown by the solid line for (Y − J) < 0.45. For redder objects the situation is less clear. To illustrate the range of (J − NB118) colours that the continua of galaxies can have in this part of the diagram, we show a set of Maraston (2005) models (see also Maraston 1998) with solar metallicity, red horizontal branch morphology, Salpeter IMF and an exponentially declining SFR with an e-folding time of 0.1 Gyr. These model spectra do not have emission lines. We have redshifted the model spectra to z = 1.75 − 2.00 as well as z = 2.20, as indicated on the figure. We have used the models with ages from 0.2 Gyr to 3 Gyr (from left to right in the figure; for z = 2.20 the oldest model is 2 Gyr). The z = 1.75−2.00 models are interesting as the (J − NB118) colour moves up and down with redshift, due to the location of the 4000 Å break and several absorption lines (including Balmer, Ca and Fe lines) in the NB118 and J filters. It is worth noting that Bruzual & Charlot (2003) models give the same behaviour. With the data and models in mind, we define a constant value of − 0.153 as the “typical” (J − NB118) colour for galaxies with (Y − J) > 0.45, as shown on the figure by the solid line. The dotted line, located 0.2 mag above the solid line, is used as one of the criteria defining candidate emission line objects (see below).
 |
Fig. 7 (J − NB118) vs. (Y − J). The blue and grey dots are objects with and without significant narrow-band excess, respectively. The contours show the density of objects after excluding likely stars. The blue dots additionally marked by a large symbol are line emitters confirmed by spectroscopy, see Fig. 8 for a legend. The solid line is meant to represent the locus of the majority of the objects. The dotted line located 0.2 mag above is one of the selection criteria. The symbols connected by coloured lines represent certain Maraston (2005) model galaxies (see text) without emission lines, placed at the 7 redshifts indicated on the panel and observed at times (from left to right) 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.5, 2.0 and 3.0 Gyr (except for z = 2.2 where 3.0 Gyr is not shown). |
It is noteworthy that the z = 2.2 models in Fig. 7 are located so much below the z = 1.95 models. This means that selecting [O ii] emitters at z = 2.2 (where [O ii] is in the NB118 filter) is difficult, since either one sets the threshold in (J − NB118) low at the price of contamination by z ≈ 1.75−2 galaxies, or one sets the threshold high at the price of only selecting [O ii] emitter with a large equivalent width (EW). Using more filters than J and Y would help; this is beyond the scope of this paper. Note that this paper is mainly based on results for NB118 emitters with spectroscopy, which are mostly objects at lower redshifts.
 |
Fig. 8 Narrow-band colour − magnitude diagram. The blue dots are objects with significant narrow-band excess, and those with a spectroscopic redshift in certain intervals are additionally marked with large symbols, as per the legend on the figure. The small grey dots are objects without significant narrow-band excess. The horizontal dotted line marks one of the selection criteria, see the text. |
Based on the analysis above, we define a (J − NB118) colour that is corrected for the fact that the NB118 filter is not located at the centre of the J-band filter. This quantity is denoted (J − NB118)corr and is essentially the (J − NB118) colour minus the solid line in Fig. 7, specifically  (7)where the last branch refers to the object not being detected in the Y-band stack at 2σ, and where the applied constant (0.07) simply is the median correction for the rest of the objects. (Of the 2308 candidate emission line objects defined below, 17 did not have a 2σY-band detection.) We note that Ly et al. (2011) used a similar functional form, with a slope below a certain broad-band colour − (z′ − J) = 0.5 in their case − and a constant thereafter.
(7)where the last branch refers to the object not being detected in the Y-band stack at 2σ, and where the applied constant (0.07) simply is the median correction for the rest of the objects. (Of the 2308 candidate emission line objects defined below, 17 did not have a 2σY-band detection.) We note that Ly et al. (2011) used a similar functional form, with a slope below a certain broad-band colour − (z′ − J) = 0.5 in their case − and a constant thereafter.
We can now define the criteria for selecting candidate emission line objects. These criteria are similar to those used in many previous studies (e.g. Geach et al. 2008; Shioya et al. 2008; Villar et al. 2008; Sobral et al. 2009, 2012, 2013; Ly et al. 2011; Nakajima et al. 2012; Lee et al. 2012).
First, we require the objects to be detected at 5σ in NB118 and at 2σ in J; we do not place any constraints on Y. Recall that throughout this paper we use errors that are based on the SExtractor flux errors scaled up by a factor to correct for the effects of correlated errors introduced by the resampling (Sect. 3.6). In principle we could remove the requirement on J, but see below.
Second, we require 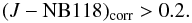 (8)This translates into a minimum observed-frame EW of 29 Å (for filter 1 at the peak transmittance of the filter) for the objects where the continuum colour (i.e. the colour in the absence of the emission line) is well modelled by Eq. (7). This is probably the case for the line emitters at z < 1.5 but not for those at z = 2.2 (i.e. [O ii]).
(8)This translates into a minimum observed-frame EW of 29 Å (for filter 1 at the peak transmittance of the filter) for the objects where the continuum colour (i.e. the colour in the absence of the emission line) is well modelled by Eq. (7). This is probably the case for the line emitters at z < 1.5 but not for those at z = 2.2 (i.e. [O ii]).
Third, we require the corrected colour to be positive at 2.5σ significance, i.e. 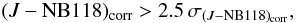 (9)where we simply calculate the uncertainty σ(J − NB118)corr by propagating the magnitude errors on NB118 and J (and Y where applicable) through Eq. (7). In the literature often a global uncertainty is used, but we have used the individual uncertainties, which automatically track the varying noise (depth) across the NB118 stack
(9)where we simply calculate the uncertainty σ(J − NB118)corr by propagating the magnitude errors on NB118 and J (and Y where applicable) through Eq. (7). In the literature often a global uncertainty is used, but we have used the individual uncertainties, which automatically track the varying noise (depth) across the NB118 stack
The above selection produces a sample of 2308 candidate emission line objects out of 57 882 objects that are detected at 5σ in NB118 and at 2σ in J (after masking of bad regions, etc.).
As stated, we have implemented the selection expressed by Eqs. (8) and (9) in terms of magnitudes. We can do this since we have required the objects to be detected in J. In principle it is better to use the corresponding equations based on counts rather than magnitudes (e.g. Bunker et al. 1995), since then objects that are undetected in J (possibly even having a slightly negative flux in J) are handled naturally. In this paper, however, we mainly base our results on objects with spectroscopy, and these are all detected in J. For reference, 23 objects are detected at 5σ in NB118 but not at 2σ in J. It is likely that most of these are unreal, i.e. due to noise or artefacts in the NB118 image.
The selection of candidate emission line objects has already been illustrated in the colour-colour plot in Fig. 7. Another view is provided by the colour − magnitude plot in Fig. 8. Note again that since we use the individual uncertainties to evaluate the significance of the narrow-band excess (Eq. (9)), the used 2.5σ selection cannot be represented by a single curve in the colour − magnitude plot.
As an alternative to the above selection method, one could use the (broad1 − narrow) vs. (narrow − broad2) colour/colour selection technique (e.g. Møller & Warren 1993; Fynbo et al. 2003; Nakajima et al. 2012).
5.2. Cross correlation with spectroscopic redshift catalogues
As detailed in Sect. 4 the filters were designed to obtain the optimal bandpass using formulas to compute the effect of cooling them to cryogenic temperatures and placing them in the converging beam. The measured bandpasses reported in Sect. 4 were measured at room temperature and in a collimated beam. To verify how well our theoretical formulae worked, the true bandpass should be measured “in situ”, i.e. with the filters located in the instrument at cryogenic temperature and vacuum, and with the light following the same path as during the observations, i.e. meeting the same optical elements and having the same superposition of rays from different angles. One way to achieve this would be using a tunable monochromatic light source combined with a device to uniformly illuminate the dome flat screen; we do not have access to such equipment. Another is to use emission line galaxies (and AGN) with spectroscopic redshifts. One of the key points in our decision to observe in the COSMOS field was exactly that many spectroscopic redshifts would become available in this field.
 |
Fig. 9 Narrow-band colour versus spectroscopic redshift. The large blue symbols are objects with significant narrow-band excess (Sect. 5.1). The symbol type indicates the spectroscopic catalogue, as per the legend given on the figure. The redshifts of strong emission lines or emission line blends selected by the NB118 filters are marked for a typical filter vacuum wavelength of 1191 nm (but note that the central wavelengths of the filters in the 4 columns of the stack differ somewhat, see the bottom row of Fig. 4). Panels b), c) and d) provide zooms, in which the dashed lines mark the line blends as shown in panel a), while the dotted lines mark the individual lines that are part of the line blends. The horizontal lines mark the redshift ranges used to define the different lines or line blends in Table 2 and in Fig. 8. The low values of the colour at z ≈ 0.9 (see panels a) and b)) are due to the Hα line being in the J band but not in the NB118. |
The largest set of redshifts used here comes from the zCOSMOS project (Lilly et al. 2007). We use the zCOSMOS-bright 20k catalogue, which essentially is a superset of the zCOSMOS-bright 10 k catalogue (Lilly et al. 2009)14. This is based on a magnitude limited (IAB < 22.5) sample. We mainly use redshifts that are classified as either secure or very secure, namely those with any of the following zCOSMOS confidence classes: 3 and 4 (stars and galaxies), 13 and 14 (broad-line AGN), 23 and 24 (serendipitous stars and galaxies), and 213 and 214 (serendipitous broad-line AGN). In addition we use redshifts with confidence class 9, corresponding to a single-line redshift where the spectrum does not show signs of the object being a broad-line AGN. Specifically we use the subclasses 9.5 + 9.4 + 9.3 (see Lilly et al. 2009). A detail to note on these single line redshifts is that there are only two possible interpretations of the line seen in the zCOSMOS optical spectrum, namely [O ii] or Hα, and therefore only two possible redshifts. Since the two possible solutions are vastly different they will not cause us any problems. Either the redshift is correct and we record a line, or the redshift is wrong and the object does not matter for our purposes. And in fact, for the sample of candidate emission line objects with redshifts (Table 2), including class 9 does not add any “unidentified” objects while adding 2 [S ii] emitters, 7 Hα+[N ii] emitters, 1 [O iii] emitter and 2 Hβ emitters. Finally, we also use class 18 (single-line redshift, broad-line AGN): this adds 2 [O iii] emitters and 1 Hβ emitter. The reported typical 1 sigma redshift uncertainty in zCOSMOS-bright is 110 km s-1.
We also use the redshift catalogue from the COSMOS AGN spectroscopic survey, as published in Trump et al. (2009). This is based on optical spectroscopy using Magellan/IMACS and MMT/Hectospec of X-ray selected objects. Again we only use redshifts that are classified as secure, which corresponds to their listed confidence classes 3 and 4.
Finally we use redshifts from early spectroscopic follow-up of objects identified as line emitters in this work (cf. Sect. 5.1) and as likely to have [O ii] in the NB118 filter based on photometric redshifts from Ilbert et al. (2009). All the 3 objects that we observed (PI: Zabl, ESO ID 089.B-0710) with VLT/X-shooter (Vernet et al. 2011) were indeed found to be [O ii] emitters at z = 2.2 (Zabl et al. in prep.).
For all redshift catalogues we performed the cross correlation with our photometric catalogue using the tskymatch2 routine in STILTS15 (Taylor 2006). We used a maximum distance of 0.5′′. For objects with a selected redshift both from zCOSMOS and Trump et al. (2009) we used the zCOSMOS value. In the vast majority of these cases the redshifts are concordant.
In Fig. 9 we plot (J − NB118)corr versus redshifts from the 3 catalogues: circles: zCOSMOS-bright 20k, squares: Trump et al. (2009), stars: X-shooter (Zabl et al. in prep.). Large, blue symbols are objects with significant narrow-band excess as defined in Sect. 5.1, and small, grey symbols are the remaining objects. Panel (a) shows the full redshift range up to z = 3.5, while panels (b), (c) and (d) show zooms near the redshifts of certain emission lines. The redshifts of a number of emission lines are marked by dashed lines. In panel (a) certain neighbouring emission lines have been shown by a single dashed line for clarity, e.g. [S ii]6718,6733, whereas panels (b), (c) and (d) additionally show the individual emission lines as dotted lines, e.g. [S ii]6718 and [S ii]6733. All rest-frame (vacuum) wavelengths were taken from the Atomic Line List16. The dashed and dotted lines correspond to a filter wavelength of 1191 nm, a number adjusted by eye to get a good match to the data in this figure. In this figure data from all the 16 NB118 filters are mixed (and not every filter has the same number of redshifts), and it should be kept in mind that the different filters are expected to have somewhat different wavelengths, as shown by the 16 filter curves in the bottom row of Fig. 4. We expand on this topic in Sect. 5.3.
The main conclusion from Fig. 9 is that the set of 16 NB118 filters do indeed function as intended, in that objects with significant NB118 excess are almost always located at the redshifts corresponding to strong emission lines. The breakdown by emission line is given in Table 2. Most of the NB118 excess objects with redshifts in the catalogues used here are z ≈ 0.8 Hα emitters.
The redshift limits z1,z2 used to define the identification with a given emission line(s) in Table 2 were calculated as the range that is within ± 0.85 × FWHM(filter) from the emission line(s) in question, using a typical filter FWHM of 12.3 nm and a typical filter wavelength of 1191 nm. In reality these values vary a bit from filter to filter. The factor of 0.85 is somewhat arbitrary, but it gives a reasonable match to the data, see the limits indicated on the zoom panels of Fig. 9, particularly panel (b) that has many galaxies. With this definition, 3 objects are unidentified. Two of these, at z = 0.375 and z = 1.854, are probably objects that are classified as emission line objects due to fluctuations in the photometry. The third object is at z = 3.302 (Fig. 9a), which is just outside the redshift interval defining Mg ii2796,2804. This object is listed in the zCOSMOS catalogue as a broad-line AGN, so it is likely that the object has a broad Mg ii emission line that could cause the observed NB118 excess.
Spectroscopically identified line emitters.
5.3. Inferred central wavelength of the filters
The plot of (J − NB118)corr versus redshift (Fig. 9) suggests that we may infer the central wavelengths of the 16 NB118 filters from emission-line objects with spectroscopic redshifts. The calculation of observed-frame wavelength from redshift (λobs = (1 + z)λrest) is most simply done for strong single (isolated) emission lines or for emission line blends where the constituent emission line are close in redshift.
 |
Fig. 10 Wavelength response of the 16 NB118 filters, as illustrated by objects with spectroscopic redshifts. These plots are as Fig. 9, except that λobs,vac = (1 + z)λrest,vac rather than z is on the x-axis. The 4 rows of the figure correspond to 4 emission lines or emission line blends, with the used rest-frame vacuum wavelength listed. The 4 columns of the figure correspond to the 4 columns of the stack (see Fig. 2), where each column contains data from 4 NB118 filters (namely filters 1 − 4, 5 − 8, 9 − 12 and 13 − 16 for Cols. 1 − 4, respectively), and where the corresponding filter curves are overplotted. The grey filter curves are those from the bottom row of Fig. 4, while the coloured ones are the curves shifted by 3.5 nm to the red to visually match the data. The vertical dotted lines indicate the centre wavelength of the 4 filters in the given panel before and after the shift. In the [S ii] panels (panels e) − h)) the hatched region indicates a redshift range where narrow-band excess is likely due to Hα rather than [S ii]. In the bottom row the theoretical sky spectrum used in Sect. 4 is shown, scaled to fit the panel. |
For our analysis we will use the single line [S iii]9533 and three line blends, for which the effective wavelengths are derived as follows. For the [S ii]6718,6733 and [O ii]3727,3730 doublets, where the intensity ratio depends on the electron density ne, we have used [S ii]6718/[S ii]6733 = 1.3 and [O ii]3730/[O ii]3727 = 1.3, which in both cases correspond to ne ≈ 102 cm-3, which is a typical value (Osterbrock & Ferland 2006). The resulting effective wavelength for [S ii] is 6724.5 Å and for [O ii] is 3728.7 Å. For the Hα+[N ii] blend of 3 lines, the doublet ratio [N ii]6585/[N ii]6550 is essentially fixed by atomic physics to a value close to 3 (e.g. Storey & Zeippen 2000), whereas the [N ii]6585/Hα ratio depends on the metallicity and on the source of photoionization and varies substantially. We have used [N ii]6585/Hα = 0.3, which in terms of N2 ≡ log ( [N ii] 6585/Hα) (e.g. Denicoló et al. 2002) corresponds to N2 ≈ − 0.5, which is a reasonable mean value (e.g. Kennicutt 1992; Gallego et al. 1997; Kauffmann et al. 2003; James et al. 2005; Moustakas & Kennicutt 2006; Pascual et al. 2007; Pérez-Montero et al. 2013; Hopkins et al. 2013). The resulting effective wavelength for Hα+[N ii] is 6568.0 Å.
Ideally we would like to analyse the data for each detector (i.e. each NB118 filter) separately, but in our combined image the data from different detectors are to some extent mixed within the 4 columns (stripes) of the image, and the number of objects with redshifts is not really large enough to allow such a split. We therefore only split the data into the 4 columns. It should also be noted that the 4 filters in a given column were chosen to be as identical as possible.
The plots of (J − NB118)corr versus inferred observed-frame wavelength is given in Fig. 10. The 4 rows of the figure correspond to the 4 emission lines/blends used ([S iii]9533, [S ii], Hα+[N ii] and [O ii]), which therefore also correspond to 4 redshift slices. The 4 columns of the figure correspond to the 4 columns of the combined image. The underlying data and the symbols in Fig. 10 are the same as in Fig. 9. The grey filter curves (identical to the coloured filter curves in the bottom row of Fig. 4) represent our calculation of where the filters should be, as operated in the instrument, i.e. at cryogenic temperature and in the converging beam. It is seen that these curves do not provide a good match to the data: in many panels there are objects with significant narrow-band excess on the red side of the filters and a lack of such objects on the blue side. If these filter curves are shifted by 3.5 nm to the red, as shown by the coloured filter curves, a much better match to the data is provided.
The 3.5 nm shift was found to be the best overall value that visually matches the data in Fig. 4, with an uncertainty that probably is 1 or 2 nm. We have also, for each of the 4 columns, calculated the weighted mean wavelength of the galaxies, using (J − NB118)corr as weight, and calculated the difference with respect to the mean predicted filter wavelengths in that column. The resulting shifts to the red for columns 1, 2, 3 and 4 were 1.7 ± 0.7 nm, 4.8 ± 1.0 nm, 5.3 ± 0.7 nm and 4.3 ± 1.1 nm, respectively, with the errors calculated using the bootstrap method. Over all columns the shift is 4.0 ± 0.4 nm.
We therefore conclude that there is a difference between the predicted filter curves and the actual achieved filter response on the sky. The data are compatible with the shift being the same for all 4 columns and for all 16 filters, but filter-to-filter differences could exist. We have re-checked all material related to the filter definitions but we have not been able to determine the cause of this shift. As detailed in Sect. 4, the calculated total blueshift from the measurements at room temperature in a collimated beam to the operating temperature in the convergent beam is 6.0 nm on average over the 16 filters. The observed 3.5 − 4 nm shift to the red could either imply that the blueshift due to temperature and convergent beam is only 2.0 − 2.5 nm instead of 6.0 nm, which is difficult to understand, or that there is some other effect at play, either some properties of the VISTA/VIRCAM optics that we have overlooked, or that the filters have been affected by their environment somehow (e.g. by the way they are mounted or by the long exposure to vacuum). We note the case of the SDSS filters that changed wavelength, see Stoughton et al. (2002, their Sect. 4.5) and Bessell (2005). These filters have a red edge defined by a multilayer interference edge coating (acting as a short-pass filter). It is believed that dehydration due to the filters being placed in vacuum caused the effective refractive index to decrease, causing a blueshift. It is not clear that this is relevant for the VIRCAM NB118 filters (where we observe a shift to the red), but it does indicate that the properties of filters can be affected by their environment.
As far as the widths of the filters are concerned, the achieved widths indicated by the data in Fig. 10 are in reasonable agreement with the predictions.
A limitation of the above analysis is that there is a degeneracy between intrinsic EW of the object and filter transmission, i.e. an object with a low value of (J − NB118)corr could either indicate an object with an intrinsically low EW or an object with an emission line that is at a wavelength where the filter has a low transmission. However, averaged over many objects, such effects will diminish. Also cosmic variance is an issue, although there should be little correlation between the 4 used redshift slices. A much improved analysis could be performed if we had objects with a spectroscopically measured EW of the emission line(s) in the NB118 window. With such data each filter curve could be derived with much better accuracy.
6. NB118 sky brightness based on observations
6.1. NB118 sky brightness in the GTO data
As detailed in Sect. 4 the VIRCAM design required us to produce 16 separate narrow-band filters, namely one for each detector. Our design goal was to obtain 16 identical filters and as shown (Fig. 4) the pre-installation measurements showed variations in bandpass which were of a magnitude that should not cause any issues. We therefore did not expect large variations in the sky brightness level from one detector to the next. In Fig. 11 we show the actual sky level in e − s-1 px-1 for all the individual GTO images plotted as a function of time. Each detector is plotted with a separate symbol/colour combination. The J-band values have been scaled down by a factor of 20 to fit on the plot; this factor reflects both the much larger width and the somewhat brighter sky of the J band compared to the NB118. The used sky levels are those listed in the headers, computed by CASU using an iterative k-sigma clipped median including masking of bad pixels but not objects, with the iteration taking care of most of the object pixels (M. Irwin, priv. comm. 2012). The values were transformed from gain-normalised ADU to electrons assuming a common gain of 4.19 e − ADU-1, cf. Sect. 3.2 and the CASU web site17. This is only approximately correct, since there are detector-to-detector differences in overall QE.
 |
Fig. 11 Sky level in e − s-1 px-1 (with 1 px being about 0.34′′ on the side) as function of time for the 6 half-nights of the GTO observing run. The data were taken in either NB118 or J band; the J-band sky level values have been scaled down by a factor of 20 to fit on the plot, as indicated on the panels. For each exposure, i.e. for each point in time, the sky level in the 16 detectors is plotted; a symbol legend is provided in panel f). In VIRCAM each detector has its own filter, and filter-to-filter variations within the set of the 16 NB118 filters are likely the reason for the large detector-to-detector variations seen for the NB118 sky levels. Dot-dashed lines mark the start of twilight. In panels a) and b), solid grey regions mark episodes where the OBs had to be restarted due to minor technical (software) problems, and dotted lines mark obtained J-band exposures for which CASU did not provide reduced images (see Sect. 3.2). The UT date for the observations in panel (a) is 2010 − 01 − 18, and each subsequent panel is one day later. |
Figure 11 shows that the narrow-band background level varies substantially from one detector to the next. The extremes are represented by detectors 1 and 13, with detector 13 on average having a 2.43 times higher level than detector 1, see Table 3. The relative background level between any two detectors remains fairly constant in time (but is not fully constant, see below). By contrast, the spread in background levels in the J band is much smaller, as is evident from Fig. 11. This raises the question what causes the large variations in the background level of the narrow-band filter.
Relative NB118 background level in the GTO data as function of detector number
One possible explanation for the variations of the background level is stray light that finds a way to the detector without passing through the filter. This effect is a potentially serious problem for any narrow-band imaging (Fynbo et al. 1999, their Sect. 2). If this were the cause, we would expect the background level to have a systematic pattern over the 4 by 4 field spanned by the detectors in the pawprint. However, no obvious pattern is seen (see Table 3). Furthermore, stray light going around the filters is also strongly excluded by an examination of dark frames taken with the dome lamps on, where essentially nothing is seen, meaning that the leak around the filters is well below 1 photon in 100 000 (W. Sutherland, priv. comm. 2012). The only remaining explanation for the enhanced sky background are imperfections in the individual filter bandpass. This could be in the form of a too wide or shifted bandpass such that airglow lines enter the bandpass, or a too large red-leak. Below we show evidence that some of the filters have a noteworthy red-leak. And in Sect. 5.3 we found that the effective filter curves on the sky are not those predicted by the laboratory measurements of filter curves.
 |
Fig. 12 Sky brightness in AB mag/arcsec2 versus time in days for all VISTA observations in the CASU QC tables. Panel a) shows the median NB118 sky brightness, with the median taken over the 16 detectors, i.e. over the 16 individual NB118 filters. Green diamonds: SV, blue triangles: UltraVISTA, red circles: GTO, grey skeletal symbols: standard stars taken at the start of the night (either in evening twilight or in the first 90 min of the night), black crosses: standard stars taken the rest of the time. Each point represents the stack made by CASU of the data coming from one OB and one pawprint position. There are therefore 18 GTO points from the 6 GTO OBs (one per night) each observing 3 pawprint positions. Panel b) shows the (NB118 − J) sky brightness difference for standard star observations taken in these two filters almost simultaneously. Again the median values over the 16 detectors are used, and symbols are as in panel a). Panel c) shows the NB118 sky brightness in the 16 individual detectors/filters minus the median NB118 sky brightness (with the latter being what is plotted in panel a). The median value in bins of one calendar month is plotted. The shown errorbar represents the standard deviation (if it could be computed). A legend is provided on the panel. The sense of the y-axis is such that e.g. detector 13 has a brighter sky and detector 1 has a darker sky. Panel d) is as panel c) but for J. These two panels have an identical scale on the y-axis in terms of mag/arcsec2 per cm on the page. The CASU magnitudes were transformed to AB using NB118(AB) = NB118(Vega) + 0.853 and J(AB) = J(Vega) + 0.937. |
6.2. NB118 sky brightness in all VISTA data and red-leak analysis
We have further investigated the NB118 background level using the CASU QC tables18, which for all VISTA data taken since the Science Verification (SV) in 2009 October list a wealth of quantities, including the sky brightness in mag/arcsec2. The images used are not the individual images (as plotted in Fig. 11), but rather the CASU stacks of images from a single OB and pawprint position. The CASU sky brightness (transformed to AB using conversions calculated by CASU19) versus time is plotted in Fig. 12. Panel (a) shows the median NB118 sky brightness, with the median being computed over the 16 detectors. The median values over time are as follows: GTO data (red circles): 17.1, SV (green diamonds): 17.4, UltraVISTA (blue triangles): 17.3, standard star fields, start of the night (grey skeletal symbols): 17.2, and standard star fields, rest of the night (black crosses): 17.3, all in mag/arcsec2. Panel (b) shows the (NB118 − J) sky brightness difference (again using the median values of the 16 detectors) for all standard star observations where the same field was observed in the two bands within a few minutes. The median value over time is 1.2 and 0.5 mag/arcsec2 for observations at the start of the night and in the rest of the night, respectively, with the division being made at 90 min into the night. This means that the J-band sky shows a stronger change from bright to dark from the start to rest of the night than the NB118 sky does. Panel (c) shows the NB118 sky brightness in the individual detectors, with the median value subtracted. Bins of one calendar month have been used. The pattern is fairly constant over time. The typical min-max span is 0.95 mag/arcsec2, in agreement with the factor of 2.43 span in the sky level for the GTO data (Table 3). The shown errorbars indicate a robust measure of the standard deviation. Particularly detectors 2 and 3 show a large standard deviation, meaning that they behave less like the other detectors (a behaviour that can also be seen e.g. in Fig. 11e). Panel (d) shows the same for the J band, and here the variation is more than an order of magnitude smaller.
The large detector-to-detector variation in the NB118 (but not in J-band) sky brightness means that for the above-mentioned standard star observations done at least 90 min into the night, detector 1 has a sky brightness in NB118 of 17.8 mag/arcsec2 that is on average 0.9 mag/arcsec2 darker than that in J, whereas detector 13 has sky brightness in NB118 of 16.8 mag/arcsec2 that is essentially identical to that in J.
The CASU QC database contains 1080 observations of standard stars where the same field was observed in H, Ks, J, Y, Z and NB118 (in that order) within 15 minutes. For each detector we have quantified the correlation between the sky brightness in these 6 filters and between the ambient temperature, by means of Spearman rank order correlation coefficients rS and linear Pearson correlation coefficients rP (e.g. Press et al. 1992). Some of these coefficients are shown in Fig. 13. The two panels differ only in the fact that panel (a) shows rS while panel (b) shows rP. The y-axis shows the correlation coefficient between the sky brightness in the given band and the sky brightness in the Y band, where the given band is either J (green triangles), NB118 (red circles, labelled by the detector number) or Ks (black crosses). The x-axis shows minus one times the correlation coefficient between the sky brightness in the given band and the ambient temperature. Positive values indicate that the sky gets brighter (i.e. smaller in mag/arcsec2) with higher temperature. It is seen that the J-band sky brightness correlates strongly with the Y-band sky brightness and not strongly with ambient temperature, whereas the opposite is the case for the Ks-band sky brightness, as expected. Interestingly, the 16 NB118 filters almost span the full range between the J and the Ks filters. At one extreme, NB118 filters 2 and 3 essentially show as strong a correlation with ambient temperature as the Ks-band filters, indicating that these NB118 filters have substantial red-leaks. These two filters were also seen to deviate from the rest of the NB118 filters in the analysis discussed above.
 |
Fig. 13 Sky brightness correlation coefficients for the 16 detectors. Green triangles: J, red circles: NB118, black crosses: Ks. The x-axes show the correlation coefficient with the ambient temperature, while the y-axis shows the correlation coefficient with the sky brightness in the Y band in the given detector. The correlation coefficients on the x-axes have been multiplied by minus one, since they would otherwise be negative due to the the sky brightness being in mag/arcsec2. Panel a) shows the Spearman rank order correlation coefficient rS while panel b) shows the linear Pearson correlation coefficient rP. The individual NB118 points are labelled with the detector number. |
 |
Fig. 14 Two measures of the red-leak for the 16 NB118 filters. The y-axis shows the level in screen flats obtained with the lights in the dome off (i.e. with the light source being the thermal emission from the dome flat screen, the dome, etc.) divided by the level in regular screen flats (i.e. with the dome flat screen illuminated by a lamp). The levels have been dark subtracted. The x-axis shows correlation coefficients between the NB118 sky brightness in the given detector (i.e. filter) and the ambient temperature using all the VISTA data contained in the CASU QC tables. The correlation coefficients have been multiplied by minus one, since they would otherwise be negative due to the sky brightness being in mag/arcsec2. Panel a) shows the Spearman rank order correlation coefficient rS while panel b) shows the linear Pearson correlation coefficient rP. The labels indicate the detector number. |
To further investigate possible red-leaks in the 16 NB118 filters, the ESO staff obtained a set of daytime test observations on 2012 November 11 and 25 to perform a test suggested by W. Sutherland. In addition to the normal screen flats, where a screen is illuminated by a lamp, special screen flats were made with the lamp switched off and the dome otherwise dark, i.e. with the illumination coming from the thermal emission from the screen and the dome. Both the “lamp on” and “lamp off” images were dark-subtracted using dark frames taken the same day. The median level in each detector was measured and converted to electrons using the gain for each detector as determined from data taken the same day. Finally, for each filter and detector, the ratio of the levels in the “lamp off” and “lamp on” images was computed. Over the 16 detectors, the median off/on ratios were 0.18% in J, 2.5% in NB118 and 48% in Ks. Comparing J with NB118 using these numbers suggest that the relative importance of red-leaks in the NB118 filters is substantially larger than in the J-band filters, but the stability of the “off” and “on” light sources between the exposures for the different filters is not fully ensured. Such problems are absent when comparing the off/on ratios for the 16 detectors of a given filter. For Ks the range was small (47.1% − 49.6%). For J the range was large (0.12% − 0.30%), but the values themselves are small. For NB118 the range was large (1.4% − 4.1%), with detectors 2 and 3 having the highest values. These ratios are shown on the y-axes of Fig. 14. The x-axis shows the correlation coefficients between NB118 sky brightness in the given detector (using 1080 nighttime observations taken over 1000 days) and ambient temperature, as discussed above and as shown in Fig. 13. In other words, Fig. 14 plots two different measures of red-leak for the 16 NB118 filters against each other, and they are indeed positively correlated.
It should be noted that the variation in red-leak strength within the set of 16 filters derived here may partly reflect differences in detector QE in the far red where the red-leaks may be located. In the spare filters the red-leaks are located near 2675 nm, see Fig. 5. We do not have the detector QE measurements for the individual detectors, only for one detector, which is plotted in Fig. 5. However, additional daytime test observations devised by V. Ivanov and obtained 2013 June 09 shed light on this question. In these tests, the filter wheel was partially out of place in such a way that two NB118 filters partially illuminated one detector. Data had to be saved directly from the real-time display and only data for detector 2 were saved. One half of this detector was illuminated by filter 1, and the other half by filter 2. As in the tests described above, “lamp off” and “lamp on” images were obtained and analysed. In terms of the off/on ratio (hereafter Q), the results were as follows. With the filter wheel in the normal position: filter 1 on detector 1: Q = 1.36%, and filter 2 on detector 2: Q = 3.23%, indicating that filter 2 has 2.4 times more red-leak than filter 1 if the two detectors were identical. With the filter wheel in the special position: filter 1 on detector 2: Q = 2.51%, and filter 2 on detector 2: Q = 3.09%, indicating that filter 2 has 1.2 times more red-leak than filter 1 when using the same detector (here detector 2). These tests indicate that the relatively large red-leak seen for NB118 filter 2 (when placed in front of detector 2 as in normal operation) is mostly due to detector 2 having a relatively large QE at the location of the red-leak(s) (whereever that may be). We speculate that the same is the case for filter 3 and detector 3. Detectors 2 and 3 are from an earlier batch than the other 14 detectors, and detectors 2 and 3 also have a slightly worse AR (anti-reflective) coating which can be seen in images of the detectors20 (W. Sutherland, priv. comm. 2013). It is therefore conceivable that detectors 2 and 3 could have a higher ratio of the QE at the red-leaks of the NB118 filters relative to the QE at main passband of the NB118 filters than the other 14 detectors. As for the absolute QE in the J and of Ks bands, our “lamp on” counts in electrons show that detectors 2 and 3 have a lower QE than the other 14 detectors.
6.3. Sky brightness near 1.19 μm from other instruments
As stated above, in the VISTA/VIRCAM NB118 data, the typical (over time) sky brightness in the typical filter (over the 16 filters) is about 17.3 mag/arcsec2 (again, AB magnitudes are used throughout). For the best filter, the value is about 17.7 mag/arcsec2, and for the worst about 16.75 mag/arcsec2. For reference, these filters probably have an average central wavelength of about 1191 nm (using the predicted values from Sect. 4 and the inferred shift of unknown origin of about 3.5 − 4 nm from Sect. 5.3) and an average FWHM of 12.3 nm. It is interesting to compare these VIRCAM NB118 sky brightness values to those from other instruments having narrow-band filters near the 1.19 μm window.
For the KPNO 4m/NEWFIRM NB118 data of Ly et al. (2011), the typical sky brightness is 18.16 mag/arcsec2 on average over the field, with the best value obtained at the field centre (18.84 mag/arcsec2) and the worst at the field edge (about 17.9 mag/arcsec2) (C. Ly, priv. comm. 2013). The central wavelength of the filter changes with distance from the field centre. At the field centre, the filter has λc = 1187.2 nm and FWHM = 11.1 nm (J. Lee, priv. comm. 2013).
For the Magellan/FourStar NB119 data of Lee et al. (2012), the typical sky brightness is 18.0 mag/arcsec2 (J. Lee, priv. comm. 2013). The filter has λc = 1190.8 nm and FWHM = 13.7 nm (J. Lee, priv. comm. 2013). Note that this filter sometimes is called NB118 instead of NB119.
For the CFHT/WIRCam lowOH2 (NB118) data of Sobral et al. (in prep.), the typical sky brightness is 18.5 mag/arcsec2 (D. Sobral, priv. comm. 2013). The filter has λc = 1187 nm and FWHM = 10 nm (D. Sobral, priv. comm. 2013).
For the VLT/ISAAC NB119 data of Willis & Courbin (2005), the typical sky brightness is 18.5 mag arcsec-2. The filter has λc = 1187 nm and FWHM = 8.95 nm.
The sky brightness in narrow-band filters is a combination of inter-line sky continuum, line emission, and possibly thermal emission entering via a red-leak. The brightness of the inter-line sky continuum is debated but is likely low. For example, Sullivan & Simcoe (2012) found the inter-line sky continuum in the J band in dark time to be 19.55 mag/arcsec2 (with an uncertainty of about ± 0.2 mag), and Tilvi et al. (2010) found the sky brightness between the OH lines near 1063 nm (which is in the Y band) to be about 21.2 mag/arcsec2.
 |
Fig. 15 Predicted sky brightness for the 16 NB118 filters as function of a hypothetical filter wavelength shift Δλ with respect to the filter curves as predicted based on laboratory measurements. The results from 3 models of the sky emission spectrum are shown: solid orange line: model 1 (Gemini Observatory, theoretical), dotted green line: model 2 (Sullivan & Simcoe 2012), dashed blue line: model 3 (see text). The predictions are based on sky continuum and emission lines near the central passband of the filters; possible red-leaks are not included. The horizontal grey line marks a representative value for the observed NB118 sky brightness in the given filter. The vertical grey line marks the wavelength shift to the red of about 3.5 nm that we infer from NB118 observations of emission line objects with spectroscopic redshifts. The mean filter wavelength λ0 (Eq. (6)) as predicted based on laboratory measurements is given on the panel. |
7. Predicted sky brightness
In this section we will calculate the predicted sky brightness for each of the 16 NB118 filters for a given model of the sky spectrum. We will do this for the filter curves as predicted based on laboratory measurements, and for these filter curves shifted in small steps in wavelength Δλ. The aim is to evaluate the influence of the wavelength shift of about 3.5 − 4 nm to the red that we have inferred using emission line objects with spectroscopic redshifts (Sect. 5.3). The aim is also to evaluate the amount of sky brightness caused by red-leaks − our red-leak indicators (Sect. 6.2) mainly provide information about the relative importance of red-leaks within the set of the 16 NB118 filters, not the absolute sky brightness due to red-leaks.
Here we will use the following 3 models for the sky background. Model 1 is the theoretical sky spectrum provided by Gemini Observatory, as described in Sect. 4. Model 2 is the observed sky spectrum from Sullivan & Simcoe (2012). Model 3, like the other two models, contains a combination of sky lines and continuum, although not directly in the form of a spectrum. The sky lines are taken from the list of wavelengths and intensities of sky emission lines as compiled from the literature (Maihara et al. 1993; Ramsay et al. 1992; Oliva & Origlia 1992; Abrams et al. 1994) by the DAzLE team (e.g., Horton et al. 2004; McMahon et al. 2008) and made available on the DAzLE web site21, and the continuum emission of 600 photons s-1 m-2 arcsec-1 μm-1 is taken from Maihara et al. (1993).
In our calculation we use the filter curves as predicted based on laboratory measurements, similar to those in the fourth row of Fig. 4, except that atmospheric absorption is not included. In the calculation we assume that the shape of the bandpasses is preserved and only a shift of the complete filter in wavelength is applied.
It is important to note that since the filter curves for the 16 NB118 filters installed in VIRCAM were only measured in a wavelength range near the central passband, our calculations of sky brightness do not include possible red-leaks.
The result in terms of sky brightness versus Δλ is given in Fig. 15. The 3 models give somewhat different results. In terms of the effect of the filters probably being about 3.5 nm redder than predicted from the laboratory measurements, i.e. the difference in sky brightness between Δλ = 3.5 nm and Δλ = 0 nm, the effect varies with filter and model. For model 1, the average is − 0.46 mag (range: − 0.04 to − 0.71). For model 2, the average is − 0.51 mag (range: − 0.09 to − 0.75). For model 3, the average is − 0.93 mag (range: − 0.34 to − 1.19). The sign is such that the sky always is brighter when the filters are shifted 3.5 nm to the red.
In terms of the absolute sky brightness at Δλ = 3.5 nm, the models vary a lot. On the figure the grey horizontal line marks the observed median (over time) NB118 sky brightness as measured by the CASU QC for UltraVISTA data (Sect. 6.2); the values for the GTO data would be about 0.1 mag brighter. The difference between the observed and the predicted sky brightness can be interpreted as the contribution due to a red-leak. For models 1 and 2, most filters seem to have a contribution from red-leaks. For model 3 the sky brightness for most filters can be explained without red-leaks. All models predicted a much darker sky for filters 2 and 3 than observed, and these two filters (combined with their respective detectors) are also those that show the strongest signs of red-leaks (Sect. 6.2). We note that our (rather uncertain) estimate of the red-leak contribution for the spare filters was typically only ~35% = 0.3 mag (Sect. 4).
To make further progress, we should base our sky spectrum on flux calibrated NIR spectra from instruments at Paranal (e.g. X-shooter) located just 1.5 km away from VISTA and taken simultaneously with the VISTA NB118 data in question. We are considering this for a future paper.
8. Summary and conclusions
We have designed and had installed a set of 16 narrow band filters centred near 1.19 μm in the ESO/VISTA instrument VIRCAM. We here report on 3 nights of GTO observations with this filter set. In particular we describe its performance in terms of sky noise, throughput and passband and we describe in detail what we have found to be the best observing and reduction strategies with this filter set.
The filters are designed to fit into a spectral region with few airglow lines and therefore relatively low sky background. The central wavelength corresponds to redshifts of z ≈ 0.8, 1.4, 2.2 and 8.8 for emission lines Hα, Hβ+[O iii], [O ii] and Lyα, respectively, which combined with the large area covered by VIRCAM in a single exposure makes it a very powerful facility for emission line surveys in the near-infrared.
We found that persistence was an important issue in our data and that persistence from bright objects could be detected not only in the following image but also in the one following that. The strength of the persistence is not the same for all detectors and we therefore designed a general process for masking which works optimally for all 16 detectors after we determine a number of detector-dependent parameters. We describe this process in detail since it will be of importance for other projects using VISTA data, but we also point out that the problem in our data was enhanced by our choice of OB nesting and make specific recommendations for which nesting to use for this kind of observations.
We found that narrow-band data from different detectors show a large variation (factor of up to 2.43) in sky background and conclude that this is most likely related to slight differences in the passbands and/or red-leaks of the narrow-band filters. This produces variations in the depth within the combined image.
From a cross correlation of catalogues of spectroscopic redshifts in the field and a preliminary catalogue of emission line objects selected in our narrow-band stack we confirm that we are able to identify emission line galaxies broadly as expected, but the passband is shifted towards slightly higher redshifts. The shift is about 3.5−4 nm towards the red; the origin of the shift is unknown.
The full scientific exploitation of the GTO data with a complete catalogue of extracted emission line objects to well defined detection limits will be presented elsewhere, but we did extract a preliminary list of emission line objects which was necessary in order to characterise the performance of the filters.
As mentioned above we have cross correlated this list with known spectroscopic redshifts and we find that we have identified objects at a large number of redshifts with a corresponding range of different emission lines in the narrow filters. In addition to the expected strong lines ([S ii]6718,6733, Hα+[N ii], Hβ+[O iii] and [O ii]3727,3730) we detect the [S iii]9533 line not usually targeted in emission-line surveys. We also find one likely Mg ii2796,2804 emitter, which is classified as a broad-line AGN by zCOSMOS.
The narrow-band component of the UltraVISTA survey was originally foreseen as a stand-alone survey called ELVIS (Emission Line galaxies with VISTA Survey, e.g. Nilsson et al. 2007).
This sequence corresponds to the nesting parameter in the observation blocks (OBs) being FJPME, with the loop over J (jitter) being outside the loop over P (pawprint); see the discussion in McCracken et al. (2012). The reverse order of J and P had been desirable.
http://www.eso.org/sci/facilities/paranal/instruments/vircam/inst/Filters_QE_Atm_curves.tar.gz − for reference, at 1190 nm the atmospheric transmission is 99.3%, the detector QE is 91.6%, and the M1 and M2 reflectivities are 97.5% and 97.8%, respectively, which likely refer to the silver coating in use at the time of the GTO observations. The other optical elements in the system (camera entrance window and lenses L1, L2 and L3) are not considered.
We used data in the field of NGC 253, ESO ID 60.A-9285(A); the VISTA SV is described in Arnaboldi et al. (2010) and at http://www.eso.org/sci/activities/vistasv/VISTA_SV.html
Acknowledgments
We thank the ESO Paranal staff, in particular Thomas Szeifert, Carlos La Fuente, Valentin Ivanov and Andres Parraguez, for assistance during the observations. We thank the CASU staff, in particular Jim Lewis, Mike Irwin and Eduardo Gonzalez-Solares, for performing the initial data processing. We thank Olivier Hérent, Patrick Hudelot and Yuliana Goranova for help with the data processing at TERAPIX. We thank Will Sutherland, Jim Emerson, Gavin Dalton, Michael I. Andersen, Sangeeta Malhotra, James Rhoads, Chun Ly, Janice Lee, Marina Rejkuba, John Moustakes, and Lise Christensen for discussions. We thank Marcus Wallace from NDC for information about the filters. We thank the referee for a constructive report that prompted us to improve both the reduction and parts of the presentation. B.M.J. thanks ESO for hospitality during a 3 month visit. We gratefully acknowledge funding for purchasing the NB118 filters from the Dark Cosmology Centre and from IDA (Instrumentcenter for Dansk Astrofysik). This paper makes use of observations processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge. This work is based on data products produced at the TERAPIX data center located at the Institut d’Astrophysique de Paris. Based in part on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium. Based in part on zCOSMOS observations made with ESO Telescopes at the La Silla or Paranal Observatories under programme ID 175.A-0839. B.M.J. and J.P.U.F. acknowledge support from the ERC-StG grant EGGS-278202. The Dark Cosmology Centre is funded by the Danish National Research Foundation. J.S.D. acknowledges the support of the European Research Council via the award of an Advanced Grant, and the support of the Royal Society via a Wolfson Research Merit Award.
References
- Abrams, M. C., Davis, S. P., Rao, M. L. P., Engleman, Jr., R., & Brault, J. W. 1994, ApJS, 93, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, K. L., Steidel, C. C., Shapley, A. E., et al. 2004, ApJ, 607, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Petr-Gotzens, M., Rejkuba, M., et al. 2010, The Messenger, 139, 6 [NASA ADS] [Google Scholar]
- Barton, E. J., Davé, R., Smith, J.-D. T., et al. 2004, ApJ, 604, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bayliss, K. D., McMahon, R. G., Venemans, B. P., Ryan-Weber, E. V., & Lewis, J. R. 2011, MNRAS, 413, 2883 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, eds. D. A. Bohlender, D. Durand, & T. H. Handley, ASP Conf. Ser., 281, 228 [Google Scholar]
- Bessell, M. S. 2005, ARA&A, 43, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Bezawada, N., & Ives, D. 2006, in Scientific Detectors for Astronomy 2005, eds. J. E. Beletic, J. W. Beletic, & P. Amico, 499 [Google Scholar]
- Bezawada, N., Ives, D., & Woodhouse, G. 2004, in SPIE Conf. Ser. 5499, eds. J. D. Garnett, & J. W. Beletic, 23 [Google Scholar]
- Bland-Hawthorn, J., van Breugel, W., Gillingham, P. R., Baldry, I. K., & Jones, D. H. 2001, ApJ, 563, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Monai, S., & Beers, T. C. 2000, AJ, 120, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Warren, S. J., Hewett, P. C., & Clements, D. L. 1995, MNRAS, 273, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Clément, B., Cuby, J.-G., Courbin, F., et al. 2012, A&A, 538, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cross, N. J. G., Collins, R. S., Mann, R. G., et al. 2012, A&A, 548, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuby, J., Hibon, P., Lidman, C., et al. 2007, A&A, 461, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalton, G. B., Caldwell, M., Ward, A. K., et al. 2006, in SPIE Conf. Ser., 6269, 30 [Google Scholar]
- Dalton, G. B., Sutherland, W. J., Emerson, J. P., et al. 2010, in SPIE Conf. Ser., 7735, 51 [Google Scholar]
- Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Emerson, J., & Sutherland, W. 2010a, The Messenger, 139, 2 [NASA ADS] [Google Scholar]
- Emerson, J. P., & Sutherland, W. J. 2010b, in SPIE Conf. Ser., 7733 [Google Scholar]
- Emerson, J. P., Irwin, M. J., Lewis, J., et al. 2004, in SPIE Conf. Ser. 5493, eds. P. J. Quinn, & A. Bridger, 401 [Google Scholar]
- Emerson, J., McPherson, A., & Sutherland, W. 2006, The Messenger, 126, 41 [NASA ADS] [Google Scholar]
- Findlay, J. R. 2012, Ph.D. Thesis, Queen Mary University of London [Google Scholar]
- Finn, R. A., Zaritsky, D., McCarthy, Jr., D. W., et al. 2005, ApJ, 630, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, A. M., & Gatley, I. 1991, in SPIE Conf. Ser. 1541, ed. T. S. J. Jayadev, 127 [Google Scholar]
- Fynbo, J. U., Møller, P., & Warren, S. J. 1999, MNRAS, 305, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. U., Møller, P., & Thomsen, B. 2001, A&A, 374, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fynbo, J. P. U., Ledoux, C., Møller, P., Thomsen, B., & Burud, I. 2003, A&A, 407, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallego, J., Zamorano, J., Rego, M., & Vitores, A. G. 1997, ApJ, 475, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Geach, J. E., Smail, I., Best, P. N., et al. 2008, MNRAS, 388, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Ghinassi, F., Licandro, J., Oliva, E., et al. 2002, A&A, 386, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grove, L. F., Fynbo, J. P. U., Ledoux, C., et al. 2009, A&A, 497, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hambly, N. C., Mann, R. G., Bond, I., et al. 2004, in SPIE Conf. Ser. 5493, eds. P. J. Quinn, & A. Bridger, 423 [Google Scholar]
- Hayashi, M., Sobral, D., Best, P. N., Smail, I., & Kodama, T. 2013, MNRAS, 430, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashino, T., Matsuda, Y., Tamura, H., et al. 2004, AJ, 128, 2073 [NASA ADS] [CrossRef] [Google Scholar]
- Hodgkin, S. T., Irwin, M. J., Hewett, P. C., & Warren, S. J. 2009, MNRAS, 394, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Driver, S. P., Brough, S., et al. 2013, MNRAS, 430, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- Horton, A., Parry, I., Bland-Hawthorn, J., et al. 2004, in SPIE Conf. Ser. 5492, eds. A. F. M. Moorwood, & M. Iye, 1022 [Google Scholar]
- Hu, E. M., Cowie, L. L., & McMahon, R. G. 1998, ApJ, 502, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, W., Hanuschik, R., de Bilbao, L., et al. 2010, in SPIE Conf. Ser. 7737, 35 [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Lewis, J., Hodgkin, S., et al. 2004, in SPIE Conf. Ser. 5493, eds. P. J. Quinn, & A. Bridger, 411 [Google Scholar]
- James, P. A., Shane, N. S., Knapen, J. H., Etherton, J., & Percival, S. M. 2005, A&A, 429, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kennicutt, R. C. 1992, ApJ, 388, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Méndez, R. H., Feldmeier, J. J., et al. 2000, ApJ, 536, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Ly, C., Spitler, L., et al. 2012, PASP, 124, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, J. R., Irwin, M., & Bunclark, P. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 91 [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lissberger, P. H. 1970, Rep. Prog. Phys., 33, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Lord, S. D. 1992, A new software tool for computing Earth’s atmospheric transmission of near- and far-infrared radiation; NASA Technical Memorandum 103957, Tech. Rep. [Google Scholar]
- Ly, C., Lee, J. C., Dale, D. A., et al. 2011, ApJ, 726, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2012, ApJ, 757, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Maihara, T., Iwamuro, F., Yamashita, T., et al. 1993, PASP, 105, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., & Rhoads, J. E. 2002, ApJ, 565, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 1998, MNRAS, 300, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Marmo, C., & Bertin, E. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 619 [Google Scholar]
- McCracken, H. J., Capak, P., Salvato, M., et al. 2010, ApJ, 708, 202 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMahon, R., Parry, I., Venemans, B., et al. 2008, The Messenger, 131, 11 [NASA ADS] [Google Scholar]
- McMurtry, C. W., Allen, T. S., Moore, A. C., Forrest, W. J., & Pipher, J. L. 2005, in SPIE Conf. Ser. 5902, eds. T. J. Grycewicz, & C. J. Marshall, 152 [Google Scholar]
- Møller, P., & Warren, S. J. 1993, A&A, 270, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Monnerville, M., & Sémah, G. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 495 [Google Scholar]
- Morelli, D. W. 1991, Interference filter handbook. A guide for specifying optimum filter performance (Santa Rosa, Ca.: Optical Coating Laboratory Inc. – OCLI) [Google Scholar]
- Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJ, 651, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2012, ApJ, 745, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K. K. 2007, Ph.D. Thesis, University of Copenhagen [arXiv:0711.2199] [Google Scholar]
- Nilsson, K. K., Orsi, A., Lacey, C. G., Baugh, C. M., & Thommes, E. 2007, A&A, 474, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, K. K., Tapken, C., Møller, P., et al. 2009, A&A, 498, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Oliva, E., & Origlia, L. 1992, A&A, 254, 466 [NASA ADS] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd edn. (Sausalito, CA: University Science Books) [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2010, ApJ, 723, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, Q. A., & Bland-Hawthorn, J. 1998, PASA, 15, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Partridge, R. B., & Peebles, P. J. E. 1967, ApJ, 147, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Pascual, S., Gallego, J., & Zamorano, J. 2007, PASP, 119, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Montero, E., Contini, T., Lamareille, F., et al. 2013, A&A, 549, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Pritchet, C. J., & Hartwick, F. D. A. 1987, ApJ, 320, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, S. K., Mountain, C. M., & Geballe, T. R. 1992, MNRAS, 259, 751 [NASA ADS] [Google Scholar]
- Reitmeyer, W. L. 1967, AJ, 72, 317 [NASA ADS] [Google Scholar]
- Rhoads, J. E., Hibon, P., Malhotra, S., Cooper, M., & Weiner, B. 2012, ApJ, 752, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Lidman, C., Cuby, J.-G., Moreels, G., & Monnet, G. 2000, A&A, 354, 1134 [NASA ADS] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007a, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007b, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Kashikawa, N., Ota, K., et al. 2012, ApJ, 752, 114 [Google Scholar]
- Shioya, Y., Taniguchi, Y., Sasaki, S. S., et al. 2008, ApJS, 175, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. E., Cohen, R. D., Burns, J. E., Moore, D. J., & Uchida, B. A. 1989, ApJ, 347, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2009, MNRAS, 398, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Matsuda, Y., et al. 2012, MNRAS, 420, 1926 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2000, ApJ, 532, 170 [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, P. W., & Simcoe, R. A. 2012, PASP, 124, 1336 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [Google Scholar]
- Tilvi, V., Rhoads, J. E., Hibon, P., et al. 2010, ApJ, 721, 1853 [NASA ADS] [CrossRef] [Google Scholar]
- Trump, J. R., Impey, C. D., Elvis, M., et al. 2009, ApJ, 696, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Gennari, S., Ciofini, M., & Testi, L. 1998, Exp. Astron., 8, 177 [Google Scholar]
- Venemans, B. P., Röttgering, H. J. A., Miley, G. K., et al. 2005, A&A, 431, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villar, V., Gallego, J., Pérez-González, P. G., et al. 2008, ApJ, 677, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, J. P., & Courbin, F. 2005, MNRAS, 357, 1348 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Creation of persistence masks
 |
Fig. A.1 Illustration of persistence in individual VIRCAM images. The top row shows a subsection of 3 NB118 images (DIT = 280 s, NDIT = 1) taken right after each other. The data are from detector 3, and the 3 subsections correspond to the same pixels on the detector. In between each image the telescope has moved, so the subsections correspond to different parts of the sky. The width of the section is 19′′, and the pixel scale is the native one of 0.34′ px-1. In the first image a star of magnitude JVega = 11.1 (2MASS) is seen. In the subsequent two images, there is a persistent image at the same detector coordinates as the star in the first image. The bottom row shows the persistence masks created by our algorithm for each image, see text. |
Most infrared detectors suffer from persistence, i.e. a sufficiently bright source will produce a signal in one or more subsequent exposures. The 16 VIRCAM detectors, of type Raytheon VIRGO 2048 × 2048 HgCdTe on CdZnTe substrate (e.g. Bezawada et al. 2004; Bezawada & Ives 2006), are reported to have low persistence22, but the effect is nevertheless easily detectable and can for certain observing patterns (i.e. an unfortunate choice of the so-called nesting) cause severe problems, as we will show below. We find that the object causing the persistence (typically a star) does not have to be extremely bright: in our stack we would see persistence from stars as faint as JVega ≈ 15 (JAB ≈ 16) had we not applied our persistence masking. Furthermore, for some of the detectors the star does not even have to be saturated to cause persistence.
At the level of the individual images, i.e. before stacking, persistence will be present in most VIRCAM images (regardless of filter). This is illustrated in the top row of Fig. A.1, where we show a small section of 3 images taken after each other. The shown section is the same on the detector but different on the sky, as the telescope was moved between each image. The first image contains a somewhat bright star (JVega ≈ 11). The two subsequent images do not contain any astronomical objects, and the source that is seen is the so-called persistent image of the star, i.e. a fake source.
 |
Fig. A.2 Illustration of persistence in the stack of our data. Left: stack made without masking the persistent images (i.e. fake sources) in the individual images. Right: stack made with masking. The circles mark the predicted locations of persistent images in the stack, see text. The circles are labelled with the J-band Vega magnitude of the star that caused the persistence in question. The diameter of the circles is 15′′. North is up and east is left |
Whether persistent images will be present in the stack depends on the number of individual images being stacked and on the observing pattern (i.e. on the type of offsets/jitters) used to obtain these images:
-
If many individual images are stacked and if random jitters havebeen used between each image, then the persistent images will not“stack up”, and sigma clipping will effectively remove these.
-
If only a few individual images are stacked, then sigma clipping will not be able to (fully) remove the persistent images.
-
If an unfortunate observing pattern is used, as is the case here (but which may be rare), then stacking many images does not help, as the the persistent images will “stack up” and sigma clipping will not remove them.
The latter situation is illustrated in Fig. A.2. The two panels on the left hand side show a stack of our NB118 data made using sigma clipping, but without applying the masking that we will describe below. The circles are located at the predicted positions of persistent images (fake sources) in the stack. The two panels on the right hand side show the stack in which the persistent images in each individual image have been masked, and it is seen that the masking removes the fake objects, while leaving real objects intact. Note that the masking operates on the individual images, not on the stack directly.
The main point of Fig. A.2 is that without masking we would have persistent images in our stack, and these could be mistaken for emission line objects, since they would mostly be present in the NB118 stack and less so in the J-band stack where most of the data come from UltraVISTA where random offsets between each image were used.
 |
Fig. A.3 Persistence in the 16 VIRCAM detectors. The figure is based on a number of image pairs taken right after each other, called image 0 and image 1. Only subsections with a somewhat bright star in image 0 and no astronomical object in image 1 were analysed (the telescope moved in between the two images). In each image the median value over the image, i.e. the background, was subtracted. For each pixel, the fluxes f0 and f1 in the two images were measured. The figure shows a plot of these, binned in f0. The persistence (i.e. detector memory effect) is seen by the fact that f1 becomes positive above a certain threshold in f0. The black solid line is a fit to the data (Eq. (A.1)). The red dashed line is the threshold in f0 at which the fit reaches a value of 3 ADU above the background, and this is used in our masking algorithm as the threshold for masking a given pixel (i.e. for excluding it when stacking the data). For detector 5 a lower threshold was manually set, as indicated by the blue dot-dashed line. The used thresholds are given on the panels and listed in Table A.1. The f0 axis is logarithmic and runs from 10 to 70 000. The units are gain-normalised ADU, as used in the individual images reduced by CASU. |
The details of Fig. A.2 are not so important, but can nevertheless be described as follows. As described in Sect. 2.2, we used an observing pattern in which the offset between the 3 pawprint positions (named paw6, paw5 and paw4, see Fig. 2) was always 5.5′ in Dec, and in which a random offset was only applied after each set of 3 pawprints. Recalling from the top row of Fig. A.1 that persistent images can sometimes be seen both in the first and the second image after a given image in which a bright star was located, we expect persistent images to be present in the stack at locations 5.5′ and 11′ north of bright stars. The circles in Fig. A.2 correspond to modified versions of the 2MASS catalogue in which 5.5′ (top panel) or 11′ (bottom panel) has been added to the Dec. In the 5.5′ case (top panel) a given bright star gives rise to two persistent images separated by about 7′′ (the circles in the figure have a diameter of 15′′) mostly along the east-west direction. One comes from the star being in paw6 and the persistent image being in paw5, and the other comes from the same star being in paw5 and the persistent image being in paw4. The telescope movements paw6 → paw5 and paw5 → paw4 must have had a small (about 3.5′′) and different component in RA (in addition to the 5.5′ in Dec) giving rise to the double appearance of these fake sources. The elongation of sources are due to the RA component of the offset being slightly different for each of the 6 nights from which we have data. In summary, the morphology of these fake sources is fully understood. It is noteworthy that the fake sources in the 11′ case (bottom panel) look like real objects and could therefore not have been excluded based on their morphology.
We will now describe the algorithm we have developed for masking the persistent images in the individual images. The algorithm uses a set of parameters, which we derived from a set of VISTA data with different background levels in order to make the algorithm more generally applicable. Specifically, we used data from this work, meaning NB118 (DIT = 280 s, NDIT = 1) and J (DIT = 30 s, NDIT = 4), and NB118 data from the VISTA SV programme23, with DIT ranging from 270 s to 860 s, all with NDIT = 1. The SV data were also chosen since some of these OBs also had an unfortunate nesting, meaning that masking of persistence is needed to make a clean stack.
We proceeded as follows. We first created a list of images taken right after each other. These images are the individual images as reduced by CASU (Sect. 3.2). We focused on a given image somewhere in the list, called image 0, and we then investigated how the pixel values in the 3 subsequent images (called image 1, image 2 and image 3) were correlated with the pixel values in image 0. When analysing each image we subtracted the median value to get a background that is approximately zero. We restricted our analysis to manually selected subsections that contained a star in image 0 and no astronomical objects in the subsequent images. For each pixel we plotted the value in image 1 (or image 2 or image 3) against the value in image 0. Since the telescope moved between the two images in question, the values should be uncorrelated. However, due to the persistence this is not the case; rather, a positive correction is always seen in the image 1 case, and for some detectors also in the image 2 case. No correlations were seen in the image 3 case.
 |
Fig. A.4 Persistence in the 16 VIRCAM detectors. This figure shows the persistence in image 2, i.e. the second image after a given image (image 0) containing somewhat bright pixels. In most aspects this figure is as Fig. A.3. One difference is that the blue dot-dashed lines show the adopted masking threshold (given on the panels and in Table A.1), which is 30% lower than the threshold derived from the fit (marked by the red dashed lines). Some detectors do not show detectable persistence in image 2, and for these no threshold was derived. |
The image 1 vs. image 0 plots for the 16 detectors are shown in Fig. A.3, with the background-subtracted level in image 1 (denoted f1) on the y-axis and the background-subtracted level in image 0 (denoted f0) on the x-axis. To reduce the noise we have binned the data in f0, and we have combined the different datasets that we analysed (see below). The persistence effect is clearly seen for all 16 detectors: when a certain threshold in f0 is reached, f1 becomes non-zero and increases with f0.
The datasets that we analysed consisted of 7 sets of images, which spanned the two filters (NB118 and J) and a range of DIT values. In each set of images we analysed two subsections. We also made versions of Fig. A.3 in which the different filters and DIT values were plotted separately, and no obvious dependence on filter or DIT were seen. The simple procedure of subtracting the median (i.e. the background) allowed datasets with different background levels to coincide in these plots, greatly simplifying the analysis.
The data points in Fig. A.3 indicate that we could in principle correct for the persistence by using f0 to predict how much persistence signal f1 should be subtracted. However, we will do something simpler and more robust: we will determine a threshold in f0 above which the pixel in image 1 should be considered unreliable and therefore be masked (i.e. be given zero weight when stacking the data). To determine this threshold for each detector, we fit functions with 3 free parameters (k1, a1 and b1) of the form 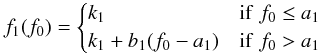 (A.1)to the data points in Fig. A.3. These fitted functions are shown as the black, solid lines in Fig. A.3; note that the fit is (piecewise) linear, but the figure uses a logarithmic x-axis. We then define the threshold (called “threshold 1”, as listed in Table A.1) above which we need to apply the masking as the f0 value at which the fit reaches 3 ADU above the constant level k1 (which is essentially zero). This threshold is shown as the red, dashed, vertical line in Fig. A.3. For detector 5 the derived threshold seemed too high given the data points, and we manually set it to a lower value, as also shown on the figure.
(A.1)to the data points in Fig. A.3. These fitted functions are shown as the black, solid lines in Fig. A.3; note that the fit is (piecewise) linear, but the figure uses a logarithmic x-axis. We then define the threshold (called “threshold 1”, as listed in Table A.1) above which we need to apply the masking as the f0 value at which the fit reaches 3 ADU above the constant level k1 (which is essentially zero). This threshold is shown as the red, dashed, vertical line in Fig. A.3. For detector 5 the derived threshold seemed too high given the data points, and we manually set it to a lower value, as also shown on the figure.
The level of 3 ADU was chosen since for our data, a persistence signal below this level would lead to a signal of less than 1σ of the noise in the stack.
Parameters used in the persistence masking algorithm.
The case of image 2 vs. image 0 is shown in Fig. A.4. For some detectors, e.g. detector 12, persistence is still seen, but only occurring above a higher threshold in f0. For each detector, a function of the same functional form as before, 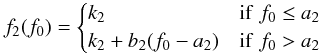 (A.2)was fitted to the data points in Fig. A.4; the fits are shown on the figure. To get the masking threshold we first calculated the level at which the fit reached 3 ADU above the constant level; this threshold is shown as the red, dashed, vertical line in the figure. Experimentation showed that slightly more masking was needed, so we multiplied the threshold by 0.7, shown by the blue, dot-dashed, vertical line in the figure. These latter thresholds are listed as “threshold 2” in Table A.1. We note that the determination of these threshold 2 values has much higher uncertainty than those for image 1, since the signal is lower (cf. Fig. A.4), which in turn is due to only a few pixels being bright enough to lead to a persistence signal in the second subsequent image. This warrants lowering the thresholds by 30%. For some detectors no persistence was seen in image 2, and for these no threshold 2 value was set (cf. Table A.1). It turned out that the stack made with the masking based on the thresholds in Table A.1 contained a few (4 in total) surviving “image 2” persistent images from detectors 1 and 2. Therefore, the used threshold 2 values for these two detectors should have been set lower; this has been indicated in Table A.1.
(A.2)was fitted to the data points in Fig. A.4; the fits are shown on the figure. To get the masking threshold we first calculated the level at which the fit reached 3 ADU above the constant level; this threshold is shown as the red, dashed, vertical line in the figure. Experimentation showed that slightly more masking was needed, so we multiplied the threshold by 0.7, shown by the blue, dot-dashed, vertical line in the figure. These latter thresholds are listed as “threshold 2” in Table A.1. We note that the determination of these threshold 2 values has much higher uncertainty than those for image 1, since the signal is lower (cf. Fig. A.4), which in turn is due to only a few pixels being bright enough to lead to a persistence signal in the second subsequent image. This warrants lowering the thresholds by 30%. For some detectors no persistence was seen in image 2, and for these no threshold 2 value was set (cf. Table A.1). It turned out that the stack made with the masking based on the thresholds in Table A.1 contained a few (4 in total) surviving “image 2” persistent images from detectors 1 and 2. Therefore, the used threshold 2 values for these two detectors should have been set lower; this has been indicated in Table A.1.
Also the image 3 vs. image 0 case was investigated, but no persistence was detected.
The analysis above shows that persistence masks can be generated simply by measuring the background-subtracted flux f0 in each pixel in image 0, and then flag the given pixel in the masks for image 1 and/or image 2 if f0 is above the thresholds listed in Table A.1. One problem remains, related to saturated stars. These stars intrinsically have high fluxes in their centres, but in the images delivered by VIRCAM these stars can have low values in their centres. Such donut shaped stars with a dip or hole in the centre are due to the CDS readout mode where each image is actually the difference of a long and a short exposure, see Sect. 3.1 and the CASU web site24. In an image containing stars of a range of magnitudes, this phenomenon leads to the following effect. Stars with peak level below the saturation threshold have the shape of the expected point spread function. When looking at increasingly brighter stars, one first sees stars with flat centres, then stars with a slight dip at the centre, and finally stars with a dip that reaches down to zero. We found that the centres of these objects with dips/holes still cause persistence in subsequent images, even if their flux values are below the thresholds of Table A.1. This has to be taken into account in any algorithm that addresses the persistence problem.
We used the above findings to generate persistence mask for each individual image in the following manner. First, we generated versions of the images in which the holes in the centres of bright stars were set to a high value. We did this by first identifying groups of connected pixels having a flux above 80% of the saturation level listed in Table A.1. For a star with a hole in the middle, such a group of pixels would be a ring around the centre of the star. Within each group of connected, high-valued pixels, a line was drawn between all the pixels with the same x-coordinate, and similarly for y, and all the pixels that these lines passed, including pixels with low values such as those forming the hole/dip, were set to a high value (specifically 1.1 times the saturation level, but the exact value is not important).
The mask was created from these modified images by marking all pixel in which the median-subtracted flux in the preceding image exceeds threshold 1, and in which the median-subtracted flux in the pre-preceding image exceeds threshold 2. These pixels were considered to be affected by persistence and therefore ignored (i.e. given zero weight) when stacking the images. Examples of the computed persistence masks are shown in the bottom row of Fig. A.1. Typically, 0.1% of the pixels in a given individual image are masked. There is some variation from detector to detector, given that some detectors (e.g. detectors 3, 12 and 13), have stronger persistence (i.e. need less bright pixels to cause persistence) than others, cf. Figs. A.3 and A.4 and Table A.1.
The algorithm works both for NDIT = 1 and NDIT > 1 images. In the case of NDIT > 1, the FITS file contains the sum of the NDIT sub-exposures. The pixel values simply need to be divided by NDIT. Care has to be taken that CASU sets the BSCALE header keyword to 1/NDIT, which makes some astronomical software (but not all) silently scale the data by this factor.
An IDL implementation of the algorithm is available upon request.
Our persistence masking algorithm was also used in the stacking of the UltraVISTA NB118 season 1 data (McCracken et al. 2012).
All Tables
All Figures
 |
Fig. 1 Schematic sky coverage. Blue hatched columns: stripes observed in this GTO work. Red filled columns: UltraVISTA ultra-deep stripes. Blue outline: UltraVISTA contiguous region. Green outline: HST/ACS region. |
| In the text | |
 |
Fig. 2 a) − c) Individual VIRCAM NB118 exposures obtained at the positions named paw6, paw5 and paw4, respectively. d) The NB118 stack. In panel a) the detector numbers are given. North is up and east is to the left. |
| In the text | |
 |
Fig. 3 Empty aperture noise measurements for the GTO NB118 data. The rectangles in panel a) show the regions used to analyse the empty aperture measurements. The detector(s) contributing data in the given region are listed, and parentheses indicate regions that have half the exposure time of the other regions. Panels b) and c) give the 2′′ diameter 5σ AB mag values for the NB118 TERAPIX stack (Sect. 3.4) and our NB118 test stack based on the CASU sky subtraction (which has about 0.1 mag lower noise, but which still may not be the best possible version of our data; Sect. 3.5), respectively. The aperture correction to total magnitude of 0.34 mag has not been subtracted. |
| In the text | |
 |
Fig. 4 Four different steps in the determination of transmittance curves shown for each of the 16 individual copies of the NB118 filter in VIRCAM. First row: collimated beam measurement at room temperature as provided by the manufacturer NDC. Second row: shift as expected due to the temperature difference. Third row: theoretical conversion to the convergent beam. Fourth row: response function including all theoretical filter transmittance, mirror reflectivity, detector QE, and atmospheric transmission (PWV = 1 mm, airmass = 1). In the plot, the 16 filters are separated into subsets of four filters corresponding to the four columns or stripes of the combined image (cf. Fig. 2d). In addition, the other 12 filters are shown in every panel in light gray. Positions and relative strengths of the sky emission lines are also included. |
| In the text | |
 |
Fig. 5 Filter curves for the 4 spare filters. These filters are relevant since they are the only ones that have two sets of measurements available: by NDC over 1100 − 1300 nm (dashed lines) and by ESO over 800 − 3000 nm (solid lines). Each colour represents one of the four filters. The left panel shows the full wavelength range covered by our measurements from the ESO laboratory. The grey line is a sky emission spectrum (see text), and the dotted line represents detector QE and mirror reflectivity (see text), but not atmospheric absorption. The right panel shows a zoom near the passband of the filters; here both NDC and ESO measurements are available. The 16 grey curves in the background show the 16 filters installed in VIRCAM (these are the filter curves shown in the top row of Fig. 4). All curves have been transformed from air to vacuum, but no further transformations have been applied. |
| In the text | |
 |
Fig. 6 Filter curves for Y, NB118 and J. |
| In the text | |
 |
Fig. 7 (J − NB118) vs. (Y − J). The blue and grey dots are objects with and without significant narrow-band excess, respectively. The contours show the density of objects after excluding likely stars. The blue dots additionally marked by a large symbol are line emitters confirmed by spectroscopy, see Fig. 8 for a legend. The solid line is meant to represent the locus of the majority of the objects. The dotted line located 0.2 mag above is one of the selection criteria. The symbols connected by coloured lines represent certain Maraston (2005) model galaxies (see text) without emission lines, placed at the 7 redshifts indicated on the panel and observed at times (from left to right) 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.5, 2.0 and 3.0 Gyr (except for z = 2.2 where 3.0 Gyr is not shown). |
| In the text | |
 |
Fig. 8 Narrow-band colour − magnitude diagram. The blue dots are objects with significant narrow-band excess, and those with a spectroscopic redshift in certain intervals are additionally marked with large symbols, as per the legend on the figure. The small grey dots are objects without significant narrow-band excess. The horizontal dotted line marks one of the selection criteria, see the text. |
| In the text | |
 |
Fig. 9 Narrow-band colour versus spectroscopic redshift. The large blue symbols are objects with significant narrow-band excess (Sect. 5.1). The symbol type indicates the spectroscopic catalogue, as per the legend given on the figure. The redshifts of strong emission lines or emission line blends selected by the NB118 filters are marked for a typical filter vacuum wavelength of 1191 nm (but note that the central wavelengths of the filters in the 4 columns of the stack differ somewhat, see the bottom row of Fig. 4). Panels b), c) and d) provide zooms, in which the dashed lines mark the line blends as shown in panel a), while the dotted lines mark the individual lines that are part of the line blends. The horizontal lines mark the redshift ranges used to define the different lines or line blends in Table 2 and in Fig. 8. The low values of the colour at z ≈ 0.9 (see panels a) and b)) are due to the Hα line being in the J band but not in the NB118. |
| In the text | |
 |
Fig. 10 Wavelength response of the 16 NB118 filters, as illustrated by objects with spectroscopic redshifts. These plots are as Fig. 9, except that λobs,vac = (1 + z)λrest,vac rather than z is on the x-axis. The 4 rows of the figure correspond to 4 emission lines or emission line blends, with the used rest-frame vacuum wavelength listed. The 4 columns of the figure correspond to the 4 columns of the stack (see Fig. 2), where each column contains data from 4 NB118 filters (namely filters 1 − 4, 5 − 8, 9 − 12 and 13 − 16 for Cols. 1 − 4, respectively), and where the corresponding filter curves are overplotted. The grey filter curves are those from the bottom row of Fig. 4, while the coloured ones are the curves shifted by 3.5 nm to the red to visually match the data. The vertical dotted lines indicate the centre wavelength of the 4 filters in the given panel before and after the shift. In the [S ii] panels (panels e) − h)) the hatched region indicates a redshift range where narrow-band excess is likely due to Hα rather than [S ii]. In the bottom row the theoretical sky spectrum used in Sect. 4 is shown, scaled to fit the panel. |
| In the text | |
 |
Fig. 11 Sky level in e − s-1 px-1 (with 1 px being about 0.34′′ on the side) as function of time for the 6 half-nights of the GTO observing run. The data were taken in either NB118 or J band; the J-band sky level values have been scaled down by a factor of 20 to fit on the plot, as indicated on the panels. For each exposure, i.e. for each point in time, the sky level in the 16 detectors is plotted; a symbol legend is provided in panel f). In VIRCAM each detector has its own filter, and filter-to-filter variations within the set of the 16 NB118 filters are likely the reason for the large detector-to-detector variations seen for the NB118 sky levels. Dot-dashed lines mark the start of twilight. In panels a) and b), solid grey regions mark episodes where the OBs had to be restarted due to minor technical (software) problems, and dotted lines mark obtained J-band exposures for which CASU did not provide reduced images (see Sect. 3.2). The UT date for the observations in panel (a) is 2010 − 01 − 18, and each subsequent panel is one day later. |
| In the text | |
 |
Fig. 12 Sky brightness in AB mag/arcsec2 versus time in days for all VISTA observations in the CASU QC tables. Panel a) shows the median NB118 sky brightness, with the median taken over the 16 detectors, i.e. over the 16 individual NB118 filters. Green diamonds: SV, blue triangles: UltraVISTA, red circles: GTO, grey skeletal symbols: standard stars taken at the start of the night (either in evening twilight or in the first 90 min of the night), black crosses: standard stars taken the rest of the time. Each point represents the stack made by CASU of the data coming from one OB and one pawprint position. There are therefore 18 GTO points from the 6 GTO OBs (one per night) each observing 3 pawprint positions. Panel b) shows the (NB118 − J) sky brightness difference for standard star observations taken in these two filters almost simultaneously. Again the median values over the 16 detectors are used, and symbols are as in panel a). Panel c) shows the NB118 sky brightness in the 16 individual detectors/filters minus the median NB118 sky brightness (with the latter being what is plotted in panel a). The median value in bins of one calendar month is plotted. The shown errorbar represents the standard deviation (if it could be computed). A legend is provided on the panel. The sense of the y-axis is such that e.g. detector 13 has a brighter sky and detector 1 has a darker sky. Panel d) is as panel c) but for J. These two panels have an identical scale on the y-axis in terms of mag/arcsec2 per cm on the page. The CASU magnitudes were transformed to AB using NB118(AB) = NB118(Vega) + 0.853 and J(AB) = J(Vega) + 0.937. |
| In the text | |
 |
Fig. 13 Sky brightness correlation coefficients for the 16 detectors. Green triangles: J, red circles: NB118, black crosses: Ks. The x-axes show the correlation coefficient with the ambient temperature, while the y-axis shows the correlation coefficient with the sky brightness in the Y band in the given detector. The correlation coefficients on the x-axes have been multiplied by minus one, since they would otherwise be negative due to the the sky brightness being in mag/arcsec2. Panel a) shows the Spearman rank order correlation coefficient rS while panel b) shows the linear Pearson correlation coefficient rP. The individual NB118 points are labelled with the detector number. |
| In the text | |
 |
Fig. 14 Two measures of the red-leak for the 16 NB118 filters. The y-axis shows the level in screen flats obtained with the lights in the dome off (i.e. with the light source being the thermal emission from the dome flat screen, the dome, etc.) divided by the level in regular screen flats (i.e. with the dome flat screen illuminated by a lamp). The levels have been dark subtracted. The x-axis shows correlation coefficients between the NB118 sky brightness in the given detector (i.e. filter) and the ambient temperature using all the VISTA data contained in the CASU QC tables. The correlation coefficients have been multiplied by minus one, since they would otherwise be negative due to the sky brightness being in mag/arcsec2. Panel a) shows the Spearman rank order correlation coefficient rS while panel b) shows the linear Pearson correlation coefficient rP. The labels indicate the detector number. |
| In the text | |
 |
Fig. 15 Predicted sky brightness for the 16 NB118 filters as function of a hypothetical filter wavelength shift Δλ with respect to the filter curves as predicted based on laboratory measurements. The results from 3 models of the sky emission spectrum are shown: solid orange line: model 1 (Gemini Observatory, theoretical), dotted green line: model 2 (Sullivan & Simcoe 2012), dashed blue line: model 3 (see text). The predictions are based on sky continuum and emission lines near the central passband of the filters; possible red-leaks are not included. The horizontal grey line marks a representative value for the observed NB118 sky brightness in the given filter. The vertical grey line marks the wavelength shift to the red of about 3.5 nm that we infer from NB118 observations of emission line objects with spectroscopic redshifts. The mean filter wavelength λ0 (Eq. (6)) as predicted based on laboratory measurements is given on the panel. |
| In the text | |
 |
Fig. A.1 Illustration of persistence in individual VIRCAM images. The top row shows a subsection of 3 NB118 images (DIT = 280 s, NDIT = 1) taken right after each other. The data are from detector 3, and the 3 subsections correspond to the same pixels on the detector. In between each image the telescope has moved, so the subsections correspond to different parts of the sky. The width of the section is 19′′, and the pixel scale is the native one of 0.34′ px-1. In the first image a star of magnitude JVega = 11.1 (2MASS) is seen. In the subsequent two images, there is a persistent image at the same detector coordinates as the star in the first image. The bottom row shows the persistence masks created by our algorithm for each image, see text. |
| In the text | |
 |
Fig. A.2 Illustration of persistence in the stack of our data. Left: stack made without masking the persistent images (i.e. fake sources) in the individual images. Right: stack made with masking. The circles mark the predicted locations of persistent images in the stack, see text. The circles are labelled with the J-band Vega magnitude of the star that caused the persistence in question. The diameter of the circles is 15′′. North is up and east is left |
| In the text | |
 |
Fig. A.3 Persistence in the 16 VIRCAM detectors. The figure is based on a number of image pairs taken right after each other, called image 0 and image 1. Only subsections with a somewhat bright star in image 0 and no astronomical object in image 1 were analysed (the telescope moved in between the two images). In each image the median value over the image, i.e. the background, was subtracted. For each pixel, the fluxes f0 and f1 in the two images were measured. The figure shows a plot of these, binned in f0. The persistence (i.e. detector memory effect) is seen by the fact that f1 becomes positive above a certain threshold in f0. The black solid line is a fit to the data (Eq. (A.1)). The red dashed line is the threshold in f0 at which the fit reaches a value of 3 ADU above the background, and this is used in our masking algorithm as the threshold for masking a given pixel (i.e. for excluding it when stacking the data). For detector 5 a lower threshold was manually set, as indicated by the blue dot-dashed line. The used thresholds are given on the panels and listed in Table A.1. The f0 axis is logarithmic and runs from 10 to 70 000. The units are gain-normalised ADU, as used in the individual images reduced by CASU. |
| In the text | |
 |
Fig. A.4 Persistence in the 16 VIRCAM detectors. This figure shows the persistence in image 2, i.e. the second image after a given image (image 0) containing somewhat bright pixels. In most aspects this figure is as Fig. A.3. One difference is that the blue dot-dashed lines show the adopted masking threshold (given on the panels and in Table A.1), which is 30% lower than the threshold derived from the fit (marked by the red dashed lines). Some detectors do not show detectable persistence in image 2, and for these no threshold was derived. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


