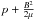| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116652 | |
| Published online | 10 December 2013 | |
Coronal heating and nanoflares: current sheet formation and heating
School of Mathematics and Statistics, University of St Andrews, North Haugh, St Andrews, Fife, KY16 9SS, UK
e-mail: ruthc@mcs.st-andrews.ac.uk
Received: 4 February 2011
Accepted: 14 November 2013
Aims. Solar photospheric footpoint motions can produce strong, localised currents in the corona. A detailed understanding of the formation process and the resulting heating is important in modelling nanoflares, as a mechanism for heating the solar corona.
Methods. A 3D MHD simulation is described in which an initially straight magnetic field is sheared in two directions. Grid resolutions up to 5123 were used and two boundary drivers were considered; one where the boundaries are continuously driven and one where the driving is switched off once a current layer is formed.
Results. For both drivers a twisted current layer is formed. After a long time we see that, when the boundary driving has been switched off, the system relaxes towards a lower energy equilibrium. For the driver which continuously shears the magnetic field we see a repeating cycle of strong current structures forming, fragmenting and decreasing in magnitude and then building up again. Realistic coronal temperatures are obtained.
Key words: magnetohydrodynamics (MHD) / magnetic reconnection / Sun: corona
© ESO, 2013
1. Introduction
The Sun’s corona is much hotter than its visible surface: the photosphere’s average temperature is 6000 K compared to over a million K in the corona. Back in 1974, Levine (1974) proposed a new theory for heating the corona involving the dissipation of many tiny little current sheets, which built on the resistive instability ideas first proposed by Parker (1972). This heating theory is better known today as nanoflare heating and was developed in a series of papers by Parker (Parker 1987, 1988). Various observational papers (e.g., Krucker & Benz 2000; Parnell & Jupp 2000; Vekstein & Jain 2003) and theoretical papers (e.g., Cargill 1993; Cargill & Klimchuk 1997, 2004; Klimchuk & Cargill 2001) lend support to this idea, but there are still many open questions. In particular, in Parker’s nanoflare heating theory the strong, localised currents in the solar corona were produced by the braiding of magnetic fields whose photospheric footpoints are moved about by convective motions. Although there are a multitude of magnetic features with a wide range of fluxes (Schrijver & Zwaan 2000; Parnell et al. 2009) which are continuously emerging, moving, cancelling, fragmenting and coalescing (Schrijver et al. 1997), it is unclear whether the braiding motions envisaged by Parker really do occur.
Tangential discontinuities, or current sheets (current layers) as they are better known, are regions where the gradient of the magnetic field and, therefore, the electric currents are very large. These currents may then dissipate due to a resistive instability, leading to magnetic reconnection, which allows the field lines to break and reconnect with some of the magnetic energy being released as heat. An aim of this paper is to follow the formation and break-up of current layers and investigate the flow of energy from the footpoint motions into the magnetic field and, through the conversion of magnetic energy, into heat in the regions of strong current. This paper investigates the heating of the plasma at the site of a single heating event.
It is well known that current layers can form at null points in both two dimensions (e.g. Green 1965; Syrovatskiǐ 1971; Bungey & Priest 1995; Craig & Litvinenko 2005; Fuentes-Fernández et al. 2011) and three dimensions (e.g., Rickard & Titov 1996; Pontin & Craig 2005; Pontin et al. 2007a,b; Masson et al. 2009; Priest & Pontin 2009; Al-Hachami & Pontin 2010; Fuentes-Fernández & Parnell 2012, 2013). They also develop at other topological features such as separators (e.g., Lau & Finn 1990; Longcope & Cowley 1996; Priest et al. 2005; Haynes et al. 2007; Parnell et al. 2010a) and separatrix surfaces (e.g., Priest et al. 2005; Mellor et al. 2005; De Moortel & Galsgaard 2006a,b). However, they may also develop at geometrical features, such as quasi-separatrix layers (e.g., Priest & Démoulin 1995; Démoulin et al. 1996; Aulanier et al. 2006; De Moortel & Galsgaard 2006a,b; Wilmot-Smith & De Moortel 2007). Indeed, a considerable body of work also exists on the formation and dissipation of current layers in initially simple fields that have been driven in a variety of different ways through shearing or rotating motions or through compressive motions (e.g., Galsgaard & Nordlund 1996a; Browning et al. 2008; Hood et al. 2009; Janse & Low 2009; Bhattacharyya et al. 2010; Huang et al. 2010).
Recently, using reduced magnetohydrodynamics (MHD), Rappazzo et al. (2007, 2008, 2010) have investigated the formation and evolution of current sheets and the cascade of energy to small-scales. In their system which is continuously driven at the photospheric boundary, they study the turbulent cascade of energy injected at large photospheric scales down to its dissipation at numerous current layers at the small scale. In their simulations, the energy equation is replaced by ∇⊥·v⊥ = 0. This means there is no information about the thermodynamic response due to any loss of magnetic energy. Here, we investigate the formation and dissipation of a single current structure using full 3D MHD, where energy is conserved if the resistivity η is greater than the numerical dissipation.
Gudiksen & Nordlund (2006) produced a model of the complete solar atmosphere. They imposed an observed velocity pattern on the photosphere and showed that all the Poynting flux injected into the corona is dissipated. However, the scale of the simulation meant that individual energy release sites were not fully resolved and so it was not possible to identify the locations and nature of these energy release sites. Recently though, a detailed analysis of the currents and reconnection in a numerical model of flux emergence has revealed that a complex web of separators through the current accumulations are responsible for the reconnection of newly emerged flux into the solar atmosphere with an overlying coronal magnetic field (Parnell et al. 2010b).
In this paper, we investigate the evolution of an initially straight magnetic field, which has first been sheared analytically and relaxed to an equilibrium. This field is then stressed by shearing motions on two boundaries similar to the models of Longbottom et al. (1998) and Galsgaard & Nordlund (1996b). Unlike in Longbottom et al. (1998), where a magnetic relaxation technique is used, our experiments use a 3D MHD code. Due to the considerable advancements in computing hardware over the past 15 years, we run simulations with grid resolutions of 5123. These are of a much higher resolution than the maximum of 1363 achieved in Galsgaard & Nordlund (1996b). Another difference to Galsgaard & Nordlund (1996b) is that we do not consider multiple random shearing of the uniform field, instead just two shears are preformed in our experiments. These create a single initial current layer, as opposed to the many transient current accumulations seen in Galsgaard & Nordlund (1996b), Rappazzo et al. (2010) and Dahlburg et al. (2012). By looking closely at the energetics of our single current layer system we investigate whether the dissipation of such a layer provides sufficient energy for either a single nanoflare on its own or many nanoflares when the system is continuously driven. Hence, we aim to determine if these types of current layers really can be the building blocks of coronal heating and, if so, what the characteristics and properties are of these building blocks.
The numerical code, basic equations and boundary conditions used in this paper are described in Sect. 2. The model is based on two shears; the first shear is described in Sect. 3 and the second shear is discussed in Sect. 4. Subsequently the evolution of the magnetic field (Sect. 5), the energetics (Sect. 6) and the current layer structure (Sect. 7) are analysed. A discussion of the results and general conclusions can be found in Sect. 8.
2. Numerical model
The simulations are carried out using the 3D MHD, Lagrangian remap, shock capturing code Lare3d (described in detail in Arber et al. 2001). The Lagrangian step is a straight forward predictor-corrector scheme and is fully 3D. After the Lagrangian step, the variables are remapped, preserving conserved quantities, onto the original grid. Artificial viscosity is used to deal with shocks and van Leer gradient limiters (van Leer 1979) are applied at the remap step to preserve monotonicity, with the appropriate shock heating applied to the energy equation. The numerical grid is staggered so that: the density, pressure and specific internal energy density are defined at the cell centres; the velocities at the vertices; the magnetic field components at the cell faces and the current components along the edges of the numerical cell. The staggered grid reduces the amount of averaging required in some of the calculations, thus reducing the associated error, and avoids the chequerboard instability. Further details of the code can be found in Arber et al. (2001).
2.1. MHD equations
The resistive MHD equations are
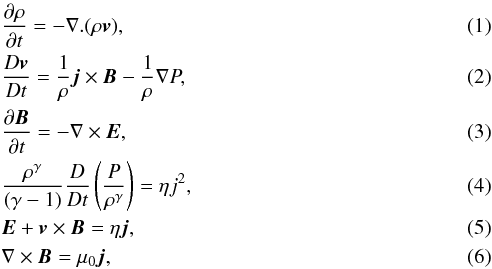 where B is the magnetic field, j is the current density, v is the velocity, E is the electric field, P is the plasma pressure, γ = 5/3 is the ratio of specific heats, ρ is the mass density, η is the resistivity and μ0 is the magnetic permeability and t is time.
where B is the magnetic field, j is the current density, v is the velocity, E is the electric field, P is the plasma pressure, γ = 5/3 is the ratio of specific heats, ρ is the mass density, η is the resistivity and μ0 is the magnetic permeability and t is time.
Lare3d runs with a normalised versions of these equations, where the normalisation is through the choice of normalising magnetic field B0, density ρ0 and length L0. Thus, we define dimensionless quantities as 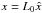 ,
, 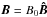 and
and 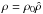 . These three basic normalising constants are then used to define the normalisation for velocity, pressure, time, current density, electric field and temperature through
. These three basic normalising constants are then used to define the normalisation for velocity, pressure, time, current density, electric field and temperature through ![\begin{eqnarray} v_0 &=& \frac{B_0}{\sqrt{\mu_0 \rho_0}}, \qquad P_0 = \frac{B_0^2}{\mu_0}, \qquad t_0 = \frac{L_0}{v_0},\nonumber \\[-1.5mm] j_0 &=& \frac{B_0}{\mu_0 L_0}, \qquad E_0 = v_0 B_0, \qquad T_0 = \frac{\tilde{\mu} v_0^2}{R}, \end{eqnarray}](/articles/aa/full_html/2013/12/aa16652-11/aa16652-11-eq21.png) (7)so that
(7)so that 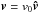 , j = j0ĵ,
, j = j0ĵ, 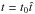 and
and 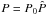 . The magnetic permeability is μ0 = 4π × 10-7 H m-1,
. The magnetic permeability is μ0 = 4π × 10-7 H m-1, 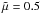 and the gas constant is R = 8.3 × 103 m2 s-2 K-1. The resistivity is normalised through
and the gas constant is R = 8.3 × 103 m2 s-2 K-1. The resistivity is normalised through 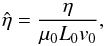 (8)or η0 = μ0L0v0. Since v0 is the normalised Alfvén speed this means that
(8)or η0 = μ0L0v0. Since v0 is the normalised Alfvén speed this means that 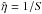 , where S is the Lundquist number.
, where S is the Lundquist number.
Dropping all of the hats on the normalised variables the final normalised resistive MHD equations, in Lagrangian form, are 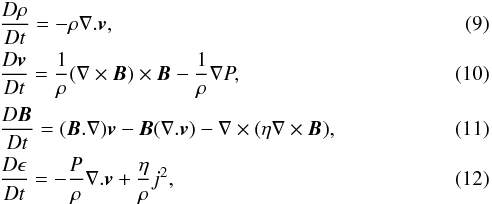 where ϵ = P/ρ(γ − 1) is the specific internal energy density. Note that, if ∇.B = 0 is initially satisfied, it remains at round-off error throughout.
where ϵ = P/ρ(γ − 1) is the specific internal energy density. Note that, if ∇.B = 0 is initially satisfied, it remains at round-off error throughout.
We neglect gravity in our simulations and initially set ρ = 1 and ϵ = 0.01, corresponding to a gas pressure of 0.00667 and plasma β of 0.013. The physical viscosity is set to zero, but Lare3d also uses an artificial viscosity to deal with shocks and includes the corresponding shock heating in (12).
In a solar context, if we choose the unit of magnetic field strength B0 = 10 G, the electron number density ne = 5 × 1014 m-3 and the unit of length L0 = 50 Mm (corresponding to a short loop over the top of a single supergranule cell), we have normalising values of velocity v0 = 975.5 km s-1, time t0 = 51 s and temperature T0 = 5.7 × 107 K.
2.2. Resistivity
The resistivity, η, is varied depending on the aim of the experiment. In the solar corona, the typical values of η are in general believed to be less than 10-10 m2s-1. Since such values are not achievable in today’s numerical experiments, we choose the smallest possible value of η we can. This is done by setting η = 0 and thus assuming an ideal evolution of the field. However, as will be shown in Sect. 6, even in this case we still get some reconnection. This is because when very fine scales are formed numerical diffusion occurs which results in reconnection. The consequences for the evolution and energetics of this numerical dissipation of the current sheet are discussed in detail in Sect. 6.
We also perform a series of resistive MHD experiments in which constant normalised η values of 10-5 and 10-4 are used. These experiments are compared with those of the “ideal” MHD runs in order to determine the effects of resistivity on the formation of the current layer and to follow the energetics of the system. The choice of η has implications for conservation of energy; too small and numerical dissipation can be important.
2.3. Boundary conditions
The equations are solved in a 3D Cartesian box, − w < x < w, − w < y < w and − L < z < L. As in Longbottom et al. (1998), we set w = 0.3, L = 0.5. We assume periodic boundary conditions in both x and y (the sides of the box) and the boundary at z = ± L is line-tied (the top and base of the box). The magnetic field components, specific internal energy density and mass density on the top and bottom boundaries have zero normal derivative, i.e. 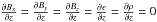 . On the top and bottom boundaries, the components of the velocities vy and vz are both set to zero and vx is discussed later in Sect. 4.
. On the top and bottom boundaries, the components of the velocities vy and vz are both set to zero and vx is discussed later in Sect. 4.
3. Initial magnetic field: first shear
The initial magnetic field we will use in our numerical simulations already includes a first shear and is analytically derived below. However, we also discuss a numerical experiment implementing the first shear in order to confirm our approach of starting from the analytical magnetic field derived and to demonstrate the limitations that should be imposed on the speed of the driver to ensure the intended displacement.
We assume the initial magnetic field has been reached by ideal MHD after a first sinusoidal shear. Such a state can be derived analytically as shown below. This initial state was also reached numerically by Longbottom et al. (1998). Assuming that the field has been sheared and that is has relaxed to an equilibrium, we can model this by considering a flux function ![\begin{equation} {\boldsymbol A} = [0,A(x,z),0]. \end{equation}](/articles/aa/full_html/2013/12/aa16652-11/aa16652-11-eq68.png) (13)The first shear will be in the y direction, as in Longbottom et al. (1998). So although there is no variation in the y direction, this shear will introduce a y component to the magnetic field, so we have
(13)The first shear will be in the y direction, as in Longbottom et al. (1998). So although there is no variation in the y direction, this shear will introduce a y component to the magnetic field, so we have ![\begin{equation} {\boldsymbol B} = \left[ -\frac{\partial A}{\partial z} , B_y(A) , \frac{\partial A}{\partial x} \right]\cdot \end{equation}](/articles/aa/full_html/2013/12/aa16652-11/aa16652-11-eq69.png) (14)The resulting force-free field satisfies the 2D Grad-Shafranov equation
(14)The resulting force-free field satisfies the 2D Grad-Shafranov equation 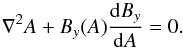 (15)Previous work, most notably that by Lothian & Hood (1989) and Browning & Hood (1989), helps to simplify our model. Lothian & Hood (1989) looked at the effect of a small twist on magnetic flux tubes. For a cylindrical loop that is much longer than it is wide, they showed that variations in the axial direction can be neglected, apart from boundary layers near the two footpoints. Hence, a theory was developed, based on straight loops with a constant cross sectional area, to show that the main properties of the loop could be explained by a simple 1D model rather than solving the 2D Grad-Shafranov equation. Mellor et al. (2005) used this idea to analytically verify the location of current accumulations when two sources are moved relative to two stationary sources. Using the approach of Mellor et al. (2005), we see that the flux function can be approximated by a function of x alone.
(15)Previous work, most notably that by Lothian & Hood (1989) and Browning & Hood (1989), helps to simplify our model. Lothian & Hood (1989) looked at the effect of a small twist on magnetic flux tubes. For a cylindrical loop that is much longer than it is wide, they showed that variations in the axial direction can be neglected, apart from boundary layers near the two footpoints. Hence, a theory was developed, based on straight loops with a constant cross sectional area, to show that the main properties of the loop could be explained by a simple 1D model rather than solving the 2D Grad-Shafranov equation. Mellor et al. (2005) used this idea to analytically verify the location of current accumulations when two sources are moved relative to two stationary sources. Using the approach of Mellor et al. (2005), we see that the flux function can be approximated by a function of x alone.
Therefore, we assume an initial magnetic field of the form ![\begin{equation} {\boldsymbol B} = [ 0, B_y(x), B_z(x) ], \end{equation}](/articles/aa/full_html/2013/12/aa16652-11/aa16652-11-eq71.png) (16)where, in order to satisfy j × B = 0, we have
(16)where, in order to satisfy j × B = 0, we have 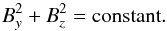 (17)As in Galsgaard & Nordlund (1996b), we choose a sinusoidal shear profile for By(x), with Bz(x) chosen to satisfy Eq. (17).
(17)As in Galsgaard & Nordlund (1996b), we choose a sinusoidal shear profile for By(x), with Bz(x) chosen to satisfy Eq. (17). ![\begin{equation} \label{our_By} {\boldsymbol B}= \left[ 0,\lambda \sin \left( \frac{\pi x}{w} \right), \sqrt{ \left( 1+ \lambda^2 \cos^2 \left( \frac{\pi x}{w} \right) \right)} \right]\cdot \end{equation}](/articles/aa/full_html/2013/12/aa16652-11/aa16652-11-eq76.png) (18)We can now calculate the footpoint displacement that generates these magnetic field components. The exact profile of the first shear is not important. All that is necessary is that the first shear produces sheared fields. Thus, the first shear we actually impose is given by
(18)We can now calculate the footpoint displacement that generates these magnetic field components. The exact profile of the first shear is not important. All that is necessary is that the first shear produces sheared fields. Thus, the first shear we actually impose is given by 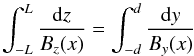 (19)which, after integrating, gives the footpoint displacement as
(19)which, after integrating, gives the footpoint displacement as 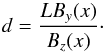 (20)For our simulations, with L = 0.5 and By, Bz, as defined above, the displacement is
(20)For our simulations, with L = 0.5 and By, Bz, as defined above, the displacement is 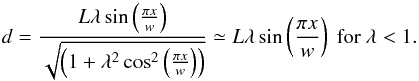 (21)As we shear on both the top and bottom boundaries, but in opposite directions, the overall maximum footpoint displacement is D = 2max(d) = 2λL.
(21)As we shear on both the top and bottom boundaries, but in opposite directions, the overall maximum footpoint displacement is D = 2max(d) = 2λL.
Hence, as we have L = 0.5 and w = 0.3, we find that the maximum shear displacement is equal to the value of λ. The particular λ used is given in the next section when implementing the second shear.
Although we present results here with the first shear taken analytically, we have also investigated it numerically by starting from a vertical magnetic field (shear parameter λ = 0) and implementing a driving profile of 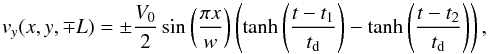 (22)where t1 is the time the driver ramps up, t2 is the time the driver starts to reduce back to zero and td is the duration over which the driver is ramped up or down. So the driving ramps up to a maximum normalised speed of V0 before reducing back to zero. This means that the footpoint displacement reaches a maximum value and does not increase after that.
(22)where t1 is the time the driver ramps up, t2 is the time the driver starts to reduce back to zero and td is the duration over which the driver is ramped up or down. So the driving ramps up to a maximum normalised speed of V0 before reducing back to zero. This means that the footpoint displacement reaches a maximum value and does not increase after that.
Importantly we note that the first shear does not excite any instabilities and there is no evidence of tearing. The Lare code has been used for reconnection studies and has successfully investigated tearing modes with both uniform and non-uniform resistivity.
The dominant velocity component is given by vy = V0zsin(πx/w))/L and this generates By = By(t)sin(πx/w). The y component of the induction equation can be expressed as 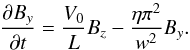 (23)We can illustrate the evolution of the maximum of By as a function of time by taking Bz = B0 as a constant. If η = 0, then we simply have the maximum of By given by
(23)We can illustrate the evolution of the maximum of By as a function of time by taking Bz = B0 as a constant. If η = 0, then we simply have the maximum of By given by 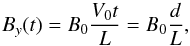 (24)where d = V0t is the distance the footpoints have been sheared and from Eq. (21) our parameter λ = d/L. However, if η ≠ 0, then the solution (as also shown by Rappazzo et al. (2010)) is
(24)where d = V0t is the distance the footpoints have been sheared and from Eq. (21) our parameter λ = d/L. However, if η ≠ 0, then the solution (as also shown by Rappazzo et al. (2010)) is 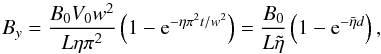 (25)where
(25)where 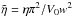 . Figure 1 shows By(t) for three values of η and for ideal MHD. Obviously, if
. Figure 1 shows By(t) for three values of η and for ideal MHD. Obviously, if 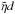 is small, then solution (25) agrees with the ideal evolution of (24). However, this assumption that
is small, then solution (25) agrees with the ideal evolution of (24). However, this assumption that 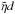 is small depends on the choices for both η and V0. The comparison between the numerical solution from the Lare code for the maximum of By as a function of time and the approximation given by Eq. (25) is exceptionally good.
is small depends on the choices for both η and V0. The comparison between the numerical solution from the Lare code for the maximum of By as a function of time and the approximation given by Eq. (25) is exceptionally good.
 |
Fig. 1 Maximum value of By as a function of time with 1283 grid points. Dashed curve is the ideal MHD case. Solid curve is η = 10-5, dot-dashed curve is η = 10-4 and triple dot-dashed curve is η = 10-3. |
During the first shear, there are no small length scales generated and the choice of the value of η is not restricted by the need to resolve any strong current regions. Choosing η = 10-5, we have conservation of total energy. With L = 0.5, w = 0.3 and V0 = 0.01, we have 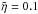 and, for t = 25, we have d = 0.25. Hence, the maximum of By will be approximately given by 0.45, rather than by 0.5 had the evolution been under ideal MHD. However, for η = 10-3, the maximum of By = 0.17. Thus, there is significant resistive slippage of the field lines for this choice of η and the field is not as sheared as expected. In fact, regardless of how long the shearing motions are applied the maximum By can reach is 0.18 for η = 10-3.
and, for t = 25, we have d = 0.25. Hence, the maximum of By will be approximately given by 0.45, rather than by 0.5 had the evolution been under ideal MHD. However, for η = 10-3, the maximum of By = 0.17. Thus, there is significant resistive slippage of the field lines for this choice of η and the field is not as sheared as expected. In fact, regardless of how long the shearing motions are applied the maximum By can reach is 0.18 for η = 10-3.
One way to reduce this slippage, for a given footpoint displacement, is to increase the value of V0. For example, increasing V0 by a factor of 5 means that, for η = 10-3, By = 0.36 for d = 0.25.
The choice for η is not too important for the first shear, and a small value of η is possible, but, it is important for the second shear as the transverse length scale, w, rapidly shortens when the current layer starts to form. The value of η needed must be increased (or the number of grid points increased significantly) to ensure that the layer is resolved and that energy is conserved. We show in Sect. 6.2 that η = 10-5 is not large enough to resolve the dissipation within the current layer during the second shear but that η = 10-4 is large enough for a 5123 grid.
Now the speed of the shearing motion becomes important once η is chosen for current sheet resolution. Too small a value for V0 and the evolution is not that intended from the driving velocity. Driving does not necessarily continue to increase the magnetic field components. Thus, we need to select V0 such that, as we stated above, the various timescales are well separated. Obviously on the Sun, the various timescales are well separated and the observed driving velocity is slow enough for sequences of equilibria but fast enough to exceed any resistive slippage. However, since computational experiments have the value of η limited by grid resolution, the speed at which the boundaries are driven is chosen as a balance between computational time and a more realistic driving velocity.
The results from the numerical simulation for the first shear can be compared with our predicted form for By (Eq. (18)). Using η = 10-5, we obtain an excellent agreement with the equilibrium predictions of analytical studies such as Browning & Hood (1989) and numerical studies such as Mellor et al. (2005) and Rappazzo et al. (2010).
4. Drivers: second shear
Next we drive a second shear in the x direction by imposing vx on the top and bottom boundaries (positive direction on the bottom boundary and negative direction on the top boundary).
We choose the same type of sinusoidal shear profile as in Sect. 3, 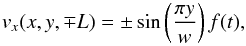 (26)where f(t) is a function, discussed in detail below, determining how fast and how much the field is sheared. The actual displacement achieved with our second shear is found from integrating vx in time and then multiplying by two, as the shear is in opposite direction on the top and bottom boundaries. Hence, we have
(26)where f(t) is a function, discussed in detail below, determining how fast and how much the field is sheared. The actual displacement achieved with our second shear is found from integrating vx in time and then multiplying by two, as the shear is in opposite direction on the top and bottom boundaries. Hence, we have 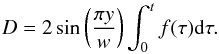 (27)Many simulations, for example varying parameter values such as the maximum first shear displacement, λ, have been carried out. We find that, as expected, an increase in the magnitude of the first shear, λ, results in a decrease in the magnitude of the second shear required to produce a localised current layer. For the results shown in this paper, we fix the value of λ at 0.5 and find that a strong localised current layer is produced with a second shear of magnitude 0.5. Note, in Longbottom et al. (1998) a first shear of magnitude 0.8 was used and a possible current sheet was formed after a shear in the second direction of 0.6−0.7.
(27)Many simulations, for example varying parameter values such as the maximum first shear displacement, λ, have been carried out. We find that, as expected, an increase in the magnitude of the first shear, λ, results in a decrease in the magnitude of the second shear required to produce a localised current layer. For the results shown in this paper, we fix the value of λ at 0.5 and find that a strong localised current layer is produced with a second shear of magnitude 0.5. Note, in Longbottom et al. (1998) a first shear of magnitude 0.8 was used and a possible current sheet was formed after a shear in the second direction of 0.6−0.7.
We run two sets of experiments which have the same spatial profiles in vx, but they have different temporal dependencies. The first set use driver 1, which continuously drives the boundaries throughout the simulation, while the second set use driver 2, which drives the boundaries up until a localised current layer forms and then the driver is switched off.
4.1. Driver 1
Driver 1 has a velocity profile that ramps up to a constant normalised value of 0.05, corresponding to a photospheric velocity of roughly 50 km s-1, namely 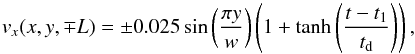 (28)where t1 and td are chosen to be 2.0 and 0.5, respectively. This velocity is high compared with observed photospheric values, but is necessary due to computational time constraints. Nonetheless, the velocity is still highly sub-Alfvénic and the magnetic field evolves slowly through a sequence of equilibria. Since the transit time for any waves propagating through the box is about one, in our dimensionless variables, they have time to settle down. Thus the evolution of the magnetic field, although sped up, will be equivalent to that found for much slower, more realistic, speeds. Mellor et al. (2005) and Galsgaard & Parnell (2005) have shown that, provided the driving speeds are slower than the Alfvén speed, it is the actual footpoint displacement that is important for the formation of current layers. The hyperbolic tanh profile is chosen so that we have a gradual rise up to our constant value. This prevents any impulsive motion at t = 0. Simulations with a slower shear were also performed. The maximum of By was found to match for both shears up to a displacement of 0.2. The maximum of jz agreed up to a displacement of 0.15 and, beyond that, the faster shear had a smaller maximum value. The maximum value of the maximum of jz, while different for the two shears, occurred at the same displacement of 0.22. So qualitatively, there was no significant different between the two cases.
(28)where t1 and td are chosen to be 2.0 and 0.5, respectively. This velocity is high compared with observed photospheric values, but is necessary due to computational time constraints. Nonetheless, the velocity is still highly sub-Alfvénic and the magnetic field evolves slowly through a sequence of equilibria. Since the transit time for any waves propagating through the box is about one, in our dimensionless variables, they have time to settle down. Thus the evolution of the magnetic field, although sped up, will be equivalent to that found for much slower, more realistic, speeds. Mellor et al. (2005) and Galsgaard & Parnell (2005) have shown that, provided the driving speeds are slower than the Alfvén speed, it is the actual footpoint displacement that is important for the formation of current layers. The hyperbolic tanh profile is chosen so that we have a gradual rise up to our constant value. This prevents any impulsive motion at t = 0. Simulations with a slower shear were also performed. The maximum of By was found to match for both shears up to a displacement of 0.2. The maximum of jz agreed up to a displacement of 0.15 and, beyond that, the faster shear had a smaller maximum value. The maximum value of the maximum of jz, while different for the two shears, occurred at the same displacement of 0.22. So qualitatively, there was no significant different between the two cases.
As already mentioned, driver 1 continuously drives the field at a constant value. Inevitably, whether we are using ideal or resistive MHD, reconnection will occur (due to either numerical diffusion or components of the induction equation). Since one of our aims is to look at the formation of a current layer we want to switch off the driver at some time so we stop driving the field and stop injecting more energy. This enables us to investigate the current layer. Hence, we run a series of experiments using a second driver, driver 2.
4.2. Driver 2
The imposed boundary shearing motion in driver 2 has the same spatial profile as driver 1, but now has a temporal variation so that it rises to a maximum speed and then reduces back to zero, similar to the driving profile implemented in Sect. 3. 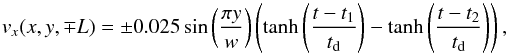 (29)where t1 and td are chosen to be 2 and 0.5, respectively, as for driver 1. The value for t2 is chosen to be 7 after a consideration of the behaviour of the maximum current as shown below. Note that if t2 is too small, no current layer forms and there is no dynamic evolution.
(29)where t1 and td are chosen to be 2 and 0.5, respectively, as for driver 1. The value for t2 is chosen to be 7 after a consideration of the behaviour of the maximum current as shown below. Note that if t2 is too small, no current layer forms and there is no dynamic evolution.
5. Evolution of the magnetic field
As already explained, the uniform field is first sheared analytically in the x direction. A cut of the magnitude of the current in the mid-plane, z = 0, shows that at this stage there is no real accumulation of current within the domain Fig. 2a. The second shear in the y direction, which is created by driving the top and bottom boundaries, moves the field at an angle of 90° to the motion of the first shear. The evolution of the magnitude of the current in the mid-plane for the experiment with driver 1 and η = 0 is illustrated in Fig. 2 for the normalised times 0,5,7 and 10. An η of zero is chosen to allow the maximum possible current to be obtained. The maximum current in this plane increases and starts to accumulate along the y-axis (Fig. 2b) until, at t = 7, an intense long thin current layer has formed (Fig. 2c). By t = 10, the current layer has dramatically evolved (Fig. 2d): the main layer has shortened and strong currents have formed in numerous smaller regions throughout the domain. This behaviour is likely to be a result of numerical reconnection occurring and will be discussed later in Sect. 6.
 |
Fig. 2 Contour plots of the logarithm of the current magnitude in the mid-plane, z = 0, for normalised times 0, 5, 7 and 10 (a)–d), respectively) for the experiment using driver 1, η = 0 and with a grid resolution of 5123. Red corresponds to a maximum of 400 while blue corresponds to a minimum value of 1. |
 |
Fig. 3 Maximum current in the domain as a function of time for the experiments with η = 0, a grid resolution of 5123 and using driver 1 (solid line and diamonds) and driver 2 (dashed line and squares). The symbols denote each time the current was recorded. |
The solid curve in Fig. 3 shows the maximum current in the whole domain as a function of time for the same case shown above (driver 1, η = 0). As we can see, the current in the domain starts off fairly small and only rises slightly over the first 5 dimensionless time units, but then the maximum current begins to rise sharply. This corresponds to the initial formation of the current layer which can be seen at t = 7 in Fig. 2c. Since η = 0, it is unlikely that this current structure is resolved. The maximum current dips slightly at about t = 8, before rising again. At about t = 8 or 9 the strong current layer starts to fragment, as seen in Fig. 2d. This is then followed by a significant decrease in maximum current as numerical effects cause it to dissipate. However, as the boundaries continue to be driven, the magnetic field continues to be stressed such that at around t = 17 the current starts to once again build up. We would expect this process to repeat since the boundaries are continuously driven.
 |
Fig. 5 As for Fig. 2, but taken at time t = 10 with η = 0, but with a) driver 1 and b) driver 2. Arrows show the projected velocity in the plane with the length of the arrows representing the magnitude of the velocity. |
If we now consider the same setup as the above experiment, except that the driver is ramped down around t = 7 (driver 2) we naturally find a similar behaviour to that shown in Figs. 2a−c. Figure 3 (dashed curve) shows that as the driver starts decreasing, the maximum current in the domain increases less rapidly than in the driver 1 case, as one might expect. After t = 7 the maximum current drops but at this time the current in the mid plane for this experiment looks the same as it does for the driver 1 experiment (compare Figs. 4a and 2c). However, by t = 10 the current in the mid-plane of the driver 2 experiment looks quite different to that seen at the same time for driver 1 (compare Figs. 4b and 2d). The main current layer is still clearly visible and a series of much shorter current sheets are found, but these are not distributed throughout the domain, instead they are clustered around the end of the main current layer forming a bubble. The drop off in maximum current that has occurred (Fig. 3) suggests that at t = 10 numerical reconnection has once again kicked in. The horizontal velocity arrows shown in Fig. 5, at this time, indicate that the flow pattern is very similar to that occurring in 2D reconnection. There is a fast outflow from the ends of the current sheets, a clear indication that numerical reconnection is occurring. It is possible that fast outflows from this numerical reconnection in the main current sheet, which are heading towards each other due to the periodic boundary conditions, lead to the formation of other short current layers and a disruption of the outflow.
The evolution of the current for both drivers reveals some interesting features which we address in the following sections. Firstly, in Sect. 6, we consider the energetics of the system, to determine whether the current really has dropped due to numerical dissipation and to investigate the effects of this for a real physical situation. Secondly, in Sect. 7, we evaluate the three-dimensional nature of the current layer at t = 7 and the magnetic structure.
6. Energy: total energy and Poynting flux
In order to properly understand the energetics, we consider, in Sect. 6.1, the ideal (η = 0) behaviour, before investigating the effects of uniform resistivity (η = constant) in Sect. 6.2.
First we discuss the total energy equation. Taking appropriate combinations of Eqs. (1) to (5), the total energy equation is 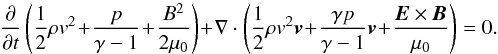 (30)Integrating over the volume of the computational box and using Gauss’s theorem, we have
(30)Integrating over the volume of the computational box and using Gauss’s theorem, we have 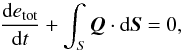 (31)where the total volume integrated energy, etot(t), given by
(31)where the total volume integrated energy, etot(t), given by 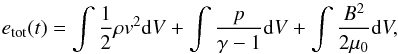 (32)is the sum of the integrated kinetic energy, internal energy and magnetic energy, respectively and
(32)is the sum of the integrated kinetic energy, internal energy and magnetic energy, respectively and 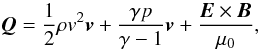 (33)is the energy flux into or out of the plasma. Since the side boundaries are periodic and the top and bottom boundaries have vz = 0, the total inflow/outflow of energy is just the Poynting flux, in dimensionless variables, namely
(33)is the energy flux into or out of the plasma. Since the side boundaries are periodic and the top and bottom boundaries have vz = 0, the total inflow/outflow of energy is just the Poynting flux, in dimensionless variables, namely 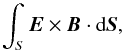 (34)where E = −v × B + ηj. The integral (34) need only be evaluated on the top (z = + L) and bottom (z = −L) boundaries because the sides are periodic. The total energy in the computational box can only increase, in response to the boundary motions, since there is a net flow of Poynting flux into the domain.
(34)where E = −v × B + ηj. The integral (34) need only be evaluated on the top (z = + L) and bottom (z = −L) boundaries because the sides are periodic. The total energy in the computational box can only increase, in response to the boundary motions, since there is a net flow of Poynting flux into the domain.
6.1. Ideal MHD energetic behaviour (η = 0)
In this section, we restrict our attention to the “ideal” evolution with η = 0. This allows us to assess the importance of numerical diffusion, which is of course a numerical error, in these simulations.
 |
Fig. 6 Volume integrated energies a) kinetic, b) internal, c) magnetic, and d) total energy as functions of time for η = 0 and driver 1 (solid) and driver 2 (dashed). For the driver 2 experiment, the start (asterisk) of the ramp down and end (triangle) of the ramp down of driver 2 are indicated. These experiments have a grid resolution 5123. |
The simulations presented are for runs with a grid resolution of 5123 (our maximum resolution). Coarser grids were also run and a similar behaviour was observed. Choosing the highest resolution for the η = 0 runs ensures there is minimal numerical diffusion of the magnetic field up to about t = 7 or 8, after the formation of the current layer. Figure 6 shows the time evolution of all energies for driver 1 (solid) and driver 2 (dashed). The asterisk denotes the time (t = 6.5) when the shearing velocity of driver 2 starts to slow down and the triangle corresponds to the time (t = 8.5) when it has completely stopped.
For both drivers the magnetic energy dominates over the other energies and is some 50−100 times larger. It is initially almost constant until about t = 3 when it begins to rise. Naturally, when driver 2 is ramped down, the energies in the two runs start to differ, with the magnetic energy for driver 1 peaking at t = 9, whilst, for driver 2, the magnetic energy levels off between t = 7 and = 8.5 The kinetic energy for both drivers remains extremely small until the current layer has formed at around t = 7, when it starts to increase. After a tiny dip the kinetic energy rises rapidly at around t = 8.5. This sudden and dramatic increase in kinetic energy is almost certainly due to numerical diffusion causing the magnetic field to reconnect. The rise is more dramatic for driver 1 than driver 2, since driver 1 is continuously driven and so, at the same time that the system is trying to dissipate the strong currents, the driver is continuing to stress the field and so maintain/rebuild the currents. In response to the reconnection, the internal energy begins to rise for both drivers, indicating that the plasma is being heated. Since driver 2 stops at t = 8 and, thus, the currents in the system are not built up again after they are dissipated, the plasma is only heated whilst the reconnection is dissipating the original current layer. Thus, the internal energy levels off, at about t = 17, to a value of 0.025 in the driver 2 case. This also corresponds to the time when the kinetic energy for driver 2 is once again almost back to zero. The magnetic energy drops off during this reconnection phase and levels off to an energy slightly below the initial magnetic energy of the numerical run (i.e., to an energy less than that after the first shear of the field). Note, that the final internal energy is only one tenth the final magnetic energy.
For driver 1, on the other hand, the internal energy continues to increase, but at a slightly lower rate, as the Poynting flux continues to add energy into the system which is converted into heat. The kinetic energy in the system is maintained significantly above zero, although at a much lower level than the high peak seen at the start of the numerical diffusion. This suggests that after the rapid onset of reconnection, which results in a drop in magnetic energy, the system adjusts to a quasi-steady state where the injection of magnetic energy, via the Poynting flux, is approximately balanced by the loss of magnetic energy through numerical reconnection. Hence, from t = 11 to t = 16 the magnetic energy is approximately constant. At t = 16, when the magnetic reconnection has essentially abated, the magnetic energy starts to increase again as the continued driving stresses the field as indicated by an increase in current (Fig. 3, solid line).
The total energy, as calculated directly by the code, is plotted in Fig. 6d. It rises continually in the experiment with driver 1, but decreases after t = 9 for driver 2.
 |
Fig. 7 Instantaneous Poynting flux (driver 1 – plus signs and driver 2 – asterisks) and the rate of change in the total energy, detot/dt, (driver 1 – solid and driver 2 – dotted line) versus time. This experiment was carried out with a grid resolution of 5123. |
The Poynting flux, as defined in (34), has been calculated numerically and is plotted in Fig. 7 for each driver, along with the rate of change of total energy (detot/dt) (where etot is determined using Eq. (32)) in the plasma. From conservation of energy (Eq. (31)), these two should lie on top of each other, but clearly they do not for t > 8. The Poynting flux corresponds to the change in total energy, as plotted in Fig. 6d, confirming that the increase in the total energy seen in this figure is due to the energy injected from the boundary driving.
For driver 1, we see that the Poynting flux matches the rate of change in total energy exactly, until a time of around t = 7. Then the effects of the numerical diffusion become significant and the two curves start to deviate. At a much later time, the two terms seem to approach each other again, before diverging at the end of the experiment. From t = 7 onwards, when the two curves do not agree, the code is not conserving energy exactly. Clearly, the lack of energy conservation will have consequences. The main concern is with the evolution of the plasma pressure and temperature. The changes in magnetic energy should be accounted for by a corresponding change in internal energy (the kinetic energy is much too small to be able to account for these changes), but, since they are not, it is difficult to trust the subsequent evolution of the plasma pressure and temperature. This is not just a consequence of our code, but something that all codes will suffer from. If numerical diffusion occurs, energy is not conserved.
If we now consider the conservation of energy in the experiment with driver 2 (Fig. 7 dotted line and asterisks) we see that the Poynting flux increases, matching the rate of change in energy exactly, until the time at which the driver is switched off: at this time the Poynting flux returns to zero as the driver ceases. However, the rate of change of total energy (as calculated from the individual components) continues to evolve after t = 8, as does the current layer. So again, the energy budget is not properly accounted for.
The simulations with η = 0 result in the formation of a strong, thin current layer. However, numerical diffusion causes magnetic reconnection and this results in a loss of energy conservation. We have conducted these η = 0 experiments as they allow for the best indication of current layer formation, the details of which we consider in the next section. However, since we are also interested in the energetic consequences of the dissipation of the current layer, we also conduct a series of constant η experiments, as discussed below.
6.2. Resistive MHD energetic behaviour (η = constant)
First, we choose an appropriate constant for η. The value of this uniform physical resistivity needs to be chosen so that it is larger than the numerical diffusion, but is still small. In particular, we aim to pick a value such that the current layers are adequately resolved. This will inevitably reduce the value of the maximum current, as discussed below.
The numerical diffusivity of the code, taking into account the size of our domain and the grid resolution used, is of the order of vA(Δx)2/2w ≈ 2.3 × 10-6, where vA ≈ 1 is the maximum Alfvén speed, 2w ≈ 0.6 is the dynamical length scale and Δx ≈ 0.6/512 = 1.2 × 10-3 is the maximum grid spacing across the current layer (for details see Arber et al. 2007). We select two values for η larger than this, namely 10-5 and 10-4.
 |
Fig. 8 Volume integrated a) kinetic, b) internal, c) magnetic, and d) total energies versus time for experiments with driver 1 and resistivities of η = 0 (solid), η = 10-5 (dotted) and η = 10-4 (dashed). These experiments were carried out with a grid resolution of 5123. |
In Fig. 8, we compare the evolution of the energies from experiments using driver 1 and with three different resistivities: η = 0, 10-5 and 10-4. Unfortunately, due to the time step restrictions and computational resources, it was only possible to run the experiment with η = 10-4 up to a time of t = 15. The initial magnetic energy (Fig. 8c) increase is smaller as η increases. This is due to the fact that the Poynting flux injected into the domain decreases as η increases (see Fig. 10). The Poynting flux depends on the size of the horizontal magnetic field component at the boundaries (as discussed by Galsgaard & Parnell 2005) which changes depending on how the magnetic field evolves (in particular how it is stressed, e.g. whether it reconnects or not). For larger η (more reconnection) these field components are reduced, leading to a reduction in the amount of energy entering the plasma.
A larger η gives not only more reconnection, but also reconnection at an earlier time. Both of these factors result in a larger increase in internal energy for larger η due to the greater Ohmic heating and its earlier onset (Fig. 8b).
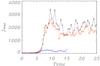 |
Fig. 9 Maximum current magnitude is shown as a function of time for the driver 1 experiments with a 5123 grid for η = 0 (black, triangles), η = 10-5 (red, squares), and η = 10-4 (blue, crosses). The symbols correspond to the times at which the current is actually recorded in each experiment. |
A plot of the temporal evolution of the maximum current (Fig. 9) clearly shows a rapid rise as the current layer starts to form just before t = 7 in the η = 0 case. There is a similar trend for η = 10-5 but the maximum current values are generally smaller. For η = 10-4, the maximum current is much smaller, reaching a maximum value of around 300. So although the maximum current still grows substantially, the rise is rapid if η is small enough, but a more steady build up if η is larger.
In all cases, the magnetic reconnection that occurs, whether numerical or associated with the imposed η, converts most of the energy injected by the Poynting flux, and stored as currents by the magnetic field, to internal energy. The kinetic energy changes are really small since only about 10% of total Poynting flux is also converted into kinetic energy (Fig. 8a). However, since the maximum current decreases with increasing η, the magnetic stresses also decrease. Thus, as η increases, the reconnection becomes weaker resulting in slower flows and, hence, a smaller maximum kinetic energy.
In Fig. 8d we plot the evolution of the total energy for the cases with driver 1, but different values of η. Not surprisingly, the total energy increases in all cases over time due to the injection of Poynting flux from the boundary driving. However, as η increases the increase in total energy decreases due to the fact that the Poynting flux crossing the boundary is smaller for larger η, as explained above. However, as we see in Fig. 8d, at a time of approximately t = 11 the total energy for the η = 10-5 case becomes larger than the η = 0 case. This does not appear to happen for the η = 10-4 case and we believe this is due to the fact that we can more accurately follow the flow of energy for this case. This is explained more fully below.
 |
Fig. 10 Poynting flux and the rate of change in the total energy (detot/dt) are shown as functions of time for experiments using a 5123 grid and driver 1 and resistivity η = 0 (black, plus signs), η = 10-5 (red, diamonds), and η = 10-4 (blue, asterisks). |
Finally, we look at the conservation of energy for each of these cases (Fig. 10), by plotting the Poynting flux (as calculated by Eq. (34)) and the rate of change of total energy, using Eq. (32). For the experiment with η = 10-4 the two terms match exactly and for this value of η we can correctly follow the flow of energy from the magnetic field to the plasma pressure and temperature. With η = 10-5, the two terms are extremely close, although there is evidence that numerical diffusion is also present after t = 7, but it is fairly small and does not dominate over our physical magnetic diffusion.
As mentioned above, there is a difference between these two terms in the η = 0 case just after η = 7 when the system abruptly switches from an ideal to a non-ideal evolution, due to the system failing to satisfy the ideal assumption. This switch in the evolution of the system occurs as the numerical diffusion begins to dominate. For the two non-zero values of η, we are confident that the numerical errors do not dominate and remain small during the simulations.
7. Current layer structure
We consider the experiment with driver 1 and η = 0 and a grid resolution of 5123 at a time of t = 7. As we have discussed above, this experiment has an ideal evolution, with no reconnection, up until approximately t = 8, unlike the constant non-zero η experiments. Shortly before t = 7 the maximum current in the experiment shows a sudden very rapid increase. Although the current continues to climb after t = 7 we pick this time because after this there is evidence of numerical diffusion. We could use either the experiment with driver 1 or driver 2, since both look almost the same, but we choose driver 1 since it has the marginally greater maximum current. Note, that at this stage the plasma pressure and temperature in this experiment should still be correct, since energy conservation still holds as no noticeable numerical diffusion has yet occurred (Fig. 10).
 |
Fig. 11 Isosurface of current at 13% of the maximum current magnitude at time a) t = 7 and b) t = 8 for the driver 1 experiment with η = 0 and a grid resolution of 5123. |
Figure 11 shows isosurfaces of the current magnitude, at approximately 13% of the maximum current in this experiment. Isosurfaces at t = 7 and t = 8 are shown in (a) and (b), respectively. We clearly see the twisted nature of the current layer. The current layer rotates from bottom to top through an angle of approximately 90°, since both the first and second shears have approximately equal magnitude. At t = 8 we see that the sheet has started to fragment due to numerical reconnection.
 |
Fig. 12 x-component of the Lorentz force, [j × B] x, across the layer (y = 0) at the mid-plane (z = 0-plane) at time t = 7. Note, that here − 0.02 < x < 0.02 to highlight the nonzero behaviour here. The experiment is the driver 1, η = 0 case with 5123 grid resolution. |
The dominant force is the Lorentz force and its x component is plotted in Fig. 12 across the layer (y = 0) at the mid-plane (z = 0). The Lorentz force is zero everywhere except inside the current layer. The width of the nonzero behaviour shown in Fig. 12 is calculated to be 0.007, which is equivalent to the width of the current layer at this resolution.
 |
Fig. 13 Slices of the current magnitude in horizontal planes a) z = 0, b) z = 0.2, and c) z = 0.4. The arrows denote the vector [Bx,By,0] in the planes. The experiment is the driver 1, η = 0 case with a grid resolution of 5123. Red corresponds to a maximum of 100 while blue corresponds to a minimum value of 0. |
7.1. Current layer rotation
Figure 11 shows a gentle rotation of the current layer from the bottom of the box to the top of the box. This rotation appears smooth and, since the plasma is very close to equilibrium when the residual Lorentz forces are analysed, we might expect to see some form of helical symmetry in the current. Hence, at t = 7, we analyse horizontal slices of the current magnitude at z = 0.0, 0.2 and 0.4 from the middle of the layer working upwards (Fig. 13). Due to symmetry the lower section of the current layer is the mirror image of these slices. These slices highlight both the strong currents in the current layers and also show the structure of the weaker current regions in the mid plane. Figure 13 shows that the current layer twists in an anticlockwise manner for increasing z (for decreasing z it rotates in the clockwise direction). The layer rotates at an approximately uniform rate with height. The angle of the current layer is approximately − 45° to the y-axis at z = 0.4, close to the top boundary and approximately half that at z = 0.2. The layer is essentially straight in each z plane but there is a slight bend in the shape at the layer ends due mainly to the imposed periodic boundaries. The arrows over plotted denote the vector (Bx,By,0). The field has a squashed elliptical structure near the current layer and there is a clear indication of anti-parallel field on either side of the current layer. The regions of stronger field (i.e. longer arrows) tend to align with the contours of the current magnitude.
 |
Fig. 14 Magnetic fieldlines drawn from starting points along the line − 0.2 < y < 0.2 at z = 0, x = 0.01 (red lines) and x = −0.01 (green lines) at t = 7 taken from the experiment using driver 1, η = 0 and 5123 resolution. |
The field lines do not cross the current layer. If they did there would be an extremely large Lorentz force. This can be seen in Fig. 14 which shows field lines plotted in both directions from the mid-plane, z = 0, with starting points along a line − 0.2 < y < 0.2 that lies either side of the current layer at x = 0.01 (red lines) and x = −0.01 (green lines). It is clear that the field lines lie along the current layer, following the same twisted structure as the isosurface of the current. In addition, it is obvious that the green and red field lines are at a different angle to each other. This is expected since the field lines lie on either side of the current layer.
We now investigate the rotation of the current layer by determining the straight line that the layer lies along at each height z. The current layer passes through x = 0 and y = 0 for all z and so we choose a value for y and determine the value of x = xmax, where xmax is the location of the maximum current. Then, we use y/xmax = tanθ(z), to calculate θ(z), the angle between the current layer and the x axis. θ = π/2 corresponds to the current layer lying along the y axis. Figure 15 shows how θ varies with z as we move up the current layer from z = −0.5 to z = 0.5 for y = 0.05. Apart from the regions near the boundaries, the twist appears linear in height.
 |
Fig. 15 Current layer angle as a function of z using y = 0.05. This is taken at t = 7 with the experiment using driver 1, η = 0 and 5123 resolution. |
7.2. Magnetic structure
The magnetic field components at the mid-plane are plotted, at t = 7, across the current layer as functions of x in Fig. 16. It is clear that there is a rapid change in the component of the magnetic field parallel to the current layer, By, across the layer and that the perpendicular component, Bx, is essentially zero. Since 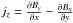 and,
and, 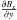 is essentially negligible, we expect the jump in By (1.62) to be approximately equal to
is essentially negligible, we expect the jump in By (1.62) to be approximately equal to 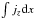 (1.61) which it is. Hence, we are satisfied that the magnetic field’s behaviour is consistent with the behaviour of the current. Bz appears to have a rapid rise inside the current layer. This is to be expected. The total pressure, i.e. the magnetic and plasma pressure, across the current layer must be continuous and this is clearly seen in Fig. 16c. The gas pressure remains small compared to the magnetic pressure. Therefore, as By vanishes at the centre of the current layer, Bz must increase rapidly at the centre of the layer to ensure that total pressure is continuous.
(1.61) which it is. Hence, we are satisfied that the magnetic field’s behaviour is consistent with the behaviour of the current. Bz appears to have a rapid rise inside the current layer. This is to be expected. The total pressure, i.e. the magnetic and plasma pressure, across the current layer must be continuous and this is clearly seen in Fig. 16c. The gas pressure remains small compared to the magnetic pressure. Therefore, as By vanishes at the centre of the current layer, Bz must increase rapidly at the centre of the layer to ensure that total pressure is continuous.
 |
Fig. 16 Magnetic field components plotted at t = 7 across the layer (y = 0) at the mid-plane. a) Shows Bx (dashed line) and By (solid line), b) shows Bz, and c) shows the total pressure ( |
We have generated a twisted current layer and the only location so far assessed is the z = 0 plane, where the layer is straight and lying along the y axis. Moving away from z = 0, the angle of the current layer changes and we must calculate magnetic field components along a cut perpendicular to the current layer at various heights. The orientation of the current layer at various values of z is determined and a cut perpendicular to the current layer at z = 0.2 is analysed here. In Fig. 17a we plot the normal and tangential components of B at z = 0.2. Here, as expected, the normal component is much smaller than the tangential. We also see in Fig. 17b that the total pressure perpendicular to the layer at z = 0.2 is similar to that at z = 0.
 |
Fig. 17 a) Normal (B⊥) and tangential (B∥) components of B across and along the current layer are plotted in the z = 0-plane (solid lines) and the z = 0.2-plane (dashed lines). Obviously, the components that show a sudden switch in sign are the B⊥ components. b) Total pressure perpendicular to the current layer in the z = 0-plane (solid line) and the z = 0.2-plane (dashed line). These are taken at t = 7 for the experiment using driver 1, η = 0 and 5123 resolution. |
The simulations were continued up to a time of t = 25 and it is interesting to see how the magnetic field and currents behave after the current layer has formed. Figure 18 shows plots of the magnetic field lines at t = 25, drawn in both directions from starting points along a line − 0.2 < y < 0.2 for x = 0, z = 0. When driver 2 is used, the magnetic field lines that lie along this line straighten out. Hence, as expected, when boundary driving stops, the magnetic field lines start to untangle and relax back towards a lower energy state.
 |
Fig. 18 Magnetic fieldlines drawn from starting points along a line − 0.2 < y < 0.2 at x = 0, z = 0 at a time t = 25 for the experiments with η = 0 and grid resolution 5123 and a) driver 1 and b) driver 2. |
However, for driver 1, when the shearing motion is continued, the field lines remain sheared and the isosurface of current still shows a fragmented current layer. Once the current layer forms and reconnection starts, the internal energy continues to rise (as shown in Fig. 6) as the Poynting flux crossing the boundaries is continually dissipated as heat.
 |
Fig. 19 Temperature at x = y = z = 0 as a function of time for the experiment using driver 1, a grid resolution of 5123 and with η = 10-5 (red, asterisks) and η = 10-4 (blue, plus signs). |
7.3. Plasma response
Figure 19 shows how the temperature at x = y = z = 0 varies, for the η = 10-5 and η = 10-4 experiments with driver 1, as a function of time. Initially the temperature is only 0.00667. What is clear is that the temperature remains low, in both cases, until the current layer forms around t = 7 and strong reconnection begins. For η = 10-5, the temperature rises to around 1.0, which corresponds to a coronal temperature of just under 6 × 107 K for our choice of physical values. The extremely rapid rise in temperature from around 0.1 to 1.1 occurs between t = 7.5 and t = 8 followed by a steep drop to around 1/5 of this value at t = 8.5. As the photospheric boundary continues to be driven, the general trend of the temperature is upwards, with a few isolated sharp peaks. For η = 10-4, a similar trend is observed, but the values are generally higher, reaching 1.4 at t = 7.5 and 1.6 at t = 14. Obviously, the larger value of η increases the Ohmic heating term and increases the temperature at the expense of the magnetic energy (see Fig. 8). The temperature response of the plasma will be investigated in more detail in future work. It is suffice to state that the temperature can easily reach the required coronal values.
8. Conclusions and future work
In this paper, we have performed a series of numerical experiments to investigate in more detail the formation of current layers. The initial field was sheared analytically in the x direction, which was justified when numerical simulations showed agreement with the analytical form used. A second, perpendicular shear was then imposed numerically through photospheric boundary motions. A choice of two different photospheric drivers were used for the second shear. While both shearing velocities are gradually ramped up to a constant value, one remains steady thereafter, while the other is ramped down to zero once the strong current layer has formed. Until the current layer formation, the magnetic energy dominates both the kinetic energy and the internal energy. The magnetic energy rises due to the stresses injected through the boundary motions. There are differences only after the twisted current structure has formed.
While the η = 0 experiment does produce the largest current values, total energy is not conserved once numerical reconnection begins. Hence, caution must be taken when following the ideal evolution. For a nanoflare model for coronal heating this is a problem, since it is not possible to account for all the energy released when the magnetic energy is reduced. The main error is in the calculation of the internal energy and, hence, the temperature and pressure. Non-zero values of η were also considered and it was shown that the total energy was indeed conserved throughout the simulations. So although physically too large, we can correctly follow the flow of energy into heat.
The current structure is twisted at a uniform rate with height. The projection of the magnetic field onto a z plane shows that the field lines are essentially elliptical in nature. The regions of strong field tend to align with the contours of the current magnitude, as one would expect. Examining the current components we find jz to be dominant, which agrees with previous numerical studies, for example Galsgaard & Nordlund (1996b).
Before the current layer forms, the boundary motions generate a Poynting flux that results in an increase in the magnetic energy. It is only after the strong currents form and reconnection starts, that this magnetic energy is released. A continued driving of the photospheric boundary, as for driver 1, means that Poynting flux continues to be fed into the system and is almost immediately converted into internal energy and, hence, temperature. Thus, if there are current layers already present in the corona, any photospheric motions that increase the stresses (currents) in the field, could produce heating. In the absence of current layers, the motions result in an increase of magnetic energy and the possible formation of current layers, but no significant heating. This is in agreement with the results found by Rappazzo & Parker (2013) who show that an initial configuration with a large-scale magnetic field develops small scales only above a magnetic intensity threshold.
Isosurfaces of temperature show that its maximum value occurs around the central plane at z = ± 0.15. The temperature at the centre of the simulation reaches a dimensionless value between 1.1 and 1.4, depending on the value of η. Although this value is quite localised, thermal conduction will spread the temperature along the field lines, reducing the maximum value. Further work is needed to understand the thermodynamic implications in detail. Using the typical values of Sect. 2.1, namely B0 = 10 G, ne = 5 × 1014 m-3 and L0 = 50 Mm, the velocities are scaled by v0 = 975.5 km s-1, the time is in units of t0 = 51 s and the temperature in units of T0 = 5.7 × 107 K. The maximum temperature is about 6 × 107 K for η = 10-5 and the rapid heating due to the rapid release of magnetic energy occurs over nearly 2 time units or 100 s. It is slightly higher when η is larger. This temperature is high but is consistent with the temperatures found by Hood et al. (2009), when considering heating by Taylor relaxation. Botha et al. (2011) showed that these high localized temperatures were reduced by a factor of 10 and spread out along the field when thermal conduction, parallel to the magnetic field, is included.
These illustrative temperatures depend on the choice of background parameters. Considering a stronger magnetic region, with B0 = 50 G, slightly denser plasma, ne = 1015 m-3, but the same length for L0, we find that the maximum temperature is now around 8 × 108 K for η = 10-5 and the rapid rise in temperature occurs within only 30 s.
There various extensions to this work that will be presented in future articles.
-
1.
Once the photospheric driving is switched off, the magnetic field tries to relax towards its lowest energy state. Since, the boundary motions have injected helicity into the plasma, the final state should be a linear force-free field with the same magnetic helicity as that at the time the driving is stopped.
-
2.
A detailed study into the reconnection process could be undertaken. There are no null points in the magnetic field and so the reconnection may be due to quasi-separator reconnection. However, this must be checked by investigating the parallel component of the electric field to see where the reconnection is occurring.
-
3.
There is some evidence that the current layer starts to fragment once reconnection begins. It is likely that there is a turbulent cascade to smaller and smaller current structures. Thus, a comparison with the work of Rappazzo et al. (2007, 2008) should be carried out.
-
4.
The inclusion of parallel thermal conduction and optically thin radiation will provide predictions of the temperature and, using forward modelling techniques, we can compare with observed properties of coronal loops.
Acknowledgments
The simulations were run on the UK MHD cluster at the University of St. Andrews funded by STFC/SRIF. R. Bowness acknowledges PhD funding from STFC.
References
- Al-Hachami, A. K., & Pontin, D. I. 2010, A&A, 512, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T. D., Haynes, M., & Leake, J. E. 2007, ApJ, 666, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., Pariat, E., Démoulin, P., & DeVore, C. R. 2006, Sol. Phys., 238, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, R., Low, B. C., & Smolarkiewicz, P. K. 2010, Phys. Plasmas, 17, 112901 [NASA ADS] [CrossRef] [Google Scholar]
- Botha, G. J. J., Arber, T. D., & Hood, A. W. 2011, A&A, 525, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., & Hood, A. W. 1989, Sol. Phys., 124, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, P. K., Gerrard, C., Hood, A. W., Kevis, R., & van der Linden, R. A. M. 2008, A&A, 485, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bungey, T. N., & Priest, E. R. 1995, A&A, 293, 215 [NASA ADS] [Google Scholar]
- Cargill, P. J. 1993, Sol. Phys., 147, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., & Klimchuk, J. A. 1997, ApJ, 478, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., & Klimchuk, J. A. 2004, ApJ, 605, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Litvinenko, Y. E. 2005, Phys. Plasmas, 12, 032301 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlburg, R. B., Einaudi, G., Rappazzo, A. F., & Velli, M. 2012, A&A, 544, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Galsgaard, K. 2006a, A&A, 451, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Galsgaard, K. 2006b, A&A, 459, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Démoulin, P., Priest, E. R., & Lonie, D. P. 1996, J. Geophys. Res., 101, 7631 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes-Fernández, J., & Parnell, C. E. 2012, A&A, 544, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuentes-Fernández, J., & Parnell, C. E. 2013, A&A, 554, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuentes-Fernández, J., Parnell, C. E., & Hood, A. W. 2011, A&A, 536, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galsgaard, K., & Nordlund, Å. 1996a, J. Geophys. Res., 101, 13445 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Nordlund, Å. 1996b, J. Geophys. Res., 101, 13445 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Parnell, C. E. 2005, A&A, 439, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, R. M. 1965, in Stellar and Solar Magnetic Fields, ed. R. Lust, IAU Symp., 22, 398 [Google Scholar]
- Gudiksen, B. V., & Nordlund, A. 2006, in 36th COSPAR Scientific Assembly, COSPAR, Plenary Meeting, 36, 3545 [NASA ADS] [Google Scholar]
- Haynes, A. L., Parnell, C. E., Galsgaard, K., & Priest, E. R. 2007, Roy. Soc. London Proc. Ser. A, 463, 1097 [Google Scholar]
- Hood, A. W., Browning, P. K., & van der Linden, R. A. M. 2009, A&A, 506, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, Y.-M., Bhattacharjee, A., & Zweibel, E. G. 2010, Phys. Plasmas, 17, 055707 [NASA ADS] [CrossRef] [Google Scholar]
- Janse, Å. M., & Low, B. C. 2009, ApJ, 690, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., & Cargill, P. J. 2001, ApJ, 553, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., & Benz, A. O. 2000, Sol. Phys., 191, 341 [Google Scholar]
- Lau, Y.-T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, R. H. 1974, ApJ, 190, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Longbottom, A. W., Rickard, G. J., Craig, I. J. D., & Sneyd, A. D. 1998, ApJ, 500, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Cowley, S. C. 1996, Phys. Plasmas, 3, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Lothian, R. M., & Hood, A. W. 1989, Sol. Phys., 122, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Mellor, C., Gerrard, C. L., Galsgaard, K., Hood, A. W., & Priest, E. R. 2005, Sol. Phys., 227, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1987, Sol. Phys., 111, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Parnell, C. E., & Jupp, P. E. 2000, ApJ, 529, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., DeForest, C. E., Hagenaar, H. J., et al. 2009, ApJ, 698, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Maclean, R. C., & Haynes, A. L. 2010a, ApJ, 725, L214 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Maclean, R. C., & Haynes, A. L. 2010b, ApJ, 725, L214 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., & Craig, I. J. D. 2005, Phys. Plasmas, 12, 072112 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007a, Phys. Plasmas, 14, 052106 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007b, Phys. Plasmas, 14, 052109 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Démoulin, P. 1995, J. Geophys. Res., 100, 23443 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Pontin, D. I. 2009, Phys. Plasmas, 16, 122101 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Longcope, D. W., & Heyvaerts, J. 2005, ApJ, 624, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., & Parker, E. N. 2013, ApJ, 773, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2007, ApJ, 657, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., & Einaudi, G. 2010, ApJ, 722, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Rickard, G. J., & Titov, V. S. 1996, ApJ, 472, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic Activity (New York: Cambridge University Press), 34 [Google Scholar]
- Schrijver, C. J., Title, A. M., van Ballegooijen, A. A., Hagenaar, H. J., & Shine, R. A. 1997, ApJ, 487, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Syrovatskiǐ, S. I. 1971, Sov. J. Exp. Theor. Phys., 33, 933 [NASA ADS] [Google Scholar]
- van Leer, B. 1979, J. Comput. Phys., 32, 101 [Google Scholar]
- Vekstein, G. E., & Jain, R. 2003, Plasma Phys. Control. Fusion, 45, 535 [Google Scholar]
- Wilmot-Smith, A. L., & De Moortel, I. 2007, A&A, 473, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Maximum value of By as a function of time with 1283 grid points. Dashed curve is the ideal MHD case. Solid curve is η = 10-5, dot-dashed curve is η = 10-4 and triple dot-dashed curve is η = 10-3. |
| In the text | |
 |
Fig. 2 Contour plots of the logarithm of the current magnitude in the mid-plane, z = 0, for normalised times 0, 5, 7 and 10 (a)–d), respectively) for the experiment using driver 1, η = 0 and with a grid resolution of 5123. Red corresponds to a maximum of 400 while blue corresponds to a minimum value of 1. |
| In the text | |
 |
Fig. 3 Maximum current in the domain as a function of time for the experiments with η = 0, a grid resolution of 5123 and using driver 1 (solid line and diamonds) and driver 2 (dashed line and squares). The symbols denote each time the current was recorded. |
| In the text | |
 |
Fig. 4 As for Fig. 2 at times a) t = 7 and b) t = 10, but with driver 2. |
| In the text | |
 |
Fig. 5 As for Fig. 2, but taken at time t = 10 with η = 0, but with a) driver 1 and b) driver 2. Arrows show the projected velocity in the plane with the length of the arrows representing the magnitude of the velocity. |
| In the text | |
 |
Fig. 6 Volume integrated energies a) kinetic, b) internal, c) magnetic, and d) total energy as functions of time for η = 0 and driver 1 (solid) and driver 2 (dashed). For the driver 2 experiment, the start (asterisk) of the ramp down and end (triangle) of the ramp down of driver 2 are indicated. These experiments have a grid resolution 5123. |
| In the text | |
 |
Fig. 7 Instantaneous Poynting flux (driver 1 – plus signs and driver 2 – asterisks) and the rate of change in the total energy, detot/dt, (driver 1 – solid and driver 2 – dotted line) versus time. This experiment was carried out with a grid resolution of 5123. |
| In the text | |
 |
Fig. 8 Volume integrated a) kinetic, b) internal, c) magnetic, and d) total energies versus time for experiments with driver 1 and resistivities of η = 0 (solid), η = 10-5 (dotted) and η = 10-4 (dashed). These experiments were carried out with a grid resolution of 5123. |
| In the text | |
 |
Fig. 9 Maximum current magnitude is shown as a function of time for the driver 1 experiments with a 5123 grid for η = 0 (black, triangles), η = 10-5 (red, squares), and η = 10-4 (blue, crosses). The symbols correspond to the times at which the current is actually recorded in each experiment. |
| In the text | |
 |
Fig. 10 Poynting flux and the rate of change in the total energy (detot/dt) are shown as functions of time for experiments using a 5123 grid and driver 1 and resistivity η = 0 (black, plus signs), η = 10-5 (red, diamonds), and η = 10-4 (blue, asterisks). |
| In the text | |
 |
Fig. 11 Isosurface of current at 13% of the maximum current magnitude at time a) t = 7 and b) t = 8 for the driver 1 experiment with η = 0 and a grid resolution of 5123. |
| In the text | |
 |
Fig. 12 x-component of the Lorentz force, [j × B] x, across the layer (y = 0) at the mid-plane (z = 0-plane) at time t = 7. Note, that here − 0.02 < x < 0.02 to highlight the nonzero behaviour here. The experiment is the driver 1, η = 0 case with 5123 grid resolution. |
| In the text | |
 |
Fig. 13 Slices of the current magnitude in horizontal planes a) z = 0, b) z = 0.2, and c) z = 0.4. The arrows denote the vector [Bx,By,0] in the planes. The experiment is the driver 1, η = 0 case with a grid resolution of 5123. Red corresponds to a maximum of 100 while blue corresponds to a minimum value of 0. |
| In the text | |
 |
Fig. 14 Magnetic fieldlines drawn from starting points along the line − 0.2 < y < 0.2 at z = 0, x = 0.01 (red lines) and x = −0.01 (green lines) at t = 7 taken from the experiment using driver 1, η = 0 and 5123 resolution. |
| In the text | |
 |
Fig. 15 Current layer angle as a function of z using y = 0.05. This is taken at t = 7 with the experiment using driver 1, η = 0 and 5123 resolution. |
| In the text | |
 |
Fig. 16 Magnetic field components plotted at t = 7 across the layer (y = 0) at the mid-plane. a) Shows Bx (dashed line) and By (solid line), b) shows Bz, and c) shows the total pressure ( |
| In the text | |
 |
Fig. 17 a) Normal (B⊥) and tangential (B∥) components of B across and along the current layer are plotted in the z = 0-plane (solid lines) and the z = 0.2-plane (dashed lines). Obviously, the components that show a sudden switch in sign are the B⊥ components. b) Total pressure perpendicular to the current layer in the z = 0-plane (solid line) and the z = 0.2-plane (dashed line). These are taken at t = 7 for the experiment using driver 1, η = 0 and 5123 resolution. |
| In the text | |
 |
Fig. 18 Magnetic fieldlines drawn from starting points along a line − 0.2 < y < 0.2 at x = 0, z = 0 at a time t = 25 for the experiments with η = 0 and grid resolution 5123 and a) driver 1 and b) driver 2. |
| In the text | |
 |
Fig. 19 Temperature at x = y = z = 0 as a function of time for the experiment using driver 1, a grid resolution of 5123 and with η = 10-5 (red, asterisks) and η = 10-4 (blue, plus signs). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.