| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322363 | |
| Published online | 22 November 2013 | |
Properties of oscillatory motions in a facular region
1 Main Astronomical Observatory, NAS, 03680 Kyiv, Ukraine
e-mail: kostik@mao.kiev.ua
2 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
3 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received: 25 July 2013
Accepted: 30 September 2013
Aims. We study the properties of waves in a facular region of moderate strength in the photosphere and chromosphere. Our aim is to statistically analyse the wave periods, power, and phase relations as a function of the magnetic field strength and inclination.
Methods. Our work is based on observations obtained at the German Vacuum Tower Telescope (Observatorio del Teide, Tenerife) using two different instruments: the Triple Etalon SOlar Spectrometer (TESOS) in the Ba ii 4554 Å line to measure velocity and intensity variations through the photosphere and, simultaneously, the Tenerife Infrared Polarimeter (TIP-II), in the Fe i 1.56 μm lines to measure the Stokes parameters and magnetic field strength in the lower photosphere. Additionally, we use the simultaneous broad-band filtergrams in the Ca ii H line to obtain information about intensity oscillations in the chromosphere.
Results. We find several clear trends in the oscillation behaviour: (i) the period of oscillation increases by 15–20% with the magnetic field increasing from 500 to 1500 G. (ii) The temperature-velocity phase shifts show a strikingly different distribution in the facular region compared to the quiet region, a significant number of cases in the range from − 180° to 180° is detected in the facula. (iii) The most powerful chromospheric Ca ii H intensity oscillations are observed at locations with strong magnetic fields (1.3–1.5 kG) inclined by 10–12 degrees, as a result of upward propagating waves with rather low phase speeds, and temperature–velocity phase shifts between 0° and 90°. (iv) The power of the photospheric velocity oscillations from the Ba ii line increases linearly with decreasing magnetic field inclination, reaching its maximum at strong field locations.
Key words: Sun: magnetic fields / Sun: photosphere / Sun: chromosphere / Sun: oscillations
© ESO, 2013
1. Introduction
There are at least two important reasons to study waves in magnetized solar regions: (i) the magnetic field modifies the properties of waves, and this provides information on the conditions of the atmosphere where these waves propagate; (ii) magnetic waves may carry enough energy to heat the material in the chromosphere and corona. In recent years, evidence has mounted that demonstrates that the magnetic field greatly influences the properties of waves not only in active regions (sunspots and plages), but also in quiet regions (network and internetwork) (see Khomenko & Calvo Santamaria 2013, for a review). Waves observed in enhanced plage, facular, and network regions share certain properties, although detailed behaviour seems to depend on the magnetic flux contained in a particular region and is apparently different for weaker network fields compared to stronger plage fields, as we explain below in detail.
Spectral and spectropolarimetric slit observations of waves in plage regions show that the maximum of oscillation power is at frequencies of around 3 mHz (below the temperature minimum cut-off frequency ~5.2 mHz) both in the photosphere and in the chromosphere (Deubner 1967; Howard 1967; Blondel 1971; Woods & Cram 1981; Deubner & Fleck 1990; Lites et al. 1993; Centeno et al. 2009; Kobanov & Pulyaev 2007; Turova 2011). The dominance of low-frequency oscillations in the chromosphere has also been reported for waves above bright network elements in the quiet Sun (Lites et al. 1993; Krijger et al. 2001; De Pontieu et al. 2003; Bloomfield et al. 2006; Tritschler et al. 2007; Vecchio et al. 2007). The two-dimensional filtergram observations give richer spatial information and demonstrate that the low-frequency 3 mHz power enhancements are only located in the intermediate surroundings of network magnetic elements at both layers (Kontogiannis et al. 2010a). In constrast, the high-frequency 5–7 mHz waves are “shadowed” in the chromosphere at the same locations, and their power is reduced (Krijger et al. 2001; Judge et al. 2001; Finsterle et al. 2004a,b; Reardon et al. 2009).
The chromospheric power distribution in stronger-field plage and facular areas is less clear. Apparently, at the edges of magnetic elements, where the field is supposed to be inclined, low-frequency 3 mHz oscillations are observed, while high-frequency 5 mHz waves are transmitted to the chromosphere at the centres of magnetic elements with a predominantly vertical field (De Pontieu et al. 2004, 2005; Hansteen et al. 2006; Jefferies et al. 2006; McIntosh & Jefferies 2006; de Wijn et al. 2009; Stangalini et al. 2011). Nevertheless, vertically propagating low-frequency 3 mHz waves are also detected in plage magnetic elements (Kobanov & Pulyaev 2007; Centeno et al. 2009). Strong complex plage areas attached to sunspot regions show the dominance of the high-frequency power at 5–7 mHz (enhanced up to 60% compared to the quiet Sun) both in the photosphere and in the chromosphere (Brown et al. 1992; Braun et al. 1992; Toner & Labonte 1993; Hindman & Brown 1998; Braun & Lindsey 1999; Donea et al. 2000; Jain & Haber 2002; Nagashima et al. 2007). These high-frequency power enhancements are called haloes in the literature on local helioseismic waves. The amplitudes of low-frequency 3 mHz photospheric waves in plages seem to be reduced compared to the quiet Sun by as much as 20–40% (Deubner 1967; Howard 1967; Blondel 1971; Woods & Cram 1981; Kobanov & Pulyaev 2007).
The phase shifts between the velocity oscillations at different heights, φ(V,V), and between the intensity and velocity oscillations at the same height, φ(I,V), have been much less investigated than the power distributions. Older slit observations provide the φ(I,V) phases that are only slightly different (on average) between the magnetic and non-magnetic areas. The magnitudes and signs of the φ(I,V) phase shifts would correspond to evanescent adiabatic acoustic-gravity waves, if one neglects the magnetic nature of these waves (Lites et al. 1993, 1982; Mein & Mein 1976; Deubner 1990). Larger φ(V,V) phase shifts are found for 3 mHz waves at the network borders compared to cell centres (Lites et al. 1982; Deubner & Fleck 1990). The network “shadow” areas show φ(V,V) phase shifts indicative of upward propagating waves at 5 mHz, but a mixture of positive and negative phase shifts for lower frequency waves at 3 mHz.
It is clear from all above that all the basic wave characteristics, such as amplitudes, phases, and dominant frequencies, depend on the magnetic structure of the region where they propagate. To get a complete picture of the wave behaviour in plage and network magnetic elements, one needs information about the magnetic field vector at photospheric and chromospheric heights. While many studies of the above-mentioned lack any magnetic information, others use photospheric magnetograms or different forms of the magnetic field extrapolation from photospheric magnetograms to obtain the magnetic field vector (Deubner 1967; De Pontieu et al. 2004; Jefferies et al. 2006; Chitta et al. 2012; Vecchio et al. 2007, 2009; Kontogiannis et al. 2010a,b). Spectropolarimetric measurements of the magnetic field vector in plage and network wave studies are scarce (Kobanov & Pulyaev 2007; Centeno et al. 2009; Stangalini et al. 2011). The later work of Stangalini et al. (2011) is a great improvement in this respect because of the 2D field of view used, rather than just one slit. However, these authors concentrate their analysis on a relatively strong pore. The behaviour of waves in weaker structures has not, to our knowledge, been studied with a similar dataset. This is one of the objectives of our paper.
A long-standing question addressed to observations is how low-frequency photospheric oscillations at 3 mHz reach chromospheric heights. It is known that, under normal conditions, waves with frequencies below the cut-off frequency (ν = 5.2 mHz) are evanescent and cannot propagate vertically to the upper layers. Their power contribution to the total spectrum is reduced, since only the evanescent tail is present there. Nevertheless, as follows from the numerous observational detections mentioned above, low-frequency waves with sufficient power are present in magnetized regions.
Michalitsanos (1973) showed that in an atmosphere where the magnetic field is inclined by γ degrees with respect to the gravity vector, the cut-off frequency is effectively lowered to a value ωccosγ, which makes the propagation of low-frequency oscillations to the chromosphere possible. This mechanism has also been considered by Bel & Leroy (1977) and Zhugzhda & Dzhalilov (1984). Numerical modelling, performed by Heggland et al. (2007, 2011), has confirmed its effectiveness as well. The observations of de Wijn et al. (2009) and Stangalini et al. (2011) indeed reveal the leakage of low-frequency waves from the photosphere to the chromosphere at the peripheral parts of rather strong magnetic elements in a plage and a pore. Stangalini et al. (2011) find a maximum transmission of 5 mHz oscillations for the field inclined by 15 degrees, and of 3 mHz oscillations for the field inclined by 25 degrees.
For the efficient working of this mechanism, a plasma β has to be below one already in the photosphere; otherwise, slow acoustic waves are not forced to propagate along the inclined magnetic field and are free to propagate in any direction. Thus, rather strong magnetic fields are required to decrease the cut-off frequency deep in the photosphere. Nevertheless, observations show the presence of energetic 3 mHz oscillations not only at the periphery of plages and pores, but also in close proximity to the network magnetic elements with weaker and mostly vertical fields (e.g. Krijger et al. 2001; Centeno et al. 2009; Vecchio et al. 2007; Kontogiannis et al. 2010a,b).
An alternative explanation was proposed by Roberts (1983) and was followed by Centeno et al. (2009). The changes in the radiative relaxation time of temperature fluctuations in small-scale magnetic elements may lead to an effective change in the cut-off frequency, introducing a formally propagating component to the wave. This mechanism allows for transmission of the 3 mHz oscillations to the chromosphere in the vertical magnetic elements, as was confirmed in the two-dimensional MHD simulation by Khomenko et al. (2008). The drawback of the latter work is in the simplified treatment of the radiative transfer by Newton’s cooling law, compared to a very detailed treatment by Heggland et al. (2007, 2011), (see the discussion in Khomenko & Calvo Santamaria 2013).
From all the above, it is evident that more observational and theoretical studies are needed to clarify the relation between waves and magnetic structures in the quiet solar regions, especially those with lower magnetic flux, such as weak plage, network, and inter-network areas. This study provides observational analysis of this sort of region. We statistically analyse the properties of waves in an isolated plage region of intermediate strength, which was observed during the minimum of solar activity in 2007. Our observational dataset includes 2D spectropolarimetric observations of the photospheric magnetic field vector, together with velocity and intensity measurements through the photosphere and the chromosphere. Below, we investigate how the different parameters of oscillations depend on the strength and inclination of the magnetic field, and we evaluate the contribution of waves to energy transport from the photosphere to the chromosphere. The same dataset was used by us to study the convection in magnetic fields (Kostik & Khomenko 2012).
 |
Fig. 1 Parameters relevant for wave propagation, calculated from the inversion. The upper row gives the magnetic field strength, inclination, and filling factor. The bottom row gives the acoustic speed, Alfvén speed, and plasma β parameter. The maps are taken at the bottom of the photosphere at constant logτ5 = −0.2. The values of density and gas pressure are calculated assuming hydrostatic equilibrium in each vertical column from the inversions and averaged over the magnetic and non-magnetic atmospheric components. |
2. Observations and data reduction
The observations were made on 2007 November 13 at the German Vacuum Tower Telescope (VTT) located at the Observatorio del Teide in Izaña, Tenerife. Three wavelength regions were observed simultaneously: Fe iλ15643–15658 Å, Ba iiλ4554 Å and Ca ii H λ3968 Å. We used two instruments simultaneously: TIP-II (Collados et al. 2007), and TESOS (Tritschler et al. 2002). On the day of the observations, there were no sunspots present on the Sun. We selected an isolated plage region unattached to any sunspot group based on filtergrams in the Ca ii H line. The observed region was located close to the solar disk centre, at approximately S05E04. The datasets and their reduction were described in detail in our previous paper (Kostik & Khomenko 2012). We recall here only those parameters that are directly relevant to the current analysis. Our dataset consists of
-
Five TIP maps of Stokes spectra ofFe i lines at1.56 μm, separated by 6 min 50 s in time and 5
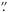 5 × 18
5 × 18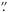 5 in size, with a pixel size of 0
5 in size, with a pixel size of 0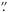 185. These data were used to recover the magnetic field strength and inclination by means of SIR inversion.
185. These data were used to recover the magnetic field strength and inclination by means of SIR inversion. -
Time series of Ba ii 4554 Å line spectra over a 5
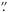 5 × 18
5 × 18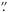 5 area, co-spatial with TIP, with a temporal cadence of 25.6 s, pixel size of 0
5 area, co-spatial with TIP, with a temporal cadence of 25.6 s, pixel size of 0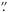 089, and a duration of 34 min 41 s. We used the Ba ii spectra to calculate the velocity and intensity fluctuations at 14 levels of the line profile, corresponding to 14 heights in the atmosphere, by means of λ-meter technique. We used the convention of positive velocity sign for upflows. Despite the consecutive wavelength points of the Ba ii line profile were not measured simultaneously, the λ-meter velocities and intensities at each of the 14 levels correspond approximately to the same moment in time, since the technique averages blue-wing and red-wing values.
089, and a duration of 34 min 41 s. We used the Ba ii spectra to calculate the velocity and intensity fluctuations at 14 levels of the line profile, corresponding to 14 heights in the atmosphere, by means of λ-meter technique. We used the convention of positive velocity sign for upflows. Despite the consecutive wavelength points of the Ba ii line profile were not measured simultaneously, the λ-meter velocities and intensities at each of the 14 levels correspond approximately to the same moment in time, since the technique averages blue-wing and red-wing values. -
Time series of Ca ii H filtergrams over 5
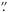 5 × 18
5 × 18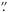 5 area, co-spatial with TIP and TESOS, with a temporal cadence of 4.93 s, pixel size of 0
5 area, co-spatial with TIP and TESOS, with a temporal cadence of 4.93 s, pixel size of 0 123, and the same duration as the TIP and TESOS series. This gives us intensity fluctuations in the low chromosphere.
123, and the same duration as the TIP and TESOS series. This gives us intensity fluctuations in the low chromosphere.
The signal-to-noise ratio of Stokes profiles in the TIP data was around 2.5 × 10-4Ic. The amplitudes of the polarization signal in the observed area were rather strong, reaching a maximum of ~ 0.03Ic in Stokes V and 0.01 − 0.02Ic in Stokes Q and U. The areas with the strongest signal in Stokes V correspond to a local darkening in the Stokes I continuum intensity.
 |
Fig. 2 Histogram of the magnetic field strength (left) and inclination with respect to the line-of-sight (right) in the observed area over the five TIP scans, as inferred from the SIR inversion. |
Stokes parameters of the Fe i 15648 and 15652 Å lines were inverted using the SIR inversion code (Stokes inversion based on response functions, see Ruiz Cobo & del Toro Iniesta 1992). We fitted all four Stokes parameters of the two Fe i lines. We slightly changed the inversion procedure compared to Kostik & Khomenko (2012) and assumed a two-component model (one magnetic and one non-magnetic component), with a filling factor as a free parameter. The temperatures and line-of-sight velocities of both atmospheres were allowed to vary independently. The magnetic field strength and orientation were assumed constant with height. Since the Stokes signals in the observed area are rather strong, they allow for robust fits. The mean error in the magnetic field strength and inclination, as given by the inversion code, is around 80 G and 7° in the strong field pixels with a more vertical field (B > 0.8 kG, γ < 20°). In the weaker field pixels (B < 0.8 kG), the error increases up to 110 G and 12°. Figure 1 gives some parameters resulting from the inversion for the first TIP map for the lower photosphere at log τ5 = −0.2. The magnetic field in the area reaches up to 2 kG. The filling factor of the magnetic atmosphere is up to 40–60% in the strongest patches. The inclination map shows coherent structures, with a more vertical field at the centres of stronger magnetic patches (in the central part of the map), inclined by 15–20 degrees in the surrounding area. At the peripheral parts of our observed region, the inclination becomes progressively higher, up to 40–50 degrees. There, the magnetic signal is not so strong. Figure 2 summarizes these results over all five maps. It shows that the magnetic field has a distribution with two dominant peaks, one in the weaker fields (with a linear decrease towards the larger fields) and another at 1.3 kG for the magnetic elements in the plage region. The distribution of inclinations peaks at low values (0–20 degrees), as was already evident from Fig. 1.
The bottom row of Fig. 1 shows maps of parameters calculated from the inversions that are directly relevant to the wave propagation, i.e. the sound and Alfvén speeds, cs and va, and the plasma β parameter, approximated as 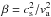 . To get gas pressure and density from the inversions, we assumed hydrostatic equilibrium in every vertical column and then averaged the pressure and density values over the magnetic and non-magnetic components with a corresponding filling factor. The sound speed map shows granulation structure with the higher values in the hotter granular areas, although the range of variation of this parameter is not so strong (7.8–8.2 km s-1). The Alfvén speed at this log τ5 is significantly greater in the central part of the map with the stronger magnetic patch. There, the values vary over a wider range than for the acoustic speed (between 6–10 km s-1). The parameter β ≥ 1 over the central part of the magnetic patch. Below log τ5 = −0.2, the values of β are greater than unity, meaning that the atmosphere is essentially gas-pressure dominated. Above log τ5 = −0.2, the plasma β becomes smaller than one, and the atmosphere is magnetically dominated. Given all the approximations and uncertainties in the inversion, these are only estimates. Nevertheless, it gives us some idea of the distribution of forces in the observed region, showing that the atmosphere is essentially magnetically dominated from the lower photosphere upwards. This defines the properties of the waves.
. To get gas pressure and density from the inversions, we assumed hydrostatic equilibrium in every vertical column and then averaged the pressure and density values over the magnetic and non-magnetic components with a corresponding filling factor. The sound speed map shows granulation structure with the higher values in the hotter granular areas, although the range of variation of this parameter is not so strong (7.8–8.2 km s-1). The Alfvén speed at this log τ5 is significantly greater in the central part of the map with the stronger magnetic patch. There, the values vary over a wider range than for the acoustic speed (between 6–10 km s-1). The parameter β ≥ 1 over the central part of the magnetic patch. Below log τ5 = −0.2, the values of β are greater than unity, meaning that the atmosphere is essentially gas-pressure dominated. Above log τ5 = −0.2, the plasma β becomes smaller than one, and the atmosphere is magnetically dominated. Given all the approximations and uncertainties in the inversion, these are only estimates. Nevertheless, it gives us some idea of the distribution of forces in the observed region, showing that the atmosphere is essentially magnetically dominated from the lower photosphere upwards. This defines the properties of the waves.
As in our previous study (Kostik & Khomenko 2012), we have split the variations in velocity and intensity from the Ba ii line profiles into two, oscillatory and convective, components based on the k − ω diagram. Below we focus our study on the oscillatory component.
 |
Fig. 3 Space-averaged power spectra (upper row, a)–c)) and dominant period of oscillations as a function of the photospheric magnetic field strength (bottom row, d)–e)). Left column: intensity oscillations in Ca ii H filtergrams (a), d)); middle column: velocity oscillations measured at the Ba ii line core (b), e)); right column: velocity oscillations measured at the Ba ii line wing (c), f)). |
 |
Fig. 4 Histograms of the phase shifts between the temperature (in anti-phase with intensity) and velocity oscillations φ(T,V) for the bottom photosphere (upper row), and the upper photosphere (bottom row). The panels on the left show the results for the facular region analysed in this paper. The panels on the right show a similar result, but for the quiet region data from Kostik et al. (2009). |
3. Results of observations
Figure 3 shows the power spectrum and the dominant periods of oscillations at three representative heights: the low photosphere, from the λ-meter velocities in the Ba ii line wings (rightmost panels); the upper photosphere from the λ-meter velocities in the Ba ii line core (middle panels); and the low chromosphere, from the Ca ii H intensity variations. The power spectra are averaged over all the spatial points irrespective of the magnetic signal (5.5′′ × 18.5′′). The power spectra have a broad distribution with peaks around 3–3.5 mHz. Some secondary peaks at lower and high frequencies are also present at all heights. The most prominent one is at lower frequencies, 1.3 mHz in the Ca ii H data. The dominant period of oscillations shows a clear dependence on the photospheric magnetic field strength. It increases by 30–60 s with B from ⟨ B ⟩ = 500 G to ⟨ B ⟩ = 1500 G at all three representative heights. We did not take a possible inclined propagation into account when calculating the relation between the dominant period and the underlying photospheric magnetic field. The periods and the magnetic field strengths are measured at the same spatial pixels. Our results mean that, on average, upper photospheric and chromospheric oscillations in a plage appear with longer periods just above the locations with stronger magnetic fields. Unfortunately, our dataset does not allow us to determine the magnetic field in the upper photosphere, which means that we are unable to determine whether the dependence between the dominant period and B would remain the same for the magnetic field measured higher up.
Phase differences between oscillating parameters provide a lot of useful information about the wave types and their propagation properties (e.g. adiabaticity or energy losses). We have calculated the phase shifts between the λ-meter intensity and velocity oscillations for the Ba ii line at two representative levels, one near the line core, corresponding to the upper photosphere; and one in the far wing, corresponding to the lower photosphere. For a better interpretation of this phase shift and for comparison with theoretical models, we converted the phase of the intensity oscillations into the phase of temperature oscillations. For that, we based it on the following qualitative argument. Since we deal with a line of a singly ionized element, an increase in temperature leads to an increase in the number of atoms in the ionized state absorbing the radiation. The line becomes deeper and its intensity decreases; i.e., the temperature and intensity oscillations are 180 degrees out of phase. Keeping this in mind, Fig. 4 presents the histograms of the distribution of the phase shifts between temperature and velocity (positive velocity direction is toward the observer), φ(T,V). The sign convention is that positive φ(T,V) mean that the oscillations of temperature lead those of velocity; the negative sign is for the opposite.
The phase shifts are frequency-dependent quantities. The φ(T,V) phase shifts in Fig. 4 are calculated at the dominant frequencies of the oscillations and are different in each spatial pixel. We used the whole field of view. The range of variation in frequencies is ν = 2.90 − 3.91 mHz (periods between 256–341 s, see Fig. 3) depending on the location. We split the whole range of φ(T,V) values in Fig. 4 into four domains: (− 180° ÷ − 90°), (− 90° ÷ 0°), (0° ÷ + 90°), and (+ 90° ÷ + 180°). If there were no magnetic field in the observed region, these four domains would correspond to different propagation behaviour of the waves, according to the well-developed theory of non-adiabatic acoustic-gravity waves in a stratified atmosphere (Whitney 1958; Noyes & Leighton 1963; Holweger & Testerman 1975). The values of φ(T,V) between 0° ÷ + 90° would mean upward propagating waves, φ(T,V) between − 180° ÷ − 90° would mean downward propagating waves, and φ(T,V) between + 90° ÷ + 180° would be evanescent non-propagating waves. This simple division is not justified once a magnetic field is introduced into the atmosphere. Later in the paper, we investigate the correlation between the magnitude and sign of φ(T,V) shift and the direction of the wave propagation. We keep the division into the sub-domains since the φ(T,V) histograms naturally split into these four regimes.
 |
Fig. 5 Phase shift between the velocities at the bottom and top of the photosphere φ(V,V) as a function of the phase shift between the velocity and temperature at the upper photosphere φ(T,V) for the plage area (upper row) and for the quiet area (bottom row). The yellow and red colours denote a greater density of points in the distribution. Negative velocity–velocity shifts, φ(V,V), mean upward waves. |
The two upper panels of Fig. 4 show histograms of the φ(T,V) phase shift for the oscillations in the Ba ii line wing (low photosphere). The two bottom panels are for the oscillations at the Ba ii line core (upper photosphere). We compare our observations in the facular region with another dataset of a similar kind, taken in the Ba ii line at the quiet solar disk centre with no detectable magnetic activity (panels on the right). The latter dataset was taken in June 2004 at the VTT and was used in our earlier work (Kostik et al. 2009). The details of the observations can be found in that paper.
The histograms of the φ(T,V) shift in the quiet region (right panels of Fig. 4) allow for an easier interpretation. At the bottom photosphere, the maximum number of cases falls into two domains: (− 180° ÷ − 90°) with 19.3% of cases, and (0° ÷ + 90°) with 62.3% of cases. According to the theory of acoustic-gravity waves, this can be interpreted as most of the waves propagating upwards in the deep photosphere. Higher up (bottom right panel), φ(T,V) shifts, and 89.9% of all points fall within the domain (+ 90° ÷ + 180°), corresponding to evanescent waves. This result is also easy to understand, since we consider waves in the 3 mHz frequency range, which are evanescent under normal conditions in the upper photosphere. The values of φ(T,V) between + 90° and + 180° fit well into the range of measurements by other authors (see e.g. the review of Deubner 1990).
The magnetic facular region shows a clearly different picture. In the lower photosphere (upper left panel of Fig. 4), most of the measured φ(T,V) values fit into the same two domains as in the quiet region (− 180° ÷ − 90° and 0° ÷ + 90°), but the relative weight of the domains is different. While in the quiet region, most of the area provides φ(T,V) between 0° ÷ + 90°, in the magnetic region the distribution between both domains is almost half and half. In addition, there are fewer points in the “evanescent” domain (+ 90° ÷ + 180°) in the facular region (3.6% vs. 12.5%).
 |
Fig. 6 Upper panels (a)–c)): power of the intensity oscillations measured from Ca ii H a); velocity oscillations at the Ba ii core b); and velocity oscillations in the Ba ii wing c), as a function of the magnetic field inclination in the photosphere. The values of inclination are averaged in time over the five TIP maps. Lower panels (d)–f)): same, but as a function of the photospheric magnetic field strength. |
Even more striking differences between the quiet and the magnetic regions are observed in the upper photosphere. The histogram of the facular region shows a significant number of points within all four phase domains, unlike in the quiet region. The maximum number of cases (46.9%) falls within the domain (0° ÷ + 90°), while only 9.3% of points in the quiet region belong there. The number of points in this domain remains almost the same in both the lower and upper photospheres in the facular region (≈46%). The number of points in the domains (+ 90° ÷ + 180°) and (− 90° ÷ 0°) has increased significantly from the bottom to the top of the photosphere. The φ(T,V) phase shifts between − 90° ÷ 0° are not present in the upper layers of the quiet photosphere. Such phase differences are not possible for the acoustic gravity waves according to the theoretical calculations. Since the difference between both regions lies essentially in the presence of the magnetic field, we suppose that waves showing φ(T,V) between − 90° and 0° in the upper photosphere are some type of magneto-acoustic waves. These types of waves are almost absent at the bottom of the photosphere of the facular region where the plasma β is around or above unity (gas-pressure-dominated region), see Fig 1. Figure 4 clearly shows that the nature of the waves propagating in the quiet and magnetized areas is fundamentally different. The interpretation of these results in terms of the wave modes is not straightforward and must rely on theoretical modelling, taking a particular magnetic field distribution in the observed region into account.
Since in general, one cannot expect the sign and magnitude of the φ(T,V) phase shift to give the direction of wave propagation, once the magnetic field was considered, we found it interesting to investigate the statistics between the measured φ(T,V) shifts and the phase shifts between the velocity oscillations at two different heights from the Ba ii line core and wings, φ(V,V). These statistics are given in Fig. 5. We compare the results for the facular region (upper panel) and the quiet region (bottom panel). In the quiet region, most of the points are located in the evanescent domain, φ(T,V) between (90° ÷ 180°). Among all the points, 73% show negative velocity phase shifts with the most frequent values above − 20°. Thus, the phase of the wave changes only slightly with height, which is compatible with their evanescent behaviour. The values of the φ(V,V) shifts measured in the quiet region are compatible with those from the earlier studies (e.g. Deubner & Fleck 1989; Fleck & Deubner 1989; Deubner et al. 1990, 1992; Khomenko et al. 2001).
In the facular region, about half of the points are located in the domain φ(T,V) between (0° ÷ 90°). The velocity phase shifts corresponding to this domain are mostly negative, but are lower in absolute value compared to the quiet region. This can be interpreted as lower upward propagation speeds of waves in the magnetic region. There is also a significant number of points in the other three domains. The areas with φ(T,V) belonging to (− 180° ÷ − 90°) give negative velocity phase shifts in most cases with higher absolute values up to 40° and a large scatter. These waves are propagating upwards with greater phase speeds. In contrast, waves with φ(T,V) belonging to (90° ÷ 180°) show mostly positive velocity phase shifts (downward propagation) with low phase velocities. Waves with φ(T,V) belonging to (− 90° ÷ 0°) show a large scatter and a slight preference for the negative velocity phase shifts. Altogether, these results are not straightforward to interpret and will need further studies.
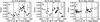 |
Fig. 7 Power of the intensity oscillations measured from Ca ii H a); Ba ii core b); and Ba ii wing c) as a function of the phase shift between the velocity and temperature oscillations, φ(T,V). The values of φ(T,V) are measured at the Ba ii line core in the panels (a), b)) and in the Ba ii line wing in panel c). |
Next, we considered the relation between the oscillation power at different heights, and the magnetic field strength and inclination, measured in the photosphere. Figure 6 gives the result. The power of oscillations is taken at the same frequency at all spatial points. As a reference frequency, we took the value of the spatially averaged dominant frequency from Fig. 3, 3.41 mHz for the Ba ii velocity oscillations, and 3.04 mHz for the Ca ii H intensity oscillations. We correlated the magnetic field strength and inclinations with the wave power at the same spatial pixel without considering a possible inclined propagation and spatial displacement of the wave front.
It appears that the power of the oscillations does indeed depend on the magnetic field inclination beyond the error bar limits at all considered heights (upper panels of Fig. 6). The photospheric velocity from the Ba ii line shows an almost linear dependence: the power increases for less inclined fields. There is a hint of another maximum of the distribution for the inclinations between 10 and 12 degrees. Altogether, the power of photospheric oscillations seems to be a maximum for the fields inclined below 12 degrees. The power distribution is different in the chromosphere. The power of Ca ii H intensity oscillations shows a clear maximum for the fields inclined by 10–12 degrees. This maximum can possibly be due to a reduction of the cut-off frequency of 3 mHz oscillations because of the inclined propagation in the low-β regime. According to Fig. 1, the plasma β is below unity in most of the observed facular region from the middle photosphere upwards. The maximum power of the photospheric oscillations at less inclined fields must be due to some other mechanism, however.
The power of oscillations also depends on the photospheric magnetic field strength (see the bottom panels of Fig. 6). In the photosphere (panels e–f), the power of the Ba ii velocity oscillations shows a non-linear dependence on B. There is a tendency for the power to increase in the strongest field areas (1.3–1.5 kG). The power of oscillations shows a minimum for the intermediate field strength and another maximum for the weakest fields. The presence of these two maxima seems to be in accordance with a hint of a two-family distribution of the power with the inclination (panels b–c). Photospheric velocity oscillations with higher power are observed above the regions where the field is strong and slightly inclined (by 10–12 degrees). Nevertheless, there are photospheric oscillations with a strong power above the regions with weak and less inclined fields. The power distribution of the chromospheric Ca ii H intensity oscillations shows only one maximum for the greatest field strength. This demonstrates that waves above the weaker field regions do not reach the chromosphere with sufficient power.
Finally, Fig. 7 shows the power of oscillations at different heights as a function of temperature-velocity phase shift φ(T,V). There are systematic differences in the power of waves at the four sub-domains of the φ(T,V) values. In the lower photosphere (panel c), the points are almost equally distributed between two domains with φ(T,V) in the range (− 180° ÷ − 90°) and (0° ÷ 90°). The power is the same in both domains within the error bar limits. The distribution of points is a replica of the φ(T,V) histogram in Fig. 4, with 94% of all cases falling into these two categories.
The power histogram for the upper photosphere (panel b) seems to be an intermediate situation between the one for the lower photosphere (c) and for the chromosphere (a). The power of the chromospheric Ca ii H intensity oscillations shows a clear maximum for the phase shifts in the domain (0° ÷ 90°). Not only is there a large number of cases of oscillations with this phase shift detected in the upper layers, but their power is also enhanced. Interpretation of this result in terms of the wave propagation needs theoretical modelling.
Summarizing all the above, we find that in the observed facular region, the most powerful waves reach the chromosphere at locations with the strong magnetic field inclined by 10–12 degrees as a result of upward propagation with rather low phase speeds. These waves have a preference for the temperature-velocity phase shifts in the range 0° ÷ 90°. The periods of the chromospheric facular oscillations are in the 5 min range, increasing with magnetic field strength.
 |
Fig. 8 Solid line: average cut-off period in the observed facular region as a function of optical depth log τ5. The dashed and dotted lines give the cut-off period for the magnetic field inclined by 12° and 50°, correspondingly. |
4. Discussion
The results of our study suggest that waves have a dominant period of around five minutes in the observed facular region of intermediate strength (Fig. 3). This dominant period is maintained both through the photosphere and in the low chromosphere. This conclusion is consistent with the previous studies of waves in enhanced network and facular regions (Deubner 1967, 1990; Howard 1967; Blondel 1971; Woods & Cram 1981; Lites et al. 1993; Krijger et al. 2001; Centeno et al. 2006; Kobanov & Pulyaev 2007; Centeno et al. 2009). At all the observed heights, the dominant period of oscillations increases by 15–20% with the magnetic field increasing from 500 to 1500 G. Our results give still more evidence that the long-period waves can propagate with sufficient power to the upper layers in magnetic regions.
One of the possible explanations of this effect, as already mentioned in the introduction, would be a decrease in the acoustic cut-off frequency due to field-aligned propagation of the slow acoustic waves in a strong magnetic field (Michalitsanos 1973; Bel & Leroy 1977; Zhugzhda & Dzhalilov 1984; Heggland et al. 2007; de Wijn et al. 2009; Heggland et al. 2011; Stangalini et al. 2011). This mechanism would be at work if the plasma β were below unity over the observed heights. The results of spectropolarimetric inversion of our infrared Stokes data suggest that β < 1 in the magnetic patch from the low photosphere upwards. Thus, the reduction of the cut-off due to the field inclination should play a role in the observed chromospheric power distribution. We checked the effectiveness of this mechanism by plotting the power of the Ca ii H oscillations as a function of photospheric magnetic field strength and inclination for waves with periods around 5 min (Figs. 6a and d). Indeed, there is a pronounced maximum of power for the magnetic field inclined by 10–12 degrees and B of 1.3–1.5 kG. In contrast, velocity oscillations in the upper photosphere from the Ba ii line core show a linear increase in power with decreasing magnetic field inclination, with a hint of a secondary maximum around 10–12 degrees (Fig. 6b). Nevertheless, the magnetic field was determined at the bottom of photosphere, so its inclination and strength may well be different at heights of the formation of Ca ii H intensity observed by the broad-band filter. Stangalini et al. (2011) find that a maximum of power of the 5 min oscillations falls at the magnetic field inclined by about 25 degrees, for the magnetic region containing an isolated pore. The difference may be due to a stronger field in the region observed by Stangalini et al. (2011) due to a different configuration of the magnetic field and thermal structure of the region, as well as to the difference in heights sampled by the observed spectral lines.
Taking the data from the inversion, we have evaluated the average cut-off period in the observed facular region, and present it in Fig. 8. The period decreases from 300 to 200 s through the photosphere. Assuming that the field keeps its inclination with height, the value of γ = 12° would give us a dashed curve for the cut-off period. This increase is obviously insufficient to allow for the efficient propagation of the five-minute waves. Only by allowing for the field inclination above 50 degrees do we reach a considerable increase in the cut-off period (the dotted line in Fig. 8). This leads to the conclusion that either the magnetic field becomes steeply more inclined by at least 50° in the photosphere or there must be some other mechanism facilitating the energy propagation of the five-minute waves.
An alternative mechanism for the propagation of the five-minute oscillations to the chromosphere is the action of radiative losses, which add a formally propagating component to the oscillations and prevent them from being evanescent (Roberts 1983; Khomenko et al. 2008). The evanescence of the acoustic-gravity waves in the quiet Sun can be evaluated by means of their phase relations, φ(T,V). We find that in the upper photosphere in the quiet area, most of measured φ(T,V) values belong to the evanescent domain (90° ÷ 180°) (Fig. 4d). Analytical treatment of non-adiabatic magnetic waves in the stratified atmosphere is significantly more complex even in the case of constant magnetic field (Babaev et al. 1995b,a; Khomenko et al. 2003). It is difficult to make theoretical predictions for the phase relations in the magnetic case. Our data reveal a striking difference between the φ(T,V) distributions in the quiet and facular regions (Figs. 4c–d). About a half of the observed facular area shows φ(T,V) phase shifts in the domain (0° ÷ 90°) that would correspond to the upward propagating acoustic waves if there were no magnetic field. There is a significant number of points with φ(T,V) in the whole interval from − 180° to 180°, unlike in the quiet region. These data confirm that wave facular areas are significantly affected by the magnetic field. Nevertheless, theoretical interpretation of these data is not immediately apparent, and we cannot yet arrive at any conclusions about the effectiveness of radiative losses of waves in the magnetic region without extensive theoretical modelling.
We have checked whether there is any relation between the sign and magnitude of the φ(T,V) phase shift and the direction of the wave propagation in the magnetic area similar to the quiet area. We did this by correlating the values of the φ(T,V) phase shifts with the velocity–velocity phase shifts at different heights, φ(V,V). On average, most of the points with φ(T,V) in the domain (0° ÷ 90°) show an upward propagation in velocity (Fig. 5). The velocity phase shifts are rather small, which can be interpreted as fairly low phase propagation speeds of these waves. In constrast, the φ(T,V) domain (90° ÷ 180°) (corresponding to evanescent acoustic-gravity waves when B = 0) shows the dominance of downward-propagating waves according to the sign of the φ(V,V) shifts.
Altogether, this leads us to conclude that most of the energetic waves with periods of around five minute reach the chromosphere as a result of the upward propagation from the photosphere in the areas with slightly inclined magnetic fields. The low φ(V,V) shifts (phase speeds) are difficult to fit into this picture, however. The propagation speed of magnetic waves is expected to be generally greater than of the acoustic waves in the atmosphere with va > cs, as follows from Fig. 1. Further observational and theoretical studies would be needed to clarify this and other remaining issues concerning the wave propagation in solar facular regions.
5. Conclusions
We have examined how the presence of a magnetic field of intermediate strength in a facular area affects the properties of waves. We statistically investigated the dependence between the periods, power, and phase relations of waves, and the magnetic field strength and inclination. Our main results can be summarized as follows:
We confirm that five-minute oscillations with sufficient power are able to propagate through the whole photosphere to the lower chromosphere. At all the observed heights, the dominant period of oscillations increases by 15% to 20% with the magnetic field increasing from 500 to 1500 G.
At the bottom of the photosphere, the phase shift between the temperature and velocity oscillations φ(T,V) in the majority of cases falls into two domains: (− 180° ÷ − 90°) and (0° ÷ 90°), both in the facular and in the quiet region. The relative weight of the points in each domain is different in the magnetic and the quiet areas. In the upper photosphere, the distributions of φ(T,V) in the quiet and facular areas are more significantly different. In the quiet area, about 90% of cases fall into the domain (90° ÷ 180°), corresponding to evanescent acoustic-gravity waves. In the magnetic facular area, the histogram shows a significant number of φ(T,V) values over the whole range, from − 180° to 180°.
By correlating the temperature-velocity, φ(T,V), and the velocity–velocity, φ(V,V), phase shifts, we find that waves with φ(T,V) between (0° ÷ 90°) show, on average, upward propagation with rather low phase speeds. Such phase shifts are detected in about half of all cases in the facular area. The most powerful oscillations in the chromospheric Ca ii H intensity have φ(T,V) between (0° ÷ 90°).
The maximum power of the photospheric oscillations appears in the areas with the magnetic field inclined by less than 12 degrees. In the chromosphere, oscillations of maximum power are observed above the areas where the photospheric magnetic field is inclined by 10 to 12 degrees and has a strength of 1.3–1.5 kG.
Acknowledgments
This work is partially supported by the Spanish Ministry of Science through projects AYA2010-18029 and AYA2011-24808.
References
- Babaev, E. S., Dzhalilov, N. S., & Zhugzhda, Y. D. 1995a, Astron. Rep., 39, No. 2, 202 [Google Scholar]
- Babaev, E. S., Dzhalilov, N. S., & Zhugzhda, Y. D. 1995b, Astron. Rep., 39, No. 2, 211 [Google Scholar]
- Bel, N., & Leroy, B. 1977, A&A, 55, 239 [NASA ADS] [Google Scholar]
- Blondel, M. 1971, A&A, 10, 342 [NASA ADS] [Google Scholar]
- Bloomfield, D. S., McAteer, R. T. J., Mathioudakis, M., & Keenan, F. P. 2006, ApJ, 652, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D. C., & Lindsey, C. 1999, ApJ, 513, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, D. C., Lindsey, C., Fan, Y., & Jefferies, S. M. 1992, ApJ, 392, 739 [Google Scholar]
- Brown, T. M., Bogdan, T. J., Lites, B. W., & Thomas, J. H. 1992, ApJ, 394, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2009, ApJ, 692, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Chitta, L. P., Jain, R., Kariyappa, R., & Jefferies, S. M. 2012, ApJ, 744, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Collados, M., Lagg, A., Díaz Garcí A, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- De Pontieu, B., Erdelyi, R., & de Wijn, A. G. 2003, ApJ, 595, L63 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., Erdelyi, R. J., & Stewart, P. 2004, Nature, 430, 536 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- De Pontieu, B., Erdélyi, R., & De Moortel, I. 2005, ApJ, 624, L61 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., McIntosh, S. W., & De Pontieu, B. 2009, ApJ, 702, L168 [NASA ADS] [CrossRef] [Google Scholar]
- Deubner, F. L. 1967, Sol. Phys., 2, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Deubner, F. L. 1990, in The Solar Photosphere: Structure, Convection and Magnetic Fields, ed. J.-O. Stenflo (Dordrecht: Kluwer), Proc. IAU Symp., 138 (Kiev), 217 [Google Scholar]
- Deubner, F.-L., & Fleck, B. 1989, A&A, 213, 423 [NASA ADS] [Google Scholar]
- Deubner, F.-L., & Fleck, B. 1990, A&A, 228, 506 [NASA ADS] [Google Scholar]
- Deubner, F.-L., Fleck, B., Marmolino, C., & Severino, G. 1990, A&A, 236, 509 [NASA ADS] [Google Scholar]
- Deubner, F.-L., Fleck, B., Schmitz, F., & Straus, T. 1992, A&A, 266, 560 [NASA ADS] [Google Scholar]
- Donea, A.-C., Lindsey, C., & Braun, D. C. 2000, Sol. Phys., 192, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Finsterle, W., Jefferies, S. M., Cacciani, A., et al. 2004a, Sol. Phys., 220, 317 [Google Scholar]
- Finsterle, W., Jefferies, S. M., Cacciani, A., Rapex, P., & McIntosh, S. W. 2004b, ApJ, 613, L185 [Google Scholar]
- Fleck, B., & Deubner, F.-L. 1989, A&A, 224, 245 [NASA ADS] [Google Scholar]
- Hansteen, V. H., De Pontieu, B., Rouppe van der Voort, L., van Noort, M., & Carlsson, M. 2006, ApJ, 647, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Heggland, L., De Pontieu, B., & Hansteen, V. H. 2007, ApJ, 666, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Heggland, L., Hansteen, V. H., De Pontieu, B., & Carlsson, M. 2011, ApJ, 743, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hindman, B. W., & Brown, T. M. 1998, ApJ, 504, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H., & Testerman, L. 1975, sp, 43, 271 [Google Scholar]
- Howard, R. 1967, Sol. Phys., 2, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, R., & Haber, D. 2002, A&A, 387, 1092 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jefferies, S. M., McIntosh, S. W., Armstrong, J. D., et al. 2006, ApJ, 648, L151 [Google Scholar]
- Judge, P. G., Tarbell, T. D., & Wilhelm, K. 2001, ApJ, 554, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., & Calvo Santamaria, I. 2013, J. Phys. Conf. Ser. 440, 012048 [Google Scholar]
- Khomenko, E. V., Kostik, R. I., & Shchukina, N. G. 2001, A&A, 369, 660 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khomenko, E. V., Collados, M., & Bellot Rubio, L. R. 2003, ApJ, 588, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., Centeno, R., Collados, M., & Trujillo Bueno, J. 2008, ApJ, 676, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Kobanov, N. I., & Pulyaev, V. A. 2007, Sol. Phys., 246, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Kontogiannis, I., Tsiropoula, G., & Tziotziou, K. 2010a, A&A, 510, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontogiannis, I., Tsiropoula, G., Tziotziou, K., & Georgoulis, M. K. 2010b, A&A, 524, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostik, R., & Khomenko, E. V. 2012, A&A, 545, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostik, R., Khomenko, E., & Shchukina, N. 2009, A&A, 506, 1405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krijger, J. M., Rutten, R. J., Lites, B. W., et al. 2001, A&A, 379, 1052 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Chipman, E. G., & White, O. R. 1982, ApJ, 253, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Rutten, R. J., & Kalkofen, W. 1993, ApJ, 414, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., & Jefferies, S. M. 2006, ApJ, 647, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Mein, N., & Mein, P. 1976, Sol. Phys., 49, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Michalitsanos, A. G. 1973, Sol. Phys., 30, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Nagashima, K., Sekii, T., Kosovichev, A. G., et al. 2007, PASP, 59, S631 [Google Scholar]
- Noyes, R. W., & Leighton, R. W. 1963, ApJ, 138, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Reardon, K. P., Uitenbroek, H., & Cauzzi, G. 2009, A&A, 500, 1239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, B. 1983, Sol. Phys., 87, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Stangalini, M., Del Moro, D., Berrilli, F., & Jefferies, S. M. 2011, A&A, 534, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toner, C. G., & Labonte, B. J. 1993, ApJ, 415, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., Schmidt, W., Langhans, K., & Kentischer, T. 2002, Sol. Phys., 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., Schmidt, W., Uitenbroek, H., & Wedemeyer-Böhm, S. 2007, A&A, 462, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turova, I. P. 2011, Astron. Lett., 37, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Vecchio, A., Cauzzi, G., Reardon, K. P., Janssen, K., & Rimmele, T. 2007, A&A, 461, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vecchio, A., Cauzzi, G., & Reardon, K. P. 2009, A&A, 494, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitney, C. A. 1958, Smithsonian Contributions to Astrophysics, 2, 365 [Google Scholar]
- Woods, D. T., & Cram, L. E. 1981, Sol. Phys., 69, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhugzhda, Y. D., & Dzhalilov, N. S. 1984, A&A, 132, 45 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Parameters relevant for wave propagation, calculated from the inversion. The upper row gives the magnetic field strength, inclination, and filling factor. The bottom row gives the acoustic speed, Alfvén speed, and plasma β parameter. The maps are taken at the bottom of the photosphere at constant logτ5 = −0.2. The values of density and gas pressure are calculated assuming hydrostatic equilibrium in each vertical column from the inversions and averaged over the magnetic and non-magnetic atmospheric components. |
| In the text | |
 |
Fig. 2 Histogram of the magnetic field strength (left) and inclination with respect to the line-of-sight (right) in the observed area over the five TIP scans, as inferred from the SIR inversion. |
| In the text | |
 |
Fig. 3 Space-averaged power spectra (upper row, a)–c)) and dominant period of oscillations as a function of the photospheric magnetic field strength (bottom row, d)–e)). Left column: intensity oscillations in Ca ii H filtergrams (a), d)); middle column: velocity oscillations measured at the Ba ii line core (b), e)); right column: velocity oscillations measured at the Ba ii line wing (c), f)). |
| In the text | |
 |
Fig. 4 Histograms of the phase shifts between the temperature (in anti-phase with intensity) and velocity oscillations φ(T,V) for the bottom photosphere (upper row), and the upper photosphere (bottom row). The panels on the left show the results for the facular region analysed in this paper. The panels on the right show a similar result, but for the quiet region data from Kostik et al. (2009). |
| In the text | |
 |
Fig. 5 Phase shift between the velocities at the bottom and top of the photosphere φ(V,V) as a function of the phase shift between the velocity and temperature at the upper photosphere φ(T,V) for the plage area (upper row) and for the quiet area (bottom row). The yellow and red colours denote a greater density of points in the distribution. Negative velocity–velocity shifts, φ(V,V), mean upward waves. |
| In the text | |
 |
Fig. 6 Upper panels (a)–c)): power of the intensity oscillations measured from Ca ii H a); velocity oscillations at the Ba ii core b); and velocity oscillations in the Ba ii wing c), as a function of the magnetic field inclination in the photosphere. The values of inclination are averaged in time over the five TIP maps. Lower panels (d)–f)): same, but as a function of the photospheric magnetic field strength. |
| In the text | |
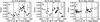 |
Fig. 7 Power of the intensity oscillations measured from Ca ii H a); Ba ii core b); and Ba ii wing c) as a function of the phase shift between the velocity and temperature oscillations, φ(T,V). The values of φ(T,V) are measured at the Ba ii line core in the panels (a), b)) and in the Ba ii line wing in panel c). |
| In the text | |
 |
Fig. 8 Solid line: average cut-off period in the observed facular region as a function of optical depth log τ5. The dashed and dotted lines give the cut-off period for the magnetic field inclined by 12° and 50°, correspondingly. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


